 Open Access
Open Access
ARTICLE
NTRU_ SSS: Anew Method Signcryption Post Quantum Cryptography Based on Shamir’s Secret Sharing
1 Ministry of Higher Education and Scientific Research, Bagdad, Iraq
2 Affiliations Computer Science, Univ. of Technology, Bagdad, 750004, Iraq
* Corresponding Author: Asma Ibrahim Hussein. Email:
Computers, Materials & Continua 2023, 76(1), 753-769. https://doi.org/10.32604/cmc.2023.039804
Received 17 February 2023; Accepted 17 April 2023; Issue published 08 June 2023
Abstract
With the advent of quantum computing, numerous efforts have been made to standardize post-quantum cryptosystems with the intention of (eventually) replacing Elliptic Curve Cryptography (ECC) and Rivets-Shamir-Adelman (RSA). A modified version of the traditional N-Th Degree Truncated Polynomial Ring (NTRU) cryptosystem called NTRU Prime has been developed to reduce the attack surface. In this paper, the Signcryption scheme was proposed, and it is most efficient than others since it reduces the complexity and runs the time of the code execution, and at the same time, provides a better security degree since it ensures the integrity of the sent message, confidentiality of the data, forward secrecy when using refreshed parameters for each session. Unforgeability to prevent the man-in-the-middle attack from being active or passive, and non-repudiation when the sender can’t deny the recently sent message. This study aims to create a novel NTRU cryptography algorithm system that takes advantage of the security features of curve fitting operations and the valuable characteristics of chaotic systems. The proposed algorithm combines the (NTRU Prime) and Shamir's Secret Sharing (SSS) features to improve the security of the NTRU encryption and key generation stages that rely on robust polynomial generation. Based on experimental results and a comparison of the time required for crucial exchange between NTRU-SSS and the original NTRU, this study shows a rise in complexity with a decrease in execution time in the case when compared to the original NTRU. It’s encouraging to see signs that the suggested changes to the NTRU work to increase accuracy and efficiency.Keywords
Building new cryptosystems is currently the cryptographic community’s primary concern. Current cryptosystems like Elliptic-curve Diffie–Hellman (ECDH), RSA, and El Gamal are easily cracked through a quantum computer utilising quantum algorithms like Shor’s, Grover’s, or other algorithms. We need post-quantum cryptosystems that can withstand quantum computer attacks [1]. Most of our modern digital infrastructure uses public-key cryptography, making it a crucial component. Yet, most, if not the entirety, of it is based on the potential vulnerability of large-scale quantum computers to the hardness guarantees regarding number theoretic problems. A global-level standardisation procedure for quantum-resistant public-key cryptographic primitives, like digital signatures and public key cryptography, has just been started by NIST in response to the impending threat posed by ongoing improvements in quantum computing [2]. Research interest in Post-Quantum Cryptography (PQC) has developed due to development of quantum computers and their effects on the security of conventional public-key cryptography. Most PQC research is carried out within the framework of the PQC standardisation process, which NIST oversees. As part of the final standardisation phase, NIST recently asked for additional research into the physical security related to PQC implementations. To assure their theoretical security, novel cryptographic primitives are first evaluated cryptanalytically [3].On the other hand, a secure cryptographic primitive in the real world may still be exposed to implementation or physical attacks. Side-channel attacks are regarded as passive physical attacks where the attacker can obtain side-channel data (such as electromagnetic (EM) radiation, power usage, execution time, etc.) that was unintentionally produced by the implementation. Secret information could be obtained by utilising such side-channel information [4]. Data hiding and encryption algorithms have a significant impact on protecting information security. Reversible data hiding (RDH) can be defined as a particular data hiding model, which has the ability of solving the issue of the permanent distortions of the conventional approaches of data hiding. This model has the ability of precisely extracting the secret messages and recovering original ones. As a result of such distinctive characteristic, RDH has become widely utilized in the sensitive images where there aren’t any permanent changes allowed to the original image [5]. It aims to hide the covert data in a cover medium such that the invader won’t know that it exists at all. In general, data hiding leads to introducing permanent distortions to cover image, and the original cover can’t be re-constructed. However, in some of the sensitive applications, like medical image sharing, military image protection, law forensics and multi-media archive management, the cover image is so important that there aren’t any distortions allowed [6]. Adding a discriminative network could lead to effectively removing the watermark information. The extensive experimentations have been carried out for the purpose of verifying the suggested concealed attack method’s feasibility. Experimental and analyses results have demonstrated that the suggested concealed attack approach has a more sufficient imperceptibility and attack ability compared with the existing watermarking attack approaches. [7,8].
Two motivations for our research are identified. The first motivation is to combine the features of NTRU, SSS and Elliptic Curve Discrete logarithm to produce the robust symmetric key. The most important feature of this algorithm is that it must have a minimum total time to key exchange. The second motivation Frequently used Cryptosystems sufficiently presented cloud data security for many years compared to all the classic attack forms, however, data theft prevails. Which is why, there is an urgent necessity for deploying quantum-safe crypto-systems that are safe for the data processing in the classical as well as the quantum spaces.
• To increase data transmission security in the cloud.
• To share the data between the owners and users securely.
• The NTRU algorithm (Nth degree Truncated Polynomial ring units) ensures high-level data security while receiving and uploading) [9].
The following are the primary contributions of the present study:
1. The primary contribution of hybrid cryptography between post-quantum cryptography and pre-quantum cryptography. The proposed algorithm combines the (NTRU Prime) and (SSS) features to improve the security of the NTRU encryption and key generation stages that rely on robust polynomial generation. Additionally, use EC digital signature algorithms only by checking the correctness of a signature.
2. First contribution A new authentication scheme depending on Shamir's Secret Sharing Scheme
3. The second contribution, key exchange secret sharing with NTRU, was proposed for preventing man in a middle (MITM) attack on the vulnerability.
4. The third contribution enhancement of the NTRU algorithm implements the lattice-based encryption schemes and key exchange protocols mentioned above using Python. Observe the running time of the algorithm to be less than other works.
5. Four contributions to reducing of limitation of NTRU include (lack of strict structure, security was not tested sufficiently, and Big-sized keys are required)
6. Final contribution implementation has good portability and scalability. Python code can be directly executed on any Python runtime environment without modification. More importantly, comparing and analysing these performance differences improves implementation for particular platforms.
The following describes the study’s overall structure: According to the secure NTRU, Section 2 offers the related works. Sections 3 include a preliminary area concerning (SSS) and (NTRU). Section 4 of the proposal consists of a thorough explanation. The NTRU-SSS results and discussion have been discussed in Sections 5, and 6 presents the conclusions.
Problem Statement
The limitations of NTRU and NTRU Prime are:
1. Security was not tested sufficiently.
2. Big-sized keys are required.
3. No strict structure.
4. Vulnerability remains undiscovered.
5. Complicated security analysis.
6. Suggest configurations that achieve 1, 3, and 5 security levels of the NIST PQC Standardization project. Since we intend to implement our framework in both low-level hardware and high-end devices, our configurations also have varied memory requirements, where NTRU reaches three levels (1, 3, and 5) but does not achieve two levels (2, 4), thus conserving two limitations [10]. Table 1 presents how the 26 NIST PQC Standardization project implementations address the five security levels.
Reference [12] M. Mosca & D. Stebila (2016) In this study, we will look at crucial exchange in PQC. Using BCNS15 protocol, which depends on ring learning with the errors problem, and Frodo, which depends upon learning with the errors problem, as 2 protocols for the quantum-resistant key exchange based upon the lattice problems examine both their own and the Transfer Layer Security (TLS) protocol’s performance and security. The Open Quantum Safe project is an open-source software for developing quantum-resistant encryption.
Harjito et al. [13] the two algorithms were compared in terms of essential generation, decryption, encryption, attack, and cloud storage implementation in the presented work. Two metrics have been used in order to compare the performance of both algorithms: the security and the running time of attempted attacks. The result of this work illustrate . The longer the time needed, the higher the bit used when using the chosen parameter for the RSA bit. The time required for key generation, decryption, and encryption operations increases with the value of the N parameter in the NTRU.
Hameed et al. [14] suggest that q-octonion algebra NTRU (QOCNTR) is a new multidimensional public key cryptosystem according to q-octonion algebra, which enhances security using a multidimensional method. The suggested cryptosystem features from earlier cryptosystems by having two public keys. This cryptosystem is essential in some applications because it might encrypt 32 messages simultaneously from 32 different or independent sources. Regarding security, QOCNTR performed better than QTRU, NTRU, and OTRU. Lastly, the results are deemed very suitable since the proposed system has a very high level of security.
Yadav et al. [15] investigated NTRU key exchange in this work and discovered it is vulnerable to MITM attacks. Similar to original Diffie-Hellman key exchange, vulnerability has been found and mitigated with zero knowledge proof (ZKP). We used the ZKP technique to address lattice-based NTRU key exchange MITM and discovered that the NTRU is still susceptible to MITM attacks even with the ZKP. The implementation results are supported, such as a MITM attack vulnerability in the NTRU key exchange using the ZKP.
Yen IARAS [16] proposes 3 different 4-way split polynomial multiplication approaches that have been derived by the use of F9 interpolation approach. In addition, we suggest a novel 5-way split polynomial multiplication algorithm, and after that, we contrast the implementation outcomes and arithmetic complexity for the techniques that have been mentioned above. We demonstrate that the novel 4- and 5-way split algorithms reduce the arithmetic complexity of multiplication over F9 by 48.6% and multiplication over F3 by 26.8% for input sizes 1280. In addition, the novel 4-way and 5-way algorithms produce faster implementation results than the most recent state-of-art techniques.
Meher et al. [17] have analyzed 2 asymmetric cryptosystems, which are –NTRU and RSA. NTRU have easily created keys that are reasonably short, low memory requirements and high speed, as the NTRU is a rather novel cryptosystem of the future.
Shuai et al. [18] have generalized the NTRU and proposed group-based NTRU-like public-key crypto-system, which has been referred to as the group-based NTRU (GTRU). After that, they have constructed high-performance GTRU for the IoT. Ultimately, security analyses have shown that the suggested GTRU for IoT had a higher security compared to the NTRU against the lattice-based attacks.
Reference [19] (B. Darong Huang, 2019) have proposed a new oblivious transfer protocol that id based upon Number Theory Research Unit Encryption and structured security location-based service (LBS) scheme in terms of that. In Comparison to Jannati and Bahrak’s protocol, it has been concluded that this model is more practical and also more efficient.
In 1996, J. Pipher, J. Hoffstein, and Joseph H. Silverman developed the lattice-based cryptographic system known as the NTRU. For the time being, Security Innovation is the owner of the patented NTRU cryptographic system [19]. Because of its quick encryption speed and low power consumption, NTRU is catching attention in addition to its exceptional security level for its scalability on platforms with constrained resources [20]. This section explains the NTRU PKC, which utilises the ring of convolution polynomials, also known as truncated polynomials. The system’s settings, key generation, decryption, and encryption are all described.
Additionally, it provides the NTRU, which is composed of (including its interior details and an example). The linear feedback shift register is finally explained [21].Benefits of NTRU :
• Provide a more secure and authorised encryption scheme.
• Getting permission and outsourcing is only permit records
- Description of NTRU
Assume that R, Rp, and Rq are convolutional polynomial rings:
Reference [22] a polynomial a ∈ R may be viewed as an Rp or Rq element by reducing its coefficients mod p or q.
- NTRU parameters
- N: represents maximum highest power in the polynomials that have been utilized in the NTRU, typically as prime number.
- p: represents minimal modulus in the NTRU, which is typically as small positive integer or polynomial of low powers.
- q: represents maximal modulus in the NTRU, which is typically as a positive integer depending upon certain examples.
- dF, gd, f d: the numbers of the non-0 coefficients in the F, f, g polynomials, respectively [23].

Even though it is a widely utilised cryptographic method, e-voting uses it less frequently. Lately, it has been put to use in a variety of applications, including authentication and randomness. Naïve version of Shamir’s secret sharing has some recognised faults, yet there are also known solutions to such issues [25]:
■ This technique does not fully satisfy all the fundamental requirements of the secret sharing concept when implemented using standard integer arithmetic. This is due to data regarding the Secret being shared leaked. With the help of a finite field, we propose an easy solution for this [26].
■ This scheme cannot be verified. There are schemes to address this problem, such as those based on publicly verifiable secret sharing (PVSS), but in our approach, as we will see below, we resolve it using our integrated mechanism.
■ The last shareholder can change the previous share when the shares are sequentially revealed, manipulating the interpolation process’ outcome [27].
The simplest solution to that issue is to make shareholders publish a hash of their shares first, preventing them from changing their shares. This is commonly referred to as “commitment.” Reference [28] Generally, most security measures rely on a single individual managing the information’s secrecy at a specific time. Yet, some particular, crucial applications demand multiple users’ security or access while they must be simultaneously present, referred to as secret sharing. Reference [29] for creating the target key that can be reconfigured to grant access to the system, a secret sharing method necessitates distributing its shares among numerous servers [30].
The following two conditions must be met to comply with SSS approach.
1. The secret key S could be re-constructed with the use of any grouping of t or more subkeys S0, S1, …, St−1.
2. Reconstructing secret key S with less than t or fewer sub-keys is not possible [31].
The SSC algorithm is made up of 2 phases, which are:
The phase of Distribution [32]:
• Take secret data represented by S.
• Specify the number of the Sites NS which receive secret pieces si.
• Specify threshold value T; data from them can reconstruct S.
• Build polynomial function f(xi), to calculate NS secret pieces, f(xi)’s degree is T − 1, the constant part of f(xi) represents original Secret, and T − 1 coefficients of it are random integers that have been selected from GF(S) [33]:
- for i = {1, … NS}
- where
- After generating NS pieces = {s1, s2 …., sns}, distribute them onto Sites [34].
Reconstruction phase:
The (k, t) SIS scheme has been utilised with the Lagrange interpolation polynomial that Thien and Lin designed (Lin & Thien, 2002) 2002, which represents an improvement on Shamir’s threshold-sharing approach (Shamir, 1979). Initially, a (k-1) order polynomial [35] Found out T pieces of data si which require to build s. Reconstruct original f(x) with the use of LaGrange interpolation equation [36]:
Example: [37] of secret sharing: let secret (s) = 5,P = 7, K = 3, N = 6, a1 = 2, a2 = 3
First, we construct a polynomial using previous information
F(
F(X)=
When
When
When
When
When X4 = 4, F(4 )= 5+ 2.40 + 3.42 mod 7 = 61 mod 7 = 5 fourth share is the pair (4, 5)
When X5 = 5, F(5) = 5 + 2. 5+ 3.52 mod 7 = 90 mod 7 = 6 fifth share is the pair (5, 6)
When X6 = 6, F(6) = 5 + 2.6 + 3.62 mod 7 = 125 mod 7 = 6 sixth share is the pair (6, 6)
The set of shares is (1, 3), (2, 0), (3, 3), (4, 5), (5, 6), (6, 6)
Let us use shares 1,4,6 to reconstruct the Secret.
= 3
F(x) =
This section presents the proposed method to modify the original NTRU algorithm by combining it with Shamir’s secret sharing to generate a new technique called (NTRU_SSS). This scheme involves three stages: key generation, Signcryption, and un-Signcryption. In the first stage, Alice generates all public parameters and sends them to Bob; in turn, Bob verifies the encrypted message, which has been recently decrypted, was sent from the honest participant by checking the correctness of a signature. The important aspect of the Signcryption scheme is to represent the most efficient others because it reduces the complexity and runs the time of the code execution. In addition, it provides a better security degree because it ensures the integrity of the sent message, the confidentiality of the data, forward secrecy when using refreshed parameters for each session, unforgeability to prevent the man-in-the-middle attack from being active or passive, and non-repudiation when the sender can’t deny the recently sent message. The block diagram (Fig. 1) presents the generation private key using Shamir’s secret sharing. Additional Elliptic curve signcryption public key and (Fig. 2) illustrated block diagram of the proposed algorithm. It also explains the key exchange and encrypted key and transfer from Alice after encryption to Bob through the cloud environment using the (NTRU_SSS) proposed algorithm. NTRU can offer classical security levels using relatively shorter length keys than other PQC algorithms. So, NTRU requires less space for key storage and less time for key transmission. Algorithm2 shows the (NTRU_SSS) algorithm of the proposed method in addition to explaining your idea in the example:
Example: N = 7, p = 3, q = 64, r1 = x + 1, m = 1551
Step 1: Alice: Request a certification.
Step2: Bob:
1- Chooses
2- Construct shares points using the SSS algorithm
:
f = X + X 2 – X 4 – X 5 + X 6
g = 1 + X 3 – X 4 –X 6
3- Sends the share points to Alice
as a Certificated Identity CI
Step3: Alice:
1- compute inverse of (f , g)
fp = 1 + 2X + X 2 + 2X 3 + 2X 4 + 2X 6
fq = 60 + X + 9X 2 + 17X 3 + 16X 4 + 62X 5 +28X 6
2- Calculates k1:
k1= 3 (60 + X + 9X 2 + 17X 3 + 16X 4 + 62X 5 +28X 6)*( 1 + X 3 – X 4 –X 6) (mod 64)
k1= 46 + 50X +2X 2 + 35X 3 + 5X 4 + 62X 5 + 56X 6 (modulo 64)
3- Encrypts the message
C = (46 + 50X + 2X 2 + 35X 3 + 5X 4 + 62X 5 + 56X 6 (modulo 64) *(x + 1) + 1551 (mod 64)
4- Establishes Elliptic Curve EC parameters:
{G: Base Point, NEC: Base Point Degree, such that GNEC = Ο, PA= dA G as a public key}
G = 7, NEC = 3, PA= 5 *7
5- Randomly Selects vEC = 0.5
6- Calculates k2 = Hash(vEC G).
k2 = 0.5 * 7, k2 = 3.5
7- Calculates:
8- Calculates:
Step4: Bob:
4- Calculates
(60 + X + 9X2 + 17X3 + 16X 4 + 62X5 +28X 6)
5- Calculates
6- Message M recovery:


Figure 1: Block diagram of proposal work

Figure 2: Block diagram of the proposed framework
This section demonstrates the suggested algorithm’s implementation and conducts performance testing on the algorithm. Every experiment runs on a Windows 10 with an i7 processor. The SSS is the foundation for the algorithm’s reconstruction. Calculate the time of the key exchange between Bob and Alice to show the approach’s efficiency. The suggested algorithm’s implementation procedure primarily entails decryption and encryption, with the encryption phase including key sharing and decryption phase including extraction, authentication, and selection decryption. Table 2 displays comparisons. The total amount of time that spent by NTRU-SSS and NTRU. Note that the suggested algorithm’s key exchange time for 128 bits is approximately 21.1 milliseconds, and Table 3 compares these times. The combined running time of the NTRU-SSS and Shamir's Secret Sharing is roughly 200 ms utilising SSS; for key size (128) Bits. Because the suggested algorithm loses some of its efficiency in boosting security, the implementation of sharing of the key takes a long time during the encryption phase. Table 4 displays results of comparing the suggested algorithm’s running time to those of other algorithms. It is clear that, compared to different algorithms, the suggested algorithm has the quickest key exchange time. Fig. 3 displays the average exchange time between NTRU and the suggested NTRU-SSS, Fig. 4 shows the average exchange time between SSS and the suggested NTRU-SSS, and Fig. 5 displays the average exchange time between ECC, AES, RSA, and the suggested NTRU-SSS.



Figure 3: Average time key exchange of NTRU and proposed NTRU-SSS
Figure 4: Average time key exchange of SSS and proposed NTRU-SSS

Figure 5: Average time key exchange of proposed NTRU-SSS and another algorithm
Several statistical and analytical measurements have been utilized for the assessment of security performance of the suggested algorithm. Table 5 shows security capabilities of the proposed algorithms SSS-NTRU and compares them with other research works; the comparison depicts that the performance of the suggested algorithm is efficient across achieving more security features, and Table 6 shows the throughput of the proposed algorithm for a variety of the key sizes.

With the use of Shamir’s secret sharing to generate private keys and key exchange cryptosystems, this study presents an improved approach for NTRU. This approach (NTRU-SSS) successfully increased the complexity and security of the polynomial generator utilised in encryption and key generation. It could be argued that NTRU-SSS is more advised for cloud storage security because the key exchange process's running time demonstrates that the suggested algorithm has a more secure resilience level. This study compared the NTRU-SSS to conventional NTRU, the conventional SSS, and other algorithms (RSA, ECC, Advanced Encryption Standard (AES), as the results showed that the NTRU-SSS required less time for key exchange and decrypted keys than the original NTRU algorithm did. The first suggested solution alters the original NTRU by creating a private key based on SSS. This shortens the time required for decryption and encryption compared to the time needed for the encryption and decryption using the original approach while adding new statistical aspects to the algorithm that make it harder to crack.
Acknowledgement: Authors should like to thank everyone who had contributed to this article but can’t include themselves.
Funding Statement: The authors had not received any specific funding for the present study.
Conflicts of Interest: The authors declare no conflicts of interest to report regarding the present study.
References
1. M. Serrhini, C. Silva and S. Aljahdali, “ Innovation in information systems and technologies to support learning research,” in Springer Nature Switzerland AG 2020, EMENA-ISTL 2019, LAIS 7, pp. 551–562, 2020. [Google Scholar]
2. M. R. Valluri, “Cryptanalysis of xinyu et al.’s NTRU-lattice based key exchange protocol,” Journal of Information and Optimization Sciences, vol. 39, no. 2, pp. 475–479, 2018. [Google Scholar]
3. A. T. Maolood, E. K. Gbashi and E. S. Mahmood, “Novel lightweight video encryption method based on ChaCha20 stream cipher and chaotic hybrid map,” International Journal of Electrical and Computer Engineering, vol. 12, no. 5, pp. 4988–5000, 2022. [Google Scholar]
4. P. Ravi, “Lattice-based key sharing schemes: A survey,” vol. 1, no. 1, pp. 1–39, 2020. [Online]. Available: https://eprint.iacr.org/2020/1276.pdf [Google Scholar]
5. X. Wang, B. Ma and M. embe, “High precision error prediction algorithm based on ridge regression predictor for reversible data hiding,” IEEE Signal Processing Letters, vol. 28, pp. 1125–1129, 2021. [Google Scholar]
6. B. Ma and Y. Shi, “A Reversible data hiding scheme based on code division multiplexing,” IEEE Transactions on Information Forensics and Security, vol. 11, no. 9, pp. 1–14, 2016. [Google Scholar]
7. Q. Li, X. Wang, C. Wang, B. Ma, S. Gao et al., “Concealed attack for robust watermarking based on generative model and perceptual loss,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 32, no. 8, pp. 5695– 5706, 2022. [Google Scholar]
8. Ch. Wang, B. Ma, Z. Xia, J. Li, Q. Li et al., “Stereoscopic image description with trinion fractional-order continuous orthogonal moments,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 32, no. 4, pp. 1998– 2012, 2022. [Google Scholar]
9. M. S. Oudah and A. T. Maolood, “New pseudo-random key generator for IoT-security model based on a novel 3D coupled map lattice,” International Journal of Intelligent Engineering and Systems, vol. 15, no. 5, pp. 139–150, 2022. [Google Scholar]
10. S. An and S. C. Seo, “Efficient parallel implementations of web-based post-quantum cryptosystems on graphics processing units,” Mathematics, vol. 8, no. 10, pp. 1–21, 2020. [Google Scholar]
11. R. N. Rodas, Y. D. Lin, S. L. Lu and K. J. Chang, “O2MD2: A new post-quantum cryptosystem with one-to-many distributed key management based on prime modulo double encapsulation,” IEEE Access, vol. 9, pp. 109260–109288, 2021. [Google Scholar]
12. D. Stebila and M. Mosca, “Post-quantum key exchange for the internet and the open quantum safe project,” LNCS, vol. 10532, pp. 14–37, 2017. [Google Scholar]
13. B. Harjito, H. N. Tyas, E. Suryani and D. W. Wardani, “Comparative Analysis of RSA and NTRU Algorithms and Implementation in the Cloud,” International Journal of Advanced Computer Science and Applications, vol. 13, no. 3, pp. 157–164, 2022. [Google Scholar]
14. E. N. Hameed and H. R. Yassein, “QOCNTR: Improved NTRU public key based on a new algebraic structure,” Mathematical Statistician and Engineering Applications, vol. 71, no. 4, pp. 5627–5633, 2022. [Google Scholar]
15. V. K. Yadav, S. Venkatesan and S. Verma, “Man in the middle attack on NTRU key exchange,” in Int. Conf. on Communication, Networks and Computing, India, vol. 839, pp. 251–261, 2019. [Google Scholar]
16. E. Yen IARAS, “New efficent characteristic three polynomial mutipliation algorithms and their application to NTRU prime,” P.H.D. Dissertation, University of Middle east Technical, Turkey, 2022. [Google Scholar]
17. K. Meher and D. Midhunchakkaravarthy, “NTRU encrypt–aquantum proof replacement to RSA cryptosystem,” International Journal of Advanced Trends in Computer Science and Engineering, vol. 9, no. 5, pp. 1–6, 2020. [Google Scholar]
18. L. Shuai, H. Xu, L. Miao and X. Zhou, “A Group-based NTRU-like public-key cryptosystem for IoT,” IEEE Access, vol. 7, pp. 75732– 75740, 2019. [Google Scholar]
19. B. Bi, D. Huang, Zeng and H. Pan, “Efficient, LBS security-preserving based on NTRU oblivious transfer,” Wireless Personal Communications, part of Springer Nature, vol. 108, no. 4, pp. 2663–2674, 2019. [Google Scholar]
20. J. Howe, M. Martinoli, E. Oswald and F. Regazzoni, “Exploring parallelism to improve the performance of frodoKEM in hardware,” Journal of Cryptographic Engineering, vol. 11, no. 4, pp. 317–327, 2021. [Google Scholar]
21. S. D. Galbraith and F. Vercauteren, “Computational problems in supersingular elliptic curve isogenies,” Quantum Information Processing, vol. 17, no. 10, pp. 1–22, 2018. [Google Scholar]
22. E. Karacan, A. Karakaya and S. Akleylek, “Quantum secure communication between service provider and sim,” IEEE Access, vol. 10, no. June, pp. 69135–69146, 2022. [Google Scholar]
23. T. Bai, S. Davis, J. Li and H. Jiang, “Analysis and acceleration of NTRU lattice-based cryptographic system,” in 15th IEEE/ACIS Int. Conf. on Software Engineering, Artificial Intelligence, Networking and Parallel/Distributed Computing (SNPD), Las Vegas, NV, USA, pp. 2–3, 30 June - 02 July 2014. [Google Scholar]
24. T. A. Jaber and B. H., “Improve NTRU algorithm based on chebyshev polynomial,” in IEEE World Congress on Information Technology and Computer Applications (WCITCA), Hammamet, Tunisia, pp. 1–5, 11-13 June 2015. [Google Scholar]
25. Y. I. Alzoubi, V. H. Osmanaj, A. Jaradat and A. Al-Ahmad, “Fog computing security and privacy for the internet of thing applications: State-of-the-art,” Security and Privacy, vol. 4, no. 2, pp. 135, 2021. [Google Scholar]
26. Q. M. Hussein and Q. M. Hussein, “Recover the NTRU private keys from known public information and public key,” Ph.D. Dissertation, University of Technology, Iraq, 2015. [Google Scholar]
27. H. C. Ukwuoma, A. J. Gabriel, A. F. Thompson and B. K. Alese, “Quantum attack-resistant security system for cloud computing using lattice cryptography,” International Journal for Information Security Research, vol. 12, no. 1, pp. 1053–1061, 2022. [Google Scholar]
28. S. Srinivasan, “Private and robust aggregate statistics collection with shamir-secret sharing,” M.S. Dissertation, University of Illinois, Chicago, 2022. [Google Scholar]
29. A. T. Maolood and A. T. Khudhair, “Towards generating a robust key based on neural networks and Chaos theory,” International Journal for Information Security Research, vol. 59, no. 3, pp. 1518–1530, 2018. [Google Scholar]
30. S. A. Abdel Hakeem and H. Kim, “Centralised threshold key generation protocol based on shamir secret sharing and HMAC authentication,” Sensors, vol. 22, no. 1, pp. 22–33, 2022. [Google Scholar]
31. M. Tejedor-Romero, D. Orden, I. Marsa-Maestre, J. Junquera-Sanchez and J. M. Guzman, “Distributed remote e-voting system based on Shamir's secret sharing scheme,” Electronics (Switzerland), vol. 10, no. 24, pp. 1–19, 2021. [Google Scholar]
32. A. A. A. Gutub and K. A. Alaseri, “Refining Arabic text stego-techniques for shares memorisation of counting-based secret sharing,” Journal of King Saud University – Computer and Information Sciences, vol. 33, no. 9, pp. 1108–1120, 2021. [Google Scholar]
33. S. VenkataRao and V. Ananth, “A Hybrid optimization algorithm and shamir secret sharing based secure data transmission for IoT based WSN,” International Journal of Intelligent Engineering and Systems, vol. 14, no. 6, pp. 498–506, 2021. [Google Scholar]
34. O. Sefraoui, A. Bouzidi, K. Ghoumid and E. M. Ar-Reyouchi, “AuSDiDe: Towards a new authentication system for distributed and decentralised structure based on shamir's secret sharing,” International Journal of Advanced Computer Science and Applications, vol. 13, no. 1, pp. 782–787, 2022. [Google Scholar]
35. P. Sarosh, S. A. Parah and G. M. Bhat, “Utilisation of secret sharing technology for secure communication: A state-of-the-art review,” Multimedia Tools and Applications, vol. 80, no. 1, pp. 517–541, 2021. [Google Scholar]
36. A. Labao and H. Adorna, “Cryptographic rational secret sharing schemes over general networks,” Cryptography, vol. 6, no. 4, pp. 50, 2022. [Google Scholar]
37. M. S. Oudah and A. T. Maolood, “Lightweight authentication model for IoT environments based on enhanced elliptic curve digital signature and shamir secret share,” International Journal of Intelligent Engineering and Systems, vol. 15, no. 5, pp. 81–90, 2022. [Google Scholar]
38. N. Mehibel and A. Hamadouche, “Authenticated secret session key using elliptic curve digital signature algorithm,” Security and Privacy, vol. 4, no. 2, pp. 1–15, 2021. [Google Scholar]
39. E. Yooni1 and K. Young Yoo, “A New elliptic curve diffie-hellman two-party key agreement protocol,” in IEEE, 2010 7th Int. Conf. on Service Systems and Service Management, Tokyo, Japanpp, pp. 1–4, 2010. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF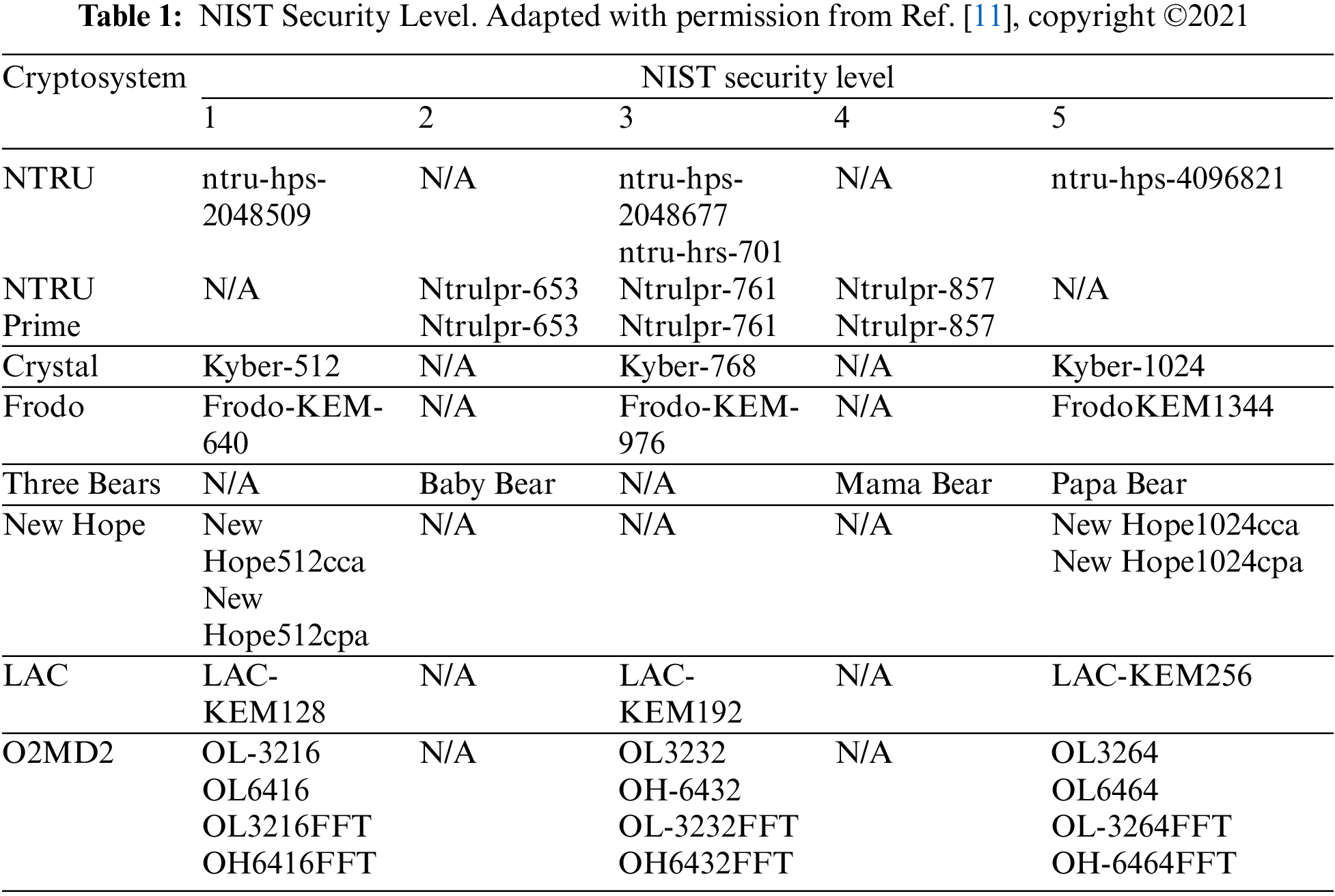

 Downloads
Downloads
 Citation Tools
Citation Tools