Blockchain Privacy Protection Based on Post Quantum Threshold Algorithm

1  Introduction

Blockchain technology emerged with the birth of Bitcoin. From the entire network, blockchain is a decentralized database platform where users are equivalent to nodes. The data are updated through the consensus mechanism between users rather than third-party platforms; thus, the data are consistent across the network [1,2]. Blockchain is a chain data structure in a single node where encrypted data, time stamps, and hash values are recorded in each block. Blockchains are formed when data blocks are joined according to transaction time [3]. Digital industries such as digital finance, smart government, smart banking, smart healthcare, and intelligent transportation extensively employ blockchains [4–6].

Encryption algorithms are adopted to realize data security in blockchain. If a single individual managed the private key, the person’s right could be exclusive. Once there is a loss, the information cannot be recovered. Regarding the distributed scheme, the whole backup sharing scheme shares the copy of the entire secret with the managers, which leads to information redundancy and increases the possibility of information leaking, while the cutting sharing scheme splits the secret into multiple pieces; only when all these pieces cooperate can the secret be decrypted, which brings difficulties to the recovery of the original information. Shamir and Balkley introduced the threshold secret-sharing scheme, with Shamir suggesting a scheme based on polynomial interpolation and Balkley proposing a system that leveraged geometric methods. Threshold secret-sharing refers to the fact that any user can encrypt private data using a public key. At the same time, the private key is jointly controlled by multiple designated secret holders. Only when a certain number of secret holders cooperate in aggregating the decryption fragments can decryption be achieved. In this way, private data that require authorization from multiple parties can be effectively protected by the threshold encryption scheme [7–9].

Based on some mathematical problems, asymmetric encryption algorithms are always used for data encryption and consensus signatures in blockchains, such as the Rivest–Shamir–Adleman (RSA) algorithm based on number decomposition, the Digital Signature Algorithm (DSA) based on discrete logarithm, and the Elliptic Curve Cryptography (ECC) algorithm. Traditional computers cannot afford to solve these mathematical problems. In the past, these algorithms were considered secure. However, with the advent of the quantum age, something is changing.

Quantum computing was an idea derived from the quantum concept in physics. Traditional computers convey information with bits, while quantum ones convey information with qubits. Quantum computers utilize the physical effects of qubits to perform computing tasks, such as quantum superposition and entanglement [10]. Thus, quantum computers can perform parallel processing, which makes them more powerful than traditional computers [11].

The advent of quantum computing has raised concerns that quantum computers could compromise public key encryption with a sufficient number of qubits. Some quantum algorithms have been proposed to solve discrete logarithm problems and factorial integer problems [12], making many of the widely used asymmetric key algorithms dangerous [13]. This article [14] noted that RSA algorithms that rely on prime number decomposition increased key size to resist quantum attacks, but this is not a permanent solution. As quantum computing advances, even public key algorithms that rely on elliptic curves will be vulnerable to threats [15]. Therefore, post-quantum algorithms have been put on the agenda of cryptography.

The paper presents a framework for managing blockchain data that employs the post-quantum threshold algorithm, effectively addressing the risks associated with a single point of private key disclosure and the potential threats quantum computing poses. The system uses the threshold algorithm to reduce the risk of key centralization and allows multiple key management nodes to decrypt and then complete the data authorization service jointly. The post-quantum threshold algorithm of the system framework uses the NTRU threshold algorithm based on the linear secret-sharing scheme proposed by Dalton [16]. The inherent complexity of the problems on NTRU lattices allows the system to resist attacks from quantum computing.

This paper is presented in the following chapters: Section 2 of the article presents research on threshold cryptography and post-quantum algorithms commonly used in blockchain applications. Section 3 reviews some concepts and the NTRU algorithm. Section 4 describes the algorithm and the proposed structure of threshold secret-sharing, and Section 5 briefly summarizes the paper.

2  Related Works

2.1 Application of Threshold Cryptography on the Blockchain

Threshold secret-sharing technology has been integrated into blockchain across many fields to protect private keys and digital signatures. To ensure data security in connecting devices, Yu et al. [17] proposed a threshold encryption protection scheme that employs blockchain and threshold secret-sharing technology to store split private keys on the blockchain, resolving privacy and security issues associated with third-party private key storage and management. To achieve the cooperative authentication of Unmanned Aerial Vehicles (UAVs) across regions, Feng et al. [18] proposed a blockchain-based UAV intelligent Internet. The cooperative domain is authenticated using a method that employs multiple signatures created through threshold secret-sharing. Their proposed scheme can resist common attacks against IoT devices. Li et al. [19] introduced an anonymous vehicle announcement aggregation protocol in intelligent transportation, establishing a blockchain-based incentive announcement network that preserves privacy. Tian et al. [20] developed a threshold multiple-signature scheme utilizing the elliptic curve cryptography algorithm, which is well-suited for multiple-signature voting in various applications, including blockchain and smart contracts.

There are also some threshold secret-sharing applications on the blockchain to meet the security requirement. The collaborative monitoring scheme presented by Lyu et al. [21] uses a threshold secret-sharing algorithm to ensure the secure sharing of secret content, which balances users’ privacy and review security. Additionally, their approach incorporates blockchain technology. Biswas et al. [22] introduced an enhanced version of Shamir’s secret-sharing scheme (SSS) into the blockchain, which prevented any fraudulent activities by dealers and participants. Additionally, the author utilized the blockchain-based secret-sharing scheme to strengthen the security of the consensus processing of Proof of Work (PoW), eliminating potential vulnerabilities. Fan et al. [23] introduced a new strategy for combating fraudulent transactions in blockchain systems through the proposition of an editable blockchain model that utilizes chameleon hash key sharing. The proposed scheme leverages chameleon hash’s polymorphic properties to ensure the edited blockchain’s structure remains intact.

2.2 Development of Post-Quantum Cryptography

Post-quantum research has garnered significant attention due to the risk quantum computing poses to classical cryptography. There have been some explorations of post-quantum algorithms in different fields. Based on lattice-based cryptography, Zhang et al. [24] provide forward security to protect data confidentiality and search privacy. The lattice-based authorization mechanism was integrated into the scheme to achieve security. After introducing the post-quantum signature scheme, Clupek et al. [25] proposed a secure digital archiving solution that could resist attacks from traditional and quantum computers. Preece et al. [26] introduced a novel framework for publicly distributed networks to address the challenge of uploading confidential industrial data to such networks. The proposed solution leverages the Diffie-Hellman Key Exchange (DHKE) technique. During the construction of DHKE, the proposed scheme can resist quantum attacks based on another type of post-quantum foundation, supersingular isogeny.

2.3 Application of Post-Quantum Algorithms on the Blockchain

To protect blockchain against quantum attacks, some scientists proposed post-quantum protocols, some made a few adjustments in verification methods on the previous blockchain model, and some built a new post-quantum blockchain system with the adoption of lattice space or quantum entanglement. Yin et al. [27] introduced a novel approach to enhance the security of the master private key by expanding a single lattice space into multiple lattice spaces. Under this approach, each transaction signature is associated with a dependent lattice space, thus ensuring randomness and security. By analyzing basic cryptographic algorithms, like hash functions in the blockchain, Fernández Caramès et al. [1] studied how to enhance the security of public key algorithms and hash functions in the blockchain and proposed a post-quantum blockchain. They extensively evaluated various cryptographic Schemes for their potential use in the blockchain. They compared their characteristics and performance to identify the most suitable options. To facilitate the verification of transactions within blockchain systems, a new blind signature scheme was proposed by Li et al. [28]. This scheme is post-quantum and utilizes the lattice hypothesis. Their proposed method utilizes bimodal Gaussian distribution and sampling rejection techniques to enhance both sec and efficiency. Holcomb et al. [29] redesigned the certificate management program and related blockchain specifications. Li et al. [30] introduced a novel signature scheme based on lattices to safeguard blockchain networks over conventional communication channels. Chalkias et al. [31] developed a scalable digital signature scheme that is resilient against quantum attacks and can be used in blockchain and decentralized systems. This scheme involved a specific chain/graph structure in reducing the cost of key generation, signature, and verification, whose performance was superior to the existing hash-based algorithms of the period. Using quantum key distribution for authentication, Kiktenko et al. [32] built a quantum-safe blockchain platform, realizing the scalability of quantum security blockchain in commercial and government applications.

Yi [33] introduced a post-quantum cryptography solution to address the issue of privacy and security for social media users. Compared to conventional social networks, the suggested approach is secure in the quantum era. Li et al. [34] enable efficient electronic medical record data management while ensuring patient privacy and security. Gao et al. [35] introduced a novel quantum blockchain scheme, employing quantum entanglement and proxy proof to achieve higher efficiency and security than traditional blockchain methods. Saha et al. [36] presented a remedy for decentralization in blockchain technology under post-quantum settings. During verification processes, they used lattice-based aggregation signatures to reduce blockchain storage space and network traffic costs. As a result, their proposed approach ensures the efficiency and applicability of post-quantum blockchain applications.

3  Preliminary

3.1 Lattice

Lattice L is a discrete subgroup of a real vector space, which is generated by n linearly independent vectors bi, the definition of which is:

L(B)=L(b1,b2,…,bn)={Ba|a∈Zn}

where  B is a set of n vectors, and these n vectors form the bases of lattice L.

In cryptography, the lattice is a mathematical structure used to create a cryptosystem resistant to quantum computer attacks. A lattice-based cryptographic system is based on the hardness of some lattice-related problems. Due to the unique cryptographic properties of lattice structures, the creation of public key encryption, digital signature, and key exchange schemes based on lattice characteristics has become a frontier in cryptography research.

3.2 NTRU

In 1998, Hoffstein, Piper, and Silverman introduced a public key encryption scheme based on the NTRU lattice. This system utilizes a polynomial ring, and the Shortest Vector Problem on the lattice ensures the security of the scheme. Compared to traditional number theory-based cryptographic schemes, NTRU can generate key pairs more quickly with the same security requirements and has advantages in encryption efficiency. Therefore, NTRU is currently the leader in cryptography for post-quantum digital signatures. Stehle and Steinfeld proposed an NTRU encryption system in 2011, which relied on the Ring Learning with Errors (RLWE) problem. In 2012, Ron Steinfeld and others proposed an NTRU encryption system with chosen ciphertext attack security on the ideal lattice. In the collection of post-quantum cryptography algorithm standardization led by American standardization research institutions, Falcon, a signature scheme based on NTRU lattice, has now successfully passed the rigorous security analysis and related performance tests of cryptologists around the world, which further deepens its security to some extent.

The following three common parameters are included in the standard NTRU scheme: positive integer N,  denotes the degree of the polynomial; the large module q and small module p should meet the requirement (q,p)=1. In the standard scheme, p=3. In addition, it is necessary to define a polynomial ring ℛ=Z[x]/(XN−1). The standard NTRU key generation process can be outlined as follows:

(1)   Two polynomials f,g are chosen, the efficient of which consists of {−1,0,1};

(2)   If the above polynomials f,g are irreversible on the polynomial ring ℛq, then the polynomials must be reselected;

(3)   Calculate the inverse of f and g on ring ℛq, called fq and gq, respectively;

(4)   The private key of the standard NTRU scheme is (f,fp), and the public key can be calculated by h=p⋅g⋅fq(mod q).

The encryption process is as follows:

(1)   Choose any random polynomial r;

(2)   Calculate the ciphertext to the plaintext messages m with y=r⋅h+m(mod q).

The decryption process is as follows:

(1)   Calculate the shared ciphertext a=f⋅y(mod q);

(2)   The plaintext can be calculated by m=fp⋅a (mod p).

3.3 Threshold Encryption

Threshold encryption algorithms include key generation algorithms, encryption algorithms, decryption algorithms, and message combination algorithms.

KeyGen(λ,n,t): there are several input parameters, including the system security parameter λ, the number of participating private computing blockchain nodes n, and the threshold value t. The algorithm outputs pk and user private key sharing sk=(skid2,…,skidn).

Enc(pk,m): input public key pk and message m in this algorithm, and output the ciphertext c;

Dec(skid,c): The input for the decryption algorithm is the private key sharing skid and ciphertext c. Once executed, the algorithm outputs the decryption share cid.

Combine(cidi1,…,cidit): input any t decryption shares cidi1,…,cidit, and output message m.

In a threshold encryption system, the data is secured via public key encryption and the key is divided among multiple participants. To decrypt the data, several participants must cooperate and complete the decryption protocol together.

3.4 Linear Secret-Sharing Scheme

The paper suggests using a linear secret-sharing scheme (LSSS) to divide the private key. The input parameters for the LSSS are t and n, and the resulting secret-sharing matrix is generated as the output. The secret-sharing matrix will be used for modular multiplication with the private key of the NTRU to generate a key-share matrix. Then, the row vector of the key share matrix is the private key share distributed to each participant. Defining the access structure is essential for establishing a linear secret-sharing scheme. A set of access policies or rules is used to construct the secret-sharing matrix.

Definition 1 (Monotone Access Structure). Let X be a finite set of users, and let 2X denote the power set of X, i.e., the set of all subsets of X. An access structure A is a collection of subsets of X, denoted by {S1,S2,⋯,Sm}, where each subset Si  is authorized to access the resource. An access structure A is said to be monotone if it can be represented as a monotone Boolean function f:2X→{0,1}, where 0 denotes unauthorized, and 1 denotes authorized. More specifically, f is said to be monotone if for any sets S and T in 2X such that S is a subset of T, f(S)≤f(T).

In this scheme, the paper mainly uses a (t−N) threshold structure, which aims that if t participants participate in decryption among N participants, decryption can succeed. Therefore, the threshold access structure is defined as follows.

Definition 2 (Threshold Access Structure). A threshold access structure constructs such an access mechanism in which a minimum number of authorized users must collaborate to gain access to a particular resource or piece of information. More formally, a threshold access structure is the following user set {S1,S2,…,Sm}, such that access is granted to the resource if and only if the number of authorized users who collaborate to access the resource is at least some threshold t. The threshold access structure can be expressed in the following mathematical form through the monotone Boolean function: f:2X→{0,1}, where X is a finite set of users and 2X denotes the set of all subsets X. The function f is defined under the condition that f(S)=1 which is enough and necessary condition |S|≥k, where |S| is the cardinality of S.

Definition 3 (Monotone Boolean Formula). Boolean variables and the logical operations of conjunction and disjunction form monotonic Boolean formulas but without negation. Mathematically, a monotone Boolean formula can be defined as follows: Let X={x1,x2,…,xn} with a finite number of Boolean variables and F is a monotone Boolean formula over X. Then F is a finite sequence of clauses, each of which is a conjunction of some of the variables in X. More formally, F can be written as F=C1∨C2∨…∨Cm, where each clause Ci is a conjunction of some of the variables in X. Intuitively, this means that a monotone Boolean formula is a logical expression that consists only of AND operations and OR operations, but no NOT operations. Since the formula is monotone, adding more variables or increasing the value assigned to a variable can only increase the output value of the formula, which is always either 0 or 1.

The conversion of a (t−N) threshold access structure into a Boolean expression is possible due to the fact that such a structure can be expressed as a monotone Boolean function. The conversion of access structures into Boolean expressions can be demonstrated by considering examples such as the (2−3) threshold access structure and the (1−3) access structure for 3 participants. Denote the 3 participants as P1,P2,P3. The former can be expressed as (P1∧P2)∨(P1∧P3)∨(P2∧P3) while the latter can be represented by (P1)∨(P2)∨(P3).

This paper utilizes the Folklore algorithm of Boneh et al. [37] on Crypto2018 to convert the Boolean expression into a secret-sharing matrix. The Folklore algorithm takes a monotone Boolean formula as input and generates an LSSS share matrix M as output.

The private key is partitioned by the linear secret-sharing algorithm in accordance with the secret-sharing matrix generated by the access structure, generating private key shares.

Definition 4 (Linear Secret-Sharing Scheme, LSSS). Suppose that P={P1,P2,…,PN} is a set of parties. A secret-sharing scheme (SS) is categorized as an LSSS if it meets two conditions while having a private key space 𝒦=Zp (p is a prime number):

a.   SS.Share(k, A): There exists a matrix M∈Zpl×N which can be called the share matrix. Each party, denoted by Pi, is assigned a partition Ti⊆{l}, {l}={0,1,2,…,l}. To generate secret shares of k, random values r1,r2,…,rn←RZp are sampled and a vector θ=M⋅(k,r2,…,rn)T is defined. The shares for Pi are comprised of the entries {θj}j∈Ti in this vector.

b.   SS.Combine(B): For any valid set  S∈A, the vector  (1,0,…,0)∈span({M[j]j∈∪i∈STi}) over Zp, by convention, M[j] represents the j-th row of matrix M. If S∈A is a valid set of parties, the coefficients {cj}j∈∪i∈STi  can be found such that

∑j∈j∈∪i∈SiTi  cj⋅M[j]=(1,0,…,0)

k=∑j∈∪i∈STi cj⋅θj

To adapt to the threshold form of the access structure, this paper uses the {0,1}−LSSS scheme proposed by Boneh et al. [37] to generate the secret-sharing matrix and then cut the private key. The {0,1}−LSSS scheme is a particular case of LSSS. It must satisfy the extra condition: For any given set S∈A, there exists a subset T⊆∪i∈STi such that k=∑j∈Twj.

4  The Proposed Architecture

4.1 System Holistic Framework

4.1.1 System Entity

In this work, we mainly provide a new blockchain data management technology based on the NTRU threshold scheme. Compared with the centralized key management scheme of the traditional technique, this paper uses the threshold method to control the critical authority. For cutting, multiple consensus nodes are used as key management nodes to manage the secret key share. For encrypted data, the data user applies to the consensus node for permission. The figure presented in Fig. 1 demonstrates the visual representation of the entities encompassed within the system, including:

(1) System manager: responsible for key generation, allocating private key shares to key management nodes, and disclosing the public key to data users in the blockchain system.

(2) Key management node (KMD): manages private key shares and handles decryption requests from data users.

(3) Data user: The individual who uses data can be referred to as the data user. Whenever the data user wishes to access the encrypted database, they send a request to the key management node. Additionally, data users have the option of encrypting their data using public keys and keeping the resulting ciphertext data in data storage nodes.

(4) Data storage node: A data storage node is responsible for storing data that has been encrypted.

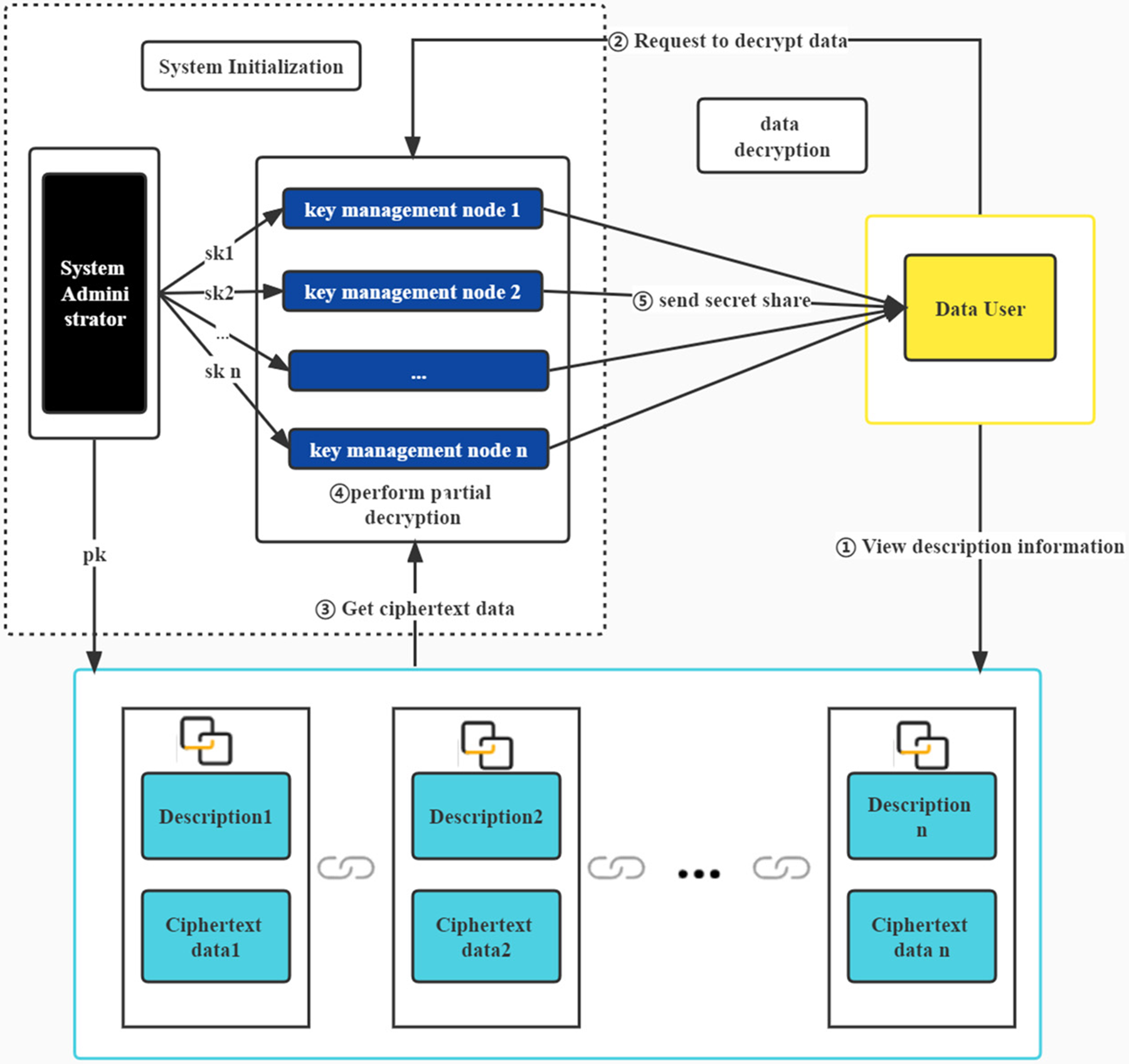
Figure 1: Flow chart of the blockchain post-quantum threshold data management system

4.1.2 Syntax of System

In the whole system process, the private key is not managed by a single node through the threshold algorithm, which increases the system’s fault tolerance and prevents the risk of privacy leakage caused by single-point key leakage. At the same time, in the process of partial decryption, the decryption share will not cause privacy leakage to the private key share of the key management node.

(1) System initialization.

During the initialization process, the system administrator initializes the system and creates a key management node. Initially, the system administrator generates a private-public key pair using NTRU-LWE public key encryption technology. Next, a secret-sharing matrix is constructed using linear secret-sharing technology. The matrix is used to compute the secret share of the private key corresponding to each node, which is subsequently sent to the corresponding key management node. The system administrator discloses his public key, encrypts the data with the public key, adds description information to this part of the data, and saves the description and ciphertext data together as a complete data file.

(2) Data users add data.

Data users can use the public key information to add data actively. After encrypting the data, add the necessary description information to this part of the data, and then save the description information and ciphertext data together as a complete data file. Then, it is stored in the data storage node.

(3) Data users apply for decryption.

Data users can also view other data files by applying decryption. The data user can view the description information of additional data. If the data user wants to decrypt the ciphertext in the file, he must submit a data decryption application to the KMD.

(4) The key management node performs partial decryption.

After the data user submits a request for decryption of the ciphertext, the decryption process does not commence directly. The KMD makes a judgment. The KMD that agrees to the demand starts to perform the decryption operation. The key management node retrieves the ciphertext data from the data storage node, uses its key share to decrypt it partially, and forwards the partially decrypted data to the data user.

(5)   The final decryption of the data user.

Once the data user receives the partially decrypted data that meets or exceeds the threshold, they can perform the final decryption to obtain the required plaintext data.

4.2 Threshold Encryption Scheme Based on NTRU

As part of the system workflow, initialization involves generating a public-private key pair using NTRU with the RLWE scheme. A secret-sharing matrix is constructed using the linear secret-sharing scheme to distribute the secret share among the key management nodes. During the decryption process performed by the data user, both partial decryption and final decryption schemes are utilized to decrypt the data. First, the NTRU with the RLWE scheme is displayed below.

4.2.1 NTRU with RLWE

(1) KeyGen: Sample f′←DZn,σ, let f=pf′+1, if f is irreversible in Rq=Zq[x]/(xn+1), then resample. Sample g←DZn,σ, if g is irreversible in Rq, then resample. Finally, administrator obtains the private key f, and the public key h=pg⋅f−1∈Rq.

(2) Encrypt(h,m): Sample e,e′ ←χ, where χ is a noise distribution on RLWE, and finally returns the ciphertext c=he+pe′+m∈Rq.

(3) Decrypt(f,c): Calculate a=f⋅c∈Rq, and return m=a mod p.

4.2.2 Key Generation and Key Share Distribution

(1) The system administrator executes the KeyGen algorithm of the NTRU with the RLWE scheme to generate the private key f that can be split, and the public key h is used to encrypt private data. Users within the system can use public key h to encrypt private information. The text data are stored in the key management node.

(2) The system manager performs key share distribution and generates secret shares based on the {0, 1}-LSSS matrix according to the threshold (t-n) structure. According to the (t-n) design, the system manager first generates a Boolean expression as algorithm 1. As the input of the Folklore algorithm, the output is a secret-sharing matrix M.

(3) The administrator utilizes the secret-sharing matrix M to divide the key, but instead of performing a multiplication operation of the secret-sharing matrix by a column vector, they employ a matrix W=(f,r2,…,rn)T for the process, where ri is a randomly chosen element in Rq. The row vector of the matrix obtained by multiplying M and W is used as a secret share and distributed to each participant. The generator matrix will contain C(n,t) rows. Then, the secret shares are allocated to the participants in lexicographical order.

For example, in the (2–3) threshold, the management node P1 obtains row 1 and row 3, the management node P2 obtains row 2 and row 5, and P3 obtains row 4 and row 6. Then, the management node P1 uses row 1 to perform the decryption operation with row 2 of the management node P2, and the management node P1 uses row 3 to complete the decryption operation with row 4 of the management node P3.

This paper implemented an adjustable (t–n) threshold code in the experiment. Figs. 2 and 3 are the (2–3) threshold matrix and (3–5) threshold matrix of the codes generated, respectively, and the LSSS matrix generation code is shown in Table 1.

Figure 2: (2–3) Threshold matrix generation result

Figure 3: (3–5) Threshold matrix generation result

4.2.3 The Key Management Node Performs a Partial Decryption Scheme

(1)   The data user views the ciphertext data description information and initiates a decryption request to the key management node for the required ciphertext data. Upon receiving the decryption request, the key management node locates the corresponding ciphertext data in the data storage node and performs partial decryption.

(2)   After the key management node Pi receives the ciphertext y, it operates ai=si⋅y+p⋅ei(mod q), where si is the key share corresponding to the key management node Pi. The polynomial ei is created independently from a discrete Gaussian distribution. The standard deviation of the coefficients in the distribution is small, and ai is the partial decrypted shares generated after decryption.

(3)   The key management node Pi sends the decryption share ai to the data user requesting decryption.

4.2.4 Data User Final Decryption Scheme

The data user collects the threshold partial decryption shares and then performs the final decryption operation m=(∑i=1tai(mod q))(mod p) to obtain the data plaintext m corresponding to the ciphertext data y.

During the process, the partially decrypted shares will not reveal the private information of the key management node’s key shares, which ensures the system’s stability.

4.3 Correctness and Security Analysis

4.3.1 Correctness

Theorem 1 The Threshold Encryption Scheme Based on NTRU satisfies correctness.

Proof. Given t valid key management nodes that have secret shares, the key management nodes first calculate ai=si⋅y+p⋅ei(mod q), where si is the key share of key management node Pi. When ai is substituted into the final decryption, the result is obtained:

(Σit(si⋅y+p⋅ei)(mod q)(mod q))(mod p)

Since p⋅eimod p=0, it gives

(Σit(si⋅y)(mod q)(mod q))(mod p)

Hence

(Σit(si)⋅y(mod q))(mod p)

Because Σitsi=f, which is the original private key, it follows that

(f⋅y(mod q))(mod p)=m

4.3.2 Security Analysis

Ensuring the security of the Threshold Encryption Scheme that is based on NTRU involves protecting the confidentiality of encrypted messages, preserving the integrity and authenticity of communications, and defending against various forms of attacks can be demonstrated using the following hybrid arguments. Assume there is a set of key shares si of key management nodes that do not satisfy the threshold condition. The partial decryption mustn’t disclose the information of the key share, and the adversary cannot learn the plaintext information from the partial decryption shares.

•   Hybrid 0: Hybrid 0 is equivalent to the actual threshold encryption scheme based on NTRU, where the key shares are less than the threshold t.

•   Hybrid 1: Hybrid 1 varies slightly from Hybrid 0, with the exception that the partial decryptions are produced from a random distribution rather than actual partial decryptions.

•   Hybrid 2: Hybrid 2 is constructed similarly to Hybrid 1, with the exception that the secret key shares are chosen at random from the entire key space rather than being the actual key shares generated in the encryption process. This allows for analysis of the security of the scheme, where attackers can only access public parameters and ciphertext without knowing the actual key sharing.

•   Hybrid 3: Hybrid 3 is constructed similarly to Hybrid 2, with the exception that the messages are generated randomly from the message space. The result in an “ideal” scenario for security analysis, where the adversary remains oblivious to both the original message being encrypted and the actual secret key shares

Assuming the hardness of the RLWE assumption, it is computationally infeasible to distinguish between Hybrid 0 and Hybrid 1. The security of the linear secret sharing scheme (LSSS) ensures that distinguishing between Hybrid 1 and Hybrid 2 is computationally infeasible in the cryptographic sense, as LSSS is responsible for generating the key shares used in both hybrids. The semantic security of basic NTRU encryption ensures that it is computationally infeasible to distinguish between Hybrid 2 and Hybrid 3. This is because the partial decryption and secret shares in both hybrids are simulated, making it impossible for an adversary to differentiate between the actual system and the theoretical model. In other words, Attackers cannot distinguish between information encrypted by real messages and information encrypted by randomly generated messages, meaning that they cannot determine what the content of the encrypted message is based on its external characteristics (such as length, size, format, etc.), thereby ensuring the confidentiality of the message. Additionally, since the NTRU lattice is used, the proposed scheme can suffice for quantum attacks.

4.4 Experiment and Efficiency Analysis

This work implements the Threshold Encryption Scheme Based on NTRU by Sagemath [38]. The share matrix is generated by the code in Table 1. The blockchain environment is simulated by a federated blockchain tool ChainMaker [39]. The program runs on Ubuntu 22.04 LTS with Intel(R) Core (TM) i7-10510U central processing unit (CPU) 1.80 GHz and 16G random access memory (RAM). The amount of time taken is documented and presented in Table 2. The parameter N is set to 256 and 512. The settings of other parameters are the same as those in [40]. It can be noted that the time consumption is within the acceptable range. Compared with the NIST PQC winning algorithm Kyber [41], the number of key generations per second of Kyber is approximately 122684, and the number of encryptions is about 154524. The number of decryptions is about 187960, and their test is implemented in C language.

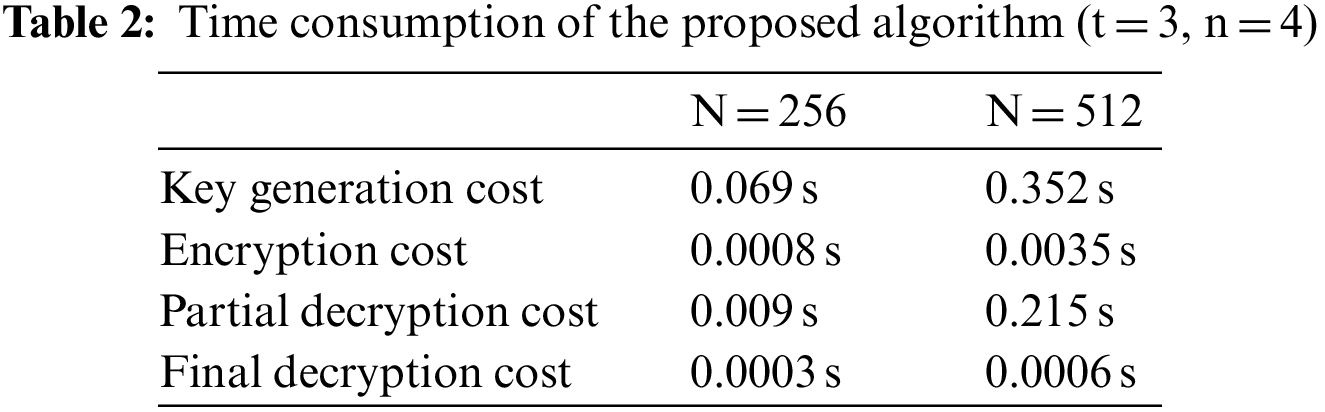
As observed in Table 2, the threshold algorithm described in this paper results in a higher consumption of resources for key generation and final decryption compared to the original NTRU. The consumption of encryption is the same as that of the original NTRU. The partial decryption process for the proposed threshold NTRU scheme is identical to that of the original NTRU, with the exception that the secret key shares are utilized instead of the private key. Additionally, the final decryption only involves a modular addition operation, which is very cheap. In comparison to threshold RSA [42], the proposed scheme in this paper is more efficient in terms of encryption and decryption, as it only requires polynomial multiplication operations. Furthermore, RSA necessitates high resource consumption power operations, whereas NTRU operates with a lower complexity of O(NlogN). In comparison, the complexity of RSA is O(N3). Compared with traditional algorithms, the algorithm in this paper has computational advantages.

5  Conclusion

This paper effectively demonstrates the blockchain data management technology based on the NTRU threshold scheme, which can realize the distributed management of keys and has significant advantages in security and quantum resistance. The NTRU algorithm encrypts plaintext data to give the system more robust security and post-quantum performance. A secret-sharing matrix generation function splits the secret into shares and disperses them among different key management nodes created using the t/n threshold structure. When a data user wants to view the entire secret, he needs to submit a request first, and the t key masters decrypt a part of the key that can be decrypted by their keys and submit this part to the data users so that the data users can use these parts for final decryption. The proposal of this scheme can effectively combine the threshold scheme and lattice encryption, improve the security of data, improve the security level of work, and provide an effective security guarantee for data management on the blockchain. In the application scenario, in addition to decrypting data through multi-party authorization in the blockchain, this solution needs to provide multiple data contributors with joint data use authorization features in areas such as anonymous electronic voting, data proxy services, and data outsourcing computing which have broad application prospects.

Funding Statement: This work was supported by the National Key R&D Program of China (2022YFB2703400).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. T. M. Fernández-Caramès and P. Fraga-Lamas, “Towards post-quantum blockchain: A review on blockchain cryptography resistant to quantum computing attacks,” IEEE Access, vol. 8, pp. 21091–21116, 2020. [Google Scholar]

2. L. Yang, “The blockchain: State-of-the-art and research challenges,” Journal of Industrial Information Integration, vol. 15, pp. 80–90, 2019. [Google Scholar]

3. T. Aste, P. Tasca and D. Matteo, “Blockchain technologies: The foreseeable impact on society and industry,” Computer, vol. 50, no. 9, pp. 18–28, 2017. [Google Scholar]

4. S. P. Mohanty, “Blockchains are everywhere,” IEEE Consumer Electronics Magazine, vol. 10, no. 5, pp. 4–5, 2021. [Google Scholar]

5. L. Zhang, J. Mao, Y. An, T. Zhang, J. Ma et al., “A systematic review of blockchain technology for government information sharing,” Computers, Materials & Continua, vol. 74, no. 1, pp. 1161–1181, 2023. [Google Scholar]

6. C. S. S. Anupama, R. Alsini, N. Supriya, E. Laxmi Lydia, S. Kadry et al., “Wind driven optimization-based medical image encryption for blockchain-enabled internet of things environment,” Computers, Materials & Continua, vol. 73, no. 2, pp. 3219–3233, 2022. [Google Scholar]

7. D. Chen, W. Lu, W. Xing and N. Wang, “An efficient verifiable threshold multi-secret sharing scheme with different stages,” IEEE Access, vol. 7, pp. 107104–107110, 2019. [Google Scholar]

8. F. Li, T. Chen and S. Zhu, “Dynamic (t, n) threshold quantum secret sharing based on d-dimensional bell state,” Physica A: Statistical Mechanics and its Applications, vol. 606, pp. 128122, 2022. [Google Scholar]

9. E. Zhang, X. Duan, S. Xiu, J. Fang, Z. Jiang et al., “Server-aided multi-secret sharing scheme for weak computational devices,” Computers, Materials & Continua, vol. 56, no. 3, pp. 401–414, 2018. [Google Scholar]

10. K. Fedorov, O. Kiktenko and I. Lvovsky, “Quantum computers put blockchain security at risk,” Nature, vol. 563, no. 7732, pp. 465–467, 2018. [Google Scholar] [PubMed]

11. X. Zhang, F. Wu, W. Yao, W. Wang and Z. Zheng, “Post-quantum blockchain over lattice,” Computers, Materials & Continua, vol. 63, no. 2, pp. 845–859, 2020. [Google Scholar]

12. P. W. Shor, “Algorithms for quantum computation: Discrete logarithms and factoring,” in 35th Annual Symp. on the Foundations of Computer Science, IEEE Computer Society Press, Los Alamitos, CA, USA, pp. 124–134, 1994. [Google Scholar]

13. C. Li, G. Xu, Y. Chen, H. Ahmad and J. Li, “A new anti-quantum proxy blind signature for blockchain-enabled internet of things,” Computers, Materials & Continua, vol. 61, no. 2, pp. 711–726, 2019. [Google Scholar]

14. J. L. Hevia, G. Peterssen, C. Ebert and M. Piattini, “Quantum computing,” IEEE Software, vol. 38, no. 5, pp. 7–15, 2021. [Google Scholar]

15. D. J. Bernstein and T. Lange, “Post-quantum cryptography,” Nature, vol. 549, no. 7671, pp. 188–194, 2017. [Google Scholar] [PubMed]

16. J. D. Dalton, “Heuristically secure threshold lattice-based cryptography schemes,” Master’s thesis, James Madison University, USA, 2021. [Google Scholar]

17. K. Yu, L. Tan, C. Yang, K. R. Choo, A. K. Bashir et al., “A blockchain-based shamir’s threshold cryptography scheme for data protection in industrial internet of things settings,” IEEE Internet of Things Journal, vol. 9, no. 11, pp. 8154–8167, 2022. [Google Scholar]

18. C. Feng, B. Liu, Z. Guo, K. Yu, Z. Qin et al., “Blockchain-based cross-domain authentication for intelligent 5G-enabled internet of drones,” IEEE Internet of Things Journal, vol. 9, no. 8, pp. 6224–6238, 2021. [Google Scholar]

19. L. Li, J. Liu, L. Cheng, S. Qiu and W. Wang et al., “CreditCoin: A privacy-preserving blockchain-based incentive announcement network for communications of smart vehicles,” IEEE Transactions on Intelligent Transportation Systems, vol. 19, no. 7, pp. 2204–2220, 2018. [Google Scholar]

20. W. Tian, J. Chai and Y. Xu, “(M, N) threshold multi-signature scheme based on ECC over finite field GF (q),” in the 2022 Int. Conf. on Blockchain Technology and Information Security, Huaihua City, Hunan, China, pp. 255–260, 2022. [Google Scholar]

21. Q. Lyu, H. Li, Z. Deng, X. Zhang, Y. Qi et al., “JRS: A joint regulating scheme for secretly shared content based on blockchain,” IEEE Transactions on Network and Service Management, vol. 19, no. 3, pp. 2957–2971, 2022. [Google Scholar]

22. A. K. Biswas, M. Dasgupta, S. Ray and M. K. Khan, “A probable cheating-free (t, n) threshold secret sharing scheme with enhanced blockchain,” Computers and Electrical Engineering, vol. 100, pp. 107925, 2022. [Google Scholar]

23. S. Fan and Y. Chen, “Editable blockchain scheme based on shamir chameleon hash secret sharing,” in 2022 IEEE 6th Information Technology and Mechatronics Engineering Conf., Chongqing, China, pp. 1125–1128, 2022. [Google Scholar]

24. X. Zhang, C. Xu, H. Wang, Y. Zhang and S. Wang, “FS-PEKS: Lattice-based forward secure public-key encryption with keyword search for cloud-assisted industrial internet of things,” IEEE Transactions on Dependable and Secure Computing, vol. 18, no. 3, pp. 1019–1032, 2021. [Google Scholar]

25. V. Clupek, L. Malina and V. Zeman, “Secure digital archiving in post-quantum era,” in 38th Int. Conf. on Telecommunications and Signal Processing, Prague, Czech Republic, pp. 622–626, 2015. [Google Scholar]

26. J. D. Preece and J. M. Easton, “Towards encrypting industrial data on public distributed networks,” in 2018 IEEE Int. Conf. on Big Data, Seattle, WA, USA, pp. 4540–4544, 2018. [Google Scholar]

27. W. Yin, Q. Wen, W. Li, H. Zhang and Z. Jin, “An anti-quantum transaction authentication approach in blockchain,” IEEE Access, vol. 6, pp. 5393–5401, 2018. [Google Scholar]

28. C. Li, Y. Tian, X. Chen and J. Li, “An efficient anti-quantum lattice-based blind signature for blockchain-enabled systems,” Information Sciences, vol. 546, pp. 253–264, 2021. [Google Scholar]

29. A. Holcomb, G. Pereira, B. Das and M. Mosca, “PQFabric: A permissioned blockchain secure from both classical and quantum attacks,” in 2021 IEEE Int. Conf. on Blockchain and Cryptocurrency, Sydney, Australia, pp. 1–9, 2021. [Google Scholar]

30. C. Li, X. Chen, Y. Chen, Y. Hou and J. Li, “A new lattice-based signature scheme in post-quantum blockchain network,” IEEE Access, vol. 7, pp. 2026–2033, 2018. [Google Scholar]

31. K. Chalkias, J. Brown, M. Hearn, T. Lillehagen, I. Nino et al., “Blockchained post-quantum signatures,” in IEEE Int. Conf. on Internet of Things, IEEE Green Computing and Communications, IEEE Cyber, Physical and Social Computing, IEEE Smart Data, Halifax, Nova Scotia, Canada, pp. 1196–1203, 2018. [Google Scholar]

32. E. O. Kiktenko, N. O. Pozhar, M. N. Anufriev, A. S. Trushechkin, R. R. Yunusov et al., “Quantum-secured blockchain,” Quantum Science and Technology, vol. 3, no. 3, pp. 035004, 2017. [Google Scholar]

33. H. Yi, “Secure social Internet of Things based on post-quantum blockchain,” IEEE Transactions on Network Science and Engineering, vol. 9, no. 3, pp. 950–957, 2022. [Google Scholar]

34. C. Li, M. Dong, J. Li, G. Xu, X. Chen et al., “Efficient medical big data management with keyword-searchable encryption in healthchain,” IEEE Systems Journal, vol. 16, no. 4, pp. 5521–5532, 2022. [Google Scholar]

35. Y. Gao, X. Chen, G. Xu, K. Yuan, W. Liu et al., “A novel quantum blockchain scheme base on quantum entanglement and DPoS,” Quantum Information Processing, vol. 19, no. 12, pp. 1–15, 2020. [Google Scholar]

36. R. Saha, G. Kumar, T. Devgun, W. J. Buchanan, R. Thomas et al., “A blockchain framework in post-quantum decentralization,” IEEE Transactions on Services Computing, vol. 16, no. 1, pp. 1–12, 2023. [Google Scholar]

37. D. Boneh, R. Gennaro, S. Goldfeder, A. Jain, S. Kim et al., “Threshold cryptosystems from threshold fully homomorphic encryption,” in 38th Annual Int. Cryptology Conf., Santa Barbara, CA, USA, pp. 565–596, 2018. [Google Scholar]

38. The Sage Developers. SageMath, the Sage Mathematics Software System (Version 9.6.0). 2022. https://www.sagemath.org [Google Scholar]

39. The ChainMaker Developers. ChainMaker. 2022. https://docs.chainmaker.org.cn/index.html [Google Scholar]

40. D. Cabarcas, P. Weiden and J. Buchmann, “On the efficiency of provably secure NTRU,” in 6th Int. Workshop on Post-Quantum Cryptography, Waterloo, ON, Canada, pp. 22–39, 2014. [Google Scholar]

41. R. Avanzi, J. Bos, L. Ducas, E. Kiltz, T. Lepoint et al., “CRYSTALS-Kyber algorithm specifications and supporting documentation,” NIST PQC Round, vol. 2, no. 4, pp. 1–43, 2019. [Google Scholar]

42. J. F. Almansa, I. Damgård and J. B. Nielsen, “Simplified threshold RSA with adaptive and proactive security,” in 24th Annual Int. Conf. on the Theory and Applications of Cryptographic Techniques, St. Petersburg, Russia, pp. 593–611, 2006. [Google Scholar]