Generation of Low-Delay and High-Stability Multicast Tree

1  Introduction

Multicast can achieve efficient data transmission for group receivers [1,2], which is widely used in various types of networks, such as the Internet [3,4], overlay networks [5], data center networks (DCNs) [6–8], and Internet-of-Things (IoT) [9–11]. Most related work constructs multicast trees to reduce transmission delay or improve multicast stability [12]. However, few works study the generation of multicast trees with low delay and high stability at the same time [13], which is a crucial challenge to be addressed in future multicast deployment.

Given a general network structure, it is a non-deterministic polynomial-hard (NP-hard) problem to construct a multicast tree with minimum delay as in [14,15]. Similarly, the construction of a multicast tree with maximum stability is also an NP-hard problem, which can be proven through the reducible principle in a polynomial time [16,17]. Without an enumeration algorithm, there is no precise solution to the minimum delay and maximum stability challenges. However, the enumeration algorithm suffers from excessive complexity, which hardly meets the practical application requirements.

To construct a high-performance multicast tree, this paper focuses on the generation of a low-delay and high-stability tree under the model of spanning tree based on stability probability, degree-constrained and edge-weighted for multicast (T-SDE) [13]. T-SDE presents a realistic multicast scenario and provides a class of algorithms on the contribution of links (CL). However, the CL algorithm fails to take advantage of degree constraint and connectivity of terminals in networks, which could not make full use of the maximum forwarding performance in the construction of a multicast tree.

This paper proposes a class of low-delay and high-stability generation algorithms of the multicast tree, which can take advantage of the degree and connectivity of a terminal. Firstly, this paper defines the ratio of fan-out to delay (RFD) of a candidate terminal to replace the contribution of link in [13], which takes out-degree constraint and interconnection characteristics of a candidate into consideration. The generation algorithms construct a multicast tree by greedy inserting a terminal with a larger RFD and higher stability probability into a multicast tree as the forwarding node, where the algorithm adjusts the weight of delay and stability by a factor k. The proposed algorithms can be deployed in various scenarios, where they can transform into each other by adjusting the impact factor k. Under different networks, this paper carries out experiments to evaluate the performance of the generation algorithms of the multicast tree. The experimental results show that our algorithm based on RFD embraces a smaller height, higher stability, and a lower transmission delay than the CL algorithm. The result indicates that RFD can make full use of the connectivity of a candidate in the construction of multicast trees, which is compatible with stability and can seamlessly substitute CL in T-SDE.

The main difference between this paper and other related work lies in the following two parts. Firstly, both the stability and delay of the multicast tree are considered in this paper. Secondly, this paper considers the change in node connectivity during the generation of a multicast tree. This paper makes three contributions as follows. First, the ratio of fan-out RFD was defined to measure the contribution of a forwarding terminal, which can take advantage of the available degree in tree construction. Second, a class of generation algorithms was proposed on RFD and the probability of stability, which provides a low delay and high stability. Finally, a detailed evaluation was conducted including comparisons with different parameters of other algorithms. In addition, the proposed algorithm on RFD can be deployed in different scenarios by adjusting the impact factor k.

The rest of this paper is organized as follows. Sections 2 and 3 present the related work of multicast and the background of this paper. Section 3 proposes the RFD based algorithms. Section 4 presents the comparative experiments. Section 5 concludes this paper.

2  Related Work

IP multicast is the first proposed mechanism that implements the function of data replication and forwarding at the network layer of Internet [1]. The possibility was [18] explored for the crowdsourced service-less video multicast in the fifth-generation (5G) radio access network (RAN), which proposes a viable solution using network function virtualization and mobile edge computing. To improve vehicle-to-vehicle collaboration in the network layer, a novel multicast protocol [19] was proposed which was specifically designed for streaming service over vehicular networks. Due to high mobility and rapid topology changes, a novel distributed tree-based multicast routing algorithm was proposed [20], which takes link failure into account. For the first time, the multicast delay was explored under a general cooperative multicast scheme [21], which proposed a two-hop relay multicast algorithm.

The key idea of the application layer multicast is to implement the function of data forwarding by terminals at the application layer among group users [6], which does not require exceptional support from routers. This multicast model does not need to change the existing network infrastructure, while the forwarding terminals bring the problem of stability and delay of the resulting multicast tree. It is a key challenge to create a low-delay and high-stability tree, which severely affects the multicast performance in overlay network multicast [12,13,16].

Multicast in data center networks focuses on the generation of the multicast tree, route management, and dynamic migration of group members. Shahbaz et al. [22] takes advantage of programmable switches and features of data center networks to improve the scalability in multi-tenant multicast. With limited storage space in a switch, [23] introduces a multi-class Bloom Filter, which supports a large amount of multicast group information. To save multicast forwarding entries in switches, a novel multicast membership management scheme was designed [24] for data center networks, which leverages the characteristics of multicast applications and software-defined networking techniques. To address scalable and load-balancing challenges, a scalable load-balanced multicast source routing was proposed for large-scale data centers [25], which can achieve a better multicast load balance than other existing schemes. Both service function chain and end-to-end delay requirements in a mobile edge cloud, [26] devised an approximation algorithm and an efficient heuristic. To deal with a huge increment of multicast flows, a preemptive scheduling approach was presented to reduce flow transmission time [27].

3  Background

This section introduces the background of our work, including the T-SDE model, stability metric and transmission delay in multicast tree construction.

3.1 T-SDE Model

T-SDE [13] comprehensively considers the factors that affect the multicast quality, which is built on the abstraction of the overlay network. In the construction of a multicast tree, the T-SDE model can reflect the characteristics of the network, which focuses on stability probability, constrained degree, and weighted edge. The T-SDE model was defined as follows [13]:

Given an undirected and connected graph G(V,E) [13]. Each node vi∈V has a probability of stability pi=p(vi)∈(0,1], and a degree constraint di=dmax(vi)∈R+. For each edge (vi,vj)∈E, eij=e(vi,vj)∈R+ denotes the transmission delay between vi and vj. The objective is to construct a multicast tree T(V,E′), which satisfies the out-degree constraint and stability requirement.

3.2 Stability Metric

The transmission interruption of a reception terminal vi is caused by the departure of itself or its ancestor. Let n denote the number of group users, stability of multicast in a period time D is calculated by the following expression [13]:

S=1−ΔT¯D+∑i=0m(pi∏j∈PVipj)∑i=0mpi⋅ΔT¯D(1)

In the above expression (1), PVi denotes the set of terminals from root v0 to vi, and ΔT¯ denotes the average interruption time.

To measure the impact of stability probability on multicast accurately without other factors, a stability degree probability factor (SDPF) is calculated by the following expression [13]:

SDPF=∑i=0n(pi∏j∈PVipj)/∑i=0npi(2)

SDPF is purely relevant to the stability probability, which is a decisive factor of multicast stability with given D and ΔT¯. SDPF is calculated from the probability of stability pi of each vi based on the morphological characteristics of the generation tree, which reflects the stability of different morphological multicast trees with the same premise [13].

3.3 Transmission Delay

The reception delay of vi is related to its position in the multicast tree, which is an accumulative delay from root v0 to vi. Without interruption, the reception delay of vi is calculated by ti=∑j∈PEiej , and it is ti=∑j∈PEiej+Δti with interrupted, where PEi denotes the transmission path from the root v0 to node vi in multicast, and Δti is the interrupted delay of vi [13]. The construction algorithm does not consider interruption, which belongs to the morphology adjustment of multicast.

The multicast tree is constructed on the contribution link (CL) and the probability of stability pi, which reflects the degree of link contribution of the forwarding terminals to the multicast tree [13]. However, these three algorithms [13] fail to consider the changes in interconnection, which hardly takes advantage of network connectivity in the process of tree construction.

4  The Proposed Algorithm

This section first analyzes the contribution of a forwarding terminal in multicast tree construction, then presents the algorithm and analysis of our generation method.

4.1 Contribution of Forwarding Terminal

Based on the above research analysis, this paper first defines the contribution of forwarding terminals. For the sake of description, this paper first presents a few symbols as shown in Table 1.

T-SDE deploys CL to measure the contribution of a candidate terminal, which is defined by the following expression:

CL(vi)=di/∑j∈PEiej.(3)

This definition considers out-degree constraint di and transmission delay ∑j∈PEiej, which fails to take the change in connectivity into account in the process of construction.

From the construction of a multicast tree, we learn that only the edge and terminal interconnected with the current terminal vi may join the tree via vi. Therefore, this paper defines the ratio of fan-out to delay (RFD) of vi as the following expression:

RFD(vi)=min(di′,di)/∑j∈PEiej(4)

In the above expression (4), di is the maximum out-degree constraint of vi, and di' is the number of neighbors of vi in the left network at the current stage. The RFD takes the dynamical connectivity of vi into consideration, which can reflect the contribution of vi factually.

In multicast tree construction, the measurement SDPF is positively correlated with pi. In terms of stability, the impact of a forwarding terminal mainly comes from pi, which affects both itself and the downstream receivers. Terminal vi with a higher pi in the upstream will influence more receivers, which provides a stable forwarding source for more nodes. A terminal vi with a small pi placed downstream will reduce its influence on receivers, so that its instability only affects a few nodes.

4.2 Construction Algorithm

To facilitate description, this article defines some symbols in the process of tree generation. Let an undirected and connected graph G(V,E) denote the network, and T(V,E′) denote target tree with E'⊆  E. Let v0∈V denote source of multicast data, and T=(∅,∅) in initial stage. The generation process of the multicast tree is to create T(V,E′) from graph G(V,E), which inserts each vertex and the associated edge of G(V,E) into the current tree.

In the construction of a multicast tree, vertices in T are referred to as VT, and the left vertices are referred to as VT¯ with VT¯=V−VT. Let ai denote the available degree of vi, where vi can accommodate children vertex when ai>0. Let AE denote edges eij=e(vi,vj) between vi∈VT¯ and vj∈VT, which is referred to as the alternative edge. Let DAE denote alternative edge AE with ai>0 for vi∈VT, where the current out degree of vi is less than di. For any eij=e(vi,vj)∈DAE with vi∈VT¯ and vj∈VT, the set of vi is referred to as the set of degree-free alternative vertices (DAV).

The construction algorithm selects vertice from DAV and the corresponding edge from DAE to insert into the current tree. Based on RFD and pi of vi, a class of low-delay and high-stability algorithms were proposed to solve the T-SDE problem approximatively. Firstly, this paper presents an algorithm on the RFD purely, as shown in Algorithm 1.

Algorithm 1 is built on RFD purely, which is referred to as the D algorithm. Similarly, this paper gives an algorithm on the probability of stability pi, where vi with the largest pi is sequentially selected to insert the tree. It is easy to get the algorithm by replacing the selection criterion in lines 10–11 of D algorithm with the largest pi. This paper refers to it as S algorithm, the detail of which is omitted to avoid repetition.

To take advantage of the RFD and pi, this paper presents the kDS algorithm, which comprehensively selects candidates to insert into T. The kDS algorithm is shown in Algorithm 2.

Algorithm kDS selects vertices with the k-largest RFD to create kRV, then selects vi with the largest pi∈kRV to insert into the current tree T. Similarly, this paper defines kSD algorithm as that in kDS algorithm. In the kSD algorithm, lines 9–14 first select kPV of which vi has the k-largest pi, and then select vi with the largest RFD from kPV to insert the current tree. This algorithm is the kSD algorithm, where details are not repeated.

These algorithms take advantage of the connectivity and stability of each vertex to construct a high-performance tree, which fully considers the change in network connectivity.

4.3 Analysis of the Construction Algorithm

Based on RFD and pi, the algorithms give an approximate solution based on a greedy strategy. The D and S algorithm are basal, which is built on one measurement. Both the kDS and kSD algorithms contains a variable k as a conditioning factor, which is determined by the efficiency of tree generation and connectivity of the network. With a large k, the kDS algorithm prefers to select a vertex with a greater pi as a forwarding terminal, and the kSD algorithm prefers to select a vertex with a larger RFD to forward data. When k=|DAV|, the kDS degenerates into S algorithm and the kSD degenerates into D algorithm. For a small k, the kDS algorithm prefers to select a vertex with a larger RFD as a forwarding terminal, and kSD prefers a vertex with a greater pi. When k=1, kDS degenerates into D algorithm, and kSD degenerates into S algorithm. By conditioning factor k, kDS and kSD can adjust the weight of delay and stability in multicast, which is applicable in various scenarios.

Both the D and S algorithms hold a time complexity of O(n2), and it is O(n3) in kDS and kSD algorithm. In a network, a terminal host can generate the multicast tree in a polynomial time.

5  Simulation Experiment

This section presents the comparison of various multicast trees in terms of stability and delay.

5.1 Experimental Settings

We carry out simulation experiments on Matlab R2016b to measure the performance of the proposed algorithm. Given an average number of neighbors, experiments are conducted in various networks to measure the properties of the multicast tree. This paper deploys the same experimental settings as [13]. Each vertex has 10 neighbors on average. For each vi, let pi∈[0.5,1] and di∈[2,5]. Let p0=1 for the root v0 which keeps away from interruption during multicast, and d0=5 for the root v0. For unicast delay between vi and vj, let eij∈[10ms,50ms]. This paper defaults k=2 in the algorithm of CL−S, kDS, and kSD. Let kDS−5 and kSD−5 denote the algorithm kDS and kSD with k=5, respectively. This paper observes the transmission delay, the stability degree probability factor (SDPF), and the height of the resulting multicast tree in various algorithms. Each result is an average on 100 different networks with the same setting.

5.2 Experimental Results

We describe the experimental result in this section. Fig. 1 shows that with the increment of network scale, where the resulting tree of the algorithm D and kDS on the RFD can obtain a smaller average transmission delay than that of CL and CL−S on CL. The average transmission delay of the multicast tree in CL is larger than that of D algorithm by about 1%, and the average delay in CL−S is larger than that of kDS by about 0.5%.

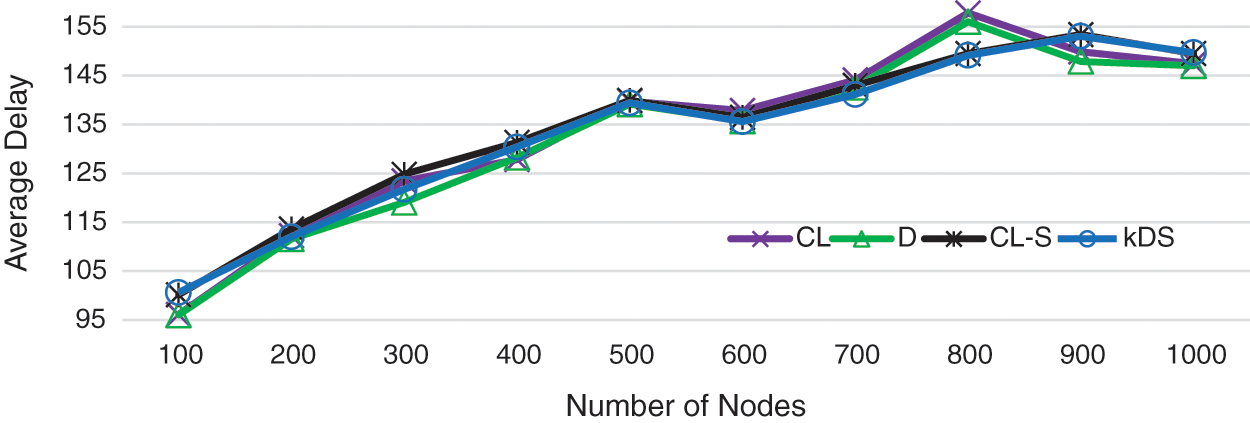
Figure 1: The average delay of multicast on the network scale

Fig. 2 shows the relationship of the maximum delay on the network scale. As we can see, with the increment of network scale, both algorithms D and kDS can obtain a smaller maximum delay than that of algorithm CL and CL−S. The maximum delay in algorithm CL is larger than that of algorithm D by about 8.9%, and the maximum delay in algorithm CL−S is larger than that of algorithm kDS by about 11.4%.

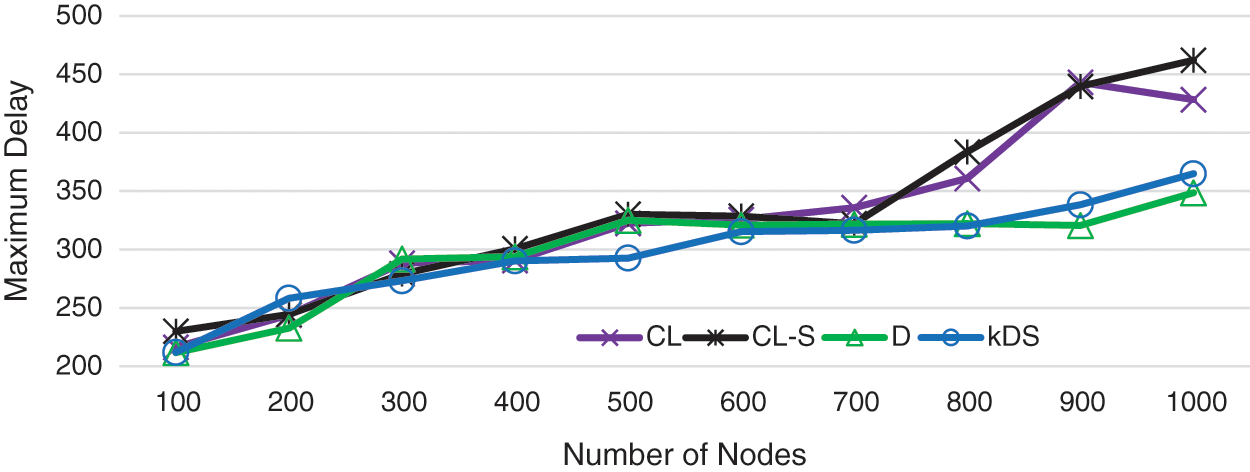
Figure 2: The maximum delay of multicast on the network scale

Fig. 3 shows that the height of the multicast tree gradually increases with the increment of the network scale. The resulting tree in algorithm CL and D shares a similar height. The height of the resulting tree in algorithm kDS is lower than that of CL−S by about 11.8% with k=2, and it is about 8.5% lower in algorithm kDS than that of CL−S with k=5.

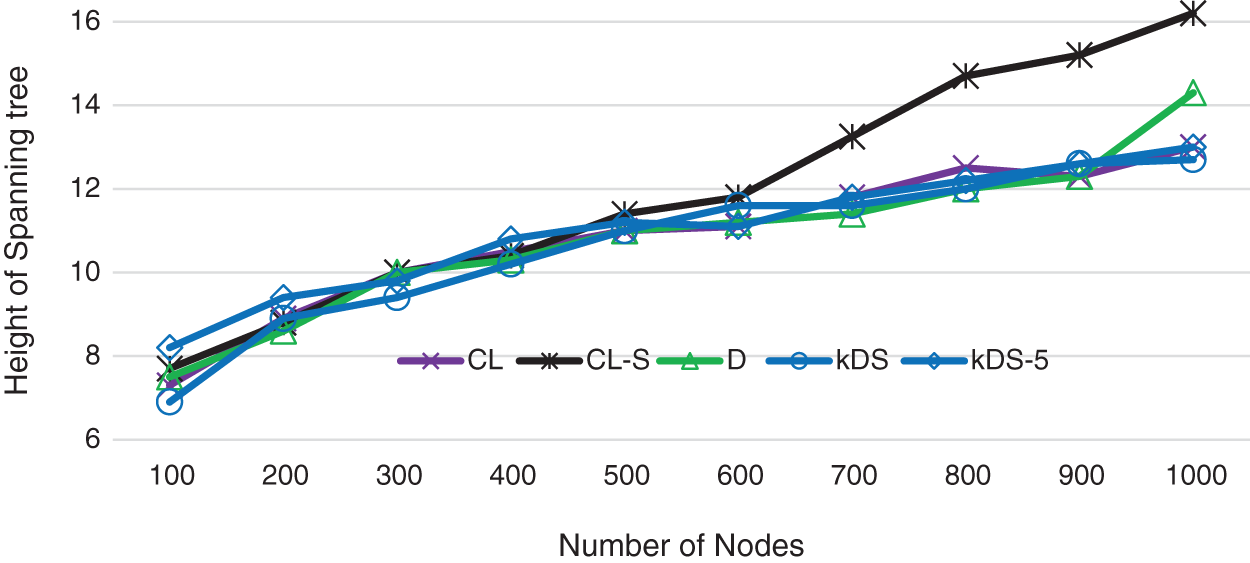
Figure 3: The height of the spanning tree on the network scale

Fig. 4 shows the relationship between the stability of multicast and network scale. We can see that algorithm S and kSD have the greatest stability where their SDPF is about 86% greater than that of algorithm D. Algorithm D shares the similar SDPF with algorithm CL, and kDS and CL−S have similar SDPF which is slightly larger than that of algorithm D and CL. The SDPF in kDS−5 is 9.3% higher than that of kDS and 9.6% higher than that of CL−S.

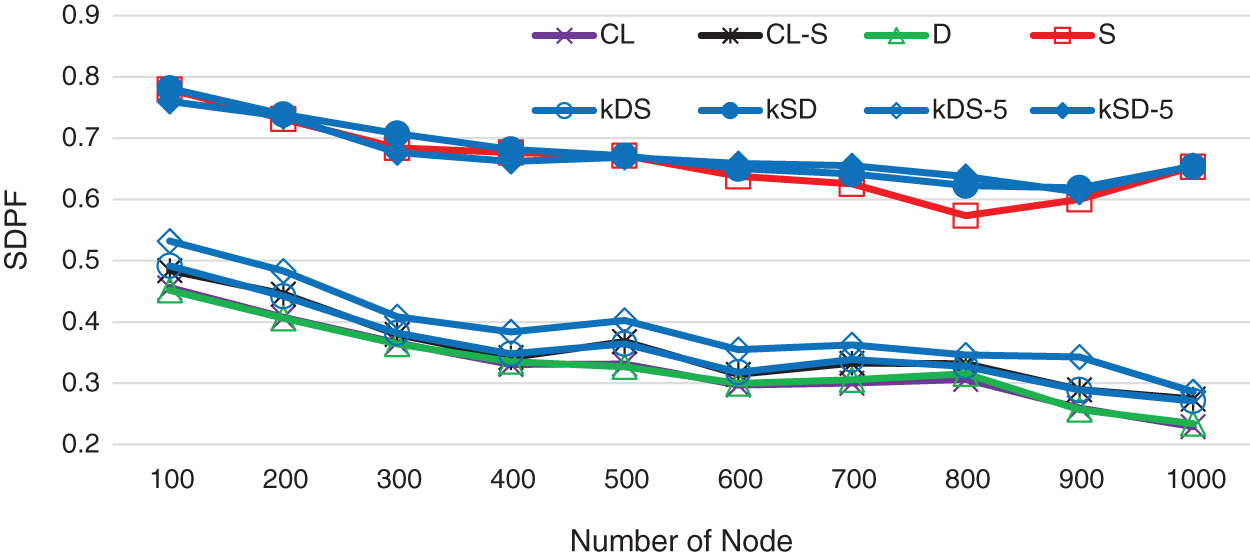
Figure 4: The SDPF on the network scale

5.3 Experimental Analysis

Experimental results show that the average delay of the multicast tree in algorithm D is lower than that of algorithm CL, and algorithm D enjoys an obvious advantage over CL in the maximum delay. During the construction of a multicast tree on greedy strategy, the ratio of fan-out to delay (RFD) can better reflect the contribution of nodes than CL. A large k brings algorithm kDS and kSD a great choice, which results in a short height and high stability of the multicast tree. In consideration of the transmission delay and stability of multicast comprehensively, the weight of stability and delay can be adjusted by changing the parameter k to improve the multicast quality. The result indicates that RFD can take full advantage of network connectivity to construct a multicast tree with a small transmission delay, and the proposed RFD is well compatible with the probability of stability and can seamlessly substitute CL in the T-SDE model.

6  Conclusion

Algorithms in the T-SDE model hardly reflect the change in network connectivity in multicast tree generation. This paper studied the construction algorithm of a low-delay and high-stability multicast tree in the T-SDE model, and algorithms based on RFD and probability of stability were proposed. The RFD proposed in this paper can reflect the changes of network connectivity during the generation of a multicast tree, which create a high-performance multicast tree. Comparative experiments show that the proposed algorithms based on RFD and probability of stability can construct a low-delay and high-stability multicast tree. For example, the average transmission delay of the multicast tree in CL algorithm is larger than that of D algorithm by about 1%, and the SDPF in kDS−5 algorithm is 9.6% higher than that of CL−S algorithm. In future research, we will continue to improve the efficiency and performance of multicast [28–30] to achieve the minimum delay and the maximal stability.

Funding Statement:: This work was supported by the Hainan Provincial Natural Science Foundation of China (620RC560, 2019RC096, 620RC562), the Scientific Research Setup Fund of Hainan University (KYQD(ZR)1877), the National Natural Science Foundation of China (62162021, 61802092, 82160345, 61862020), the key research and development program of Hainan province (ZDYF2020199, ZDYF2021GXJS017), and the key science and technology plan project of Haikou (2011-016).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. S. Deering, “Multicast routing in internetworks and extended LANs,” ACM Transactions on Computer System, vol. 8, no. 2, pp. 85–110, 1990. [Google Scholar]

2. Y. Dong, L. Song, R. Xie and W. Zhang, “ltra-low latency, stable, and scalable video transmission for free-viewpoint video services,” IEEE Transactions on Broadcasting, vol. 68, no. 3, pp. 636–650, 2022. [Google Scholar]

3. W. Wu, J. Liu and T. Huang, “The source-multicast: A sender-initiated multicast member management mechanism in SRv6 networks,” Journal of Network and Computer Applications, vol. 153, no. 3, pp. 102505, 2020. [Google Scholar]

4. Q. Liu, H. Ren, R. Tang and J. Yao, “Optimizing co-existing multicast routing trees in IP network via discrete artificial fish school algorithm,” Knowledge Based Systems, vol. 191, no. 3, pp. 105276, 2019. [Google Scholar]

5. Y. Chu, S. Rao and H. Zhang, “A case for end system multicast,” IEEE Journal on Selected Areas in Communications, vol. 20, no. 8, pp. 1456–1471, 2002. [Google Scholar]

6. M. Shahbaz, L. Suresh, J. Rexford, N. Feamster, O. Rottenstreich et al., “Elmo: Source routed multicast for public clouds,” IEEE/ACM Transactions on Networking, vol. 28, no. 6, pp. 2587–2600, 2020. [Google Scholar]

7. D. Li, H. Cui, Y. Hu, Y. Xia and X. Wang, “Scalable data center multicast using multi-class Bloom Filter,” in Proc. 2011 19th IEEE Int. Conf. on Network Protocols, Vancouver, BC, Canada, pp. 266–275, 2011. [Google Scholar]

8. K. Ambika and M. B. Moses, “Tar-aft: A framework to secure shared cloud data with group management,” Intelligent Automation & Soft Computing, vol. 31, no. 3, pp. 1809–1823, 2022. [Google Scholar]

9. E. Garro, M. Fuentes, J. Carcel, H. Chen D. Mi et al., “5G mixed mode: NR multicast-broadcast services,” IEEE Transactions on Broadcasting, vol. 66, no. 2, pp. 390–403, 2020. [Google Scholar]

10. J. Almutairi and M. Aldossary, “Exploring and modelling IoT offloading policies in edge cloud environments,” Computer Systems Science and Engineering, vol. 41, no. 2, pp. 611–624, 2022. [Google Scholar]

11. K. Imran, N. Anjum, S. Mahfooz, M. Zubair, Z. Yang et al., “Cluster-based group mobility support for smart IoT,” Computers, Materials & Continua, vol. 68, no. 2, pp. 2329–2347, 2021. [Google Scholar]

12. J. Su, J. Cao and B. Zhang, “A survey of the research on ALM stability enhancement,” Chinese Journal of Computers, vol. 32, no. 3, pp. 576–590, 2009. [Google Scholar]

13. L. Huo, D. Li and Y. Tan, “Algorithms of spanning tree based on the stability probability and contribution link of nodes for ALM,” Journal of Computer Research and Development, vol. 49, no. 12, pp. 2559–2567, 2012. [Google Scholar]

14. E. Brosh, A. Levin and Y. Shavitt, “Approximation and heuristic algorithms for minimum-delay application-layer multicast trees,” IEEE/ACM Transactions on Networking, vol. 15, no. 2, pp. 473–484, 2007. [Google Scholar]

15. S. Shi and JS. Turner, “Multicast routing and bandwidth dimensioning in overlay networks,” IEEE Journal on Selected Areas in Communications, vol. 20, no. 8, pp. 1444–1455, 2002. [Google Scholar]

16. V. Roca and A. El-Sayed, “A host-based multicast (HBM) Solution for group communications,” in Proc. of the 1st Int. Conf. on Networking, Colmar, France, pp. 610–619, 2001. [Google Scholar]

17. G. Tan and S. A. Jarvis, “Improving the fault resilience of overlay multicast for media streaming,” IEEE Transactions on Parallel and Distributed Systems, vol. 18, no. 6, pp. 721–734, 2007. [Google Scholar]

18. K. Zahoor, K. Bilal, A. Erbad and A. Mohamed, “Service-less video multicast in 5G: Enablers and challenges,” IEEE Network, vol. 34, no. 3, pp. 270–276, 2020. [Google Scholar]

19. D. R. Chowdhury, S. Nandi and D. Goswami, “Video streaming over IoV using IP multicast,” Journal of Network and Computer Applications, vol. 197, no. 3, pp. 103259, 2022. [Google Scholar]

20. S. Babu and A. R. K. Parthiban, “DTMR: An adaptive distributed tree-based multicast routing protocol for vehicular networks,” Computer Standards & Interfaces, vol. 79, no. 2, pp. 103551, 2022. [Google Scholar]

21. B. Yang, Z. Wu, Y. Shen and S. Shen, “On delay performance study for cooperative multicast MANETs,” Ad Hoc Networks, vol. 102, no. 4, pp. 102117, 2020. [Google Scholar]

22. M. Shahbaz, L. Suresh, J. Rexford, N. Feamster, O. Rottenstreich et al., “Elmo: Source routed multicast for public clouds,” IEEE/ACM Transactions on Networking, vol. 28, no. 6, pp. 2587–2600, 2020. [Google Scholar]

23. D. Li, H. Cui, Y. Hu, Y. Xia and X. Wang, “Scalable data center multicast using multi-class bloom filter,” in Proc. of the 19th IEEE Int. Conf. on Network Protocols, Vancouver, BC, Canada, pp. 266–275, 2011. [Google Scholar]

24. Y. Cheng, D. Li, J. Zhu, H. Liu, K. Chen et al., “Managing multicast membership for software defined data center network,” in Proc. of the IEEE 92nd Vehicular Technology Conf. (VTC2020-Fall), Victoria, Canada, pp. 1–5, 2020. [Google Scholar]

25. J. Alqahtani, B. Hamdaoui and R. Langar, “Ernie: Scalable load-balanced multicast source routing for cloud data centers,” IEEE Access, vol. 9, pp. 168816–168830, 2021. [Google Scholar]

26. H. Ren, Z. Xu, W. Liang, Q. Xia, P. Zhou et al., “Efficient algorithms for delay-aware NFV-enabled multicasting in mobile edge clouds with resource sharing,” IEEE Transactions on Parallel and Distributed Systems, vol. 31, no. 9, pp. 2050–2066, 2020. [Google Scholar]

27. L. Luo, K. Foerster, S. Schmid and H. Yu, “Optimizing multicast flows in high-bandwidth reconfigurable datacenter networks,” Journal of Network and Computer Applications, vol. 203, no. 4, pp. 103399, 2022. [Google Scholar]

28. H. Zhang, X. Shi, X. Yin, Z. Wang, H. Geng et al., “DA&FD-deadline-aware and flow duration-based rate control for mixed flows in DCNs,” IEEE/ACM Transactions on Networking, vol. 27, no. 6, pp. 2458–2471, 2019. [Google Scholar]

29. M. Beshley, N. Kryvinska, H. Beshley, M. Medvetskyi L. Barolli et al., “Centralized qos routing model for delay/loss sensitive flows at the sdn-IoT infrastructure,” Computers, Materials & Continua, vol. 69, no. 3, pp. 3727–3748, 2021. [Google Scholar]

30. A. Latif, R. Parameswaran, S. Vishwarupe, A. Khreishah, Y. Jararweh et al., “MediaFlow: Multicast routing and in-network monitoring for professional media production,” IEEE Transactions on Network and Service Management, vol. 19, no. 2, pp. 1862–1875, 2022. [Google Scholar]