A New Multi Chaos-Based Compression Sensing Image Encryption

1  Introduction

Nowadays, the Internet offers a simple and low-cost means of transmitting and receiving real-time information. Threats to digital information technology have increased over the past decade because of the Internet’s heterogeneity. Security is a crucial issue in the communication process to secure multimedia content from unauthorized copying, usage, and alteration. Many encryption techniques have been created by specialists and scholars to give security and protection to multimedia materials. Because the fundamental properties of digital images differ from those of text, academics are proposing new approaches in place of established cryptographic procedures. The majority of proposed methods are pixel permutation-based and hence inadequately guard against well-known cryptographic attacks [1,2]. A tight association between chaos and encryption has been investigated in recent years. Chaotic systems differ from conventional algorithms in terms of sensitivity to beginning circumstances, non-periodicity, non-convergence, and pseudo-randomness [3]. As a result of these characteristics, chaotic systems may readily be utilized to develop image encryption approaches that surpass existing algorithms [4]. Typically, the chaos-based encryption method for images involves two crucial stages: chaotic pixel shuffling for confusion and chaotic pixel value changes for dispersion [5].

Matthew presented the first efficient chaos-based cryptographic encryption technique in 1989 [6]. Fridrich [7] utilized a two-dimensional baker map to encrypt and randomize a N × N image. The researcher emphasized the connection between discretized chaos and cryptography. To improve the encryption speed and enhance the security level, Mao et al. [8] extended the 2D baker map into a 3D chaotic map. According to researchers, the 3D map can achieve 2–3 times quicker processing than a two-dimensional map. Mazloom et al. [9] presented a unique technique of Connected Nonlinear Chaotic Map (CNCM) to solve the disadvantages of chaotic one-dimensional maps. The proposed technique is considered to be more advanced and secure, mainly due to the coupling nature of the Chaotic Neuron Cellular Network (CNCM) and the utilization of a 240-bit secret key. Authors in paper [10] utilized 2 chaotic maps for encrypting images. Zhang et al. [11] broke the algorithm proposed in [10] due to the shortcomings of the permutation approach, which cannot break the bit planes. Researchers enhanced the original image encryption scheme’s overall security. In the encryption approach proposed by Seyedzadeh et al. [12], a 2D piecewise nonlinear chaotic map is linked to obtain improved values for a range of security parameters, such as entropy, Number of Pixel Change Rate (NPCR), and Unified Average Changing Intensity (UACI). To alleviate the shortcomings of the logistic map, various writers developed spatiotemporal chaotic maps for image encryption [13,14]. The technique presented in these papers may be widely implemented in various image encryption systems to improve security. Wang et al. [15] presented the concept of block encryption as a result of dynamic patterns generated by a large number of chaotic maps. The final ciphertext is constructed by employing random sequences, shifting operations, and Exclusive-OR as well as a few rounds. The approach is used to minimize the correlation of the R, G, and B components of a color image. Wang et al. [16] developed a novel technique to address the shortcomings of a Cat Map. Despite the various image encryption techniques that have been developed, many researchers still strive to enhance security while achieving faster processing times. To our understanding, no approach has been reported to date that addresses both encryption and noise resistance simultaneously. The problem statement highlights the challenge of dealing with the noisy effects and compression during the encryption process.

Problem statement is discussed with the help of example. This article addresses two critical issues: the effects of noise and compression. Fig. 1a displays the original Cameraman image, while Figs. 1b to 1d show the distorted images for different signal-to-noise ratio (SNR) values. It can be seen clearly in Fig. 1 that image quality diminishes with decreasing SNR. The primary concern is whether it is possible to recover the original plaintext image if a encoded image is distorted by channel noise. Encrypting the Cameraman image and transporting it via an AWGN channel with SNR values varying from 30 to 10 is the best way to demonstrate these effects. It is clear from Fig. 2 that accurate decryption is impossible. It is because only 16 bytes or 44 blocks are used by the 128-bit advanced encryption standard (AES) algorithm at one time. If a single pixel value in a 44-block encrypted AES image is altered by one bit, the entire 44-block cannot be properly decoded. As a result, if the pixel values change during transmission, AES cannot decrypt the original image. One should examine whether the original unencrypted image can still be retrieved after compressing an encrypted image. It has been previously stated that traditional encryption methods are not appropriate for use in compressed scenarios or channels with noise.

Figure 1: The impact of noise is shown in Fig. 1, where (a) represents the original Cameraman image, (b) represents AWGN with SNR of 30 dB, (c) represents AWGN with SNR of 20 dB, and (d) represents AWGN with SNR of 10 dB

Figure 2: The impact of noise is shown in Fig. 1, where Fig. 2a represents the original Cameraman image, Fig. 2b represents the encrypted image. Fig. 2c shows the encrypted image affected by AWGN with SNR ranging from 10 dB to 30 dB. Fig. 2d represents the decrypted

2  Preliminaries

Our suggested system is built around three primary components: chaotic maps, orthogonal matrices, and discrete cosine transform (DCT). In this section, we will study chaotic maps and DCT to have a better grasp of the suggested system. Using a logistic map as an illustration of a chaotic map’s power is essential to illustrate the concept. The DCT, which may be employed in the PE process, is also explained in the next section.

2.1 Chaotic Maps

An insect population model was devised by scientist May in 1976 [17]. There is a relationship between the discrete logistic map, which is the suggested scheme’s discrete version, and the logistic equation. Because of this, iterative maps and difference equations are two terms typically used to describe the discrete insect population scheme. The discrete representation of a 1−D logistic map is mathematically described as:

zn+1=μzn(1−zn)(1)

where z0∈(0,1) and μ∈(0,4) are the logistic map’s starting values. When the values of μ are 3 and 4 the logistic map exhibits oscillatory behavior for the iteration greater than 1. A basic question is what range of μ can be utilized for encryption purposes. In it has been demonstrated that when 3.57≤μ≤4 is reached, the Logistic map enters a state of chaos and shows extremely complicated behavior. Authors in Ref. [18] introduced an Improved Sine-Tangent (IST map as a novel technique for image encryption. The map is mathematically defined as follows:

yn+1=sin (α tan (3 yn2 − 1.5))(2)

where yn ∈ (−1, 1) is the output of the nth iteration, α∈ (0, 1) is the control parameter. We employ one-dimensional PWLCM to randomly dilute an image. A skew tent map is a common example of a 1-D PWLCM. Mathematically skew tent map f:[0,1]→[0,1] can expressed as [19]:

zn+1=f(zn,λ)={znλ,if zn∈[0,λ]1−zn1−λ,if zn∈(λ,1](3)

where Znϵ [0,1] is the initial state of 1D-PWLCM, and λ ϵ(0,1] is the control parameter.

2.2 Discrete Cosine Transform

The time complexity of a cryptosystem can be reduced through the use of PE. Increasing computing effectiveness can be obtained by encrypting only a fraction of multimedia material. While performing PE, many academics focus on the lower frequency coefficients rather than the higher frequency ones. Consider the case where ψ denotes the DCT of a plaintext image. DCT and inverse DCT are denoted by the following equations:

ψ(u,v)=2n×nΛ(u)Λ(v)∑x=0n−1⁡∑y=0n−1⁡P(x,y)cos[(2y+1)uπ2n]×cos[(2x+1)vπ2n](4)

P(x,y)=2n×nΛ(u)Λ(v)∑x=0n−1⁡∑y=0n−1⁡ψ(u,v)cos[(2y+1)uπ2n]×cos[(2x+1)vπ2n](5)

where n×n is the size of image and Λ(u) and Λ(v) can be written:

Λ(u)=Λ(v)={12foruv=01otherwise

3  Proposed Scheme

This section divides the proposed system into two parts: image encryption through a chaos-based [20] orthogonal matrix and the whole encryption/decryption procedure. The Gram–Schmidt method is used to build an orthogonal matrix in the proposed technique. This algorithm takes a random matrix as input and produces an orthogonal matrix as output. Singular Value Decomposition (SVD) [21] is another approach for orthogonal matrix production that may potentially be employed. However, this algorithm has been preferred for orthogonal matrix generation because of its complexity.

3.1 Orthogonal Matrix for Image Encryption

Suppopse, we have n × n orthogonal matrix Q, which can be expressed by Q={q→1, q→2, q→3, …, q→n}, where q→i ∈ Rn, ∀i : 1≤i≤n. The symbol Rn denotes an indefinitely large collection of vectors, where every q→i has n components.

Rn⇒ [a1a2...an], ai∈R, ∀i :1≤i≤n

Each vector in Q is perpendicular and linearly independent of the others, forming the basis for the subspace covered by Q. When all of the vectors in matrix Q are normalized, Q is referred to as an orthonormal set. If q→ denotes the column vector in Rn and ||⋅|| denotes the Euclidean distance of any vector, then Q is an orthonormal set if and only if ‖q→i‖=a12+a22+⋯+an2=1, ∀i :1≤i≤n. The fundamental features of orthogonal matrices are summarized in [22] and is represented as follows:

1.    Q−1=QT

2.    ||x→||=||Q x→||

3.    QTQ=QQT=I=identiy matrix

C=QP(6)

P=Q−1C(7)

Proposition 1

When Q is an orthogonal matrix, accurate decryption of the P is always possible.

Proof

Eq. (7) can be written as:

P=Q−1C=QTC=QTQP⏟I=IP(8)

When a matrix P is multiplied by the identity matrix I, the values of matrix P stay unaltered. Eq. (8) demonstrates that decryption of the image is always achievable. When the relevant characteristics of orthogonal matrix Q are used, the decryption transformation may be calculated easily. The fundamental image encryption described in Eq. (6) can be modified so that the intruder obtains no information about the image. Reiterating Eq. (6) will produce this type of diffusion. The use of several orthogonal matrices raises the ciphertext C’s complexity to guard against statistical and differential attacks. By iterating the chaos map, many orthogonal matrices are created using the Gram–Schmidt process. Eq. (6) may be iterated mathematically as follows:

CN=QN⋯Q2Q1P⏟C1⏞C2(9)

where C1,  C2 and CN , respectively represent the ciphertext after the first, second, and Nth iterations, where C1,  C2 and CN  , is the ciphertext after 1st, 2nd and Nth iterations, respectively.

Proposition 2

The decryption is still achievable despite the fact that the image P has been pre-multiplied by even more than an orthogonal matrix:

P=Q1−1Q2−1⋯QN−1C

P=Q1TQ2T⋯QNTQN⏟I⋯ Q2Q1P

P=Q1TQ2TQ2⏟I ⋯ Q1P

P=Q1TQ1⏟IP

3.2 The Proposed Algorithm

The proposed work steps are discussed in this section, with a focus on the approach for PE which is depicted in Fig. 3. Let P0 be the iput image. Details step of the proposed work is given below.

1.    DCT of Pi is taken, then partition DCT to get ϕi.

2.    Iterating the Logistic map to get random values.

3.    The Gram–Schmidt procedure is used to generate an orthogonal matrix using the random values obtained in step 2.

4.    Perform the multiplication of ϕi with orthogonal matrix to get ϕ¯i.

5.    Replace ϕi with ϕ¯i to get ψ¯i.

6.    Calculate the inverse DCT of ψ¯i to get P¯i.

7.    Convert P¯i into blocks of size B×B.

8.    Iterate the IST using the initial control parameters and  randomly permute the blocks using random uses obtained through IST. To add an additional permutation layer, iterate 1D-PWLCM and permute the blocks using random values.

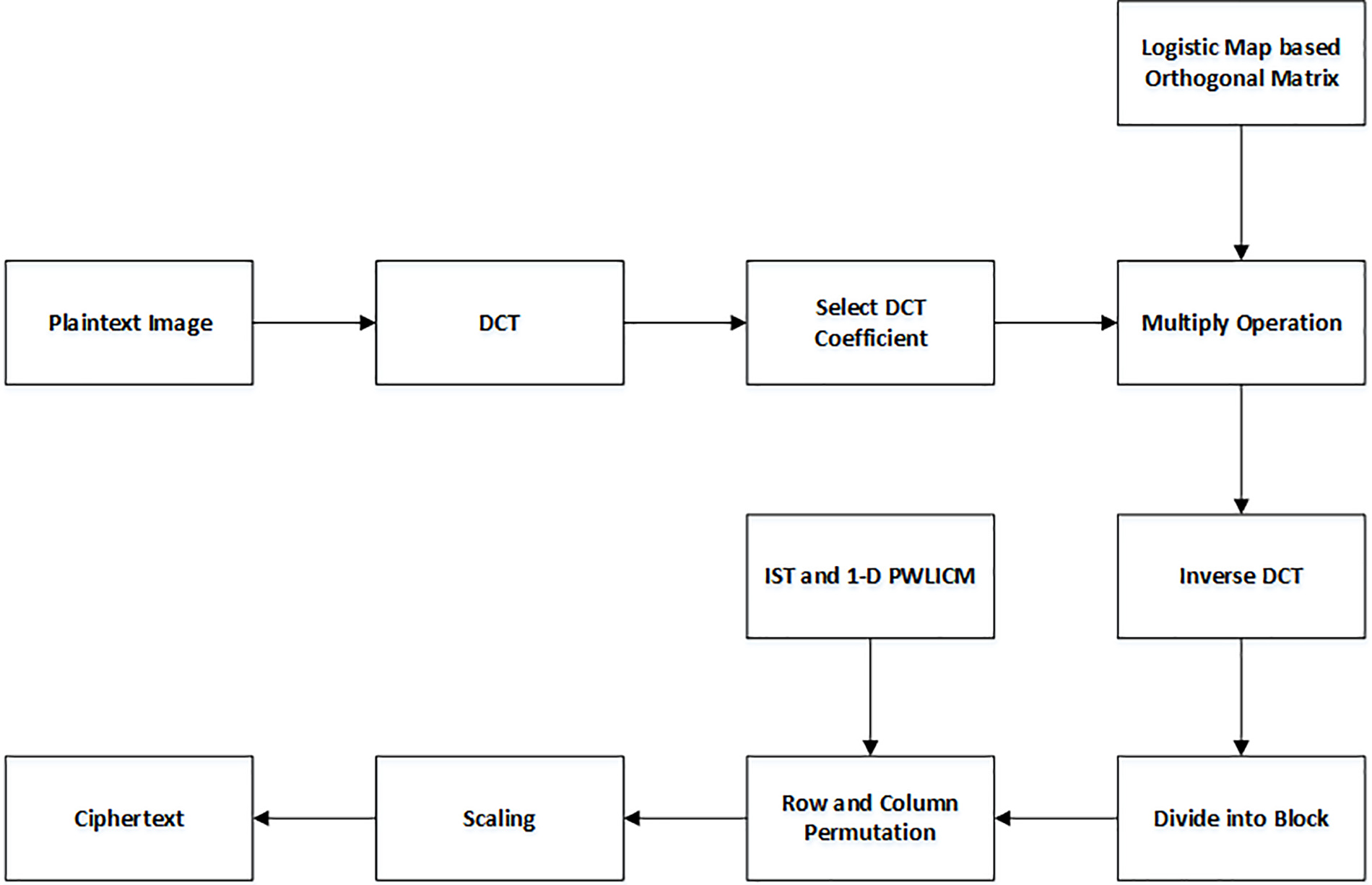
Figure 3: Block diagram of the proposed technique

Grayscale images should use pixel values ranging from 0 to 255. To produce the final ciphertext C, the permuted blocks are quantized and scaled to maintain the pixel values between 0 and 255.

4  Experimental Results

Results from our experiments are presented in this section to highlight the method’s fundamental characteristics. It has a high PSNR of decrypted output due to noise resilience and compressed sensing. The experiments are carried out on a variety of photographs kept in our database. Both the frequency and spatial domains of these images are encrypted. For the sake of consistency, all images in this article are 256 × 256 pixels in size. However, the proposed approach is adaptable to different sizes. To demonstrate the utility of our suggested technique, Figs. 4 and 5 illustrate the results for partial and complete encryption, respectively. These findings show that neither entire nor PE photos provide any meaningful details about the original image. Full encryption, on the other hand, encrypts the entire piece of text; hence, it seems identical to PE. Since just a tiny portion of the data is encrypted, PE takes less time to encrypt and decode than full encryption, as discussed in Section 5.

Figure 4: Encryption using N = 4, B = 16 and K = 128. (a) Plaintext Cameraman image. (b) Encrypted Cameraman image. (c) Plaintext newton image. (d) Encrypted newton image

Figure 5: Encryption with N = 4 and B = 16 and K = 256. (a) Encrypted Cameraman image. (b) Encrypted newton image

4.1 Robustness to Noise

When signals are sent via an AWGN (also known as channel noise), they are typically distorted. Even when the original picture is corrupted by AWGN, traditional decryption techniques are unable to recover it. Fig. 6 shows the impact of AWGN at an SNR of 40 dB on decoded images received. As demonstrated in Fig. 6, the recovered images have a high PSNR and are perceptually comparable to the original images. PSNR values for our suggested strategy at various SNR levels are shown in Table 1. As seen in the figure, Table 1 indicates that the presented system provides noise-tolerating flexibility while retaining an acceptable high PSNR even at low SNR levels.

Figure 6: The outcome of applying JPEG compression with a Quality Factor set to 100. (a) Original Cameraman image (b) decryption result (PSNR = 40.06 dB). (c) Newton image (d) decryption result (PSNR = 37.74 dB)

4.2 Robustness to Compression

Bitmap files store plaintext images and have a size of 65 KB. The method explained in this section can be used to encrypt an image and save it as a Bitmap file without any additional compression. This approach utilizes quantization and scaling, resulting in the encrypted images having the same size as the plaintext images 65 KB. Even though the encrypted data has been compressed, encrypted files of original size can still be decrypted using JPEG compression. When the JPEG-compressed data is decoded, various PSNRs are produced, depending on the Quality Factor (QF) used. The decrypted output quality is found to be excellent, with a high PSNR as evidenced by Tables 2–5 which display the JPEG-compressed files and PSNR values for various quality levels. As the QF value is reduced, the quality of degrades. While the PSNR results are outstanding at QF = 100, the compression ratio is insufficient compared with original size.

4.3 The Effect of Different Parameters on Computational Complexity

The encryption technique proposed in this paper has mainly focused on processing time that is determined by three parameters: N, B and K. The most essential parameter in these parameters is K. The amount of these coefficients have an effect on the number of chaos map iterations and the size of the matrix. The choice of a substantial number of DCT elements is made when the level of security is high, as a result, the iterations is increased, and the size of the matrix is also increased. As a result, the processing time required to encrypt more DCT pieces is visibly long. The time required to process full encryption is entirely influenced by N and B. The effect of JPEG compression is highlighted in Fig. 6 with different PSNR.

5  Security and Performance Evaluation

It is imperative to ensure the security of an image encryption method and verify its ability to withstand various forms of attacks. This section thoroughly examines the dependability of the proposed technique.

5.1 Key Space Analysis

To evaluate an encryption algorithm, it is common to perform key space analysis. This analysis examines the size and complexity of the key space, which is a critical factor in preventing brute force attacks. The larger the key space, the more challenging it becomes for an attacker to break the encryption. In addition, image encryption methods that use chaotic systems are often considered more secure due to erodicity and initial conditions. As a result, the proposed encryption technique will be assessed for its reliability and ability to resist various forms of attacks. If the key space is more than 2100, an algorithm is secure [23]. The key space of the presented strategy is  1090. It is clear that, this space is sufficiently large even after a single iteration.

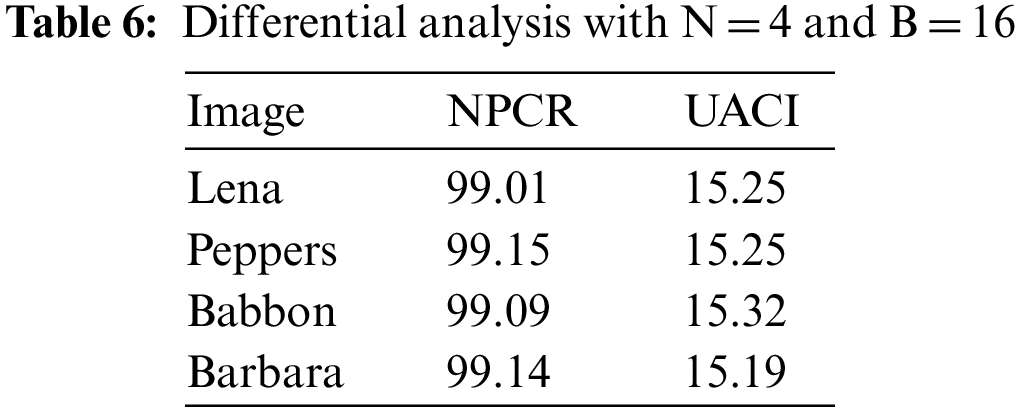
5.2 Analysis of Differential Attack

Differential attacks on image encryption may be evaluated largely using two frequently used metrics: NPCR and UACI [24,25]. Let C(i, j) and C′(i,j) denote the ciphertext image before and following a one-pixel modification in the plaintext image. These metrics can be mathematically expressed as:

NCPR=∑i,jD(i,j)m×n×100%(10)

UACI=1m×n[∑i,j|C(i,j)−C′(i,j)|255]×100%(11)

D(i, j) equals 1 if (i,j)≠C′(i,j); else, 0. Tables 6 and 7 indicate NPCR and UACI for both complete and partly encrypted images. Both tables demonstrate that the NPCR for both total and PE is more than 99%. UACI values are greater in the event of complete encryption than in the case of PE. The greater the UACI number, the more secure the encryption is, but the slower the processing speed is in comparison to PE.

5.3 Analysis of Statistical Attack

By inventing statistical assaults on ciphertext images, an intruder can learn about plaintext images. Therefore, any statistical attacks should be able to be withstood by an image encryption approach. We use histogram analysis and correlation analysis to demonstrate protection against statistical assaults.

5.3.1 Analysis of Histogram

An image encryption technique is to be regarded as secure if the histogram’s output of plaintext and ciphertext images are completely distinct. The ciphertext picture’s histogram should not give any details of the image. Comprehensive Encryption (CE) histogram analysis findings are shown in Fig. 7. Fig. 7 demonstrates that the histogram of the encrypted image bears a close resemblance to the Gaussian distribution function. According to these findings, the frequency distribution of the plaintext picture is hidden behind the encrypted histogram. For all test photos, similar Gaussian distribution functions are generated when PE is used.

Figure 7: Histogram analysis. (a) Histogram of original Cameraman. (b) Histogram of encrypted Cameraman. (c) Histogram of original newton. (d) Histogram of encrypted newton

5.3.2 Analysis of Correlation

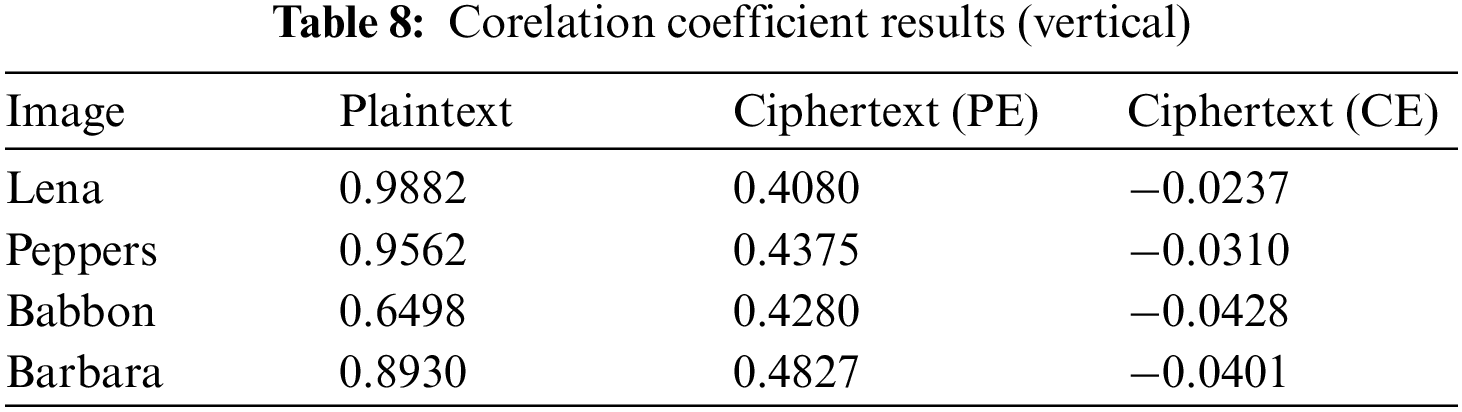
The neighouring points (pixels) in a plaintext image have an intrinsic correlation. When it comes to extremely reliable image encryption, low correlation coefficients in both directions are generally necessary [26]. Table 8 indicates that the horizontal connection between encrypted images is high and smooth for both whole and partial images. This horizontal correlation is crucial in compression, as discussed in Section 4.2.

5.4 Analysis of Time

Using the MATLAB software R2021a, the suggested technique was evaluated with all image sizes of 256×256. The CPU had a processing speed of 3.4 GHz and 4 GB. Table 9 shows the time necessary to encrypt an image using the given techniques. Table 9 illustrates that PE takes less time than total encryption. PE data appears to be a good option. However, as discussed in earlier sections, CE provides greater security. As a result, there is a trade-off between processing speed and security.

6  Conclusion and Future Work

This study presents a novel and efficient approach to image encryption that utilizes the unique characteristics of chaotic maps and orthogonal matrices. Because of the ability of the proposed technique to endure channel noise and JPEG compression, the proposed system is particularly well-suited for use with big data. Even with low SNR values, the suggested technique can retrieve perceptually identical plaintext. When photos are compressed, the quality changes with the encrypted image size. In contrast to standard techniques, from the ciphertext image, the original image may still be deciphered. Furthermore, the suggested approach is usable in a variety of contexts with varying security and processing time requirements. To minimize processing time, only a small fraction of DCT coefficients are encrypted in the frequency domain. However, security evaluations indicate that encrypting all pixels in the spatial domain leads to higher security. The proposed approach employs a symmetric key for both encryption and decryption, which means that the same secret key is used for both operations. The encoded image can only be decoded using the same secret key. In future, our aim is to proposed public key encryption along with compression. Further security may be achieved by using the concept of spatiotemporal chaos and multi-chaos approaches. Moreover, we aim to perform cipertext and plaintext attacks analysis in future.

Acknowledgement: The researchers would like to thank the Deanship of Scientific Research, Qassim University for funding the publication of this project.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. C. M. Kumar, R. Vidhya and M. Brindha, “An efficient chaos based image encryption algorithm using enhanced thorp shuffle and chaotic convolution function,” Applied Intelligence, vol. 52, no. 3, pp. 2556–2585, 2022. [Google Scholar]

2. J. Ahmad and S. O. Hwang, “Chaos-based diffusion for highly autocorrelated data in encryption algorithms,” Nonlinear Dynamics, vol. 82, no. 4, pp. 1839–1850, 2015. [Google Scholar]

3. J. Ahmad and S. O. Hwang, “A secure image encryption scheme based on chaotic maps and affine transformation,” Multimedia Tools and Applications, vol. 75, no. 21, pp. 13951–13976, 2016. [Google Scholar]

4. A. P. Kari, A. H. Navin, A. M. Bidgoli and M. Mimia, “A new image encryption scheme based on hybrid chaotic maps,” Multimedia Tools and Applications, vol. 80, no. 2, pp. 2753–2772, 2021. [Google Scholar]

5. M. Z. Talhaoui and X. Wang, “A new fractional one dimensional chaotic map and its application in high-speed image encryption,” Information Sciences, vol. 550, pp. 13–26, 2021. [Google Scholar]

6. R. Matthews, “On the derivation of a “chaotic” encryption algorithm,” Cryptologia, vol. 13, no. 1, pp. 29–42, 1989. [Google Scholar]

7. J. Fridrich, “Symmetric ciphers based on two-dimensional chaotic maps,” International Journal of Bifurcation and Chaos, vol. 8, no. 6, pp. 1259–1284, 1998. [Google Scholar]

8. Y. Mao, G. Chen and S. Lian, “A novel fast image encryption scheme based on 3D chaotic baker maps,” International Journal of Bifurcation and Chaos, vol. 14, no. 10, pp. 3613–3624, 2004. [Google Scholar]

9. S. Mazloom and A. M. Eftekhari-Moghadam, “Color image encryption based on coupled nonlinear chaotic map,” Chaos, Solitons & Fractals, vol. 42, no. 3, pp. 1745–1754, 2009. [Google Scholar]

10. Z. L. Zhu, W. Zhang, K. W. Wong and H. Yu, “A chaos-based symmetric image encryption scheme using a bit-level permutation,” Information Sciences, vol. 181, no. 6, pp. 1171–1186, 2011. [Google Scholar]

11. Y. Q. Zhang and X. Y. Wang, “Analysis and improvement of a chaos-based symmetric image encryption scheme using a bit-level permutation,” Nonlinear Dynamics, vol. 77, no. 3, pp. 687–698, 2014. [Google Scholar]

12. S. M. Seyedzadeh and S. Mirzakuchaki, “A fast color image encryption algorithm based on coupled two-dimensional piecewise chaotic map,” Signal Processing, vol. 92, no. 5, pp. 1202–1215, 2012. [Google Scholar]

13. Y. Q. Zhang and X. Y. Wang, “Spatiotemporal chaos in mixed linear–nonlinear coupled logistic map lattice,” Physica A: Statistical Mechanics and Its Applications, vol. 402, pp. 104–118, 2014. [Google Scholar]

14. Y. Q. Zhang, X. Y. Wang, J. Liu and Z. L. Chi, “An image encryption scheme based on the MLNCML system using DNA sequences,” Optics and Lasers in Engineering, vol. 82, pp. 95–103, 2016. [Google Scholar]

15. X. Y. Wang and Q. Yu, “A block encryption algorithm based on dynamic sequences of multiple chaotic systems,” Communications in Nonlinear Science and Numerical Simulation, vol. 14, no. 2, pp. 574–581, 2009. [Google Scholar]

16. X. Wang, L. Liu and Y. Zhang, “A novel chaotic block image encryption algorithm based on dynamic random growth technique,” Optics and Lasers in Engineering, vol. 66, pp. 10–18, 2015. [Google Scholar]

17. R. M. May, “Simple mathematical models with very complicated dynamics,” in The Theory of Chaotic Attractors, New York, NY: Springer, pp. 85–93, 2004. [Google Scholar]

18. A. Belazi, S. Kharbech, M. N. Aslam, M. Talha, W. Xiang et al., “Improved sine-tangent chaotic map with application in medical images encryption,” Journal of Information Security and Applications, vol. 66, pp. 103131, 2022. [Google Scholar]

19. R. A. Elmanfaloty and E. Abou-Bakr, “An image encryption scheme using a 1D chaotic double section skew tent map,” Complexity, vol. 2020, pp. 1–18, 2020. [Google Scholar]

20. G. Ye, “Image scrambling encryption algorithm of pixel bit based on chaos map,” Pattern Recognition Letters, vol. 31, no. 5, pp. 347–354, 2010. [Google Scholar]

21. T. Huang, R. Zhao, L. Bi, D. Zhang and C. Lu, “Neural embedding singular value decomposition for collaborative filtering,” IEEE Transactions on Neural Networks and Learning Systems, vol. 33, pp. 6021–6029, 2021. [Google Scholar]

22. T. S. Shores, “Matrix algebra,” in Applied Linear Algebra and Matrix Analysis, NY, USA: Springer, pp. 55–144, 2007. [Google Scholar]

23. H. Liu and X. Wang, “Image encryption using DNA complementary rule and chaotic maps,” Applied Soft Computing, vol. 12, no. 5, pp. 1457–1466, 2012. [Google Scholar]

24. X. Wang and D. Luan, “A novel image encryption algorithm using chaos and reversible cellular automata,” Communications in Nonlinear Science and Numerical Simulation, vol. 18, no. 11, pp. 3075–3085, 2013. [Google Scholar]

25. X. Y. Wang, F. Chen and T. Wang, “A new compound mode of confusion and diffusion for block encryption of image based on chaos,” Communications in Nonlinear Science and Numerical Simulation, vol. 15, no. 9, pp. 2479–2485, 2010. [Google Scholar]

26. M. B. Younas and J. Ahmad, “Comparative analysis of chaotic and non-chaotic image encryption schemes,” in Int. Conf. on Emerging Technologies (ICET), Islamabad, Pakistan, IEEE, pp. 81–86, 2014. [Google Scholar]