A Whale Optimization Algorithm with Distributed Collaboration and Reverse Learning Ability

1  Introduction

The advantages of the digital economy are reflected in today’s society [1]. Based on digitization, the helpful information mining in data becomes critical. The optimization problem in data mining has always been the research object for many scholars [2]. As more and more factors are considered, the optimization operation steps are complex when using traditional methods. If the solution space of the optimization problem is high-dimensional, these traditional methods cannot solve it.

With the development of scientific research, the swarm intelligence algorithm based on bionics has been gradually applied to solve optimization problems [3–5]. Ant colony algorithm to simulate the process of ants searching for food [6], wolf swarm algorithm to simulate the predation behavior and prey distribution of wolves [7], WOA algorithm to simulate the hunting behavior of humpback whales [8], and particle swarm optimization algorithm (PSO) to simulate the foraging of birds [9] are all belong to swarm intelligence algorithms. The application performance of swarm intelligence algorithms has been fully proven in many industry problems [10–13].

WOA algorithm is one of the algorithms with good performance. The basic WOA algorithm mainly obtains the optimization target through searching, encircling, and attacking the prey. The WOA algorithm has a simple principle, few parameters that need to be adjusted during the iterative search, and better optimization accuracy [14]. Meanwhile, the WOA algorithm also has some shortcomings. The convergence accuracy and speed still need to be further improved in practical application.

Scholars have improved the WOA algorithm from different aspects and made many research achievements. First, some scholars optimized the relevant parameters of the WOA algorithm. Second, other theories or operators are introduced into the WOA algorithm. Third, scholars used multi-population or multiple search strategies to search the optimal solution. The performance of the standard WOA algorithm has been improved based on the above improvement ideas. But through early experimental research, it is found that the WOA algorithm performance is still possible to improve further, especially in large-scale optimization problems.

This paper studies the WOA algorithm and proposes a novel DCRWOA algorithm. In the proposed DCRWOA algorithm, the double population search strategy is constructed based on distributed collaboration. Meanwhile, the reverse learning strategy is adopted in the population search process to help individuals quickly jump out of the non-ideal search area. At the same time, the adjustment equations of relevant parameters are further improved. Through experimental research, the performance of the WOA algorithm can be improved as a whole. The research results provide a better method for solving practical optimization problems.

The rest of the paper is organized as follows: Literature review is presented in Section 2. Section 3 introduces the basic WOA algorithm. Section 4 presents specific ideas for WOA algorithm improvement. Numerical experiments and analysis of results are carried out in Section 5. Section 6 further verifies the actual engineering application performance of the proposed algorithm by optimizing shield construction parameters. Section 7 concludes the paper and recommends future direction.

2  Literature Review

After the WOA algorithm was proposed in 2016, it has attracted the attention of many scholars. The WOA algorithm is also gradually applied in many fields. When using WOA algorithm to solve practical optimization problems, it is also found that the performance still needs to be improved. Therefore, scholars have made many explorations on the performance of the WOA algorithm.

To study the diverse scales of optimal power flow, Nadimi-Shahraki et al. [15] explored the effective combination of the WOA algorithm and a modified most flat optimization algorithm. Tawhid et al. [16] combined the WOA algorithm and the flower pollination algorithm to reconstruct a hybrid algorithm to solve complex nonlinear systems and unconstrained optimization problems. Khashan et al. [17] studied the adjustment methods of parameters A and C in the WOA algorithm. They proposed an adjustment method based on nonlinear random changes and inertial weight strategy update. From the perspective of improving the global convergence speed and overall performance of the WOA algorithm, Kaur et al. [18] introduced chaos theory into the WOA algorithm, and experimental tests indicated that chaos mapping is beneficial to improving the WOA algorithm performance. Deepa et al. [19] proposed a WOA algorithm based on the Levy flight mechanism for the coverage optimization problem of wireless sensor networks. The improved WOA algorithm enhances and balances the exploration ability. Long et al. [20] proposed an improved whale optimization algorithm (IWOA). In IWOA algorithm, the opposite learning strategy is adopted to initialize population, and the diversity mutation operation is applied to reduce the probability of falling into local extremum. Kong et al. [21] proposed a novel search strategy and the adaptive weight adjustment method to improve the WOA algorithm performance (AWOA). Farinaz et al. [22] grouped selection according to the individual fitness value, which is beneficial to improving the global search ability of the WOA algorithm. Ning et al. [23] comprehensively analyzed and improved the WOA algorithm regarding mutation operation, convergence factor and population initialization to improve the convergence speed and accuracy. Aimed at convergence speed, stability, and the ability to avoid falling into the local extremum, Liu et al. [24] introduced the roulette method in the search stage of the WOA algorithm. They adopted the two groups with different evolution mechanisms to balance the search capabilities. In addition, the quadratic interpolation method is used to update the individual position of the whale.

As the complexity of the actual project increases, more factors will be considered. The requirements for the algorithm also become higher and higher. Therefore, the performance of the WOA algorithm still needs to be improved to solve more and more complex optimization problems.

3  WOA Algorithm

The design idea of the WOA algorithm is derived from the hunting behavior of humpback whale [25]. The hunting process of humpback whales includes shrink hunting, spring bubble net predation and random search [26].

In the WOA algorithm, the shrink surrounding strategy is implemented when the random value p < 0.5 and |A| < 1. The position update equation is:

X(t+1)=Xp(t)−A⋅|C⋅Xp(t)−X(t)|(1)

where Xp is the position of the optimal individual, A and C are calculated and determined by Eqs. (2) and (3), and t is the current iteration number.

A=2a⋅rand1−a(2)

C=2⋅rand2(3)

where a is the convergence factor, determined by Eq. (4). rand1 and rand2 are random values between [0, 1].

a=2−2t/tmax(4)

where tmax is the maximum number of iterations.

The random search strategy is performed when p < 0.5 and |A| ≥ 1. Eq. (5) is adopted to update the position.

X(t+1)=Xrand(t)−A⋅|C⋅Xrand(t)−X(t)|(5)

When the random value p ≥ 0.5, the WOA algorithm will execute the spiral bubble net predation, simulating the spiral movement of the whale predation process. In this case, Eq. (6) is used to update the position.

X(t+1)=|Xp(t)−X(t)|⋅ebl⋅cos⁡(2πl)+Xp(t)(6)

where b is a constant that defines the shape of the logarithmic spiral. l is a random value between [−1, 1].

4  DCRWOA Algorithm

4.1 Population Initialization Based on Good-Point-Set

The distribution of the initial population affects the algorithm performance. If there is no prior knowledge, the random method is generally adopted to initialize the population. The individual diversity obtained by the random method is generally not guaranteed, and the performance is unstable. Yan et al. proposed a good-point-set method that can uniformly select points [27]. The basic principle is that let Gs be the unit cube in s-dimensional Euclidean space. If r ∈ Gs, then

Pn(k)={({r1(n)⋅k},{r2(n)⋅k},…,{rs(n)⋅k}),1≤k≤n}(7)

The deviation φ(n) satisfies φ(n) = C(r, ε)n−1+ε, and C(r, ε) is only related to r and ε. Then Pn(k) is a good-point-set, and the excellent point r = {2cos(2πk/p), 1 ≤ k ≤ s}, p is the smallest prime number satisfying the condition of (p-3)/2 ≥ s.

Fig. 1 shows the population distribution in a two-dimensional space initialized by the random and good-point-set methods. The population distribution initialized based on the good-point-set method is more uniform and the population diversity is higher, which plays an important function in avoiding falling into some local extreme values.

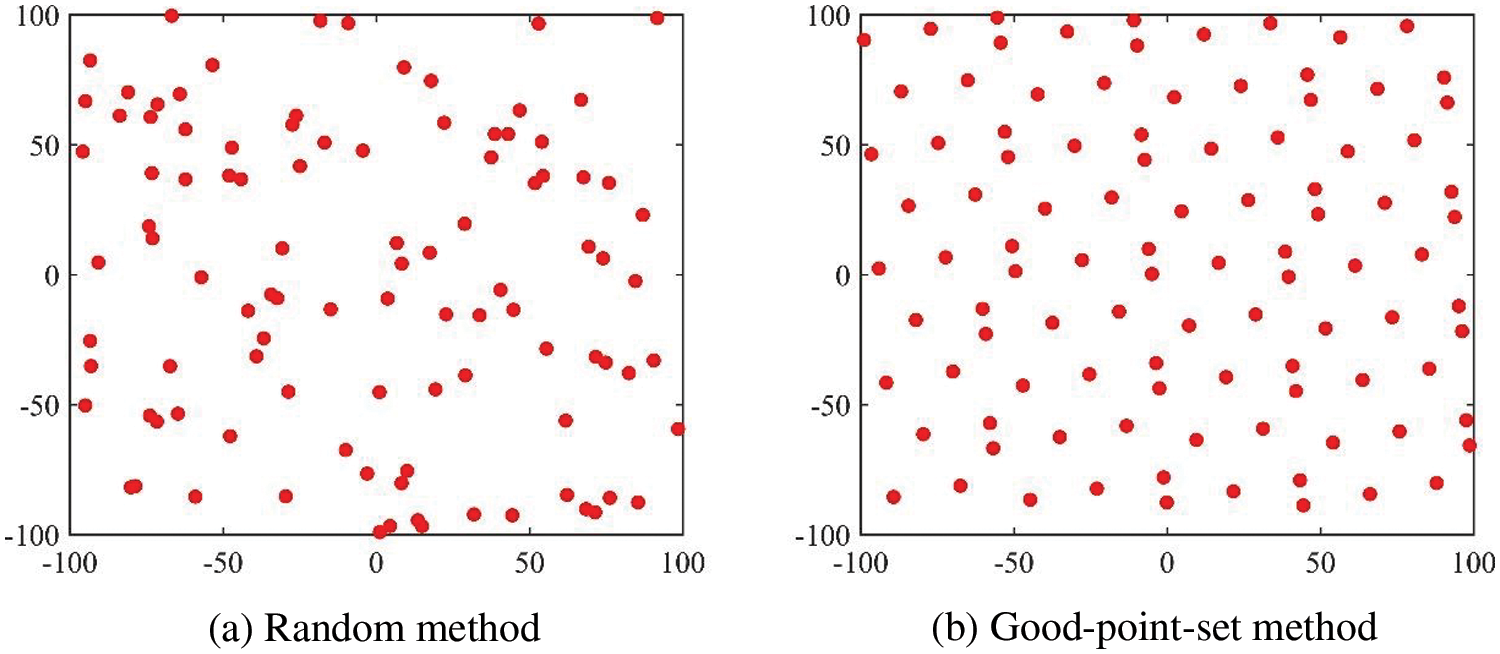
Figure 1: Population initialization distribution

4.2 Improvement of Adjustment Equation for Convergence Factor

The convergence factor affects the search performance [28]. The higher the convergence factor value, the better the global search ability. When the value is small, the local search is performed. The function of the convergence factor is the same as that of the inertia weight in the PSO algorithm. According to the previous research about the inertia weight in the PSO algorithm [29], the optimal exponential form to adjust the inertia weight value is the circular formula. Therefore, for the adjustment of the convergence factor that affects the search ability in the WOA algorithm, the proposed nonlinear adjustment equation is Eq. (8).

a=amin(amaxamin)(1−(tT)2)(8)

where amax and amin are the maximum and minimum values of the convergence factor. If they are used for global search group update, their values are 2 and 1, respectively. If they are used for local search group update, their values are 1.5 and 1, respectively. t is the current number of iterations, and T is the total number.

According to Eq. (8), the convergence factor decreases from the maximum to the minimum. The exponential form of the exponential function is a circular formula, and the exponential value decreases from 1 to 0. Therefore, the convergence factor value decreases slowly and can maintain an enormous value for a long time in the early stage of the iteration, which can ensure the global search performance.

4.3 Double Population Search Strategy Based on Distributed Collaboration

A novel double population search strategy is proposed in this paper based on the distributed collaboration. In this strategy, two groups are set. One group is responsible for the global search. Another group is responsible for the local search. These two groups complete the optimal value search through collaboration, as shown in Fig. 2.

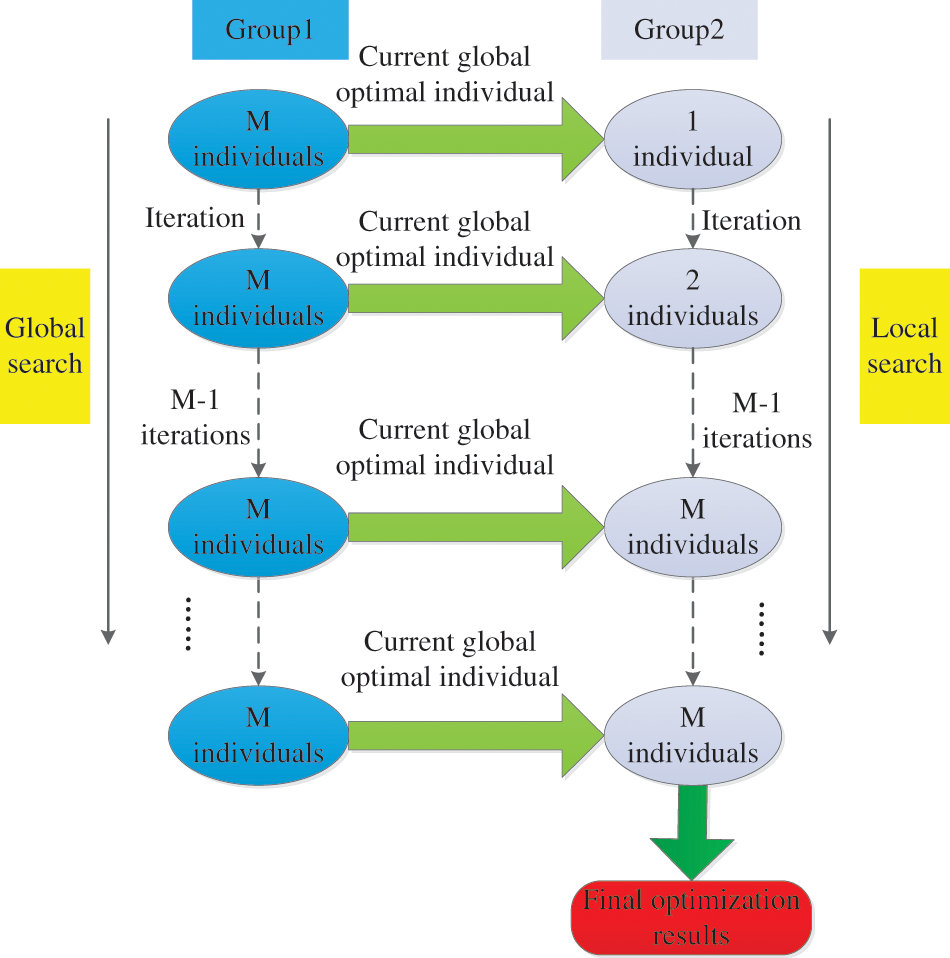
Figure 2: Double population search strategy based on distributed collaboration

The initial population of group 1 is generated by the good-point-set method. The best individual of each iteration in group 1 is put into group 2. Therefore, the population size of group 2 increases gradually with the increase of iteration times. When the number of iterations exceeds the population size of group 1, one individual in group 2 is eliminated according to the individual fitness value after each iteration in this study.

4.4 Hybrid Reverse Learning Strategy and Inertia Weight

In the iterative process, especially for large-scale optimization problems, some individuals may search in the non-ideal area for a long time, which affects the convergence speed and accuracy. The reverse learning strategy is adopted to solve this problem in this paper. The optimal and worst individuals are considered. Let the upper and lower boundaries of the whale position vector be ub and lb, respectively. The optimal individual position is represented by XLeader. The reverse learning operation formula is shown in Eq. (9).

XLeader(t+1)=lb+(ub−XLeader(t))(9)

The position of the worst individual is represented by XWorse and is updated with hybrid reverse learning, as shown in Eq. (10).

XWorse(t+1)=lb+rand⋅(ub−XWorse(t))(10)

The adjustment equation of inertia weight is improved as Eq. (11) or takes the value 1.

w=0.0001∗(XLeader(t)−XWorse(t))+0.0001∗(ub−lb)/t(11)

Inertial weight greatly influences the convergence speed and accuracy of the algorithm. Eq. (11) can be seen as consisting of two parts before and after the plus sign. When there is a large gap between the positions of the best individual and the worst individual in the late iteration, the former part in Eq. (11) will influence the inertial weight value. Improving the iterative search step will make the poor individual update in an extensive range. The latter part can help the algorithm jump out of the local extremum quickly when individuals fall into the local extremum in the early stage.

Therefore, the Eqs. (1) and (6) are updated as follows:

X(t+1)=w⋅Xp(t)−A⋅|C⋅Xp(t)−X(t)|(12)

X(t+1)=|Xp(t)−X(t)|⋅ebl⋅cos⁡(2πl)+w⋅Xp(t)(13)

4.5 Impact Analysis of the Used Two Strategies on Algorithm Performance

Based on the distributed idea, the double population search strategy is used to assign the global and local searches to one population, respectively. The global and local searches are performed during the whole iteration process. Especially for large-scale optimization problems, it is helpful to reduce the possibility of individuals falling into local extremum. Meanwhile, the double population search strategy can also improve the search population diversity.

The reverse learning strategy is adopted to solve the problem that the algorithm can easily fall into the non-ideal search area in solution space. For optimization problems with complex solution space, high dimensions and many local extreme points, some individuals are easy to search in the non-ideal area for a long time during the algorithm iteration process, which affects the convergence accuracy and speed. The reverse learning strategy introduced can help these individuals jump out of the non-ideal area quickly, which plays a crucial role in solving large-scale optimization problems.

4.6 DCRWOA Algorithm Flowchart

The flowchart of the DCRWOA algorithm proposed in the paper is shown in Fig. 3.

Figure 3: The flowchart of the DCRWOA algorithm

5  Numerical Experiments and Analysis of Results

5.1 Experimental Setup

The international standard classical test functions are selected for experimental analysis. The test functions are shown in Table 1.

The DCRWOA algorithm is compared with the WOA, improved whale optimization algorithm (IWOA), and whale optimization algorithm with adaptive adjustment of weight and search strategy (AWOA) to comprehensively test the algorithm performance. The dimensions selected in the experiment include 10, 50, 100, and 200 to study the optimization performance in different dimensions. The four algorithms run 30 times in all functions. The selected metrics include the minimum value, mean value, standard deviation, and average number of iterations to converge to the final optimal value. The relevant algorithm parameters are set as follows: the population size is 30, the maximum number of iterations is 300, and the constant b that defines the logarithmic spiral shape is 1 [30,31].

5.2 Experiment Results and Analysis

The obtained minimum, mean and standard deviation values in dimension 10 are shown in Table 2. The values of minimum, mean, and standard deviation obtained by the DCRWOA algorithm in functions f1, f2, f3, f4, f6, f7 and f9 are all 0, indicating that it can stably converge to the theoretical optimal value. Similarly, the theoretical optimal value can be obtained by the AWOA algorithm in f1, f2, f3, f7 and f9. Although the minimum values in f4 and f6 obtained by the AWOA algorithm and in f9 obtained by WOA and IWOA algorithms are 0, the mean values are not 0. Therefore, there are obtained values that are not 0 in 30 independent runs, indicating that these algorithms have an unstable performance to obtain the theoretical optimal value in these functions.

Except that the values of minimum, mean, and standard deviation obtained by the AWOA algorithm and DCRWOA algorithm in functions f1, f2, f3, f7, f8 and f9 are equal, the numerical synthesis in other functions shows that the accuracy and stability of DCRWOA algorithm are better than that of WOA, IWOA and AWOA algorithms. The mean values obtained by the AWOA algorithm and DCRWOA algorithm are used to analyze whether their experimental results are significantly different based on the Friedman test. The detection value p = 0.045 < 0.05. Thus, the obtained results by AWOA and DCRWOA algorithms are significantly different. The iteration curves in f1, f2, f3, f7, f8 and f9 are shown in Fig. 4

Figure 4: Iteration curves in f1, f2, f3, f7, f8 and f9

The iteration curves in Fig. 4 indicate that the DCRWOA algorithm has faster speed to converge to the theoretical optimal value. The average iteration number that converges to the final optimal value is shown in Fig. 5.

Figure 5: Average number of iterations required in dimension 10

The iteration number that the DCRWOA algorithm obtains for the final optimal value is controlled at about 20, which is much lower than that of the AWOA algorithm. Therefore, although these two algorithms can converge to the theoretical optimal value in these six functions, the AWOA algorithm convergence speed is significantly slower than that of the DCRWOA algorithm. Based on the above analysis, the DCRWOA algorithm has high accuracy, stability and fast convergence speed compared with the other three algorithms in 10 dimensions.

The obtained experimental data in dimensions 50, 100, and 200 are shown in Tables 3–5, respectively.

In 50, 100 and 200 dimensions, the WOA algorithm can stably obtain the theoretical optimal value in function f9 with dimension 200. The IWOA algorithm can stably obtain the theoretical optimal value in function f9 with dimensions 50 and 100. In functions f1, f2, f3, f7 and f9 with dimensions 50, 100 and 200, the AWOA algorithm can obtain the theoretical optimal value. According to Tables 3 to 5, the values of minimum, mean, and standard deviation obtained by the DCRWOA algorithm in the functions f1, f2, f3, f4, f6, f7, and f9 are also 0. Therefore, the DCRWOA algorithm can still stably obtain the theoretical optimal value of 0 in these six functions with dimensions 50, 100 and 200.

DCRWOA and AWOA algorithms also have the same convergence results in function f8. The mean values obtained by the AWOA algorithm and DCRWOA algorithm in these three dimensions are used to analyze whether their experimental results are significantly different. All values of p obtained by Friedman in three dimensions are less than 0.05. Therefore, the performance of AWOA and DCRWOA algorithms are significantly different. For other functions with unequal convergence results, the values in Tables 3 to 5 also indicate that the DCRWOA algorithm has better convergence accuracy and stability than those of the other three comparison algorithms.

For these six functions where DCRWOA and AWOA algorithms have the same convergence results, the average iteration number of the two algorithms to obtain the final optimization value is counted. The results are shown in Figs. 6 to 8.

Figure 6: Average number of iterations required in dimension 50

Figure 7: Average number of iterations required in dimension 100

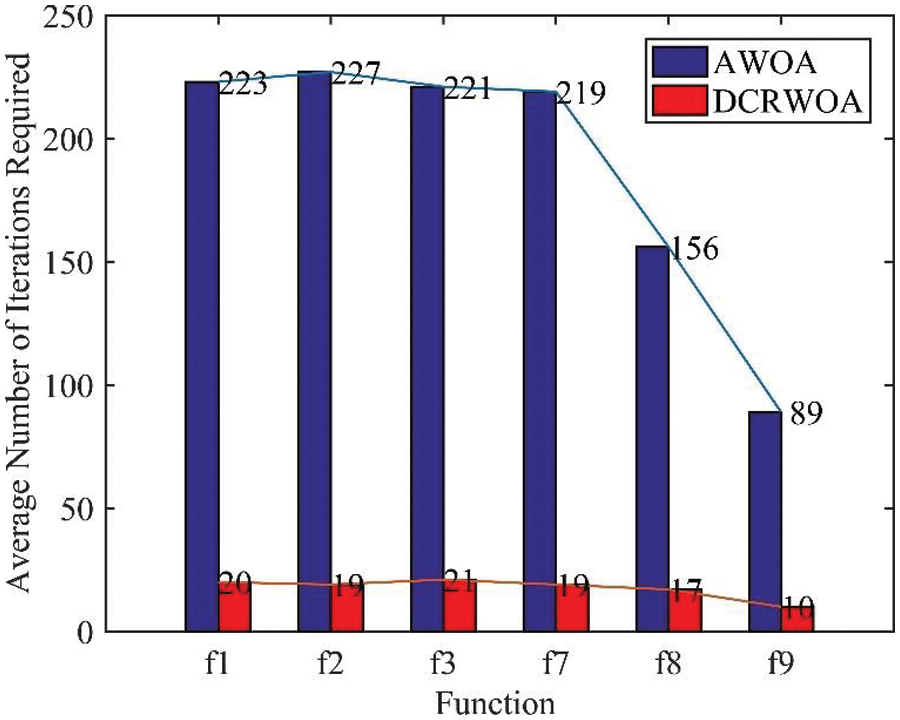
Figure 8: Average number of iterations required in dimension 200

The average number of iterations required for the DCRWOA algorithm is still only about 20 in 50, 100 and 200 dimensions. The minimum iteration number is only 10. AWOA algorithm requires significantly more iterations than the DCRWOA algorithm. Therefore, the DCRWOA algorithm has fast convergence speed.

5.3 Comparative Analysis with Other Swarm Intelligence Algorithms

To further demonstrate the performance of the DCRWOA algorithm, it is compared with improved inertia weight decreasing speed particle swarm optimization algorithm (IIWDSPSO), genetic algorithm (GA), linear decreasing inertia weight particle swarm optimization algorithm (LDIWPSO) and random inertia weight particle swarm optimization algorithm (RIWPSO). The parameter settings in the DCRWOA algorithm are the same as the above experimental values. In the PSO algorithm and its improved algorithm, c1 = 2, c2 = 2. The crossover and mutation probability values are 0.6 and 0.8, respectively. Ten functions in Table 1 are selected for iterative experiments when the dimension is 100. The final iteration curves are shown in Fig. 9

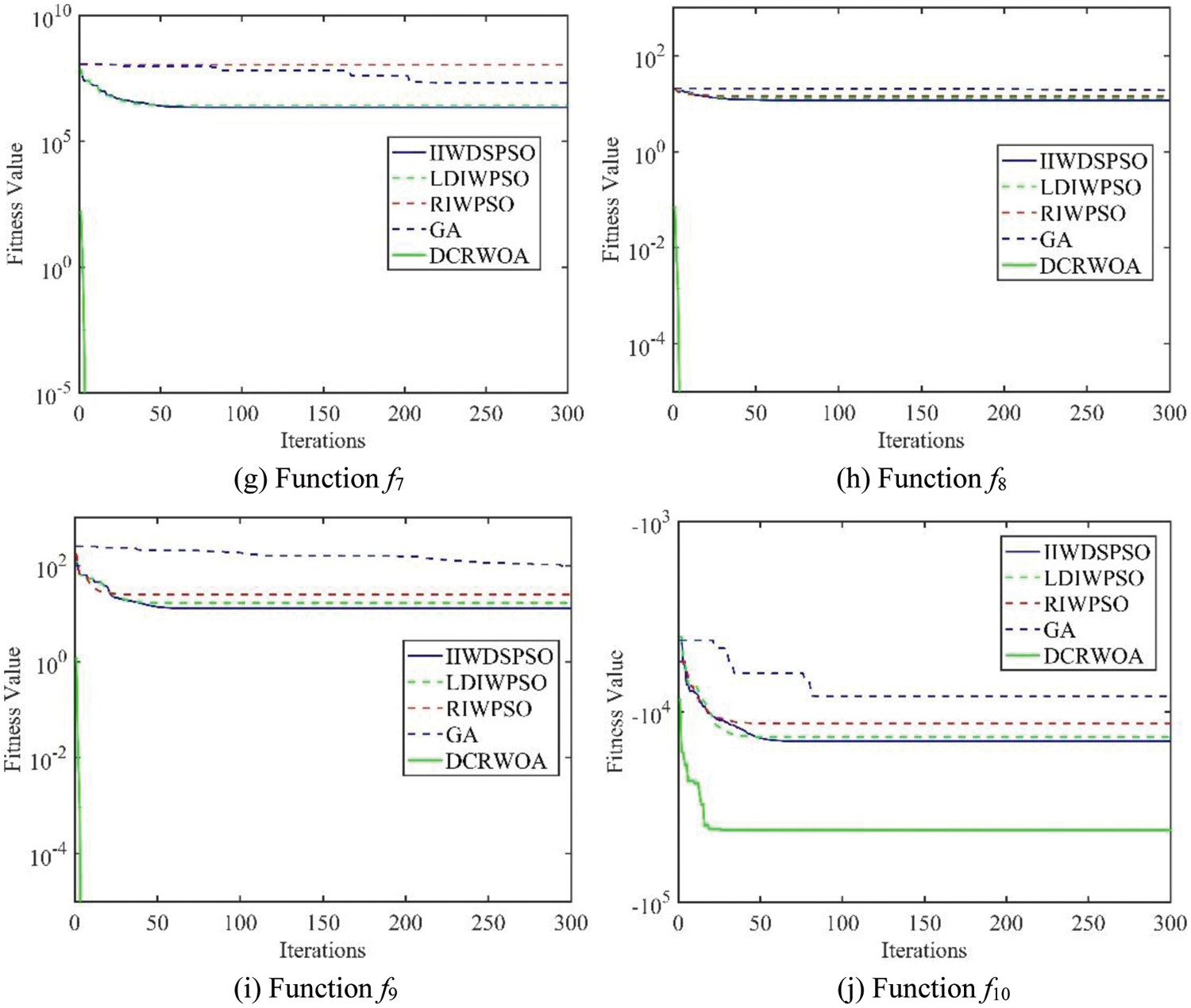
Figure 9: Iteration curves in 10 test functions

According to Fig. 9, the iteration curves corresponding to the DCRWOA algorithm are the lowest. IIWDSPSO, GA, LDIWPSO, and RIWPSO algorithms also don’t converge to the theoretical optimal value in any function. The convergence accuracy of the DCRWOA algorithm is significantly better than the four algorithms compared. Moreover, the change trend of the iteration curves indicates that the four selected comparison algorithms are easy to fall into local extremum, compared with DCRWOA algorithm. Therefore, the DCRWOA algorithm is superior to the other four algorithms in terms of convergence accuracy and ability to avoid falling into local extremum.

Based on the above experiment results and analysis, the proposed DCRWOA algorithm has high convergence accuracy and stability in each dimension. Therefore, no matter whether the optimization problem is simple or complex, the DCRWOA algorithm can solve it well. Because the DCRWOA algorithm has double population with distributed collaboration, the global and local search abilities are better in the entire iteration process. The values of the average iteration number also indicate that the DCRWOA algorithm has fast convergence speed. Through the reverse learning strategy, the DCRWOA algorithm can quickly jump out of the non-ideal search area in the solution space of large-scale problems to avoid many invalid searches. Thus, the DCRWOA algorithm guided by the double population search and reverse learning strategy proposed in this paper is very suitable for solving optimization problems in various dimensions.

6  Case Application

To verify the application performance of the DCRWOA algorithm, the optimization of shield construction parameters is selected as an application case. Shield tunneling is carried out in the underground space. The ground settlement is the most concerned. The critical factors affecting ground settlement are the shield machine operation parameters. Therefore, how to optimize the shield operation parameters is essential for construction.

Before optimizing the shield construction parameters to minimize the ground settlement value, it is first necessary to establish their nonlinear relationship model. The tunneling parameters include cutter head torque, shield thrust, earth pressure, the ratio of tunneling speed and cutter speed R, slag amount and synchronous grouting amount. The paper selects the shield construction operation parameters and the detected ground settlement of the Chang Zhu Tan intercity railway project as the modeling samples. Geometric condition and formation condition parameters are also considered in the model. The geometric condition parameter is the ratio of buried depth H and diameter excavation D. The formation condition parameters are groundwater level and earthwork heavy.

The method of support vector regression (e-SVR) is used to establish a nonlinear relationship model. After training the e-SVR model with sample data, the sample fitting is shown in Fig. 10.

Figure 10: Sample fitting

Based on the obtained relationship model, the DCRWOA algorithm and other improved WOA algorithm compared in simulation experiments are used to optimize the shield construction operation parameters. In the optimized geographical location range, the geometric condition parameter of H/D is 3.7, groundwater level is 28.8 and earth heavy is 20.65. The final optimization results are shown in Table 6.

According to values in Table 6, the ground settlement values obtained by the DCRWOA algorithm and IWOA algorithm are relatively close. But the ground settlement value obtained by the DCRWOA algorithm is still the smallest. By comparing the corresponding shield operation construction parameter values from these two algorithms, thier values are very close, which also shows the accuracy of the shield operation parameters obtained by the DCRWOA algorithm. Combined with the performance analysis of the DCRWOA algorithm based on the classical test functions, the accuracy of shield operation parameters obtained by the DCRWOA algorithm is more guaranteed.

There are many factors affecting the actual construction operation, so it is unrealistic to take all factors into account. The actual construction parameters must be adjusted according to the optimized operation parameters. Undoubtedly, the first step of parameter optimization plays a vital role in the further adjustment of parameters. The DCRWOA algorithm proposed in the paper provides a very accurate and efficient method for optimizing shield construction parameters.

7  Conclusion & Future Work

The DCRWOA algorithm with distributed collaboration and reverse learning ability is proposed in this paper. In the DCRWOA algorithm, the novel double population search strategy is constructed based on the distributed idea. The reverse learning strategy is introduced to help individuals jump out of the non-ideal search area. Based on these two strategies and the adjustment of the related parameters, the performance of the WOA algorithm is improved.

Based on experimental data analysis, the results indicate that the convergence accuracy and stability of the DCRWOA algorithm proposed in the paper are optimal in different dimensions. And some optimization results are the theoretical optimal value. In addition, compared with the other algorithms in the experiment, the DCRWOA algorithm only needs few iterations to converge to the final optimization value and has faster convergence speed. The practical engineering application also verifies that the DCRWOA algorithm has high comprehensive performance.

In the future, the knowledge model of the learning-based swarm intelligence algorithm is the main research direction. The knowledge model is adopted to guide the iterative process of the algorithm. Meanwhile, expanding the application field of the improved swarm intelligence algorithm is also a research work.

Funding Statement: This study was supported by Anhui Polytechnic University Introduced Talents Research Fund (No. 2021YQQ064) and Anhui Polytechnic University Scientific Research Project (No. Xjky2022168).

Conflicts of Interest: The authors declare they have no conflicts of interest to report regarding the present study.

References

1. B. Urh, M. Senegacnik and T. Kern, “Digital transformation reduces costs of the paints and coatings development process,” Pitture e Vernici, vol. 96, no. 6, pp. 18–21, 2020. [Google Scholar]

2. M. Li, Z. Hui, X. Weng and H. Tong, “Cognitive behavior optimization algorithm for solving optimization problems,” Applied Soft Computing, vol. 39, no. c, pp. 199–222, 2016. [Google Scholar]

3. C. V. Kumar and M. R. Babu, “A novel hybrid grey wolf optimization algorithm and artificial neural network technique for stochastic unit commitment problem with uncertainty of wind power,” Transactions of the Institute of Measurement and Control, vol. 2021, no. 3, pp. 014233122110019, 2021. [Google Scholar]

4. M. R. Bonyadi and Z. Michalewicz, “Impacts of coefficients on movement patterns in the particle swarm optimization algorithm,” IEEE Transactions on Evolutionary Computation, vol. 21, no. 3, pp. 378–390, 2017. [Google Scholar]

5. G. Y. Hou, Z. D. Xu, X. Liu and C. Jin, “Improved particle swarm optimization for selection of shield tunneling parameter values,” Computer Modeling in Engineering and Sciences, vol. 118, no. 2, pp. 317–337, 2019. [Google Scholar]

6. H. Motameni, K. R. Kalantary and A. Ebrahimnejad, “An efficient improved ant colony optimization algorithm for dynamic software rejuvenation in web services,” IET Software, vol. 14, no. 4, pp. 369–376, 2020. [Google Scholar]

7. G. Venkanna and D. Bharati, “Optimal text document clustering enabled by weighed similarity oriented jaya with grey wolf optimization algorithm,” The Computer Journal, vol. 64, no. 6, pp. 960–972, 2021. [Google Scholar]

8. S. G. Ismail, D. Ashraf and H. A. Ella, “A new chaotic whale optimization algorithm for features selection,” Journal of Classification, vol. 35, pp. 300–344, 2018. [Google Scholar]

9. W. Zhang and Y. Huang, “Using big data computing framework and parallelized PSO algorithm to construct the reservoir dispatching rule optimization,” Soft Computing, vol. 24, pp. 8113–8124, 2020. [Google Scholar]

10. D. W. Gong, S. Jing and Z. Miao, “A set-based genetic algorithm for interval many-objective optimization problems,” IEEE Transactions on Evolutionary Computation, vol. 22, no. 99, pp. 47–60, 2018. [Google Scholar]

11. A. Ghodousian and M. R. Parvari, “A modified PSO algorithm for linear optimization problem subject to the generalized fuzzy relational inequalities with fuzzy constraints (FRI-FC),” Information Sciences, vol. 418, pp. 317–345, 2017. [Google Scholar]

12. A. Hra, A. Bh, B. As and C. HAL, “Optimization model for integrated river basin management with the hybrid WOAPSO algorithm,” Journal of Hydro-Environment Research, vol. 25, pp. 61–74, 2019. [Google Scholar]

13. X. Zhou, J. Lu, J. H. Huang, M. S. Zhong and M. W. Wang, “Enhancing artificial bee colony algorithm with multi-elite guidance,” Information Sciences, vol. 543, pp. 242–258, 2021. [Google Scholar]

14. S. Mirjalili and A. Lewis, “The whale optimization algorithm,” Advances in Engineering Software, vol. 95, pp. 51–67, 2016. [Google Scholar]

15. M. H. Nadimi-Shahraki, A. Fatahi, H. Zamani, S. Mirjalili and D. Oliva, “Hybridizing of whale and moth-flame optimization algorithms to solve diverse scales of optimal power flow problem,” Electronics, vol. 11, no. 5, pp. 831, 2022. [Google Scholar]

16. M. A. Tawhid and A. M. Ibrahim, “Solving nonlinear systems and unconstrained optimization problems by hybridizing whale optimization algorithm and flower pollination algorithm,” Mathematics and Computers in Simulation, vol. 190, pp. 1342–1369, 2021. [Google Scholar]

17. N. Khashan, M. A. Elhosseini and A. Y. Haikal, “Biped robot stability based on an A-C parametric whale optimization algorithm,” Journal of Computational Science, vol. 31, pp. 17–32, 2019. [Google Scholar]

18. G. Kaur and S. Arora, “Chaotic whale optimization algorithm,” Journal of Computational Design & Engineering, vol. 5, pp. 275–284, 2018. [Google Scholar]

19. R. Deepa and R. Venkataraman, “Enhancing whale optimization algorithm with levy flight for coverage optimization in wireless sensor networks,” Computers & Electrical Engineering, vol. 94, pp. 107359–107359, 2021. [Google Scholar]

20. W. Long, S. H. Cai, J. J. Jiao and M. Z. Tang, “Improved whale optimization algorithm for large scale optimization problems,” Systems Engineering-Theory & Practice, vol. 37, no. 11, pp. 2986–2994, 2017. [Google Scholar]

21. Z. Kong, Q. F. Yang, J. Zhao and J. J. Xiong, “Adaptive adjustment of weights and search strategies-based whale optimization algorithm,” Journal of Northeastern University (Natural Science), vol. 41, no. 1, pp. 35–43, 2020. [Google Scholar]

22. H. E. Farinaz and S. E. Faramarz, “Group-based whale optimization algorithm,” Soft Computing, vol. 24, no. 5, pp. 3647–3673, 2020. [Google Scholar]

23. G. Y. Ning and D. Q. Cao, “Improved whale optimization algorithm for solving constrained optimization problems,” Discrete Dynamics in Nature and Society, vol. 2021, no. 12, pp. 1–13, 2021. [Google Scholar]

24. J. S. Liu, Z. Y. Zheng and Y. Li, “An interactive evolutionary improved whale algorithm and its convergence analysis,” Control and Decision, vol. 38, no. 1, pp. 75–83, 2023. [Google Scholar]

25. P. Dinakara, V. V. Reddy and T. G. Manohar, “Optimal renewable resources placement in distribution networks by combined power loss index and whale optimization algorithms,” Journal of Electrical Systems & Information Technology, vol. 5, no. 2, pp. 175–191, 2017. [Google Scholar]

26. M. A. Elaziz, S. Lu and S. He, “A multi-leader whale optimization algorithm for global optimization and image segmentation,” Expert Systems with Applications, vol. 175, no. 12, pp. 114841, 2021. [Google Scholar]

27. H. Yan, Y. Cao and J. Yang, “Statistical tolerance analysis based on good point set and homogeneous transform matrix,” Procedia Cirp, vol. 43, pp. 178–183, 2016. [Google Scholar]

28. X. Shi and M. Li, “Whale optimization algorithm improved effectiveness analysis based on compound chaos optimization strategy and dynamic optimization parameters,” in Proc. ICVRIS, Jishou, China, pp. 338–341, 2019. [Google Scholar]

29. Z. D. Xu, G. Y. Hou, L. Yang and X. J. Huang, “Selection of shield construction parameters in specific section based on e-SVR and improved particle swarm optimization algorithm,” China Mechanical Engineering, vol. 33, no. 24, pp. 1–10, 2022. [Google Scholar]

30. Q. V. Pham, S. Mirjalili, N. Kumar and M. Alazab, “Whale optimization algorithm with applications to resource allocation in wireless networks,” IEEE Transactions on Vehicular Technology, vol. 69, no. 4, pp. 4285–4297, 2020. [Google Scholar]

31. J. Luo and B. Shi, “A hybrid whale optimization algorithm based on modified differential evolution for global optimization problems,” Applied Intelligence, vol. 49, no. 1, pp. 1–19, 2019. [Google Scholar]