Multi-View & Transfer Learning for Epilepsy Recognition Based on EEG Signals

1  Introduction

Epilepsy is a brain disorder caused by damage to neurons in the brain, resulting in the abnormal firing of neuronal cells, which temporarily prevents the brain from working normally [1,2]. Due to the different starting locations and transmission modes of abnormal electrical activity in the brain, epilepsy has various complex clinical manifestations, but sometimes there are no obvious seizure characteristics, so clinicians can only determine whether a patient has a seizure by observing changes in the EEG signals. Therefore, EEG signals play a very important role in the clinical diagnosis of patients with epilepsy [3].

With the development of AI, intelligent algorithms are widely used for epileptic EEG signals recognition. In general, the AI-based EEG signals recognition process includes the steps of EEG signals acquisition, feature extraction, feature selection, and modeling, as shown in Fig. 1. In this research field, Anusha et al. extracted time and frequency domain features from EEG signals, and proposed an automated epileptic EEG diagnosis system based on artificial neural network (ANN) [4]. Tao et al. used variational mode decomposition (VMD) to decompose the epileptic EEG signals, combined with an autoregressive (AR) model for quadratic feature extraction, and then employed random forest (RF) for epilepsy diagnosis [5]. Wang proposed a classification model based on wavelet analysis and support vector machine (SVM) for epilepsy diagnosis [6]. The above-mentioned studies demonstrated that intelligent algorithms achieved promising performance for epilepsy recognition based on the epileptic EEG signals. However, the EEG signals of epileptic patients are complex, and the potential information contained in the EEG signals can no longer be captured more adequately and comprehensively by using only the algorithmic domain features from a single view. Therefore, more and more multi-algorithmic domain features are extracted and analyzed based on an assumption that different kinds of domain features can provide complementary patterns for epilepsy recognition. The analysis algorithms for multi-algorithmic domain features belong to the category of multi-view learning in AI [7].

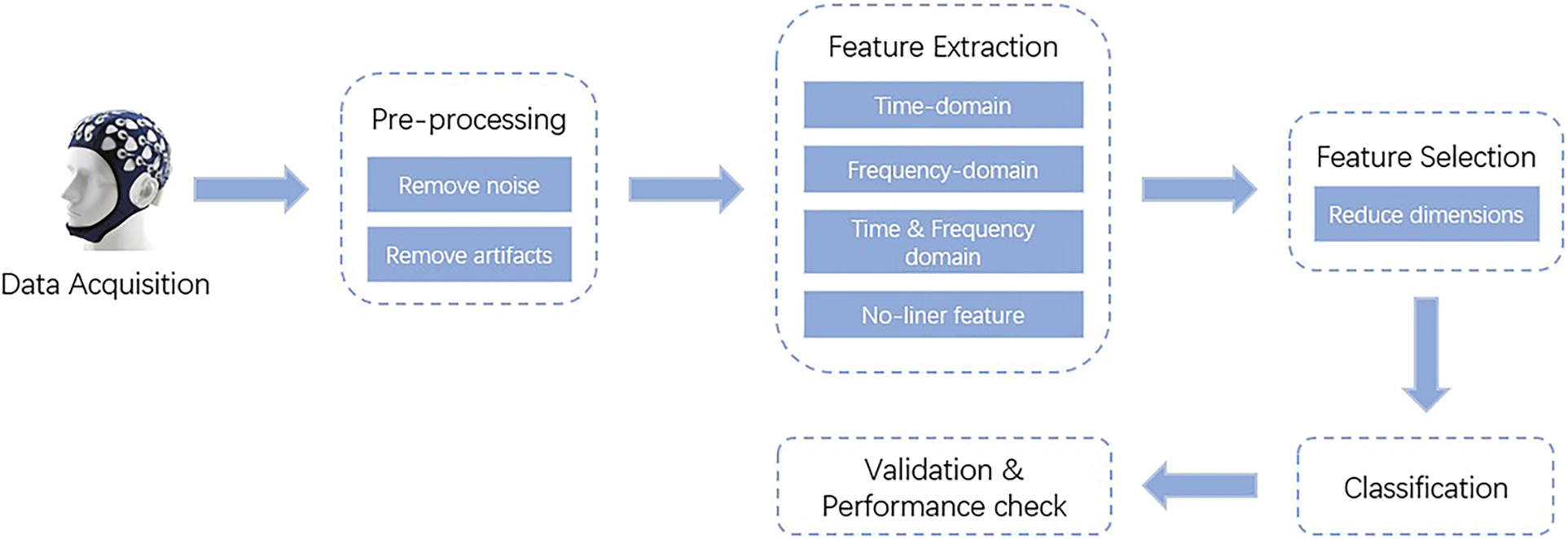
Figure 1: Epilepsy diagnosis based on EEG sensing signals

Multi-view learning exploits the consensus and complementary information contained in multi-view data to explore potential correlations between views, and thus achieve a learning model with promising performance and robustness [8]. For example, to handle high-dimensional data, Li et al. used a feature partition strategy to organize all features into different subsets and taken each subset as a view. Then the authors proposed a semi-supervised multi-view learning method [9]. Jiang et al. proposed an algorithm of collaborative probabilistic latent semantic analysis (C-PLSA) to transform the problem of maximizing the consistency of clustering results from two views into a regularization problem [10]. Tzortzis et al. proposed kernel-based multi-view learning algorithms by using a kernel matrix to represent data from different views [11]. Zhao et al. found that learning by tandem method for multi-view data usually leads to overfitting when the training sample size is small [12]. Therefore, the authors proposed a weighting strategy to emphasize the importance of high-quality views.

Data labeling is a very time-consuming and labor-intensive task, which has led to the scarcity and high cost of high-quality labeled data. Therefore, transfer learning emerges as the requirement of real applications. Transfer learning refers to leveraging knowledge from source domains with high-quality labeled data and applying it to the target domain with no labeled data or few labeled data. Zhang et al. experimentally verified the feasibility of using transfer learning to address attention-deficit/hyperactivity disorder (ADHD) recognition problems [13]. Duan et al. accelerated the transfer process by applying the model-agnostic meta-learning (MAML) algorithm when dealing with the cross-topic EEG classification problem [14]. Took et al. proposed a new convolutional neural network (CNN) algorithm for recognizing epileptic EEG signals by focusing on the first layer of the network to adapt to each task. The new CNN achieved 12% accuracy improvement [15].

In clinical data analysis, although transfer learning reduces the cost of data labeling, it is easy to lead to the disclosure of the privacy of patients in the source domain. In addition, the analysis of clinical data from a single view often ignores the high-order characteristics contained in clinical data.

Driven by the above-mentioned motivations, in this paper, we propose a multi-view & transfer learning algorithm for epilepsy recognition based on the EEG signals. The main contributions of this paper are as follows.

1)   We develop a knowledge transfer mechanism to leverage multi-view knowledge from the source domain, instead of directly transferring features, which can protect the privacy of the source domain.

2)   When leveraging multi-view knowledge, we embed view weighting and manifold regularizations into the transfer mechanism to detect the importance of views and improve the generalization ability.

3)   The effectiveness of the proposed algorithm is verified through EEG signals. Its excellent performance against existing state-of-the-art algorithms is demonstrated by the promising extensive experimental results.

The rest of the paper is organized as follows. In Section 2, we review some of studies related to this study. Then, in Section 3, we detail the knowledge transfer mechanism, the multi-view weighting mechanism, and the optimization process of the proposed algorithm, respectively. In Section 4, we report the experimental results. Finally, a summary is presented in Section 5.

2  Related Work

In this section, we will briefly review some related studies regarding multi-view learning, transfer learning and their combinations.

2.1 Multi-View Learning

With the rapid development of data collection and processing technologies, more and more complex data with different views or modalities are emerging. Generally, we call them multi-view data. Some toy examples of multi-view data are illustrated in Fig. 2. For example, in natural language processing, the same semantic meaning can be described by different languages, and each language corresponds to a view. When depicting objects, the morphology of the whole object can be depicted by images from different angles, each angle corresponds to a view. In clinical diagnosis, X-ray images, electrocardiograms, and clinical examination results can be taken as different views/modalities. In EEG signals analysis, time-domain, frequency-domain and time-frequency-domain can be extracted by wavelet packet decomposition (WPD), short-time Fourier transform (STFT), kernel principal component analysis (KPCA) etc. Each type of features can be taken as a view. These views have different feature spaces, but they all describe the same object, reveal different characteristics of the object.

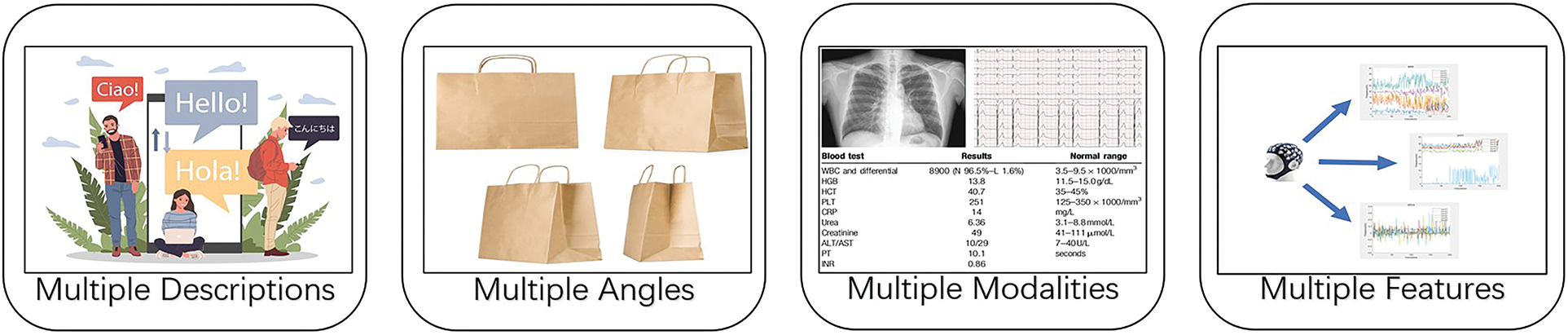
Figure 2: Multi-view data

In earlier studies, most traditional algorithms for epileptic EEG signals analysis were single-view based, which not only fail to tap the consensus and complementary information of each view, but also may lead to dimensional disasters. In subsequent studies, some scholars demonstrated that multi-view learning has better classification performance than single-view learning [16,17]. Jiang et al. proposed a multi-view Takagi-Sugeno-Kang fuzzy system. This system uses multi-view data to enable the model to produce more comprehensive and reasonable results than traditional single-view learning models [18]. Zhu et al. proposed a novel double-index-constrained, multi-view, fuzzy clustering algorithm (DIC-MV-FCM), which has better clustering performance than traditional clustering algorithms when dealing with multi-view EEG signals [19]. Although all of the above studies demonstrated the advantages of multi-view learning over single-view learning, none of them focused on the possible overfitting effects of multi-view learning in the model training process.

2.2 Transfer Learning

Transfer learning is a machine learning technique whose main idea is to exploit the similarities between data, models and tasks. Transfer learning attempts to learn a model by applying the pre-learned knowledge in a domain with sufficient training data to a new domain and increase the generalization performance of the model. Transfer learning can usually be classified as instance transfer, feature transfer, relationship transfer, and model transfer [20]. In transfer learning, the domain where the learning is performed in advance is called the source domain and domain that accepts the knowledge learned in advance is called the target domain. Instance-based transfer is done by changing the existence form of samples to reduce the difference between source and target domain; feature-based transfer is done by mapping the source and target domain in some feature space and minimizing the distance between them through feature transformation; relationship-based transfer is done by creating a mapping of the correlation knowledge between two domains; model-based transfer is done by sharing certain parameters between the source domain model and the target domain model and adjusting them to accomplish knowledge transfer.

Transfer learning has also received extensive attention from researchers in the research field related to EEG signals processing. Jeng et al. proposed a transfer learning framework based on low-dimensional topic representation to address the problem of human variability in brain-computer interface [21]. Sameri et al. used a multi-stage fine-tuning approach during transfer learning to train end-to-end CNN models to learn discriminative features from EEG signals [22]. Zhang et al. proposed a Kullback–Leibler divergence-based transfer learning algorithm to deal with the effects of the non-stationarity of the motor imagery EEG signals [23].

In epilepsy diagnosis studies, Wang et al. found that in some scenarios, the classification of epileptic EEG signals was not finely delineated. Therefore, they utilized sub-band mean amplitude spectrum map (MAS) of multichannel EEG for signal representation and used three commonly used deep convolutional neural networks for feature transfer learning separately, achieving classification performance of prefrontal epilepsy signals on a fine time scale [24]. Song et al. proposed a new EEG-based epilepsy detection strategy, the main idea of which is to use an improved transfer learning model to decode EEG models in the nonlinear dynamic domain, and this framework does not lose important nonlinear features to a certain extent, a property that makes the model outperform seven well-known neural network transfer learning models and provides new insights into EEG decoding [25]. Although transfer learning algorithms have been extensively used in the study of EEG signals, there are still relatively few transfer learning-based algorithms for seizure detection, necessitating additional study and performance validation.

2.3 Multi-View & Transfer Learning

Multi-view learning, which involves learning from several views, can enhance a model’s performance by enabling it to comprehend information from various views more thoroughly. Transfer learning enables us to use information from similar issues to aid the model in problem-solving, which can enhance the model’s generalization capabilities and stability. Therefore, by including a multi-view learning algorithm into transfer learning, it is possible to avoid both the one-sided description of single-view data as well as the lack of experimental data.

Currently, there are not many studies using multi-view learning algorithms in the field of transfer learning. At first, Xu et al. chose the adaboost algorithm to implement multi-view transfer learning, and although the experimental results proved the feasibility of the algorithm, this algorithm was developed based on two-view data and did not make good use of multi-view learning [26]. With the change of research direction, this type of algorithm is mostly used in the research of object classification. For instance, Liu et al. was studied on categorizing moving objects in traffic scenes used the adaboost-based multi-view transfer learning technique. A modest number of labeled target scene instances in this system can greatly enhance performance and reduce labeling time and labor requirements [27]. Bian et al. considered that using deep neural networks for automatic dermatological classification would largely limit the scalability of the model, and proposed a multi-view filtered transfer learning network to represent the discriminative information from different image views with a reasonable weighting strategy [28]. In the research area related to EEG sensing signals processing, Jiang et al. proposed an online multi-view transfer learning model with high interpretability for identifying fatigue driving based on EEG sensing signals, considering that the existing classification models are based on single-view data and are not interpretable transfer learning models. In this model, features in both the source and target domains are multi-view data, allowing more pattern information to be utilized during model training [29]. Abbas et al. proposed a real-time driver inattention and fatigue detection system by extracting hybrid features from multi-view cameras and biosignal sensors [30]. Although multi-view transfer learning algorithms have been used in the study of EEG sensing signals, further research and performance validation are still required for the algorithms that have been explored for seizure identification.

2.4 Motivation

1)   Considering the lack of experimental data, traditional transfer learning algorithms can transfer data or model knowledge from different source domains to exploit patterns related to the target. However, the transfer learning process requires knowledge sharing and exchange among participants, which poses a greater risk to the data privacy of participants.

2)   Most of the epileptic EEG sensing signals classification methods learn only a single algorithmic domain feature. This makes it possible for some specific information from different views to be interfered with by some noisy features (e.g., Gaussian noise) during the feature learning process. This specific information contributes to the most discriminative features of important category cues for EEG sensing signals recognition tasks. Therefore, feature extraction should be performed from various algorithmic domain views.

3)   Traditional learning models can only perform a simple splicing process when faced with multi-view data, but this simple processing renders the previously done feature extraction work meaningless. In addition, in the case of a small number of training samples, this simple splicing process for features will make overfitting in the operation.

Based on the above motivations, we propose a multi-view transfer learning algorithm. In order to solve the above problems, this paper introduces a knowledge transfer mechanism, which aims to avoid the mutual contact of multiple participants in the transfer learning process, and chooses to protect the privacy of participants by directly using the multi-view knowledge of the source domain. And the multi-view weighting mechanism is used to measure the advantages and disadvantages of multiple views to describe the object more comprehensively and scientifically as possible.

3  Multi-View & Transfer Learning for Epilepsy Recognition

3.1 Notations

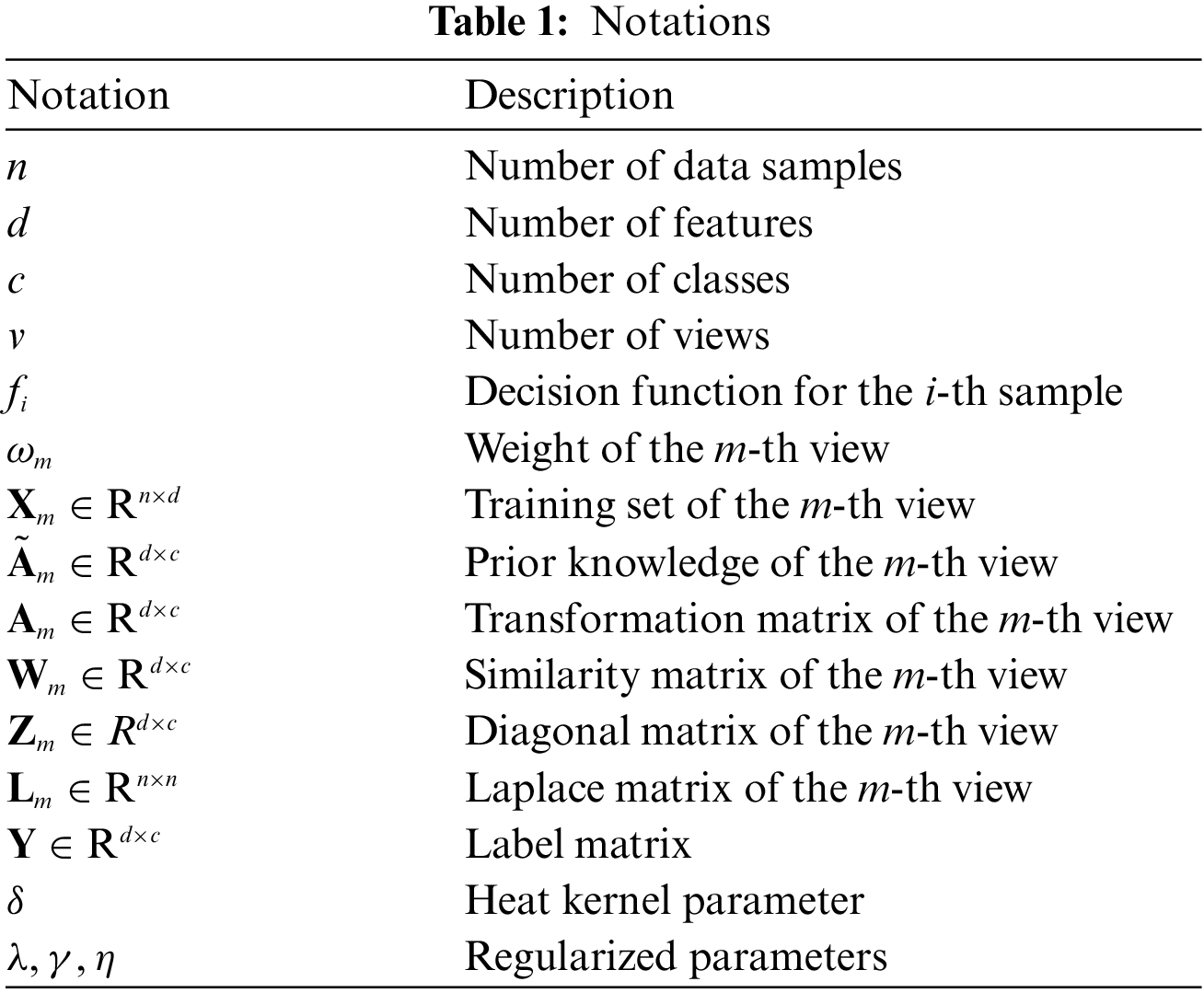
In this study, some of important notations are listed in Table 1. Usually, bold numbers represent vectors, and un-bold italics represent scalars.

3.2 Multi-View & Transfer Learning

3.2.1 Knowledge Transfer with Privacy Protection

In machine learning, the empirical risk is usually used to describe how well the AI algorithm fits the training data. Suppose we have a training set denoted as {X, Y}, the empirical risk can be represented as ‖XA−Y‖F2. A is the transformation matrix, aiming at transforming the feature space to the label space. A is also the knowledge learned from the training set. In this paper, we assume that if two domains are related, then the transformation matrices of two domains are also similar to each other. Therefore, in order to leverage knowledge from the source domain to the target domain, based on the above-mentioned assumption, we can minimize the following term,

‖A−A~‖F2(1)

where A is the transformation matrix of the target domain, and A~ is the transformation matrix of the source domain. A~ is the knowledge from the source domain. Notably, A~ does not contain any feature information, therefore, the privacy of the source domain is well-protected.

3.2.2 Multi-View Weighting

To explore the consistent or complementary information from different views, in this paper, we develop a multi-view weighting mechanism based on the information theory. To be specific, a view weighting penalty term based on “Shannon entropy” is introduced to measure the weight of each view, which is defined as follows,

∑m=1vωmln⁡ωm(2)

where v is the number of views, ωm is the weight of the m-th view. By minimizing (2), the view which contains form pattern information is assigned bigger weight.

3.2.3 The Compactness Graph

Minimizing empirical risk to the maximum extent can easily lead to overfitting. In manifold learning, it is usually assumed that samples sharing the same labels should be kept close together in the transformed space. Based on this assumption, the compactness graph is introduced in this paper to handle overfitting problems. To be specific, we use the following equation to capture the relationship between training samples in the compactness graph,

Wij={e−‖xi−xj‖2/δ if xi and xjhave the same labels0,otherwise(3)

where δ is the heat kernel parameter. According to [31], if Wij can capture the relationship that the samples sharing the same labels should be kept close together, then any two transformed samples fi and fj with the same labels have a bigger weight Wij. Therefore, to keep the compactness of samples in the transformed space, we can minimize the following equation,

minf∑ij‖fi−fj‖2Wij(4)

where fi and fj are any two transformed samples of xi and xj by the transformation matrix A. By introducing the Laplacian matrix, it is easy to find that (4) can be simplified into the following objective,

minAtr(AmTXmTLmXmAm)(5)

where L is the Laplacian matrix which can be computed by L=Z−W. Z is a diagonal matrix and its diagonal entries can be computed by Zij=∑jWij.

3.2.4 Objective and Optimization

Based on the above-mentioned components, we propose a new multi-view & transfer learning algorithm MVTL-LSR. The objective is formulated as follows,

JMVTL−LSR=minAm,ωm⁡∑m=1vωm‖XmAm−Y‖F2+λ∑m=1vtr(AmTXmTLmXmAm)+η∑m=1vωmlnωm+γ∑m=1v‖Am−A~m‖F2(6)

s.t.∑m=1vωm=1

where λ>0, η>0 and γ>0 are trade-off parameters to balance the effects of different components in the objective function. Since the objective is convex, the updated rules regarding ωm and Am has closed-form solution. Therefore, it is straightforward to use an alternative iteration strategy to optimize the objective.

Firstly, when ωm is fixed, the following theorem can be used to the optimal Am.

Theorem 1: Given ωm, then the optimal Am can be computed by

Am=(ωmXmTXm+λXmTLmXm+γI)−1(XmTY+γA~m)(7)

Proof. Given an arbitrary ωm, the objective in (6) can be re-formulated as

JMVTL−LSR(Am)=minAm,ωm⁡∑m=1vωm‖XmAm−Y‖F2+λ∑m=1vtr(AmTXmTLmXmAm)+γ∑m=1v‖Am−A~m‖F2(8)

By setting the partial derivative of JMVTL−LSR(Am) with respect to Am to 0, we have

∂JMVTL−LSR(Am)∂Am=0

⇒2ωmXmTXmAm−2XmTY+2λXmTLmXmAm+2γ(Am−A~m)=0

⇒(ωmXmTXm+λXmTLmXm+γI)Am=XmTY+γA~m

Therefore, Am can be expressed as

Am=(ωmXmTXm+λXmTLmXm+γI)−1(XmTY+γA~m)(9)

Thus, the proof is finished.

Secondly, when Am is fixed, the following theorem can be used to the optimal ωm.

Theorem 2: Given Am, then the optimal ωm can be computed by

ωm=e−‖ XmAm−Y ‖F2η∑m′=1ve−‖ Xm′Am′−Y ‖F2η(10)

Proof. Given an arbitrary Am, the objective in (6) can be re-formulated as

JMVTL−LSR(ωm)=minAm,ωm∑m=1vωm‖XmAm−Y‖F2+η∑m=1vωmln⁡ωm(11)

s.t.∑m=1vωm=1

By setting the partial derivative of JMVTL−LSR(ωm) with respect to ωm to 0, we have

∂JMVTL−LSR(ωm)∂ωm=0

⇒‖XmAm−Y‖F2+η(ln⁡ωm+1)+ξ=0

⇒ln⁡ωm=−ξ−‖XmAm−Y‖F2η−1

⇒ωm=e−ξ−‖XmAm−Y‖F2η−1=e−−ξηe−‖XmAm−Y‖F2ηe−1

Owing to ∑m=1vωm=1, we have

∑m=1ve−−ξηe−‖XmAm−Y‖F2ηe−1=1

⇒e−−ξηe−1=1∑m=1ve−‖XmAm−Y‖F2η

By substituting e−−ξηe−1 to ωm, we have

ωm=e−‖XmAm−Y‖F2η∑m′=1ve−‖Xm′Am′−Y‖F2η(12)

Thus, the proof is finished.

3.2.5 Algorithm

Based on the updated rules of Am and ωm, the algorithm of MVTL-LSR can be derived as follows.

Based on Algorithm 1, the testing algorithm of MVTL-LSR can be deduced as follows.

Remark 1: In Algorithm 1, it is first necessary to set γ to 0 and find the transfer knowledge A~m in the source domain.

Remark 2: In Algorithm 1, the condition to end the iteration is ‖Am(t)−Am(t−1)‖≤10−4, where 10−4 is the termination condition set by this algorithm, and you can set the threshold value according to the actual scenario of your algorithm.

Remark 3: The time complexity of this algorithm mainly consists of the computation complexity of the transformation matrix A and the computation complexity of the view weight ω. The computation complexity of the transformation matrix A for a single view is O(2d3+d2c), where d is the dimension of the input feature space and c is the number of classes. The computation complexity of the view weight ω of a single view is O(nc), where n is size of the training set. Therefore, the time complexity of Algorithm 1 is O(2d3+d2c+nc). Obviously, the computational complexity of Algorithm 1 mainly depends on d3, which indicates that Algorithm 1 is suitable for large-scale low-dimensional datasets.

4  Experimental Studies

4.1 EEG Sensing Signals Processing

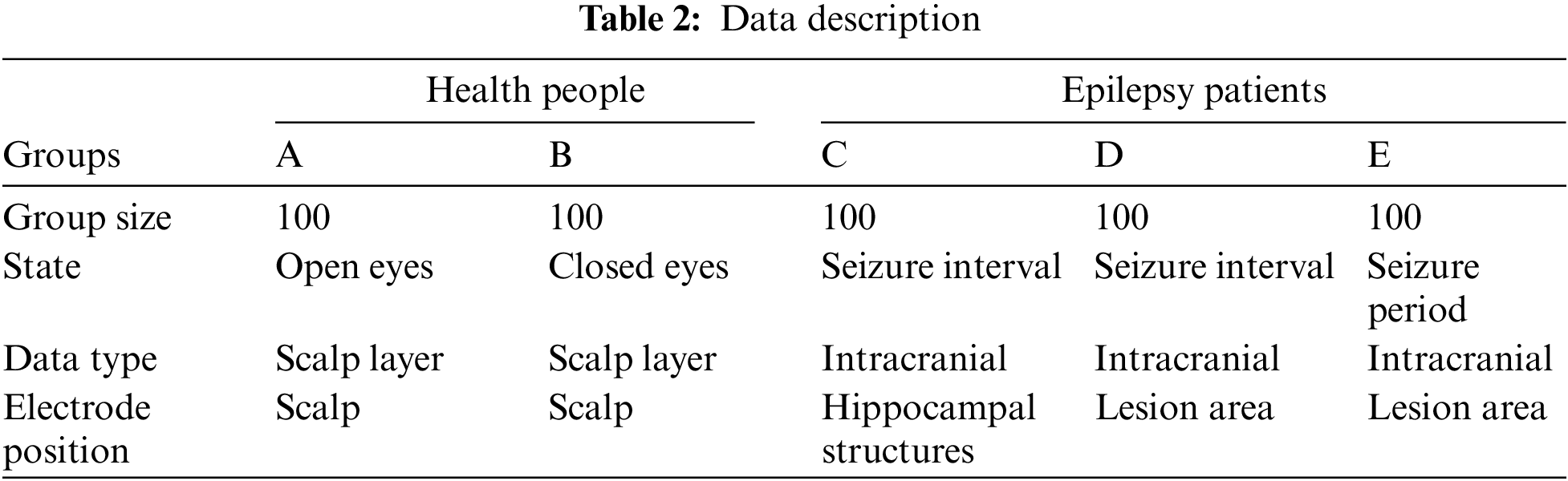
The epilepsy EEG signals licensed and provided by the University of Bonn, Germany, are used in this study. The dataset consists of 5 sub-datasets (Set A, Set B, Set C, Set D, and Set E). Each sub-dataset contains 100 single-channel EEG segments with a duration of 23.6 s and a sampling frequency of 173.61 Hz. A brief description of the five sub-datasets is presented in Table 2.

In the stage of EEG signals acquisition, the obtained signals often contain different kinds of noises [32–34], which may affect the physician’s analysis and diagnosis. Therefore, it is important to pre-process the EEG signals before the beginning of the next stage. Fig. 3 shows a toy example of the collected EEG signals.

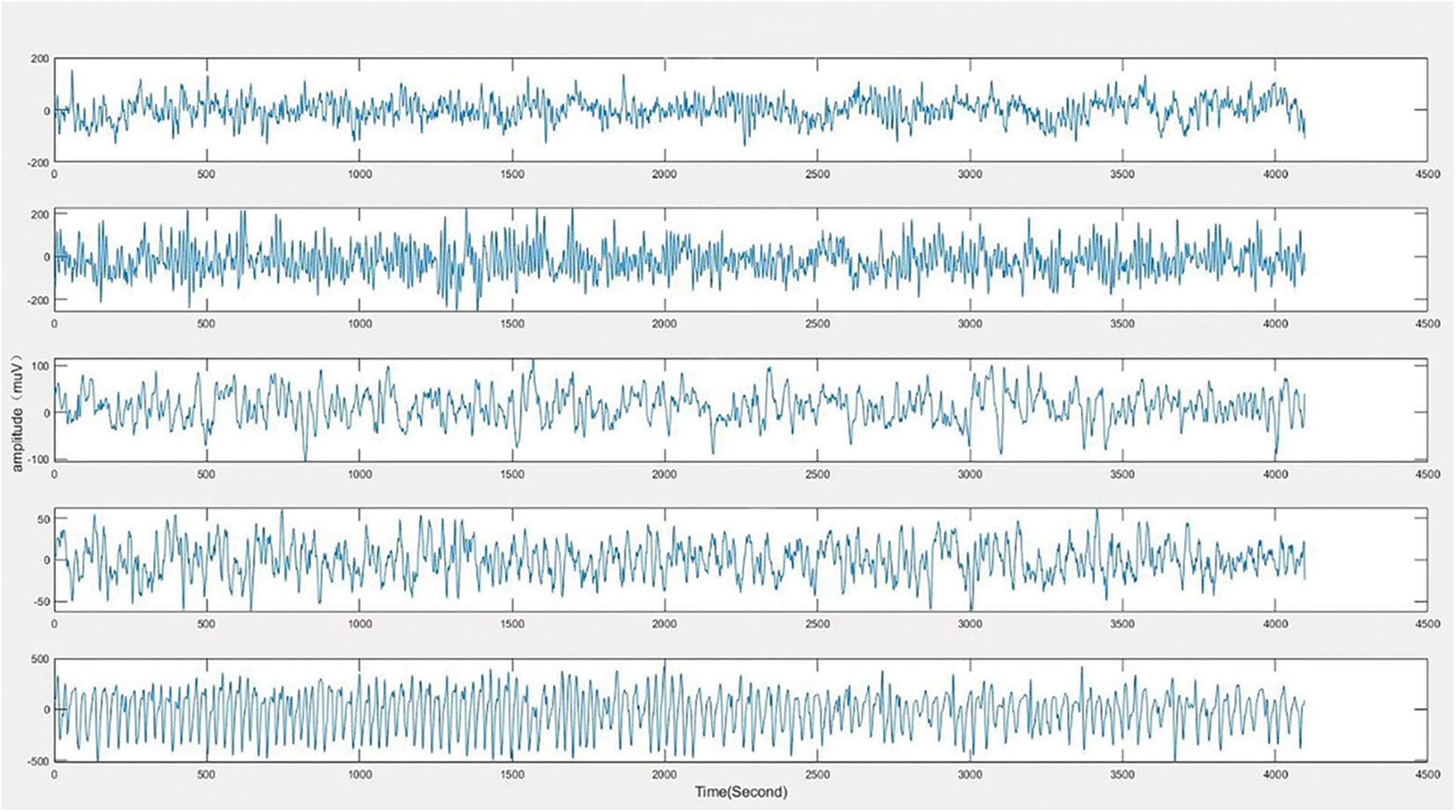
Figure 3: Collected EEG signals of 5 individuals from sub-datasets A, B, C, D, and E, respectively

In recent years, with the continuous research for EEG signals, more and more feature extraction methods have been proposed to process the raw data. To better study the information contained in EEG signals, we select three classical feature extraction methods, i.e., WPD [35], STFT [36] and KPCA [37], to extract the time-domain features, frequency-domain features and time-frequency features, respectively, as shown in Fig. 4.

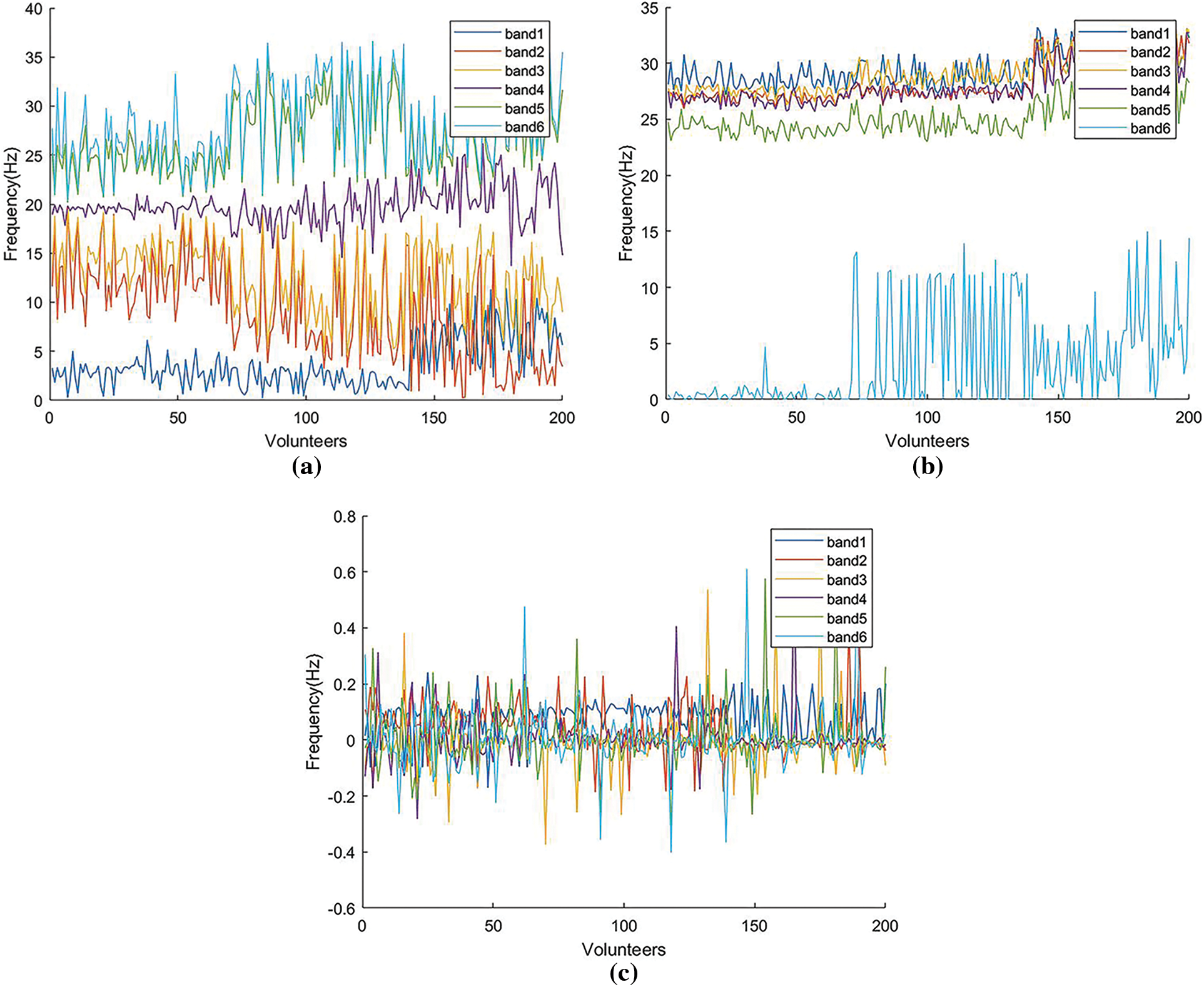
Figure 4: Features extracted by WPD, STFT and KPCA. (a) WPD. (b) STFT. (c) KPCA.

4.2 Transfer Scenarios

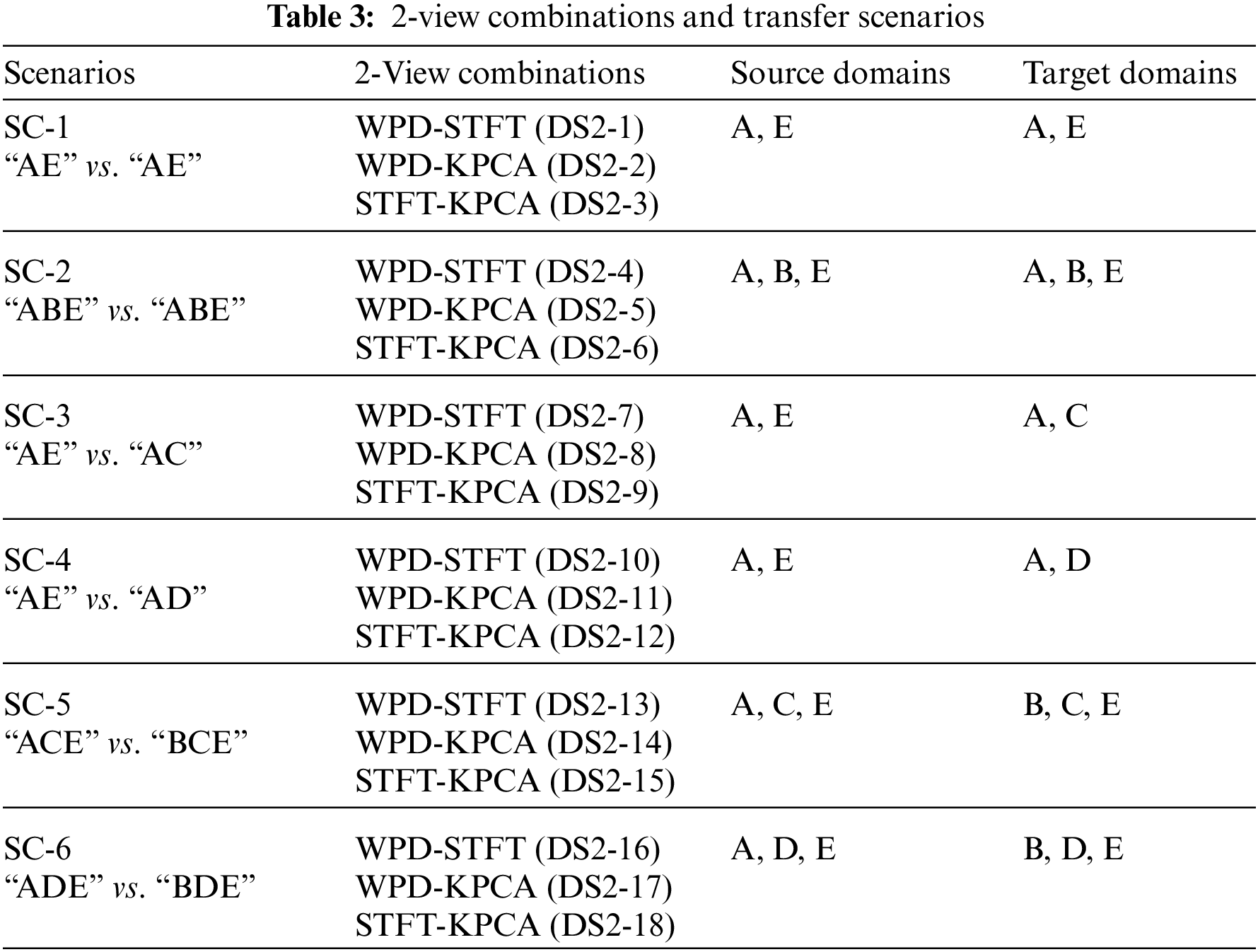
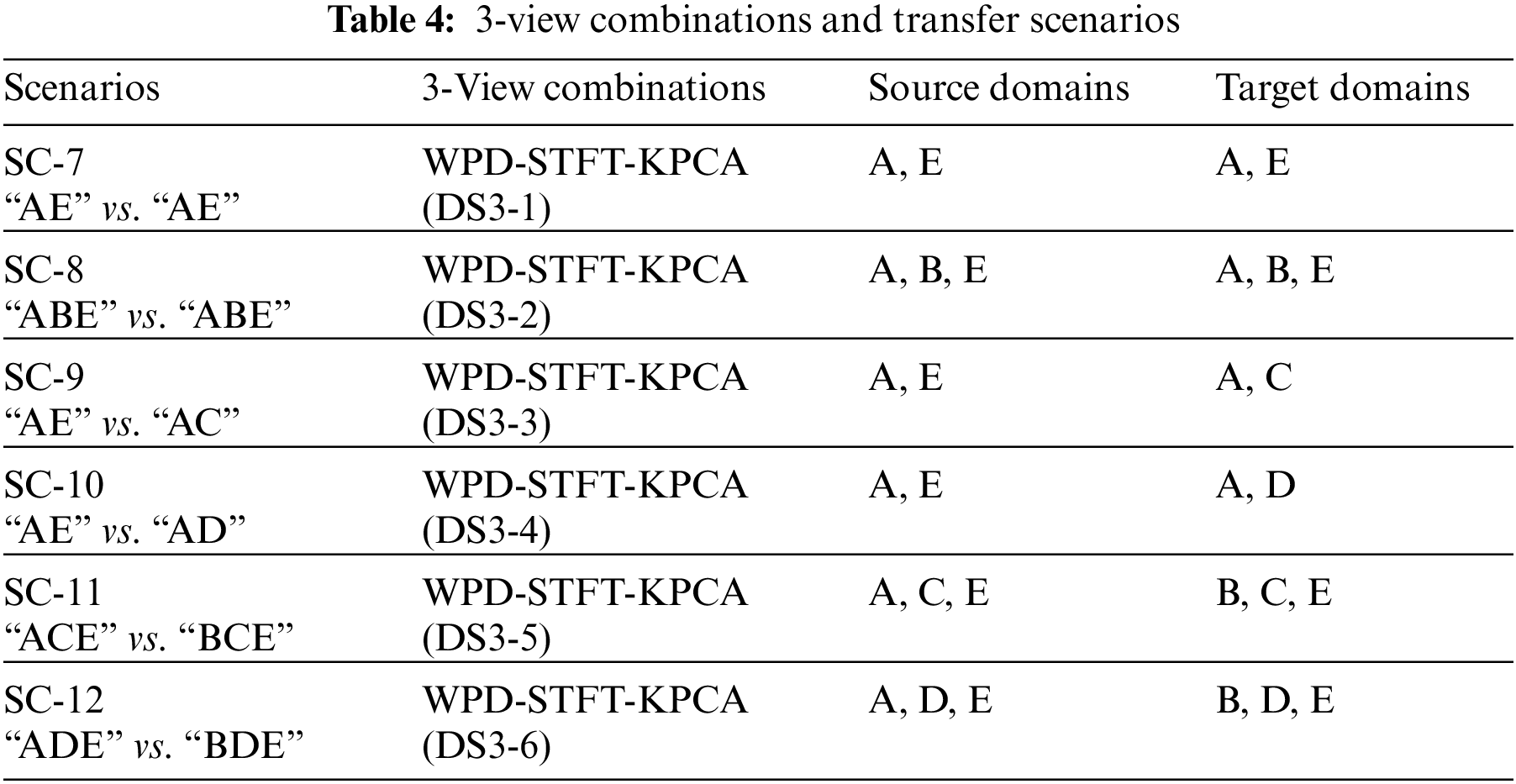
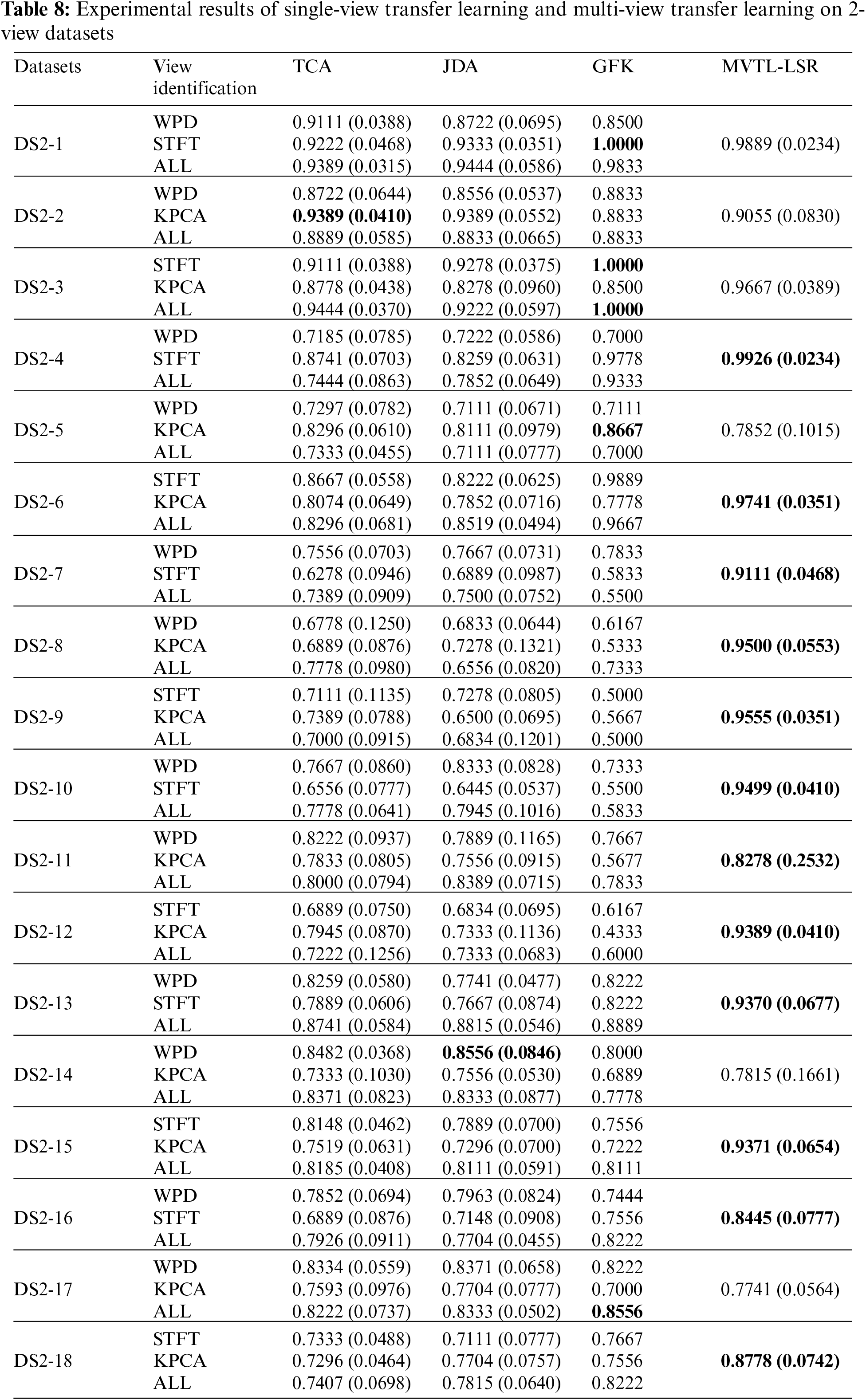
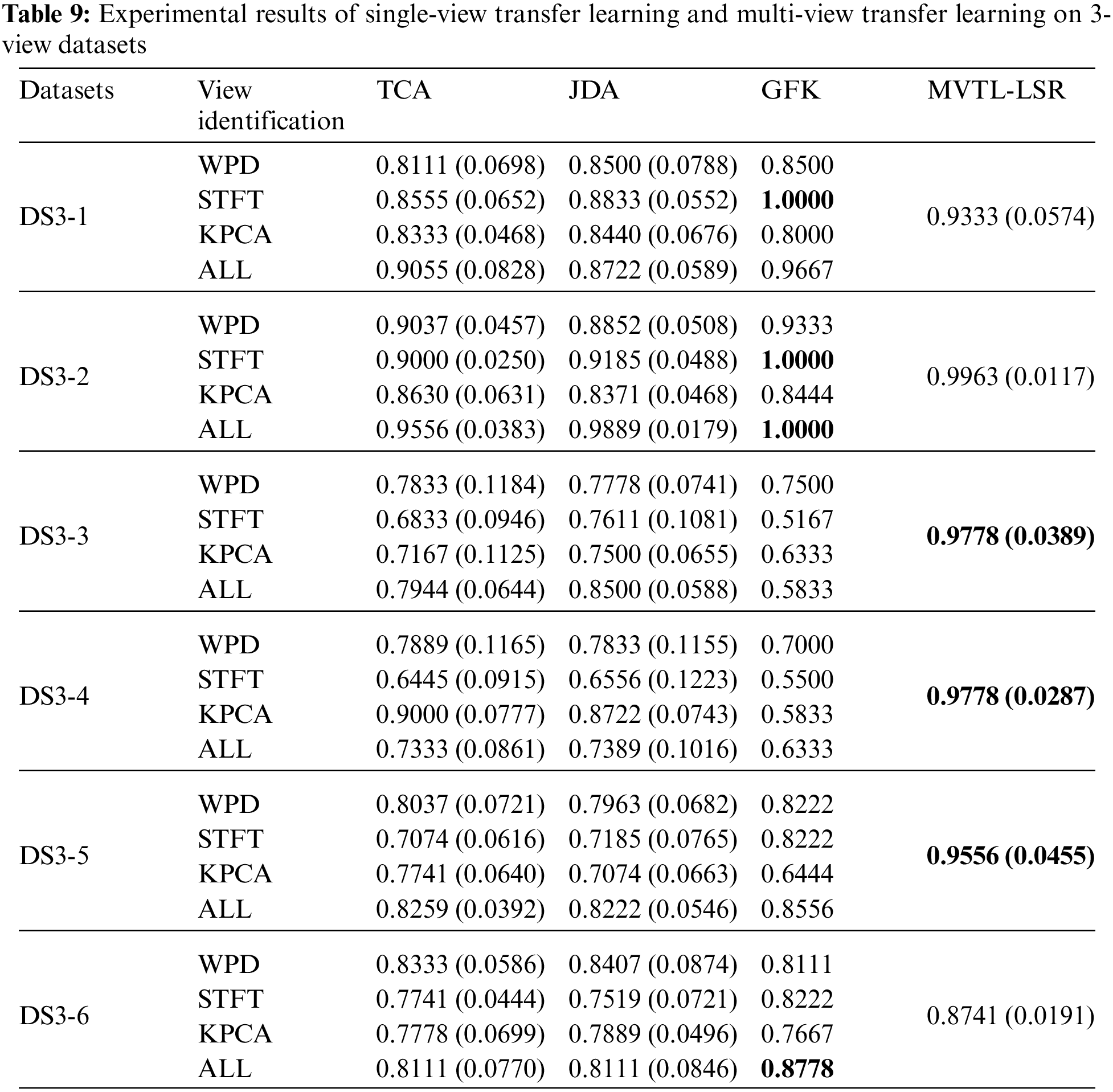
Unlike previous studies using the Bonn dataset, this study treats each feature space as a view. Therefore, we have three views in this study. In addition, since the data distributions of A, B, C, D and E are different, we generate 6 different transfer scenarios by grouping different sub-datasets. For example, we randomly select 70% samples from A and E to generate a source domain, and select the rest 30% samples from A and randomly select 30% samples from D to generate the corresponding target domain. Therefore, in this study, we generate 12 transfer scenarios including 6 2-view scenarios and 6 three-view scenarios, as shown in Tables 3 and 4.

4.3 Experimental Settings

To highlight the performance of the suggested algorithm, four state-of-the-art algorithms are introduced for comparison.

Baseline 1 (MV-NTL-LSR as BL1), which is a multi-view machine learning algorithm. MV-NTL-LSR is trained on the source domain and directly tested on the target domain. MV-NTL-LSR is a non-transfer regression algorithm.

Baseline 2 (MV-NR-LSR, as BL2), which is a multi-view transfer learning algorithm. MV-NR-LSR is trained on the source domain and tested on the target domain by leveraging knowledge learned from the source domain.

Baseline 3 (BL3), which are three single-view transfer learning algorithms, i.e., geodesic flow kernel (GFK), transfer component analysis (TCA), and joint distribution adaptation (JDA), having the following two forms of input data: (i) transfer learning with single-view data; and (ii) transfer learning with multiple-view data stitched and merged into single-view data.

Baseline 4 (BL4), which is the coupled local-global adaptation (CLGA) algorithm proposed by Liu et al. [38]. It transfers the source domain knowledge into the target domain for training in each scenario and updates the view weights in real-time.

All algorithms are implemented in MATLABR2020a and run on a PC with Intel (R) Core (TM) i7-7500U, 8.00 GB with the Windows operating system. Parameter settings are shown in Table 5. 5-cross validation combined with the grid search strategy is used to search for the optimal parameters. All experiments are repeated 10 times and the average accuracy and the standard deviation are recorded.

4.4 Experimental Results and Analysis

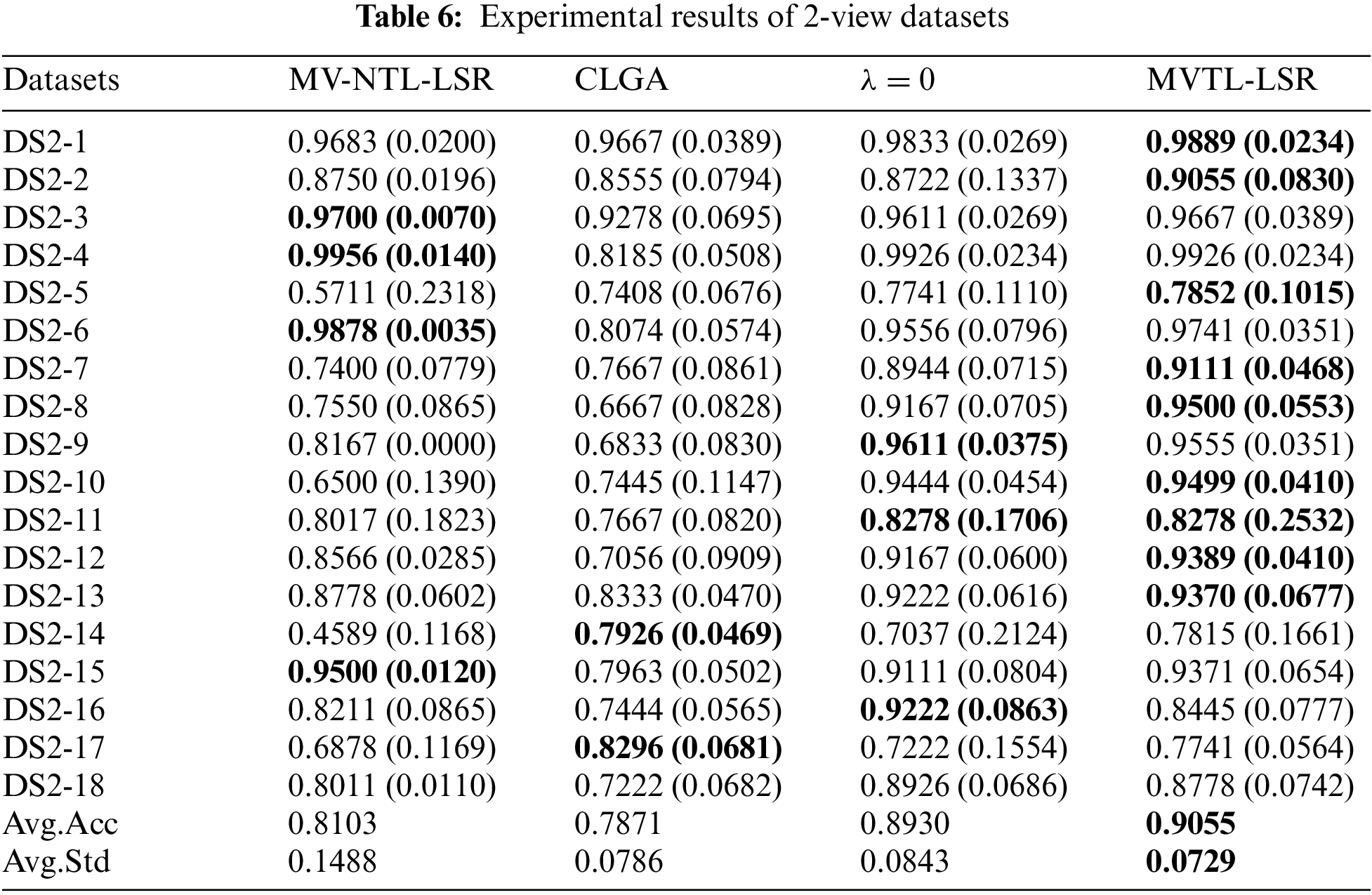
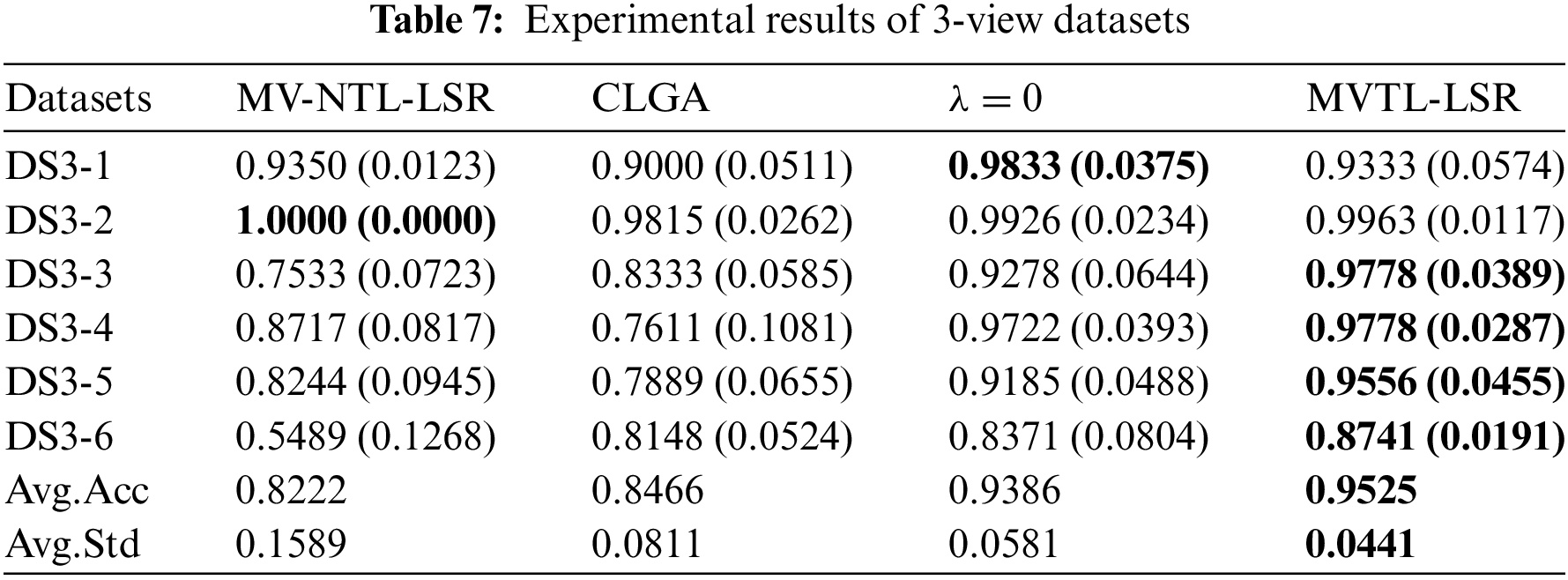
In this section, the average classification performance of the four baselines and the proposed MVTL-LSR are reported, as shown in Tables 6–9. As can be seen that, in scenarios 1, 2, 7, and 8, the classification performance of BL1 and the single-view transfer learning algorithm performs well because the data distributions in the source and target domain are the same. In other scenarios, the proposed MVTL-LSR algorithm achieves the best classification performance on both 2-view and 3-view data sets. Additionally, the comparison results exhibit the following characteristics.

1)   Since BL1 is a straightforward multi-view learning algorithm without knowledge transfer, it is unable to adapt to situations in which the distribution of data in the source and target domains is different. In scenarios 1, 2, 7 and 8, BL1 has similar performance to the proposed MVTL-LSR. However, in other scenarios, MVTL-LSR performs significantly better than BL1. Therefore, the present algorithm is not picky about transfer scenarios.

2)   Regularization is not used in BL2 to prevent the algorithm from overfitting. Comparing BL2 with the proposed MVTL-LSR, it can be found that the classification performance of MVTL-LSR is better than that of BL2.

3)   In BL3, three classical single view transfer learning algorithms are selected for comparison. In scenarios 1, 2, 7 and 8, since the data distribution of the source domain and target domain is the same, on some views, BL3 performs better than MVTL-LSR. We also report the multi-view results of BL3 by directly putting features of each view together. Direct feature stitching is the first solution to multi-view learning, but we prove that it is not the best data processing method through comparison. Measuring the weight of each view can achieve better performance.

4.5 Parameter Sensitivity Analysis

In this section, we perform a sensitivity analysis of the parameters for MVTL-LSR. There are a penalty coefficient λ and two trade-off coefficients η and γ in the proposed objective. In addition, a parameter is used to describe the number of instances ratio in the specific process of conducting the experiment, i.e., R.

4.5.1 Sensitivity Study of Instance-to-Number Ratio

Since the number of instance ratio are randomly selected for optimization in the classification problem, in this experiment we verify the effect of different R values on the overall accuracy of MVTL-LSR. The experimental results for R values between 0.1 and 0.9 are shown in Fig. 5. From the figure, we can observe that the accuracy of MVTL-LSR classification varies with increasing R-value. Based on these experimental results, we show that setting the number of instances ratio R to 0.7 for classification will be for getting more desirable experimental results.

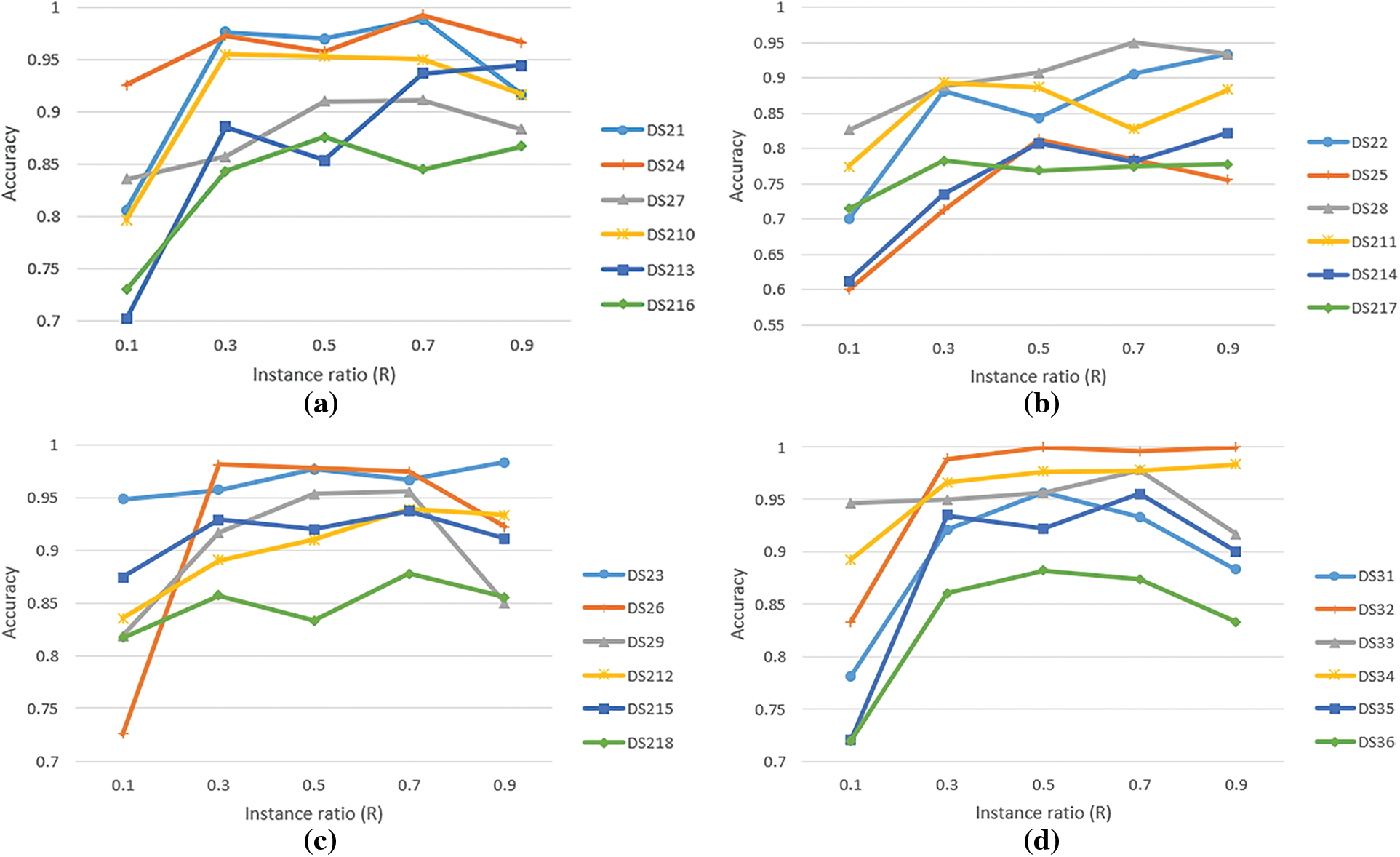
Figure 5: Sensitivity analysis of the dataset instance ratio from different views (a. WPD-STFT; b. WPD-KPCA; c. STFT-KPCA; d. WPD-STFT-KPCA)

4.5.2 Sensitivity Study of λ

In this section, we control the generalization error of the metric with the transformation matrix A by adding a penalty term r(A). Thus, λ in Eq. (5) is the penalty coefficient of the penalty term. To visualize the effect of the penalty term on the accuracy of MVTL-LSR, we sampled three datasets to compare the training accuracy with the testing accuracy, as shown in Fig. 6. From the figure, we can observe that the test accuracy is greater than the training accuracy for λ∈[10−5,105], which indicates the good generalization performance of this algorithm.

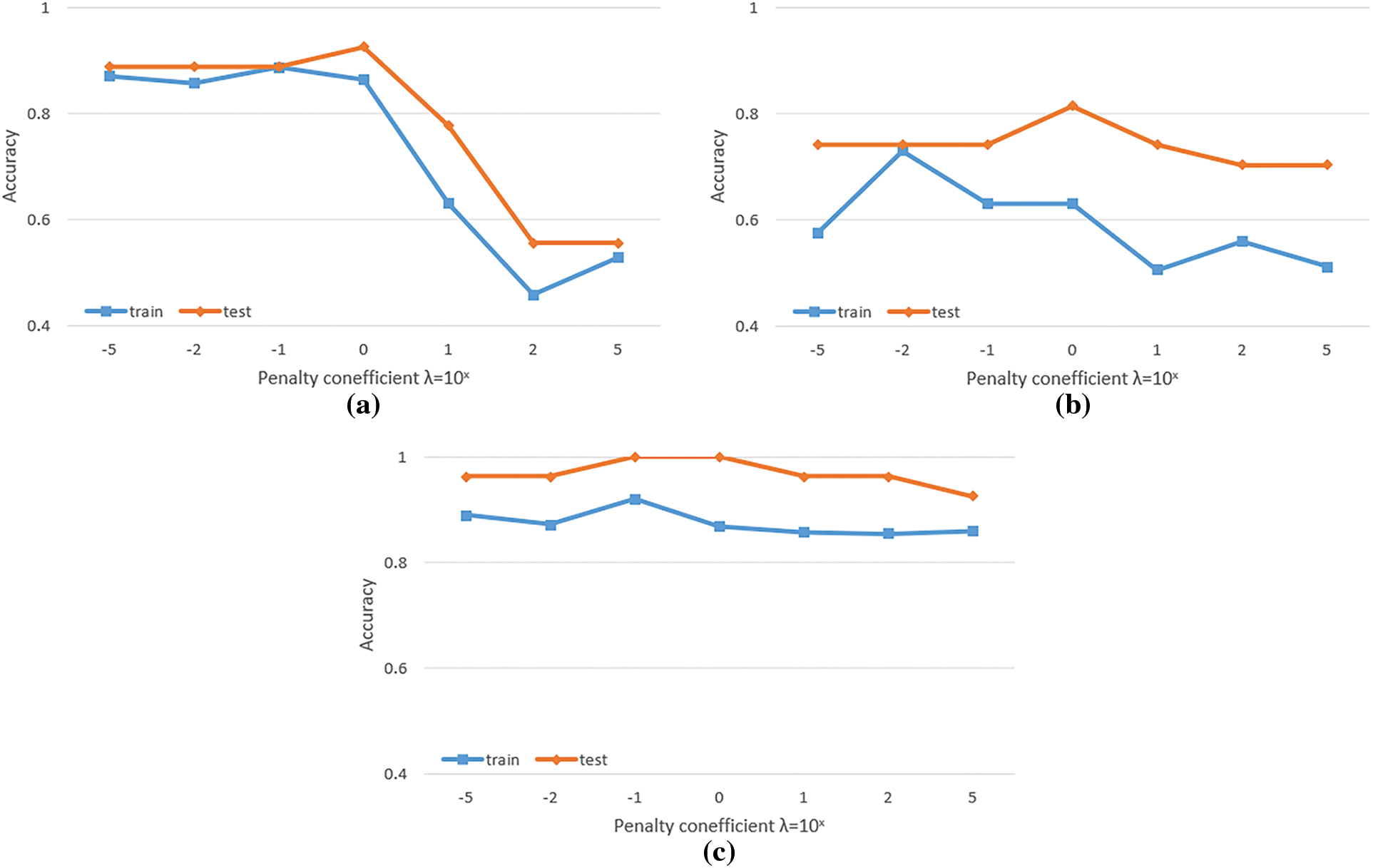
Figure 6: Sensitivity analysis of penalty coefficient λ (a. DS2-16; b. DS2-17; c. DS2-18)

4.5.3 Sensitivity Study of η, γ

Here, we investigated the sensitivity analysis of two trade-off parameters, namely η and γ, in the target algorithm of the MVTL-LSR Eq. (3). For simplicity, we chose to conduct experiments on the scenario DS2-1 dataset, and the results are shown in Fig. 7. It is observed from the figure that MVTL-LSR performs well and is stable when η is set to a relatively large value, such as η≥0.1, and γ is in a large range [10−3,103].

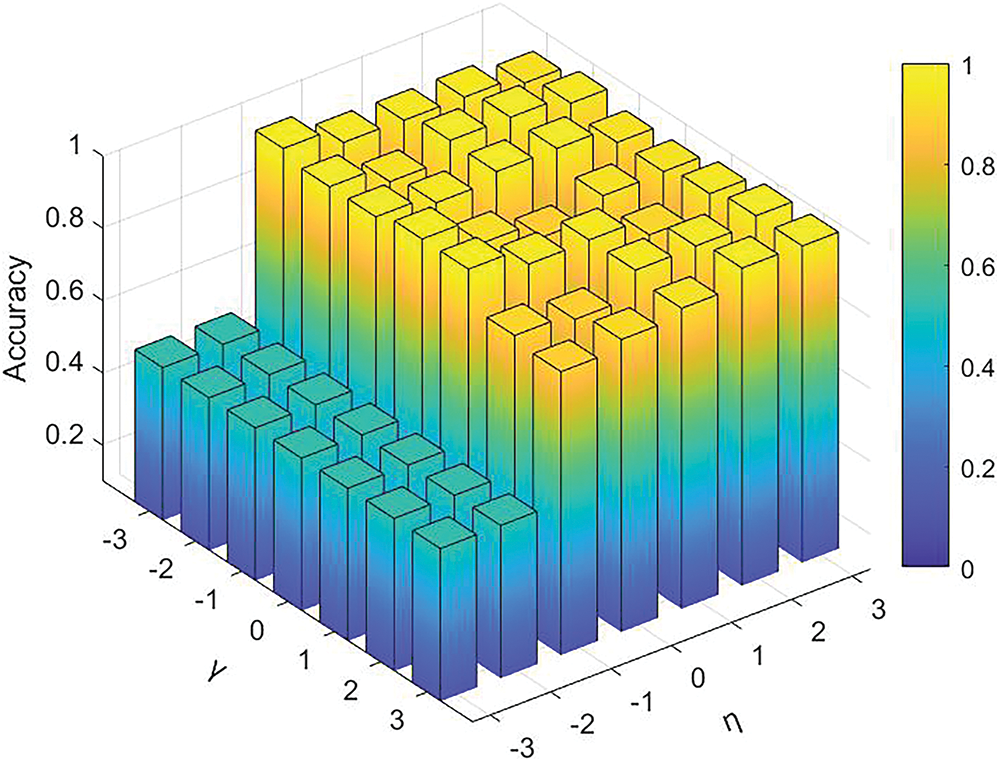
Figure 7: Sensitivity analysis of η and γ

4.5.4 Non-Parametric Statistical Analysis

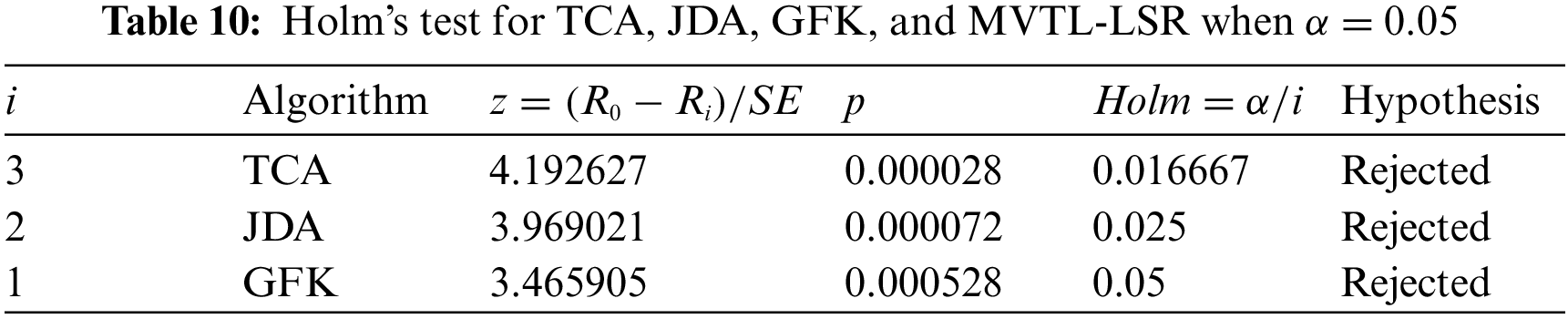
To verify the significant differences between these seven algorithms on 12 scenarios, Friedman’s rank test and Holm’s post hoc test are used. To ensure the comparability of the experimental results, we chose to use the accuracy obtained by the feature stitching method for the subsequent analysis. Depending on the algorithms, we divided them into two groups. One group is single-view transfer learning algorithms (TCA, JDA, GFK, and MVTL-LSR), and the other group is multi-view transfer learning algorithms (MV-NTL-LSR, MV-NR-LSR, CLGA, and MVTL-LSR). The confidence level α set to 0.05.

First, the Friedman rank test is used to calculate the average rank of each group of algorithms. Figs. 8 and 9 shows the ranking results of each group of algorithms. The p value indicates that there are significant differences between each group of algorithms, and MVTL-LSR is the best in each group.

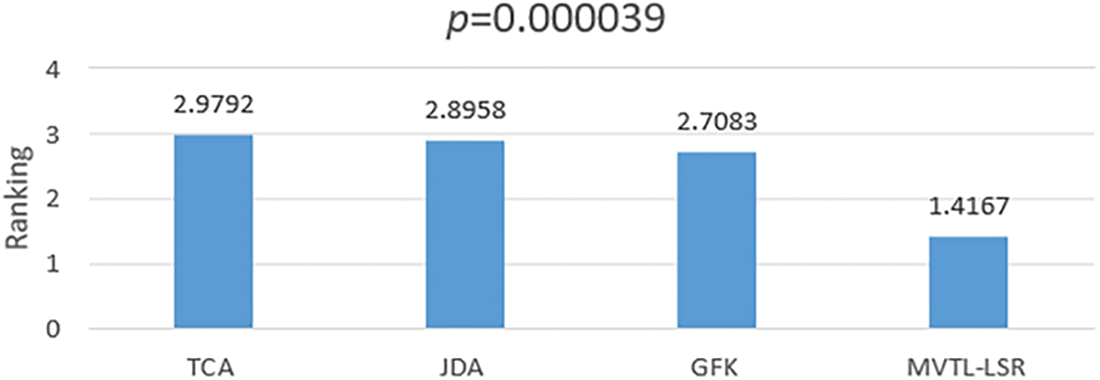
Figure 8: Rank test of TCA, GDA, GFK and MVTL-LSR

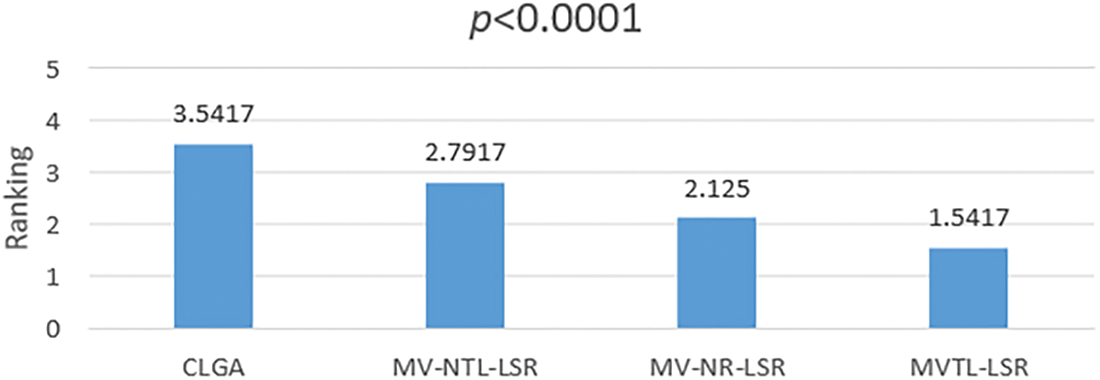
Figure 9: Rank test of CLGA, MV-NTL-LSR, MV-NR-LSR and MVTL-LSR

Secondly, Holm post test is performed on the two groups of algorithms to observe the performance difference between them. The test results for each group are presented in Tables 10 and 11. All algorithms in each group are ranked by the z-values obtained during testing. In the Holm test, the hypothesis that the unadjusted p-value is smaller than the Holm value is rejected. From the observations in Tables 10 and 11, we can see that MVTL-LSR performs the best in comparison with single-view algorithms as well as multi-view algorithms, which indicates that MVTL-LSR is an effective multi-view transfer learning algorithm. Although the MV-NR-LSR hypothesis is not rejected, its corresponding lower p-value still indicates the competitive nature of the MVTL-LSR algorithm.

5  Conclusions

In this study, we propose a multi-view transfer learning algorithm for epileptic EEG signals recognition. First, transformation matrix as knowledge is transformed to the target domain, instead of directly transferring samples or features. In this manner, the security of the source domain data is properly protected on the basis of promising performance. Secondly, the manifold regularization term is introduced to improve the generalization ability of the model. Also, Shannon entropy is introduced to adaptively learn the weight coefficients of each view, which makes it possible to emphasize the contribution of high-quality views in the multi-view learning process. Finally, in the experimental study, we simulate several scenarios to verify the effectiveness of the proposed multi-view transfer learning algorithm. And its superior performance against existing methods is demonstrated through extensive experiments.

The limitation of this study mainly lies in the high computational complexity with respect to the dimension of the input feature space. In our future work, we expect to find a more efficient method to reduce the computational complexity.

Funding Statement:: This work was supported in part by the National Natural Science Foundation of China (Grant No. 82072019), the Shenzhen Basic Research Program (JCYJ20210324130209023) of Shenzhen Science and Technology Innovation Committee, the Shenzhen-Hong Kong-Macau S&T Program (Category C) (SGDX20201103095002019), the Natural Science Foundation of Jiangsu Province (No. BK20201441), the Provincial and Ministry Co-constructed Project of Henan Province Medical Science and Technology Research (SBGJ202103038 and SBGJ202102056), the Henan Province Key R&D and Promotion Project (Science and Technology Research) (222102310015), the Natural Science Foundation of Henan Province (222300420575), and the Henan Province Science and Technology Research (222102310322). The Jiangsu Students' Innovation and Entrepreneurship Training Program (202110304096Y).

Availability of Data and Materials: The source code will be available on https://github.com/didid5/MVTL-LSR.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. R. Mirnezami, J. Nicholson and A. Darzi, “Preparing for precision medicine,” New England Journal of Medicine, vol. 366, no. 6, pp. 489–491, 2012. [Google Scholar] [PubMed]

2. J. C. Wilson, S. Toovey, S. S. Jick and C. R. Meier, “Previously diagnosed influenza infections and the risk of developing epilepsy,” Epidemiology and Infection, vol. 143, no. 11, pp. 2408–2415, 2015. [Google Scholar] [PubMed]

3. S. J. Smith, “EEG in the diagnosis, classification, and management of patients with epilepsy,” Journal of Neurology, Neurosurgery and Psychiatry, vol. 76, no. 2, pp. 2–7, 2005. [Google Scholar]

4. K. S. Anusha, M. T. Mathews and S. D. Puthankattil, “Classification of normal and epileptic EEG signal using time & frequency domain features through artificial neural network,” in 2012 Int. Conf. on Advances in Computing and Communications, Cochin, India, pp. 98–101, 2012. [Google Scholar]

5. Z. Tao, W. Chen and M. Li, “AR based quadratic feature extraction in the VMD domain for the automated seizure detection of EEG using random forest classifier,” Biomedical Signal Processing and Control, vol. 31, no. 2, pp. 550–559, 2017. [Google Scholar]

6. Y. Wang, “Classification of epileptic electroencephalograms signals using combining wavelet analysis and support vector machine,” Journal of Medical Imaging and Health Informatics, vol. 8, no. 1, pp. 62–65, 2018. [Google Scholar]

7. I. Muslea, S. Minton and C. A. Knoblock, “Active learning with multiple views,” Journal of Artificial Intelligence Research, vol. 27, no. 1, pp. 203–233, 2006. [Google Scholar]

8. S. Sun, W. Dong and Q. Liu, “Multi-view representation learning with deep gaussian processes,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 43, no. 12, pp. 4453–4468, 2021. [Google Scholar] [PubMed]

9. K. Li, X. Q. Meng, Z. Cao and X. Sun, “Multi-view learning for high dimensional data classification,” in 2009 Chinese Control and Decision Conference, Guilin, China, pp. 3766–3770, 2009. [Google Scholar]

10. Y. Jiang, J. Liu, Z. Li and H. Lu, “Collaborative PLSA for multi-view clustering,” in Proc. of the 21st Int. Conf. on Pattern Recognition, Tsukuba, Japan, pp. 2997–3000, 2012. [Google Scholar]

11. G. Tzortzis and A. Likas, “Kernel-based weighted multi-view clustering,” in 2012 IEEE 12th Int. Conf. on Data Mining, Brussels, Belgium, pp. 675–684, 2012. [Google Scholar]

12. J. Zhao, X. Xie, X. Xu and S. Sun, “Multi-view learning overview: Recent progress and new challenges,” Information Fusion, vol. 38, pp. 43–54, 2017. [Google Scholar]

13. Z. Zhang and X. Li, “Use transfer learning to promote identification ADHD children with EEG recordings,” in 2019 Chinese Automation Congress, Hangzhou, China, pp. 2809–2813, 2019. [Google Scholar]

14. T. Duan, M. A. Shaikh, M. Chauhan, J. Chu, R. K. Srihari et al., “Meta learn on constrained transfer learning for low resource cross subject EEG classification,” IEEE Access, vol. 8, pp. 224791–224802, 2020. [Google Scholar]

15. C. C. Took, S. Alty, D. M. Lopez, A. Valentin, G. Alarcon et al., “Transfer learning of EEG for analysis of interictal epileptiform discharges,” in 2021 Int. Conf. on e-Health and Bioengineering, Iasi, Romania, pp. 1–4, 2021. [Google Scholar]

16. D. Yarowsky, “Unsupervised word sense disambiguation rivaling supervised methods,” in Proc. of the 33rd Annual Meeting of the Association for Computational Linguistics, Cambridge, Massachussets, USA, pp. 189–196, 1995. [Google Scholar]

17. A. Blum and T. Mitchell, “Combining labeled and unlabeled data with co-training,” in Proc. of the Eleventh Annual Conf. on Computational Learning Theory, Madison, Wisconsin, USA, pp. 92–100, 1998. [Google Scholar]

18. Y. Jiang, Z. Deng, F. L. Chung, G. Wang, P. Qian et al., “Recognition of epileptic EEG signals using a novel multi-view TSK fuzzy system,” IEEE Transactions on Fuzzy Systems, vol. 25, no. 1, pp. 3–20, 2017. [Google Scholar]

19. J. Zhu, K. Li, K. Xia, X. Q. Gu, J. Xue et al., “A novel double-index-constrained, multi-view, fuzzy-clustering algorithm and its application for detecting epilepsy electroencephalogram signals,” IEEE Access, vol. 7, pp. 103823–103832, 2019. [Google Scholar]

20. S. J. Pan and Q. Yang, “A survey on transfer learning,” IEEE Transactions on Knowledge and Data Engineering, vol. 22, no. 10, pp. 1345–1359, 2010. [Google Scholar]

21. P. Jeng, C. S. Wei, T. P. Jung and L. C. Wang, “Low-dimensional subject representation-based transfer learning in EEG decoding,” IEEE Journal of Biomedical and Health Informatics, vol. 25, no. 6, pp. 1915–1925, 2021. [Google Scholar] [PubMed]

22. J. Sameri, H. Zarooshan and M. R. J. Motlagh, “A deep transfer learning training strategy for inter-subject classification of EEG signal,” in 2021 28th National and 6th Int. Iranian Conf. on Biomedical Engineering (ICBME), Tehran, Iran, Islamic Republic of Iran, pp. 188–192, 2021. [Google Scholar]

23. Y. Zhang, H. Li, H. Dong, Z. Dai, X. Chen et al., “Transfer learning algorithm design for feature transfer problem in motor imagery brain-computer interface,” China Communications, vol. 19, no. 2, pp. 39–46, 2022. [Google Scholar]

24. Y. Wang, J. Cao, J. Wang, D. Hu and M. Deng, “Epileptic signal classification with deep transfer learning feature on mean amplitude spectrum,” in 2019 41st Annual Int. Conf. of the IEEE Engineering in Medicine and Biology Society, Berlin, Germany, pp. 2392–2395, 2019. [Google Scholar]

25. Z. Song, B. Deng, J. Wang, G. Yi and W. Yue, “Epileptic seizure detection using brain-rhythmic recurrence biomarkers and ONASNet-based transfer learning,” IEEE Transactions on Neural Systems and Rehabilitation Engineering, vol. 30, pp. 979–989, 2022. [Google Scholar] [PubMed]

26. Z. Xu and S. Sun, “Multi-view transfer learning with adaboost,” in 2011 IEEE 23rd Int. Conf. on Tools with Artificial Intelligence, Boca Raton, FL, USA, pp. 399–402, 2011. [Google Scholar]

27. J. Liu, Y. Wang, Z. Zhang and Y. Mo, “Multi-view moving objects classification via transfer learning,” in The First Asian Conf. on Pattern Recognition, Beijing, China, pp. 259–263, 2011. [Google Scholar]

28. J. Bian, S. Zhang, S. Wang, J. Zhang and J. Guo, “Skin lesion classification by multi-view filtered transfer learning,” IEEE Access, vol. 9, pp. 66052–66061, 2021. [Google Scholar]

29. Y. Jiang, Y. Zhang, C. Lin, D. Wu and C. T. Lin, “EEG-based driver drowsiness estimation using an online multi-view and transfer TSK fuzzy system,” IEEE Transactions on Intelligent Transportation Systems, vol. 22, no. 3, pp. 1752–1764, 2021. [Google Scholar]

30. Q. Abbas, M. E. A. Ibrahim, S. Khan and A. R. Baig, “Hypo-driver: A multiview driver fatigue and distraction level detection system,” Computers, Materials & Continua, vol. 71, no. 1, pp. 1999–2017, 2022. [Google Scholar]

31. X. Fang, Y. Xu, X. Li, Z. Lai, W. K. Wong et al., “Regularized label relaxation linear regression,” IEEE Transactions on Neural Networks and Learning Systems, vol. 29, no. 4, pp. 1006–1018, 2018. [Google Scholar] [PubMed]

32. J. R. Millan and J. Mourino, “Asynchronous BCI and local neural classifiers: An overview of the adaptive brain interface project,” IEEE Transactions on Neural Systems and Rehabilitation Engineering, vol. 11, no. 2, pp. 159–161, 2003. [Google Scholar] [PubMed]

33. F. Liao and F. Wang, “Deriving respiratory signals from ECG by filtering method,” in 2011 3rd Int. Conf. on Computer Research and Development, Shanghai, China, pp. 456–459, 2011. [Google Scholar]

34. C. S. Liu, Y. Tang and J. T. Tang, “Removal of ocular artifact from EEG based on ICA,” Computer Engineering and Applications, vol. 43, no. 17, pp. 230–232, 2007. [Google Scholar]

35. S. Li, “Speech denoising based on improved discrete wavelet packet decomposition,” in 2011 Int. Conf. on Network Computing and Information Security, Guilin, China, pp. 415–419, 2011. [Google Scholar]

36. C. W. N. F. C. W. Fadzal, W. Mansor, L. Y. Khuan and A. Zabidi, “Short-time fourier transform analysis of EEG signal from writing,” in 2012 IEEE 8th Int. Colloquium on Signal Processing and Its Applications, Malacca, Malaysia, pp. 525–527, 2012. [Google Scholar]

37. B. Schölkopf, A. Smola and K. R. Müller, “Kernel principal component analysis,” in Int. Conf. on Artificial Neural Networks, Lausanne, Switzerland, pp. 583–588, 1997. [Google Scholar]

38. J. Liu, J. Li and K. Lu, “Coupled local-global adaptation for multi-source transfer learning,” Neurocomputing, vol. 275, no. 3, pp. 247–254, 2018. [Google Scholar]