An Efficient Three-Party Authenticated Key Exchange Procedure Using Chebyshev Chaotic Maps with Client Anonymity

1  Introduction

The term “Internet of Things (IoT),” which is widely described as “a global network of networked devices uniquely reachable, based on standard communication protocols,” may have been coined by Kevin Ashton from Procter & Gamble in 1998 [1]. Since then, usage of IoT has sharply increased in part because of the digital revolution (such as widespread connectivity even in developing nations and the ongoing improvement of information and communication technologies). Mobile users may make payments for goods online, pay bills, and conduct other electronic transactions by subscribing to various remote services thanks to the rapid development of low-power and highly efficient networks. Despite being very portable, mobile computing devices are typically insecure and superficial to steal or lose. Without security measures, an unauthorized person might access the data kept on them. For instance, if the data is “sniffed out of the air” during wireless connections or any malware is introduced, intruders may obtain access illegally. Even more severe consequences, such as disabled devices, the loss of personal data, the revelation of non-public data, or charges of misused usage against the device owner, may occur from a lack of authentication and privacy. In addition to the data they hold, mobile computing devices pose a serious security risk since they may give clients access to other services that store or show non-public data. Before distant servers offer clients services for nearly all of these transactions, mutual authentication and client privacy is necessary for the key exchange. Applications for industrial networks [2], wireless sensor networks [3,4], dispersed networks [5–7], as well as Radio Frequency Identification (RFID) systems [8–10] in particular, place a high priority on authentication and privacy.

Many analogous procedures [11–14] have been proposed by researchers to ensure the security of secret keys that are exchanged over an insecure public network, including the Authenticated Key Exchange Procedure (AKEP) based on passwords. The AKEP based on password enables two parties to agree on a standard session key across an insecure public network while maintaining a single memorable password [15–17]. Generally speaking, provided clients use strong passwords that offer adequate entropy, password-based authentication can withstand brute force and dictionary assaults. However, one inherent issue with password-based authentication exists: consumers struggle to memorize long text sequences. Therefore, even though they are aware that the passwords might not be secure, most clients choose memorable passwords, making it difficult to defend against numerous attacks.

Bellovin et al. [18] first introduced the AKEP based on the password procedure in 1992. After ten years, other related procedures have been presented, including the two-party AKEP [11,12] and the three-party AKEP [19,20]. Two-party AKEPs, on the other hand, are not appropriate in the significant peer-to-peer architecture, according to Hassan et al. [21]. Some of the three-party AKEPs are also insufficiently efficient or secure for usage in real-world applications. Recently, in 2005 and 2007, respectively, Abdalla et al. [22], Lu et al. [23], and Algubili et al. [24] introduced three effective three-party AKEPs. Sadly, both methods were still susceptible to offline or online dictionary attacks that were undetectable.

Three-party AKEP based on the password was suggested by Deng et al. [25] in 2009, and it was deemed secure by the universal compostable framework. Deng et al. AKEP, however, is vulnerable to an offline dictionary attack by any other client, according to Yuan et al. [26]. Huang’s [27] procedure could not withstand undetectable online dictionary attacks and key-compromise impersonation attacks, according to Yoon et al. [28], who presented a protocol in 2011. Later, Yoon et al. [29] introduced a different procedure and demonstrated how Lou et al. [30] procedure was susceptible to an attacker’s off-line password guessing attempts. The security flaws in Huang’s [27] procedure were later discovered by Wu et al. [31], who also suggested a three-party AKEP based on the password to fix the issues with Huang’s procedure. The procedure developed by Wu et al. required the most difficult computations due to its numerous exponential computations. Also, their procedure was unable to guarantee client anonymity. Table 1 provides a brief comparison of related research with our proposed AKEP.

1.1 Motivation

It is challenging to create a three-party AKEP that is both lightweight and secure. Numerous three-party-AKEP have been put forth and afterward shown to be insecure. For instance, Zhang et al. [32] suggested a three-party-AKEP based on the standard model’s verification feature in 2019. It employs anonymous authentication for server and client authentication to strengthen procedure security, which raises computation costs. A three-party-AKEP based on the verification element on the ideal lattice was proposed by Shu et al. [33] in 2021. It reduces space complexity but requires six rounds of communication to negotiate a session key, increasing communication overhead. Peikert’s [34] error reconciliation mechanism was adopted by Shu et al. [33].

1.2 Contribution

This paper introduced a three-party-AKEP with user anonymity using Chebyshev chaotic maps to increase security and efficiency.

•   The presented three-party AKEP encrypts and decrypts the data sent by the user or the server using Chebyshev chaotic maps.

•   The presented three-party AKEP can also offer client and server mutual authentication and client anonymity to ensure that clients’ identities, which are conveyed via an insecure public network, are guaranteed.

•   The presented three-party AKEP has low computing and communication costs and can fend off various attacks, according to the security, statistical experiment and performance analysis.

1.3 Paper Organization

The rest of this paper is structured as follows. The definitions of Chebyshev chaotic maps are introduced briefly in Section 2. Section 3 presents the proposed AKEP. In Section 4, we analyze the projected AKEP and demonstrate that it can withstand several attacks. Section 5 will examine the performance of our AKEP using the former protocols and statistical experiments. Finally, in Section 6, we present our conclusion.

2  Background and Material

The section provides a brief overview of the trigonometry in Galois fields, Chebyshev polynomials over Galois fields that are used in the proposed procedure, and the necessary security notations.

2.1 Trigonometry in Galois Fields (𝒢ℱ)

Here we assume that calculations over 𝒢ℱ(𝓆1), where 𝓆1=𝓅ı, where ı is a positive (+) integer and 𝓅 is an odd prime, are done modulo an irreducible polynomial f(𝓋) of degree whose coefficients are in 𝒢ℱ(𝓅).

Definition 1. The set 𝒢𝒥(𝓆1)={𝓈+𝓉𝓇,∀𝓈,𝓉∈𝒢ℱ(𝓆1)} contains the Gaussian integers over 𝒢ℱ(𝓆1) in a way that 𝓇2=−1 is a quadratic non-residue over 𝒢ℱ(𝓆1), i.e., 𝓆1≡3(mod 4). Specifically, the extension field 𝒢ℱ(𝓆12) is isomorphic to the “complex” structure 𝒢ℱ(𝓆1), where each component χ=𝓈+𝓉𝓇 is composed of two parts, 𝓈={χ} (the “actual” part) and 𝓉={χ} (the “imaginary” part).

Definition 2. Let χ>0 represent an element of 𝒢ℱ(𝓆1), where 𝓆1≡3(mod4) and has the multiplicative order indicated by ord (χ). The τ−trigonometric functions identified with τ−cosine and τ−sine are calculated modulo f(𝓋) as

cosχ(𝓏): =χ𝓏+χ−𝓏2 and sinχ(𝓏): =χ𝓏−χ−𝓏2𝓇(1)

In this case, we modify the notational scheme established in [35]. Properties like the unit circle and the addition of arcs [35] are naturally shared by the τ−trigonometric functions and the conventional real-valued trigonometric functions. The τ-cosine function has period ord(χ) and even symmetry, as shown in Eq. (1).

cosχ(𝓏)=cosχ(−𝓏(mod ord(χ)))(2)

The description of the τ-cosine function also depends heavily on the surrounding lemmas. Reference [36] discusses how to prove lemmas, assertions, and theorems.

Lemma 1. For 1≤𝓏,𝓋≤⌊ord(χ)−1)/2⌋, where ⌊.⌋ denotes the flour function of the argument, cosχ(𝓋)=cosχ(𝓏)⇔𝓋=𝓏.

Definition 3. The unimodular set of 𝒢𝒥(𝓆1), signified by 𝒢1, is the prearrangement of exponents χ=(𝓈+𝓉𝓇,)∈𝒢𝒥(𝓆1), such that 𝓈2+𝓉2≡1(mod f(𝓋)).

Proposition 1.χ𝓆1+1≡|χ|2≡𝓈2+𝓉2≡1(mod f(𝓋)).

Proposition 2. The structure (𝒢1,*) is a cyclic group of order (𝓆1+1).

Lemma 2. If χ=(𝓈+𝓉𝓇,)∈𝒢𝒥(𝓆1) is a unimodular exponent, then cosχ(𝓏)=ℛ{χ𝓏},𝓏=0,1,…,ord(χ)−1.

Example 1. Consider 𝒢ℱ(27). The primitive polynomial f(𝓋)=𝓋3+2𝓋+1 is used to make the Galois field. Let χ1=(𝓋2+2𝓋)+(𝓋2+𝓋+1)𝓇 be a unimodular element with order ord(χ1)=28 in 𝒢𝒥(27). Table 2 includes all possible values for cosχ1(𝓏). By choosing a specific element χ1∈𝒢𝒥(𝓆1) with multiplicative order ord{𝒥χ1}, its τ−cosine function may be expressed as cosχ1(𝓏):Ɀord(χ1)→𝒥χ1, where 𝒵ord(χ1) is the set of integers modulo ord(χ1) and 𝒥χ1 is the image set of cosχ1. Note that  ord{𝒥χ1}=15, which means that the function arccosχ1(𝓏) is not defined for each 𝓏∈𝒢ℱ(27).

Even if χ1∈𝒢𝒥(𝓆1) has the highest possible multiplicative order (𝓆1+1), as shown in Example 1, the function arccosχ1(𝓏) is not described for all 𝓏∈𝒢ℱ(𝓆1). Thus, we must select a component χ2(≠χ1) yielding 𝒥χ1∪𝒥χ2=𝒢ℱ(𝓆1) in order to calculate the inverse τ-cosine function of the components that are in 𝒢ℱ(𝓆1) but not in 𝒥χ1. The following theorem provides evidence for the existence of such a factor.

Theorem 1. Let χ1∈𝒢𝒥(𝓆1) be a unimodular component such that ord χ1=𝓆1+1 and χ2∈𝒢𝒥(𝓆1) such that ord (χ2)=𝓆1−1. Then, 𝒥χ1∪𝒥χ2=𝒢ℱ(𝓆1).

Example 2. Let χ2=𝓋 be a component of order 26 in 𝒢ℱ(27), corresponding to the Galois fields produced by the fundamental polynomial f(𝓋)=𝓋3+2𝓋+1. The full range of values for cosχ2(𝓏) is displayed in Table 3. Be aware that if we consider the set 𝒥χ1 (see Example 1), we have 𝒥χ1∪𝒥χ2=𝒢ℱ(𝓆1) because χ2 was chosen by Theorem 1.

2.2 Chebyshev Polynomials (CP) over Galois Fields

In this section, we will look at the properties of CP over Galois fields. There is a definition in [37] that uses the τ-cosine function and is in perfect relationship with the CP over ℛ (real numbers) [38].

Definition 4. The CP over 𝒢ℱ(𝓆1) are defined as

Υ𝒹(𝓏):=cosχ(𝒹×cosχ−1(𝓏))(mod f(𝓋)),(3)

It can be seen that Eq. (3) is analogous to the arc τ-cosine products. Using the De Moivre, we may generalize a similar situation to real numbers. This yields polynomials of degree 𝒹 as far as τ-cosines of the respective arcs [38]. However, a simple recurrence relation can be used to obtain Chebyshev chaotic maps for various approximations of 𝒹. This relationship is determined from Definition 4 for Galois fields via the formula for adding arcs [35], which is

Υ𝒹(𝓏)=2𝓏Υ𝒹−1(𝓏)−Υ𝒹−2(𝓏)(modf(𝓋)),(4)

where 𝓏∈𝒢ℱ(𝓆),𝒹∈𝒩,Υ0(𝓏)=1 and Υ1(𝓏)=𝓏. The following is the periodicity of CP modulo f(𝓋).

Proposition 3. Let χ>0 be an exponent of 𝒢𝒥(𝓆) such that ord(χ)=𝒩. If 𝓏∈𝒥χ,then Υ𝒶𝒩±𝒹(𝓏)=Υ𝒹(𝓏),𝒶∈𝓏.

Proof: From Definition 4, we have

Υ𝒶𝒩±𝒹(𝓏)=cosχ((𝒶𝒩±𝒹)×cosχ−1(𝓏)))(mod f(𝓋)))

After using the formula for the extension of arcs, we can reformulate the preceding statement as

Υ𝒶𝒩±𝒹(𝓏)=cosχ(𝒶𝒩×cosχ−1(𝓏))cosχ(𝒹×cosχ−1(𝓏))

∓sinχ(𝒶𝒩×cosχ−1(𝓏))sinχ(𝒹×cosχ−1(𝓏))

Since ord(χ)=𝒩, applying Definition 2, we know that

cosχ(𝒶𝒩×cosχ−1(𝓏))=1 and sinχ(𝒶𝒩×cosχ−1(𝓏))=0. As a result, we may simplify the last requirement to

Υ𝒶𝒩±𝒹(𝓏)=cosχ(𝒹×cosχ−1(𝓏))=Υ𝒹(𝓏)

If we need to estimate Υ𝒹(𝓏) for specific values of 𝓏, and prime power, the restriction that Definition 4 imposes on 𝓏∈𝒥χ can be eliminated. In this sense, it is possible to use Eq. (4) without relying on the calculation of τ-trigonometric functions.

The semigroup possessions and the chaotic possessions are two significant characteristics that the Chebyshev polynomials display [39,40].

(1) The semigroup possessions:

Υ𝓋(Υ𝓊(𝓋))=cos⁡(𝓋cos−1⁡(cos⁡(𝓊cos−1⁡(𝓋))))

=cos⁡(𝓋𝓊cos−1⁡(𝓋))=Υ𝓊𝓋(𝓋)

=Υ𝓊(Υ𝓋(𝓋))

𝓋 and 𝓊 are (+) integer numbers and 𝓋∈[−1,1].

(2) The chaotic possessions:

The Chebyshev polynomial map Υ𝓀(𝓋): [−1,1]→[−1,1] of degree 𝓀 is a chaotic map when the degree 𝓀>1 and the (+) Lyapunov exponent λ=ln ⁡𝓀>0. Its invariant density is 𝒻*(𝓋)=1/(π1−𝓋2).

It is challenging to solve in polynomial time the following two CP problems [36,38,39]:

(a)   The discrete logarithm problem (DLP) is defined as the task of determining the number 𝓋 such that Υ𝓋(𝓋)=𝓌 given the two elements 𝓋 and 𝓌.

(b)   The Diffie-Hellman problem (DHP) is defined as the task of computing the value Υ𝓋𝓊(𝓋) given three elements 𝓋, Υ𝓋(𝓋), and Υ𝓊(𝓋).

3  The AKEP Based on Chebyshev Chaotic Maps

The projected procedure with user anonymity using extended chaotic maps is detailed in depth in this section. Table 4 summarizes the notations utilized in our protocol.

At first, the distant server 𝒥𝒮 chooses a random numbers 𝓊∈R𝒢ℱ(𝓆1) and 𝓋∈R𝒢ℱ(𝓆1), then calculates its public key 𝒫≡Υ𝓊(𝓋)(modf(𝓋)). The remote server 𝒥𝒮 conceals its private key 𝓊. In our protocol, we assume that the clients, 𝒞1 and 𝒞2, have previously established the remote server 𝒥𝒮’s shared secret key-sharing passwords 𝓅𝓌𝒹𝒞1 and 𝓅𝓌𝒹𝒞2. The remote server 𝒥𝒮 distributes the public constraints (𝒫,𝓋,ℏ(⋅),f(𝓋)) to all network participants. Fig. 1 depicts a simplified depiction of the suggested protocol. The following steps summarize the details of the proposed protocol from this point forward:

Figure 1: Chebyshev-based Decisional Diffie-Hellman problem

(1) Client 𝒞1 selects an integer 𝓋 at random and calculates the following:

   R𝒞1≡Υ𝓋(𝓋)(mod f(𝓋)), Υ𝒞1≡Υ𝓋(𝒫)(mod f(𝓋)), 𝒞1IDi=𝒞1⨁ℏ(Υ𝒞1),

   Υ𝒞1,𝓈=ℏ(𝒞1∥𝒞2∥𝒥𝒮∥𝒞1IDi∥𝓅𝓌𝒹𝒞1∥Υ𝒞1∥𝓉1).

   Client 𝒞1 sends (𝒞1IDi,R𝒞1,Υ𝒞1,𝓈,𝓉1) to client 𝒞2.

(2) The client then sends back the response (𝒞1IDi,R𝒞1,Υ𝒞1,𝒮,𝓉1).

   𝒞2 selects an integer at random. 𝓌 and calculates the following

   R𝒞2≡Υ𝓌(𝓋)(mod f(𝓋)), Υ𝒞2≡Υ𝓌(𝒫)(modf(𝓋)),𝒞2IDi=𝒞2⨁ℏ(Υ𝒞2),

   Υ𝒞2,𝒮=ℏ(𝒞2∥𝒥𝒮∥𝒞2IDi∥𝓅𝓌𝒹𝒞2∥Υ𝒞2).

   The second client, 𝒞2, then transmits the remote server, 𝒥𝒮, the following data: (𝒞1IDi,R𝒞1,Υ𝒞1,𝒮,𝒞2IDi,R𝒞2,Υ𝒞2,𝒮,𝓉1).

(3) When receiving (𝒞1IDi,R𝒞1,Υ𝒞1,𝓈,𝒞2IDi,R𝒞2,Υ𝒞2,𝓈,𝓉1), the server 𝒥𝒮 first verifies the accuracy of 𝓉1 by determining whether the equation 𝓉′−𝓉1>Δ𝓉 holds, where 𝓉′ is the time at which the server gets the messages from 𝒞2. Δ𝓉 stands for the predefined. In the event that the equation is incorrect, the server 𝒥𝒮 computes Υ𝒞1′≡Υ𝓊(R𝒞1)(mod f(𝓋)), Υ𝒞2′≡Υ𝓈(R𝒞2)(mod f(𝓋)), 𝒞1′=𝒞1IDi⨁ℏ(Υ𝒞1′), and 𝒞2′=𝒞2IDi⨁ℏ(Υ𝒞2′) and uses them to check Υ𝒞1,𝓈 and Υ𝒞2,𝓈 respectively. The protocol is ended by 𝒥𝒮 if the values are incorrect. If not, 𝒥𝒮 calculates Υ𝓈,𝒞1=ℏ(𝒞1′∥𝒞2′∥Υ𝓈∥𝓅𝓌𝒹𝒞1∥Υ𝒞1′), Υ𝓈,𝒞2=ℏ(𝒞1′∥𝒞2′∥𝒥𝒮∥𝓅𝓌𝒹𝒞2∥Υ𝒞2′), and 𝒞1IDj=𝒞1′⨁ℏ(Υ𝒞2′), and then sends (Υ𝓈,𝒞1,Υ𝓈,𝒞2,𝒞1IDj) to client 𝒞2.

(4) After receiving (Υ𝓈,𝒞1,Υ𝓈,𝒞2,𝒞1IDj), client 𝒞2 computes 𝒞1″=𝒞1IDj⨁ℏ(Υ𝒞2) and uses Υ𝒞2 to validate Υ𝓈,𝒞2. Client 𝒞2 stops the protocol if the value is invalid. Else, both server 𝒥𝒮 and client 𝒞2 are authenticated, and client 𝒞2 calculates the shared session key SK≡Υ𝓌(R𝒞1)(mod f(𝓋)) and 𝓈𝒞1𝒞2=ℏ(SK∥𝒞1″∥𝒞2). Lastly, 𝒞2 sends (R𝒞2,Υ𝓈,𝒞1,𝓈𝒞1𝒞2) to client 𝒞1.

(5) Client 𝒞1 initially verifies the legitimacy of Υ𝓈,𝒞1 using Υ𝒞1 after obtaining (R𝒞2,Υ𝓈,𝒞1,𝓈𝒞1𝒞2). The protocol is ended by 𝒞1 if the value is invalid. If not, client 𝒞1 calculates the shared session key SK≡Υ𝓋(R𝒞2)(mod f(𝓋)) and verifies that 𝓈𝒞1𝒞2=ℏ(SK∥𝒞1∥𝒞2) is valid. 𝒞1 ends the protocol if it doesn’t hold. Otherwise, the shared session key SK is agreed upon, and the server 𝒥𝒮 and user 𝒞1 are both authenticated. Client 𝒞1 and 𝒞2 can communicate securely using the shared session key SK. One session is all that the shared session key SK is used for.

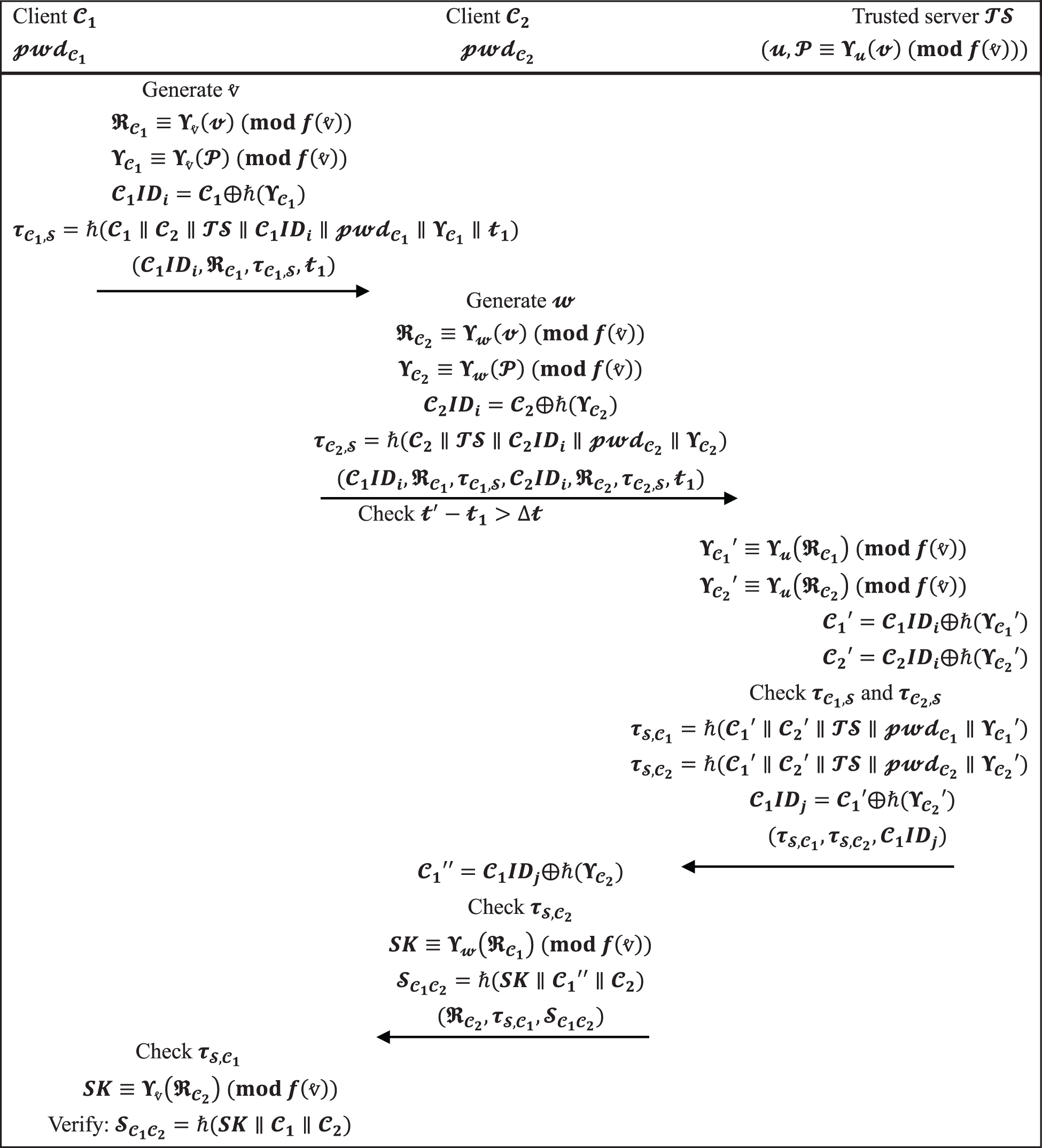
4  Security Investigation and Discussion

In this segment, we examine the security and performance of our presented procedure and demonstrate its ability to withstand various attacks. Here, we explain several security analyses in our proposed process.

Proposition 4.1: The presented AKEP can accomplish off-line dictionary attacks.

Proof: The attacker might deduce the password from the element Υ𝒞1,𝓈 or Υ𝒞2,𝓈 in the messages (𝒞1IDi,R𝒞1,Υ𝒞1,𝓈,𝓉1) or (𝒞1IDi,R𝒞1,Υ𝒞1,𝓈,𝒞2IDi,R𝒞2,Υ𝒞2,𝓈,𝓉1). Client 𝒞1 and 𝒞2 generate Υ𝒞1 or Υ𝒞2, respectively, according to the difficulty of the chaotic map based DLP issue, and without knowing either of these, the attacker cannot validate the password. Because of this, our procedure is secure from dictionary attacks in the background.

Proposition 4.2: The presented AKEP can accomplish undetectable online dictionary attacks.

Proof: The attacker may attempt to impersonate a legitimate client by intercepting the messages (𝒞1IDi,R𝒞1,Υ𝒞1,𝓈,𝓉1) or (𝒞1IDi,R𝒞1,Υ𝒞1,𝓈,𝒞2IDi,R𝒞2,Υ𝒞2,𝓈,𝓉1). However, unless the attacker has successfully guessed the correct password, they are unable to send a new valid message (𝒞1IDi,R𝒞1,Υ𝒞1,𝓈,𝒞2IDi,R𝒞2,Υ𝒞2,𝓈,𝓉1) to the trustworthy server. Additionally, the attacker will run into the the chaotic map-based DLP issue if they attempt to guess the password. As a result, our presented procedure can withstand attacks using an undetected online dictionary.

Proposition 4.3: The presented AKEP can accomplish detectable online dictionary attacks.

Proof: The attacker may attempt to impersonate a legitimate client by intercepting the messages (𝒞1IDi,R𝒞1,Υ𝒞1,𝓈,𝓉1) or (𝒞1IDi,R𝒞1,Υ𝒞1,𝓈,𝒞2IDi,R𝒞2,Υ𝒞2,𝓈,𝓉1). However, unless the attacker has successfully guessed the correct password, they are unable to send a new valid message (𝒞1IDi,R𝒞1,Υ𝒞1,𝓈,𝒞2IDi,R𝒞2,Υ𝒞2,𝓈,𝓉1) to the trustworthy server. Additionally, the server will verify that Υ𝒞1,𝓈 and Υ𝒞2,𝓈 are valid. Therefore, if an attacker sends an invalid message to the server, the attacker will be found. In that instance, our presented procedure is secure against detectable online dictionary attacks.

Proposition 4.4: The presented AKEP can counterattack replay and impersonation attacks.

Proof: A client’s messages may be intercepted by the attacker, who may then replay them to the server in the subsequent run. However, by verifying the accuracy of the timestamp 𝓉1, the server was able to identify the attack. The attacker may potentially eavesdrop on server messages and repeat them to the client. However, the new random integers 𝓋 and 𝓌 were produced by the clients. The attack might then be discovered by clients 𝒞1 and 𝒞2, respectively, by confirming the accuracy of Υ𝓈,𝒞1 and Υ𝓈,𝒞2. Any changes to the preceding parameters during the authentication phase result in discrepancies between the supplied parameters and the received hash value, and the authentication request fails. An attacker cannot replay or change the server authentication message using the same reasoning described previously. As a result, our presented procedure is resistant to both replay and user impersonation attacks.

Proposition 4.5: The presented AKEP can achieve user anonymity.

Proof: The attacker may listen in on the client’s conversation with the trusted server and attempt to identify the client’s true identity to gather some of the client’s security-sensitive data. The real identities of clients 𝒞1 and 𝒞2 are shielded in our proposed procedure by 𝒞1IDi=𝒞1⨁ℏ(Υ𝒞1), and 𝒞2IDi=𝒞2⨁ℏ(Υ𝒞2), respectively. The attacker will have to calculate Υ𝒞1 and Υ𝒞2 and deal with the chaotic map-based DLP problem. As a result, our presented procedure can offer the user a high level of anonymity.

Proposition 4.6: The presented AKEP can accomplish mutual authentication.

Proof: Mutual authentication between the client and the server is possible with our presented procedure. Step 3 of our procedure requires the server 𝒥𝒮 to validate Υ𝒞1,𝓈 and Υ𝒞2,𝓈 to authenticate clients 𝒞1 and 𝒞2. To authenticate server 𝒥𝒮, clients 𝒞1 and 𝒞2 must also verify the validity of Υ𝓈,𝒞1 and Υ𝓈,𝒞2. If an attacker attempts to forge messages, they will encounter both chaotic map-based DLP and chaotic map-based DHP issues. As a result, because both the client and the trusted server can authenticate each other, mutual authentication is achieved. As a result, mutual authentication is achieved because both the client and the trusted server can authenticate each other.

Proposition 4.7: The presented AKEP can prevent denial-of-service (DoS) attacks.

Proof: When 𝒞2 receives the message (𝒞1IDi,R𝒞1,τ𝒞1,𝓈,𝓉1) from 𝒞1, 𝒞2 first verifies the timestamp’s accuracy. If it is invalid, 𝒞2 throws the message away. If not, it calculates a value to compare with the received value: (𝒞1IDi,R𝒞1,Υ𝒞1,𝓈,𝒞2IDi,R𝒞2,Υ𝒞2,𝓈,𝓉1). DoS occurs when an attacker uses the same or different identities to access a specific resource in a hugely and simultaneously. Because the system can preserve the session, access by the same identity to the same resource can be restricted to only one session at a time. The genuine identities of clients 𝒞1 and 𝒞2 are concealed in our suggested process by 𝒞1IDi=𝒞1⨁ℏ(Υ𝒞1) and 𝒞2IDi=𝒞2⨁ℏ(Υ𝒞2), respectively. However, the presented procedure can mitigate DoS attacks to some extent. As described in Section 3(3), the proposed procedure exploits the advantages of timestamp. The proposed procedure can resist such DoS attacks.

Proposition 4.8: The presented AKEP can accomplish Bergamo et al.’s attack [41].

Proof: This attack is conceivable in two scenarios. First, an attacker must have the relevant parameters 𝓋, Υ𝓋(𝓋) and Υ𝓌(𝓋); second, if numerous Chebyshev polynomials reach the same crossing point, the adversary will be able to recover the encrypted text due to the periodicity of cosine functions. The suggested protocol substitutes Υ𝓋(𝓋) and Υ𝓌(𝓋) inside 𝒞1IDi=𝒞1⨁ℏ(Υ𝒞1) and 𝒞2IDi=𝒞2⨁ℏ(Υ𝒞2), where Υ𝒞1≡Υ𝓋(𝒫)(mod f(𝓋)) and Υ𝒞2≡Υ𝓌(𝒫)(mod f(𝓋)) correspondingly. Adversaries cannot obtain these polynomials unless they know the hash values of Υ𝒞1and Υ𝒞2, which are transmitted to the client over a secure channel. Furthermore, the protocol’s use of augmented Chebyshev polynomials over Galois fields makes Bergamo et al.'s attack unachievable.

5  Analysis

5.1 Statistical Experiments

Statistical experiments will be used to demonstrate the Chebyshev-based Decisional Diffie-Hellman (CDDH) assumption. A fast graphical tool for comparing two probability distributions in statistics is the quantile-quantile plot (Q−Q plot) [42]. The sample quintiles and theoretical quintiles are contrasted visually. The experimental result will be roughly on the reference line “𝒴=𝒳,” where 𝒳 represents the first data sample, and 𝒴 represents the second data sample, if two data samples are taken from the same distribution. As a result, the Q−Q plot, a non-parametric approach, is widely used in cryptosystem security analysis to demonstrate the distribution indistinguishability among privacy data and uniformly random data. This technique has previously been used to demonstrate the security of proposed procedures [43]. Small size parameters are sufficient in the experiment for the distribution of given arrays. Let (𝓍0=𝒫,𝓍1=Υ𝒞1≡Υ𝓋(𝒫), 𝓍2=Υ𝒞2≡Υ𝓌(𝒫),𝓍3=SK≡Υ𝓌(Υ𝓋(𝓋))=Υ𝓋(Υ𝓌(𝓋))) be a CD DH tuple. The goal is to determine whether 𝓍3≡Υ𝓋(Υ𝓌(𝓋))=Υ𝓋𝓌(𝓋)=Υℓ(𝓋), where ℓ=𝓋𝓌 or not. Meanwhile, if 𝒞=f(𝓋)=1319,𝓍0=2,𝓋=460, and 𝓌=981, then 𝓍1=861 and 𝓍2=1182, with 𝓋 and 𝓌 unknown to the challenger and adversary. Let y=Υt(𝓍i)(mod 𝒸) be a Chebyshev map for i=1,2. We consider the case where i=1 without losing generality. Now, by sampling 1500 times, we utilize the Q–Q plot to display the distributions of y and 𝓍3 before tallying the frequency with which each Z𝒸 component appears. In the event, that the two distributions are identical, the resulting graph will be a straight line.

``𝒴=𝒳''

The vertical axis shows estimated quintiles from the y sample set and the horizontal axis shows estimated quintiles from the 𝓍3 sample set. Using Maple-17, the statistical experiment is run.

Fig. 1 depicts a comparison of the distributions of y and 𝓍3. Because the graph is a straight line, Υt1(𝓍1) is statistically equivalent to Υt3(𝓍0). Although the Q−Q plot cannot provide theoretical proof of the security, it can provide evidence when the theoretical proof is challenging to achieve.

In addition, we provide the Chebyshev polynomial’s function image for random ℓ: y=Υtℓ(𝓍0)(mod f(𝓋)). The period of Υℓ(𝓍0)(mod f(𝓋)) is 𝒸−12, as seen in Fig. 2. In reality, it has been demonstrated that the period of Υ𝒹(𝓍)(mod  c) for the odd prime is a divisor of c−1 when the roots of ξ2−2𝓍0ξ+1=0 are in GF𝒸 [43] and the period of Υ𝒹(𝓍) (mod 𝒸) is a divisor of c−1 when the roots are in  GF𝒸2. Therefore, we choose a prime c=2c0+1, where c0 is likewise a prime, to prevent a short period of Υℓ(𝓍0)(mod c). Furthermore, the procedure’s randomness is based on the pseudo-randomness of Υℓ(𝓍0)(mod c).

Figure 2: Chebyshev polynomials image map

5.2 Efficiency and Performance Analysis

To illustrate the security performance and effectiveness of our new design, we will compare the security properties of our given AKEP with four previous AKEPs introduced by Wu et al. [31], Yanrong et al. [44], Guo et al. [45], and Lee [46] in Table 5. In Table 5, we can see that our AKEP is more secure than other AKEPs. To express the execution time necessary for modular multiplication, one-way hash function, chaotic map operation, group modular exponentiation, and symmetric encryption/decryption operation, notations such as †𝓂, †𝒽, †c †𝑒, and †s, are used to show our evaluation results. Table 6 shows the client as 𝒞 and the server as 𝒥𝒮. Table 6 and Fig. 3 shows how our novel AKEP compares to similar procedures such as Wu et al. [31], Yanrong et al. [44], Guo et al. [45], and Lee [46] in terms of communication costs. We arrive at the subsequent communication time figures with unit hashing time based on the experimental findings in [47–51]: †𝑒=600†h, †𝓂=2.5†h,†s=†h and †h=†c. We obtain the subsequent order of computational complexity using this above relation: †h≈†c≈†s<†𝓂<†e. By the way, we know that the running time of †h is 0.503 ms [51]. The total communication costs of the work of Wu et al. [31], the work of Yanrong et al. [44], the work of Guo et al. [45], the work of Lee [46], and the projected protocol are 3022.03, 13.59, 11.07, 10.06, and 8.56 ms, respectively. According to the study findings in Fig. 3, the presented AKEP has by far the lowest interaction value. In terms of runtime, the proposed AKEP frequently produces tests that outperform the other procedures.

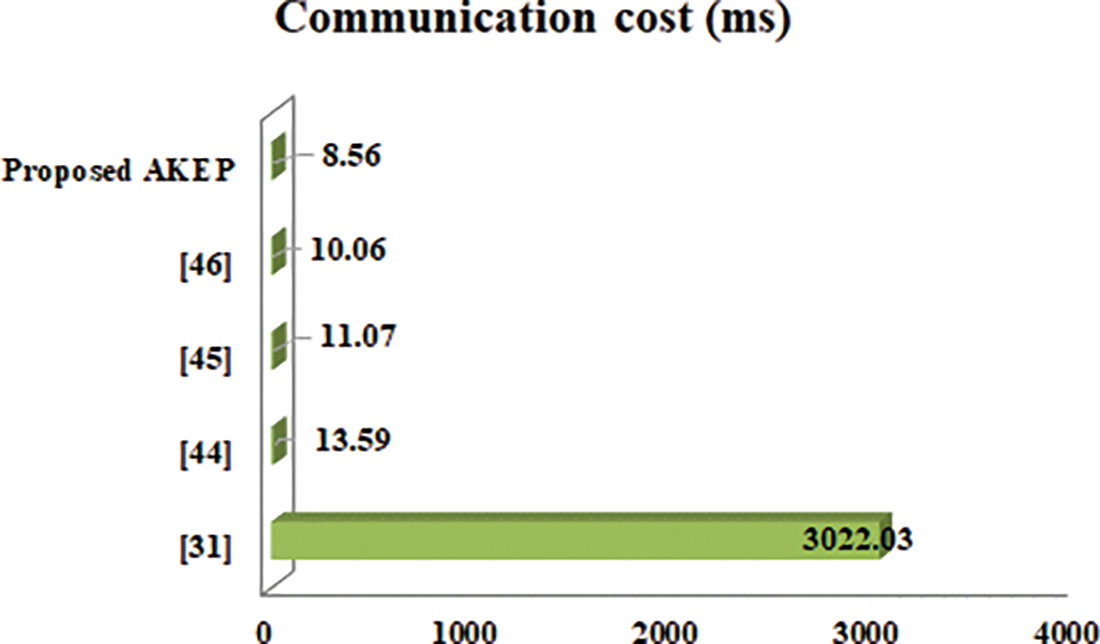
Figure 3: The total communication costs

6  Conclusion

In this paper, we propose a three-party password-based AKEP with client anonymity that uses Chebyshev chaotic maps and is more efficient and secure than previous procedures. Chebyshev chaotic maps are used to encrypt and decrypt data transmitted by either the client or the server to increase security and efficiency. Because it solely employs hash and XOR operations, we were able to show through security and performance studies that our AKEP is more effective and secure than others. To protect client identification when transferring data over an insecure public network, our AKEP may also offer client anonymity. In the future, we plan to provide efficient, lightweight, provably secure authentication protocols for the Internet of Things based on authenticated key exchange procedures using Chebyshev chaotic maps.

Acknowledgement: The authors would like to thank anonymous reviewers of Computers, Materials & Continua Journal for their careful and helpful comments. Prof. Monia Hadj Alouane-Turki extends her appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through Small Groups. Project under grant number (RGP.1/257/43).

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. L. Atzori, A. Iera and G. Morabito, “The internet of things: A survey,” Computer Networks, vol. 54, no. 15, pp. 2787–2805, 2010. [Google Scholar]

2. A. Valenzano, L. Durante and M. Cheminod, “Review of security issues in industrial networks,” IEEE Transactions on Industrial Informatics, vol. 9, no. 1, pp. 277–293, 2013. [Google Scholar]

3. V. C. Gungor and G. P. Hancke, “Industrial wireless sensor networks: Challenges, design principles and technical approaches,” IEEE Transactions on Industrial Electronics, vol. 56, no. 10, pp. 4258–4265, 2009. [Google Scholar]

4. D. Liu, M. C. Lee and D. Wu, “A node-to-node location verification method,” IEEE Transactions on Industrial Electronics, vol. 57, no. 5, pp. 1526–1537, 2010. [Google Scholar]

5. C. Chang and C. Lee, “A secure single sign-on mechanism for distributed computer networks,” IEEE Transactions on Industrial Electronics, vol. 59, no. 1, pp. 629–637, 2012. [Google Scholar]

6. G. Wang, J. Yu and Q. Xie, “Security analysis of a single sign-on mechanism for distributed computer networks,” IEEE Transactions on Industrial Informatics, vol. 9, no. 1, pp. 294–302, 2013. [Google Scholar]

7. L. Barolli and F. Xhafa, “JXTA-Overlay: A P2P platform for distributed, collaborative and ubiquitous computing,” IEEE Transactions on Industrial Electronics, vol. 58, no. 6, pp. 2163–2172, 2010. [Google Scholar]

8. Y. Huang, W. Lin and H. Li, “Efficient implementation of RFID mutual authentication protocol,” IEEE Transactions on Industrial Electronics, vol. 59, no. 12, pp. 4784– 4791, 2012. [Google Scholar]

9. B. Wang and M. Ma, “A server independent authentication scheme for RFID systems,” IEEE Transactions on Industrial Informatics, vol. 8, no. 3, pp. 689–696, 2012. [Google Scholar]

10. B. Fabian, T. Ermakova and C. Muller, “SHARDIS: A privacy enhanced discovery service for RFID-based product information,” IEEE Transactions on Industrial Informatics, vol. 8, no. 3, pp. 707–718, 2012. [Google Scholar]

11. T. Y. Chang, M. S. Hwang and W. P. Yang, “A communication-efficient three-party password authenticated key exchange protocol,” Information Sciences, vol. 181, no. 1, pp. 217–226, 2011. [Google Scholar]

12. T. Y. Chang, W. P. Yang and M. S. Hwang, “Simple authenticated key agreement and protected password change protocol,” Computers & Mathematics with Applications, vol. 49, no. 5–6, pp. 703–714, 2005. [Google Scholar]

13. T. F. Lee, T. Hwang and C. L. Lin, “Enhanced three-party encrypted key exchange without server public keys,” Computers & Security, vol. 23, no. 7, pp. 571–577, 2004. [Google Scholar]

14. S. W. Lee, H. S. Kim and K. Y. Yoo, “Efficient verifier-based key agreement protocol for three parties without server’s public key,” Applied Mathematics and Computation, vol. 167, no. 2, pp. 996–1003, 2005. [Google Scholar]

15. D. He, Y. Chen and J. Chen, “Cryptanalysis and improvement of an extended chaotic maps-based key agreement protocol,” Nonlinear Dynamics, vol. 69, no. 3, pp. 1149–1157, 2012. [Google Scholar]

16. J. W. Lo, J. Z. Lee, M. S. Hwang and Y. P. Chu, “An advanced password authenticated key exchange protocol for imbalanced wireless networks,” Journal of Internet Technology, vol. 11, no. 7, pp. 997–1004, 2010. [Google Scholar]

17. J. W. Lo, S. C. Lin and M. S. Hwang, “A parallel password-authenticated key exchange protocol for wireless environments,” Information Technology and Control, vol. 39, no. 2, pp. 146–151, 2010. [Google Scholar]

18. S. M. Bellovin and M. Merritt, “Encrypted key exchange: Password-based protocols secure against dictionary attacks,” in Proc. of IEEE Computer Society Symp. on Security and Privacy, Oakland, CA, USA, pp. 72–84, 1992. [Google Scholar]

19. C. C. Lee, R. X. Chang and H. J. Ko, “Improving two novel three-party encrypted key exchange protocols with perfect forward secrecy,” International Journal of Foundations of Computer Science, vol. 21, no. 6, pp. 979–991, 2010. [Google Scholar]

20. C. C. Lee and Y. F. Chang, “On security of a practical three-party key exchange protocol with round efficiency,” Information Technology and Control, vol. 37, no. 4, pp. 333–335, 2008. [Google Scholar]

21. M. I. Hassan and A. Abdullah, “A new grid resource discovery framework,” The International Arab Journal of Information Technology, vol. 8, no. 1, pp. 99–107, 2011. [Google Scholar]

22. M. Abdalla and D. Pointcheval, “Interactive Diffie-Hellman assumptions with applications to password-based authentication,” Lecture Notes in Computer Science, vol. 3570, pp. 341–356, 2005. [Google Scholar]

23. R. Lu and Z. Cao, “Simple three-party key exchange protocol,” Computers & Security, vol. 26, no. 1, pp. 94–97, 2007. [Google Scholar]

24. B. H. T. Algubili, N. Kumar, H. Lu, A. A. Yassin, R. Boussada et al., “EPSAPI: An efficient and provably secure authentication protocol for an IoT application environment,” Peer-to-Peer Networking and Applications, vol. 15, pp. 2179–2198, 2022. [Google Scholar]

25. M. Deng, J. Ma and F. Le, “Universally composable three party password-based key exchange protocol,” China Communications, vol. 6, no. 3, pp. 150–154, 2009. [Google Scholar]

26. W. Yuan, L. Hu, H. Li and J. Chu, “Offline dictionary attack on a universally composable three-party password-based key exchange protocol,” Procedia Engineering, vol. 15, no. 11, pp. 1691–1694, 2011. [Google Scholar]

27. H. F. Huang, “A simple three-party password-based key exchange protocol,” International Journal of Communication Systems, vol. 22, no. 7, pp. 857–862, 2009. [Google Scholar]

28. E. J. Yoon and K. Y. Yoo, “Cryptanalysis of a simple three-party password-based key exchange protocol,” International Journal of Communication Systems, vol. 24, no. 4, pp. 532–542, 2011. [Google Scholar]

29. E. J. Yoon and K. Y. Yoo, “Cryptanalysis of an efficient three-party password-based key exchange scheme,” Procedia Engineering, vol. 29, no. 5, pp. 3972–3979, 2012. [Google Scholar]

30. D. C. Lou and H. F. Huang, “Efficient three-party password-based key exchange scheme,” International Journal of Communication Systems, vol. 24, no. 4, pp. 504–512, 2011. [Google Scholar]

31. S. Wu, K. Chen and Y. Zhu, “Enhancements of a three-party password-based authenticated key exchange protocol,” International Arab Journal of Information Technology, vol. 10, no. 3, pp. 215–221, 2013. [Google Scholar]

32. Q. Zhang, P. Chaudhary, S. Kumari, Z. Kong and W. Liu, “Verifier-based anonymous password-authenticated key exchange protocol in the standard model,” Mathematical Biosciences and Engineering, vol. 16, no. 5, pp. 3623–3640, 2019. [Google Scholar] [PubMed]

33. Q. Shu, S. B. Wang, B. Hu and L. D. Han, “Verifier-based three-party password-authenticated key exchange protocol from ideal lattices,” Journal of Cryptologic Research, vol. 8, no. 2, pp. 294–306, 2021. [Google Scholar]

34. C. Peikert, “Lattice cryptography for the internet,” in Proc. of the Int. Workshop on Post-quantum Cryptography, Waterloo, ON, Canada, pp. 197–219, 2014. [Google Scholar]

35. R. M. Campello de Souza, H. M. A. de Oliveira Kauffman, A. N. Kauffman and A. J. A. Paschoal, “Trigonometry in finite fields and a new Hartley transform,” in Proc. of IEEE Int. Symp. Information Theory (ISIT’98), Cambridge, MA, USA, pp. 293, 1998. [Google Scholar]

36. J. B. Lima, D. Panariob and R. M. Campello de Souza, “Public-key encryption based on Chebyshev polynomials over GF(q),” Information Processing Letters, vol. 111, pp. 51–56, 2010. [Google Scholar]

37. J. B. Lima, R. M. Campello de Souza and D. Panariob, “Security of publickey cryptosystems based on Chebyshev polynomials over prime finite fields,” in Proc. IEEE Int. Symp. Information Theory (ISIT 2008), Toronto, ON, Canada, pp. 1843–1847, 2008. [Google Scholar]

38. J. C. Mason and D. C. Handscomb, Chebyshev polynomials. Boca Raton, Florida: Chapman & Hall/CRC, 2003. [Google Scholar]

39. C. Meshram, C. C. Lee, S. G. Meshram and A. Meshram, “OOS-SSS: An efficient online/offline subtree-based short signature scheme using chebyshev chaotic maps for wireless sensor network,” IEEE Access, vol. 8, no. 1, pp. 80063–80073, 2020. [Google Scholar]

40. C. Meshram, C. C. Lee, A. S. Ranadive, C. T. Li, S. G. Meshram et al., “A subtree-based transformation model for cryptosystem using chaotic maps under cloud computing environment for fuzzy user data sharing,” International Journal of Communication Systems, vol. 33, no. 7, pp. e4307, 2020. [Google Scholar]

41. P. Bergamo, P. D’Arco, A. De Santis and L. Ko Carev, “Security of public-key cryptosystems based on Chebyshev polynomials,” IEEE Transactions on Circuits and Systems, vol. 52, no. 7, pp. 1382–1393, 2005. [Google Scholar]

42. J. Li, L. Wang, L. Wang, X. Wang, Z. Huang et al., “Verifiable chebyshev maps-based chaotic encryption schemes with outsourcing computations in the cloud/fog scenarios,” Concurrency and Computation: Practice and Experience, vol. 31, no. 5, pp. e4523, 2018. [Google Scholar]

43. D. Kahrobaei, C. Koupparis and V. Shpilrain, “Public key exchange using matrices over group rings,” Groups, Complexity, Cryptology, vol. 5, no. 1, pp. 11–97, 2013. [Google Scholar]

44. L. Yanrong and Z. Dawei, “A chaotic-map-based password-authenticated key exchange protocol for telecare medicine information systems,” Security and Communication Networks, vol. 2021, pp. 1–8, 2021. https://doi.org/10.1155/2021/7568538 [Google Scholar] [CrossRef]

45. X. Guo and J. Zhang, “Secure group key agreement protocol based on chaotic hash,” Information Sciences, vol. 180, no. 20, pp. 4069–4074, 2010. [Google Scholar]

46. T. -F. Lee, “Enhancing the security of password authenticated key agreement protocols based on chaotic maps,” Information Sciences, vol. 290, pp. 63–71, 2015. [Google Scholar]

47. C. Meshram, S. G. Meshram, R. W. Ibrahim, H. A. Jalab, S. S. Jamal et al., “Conformal chebyshev chaotic maps based remote user password authentication protocol using smart card,” Complex & Intelligent Systems, vol. 8, pp. 973–987, 2022. [Google Scholar]

48. M. B. Algehawi and A. Samsudin, “A new identity-based encryption (IBE) scheme using extended Chebyshev polynomial over finite fields Zp,” Physics Letters A, vol. 374, pp. 4670–4674, 2010. [Google Scholar]

49. M. H. Ibrahim, S. Kumari, A. K. Das, M. Wazid and V. Odelu, “Secure anonymous mutual authentication for star two-tier wireless body area networks,” Computer Methods and Programs in Biomedicine, vol. 135, no. 1, pp. 37–50, 2016. [Google Scholar] [PubMed]

50. C. Meshram, A. L. Imoize, S. S. Jamal, P. Tambare, A. R. Alharbi et al., “An efficient three-factor authenticated key agreement technique using FCM under HC-IoT architectures,” Computers, Materials & Continua, vol. 72, no. 1, pp. 1373–1389, 2022. [Google Scholar]

51. C. Meshram, A. L. Imoize, S. S. Jamal, A. Aljaedi and A. R. Alharbi, “SBOOSP for massive devices in 5G WSNs using conformable chaotic maps,” Computers, Materials & Continua, vol. 71, no. 3, pp. 4591–4608, 2022. [Google Scholar]