APST-Flow: A Reversible Network-Based Artistic Painting Style Transfer Method

1  Introduction

With the improvement of hardware computing capability, large-scale deep learning, as an important method in the field of artificial intelligence, has made significant progress in many applications [1–6]. In recent years, image processing tasks [7–10] have gradually become a research hotspot. One potential application is artistic painting style transfer (APST), which is to transfer the style of an artistic painting to another painting or real image so that the generated image has the style of the former while retaining the content of the latter. It has rich application scenarios, such as quickly providing painters with different styles of reference image examples [11,12], and efficient post-production video rendering [13]. Nevertheless, the current main deep generative models, such as Variational Auto-encoder (VAE) [14] and Generative Adversarial Network (GAN) [15], suffer from the loss of generated details caused by the incompact feedforward process and the uncertainty of the generated content through the noise-driven network. Therefore, this paper attempts to introduce a more compact analysis framework into the APST to alleviate the above bottlenecks.

Early studies of artistic painting style transfer focused on how manual design synthesizes the spatial details of a particular style, such as highlighting the detailed features of a certain style by planning the generation process via modeling textures and brushstrokes [11,16,17]. Wang et al. [11] proposed a watercolor painting style transfer framework, which realizes the drawing of different features of watercolor painting through several sets of filters. Efros et al. implemented an image texture synthesis method based on an image mosaic, which renders textures obtained from different images [16]. Wang et al. [17] formulated an algorithm for the automatic diffusion synthesis of color inks, which simplifies the feature extraction process through brightness and color segmentation, and uses texture synthesis technology to simulate the diffusion effect of color inks. The above methods usually design synthesis details for a specific type of migration scene, nevertheless the modeling of different types of art paintings is quite different, which is not conducive to the expansion of new application scenarios. In recent years, deep generative networks have been successfully applied to the field of artistic painting transfer. Gatys et al. [18,19] first applied Gram loss in deep network feature mapping to represent image artistic style, which initiated the research on neural painting style transfer. After that, a large number of artistic painting transfer methods based on deep generative networks have been proposed, which can be roughly divided into two categories: those based on the en-decoding process and those based on adversarial generative learning.

Referring to image segmentation, some scholars [20,21] verified that the method of decoding and restoring the features extracted by the encoder can be used for painting style transfer tasks. In 2017, Huang et al. proposed an en-decoder architecture-based style transfer model [22]. They introduced an adaptive normalization module (AdaIN) to recombine the content and style features of the encoded image so that the generated image has the same feature distribution as the artistic painting. Then Park et al. [23] suggested SANet, which can represent global and local style patterns and maintain the content structure without losing the richness of the style. Based on this, AdaAttN [24] improved attention to consider both low and high-level features, and the final effect is more stable than SANet. Similarly, the en-decoding scheme proposed by Li et al. [25] uses the Whitening and Coloring Transform (WCT) to match the feature covariance of the content map with a given style, to statistically model the encoded content. The Avatar-Net [20] proposed by Sheng et al. uses a multi-scale decoding network to gradually learn the overall style decoding process to achieve adaptive style transfer. The en-decoder architecture performs well in general adaptive style transfer tasks, but the model feedforward process is not compact, resulting in a loss of detail in the generated results. In addition, the neglect of the strong correlation between the encoder and decoder usually leads to large training parameters and difficulty in convergence. Some studies [26,27] suggested using the single decoding method [12] for style transfer of artistic paintings, that is, image style transfer through a feedforward network and enhancement losses. This solution simplifies the model structure to a certain extent, but the quality of the generated image details is still poor. Also, it is suitable for general style transfer tasks, but not for advanced semantic transfer tasks such as representation and transfer of artistic painting styles. By contrast, the methods based on GANs not only avoid the low training efficiency caused by the separated en-decoding modules but also facilitate the loss design for different artistic painting transfer task scenes. For example, Lin et al. [15] proposed to extract multi-scale image edges and use generative adversarial learning to generate corresponding ink paintings from sketches. Zhang et al. [9] designed the corresponding loss function according to the three details of ink painting: gaps, edges, and ink diffusion, and used GAN to generate ink paintings from real images. Zeng et al. [10] applied the one-side cycle of the CycleGAN as the cycle consistency loss and used AdaIN [22] to edit the decoded information to get the final style painting. Different from the aforementioned approaches [9,15], this method enhances task performance from overall style learning. Cao et al. [28] achieved good results by proposing a dual-domain generator and a dual-domain discriminator using spatial and frequency domain features. Due to these scene-oriented improvements and efficient learning strategies of GANs, GAN-based solutions generally outperform en-decoding schemes in generation quality. Nevertheless, these methods cannot get accurate mapping through learning, and there are deviations in the generated content caused by the introduction of noise in the training and even artifacts of unknown meaning in the generated results. Moreover, designing an enhanced GAN-based model for specific tasks will lead to a large number of training parameters and difficulties in model convergence.

In conclusion, the above studies provide solutions for the transfer of artistic painting style, but there are still some shortcomings. (1) The existing deep generation model does not have an accurate inference mechanism for latent variable mapping, which leads to inherent image semantic errors and deviations in the generated results, as well as inaccurate reconstruction of image contents. (2) The feedforward process of the separated en-decoding architecture is not compact, resulting in the loss of image details in the deep generation process and the inefficiency of convergence caused by large model parameters. (3) Most of the existing style transfer models fail to thoroughly evaluate the generation quality on both global style and local details, so it is difficult to significantly improve the overall quality of generated images.

To address the above problems, this paper introduces a reversible network using multiplexing modules for parameter sharing via the en-decoding procedures. With this novel architecture, the accuracy of cross-domain feature transfer is improved and the loss of details is reduced, resulting in an efficient transfer of artistic style. Recently, Flow-based models [29–32], as a subclass of deep generative models, learn the latent spatial variables of high-dimensional observations through a reversible transformation of a series of network layers, to establish an unbiased, accurate reversible mapping from the complex distribution of observation variables to the Gaussian distribution. Based on the reversible architecture, this paper attempts to achieve accurate mapping and transfer of content and style features in the transfer scene of artistic paintings. To the best of our knowledge, this is the first time a deep reversible network has been used for artistic painting generation. In detail, an existing Flow-based reversible model as Glow [31] is adopted and a multi-scale Wavelet architecture is formulated to enhance the accuracy inference of spatial features and improve model convergence. Also, an adaptive edge extractor such as Bi-Directional Cascade Network (BDCN) [33] is applied to adaptively learn edge salient information. Moreover, a style tester is implemented to check the overall style to ensure that the details of generated content are style consistent. The main contributions are as follows:

•   This paper proposes a novel framework APST-Flow for artistic painting style transfer. This framework introduces a reversible Flow network with shared en-decoder parameters and Wavelet Additive Coupling (WAC) layers to accurately infer the mapping of image content and style to latent variable space, thereby reducing the deviation of generated results and accelerating model convergence.

•   APST-Flow applies an adaptive painting stroke edge loss Lbrush to guide the learning of artistic painting-specific brushstroke effects to generate salient details. Also, a multi-scale edge loss of content and style images is calculated to constrain the local edge details. Besides, the adversarial training of the generator is guided by the discriminator according to the adaptation task, so as to optimize the overall generated results.

•   To enhance the style transfer performance, this paper formulates a style consistency checking network (T), which makes full use of the reverse reconstruction network to calculate the checking loss Lsn without additional memory resources, and adds noise to drive the style encoder to improve the generalization ability. Furthermore, this network can help the generation module learn global style features by detecting the error between the inversely reconstructed image and the input image.

The rest of this paper is organized as follows. Section 2 reviews related work, as a brief introduction to artistic style transfer and Flow-based models. Section 3 illuminates the proposed APST-Flow with the network modules, procedures, and losses. In Section 4, qualitative and quantitative experiments are established and the results are discussed on different data sets. The major conclusions are presented in Section 5.

2  Related Work

2.1 Image Style Transfer Based on Deep Learning

Image style transfer has gradually become a popular vision application in recent years. Its purpose is to retain the content of one image of the two given images and the style of the other. In 2015, Gatys et al. [18,19] introduced Gram loss in deep features to represent image style, which led to extensive research on neural style transfer by subsequent scholars. Many neural style transfer methods have been proposed in recent years. In this paper, these methods are categorized into application scenarios with ink painting style transfer [8–10,15,26,27], sketch style transfer [34–38], and other artistic painting style transfer [39–41].

In the study of artistic style transfer, the transfer scheme of ink painting has made remarkable progress. Based on the basic framework proposed in [12], Li et al. [26] generated Chinese landscape paintings from real landscapes and used three MXDoG-based losses to guide the network to learn the spatial abstract elements of artistic paintings. Zhou et al. [27], through improved the inception convolution in [12], reduced the number of parameters of the rendering module while ensuring the quality of generated results. Lin et al. [15] proposed extracting image edges at multiple scales and using GAN to generate ink paintings from sketches. Zhang et al. [9] proposed the corresponding training objective functions according to the three characteristics of ink paintings: gaps, edges, and ink diffusion. Zeng et al. [10] adopted the one-side cycle of the CycleGAN architecture as the cycle consistency loss, and then used AdaIN [22] to edit the decoded information. To simulate the manual painting process, He et al. [8] first used SketchGAN to generate the edge map of ink painting, and then adopted PaintGAN to generate ink painting from the edge map. The model uses an edge map rather than a real image as the condition, so interpolation can be used to generate non-existent ink paintings. Significant progress is also made in the transfer scheme of sketches. For example, Zhang et al. [36] suggested inputting real graphs into a Branched Fully Convolutional Neural Network (BFCN) to generate structure sketches and texture sketches respectively. Some studies choose to improve the generation quality from the generated details. For example, Wan et al. [35] used a high-resolution network instead of a generative network for details in sketches and utilized a Laplacian of Gaussian (LoG) filter to establish a detailed loss. In [38], an image detail denoising method was used to improve the generated results of ordinary GAN and achieve sketch transfer. Nevertheless, some others improved existing models from the overall sketch style. For example, Yan et al. [34] implied that identity information was rather important in the transfer task of a real graph to pictorial style, so identity loss was introduced in adversarial learning and cycle consistency loss was added to assist adversarial learning. Yu et al. [37] proposed a composition-aided generative adversarial network (CA-GAN), which takes the real image and its corresponding face composition information as paired inputs and uses a perceptual loss function to generate constraints.

In addition, there is extensive research on the transfer of other styles. Zhang et al. [39] replaced the traditional decoder with residual U-Net in the transfer task of black and white sketches to color illustrations and used the discriminator improved by CA-GAN for discrimination. Chen et al. [40] formulated a dual style-learning network for the transfer of artistic painting. This network takes the overall style and the detailed style as the two supervision directions of artistic painting, uses Style Control Block (SCB) to control the style factors, and has good performance in a variety of oil paintings. Lin et al. [41] introduced a Laplacian pyramid network (LapTsyle) as a feedforward scheme in the style transfer of artistic paintings such as oil paintings. The above methods are all artistic painting transfer schemes based on deep generative networks, most of which are based on GANs. Although they are efficient in generative model training, statistical learning based on noise-driven generative networks will lead to uncertainty in the generated content and details.

2.2 Image Generation Based on Reversible Networks

As a kind of reversible network, Flow-based models were first applied to the image and video generation tasks [29]. The Non-linear Independent Components Estimation (NICE) [29] constructed a reversible neural network module and applied the maximum likelihood estimation learning criterion to fit the feature distribution of complex images. NICE could accurately sample from latent variables and generate corresponding images through network mapping. But it simply stacked fully connected layers and failed to give the general use for convolutional layers. RealNVP [30] further normalized the coupling layer based on the reversible idea of NICE, and successfully introduced a convolutional layer into the coupling model to better address high-dimensional image problems. Assuming that the input picture is x∈RD, the latent variable is z∈RD, then the bidirectional mapping is established according to the Flow model described in [30], where the forward reasoning is f:x→z, and the reverse reasoning is g≜f−1:z→x. This mapping can be obtained by using the equation of the maximum likelihood criterion:

pX(x)=pZ(z)|det(∂g(z)∂z)|−1(1)

where x=g(z) and J(z)=∂x/∂z are Jacobi matrices of x with respect to z. Further, the design of multi-scale layers is proposed to implement a simplified reversible network algorithm based on Jacobian determinant [30], that is, the input x is divided into x1 and x2 equally in the channel dimension. Then the output y1 and y2 will be expressed as:

{y1=x1y2=x2exp⁡⨀(s(x1))+t(x1)(2)

where s(⋅) and t(⋅) are arbitrarily complex neural networks (i.e., CNNs for learning features). Then, the derivative of y with respect to x1 and x2 is obtained as a triangular determinant, where the diagonal is the product of exp(s(x1)). Therefore, efficient calculation of the Jacobian determinant can be achieved, which not only reduces calculation but also provides a strong regularization effect, thereby enhancing the generation quality.

Different from RealNVP, the subsequently proposed Glow [31] mainly introduced the Actnorm layer before the input to replace the Batch Normal (BN) layer. The Actnorm layer, as an alternative to the BN layer, performs a per-channel affine transformation on the input tensor x:

yi,j=w⊙xi,j+b(3)

where i and j are the spatial positions on the tensor; w and b are the scale and deviation parameters of the affine transformation, which are learnable in model training. Its inverse function is:

xi,j=(yi,j−b)/w(4)

Since the affine coupling layer only processes half of the feature images, the channel dimensions of the feature images need to be permuted so that each dimension can affect all the dimensions. The reversible 1 × 1 convolution operation is as follows:

yi,j=Wxi,jxi,j(5)

where W is a c × c weight matrix, where c is the channel dimension of the tensors x and y. Its inverse function is:

xi,j=W−1yi,j(6)

Based on the above work, three restrictive designs based on the previous Flow are further improved in Flow++ [32]: the use of uniform noise for dequantization, the use of affine Flow without expression, and the application of pure convolution conditional reflective networks in the coupling layer. In addition, C-Glow [42] applied a conditional Flow for structured output learning, adding a conditional before the network. SR-Flow [43] utilized a super-resolution method based on standardized Flow, which added a conditional affine coupling layer and adopted a multi-scale method to enlarge the resolution of the generated images. The Wavelet Flow [44] adopted the Wavelet transform scheme to achieve the super-resolution image analysis and to construct a multi-scale Flow network. BeautyGlow [45] implemented the transformation matrix to learn and extract the latent codes of the features before and after makeup and added the style codes in the latent variable domain to complete the makeup task. ArtFlow [46] is based on a general style transfer model, which encoded images through the exact reversibility of the Flow model, then fused the image feature style, and finally obtained a style transfer image through reverse decoding. Different from ArtFlow [46], this paper attempts to use the multi-scale style inference based on the reversible en-decoder architecture, formulate an adaptive edge extractor as BDCN [33] to adaptively learn edge salient information, and also implement a style consistency tester to ensure the details of generated content are style consistent.

3  The Proposed Method

As mentioned above, given the real scene image Ic as the content image and the artistic painting image Is as the style image, the image Ics is generated through artistic painting style transfer. And the generated image has the artistic style of Is, while preserving the scene content of Ic. To solve the problems such as the loss of details in generated images and difficult convergence of training[8–10,15,26,27], this paper proposes to use three modules to complete the style transfer task: A Wavelet additive coupling layer-based Flow network (WAC-Flow) as the generator (G), a discriminator (D) similar to the discrimination network described in PatchGAN [47], and a style consistency checking network as the tester (T), which corresponds to the reverse transfer process of the generator (G). As shown in Fig. 1, generator G uses the reversible WAC-Flow model as the en-decoder for the content image Ic and the style image Is, and AdaIN as the style transferor. The encoder and decoder share the same network module, which reduces the scale of trainable parameters and allows accurate inference of the mapping of image content to the latent variable space, thereby reducing the loss of content details. The discriminator D uses the discrimination network in [47] to discriminate the generated stylized images and generate the discriminant loss LGAN, to optimize the generator G by adversarial training. In addition, the tester T uses noise as an input to drive the style encoder and utilizes the reversibility of WAC-Flow to construct the loss Lsn, to check the global features of the generated stylized images and enhance the generalization ability of the model.

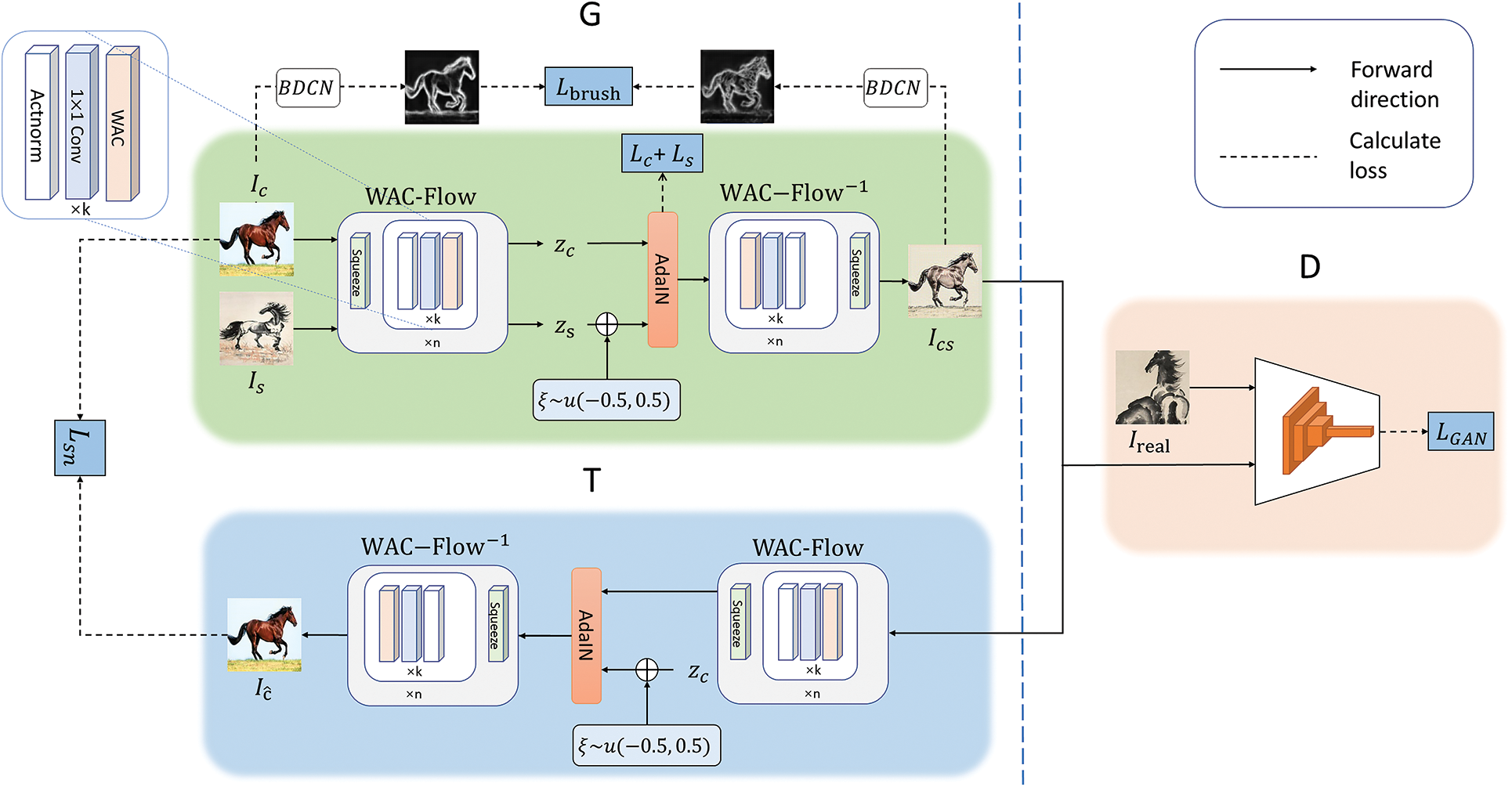
Figure 1: The APST-Flow model proposed in this paper. It contains a generator G, a discriminator D, and a tester T, among which G involves the adaptive paint stroke edge loss Lbrush and style transfer losses Lc and Ls, D involves loss LGAN, and T involves the style noise consistency loss Lsn. Repeated modules in WAC-Flow are shown in the upper left corner

3.1 Generative Network Based on WAC-Flow Model

3.1.1 Image Encoding and Decoding Using WAC-Flow

In style transfer tasks, most of the previous studies use linear networks as generators and employ adversarial learning strategies to train the network. However, the pooling operation leads to the loss of spatial information, and the cumulation of these irreversible operations may disturb the generation of images and cause detail loss. The Flow model theoretically has perfect reconstruction and also is a generative model that can establish an accurate mapping between the image domain and the latent space. Therefore, this paper will extend this reversible model to artistic style transfer scenarios.

In this paper, the existing reversible model is used as the basic module of image en-decoding processing, and its basic working principle can be expressed as:

{zc=f(Ic)zs=f(Is)Ics=f−1(AdaIN(zc,zs))(7)

where the mappings f:RD→RD and f−1:RD→RD are the forward and reverse transformation processes of the Flow module. And, the optimization objective function of f is:

arg⁡minθEx[−log⁡pθ(x)]=Ex[−log⁡pz(fθ(x))−logdet|∂fθ(x)∂x|](8)

where θ is the parameter that can be learned, pθ(x) is the complex distribution of the image domain, det|⋅| is the Jacobian determinant, and pz(⋅) is the Gaussian distribution of the latent space. In view of the particularity of the artistic painting style transfer task, a WAC-Flow model consisting of four fully reversible components is proposed in this paper.

Wavelet Additive Coupling (WAC) layer. Since this paper is the first study to apply a deep reversible network [31] to artistic painting style transfer, the existing reversible model needs to be regularized accordingly. The reversible model RealNVP proposed in [30] contains a reversible transform encapsulated as an affine coupling layer, which can efficiently update part of the input vector or latent vector. To enhance the model’s ability to represent spatial details, herein Haar Wavelet is introduced into the traditional affine coupling layer, as shown in Fig. 2. Moreover, discrete Wavelet is used to obtain high-frequency information that is not easy to extract from images, and to strengthen the learning of spatial edges and textures. Due to the orthogonality of the discrete Wavelet basis function, the correlation interference caused by the redundant representation between the two feature points in the transform space can be eliminated, and a significant representation of the image latent variables can be obtained. In this paper, a multi-scale discrete Wavelet pyramid is used to enhance the adaptability of the coupling layer to the style transfer task. The equations for the forward and reverse feed of a single WAC layer are expressed as:

{Forward−feed:{x1,x2=split(x)y1=x1y2=Khaar−1(Khaar(hconv(x1)))+x2y=concat(x1,x2)Inverse−feed:{y1,y2=split(y)x1=y1x2=Khaar−1(Khaar(hconv(y1)))−y2x=concat(y1,y2)(9)

where the equation for the transformation processing based on Haar Wavelet, including forward analysis Khaar and reverse reconstruction Khaar−1, is:

Haar−Wavlet:{Il:{Il,Dl}=Khaar,l(Il−1)I^l−1:{I^l−1,D^l−1}=Khaar,l−1−1(Il,hconv,l(Dl)),l∈1,2,…L(10)

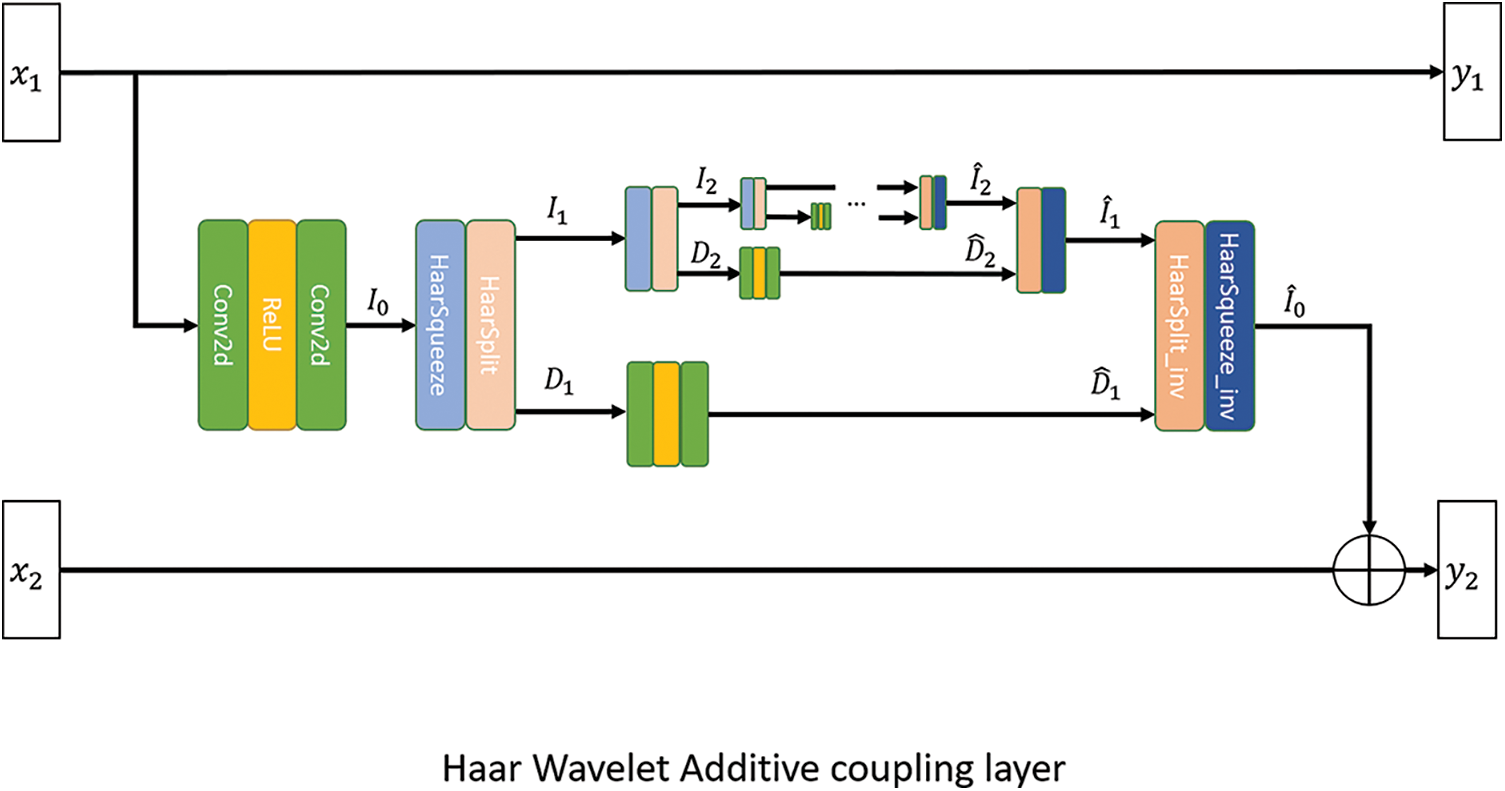
Figure 2: The structure of the proposed WAC layer. The left side is the inputs x1,x2. Notice x1 is used to generate features through multi-scale Wavelet transformation, which restores image features by levels in turn and then added on x2 as output y2, and output y1 equals x1

In Eq. (9), the function split() splits the tensor in half along the channel dimension, the function concat() connects the two tensors along the channel dimension, and hconv() is a simple convolution operation. It is worth noting that the Wavelet forward decomposition decomposes the input information Il−1:I∈R2l×2l×C into low-frequency output Il:I∈R2l−1×2l−1×C and high-frequency output Dl:D∈R2l−1×2l−1×3C through the discrete Wavelet kernel Khaar (channel). This transformation is recursive, l∈1,2…L is the recursive scale, the initial input is Il−1=I0, and finally D1,D2,…,DL is obtained after transformation. Then, the forward Wavelet transform is restored by the discrete Wavelet reverse kernel Khaar−1 (channel), which can recursively fuse the processed high-frequency information hconv,l(Dl) and low-frequency information Il and restore it to the scale of the next level and ultimately to I^0≈I0 after several iterations. Here, I^0 and I0 have the same size and shape. In other words, through the forward channel and reverse channel of the Wavelet, recursive reduction allows the input and output to have the same shape.

In addition to the proposed WAC layer, the details of the remaining major components of the reversible network are given below.

Reversible 1 × 1 convolutional layer. Following Glow [31], a learnable reversible 1 × 1 convolutional layer is used for flexible channel arrangement, which can be calculated from Eqs. (5) and (6).

Actnorm layer. An activation normalization layer (Actnorm) is used as an alternative to batch normalization following Glow [31]. The Actnorm layer performs a per-channel affine transformation on the tensor x, as calculated by Eqs. (3) and (4).

Squeeze layer. In addition to the aforementioned reversible transformations, squeeze operations are embedded in some parts of the model. The encapsulated squeeze layer is suitable for realizing multi-scale architecture, for example, dividing an image into sub-images of shape 2 × 2 × c and then reshaping them to 1 × 1 × 4c. Before the output of the current level is transmitted to the next level, half of the dimensions of the outputs are decomposed and dumped into the latent space to reduce computational cost and the number of parameters.

By stacking the above four operating components in a specific order, the generative network WAC-Flow can be obtained, which realizes the bidirectional mapping from the input image to the latent variable domain, and obtains their spatial features. Specifically, in the encoding process, the real image Ic and the artistic image Is are respectively input into WAC-Flow to obtain their latent variables zc and zs. In the decoding process, the latent variable zcs transferred by AdaIN is input into the reverse model of WAC-Flow, and the transferred image is obtained by decoding. It should be pointed out that in the training stage, WAC-Flow shares parameters with its inverse model, and there is roughly no information loss in the process of en-decoding.

3.1.2 Style Feature Transfer Using AdaIN

After the image is mapped to the latent variable space through WAC-Flow, the content features and style features should be combined for transfer. Moreover, the content of the latent variable domain should be edited to match the Tester T. To achieve this function, this paper selects the module AdaIN that can combine content features and style features in the latent space to complete the transfer. This module aligns the normalized channel mean and variance of the content image with the style image, so that the generated image adaptively has the same feature distribution as the artistic image, and introduces a Gaussian distribution to enhance the generalization ability of the model. If zc and zs respectively are the feature codes of the content image and style image obtained through WAC-Flow mapping, and ξ is the noise distribution, then the AdaIN layer can be given by:

hAdaIN(zc,zs+ξ)=σ(zs+ξ)(zc−μ(zc)σ(zc))+μ(zs+ξ)(11)

where μ(zc) and σ(zc) are the mean and standard deviation of the content image features, respectively; μ(zs+ξ) and σ(zs+ξ) are the mean and standard deviation of the features of the noised style image respectively; zs+ξ is the result of adding noise to the style latent variable for the tester T, and ξ∼u(−0.5,0.5). In this way, the content and style representation of the image can be separated. Then, the WAC-Flow code is inversely mapped to the image space through the stylized decoding process integrated with the AdaIN module.

The additional loss of the AdaIN layer in the generator G is the weighted combination of the content loss Lc and the style loss Ls:

Lc=||e(f−1(zcs))−zcs||2(12)

Ls=∑i=1…L||μ(ϕi(f−1(zcs)))−μ(ϕi(Is))||2+∑i=1…L||σ(ϕi(f−1(zcs)))−σ(ϕi(Is))||2(13)

where zcs is the output code of AdaIN, Is is the style image, f−1 is the decoder, e is all the layers prior to relu4_1 pre-trained for fixed VGG-19, ϕi is the layer in VGG19 used to calculate style loss. In the experiment, relu1_1, relu2_1, relu3_1, and relu4_1 layers with the same weights are used, and μ and σ are the mean and standard deviation of the feature image, respectively. To obtain the content loss Lc, the Euclidean distance between the target features and the output image features needs to be calculated. As for the style loss Ls, the mean and variance of the channel corresponding to feature code are used to represent the image style instead of the Gram matrix [18,19]. The decoder f−1 is trained to trade off between Lc and Ls rather than to reconstruct a perfect input image.

3.1.3 Loss of Adaptive Painting Stroke Edges

In order to generate images that are more suitable for artistic painting style transfer, the model needs to learn a typical feature of artistic paintings, i.e., edge features. For example, traditional ink painting is outlined with brushes, which not only clearly depicts the outline of the object but also embellishes the details. In a sketch, by contrast, the color is applied thickly with a pencil, while the outline is sketched with a single stroke. To unify the edges of different thicknesses in modeling art paintings, and also define and distinguish them to guide the generation, a stroke constraint is introduced in the generator G to strengthen the edge consistency between the real and generated images. This adaptive stroke edge loss can extract specific multi-scale edges in each image. It is more flexible and accurate than Holistically-Nested Edge Detection (HED) [48] which can only extract fixed-scale edges and thus is suitable for tasks on artistic painting datasets.

In this paper, the Bi-Directional Cascade Network (BDCN) is used to extract adaptive multi-scale edges from the input image, to simulate strokes of different thicknesses. It uses multiple IDB (ID block) layers to extract edge maps of specific scales that are learned by the network itself. The effect of edge extraction varies with different scales. The shallow layer is better at extracting the edge of details better, while the deep layer extracts the edge of the target better. The network allows each intermediate layer to learn its own appropriate scale, and finally fuses the outputs of all layers.

Specifically, the pre-trained BDCN is used to extract the edge of the original image to get B(Ic), and the edge of the transferred image is extracted to obtain B(G(Ic)). Then, a balanced cross-entropy loss is computed with B(Ic) as the true guidance, so that the generator network can learn to get the appropriate strokes. Therefore, the stroke edge loss can be expressed as:

Lbrush(G,B,Ic)=EIc∼Pdata(Ic)[1N∑i=1NαB(Ic)ilog⁡B(G(Ic))i]+β(1−B(Ic)i)log⁡(1−B(G(Ic)i))(14)

where G is a generator that uses WAC-Flow to generate stylized image from the original image, N is the total number of pixels in the edge map of the original image or the transferred image, and α and β are two parameters for balancing edge and non-edge pixels respectively.

{α=λ⋅|Y+|/(|Y+|+|Y−|)β=|Y+|/(|Y+|+|Y−|)(15)

where λ controls the proportion of positive and negative samples in α. |Y+| and |Y−| are the sums of non-edge and edge probabilities for each pixel in B(x), respectively.

3.2 A Tester Based on Style Consistency Loss

This study believes that various styles have certain commonalities. For example, the style of artistic paintings has its unique characteristics, so the generated pictures are expected to have a general style rather than a specific style. Previous style transferors only normalize the style of each image, thus this paper formulates a style noise consistency loss Lsn to guide the generalization of the generative model. It uses the reverse reconstruction ability of WAC-Flow to input the stylized image Ics as content information and the content image Ic as style information, and reversely reconstruct the stylized image Ics back to the original content image I^c. This can improve the model utilization and further optimize the model so that it can be applied to more types of artistic style transfer tasks.

In view of the above considerations, this paper adopts a tester T, corresponding to the blue part in Fig. 1, where it can produce a style noise consistency loss Lsn. As mentioned above, the generator G has added style noise to Is before it is fed to the tester T, so z~s=zs+ξ, where ξ∼u(−0.5,0.5). In the tester T, the latent space code of Ic is processed with style noise again: z~c=zc+ξ, where ξ∼u(−0.5,0.5). After that, the obtained code z~c as the style code and zcs as the content code are input into the AdaIN layer so as to obtain the latent variable z~cs after transfer. Finally, the transfer result z~cs is reconstructed from Ic to I^c through the reverse decoder f−1. To ensure that the reconstructed image I^c after style noise processing is consistent with the input content image Ic in content and style, the loss is constructed:

Lcyc(G,T,Ic,Is)=||T(G(Ic,Is),zc)−Ic||1(16)

LMS−SSIM(G,T,Ic,Is,zc)=1−SSIM(T(G(Ic,Is),zc),Ic)(17)

Lsn(G,T,Ic,Is,zc)=Lcyc(G,T,Ic,Is)+LMS−SSIM(G,T,Ic,Is,zc)(18)

where ||⋅||1 is the L1 loss, G is the module that generates the style image from the original image, and T is the module that restores the style image to the original image. Specifically, G can be expressed as:

G(Ic,Is)=f−1(AdaIN(f(Ic),f(Is)+ξ))(19)

And T can be expressed as:

T(Ics,zc)=f−1(AdaIN((zc+ξ)+f(Ics)))(20)

where the noise ξ∼u(−0.5,0.5). Further, the loss Multi-scale Structural Similarity Index Measure (MS-SSIM) can be obtained by computing the value of Structural Similarity Index Measure (SSIM) at multiple scales:

SSIM(x,y)=[lM(x,y)]αM∏j=1M[cj(x,y)]βj[sj(x,y)]γj(21)

Then, the multi-scale SSIM and L1 loss are combined to regularize the generator output after style noise treatment, including Ics and I^c. In addition, the similarity constraints of I^c and Ic spatial features are added, so that the image style of the generated Ics is not limited to a single image, and the generalization ability of image style representation is enhanced. The tester of WAC-Flow and its inverse structure share the corresponding parameters with the generator G, thus the storage and computation for parameters are not large.

3.3 Discriminator and Combined Loss

For artistic paintings, the processing of details is crucial, and generating reasonable details can improve the authenticity of the image. To ensure the generative model can focus on the generated details of the artistic painting image while considering the influence of different parts of the generated image, this paper adopts the discriminator in PatchGAN and its loss to further improve the effect of image style transfer. Different from the common GAN discriminator that maps the input to a real number, that is, the probability of the input sample being a true sample, the PatchGAN discriminator maps the input to a N × N (patch) matrix X. Each Xij corresponds to the probability of the sample in the area where the patch is located being true. It comprehensively considers the discriminative output of each patch of the image, and thus can enhance the spatial detail quality of the generated artistic painting image. In this paper, the discriminator D is used to calculate the patch average discriminant distance D(X)=1N×N∑ijDij(xij) of the generated stylized image, thus establishing the adversarial generative network loss:

LGAN(Ic,Is,Ireal)=EIreal∼Pdata(Ireal)[log⁡D(Ireal)]+EIc,Is∼Pdata(Ic,Is)[1−log⁡D(G(Ic,Is))](22)

where G is the generator that transfers input images to stylized images through the proposed reversible network, and D is the PatchGAN discriminator. The optimization goal here is to minimize the loss of the generator G and maximize the loss of the discriminator D, namely:

minGmaxDLGAN(Ic,Is,Ireal)(23)

The objective function is optimized by the training strategy of cyclic confrontation in the data batch. The discriminator (D) and the generator (G) are optimized in turn through adversarial learning, and finally the ideal style image generation effect is obtained. In summary, the combined loss proposed in this paper is:

L(G,T,D,B)=αLc+βLs+γLbrush(G,B,Ic)+μLGAN(G,D,Ic,Is,Ireal)+ωLsn(G,T)(24)

where parameters like α, β, γ, μ, and ω are a linear combination for control of these losses. The final optimization objective is:

ℋ=argminT,G,BmaxDL(G,T,D,B)(25)

The transfer method of artistic painting style proposed in this paper can be analyzed from the aspects of detail processing and overall style. The reversible WAC-Flow model not only provides an approach to obtaining the unbiased transfer map of generated content but also constructs a compact en-decoder feedforward structure to meet the requirement of lossless spatial details in artistic painting transfer tasks. Furthermore, an adaptive paint stroke edge loss is introduced to constrain the learning of style painting edges. As for the overall style, this paper proposes a tester T, which can satisfy the overall style requirements of artistic paintings, guide the optimization process of the generative model, and obtain good style generalization performance. Fig. 3 illuminates the overall flowchart of APST-Flow and the detailed algorithm of the Flow-based module.

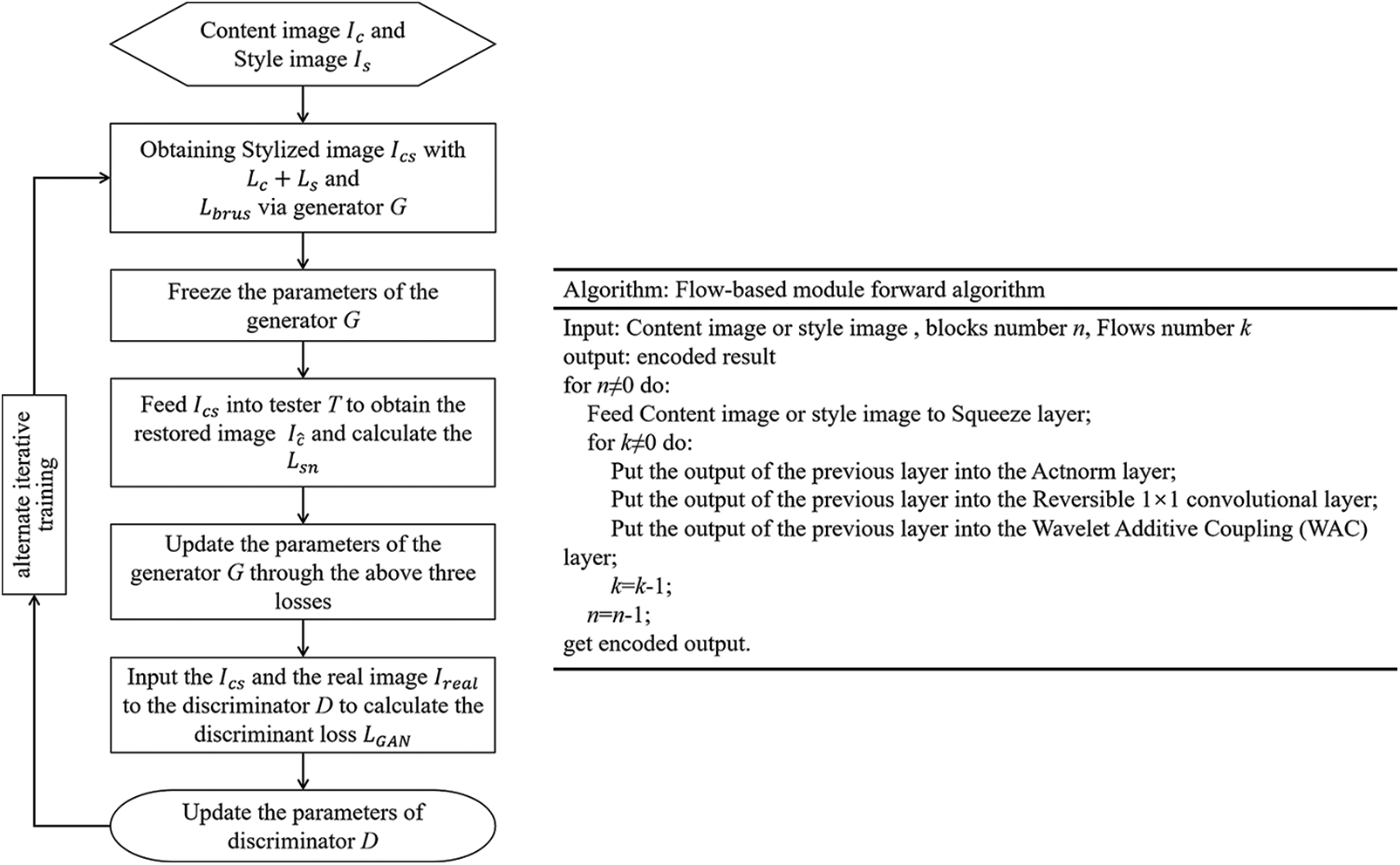
Figure 3: The flowchart of APST-flow and the algorithm table of the flow-based module

4  Experimental Results and Discussion

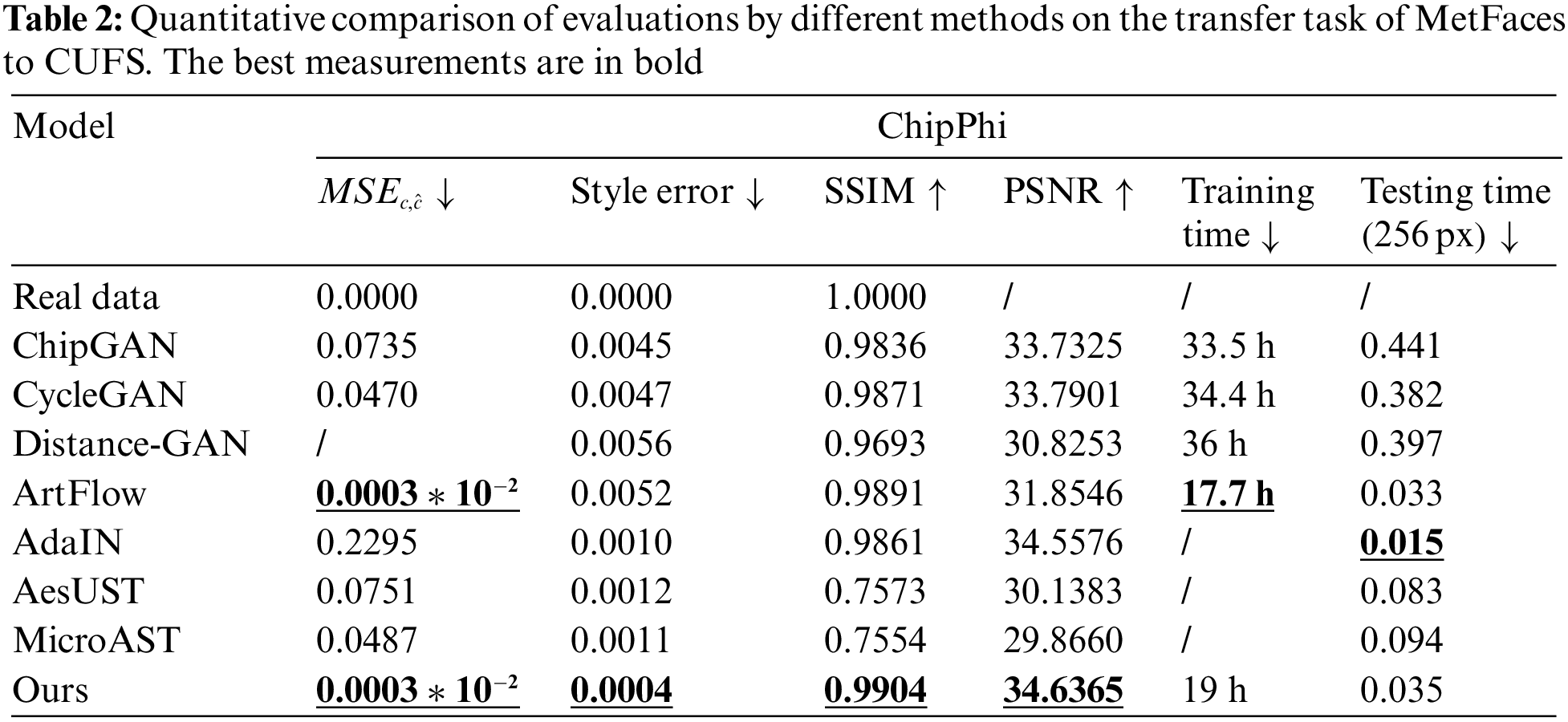
The proposed method was evaluated according to the main performance indicators of the generation results according to different artistic painting style transfer tasks. Specifically, the existing models of artistic painting style transfer were tested and compared, including ChipGAN [9], CycleGAN [49], Distance-GAN [50], AdaIN [22], ArtFlow [46], etc. To ensure test fairness, the default parameter configurations of the above models were performed, and the same image set was used to train for model convergence. After that, the same images were selected from the test set for qualitative and quantitative evaluation and comparison (the details are given below). For the experimental computing platform, the ubuntu18.04.6 system equipped with the intel®Core i5—9400F CPU 2.90 GHz × 6 and the NVIDIA GeForce RTX 2070 8G GPU was adopted.

4.1 Experimental Settings

Two scenarios were set for the experiment, one was the style transfer from real image to artistic painting, and the other was the style transfer from artistic painting to artistic painting. Three representative datasets were adopted: ChipPhi [9], MetFaces [51], and CUHK Face Sketch Database (CUFS) [52]. Among them, the ChipPhi set collected in ChipGAN [9] contains 1478 real horse photos and 822 ink paintings of horses. It serves as an evaluation test set for the ink style transfer models [9,10] and can be used for transfer experiments from real pictures to ink paintings. The MetFaces set contains 1336 images of western artistic face paintings, including oil paintings, prints, gouache, etc. The CUFS set is composed of 606 face sketch images of different races. These two sets can be used for the experiment of style transfer from other artistic paintings to sketches. For better training effect, CUFS was reversed and trimmed to increase the number of sketches to a total of 1212.

To evaluate the style transfer from real pictures to artistic paintings, MSEc,c^, Style Error, training time, and testing time were used as evaluation indexes to quantitatively evaluate the generated results. These evaluations comprehensively compared the results of different model architectures, loss functions, and related parameters. The average of 50 results for each method was selected as the final result. Here, MSEc,c^ refers to the Mean Squared Error (MSE) between the fake content image I^c restored from the generated stylized image Ics and the content image Ic. The MSE evaluation indicator is given by:

MSE=1N∑i=1N(yi−y^i)2(26)

The other evaluation index, Style Error, calculates the distance of the style features between the generated stylized image Ics and the style image Is. As described in Eq. (6), it calculates the Euclidean distance between the variance σ and the mean μ of the stylized image Ics and the style image Is via the VGG19 specific layer ϕi, respectively. SSIM is designed to evaluate the similarity of two images (Ics and Is) in terms of brightness, contrast, and structure, and is a commonly used evaluation indicator for style transfer tasks.

SSIM(G)=(2μxμy+C1)(2σxy+C2)(μx2+μy2+C1)(σx2+σy2+C2)(27)

Peak Signal-to-Noise Ratio (PSNR) is also a widely used image evaluation index, and it is based on the error between corresponding pixels. PSNR is calculated by the following formula, where MAXI represents the maximum of the pixel color.

PSNR=20⋅log10⁡(MAXIMSE)(28)

In this paper, the APST-Flow model details are realized on the PyTorch framework. The Adam optimizer (0.5, 0.999) was applied to train APST-Flow for 60,000 iterations, with batch size of 1, initial learning rate of 1e-4, and learning rate decay of 0. The WAC-Flow had 2 blocks, each of which contained 2 Flows, and the scale of the discrete Wavelet pyramid in WAC was set as L = 2. On a single RTX 2070 GPU, the APST-Flow was trained for about 24 h. In the linear combination of the total loss function, the coefficients of content loss and style loss were set to 1 and 0.1 respectively, the coefficient of edge loss to 0.1, and the coefficients of other loss terms to 1.0 by default.

4.2 Experimental Results and Discussion

To verify the effectiveness of the proposed method, it is compared both qualitatively and quantitatively on two tasks with several state-of-the-art models including ChipGAN [9], AdaIN [22], ArtFlow [46], CycleGAN [49], Distance-GAN [50], AesUST [53], and MicroAST [54].

4.2.1 Qualitative Comparison

Fig. 4 shows the comparison between the generated results of the proposed model and existing transfer methods in the transfer task from real images to ink paintings on the ChipPhi set. As can be seen from the figure, only our method and ArtFlow which also uses the Flow model can roughly separate the main part of the horse and generate the necessary gaps in ink paintings. For example, as shown in the 2nd and 5th rows of Fig. 4, the other 6 methods except our method have complex artifacts in the shadow behind the horse, which affects the overall generation effect. Although ChipGAN, Distance-GAN, and CycleGAN have removed artifacts to a certain extent, their overall generation effect is not ideal, that is because the style tester T in our method can maintain the overall style. In addition, as shown in lines 3 and 6, the other 6 methods do not work efficiently on background segmentation, while our method has clearer lines and better shows ink painting style in the simulation of brush strokes. These illustrate that our model can well achieve ink painting style transfer of brushstrokes. From the generated results of ChipGAN in the 6th row, it can be observed that the leaves on the left side are generated as horse tails and the ears are missing. In contrast, our results preserve the image content while transferring the style well. This is attributed to the ability of WAC-Flow to preserve the content details in style transfer tasks.

Figure 4: The style transfer from real pictures to ink paintings on the ChipPhi set. The left side of the dotted line is the input content image and style image, and the right side is the generated images by APST-Flow and the comparative methods

To verify the effectiveness of the proposed model, its performance on the task of style transfer between artistic paintings is also evaluated. Fig. 5 shows the comparison between the proposed model and the existing methods in the task from the artistic face painting set MetFaces to the face sketch set CUFS. As shown in Fig. 5, ChipGAN, Distance-GAN, and CycleGAN have content deviations in the generated sketches, and part of the content cannot be generated. Also, they have many artifacts on the generated texture, making them difficult to preserve the style of the sketch. Moreover, AdaIN, ArtFlow, AesUST, and MicroAST fail to learn the characteristics of sketches well, and the generated images lack the texture of sketches. AdaIN and AesUST learn only the color features of sketches, and it still maintains the texture of oil paintings. Although ArtFlow retains the general content of the content image, the generated pencil texture is blurred, and the strokes are still in the style of oil paintings rather than sketches. MicroAST generated colors that should not appear in the sketch. Only the proposed method can transfer the style features of sketches well without any bias in content. This is mainly because the WAC-Flow network and the discriminator D of PatchGAN in our model are more focused on detail generation than the other models. At the same time, due to the precise content-preserving ability of the reversible network, our model can preserve more reasonable details than the irreversible transfer models.

Figure 5: Results of the MetFaces to CUFS transfer task. The left side of the dotted line is the input content image and style image, and the right side is the generated images by APST-Flow and the comparative methods

To visualize the content deviations, a set of reconstruction experiments are performed, as shown in Fig. 6. Several methods (ChipGAN, AdaIN, CycleGAN) that allow reconstruction is selected for comparison. The generated image Ics is reconstructed into I^c, which is qualitatively compared with the content image. Obviously, except for our method, the other schemes cannot reconstruct the generated image accurately and completely. ChipGAN and CycleGAN can retain most texture details of the content image, with some deviations, whereas the result of AdaIN is completely based on the generated image, and it differs most significantly from the content image. This demonstrates the unbiased mapping ability of the proposed reversible model to completely transfer the original content image Ic, as well as the ability to fully retain the details in the transfer processing.

Figure 6: Comparison of the results of the four methods for reconstructing the content image Ic into the reconstructed image Ic^. The first and second rows show the content image and the style image respectively, and the third row is the result Ic^ restored by the method in the corresponding column

In addition to horses, various categories of pictures, such as cats, dogs, human faces, and fruits, are selected as the test set. The two models previously trained by the real picture to ink painting transfer task and MetFaces to CUFS transfer task are used to generate these images into ink paintings and sketches. The final results are shown in Fig. 7. It can be seen that the transfer results of different types of images conform to the style of artistic paintings while retaining the content of the original images, indicating that our model has high style transfer efficiency and strong generalization ability.

Figure 7: Transfer results of various images by APST-Flow. Each group has three columns, the first of which is the content image, the second is the results of transferring to ink paintings, and the third is the results of transferring to sketches

In conclusion, ChipGAN, Distance-GAN, and CycleGAN generate a certain degree of content deviation and background artifacts. AdaIN and MicroAST produce textures that are not realistic enough and have artifacts. ArtFlow has messy brushstrokes. They cannot faithfully reflect the style features of ink paintings and sketches. AesUST produces sketchy textures that are too strong. Compared with these methods, our method can well transfer the style of artistic paintings without changing the content. Our method can generate images with reasonable style on both tasks, and the trained model can be applied to the other types of input and achieve reasonable generation results. This is because the proposed WAC-Flow reversible network can preserve the content details, and the adaptive stroke loss can improve the effect of edge transition. Thus, it achieves excellent results in qualitative comparison with the other methods. Furthermore, the style-checking network can ensure the consistency of the overall style and enhance the generalization ability of the model transfer, so it can generate high-quality results in the other types of images.

4.2.2 Quantitative Comparison

Since the generated images are sometimes difficult to evaluate with the naked eye, multiple sets of quantitative tests are conducted for a fair comparison. MSEc,c^, Style Error, SSIM, and PSNR are used as evaluation indicators for quantitative comparison. It can be seen from Tables 1 and 2 that our method has better results on most indicators and requires less training time. In addition, the SSIM index also has the best performance due to the unbiased mapping ability of the reversible model, and this is also reflected in ArtFlow. Our method also has an advantage in style loss, presumably due to the fact that WAC-Flow can process deeper features. This shows that the proposed method can not only preserve the content information of images but also learn the style features of paintings well. The image generated by our method is better than those of the other methods in image evaluation indicators PSNR. Our method has the most obvious improvement in the transfer task from real pictures to ink paintings. Specifically, compared with the previous best method ArtFlow, ours improves PSNR by 1.5975 and SSIM by 0.0583 and decreases Style Error by 0.005. In the MetFaces to CUFS transfer tasks, our method outperforms the previous best method by 0.0789 and 0.0013 in PSNR and SSIM indicators, respectively, and reduces Style Error by 0.0006. This shows that the proposed method achieves the best transfer effect on the two tasks, and the greatest improvement is achieved in the real to ink painting task. In terms of training time, AdaIN, AesUST, and MicroAST use the pre-trained model. ChipGAN is cyclic training, which has two identical generators and discriminators, and ArtFlow is one-way training. Our model is also one-way training but has some more cyclic constraints than ArtFlow, so our method is shorter than ChipGAN but longer than ArtFlow in training time. Nevertheless, our model has a longer test time than AdaIN, which may be ascribed to the lightweight model of AdaIN.

4.2.3 Ablation Experiment

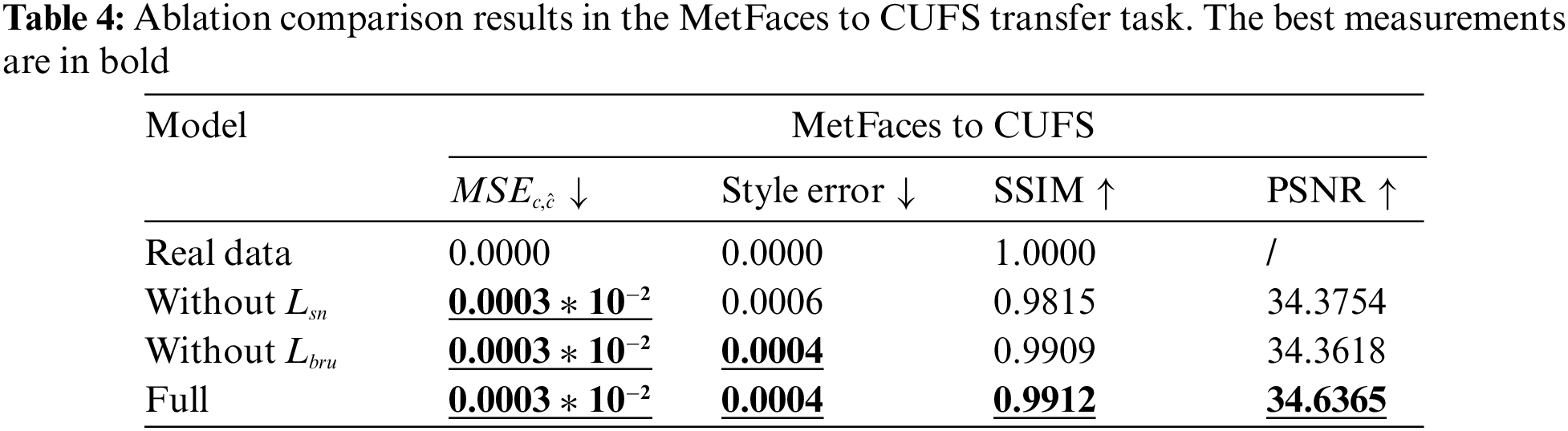
To verify the effectiveness of the proposed loss, ablation experiments are performed on the two losses. In Fig. 8, “Without Lsn” refers to removing the tester T from the model, and “Without Lbrush” refers to removing the adaptive painting stroke edge loss. The first and fifth columns of the test results are the input real images. The three columns following the first column are the ablation comparison of sketches and the three following the fifth column are the ablation comparison of ink paintings. It can be seen from the generation results on the ChipPhi set that the generated images without Lbrush are blurrier on the whole, and though have an advantage in the definition of content and texture, there are lots of artifacts at the edges. The results without Lsn are close to the real image in the generation of edges, while the results without Lbrush have poor generation effect, especially in gap processing. For example, many artifacts can be observed in the images in the second and sixth columns, but not in the results without Lbrush or with the full model. On the MetFaces to CUFS transfer task, the results without Lbrush partly retain the color and fail to completely transfer the black and white style of sketches, as shown in the first and third rows. Also, the generated result is more like the original image with changed colors and lacks the sketch style in the stroke texture. The generated images without Lsn are better than those without Lbrush in texture details but still cannot achieve high-quality results in color generation.

Figure 8: Ablation results for both two tasks. The left half is the result of the MetFaces to CUFS transfer task, and the right half is the result of the real image to ink painting transfer task

In the experiment, it is found that the stroke contour, gap, and texture details of ink paintings can be well learned by using these two losses at the same time, with the best generation effect. To demonstrate the effectiveness of the proposed WAC-Flow network, Fig. 9 with obvious visualization is chosen to show our experimental results. The first column on the left is the content image, and the two on the right are the generated results by Glow and WAC-Flow respectively. It can be seen that the generation effect by WAC-Flow not only retains the original outline but also generates fine texture details. For example, as shown in the horse's neck in the first and third columns, the images generated with WAC-Flow are closer to ink painting in texture than those with Glow, and the transition is natural and closer to the real painting. The reason is that the proposed method can better distinguish content and texture, and generate texture features that are more in line with the content.

Figure 9: Comparative experiment with/without WAC. The first row is the input content image, the second is the generated image by Glow, and the third is the generated result with the WAC network

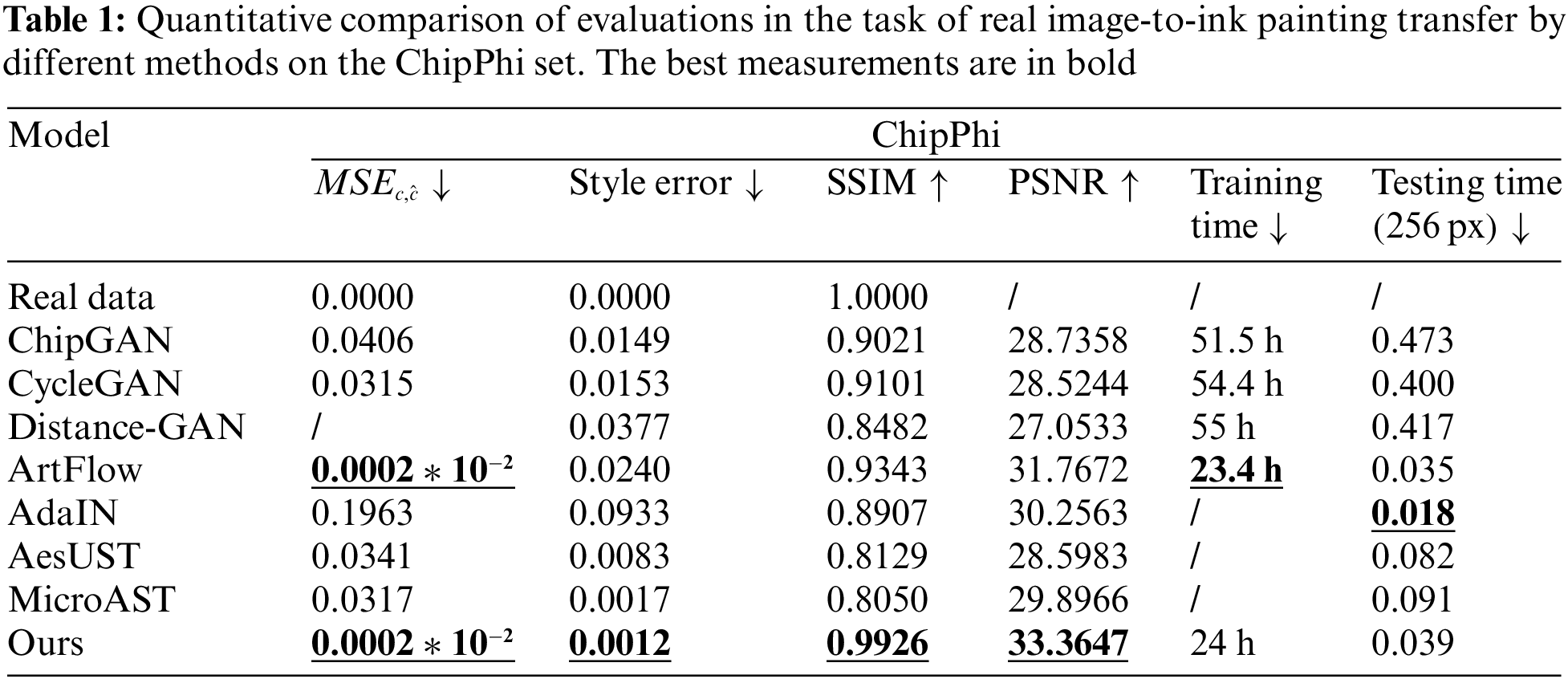
The quantitative analysis results are presented in Tables 3 and 4. The values of MSEc,c^ in the ablation results are the same, which means that the models without Lsn or Lbrush can fully save the content without content offset. This also demonstrates the advantage of unbiased mapping in full mode. In the image-to-ink painting transfer task, the model without Lsn module performs the best on Style Error, which is less than the full model by 0.0009. The reason for the poorer performance of the full model may lie in the large deviation between the overall style and the specific style, but it is slightly better than the model without Lsn on the generation effect. Furthermore, the model without Lsn module is slightly lower than that without Lbrush module in SSIM and PSNR. It has a poorer generation effect than the full model. In the MetFaces to CUFS transfer task, the ablation results are similar. On the whole, the model without Lsn module is inferior to the model without Lsn module, except in PSNR, the former exceeds the latter by 0.014. All indicators of the full model are the best, proving that the proposed method can achieve the best performance.

Unlike CycleGAN, Distance-GAN, ChipGAN, or AdaIN which will cause artifacts and loss of content, the proposed en-decoder shared framework can generate excellent transfer results without missing more content. It is because our model utilizes the reversibility of WAC-Flow to achieve compact feedforward en-decoding processing. Compared with ArtFlow [46], which is also an en-decoding style transfer scheme, our method shows a significant advantage in the transfer tasks, which is ascribed to the multiple improvements in content details and overall style. Consequently, our method can be applied in many scenes of reality, such as providing inspiration for artistic painting. Although the proposed method is excellent, it still requires optimizing numerous model parameters, which makes the generation process inefficient. Additionally, the model cannot realize the adaptive transfer of different artistic painting styles, thus its generalization ability needs to be further enhanced.

5  Conclusions

Aiming at the problems of content detail deviation and the difficult convergence of model training in APST, this paper proposes a novel style transfer network APST-Flow based on a multi-scaled reversible model. Experiments on different scenarios demonstrate that APST-Flow can effectively and accurately guide the style transferring process and outperforms the state-of-the-art baselines in both qualitative and quantitative evaluations. In addition, the loss Lbrush can effectively guide the learning of style strokes, and the PatchGAN discriminator reduces the uncertainty of generated results so that the reversible WAC-Flow generates high-quality details. The introduced discriminant module T can globally enhance the generalization ability, thereby improving the generative performance on various APST tasks. Compared with existing baselines, APST-Flow improves PSNR and SSIM by 1.5975 and 0.0583 respectively on the ChipPhi set and by 0.0789 and 0.0013 in the MetFaces to CUFS transfer task. The competitive results verify that APST-Flow achieves high-quality generation with less content deviation and enhanced generalization, thereby can be further applied to more APST scenes. The limitations lie in the parameter scale being still too large and the ability to adapt and transfer various styles cannot be totally satisfied. Further work might be carried out in two folds: improve the generator by incorporating the concept of super-resolution to generate more general art-style paintings, and integrate the attention mechanism to control the distribution of stylization to generate more interpretable style transfer results.

Funding Statement: The authors appreciate the financial support from National Natural Science Foundation of China (62062048).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. O. Russakovsky, J. Deng, H. Su, J. Krause, S. Satheesh et al., “Imagenet large scale visual recognition challenge,” International Journal of Computer Vision, vol. 115, no. 3, pp. 211–252, 2015. https://doi.org/10.1007/s11263-015-0816-y [Google Scholar] [CrossRef]

2. J. X. Chen, “The evolution of computing: AlphaGo,” Computing in Science & Engineering, vol. 18, no. 4, pp. 4–7, 2016. https://doi.org/10.1109/MCSE.2016.74 [Google Scholar] [CrossRef]

3. U. A. Bhatti, Z. Yu, J. Chanussot, Z. Zeeshan, L. Yuan et al., “Local similarity-based spatial-spectral fusion hyperspectral image classification with deep CNN and Gabor filtering,” IEEE Transactions on Geoscience and Remote Sensing, vol. 60, pp. 1–15, 2021. [Google Scholar]

4. A. Bochkovskiy, C. -Y. Wang and H. -Y. M. Liao, “Yolov4: Optimal speed and accuracy of object detection,” arXiv preprint arXiv:2004.10934, 2020. [Google Scholar]

5. H. Cate, F. Dalvi and Z. Hussain, “Deepface: Face generation using deep learning,” arXiv preprint arXiv:1701.01876, 2017. [Google Scholar]

6. U. A. Bhatti, M. Huang, D. Wu, Y. Zhang, A. Mehmood et al., “Recommendation system using feature extraction and pattern recognition in clinical care systems,” Enterprise Information Systems, vol. 13, no. 3, pp. 329–351, 2019. https://doi.org/10.1080/17517575.2018.1557256 [Google Scholar] [CrossRef]

7. A. Xue, “End-to-end Chinese landscape painting creation using generative adversarial networks,” in Proc. IEEE/CVF Winter Conf. on Applications of Computer Vision, Waikoloa, HI, USA, pp. 3863–3871, 2021. [Google Scholar]

8. B. He, F. Gao, D. Ma, B. Shi and L. -Y. Duan, “ChipGAn: A generative adversarial network for Chinese ink wash painting style transfer,” in Proc. 26th ACM Int. Conf. on Multimedia, Seoul, Korea, pp. 1172–1180, 2018. [Google Scholar]

9. F. Zhang, H. Gao and Y. Lai, “Detail-preserving CycleGAN-AdaIN framework for image-to-ink painting translation,” IEEE Access, vol. 8, pp. 132002–132011, 2020. https://doi.org/10.1109/ACCESS.2020.3009470 [Google Scholar] [CrossRef]

10. C. Zeng, J. Liu, J. Li, J. Cheng, J. Zhou et al., “Multi-watermarking algorithm for medical image based on KAZE-DCT,” Journal of Ambient Intelligence and Humanized Computing, vol. 32, no. 9, pp. 1–9, 2022. https://doi.org/10.1007/s12652-021-03539-5 [Google Scholar] [CrossRef]

11. M. Wang, B. Wang, Y. Fei, K. -L. Qian, W. Wang et al., “Towards photo watercolorization with artistic verisimilitude,” IEEE Transactions on Visualization and Computer Graphics, vol. 20, no. 10, pp. 1451–1460, 2014. https://doi.org/10.1109/TVCG.2014.2303984 [Google Scholar] [PubMed] [CrossRef]

12. J. Johnson, A. Alahi and L. Fei-Fei, “Perceptual losses for real-time style transfer and super-resolution,” in European Conf. on Computer Vision, Amsterdam, Netherlands, pp. 694–711, 2016. [Google Scholar]

13. W. Li, L. Wen, X. Bian and S. Lyu, “Evolvement constrained adversarial learning for video style transfer,” in Asian Conf. on Computer Vision, Perth, Australia, pp. 232–248, 2018. [Google Scholar]

14. D. P. Kingma and M. Welling, “Auto-encoding variational bayes,” arXiv preprint arXiv:1312.6114, 2013. [Google Scholar]

15. D. Lin, Y. Wang, G. Xu, J. Li and K. Fu, “Transform a simple sketch to a chinese painting by a multiscale deep neural network,” Algorithms, vol. 11, no. 1, pp. 4, 2018. https://doi.org/10.3390/a11010004 [Google Scholar] [CrossRef]

16. A. A. Efros and W. T. Freeman, “Image quilting for texture synthesis and transfer,” in Proc. 28th Annual Conf. on Computer Graphics and Interactive Techniques, New York, NY, USA, pp. 341–346, 2001. [Google Scholar]

17. C. M. Wang and R. -J. Wang, “Image-based color ink diffusion rendering,” IEEE Transactions on Visualization and Computer Graphics, vol. 13, no. 2, pp. 235–246, 2007. https://doi.org/10.1109/TVCG.2007.41 [Google Scholar] [PubMed] [CrossRef]

18. L. Gatys, A. S. Ecker and M. Bethge, “Texture synthesis using convolutional neural networks,” in Advances in Neural Information Processing Systems, Montreal Canada: Curran Associates, Inc., pp. 262–270, 2015. [Google Scholar]

19. L. A. Gatys, A. S. Ecker and M. Bethge, “A neural algorithm of artistic style,” arXiv preprint arXiv:1508.06576, 2015. [Google Scholar]

20. V. Badrinarayanan, A. Kendall and R. Cipolla, “SegNet: A deep convolutional encoder-decoder architecture for image segmentation,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 39, no. 12, pp. 2481–2495, 2017. https://doi.org/10.1109/TPAMI.2016.2644615 [Google Scholar] [PubMed] [CrossRef]

21. J. Long, E. Shelhamer and T. Darrell, “Fully convolutional networks for semantic segmentation,” in Proc. IEEE Conf. on Computer Vision and Pattern Recognition, Boston, MA, USA, pp. 3431–3440, 2015. [Google Scholar]

22. X. Huang and S. Belongie, “Arbitrary style transfer in real-time with adaptive instance normalization,” in Proc. IEEE Int. Conf. on Computer Vision, Venice, Italy, pp. 1501–1510, 2017. [Google Scholar]

23. D. Y. Park and K. H. Lee, “Arbitrary style transfer with style-attentional networks,” in Proc. IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Long Beach, CA, USA, pp. 5880–5888, 2019. [Google Scholar]

24. S. Liu, T. Lin, D. He, F. Li, M. Wang et al., “AdaAttN: Revisit attention mechanism in arbitrary neural style transfer,” in Proc. of the IEEE/CVF Int. Conf. on Computer Vision, on-line, pp. 6649–6658, 2021. [Google Scholar]

25. Y. Li, C. Fang, J. Yang, Z. Wang, X. Lu et al., “Universal style transfer via feature transforms,” in Advances in Neural Information Processing Systems, Long Beach, CA, USA: Curran Associates, Inc., pp. 385–395, 2017. [Google Scholar]

26. B. Li, C. Xiong, T. Wu, Y. Zhou, L. Zhang et al., “Neural abstract style transfer for chinese traditional painting,” in Asian Conf. on Computer Vision, Perth, Australia, pp. 212–227, 2018. [Google Scholar]

27. R. Zhou, J. H. Han, H. S. Yang, W. Jeong and Y. S. Moon, “Fast style transfer for chinese tranditional ink painting,” in 2019 IEEE 9th Int. Conf. on Electronics Information and Emergency Communication (ICEIEC), Beijing, China, pp. 586–588, 2019. [Google Scholar]

28. J. Cao, Y. Hong and L. Niu, “Painterly image harmonization in dual domains,” arXiv preprint arXiv:2212.08846, 2022. [Google Scholar]

29. L. Dinh, D. Krueger and Y. Bengio, “Nice: Non-linear independent components estimation,” arXiv preprint arXiv:1410.8516, 2014. [Google Scholar]

30. L. Dinh, J. Sohl-Dickstein and S. Bengio, “Density estimation using real NVP,” arXiv preprint arXiv:1605.08803, 2016. [Google Scholar]

31. D. P. Kingma and P. Dhariwal, “Glow: Generative flow with invertible 1 × 1 convolutions,” in Advances in Neural Information Processing Systems, Montréal, Canada: Curran Associates, Inc., pp. 10236–10245, 2018. [Google Scholar]

32. J. Ho, X. Chen, A. Srinivas, Y. Duan and P. Abbeel, “Flow++: Improving flow-based generative models with variational dequantization and architecture design,” in Int. Conf. on Machine Learning, Long Beach, CA, USA, pp. 2722–2730, 2019. [Google Scholar]

33. J. He, S. Zhang, M. Yang, Y. Shan and T. Huang, “BDCN: Bi-directional cascade network for perceptual edge detection,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 44, no. 1, pp. 100–113, 2020. https://doi.org/10.1109/TPAMI.2020.3007074 [Google Scholar] [PubMed] [CrossRef]

34. L. Yan, W. Zheng, C. Gou and F. -Y. Wang, “IsGAN: Identity-sensitive generative adversarial network for face photo-sketch synthesis,” Pattern Recognition, vol. 119, no. 4, pp. 108077, 2021. https://doi.org/10.1016/j.patcog.2021.108077 [Google Scholar] [CrossRef]

35. W. Wan, Y. Yang and H. J. Lee, “Generative adversarial learning for detail-preserving face sketch synthesis,” Neurocomputing, vol. 438, no. 2, pp. 107–121, 2021. https://doi.org/10.1016/j.neucom.2021.01.050 [Google Scholar] [CrossRef]

36. D. Zhang, L. Lin, T. Chen, X. Wu, W. Tan et al., “Content-adaptive sketch portrait generation by decompositional representation learning,” IEEE Transactions on Image Processing, vol. 26, no. 1, pp. 328–339, 2016. https://doi.org/10.1109/TIP.2016.2623485 [Google Scholar] [PubMed] [CrossRef]

37. J. Yu, X. Xu, F. Gao, S. Shi, M. Wang et al., “Toward realistic face photo-sketch synthesis via composition-aided GANs,” IEEE Transactions on Cybernetics, vol. 51, no. 9, pp. 4350–4362, 2020. https://doi.org/10.1109/TCYB.2020.2972944 [Google Scholar] [PubMed] [CrossRef]

38. N. Wang, W. Zha, J. Li and X. Gao, “Back projection: An effective postprocessing method for GAN-based face sketch synthesis,” Pattern Recognition Letters, vol. 107, no. 3, pp. 59–65, 2018. https://doi.org/10.1016/j.patrec.2017.06.012 [Google Scholar] [CrossRef]

39. L. Zhang, Y. Ji, X. Lin and C. Liu, “Style transfer for anime sketches with enhanced residual U-net and auxiliary classifier GAN,” in 2017 4th IAPR Asian Conf. on Pattern Recognition (ACPR), Nanjing, China, pp. 506–511, 2017. [Google Scholar]

40. H. Chen, L. Zhao, Z. Wang, H. Zhang, Z. Zuo et al., “Dualast: Dual style-learning networks for artistic style transfer,” in Proc. IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Nashville, TN, USA, pp. 872–881, 2021. [Google Scholar]

41. T. Lin, Z. Ma, F. Li, D. He, X. Li et al., “Drafting and revision: Laplacian pyramid network for fast high-quality artistic style transfer,” in Proc. of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Nashville, TN, USA, pp. 5141–5150, 2021. [Google Scholar]

42. Y. Lu and B. Huang, “Structured output learning with conditional generative flows,” in Proc. of the AAAI Conf. on Artificial Intelligence, New York, NY, USA, vol. 34, pp. 5005–5012, 2020. [Google Scholar]

43. A. Lugmayr, M. Danelljan, L. V. Gool and R. Timofte, “Srflow: Learning the super-resolution space with normalizing flow,” in European Conf. on Computer Vision, Glasgow, KY, USA, pp. 715–732, 2020. [Google Scholar]

44. J. J. Yu, K. G. Derpanis and M. A. Brubaker, “Wavelet flow: Fast training of high resolution normalizing flows,” Advances in Neural Information Processing Systems, vol. 33, pp. 6184–6196, 2020. [Google Scholar]

45. H. -J. Chen, K. -M. Hui, S. -Y. Wang, L. -W. Tsao, H. -H. Shuai et al., “Beautyglow: On-demand makeup transfer framework with reversible generative network,” in Proc. IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Long Beach, CA, USA, pp. 10042–10050, 2019. [Google Scholar]

46. J. An, S. Huang, Y. Song, D. Dou, W. Liu et al., “Unbiased image style transfer via reversible neural flows,” in Proc. IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Nashville, TN, USA, pp. 862–871, 2021. [Google Scholar]

47. P. Isola, J. -Y. Zhu, T. Zhou and A. A. Efros, “Image-to-image translation with conditional adversarial networks,” in Proc. IEEE Conf. on Computer Vision and Pattern Recognition, Honolulu, HI, USA, pp. 1125–1134, 2017. [Google Scholar]

48. S. Xie and Z. Tu, “Holistically-nested edge detection,” in Proc. IEEE Int. Conf. on Computer Vision, Santiago, Chile, pp. 1395–1403, 2015. [Google Scholar]

49. J. -Y. Zhu, T. Park, P. Isola and A. A. Efros, “Unpaired image-to-image translation using cycle-consistent adversarial networks,” in Proc. IEEE Int. Conf. on Computer Vision, Venice, Italy, pp. 2223–2232, 2017. [Google Scholar]

50. S. Benaim and L. Wolf, “One-sided unsupervised domain mapping,” in Advances in Neural Information Processing Systems, Long Beach, California, USA: Curran Associates, Inc., pp. 752–762, 2017. [Google Scholar]

51. T. Karras, M. Aittala, J. Hellsten, S. Laine, J. Lehtinen et al., “Training generative adversarial networks with limited data,” Advances in Neural Information Processing Systems, vol. 33, pp. 12104–12114, 2020. [Google Scholar]

52. X. Wang and X. Tang, “Face photo-sketch synthesis and recognition,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 31, no. 11, pp. 1955–1967, 2008. https://doi.org/10.1109/TPAMI.2008.222 [Google Scholar] [PubMed] [CrossRef]

53. Z. Wang, Z. Zhang, L. Zhao, Z. Zuo, A. Li et al., “AesUST: Towards aesthetic-enhanced universal style transfer,” in Proc. 30th ACM Int. Conf. on Multimedia, Lisboa, Portugal, pp. 1095–1106, 2022. [Google Scholar]

54. Z. Wang, L. Zhao, Z. Zuo, A. Li, H. Chen et al., “MicroAST: Towards super-fast ultra-resolution arbitrary style transfer,” arXiv preprint arXiv:2211.15313, 2022. [Google Scholar]