Robust Watermarking Algorithm for Medical Volume Data Based on Polar Cosine Transform and 3D-DCT

1  Introduction

In the current Internet of Medical Things (IoMT), new diagnosis and treatment modes such as telemedicine, medical virtual reality technology and intelligent medicine are emerging. From the discovery of X-ray to now, there is three-dimensional imaging based on Computer Tomography (CT), Magnetic Resonance (MR) and ultrasound, which provide more accurate information for doctors’ medical diagnosis and clinical management [1]. Compared with two-dimensional images, three-dimensional volume data is more intuitive, which is beneficial for doctors to observe the health status of the tissues or organs represented by the images, and can help doctors to make preoperative planning, communicate with patients and train professional medical personnel [2].

In practice, doctors generally embed personal information or diagnoses of patients into medical images. For clinical management or referral purposes, these medical data will be transmitted between hospitals or institutions. To make patient data more private and secure, digital watermarking technology from the field of information hiding is applied. The three-dimensional volume data are often subjected to geometric operations such as rotation, scaling, and translation. For example, many important areas of interest to doctors are often inside the volume of data. At this time, the rotation and cutting of medical volume data can provide more reliable data for diagnosis and treatment, and can be used for better quantitative and qualitative analysis [3,4]. This requires the watermarking algorithm to withstand geometric attacks efficiently, so it can be better used for medical data protection.

The usual methods mainly include the algorithm based on transformation, feature points, dimension reduction and so on. Among them, Discrete Cosine Transform (DCT), Discrete Fourier Transform (DFT), Discrete Wavelet Transform (DWT), Log Polar Transform (LPT), etc. based on transformation [5], Zernike moments and local features, etc. based on feature points [6,7], Compressed Sensing (CS) and Singular Value Decomposition (SVD), etc. based on dimension reduction [8,9]. Loan et al. [10] proposed a blind watermarking scheme. In the scheme, the Y component of the pre-processed YCbCr image was chosen as the watermark embedding component and the image was divided into several square blocks of side length 16, which were further divided into sub-blocks of side length 8. The differences of the pre-selected DCT coefficients of the neighboring blocks were calculated and adjusted to the specified range by an adaptive process to facilitate the correct extraction. Zhang et al. [11] proposed a robust watermarking algorithm based on pseudo-Zernike moments. Initially, the low-frequency image was extracted by contourlet transform, and then the blob Harris detection operator was used to extract the feature points of the low-frequency image. The stable and non-overlapping feature regions were optimized and the Zernike moment of each rectangular feature region was computed. The watermark information was embedded in the amplitude of the regularized Zernike moment quantized modulation. The comparison of watermark technologies is shown in Table 1.

At the same time, the above methods are all applied to two-dimensional images, and in the current IoMT, the proportion of three-dimensional imaging data is gradually increasing. Therefore, we proposed a robust watermarking algorithm for medical volume data based on Polar Cosine Transform (PCT) and 3D-Discrete Cosine Transform (3D-DCT). PCT is a kind of polar harmonic transformation proposed by Yap et al., and has good rotation invariance [14]. The algorithm proposed in this paper combines the good distinguishability and rotation invariance of PCT and the good resistance of 3D-DCT to conventional attacks. By combining the feature extraction algorithm PCT and 3D-DCT with the perception hash, the binary feature sequence of the original volume data was obtained, and Exclusive OR (XOR) line by line with the binary watermark encrypted by Sine and Piecewise linear chaotic Mapping (SPM), and the key was obtained and stored in the authentication authority. Similarly, after obtaining the binary feature sequence of the volume data to be tested, and performing line by line XOR with the key stored in the authentication authority, the recovered watermark was extracted after decryption.

The main contributions of this paper are as follows:

1)   The watermark is encrypted by SPM system, which greatly improves the generation efficiency of chaotic sequences without reducing the security;

2)   The combination of zero watermark and third-party technology avoids the modification of medical data when embedding watermark in previous algorithms, meets the strict requirements of medical data quality in medical diagnosis, and greatly improves the embedding capacity of watermark. Since zero watermark does not change the host information, there is no capacity limitation problem. As long as the third party has enough storage space, the original watermark can be as large as possible, so that the capacity of zero watermark generated by XOR of medical data feature vector and encrypted original watermark is unlimited.

3)   The algorithm is robust, and can resist various geometric attacks including rotation and cropping, which are frequently used in processing medical volume data, and also has a good performance against conventional attacks.

2  Related Work

2.1 Polar Cosine Transform

Polar harmonic transformation was proposed by Yap et al. It is a type of orthogonal moment whose domain is unit circle. Polar harmonic transformations (PHTS) include Polar Complex Exponential Transform (PCET), Polar Sine Transform (PST) and Polar Cosine Transform (PCT) [15,16]. For an image  f(r,θ), r is the polar diameter, θ is the polar angle, the PCT moment with order n and repeatability l is defined as Eq. (1).

Mnl=∫02π∫01[Hnl(r,θ)]∗f(r,θ)rdrdθ(1)

Among, n,|l|=0,1,2,⋯+∞, [Hnl(r,θ)]∗ is the complex conjugate of the PCT kernel function Hnl(r, θ). Kernel function is defined as Eq. (2).

Hnl(r,θ)=Rn(r)eilθ=λcos(πnr2)eilθλ={ 1π,n=02π,n≠0(2)

Among, λ is the coefficient of the kernel function  Hnl(r, θ). The kernel function consists of radial part Rn(r) and angular part eijθ, and Rn(r) satisfies the orthogonal condition given by Eq. (3). Where δnn′ is the Kronecker delta and [Rn′(r)]∗ is the conjugate of Rn′(r).

∫01Rn(r)  [ Rn′(r) ]∗rdr=12δnn′δnn′={ 1,n=n′0,n≠n′(3)

The orthogonality of the basis function ensures no information redundancy in the moment set, thus improving the distinguishability between images [17,18].

The image f(r,θ) is defined in a discrete domain [m,n], where 1≤m≤M,1≤n≤N, and M and N are the number of rows and columns of the image.

First, the image f(m,n) defined in the discrete domain [m,n] is transformed into the rectangular coordinate system established with the image point (N/2,M/2) as the origin. Then, the image f(x,y) defined in the rectangular coordinate system is transformed into the polar coordinate system with the origin as the pole and the positive direction of the X axis as the polar axis. Normalize the polar diameter to R=max((N−1)/2,(M−1)/2), and project it onto the inner circle of the image with the pole as the origin and R as the radius.

Take the point (m,n) located in the first quadrant as an example, its corresponding relationship with the point (x,y) in the rectangular coordinate system is as Eq. (4).

x=(n−1)−(N−1)2,y=(M−1)2−(m−1)(4)

The correspondence between the point (x,y) and the point (rr,θ) is as Eq. (5).

rr=x2+y2,θ=sin−1⁡yx2+y2(5)

Similarly, the coordinate transformation relationship of other quadrant image points can be obtained. Coordinate transformation process as shown in Fig. 1.

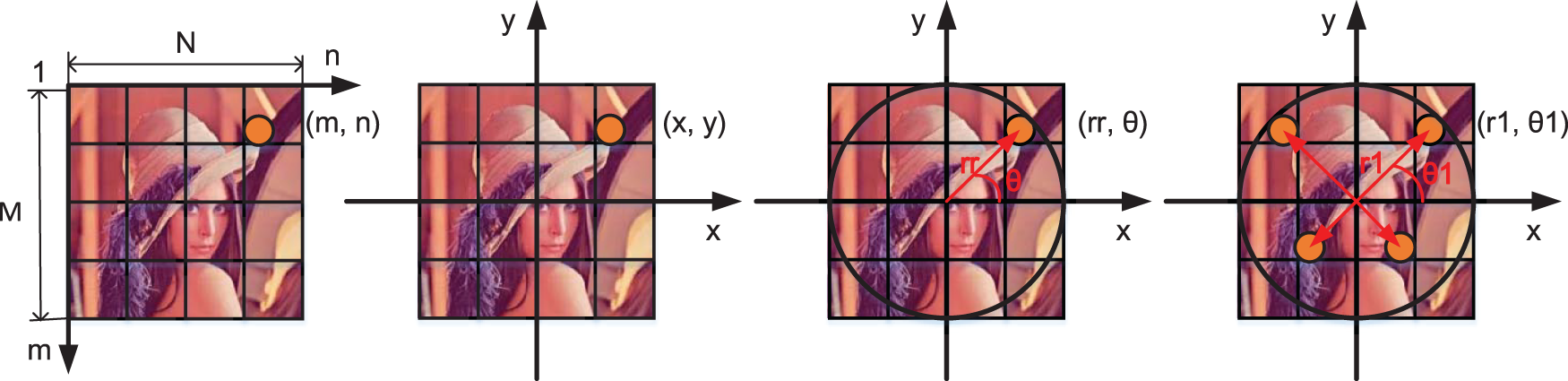
Figure 1: Coordinate transformation process in polar cosine transform (PCT) moment calculation

The PCT moment calculation formula is given by Eq. (6).

Mnl=∑x=0M−1∑y=0N−1[ Hnl(x,y) ]∗f(x,y){ x=rcosθy=rsinθ(6)

2.2 SPM Chaotic Mapping

SPM is an efficient one-dimensional composite chaotic map, which combines sine map and piecewise linear chaotic mapping, expands the scope of chaotic mapping and ensures the ergodicity of the results, and greatly improves the generation efficiency of chaotic sequences without reducing the security [19]. The mathematical formula is as Eq. (7), where, when η∈(0,1) and  μ∈(0,1), the system is in a chaotic state, and x(1)=r, r is a random number between 0 and 1, which is generated by random number seeds. Among, mod(⋅) stands for the remainder operation. The result of the composite operation is remaindered at 1 to generate a random sequence of specified length whose value is in (0, 1).

x(t+1)={mod(x(t)η+μsin⁡(πx(t))+r,1),0≤x(t)<ηmod(x(t)/η0.5−η+μsin⁡(πx(t))+r,1),η≤x(t)<0.5mod((1−x(t))/η0.5−η+μsin⁡(π(1−x(t)))+r,1),0.5≤x(t)<1−ηmod(1−x(t)η+μsin⁡(π(1−x(t)))+r,1),1−η≤x(t)<1(7)

3  Proposed Algorithm

3.1 Extraction of Feature Vector

For zero watermarking, it relies on the extracted features of the data to be embedded, since the key is generated based on the data features after the perceptual hashing. We chose standard Magnetic Resonance Imaging (MRI) brain volume data (128 × 128 × 27) as the subject. Because the coefficients of PCT have good rotation invariance and meet the orthogonal characteristic, the contribution of each transform coefficient to the image is unique and the redundancy between image features is minimal. First, PCT transform was performed on each slice, and then 3D-DCT transform was performed on the reconstructed 3D feature matrix. To extract the visual feature vector of the volume data by drawing on the concept of binary perceptual hash. The transformation rule was: when the coefficient was greater than or equal to the average value of the coefficients, binarized it to “1”; otherwise, binarized it to “0”. The perceptual hash threshold was the average of the coefficients, and the sequence of binary data features was chosen to be 32 bits long. As shown in Fig. 2, we randomly selected five different volume data to verify the discrimination of the extracted visual feature vectors. Then, the Normalized Correlation Coefficient (NC) value between them was calculated. From the results in Table 2, the correlation coefficient between different volume data is low, and different volume data can be distinguished. Only when the shape is consistent, the NC is equal to 1.00. While brain volume data 1 and brain volume data 2 are both brain volume data, so the correlation coefficient is relatively high, which is 0.50, which further illustrates the good performance of the algorithm for 3D contour feature extraction of medical volume data.

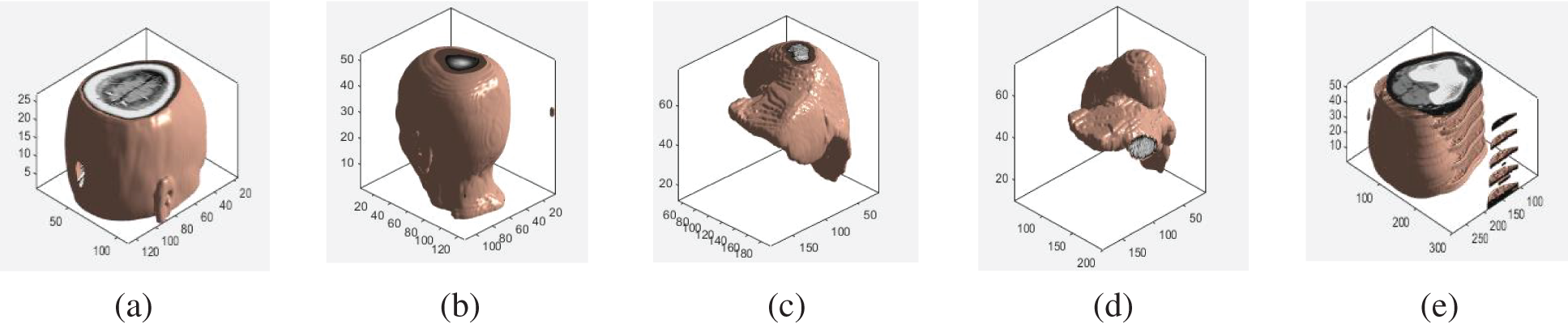
Figure 2: Different volume data: (a) Brain 1; (b) Brain 2; (c) The liver 1; (d) The liver 2; (e) Leg bone

3.2 Watermark Encryption

The watermark encryption was completed by applying the SPM composite chaotic mapping to scramble the watermark. The specific process is depicted in Fig. 3.

1)   Selected the key coefficient r=rng(7),η=0.4,μ=0.3. It can be seen from Eq. (7) that the system is in a chaotic state at this time. Let x(1)=r∈(0,1), r was a random number generated by the random number seed rng(7), and then a pseudo-random sequence was generated;

2)   Sorted the generated pseudo-random sequence in ascending order according to the value, and then scrambled the pixels at the corresponding positions by utilizing the changes in the position space before and after the sorting to obtain the encryption watermark.

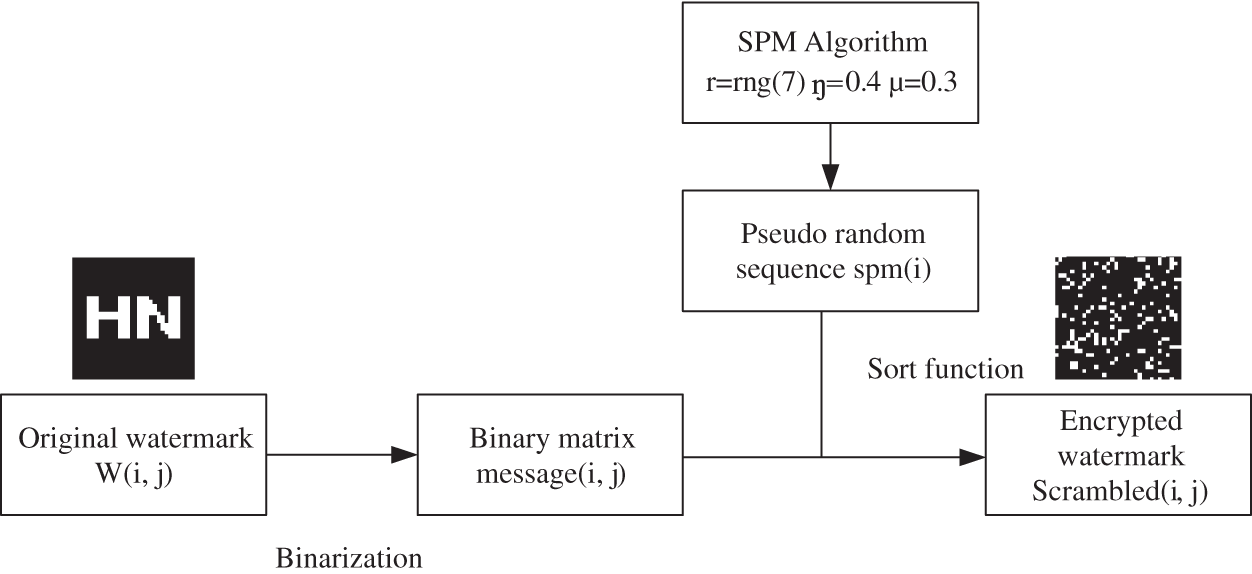
Figure 3: The flow-process diagram of watermark encryption

3.3 Watermark Embedding and Extraction

The embedding procedure of watermark for volume data is depicted in Fig. 4. First, the medical volume data G(i,j,k) was transformed by PCT and 3D-DCT, and the transform coefficients F2(1:4,1:2,1:4) were selected for perceptual hash. Thus, the 32-bits visual feature vector V(j) was obtained. Then, the logical key was obtained by line by line XOR of the binary data feature sequence and watermark encrypted by the SPM algorithm.

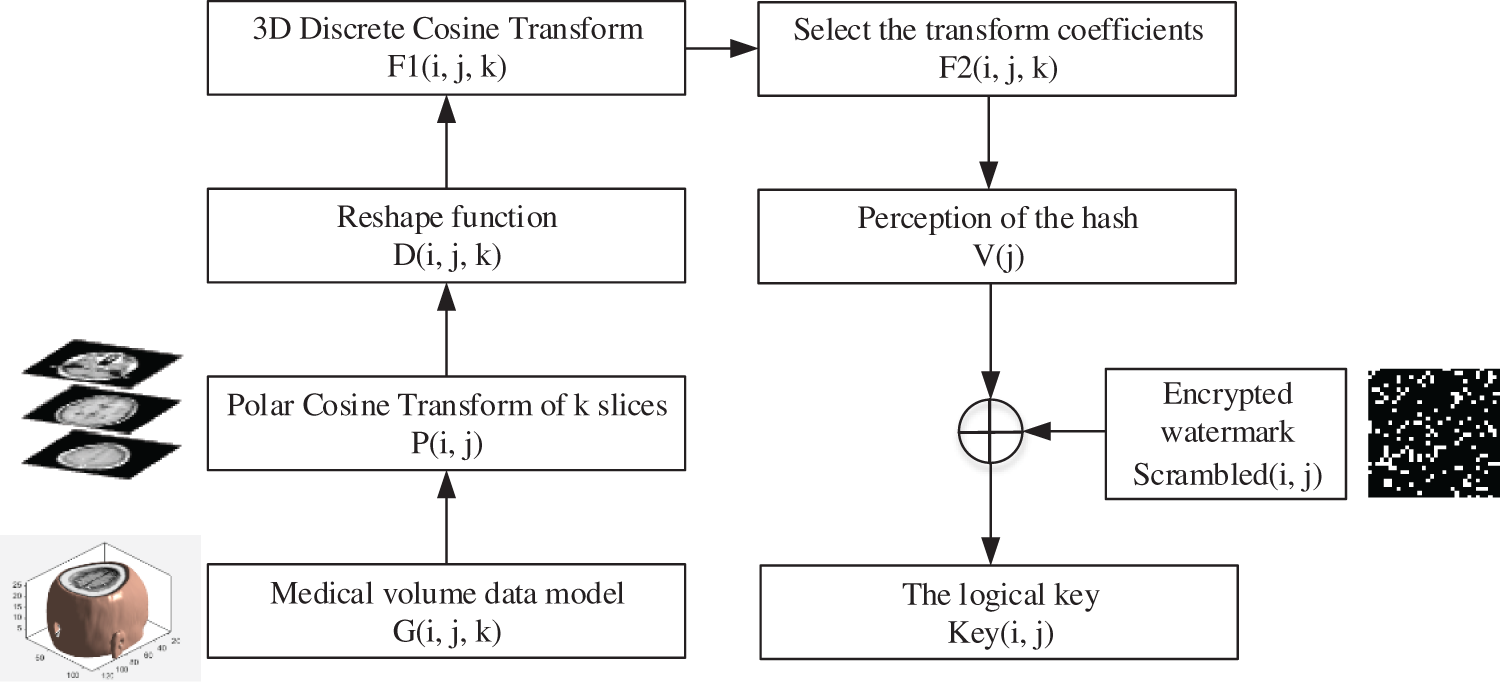
Figure 4: The flow-process diagram of watermark embedding

The extraction procedure of watermark of volume data is depicted in Fig. 5. The watermark extraction process also required the acquisition of the sequence of binary data features. For example, rotated the medical volume data G(i,j,k) by 70 degrees to obtain the tested data G′(i,j,k), then performed PCT and 3D-DCT transform on it, selected the transform coefficients F2′(1:4,1:2,1:4) for the perceptual hash, and obtained the 32-bits visual feature vector V′(j). Then, the feature vector V′(j) and the logical key Key(i,j) stored in the third party were XOR line by line to extract the encrypted watermark  Scrambled′(i,j).

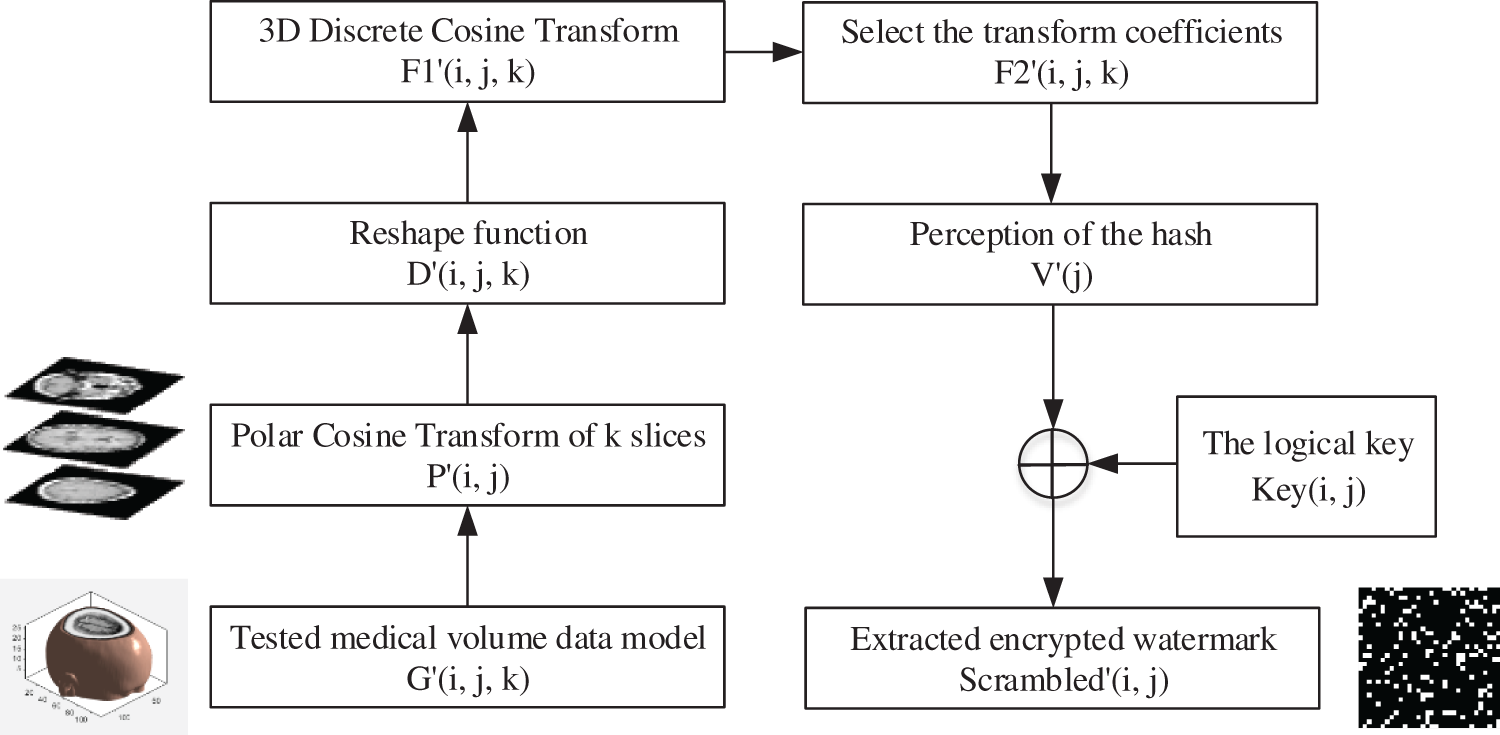
Figure 5: The flow-process diagram of watermark extraction

3.4 Watermark Decryption

The decryption process is as Fig. 6. First, the extracted encrypted watermark  Scrambled′(i,j) was binarized to acquire the watermark  message′(i,j), and next the pseudo-random sequence spm(i) generated by SPM algorithm and sort function were used to restore the scrambled position space and the pixels corresponding to it to acquire the recovered watermark  W′(i,j).

Figure 6: The flow-process diagram of recovery

4  Experimental Results

4.1 Settings

We selected MATLAB 2020b as the experiment platform, and used standard MRI brain volume data (128 × 128 × 27) as the experiment data, the original watermark size was 32 × 32 (see Fig. 7).

Figure 7: (a) The brain volume data; (b) the original watermark; (c) standard MRI brain slices

The peak signal-to-noise ratio (PSNR) of volume data is calculated as Eq. (8). M, N, H, respectively, represent the dimensions of volume data, G(i,j,k) and G′(i,j,k) respectively represent the voxel value of the corresponding position of the original volume data and the attacked volume data.

PSNR=10lg⁡[MNHmaxi,j,k(G(i,j,k))2∑i∑j∑k(G(i,j,k)−G′(i,j,k))2](8)

The Normalized Correlation Coefficient (NC) is computed as Eq. (9); W(i,j) and W′(i,j) represent the value of the corresponding position of the original watermark and the recovered watermark respectively.

NC=∑i∑jW(i,j)W′(i,j)∑i∑jW2(i,j)(9)

The Bit Error Ratio (BER) is calculated as Eq. (10). E(i,j) means whether the value of the corresponding position of the recovered watermark is error. L1 and L2 are the watermark row and column sizes.

E(i,j)={1,W(i,j)≠W′(i,j)0,W(i,j)=W′(i,j),BER=∑i∑jE(i,j)L1L2(10)

4.2 Conventional Attacks

4.2.1 Gaussian Noise Attacks

Gaussian noise assaults are performed on the brain volume data with varying intensities. The noise intensity is from 3% to 25% (see Table 3). It can be seen that the brain volume data and the corresponding slices are severely blurred with a noise strength of 10%, and the PSNR is 3.33 dB. Only the blurred contour can be seen, but the NC value of the extracted watermark is 0.80 (see Fig. 8); when the noise intensity continues to increase by 25%, the PSNR has decreased to 0.07 dB, and the NC value is still 0.70. In other words, the watermarking algorithm is able to withstand Gaussian noise attacks.

Figure 8: Noise attacks-Gaussian

4.2.2 JPEG Compression Attacks

When JPEG compression assaults are carried out on brain volume data, the block effect becomes increasingly noticeable as the quality of the compression is degraded. The image clearly demonstrates a block effect when the compression quality is set to 1%. However, even if the compression quality is 1%, the NC value is 1 (see Fig. 9), and for attacks with different compression qualities such as 2%, 4%, and 8% (see Table 4), the NC value is 1, which indicates that the watermark algorithm can withstand JPEG compression attacks efficiently.

Figure 9: Compression attacks-JPEG

4.2.3 Median Filter Attacks

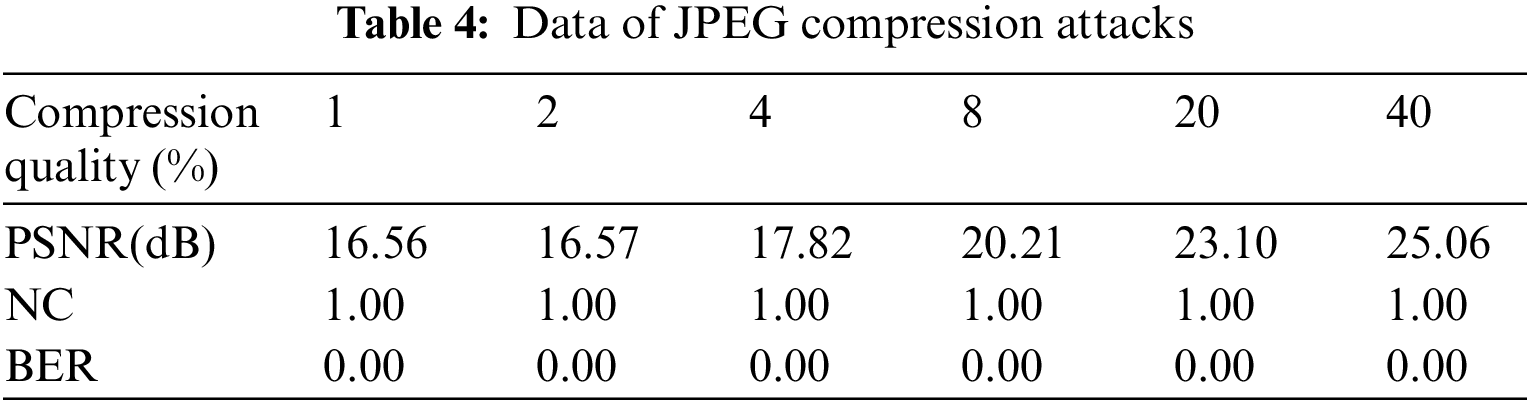
After [7 × 7] 20 median filtering attacks, the NC value is still 1 (see Fig. 10). Even after [11 × 11] 20 median filtering attacks, the NC value is still 0.89. Moreover, it can be found in Table 5 that the proposed algorithm works well against the median filtering attack.

Figure 10: Median filtering attacks (20 times)

4.3 Geometric Attacks

4.3.1 Rotation Attacks

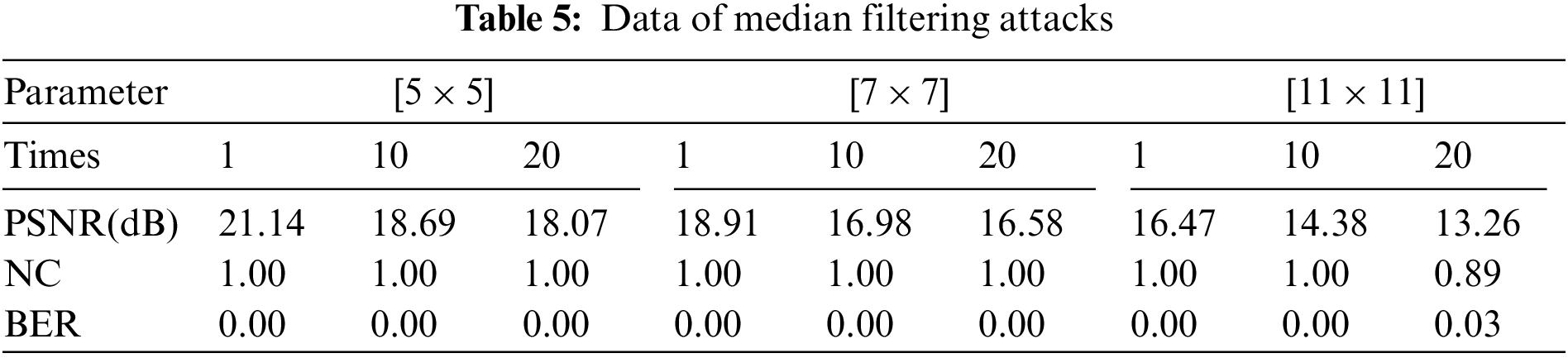
Anti-geometric attacks is one of the difficulties in watermarking algorithms, and most of the existing algorithms are not very good at anti-rotation attacks. In this experiment, the brain volume data are subjected to clockwise rotation attacks of 5 degrees to 80 degrees. It can be seen that when rotating clockwise from 5 degrees to 50 degrees, the NC value is all 1. From 50 degrees, the NC value starts to drop slowly. However, even with an 80 degree rotation, the NC value is still 0.80, which is much larger than 0.50, and the information in the watermark is still clear and identifiable. And it can be found in Fig. 11 and Table 6 that the algorithm is very robust to rotation attacks and further verifies the good rotation invariance of PCT moments.

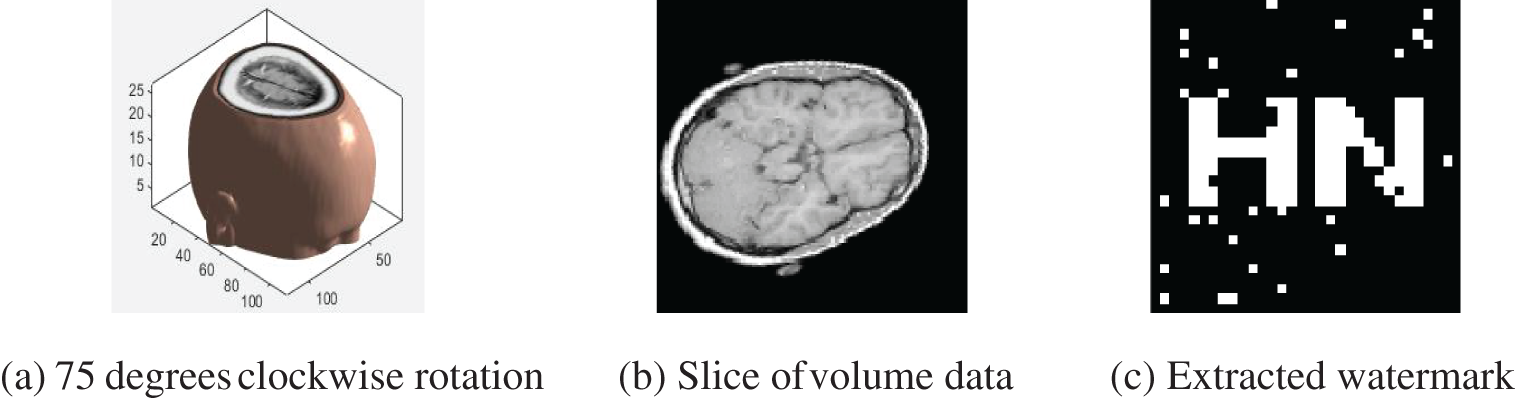
Figure 11: Clockwise rotation attacks

4.3.2 Scaling Attacks

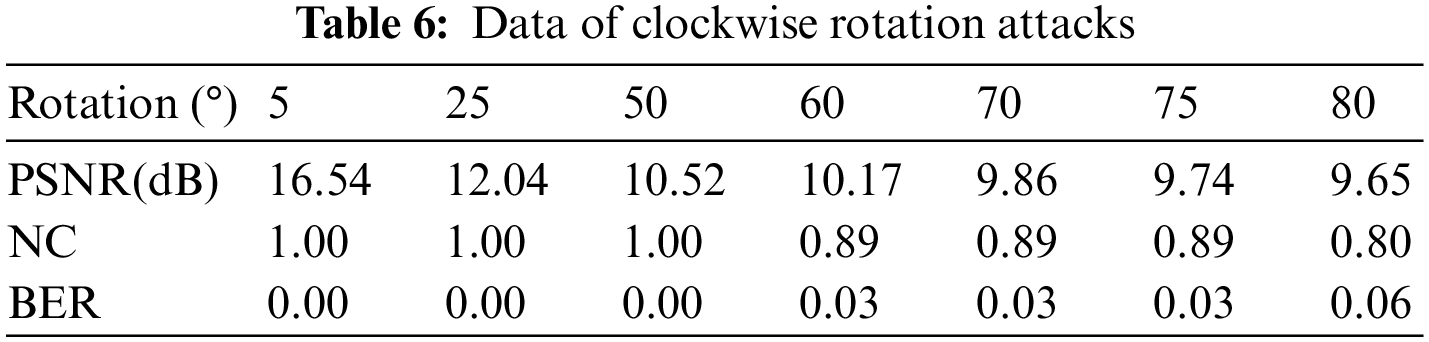
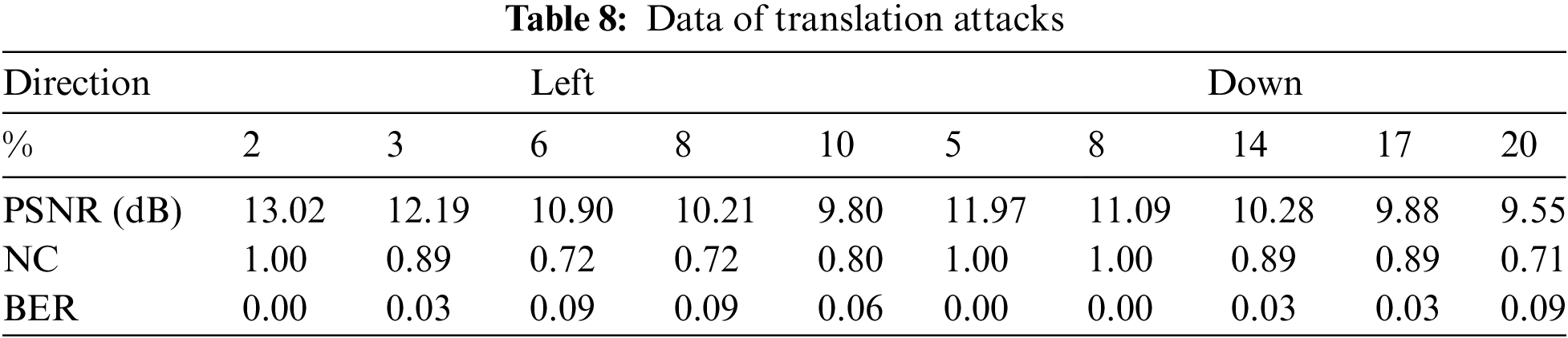
As shown in Fig. 12 and Table 7, when the watermark is enlarged by 4 times, the NC value is still 1, while when the watermark is reduced by 0.75 times and 0.5 times, the NC value is 1 and 0.80, respectively. Even if the watermark is reduced by 0.375 times, the NC value is still 0.70, higher than 0.50. Hence, the watermarking algorithm can withstand scaling attacks.

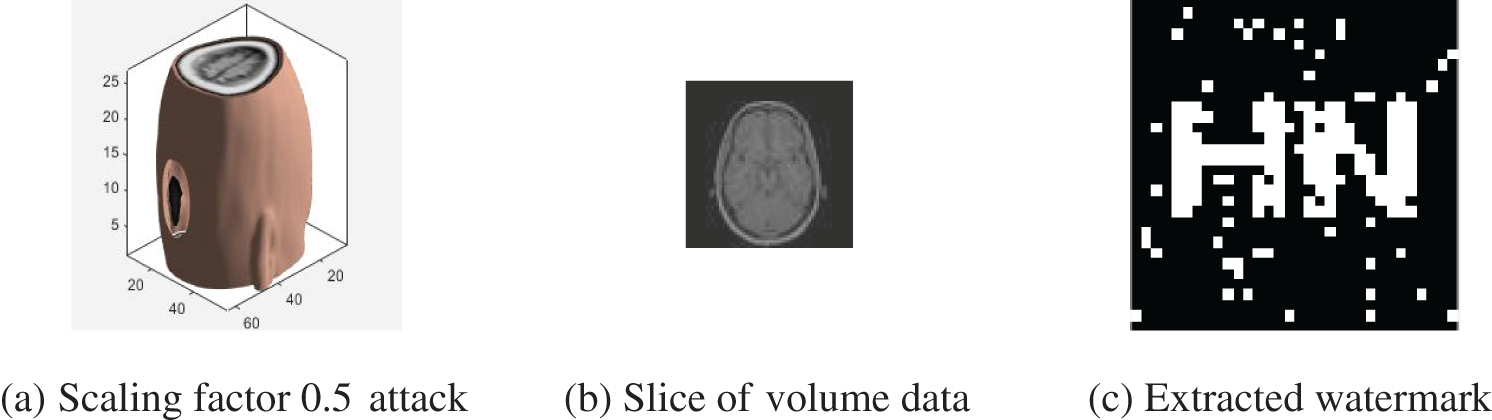
Figure 12: Scaling attacks

4.3.3 Translation Attacks

Different types of the translation attacks on brain volume data are performed. When the left translation is 10%, the NC value is 0.80(see Figs. 13a–13c). Perform 5% to 20% vertical downward translation attacks on the volume data in turn. When the translation percentage is 5% to 8%, the NC value remains 1. When the translation percentage is greater than 8%, the NC value begins to decrease slowly. It can be seen from Figs. 13d–13f that when the down translation is 17%, the detail information of the lower part of the brain has been lost, and the NC value is still as strong as 0.89. As the down translation is 20%, the brain information is lost by nearly one-fifth. The NC value is still as strong as 0.80, much greater than 0.50, and the information contained in the watermark can still be obtained. Moreover, it can be found in Table 8 that the algorithm is nicely resistant to translation attacks.

Figure 13: Translation attacks

4.3.4 Cropping Attacks

When the brain volume data is subjected to the Z-axis cropping attacks in the range of 3% to 25% (see Table 9), it can be seen that when the cutting ratio is 25%, the contour of the data has changed greatly, and the upper data is seriously lost. Even in this case, the NC value is still as steep as 0.89 (see Fig. 14), indicating that the algorithm can resist the Z-axis cropping attacks nicely.

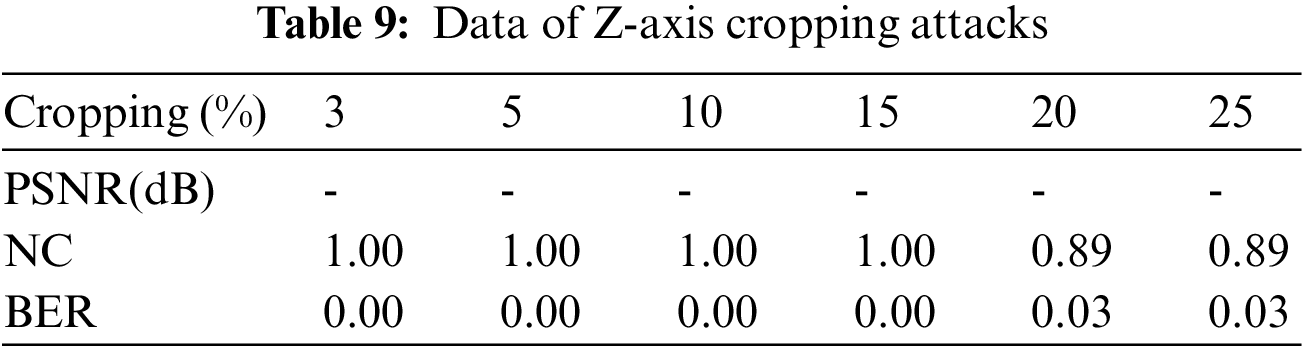
Figure 14: Z-axis cropping attacks

4.4 Comparison

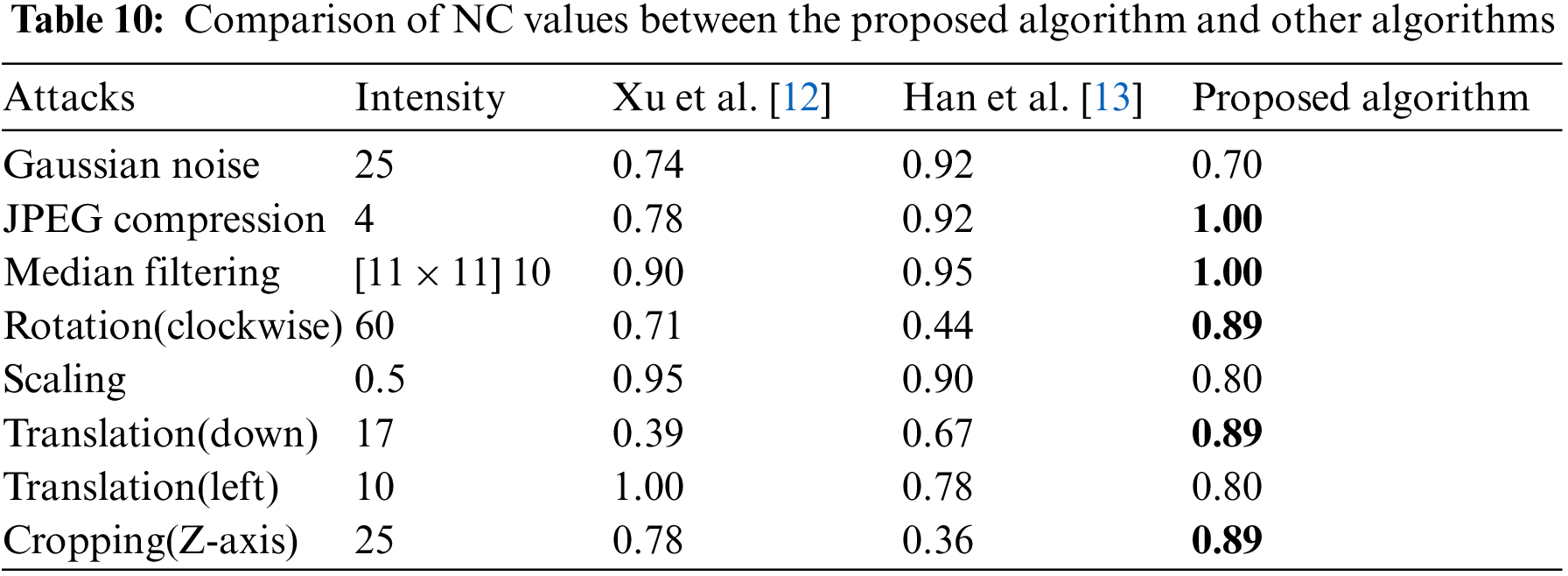
To further validate the stability of the approach, standard brain volume data (128 × 128 × 27) was used for comparison testing. We compare this algorithm with the algorithm proposed by Xu et al. [12] and the algorithm proposed by Han et al. [13]. It can be observed that the method suggested in this research is superior to the two comparison algorithms in anti-JPEG compression assaults, rotation assaults, downward translation assaults and Z-axis cropping assaults. When using the same strength assaults, the NC value is substantially greater than the comparison procedure.

The NC value curve of the proposed approach is a straight line with a constant value of 1 (see Fig. 15b), which is superior to the NC value curves of the two compared algorithms in terms of anti-JPEG compression assaults. The benefit becomes more noticeable as compression quality decreases. Downward translation assaults are well resisted by the suggested approach. Starting at 11% of the translation percentage, the NC value declines dramatically to below 0.50 in the technique described by Xu et al. [12]. The stability of the suggested algorithm’s performance, however, is a major advantage. When compared to 0.32 [12] and 0.50 [13] (see Fig. 15g), 0.71 is still significantly greater even when the proportion of translation approaches 20%. Perhaps most notably, the suggested method performs exceptionally well against rotation assaults. The NC value of the suggested method is 1, which is greater than the NC value of the two compared algorithms, if the rotation degree is between 5 and 50 degrees in the clockwise direction. This benefit becomes increasingly noticeable as the rotation degree rises. At 70 degrees of rotation, both the Xu et al. [12] and Han et al. [13] algorithms achieve NC values below 0.50 (0.35 for the latter) and 0.54 for the former. At 80 degrees of rotation, the NC value of the proposed method remains at 0.80, which is much higher than the NC values of the two compared algorithms (see Fig. 15d). The suggested technique also performs well when it comes to protecting against Z-axis cropping assaults. Even with as much as 25% cropping, it maintains a respectable performance of 0.89 (see Fig. 15h).

Figure 15: Comparison of algorithms under different attacks

For median filtering assaults, the NC value is 0.89 (see Fig. 15c) only as the filter parameters set to [11 × 11] 20 times. This is 0.01 lower than the approach suggested by Xu et al. [12]. The primary reason why the proposed algorithm’s performance is worse than that of the comparison method is because the emphasis is different, particularly in regards to anti-Gaussian noise assaults and the like (see Figs. 15a, 15e, 15f). The suggested approach is founded on both PCT and 3D-DCT, in contrast to Xu et al. [12], which is based on 3D DWT-DCT and Han et al. [13], which is based on 3D DWT-DFT and both of which focus on extracting the contour characteristics of volume data. After features are extracted from each slice of volume data, the proposed approach applies 3D-DCT to the resulting 3D feature matrix. Since it takes both the volume data’s contour information and the internal slice’s detailed information into account, with the latter receiving greater attention, its performance suffers when the latter’s detailed information is corrupted. Slice details are also highly essential in clinical diagnosis and therapy, and the performance hit from honing down on those aspects is tolerable. As an added bonus, even though the proposed algorithm performs worse than the comparison algorithm in anti-Gaussian noise assaults, scaling assaults, and left translation assaults, the average NC value of the poor performance points is also around 0.70 and higher than 0.50 in the test range, and the information contained in the watermark can still be obtained better. Table 10 displays the comparative results of NC values for the proposed approach and other techniques.

In the future, we will consider using regional XOR and ternary quantization techniques to reduce the false alarm rate of zero watermarks and expand the applicability [20,21]. And combine multiscale knowledge learning technology which uses the semantic, texture, edge and frequency domain information of the medical data as multiscale knowledge features to further improve the robustness [22–26].

5  Conclusion

A robust watermarking approach for medical volume data is described in this research to address the security issue of rising three-dimensional data in the IoMT. This approach extracts the sequence of binary data features from the volume data using the PCT and 3D-DCT transforms, and then combines the perceptual hash to embed and extract the watermark. Using the zero watermark and third-party concepts, the watermark is implanted without altering the quality of medical data, and the security and accuracy of the data are taken into account. Furthermore, the binary watermark is encrypted using the multi-sensitive starting value SPM composite chaotic map, which increases the watermark system’s secrecy. The experimental findings suggest that the method can withstand conventional and geometric assaults, particularly geometric assaults such as rotation and cropping. In practice, doctors frequently execute geometric operations on volume data to improve qualitative and quantitative analysis, which necessitates that the watermark encoded in the transmitted medical data be resistant to geometric assaults. This is something that the method suggested in this work is capable of. It offers the benefits of high security and resilience, and it can better safeguard the security of large amounts of data.

Acknowledgement: Thanks for editors and reviewers in providing suggestions for improving the manuscript.

Funding Statement: This work was supported in part by the Natural Science Foundation of China under Grants 62063004, the Key Research Project of Hainan Province under Grant ZDYF2021SHFZ093, the Hainan Provincial Natural Science Foundation of China under Grants 2019RC018 and 619QN246, and the postdoctor research from Zhejiang Province under Grant ZJ2021028.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. J. L. Byl, R. Sholler, J. M. Gosnell, B. P. Samuel and J. J. Vettukattil, “Moving beyond two-dimensional screens to interactive three-dimensional visualization in congenital heart disease,” The International Journal of Cardiovascular Imaging, vol. 36, no. 8, pp. 1567–1573, 2020. [Google Scholar] [PubMed]

2. J. Liu, J. X. Ma, J. B. Li, M. X. Huang, N. Sadiq et al., “Robust watermarking algorithm for medical volume data in internet of medical things,” IEEE Access, vol. 8, pp. 93939–93961, 2020. [Google Scholar]

3. S. Roy, M. S. Brown and G. L. Shih, “Visual interpretation with three-dimensional annotations (VITAThree-dimensional image interpretation tool for radiological reporting,” Journal of Digital Imaging, vol. 27, no. 1, pp. 49–57, 2014. [Google Scholar] [PubMed]

4. J. Wu, H. T. Zhai, J. Xia, Z. M. Cui and F. Ye, “Research and realization of medical volume data interactive cutting,” Journal of Algorithms & Computational Technology, vol. 4, no. 3, pp. 349–361, 2010. [Google Scholar]

5. T. F. Li, J. B. Li, J. Liu, M. X. Huang, Y. W. Chen et al., “Robust watermarking algorithm for medical images based on log-polar transform,” EURASIP Journal on Wireless Communications and Networking, vol. 2022, no. 1, pp. 1–11, 2022. [Google Scholar]

6. M. Hamidi, H. M. Ei, H. Cherifi and H. M. Ei, “A hybrid robust image watermarking method based on DWT-DCT and SIFT for copyright protection,” Journal of Imaging, vol. 7, no. 10, pp. 218–218, 2021. [Google Scholar] [PubMed]

7. K. Sonal, K. Geeta and S. K. Singara, “Extended visual cryptography-based copyright protection scheme for multiple images and owners using LBP–SURF descriptors,” The Visual Computer, vol. 37, no. 6, pp. 1481–1498, 2021. [Google Scholar]

8. C. D. Wang, Y. Bai and X. L. Mo, “Data secure transmission model based on compressed sensing and digital watermarking technology,” Wuhan University Journal of Natural Sciences, vol. 19, no. 6, pp. 505–511, 2014. [Google Scholar]

9. X. L. Zhao, G. Q. Wang and X. B. Xu, “Robust digital watermarking algorithm based on DCT-SVD and QR code,” in Proc. AIPR, Xiamen, Fujian Province, China, pp. 187–191, 2020. [Google Scholar]

10. N. A. Loan, N. N. Hurrah, S. A. Parah, J. W. Lee, J. A. Sheikh et al., “Secure and robust digital image watermarking using coefficient differencing and chaotic encryption,” IEEE, vol. 6, pp. 19876–19897, 2018. [Google Scholar]

11. T. Q. Zhang, L. Zhou, X. M. Liang and W. Xu, “A robust watermarking algorithm based on blob-harris and NSCT-zernike,” Journal of Electronics & Information Technology, vol. 43, no. 7, pp. 2038–2045, 2021. (in Chinese). [Google Scholar]

12. L. Xu, J. B. Li* and W. B. Fu, “A robust watermarking algorithm of encrypted medical volume data based on 3D DWT and 3D DCT,” in Proc. AICE and NCS, Sydney, Australia, 2016. [Google Scholar]

13. B. R. Han, J. B. Li and L. Zong, “Application of chaotic neural network and 3D DWT-DFT in medical volume data watermarking,” Applied Mechanics and Materials, vol. 2700, no. 411–414, pp. 1209–1212, 2013. [Google Scholar]

14. P. T. Yap, X. D. Jiang and A. C. Kot, “Two-dimensional polar harmonic transforms for invariant image representation,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 32, no. 7, pp. 1259–1270, 2009. [Google Scholar]

15. S. R. Qi, Y. S. Zhang, C. Wang, J. T. Zhou and X. C. Cao, “A survey of orthogonal moments for image representation: Theory, implementation, and evaluation,” ACM Computing Surveys (CSUR), vol. 55, no. 1, pp. 1–35, 2021. [Google Scholar]

16. B. Wang, “Study on multi-purpose dual watermarking algorithm for digital image based on compressive sensing and polar cosine transform,” M.S. thesis, Xi’an University of Technology, China, 2019. [Google Scholar]

17. D. Pooja, “Effective image retrieval using polar cosine transform and local binary patterns,” in Proc. IICIP, India, pp. 1–6, 2016. [Google Scholar]

18. L. D. Li, S. S. Li, A. Abraham and J. S. Pan, “Geometrically invariant image watermarking using polar harmonic transforms,” Information Sciences, vol. 199, pp. 1–19, 2012. [Google Scholar]

19. D. H. Ban, X. Lv and X. Y. Wang, “Efficient image encryption algorithm based on 1D chaotic map,” Computer Science, vol. 47, no. 4, pp. 278–284, 2020. (in Chinese). [Google Scholar]

20. D. Y. Wu, S. Hu, M. M. Wang, H. B. Jin, C. B. Qu et al., “Discriminative zero-watermarking algorithm based on region XOR and ternary quantization,” Journal on Communications, vol. 43, no. 2, pp. 208–222, 2022. (in Chinese). [Google Scholar]

21. W. B. Wang, F. L. Liu, D. F. Gong and S. L. Liu, “Analysis of false alarm problem of watermarking method based on singular value decomposition,” Computer Engineering, vol. 46, no. 11, pp. 273–278, 2020. [Google Scholar]

22. B. Fan, Z. Li and J. Gao, “Deep robust watermarking algorithm based on multiscale knowledge learning,” Journal of Computer Applications, vol. 42, no. 10, pp. 3102, 2022. (in Chinese). [Google Scholar]

23. C. Gong, J. Liu, M. Gong, J. B. Li, U. A. Bhatti et al., “Robust medical zero-watermarking algorithm based on Residual–DenseNet,” IET Biometrics, vol. 11, no. 6, pp. 547–556, 2022. [Google Scholar]

24. U. A. Bhatti, M. X. Huang, D. Wu, Y. Zhang, A. Mehmood et al., “Recommendation system using feature extraction and pattern recognition in clinical care systems,” Enterprise Information Systems, vol. 13, no. 3, pp. 329–351, 2019. [Google Scholar]

25. U. A. Bhatti, Z. Y. Yu, J. Chanussot, Z. Zeeshan, L. W. Yuan et al., “Local similarity-based spatial–spectral fusion hyperspectral image classification with deep CNN and gabor filtering,” IEEE Transactions on Geoscience and Remote Sensing, vol. 60, pp. 1–15, 2021. [Google Scholar]

26. U. A. Bhatti, Z. Y. Yu, J. B. Li, S. A. Nawaz, A. Mehmood et al., “Hybrid watermarking algorithm using clifford algebra with arnold scrambling and chaotic encryption,” IEEE Access, vol. 8, pp. 76386–76398, 2020. [Google Scholar]