Designing Pair of Nonlinear Components of a Block Cipher over Gaussian Integers

1  Introduction

Cryptography was widely used in military, diplomatic, and government applications until the 1970s. In the 1980s, the telecommunications and financial industries installed hardware cryptographic devices. The mobile phone system was the first cryptographic application in the late 1980s. Nowadays, everyone uses cryptographic applications in their daily lives. Our daily lives are commonly dependent on the secure transmission of information and data. Online shopping, cell phone messages and calls, ATMs, electronic mail, facsimile, wireless media, and data transfer over the internet all require a system to maintain the secrecy and integrity of private information. In an antagonistic environment, cryptography provides a way for everyone to communicate securely. Cryptography plays a major role in the security of data. Encryption of a message ensures that the meaning is concealed in it so that someone who reads the message cannot understand anything out of it unless people crack the message [1].

In cryptography, the S-box plays a major role in maintaining safe communication. In 1949, Shannon proposed the concept of an S-box. In creating confusion in data, S-boxes play a key role. According to Shannon, hiding the relationship between the key and cipher text is known as confusion, while hiding the statistical relationship between plain text and cipher text is known as diffusion. In other words, the plain text's non-uniformity in the distribution of individual letters should be redistributed into the cipher text's non-uniformity in the distribution of much larger structures, which is significantly much harder to detect [2].

In literature, for creating confusion very well-known S-boxes are available in data and information, such as data encryption standard (DES), advanced encryption standard (AES), affine power affine, Gray, Skipjack, Xyi, and Residue Prime Substitution boxes. In 1974, the National Bureau of Standards requested an American company to create a strong cryptosystem that could be used in unclassified U.S. applications. So, DES was developed by IBM and was adopted by NIST (then called the National Bureau of Standards) on January 15, 1977. It soon became the most widely used cryptosystem in the world. However, from the very beginning, DES attracted criticism for not having a sufficiently large key space to make it secure. The size of the key space in DES is  256. From early on, attempts were made to build a special-purpose machine devoted exclusively to the task of breaking the DES code. In 1998 a massively parallel network computer, called “DES Cracker,” was built by Electronic Frontier Foundation EFF that could search 88 billion DES keys per second. It succeeded in finding a DES secret key in 56 h. In 1999, working in conjunction with a worldwide network of 100,000 computers, the DES Cracker could search 245 billion keys per second and succeed in finding a secret DES key in a little more than 22 h. It was thus clear that DES was no longer a secure cryptosystem [3]. Therefore it was necessary to phase out the DES and adopt a more secure encryption standard.

A brief description of the latest cryptosystem is approved for general use by the National Institute of Standards and Technology (NIST). It is called the Advanced Encryption Standard (AES) and was adopted, effective May 26, 2002, as the official Federal Information Processing Standard (FIPS) to be used by all U.S. government organizations to protect sensitive information. It is also expected to be used by other organizations, institutions, and individuals all over the world. The enciphering algorithm in AES was designed by two Belgian cryptographers, Dr. Joan Daeman and Dr. Vincent Rijmen. It was given the name Rijndael (pronounced “rhine dahl”). The basic structure of the Rijndael algorithm is that of an iterated block cipher, but with some additional features. Before considering the Rijndael algorithm, we will move towards an iterated block cipher which is present in [4].

For creating confusion on data, for the construction of S-boxes, many researchers used different schemes with algebraic and statistical structures. The authors proposed S-boxes over the permutation of the symmetric group in [5]. The construction of S-boxes over the action of the quotient of a modular group by using a secure scheme is given in [6]. The construction of the S-box based on the subgroup of the Galois field is given in [7]. The author proposed a strong encryption scheme by using a modified Chebyshev map, AES S-boxes, and a symmetric group of permutations [8].

In [9], the authors proposed a new scheme for the construction of the S-box based on the linear fractional transformation (LFT) and permutation function. In [10], the author proposed S-box over the Mobius group and finite field. The author proposed S-box on a nonlinear chaotic map in [11]. The authors proposed S-boxes over the second coordinate of EC in [12]. Adnan et al. [13], designed the construction of a non-linear component of block cipher by means of a chaotic dynamical system and symmetric group. In [14], the author constructed cyclic codes over quaternion integers, these quaternion structures can be helpful for the construction of S-boxes.

An S-box generator is appropriate for cryptographic purposes if it can efficiently make highly dynamic S-boxes with good cryptographic properties or tests like nonlinearity, bit independence criterion, strict avalanche criterion, linear approximation probability, and differential approximation probability. The key contributions of our proposed study are given below:

•   Propose an algorithm to generate pair of S-boxes by the cyclic group over the residue class of Gaussian integers.

•   Security Analysis.

•   The advantages of the proposed algorithm over GI with some of the existing algorithms over EC.

This paper is structured as follows: Basic definitions, cyclic group over the residue class of Gaussian integers, and some fundamental results are elaborated in Section 2. The scheme of the pair of new S-boxes is proposed in Section 3. Analysis of the proposed S-boxes including nonlinearity, bit independence criterion, strict avalanche criterion, linear approximation probability, and differential approximation probability investigated in Section 4. The comparison of the proposed S-boxes with some of the existing S-boxes are given in Section 5. Conclusions and future directions are given in Section 6.

2  Preliminaries

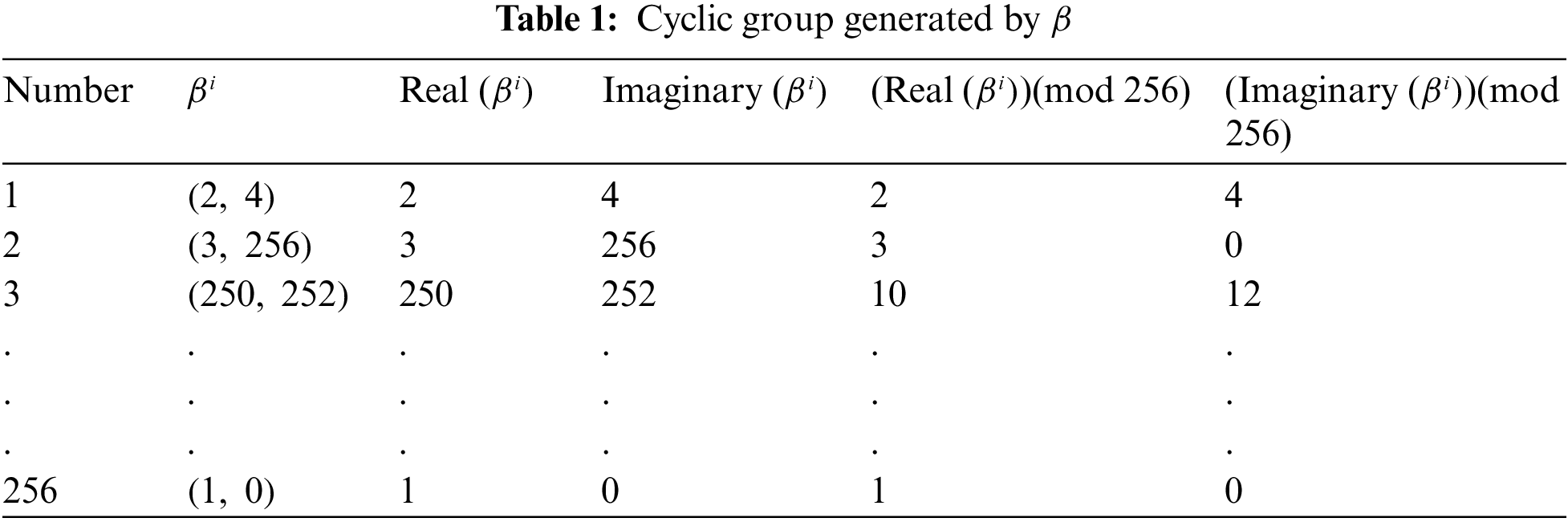
This section provides the key concepts and basic findings that will be used in the study of upcoming sections. First of all, we recall the definition of Gaussian integers, cyclic group over a residue class of Gaussian integers, and some fundamental results.

Gaussian Integers

By following [[15], Section 2], Gaussian integers are a subset of complex numbers which have integers as real and imaginary parts;

1.    Z[i]={b0+b1i: b0, b1∈Z}, where Z is the set of integers.

2.    Multiplicative identity is 1.

3.    i2=−1 

Let h=b0+b1i be an element of the Gaussian integer ring, then the conjugate of h is  h¯=b0−b1i. The norm of h is the sum of the squares of the real part and the coefficient of the vector part of h;

p=n(h)=hh¯=b02+b12

A Gaussian integer has only two parts, one is the scalar part b0 and the other is the vector part  b1i.

Addition of two Gaussian Integers

Let h=a1+b1i and k=a2+b2i are two Gaussian integers then, the sum of two Gaussian integers is also a Gaussian integer defined as;

h+k=(a1+b1i)+(a2+b2i)=(a1+a2)+i(b1+b2)=a3+b3

Multiplication of two Gaussian Integers

Let h=a1+b1i and k=a2+b2i are two Gaussian integers then, the multiplication of two Gaussian integers is also a Gaussian integer defined as;

hk=(a1+b1i)(a2+b2i)=(a1a2−b1b2)+i(a1b2+a2b1)=(a1a2−b1b2 ,a1b2+a2b1)=a4+b4i

Theorem: In [[15], Section 2], the set of natural numbers for each odd rational prime  p, there is a prime  h∈Z[i], such that  N(h)=p=hh¯. In particular, p is not prime in Z[i].

Theorem: In [[16], Theorem 6.3], if the norm of a Gaussian integer N(h) is prime in Z, then the Gaussian integer h is prime in Z[i].

Definition: In [[17], Section 2], let Z[i] be the set of Gaussian integers and Z[i]h be the residue class of Gaussian integers over modulo h, h=a+bV. Then, the modulo function

ω:Z[i]={c+dV:c,d∈Z}→Z[i]h

Then, ω(u)=z (mod h)=u−[uh¯hh¯]h.

Where  z∈Z[i]h and [.] are rounding to the nearest integer. The rounding of a Gaussian integer can be done by rounding the real part and coefficients of the imaginary part separately to the closest integer.

Theorem: In [[17], Theorem 7.12], let h be a Gaussian prime, and the number of Gaussian integers modulo h is the norm of h. If ρ≠0 (mod h), then ρn(h)−1≡1(mod h).

Theorem: In [[17], Theorem 2], If c and d are two relatively prime integers, then Z[i]/⟨c+di⟩ is isomorphic to  Zc2+d2.

3  Redesign of Pair of n × n S-Boxes Over Gaussian Integers

Numerous procedures can be used to generate confusion in a security system. S-box is one of the most efficient techniques in modern cryptosystems. The S-boxes are generally constructed through the class of GI, which is the multiplicative cyclic group. Consequently, there is a good choice to design a variety of S-boxes over the residue class of GI, which provides a marvelous perspective for secure and consistent cryptosystems. The following steps are helpful for the construction of S-boxes over the residue class of GI (Multiplicative cyclic group);

Step 1: Construct a cyclic group of order p−1 over the residue class of GI.

Step 2: Separate real and imaginary parts of the cyclic group constructed in Step 1.

Step 3: Apply modulo 2n over the separated parts in Step 2.

Step 4: Select the first 2n non-repeated elements from the elements of Step 3.

Step 5: Apply permutation through affine mapping as

f(x)=(ax+b)(mod 2n)

where b∈Z2n and a be the units element of Z2n.

Step 6: Get a pair of S-boxes.

3.1 Pair of 4 × 4 S-Boxes Over the Residue Class of GI

Let  h=1+16i, p=n(h)=12+162=257, and  β=2+4i=(2, 4), then the cyclic group generated by β as follows;

Select the first 16 non-repeated elements from the last two columns of Table 1, then apply the affine permutation mapping, f(x)=(3x+5)(mod 16), and get the pair of S-boxes separately in Tables 2 and 3.

3.2 Pair of 8 × 8 S-Boxes Over the Residue Class of GI

Let  h=14+61i,  p=n(h)=3917, and  β=1+11i=(1, 11), then the cyclic group generated by β as follows;

Select the first 256 non-repeated elements from the real part of Table 4. Then apply the affine permutation map f(x)=(165x+120)(mod 256), and get the S-box for the real part of GI in Table 5.

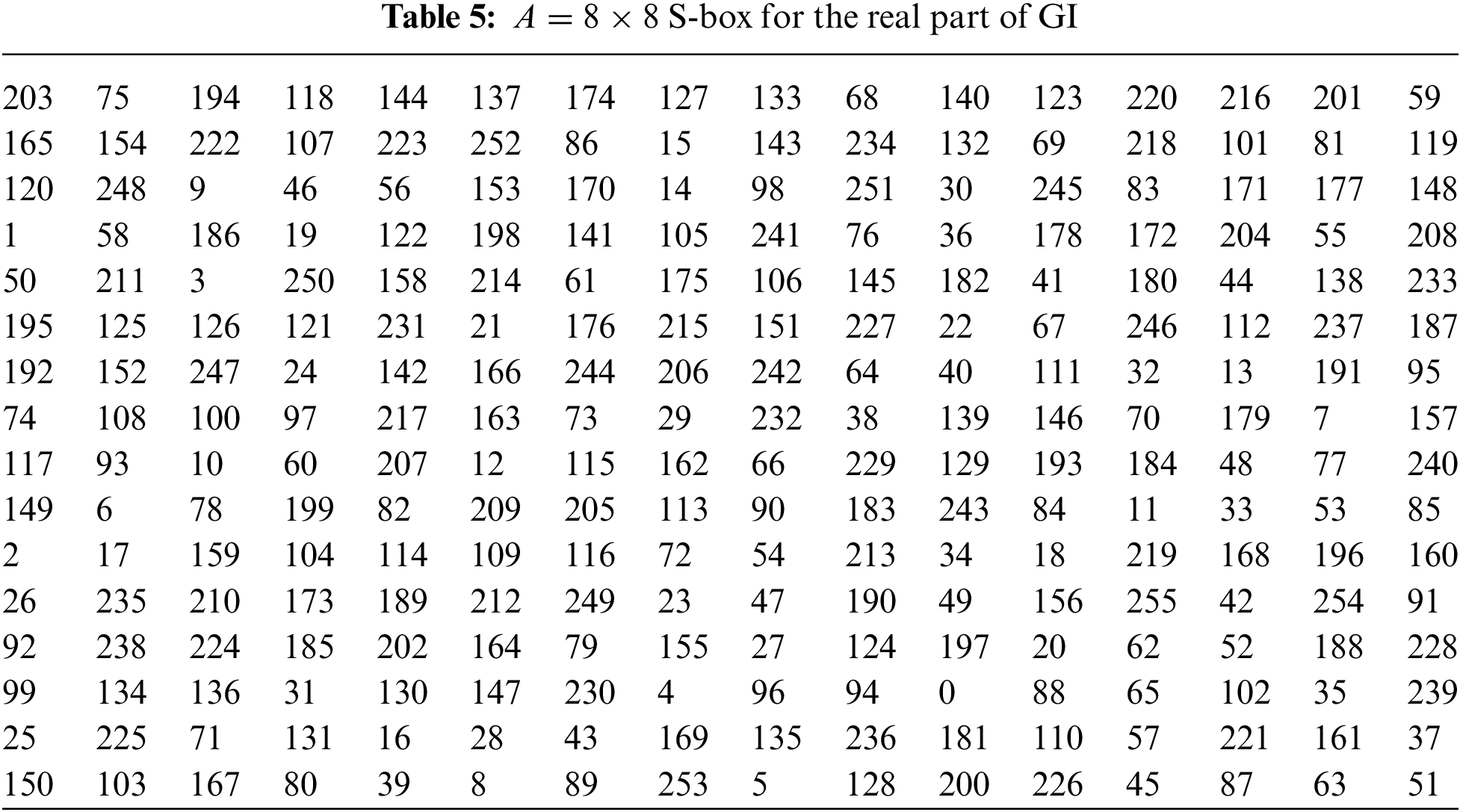
Select the first 256 non-repeated elements from the imaginary part of Table 4. Then apply the affine permutation map f(x)=(165x+119)(mod 256), and get S-box for the imaginary part of GI in Table 6.

3.3 Pair of 8 × 8 S-Boxes Over the Residue Class of GI

Let  h=19+50i, p=n(h)=2861, and  β=1+7i, then apply a similar process like 3.2 and 3.3, then get a pair of S-boxes over the residue class of GI in Tables 7 and 8.

3.4 Inverse S-Boxes

The S-boxes A, B, C, and D in 3.2,  and 3.3 are invertible and bijective. The procedure of inverse S-boxes over the residue class of GI is defined by applying inverse permutation through the following affine mapping h(x)=(cx+d)(mod 2n), where c is the multiplicative inverse of a under modulo 2n and d is the additive inverse of cb  under modulo 2n.

The Inverse S-box of A is defined by the map, h1(x)=(45x+232)(mod 256) in Table 9.

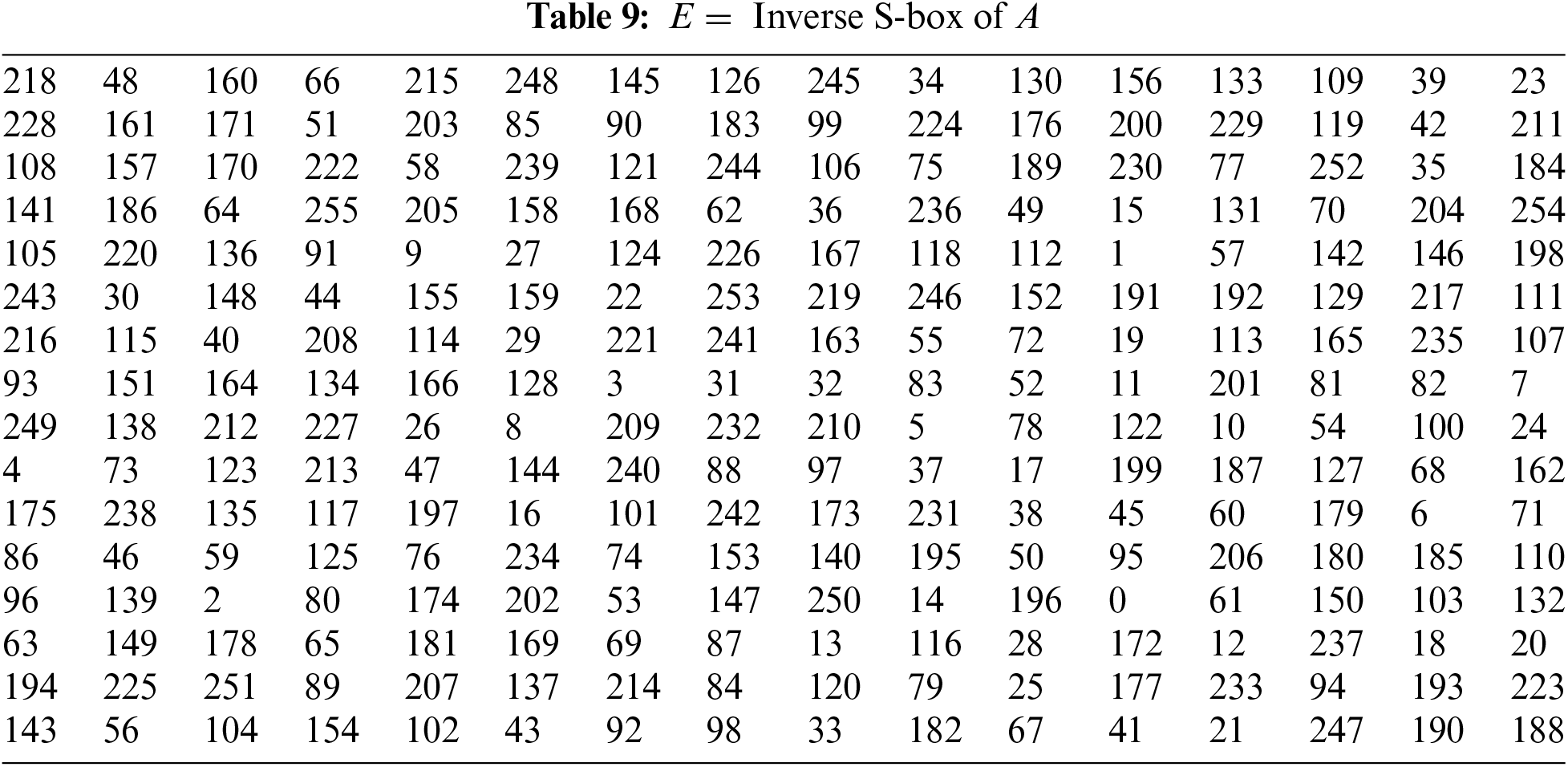
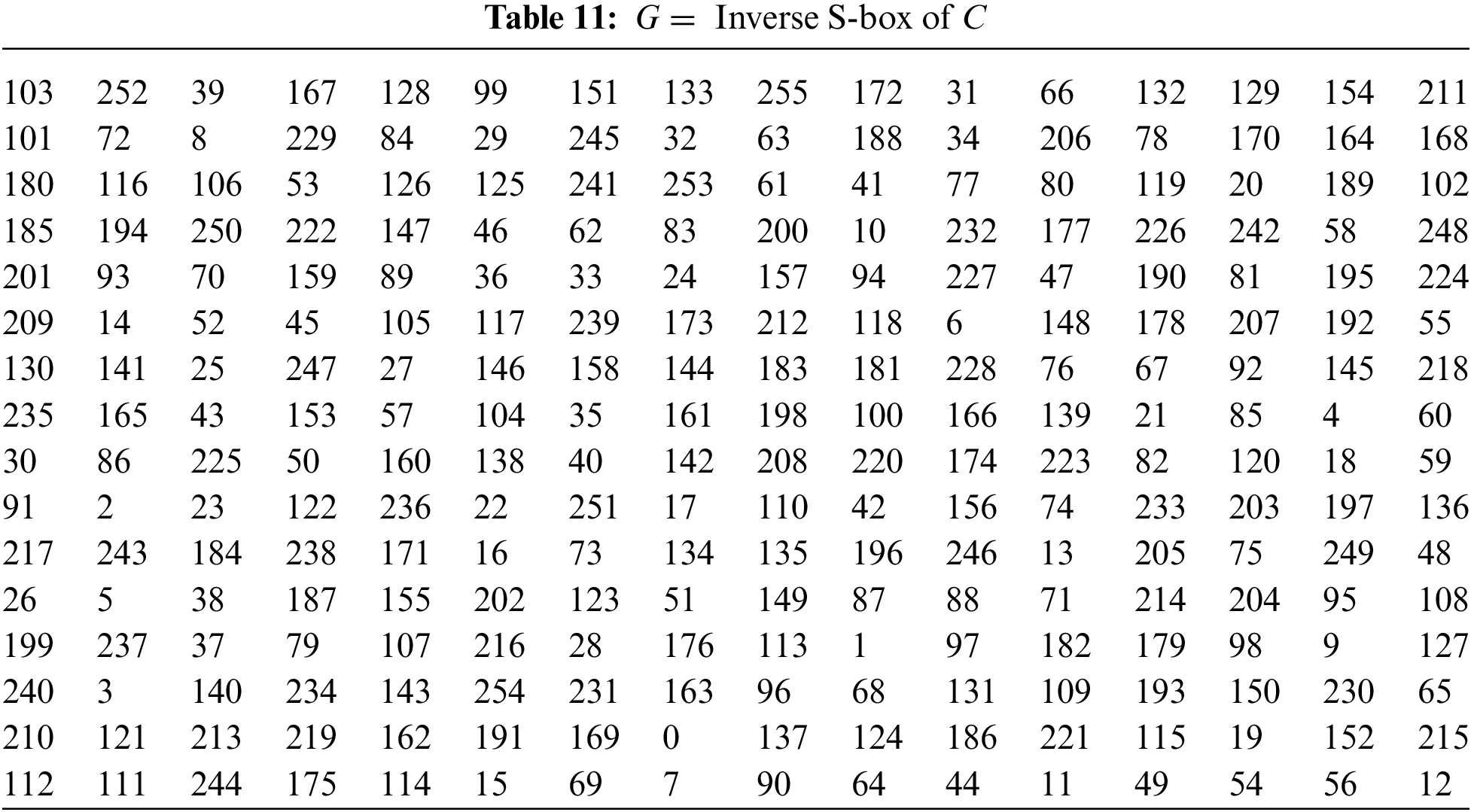
The inverse S-box of B is defined by the map, h2(x)=(45x+21)(mod 256) in Table 10.

The inverse S-box of C for the real part of GI is given in Table 11.

The inverse S-box of D for the imaginary parts of GI is given in Table 12.

4  Analysis of S-Boxes

In this section, we will present some useful analyses of the proposed S-box like as; Nonlinearity, bit independence criterion, strict avalanche criterion, linear approximation probability, and differential approximation probability.

4.1 Nonlinearity (NL)

The NL of a Boolean function can be defined as the distance between the function and the set of all affine functions. In other words, we can say that; Non-linearity is the number of bits that must be changed in the truth table of a Boolean function to reach the closest affine function. The upper bound of NL for the S-box is N(f)=2n−1−2n2 −1 [18]. The optimal value of the NL of the S-box is 120. The NL results of the proposed 8×8 S-boxes A, B, C, and D are given in Table 13.

The maximum nonlinearity of all proposed S-boxes A, B, C, and D is 108. The minimum nonlinearity of proposed S-boxes A, B, C, and D are 106, 104, 104, and 106. The average nonlinearity of proposed S-boxes A, B, C, and D are 107.5, 106.5, 106.75, and 106.75.

4.2 Bit Independence Criterion (BIC)

The output BIC was also first introduced by Webster and Tavares, which is explained in [18], which is another desirable property for any cryptographic design. It means that all the avalanche variables should be pair-wise independent for a given set of avalanche vectors generated by the complementing of a single plaintext bit. The average value of BIC is 12. The BIC analysis with the pair of proposed S-boxes A, and B are given in Tables 14 and 15. The BIC of the proposed S-boxes generated by GI is up to the standard in the sense of encryption strength.

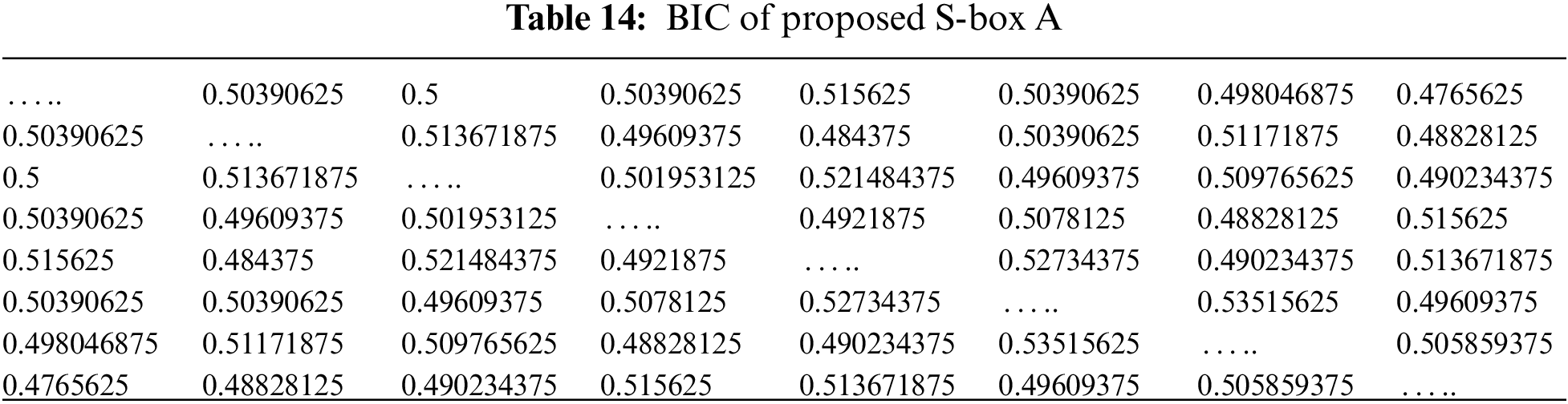
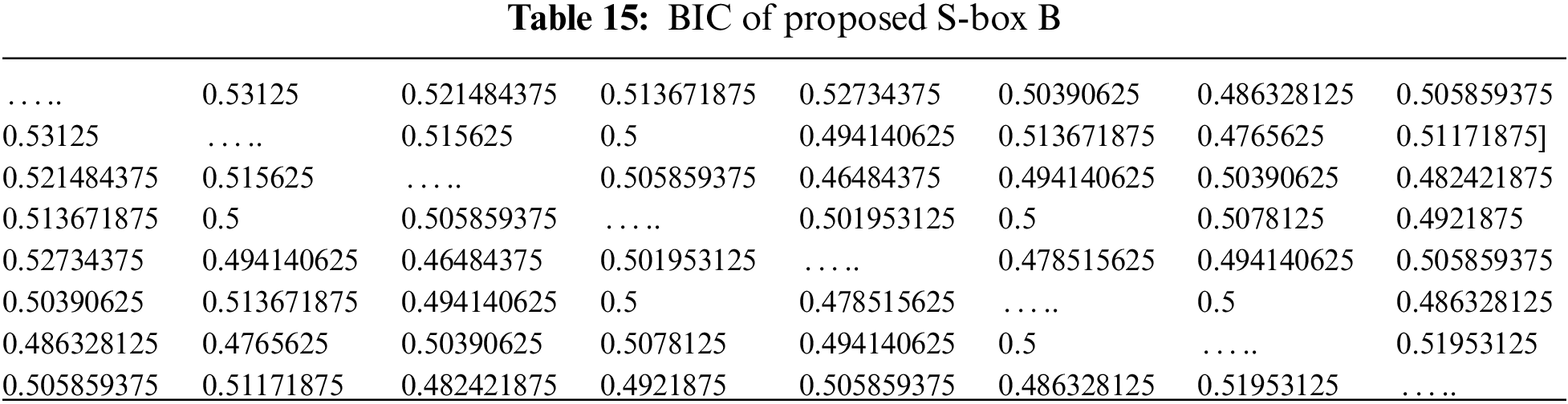
The maximum (Max), average (Ave), and minimum (Min) BIC values of proposed S-boxes (A, B, C, and D) are (0.625, 0.609, 0.609, and 0.578), (0.047, 0.47, 0.47, and 0.47), and (0.375, 0.375, 0.375, and 0.391). The DAP comparison of proposed S-boxes with S-boxes on EC from the literature are given in the comparison section.

4.3 Linear Approximation Probability (LAP)

LAP is the maximum value of the imbalance of an event. The parity of the input bits selected by the mask Γu is equal to the parity of the output bits selected by the mask Γv. According to Matsui's original definition, linear approximation probability (or probability of bias) of a given s-box is defined in [18];

LP=maxΓu, Γv=0|#{u: u.Γu=S(u). Γv2n−12|

where, Γu and Γv are input and output masks, respectively; X is the set of all possible inputs and 2n is the number of its elements. We have calculated the linear approximation probability of proposed S-boxes. We will compare it with some well-known S-boxes in Comparison Table 22. The maximum values of LAP of proposed S-boxes are given in Table 16, which are not so bad against linear attacks.

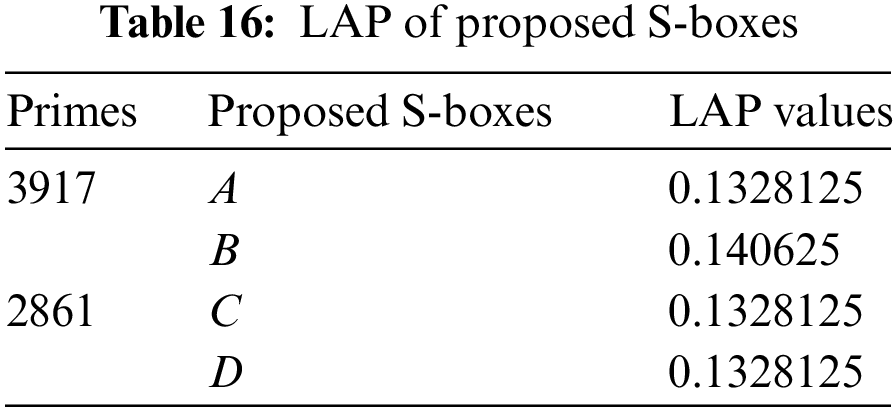
4.4 Differential Approximation Probability (DAP)

The nonlinear transformation S-box should ideally have differential uniformity. An input differential Δui should uniquely map to an output differential Δvi, thereby ensuring a uniform mapping probability for each i. The differential approximation probability DAP of a given S-box is a measure of differential uniformity and is defined as

DPs(Δu→Δv)=[#{u∈X: S(u)⊕S(u⊕Δu)=Δv}2m]

The DAP results of proposed S-boxes A  and B are given in Tables 17 and 18.

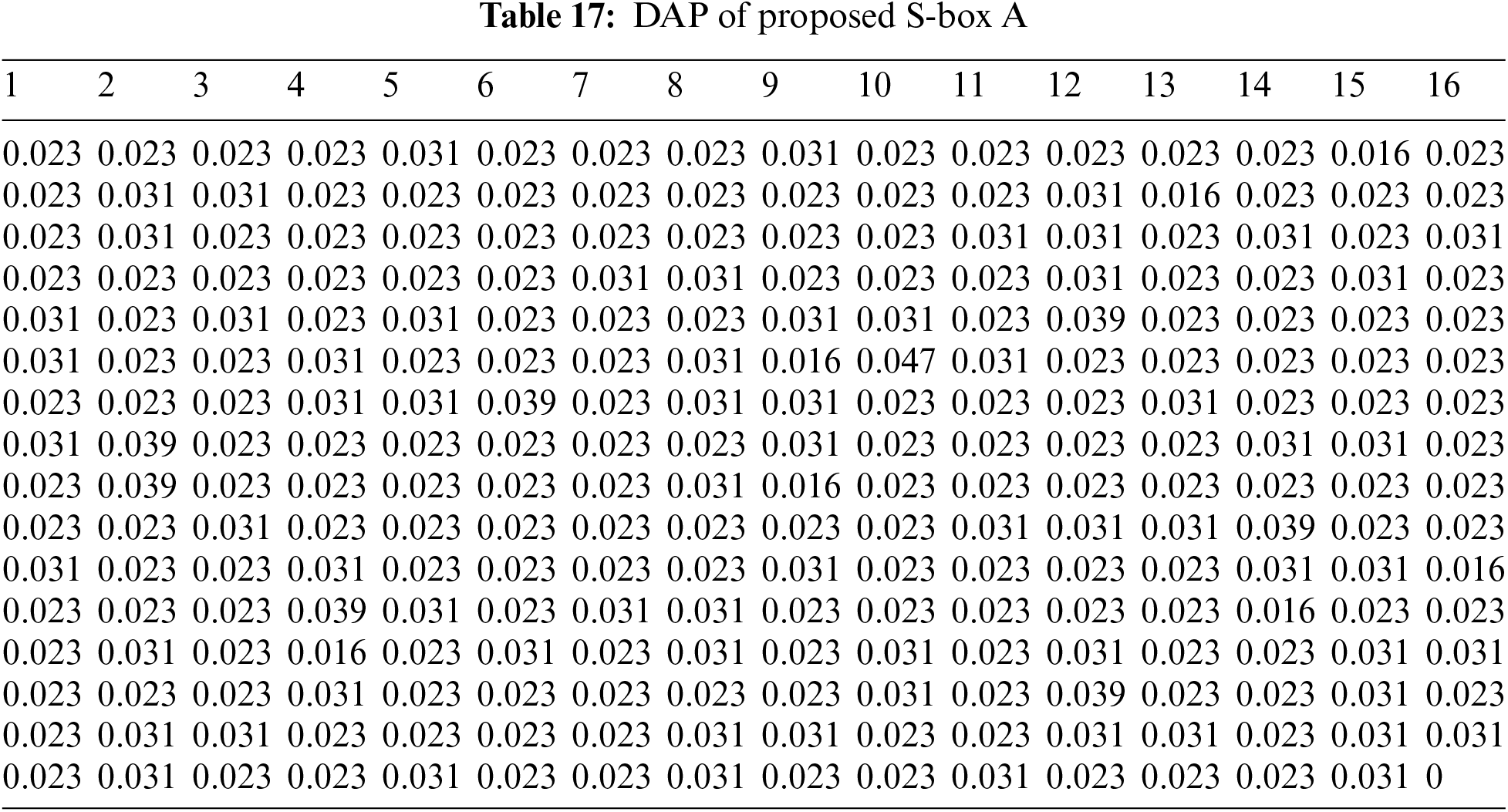
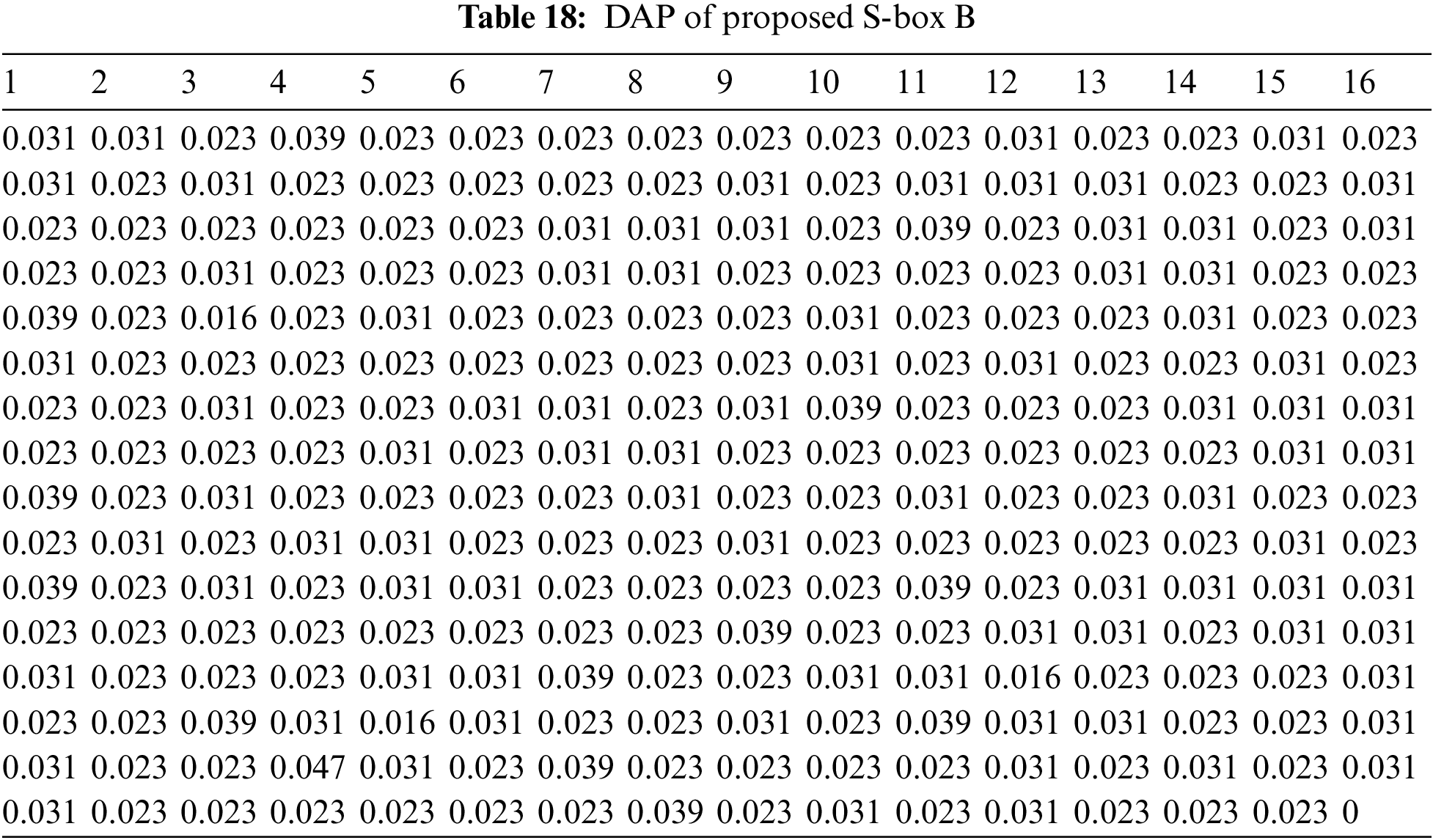
The Max. DAP values of proposed S-boxes A, B, C, and D are 0.047, 0.47, 0.47, and 0.47. The DAP comparison of proposed S-boxes with S-boxes on EC from the literature are given in the comparison section.

4.5 Strict Avalanche Criterion (SAC)

An S-box satisfies SAC if a single bit changes on the input results in a change on half of the output bits. Note that when S-box is used to build an S-P network, then a single change on the input of the network causes an avalanche of changes. The SAC results of the proposed S-boxes A and B are given in Tables 19 and 20. We have come to a close that the value of the proposed S-boxes is approximately equal to 12. So, we conclude that we can make use of proposed S-boxes in block cipher for secure communication.

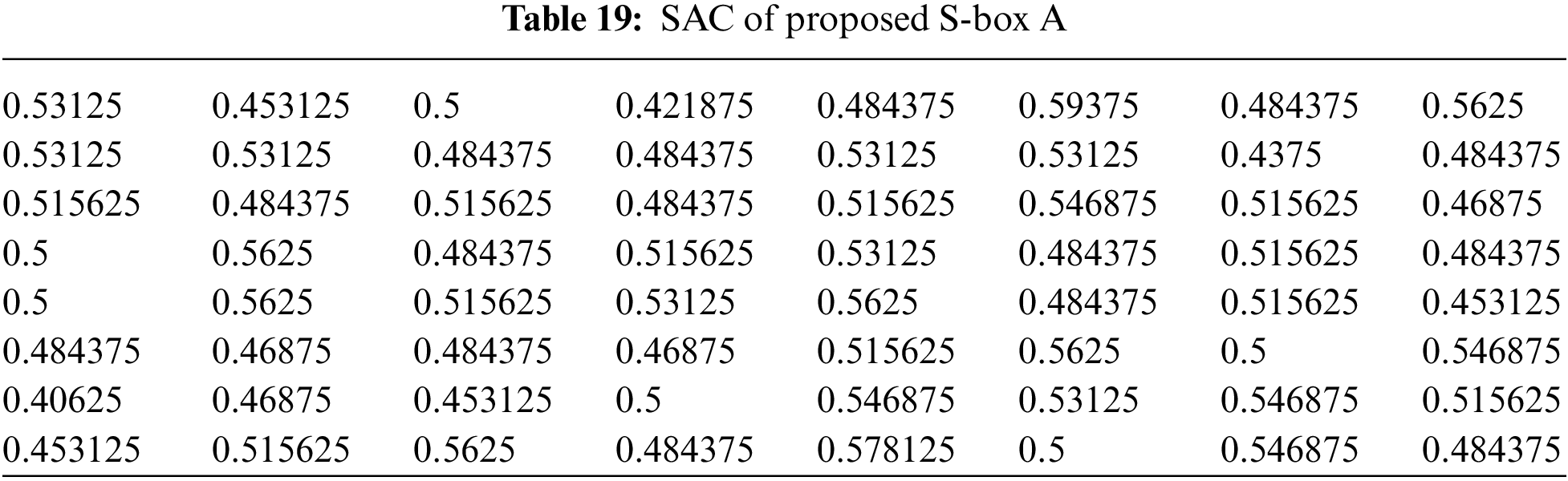
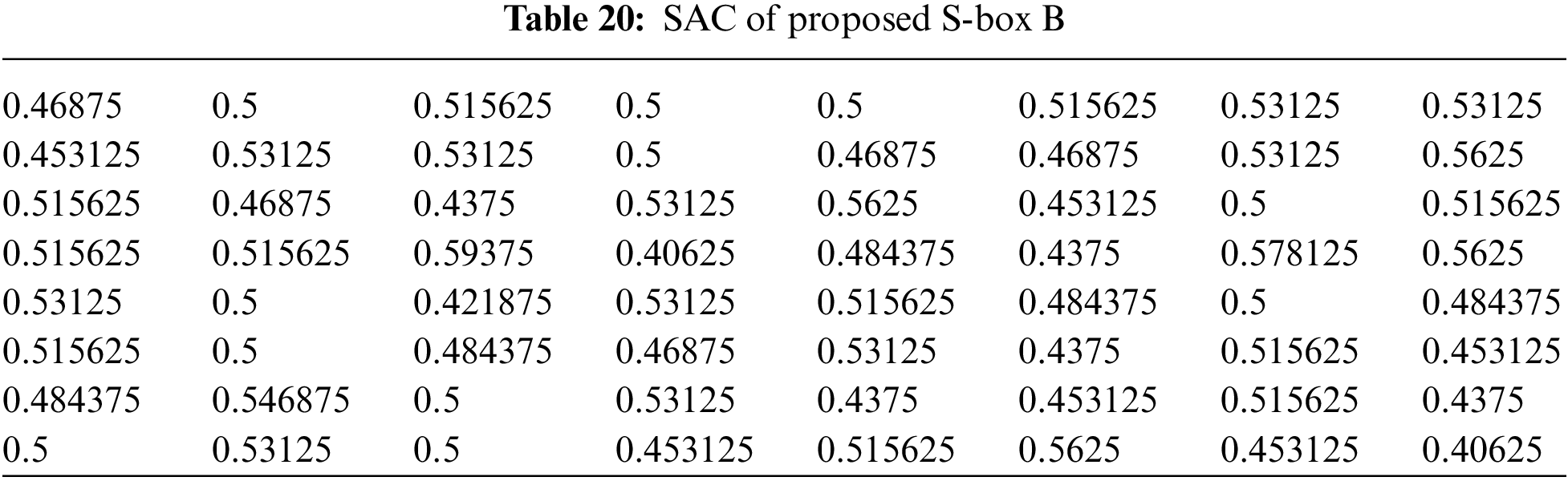
The Max SAC values of proposed S-boxes A, B, C, and D are 0.594, 0.594, 0.594, and 0.594. The minimum SAC values of the proposed S-boxes A, B, C, and D are 0.406, 0.406, 0.406, and 0.422. The average SAC values of the proposed S-boxes A, B, C, and D are 0.5, 0.5, 0.5, and 0.508. Hence, we conclude that the proposed S-boxes satisfied the SAC close to the optimal possible value.

5  Comparison

The former tests are applied on well-known S-boxes over EC presented in [19,20] to compare with the proposed S-boxes A, B, C, and D over GI. The analysis of EC and GI for the same primes with different parameters is presented in Table 21, and Figs. 1–5.

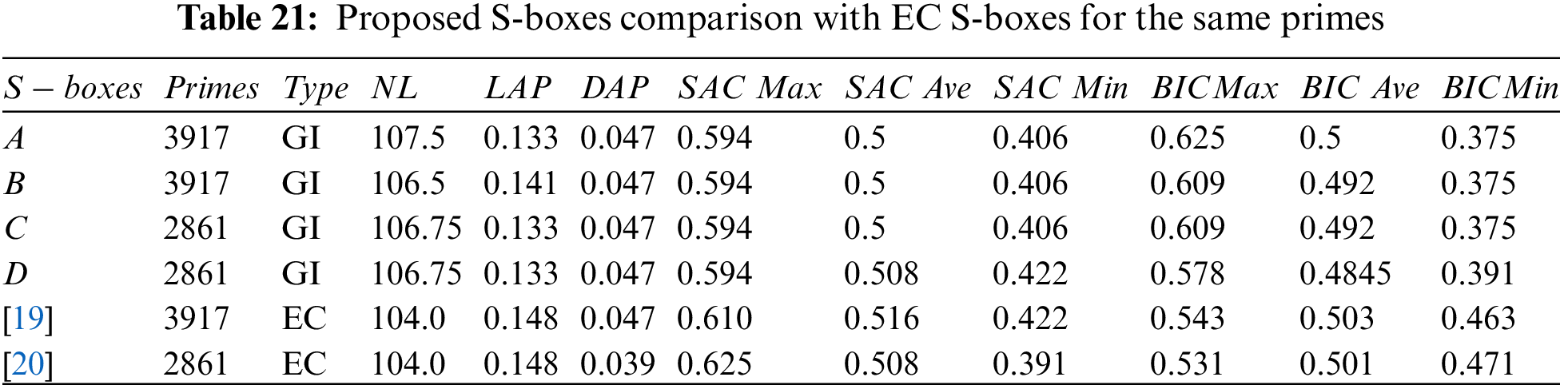
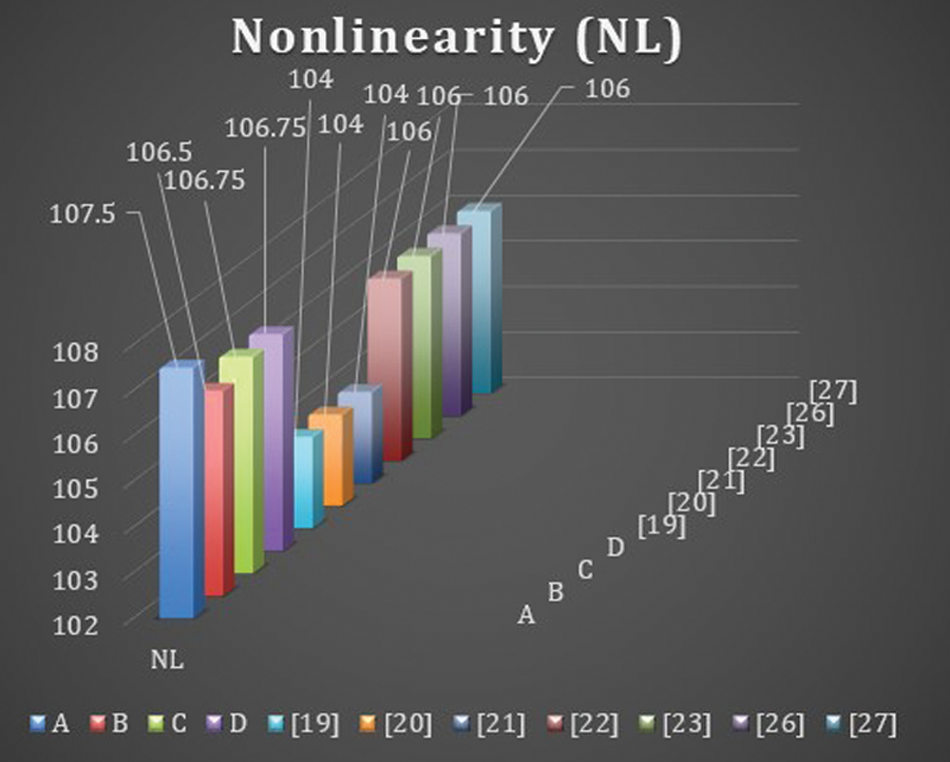
Figure 1: Nonlinearity

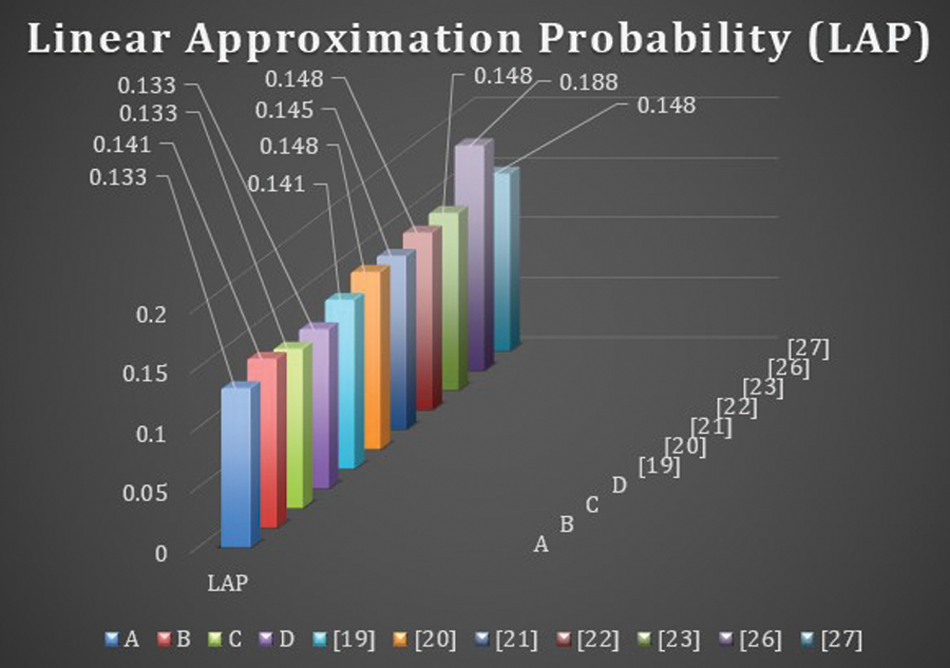
Figure 2: Linear approximation probability

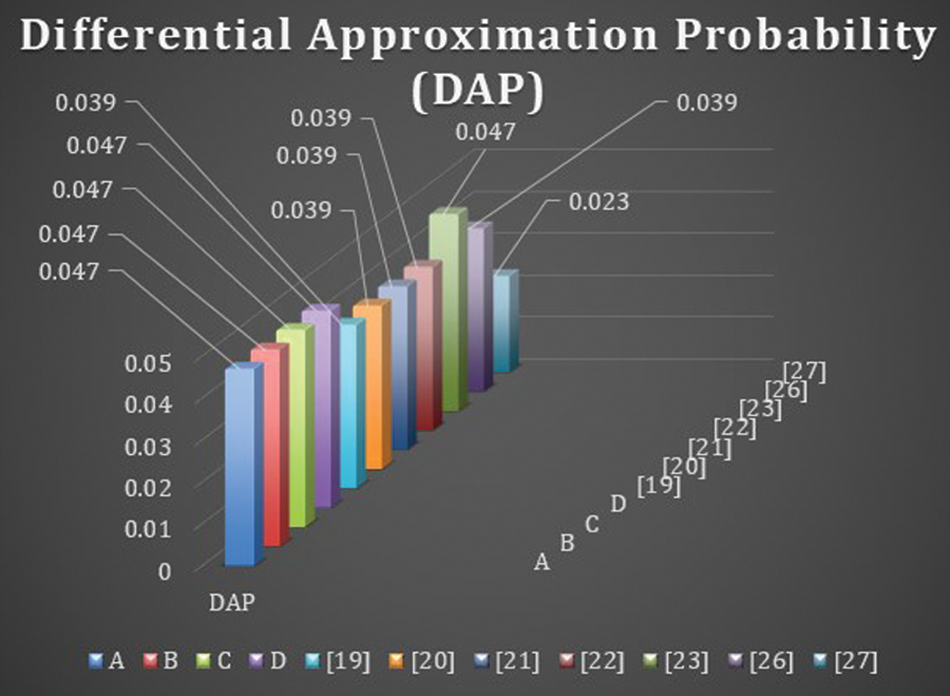
Figure 3: Differential approximation probability

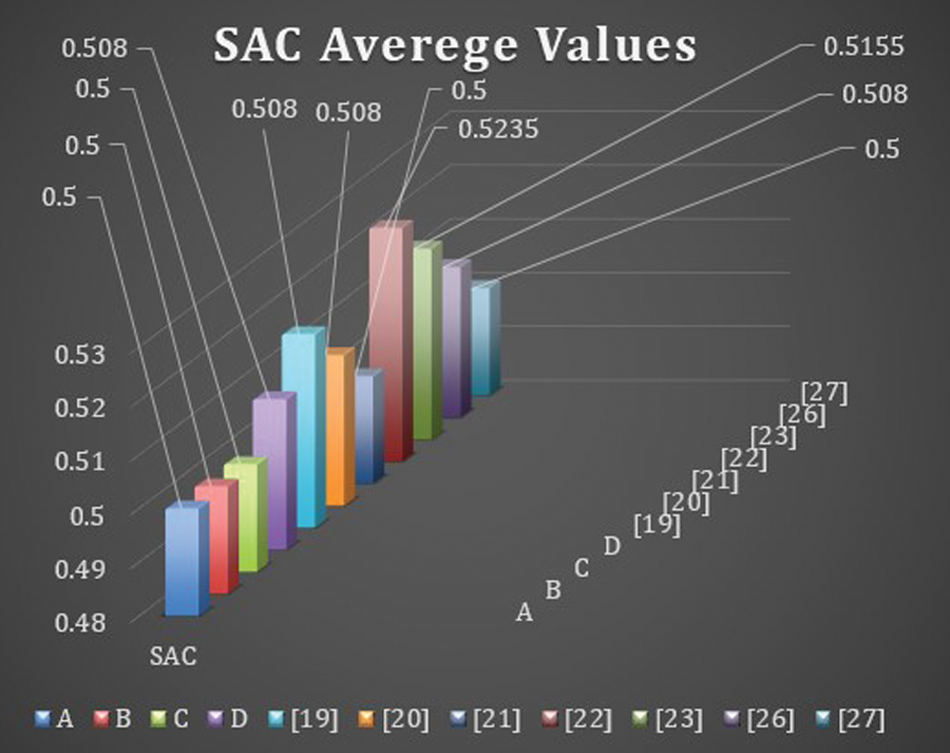
Figure 4: SAC average values

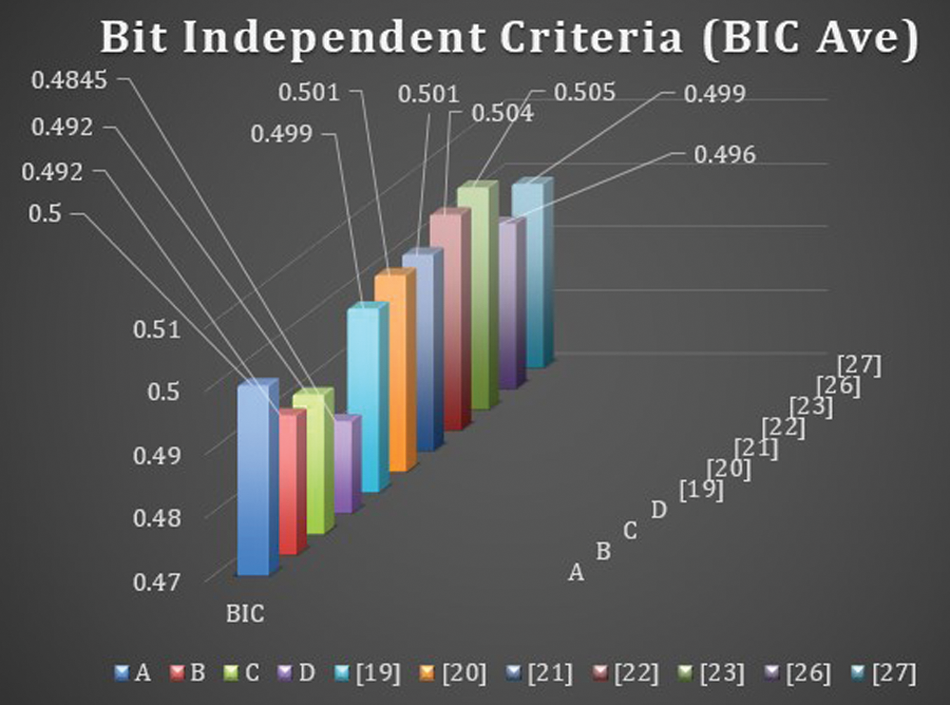
Figure 5: Bit independent criteria

Similarly, the comparison of S-boxes over EC presented in [19–27] with the proposed S-boxes A, B, C, and D over GI by some tests of S-boxes. The analysis of EC and GI for different primes with different parameters is presented in Table 22, and Figs. 1–5.

It is observed that the value of nonlinearity of the proposed S-boxes is better than with EC S-boxes. The fascinating features of the proposed technique by using affine mapping provide S-boxes pair at a time by fixing three parameters a, b, and  p. But the prime field dependent on the EC by different techniques provides one S-box at a time by fixing three parameters a, b, and  p. The nonlinearity of the proposed S-boxes is given in Table 22, and Figs. 1–5. The LAP results of the proposed S-boxes are less than the S-boxes presented in [19–27] This fact reveals that the proposed S-boxes create high confusion in the data and higher resistance against linear attack [24] as compared to [19–27]. The SAC and BIC results of proposed S-boxes are comparable with other S-boxes used in Tables 21, 22, and Figs. 1–5. Thus, the S-box generated by the proposed technique and S-boxes presented in Tables 21, 22, and Figs. 1–5 create diffusion in the data of equal magnitude. The DAP of proposed S-boxes is comparable to the DAP of S-boxes in [19–27]. Thus, the proposed technique generates S-box with high resistance against differential cryptanalysis [25] as compared to the others. The analysis results of newly generated paired S-boxes by the cyclic group of GI are listed in Tables 21, 22, and Figs. 1–5. It is evident from Tables 21, 22, and Figs. 1–5 that the performance of paired S-boxes by the cyclic group over GI is comparable with the S-boxes over EC.

6  Conclusion and Future Directions

A novel S-box construction technique is presented in this article. The fascinating features of the proposed technique by using affine mapping provide S-boxes pair at a time by fixing three parameters a, b, and  p. But the prime field dependent on the EC by different techniques provides one S-box at a time by fixing three parameters a, b, and  p. For the generation of cryptographically strong proposed S-boxes prime p which is greater than or equal to 257 and  a, b belongs to the cyclic group over the residue class of Gaussian integers. Several tests are applied to the newly proposed S-boxes and analyze their cryptographic strength. Furthermore, the cryptographic properties of proposed S-boxes are compared with some of the existing prevailing S-boxes over EC. Experimental results showed that the proposed algorithm is capable of generating paired S-boxes with high resistance against linear and differential attacks.

The proposed S-boxes over the residue class of GI can be extended to the S-boxes over the residue class of quaternion and octonion integers. Furthermore, we can use these structures in watermarking and image encryption.

Funding Statement: The third author is supported by Minciencias Convocatoria 891.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. K. Ruohonen, “Mathematical cryptology,” Lecture Notes, vol. 1, no. 1, pp. 1–138, 2010. [Google Scholar]

2. C. E. Shannon, “Communication theory of secrecy systems,” The Bell System Technical Journal, vol. 28, no. 4, pp. 656–715, 1949. [Google Scholar]

3. M. M. Hoobi, “Strong triple data encryption standard algorithm using nth degree truncated polynomial ring unit,” Journal of Science, vol. 3, no. 3, pp. 1760–1771, 2017. [Google Scholar]

4. A. Fathy, I. F. Tarrad, H. F. A. Hamed and A. I. Awad, “Advanced encryption standard algorithm, issues and implementation aspects,” in Int. Conf. on Advanced Machine Learning Technologies and Applications, Berlin, Heidelberg, Springer, vol.12, no. 2, pp. 516–523, 2012. [Google Scholar]

5. A. Anees and Y. P. P. Chen, “Designing secure substitution boxes based on permutation of symmetric group,” Neural Computing and Applications, vol. 2, no. 11, pp. 7045–7056, 2020. [Google Scholar]

6. I. Shahzad, Q. Mushtaq and A. Razaq, “Construction of new S-box using action of quotient of the modular group for multimedia security,” Security and Communication Networks, vol. 19, no. 1, pp. 1–13, 2019. [Google Scholar]

7. T. Shah and A. Qureshi, “S-box on subgroup of galois field,” Cryptography, vol. 3, no. 2, pp. 1–9, 2019. [Google Scholar]

8. I. Hussain, A. Anees, A. H. Alkhaldi, M. Aslam, N. Siddiqui et al., “Image encryption based on Chebyshev chaotic map and S8 S-boxes,” Optica Applicata, vol. 49, no. 2, pp. 317–330, 2019. [Google Scholar]

9. L. C. N. Chew and E. S. Ismail, “S-box construction based on linear fractional transformation and permutation function,” Symmetry, vol. 12, no. 5, pp. 826–842, 2020. [Google Scholar]

10. B. Arshad, N. Siddiqui, Z. Hussain and M. E. U. Haq, “A novel scheme for designing secure substitution boxes (S-boxes) based on mobius group and finite field,” Wireless Personal Communications, vol. 135, no. 124, pp. 3527–3548, 2022. [Google Scholar]

11. I. Hussain, T. Shah, M. A. Gondal and H. Mahmood, “A novel image encryption algorithm based on chaotic maps and GF (28) exponent transformation,” Nonlinear Dynamics, vol. 72, no. 1, pp. 399–406, 2013. [Google Scholar]

12. U. Hayat, N. A. Azam and M. Asif, “A method of generating 8× 8 substitution boxes based on elliptic curves,” Wireless Personal Communications, vol. 101, no. 1, pp. 439–451, 2018. [Google Scholar]

13. A. Javeed, T. Shah and A. Ullah, “Construction of non-linear component of block cipher by means of chaotic dynamical system and symmetric group,” Wireless Personal Communications, vol. 112, no. 1, pp. 467–480, 2020. [Google Scholar]

14. M. Sajjad, T. Shah, M. M. Hazzazi, A. R. Alharbi and I. Hussain, “Quaternion integers based higher length cyclic codes and their decoding algorithm,” Computers, Materials & Continua, vol. 73, no. 1, pp. 1177–1194, 2022. [Google Scholar]

15. G. Davidoff, P. Sarnak and A. Valette, “Elementary number theory, group theory, and ramanujan graphs,” Cambridge University Press, vol. 55, no. 1, pp. 45–80, 2003. [Google Scholar]

16. K. Conrad, “The Gaussian integers,” Preprint, Paper Edition, vol. 10, no. 2, pp. 1–13, 2018. [Google Scholar]

17. K. Huber, “Codes over Gaussian integers,” IEEE Transactions on Information Theory, vol. 40, no. 1, pp. 207–216, 1994. [Google Scholar]

18. M. I. Haider, A. Ali, D. Shah and T. Shah, “Block cipher's nonlinear component design by elliptic curves: An image encryption application,” Multimedia Tools and Applications, vol. 80, no. 3, pp. 4693–4718, 2021. [Google Scholar]

19. U. Hayat and N. A. Azam, “A novel image encryption scheme based on an elliptic curve,” Signal Processing, vol. 155, no. 1, pp. 391–402, 2019. [Google Scholar]

20. G. Dresden and W. M. Dymàčcek, “Finding factors of factor rings over the Gaussian integers,” The American Mathematical Monthly, vol. 112, no. 7, pp. 602–611, 2005. [Google Scholar]

21. N. Siddiqui, A. Naseer and M. E. U. Haq, “A novel scheme of substitution-box design based on modified pascal’s triangle and elliptic curve,” Wireless Personal Communications, vol. 116, no. 4, pp. 3015–3030, 2021. [Google Scholar]

22. N. A. Azam, U. Hayat and I. Ullah, “Efficient construction of a substitution box based on a mordell elliptic curve over a finite field,” Frontiers of Information Technology & Electronic Engineering, vol. 20, no. 10, pp. 1378–1389, 2019. [Google Scholar]

23. U. Hayat, N. A. Azam, H. R. G. Ruiz, S. Naz and L. Batool, “A truly dynamic substitution box generator for block ciphers based on elliptic curves over finite rings,” Arabian Journal for Science and Engineering, vol. 46, no. 9, pp. 8887–8899, 2021. [Google Scholar]

24. B. Collard and F. X. Standaert., “Experimenting linear cryptanalysis,” in Advanced Linear Cryptanalysis of Block and Stream Ciphers, 1st ed., vol. 1. Du Levant 3, B-1348, Louvain-la-Neuve, Belgium: IOS Press, pp. 1–28, 2011. [Google Scholar]

25. E. Biham and A. Shamir, “Differential cryptanalysis of DES-like cryptosystems,” Journal of Cryptology, vol. 4, no. 1, pp. 3–72, 1991. [Google Scholar]

26. N. A. Azam, U. Hayat and I. Ullah, “An injective S-box design scheme over an ordered isomorphic elliptic curve and its characterization,” Security and Communication Networks, vol. 80, no. 3, pp. 220–229, 2018. [Google Scholar]

27. I. Ullah, U. Hayat and M. D. Bustamante, “Image encryption using elliptic curves and rossby/drift wave triads,” Entropy, vol. 22, no. 4, pp. 454–473, 2020. [Google Scholar] [PubMed]