Traffic Management in Internet of Vehicles Using Improved Ant Colony Optimization

1  Introduction

The Internet of Things (IoT) is a network of ubiquitous gadgets, including computers, tablets, vehicles, and smartphones. Communication linkage between multiple gadgets, the IoT network creates a heterogeneous network [1]. For example, the Internet of Automobiles (IoV) facilitates Internet-based communication and data sharing between vehicles. However, traffic management remained the key issue with IoV. Several heuristics and algorithms have been suggested to select the shortest route between the source and the destination [2]. Among the multiple pathways between the source and destination, the best one should be picked, taking time and distance into account. However, choosing the best route without considering the dynamics of traffic features (such as traffic flow and vehicle speed) is challenging [2].

The word “path planning” refers to finding the best and least congested routes. Path planning has recently attracted the attention of experts working in the field of automobiles [3]. Numerous methods, such as the potential field method, evolutionary algorithm, simulated annealing algorithm, particle swarm optimization, fuzzy logic, and dynamic window approach, have been suggested for effective path planning [4–9].

The Capacitated Vehicle Routing Problem (CVRP) and the Vehicle Routing Problem with Time Window (VRPTW) handle the issue of finding the best routes for more than 100 automobiles (CVRP). In [9], VRPTW, a nonlinear problem, is solved using a Non-dominated Sorting Genetic Algorithm (NSGA). When tackling the VRPTW, the Tabu Search (TS) performs significantly better than the NSGA. A simple but effective hybrid Genetic Algorithm (GA) is suggested in [10] as a solution to this issue. Using real-world data and domain knowledge in GA, the researchers developed a brand-new heuristic standard for vehicle routing. A fuzzy routing solution has also been developed for the location-routing problem in-vehicle networks [11]. Researchers in [12] developed a hybrid route planning system for cars that are based on particle swarm optimization (PSO) and swarm algorithm (SA). However, the approaches lack flexibility and resilience and are quite vulnerable to local optimization. Dorigo [13] first introduced ACO in the early 1990s. This novel meta-heuristic method determines the foraging behavior of ants [14]. This algorithm has emerged as an effective evolutionary approach for handling complex optimization problems. The ACO solves challenges such as vehicle routing, network shortest path finding, and secondary distribution well because of distributed and parallel processing features. In [15], the authors obtained declined average waiting and transit time by formulating the path planning issue in IoV as an ACO optimization. Compared with the state-of-the-art methods, researchers in [16] suggested a distributed ACO for vehicular networks and enhanced network performance.

Researchers in [17] proposed a new navigation strategy for mobile robots working in dynamic situations by utilizing the ACO’s heuristic characteristics. The current swarm intelligence (SI) based routing protocols handle one or two indicators simultaneously while determining the optimum path. They do not consider the correlation between many indices. However, this search strategy is not appropriate for the situation where it is necessary to optimize numerous indices or pathways. The authors of [18] presented an ACO method based on fuzzy logic for path planning; however, they did not account for the dynamic character of the IoV environment, such as the cars’ potential future arrivals. The ACO’s resilience and powerful computational capability have attracted many applications for automobile traffic management. The optimal path is not necessarily to be the shortest distance path. Other factors include safety, a breathtaking view, reduced traffic, and a small number of junctions. Currently, there is no practical method for quick and accurate planning of these dynamic pathways. The best path is derived using nonlinear optimization with fuzzy logic and the SI in [19], which presents a novel routing protocol based on fuzzy ant colony optimization (FACO).

2  Literature Review

The Vehicular Ad hoc Networks (VANET) communication model uses roadside equipment and vehicle-to-vehicle communication to convey information between the cars [19]. However, decreasing the latency and enhancing network performance between the cars is one of the problems with the existing IoV [20]. Path planning algorithms, such as Dijkstra, are employed to regulate traffic, but they do not function well in dynamic situations like those seen in automotive networks [21].

The researchers improved the optimization technique and path-planning model for the IoV [22]. They offer a model so exact that it considers the steering window constraint and integrates length, energy calculation, and collision risk using an objective function. Based on this concept, they created a nature-inspired ACO algorithm to choose the best course. This technique is referred to as the Pheromone-Assisted Ant Colony System (AP-ACS) because it combines the alarm pheromone with the conventional guiding pheromone. This pheromone warns ants away from inefficient locations, preventing them from doing pointless searches and improving the efficacy of the search. Three heuristic metrics have been devised specifically to give ants the extra information they need for path planning in the interim. The authors conducted scale-based comparisons between AP-ACS and the present methods in various real-world settings. Their research revealed that the AP-ACS beat similar methods concerning accuracy, stability, and efficiency while handling constraints well. Due to ACO’s drawbacks, such as sluggish convergence and the ease with which it gets locked in a local optimum, [23] presented a better ACO algorithm-based vehicle path planning. To create a place for moving vehicles, it utilizes the grid approach. In a local optimum, a hybrid ant colony of common and scout ants is used to evade traps. By conserving elite ants for accelerating convergence, the pheromone process is enhanced by raising the ants’ sensitivity to the best path. In an area with various barriers, the fastest route with the lowest chance of collision must be designed. The outcomes showed that the method is efficient and useful. According to the available IoV studies, there exists a need for a study that considers dynamics such as potential congestion when determining the ideal path [24].

Considering the previously stated methods, this work demonstrates the use of fuzzy logic in conjunction with ACO, which dynamically chooses the best vehicle route based on various indices. The benefits of the enhanced ACO and the FL are merged to identify the optimal path from the origin and destination using several ideal factors. Given the dynamic nature of IoV, the best path, in this case, is the one whose variables fully satisfy all user expectations. The following are the main contributions of this work:

•   To solve the issue that the standard ACO is vulnerable to local optimization, an improved ACO has been developed.

•   It has suggested a novel future congestion-based ACO that estimates the dynamic nature of the IoV and calculates the optimal path considering the future arrival of the vehicles.

The remaining portions of the article are structured as follows: The proposed method for planning courses for cars is established in Section 4; Section 2 examines the ACO and fuzzy logic; Section 3 introduces the path guidance system for IoV; Section 4 concludes; and Section 5 includes sections on future suggestions.

3  Problem Formulation

A directed graph G = (V, E, D) is used to describe the proposed network model, where V stands for the number of cars in an IoV network, E stands for the collection of directed edges, and D stands for the separation between the source and destination. Table 1 a list of the annotations is presented that has been used.

3.1 Optimization Model

An ILP is used to formulate the path planning optimization problem in IoV. The ILP’s primary goal is to choose the best routes with the least congestion and travel time. Mathematically,

min∑i=1N∑j=1NαijCij(1)

∑(i,j)∈(i,j)out (i)|fmi,j|=∑(i,j)∈(i,j)in (i)|fmi,j|,∀i,j∈E∖{xm, zt}(2)

∑(i,j)∈(i,j)out (xm)|fmi,j|=∑(i,j)∈(i,j)in (zt)|fmi,j|=|fL|(3)

αij={1 if Eij=10 otherwise(4)

As stated in Eq. (1), the goal of the optimization issue is to zt the cost in terms of congestion and distance for designing a vehicle’s path. Each flow fm that is a member of FL has a unique source and destination node, Cij denotes the cost of each edge (i, j), and Eqs. (2) and (3) outline the restrictions related to the flow of conservation. Eq. (4) shows the choice of taking the path or not. The literature frequently uses ACO to enhance the design of vehicle network paths. Finding the quickest path while considering distance and congestion may be portrayed as the ant species’ foraging behavior. An arrival time of backward information can be used to update the value of the pheromone Eij.

3.2 Ant Colony Optimization

The proposed ACO uses a backward and forward ant procedure to search the optimal locations to reach the destination. The IoV technology, such as Road Side Unit (RSU), IoT gateways, and base stations, are used to collect information such as the number of cars, density of cars, and car speed. Mathematically, the congestion on the road can be calculated as follows,

Ci=1−Spnvimaxsp(5)

The above Equation represents the congestion on the network. The lower the value of Ci, the less congested the road is, and less traffic density is considered. The sp p stands for vehicle speed, the nvi displays the number of vehicles parked along the edge of the road, and the maxsp is the top speed of the vehicles.

Say the current node for an ant k is denoted by the letter i. Based on the distance between nodes j and i and the quantity of pheromones on edge ij, the ant k will travel from node I to an unvisited node j at time t. When there are several unvisited nodes, it is more likely that ant k will select node j, as shown by:

Pikj(t)={{[Tij(t)]α.[nij(t)]β[∑Tis(t)]α.[nis(t)]β}0 otherwise, j∈allowedj(6)

where ηij is the fuzzy value on edge ij visibility, the amount of pheromone on edge ij is denoted by Tij; allowedj denotes the set of contender nodes from where the ant k can select one, signifies the importance (weight) of the heuristic data (visibility) in selecting a path, and denotes the importance (weight) of concentration of pheromone in selecting a path.

3.3 ACO-Based Future Congestion System

The proposed future congestion metric also models the arrival of the vehicles in the future while searching for the optimal paths. Mathematically, it can be written as,

ECi,jk=Ci,jk+1−Vi,jkCi,jk(7)

where Ci,jk denotes the capacity of the vehicle in the k lane. The Vi,jk shows the vehicle in the kth lane and Ei,j, represents the edge or route i,j.ECi,jk represents the expected congestion on edge or route i j, on the kth lane.

4  Pheromone Update

The arrival time of the retreating ant updates the pheromone value of the edge (i,j).

Tij(t+1)=(1−ρ)Tij(t)+∑k=1nΔTijk(8)

where ΔTijk is the quantity of pheromones that ant k left in current iterations; n denotes the number of ants; and the evaporation rate of pheromone is denoted by ρ;

δTijk={ { 1sp+1nvi+1ECi,jk },edge  (i,j)is selected by ant k0 otherwise​​​(9)

where sp indicates the vehicles’ speeds, nvi represents the number of vehicles, maxsp is the maximum speed of the vehicles and ECi,jk predicts the future congestion on the kth lane.

The proposed algorithm for traffic management is shown by Algorithm 1. Initially, the ants are generated, and their position is located. After that, the vehicles acting as an ant calculates the congestion using the Equation as seen in the algorithm step 7. After that, the expected congestion is calculated as shown in step 8. Finally, the optimal route information is updated in the ant database.

4.1 Fuzzy Logic

Lotfi A. Zadeh, in 1965, presented the idea of a fuzzy set derived from a common set. Instead of the characteristic function, the membership function having a value of either one or zero defines the fuzzy set [25]. Membership implies that each object has the probability of being an element of the set. The membership values lie within [0, 1]. If the value of 4 memberships is 1, the item is an element of the set; if it is 0, the object is not a member of the set. Assilian and Mamdani devised sophisticated fuzzy logic processes in the 1970s, especially without rigorous models [26]. The fuzzy logic control methodology uses conditional sentences in place of equations. Inference refers to deriving a rule that needs characterization through a membership function. The truthfulness of every proposition can be evaluated through inference. The mechanism of an elementary FL control system is explained in Fig. 1. Fig. 1 illustrates three key steps for attaining FL control: fuzzification, rule evaluation, and defuzzification.

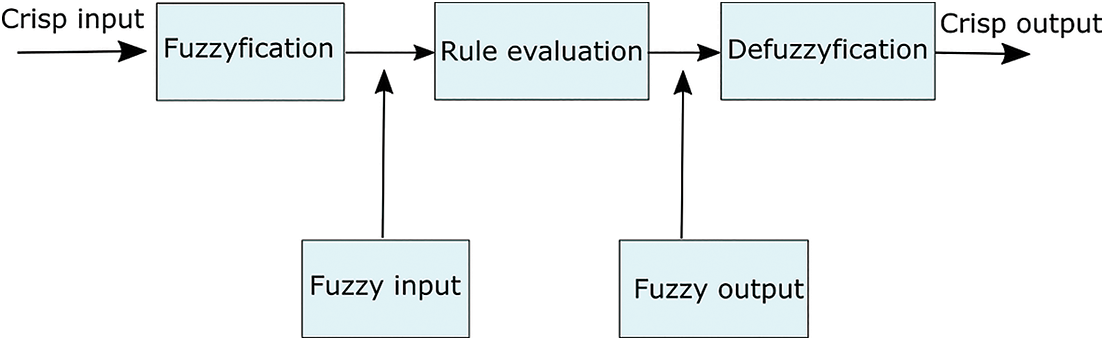
Figure 1: A fuzzy control system

4.2 Fuzzification

The implementation of every fuzzy logic control system might be done in terms of fuzzy rules, like:

Rule 1: if N is q1 & M is p1, then R is g1

Rule 2: if N is q2 & M is p2, then R is g2

Where the fuzzy parameters gi, qi, and pi are described by membership functions; R is the response variable; N and M are conditional variables. Considering that conditional variable are generally computed as one, Mamdani presented the fuzzy procedure for any membership function and the two rules: taking D2 and D1 as intervals, the conditional variable’s memberships were measured as μq2(n) and μp2(m) for Rule 2, and as μq1(n) and μp1(m) for Rule 1, followed by the matching of the computed values with the equivalent fuzzy variables.

4.3 Rule Evaluation

Regarding the rules, the control rules that satisfy N = n and M = m are connected as follows:

Rule 1: μ1 = μp1 (m) and μq1 (n);

Rule 2: μ2 = μp2 (m) and μq2 (n);

where the min function, μ1, and μ2, are used to calculate the truth degrees of rules 1 and 2, respectively.

The collection of all fuzzy subsets, gi(R), is used to represent the output of the FL control system (g(R)) by utilizing D3 as the output variable interval. The membership μgi(R) of the output provides the total of all memberships.

μg(R)=μc1(R)∗μc2(R)(10)

where, ∗, signifies the largest operation for evaluating Mamdani-type rules.

4.4 Defuzzification

The fuzzy output, or the result of inference, is converted into real values and used as an input for the FL control system. Since a non-fuzzy result is necessary, it is possible to determine the quantitative value of the FL control system output by μgi(R). The area of gravity (COA) procedure is generally used

ZCOA=∫µA(Z)dzµA(Z)d(11)

Here, ∫Z signifies the membership of all elements in the subset of fuzzy output as an integral on the continuous domain Z. There are equal areas on both sides of the ZCOA.

5  Simulation Results

Using the Intel Core i7-4790 CPU running at 3.6 GHZ machine, MATLAB is installed to run the simulations. Table 2 shows the simulation parameters. The average waiting and travel time are measured in ticks. In the simulation setting, where there is a high vehicle density, the distribution of the vehicles is random. The density of the vehicles ranges from 10% to 60% in each direction of the simulation environment. The environment will be considered congested if the vehicle’s density is greater than 60%. The evaluation for average waiting time of the vehicles is evaluated using three scenarios in the IoV. 1) Single intersection: The vehicle at a given junction node decides to move in different paths; 2) Multiple lanes at the intersection: a situation in which a single car travels down more than one lane; 3) numerous intersections: a scenario in which a single vehicle travels through more than one intersection to represent a large-scale network (Figs. 2–4).

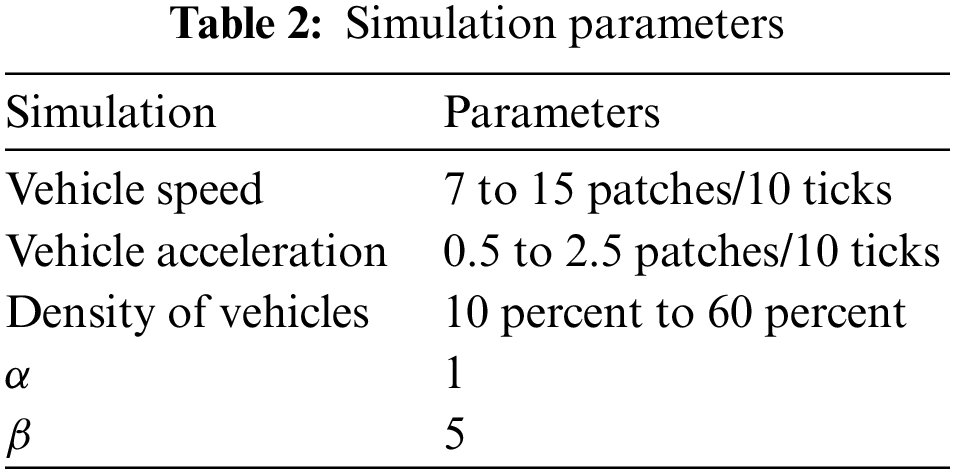
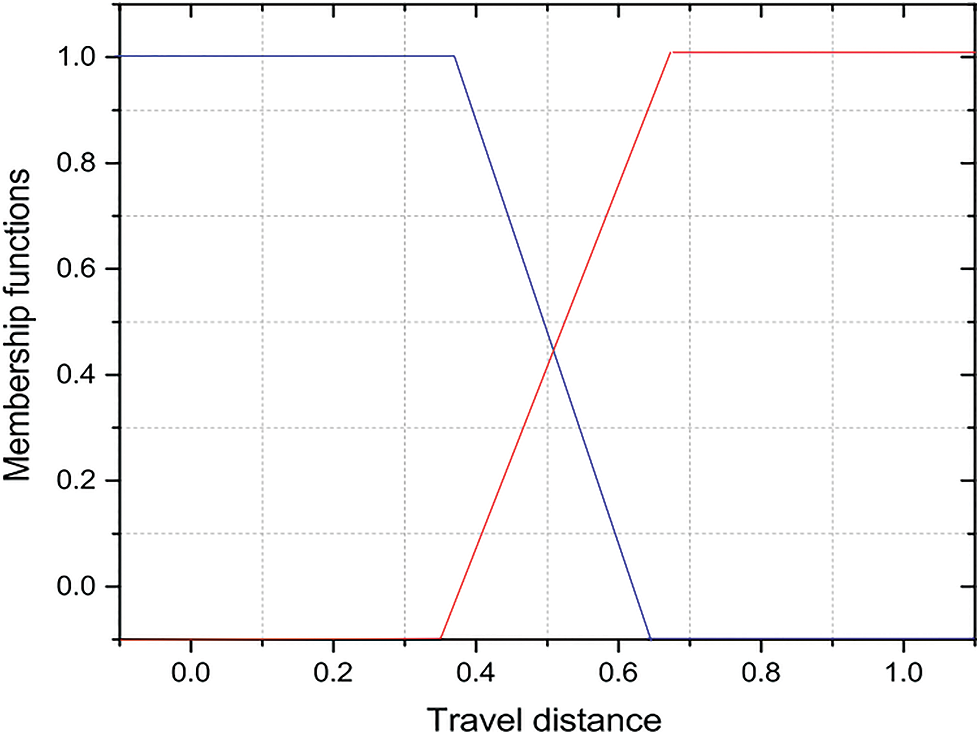
Figure 2: Average travel time

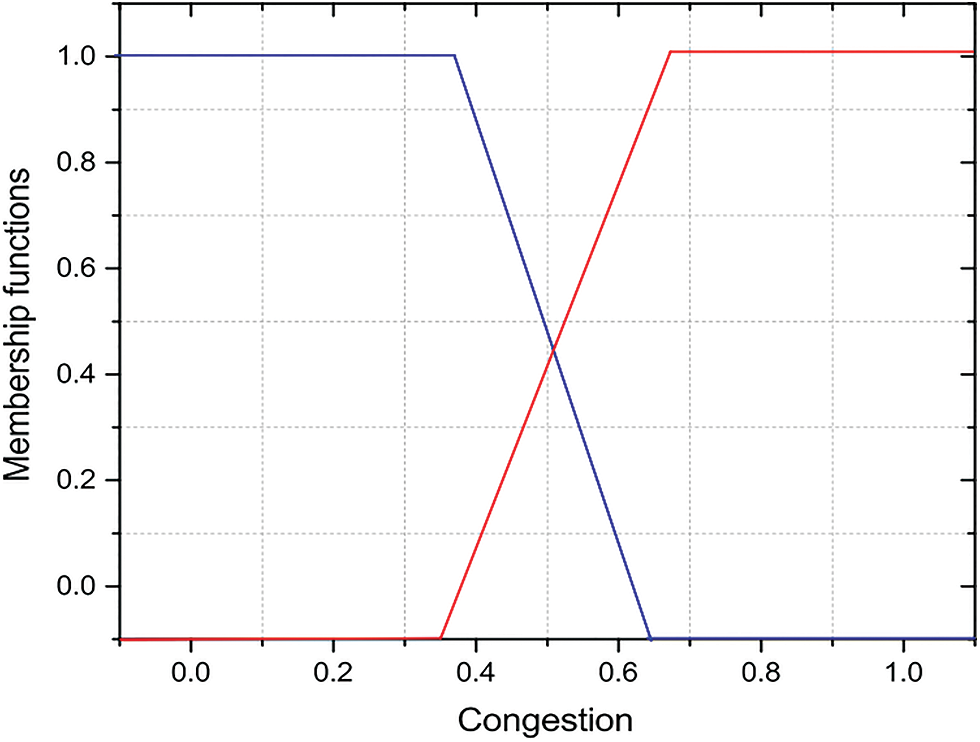
Figure 3: Congestion plot

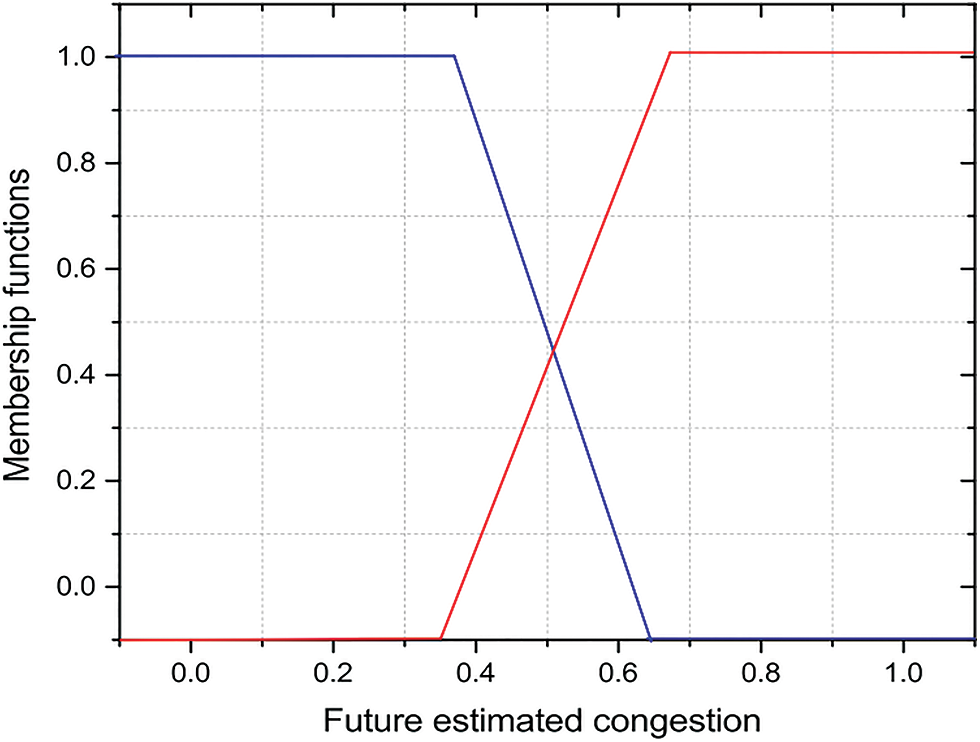
Figure 4: Future estimated congestion

Figs. 2 to 4 show the membership functions of the proposed algorithm. The membership functions significantly enhance the performance of the fuzzy representation. The membership function can graphically represent the fuzzy set. The fuzzy rules for searching the optimal paths are based on the inputs of travel distance, congestion, and future estimated congestion. The trapezoidal membership function has been used to calculate the optimal paths for each input. Fig. 2 exhibits a trip distance’s membership function, Fig. 3 the congestion’s membership function, and Fig. 4 the anticipated future congestion’s membership function.

Fig. 5 shows the fuzzy logic system for the proposed algorithm. The inputs for the Fuzzy system are the travel distance, congestion, and estimated future congestion based on the trapezoidal membership function. Finally, the defuzzification process is completed, and the value of the pheromone is updated.

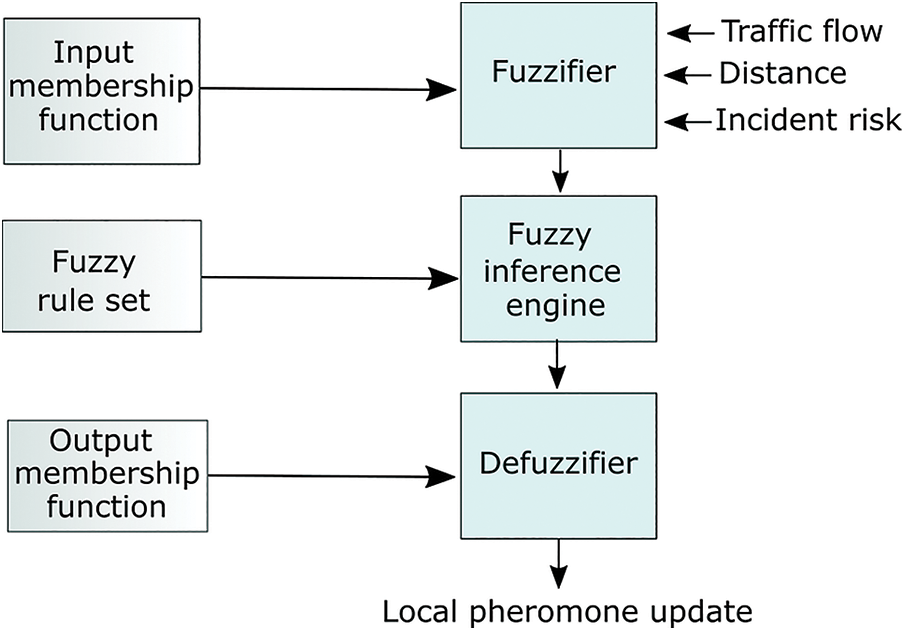
Figure 5: Fuzzy logic control system of the proposed algorithm

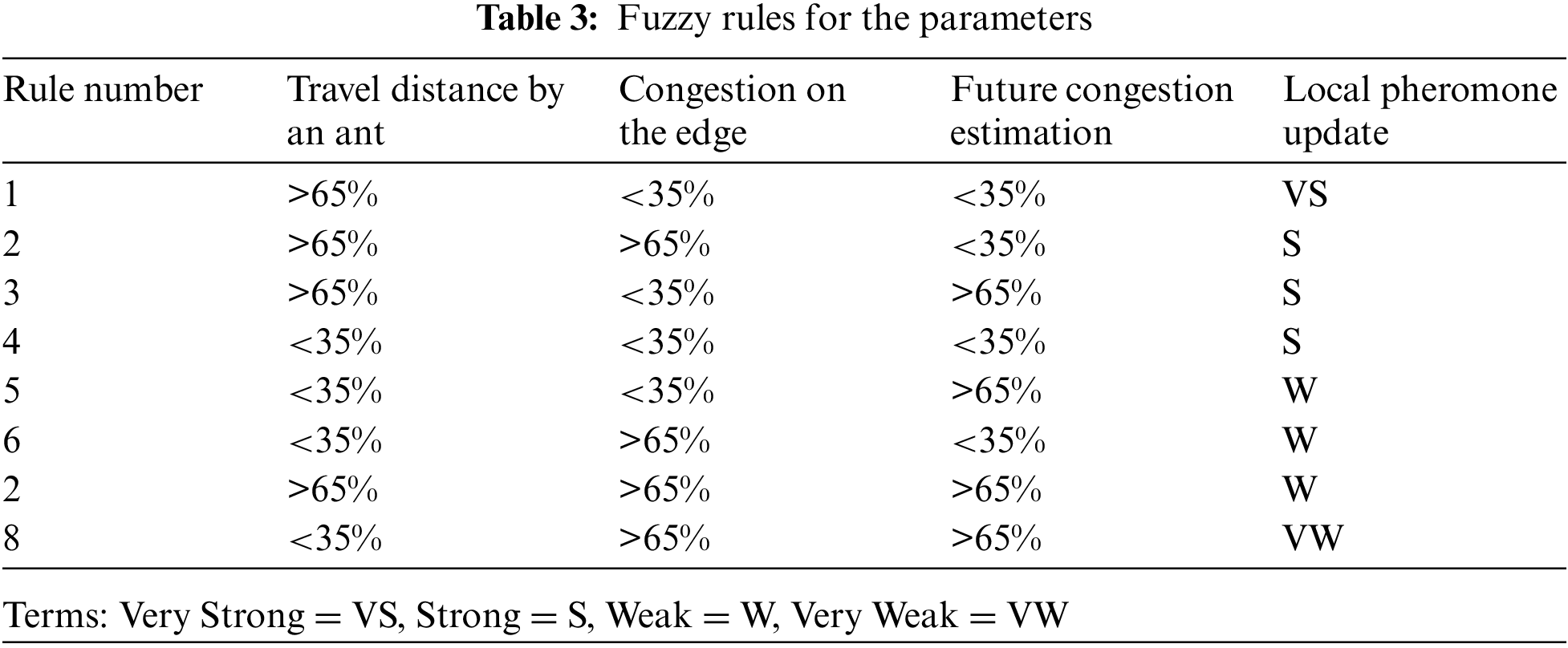
The readability and clarity of road networks are crucial in path planning. However, the road network information is either static or dynamic. It is impossible to digitize the dynamic information, so it is rarely considered in evaluating paths. A novel concept named “Future Congestion” has been suggested in this paper, as presented in Fig. 5. For an actual path with a Ln length, three dynamic parameters, including the travel speed, congestion, and future expected congestion are integrated while searching for an optimal path (Table 3).

Comparison of offline optimization technique with proposed ACO: The problem of searching for the optimal path in a dynamic IoV network is formulated as an ILP. There are two approaches, one for evaluating results for offline comparison and the other for evaluating results for online comparison. The offline comparison is made using a proposed optimization technique, as discussed in Section 3. ILP can search for the optimal paths as it considers that the network already has all the information. On the other hand, the network dynamics cannot be calculated in advance, so online comparison takes the current network states as input and searches for an optimal path. ILP finds the optimal paths as compared to heuristics. It is clear in Fig. 6 that the proposed ACO has a moderate deviation from ILP and is considered an effective approach for finding the optimal path, considering the time complexity of the algorithms. The proposed approach considers the congestion, future congestion, and travel distance for finding the optimal path and can be mathematically defined as:

P∗=∑i=1,j=1kDi,j[1+Ei,j+Ci (1+Si,j)](12)

Figure 6: Comparison of proposed ACO and integer linear program optimization with average travel time

The simulation results show a decrease in path with the traffic flow. Among various factors, just the road distance is considered in the actual path. However, the proposed approach considers the congestion, FC, and travel distance, making it closer to the real conditions. Concerning the actual path length, the ideal result is attained by the proposed algorithm in comparison with [19].

Average travel time: The suggested algorithm’s average journey time is displayed in Fig. 7 alongside well-known techniques. The proposed approach beats the benchmark systems by 27.6% and 13.4% when compared to the ACO [15] and [19], respectively, which incorporate virtual path length with dynamic parameters when identifying the best path. As the number of cars rises, the average wait time also increases. The proposed algorithm efficiently adapts to the dynamic situation of vehicles in an IoV environment such as FC while finding the optimal path. The vehicles are connected, and based on the collaboration among vehicles, the suggested technique can make dynamic and intelligent decisions, especially in the case of higher vehicle densities. The connected vehicles can adaptively balance the pheromone value based on actual traffic information. On the other hand, the benchmark scheme does not consider the real conditions of the road while searching for the optimal path in terms of waiting time.

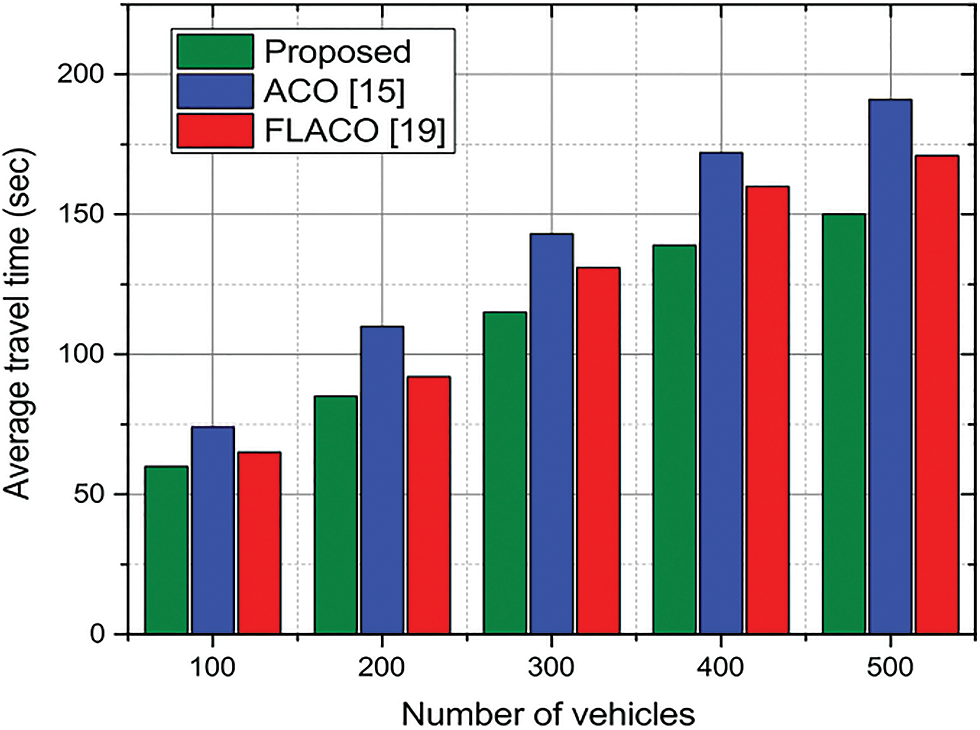
Figure 7: Average travel time

Average Waiting Time: Fig. 8 illustrates the typical wait time. The suggested fuzzy-based ACO strategy yields an average time slower than state-of-the-art methods. The suggested method computes pheromone values using real-time traffic flow data. The recommended approach can reduce average waiting times by adopting a virtual route length based on dynamic measurements and can produce pheromone values based on exchanging information about real-time traffic flow. On the other hand, the dynamic circumstances of the IoT network cannot be modeled by the benchmark systems.

Figure 8: Average waiting time

Optimal Path: The scheme is compared with the traditional ACO and the improved FLACO [19] that considers dynamic path planning. The red line in Fig. 9 shows the classical ACO, the blue line shows the improved ACO, and the black line shows the proposed future congestion-based estimation technique while finding the optimal path from source S to destination D.

Figure 9: Optimal path considering the future congestion

Fig. 9 shows the comparison of the proposed scheme with the benchmark techniques while searching for the optimal path. The red line shows the path from S to D in ACO [15]. It performs well in the case of static environments; however, its performance degrades if the nature of the environment is dynamic. [19] It considers the dynamic nature and uses a fuzzy approach to find the optimal path. Consequently, it does not consider future congestion while searching for optimal paths. The proposed scheme considers the dynamic nature of the vehicles in the IoV while considering future congestion while forwarding the optimal path. Thus, the proposed scheme performs best compared to benchmark techniques.

6  Conclusion

This paper presents a novel ACO-based technique that considers future congestion while searching for optimal paths. The algorithm searches the paths while considering the expected future arrival of cars in the network. The results show that our approach has optimized the network resources and reduced the delay of the IoV network as it calculates the paths with a future estimation of congestion on the paths. The execution of the proposed work is tested by running simulations on a road network topology and comparing results with the improved ACO and the classic ACO. The proposed method outperformed in finding the most cost-efficient route compared to the other two algorithms. In the future, this approach can be optimized further (e.g., reduction in computing time), and its application needs to be extended to planning paths for a group of vehicles.

Funding Statement: This work was supported by “Human Resources Program in Energy Technology” of the Korea Institute of Energy Technology Evaluation and Planning (KETEP), granted financial resources from the Ministry of Trade, Industry & Energy, Republic of Korea. (No. 20204010600090).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. X. Wang, Z. Ning, X. Hu, L. Wang and L. Guo, “Future communications and energy management in the internet of vehicles: Toward intelligent energy-harvesting,” IEEE Wireless Communications, vol. 26, no. 7, pp. 87–93, 2019. [Google Scholar]

2. V. Vijayaraghavan and J. Rian Leevinson, “Intelligent traffic management systems for next generation IoV in smart city scenario,” Connected Vehicles in the Internet of Things, vol. 21, no. 7, pp. 123–141, 2020. [Google Scholar]

3. N. Alawadhi, I. A. Shaikhli, A. Akandari and M. Tahir, “Optimal path planning for urban vehicles using internet of things: A new navigation perspective,” Journal of Computational Theoretical Nanoscience, vol. 16, no. 4, pp. 1074–1080, 2019. [Google Scholar]

4. J. Ni, L. Wu, P. Shi and S. X. Yang, “A dynamic bioinspired neural network based real-time path planning method for autonomous underwater vehicles,” Computational Intelligence Neuroscience, vol. 2017, no. 6, pp. 1–16, 2017. [Google Scholar]

5. R. M. C. Santiago, A. L. De Ocampo, A. T. Ubando and E. P. Dadios, “Path planning for mobile robots using genetic algorithm and probabilistic roadmap,” in 2017 IEEE 9th Int. Conf. on Humanoid, Nanotechnology, Information Technology, Communication and Control, Environment and Management (HNICEM), NY, USA, pp. 1–5, 2017. [Google Scholar]

6. F. Y. Vincent, A. P. Redi, Y. A. Hidayat and O. J. Wibowo, “A simulated annealing heuristic for the hybrid vehicle routing problem,” Applied Soft Computing, vol. 53, no. 42, pp. 119–132, 2017. [Google Scholar]

7. K. Jyothi and J. C. Jackson, “A Time-based approach for solving the dynamic path problem in vanets–an extension of ant colony optimization,” Journal of Engineering Science Technology, vol. 13, no. 6, pp. 813–821, 2018. [Google Scholar]

8. W. Yang, L. Zheng, Y. Li, Y. Ren and Y. Li, “A trajectory planning and fuzzy control for autonomous intelligent parking system,” SAE Technical, vol. 2, no. 1, pp. 0148–7191, 2017. [Google Scholar]

9. B. Ombuki, B. J. Ross and F. Hanshar, “Multi-objective genetic algorithms for vehicle routing problem with time windows,” Applied Intelligence, vol. 24, no. 5, pp. 17–30, 2006. [Google Scholar]

10. A. Mungwattana, T. Manisri, K. Charoenpol and G. K. Janssens, “A solution for the bi-objective vehicle routing problem with time windows using local search and genetic algorithms,” International Journal for Traffic Transport Engineering, vol. 6, no. 5, pp. 1–21, 2016. [Google Scholar]

11. A. Nadizadeh and B. Kafash, “Fuzzy capacitated location-routing problem with simultaneous pickup and delivery demands,” Transportation Letters, vol. 11, no. 4, pp. 1–19, 2019. [Google Scholar]

12. J. Yin and W. Fu, “A hybrid path planning algorithm based on simulated annealing particle swarm for the self-driving car,” in 2018 Int. Computers, Signals and Systems Conf. (ICOMSSC), NY, USA, pp. 696–700, 2018. [Google Scholar]

13. H. T. Zhao, X. P. Zhu, C. He and Y. Y. Zhu, “Ant colony optimization based dynamic scheduling routing algorithm in internet of vehicles,” in 2019 IEEE Int. Conf. on Consumer Electronics-Taiwan (ICCE-TW), NY, USA, pp. 1–2, 2019. [Google Scholar]

14. M. Dorigo, V. Maniezzo and A. Colorni, “Ant system: Optimization by a colony of cooperating agents,” IEEE Transactions on Systems, vol. 26, no. 12, pp. 29–41, 1996. [Google Scholar]

15. P. M. Kumar, G. Manogaran, R. Sundarasekar and R. Varatharajan, “Ant colony optimization algorithm with internet of vehicles for intelligent traffic control system,” Computer Networks, vol. 144, no. 31, pp. 154–162, 2018. [Google Scholar]

16. K. H. N. Bui and J. J. Jung, “ACO-Based dynamic decision making for connected vehicles in IoT system,” IEEE Transactions on Industrial Informatics, vol. 15, no. 4, pp. 5648–5655, 2019. [Google Scholar]

17. R. Kuo, B. Wibowo and F. Zulvia, “Application of a fuzzy ant colony system to solve the dynamic vehicle routing problem with uncertain service time,” Applied Mathematical Modelling, vol. 40, no. 6, pp. 9990–10001, 2016. [Google Scholar]

18. B. F. Ibrahim, M. Toycan and H. A. Mawlood, “A comprehensive survey on VANET broadcast protocols,” in 2020 Int. Conf. on Computation, Automation and Knowledge Management (ICCAKM), NY, USA, pp. 298–302, 2020. [Google Scholar]

19. Q. Song, Q. Zhao, S. Wang and X. Chen, “Dynamic path planning for unmanned vehicles based on fuzzy logic and improved ant colony optimization,” IEEE Access, vol. 8, no. 11, pp. 62107–62115, 2020. [Google Scholar]

20. J. Tian, Q. Han and S. Lin, “Improved delay performance in VANET by the priority assignment,” Earth and Environmental Science, vol. 4, no. 1, pp. 012081, 2019. [Google Scholar]

21. D. Medhi and K. Ramasamy, “Network routing,” Algorithms, Protocols, and Architectures, vol. 2, no. 6, pp. 1–6, 2017. [Google Scholar]

22. Y. N. Ma, Y. J. Gong, C. F. Xiao, Y. Gao and J. Zhang, “Path planning for autonomous underwater vehicles: An ant colony algorithm incorporating alarm pheromone,” IEEE Transactions on Vehicular Technology, vol. 68, no. 1, pp. 141–154, 2018. [Google Scholar]

23. P. H. Suganthi and M. Subha, “Path navigation in ACO using mobile robot,” International Journal of Trend in Scientific Research and Development, vol. 3, no. 3, pp. 164–169, 2019. [Google Scholar]

24. A. Azhar, S. Rubab, M. M. Khan, Y. A. Bangash et al., “Detection and prediction of traffic accidents using deep learning techniques,” Cluster Computing, vol. 10, no. 2, pp. 1–17, 2022. [Google Scholar]

25. Y. Sun, J. Xu, H. Qiang and G. Lin, “Adaptive neural-fuzzy robust position control scheme for maglev train systems with experimental verification,” IEEE Transactions on Industrial Electronics, vol. 66, no. 3, pp. 8589–8599, 2019. [Google Scholar]

26. E. H. Mamdani, “Applications of fuzzy algorithms for control of simple dynamic plant,” IEEE Consumer, vol. 121, no. 6, pp. 1585–1588, 1974. [Google Scholar]