Memory-Occupied Routing Algorithms for Quantum Relay Networks

1  Introduction

Quantum technology has developed rapidly, and some research directions have gradually become popular, such as quantum entanglement [1], quantum correlation [2–5], quantum computer [6–8], quantum computing [2,3], quantum machine learning [4], quantum image protocol [5], etc. Quantum relay networks based on teleportation and entanglement exchange are also under rapid development [9–13]. The earliest scheme of universal BB84 Quantum Key Distribution (QKD) was proposed by C. Bennet and G. Prasard in 1984 [14]. Bennett proposed a communication mode that can transmit quantum information by quantum means by using Einstein-Podolsky-Rosen (ERP) pair as a quantum channel in 1993, named quantum teleportation [15]. In quantum teleportation, remote transmission of any unknown quantum state can be accomplished only by local operation and classical communication and the distribution of quantum entanglement resources without sending information particles.

In the implementation of the quantum relay network, the selection of entangled particles, the working wavelength of a quantum storage system, and the loss of optical fiber are essential to limit the entanglement transmission distance. As a result, the quantum network is still in the primitive demonstration stage, and there is still a considerable distance to the realization of the quantum network. But studies and experiments are constantly updated [16–20], and scholars have studied various routing algorithms under the setting of quantum teleportation. They abstract basic physical processes at different levels and propose their network models, routing metrics, and routing algorithms under network topologies such as equilateral network, ring network, square network, and random graph [21–27]. Some of them propose concepts including the three steps of quantum transportation, time slot, and routing contention, which gradually advances the routing algorithm for quantum networks.

Meanwhile, recent research on quantum repeaters and memories can be divided into two directions: repeaters with and without memory function. For the mixed-function repeater, it can realize both the memory function and the entanglement swapping process. When the memory and repeater are independent, quantum channels can also be established by the entanglement distribution with the memories, and the entanglement swapping in repeaters.

However, the routing metrics recently proposed tend to consider more physical configuration. It considers the influence factor of entanglement cavity routing metrics in [16]. Reference [17] considers various routing factors in network layers without the effect of repeater distance and mutual exclusion. And most research on routing algorithms is repeater-occupied rather than memory-occupied under the limitations of quantum storage, such as the newly proposed routing algorithms contention-free path selection at runtime algorithm Q-CAST [22] and redundant entanglement provisioning and selection algorithm (REPS) [23]. Therefore, the motivation of this paper is to design memory-occupied routing algorithms in arbitrary connected mesh graph quantum networks to improve the network throughput.

We introduce a more comprehensive routing metric E to measure the throughput based on our previous work [28]. Routing metric E is not applicable in the case of multiple information pairs and possible route contention because it is only suitable for single-source transmission in a linear quantum network. Therefore, some improvements were made to E to correctly measure throughput in the case of multiple information pairs and possible route contention.

Furthermore, this paper abstracts a quantum network based on quantum teleportation and proposes a topology model that takes both network and physical layer factors into consideration. We investigate how to minimize route congestion when sending numerous source-destination (SD) pairs simultaneously, modify the Floyd algorithm to solve the All Pairs Shortest Path (APSP) problem, and propose exclusive memory routing algorithms Q-GMOA and Q-RMOA. These algorithms have a greater data transmission rate than that of exclusive repeaters and random routing, according to the evaluation. We summarize the main contributions of this paper as follows:

(1)   Present a well-designed transmission model and modify routing metrics E to correctly measure throughput under this model.

(2)   Propose exclusive memory-occupied routing algorithms Q-GOMA and Q-ROMA.

(3)   Extensive simulations to demonstrate the superior performance of the proposed memory-occupied algorithms.

The structure of this paper is as follows. The second chapter is related work, the third chapter puts forward an algorithm model and detailed explanation of factors. The fourth chapter puts forward the routing algorithm. The fifth chapter shows experimental and data results. The sixth chapter discusses the conclusion and future work.

2  Related Work

In the development of quantum networks, network topologies and routing algorithms emerge one after another. In this process, many scholars have used the topologies and routing algorithms in classical networks for reference by grasping the characteristics of quantum networks. For example, the current vision of the global quantum network is the combination of quantum satellite and fiber quantum network. Fiber quantum networks can complete quantum communication tasks at the metropolitan and intercity scales. At present, the development stage of the quantum network can be roughly divided into the following stages in Fig. 1 [29].

Figure 1: Development stages of quantum networks

The results of the previous study indicate that storage and on-demand retrieval in quantum networks are already available, although efficiency is still to be improved, and quantum relay stations need to improve the transmission rate of optical qubits [30]. A range of quantum repeaters for simple applications has been thoroughly studied [31–33]. But future quantum networks will need to be able to serve multiple applications and users.

At the same time, many algorithms related to graph theory are also used in the design of quantum networks. Shi and Qian chose the Yen algorithm in K-Shortest in the process of choosing the main path and the alternative path in their proposed routing algorithm Q-CAST [22]. Van Meter et al. used the Dijkstra algorithm to sort candidate paths in the quantum relay network and evaluated the ability of the algorithm to select paths [34]. Pant et al. consider how, in mesh networks, a quantum network node is equipped with limited quantum processing capability to simultaneously distribute high-rate entangled users between multiple pairs through lossed-optical link connections [35]. Pirandola studied multi-path routing in a diamond network, and extended the release of the widest path solving algorithm and maximum flow problem algorithm in traditional networks to quantum communication settings [36]. Das studied the quantification of network robustness by using the seepage theory under the lattice and bow equidistance topology of the repeater without memory function [37].

However, the existing routing metric policies tend to be more physical configuration, for example, some scholars consider the influence factor of entanglement cavity routing metrics [16,21,22] and tend to calculate routing metrics without considering the influence of the distance relay and mutexes effect [17]. Therefore, this paper uses routing metric E, which considers the influence factors in the network layer, to quantify throughput [28]. But route metric E is suitable for linear link single-source entanglement, and is not applicable in the case of multiple information pairs and possible route contention. Therefore, some modifications were made to measure throughput correctly in our experiments. In this paper, we use E’s analysis results within the scope of arbitrary network structure as the following setting:

(1)   Use an arbitrary network structure rather than a linear topology in our previous work [28].

(2)   Distance among nodes is set within the scope of the E analysis results, which build a quantum network in an arbitrary network structure with a range. And considering the deployed equilibrium problems of repeaters during the deployment phase can improve the throughput.

(3)   A range of deployment of repeaters is feasible to realize in an actual network.

For the above reasons, this paper abstracts the quantum network based on quantum teleportation and establishes a data transmission model. Then we explore how to design routing algorithms to improve throughput based on this model. Besides, a greedy algorithm is designed to evaluate the network throughput under different conditions with and without route contention.

3  Algorithmic Model

We will present a foundational network architecture and the transmission model, and describe the parameters in detail in this chapter.

3.1 Design of Network Architecture

In the previous routing algorithms in model design, network topologies are mostly linear, ring and star. However, the network topology is a connected mesh structure in reality rather than a fixed construction. In this paper, we abstract the quantum network based on quantum teleportation and establish a transmission model based on our work [28]. And the distance among network nodes is set under the analysis of E within the scope of arbitrary mesh network structure. To distinguish it from the path set E, write E as EXTsdij.

This paper focuses on the design of routing algorithms and only models the quantum swapping process without considering the traditional network transmission process in the quantum transportation process. In the process of data transmission, the main factors affecting throughput are the generation of entanglement pair, the transmission rate of entanglement pair in the fiber, and the process of quantum exchange of repeater. These influencing factors and parameters of the network model are listed in Table 1:

In order to visualize the parameters more clearly, Fig. 2 shows the transmission process and the setting of some basic parameters:

(1)   In the initial stage, each node k has a rated number of W memory, where the memory has the broken probability of Phik, and the actual memory number of nodes is denoted as wk.

(2)   In the phase of quantum entanglement establishment, entanglement generation and transmission processes are required for the successful entanglement establishment between two nodes. The probability of successful entanglement generation is set as basep, and the probability of successful entanglement transmission is set as p. p decreases exponentially with the increase of distance while establishing entanglement.

(3)   In the phase of entanglement swapping, the probability of successful quantum exchange in node i is set as q.

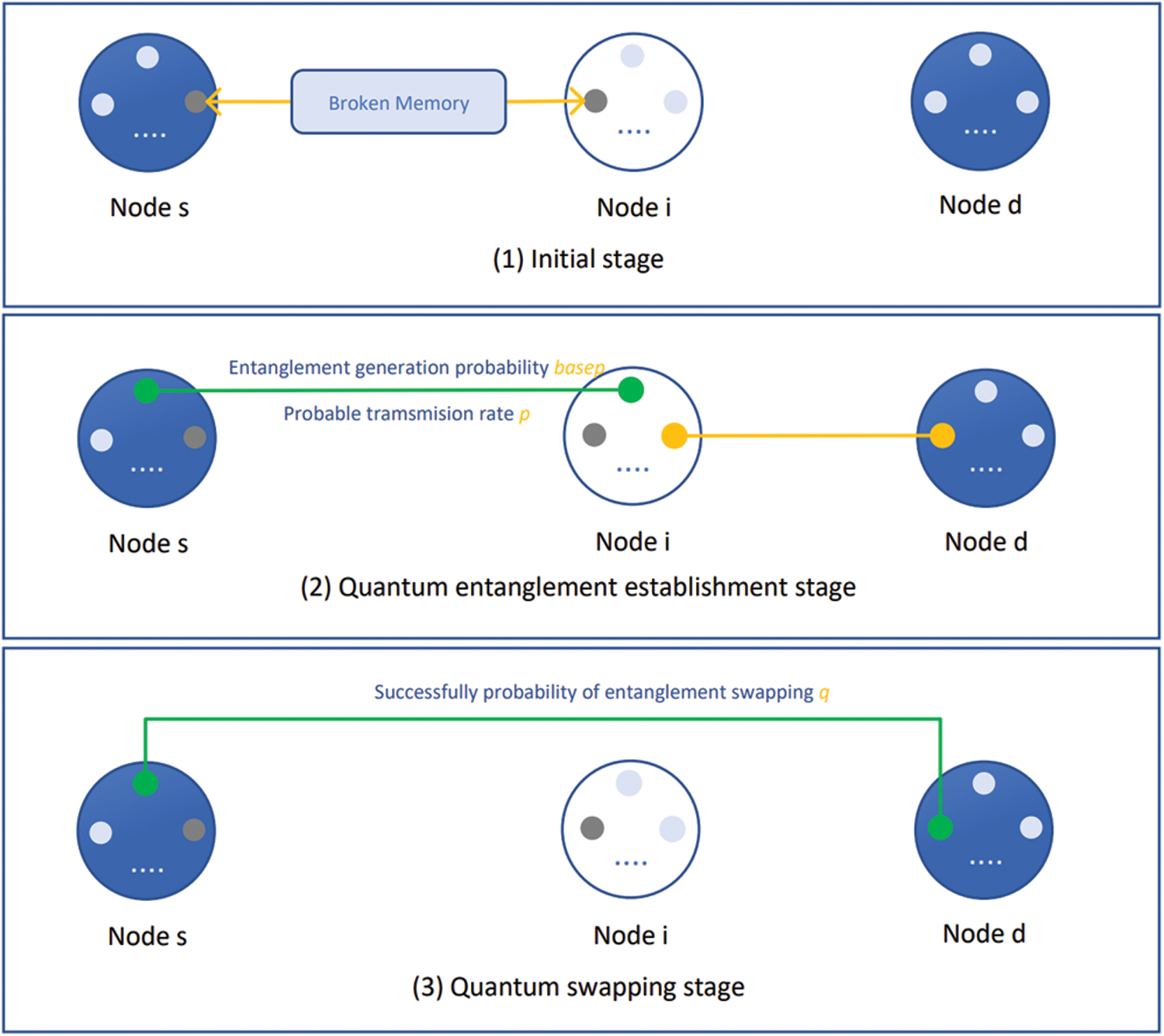
Figure 2: Analysis of the transmission process and basic parameters

The routing model proposed in this paper is to maximize the network throughput by solving the path set PSD under the condition of the given source-destination pair set SD.

3.2 Detailed Model

We will define the transmission model in detail in this section.

Definition 1: Problem Model

Given a quantum network whose topology is an arbitrary connected graph G = (V, E). For simplicity, there are no rings and no parallel edges.

V is a set of nodes, and for any node vi = ((xi, yi, zi), wi) belongs to V, whose position coordinates are (xi, yi, zi), with wi as the actual number of repeaters. The actual memory is the value of the rated memory obtained by the normal operation with the probability of phi. For simplicity, for each node vi, there is a fixed probability of p succeeding during the Bell state measurement.

E is the edge set. For any eij = ((vi, vj), kij ), the loss rate of the physical fiber channel is kij. The distance of eij can be calculated by the node coordinates of vivj, and the distance range of eij is the analysis result range of routing metric Eth under the above parameters.

Problem Description: For source-destination pair set SD in a given simultaneous time slot, find solution path set PSD to maximize network throughput Eth.

This problem can be reduced to the multi-source multi-destination shortest path problem, namely All-Pair Shortest Paths (APSP). Floyd-Warshall and Multiple Dijkstra are both classical algorithms for APSP in graph theory. In recent years, some new optimized solutions to APSP problems have appeared [38–40]. Due to the characteristics of the future quantum network, the amount of memory is limited and the cost of optical fiber deployment is reduced, the network is more likely to present the characteristics of a dense graph. Therefore, the dense graph-friendly Floyd-Warshall algorithm is used in this paper to solve the APSP problem.

4  Routing Algorithm Design

After the introduced model in the previous chapter, this section elaborates on routing algorithms for the proposed model. The principle of routing algorithms is introduced, and then goes four algorithms of different designs. In chapter 5, numerical results and conclusions are analyzed.

4.1 Analysis of Algorithm

According to the model analysis in the previous chapter, the proposed model can be determined as an APSP problem under the setting of quantum networks. This paper intends to find the appropriate path set (PSD) for source-destination (SD) pairs under the numerous parameters of quantum networks to maximize network throughput.

First of all, the quantum network topology in this paper is set as a connection graph. The physical distance between each node and the neighbors is within a range, which is obtained from the analysis of E. For instance, in a 100 km * 100 km network, 20 points are randomly distributed, and the channel distance is set within the range of 0 km−141.4 km. According to the analysis result of E, it can be deduced that the network can get the highest transmission rate with 0–18 nodes, and the average distance of optical fiber is set from 5.5 km to 28 km. There is a special condition that although the random network is unpredictable, there is an average point within the range of 5 km * 5 km in this network, which means the distance between each point should be 0–11.8 km, and the average value is 5.9 km. According to the distance setting, 0–5.5 km is less than the set minimum of 5.5 km, such a short circuit is not connected unless there is no adjacent node that meets the condition. In the transmission process of selecting the next hop in the quantum network, selecting the nearest neighbor does not necessarily have a higher transmission rate, since the excess BSM process caused by the short distance may offset the advantage of distance.

Since the problem is a deformed APSP, finding the shortest path from each node to the other is significant, namely the path with the highest possible transmission rate. In this case, the traditional measure of “cost” corresponds to possible transmission indicators such as distance. And the smaller the metric, the higher the transmission efficiency, which is the opposite of our original intention to choose a higher transfer rate. Therefore, the Floyd-Warshall algorithm should be modified to obtain the path with the highest rate, by taking the possible rate as the metric and selecting the path with the highest transmission rate as the optimal path each time. The key pseudocode is shown in Fig. 3:

Figure 3: Algorithm 1 modified floyd algorithm

The input of this code is Dists, matrixw, base, k, q. Dists is the node distance matrix. The memory storage matrix of the node is matrixw, the success rate of entanglement pair generation is basep, k refers to the propagation loss index on the fiber, and q is the BSM success rate of the intermediate process. After the algorithm, we can get the optimal path from each node to the other nodes by Route and the corresponding distance matrix matrixE.

The main purpose of lines 5 to 12 of the pseudo-code is to calculate the transmission rate of the directly connected path. Line 9 is the setting of the cast principle according to the calculation principle of E, which is the amount of available memory for two nodes is the minimum amount of memory for each node. Line 11 computes the potential success rate of a successful entanglement on a direct link. The 12th line measures the probability that there is one successful entanglement at least between the two nodes when minw memory is available, that is, the transmission rate between the two nodes. Lines 13–20 refer to the Floyd algorithm, which updates the transmission rate matrix (line 19) and set k node as the next hop from i to j (line 20) if the calculated transmission rate can be greater than the existing rate by adding a new node k in Line 17.

After the modified Floyd algorithm, each node has the global network knowledge of the network including the distance to each node and the optimal path. We randomly generated multiple SD pairs for experiments, and multiple SD pairs are not repeated. Different numbers of SD pairs are constructed respectively to achieve the effect of testing different network traffic.

During data transmission, routing contention may occur when multiple SD pairs are transmitted at the same time, affecting transmission efficiency. In order to solve the problem, connections can be queued for the next time point, or a suboptimal path can be selected for direct transmission. Since the concept of the time slot is not referenced in this paper, the algorithm is only designed in a broad sense, and the latter method is chosen to avoid contention. In addition, to avoid route contention, when a node is selected, we can choose to occupy a repeater node or memory. The method of occupying the repeater is commonly used in the previous research, which is very practical in the small traffic network and can simply and quickly avoid the data conflict caused by contention. The way of occupying memory has also been studied [19,20], mainly through occupying memory through links and setting capacity limits of memory to conduct experiments and evaluation. Based on this knowledge, this paper proposes a greedy memory-occupied routing algorithm to solve the problem of routing contention and designs three algorithms for experimental comparison.

4.2 Routing Algorithm

This section introduces a greedy memory-occupied routing algorithm Q-GMOA in Section 4.2.1 and a random memory-occupied routing algorithm Q-RMOA to improve the utilization of the quantum networks and design two algorithms in Sections 4.2.2 and 4.2.3 for comparison.

4.2.1 Greedy Memory-Occupied Algorithm Q-GMOA

We proposed a greedy routing algorithm Q-GMOA by occupying repeaters which set the smallest unit to be memories rather than repeaters in Fig. 4. One memory can only serve one SD pair at a time slot, which means one memory cannot be used as the relay for other SD pairs after being assigned to an SD pair. One repeater contains a certain number of memories so that multiple links can be established at the same time.

Figure 4: Algorithm 2 greedy memory-occupied algorithm Q-GMOA

Algorithm 2 provides the key code of the Greedy Memory-Occupied Algorithm. The parameters are Network topology Network, the actual amount of memories matrixw, the loss coefficient k on the optical fiber, the success rate q of the entanglement swapping inside the node, and the set of source-destination pairs SDPair. Network includes information on node position and distance, adjacency matrix, and other information.

The purpose of the algorithm is to obtain the path set PSD that can achieve the optimal throughput Eth for a given SD pairs SDPair. These target values are defined at the beginning of the algorithm (1–4), and the set of source S, destination D, and amount of SD pair SDnum are introduced. Lines 5 to 22 are a loop algorithm that loops SDnum times for each round of SD pairs calculation. The 6th line uses the modified Floyd algorithm to find the All-Pairs Shortest path, and the path matrix Route and throughput matrix matrixE can be obtained. Line 7 finds the values S and D with index of the SD pairs that can achieve maximum throughput in the current SDPair. Lines 8 and 9 check the calculated transmission rate between s and d. It means there is a break in the network and no suitable path for s and d if ext equals to zero. In addition to this situation, we can carry out the subsequent operation regularly, which mainly aims to update the matrixw. Line 10 updates the throughput Eth, and line 11 computes the path from s to d based on Route, and assigns the value to the PSD in line 12. Lines 13 to 18 update the amount of memory in the source and destination nodes minus one, and the amount of memory in the intermediate nodes minus two to intention the routing contention. In the 19–20 lines, source node set S and destination set D are updated to avoid double calculations. Then print the process data in lines 21–22 for review.

4.2.2 Greedy Repeater-Occupied Algorithm

The greedy routing algorithm for occupying repeaters is a very resource-intensive approach, where a repeater can only serve one SD pair at a time slot. After the repeater is assigned to an SD pair, it cannot be used as the relay for other SD pairs. This algorithm is commonly used as a basic concept for abstract quantum network settings in routing algorithms for its simplicity, which is shown in Fig. 5.

Figure 5: Algorithm 3 greedy repeater-occupied algorithm

But the defects can be identified in the basic principle: 1) The node utilization rate is low, resulting in the waste of resources; 2) There is a great probability to generate outlying points or disconnected subgraphs when there are an amount of SD pairs, resulting in network disconnection. The algorithm goes as follows:

Algorithm 3 is similar to that used in occupying repeaters algorithm besides the process of updating the memory amount after calculating the path in lines 13–18. In the pseudo-code of the algorithm, it can be determined that the setting of line 15 will cause a considerable waste of memory resources.

4.2.3 Random Memory-Occupied Algorithm Q-RMOA

Random strategies have poor efficiency after experimental assessment, so we add route selection in transit on the basis of the random strategy to improve the transmission rate, which is different from the greedy method which calculated paths before the connection is established. This method can reduce the cost of route calculation by calculating the path offline and updating the routing table until transmission problems occur. According to the occupation mode, we propose random memory-occupied algorithm Q-RMOA and the comparative random repeater-occupied algorithm.

The strategy Q-RMOA is to randomly select SD pairs instead of choosing s and d with the highest transmission rate at each loop in Algorithm 2 and Algorithm 3. If the paths of each SD pair are independent, the results of the random and greedy path selection method are the same. The pseudo-code goes as Algorithm 4 in Fig. 6.

Figure 6: Algorithm 4 random memory-occupied algorithm Q-RMOA

The random path selection algorithm in memory is the same as the input parameters for the first line to 9 lines. The main function of the while loop in lines 10 to 30, is to dynamically select routes during transmission. If the degree of the next-hop node is 0, go back to the previous node and find a new path until an appropriate path is found. Line 12 is calculated in two parts, depending on whether the next hop is the final node. If the next-hop is not the current node and connectable, the transfer rate to the next-hop is calculated and the path and the current source node are updated (lines 14–18). If the next-hop is not available, the path from the current node to the final node is recalculated at line 30. If the transmission rate equals zero, we need to roll back a source node and repeat the loop until path is empty. On the other hand, update path and throughput ext when the next hop is the final node. Then in line 31, the process of intermediate BSM needs to be taken into account. Finally, lines 33 to 39 update the memory count, S, and D, for the next round of SD pair calculations.

The comparative random strategy is more conventional, and its principle is that each SD pair establishes a connection according to the path of the initial calculation. If there is no way to contact the next node due to the dynamic memory problem during the transmission, the path from this node to the destination node d would be recalculated. The pseudo-code is the same as Algorithm 4 besides lines 33–38, the process of updating the amount of memory is shown in Fig. 7. This method is also similar to Algorithm 3, which also causes the waste of repeater nodes.

Figure 7: Algorithm 5 random repeater-occupied algorithm

4.2.4 Summary

The biggest difference between the proposed two algorithms Q-GMOA and Q-RMOA and the comparison algorithms is that they choose to occupy memory instead of repeater, which will greatly improve the node efficiency of repeater. The difference between greedy algorithm and random algorithm lies in the order of SD pairs. When the greedy algorithm transmits an SD pair in this time slot, it selects the SD pair with the highest initial estimated transmission rate instead of random selection. The transmission rates of the four methods can be verified by experiments.

5  Numerical Result

Several experiments are taken to measure the trend of routing measurement changes under the proposed routing algorithm Q-GMOA and its comparative algorithm. The advantages of the proposed algorithm Q-GMOA are examined and analyzed according to the results.

5.1 Experimental Settings

An Experimental simulation is carried out in an arbitrary connected network, which is connected by random nodes, and edges are set within the range of E analysis results to increase the throughput during the deployment stage. The size of the network varies from 50 km to 300 km, 100–500 nodes are stochastically distributed in the network, and 5–50 SD pairs are randomly generated. The topology in one experiment is shown in Fig. 8.

Figure 8: Visualized network with repeaters and channels

In the configuration of repeaters and memories, the actual amount of memory in repeater node is determined by independently repeated experiments to check its availability. Then we set the loss coefficient k on the optical fiber as 0.04, the success rate of generating entangled pairs basep as (0.8, 1). And the probability of a successful BSM q equals to 0.99, the rated size of memory W in the repeater is {4, 8, 12, 16}, and the normal usage rate Phi ranges from (0.8, 1). Experiments are carried out based on the network topology and the device configuration.

5.2 Experimental Conclusion and Analysis

Fig. 9 shows the numerical results of different algorithms for W = 4, 8, 12, 16 when the network area is 300 km * 300 km, 100 nodes are random distributed, basep = 0.99, k = 0.04, q = 0.99, Phi = 1. The distance between subsequent optical fibers is between 7.14 km to 13.125 km.

Figure 9: Throughput changes at W = 4,8,12,16

The X-axis represents the number of SD pairs and the Y-axis represents throughput Eth. The graph on the upper left shows the throughput changes of the four algorithms when W = 4 while with W= 16 in the upper right. It can be observed according to the experimental results of the four graphs:

(1)   The throughput of Q-GMOA is higher than that of Q-RMOA, the strategy of greedy is significantly better than random algorithms.

(2)   The throughput of random repeater-occupied algorithm is the lowest. And the throughput does not improve with the increase of the number of memory, and the gap with memory-occupied strategy gradually increases. The strategy of occupying memory is significantly better than that of occupying repeater. Although the random route selection process is relatively simple and does not need to find the largest SD pair, the result of using the greedy algorithm of occupying memories algorithm is 2–5 times better than random path selection in the case of rated memory is small, as shown in Fig. 10, when W = 4.

(3)   The transmission rate of the random repeater-occupied algorithm is higher than that of the greedy repeater-occupied algorithm. The reason is that the random method is not only different from the greedy algorithm in the path selection strategy but also uniquely adds the strategy of selecting paths while transforming, thus greatly improving the overall efficiency.

Figure 10: Throughput changes at W = 4,8,12,16

Fig. 10 is a process diagram saved for each round of the experiment, the X-axis is the rated amount of memory in the repeater, the Y-axis is the number of SD pairs, and the Z-axis is throughput. We can recognize the throughput obtained by using the four algorithms when the number of SD pairs changes and the number of memory changes.

Besides, the average transmission rate Eth/sizeof(SD) is calculated according to the simulation, and the average transmission rate when W = 16 of the four algorithms is 0.1674, 0.0108, 0.1134, 0.0284. It can be seen that the throughput of the greedy algorithm Q-GMOA is higher than that of the random algorithm Q-RMOA.

6  Discussion and Future Work

In this paper, an abstract model of the quantum relay network is established, which is based on quantum teleportation and takes both network and physical layer factors into consideration. And we proposed memory-occupied routing algorithms Q-GMOA and Q-RMOA to solve the routing contention problem that multiple SD pairs are simultaneously transmitted. Experiments show that in this network model, the use of the memory-occupied strategy can significantly improve node utilization and data transmission rate compared with the repeater-occupied strategy.

However, this greedy approach is only to find the maximum transmission throughput at each step. When the range of network structure is relatively large, this is only a local optimal solution, which may occupy the node resources of the next SD pair, and the maximum found may not be the global optimal solution. A more subtle approach would be to prioritize SD pairs unrelated to occupied paths, which will be done in future work.

Furthermore, the design of this paper is relatively simple, and some topics can be optimized in the work. In future work, the concept of time slot and the time of decoherence will be added, and the average time slot transmission rate will be considered to simulate with more real data parameters. After adding the concept of time slot, we need to consider which calculation process is offline or online and whether we need the concept of master path recovery path and get the time and space complexity of data or not.

Acknowledgement: We are thankful to all the collaborating partners.

Funding Statement: This work was supported by the Fundamental Research Funds for the Central Universities (2021RC239), the Postdoctoral Science Foundation of China (2021 M690338), the Hainan Provincial Natural Science Foundation of China (620RC562, 2019RC096, 620RC560), the Scientific Research Setup Fund of Hainan University (KYQD(ZR)1877), the Program of Hainan Association for Science and Technology Plans to Youth R&D Innovation (QCXM201910) and the National Natural Science Foundation of China (61802092, 62162021).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. D. L. Khokhlov, “Interpretation of the entangled states,” Journal of Quantum Computing, vol. 2, no. 3, pp. 147–150, 2020. [Google Scholar]

2. A. Mohamed, A. Farouk, M. Yassen and H. Eleuch, “Quantum correlation via skew information and bell function beyond entanglement in a two-qubit heisenberg XYZ model: Effect of the phase damping.” Applied Sciences, vol. 10, no. 11, pp. 3782–3795, 2020. [Google Scholar]

3. R. Abdelghany, A. Mohamed, M. Tammam and A. Obada, “Dynamical characteristic of entropic uncertainty relation in the long-range ising model with an arbitrary magnetic field.” Quantum Information Processing, vol. 19, no. 11, pp. 1–14, 2020. [Google Scholar]

4. A. Mohamed, A. Abdel-Aty, M. Qasymeh and H. Eleuch, “Non-local correlation dynamics in two-dimensional graphene.” Scientific Reports, vol. 12, no. 1, pp. 1–12, 2022. [Google Scholar]

5. M. Hashem, A. Mohamed, S. Haddadi, Y. Khedif, M. Pourkarimi et al., “Bell nonlocality, entanglement, and entropic uncertainty in a heisenberg model under intrinsic decoherence: DM and KSEA interplay effects.” Applied Physics, vol. B128, no. 4, pp. 1–10, 2022. [Google Scholar]

6. A. Homid, M. Sakr, A. Mohamed, M. Abdel-Aty and A. Obada, “Rashba control to minimize circuit cost of quantum Fourier algorithm in ballistic nanowires.” Physics Letters, vol. A383, no. 12, pp. 1247–1254, 2019. [Google Scholar]

7. A. Obada, H. Hessian, A. Mohamed and A. Homid, “Efficient protocol of N N-bit discrete quantum Fourier transform via transmon qubits coupled to a resonator.” Quantum Information Processing, vol. 13, no. 2, pp. 475–489, 2014. [Google Scholar]

8. A. Obada, H. Hessian, A. Mohamed and A. Homid, “Implementing discrete quantum Fourier transform via superconducting qubits coupled to a superconducting cavity.” JOSA, vol. B30, no. 5, pp. 1178–1185, 2013. [Google Scholar]

9. S. Sahoo, A. Mandal, P. Samanta, I. Basu and P. Roy, “A critical overview on quantum computing,” Journal of Quantum Computing, vol. 2, no. 4, pp. 181–192, 2020. [Google Scholar]

10. P. Gao, M. Perkowski, Y. Li and X. Song, “Novel quantum algorithms to minimize switching functions based on graph partitions,” Computers Materials & Continua, vol. 70, no. 3, pp. 4545–4561, 2022. [Google Scholar]

11. Y. Huang, X. Li, Y. Zhu, H. Lei, Q. Zhu et al., “Learning unitary transformation by quantum machine learning model,” Computers, Materials & Continua, vol. 68, no. 1, pp. 789–803, 2021. [Google Scholar]

12. G. Qu, H. R. Sun and M. Zheng, “An efficient quantum image steganography protocol based on improved EMD algorithm,” Quantum Information Processing, vol. 20, no. 53, pp. 1–29, 2021. [Google Scholar]

13. Y. Xu, “Entanglement of remote quantum memories,” Ph.D. dissertation, University of Science and technology of China, China, 2020. [Google Scholar]

14. C. Bennett and G. Brassard, “Quantum cryptography: Public key distribution and coin tossing,” arXiv preprint arXiv:2003.06557, 2020. [Google Scholar]

15. C. Bennett, G. Brassard, C. Crépeau, R. Jozsa, A. Peres et al., “Teleporting an unknown quantum state via dual classical and einstein-podolsky-rosen channels,” Physical Review Letters, vol. 70, no. 13, pp. 1895, 1993. [Google Scholar] [PubMed]

16. H. Briegel, W. Dür, J. I. Cirac and P. Zoller, “Quantum repeaters: The role of imperfect local operations in quantum communication,” Physical Review Letters, vol. 81, no. 26, pp. 5932, 1998. [Google Scholar]

17. T. Satoh, F. Le Gall and H. Imai, “Quantum network coding for quantum repeaters,” Physical Review, vol. A86, no. 3, pp. 032331, 2012. [Google Scholar]

18. M. Epping, H. Kampermann and D. Bruß, “Graph state quantum repeater networks,” arXiv preprint ArXiv:1504.06599, 2015. [Google Scholar]

19. D. Bouwmeester, J. Pan, K. Mattle, M. Eibl, H. Weinfurter et al., “Experimental quantum teleportation,” Nature, vol. 390, no. 6660, pp. 575–579, 1997. [Google Scholar]

20. X. Wang, X. Cai, Z. Su, M. Chen, D. Wu et al., “Quantum teleportation of multiple degrees of freedom of a single photon,” Nature, vol. 518, no. 7540, pp. 516–519, 2015. [Google Scholar] [PubMed]

21. C. Marcello, “Optimal routing for quantum networks,” IEEE Access, vol. 5, pp. 22299–22312, 2017. [Google Scholar]

22. S. Shi and C. Qian, “Concurrent entanglement routing for quantum networks: Model and designs,” in Proc. of the Annual Conf. of the ACM Special Interest Group on Data Communication on the Applications, Technologies, Architectures, and Protocols for Computer Communication, Virtual Event, NY, USA, pp. 62–75, 2020. [Google Scholar]

23. Y. Zhao and C. Qiao, “Redundant entanglement provisioning and selection for throughput maximization in quantum networks,” in IEEE INFOCOM 2021-IEEE Conf. on Computer Communications, Vancouver, BC, Canada, pp. 1–10, 2021. [Google Scholar]

24. W. Kozlowski and S. Wehner, “Towards large-scale quantum networks,” in Proc. of the Sixth Annual ACM Int. Conf. on Nanoscale Computing and Communication, Dublin, DUB, Ireland, pp. 1–7, 2019. [Google Scholar]

25. L. Le and T. Nguyen, “DQRA: Deep quantum routing agent for entanglement routing in quantum networks,” IEEE Transactions on Quantum Engineering, vol. 3, pp. 1–12, 2022. [Google Scholar]

26. S. Pirandola, J. Eisert, C. Weedbrook, A. Furusawa and S. L. Braunstein, “Advances in quantum teleportation,” Nature Photonics, vol. 9, no. 10, pp. 641–652, 2015. [Google Scholar]

27. S. Pirandola, R. Laurenza, C. Ottaviani and L. Banchi, “Fundamental limits of repeaterless quantum communications,” Nature Communications, vol. 8, no. 1, pp. 1–15, 2017. [Google Scholar]

28. J. Yao, K. Zou, D. Li and Z. Jiang, “Optimal deployment design of repeaters and memories in quantum networks,” in 2021 IEEE 23rd Int Conf on High Performance Computing & Communications; 7th Int Conf on Data Science & Systems; 19th Int Conf on Smart City; 7th Int Conf on Dependability in Sensor, Cloud & Big Data Systems & Application (HPCC/DSS/SmartCity/DependSys), Haikou, China, pp. 361–368, 2021. [Google Scholar]

29. S. Wehner, D. Elkouss and R. Hanson, “Quantum internet: A vision for the road ahead,” Science, vol. 362, no. 6412, pp. 1–9, 2018. [Google Scholar]

30. A. Delteil, Z. Sun, S. Fält and A. Imamoğlu, “Realization of a cascaded quantum system: Heralded absorption of a single photon qubit by a single-electron charged quantum dot,” Physical Review Letters, vol. 118, no. 17, pp. 177401, 2017. [Google Scholar] [PubMed]

31. S. Guha, H. Krovi, C. Fuchs, Z. Dutton, J. Slater et al., “Rate-loss analysis of an efficient quantum repeater architecture,” Physical Review, vol. A92, no. 2, pp. 022357, 2015. [Google Scholar]

32. M. Pant, H. Krovi, D. Englund and S. Guha, “Rate-distance tradeoff and resource costs for all-optical quantum repeaters,” Physical Review, vol. A95, no. 1, pp. 012304, 2017. [Google Scholar]

33. S. Pirandola, “Capacities of repeater-assisted quantum communications,” arXiv preprint arXiv:1601.00966, 2016. [Google Scholar]

34. R. Van Meter, T. Satoh, T. Ladd, W. Munro and K. Nemoto, “Path selection for quantum repeater networks.” Networking Science, vol. 3, no. 1, pp. 82–95, 2013. [Google Scholar]

35. M. Pant, H. Krovi, D. Towsley, L. Tassiulas, L. Jiang et al., “Routing entanglement in the quantum internet,” Npj Quantum Information, vol. 5, no. 1, pp. 1–9, 2019. [Google Scholar]

36. S. Pirandola, “End-to-end capacities of a quantum communication network,” Communications Physics, vol. 2, no. 1, pp. 1–10, 2019. [Google Scholar]

37. S. Das, S. Khatri and J. Dowling, “Robust quantum network architectures and topologies for entanglement distribution,” Physical Review, vol. A97, no. 1, pp. 012335, 2018. [Google Scholar]

38. M. Enayattabr, A. Ebrahimnejad, H. Motameni and H. Garg, “A novel approach for solving all-pairs shortest path problem in an interval-valued fuzzy network,” Journal of Intelligent & Fuzzy Systems, vol. 37, no. 5, pp. 6865–6877, 2019. [Google Scholar]

39. A. Pradhan and G. Mahinthakumar, “Finding all-pairs shortest path for a large-scale transportation network using parallel floyd-warshall and parallel dijkstra algorithms,” Journal of Computing in Civil Engineering, vol. 27, no. 3, pp. 263–273, 2013. [Google Scholar]

40. I. Toroslu, “Improving the floyd-warshall all pairs shortest paths algorithm,” arXiv preprint arXiv:2109.01872, 2021. [Google Scholar]