A Novel Approach for Security Enhancement of Data Encryption Standard

1  Introduction

With rapid development in the field of information technology, it is observed that communication over electronics channels and broadcasting of digital data over the internet is increased. Accordingly, the security of sensitive information against prohibited copying and dissemination has become tremendously imperative. Cryptography is the study of secure communication which is contemplated as a recognized branch of science for the last 60 years. However, it is quite a new area of study comparable to other areas of sciences as each moment carries continual developments. Cryptography is divided into two sub-branches; asymmetric key cryptography, and symmetric key cryptography. This classification is based on the secret key that is used during encryption and decryption. In symmetric-key cryptography, the communicating parties share a secret key confidentially. The algorithms such as Lucifer, DES, Advanced encryption standard (AES), and the International data encryption algorithm (IDEA) are the prominent examples of symmetric key cryptography.

Data encryption standard (DES) is a symmetric key algorithm designed by IBM. It was adopted and published by the US National Institute of Standard Technology (NIST) in 1971, as a federal information processing scheme. The aim was to provide a secure cryptosystem for the security of sensitive data and information during transmission. This algorithm became a distinguished and broadly used algorithm [1]. In the same way, a considerable number of cryptanalytic papers on DES were published since its acceptance in 1971. In 1977, Diffie and Hellman proposed a parallel machine for the comprehensive search of the complete keyspace [2]. The author claimed was, that very-large-scale integration (VLSI) chips are constructed and each chip probably searches one key per microsecond. The construction of the search machine contains millions of such chips and all working in parallel mode. Each chip is credible to search 1012 keys per second. The order of the set of all keys of DES is 7×1016 and can be approximately searched in 105 seconds that is almost 24 h. The estimated cost of this machine was $ 20 million and hence the cost per solution was $ 5000. In 1980 Hellman presented a time-memory tradeoff technique for the chosen plaintext attack [3]. The time memory tradeoff method takes vu  words of memory and performed u2 operations. Since vu2 equivalent to the total number of all possible keys for DES. Therefore, this technique is the same as the Differential Cryptanalysis of DES-like Cryptosystems which takes about 238 times and 238 memory with 256 pre-processing time for a special case m=t. The author suggested a special machine that produced about a hundred solutions with an average time of 24 h. The approximate cost of that machine was $ 4 million, so the cost per solution was about $ 1–$ 100. The processing time for the same machine was estimated and was required two years or three years. In 1985, Evertse and Chaum showed that the meet-in-the-middle attack can decrease the key search for DES [4]. The reduction factors are 219, 29 and  22 for the reduced number of rounds 4, 5 and 6 respectively. They also claimed that a somewhat altered form of DES having seven rounds can be cracked through the reduction factor of 2. Besides this, they showed that a meet-in-the-middle attack of the same kind is not appropriate for eight or more round reduced DES. In 1987, Davies described a new kind of cryptanalytic attack on DES called it known-plaintext attack [5]. They assumed that sufficient data might produce sixteen linear relationships amid the key bits. Accordingly, it decreases the size of the key search up to 240. The correlation among the outputs of the adjacent S-boxes was the main target of the plaintext attack. Since the correlation can disclose the linear relationship between the four bits of the key that is utilized to adjust these S-boxes as an input bit. Moreover, the consequence of the splits 32-bit of DES receives these outputs independently. Thus, each pair of the adjacent S-boxes can be exploited twofold, yielding 16 bits of key information. In 1991, Eli Biham and Adil Shamir designed the differential attacks which applied to various DES-like substitution permutation cryptosystems [5]. This was a powerful attack, which used just the pairs of ciphertexts and broke the DES in a few minutes. According to [6], any modification in the algorithm, for instance, key scheduling of the algorithm, substituting the permutation step by any other permutation, or the change the order of the eight S-boxes cannot make the algorithm less successful against the differential attack. A complete review of these attacks shows that the main targets of this cryptanalysis are the substitution phase which is the only nonlinear part of the algorithm. Since the S-boxes used in the algorithm were not cryptographically strong and thus the DES proved to be insecure against differential attacks.

S-box is one of the most important components in block ciphers, which is used to confuse the relationship between the cipher data and the input key during the process of encryption. Since the confusion-creating capability of the cipher relies on the quality of the S-box. Therefore, the construction of good quality S-box has attracted the cryptographic research community. The S-box construction schemes based on all isomorphic Galois field GF(28) is given in [6]. In [7], the author presented a novel S-box construction scheme using a chaotic skew tent map and its image encryption application. The nonlinear dynamical system exhibits desirable properties that are useful for confusion, so these are widely used for S-box construction [8–10].

Keeping the above facts in view, this manuscript proposed a novel 6×6 cryptographically strong S-boxes. The proposed S-boxes are then deployed in the Feistel function (FF) of the DES to achieve the substitution transformation which is the necessary step for the confusion criterion. The cryptographic characteristics of the new S-boxes are then analyzed over different analyses such as Differential approximation probability (DP), linear approximation probability (LP), Nonlinearity, strict avalanche criterion (SAC) and bit independent criterion (BIC). The results show that the proposed S-boxes are bijective, highly nonlinear and low costly than AES 8-bit S-box to implement and are almost identical in the term of linear, differential and algebraic properties. Hence, the essential criterion for the substitution step of the DES algorithm is successfully achieved. The major contribution of this paper is to strengthen the DES algorithm against linear and differential attacks.

The rest of this manuscript is organized as follows. In Section 2, we introduced some basic definitions. Section 3 is dedicated to the general principle of DES. The construction of the proposed S-box construction scheme is presented in Section 4. Section 5 is devoted to the performance analyses of the suggested S-boxes. The modified DES is examined using a specific ciphertext and compared the results with the DES in Section 6. Section 7 concluded the discussion.

2  Preliminaries

We denote the direct product of n copies of the field  Zp by Zpn where p is a positive prime integer. The 2-ary function having a range in Z2 is denoted by f throughout in this study namely Boolean functions, which is defined as f:Z2n→Z2. However, the function F:Z2n→Z2m is called a vectorial Boolean function.

2.1 Definition

Let f:Z2n→Z2 be a Boolean function. Then the nonlinearity of f can be defined as the smallest hamming distance among the set of all affine Boolean functions and the function  f. The nonlinearity of the function f is denoted by Nf. Mathematically it can be written as;

Nf=min{d(f,a): a∈A }(1)

where d(f,a) denote the Hamming distance between f and a. The symbol A signifies the set of all affine Boolean functions. Accordingly, the maximum possible Nf value of a function  f is equal to 2n−1−2n2−1.

2.2 Definition

Followed by [11], a function  F:Zpm→Zpn is said to exhibit the avalanche effect if and only if the following equation holds.

∑y∈Zpm⁡wt(F(y)⊕F(X⊕Cim))=n⋅2m−1. (2)

For all  i (1≤i≤m), Eq. (2), implies that the average of one-half of the output bits must be changed whenever one bit is complemented by the input data.

2.3 Definition

Followed by [11], let F:Zpm→Zpn be a function and defined a set

∂(x,y)=|{x |F(z+x)−F(z)=y}|(3)

The positive integer △F is called differential △F− uniform. The mathematical representation is defined as:

△F=maxx∈Zpm,   x≠0y∈Zpn⁡∂(x,y)(4)

3  General Outline of DES

DES is a symmetric key encryption scheme, which encrypts a 64-bits block of data. Thus, the input size of the algorithm is 64-bits and the output size is also 64-bits. The length of the key is 56-bits and it is mostly expressed as the block of 64-bits. The 56-bits are used as input key and the remaining eight least significant bits are utilizes for the parity check purpose. DES is consisting of two modules that are product cipher and Feistel cipher. The product cipher is used to combines two or more transformations because the combinations of ciphers are more secure than separated ciphers. A Feistel cipher is the iterated cipher that consists of the sequential repetition of the round functions. The formal definition of the FF is given as follows.

The Feistel Function (FF) is an iterated cipher that maps plaintext of size n=2m. We denote the left t-bits block and right t-bits block of the plaintext by ℒ0  and  ℜ0 respectively. Assume that the FF is consist of r rounds and the output of the rth round is the ciphertext, thus we denote the ciphertext by (ℒr, ℜr). The Feistel for ith round (for 1≤i≤r) is defined as follows;

(ℒi−1, ℜi−1)↦(ℒi, ℜi)(5)

(ℒi, ℜi)={ℒi=ℜi−1ℜi=ℒi−1⊕f(ℜi−1,𝒦i)(6)

where 𝒦i is the subkey derived through the key schedule algorithm. In DES the number of rounds r=16 and the subkeys size 𝒦i is 48-bits.

The FF is bijective and thus reversible. So, the same key is used for the encryption and decryption procedure. The Xor is used in the function to combine the output of the round function with the left half using the following equation.

ℒi−1⊕f(ℜi−1,𝒦i)⊕f(ℜi−1,𝒦i)=ℒi−1(7)

Eq. (7), demonstrates that the DES algorithm is independent of the design of the FF. The invertibility of FF does not produce an impact on the invertibility of the DES algorithm. Accordingly, if the function FF is invertible or not, though the DES scheme is always invertible.

4  Construction of Galois Fields GF(26) and S-Boxes

The field of order p is a prime field that is denoted by Zp . A polynomial p(y)∈Zp[y] that cannot factor in the product of polynomials in  Zp[y] is called irreducible polynomials. Let p(y) be an irreducible polynomial in principle ideal domain  Zp[y],. Therefore, the ideal generated by p(y) is a maximal ideal in  Zp[y]. The ideal generated by p(y) is denoted by ⟨p(y)⟩ and it is defined as;

⟨p(y)⟩={a(y):a(y)=p(y).h(y), for some h(y)∈ Zp[y] }.(8)

Thus, the quotient ring Zp[y]⟨p(y)⟩ is a finite field of order pn, which is known as Galois field  GF(pn), where m is the degree of the polynomial p(y). The field Zp[y]⟨p(y)⟩  consists of all polynomials in the form of the element of the principal ideal domain Zp[y] having a degree strictly less than m. The subtraction and addition operations perform over the field   Zp, that are the same operations as performed in Zp[y]. However, the product of the polynomials performs modulo p(y). A polynomial f(y)∈Zp[y]⟨p(y)⟩  is said to be the multiplicative inverse of the non-zero polynomial g∈Zp[y]⟨p(y)⟩ , if and only if f(y)g(y)≡1 mod p(y).

4.1 Construction of Galois Fields

This main interest of this study is Galois field s GF(26) of order  26. To construct the Galois field GF(26),  initially choose a degree 6 primitive irreducible polynomial p(y) in Z2[y] and find the root β of the polynomial p(y) i.e., p(β)=0. Subsequently, generate the multiplicative cyclic group GF(26)−{0}  from the root β by computing all βi for 1≤i≤26−1. Hence each nonzero element of the field GF(26)  can be expressed as the power of the primitive element β. We consider the set {pi(y)∈Z2[y]:pi(y)  is irreducible and  1≤i≤6} of all primitive irreducible polynomials of degree 6, to construct corresponding the Galois Fields Zp[y]⟨pi(y)⟩, 1≤i≤6. Next, these Galois fields are then utilized to construct 6×6 S-boxes. The degree 6 primitive irreducible polynomials and their corresponding Galois fields are listed in Table 1.

4.2 Construction of 6 × 6 S-Boxes

The construction of the S-box required a nonlinear bijective map. In the proposed work, we have used the multiplicative inverse function module degree 6 primitive irreducible polynomial pi(y) as a power permutation for the construction of S-boxes. The mapping is defined as follows:

gi:Z2[y]⟨pi(y)⟩→Z2[y]⟨pi(y)⟩

gi(w)={w−1        if w≠00             if w=0(9)

The images gi(w) for all 0≤w≤63 are then converted into an 8×8 lookup table, which is the required S-box. Thus, for each degree 6 primitive irreducible pi(w) for 1≤i≤6 one can obtain different S-box denoted by Si. Tables 2a–2f depicted the generated S-boxes corresponding to different primitive irreducible polynomials and Galois field Z2[y]⟨pi(y)⟩. Section 5, analyzed the proposed S-boxes with well-known analyses such as nonlinearity, BIC, SAC, LP and DP to examine the quality of the S-boxes.

4.3 Theorem

In [12], Let l be an affine transformation and g be the power permutation with good cryptographic properties in the Galois field GF(2m), then the affine power affine (APA) composition is defined as follows:

S(x)=l∘g∘l(10)

The Eq. (10) preserves the cryptographic properties of g and takes on stronger algebraic complexity.

4.4 Remark

A composition function of an affine function with a function g on the right-hand side or the left-hand side preserved the properties of linearity and differential uniformity of a function g.

5  Performance Analyses

An efficient cryptosystem should be secure against all kinds of attacks. Since the security of the block ciphers depends on the choice of the S-box, therefore this section we thoroughly analyzed the performance of the proposed 6×6 S-boxes to figure out the best S-box. The good quality S-box of these S-boxes is then deployed in the proposed modified DES. Besides, we will also compare the obtained results with the super AES 8-bits S-box.

5.1 Nonlinearity

In Section 2, the definition of nonlinearity for the Boolean function has been already discussed. The general formula to calculate the upper bound of the nonlinearity of the function f:Z2m→Z2 that is 2m−1−2m2−1 [13]. Therefore, the maximum possible nonlinearity for  m=6 is Nmax=28. The nonlinearity of all S-boxes is calculated, the resultant values are listed in Tables 3a–3f. It can be seen that overall, the average nonlinearity analyses of the S-boxes are quite good and capable to resist linear attacks. Moreover, from the tables, one can observe that the average nonlinearity of the S-box S1 is equal to S2. Similarly, the average nonlinearity value of S3 is equal to S4 and the S5 average nonlinearity value is the same as S6. Therefore, the pair consists of S5 and S6 is the best with respect to nonlinearity analysis.

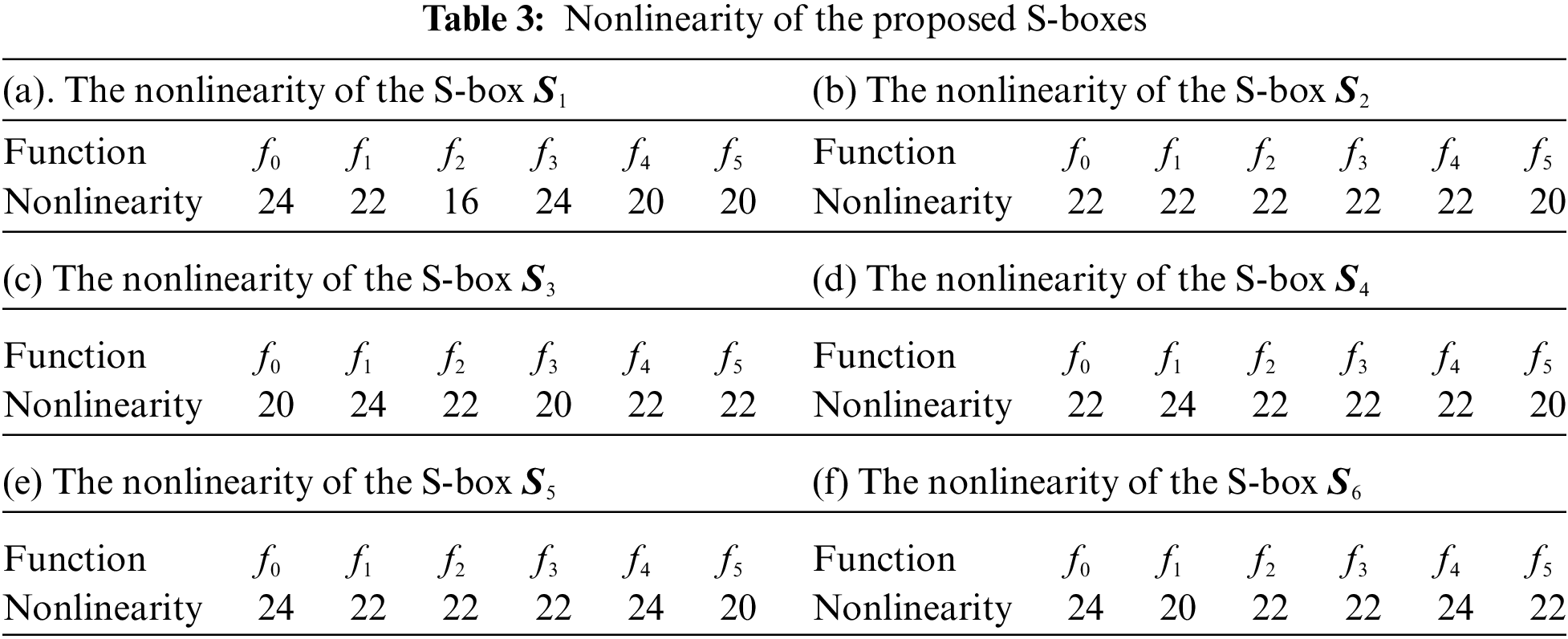
5.2 Differential Cryptanalysis

Differential approximation probability (DP) analysis is used to measure the differential uniformity of the S-box. The minimum possible value of differential uniformity for m×n S-box is δ(S)= 2m−n+1 [14]. Thus, for the 6-bit S-box, m=n=6,δmin=2. The S-box having minimum differential uniformity is known as almost perfect nonlinear [15]. We have calculated the differential distribution matrix Λ(S) of all the generated S-boxes, shown in Tables 4a–4f. As can be seen in the tables that the differential distribution table of all the 6-bit S-boxes are consist of 4,6 and 8 except the element  λ63 and the S-box S5 also contain 10. Therefore, the differential approximation probability is 0.1250 for the S-boxes S1,…,S4 and S6, however the differential probability of the S-box S5 is 0.1563. Overall, the differential approximation values of all S-box are approximately equal to the DP value of the AES S-box, nowadays considered as a super S-box. Accordingly, the modified DES S-boxes have enough strength against the differential cryptanalysis attack.

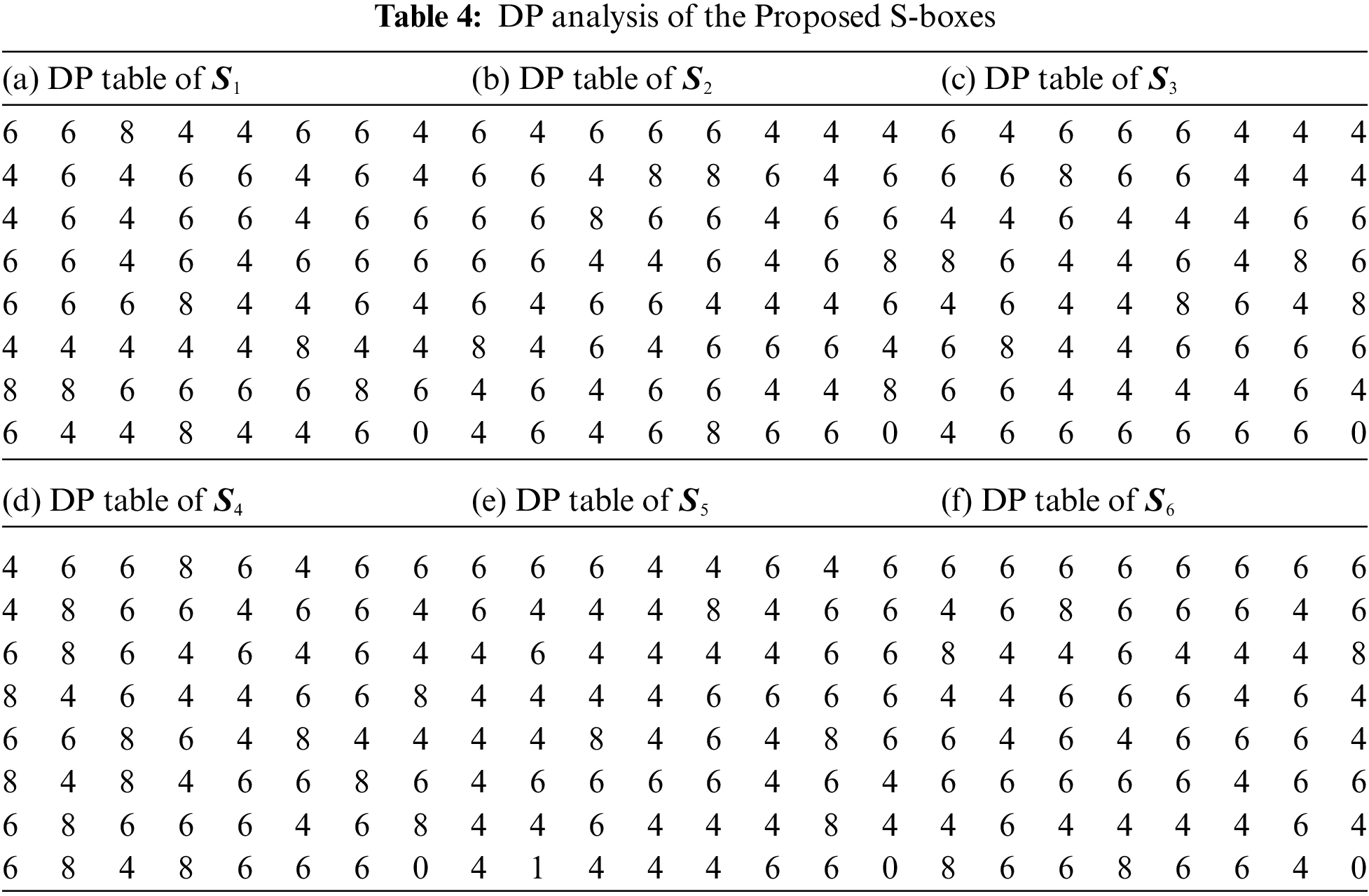
5.3 Strict Avalanche Criterion

In general, an S-box is considered a lookup table of Boolean functions from Z2m to Z2n for m≥n [16]. Feistel has suggested an important criterion for the designation of cryptographic function. A Boolean function f:Z2m→Z2n is said to be exhibit the avalanche effect if

 ∑u∈Z2m⁡wt(f(u)⊕f(u⊕cin))=n2m−1.(11)

For all 1≤i≤m, where cin is a vector consist of all zeroes except at the ith position. Accordingly, this definition means, that a Boolean function is said to fulfill the avalanche criterion if and only if the average half of the output bits change, whenever one changes a single bit in the output bits. This implies that if a single input bit changes, then the output bits will change with 0.5 probability. According to Adams, C., & Tavares, S the function of Hamming weight 2m−1 for all output, m-bits leads the S-box with the good avalanche. Because every vector fj complements the input bit xb according to alteration in the location from the position fji and fjk for some positive integer j and k. If the vector fj contains equal number ones and zeroes, then for all possible inputs with complementing the bit xb yields the function yi to be inverted 50%. Therefore, for all f1,f2,…,fn with the property of hamming weight 2m−1 by inverting a bit xb inverts on average half bits in y1,y2,….yn. Since all the Boolean functions of the proposed S-boxes are complete, therefore the proposed S-boxes successfully satisfy SAC with an average probability approximately equal to 0.5 as can be seen in Tables 5a–5g.

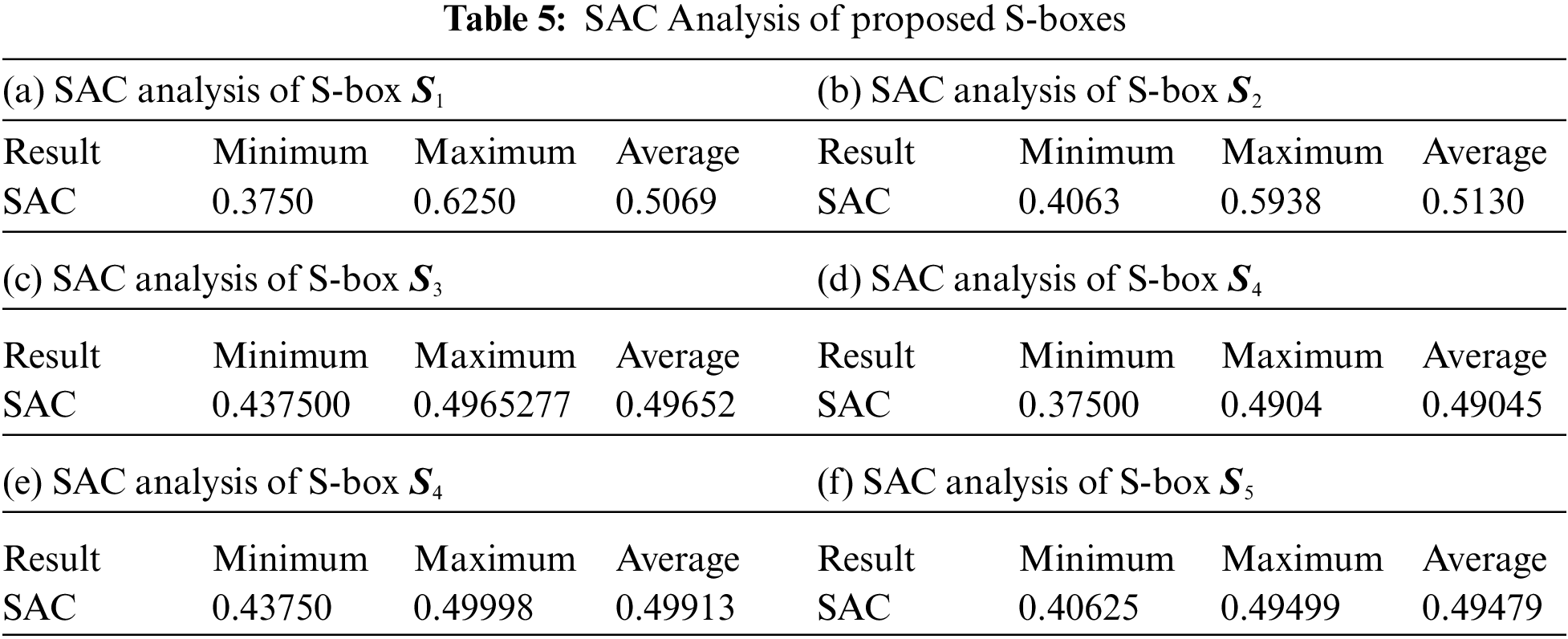
5.4 Linear Approximation Probability

Linear approximation probability (LP) analysis is used to investigate the maximum value of the imbalance of the scheme. Let Li and Lo be the input and the output mask respectively. According to the Mastui original definition of LP. The order of equal output bits selected by the mask Lo is equivalent to the equality of the input bits select by the mask  Li. Mathematically it can be written as follows:

LP=maxLi,Lo≠0|{i∈Z|i.Li=S(i).Lo}2n−12| (12)

where the order of the set of in input value is 2n. In Tables 6a–6f the values of maximum linear approximation probability of the S-boxes S2,S3  and S4  are same that is equal to 0.187500. Similarly, the resultant linear approximation value of the S-box S5 and S6 are same equal to 0.2187500. The result of S1 is equal to 0.25000 as shown in the tables. Since the probability results of all S-box are near zero therefor all S-boxes are secure against linear cryptanalysis.

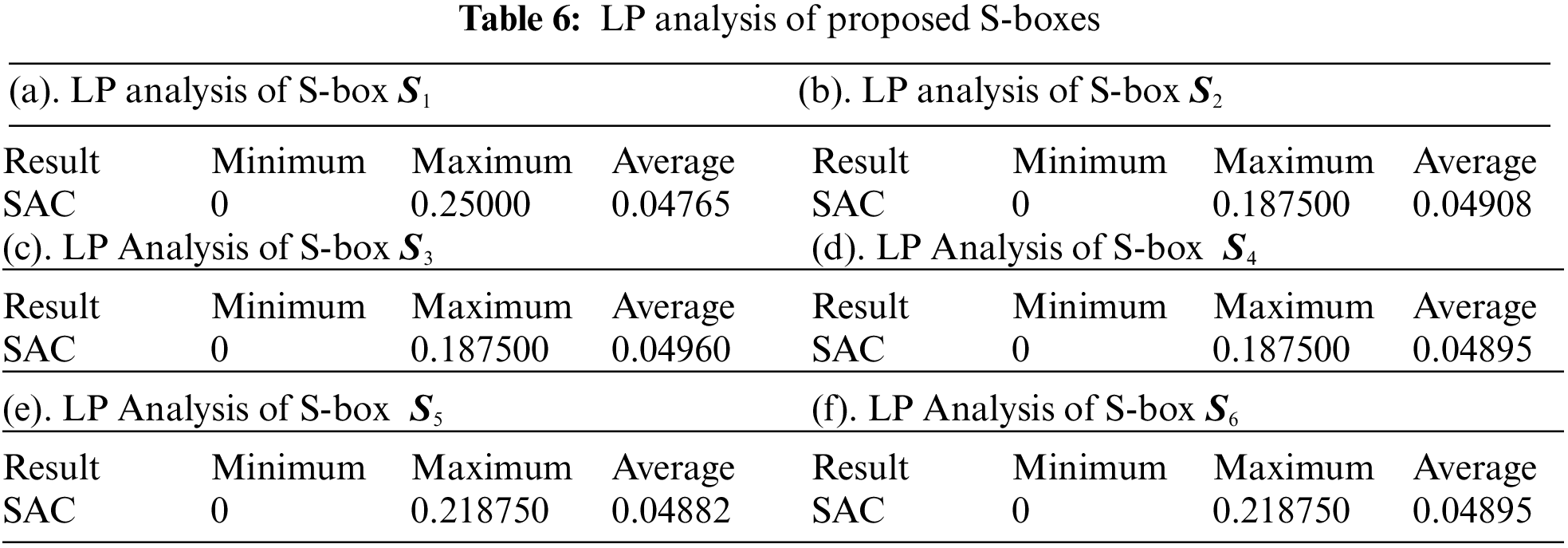
The performance analyses demonstrate that the results of all analyses of the proposed S-boxes are quite better. According to Theorem 2, the APA transformations preserve the cryptographic properties of the S-box, so we used the APA transformation to increase the number of good quality S-boxes and robust their algebraic complexity. In the next section, we deployed the APA transformation in the Feistel network to enhanced the security of the DES algorithm.

6  Modified DES Algorithm

DES is a sixteen-round cryptosystem, each round is the combination of bits permutation, expansion of bits, substitution step and XOR operation. The practice of the bit permutation step is to rearrange the order of the data to aim to produce diffusion in the ciphered data. The usage of an exclusive XOR operation is to mix the round key with the plain data. The S-box is used to produce confusion in the ciphered data. In these operations the S-box is the only nonlinear component in the DES, thus the modification in any other operation of the algorithm would not make them less successful. Thus, in this study, we modified the DES algorithm by fitting a good quality 6-bit S-box in the FF and keep the other operation unchanged. The modified DES attains the following obligatory criteria.

i.   Enhance the key space.

ii.   Highly nonlinear output functions; the maximum distance from the linear functions.

iii.   Successfully resist the linear and differential cryptanalysis.

iv.   High nonlinearity is attained; degrees of the output bit functions are increased.

v.   Efficient construction is easily implemented in hardware and software.

6.1 Generation of Key Dependent 6-Bits S-Boxes

The Key size of the modified DES is increased up to 12n+56-bits. The first 56-bit of the key that is used to derive the sixteen round keys  ki. There is no change in deriving round keys. The last 12n-bits are divided into 2n sub-blocks of 6-bits. Afterward, transforms the sub-blocks into the decimal form which is, of course, the elements of the Galois field  GF(26). The obtained elements are then used as parameters of APA transformation. For instance, let a1, a2,…,a2i be the obtained elements. Then the APA transformation can be written as follows:

S(w)=(a2i−1(…a7(a5(a3(a1(w−1)⊕ a2)⊕a4)⊕ a6)⊕ a8…)⊕a2i(13)

where w  and ai are the elements of the Galois field  GF(26) having a range between 0 and 63. Accordingly, for each different combination of ai≠0, one can obtain different S-boxes of the same cryptographic properties and algebraic complexity. The purpose of the APA transformation is: First, to increase the key space of the algorithm, increase the algebraic complexity of the S-box and generate a considerable number of key-dependent S-boxes having the same cryptographic properties. For the decryption, the same key generates the inverse of the S-box using the inverse of the transformation  S given in Eq. (13).

6.2 Modified DES Feistel Network

The Feistel network was introduced by Horst Feistel. In general, it is a transformation of a function into a permutation, which is called F function. The FF is the nonlinear, reversible and key-dependent mapping, that maps an input string of data into the output string of data. The Feistel network has been widely used in many block ciphers such as in DES, GOST [13], Khufu and Khafre [14], RC5 [15], FEAL [17], Blowfish [18] and LOKI [19]. In this study, the Feistel network used in the DES is of our specific interest. The Feistel network plays a vital role in the security of DES. The input string of F-function in a round i is the right half output Ri−1 of round  i−1. The detailed procedure of the modified F-function is as: the modified F-function initially uses the E expansion and expands the 32-bit input data into 48-bit blocks. Afterward, the F-function carries out the XORed operation and mixed the 48-bit with the round key  Ki. After the xor operation, the scheme divides the 48-bit block into eight 6-bit sub-blocks and substitutes each sub-block with the generated 6×6 S-box. The substitution method is: the first three most significant bits (MSB) selects the column of the S-box and the least significant three-bit (LSB) selects the row of the S-box. The output data are then again fed into eight different DES S-boxes. The detailed procedure of the modified Feistel network is demonstrated in Fig. 1.

Figure 1: Flow Chart of the Modified F-function

Example: Let I=45 be the input for the S-box S1. The decimal representation of 45 is 101101x. From the decimal representation, the MSB of the input I is 101x=5 indicates the fifth row of the S-box S1, the counts of the rows start from zero to 0. Similarly, the decimal representation of the input LSB is again 101x=5 indicates the fifth column of the S-box S1, the counts of the column start from zero 0. Thus, if the input I is substitute with the S-box given in Table 1, then the output of the S-box is S1(45)=53.

6.2.1 Key Compliment

The order of the key space of the DES algorithm is equal to 252. In that keyspace, half of the keys can be obtained by complimenting bitwise the other half keys. Since the DES cipher holds the following properties.

E(P,K)=C    ⇒  C¯=E(P¯,K¯)(14)

This property of the DES cipher makes the brute force attack simpler. The attacker has to check half possible keys to break the DES through a brute force attack. However, the S-boxes deployed in the modified DES are key-dependent, which does satisfy the following property.

S(P,k)=C   ⇏  C¯=S(P¯,k¯)(15)

Implies that

ME(P,K)=C    ⇏  C¯=ME(P¯,K¯)(16)

where ME denote the modified DES cipher, K denote the Modified DES key, S denote the substitution cipher of the scheme and k signify the subblock of the keys K that are used to generate the S-box S. Since the modified DES scheme does not hold the property given in Eq. (13). Hence, the attackers have to check all the keys in case of a brute force attack. We have examined the claim about the compliment property while using arbitrary key and plaintext on both DES and modified DES ciphers, the outcome is depicted in Table 7. From the table, it can be seen that the compliments of the DES cipher are equal to the ciphertext obtained as a result of using the key and plaintext compliment. However, the compliment of Modified DES ciphertext is not equal to the ciphertext given in the compliment row.

6.2.2 The Brute Force Attack

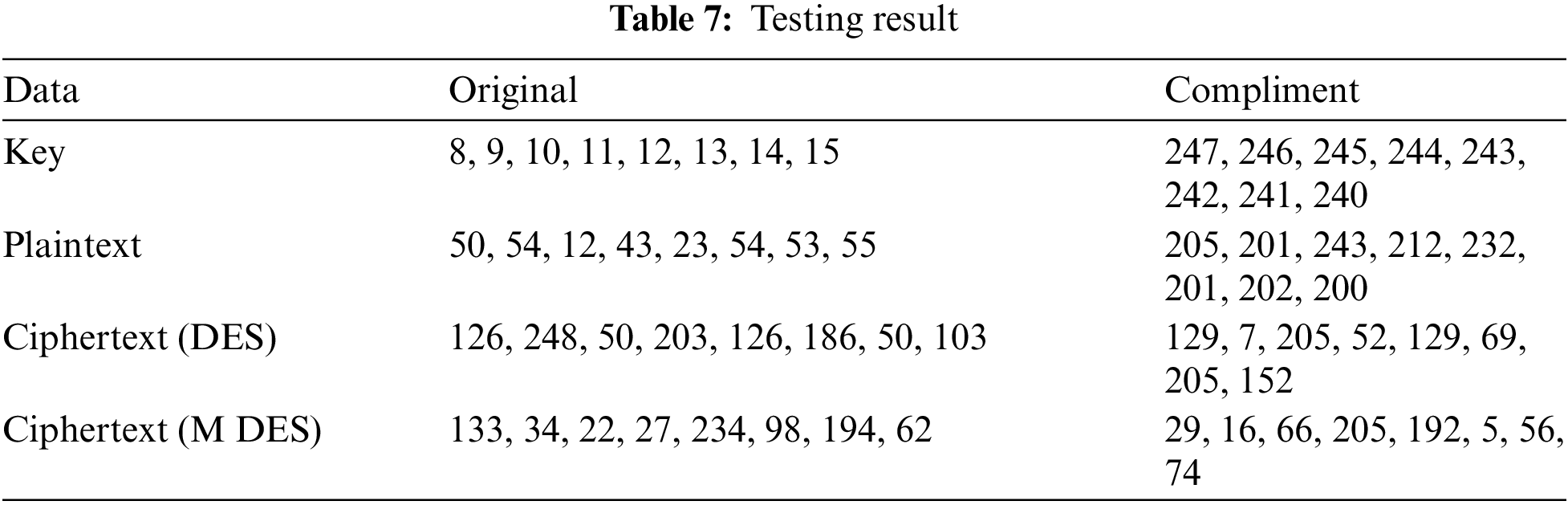
A brute force attack is a classical attack, that is used to check all the possible keys until the correct key is found. In this era, symmetric ciphers with 100-bits key or less are susceptible to brute force attack. The DES algorithm uses 56-bit keys and therefore, it was proved to be insecure against brute force attacks. The modified DES algorithm uses 12n+56-bits. Accordingly, for n≥5,  the algorithm will be able to resist the brute force attack. Since the modified DES algorithm is almost secure against linear and differential attacks, so the algorithm will be secure for  n=1, if all the round keys Ki are derived independently or by another complex method.

7  Conclusion

The DES algorithm was proved to be insecure against brute force attack, differential and linear cryptanalysis. The reason for breaking the algorithm was the small key space and weak S-box used in the substitution part of the algorithm. In this latter, we proposed an algorithm for the construction of 6×6 S-boxes based on Galois field  GF(26). The S-boxes are analyzed with different analyses and we found it secure against linear and differential attacks. Thus, we improved the DES algorithm by adding the construction method in the substitution part of the algorithm and strengthened the algorithm against brute force attack, linear and differential attacks.

Funding Statement: The authors extend their gratitude to the Deanship of Scientific Research at King Khalid University for funding this work through the research groups program under grant number R. G. P. 2/150/42.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. FIPS 46, “Data Encryption Standard,” in Federal Information Processing Standard, Washington D. C., USA: National Bureauof Standards, U.S. Department of Commerce, 1977. [Google Scholar]

2. W. Diffie and M. E. Hellman, “Special feature exhaustive cryptanalysis of the NBS data encryption standard,” Computer, vol. 10, no. 6, pp. 74–84, 1977. [Google Scholar]

3. M. E. Hellman, “A cryptanalytic time-memory trade-off,” IEEE Transactions on Information Theory, vol. 26, no. 4, pp. 401–406, 1980. [Google Scholar]

4. D. Chaum and J. H. Evertse, “Cryptanalysis of DES with a reduced number of rounds,” in Conf. on the Theory and Application of Cryptographic Techniques, Berlin, Heidelberg, Springer, 1985. [Google Scholar]

5. E. Biham and A. Shamir, “Differential cryptanalysis of DES-like cryptosystems,” Journal of CRYPTOLOGY, vol. 4, no. 1, pp. 3–72, 1991. [Google Scholar]

6. T. Shah and D. Shah, “Construction of highly nonlinear S-boxes for degree 8 primitive irreducible polynomials over ℤ 2,” Multimedia Tools and Applications, vol. 78, no. 2, pp. 1219–1234, 2019. [Google Scholar]

7. F. A. Khan, J.Ahmed, J. S. Khan, J. Ahmad,M. A. Khan et al., “A new technique for designing 8× 8 substitution box for image encryption applications,” in 2017 9th Computer Science and Electronic Engineering (CEEC), Colchester, UK: IEEE, pp. 7–12, 2017. [Google Scholar]

8. M. A. Khan, J. Ahmad, Q. Javaid and N. A. Saqib, “An efficient and secure partial image encryption for wireless multimedia sensor networks using discrete wavelet transform, chaotic maps and substitution box,” Journal of Modern Optics, vol. 64, no. 5, pp. 531–540, 2017. [Google Scholar]

9. A. Qayyum, J. Ahmad, W. Boulila, S. Rubaiee, A. Arshad et al., “Chaos-based confusion and diffusion of image pixels using dynamic substitution,” IEEE Access, vol. 8, pp. 140876–140895, 2020. [Google Scholar]

10. A. Arshad, S. Shaukat, A. Arshid, A. Eleyan, S. A. Shah et al., “Chaos theory and its application: An essential framework for image encryption,” Chaos Theory and Applications, vol. 2, no. 1, pp. 17–22, 2020. [Google Scholar]

11. K. Nyberg, “Differentially uniform mappings for cryptography,” in Workshop on the Theory and Application of Cryptographic Techniques, Springer, Berlin, Heidelberg, pp. 55–64, 1993. [Google Scholar]

12. L. Cui and Y. Cao, “A new S-box structure named affine-power-affine,” International Journal of Innovative Computing, Information and Control, vol. 3, no. 6, pp. 751–759, 2007. [Google Scholar]

13. I. A. Zabotin, G. P. Glazkov and V. B. Isaeva, “Cryptographic protection for information processing systems: Cryptographic transformation algorithm.” Government Standard of the USSR, Government Committee of the USSR for Standards, pp. 28147–28189, 1989. [Google Scholar]

14. R. C. Merkle, “A fast software one-way hash function,” Journal of Cryptology, vol. 3, no. 1, pp. 43–58, 1990. [Google Scholar]

15. R. L. Rivest, “The RC5 encryption algorithm,” in Int. Workshop on Fast Software Encryption, Springer, Berlin, Heidelberg, pp. 86–96, 1994. [Google Scholar]

16. P. P. Mar and K. M. Latt, “New analysis methods on strict avalanche criterion of S-boxes,” World Academy of Science, Engineering and Technology, vol. 2, no. 2, pp. 150–154, 2008. [Google Scholar]

17. A. Shimizu and S. Miyaguchi, “Fast data encipherment algorithm FEAL,” in Workshop on the Theory and Application of Cryptographic Techniques, Springer, Berlin, Heidelberg, pp. 267–278, 1988. [Google Scholar]

18. B. Schneier, “Other block ciphers,” in Applied Cryptography, Second Edition, New York, USA: John Wiley and Sons, pp. 319–325, 1996. [Google Scholar]

19. L. P. Brown, M. Kwan, J. Pieprzyk and J. Seberry, “Improving resistance to differential cryptanalysis and the redesign of LOKI,” in Int. Conf. on the Theory and Application of Cryptology, Springer, Berlin, Heidelberg, pp. 36–50, 1991. [Google Scholar]