A New Prediction System Based on Self-Growth Belief Rule Base with Interpretability Constraints

1  Introduction

As the premise of intelligent decision making, the prediction system can make predictions and judgments about the future development trend and level of things. With the further development of industrialization, a series of environmental pollution problems, such as hazy weather and sandstorms, have caused harm to human physical and mental health. Air quality prediction can scientifically guide people’s daily activities and behaviors and improve their quality of life, which is of great significance to environmental monitoring and governance [1,2].

In the current research, the methods of prediction systems can be roughly divided into the following three categories: physical knowledge methods [3], qualitative model methods [4], and data-driven methods [5]. The method based on physical knowledge is established through system principles and some engineering laws. Li et al. proposed a simplified multi-particle model for the remaining useful life prediction of lithium-ion batteries, which improves the computational efficiency [6]. Chaibi et al. proposed a quasi-steady-state thermal model (QSTM) to predict solar photovoltaic thermal performance and provided a physical modeling guideline for other researchers on solar photovoltaic thermal systems [7]. However, as the complexity of the actual system increases, the system will have nonlinearity and uncertainty, so the difficulty of accurately establishing a prediction model increases. Qualitative-based methods are used through expert knowledge and observation data. Tan et al. proposed a model of Mamdani-type fuzzy inference system to predict the tensile properties of cast alloys, which has high accuracy and good stability [8]. However, now that expert knowledge can be uncertain, the model’s accuracy will be affected. The data-driven model is built by training on a large amount of data. Li et al. proposed a method combining a numerical algorithm and support vector machine (SVM) to predict the friction torque of helical gears, and this method has a good prediction effect [9]. Wang et al. proposed a model combining the chi-square test (CT) and long-term short-term memory (LSTM) network to predict the air quality index, which has good accuracy compared with other machine models [10]. Phruksahhiran et al. proposed an ensemble forecasting method for geographically weighted predictors that incorporates additional predictor variables [11]. However, this method belongs to the black-box model. Because of the invisible internal structure of the model, the prediction results cannot be reasonably interpreted.

In a prediction system for practical engineering, there are two common problems. First, the problem of uncertain information coexistence cannot be effectively handled, such as coexisting fuzzy information and ignorance, reducing the model accuracy. Second, the data-driven model is built on a large amount of data; because the modeling process is not transparent, the rationality of the output results is difficult to convince. The belief rule base (BRB) can effectively solve the above problems [12–14]. It uses a general rule-based reasoning method and has the ability of nonlinear modeling [15], which can effectively address the problem of the coexistence of uncertain information. Moreover, BRB has a transparent and reliable inference engine based on evidence reasoning (ER) algorithms. Thus, BRB is suitable for many fields, such as medical decisions [16,17] and health-state assessments [18].

However, three problems that exist in the BRB model need to be solved. First, expert knowledge can provide a roughly correct direction in the prediction system. However, in current research [19–21], many methods do not fully utilize expert knowledge. Second, many BRB models were optimized for higher accuracy, but interpretability was not considered. This leads to the breaking of interpretable properties such as BRB rule consistency and transparent reasoning. For example, Zhou et al. proposed that building an interpretable model was the future development direction of BRB [22]. Rule-based modeling methods can extract rules from expert knowledge, which leads to models with strong interpretability but low accuracy. Rule-based modeling methods can also learn rules from observational data, which leads to models with good accuracy but poor interpretability. This shows that models with high accuracy and interpretability are incompatible [14]. Hence, how to improve accuracy while maintaining interpretability also needs handling. Third, BRB is a new intelligent expert system, and it has the advantages of expert systems and data-driven models [22]. Thus, maximizing the cooperation between the two characteristics is a problem. Thus, the self-growth BRB model with interpretability constraints (SBRB-I) is proposed. The SBRB-I model flexibly converts expert knowledge into parameters of belief rules and brings expert knowledge into the optimization process of the model. The SBRB-I model adopts a self-growth learning strategy optimization method with interpretability constraints that maintains the balance between the accuracy and interpretability of the SBRB-I model. Moreover, the SBRB-I model can use expert knowledge to guide data mining, and the knowledge found in data mining becomes supplementary knowledge of the expert system, so the advantages of BRB are brought into full play.

The contributions of this paper are as follows: 1) A new self-growth BRB model with interpretability constraints is proposed. 2) To ensure the interpretability of the SBRB-I model, an optimization algorithm with interpretability constraints is proposed.

The structure of the rest of the paper is as follows. In Section 2, the problems of the prediction model are formulated, and a new prediction model SBRB-I is introduced. The interpretability of the SBRB-I model, including inference interpretability and optimization interpretability, is introduced in Section 3. In Section 4, the reasoning process and optimization process of the SBRB-I model are given. Then, a case study is implemented to verify the effectiveness of the proposed model in Section 5. This paper is concluded in Section 6.

2  Problem Description

2.1 Problems with the Prediction System

In prediction systems, model construction and optimization have a great impact on prediction accuracy and interpretability. In this section, the problem of the prediction system is formulated.

Problem 1: In engineering practice, it is necessary to build a model that improves accuracy while ensuring interpretability. The model should have the following characteristics: 1). It can deal with uncertain factors in complex environments to ensure the model’s accuracy. The actual system is affected by uncertain factors in a complex environment, and the accuracy of the model will be reduced. 2). Based on the data-driven black-box model, the operation mechanism of the model is not considered, and the internal structure of the model is not visible. Thus, the first problem to be solved is how to ensure the structural interpretability of the model.

y=f(x,w)(1)

where y is the output result of the model, w is the parameter set of the prediction model, and x is the input of the model.

Problem 2: Build an interpretable optimization process. In prediction systems, the usual optimization algorithms do not consider the interpretability of the BRB model. As any optimization algorithm is random, the interpretability of the model has been destroyed. Thus, the second problem is how to design efficient interpretability constraints to ensure the interpretability of the model.

w=g(y,x,O,X)(2)

where O is the interpretability constraint and X is the parameter of the optimization algorithm.

2.2 The SBRB-I Model

In a prediction model, the belief rule base is composed of a set of belief rules. The kth belief rule is as follows:

IF x1 is A1k∧x2 is A2k∧⋯∧xTk is ATkk,THEN y is{(D1,β1,k),(D2,β2,k),…,(DN,βN,k)},(∑n=1N⁡βn,k≤1),with rule weight θk,k∈{1,2,…,L}.and attribute weight δ1,δ2,…,δi,i∈{1,2,…,Tk}.(3)

where X1,X2,…,XTk is the antecedent attribute of the kth rule, A1k,A2k,…,ATkk is the reference value for the antecedent attribute X1,X2,…,XTk. Tk is the number of attributes in the kth rule. βnk is the belief of the result Dn. θk is the weight of the kth belief rule. δ1,δ2,…,δi is the weight of the ith attribute. L is the number of rules. The overall structure of the new prediction system based on SBRB-I is shown in Fig. 1.

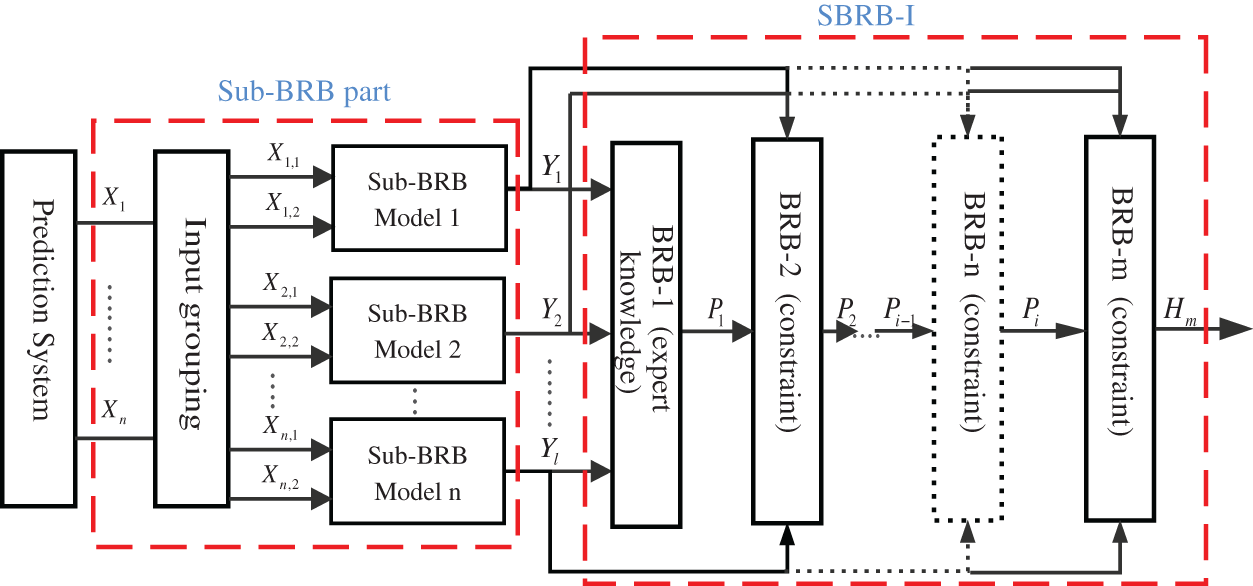
Figure 1: The overall structure of the prediction system

3  The Interpretability of SBRB-I

In Section 3.1, the interpretability of the reasoning process of the SBRB-I model is described. Then, in Section 3.2, the optimized interpretability of the SBRB-I model is described.

3.1 The Interpretability of Reasoning

In the SBRB-I model, the ER algorithm is used as the inference engine; it is a reasoning calculation process based on evidence fusion, and the interpretability is reflected in the causal relationship between the processes. In building the model, the interpretability of the reasoning process refers to sufficient and clear explanations when dealing with uncertain information [23]. The ER algorithm has many clear and explicit semantics, which can fully describe and transform various uncertain information. In the running of the model, the weighted belief distribution of evidence is calculated by the orthogonal sum operator. Moreover, the ER algorithm ensures the traceability of the evidence combination process through strict probabilistic reasoning, and the reasoning result ensures interpretability in the form of a belief distribution [24]. Thus, the ER algorithm has received attention due to its interpretability characteristics, such as transparency, reliability, and traceability of output results [25,26].

3.2 The Interpretability of Optimization

In the current study, Cao et al. established eight general interpretability criteria for the BRB in Fig. 2 [14]. Therefore, this offers a theoretical foundation for constructing the SBRB-I model. The interpretability constraints of optimization are as follows:

Figure 2: General interpretability BRB criteria

Criteria 8. The optimized belief rules satisfy the actual system.

Belief rules can give a clear input-output relationship of the prediction system, and it is the main interpretable aspect of BRB [25]. Expert knowledge can be transformed into parameters and incorporated into the model through belief rules, which allows the model to generate reasonable and convincing predictions. However, because any optimization algorithm is random, the model produces many incorrect rules. For example, the 28th rule of pipeline leak detection [27] is shown in Table 1. When the “negative very small (NVS) AND positive large (PL)” condition is reached, the belief degrees of “leakage size is zero” and “leakage size is very high” are 0.53 and 0.33, respectively. This belief distribution is impractical and unreasonable. A reasonable belief distribution does not lead to a high degree of confidence in contradictory results at the same time. Therefore, interpretability constraints should be added to the model optimization process.

Rulek∼Ok (k=1,2,…,L)(4)

Ok∈{{β1≤β2≤⋯≤βn}or {β1≥β2≥⋯≥βn}or {β1≤⋯≤max(β1,β2,…βn)≥⋯≥βn}}(5)

where Ok is the constraint on the belief distribution in the kth rule. In different prediction systems, interpretability constraints should conform to the system mechanism and general knowledge.

In recent years, BRB has been widely used due to its interpretability [25,26]. However, BRB still has two problems in practical prediction systems. Expert knowledge is an important source of BRB interpretability. Moreover, expert knowledge is helpful to establish the model’s structure and to guide the direction of model optimization [20]. Thus, the first guideline is how to effectively use expert knowledge.

Guidelines 1: Expert knowledge is used to determine the optimal feasible region.

For interpretable BRB models, the feasible region of optimization is a local judgment based on experts [25]. Thus, the initial population in the optimization algorithm needs to be adjusted, as shown in Fig. 3. In other words, the search domain of the optimization algorithm should be reduced to form a solution space centered on expert knowledge. Thus, the interpretability constraints are as follows:

Xi→Ek(i=1,2,…,n)(6)

where Xi is the current solution vector, → is the operation of moving, Ek is the solution vector of expert knowledge, and n is the number of solution vectors used for optimization. The adjusted initial population can carry part of the available information from expert knowledge, making the optimized results more convincing and interpretable.

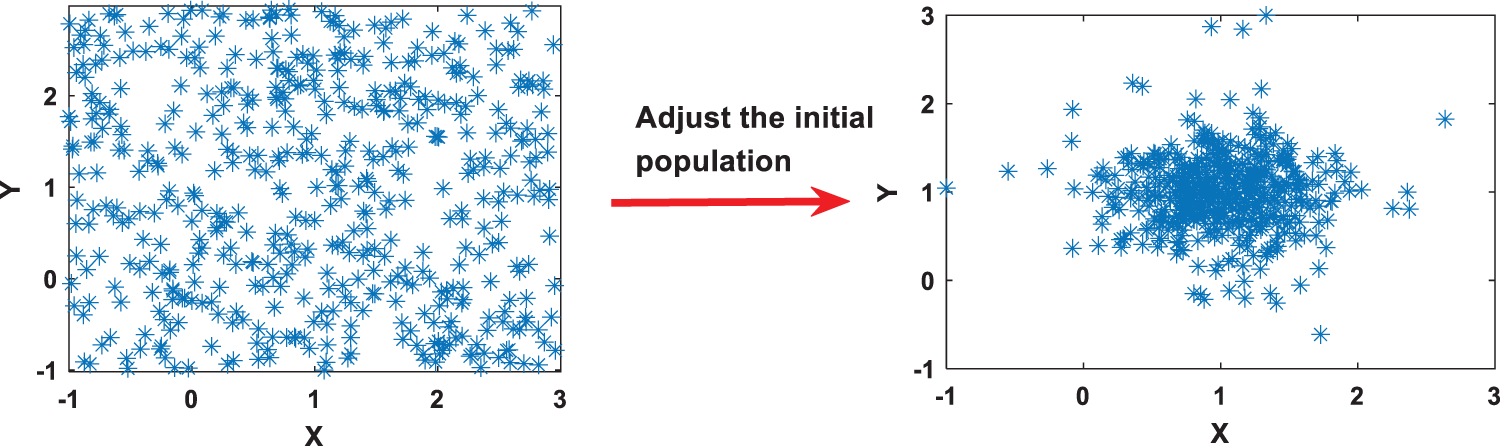
Figure 3: Adjustment of the initial population

BRB is a new intelligent expert system that combines an expert system and a data-driven model. However, because of the complexity of the prediction system, experts face difficulties in developing a deep understanding of the system. Moreover, BRB is typically optimized as a data-driven model, ignoring the characteristics of expert systems [22]. Thus, the second guideline is how to exploit the individual capabilities of BRB’s expert system and data-driven model.

Guidelines 2: A new self-growth learning strategy.

As shown in Fig. 4, a self-growth learning strategy is used that combines any available expert knowledge about the optimal solution, which enables the algorithm to quickly jump to the optimal position [19,21]. Moreover, expert knowledge can guide the direction of population optimization during the optimization process, which helps quickly improve the convergence of the objective function [20]. There are two types of expert knowledge: 1. Expert knowledge accumulated through the analysis of practical systems by domain experts. 2. Expert knowledge optimized by correlation functions [20]. Thus, expert knowledge and knowledge discovered by data mining can cooperate to maximize their individual capabilities: the knowledge obtained through data-driven analysis is used as the supplementary source of the expert system, and expert knowledge of the expert system can guide the optimization direction of the model [28,29]. Moreover, expert knowledge is an important source of interpretable BRBs [14]. Any optimization algorithm has randomness, and the self-growth learning strategy effectively utilizes expert knowledge for optimization, which makes the model optimization process more convincing and interpretable.

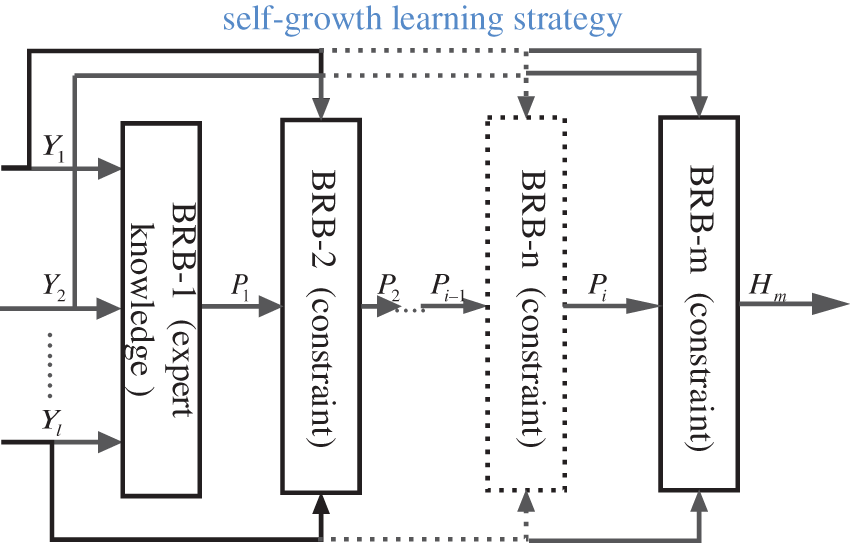
Figure 4: Self-growth learning strategy

In this strategy, adding constraints can effectively prevent the parameters from being overoptimized.

T1≤c1 or T2≥c2 or ⋯ or Tn≥cn(7)

where T1,T2,…,Tn is a series of requirements to stop self-growth, and c1,c2,…cn is the threshold given by the actual system.

The interpretability of the SBRB-I model is as follows [12,13]: 1. By using the method of modeling based on IF-THEN rules, the structure and expression of the model are clear and understandable. 2. Have a transparent and reliable reasoning process. The logic and understanding of the ER algorithm are in line with the human thinking process, so it can be more accepted by humans. 3. The model can be integrated into the system mechanism or expert knowledge of the actual system, which will help humans better understand the model. 4. Optimization with interpretability constraints ensures that interpretability is not destroyed during the optimization process. 5. A self-growth process guided by expert knowledge can make the optimized solution more trustworthy.

4  The Prediction System Model Based on SBRB-I

4.1 The Reasoning Process of the Model

In the SBRB-I prediction model, the ER algorithm is used as the inference engine. As shown in Fig. 5, the reasoning process mainly consists of the following four steps:

Step 1: Input transformation. Quantitative and qualitative information can be transformed into belief distributions [20] as follows:

S(xi)={(Ai,j,ai,j),i=1,…,M;j=1,…,Ji}(8)

where Ai,j is the jth parameter value corresponding to the ith input and ai,j is the matching degree of Ai,j.

Step 2: The weights are activated, and the activation weight of the rule is as follows:

wk=θk∏i=1T⁡(aik)δi¯/(∑l=1L⁡θl∏i=1T⁡(aik)δi¯),δi¯=δi/(maxi=1,…,Tk⁡{δi})(9)

where θk∈[0,1]. δi¯ is the normalized ith previous attribute weight. δi¯ is the normalized ith antecedent attribute weight.

Step 3: The final belief is generated by analyzing ER as follows:

βj=[∏k=1L(ωkβj,k+λj,ik)−∏k=1L(λj,ik)][∑j=1N∏k=1L(ωkβj,k+λj,ik)−(N−1)∏k=1L(λj,ik)]−[∏k=1L(1−ωk)]′(10)

λj,ik=1−ωk∑i=1N⁡βi,k(11)

Step 4: Finally, all beliefs were updated. The final belief distribution is as follows:

S(A∗)={(Dj,βj);j=1,…,N}(12)

where A∗ is the input vector. The utility of the output can be expressed as follows:

u(S(A∗))=∑j=1N⁡u(Dj)βj(13)

where u(Dj) is the utility of the result.

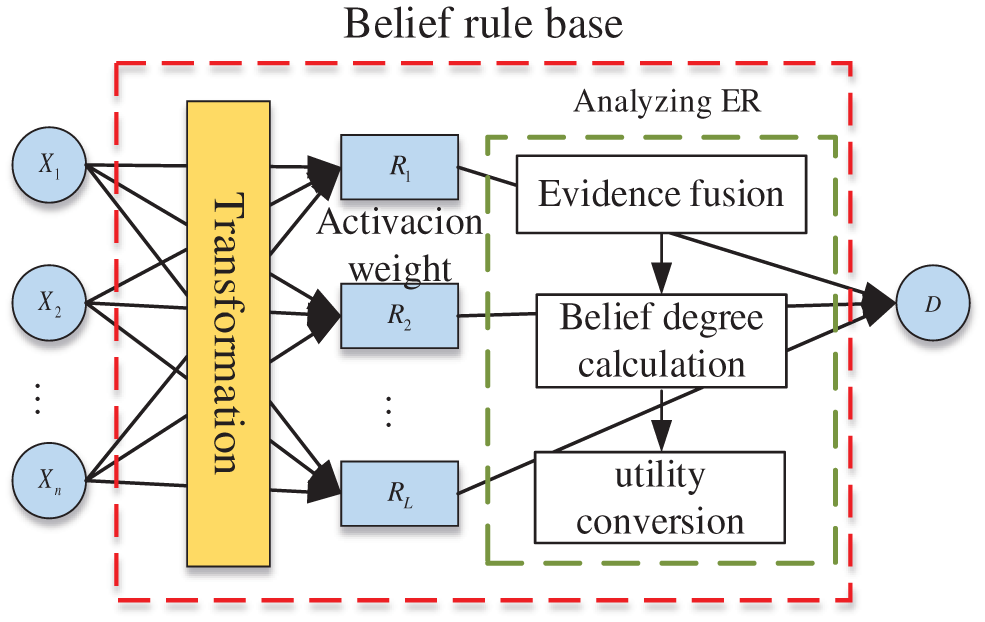
Figure 5: The reasoning process of the BRB

4.2 Optimization Process of the Model

In the current research, BRB is optimized by many algorithms, including the projection covariance matrix adaptation evolution strategy (P-CMA-ES) [14,23] and the particle swarm optimization algorithm (PSO) [12,22]. The BRB is optimized by the Whale Optimization Algorithm (WOA) algorithm in this paper [30]. The WOA is a new natural heuristic metaheuristic optimization algorithm, and this algorithm has the following advantages: 1) Fewer parameters and is easy to understand. 2) Fast optimization speed. 3) Local optima can be avoided. 4) It can be widely used in various fields.

To obtain higher accuracy, a self-growth learning strategy is proposed. At the same time, interpreted constraints are designed. Fig. 6 shows the model optimization process. Modifications to the original algorithm are marked in green, and the specific steps are as follows:

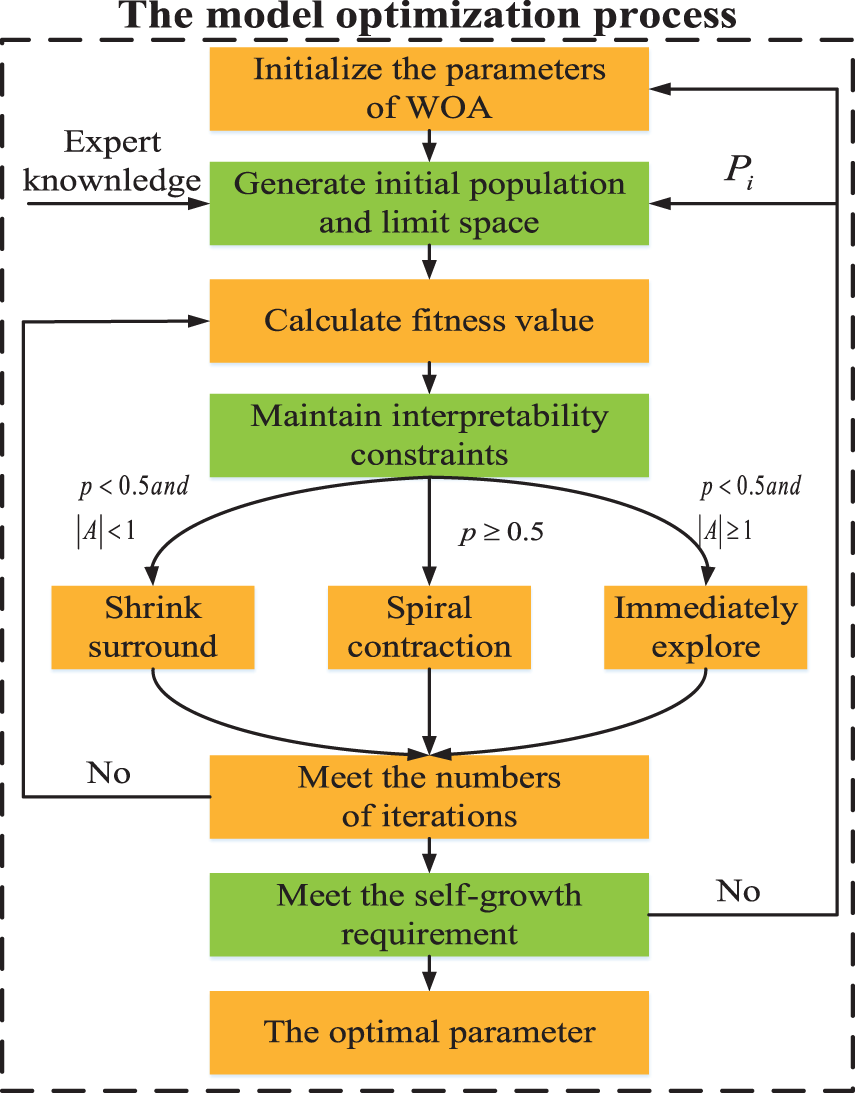
Figure 6: The modified WOA optimization algorithm

Step 1: (Initial operation): Initialize the population size of whales N, the number of iterations t, and the search space is d dimension.

Step 2: (Sampling operation): Each whale was randomly sprinkled. The position of the ith whale is as follows:

Xi=rand⋅(ub−lb)+lb(14)

The value range of Xi is [lb,ub], rand is a random number of [0,1]. lb is the minimum value of the parameter boundary, ub is the maximum value of the parameter boundary.

To exploit the individual capabilities of BRB expert systems and data-driven models, expert knowledge is integrated into the initial population of algorithms, which increases the convergence speed of the algorithm [19,20]. The optimized knowledge is continuously put into the initial population, which is the process of self-growth as follows:

{Ek=expert→  if  i=1Xn=Pi  if  i≠1(15)

where n∈[1,N], Ek is the solution vector of expert knowledge. expert→ is expert knowledge. Xn is the nth whale that has undergone the ith self-growth. Pi is the expert knowledge after the ith self-growth optimization.

Then, to make the initial population carry more expert knowledge information, whales move closer to whales with expert knowledge, forming a solution space centered on expert knowledge.

Xi→Ek(i=1,2,…,n)(16)

Specific operation: Turn off the random searchability of the WOA algorithm. Only spiral contraction and contraction surrounding mechanisms are retained. The formulas are Eqs. (19)–(22) and (25).

Remark: After the limit operation, all vector parameters of the WOA algorithm are restored to the original value.

Step 3: (Calculate fitness value): The mean square error (MSE) is used as the fitness function.

min{ψ(θ,δ,β)}s.t. 0≤θ≤1,0≤δ≤1,0≤β≤1,∑n=1N⁡βn,k≤1(17)

where ψ(θ,δ,β) is the error value between the real value and outputs.

Step 4: (Constraint operation): Adjust the belief distribution of the ith solution vector, which cannot meet the interpreted belief distribution.

Rulek∼Ok(k=1,2,…,L)(18)

Step 5: (Move operation):

When p<0.5 and |A|<1, whales can find their prey and surround it. Through the best search agent, centered on the optimal whale individual, all whales surround it as follows:

X→(t+1)=X∗→(t)−A→⋅|C→⋅X∗→(t)−X→(t)|(19)

A→=2a→⋅r→1−a→(20)

C→=2⋅r→2(21)

a→=2−2t/tmax(22)

where r→1, r→2, p is a random number of [0,1]. X→(t) is the current solution vector, X∗→(t) is the location of the prey, A→⋅|C→⋅X∗→(t)−X→(t)| is the enclosing step, a→ is the convergence factor, which decreases linearly from 2 to 0 with the increase of the number of iterations. A→, C→ is the coefficient vector. t is the current number of iterations, and tmax is the maximum number of iterations.

When p<0.5 and |A|≥1, whales can look for prey at random by randomly searching for agents as follows:

X→(t+1)=X→rand−A→⋅D→(23)

D→=|C→⋅X→rand−X→(t)|(24)

where X→rand is the randomly selected whale position vector.

When p≥0.5, using the bubble net predation of whales, whale prey in a spiral contraction as follows:

X→(t+1)=D′→⋅ebl⋅cos(2πl)+X∗→(t)(25)

D′→=|X∗→(t)−X→(t)| is the distance between the whale and prey. b is the constant of the number helix shape. l is a random number of [0,1].

Step 6: (Meet the requirements): Until the mth self-growth meets one of the requirements, the self-growth stops as follows:

Fm=Hm−Hm−1(26)

(Fm≤e)or(Q≥Qmax)(27)

where Fm is the training error between the mth self-growth and the m−1th self-growth, e is the threshold for stopping self-growth, Q is the current total number of self-growth iterations, and Qmax is the largest self-growth iteration.

5  Case Study

An example of predicting the air quality index (AQI) is given to demonstrate the effectiveness of the proposed model. The experimental data set is from China’s air quality online monitoring and analysis platform from January 2020 to October 2020 in Beijing. Serious air pollution endangers people’s physical and mental health and has become a common threat to the world. Predicting air quality in an interpretable way can help guide future environmental governance. Therefore, the establishment of an accurate and reliable air quality prediction system is of great significance. Thus, SBRB-I is a good choice for predicting air quality.

5.1 Establishment of the Initial SBRB-I Model

5.1.1 Input Grouping

In the actual air quality prediction system, the AQI is based on air quality standards and the impact of various pollution factors on the ecological environment, which comprehensively reflects the pollution degree of PM2.5,NO2,CO,O3,SO2,PM10. To build the initial SBRB-I model, first, these attributes are divided into groups as follows: PM2.5,PM10 is the particle size index of particulate matter. The comprehensive reaction affects the atmospheric transparency and the degree of injury to the human respiratory tract. SO2,NO2 can form acid rain and damage the environment, affecting the hair coloring rate of respiratory tract infection. O3,CO are toxic gases. It comprehensively reflects the toxic content in the air. The initial establishment model is shown in Fig. 7.

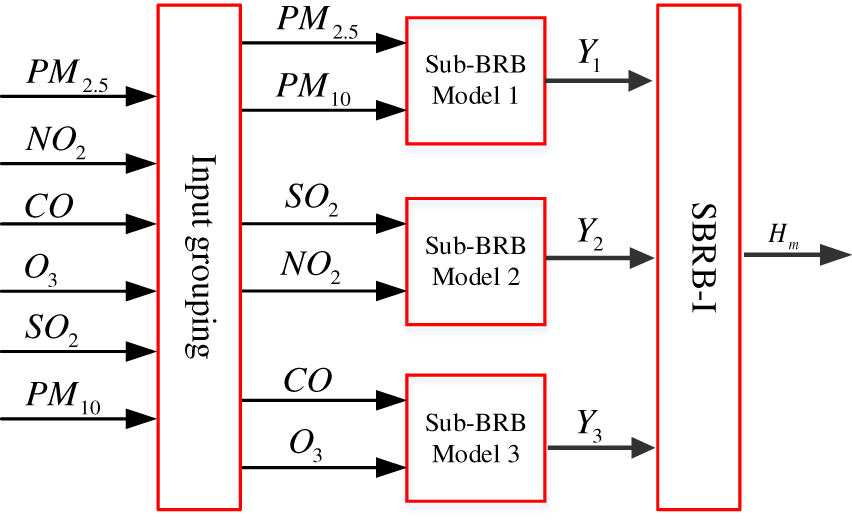
Figure 7: The initial establishment model

5.1.2 Select Reference Point

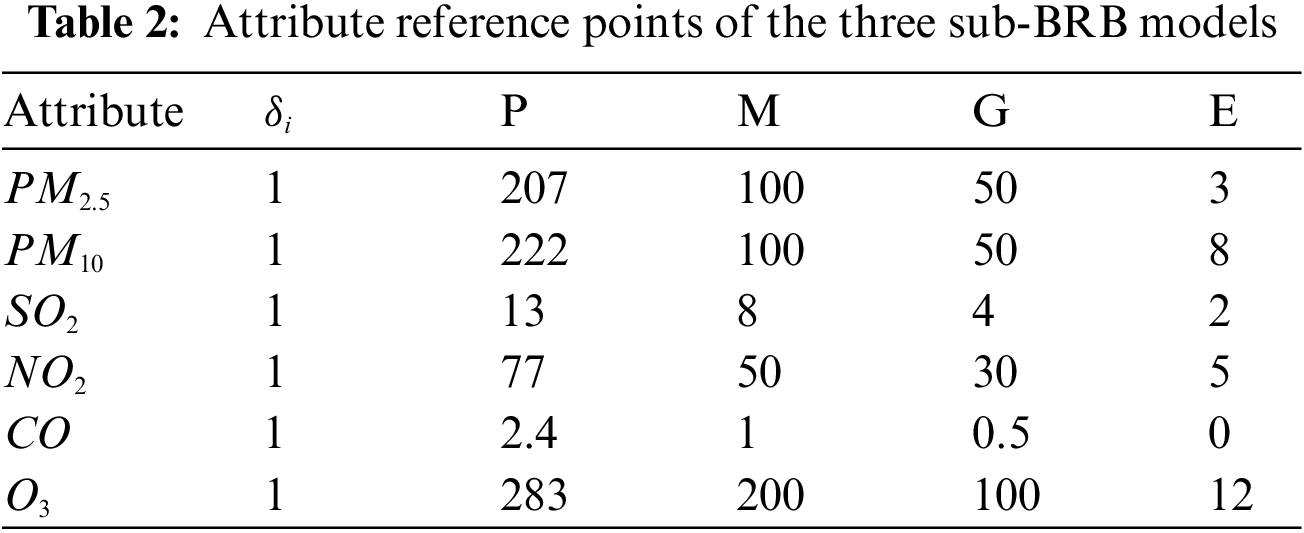
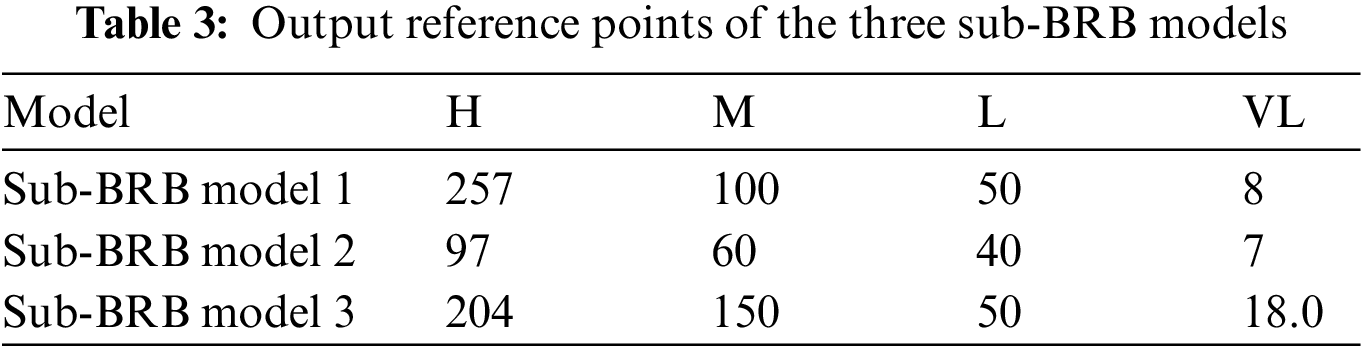
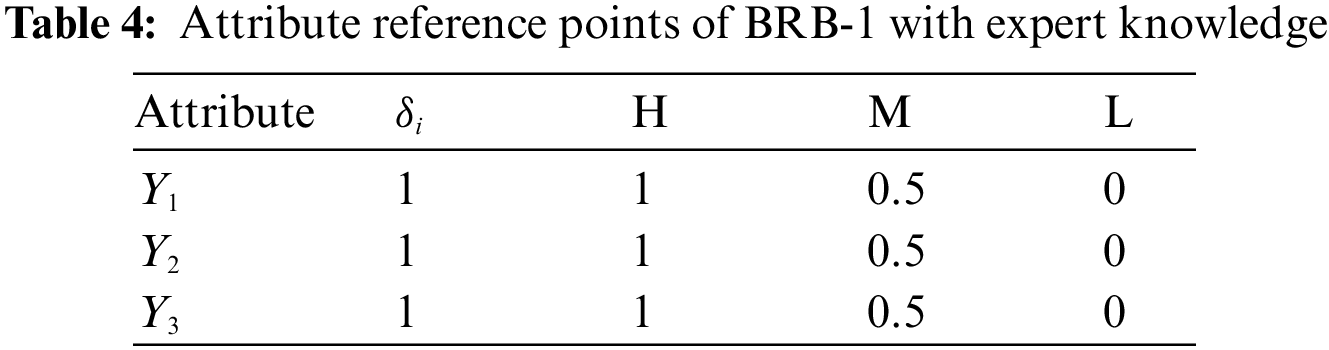
Second, these three groups are put into the sub-BRB model. Expert knowledge can be obtained through mechanism analysis of actual systems and long-term practice accumulation [14]. Therefore, the initial model constructed by expert knowledge has strong interpretability and is easily understood by users [17]. Moreover, the selection of the model reference value is determined by analyzing the actual system and using the method of statistical analysis of data. Thus, in the actual air quality prediction system, each attribute is described by four semantic values, that is, “excellent” (E), “good” (G), “medium” (M), and “poor” (P). The reference values are given in Table 2. In life, four reference points are used to describe the degree of air pollution, that is, “high” (represented by H), “medium” (represented by M), “low” (represented by L) and “very low” (represented by VL). The referential values are given in Table 3, the sub-BRB model is optimized by a self-growth learning strategy, so Y1,Y2,Y3 are generated, and then Y1,Y2,Y3 are normalized.

Third, Y1,Y2,Y3 is taken as input to SBRB-I. In Table 4, the reference values of the attributes are demonstrated. Moreover, five reference values are used to express the quality of the air quality index, that is, “Serious” (S), “Bad” (B), “Medium” (M), “Good” (G), and “Excellent” (E). The referential values are shown in Table 5.

5.2 Analysis of Experimental Results

The initial parameters of the WOA are as follows: population size N is 20, the number of iterations t for each self-growth is 50, 25 is used to limit the solution space, and 25 is used for optimization. The search space d is 165-dimensional. The maximum number of self-growth iterations Qmax is 3000. The threshold e for self-growth to be stopped is 1−6.

As shown in Fig. 8, the MSE decreases with the increase in the number of self-growths. When reaching the 42nd layer, point A is the best point for self-growth, and the MSE value is 0.0046. However, the MSE of the initial SBRB-I model constructed with expert knowledge was 0.0117. According to the experimental results, the accuracy of the model is improved by 60.68%. The comparison between the prediction results of the SBRB-I model and the real value is shown in Fig. 9. To prove whether the selection of the threshold is effective, self-growth is continued. As seen from part C, the MSE value gradually increases, and overfitting occurs at the position after self-growth stops. The effective selection of threshold e can prevent the overoptimization of parameters and fitting.

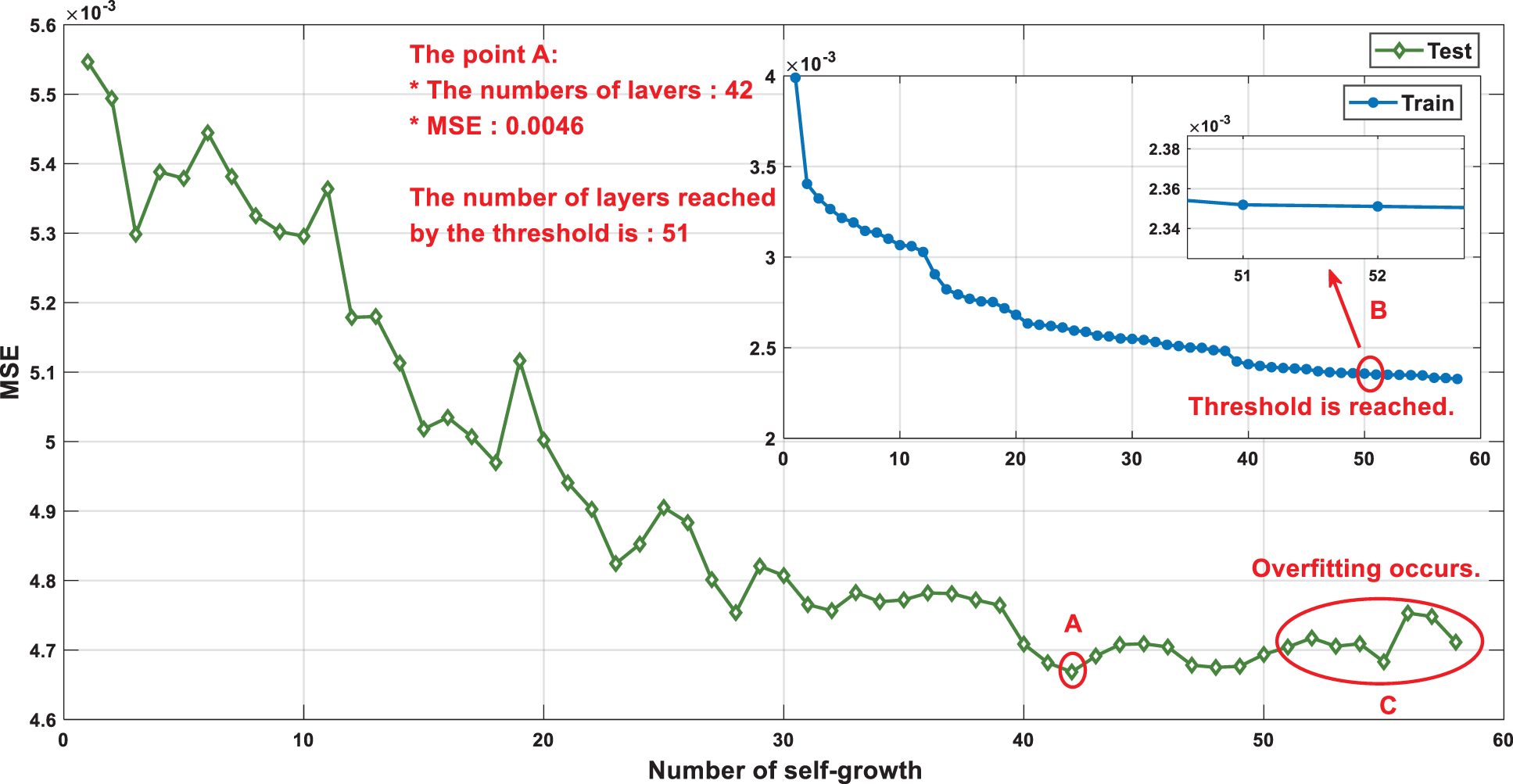
Figure 8: Optimization process of the SBRB-I(42) model

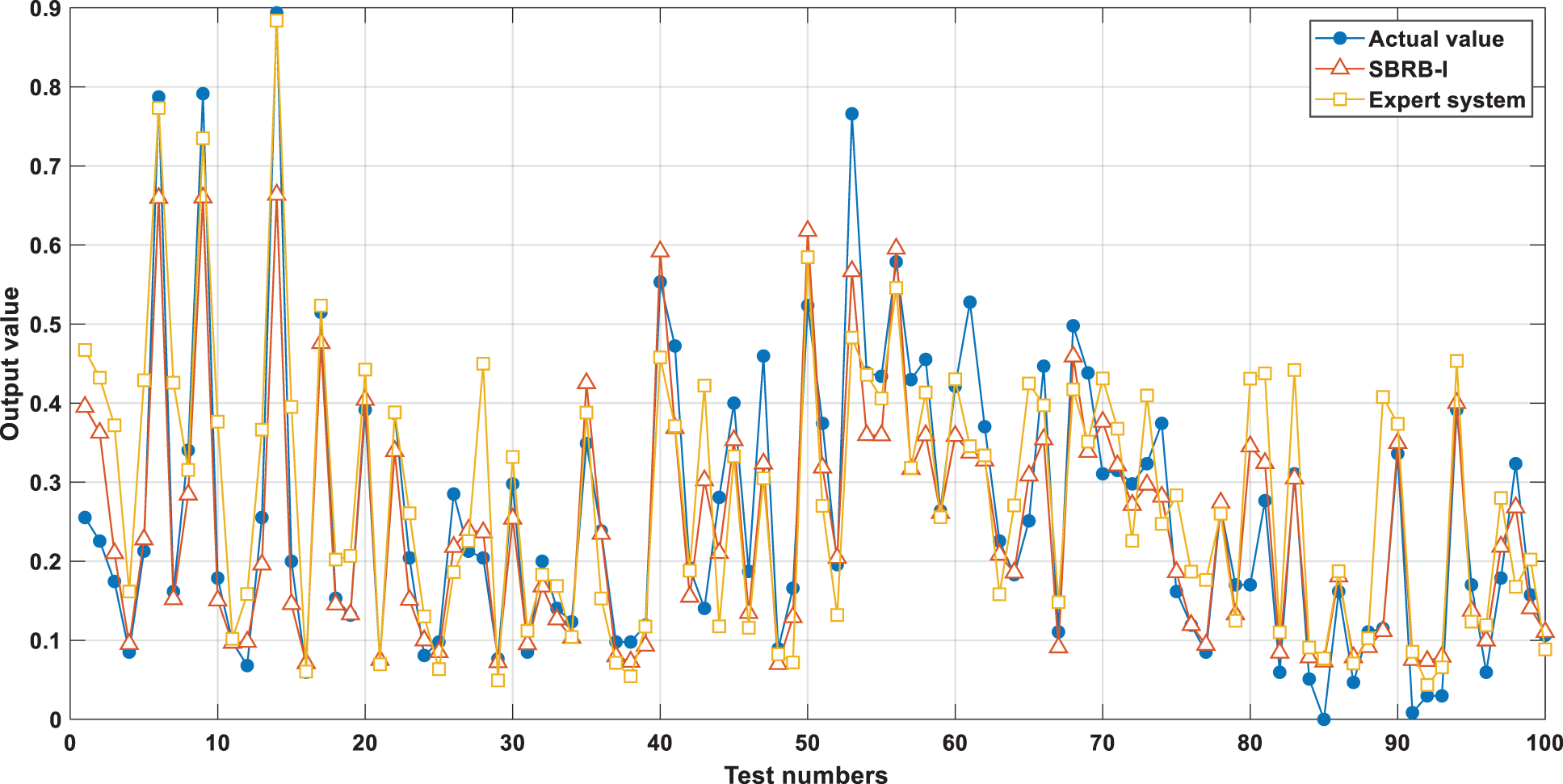
Figure 9: Output result comparison

The Euclidean distance shows the similarity between two vectors, as shown in Fig. 10 [28]. Euclidean distance represents the linear distance between two points, which can well describe the similarity between two vectors, while other distance measurement methods cannot measure the linear distance well [31]. It can be concluded that the optimization process of the SBRB-I(42) model is an optimization process close to expert knowledge. This further realizes that the interpretability SBRB-I(42) model of the optimization process is a feasible region based on the local judgment of expert knowledge [14]. However, the WOA-BRB model does not have such capability. Moreover, this proves that the SBRB-I(42) model can utilize expert knowledge to guide the optimization direction of the data-driven model. The optimized solution vector maintains a high similarity with expert knowledge, which can retain more characteristics of expert knowledge information, making the optimized model more interpretable.

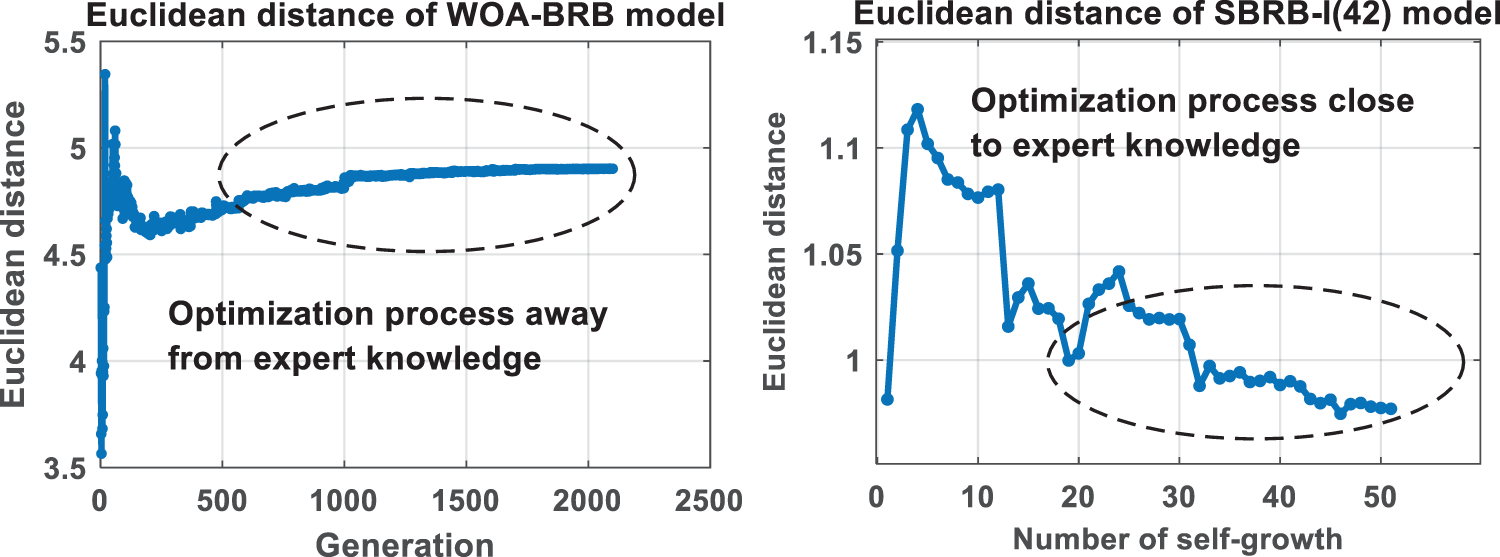
Figure 10: Euclidean distance variation

As shown in Fig. 11, the SBRB-I(42) model has a better fit with expert knowledge, and it can better retain the characteristics of expert knowledge information. For example, in Rules 4, 7, 10, 11 and 15, the SBRB-I model can better represent the behavior of the actual system. Because the optimized knowledge is highly similar to the initial expert knowledge, SBRB-I(41) realizes that the knowledge of data-driven model mining can be a supplementary source for expert systems. That is, the SBRB-I(42) model realizes cooperation between the BRB expert system and the data-driven model. However, the WOA-BRB model generates many belief rules that are inconsistent with common sense.

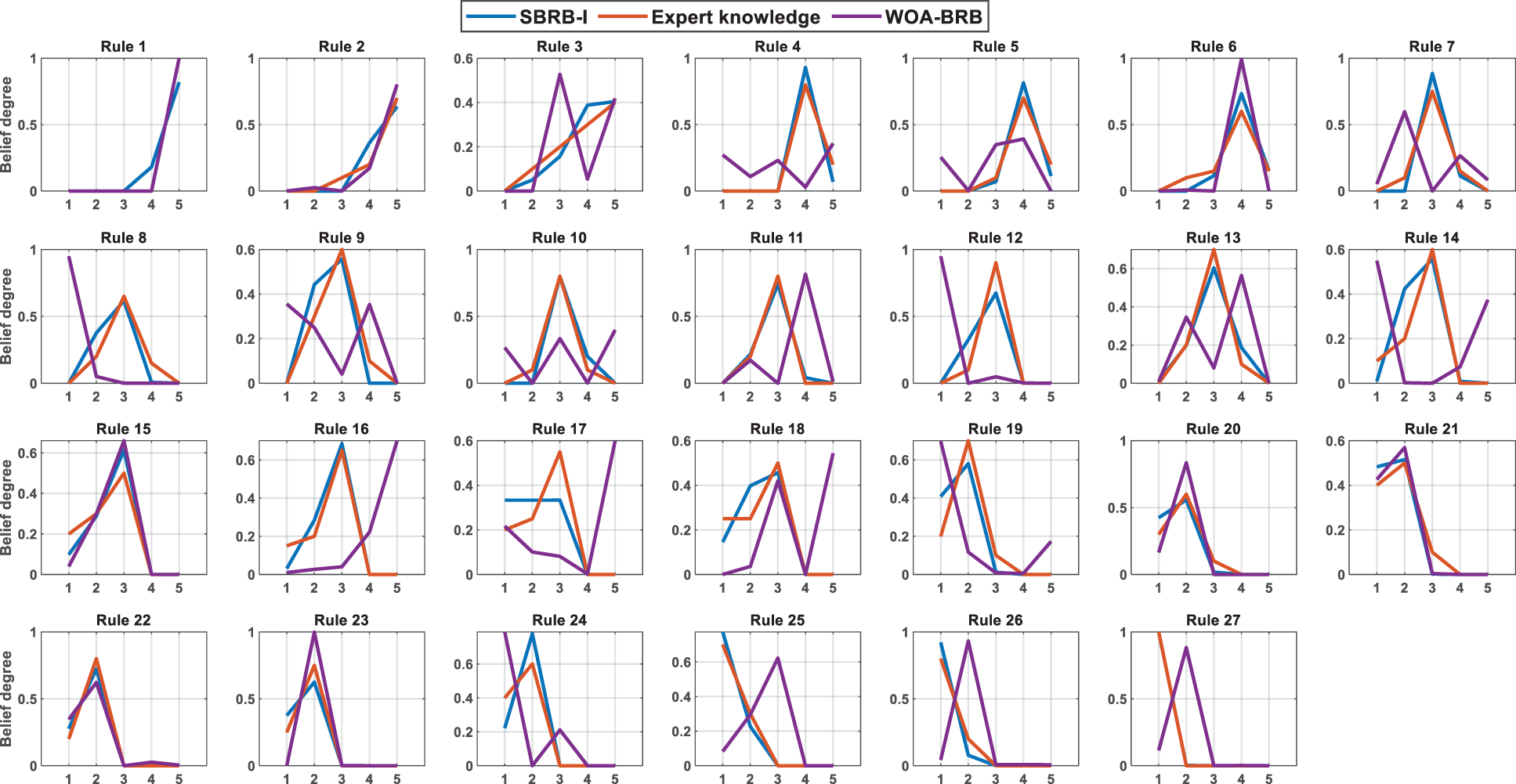
Figure 11: The belief distribution of SBRB-I(42) models

5.3 Comparison of Different Models

In Table 6, under the condition of 2100 iterations, the optimization process is repeated 20 times for different BRB models. SBRB(1) has a lower standard deviation compared with WOA-BRB, which shows that the self-growth learning strategy makes the SBRB model more robust. The convergence speed of the WOA-BRB and SBRB(1) is shown in Fig. 12. SBRB(1) is represented by a red curve, and WOA-BRB is represented by a blue curve. As seen from part D, due to SBRB(1) integrating expert knowledge into the optimization process, SBRB(1) is a better starting point for optimization than WOA-BRB. Part E shows that SBRB(1) converges faster than the WOA-BRB. This shows that expert knowledge introduced into the initial population of the algorithm can effectively accelerate the convergence rate and improve the optimization process [20,21]. Thus, this demonstrates the effectiveness of the self-growth learning strategy proposed in this paper.

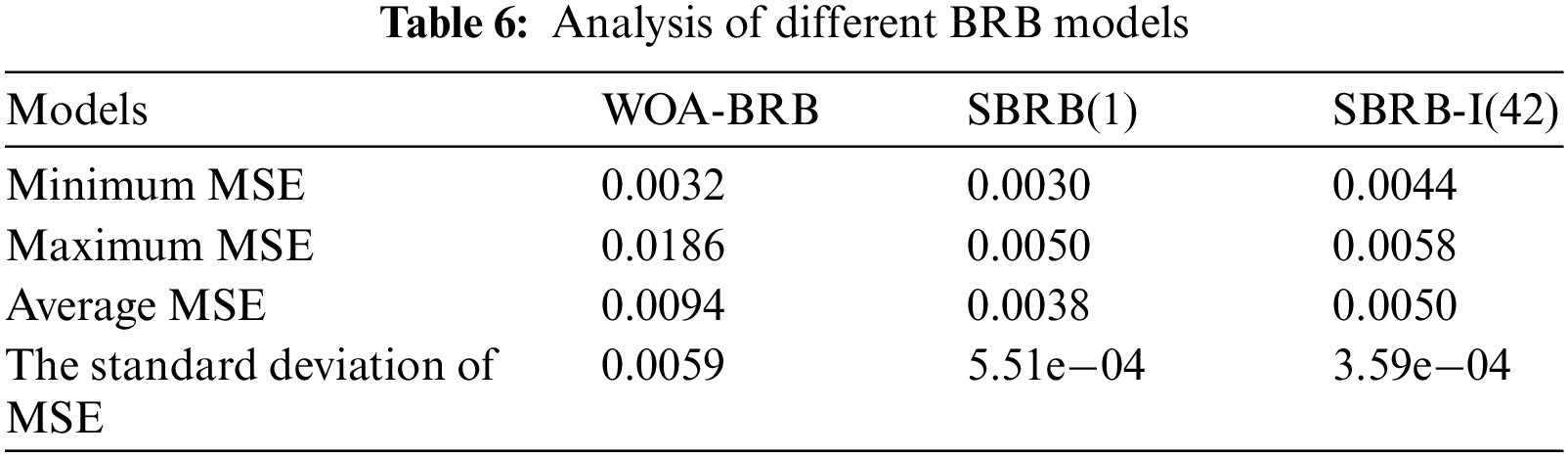
Figure 12: The convergence speed of different BRB models

The projection covariance matrix adaptation evolution strategy (P-CMA-ES), gray wolf optimization algorithm (GWO), differential evolution algorithm (DE), backpropagation neural network (BPNN), radial basis function (RBF), deep belief networks (DBN), long short-term memory (LSTM) and decision tree are used for experimental comparison. In Table 7, while other models have close to the same accuracy as SBRB-I, SBRB-I is more interpretable than the ones. Compared with P-CMA-ES-BRB, DE-BRB and GWO-BRB, the interpretability of SBRB-I can be seen in the following aspects: 1. The belief distribution of SBRB-I conforms to the actual system, while the other models do not have such interpretability. 2. The SBRB-I model is optimized in the solution space of the local judgment of experts. The optimized solution can retain the characteristics of expert knowledge information and is more interpretable.

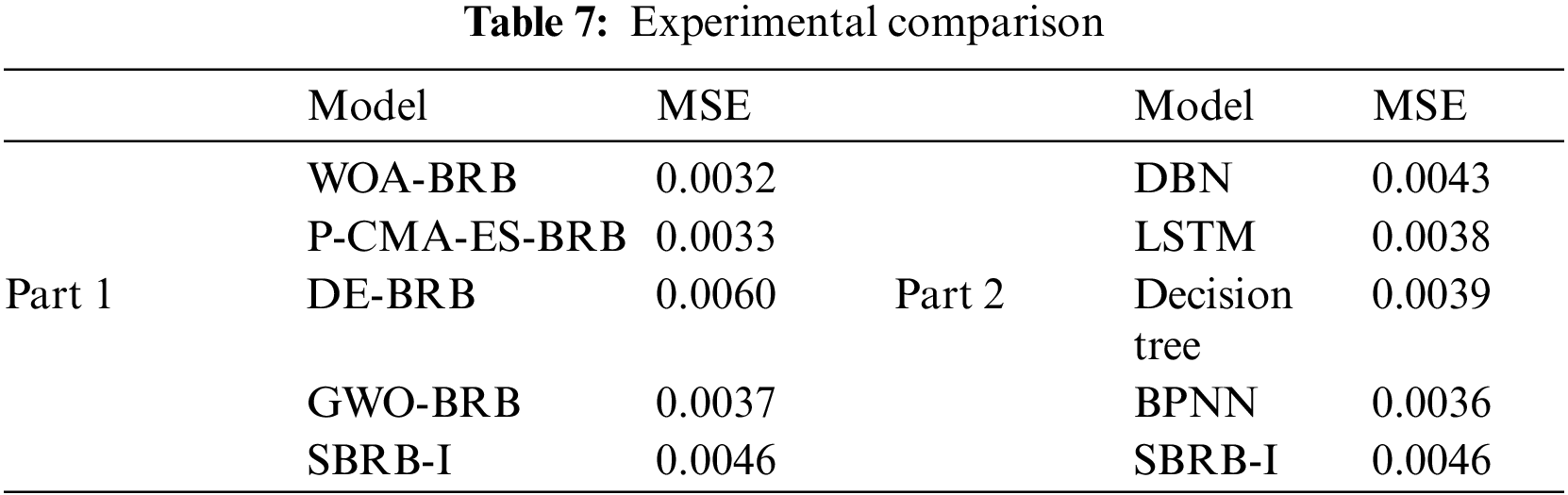
Compared with the BPNN, RBF, DBN, LSTM prediction models, the interpretation of SBRB-I can be described as follows: 1. The SBRB-I model is a modeling method based on IF-THEN rules, and its output can be traced back. However, the prediction models of BPNN and RBF are essentially black-box models with few parameter meanings, and their input–output relationships are difficult to interpret. 2. SBRB-I has a clear and transparent reasoning calculation process, while the internal structure of prediction models such as BPNN is invisible. 3. The expert knowledge and system mechanism can be integrated into the SBRB-I model, so the SBRB-I model is much more easily understood by users.

5.4 The Interpretability of SBRB-I Model is Introduced

The SBRB-I model is an interpretable model, and it can provide guidance on air quality governance through its analysis [32]. The effect of the Sub-BRB model on the air quality index is shown in Fig. 13. Model 1 has the greatest impact on the AQI, which is consistent with the judgment of the expert model. Through the analysis in Section 5.1, Model 1 represents the particle size index of particles in the air. Thus, one of the measures to improve the air quality in Beijing is to reduce the content of PM 2.5 and PM 10 in the air.

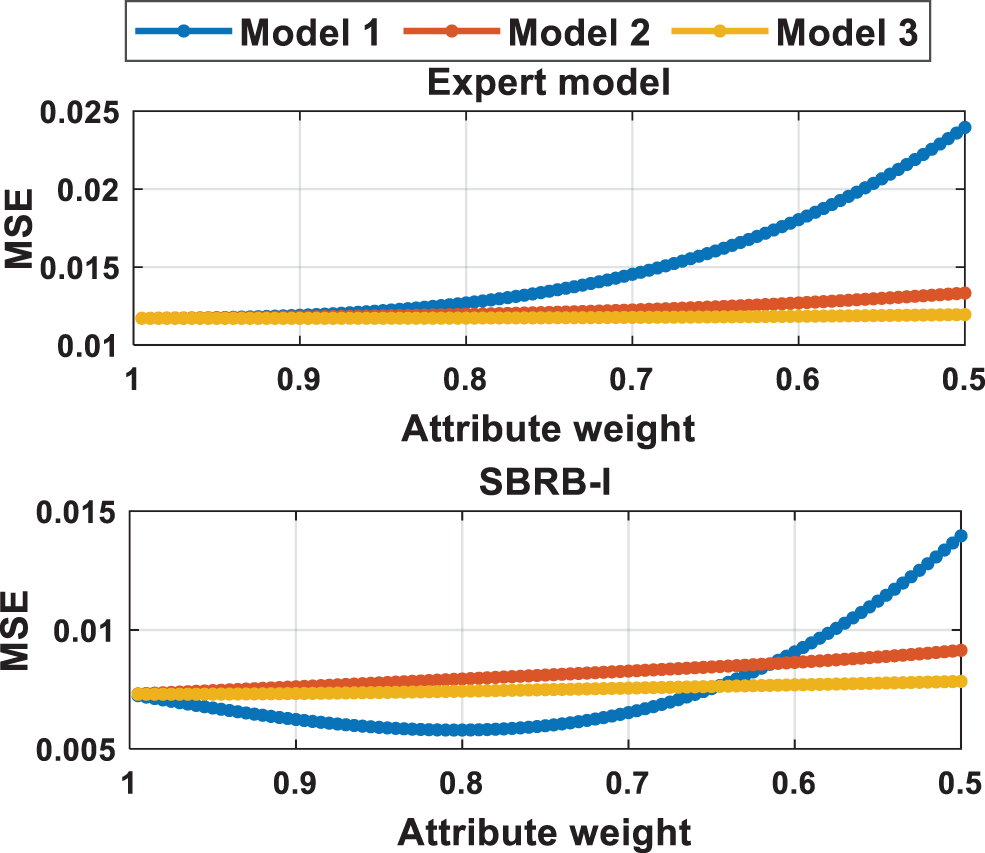
Figure 13: Sensitivity analysis of the SBRB-I model

6  Conclusion

Interpretability and accuracy are important requirements to achieve reliable and accurate prediction systems. However, in the current study, three problems need to be solved for interpretability of BRBs: expert knowledge is not used effectively, how to improve model accuracy while maintaining interpretability and how to make expert systems and data-driven models cooperate effectively.

There are two innovations in this paper. For the first problem, one interpretability guideline is designed. Expert knowledge is used to form a local optimization space based on expert judgment. Moreover, expert knowledge is also integrated into the optimization process, which improves the convergence speed when optimizing and enhances the model’s interpretability. For the second and third problems, a new prediction system based on a self-growth BRB with interpretability constraints (SBRB-I) is proposed. The SBRB-I model uses any available knowledge to guide the optimization direction, including domain expert knowledge and knowledge optimized by correlation functions. The SBRB-I model realizes cooperation between BRB’s expert system and the data-driven model. Moreover, the optimization process guided by experts and the limitation of interpretability constraints makes the knowledge after model optimization highly similar to the expert knowledge. Therefore, the knowledge optimized by the data-driven model can be used as a supplementary source of expert systems. Finally, a case study of the prediction system of the air quality index is conducted to verify the effectiveness of the proposed model. SBRB-I can improve prediction accuracy while maintaining interpretability.

SBRB-I proposed in this paper is an exploration. More interpretability constraints have been added to this model, which enhances its interpretability. At the same time, after limiting the constraint space, it is necessary to improve the local search ability of the algorithm, which will obtain better prediction results. Finally, the number of iterations of each self-growth needs to be further studied.

Acknowledgement: We thank the anonymous reviewers for their valuable comments and suggestions which helped us to improve the content and presentation of this paper.

Funding Statement: This work was supported in part by the Postdoctoral Science Foundation of China under Grant No. 2020M683736, in part by the Natural Science Foundation of Heilongjiang Province of China under Grant No. LH2021F038, in part by the innovation practice project of college students in Heilongjiang Province under Grant Nos. 202010231009, 202110231024, and 202110231155, in part by the basic scientific research business expenses scientific research projects of provincial universities in Heilongjiang Province Grant Nos. XJGZ2021001, and in part by the Education and teaching reform program of 2021 in Heilongjiang Province under Grant No. SJGY20210457.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. J. Debnath, D. Majumder and A. Biswas, “Air quality assessment using weighted interval type-2 fuzzy inference system,” Ecological Informatics, vol. 46, pp. 133–146, 2018. [Google Scholar]

2. C. J. Liang, J. J. Ling, C. W. Jheng and M. C. Tsai, “A rolling forecast approach for next six-hour air quality index track,” Ecological Informatics, vol. 60, pp. 101153, 2020. [Google Scholar]

3. D. M. Lima, B. M. Lima and J. E. Normey-Rico, “A predictor for dead-time systems based on the Kalman Filter for improved disturbance rejection and robustness,” Journal of Process Control, vol. 105, pp. 108–116, 2021. [Google Scholar]

4. X. W. Gu and Q. Shen, “A Self-adaptive fuzzy learning system for streaming data prediction,” Information Sciences, vol. 579, pp. 623–647, 2021. [Google Scholar]

5. L. G. Cui, Y. Q. Tao, J. Deng, X. L. Liu, D. Y. Xu et al., “BBO-BPNN and AMPSO-BPNN for multiple-criteria inventory classification,” Expert Systems with Applications, vol. 175, pp. 114842, 2021. [Google Scholar]

6. X. Y. Li, G. D. Fan, G. Rizzoni, M. Canova, C. B. Zhu et al., “A new particle predictor for fault prediction of nonlinear time-varying systems,” Developments in Chemical Engineering & Mineral Processing, vol. 13, no. 3–4, pp. 379–388, 2005. [Google Scholar]

7. Y. Chaibi, T. El Rhafiki, R. Simon-Allue, I. Guedea, C. Luaces et al., “Physical models for the design of photovoltaic/thermal collector systems,” Solar Energy, vol. 226, pp. 134–146, 2021. [Google Scholar]

8. H. Tan, V. Tarasov, A. E. W. Jarfors and S. Seifeddine, “A design of fuzzy inference systems to predict tensile properties of as-cast alloy,” The International Journal of Advanced Manufacturing Technology, vol. 113, no. 3–4, pp. 1111–1123, 2021. [Google Scholar]

9. W. L. Li, W. Y. Lin and J. Y. Yu, “Predicting contact characteristics for helical gear using support vector machine,” Neurocomputing, vol. 174, pp. 1156–1161, 2016. [Google Scholar]

10. J. Y. Wang, J. Z. Li, X. X. Wang, J. Wang and M. Huang, “Air quality prediction using CT-LSTM,” Neural Computing and Applications, vol. 33, no. 10, pp. 4779–4792, 2020. [Google Scholar]

11. N. Phruksahiran, “Improvement of air quality index prediction using geographically weighted predictor methodology,” Urban Climate, vol. 38, pp. 100890, 2021. [Google Scholar]

12. L. L. Chang, Z. J. Zhou, H. C. Liao, Y. W. Chen, X. Tan et al., “Generic disjunctive belief rule base modeling, inferencing, and optimization,” IEEE Transactions on Fuzzy Systems, vol. 27, no. 9, pp. 1866–1880, 2019. [Google Scholar]

13. Y. Cao, Z. J. Zhou, G. Y. Hu, C. H. Chang, S. W. Tang et al., “A new multilayer belief rule base model for complex system modeling,” IEEE Systems Journal, vol. 16, no. 3, pp. 4301–4312, 2021. [Google Scholar]

14. Y. Cao, Z. J. Zhou, C. H. Hu, W. He and S. W. Tang, “On the interpretability of belief rule-based expert systems,” IEEE Transactions on Fuzzy Systems, vol. 29, no. 11, pp. 3489–3503, 2021. [Google Scholar]

15. J. B. Yang, J. Liu, J. Wang, H. S. Sii and H. W. Wang, “Belief rule-base inference methodology using the evidential reasoning approach-RIMER,” IEEE Transactions on Systems, Man, and Cybernetics-Part A: Systems and Humans, vol. 36, no. 2, pp. 266–285, 2006. [Google Scholar]

16. G. L. Kong, D. L. Xu, J. B. Yang, X. F. Yin, T. B. Wang et al., “Belief rule-based inference for predicting trauma outcome,” Knowledge-Based Systems, vol. 95, pp. 35–44, 2016. [Google Scholar]

17. J. Wu, Q. W. Wang, Z. L. Wang and Z. G. Zhou, “AutoBRB: An automated belief rule base model for pathologic complete response prediction in gastric cancer,” Computers in Biology and Medicine, vol. 140, pp. 105104, 2022. [Google Scholar]

18. Z. C. Feng, W. He, Z. J. Zhou, X. J. Ban, C. H. Chang et al., “A new safety assessment method based on belief rule base with attribute reliability,” IEEE-CAA Journal of Automatica Sinica, vol. 8, no. 11, pp. 1774–1785, 2021. [Google Scholar]

19. Q. Q. Fan, X. F. Yan and Y. Xue, “Prior knowledge guided differential evolution,” Soft Computing, vol. 21, no. 22, pp. 6841–6858, 2017. [Google Scholar]

20. A. Ramachandran, S. Gupta, S. Rana, C. Li and S. Venkatesh, “Incorporating expert prior in Bayesian optimisation via space warping,” Knowledge-Based Systems, vol. 195, pp. 105663, 2020. [Google Scholar]

21. J. T. Vastola, J. C. Lu, M. J. Casciato, D. W. Hess and M. A. Grover, “A framework for initial experimental design in the presence of competing prior knowledge,” Journal of Quality Technology, vol. 45, no. 4, pp. 301–329, 2013. [Google Scholar]

22. Z. J. Zhou, G. Y. Hu, C. H. Hu, C. L. Wen and L. L. Chang, “A survey of belief rule-base expert system,” IEEE Transactions on Systems Man Cybernetics-Systems, vol. 51, no. 8, pp. 4944–4958, 2021. [Google Scholar]

23. J. B. Yang and D. L. Xu, “Evidential reasoning rule for evidence combination,” Artificial Intelligence, vol. 205, pp. 1–29, 2013. [Google Scholar]

24. Z. J. Zhou, Y. Cao, C. H. Hu, S. W. Tang, C. C. Zhang et al., “Interpretability and development of rule-based modeling methods,” Acta Automatica Sinica, vol. 47, no. 6, pp. 1201–1216, 2021. [Google Scholar]

25. Z. J. Zhou, S. W. Tang, C. H. Hu, Y. Cao and J. Wang, “Evidence reasoning theory and its application,” Acta Automatica Sinica, vol. 47, no. 5, pp. 15, 2021. [Google Scholar]

26. Z. J. Zhou, Y. Cao, G. Y. Hu, Y. M. Zhang, S. W. Tang et al., “New health-state assessment model based on belief rule base with interpretability,” Science China (Information Sciences), vol. 64, no. 7, pp. 172214, 2021. [Google Scholar]

27. Y. W. Chen, J. B. Yang, D. L. Xu, Z. J. Zhou, D. W. Tanga et al., “Inference analysis and adaptive training for belief rule based systems,” Expert Systems with Applications, vol. 38, no. 10, pp. 12845–12860, 2011. [Google Scholar]

28. F. Alonso, L. Martínez, A. Pérez and J. P. Valente, “Cooperation between expert knowledge and data mining discovered knowledge: Lessons learned,” Expert Systems with Applications, vol. 39, no. 8, pp. 7524–7535, 2012. [Google Scholar]

29. A. Cano, A. R. Masegosa and S. Moral, “A method for integrating expert knowledge when learning Bayesian networks from data,” IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), vol. 41, no. 5, pp. 1382–1394, 2011. [Google Scholar]

30. S. Mirjalili and A. Lewis, “The whale optimization algorithm,” Advances in Engineering Software, vol. 95, pp. 51–67, 2016. [Google Scholar]

31. A. Zhang, F. Gao, M. Yang and W. H. Bi, “A new rule reduction and training method for extended belief rule base based on DBSCAN algorithm,” International Journal of Approximate Reasoning, vol. 119, pp. 20–39, 2020. [Google Scholar]

32. Z. C. Feng, Z. J. Zhou, C. H. Hu, L. L. Chang, G. Y. Hu et al., “A new belief rule base model with attribute reliability,” IEEE Transactions on Fuzzy Systems, vol. 27, no. 5, pp. 903–916, 2019. [Google Scholar]