 Open Access
Open Access
ARTICLE
Dynamic S-Box Generation Using Novel Chaotic Map with Nonlinearity Tweaking
1 School of Systems and Technology, University of Management and Technology, Lahore, 54700, Pakistan
2 Department of Computer Science, University of Engineering and Technology, Lahore, 54700, Pakistan
3 Department of Computer Engineering, Jamia Millia Islamia, New Delhi, 110025, India
4 Department of Information Technology, College of Computer and Information Sciences, Princess Nourah bint Abdulrahman University, P.O. Box 84428, Riyadh, 11671, Saudi Arabia
5 Security Engineering Lab, Computer Science Department, Prince Sultan University, Riyadh, 11586, Saudi Arabia
6 Department of Electronics and Electrical Communications Engineering, Faculty of Electronic Engineering, Menoufia University, Menouf, 32952, Egypt
* Corresponding Author: Musheer Ahmad. Email:
Computers, Materials & Continua 2023, 75(2), 3011-3026. https://doi.org/10.32604/cmc.2023.037516
Received 07 November 2022; Accepted 15 January 2023; Issue published 31 March 2023
Abstract
A substitution box (S-Box) is a crucial component of contemporary cryptosystems that provide data protection in block ciphers. At the moment, chaotic maps are being created and extensively used to generate these S-Boxes as a chaotic map assists in providing disorder and resistance to combat cryptanalytical attempts. In this paper, the construction of a dynamic S-Box using a cipher key is proposed using a novel chaotic map and an innovative tweaking approach. The projected chaotic map and the proposed tweak approach are presented for the first time and the use of parameters in their working makes both of these dynamic in nature. The tweak approach employs cubic polynomials while permuting the values of an initial S-Box to enhance its cryptographic fort. Values of the parameters are provided using the cipher key and a small variation in values of these parameters results in a completely different unique S-Box. Comparative analysis and exploration confirmed that the projected chaotic map exhibits a significant amount of chaotic complexity. The security assessment in terms of bijectivity, nonlinearity, bits independence, strict avalanche, linear approximation probability, and differential probability criteria are utilized to critically investigate the effectiveness of the proposed S-Box against several assaults. The proposed S-Box’s cryptographic performance is comparable to those of recently projected S-Boxes for its adaption in real-world security applications. The comparative scrutiny pacifies the genuine potential of the proposed S-Box in terms of its applicability for data security.Keywords
It is evident that the role of information in every aspect of our everyday lives and the modern industrial revolution are changing the planet. Reliance on Internet technology is increasing as it grows more and more integrated into many facets of our lives. Organizations need to store the data and share it with different users at different levels via the Internet or other networking protocols. During this interchange of data and information, there is a very real risk of data loss and misuse caused by malware or other harmful software. An organization that maintains digital data or financial information needs to keep it well-protected from intruders. Protecting data and information resources from illegitimate access and usage has become crucial. When data is kept on public networks, the need to shield data and systems is more demanding [1]. Consequently, an increasing number of researchers are investigating cryptographic techniques to enhance the sanctuary of information being communicated over the Internet [2]. These techniques assist users in transmitting data and information in a protected way over an apprehensive network. Assailants use cryptanalytical practices to enervate this protection of data, and therefore diverse cryptosystems have been contrived for the fortification of the data to defy these illegitimate practices [3].
Along with other arithmetic operations, permutation and substitution processes are extensively used in different phases of modern block ciphers. The permutation process is used to change the locations of bits/bytes in the original message to make it disordered and achieves the diffusion principle of cryptography. A substitution process replaces plaintext bits/bytes randomly with other bits/bytes to produce visually meaningless and futile data called ciphertext. This substitution of the original data into meaningless data is carried out in a nonlinear fashion and the process achieves the confusion principle of cryptography. A substitution box plays a crucial part in the encryption of data and is a fundamental part of modern block encryption algorithms (block ciphers). It facilitates an encryption algorithm to accomplish the confusion activity by carrying out a nonlinear transfiguration between the plaintext and ciphertext bits/bytes. The encryption algorithms using static S-Boxes always employ the same S-Box for the plaintext-ciphertext transformation. Such S-Boxes have weaknesses that make it possible for intruders to get the clue of plaintext from the ciphertext’s characteristics [4]. In comparison to static S-Boxes, dynamic S-Boxes are mostly reliant on the cipher key and are sturdy, robust, and more efficacious in accomplishing the confusion of data. Researchers in the cryptography domain over time have ornated numerous S-Box generation methods using various techniques like linear fractional transformation [5,6], DNA computing [7,8], elliptic curves [9–12], compressive sensing [13–17], cellular automata [18], optimization techniques [19,20].
Recently, chaos theory has been a major focus and gained the attention of many S-Box designers to create this nonlinear component of modern block ciphers [21,22]. In order to build robust S-Boxes, authors in [23] developed a novel technique based on Logistic chaotic map that employed the idea of matrix rotation and affine transformation to generate key-dependent S-Boxes. Four steps that make up the suggested process for S-Box construction include the calculation of the Galois Field inverse, creating keys using Logistic map, computing the rotational matrix, and ultimately creating a new S-Box. Alghafis et al. [24] presented an S-Box construction technique based on a three-dimensional Liu chaotic system. The resultant S-Box is utilized along with other chaotic systems for image encryption and the outcomes reflect the robustness of the substitution process. Lu et al. [25] projected a new compound chaotic map that is a composition of two chaotic maps (Sine map and Logistic map) and employed this compound map for the creation of an S-Box. The compound chaotic map offers more chaotic behaviour, improved chaotic map features, and computational efficiency. However, the nonlinearity score of the resultant S-Box is not an encouraging one. A method for producing S-Box using a 1-D chaotic map was proposed by Tanyildizi et al. [26]. Liu et al. [27] created an improved coupling quadratic map (ICQM). Using this map, a key-dependent strong S-Box was designed. The outcomes of the experiments demonstrated the viability of the suggested S-Box construction strategy. Riaz et al. [28] suggested a compound chaotic map that is based on the Tent map and Chebyshev map for constructing an effectual S-Box that is employed for the encryption of images.
Many other researchers [29–48] have proposed chaos-based S-Box construction techniques using other concepts. Despite the fact that chaotic maps are frequently utilized to construct S-Boxes, these maps also have accompanying shortcomings [49]. The number of potential S-Boxes and the associated recital are improvised by using heuristics, optimization algorithms, and transformation techniques. For the creation of robust S-Boxes, Zahid et al. [50] offered an innovative permutation method and inventive polynomial algorithm. This permutation-based method is incredibly simple and effective. As cryptanalytic efforts are increasing day by day, new substitution boxes need to be designed all the time with improved and more reliable performance. This paper proposes to present the construction technique of a new S-Box to protect data to resist security assaults with the help of a novel chaotic map and a tweaking approach to improvise the nonlinearity feature of the S-Box.
The major contributions of this paper are summarized as follows:
■ A novel 1-D discrete chaotic map is proposed which has frail free dynamics and performance.
■ Dynamic S-Box generation method is developed to get a strong final S-Box.
■ A tweaking approach is presented that improvises the nonlinearity feature of the S-Box.
■ The performance analysis and comparative study are carried out to validate the effective performance of the proposed method.
Descriptions of the remaining parts of this research paper are organized as follows. A novel chaotic map-based method for the creation of an S-Box is elaborated in Section 2. The performance and comparison analysis of S-Boxes based on various parameters and pertinent security analyses is described in Section 3. Constraints associated with the projected chaotic map are described in Section 4. The conclusion of our work is reported in Section 5.
2 Proposed Approach for S-Box Design
In recent times, many researchers have utilized chaotic maps for the construction of new strong S-Boxes. Because these maps have the capability to offer decent cryptographic-suited features. A chaotic map is very sensitive to initial conditions, possesses the competence to generate randomness in outcomes, and is non-periodic in nature. These assets of chaotic maps help to achieve confusion and diffusion aspects of cryptographic systems. These benefits motivated us to design a novel chaotic map to generate dynamic S-Boxes which further can be utilized in the structure of new cryptosystems. The process for engendering the key-dependent and dynamic S-Boxes comprises of subsequent three steps:
■ Novel Chaotic map design
■ Initial S-Box construction
■ Tweaking approach to improvise the nonlinearity of the final S-Box
For the construction of the proposed S-Box, a novel chaotic map (named as AZ Map) as specified mathematically in Eq. (1) is proposed.
Xn+1={1.1∗R∗Xn 0.0<Xn<0.5 0.55∗R∗(Xn)3 0.5≤Xn<1.0(1)
where, R = (2 + A)0.5 and A, Xn ∈ (0.0, 1.0). The values of the variables A and Xn as stated in Eq. (1) are provided using the cipher key. The proposed 1-D chaotic map is very delicate to the initial values of the variables, set conditions, and provides assistance for the augmentation of the cryptographic strength of S-Box to limit security assaults. Authors in [51] described the bifurcation diagram and Lyapunov exponent as the analytical metrics/methods to show the chaos present in a system. The recital of the proposed chaotic map is compared to that of the classical Logistic map and Tent map [45] in terms of the bifurcation diagram and Lyapunov exponent in Figs. 1 and 2, respectively. The presented diagrams and comparison analysis confirmed that the new chaotic map embraces a significant amount of chaotic intricacy as it spans greater spatial regions than those of the other two chaotic maps.

Figure 1: Bifurcation diagrams of (a) logistic map, (b) tent map, and (c) proposed AZ chaotic map

Figure 2: Lyapunov exponents of (a) logistic map, (b) tent map, and (c) proposed AZ chaotic map
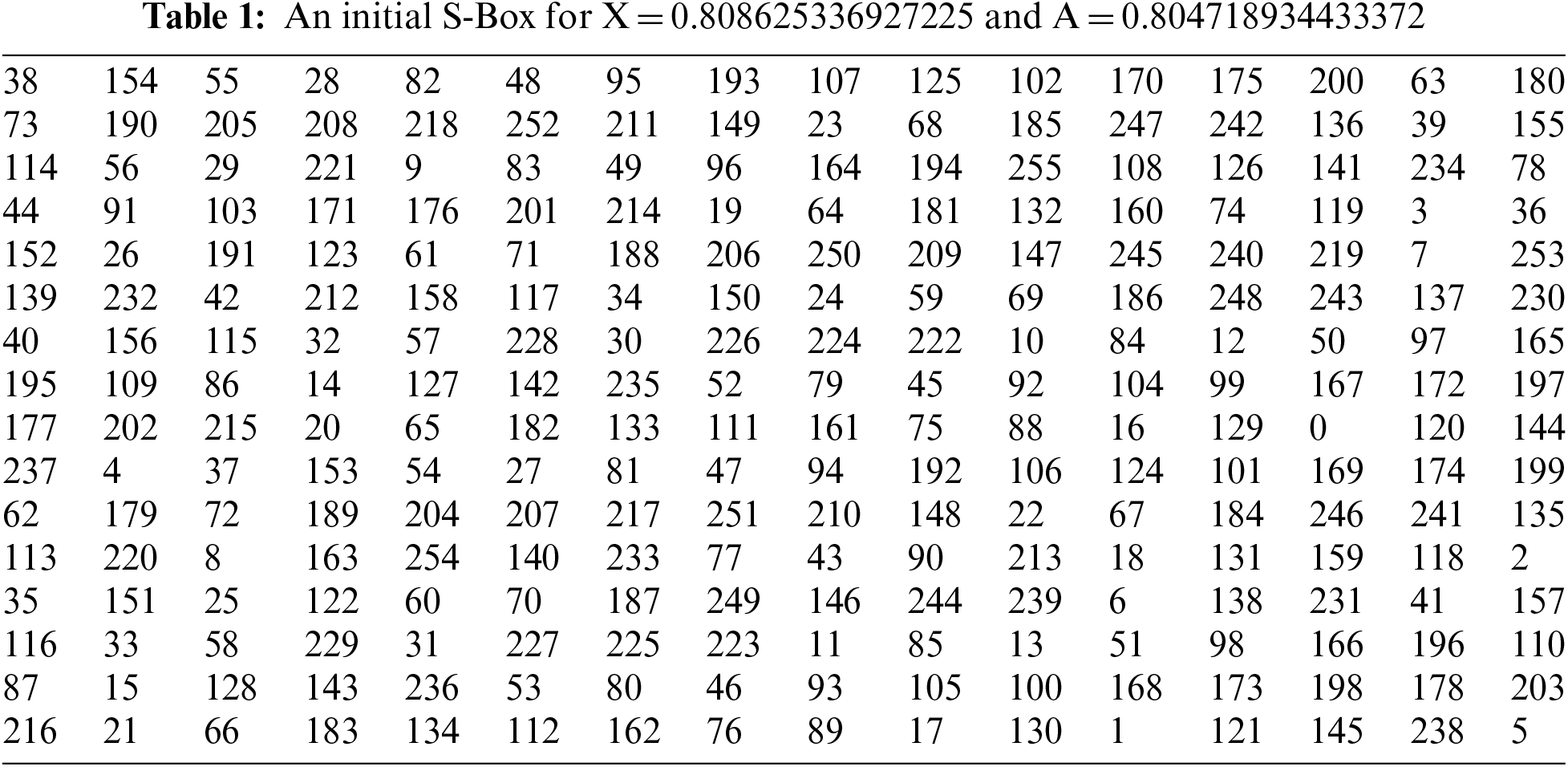
Using Eq. (1) and flowchart shown in Fig. 3, an initial S-Box is generated. Table 1 provides an illustration of a preliminary S-Box obtained.
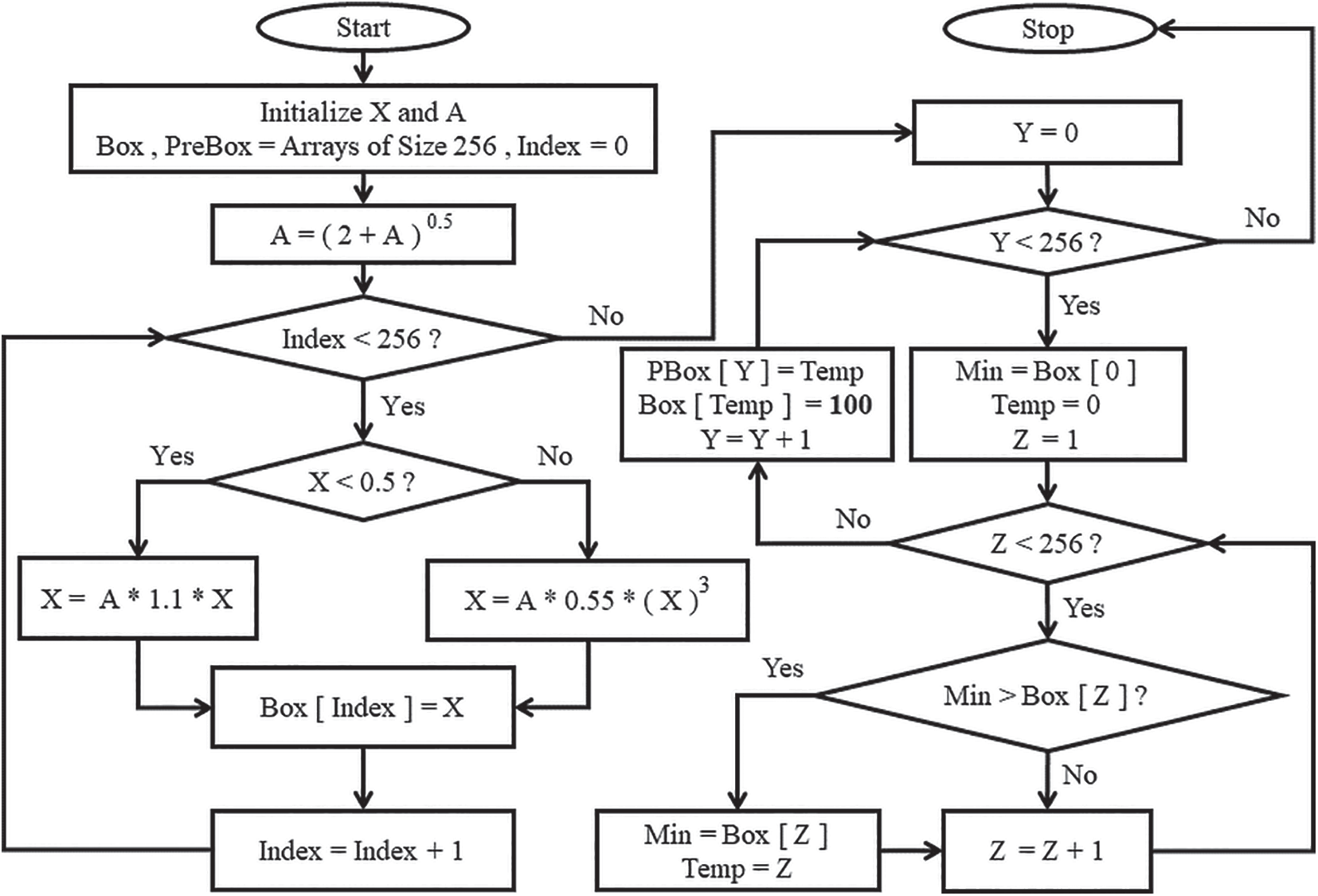
Figure 3: Preliminary S-Box creation procedure
2.3 Tweaking Approach for Final S-Box Generation
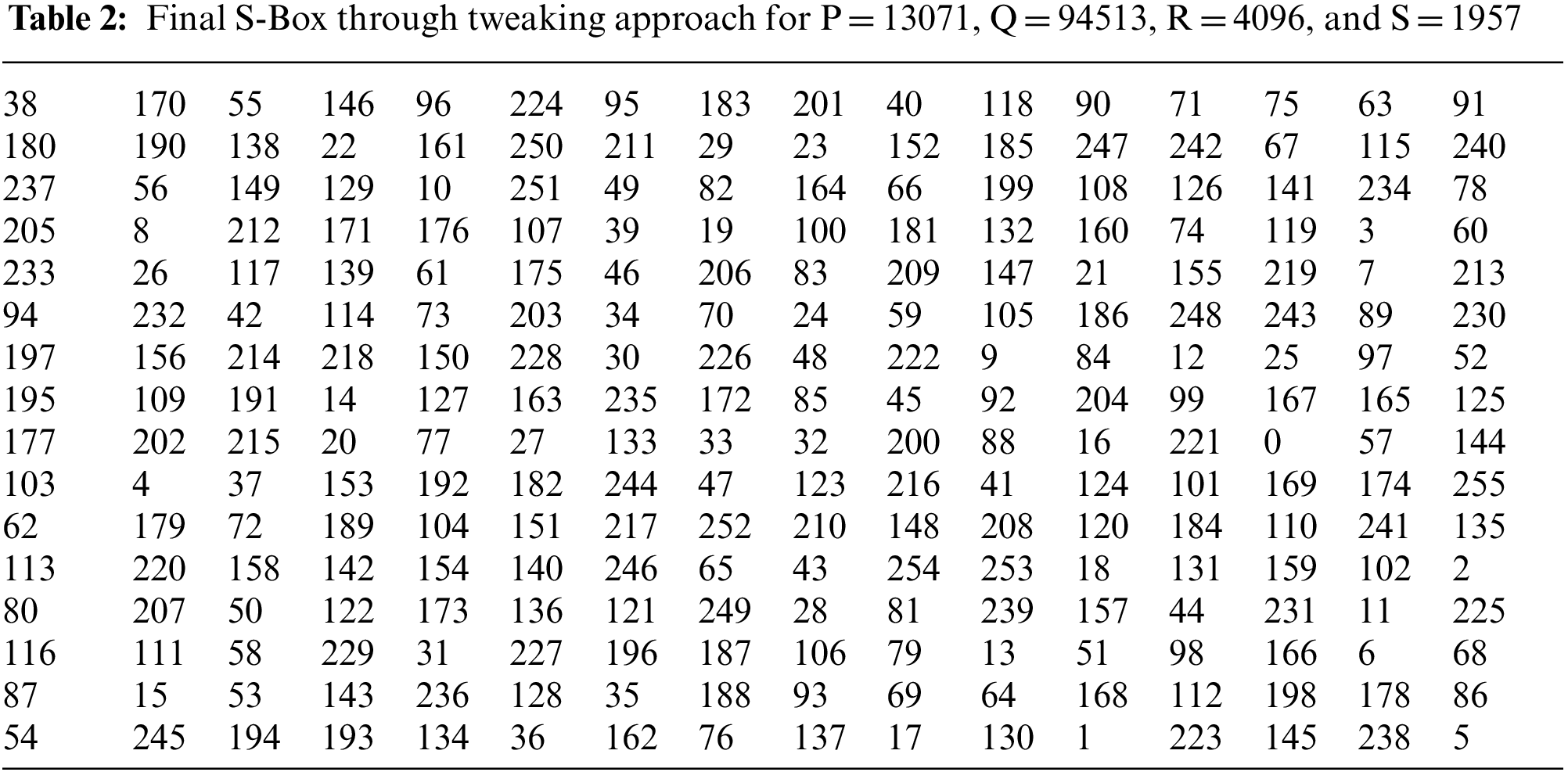
The final S-Box is created by processing an initial S-Box created by Fig. 3 with a novel tweak approach depicted in Fig. 4. The proposed tweak approach uses cubic polynomials in its working and assists in enhancing the nonlinearity of the initial S-Box by permuting the S-Box elements. The suggested tweak method is dynamic and is reliant on the values of the parameters supplied by the cipher key. Values, P = 13071, Q = 94513, R = 4096, and S = 1957 are selected for computation and demonstration purposes. Novel tweak approach permutes values of an initial S-Box through Fig. 4 and yields the final S-Box as presented in Table 2.
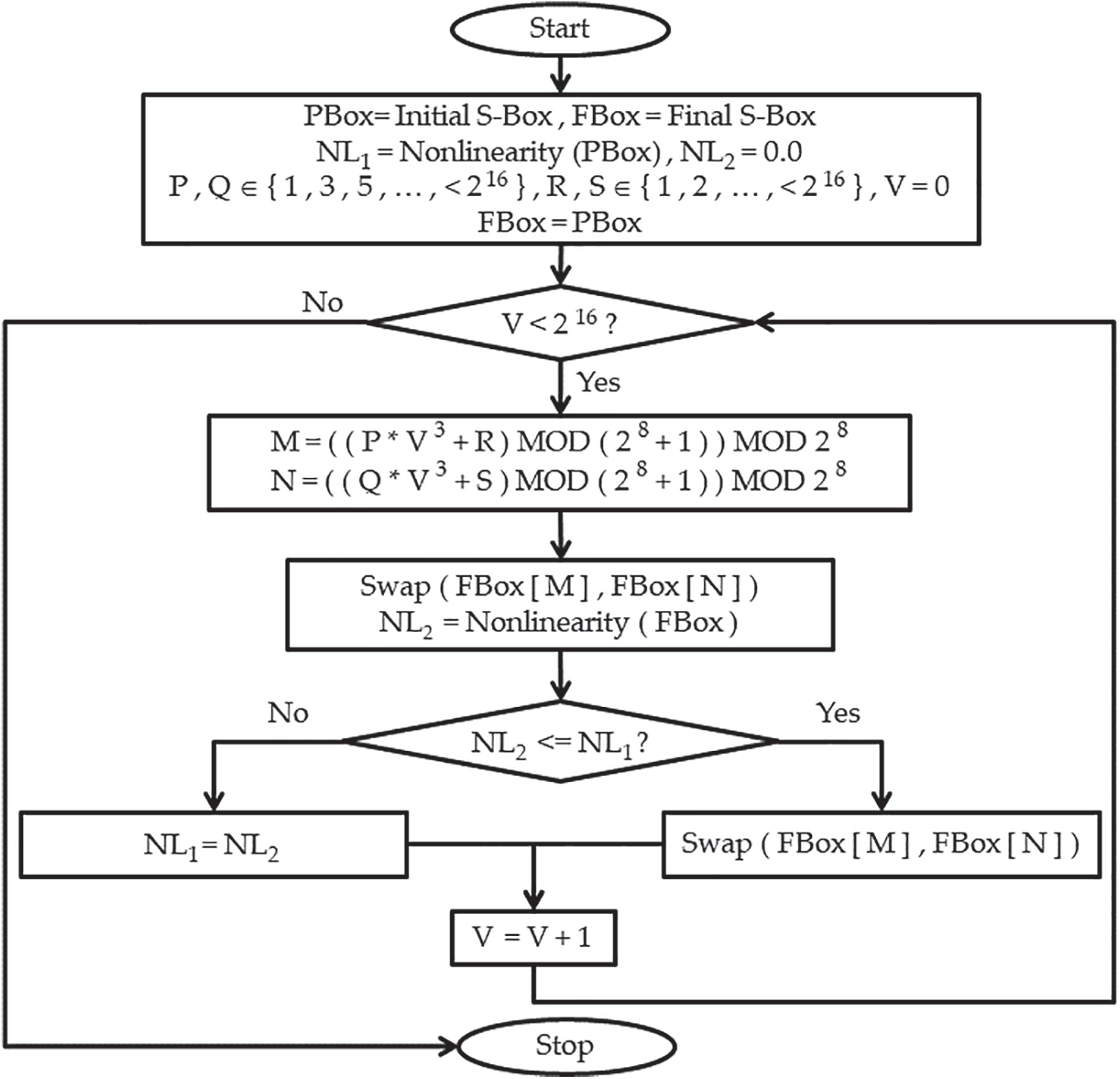
Figure 4: Tweaking approach for final S-Box generation
3 Security Assessment of Proposed S-Box
The development of new S-Boxes is a significant research contribution in the realm of information security. After the creation of an S-Box, it is examined to determine its strength against various linear and differential assaults. The strength of the projected S-Box has been evaluated through a critical analysis using the following predetermined criteria:
■ FPA–Fixed Points Analysis
■ Bijectivity Test
■ NL–Nonlinearity
■ SAC–Strict Avalanche Criterion
■ BIC–Bit Independence Criterion
■ LP–Linear Approximation Probability
■ DP–Differential Approximation Probability
3.1 Fixed Points Analysis (FPA)
If there is any fixed point (FP) in an S-Box, an attacker may be able to decipher the original data from the seized ciphertext. Therefore, the presence of any number of fixed points causes the weakness of the final S-Box. This criterion was applied to the projected S-Box of Table 2, and no fixed points were discovered throughout the whole table.
For an m × n S-Box, this attribute must convert a distinct input of m bits to a distinct output of n bits. An S-Box must reflect this input-output mapping as one-to-one [51]. Proposed 8 × 8 S-Box shown in Table 2 has 256 distinct values ranging from 0 to 255. The projected S-Box satisfies this bijectivity criterion very well as every possible unique input has a unique output associated with it.
A crucial feature in assessing the effectiveness of a substitution box is nonlinearity [52]. An S-Box is the only nonlinear element of today’s block ciphers in particular. The strength of an S-Box against various linear and differential assaults is feeble if it is built in such a way that the conversion between original data and scrambled data is linear. A large value of nonlinearity is required for an effective defense against these malevolent efforts [53].
With the help of Eq. (2) as follows, the value of nonlinearity of a Boolean function T is determined.
NL(T)=2n−1− 12(Smax(T))(2)
where, Smax (T) = Walsh-Hadamard Spectrum of a Boolean function T having n bits.
Table 3 lists the nonlinearity values of different Boolean functions of the projected S-Box.

Table 4 demonstrates that the minimum, maximum, and average nonlinearity scores of projected S-Box are 110, 112, and 110.75 respectively. The NL scores of the proposed S-Box are compared to those of designed in recent times in Table 4. It is clear from Table 4 that the proposed S-Box has a stronger resistance against assaults like linear cryptanalysis as its NL scores (min, max, and avg) are higher than the NL scores of the majority of the other S-Boxes.
3.4 Strict Avalanche Criterion (SAC)
Tavares and Webster were the first to present the Strict Avalanche Criterion (SAC) [68]. In order to comply with this criterion, 50% bits of the ciphertext due to the application of a cipher must alter for any change to one of the input bits. A dependency matrix is used to compute the SAC score of a substitution box. Values of this matrix for the projected S-Box have been calculated and quantified in Table 5.
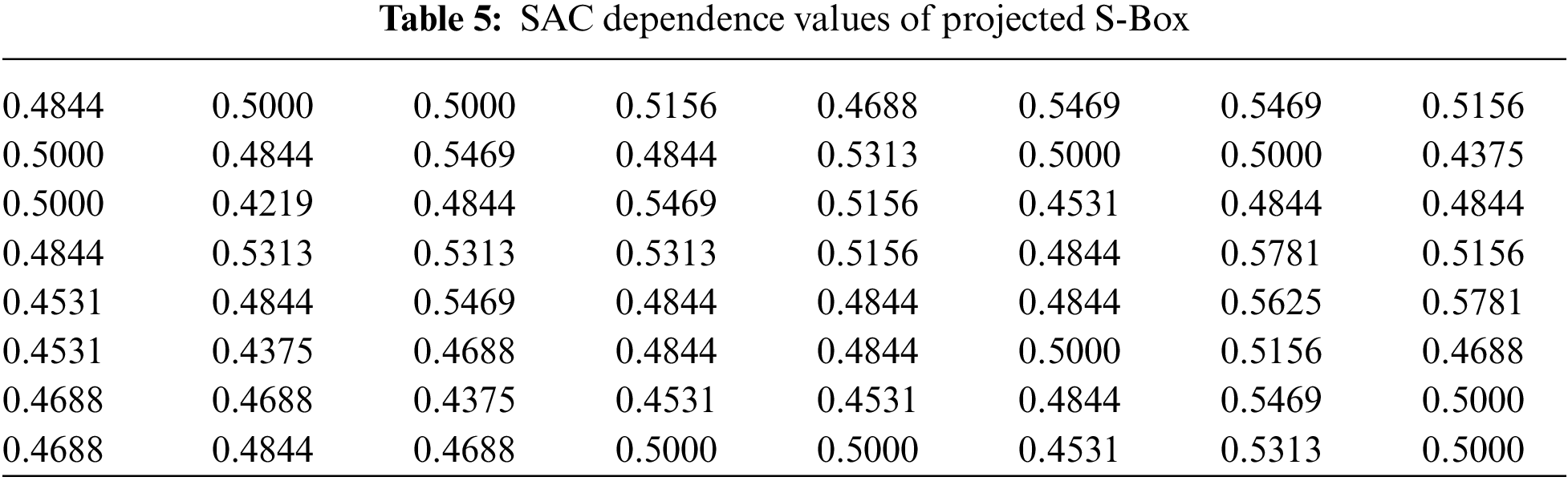
A SAC value of 0.5 for an S-Box is considered an ideal score. The projected S-Box has an average SAC score equal to 0.496 which is very close to the ideal value.
3.5 Bit Independence Criterion (BIC)
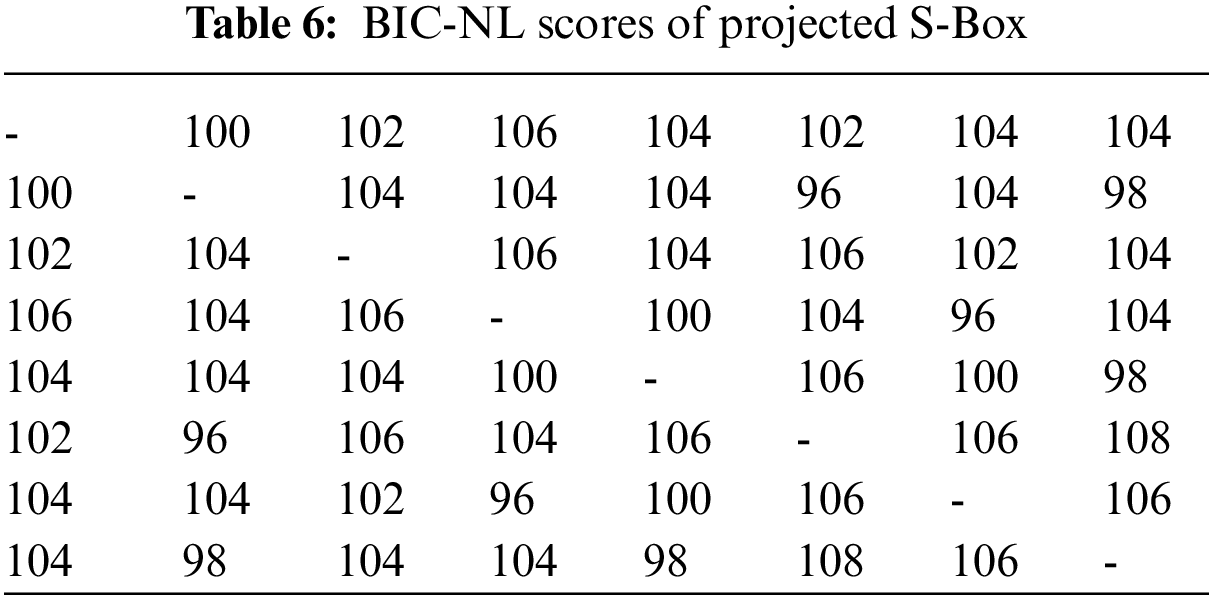
Tavares and Webster developed Bit Independence Criterion (BIC) which is another standard for assessing S-Box recitals [68]. This criterion states that if input bits change in any way, changes in output bits should be independent of each other. BIC-NL values of the projected S-Box are described in Table 6, whereas the average BIC-NL score is 102.9.
3.6 Linear Approximation Probability (LP)
Matsui put forth linear cryptanalysis as a statistical attack to test the strengths and weaknesses of the Data Encryption Standard (DES) in 1993 [69]. Linear cryptanalysis crooks the probability of the existence of linear relationships between different inputs (key, plaintext) and output (ciphertext) of a cryptosystem. Today, linear cryptanalysis helps cryptanalysts to look into the feebleness of modern-day block ciphers. DES cipher showed severity and compromise against linear cryptanalysis and consequently, the National Institute of Standards and Technology (NIST) developed Advanced Encryption Standard (AES) to prevent such malicious efforts by attackers [70]. If the probability of a linear relationship between inputs and output (called linear probability) for a substitution box is computed and emanated to be small, it shows that the S-Box under consideration is robust against linear cryptanalysis. Eq. (3) is used to calculate the value of Linear Probability (LP) for an S-Box.
LP=maxtx, ty≠0 |#{x∈V|x.tx =S(x). ty} 2n−1 2 |(3)
where, tx = Input mask, ty = Output mask, and V = {0, 1, … , 2n −1}.
The projected S-Box has a very low value of LP as 0.125, demonstrating its efficacy against linear cryptanalysis.
3.7 Differential Approximation Probability (DP)
Biham and Shamir introduced differential cryptanalysis as a brand-new method of assault against the Data Encryption Standard (DES) [71]. All cryptosystems that utilize substitution and permutation operations like those of DES, are vulnerable to this attack. Using differential cryptanalysis, an attacker attempts to identify dissimilarities between related scrambled plaintexts and tries to exploit the non-uniformity in existences of differences between plaintext and ciphertext. Original plaintexts may vary by one or more bits.
The strength of an S-Box against this attack is assessed using values of differential uniformity (DU) and differential probability (DP). For a given substitution box B, its differential uniformity (DU) is determined by Eq. (4).
DU=MaxΔa≠0,Δb[#{a∈P|B(a)⊕B(a⊕Δa)=Δb}](4)
where, ‘P’ stands for all potential inputs. Table 7 shows DU score of projected S-Box as 0.039 that is very low and specifies that the projected S-Box has the power to resist against differential cryptanalysis. Table 8 compares SAC, SAC-Offset, BIC-NL, LP and DP values of projected S-Box with those of various recently designed S-Boxes.
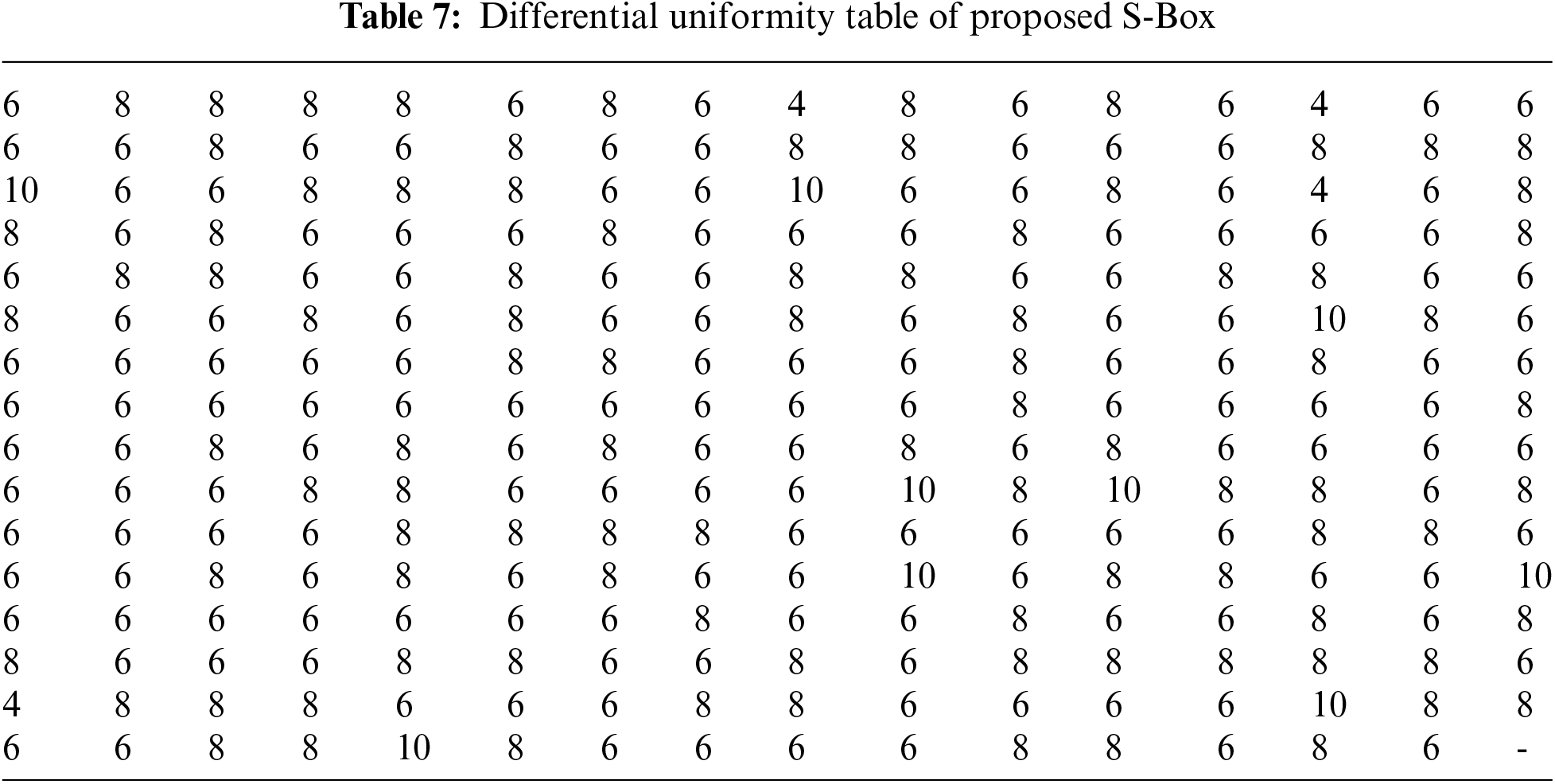
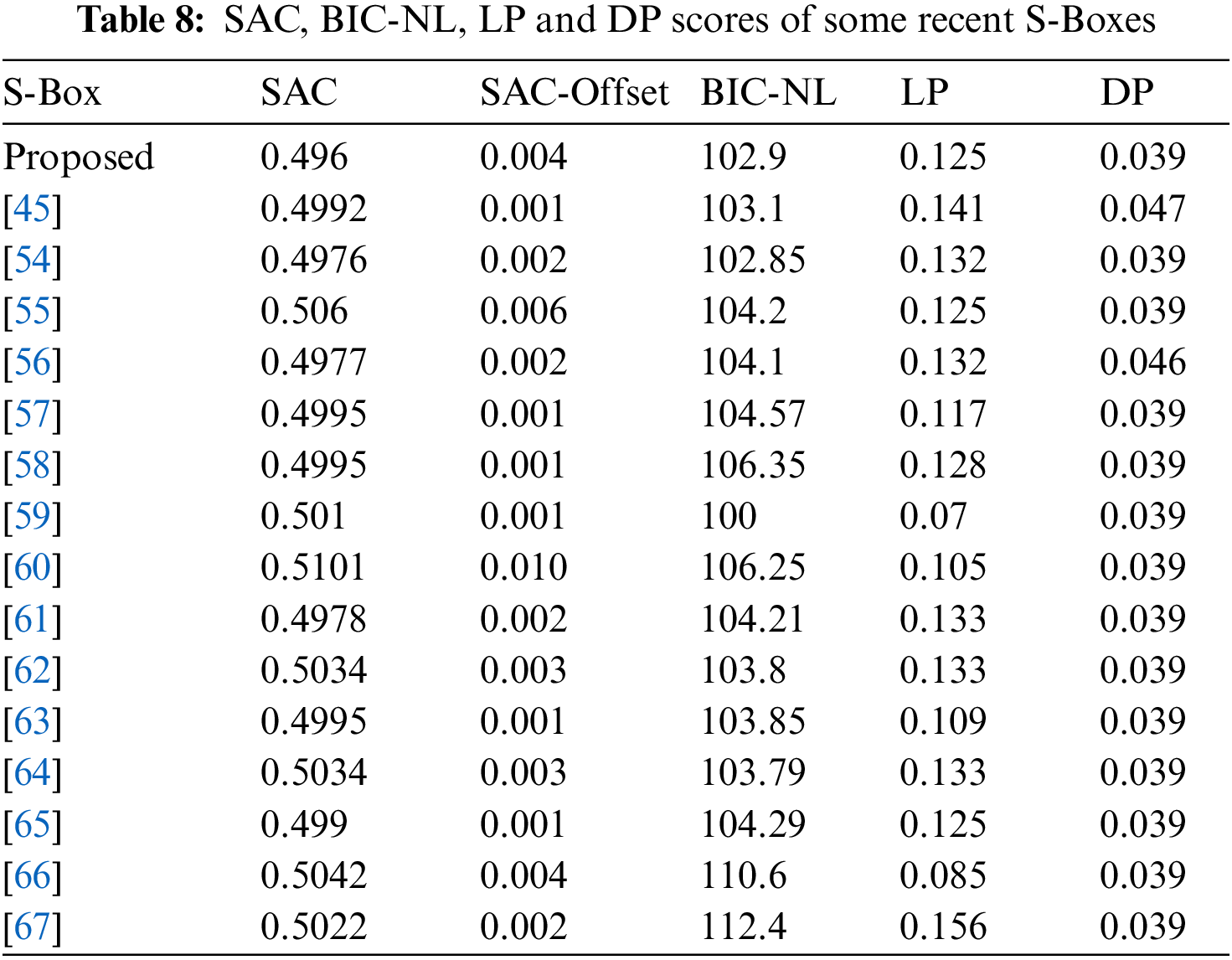
Table 8 clearly demonstrates that 0.004 is the offset value of SAC of projected S-Box. This low value of SAC offset validates that the projected S-Box has a great potential for usage in real life applications where security is the need of time. Similarly, low values of LP and DP are evidence of its effectiveness against such assaults.
The computational efficiency of the method to generate the projected S-Box was evaluated using Visual C# and Windows 10 on an Intel-core i7 CPU (2.2 GHz) system with 8 GB RAM. The projected method’s computational effectiveness was analyzed for both initial and final S-Boxes. The conception of the final S-Box is reliant on a novel tweak approach to improvise the cryptographic forte of the already generated S-Box. More than 106 diverse preliminary S-Boxes were engendered with the help of parameters through different initial values and computed their respective generation time. Similarly, overall times spent on the creation of final S-Boxes were measured. Table 9 enumerates the average times taken for the creation of these initial and final S-Boxes.

Table 9 shows that the construction time for initial S-Boxes is very motivational. Nevertheless, the projected approach takes a little longer to produce the final S-box. Novel tweak approach used in the proposed method significantly increases the cryptographic fort of the final S-Box. The need to protect one’s data is very important, and this need should never be neglected keeping in mind the speeds offered by today’s CPUs. Fig. 5 shows how the nonlinearity values of initial S-Boxes were enhanced while still being computationally efficient.
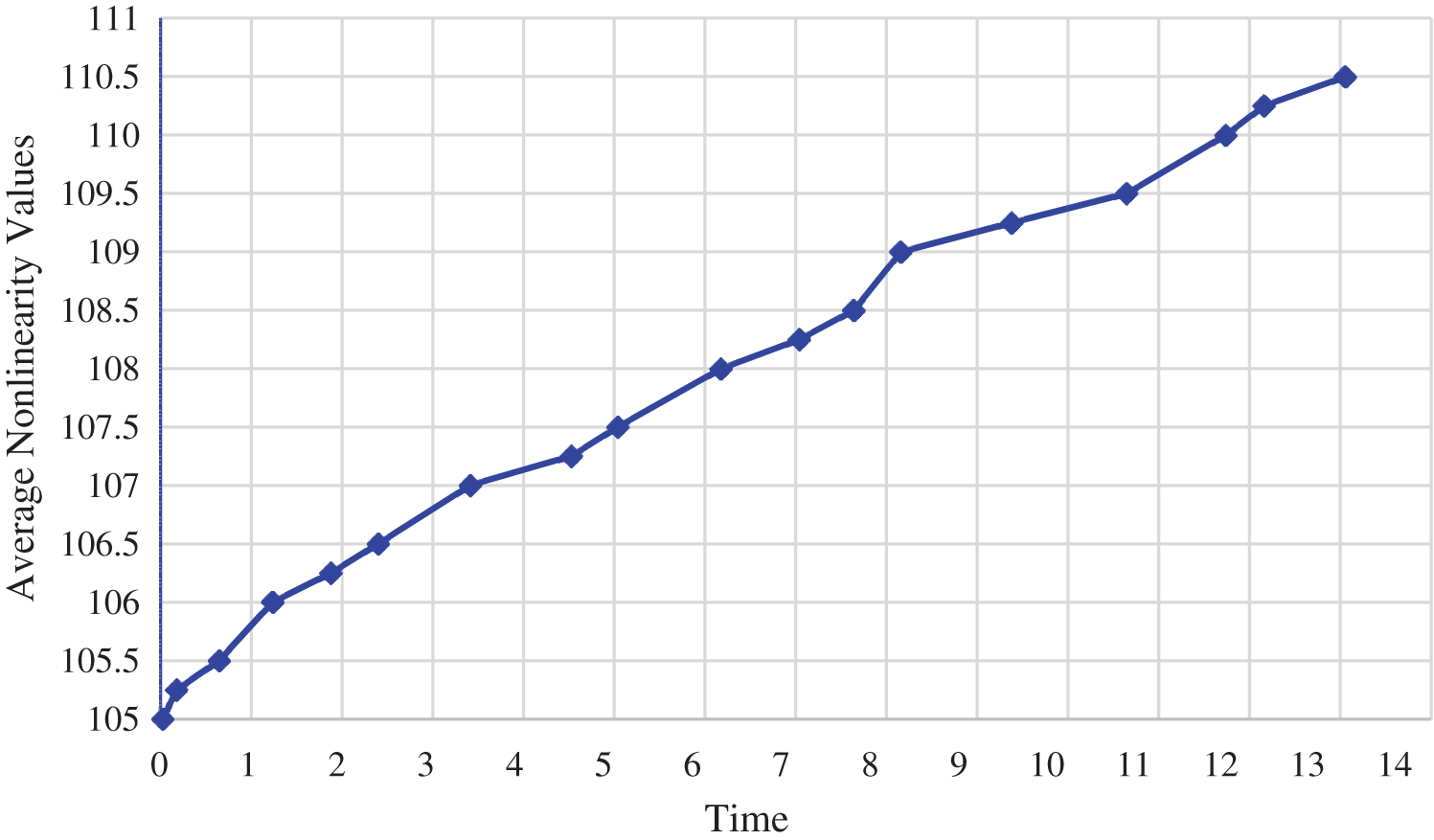
Figure 5: Nonlinearity evolution of initial S-box through tweaking approach w. r. t. time (secs)
Being dynamic and key dependent in nature, the projected method with the selection of distinct preliminary values for the parameters aids in the development of a fresh S-Box every time. Table 10 lists the parameters employed in our proposed method together with their associated ranges and key spaces.

It can be seen that the projected method’s entire key space is ∼4.7 × 1048 ∼2162 that is really a gigantic space for assailants. As a result, our suggested method is particularly resistant to intruders’ use of brute force approach.
The construction method of an innovative, key-dependent, and dynamic substitution box to protect data is presented in this research article to defy security assaults using a novel chaotic map. A novel tweak approach, dynamic in nature, permutes the values of an initial S-Box to enhance its cryptographic fort. The usage of parameters in projected chaotic map and the proposed tweak approach makes the generated S-Box dynamic and key dependent. A small variation in values of these parameters results in a completely different unique S-Box. Further comparative analysis and exploration confirmed that the projected chaotic map exhibits a significant amount of chaotic complexity. Cryptographic fort evaluation of the final S-Box using well-defined criteria is performed. To check its potential for use in contemporary ciphers, its cryptographic strength is equated with those of the state-of-the-art S-Boxes. This analytical assessment certifies that the S-Boxes using proposed approach have profound aptness in cryptography domain.
Acknowledgement: Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R66), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Funding Statement: Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2023R66), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. A. A. A. El-Latif, B. A. E. Atty, W. Mazurczyk, C. Fung and S. E. V. Andraca, “Secure data encryption based on quantum walks for 5G internet of things scenario,” IEEE Transactions on Network and Service Management, vol. 17, no. 1, pp. 118–131, 2020. [Google Scholar]
2. M. A. M. Escobar, C. C. Hernandez, F. A. Perz, R. M. L. Gutierrez and O. R. A. D. Campo, “A RGB image encryption algorithm based on total plain image characteristics and chaos,” Signal Processing, vol. 109, pp. 119–131, 2015. [Google Scholar]
3. S. Ibrahim and A. M. Abbas, “Efficient key-dependent dynamic S-boxes based on permutated elliptic curves,” Information Sciences, vol. 558, pp. 246–264, 2021. [Google Scholar]
4. K. Mohamed, M. N. M. Pauzi, F. H. H. M. Ali, S. Ariffin and N. H. N. Zulkipli, “Study of S-box properties in block cipher,” in Proc. I4CT, Langkawi, Malaysia, pp. 362–366, 2014. [Google Scholar]
5. L. Chew, N. Chew and E. S. Ismail, “S-Box construction based on linear fractional transformation and permutation function,” Symmetry, vol. 12, no. 5, pp. 1–16, 2020. [Google Scholar]
6. A. Qureshi and T. Shah, “S-Box on subgroup of galois field based on linear fractional transformation,” Electronics Letters, vol. 53, no. 9, pp. 604–606, 2017. [Google Scholar]
7. F. A. Kadhim, G. H. A. Majeed and R. S. Ali, “Proposal new S-box depending on DNA computing and mathematical operations,” in Proc. AIC-MITCSA, Baghdad, Iraq, pp. 142–147, 2016. [Google Scholar]
8. A. H. Al-Wattar, R. Mahmod, Z. A. Zukarnain and N. I. Udzir, “A new DNA-based S-box,” International Journal of Engineering & Technology, vol. 15, no. 4, pp. 1–9, 2015. [Google Scholar]
9. U. Hayat, N. A. Azam and M. Asif, “A method of generating 8 × 8 substitution boxes based on elliptic curves,” Wireless Personal Communications, vol. 101, no. 1, pp. 439–451, 2018. [Google Scholar]
10. N. A. Azam, U. Hayat and I. Ullah, “An injective S-box design scheme over an ordered isomorphic elliptic curve and its characterization,” Security and Communication Networks, vol. 18, no. 2, pp. 1–9, 2018. [Google Scholar]
11. G. Murtaza, N. A. Azam and U. Hayat, “Designing an efficient and highly dynamic substitution-box generator for block ciphers based on finite elliptic curves,” Security and Communication Networks, vol. 21, no. 1, pp. 1–14, 2021. [Google Scholar]
12. U. Hayat, N. A. Azam, H. R. G. Ruiz, S. Naz and L. Batool, “A truly dynamic substitution box generator for block ciphers based on elliptic curves over finite rings,” Arabian Journal of Science and Engineering, vol. 46, pp. 8887–8899, 2021. [Google Scholar]
13. X. Chai, H. Wu, Z. Gan, Y. Zhang, Y. Chen et al., “An efficient visually meaningful image compression and encryption scheme based on compressive sensing and dynamic LSB embedding,” Optics and Lasers in Engineering, vol. 124, no. 1, pp. 1–19, 2020. [Google Scholar]
14. X. Chai, X. Zheng, Z. Gan, D. Han and Y. Chen, “An image encryption algorithm based on chaotic system and compressive sensing,” Signal Processing, vol. 148, pp. 124–144, 2018. [Google Scholar]
15. Y. Yang, B. Guan, J. Li, D. Li, Y. Zhou et al., “Image compression-encryption scheme based on fractional order hyper-chaotic systems combined with 2D compressed sensing and DNA encoding,” Optics & Laser Technology, vol. 119, no. 1, pp. 1–14, 2019. [Google Scholar]
16. H. Wang, D. Xiao, M. Li, Y. Xiang and X. Li, “A visually secure image encryption scheme based on parallel compressive sensing,” Signal Processing, vol. 155, pp. 218–232, 2019. [Google Scholar]
17. X. Chai, Z. Gan, Y. Chen and Y. Zhang, “A visually secure image encryption scheme based on compressive sensing,” Signal Processing, vol. 134, pp. 35–51, 2017. [Google Scholar]
18. B. R. Gangadari and S. R. Ahamed, “Design of cryptographically secure AES like S-box using second-order reversible cellular automata for wireless body area network applications,” Healthcare Technology Letters, vol. 3, no. 3, pp. 177–183, 2016. [Google Scholar] [PubMed]
19. A. A. Alzaidi, M. Ahmad, H. S. Ahmed and E. A. Solami, “Sine-cosine optimization-based bijective substitution-boxes construction using enhanced dynamics of chaotic map,” Complexity, vol. 2018, no. 4, pp. 1–16, 2018. [Google Scholar]
20. Y. Wang, K. W. Wong, C. Li and Y. Li, “A novel method to design S-box based on chaotic map and genetic algorithm,” Physics Letters A, vol. 376, no. 6–7, pp. 827–833, 2012. [Google Scholar]
21. M. M. Dimitrov, “On the design of chaos-based S-boxes,” IEEE Access, vol. 8, pp. 117173–117181, 2020. [Google Scholar]
22. W. Yan and Q. Ding, “A novel S-box dynamic design based on nonlinear-transform of 1D chaotic maps,” Electronics, vol. 10, no. 11, pp. 1–11, 2021. [Google Scholar]
23. M. S. M. Malik, M. A. Ali, M. A. Khan, M. E. U. Haq, S. N. M. Shah et al., “Generation of highly nonlinear and dynamic AES substitution-boxes (S-boxes) using chaos-based rotational matrices,” IEEE Access, vol. 8, pp. 35682–35695, 2020. [Google Scholar]
24. A. Alghafis, N. Munir, M. Khan and I. Hussain, “An encryption scheme based on discrete quantum map and continuous chaotic system,” International Journal of Theoretical Physics, vol. 59, pp. 1227–1240, 2020. [Google Scholar]
25. Q. Lu, C. Zhu and X. Deng, “An efficient image encryption scheme based on the LSS chaotic map and single S-box,” IEEE Access, vol. 8, pp. 25664–25678, 2020. [Google Scholar]
26. E. Tanyildizi and F. Ozkaynak, “A new chaotic S-box generation method using parameter optimization of one-dimensional chaotic maps,” IEEE Access, vol. 7, pp. 117829–117838, 2019. [Google Scholar]
27. H. Liu, A. Kadir and C. Xu, “Cryptanalysis and constructing S-box based on chaotic map and backtracking,” Applied Mathematics and Computation, vol. 376, pp. 1–11, 2020. [Google Scholar]
28. F. Riaz and N. Siddiqui, “Design of an efficient cryptographic substitution box by using improved chaotic range with the golden ratio,” International Journal of Computer Science and Information Security, vol. 18, no. 1, pp. 89–94, 2020. [Google Scholar]
29. E. A. Solami, M. Ahmad, C. Volos, M. N. Dojia and M. M. S. Beg, “A new hyperchaotic system-based design for efficient bijective substitution-boxes,” Entropy, vol. 20, no. 7, pp. 1–17, 2018. [Google Scholar]
30. Y. Tian and Z. Lu, “S-Box: Six-dimensional compound hyperchaotic map and artificial bee colony algorithm,” Journal of Systems Engineering and Electronics, vol. 27, no. 1, pp. 232–241, 2016. [Google Scholar]
31. A. Ullah, S. S. Jamal and T. Shah, “A novel construction of substitution box using a combination of chaotic maps with improved chaotic range,” Nonlinear Dynamics, vol. 88, no. 7, pp. 2757–2769, 2017. [Google Scholar]
32. S. S. Jamal, M. U. Khan and T. Shah, “A watermarking technique with chaotic fractional S-box transformation,” Wireless Personal Communications, vol. 90, no. 4, pp. 2033–2049, 2016. [Google Scholar]
33. F. Özkaynak and S. Yavuz, “Designing chaotic S-Boxes based on time-delay chaotic system,” Nonlinear Dynamics, vol. 74, no. 3, pp. 551–557, 2013. [Google Scholar]
34. Y. Tian and Z. Lu, “Chaotic S-box: Six-dimensional fractional Lorenz–Duffing chaotic system and O-shaped path scrambling,” Nonlinear Dynamics, vol. 94, no. 3, pp. 2115–2126, 2018. [Google Scholar]
35. F. Özkaynak, “Construction of robust substitution boxes based on chaotic systems,” Neural Computing and Applications, vol. 31, no. 8, pp. 3317–3326, 2019. [Google Scholar]
36. F. Özkaynak, V. Çelik and A. B. Özer, “A new S-box construction method based on the fractional-order chaotic chen system,” Signal, Image and Video Processing, vol. 11, no. 4, pp. 659–664, 2017. [Google Scholar]
37. M. A. Khan, A. Ali, V. Jeoti and S. Manzoor, “A chaos-based substitution box (S-box) design with improved differential approximation probability (DP),” Iranian Journal of Science and Technology, Transactions of Electrical Engineering, vol. 42, no. 2, pp. 219–238, 2018. [Google Scholar]
38. M. Khan and Z. Asghar, “A novel construction of substitution box for image encryption applications with gingerbreadman chaotic map and S8 permutation,” Neural Computing and Applications, vol. 29, no. 4, pp. 993–999, 2018. [Google Scholar]
39. X. Wang, A. Akgul, U. Cavusoglu, V. T. Pham, D. V. Hong et al., “A chaotic system with infinite equilibria and its S-box constructing application,” Applied Sciences, vol. 8, no. 11, pp. 1–12, 2018. [Google Scholar]
40. Ü. Çavuşoğlu, A. Zengin, I. Pehlivan and S. Kaçar, “A novel approach for strong S-box generation algorithm design based on chaotic scaled zhongtang system,” Nonlinear Dynamics, vol. 87, no. 2, pp. 1081–1094, 2017. [Google Scholar]
41. X. Wang and Q. Wang, “A novel image encryption algorithm based on dynamic S-boxes constructed by chaos,” Nonlinear Dynamics, vol. 75, no. 3, pp. 567–576, 2014. [Google Scholar]
42. Z. Hua and Y. Zhou, “Dynamic parameter-control chaotic system,” IEEE Transactions on Cybernetics, vol. 46, no. 12, pp. 3330–3341, 2015. [Google Scholar] [PubMed]
43. H. Liu, F. Wen and A. Kadir, “Construction of a new 2D chebyshev-sine map and its application to color image encryption,” Multimedia Tools and Applications, vol. 78, no. 12, pp. 15997–16010, 2019. [Google Scholar]
44. X. Wang, Ü. Çavusoglu, S. Kacar, A. Akgul, V. T. Pham et al., “S-Box based image encryption application using a chaotic system without equilibrium,” Applied Sciences, vol. 9, no. 4, pp. 1–17, 2019. [Google Scholar]
45. T. S. Ali and R. Ali, “A novel color image encryption scheme based on a new dynamic compound chaotic map and S-box,” Multimedia Tools and Applications, vol. 81, no. 1, pp. 20585–20609, 2022. [Google Scholar] [PubMed]
46. Z. Man, J. Li, X. Di, Y. Sheng and Z. Liu, “Double image encryption algorithm based on neural network and chaos,” Chaos, Solitons & Fractals, vol. 152, no. 1, pp. 1–16, 2021. [Google Scholar]
47. Z. Man, J. Li, X. Di and O. Bai, “An image segmentation encryption algorithm based on hybrid chaotic system,” IEEE Access, vol. 7, no. 1, pp. 103047–103058, 2019. [Google Scholar]
48. Z. Liu, J. Li and X. Di, “A new hyperchaotic 4D-FDHNN system with four positive lyapunov exponents and its application in image encryption,” Entropy, vol. 24, no. 7, pp. 1–28, 2022. [Google Scholar]
49. I. Gagnon, A. April and A. Abran, “An investigation of the effects of chaotic maps on the performance of metaheuristics,” Engineering Reports, vol. 3, pp. 1–14, 2021. [Google Scholar]
50. A. H. Zahid, H. Rashid, M. M. U. Shaban, S. Ahmad, E. Ahmed et al., “Dynamic S-box design using a novel square polynomial transformation and permutation,” IEEE Access, vol. 9, pp. 82390–82401, 2021. [Google Scholar]
51. A. Manzoor, A. H. Zahid and M. T. Hassan, “A new dynamic substitution box for data security using an innovative chaotic map,” IEEE Access, vol. 10, pp. 74164–74174, 2022. [Google Scholar]
52. Y. Wang, Z. Zhang, L. Y. Zhang, J. Feng, J. Gao et al., “A genetic algorithm for constructing bijective substitution boxes with high nonlinearity,” Information Science, vol. 523, pp. 152–166, 2020. [Google Scholar]
53. K. M. Ali and M. Khan, “A new construction of confusion component of block ciphers,” Multimedia Tools and Applications, vol. 78, no. 22, pp. 32585–32604, 2019. [Google Scholar]
54. Z. Jiang and Q. Ding, “Construction of an S-box based on chaotic and bent functions,” Symmetry, vol. 13, no. 4, pp. 1–11, 2021. [Google Scholar]
55. A. H. Zahid, L. O. A. I. Tawalbeh, S. Member, M. Ahmad and A. K. Farhan, “Efficient dynamic S-box generation using linear trigonometric transformation for security applications,” IEEE Access, vol. 9, pp. 98460–98475, 2021. [Google Scholar]
56. J. Liu, X. Tong, M. Zhang and Z. Wang, “The design of S-box based on combined chaotic map,” in Proc. AEMCSE, ShenZhen, China, pp. 350–353, 2020. [Google Scholar]
57. T. Farah, R. Rhouma and S. Belghith, “A novel method for designing S-box based on chaotic map and teaching–learning-based optimization,” Nonlinear Dynamics, vol. 88, no. 2, pp. 1059–1074, 2017. [Google Scholar]
58. H. Zhu, X. Tong, Z. Wang and J. Ma, “A novel method of dynamic S-box design based on combined chaotic map and fitness function,” Multimedia Tools and Applications, vol. 79, no. 17–18, pp. 12329–12347, 2020. [Google Scholar]
59. D. Lambić, “A new discrete-space chaotic map based on the multiplication of integer numbers and its application in S-box design,” Nonlinear Dynamics, vol. 100, no. 1, pp. 699–711, 2020. [Google Scholar]
60. A. Shafique, “A new algorithm for the construction of substitution box by using chaotic map,” The European Physical Journal Plus, vol. 135, no. 2, pp. 1–13, 2020. [Google Scholar]
61. D. Lambić, “S-Box design method based on improved one-dimensional discrete chaotic map,” Journal of Information and Telecommunication, vol. 2, no. 2, pp. 181–191, 2018. [Google Scholar]
62. D. Lambić, “A novel method of S-box design based on discrete chaotic map,” Nonlinear Dynamics, vol. 87, pp. 2407–2413, 2017. [Google Scholar]
63. H. S. Alhadawi, M. A. Majid, D. Lambić and M. Ahmad, “A novel method of S-box design based on discrete chaotic maps and cuckoo search algorithm,” Multimedia Tools and Applications, vol. 80, no. 5, pp. 7333–7350, 2021. [Google Scholar]
64. D. Lambić, “A novel method of S-box design based on chaotic map and composition method,” Chaos, Solitons & Fractals, vol. 58, pp. 16–21, 2014. [Google Scholar]
65. S. Ibrahim, H. Alhumyani, M. Masud, S. S. Alshamrani, O. Cheikhrouhou et al., “Framework for efficient medical image encryption using dynamic S-boxes and chaotic maps,” IEEE Access, vol. 8, pp. 160433–160449, 2020. [Google Scholar]
66. M. Long and L. Wang, “S-Box design based on discrete chaotic map and improved artificial bee colony algorithm,” IEEE Access, vol. 9, pp. 86144–86154, 2021. [Google Scholar]
67. F. Masood, J. Masood, L. Zhang, S. S. Jamal, W. Boulila et al., “A new color image encryption technique using DNA computing and chaos-based substitution box,” Soft Computing, vol. 26, no. 1, pp. 7461–7477, 2022. [Google Scholar]
68. A. F. Webster and S. E. Tavares, “On the design of S-boxes,” in Proc. CRYPTO’85, Santa Barbara, CA, USA, pp. 523–534, 1986. [Google Scholar]
69. M. Matsui, “Linear cryptanalysis method for DES cipher,” in Proc. EUROCRYPT’93, Lofthus, Norway, pp. 386–397, 1994. [Google Scholar]
70. H. M. Heys, “A tutorial on linear and differential cryptanalysis,” Cryptologia, vol. 26, no. 3, pp. 189–221, 2002. [Google Scholar]
71. E. Biham and A. Shamir, “Differential cryptanalysis of DES-like cryptosystems,” Journal of Cryptology, vol. 4, no. 1, pp. 3–72, 1991. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF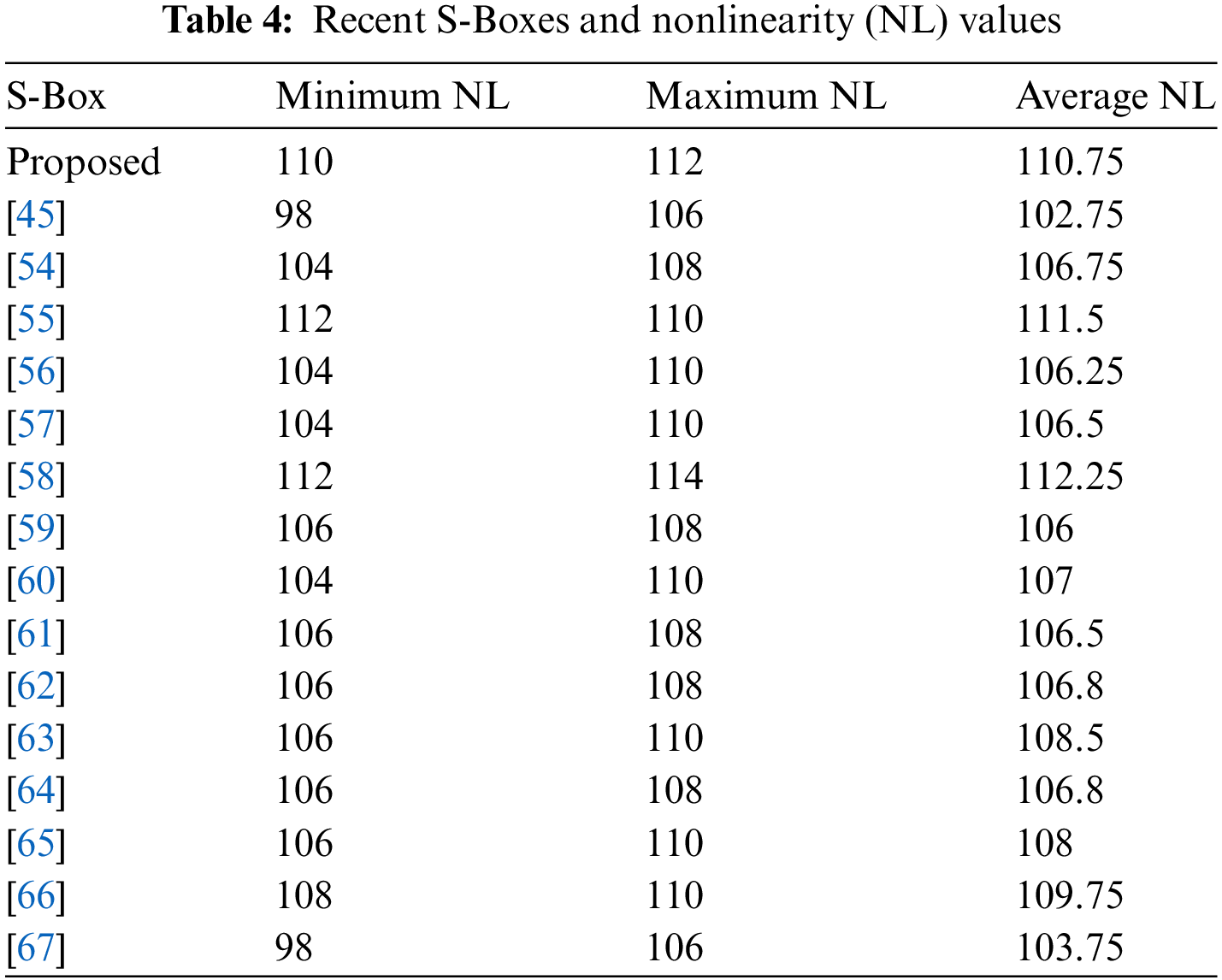
 Downloads
Downloads
 Citation Tools
Citation Tools
