Automated Colonic Polyp Detection and Classification Enabled Northern Goshawk Optimization with Deep Learning

1  Introduction

One of the leading factors of death relevant to the intestinal tract is the cancer cell development in its many body parts. Still, initial cancer detection is at earlier stages, and a proper examination of everyone above 50 years could minimize the death ratio among these patients [1]. Specifically, colonic polyps (benign tumours or growth that arises on the inner colon surface) contain a high existence and are the precursor of colon cancer growth. Endoscopy is a very common technique to identify colon polyps. Various researchers have shown that automated detection of the image region that comprises polyps in the colon is utilized to assist authorities in decreasing polyp miss rates [2]. The automated identification of polyps in a computer-aided diagnosis (CAD) mechanism was generally executed via a statistical analysis related to spatial features, color, texture, or shape implemented in the video frames [3]. The major problems for the detection were the diverse aspects of textures, color, and shape of polyps, which are influenced [4], for instance, by the viewing angle, the distance from the camera which is capturing, or also by the colon insufflation along with the degree of colon muscular contraction.

Once the detection is completed, the colonic polyps are categorized into 3 different classes: malignant, hyperplasic, and adenomatous [5]. The “pit-pattern” method helps detect tumorous lesions after identifying suspicious areas. In this method, the mucosal surfaces of the colon are categorized into five kinds labelling the distribution, size, and shape of the pit structures [6]. In the artificial intelligence (AI) domain, deep-learning (DL) computational methods, made up of many processing layers, could study various levels of abstraction for data representation. Such data abstractions have intensely enhanced the visual object recognition application and existing computer vision (CV) and, in a few cases, exceeded human performance. DL methods are used in self-driving cars and autonomous mobile robots [7]. The formulation of DL methods recently became realistic owing to large amounts of training data available via the World Wide Web (WWW), public data repository, and new high-performance computation abilities, which were mostly because of the new generation of graphics processing units (GPUs) required for optimizing such methods [8]. As per recent research, DL has given superior outcomes in the area of CV and object detection. It has overcome the human potentiality in task recognition and playing games. In medical imaging, DL has also offered promising outcomes [9]. The tasks, namely classification, detection, recognition, and medical images, have become easier. AI systems compile the automatic diagnosis mechanism of endoscopic images with maximum accuracy compared to a trained specialist or expert [10]. Thus, automated detection systems that are faster and more reliable have to be developed.

This manuscript devises a new Northern Goshawk Optimization with Transfer Learning Model for Colonic Polyp Detection and Classification (NGOTL-CPDC) model. The NGOTL-CPDC technique aims to investigate endoscopic images for the automated detection of colonic polyps. To accomplish this, the NGOTL-CPDC technique comprises of adaptive bilateral filtering (ABF) technique as a noise removal process and image pre-processing step. Besides, the NGOTL-CPDC model applies the Faster SqueezeNet model for feature extraction purposes in which the hyperparameter tuning process is performed using the NGO optimizer. Finally, the fuzzy Hopfield neural network (FHNN) method can be leveraged for colonic poly detection and classification. A widespread simulation analysis is carried out to ensure the improved outcomes of the NGOTL-CPDC model.

2  Literature Review

In [11], trained recurrent neural network (RNN) and convolutional neural network (CNN) on biopsy histopathology whole-slide images (WSIs) of the colon and stomach. The model was well-trained to categorize WSI into non-neoplastic, adenocarcinoma, and adenoma. Hsu et al. [12] suggested a colorectal polyp image recognition and classification methodology via deep learning and grayscale image. Polyp recognition and classification have been implemented by the CNN method. Information for polyp recognition was classified into 5 classes and tested under fivefold validation. Rodriguez-Diaz et al. [13] developed a CAD method which seeks to improve the interpretability and transparency of outcomes by producing an intuitive visualization of the method forecasted histology through the polyp surface. Then, a DL method with semantical segmentation was proposed to describe polyp boundaries and a DL method for classifying sub-region within a segmented polyp.

Li et al. [14] designed a new and scalable diagnosis technique based on deep neural network (DNN) and fast Region-based CNN (Fast RCNN) by raising the combination of feature mappings at distinct levels. Mahmood et al. [15] propose the application of cinematic rendering in DL, where the authors present a model to adjust synthetic data-driven networks through cinematically rendering CT datasets for monocular depth approximation in endoscopy. The experimental study demonstrates that: CNN trained on a synthetic dataset and adjusted on a photorealistic cinematically rendered dataset can be adapted better for real-time medical imaging and illustrate high performance than the network without fine-tuning. Ribeiro et al. [16] address the transfer learning through CNN for automatically classifying colonic polyps in eight endoscopic image datasets attained through distinct modalities. Therefore, the authors have explored if the training approach, the structure, the nature of the images, the number of classes, and the number of images in the training stage might affect the outcomes.

But, still, it remains a challenge. Due to the continuous deepening of the algorithm, the various parameters of DL methods also quickly rise, which leads to model over-fitting. Simultaneously, distinct hyperparameters have a greater influence on the effectiveness of the CNN module, especially the learning rate. Also, it needs to adapt the learning rate parameter to obtain improved performance. Therefore, this study addresses the parameter optimization problem using the NGO algorithm.

3  The Proposed Model

This work devised a new NGOTL-CPDC algorithm for Colonic Polyp Detection and Classification on biomedical images. The presented NGOTL-CPDC algorithm intends to inspect the endoscopic images for automated detection of the colonic polyp. The NGOTL-CPDC technique applies ABF pre-processing, Faster SqueezeNet-driven feature extraction, FHNN classification, and NGO-based parameter tuning. Fig. 1 illustrates the working procedure of the NGOTL-CPDC approach.

Figure 1: Working process of NGOTL-CPDC approach

3.1 Image Pre-processing: ABF Technique

In this work, the NGOTL-CPDC technique comprises of ABF technique as a noise removal process and image pre-processing step. In the study, ABF is employed on the input images for noise reduction, and the mathematical formula of the presented method is shown below [17]:

ABFxo,yo=∑x=x0−Nx0+N∑y=y0−Ny0+Nexp((x−x0)2+(y−y0)2∇d2)×exp⁡(−(G[m,n]−G[x0,y0]−δ[x0,y0])22∇r2[x0,y0](1)

Once ∇−r and δ are set, the ABF is degraded to a standard 2-way filter. A lower frequency filter, constant frequency, is adapted for ABF. Furthermore, by increasing the edge gradient and computation of Δ, ABF sharpens the image given as follows.

δ[x0,y0]={MAXIMUM(βx0,y0)−G[x0,y0],if Ωx0,y0>0MINIMUM(βx0,y0)−G[x0,y0],if Ωx0,y0>00,if Ωx0,y0=0(2)

The size of the input image window represents (2W + 1) × (2W + 1). Each pixel can be denoted by β−(x−(0,)y−0) via center point [x−(0,)y−0]. Consider MAXIMUM and MINIMUM to characterize every data value retrieval function. The efficacy of ABF has an effective range filter and fixed douchean filter. Now ∇−(d)=1 is set, and ∇−(r) adjusts the s value.

3.2 Feature Extraction: Faster SqueezeNet Model

At this stage, the NGOTL-CPDC model exploited the Faster SqueezeNet model for feature extraction. To enhance the real-time and accuracy performance of the classifier method, Fast SqueezeNet has been developed [18]. To avoid over-fitting, BatchNorm and residual structure are added. Like DenseNet, we employ concat to interconnect various layers to enhance the expression of the few initial layers in the network. Fast SqueezeNet comprises a global average pooling layer, 1 BatchNorm layer, 3 block layers, and 4 convolution layers. Mainly, Fast SqueezeNet is enhanced as follows:

(1) To further enhance the data flow between layers, the study proposed a different connection mode and imitated the DenseNet structure. This comprises a fire module and pooling layer, and lastly, the 2 concat layers were interconnected to the following convolution layers and are given below.

The present layer gets each feature map of the previous layer and uses x0, …, xl−1 as input, and it is expressed as follows

xl=Hl([x0,x1,…,xl−1]),(3)

In Eq. (3), [x0,x1,…,xl−1] represents the connection of feature graphs produced in layers 0,1, …, l−1 and Hl (.) concatenates more than one input. Now, x0 signifies themax pooling layer, x1 signifies the Fire layer, and xl indicates the concat layer. Fig. 2 portrays the framework of SqueezeNet.

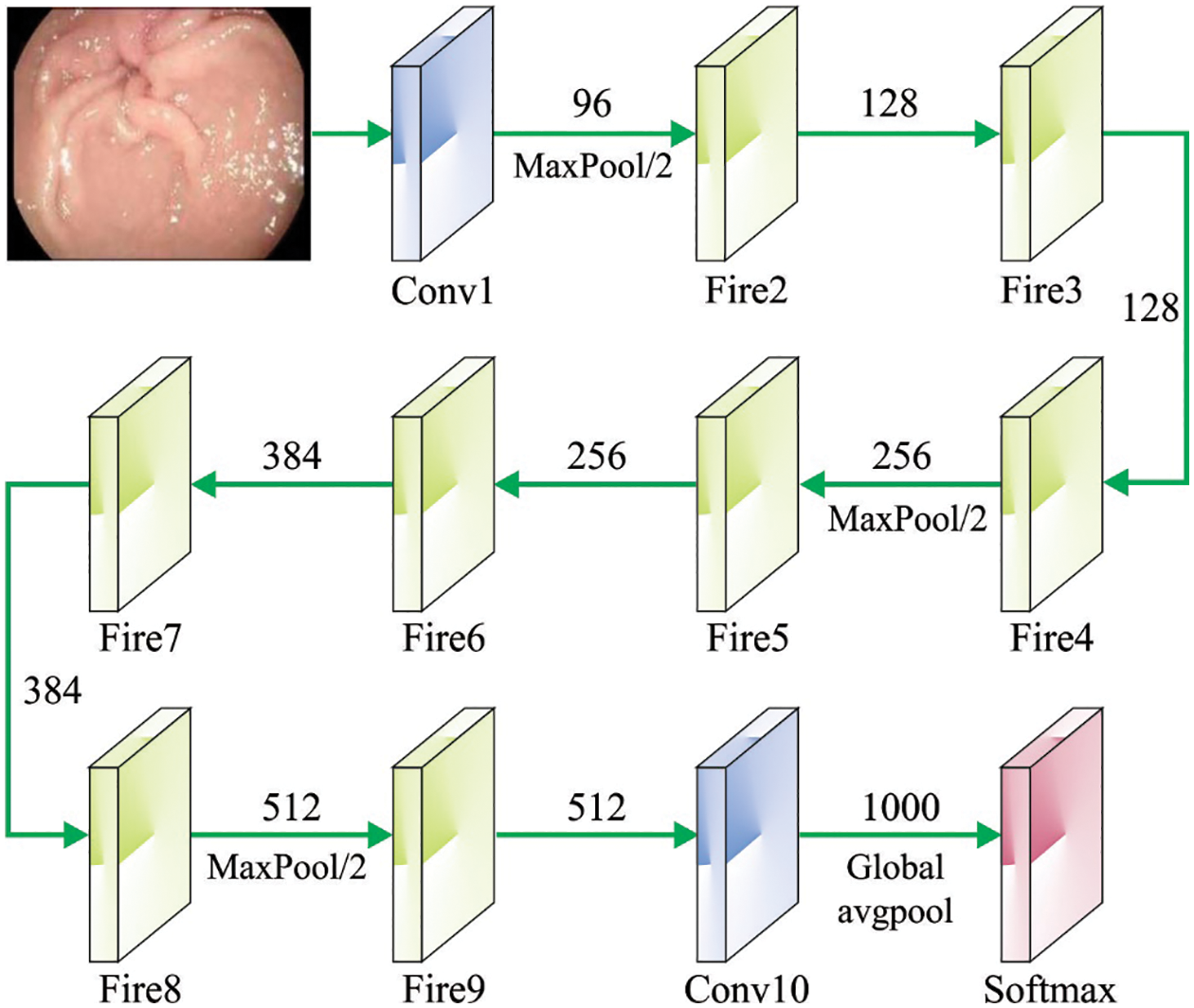
Figure 2: Structure of SqueezeNet model

Without improving the network variables count, the efficiency of the network is improved in the earlier phases, and simultaneously, the two-layer network might communicate data.

(2) We learn from ResNet architecture and present distinct components comprising fire module and pooling layer for good network convergence. At last, afterwards adding the two layers, it is interconnected with the following convolution layer.

In ResNet, the shortcut connection exploits identity mapping that implies the input of the convolutional stack was added straightaway to the output of the convolutional stack. Formally, representing the desired mapping as (x), then let the stacked non-linear layer fit other mappings of F(x):=H(x)−x. The original mapping was re-casted into F(x)+x.

The Adam optimizer is employed for training the Faster SqueezeNet module. This process is extensively applied to the DL model that needs a computer adaptive learning rate for distinct variables, the initial order, and gradient-based descent with smaller memory [19]. This technique is computationally effective and easier to implement and has shown to be effective compared to Rprop and RMSprop optimizers. The rescaling procedure of the gradients depends on the magnitude of the updating variable. The Adam optimizer works with a limited gradient and doesn’t need a stationary object. Then, calculate past squared gradients mt and vt and the decaying average of past, correspondingly:

mt=β1mt−1+(1−β1)gt(4)

vt=β2vt−1+(1−β2)gt2(5)

mt and vt are approximations of the initial moment (the mean) and subsequent moment (uncentred variance) correspondingly. mt and vt are set as a vector of 0′s, the author of Adam observes that they are biased to zero, particularly in the first-time step, and particularly after the decay rate becomes smaller (viz. β1 and β2 are closer to 1). It counteracts the bias by calculating bias-corrected 1st- and 2nd-moment approximations:

m^t=mt1−β1t(6)

v^t=vt1−β2t(7)

Then, they employ this to upgrade the parameter:

θt+1=θt−ηv^t+ε1m^t(8)

Here, we employ the default values: β1=0.9, β2=0.999 and ε=10−8, and the learning rate η=0.001.

3.3 Hyperparameter Tuning: NGO Algorithm

The NGO algorithm with the Faster SqueezeNet method was employed for colonic poly detection and classification. The simulation of NGOs during hunting was applied in designing the suggested method to update the population member [20]. In this strategy, the 2 major behaviors of northern goshawk are given below.

(i)   Prey identification and attack and

(ii)   Chase and escape operations.

PHASE 1: PREY IDENTIFICATION (EXPLORATION)

During this stage, select prey at random and quickly assault them. This stage raises NGOs’ exploration ability because of the random choice of prey in the search domain. This stage results in a global search of the search domain to identify the optimum region. In the following, the mathematical expression of this phase can be given.

Pi=Xk,i=1,2,…,N,k=1,2,…,i−1,i+1,…,N,(9)

xi,jnew,P1={xi,j+r(pi,j−Ixi,j),FPi<Fi,xi,j+r(xi,j−pi,j),FPi≥Fi,(10)

Xi={Xinew,P1,Finew,P1<Fi,Xi,Finew,P1≥Fi,(11)

Now, Pi indicates the location of prey for i-th northern goshawk, FPi denotes the value of the objective function, k shows a random integer within [1, N], Xinew,P1 denotes the novel status for the i-th solution, xijnew,P1 indicates the j-th dimensions, Finew,P1 shows the objective function value depends on the initial stage of NGO, r indicates an arbitrary value within [0,1]. I show a random integer 1 or 2. r, and I parameters are random values utilized for randomly generating NGO behaviors in search and update.

PHASE 2: CHASE AND ESCAPE OPERATION (EXPLOITATION)

Afterwards, the northern goshawk will attack the prey, and they will try to escape. Consequently, they continue to chase the target in the tail and chase procedure. Because of the higher speed of northern goshawks, they chase the prey in nearly all situations and ultimately hunt. Simulation of these behaviors increased exploitation ability for local search of search domain. In this work, it can be considered that hunting was close to an assault location having a radius R. The chasing procedure among the prey and northern goshawk and the mathematical expression of this phase is shown below.

xi,jnew,P2=xi,j+R(2r−1)xi,j,(12)

R=0.02(1−tT),(13)

Xi={Xinew,P2,Finew,P2<Fi,Xi,Finew,P2≥Fi.(14)

Now, t denotes the iteration count, T represents the maximal iteration count, Xinew,P2 denotes the novel status for ani-th solution, xi,jnew,P2 indicates the j-th parameter, Finex, and P2 denotes the value of the objective function.

Afterwards, each member of the population was upgraded based on the first and second stages of the presented method, an iteration of the model was finished, and the main function, the optimal proposed solution, and the new value of the population member were defined. Then, the model will enter the following iteration and update the population member by using Eqs. (9) to (14) until the final iteration of the model is accomplished. The better solution attained in the model iteration was initiated as a quasi-optimum solution for optimization issues at the end and after the complete implementation of the NGO. The different phases of the NGO method are indicated as pseudocode in Algorithm 1.

The Fitness function of the NGO technique can be derived to accomplish better classification performance. It describes a positive integer to characterize the improved efficiency of the candidate solution. Considering the reduction of classification error rate in this work as the fitness function. The worse solution has an improved error rate, and the optimal solution attains the least error rate.

fitness(xi)=Classifier Error Rate(xi)

=number of misclassified samplesTotal number of samples∗100(15)

3.4 Image Classification: FHNN Model

To detect and classify colonic polyps, the FHNN method is used. A fuzzy neural network (NN) is a group of computation intelligence and is a great alternative to processing datasets with uncertainty [21]. They could process the data and recognize the pattern to detect the fault occurrence, which defines the location and type of the fault.

The mathematical equation of the Hopfield network is given as follows:

dxjdt=∑i=1nTijyi+uj

yj=F(xj),j=1,…,n(16)

where is the number of neurons, xj are states, the neural synaptic weights are demonstrated as TijIj are the bias input, yj indicates the output, and lastly, F(X) refers to a Gaussian fuzzy set in the following:

F(xj)=e−0.5(xj−mk,jσk,j)2(17)

In Eq. (17), mk,j and σk,j denotes the centre and spread of the Gaussian function, correspondingly. Details on the feedforward formula and parameter updating are presented in Appendix.

An algorithm based on NN programming has complex disadvantages and various benefits. The most significant factor in selecting the kind of network is the network structure (consisting of the number of neurons in each layer, the number of layers, parameters of learning algorithms, activation of functions, etc.).

4  Results and Discussion

The proposed model is simulated using Python 3.6.5 tool. The proposed model experiments on PC i5-8600k, GeForce 1050 Ti 4 GB, 16 GB RAM, 250 GB SSD, and 1 TB HDD. The parameter settings are learning rate: 0.01, dropout: 0.5, batch size: 5, epoch count: 50, and activation: ReLU. The experimental validation of the NGOTL-CPDC method on colonic polyp classification takes place on an endoscopic image dataset. Table 1 depicts the details of the dataset. A few samples of Non-polyp and polyp images are demonstrated in Fig. 3. The dataset holds 375 polyp images and 742 non-polyp images.

Figure 3: Sample images (a) Non-polyp, (b) Polyp

The confusion matrices created at the time of colonic polyp classification are depicted under training (TR) and testing (TS) data in Fig. 4. The NGOTL-CPDC model has exhibited the effectual identification of polyp and non-polyp samples in both cases.

Figure 4: Confusion matrices of NGOTL-CPDC approach (a–b) TR and TS databases of 80:20 and (c–d) TR and TS databases of 70:30

Table 2 provides a brief set of colonic polyp classification outcomes of the NGOTL-CPDC method with 80% of the TR database and 20% of TS data. The classification results of the NGOTL-CPDC method on 80% of the TR database are depicted in Fig. 5. The figure revealed the NGOTL-CPDC method has enhanced outcomes on both class labels. For example, on polyp image classification, the NGOTL-CPDC approach has attained accuy, precn, recal, Fscore, and Jaccardindex of 98.54%, 98.59%, 96.89%, 97.73%, and 95.56%, respectively.

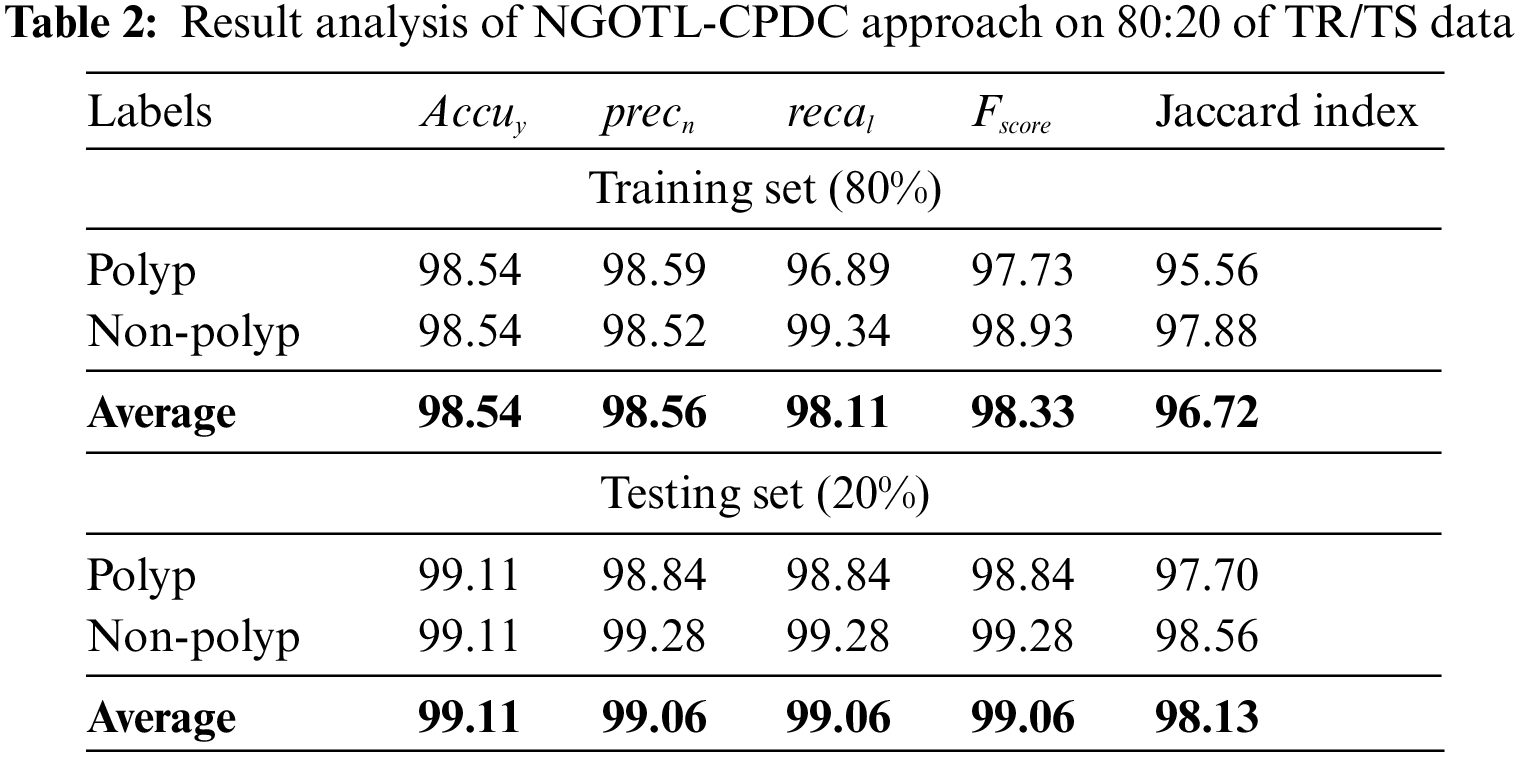
Figure 5: Result analysis of NGOTL-CPDC method under 80% of TR data

Meanwhile, on non-polyp image classification, the NGOTL-CPDC method has achieved accuy, precn, recal, Fscore, and Jaccardindex of 98.54%, 98.52%, 99.34%, 98.93%, and 97.88% correspondingly.

The classification outcomes of the NGOTL-CPDC method on 20% of the TS database are portrayed in Fig. 6. The figure exposes the NGOTL-CPDC algorithm has attained enhanced results on both class labels. For example, on polyp image classification, the NGOTL-CPDC approach has attained accuy, precn, recal, Fscore, and Jaccardindex of 99.11%, 98.84%, 98.84%, 98.84%, and 97.70% correspondingly. Concurrently, on non-polyp image classification, the NGOTL-CPDC approach has gained accuy, precn, recal, Fscore, and Jaccardindex of 99.11%, 99.28%, 99.28%, 99.28%, and 98.56% correspondingly.

Figure 6: Result analysis of NGOTL-CPDC approach in 20% of TS data

Table 3 presents the detailed colonic polyp classification outcomes of the NGOTL-CPDC approach with 70% of the TR and 30% of the TS databases. The classification results of the NGOTL-CPDC algorithm on 70% of the TR database are depicted in Fig. 7. The figure exposed that the NGOTL-CPDC approach has obtained enhanced results on both class labels. For example, on polyp image classification, the NGOTL-CPDC method has obtained accuy, precn, recal, Fscore, and Jaccardindex of 99.10%, 99.16%, 97.93%, 98.54%, and 97.13% correspondingly. Concurrently, on non-polyp image classification, the NGOTL-CPDC approach has reached accuy, precn, recal, Fscore, and Jaccardindex of 99.10%, 99.08%, 99.63%, 99.35%, and 98.71% correspondingly.

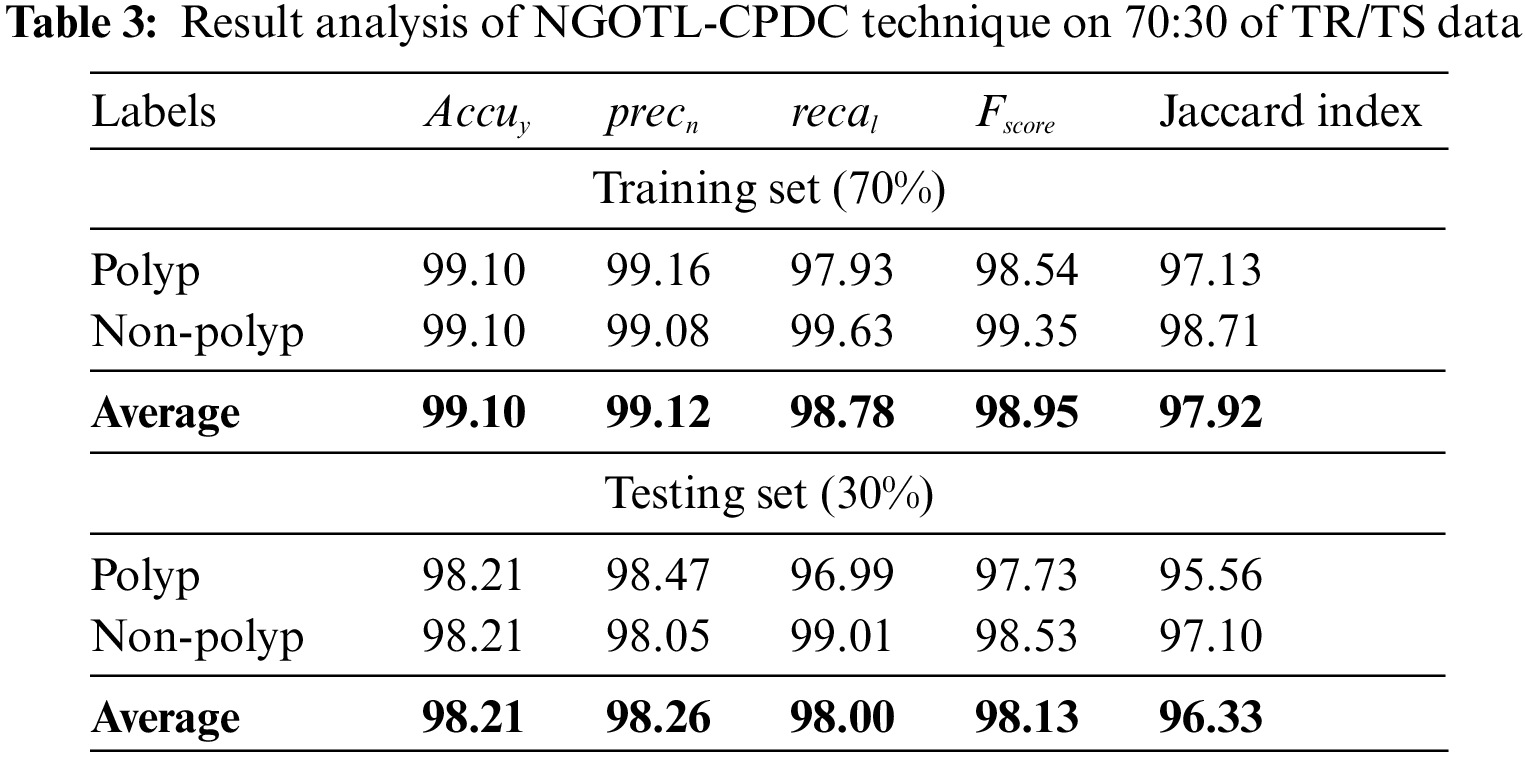
Figure 7: Result analysis of NGOTL-CPDC technique under 70% of the TR database

The classification results of the NGOTL-CPDC technique on 30% of the TS database are depicted in Fig. 8. The figure showed the NGOTL-CPDC algorithm had obtained enhanced results on both class labels. For example, on polyp image classification, the NGOTL-CPDC approach has reached accuy, precn, recal, Fscore, and Jaccardindex of 98.21%, 98.47%, 96.99%, 97.73%, and 95.56% correspondingly. Meanwhile, on non-polyp image classification, the NGOTL-CPDC technique has gained accuy, precn, recal, Fscore, and Jaccardindex of 98.21%, 98.05%, 99.01%, 98.53%, and 97.10% correspondingly.

Figure 8: Result analysis of NGOTL-CPDC approach on 30% of the TS database

The training accuracy (TACC) and validation accuracy (VACC) achieved by the NGOTL-CPDC method on the test database is displayed in Fig. 9. The simulation values inferred that the NGOTL-CPDC technique had achieved maximal values of TACC and VACC. Certainly, the VLA is superior to TRA.

Figure 9: TACC and VACC analysis of NGOTL-CPDC technique

The training loss (TLS) and validation loss (VLS) gained by the NGOTL-CPDC technique on the test database are established in Fig. 10. The experimental result implicit that the NGOTL-CPDC method has exhibited minimal values of TLS and VLS. The VLL seems to be less than TRL.

Figure 10: TLS and VLS analysis of NGOTL-CPDC approach

A clear precision-recall review of the NGOTL-CPDC methodology on the test database is shown in Fig. 11. The figure exhibits the NGOTL-CPDC method has enhanced precision-recall values in every class label.

Figure 11: Precision-recall analysis of the NGOTL-CPDC method

The detailed ROC study of the NGOTL-CPDC method on the test database is represented in Fig. 12. The results signified the NGOTL-CPDC algorithm had revealed its ability to classify different classes on the test database.

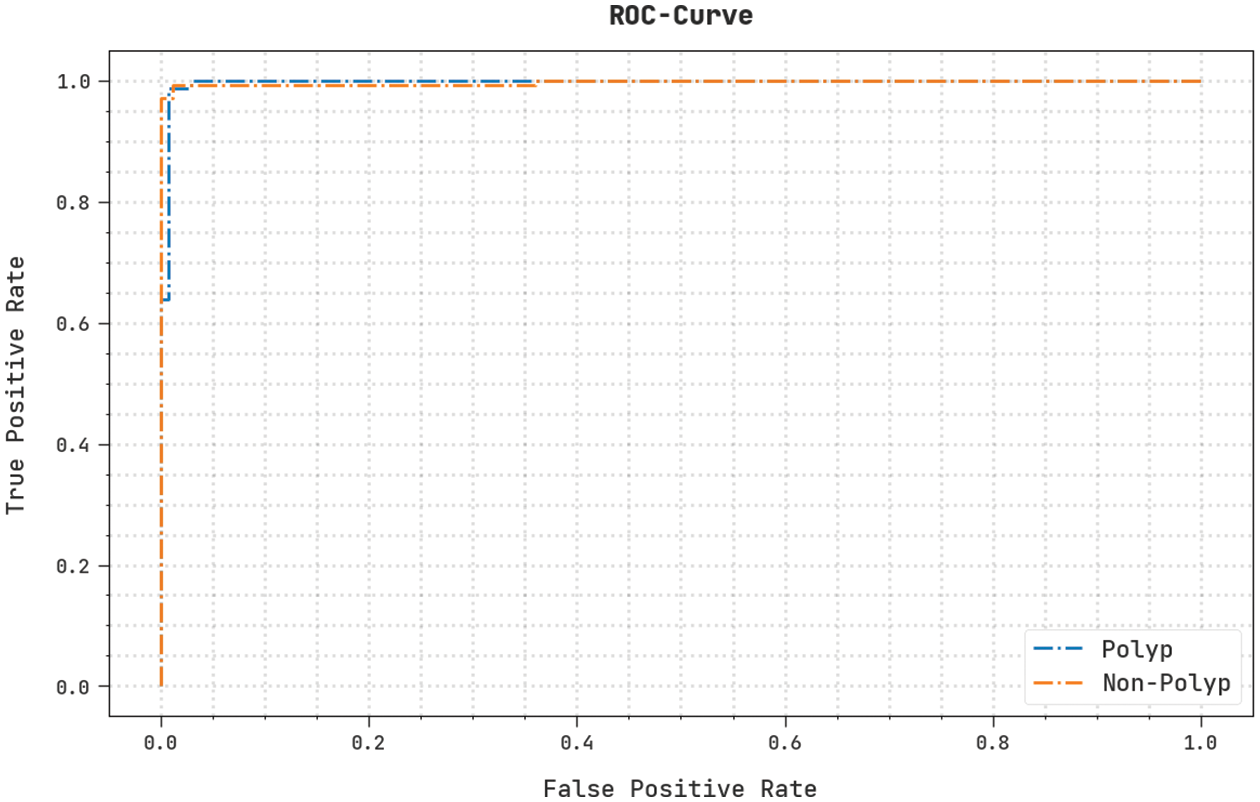
Figure 12: ROC curve analysis of NGOTL-CPDC technique

Table 4 illustrates a comparative result analysis of the NGOTL-CPDC model with other DL models in terms of accuy and computational time (CT) [22]. The outcomes specified that the NGOTL-CPDC method had achieved better performance with maximum accuy and minimal CT values. For instance, based on accuy, the NGOTL-CPDC model has shown improved outcomes with an accuy of 99.11%. In contrast, the modified ResNet-50, Mask R-CNN, Inception v3, CNN-based transfer learning (CNN-TFL), and VGG-16 models have demonstrated degraded results with accuy of 98.99%, 92.54%, 97.68%, 94.45%, and 98.12% respectively.

Finally, based on CT, the NGOTL-CPDC technique has revealed enhanced outcomes with CT of 5.36 s. In contrast, the modified ResNet-50, Mask R-CNN, Inception v3, CNN-TFL, and VGG-16 approaches have degraded results with CT of 10.67, 6.80, 11.06, 10.57, and 8.19 s correspondingly. From the detailed discussion, it is assumed that the NGOTL-CPDC method exhibited maximum performance in the colonic polyp classification process.

5  Conclusion

This work devised a new NGOTL-CPDC model for Colonic Polyp Detection and Classification on biomedical images. The NGOTL-CPDC method aims to investigate endoscopic images for automated colonic polyp detection. To accomplish this, the NGOTL-CPDC technique comprises of ABF technique as a noise removal process and image pre-processing step. Besides, the NGOTL-CPDC model applies the Faster SqueezeNet model for feature extraction purposes in which the hyperparameter tuning process is performed using the Adam optimizer. Finally, the NGO algorithm with the FHNN model is utilized for colonic poly detection and classification. A widespread simulation analysis is carried out to ensure the improved outcomes of the NGOTL-CPDC model. The comparison study demonstrates the enhancements of the NGOTL-CPDC model on the colonic polyp classification process on medical test images with maximum accuracy of 99.11%. In future, multimodal data classification model can be derived to extend the proposed model. Besides, large-scale real-time datasets can be used to test the consistent performance of the proposed model.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. W. Wang, J. Tian, C. Zhang, Y. Luo, X. Wang et al., “An improved deep learning approach and its applications on colonic polyp images detection,” BMC Medical Imaging, vol. 20, no. 1, pp. 83, 2020. [Google Scholar] [PubMed]

2. S. A. Azer, “Challenges facing the detection of colonic polyps: What can deep learning do?,” Medicina, vol. 55, no. 8, pp. 473, 2019. [Google Scholar] [PubMed]

3. N. Ito, H. Kawahira, H. Nakashima, M. Uesato, H. Miyauchi et al., “Endoscopic diagnostic support system for ct1b colorectal cancer using deep learning,” Oncology, vol. 96, no. 1, pp. 44–50, 2018. [Google Scholar] [PubMed]

4. S. Tanwar and S. Vijayalakshmi, “Comparative analysis and proposal of deep learning based colorectal cancer polyps classification technique,” Journal of Computational and Theoretical Nanoscience, vol. 17, no. 5, pp. 2354–2362, 2020. [Google Scholar]

5. K. Bora, M. K. Bhuyan, K. Kasugai, S. Mallik and Z. Zhao, “Computational learning of features for automated colonic polyp classification,” Scientific Reports, vol. 11, no. 1, pp. 4347, 2021. [Google Scholar] [PubMed]

6. E. J. Gong, C. S. Bang, J. J. Lee, S. I. Seo, Y. J. Yang et al., “No-code platform-based deep-learning models for prediction of colorectal polyp histology from white-light endoscopy images: Development and performance verification,” Journal of Personalized Medicine, vol. 12, no. 6, pp. 963, 2022. [Google Scholar] [PubMed]

7. W. S. Liew, T. B. Tang, C. H. Lin and C. K. Lu, “Automatic colonic polyp detection using integration of modified deep residual convolutional neural network and ensemble learning approaches,” Computer Methods and Programs in Biomedicine, vol. 206, no. 2, pp. 106114, 2021. [Google Scholar] [PubMed]

8. C. Ho, Z. Zhao, X. F. Chen, J. Sauer, S. A. Saraf et al., “A promising deep learning-assistive algorithm for histopathological screening of colorectal cancer,” Scientific Reports, vol. 12, no. 1, pp. 1–9, 2022. [Google Scholar]

9. L. D. Tamang and B. W. Kim, “Deep learning approaches to colorectal cancer diagnosis: A review,” Applied Sciences, vol. 11, no. 22, pp. 10982, 2021. [Google Scholar]

10. J. Escorcia-Gutierrez, M. Gamarra, P. P. Ariza-Colpas, G. B. Roncallo, N. Leal et al., “Galactic swarm optimization with deep transfer learning driven colorectal cancer classification for image guided intervention,” Computers and Electrical Engineering, vol. 104, no. 40, pp. 108462, 2022. [Google Scholar]

11. O. Iizuka, F. Kanavati, K. Kato, M. Rambeau, K. Arihiro et al., “Deep learning models for histopathological classification of gastric and colonic epithelial tumours,” Scientific Reports, vol. 10, no. 1, pp. 1–11, 2020. [Google Scholar]

12. C. M. Hsu, C. C. Hsu, Z. M. Hsu, F. Y. Shih, M. L. Chang et al., “Colorectal polyp image detection and classification through grayscale images and deep learning,” Sensors, vol. 21, no. 18, pp. 5995, 2021. [Google Scholar] [PubMed]

13. E. Rodriguez-Diaz, G. Baffy, W. K. Lo, H. Mashimo, G. Vidyarthi et al., “Real-time artificial intelligence-based histologic classification of colorectal polyps with augmented visualization,” Gastrointestinal Endoscopy, vol. 93, no. 3, pp. 662–670, 2021. [Google Scholar] [PubMed]

14. J. Li, J. Zhang, D. Chang and Y. Hu, “Computer-assisted detection of colonic polyps using improved faster R-CNN,” Chinese Journal of Electronics, vol. 28, no. 4, pp. 718–724, 2019. [Google Scholar]

15. F. Mahmood, R. Chen, S. Sudarsky, D. Yu and N. J. Durr, “Deep learning with cinematic rendering: Fine-tuning deep neural networks using photorealistic medical images,” Physics in Medicine & Biology, vol. 63, no. 18, pp. 185012, 2018. [Google Scholar]

16. E. Ribeiro, M. Häfner, G. Wimmer, T. Tamaki, J. J. Tischendorf et al., “Exploring texture transfer learning for colonic polyp classification via convolutional neural networks,” in IEEE 14th Int. Symp. on Biomedical Imaging (ISBI), Melbourne, VIC, Australia, pp. 1044–1048, 2017. [Google Scholar]

17. P. V. Sudeep, S. I. Niwas, P. Palanisamy, J. Rajan, Y. Xiaojun et al., “Enhancement and bias removal of optical coherence tomography images: An iterative approach with adaptive bilateral filtering,” Computers in Biology and Medicine, vol. 71, no. 1–2, pp. 97–107, 2016. [Google Scholar] [PubMed]

18. Y. Xu, G. Yang, J. Luo and J. He, “An electronic component recognition algorithm based on deep learning with a faster SqueezeNet,” Mathematical Problems in Engineering, vol. 2020, no. 2, pp. 1–11, 2020. [Google Scholar]

19. M. Jangid and S. Srivastava, “Handwritten devanagari character recognition using layer-wise training of deep convolutional neural networks and adaptive gradient methods,” Journal of Imaging, vol. 4, no. 2, pp. 41, 2018. [Google Scholar]

20. M. Dehghani, Š. Hubálovský and P. Trojovský, “Northern goshawk optimization: A new swarm-based algorithm for solving optimization problems,” IEEE Access, vol. 9, pp. 162059–162080, 2021. [Google Scholar]

21. J. Wang, X. Liu, J. Bai and Y. Chen, “A new stability condition for uncertain fuzzy hopfield neural networks with time-varying delays,” International Journal of Control, Automation and Systems, vol. 17, no. 5, pp. 1322–1329, 2019. [Google Scholar]

22. W. S. Liew, T. B. Tang, C. H. Lin and C. K. Lu, “Automatic colonic polyp detection using integration of modified deep residual convolutional neural network and ensemble learning approaches,” Computer Methods and Programs in Biomedicine, vol. 206, no. 2, pp. 106114, 2021. [Google Scholar] [PubMed]