A Universal Activation Function for Deep Learning

1  Introduction

Recently, deep learning has shown very good results in computer vision fields such as image classification [1–5], object recognition [6–11], object tracking [12,13], etc. with the help of large-capacity artificial intelligence learning data and high-end computing resources. In addition, research is being actively conducted in fields such as speech recognition [14–16] and natural language processing [17–20]. The activation function is very important because it transfers the value extracted from the previously hidden layer to the input of the next layer for learning the artificial neural network. If an artificial neural network uses a linear function as an activation function, it has no meaning in deeply constructing the neural network, so it uses a nonlinear function as an activation function. That is, a model designed with a deep structure may function like a model without a hidden layer. Currently, various nonlinear functions such as Sigmoid [21], Hyperbolic tangent (Tanh) [22], Rectifier Linear Unit (ReLU) [23], Parametric ReLU (PReLU) [24], Randomized ReLU (RReLU) [25], Leaky ReLU (LReLU) [26], Swish [27], Exponential Linear Unit (ELU) [28] and others [29–32] are available as activation functions of artificial neural networks. By using these nonlinear functions as an activation function, it is possible to construct a deep neural network. However, with Sigmoid and tanh, it is not a serious problem in shallow artificial neural networks, but as the model deepens, the gradient becomes zero when updating numerous weights in the back propagation process of deep learning, resulting in a problem that learning no longer progresses. ReLU has been introduced to solve this vanishing gradient problem, but if most input values are in the negative range, the weight may not be updated while returning 0 to the output value of the activation function. To solve this Dying Node problem, several studies have been conducted, such as reducing the Learning Rate or modifying the ReLU. However, researchers need a lot of time and effort to apply and evaluate various existing activation functions in their own research. Therefore, in this paper, we propose a UA that can easily generate and implement a new type of activation function as well as an activation function similar to the traditional activation function. The UA uses three hyperparameters that determine the shape of the activation function according to the range of input values. Researchers can use various types of activation functions by appropriately modifying the three hyperparameters. The contribution goals to be achieved in this study through a UA are as follows.

•   The UA is proposed to improve the usability of the activation function of the researcher and the performance of the existing neural network.

•   The UA introduced the k, m, and L hyperparameters, allowing researchers to generate various activation functions.

•   We evaluate UAs by implementing Visual Geometry Group (VGG) 16, VGG19, Residual Network (ResNet) 50, and CustomNet and show similar or better performance compared to traditional activation functions.

•   Using CIFAR10, CIFAR100 [33] and Horses or Humans benchmark datasets with different classes and resolutions of images, we have secured the reliability of experimental performance evaluation and can be used in various areas.

The structure of this paper describes the related activation functions in Section 2 and the dataset to be used for experimental performance evaluation in Section 3. Section 4 describes the UA proposed in this study, and Section 5 describes the methods and results of experimental performance evaluation. Section 6 concludes this study.

2  Related Works

2.1 Sigmoid

Sigmoid was mainly used in early artificial neural networks and is also called a logistic function. Sigmoid began to be used to obtain nonlinear values from linear multi-perceptrons and can be expressed as Eq. (1). Sigmoid is limited to a value between 0 and 1, so a very large positive number has a value close to 1 and a very large negative number has a value close to 0. Sigmoid in shallow artificial neural networks is not a serious problem, but it can cause serious problems due to the vanishing gradient in which the gradient approaches zero as the model deepens. Due to these disadvantages, recently it has been only used for binary classification and not for hidden layers of models.

f(x)=11+e−x(1)

2.2 ReLU

ReLU is proposed to solve the vanishing gradient problem of Sigmoid and Tanh. ReLU can be expressed as Eq. (2) and is an identity function for a positive input value and outputs 0 for a negative input value. This function has the advantage of speeding up the learning speed because it is easy to calculate the differential, but it may cause a dying node problem.

f(x)={x, (x>0)0, (x≤0)(2)

2.3 Swish

Swish is an activation function devised by Google to replace ReLU and shows a simple form of multiplying the input by the sigmoid as shown in Eq. (3). Swish outperforms ReLU when training models in deep layers. By not limiting the range of output values in positive numbers, the vanishing gradient problem can be solved, and the dying node problem can be solved by allowing some small negative output values. And the output feature map responds small to small changes and large to large changes so that the optimizer can find the optimal minima.

f(x)=x1+e−x(3)

3  Datasets

The datasets used in the experiments in this study utilize one of the most used benchmark datasets, Canadian Institute for Advanced Research (CIFAR) 10, CIFAR100, and Horses or Humans. CIFAR10 consists of 10 classes, 32 × 32 images, 50,000 training images and 10,000 test images. The CIFAR100 consists of 100 classes, 32 × 32 images, 50,000 training images and 10,000 test images. Horses or Humans consists of two classes, 300 × 300 images, 1027 training images and 256 test images. Fig. 1 shows a dataset sample. Table 1 summarizes and shows the information of each data.

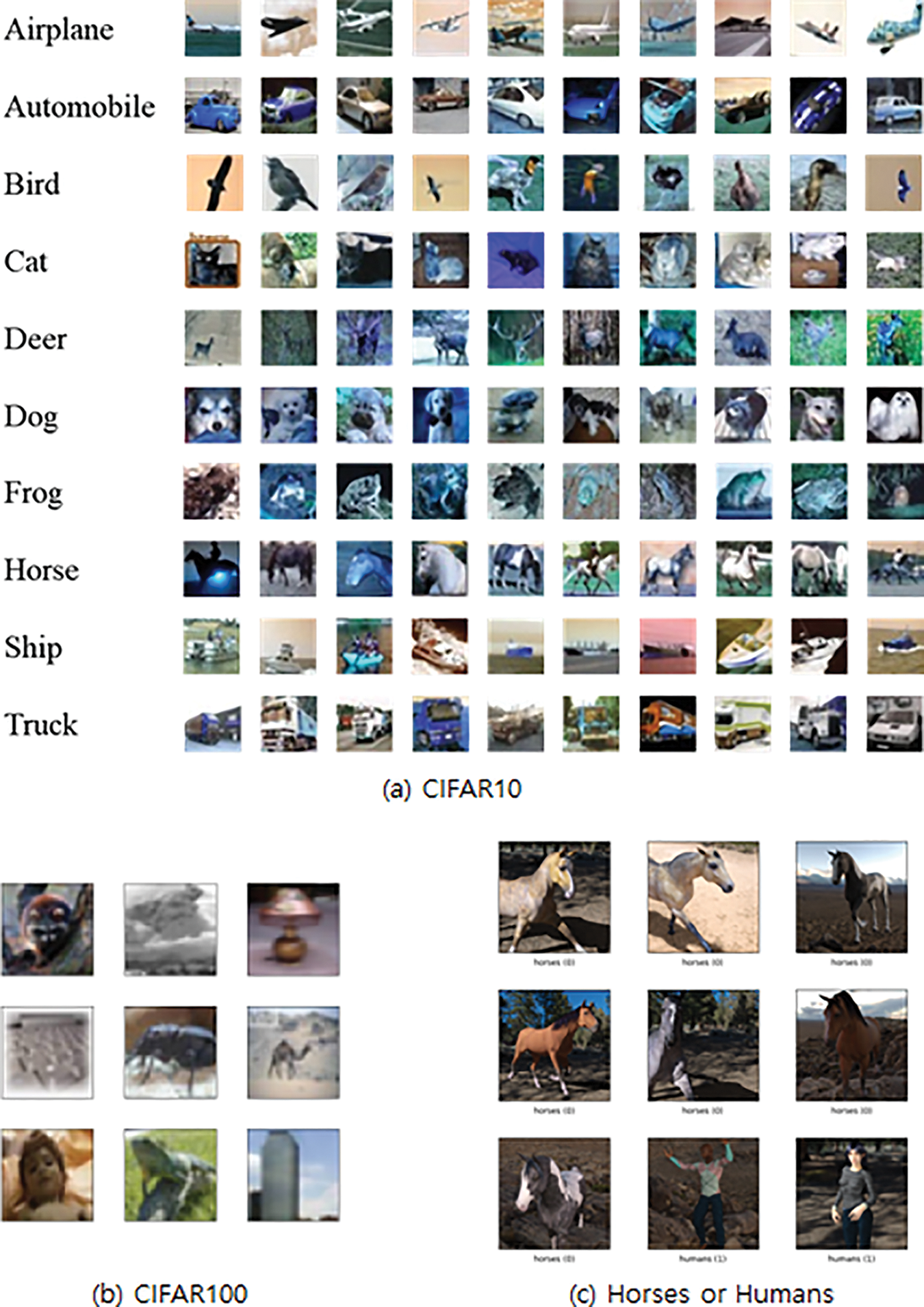
Figure 1: Sample image of CIFAR10, CIFAR100, horses or humans dataset

4  Universal Activation Function

The formula for UA proposed in this paper is shown in Eq. (4).

Universal activation function(x)={xkx>Lxk(L+x)m(L+x)m+(L−x)m|x|≤L0x<−L(4)

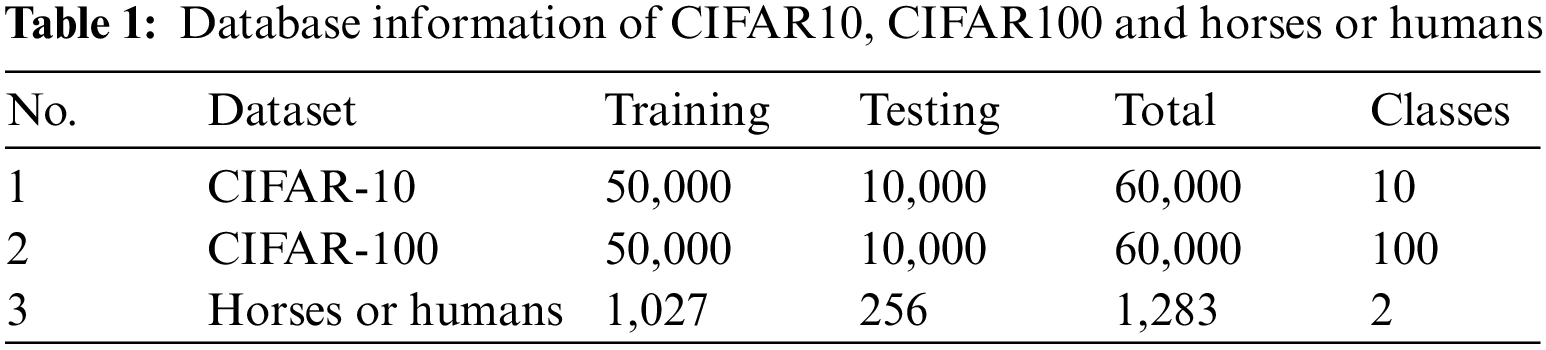
The x of a UA means the input value, and the k, m, and L hyperparameters determine the form of the activation function. The value of k determines the shape of the graph of the interval in which the input value is greater than L. The value of m gently adjusts the shape of the graph so that the value of the slope does not change rapidly. The value of L is the criterion for dividing the activation function into three intervals. Researchers can set three parameters appropriately to generate a desired type of activation function. And a visualizer was developed to visualize these activation functions. The visualizer allows visualization by selecting the desired activation function among Swish, Sigmoid, ReLU, and ELU, and when UA is selected, a graph of the activation function is output according to the applied hyperparameters. Figs. 2–4 show the ReLU, Sigmoid, and Swish activation functions generated using a UA through the visualizer.

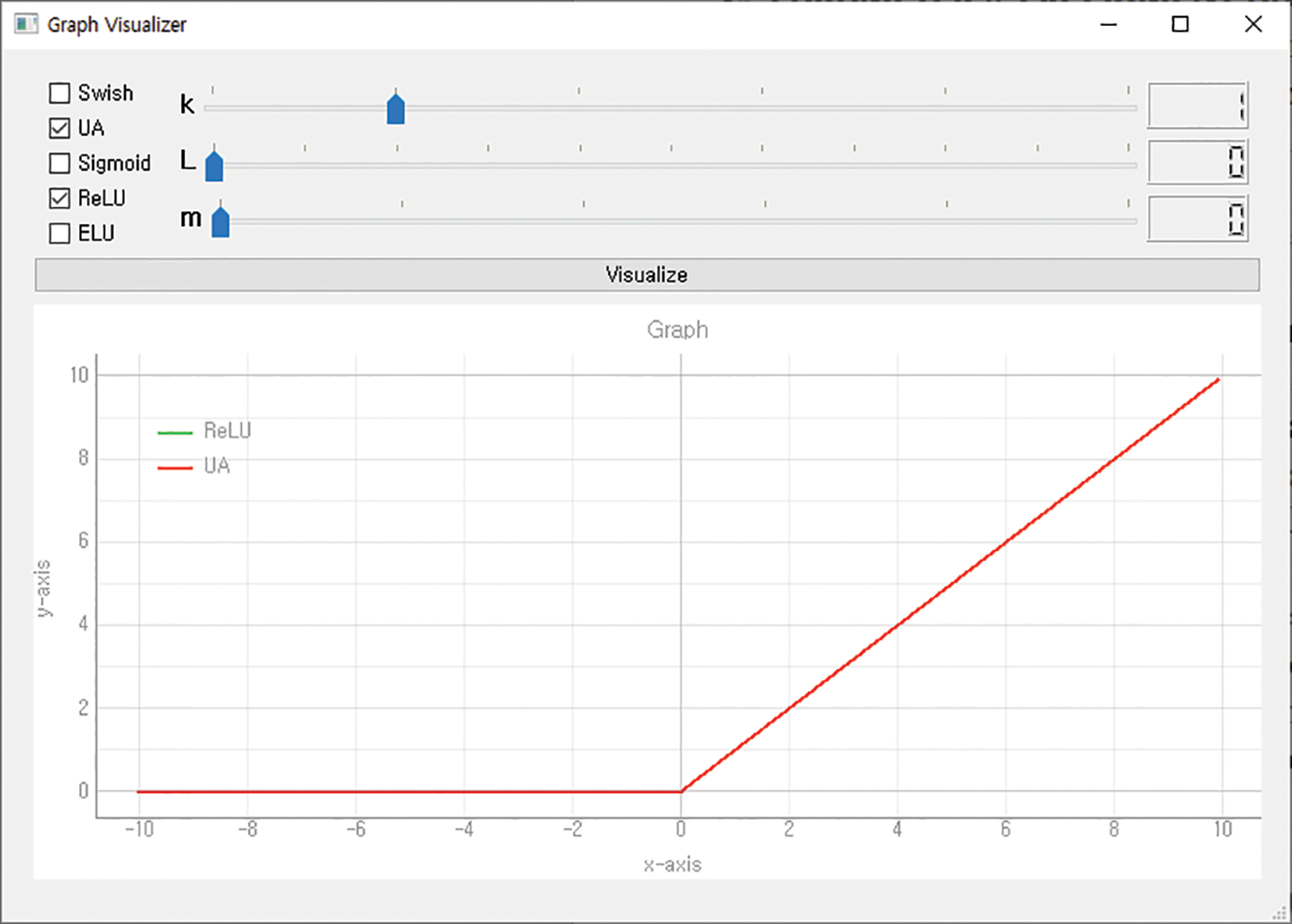
Figure 2: ReLU generated using UA

Figure 3: Sigmoid generated using UA

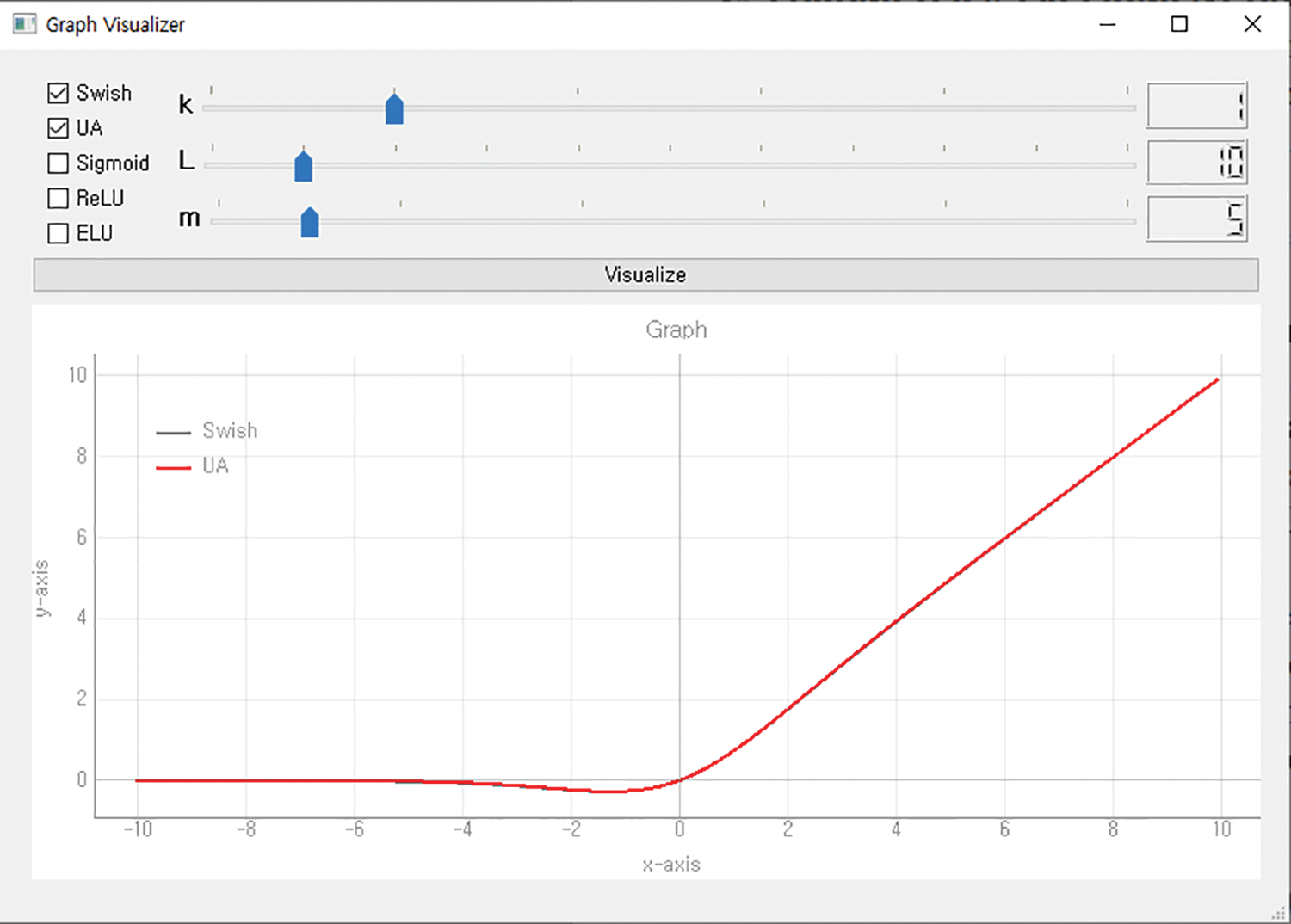
Figure 4: Swish generated using UA

To check the similarity between the traditional activation function and the UA, the output vector of the activation function for random input vector was calculated and the results were prepared in Table 2.

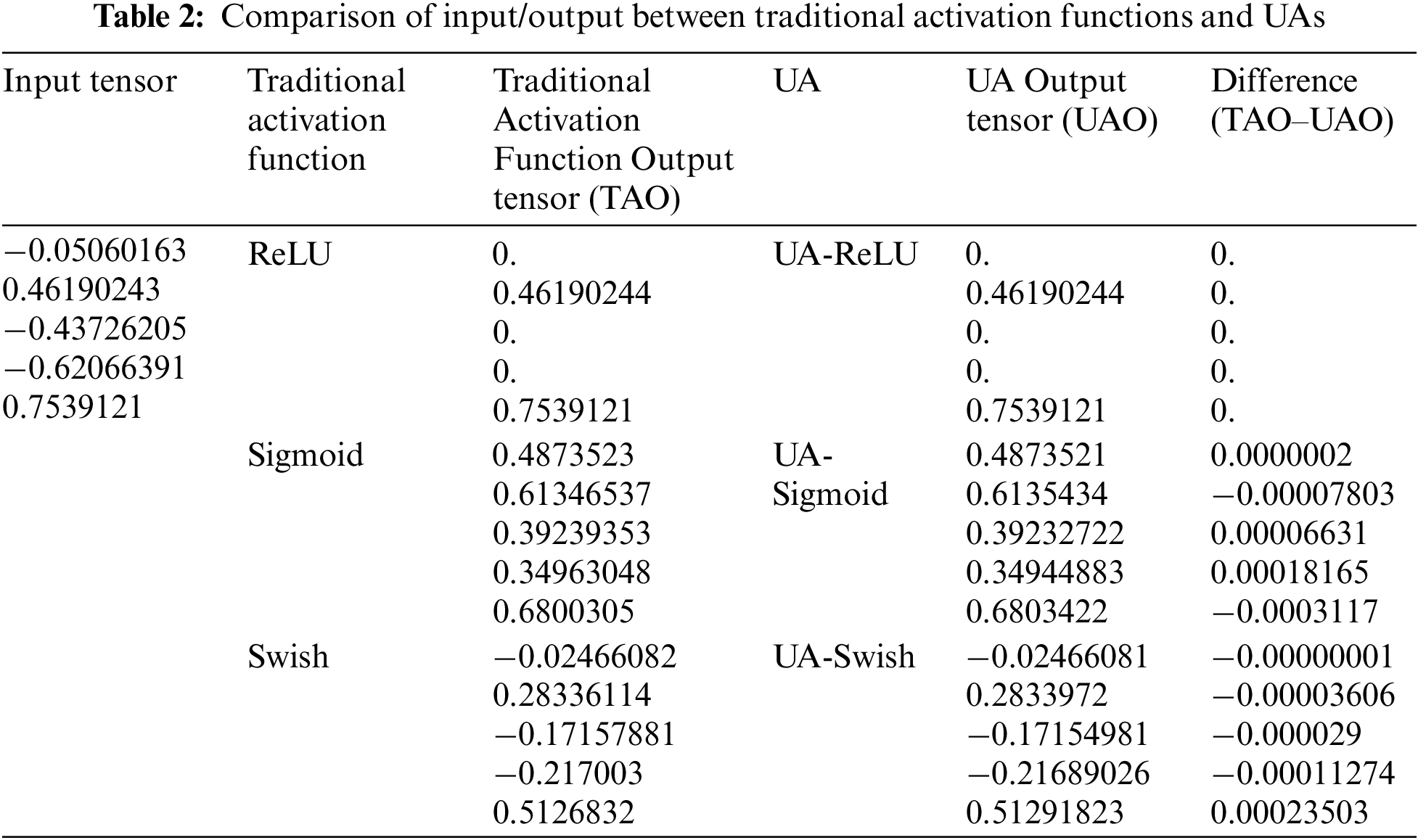
According to Table 2, for any input vector, ReLU and UA-ReLU have the same output vector. In the case of sigmoid and swish, there are some errors, but it is proved that there are no performance issues through experimental performance evaluation. The UA proposed in this paper can generate various types of activation functions as well as functions like traditional activation functions by adjusting three parameters. Therefore, various researchers will be able to easily use the activation function by changing the parameters to create an activation function suitable for the data and research purpose.

5  Experimental Performance Evaluation

5.1 Environment and Method

The activation function visualizer developed in this study was developed in Windows 10 with Python programming language. Experimental performance evaluation was performed in Docker container of Ubuntu 20.04 OS and implemented using Python programming language and Keras library. The hardware of the PC consists of an NVIDIA GeForce Ray Tracing (RTX) 3080 GPU, an Advanced Micro Devices (AMD) Ryzen 7 5700X CPU and 64 GB of RAM.

For the experimental performance evaluation of the UA, a custom neural network consisting of three Conv layers, three Pooling layers, and one fully connected layer was utilized to minimize the value lost as the neural network deepens, as well as CNN won the ImageNet Large Scale Visual Recognition Challenge (ILSVRC). The architecture of CustomNet is shown in Fig. 5. All three Conv layers used 3 × 3 filters, and MaxPool layers used 2 × 2 filters. The Conv1 layer used 32 kernels, the Conv2 layer used 64 kernels, and the Conv3 layer used 128 kernels. The output vector dimension of the FC1 layer was set to 256.

Figure 5: CustomNet model architecture

The CIFAR10, CIFAR100, Horses or Humans datasets were used to evaluate the experimental performance of this study, and the hyperparameters applied to each neural network are shown in Table 3.

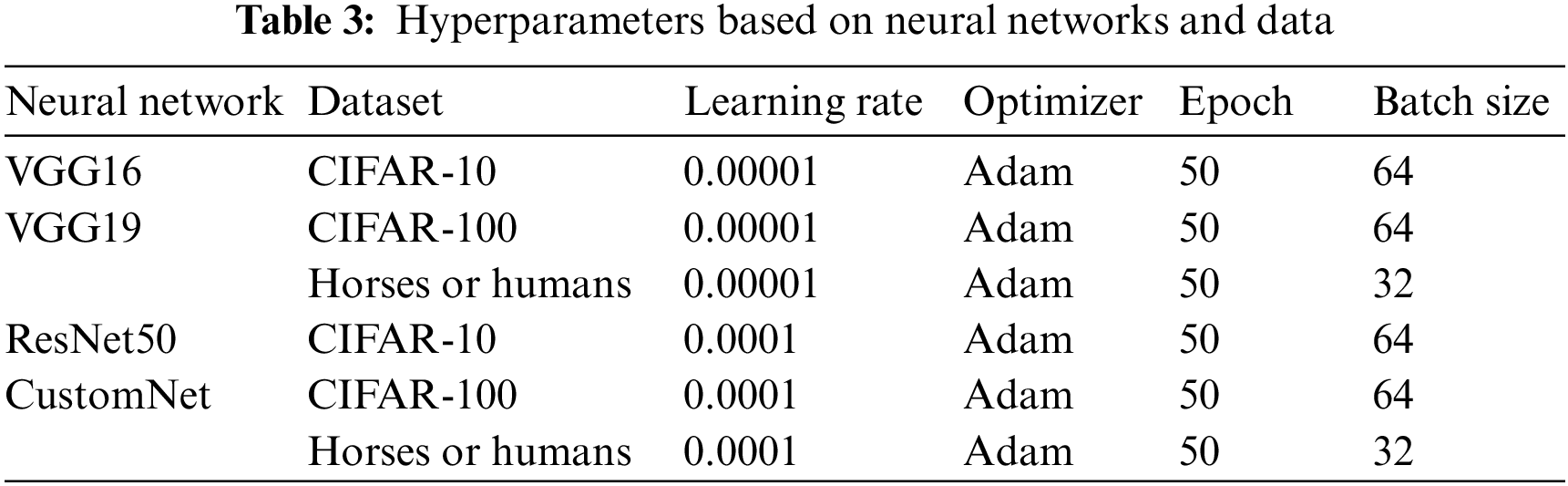
To confirm the performance according to the activation function, the weight decay scheduler was not used for the learning rate, and a CNN model that was not pre-trained was used. And Adam Optimizer [34] was used for fast weight convergence. Additionally, we used the CIFAR10 dataset to perform an experimental performance evaluation based on changes in hyperparameters that determine a UA.

5.2 Results and Analysis

5.2.1 Experimental Performance Evaluation Results for CIFAR-10

Table 4 shows the results of learning the CIFAR10 using traditional activation functions (ReLU, Swish) and UAs (UA-ReLU, UA-Swish). Fig. 6 is a visualization for intuitive understanding of the results.

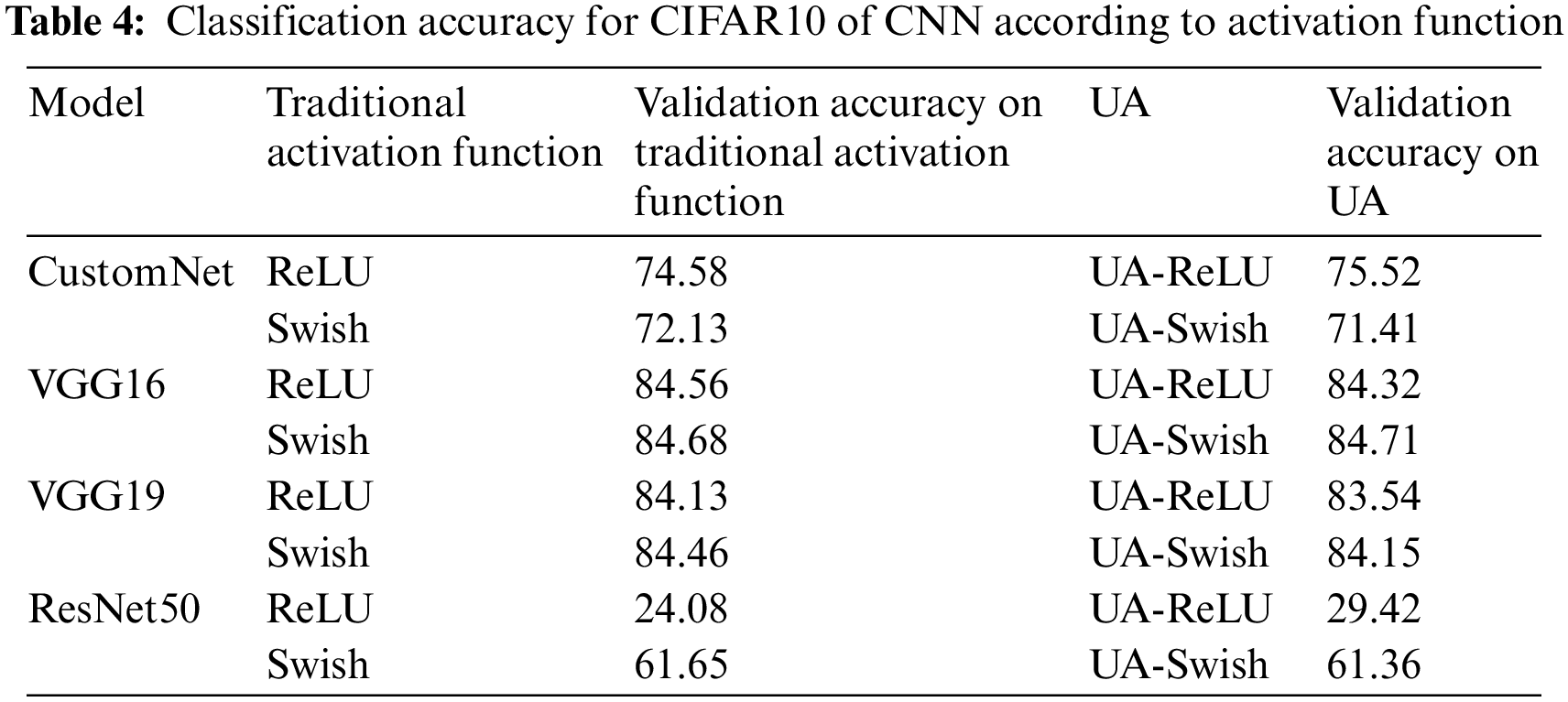
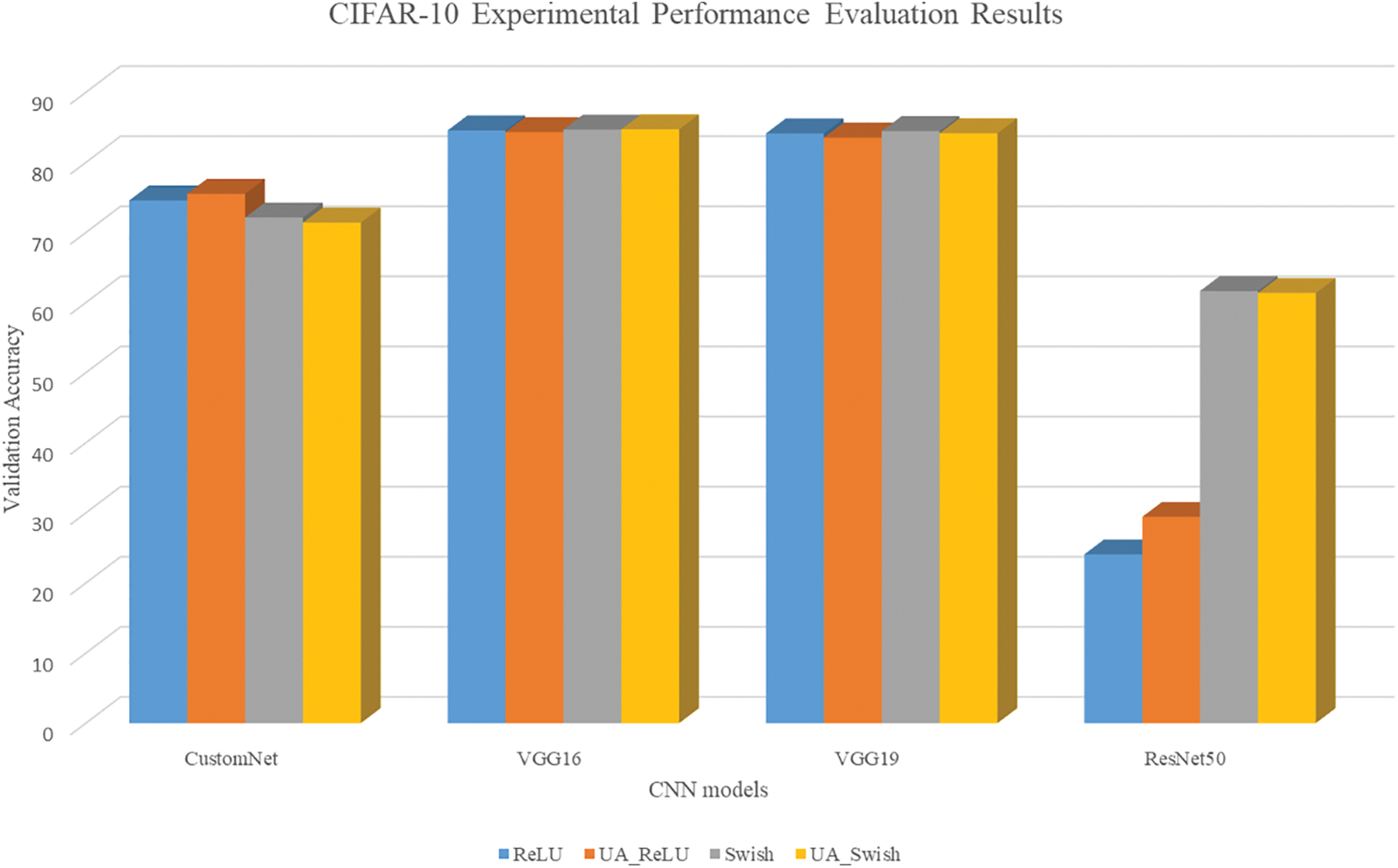
Figure 6: CIFAR10 results bar graph

The results show that the validation accuracy of the traditional activation function and the UA is mostly derived similarly for the entire model. For ResNet50, UA-ReLU has improved accuracy by about 5.3% compared to ReLU. The reason why ResNet50 is less accurate than other neural networks is that the neural network is composed of layers deeper than the resolution of a given dataset, so it is judged that it has not been learned normally because many features of the image have been lost in the hidden layer.

5.2.2 Experimental Performance Evaluation Results for CIFAR-100

Table 5 shows the results of learning the CIFAR100 using traditional activation functions and UAs. Fig. 7 is a visualization for intuitive understanding of the results.

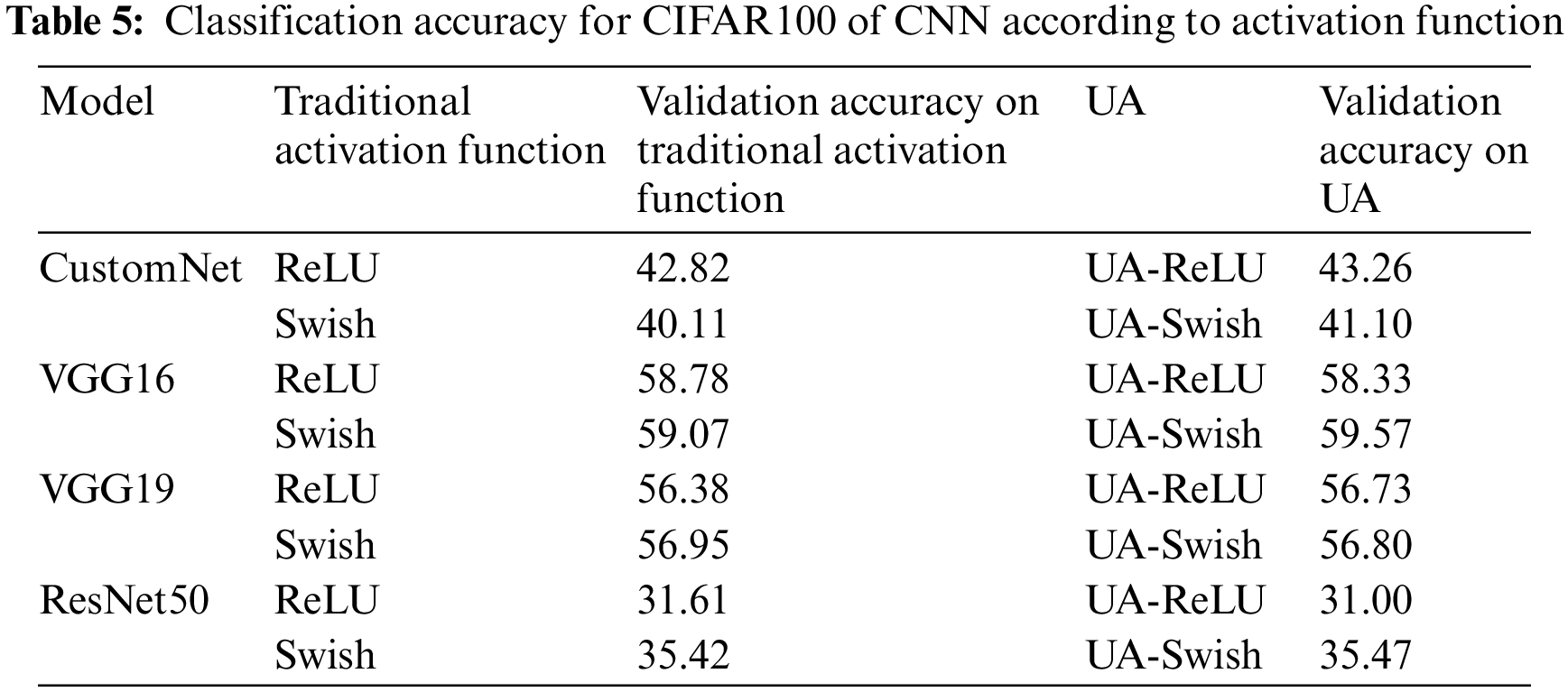
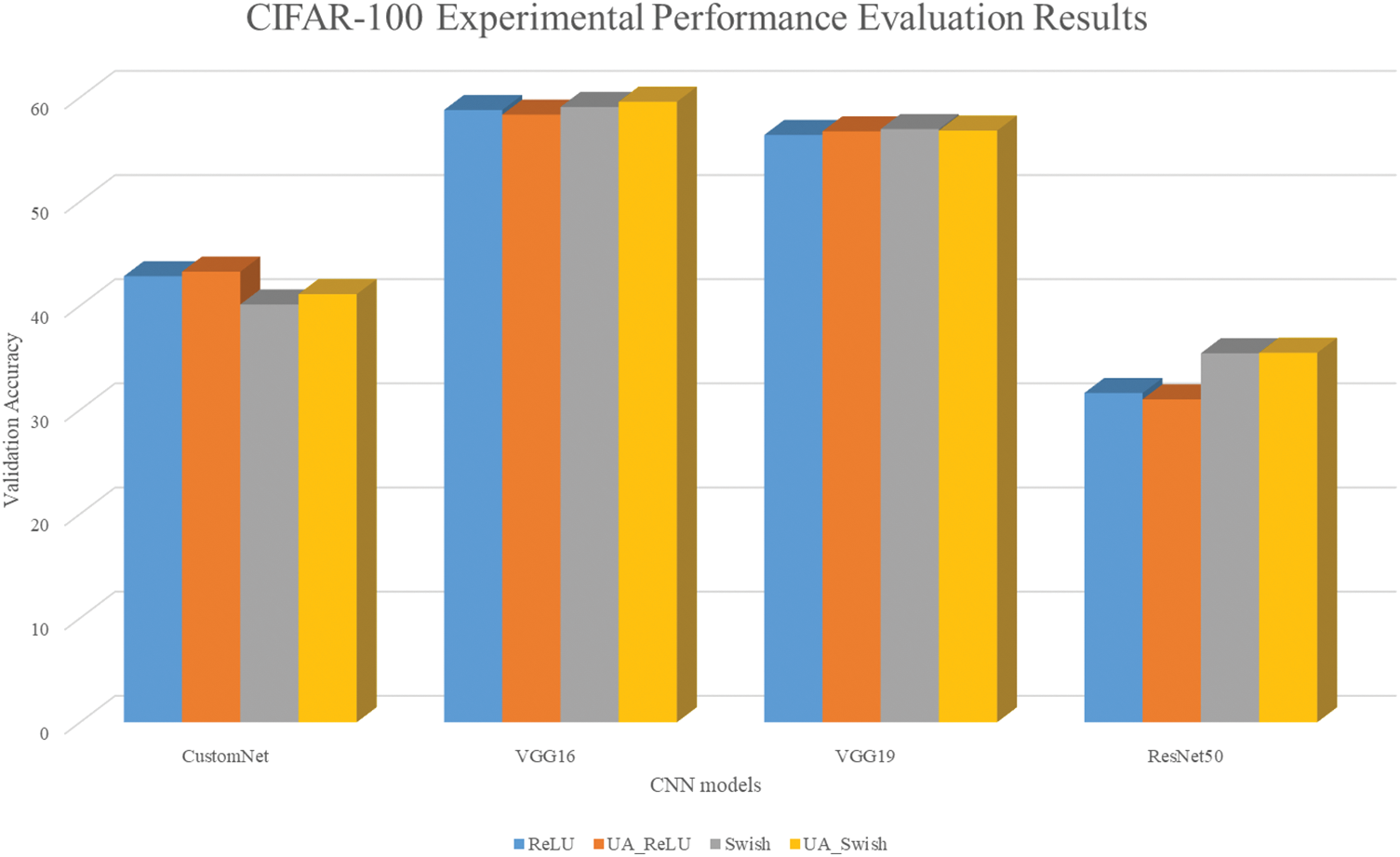
Figure 7: CIFAR100 results bar graph

As a result of learning the CIFAR100 dataset, most of them show similar accuracy, and the accuracy is generally slightly higher when UA is applied. Like the CIFAR10 dataset, it is judged that the accuracy of ResNet50 is low because the resolution of the given dataset is low and many image features are lost in the hidden layer.

5.2.3 Experimental Performance Evaluation Results for Horses or Humans

Table 6 shows the results of learning the Horses or Humans using traditional activation functions and UAs. Fig. 8 is a visualization for intuitive understanding of the results.

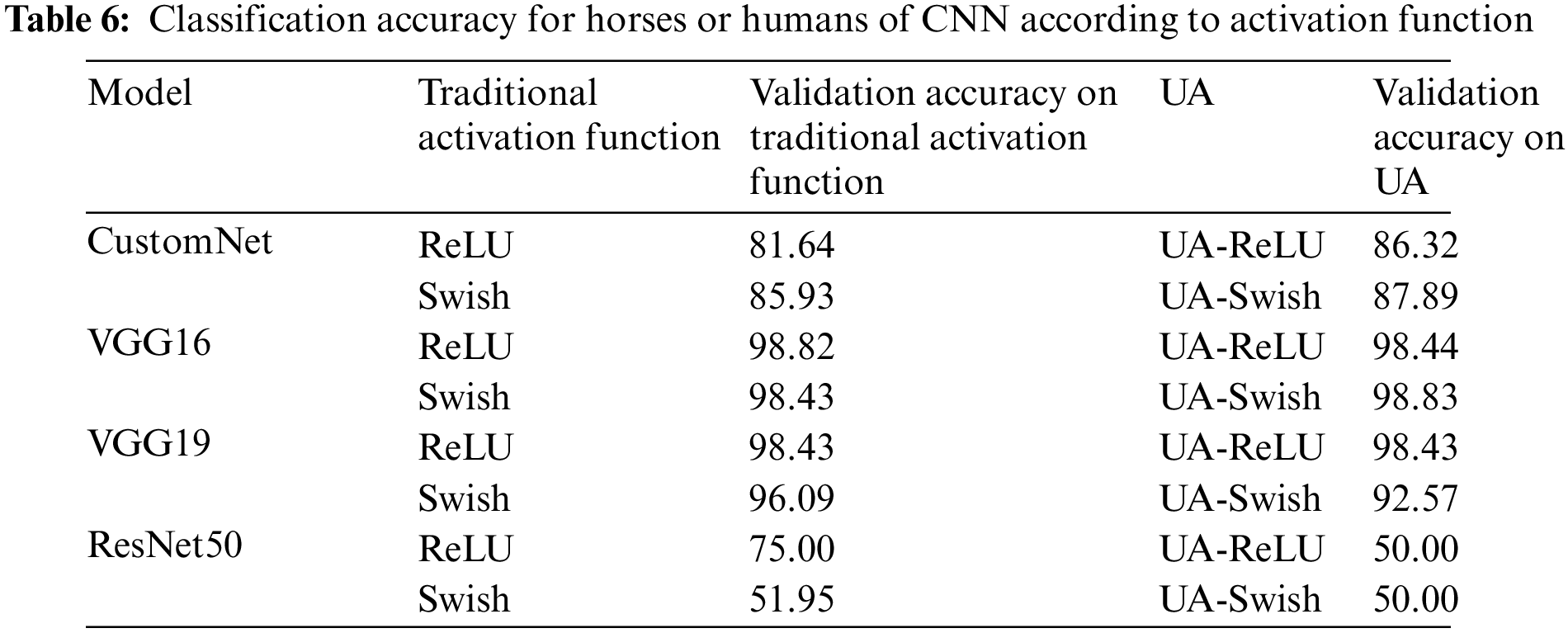
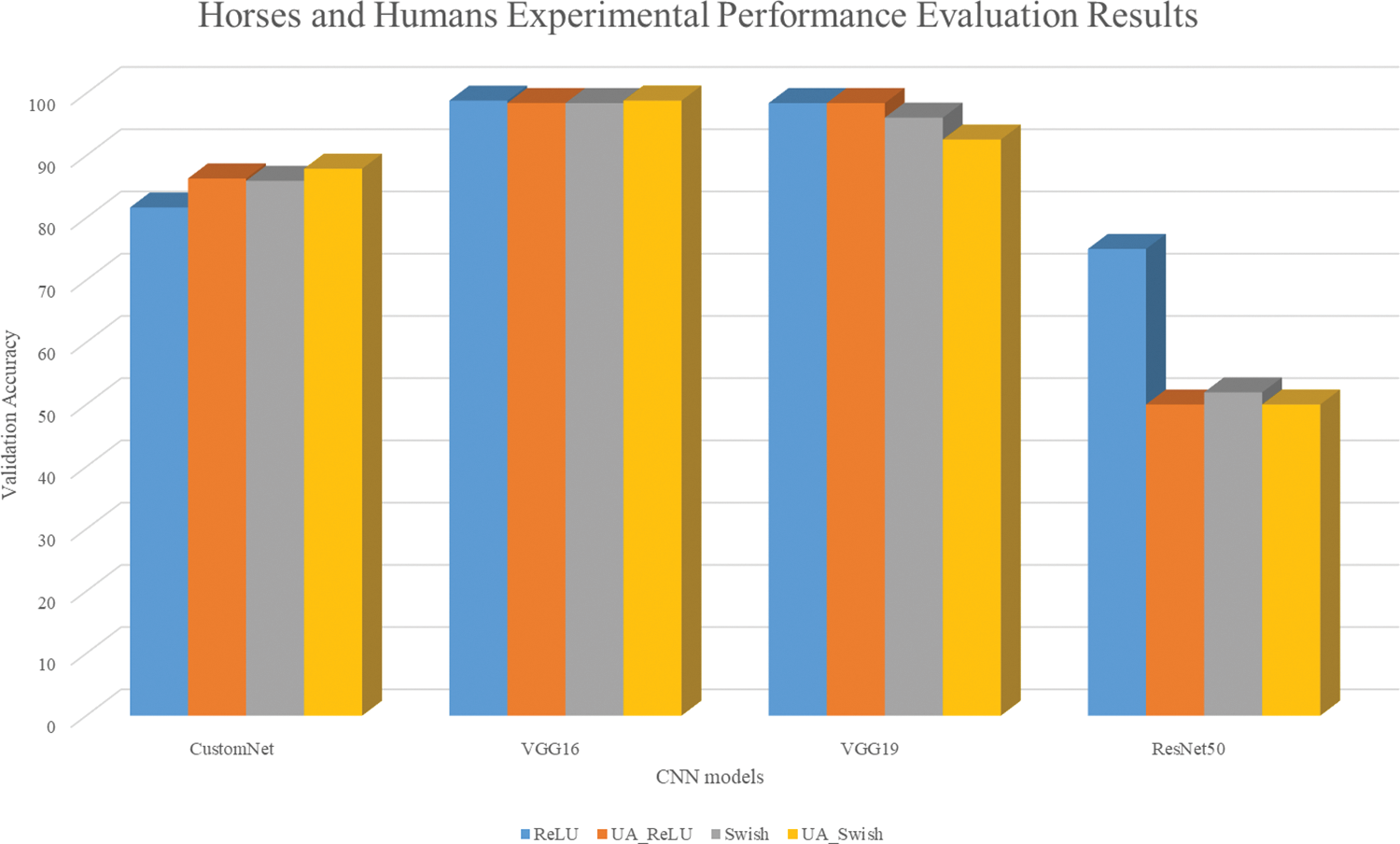
Figure 8: Horses or humans results bar graph

As a result of learning from the Horses or Humans dataset, CustomNet had higher accuracy when applying a UA. The VGG16 showed similar accuracy and the VGG19 showed similar accuracy for ReLU, but the accuracy was approximately 3.5% lower for UA-Swish. In the case of ResNet50, it is judged that it was not learned normally, such as the CIFAR10 and CIFAR100 dataset learning results.

5.2.4 Experimental Performance Evaluation Results of UA According to Hyper-Parameter

Considering the diversity of the study, three hyperparameters of the UA were changed to generate activation functions similar to ELU not covered in the previous section, and the experimental performance evaluation was conducted using the CIFAR10 dataset. Table 7 shows the hyperparameters of the three UAs and the results of learning CIFAR10.

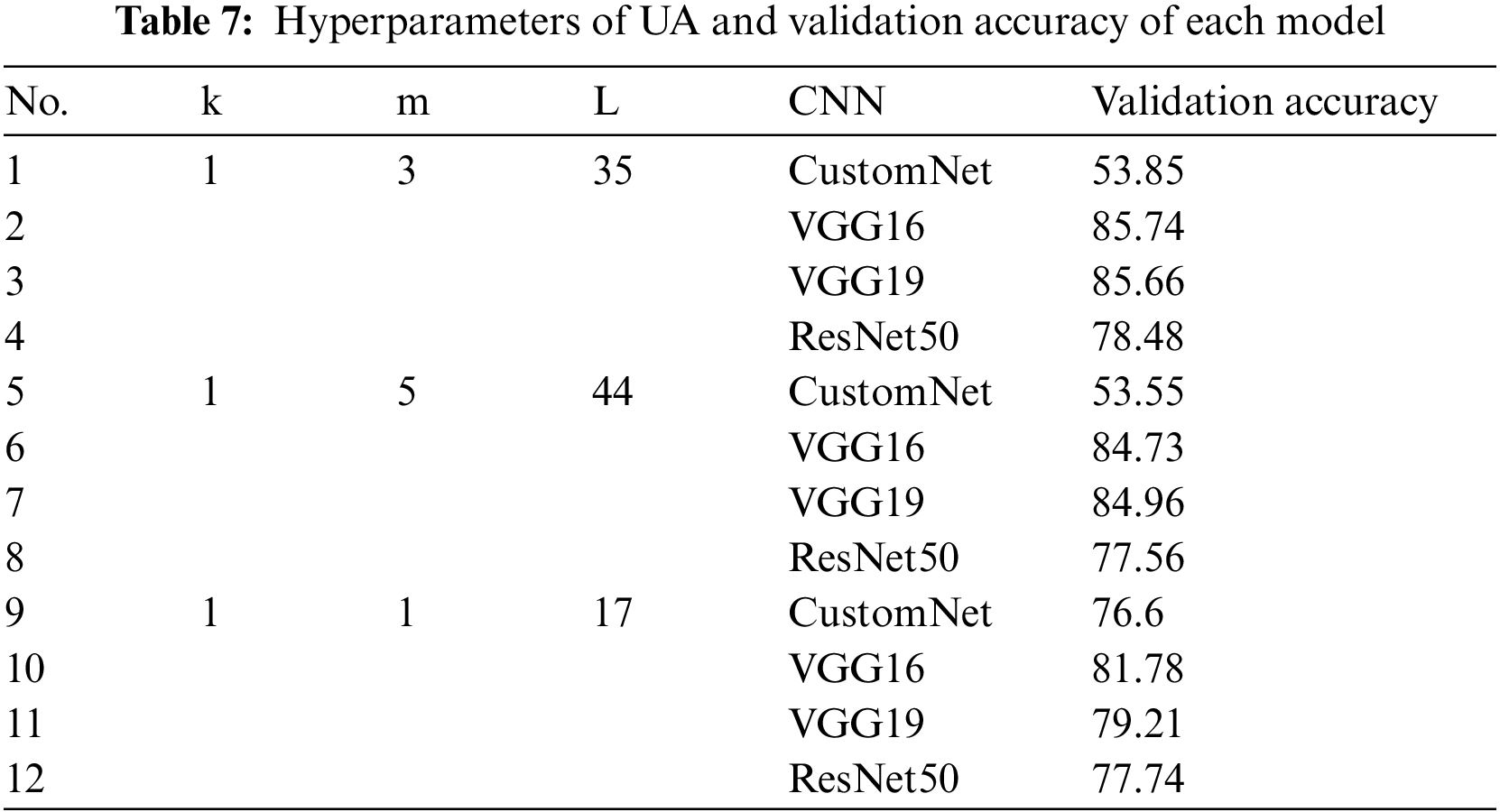
The hyperparameters of the first UA were set to k = 1, m = 3, and L = 35. Fig. 9 shows the first UA graph, and Fig. 10 visualizes the results.

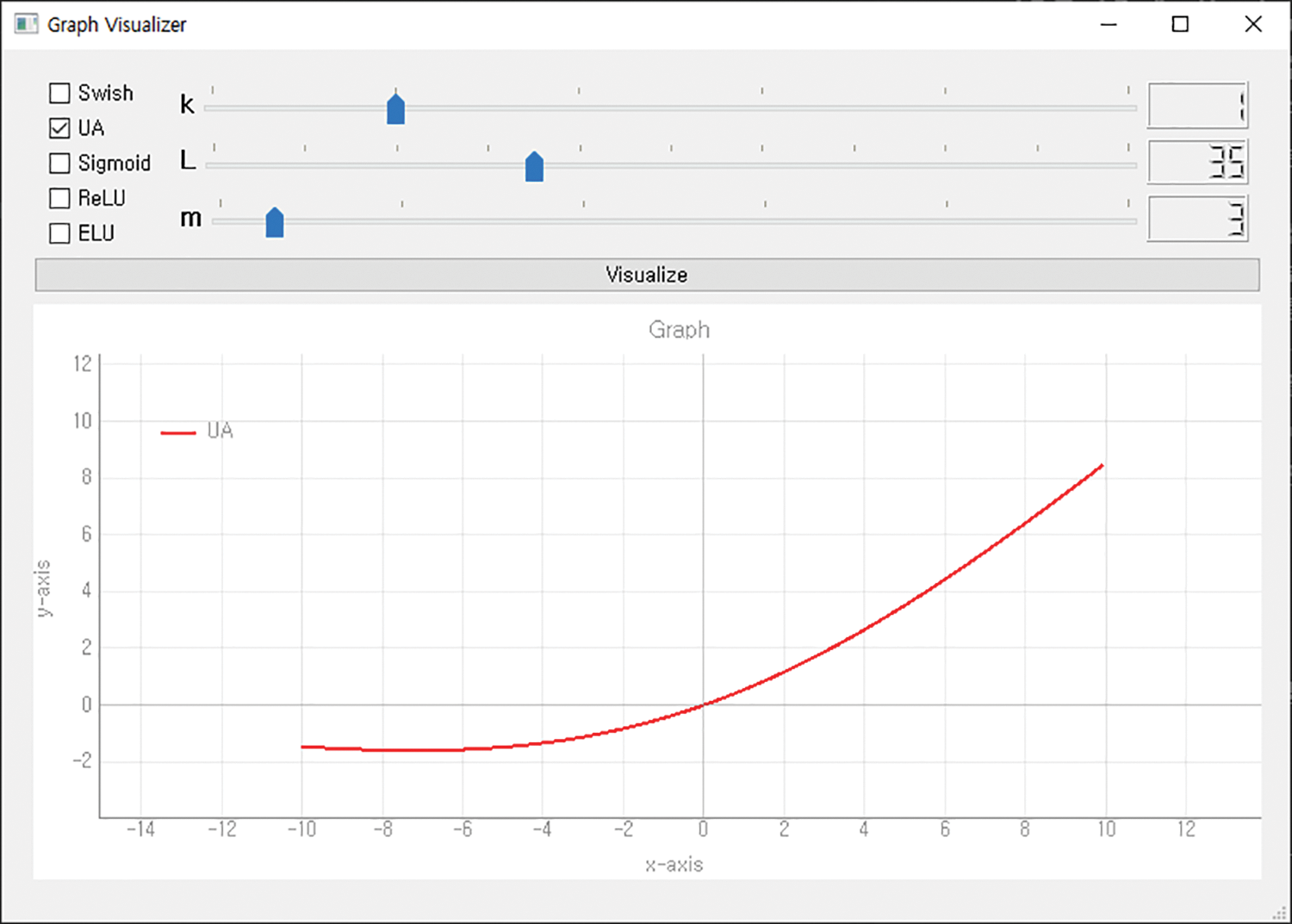
Figure 9: Graph of UA (k = 1, m = 3, L = 35)

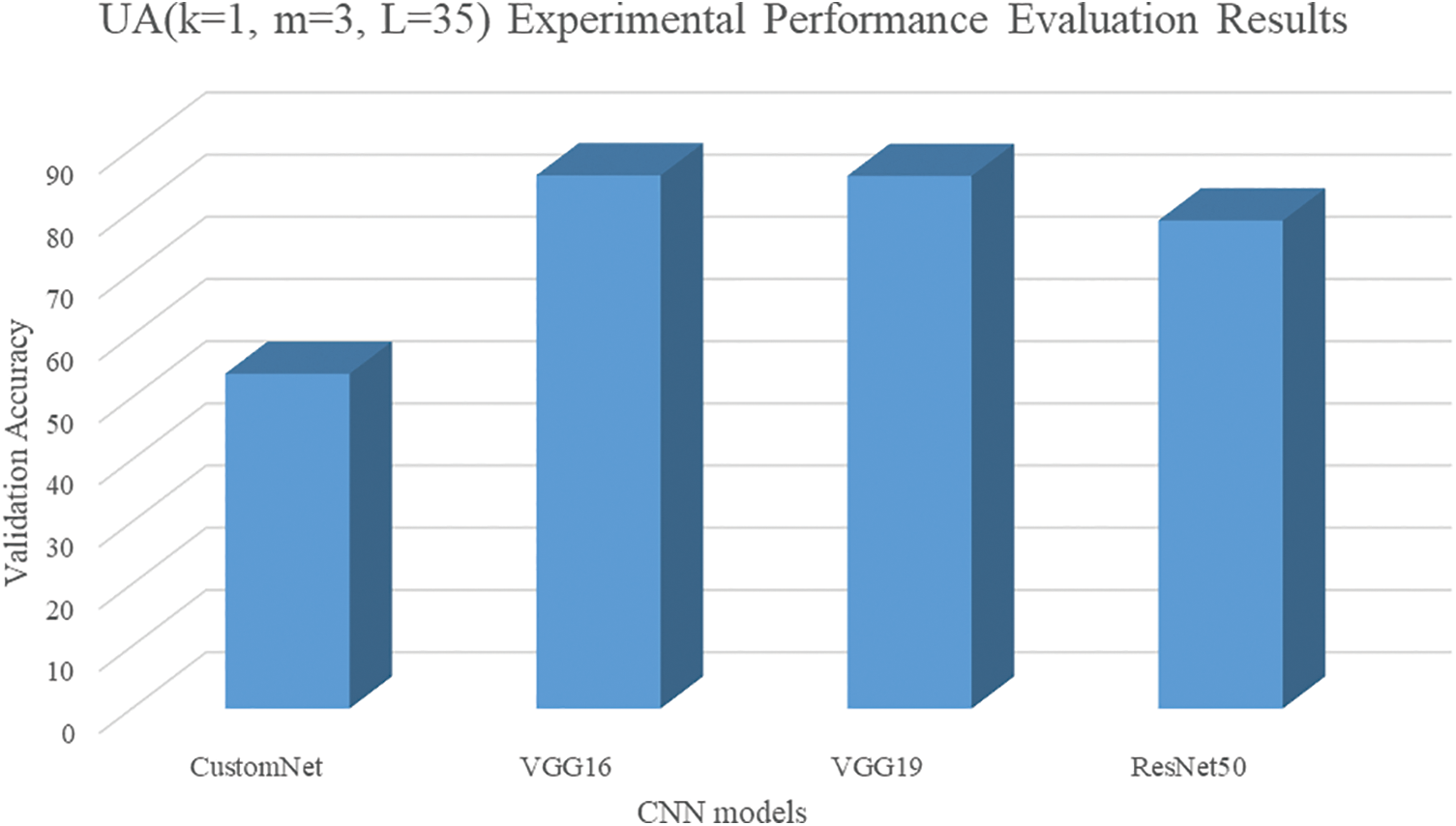
Figure 10: Results of UA (k = 1, m = 3, L = 35)

The accuracy of the neural network to which the first general-purpose activation function was applied was found to be about 19.56% lower than the average accuracy of the model trained with four activation functions (ReLU, Swish, UA-ReLU, UA-Swish) for CustomNet. However, in the case of VGG16 and VGG19 neural networks, about 1.2% and 1.6% accuracy improvements were found. In the case of ResNet50, it seems that the image features are lost in the hidden layer, but there was a performance improvement of about 34.4% compared to the result of applying the four activation functions.

The hyperparameters of the second UA were set to k = 1, m = 5, and L = 44. Fig. 11 shows the second UA graph, and Fig. 12 visualizes the results.

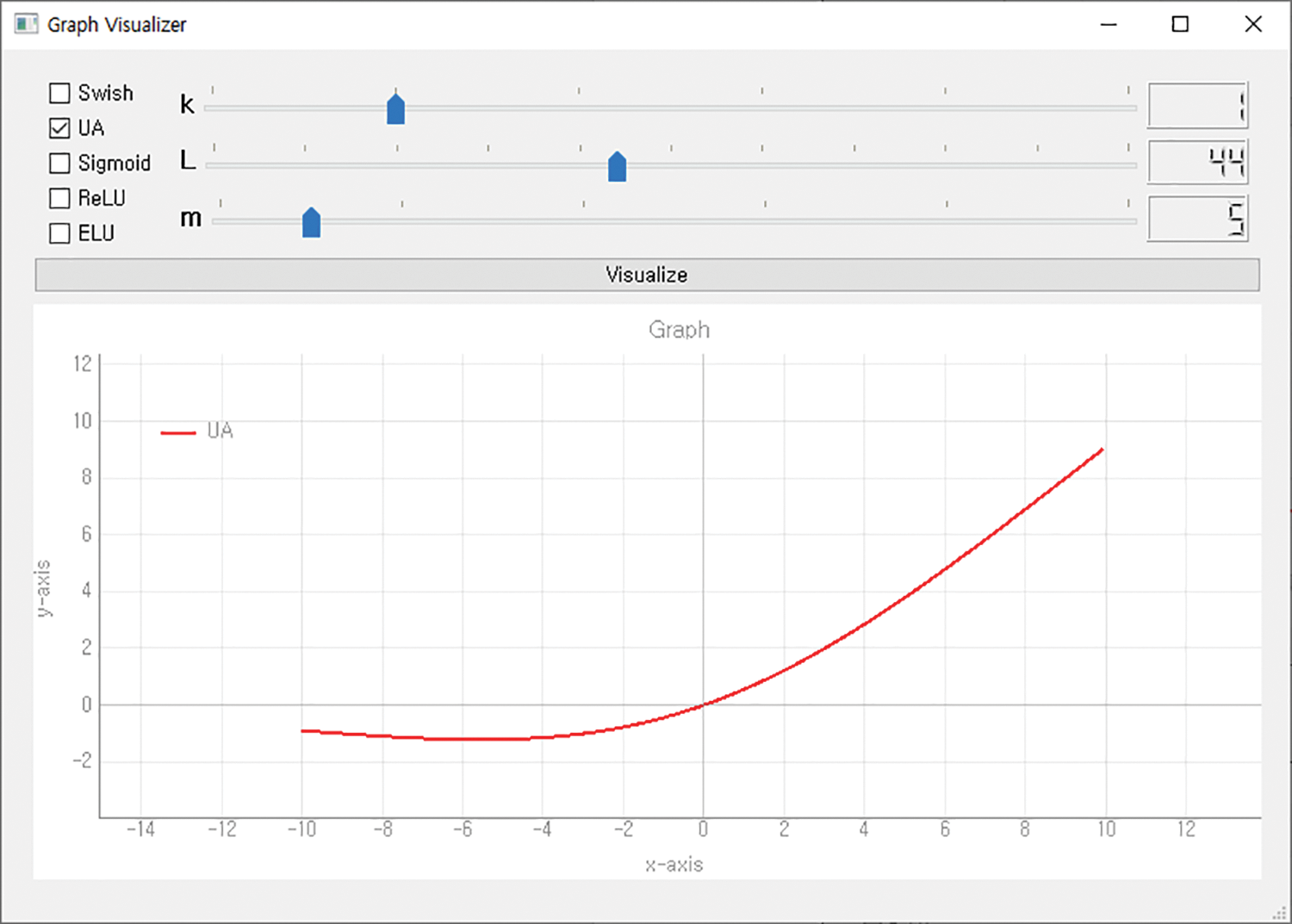
Figure 11: Graph of UA (k = 1, m = 5, L = 44)

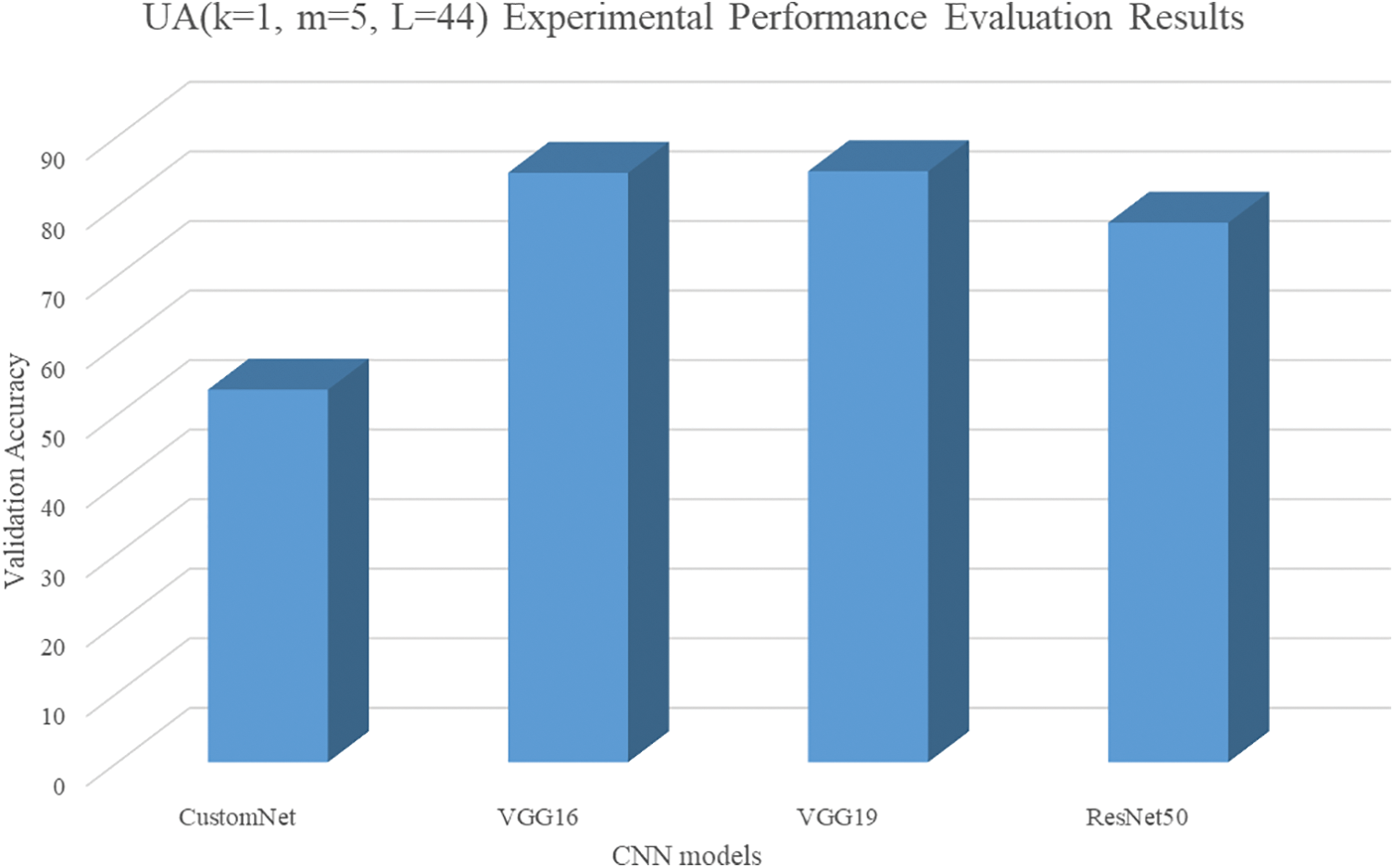
Figure 12: Results of UA (k = 1, m = 5, L = 44)

The accuracy of applying the second UA was like that of the first UA applied to CustomNet. In the case of VGG16 and VGG19, there was a slight improvement in performance compared to the four activation functions, but the case of applying the first UA showed better accuracy. ResNet50 also had the loss of image features of the hidden layer, but there was a performance improvement of about 33.4%.

The hyperparameters of the third UA were set to k = 1, m = 1, and L = 17. Fig. 13 shows the third UA graph, and Fig. 14 visualizes the results.

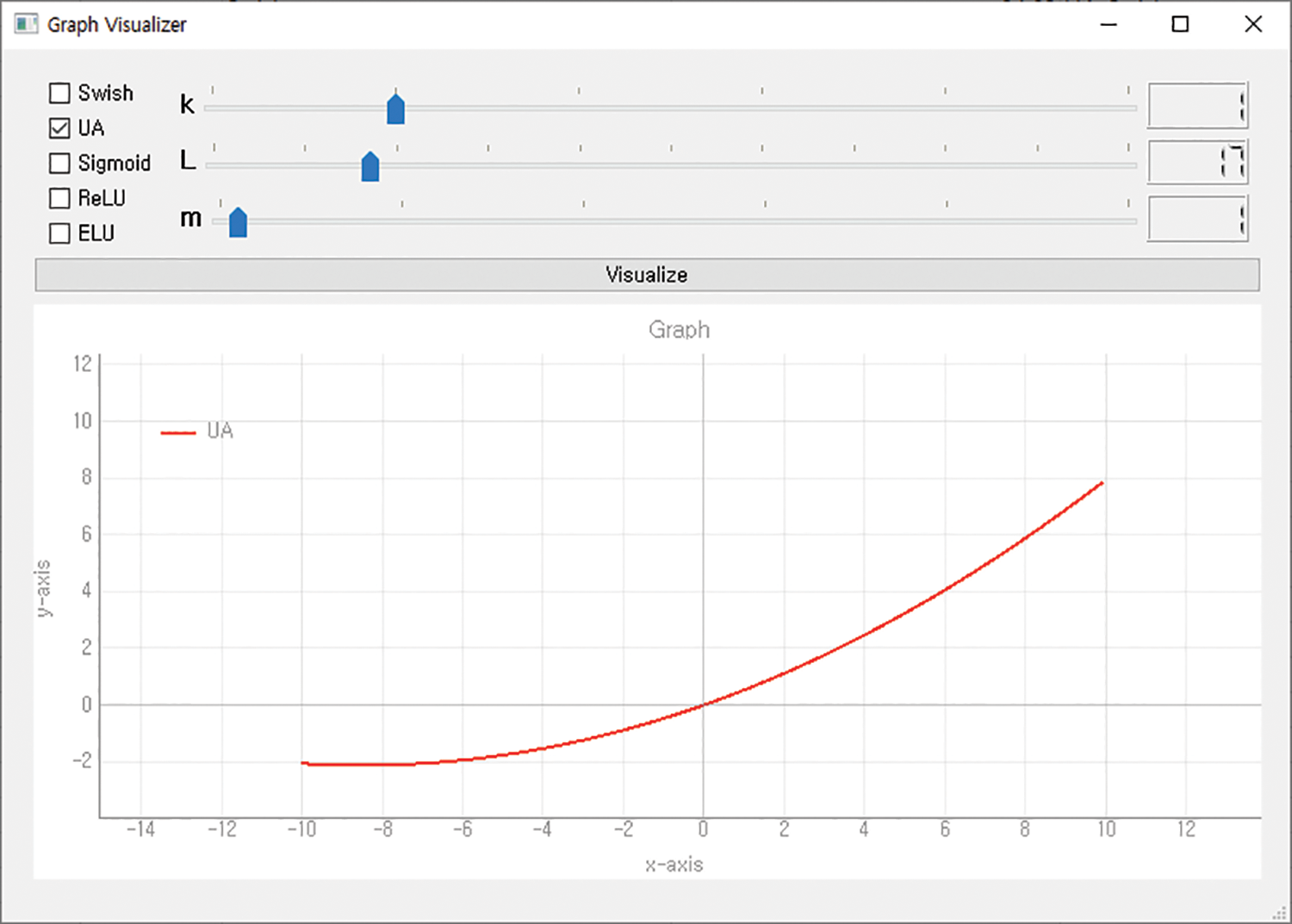
Figure 13: Graph of UA (k = 1, m = 1, L = 17)

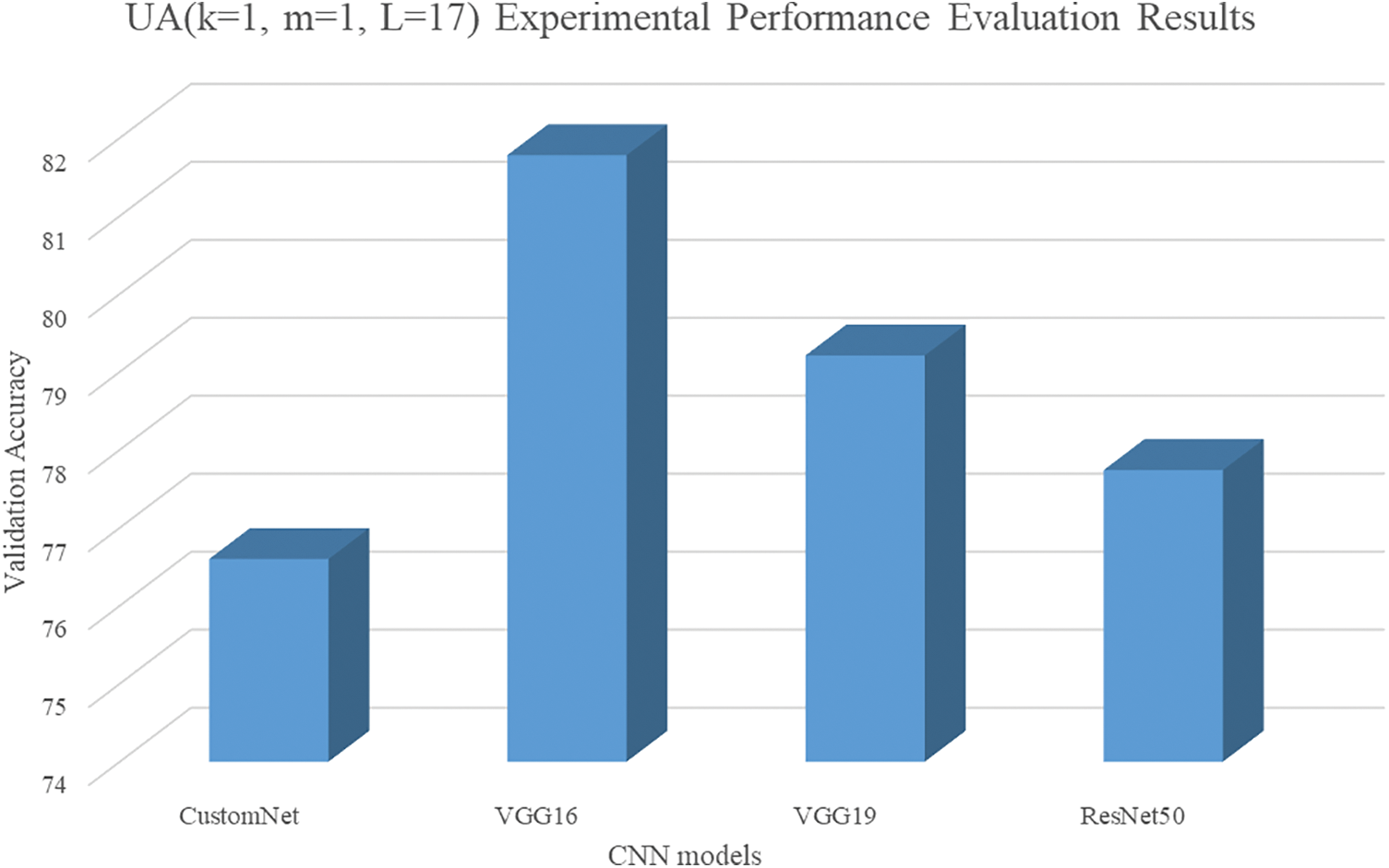
Figure 14: Results of UA (k = 1, m = 1, L = 17)

As a result of the third UA, CustomNet achieved 76.6% accuracy, unlike the application of the first and second UA, and improved accuracy by about 3.2% over the average accuracy of the models trained with the four activation functions. In the case of VGG16 and VGG19, there was a performance degradation of about 2.8% and 4.9%. For ResNet50, we achieved 77.74% accuracy and there was a loss of image features of the hidden layer, but there was a performance improvement of about 33.6%.

6  Conclusion

In this paper, the UA is proposed to improve the performance of deep learning and the usability of the activation function of researchers. The UA consists of three hyperparameters k, m, and L that determine the form of the activation function. By properly setting the hyperparameters, researchers can generate activation functions like traditional activation functions as well as various types of activation functions. We trained self-defined CNNs to minimize loss due to depth of neural networks by leveraging various benchmark datasets for comparison and experimental performance evaluation of traditional activation functions and UAs. As a result, the traditional activation function and the UA showed generally similar performance. In addition, three new types of activation functions were generated by changing the hyperparameters of the UA, and experimental performance evaluation was conducted using CIFAR10 and CNNs. In the experimental performance evaluation process, there were neural networks with improved performance for all three UAs, but there were also cases with improved performance in a specific neural network. Therefore, based on the results of this study, various researchers can easily generate and utilize new activation functions, so that technological advancement can be expected in various fields using deep learning. However, the traditional activation function was superior due to the complexity of the UA in terms of deep learning speed. In future studies, we will solve the problem of lowering the learning speed due to the complexity of the UA.

Acknowledgement: This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. 2022R1F1A1062953).

Funding Statement: This work was supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. 2022R1F1A1062953).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. A. Krizhevsky, I. Sutskever and G. E. Hinton, “Imagenet classification with deep convolutional neural networks,” Advances in Neural Information Processing Systems, vol. 25, pp. 1097–1105, 2012. [Google Scholar]

2. K. Simonyan and A. Zisserman, “Very deep convolutional networks for large-scale image recognition,” 2014. [Online]. Available: https://arxiv.org/abs/1409.1556 [Google Scholar]

3. C. Szegedy, W. Liu, Y. Jia, P. Sermanet, S. Reed et al., “Going deeper with convolutions,” in Proc. Conf. on Computer Vision and Pattern Recognition, Boston, MA, USA, pp. 1–9, 2015. [Google Scholar]

4. K. He, X. Zhang, S. Ren and J. Sun, “Deep residual learning for image recognition,” in Proc. Conf. on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, pp. 770–778, 2016. [Google Scholar]

5. T. Abbas, S. F. Ali, M. A. Mohammed, A. Z. Khan, M. J. Awan et al., “Deep learning approach based on residual neural network and SVM classifier for driver’s distraction detection,” Applied Sciences, vol. 12, no. 13, pp. 6626, 2022. [Google Scholar]

6. R. Girshick, J. Donahue, T. Darrell and J. Malik, “Rich feature hierarchies for accurate object detection and semantic segmentation,” 2014. [Online]. Available: https://arxiv.org/abs/1311.2524 [Google Scholar]

7. J. Redmon, S. Divvala, R. Girshick and A. Farhadi, “You only look once: Unified, real-time object detection,” in Proc. Conf. on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, pp. 779–788, 2016. [Google Scholar]

8. R. Girshick, “Fast R-CNN,” in Proc. of the IEEE Int. Conf. on Computer Vision, NW Washington, DC United States, pp. 1440–1448, 2015. [Google Scholar]

9. A. Bochkovskiy, C. Y. Wang and H. Y. M. Liao, “YOLOv4: Optimal speed and accuracy of object detection,” 2020. [Online]. Available: https://arxiv.org/abs/2004.10934 [Google Scholar]

10. H. J. Mohammed, S. Al-Fahdawi, A. S. Al-Waisy, D. A. Zebari, D. A. Ibrahim et al., “ReID-DeePNet: A hybrid deep learning system for person re-identification,” Mathematics, vol. 10, no. 19, pp. 3530, 2022. [Google Scholar]

11. O. I. Obaid, M. A. Mohammed, A. O. Salman, S. A. Mostafa and A. A. Elngar, “Comparing the performance of pre-trained deep learning models in object detection and recognition,” Journal of Information Technology Management, vol. 14, no. 4, pp. 40–56, 2022. [Google Scholar]

12. A. Bewley, Z. Ge, L. Ott, F. Ramos and B. Upcroft, “Simple online and realtime tracking,” in 2016 IEEE International Conf. on Image Processing (ICIP), Phoenix, Arizona, USA, pp. 3464–3468, 2016. [Google Scholar]

13. N. Wojke, A. Bewley and D. Paulus, “Simple online and realtime tracking with a deep association metric,” in 2017 IEEE International Conf. on Image Processing (ICIP), Beijing, China, pp. 3645–3649, 2017. [Google Scholar]

14. A. V. D. Oord, S. Dieleman, H. Zen, K. Simonyan, O. Vinyals et al., “WaveNet: A generative model for raw audio,” 2016. [Online]. Available: https://arxiv.org/abs/1609.03499 [Google Scholar]

15. Y. Ren, C. Hu, X. Tan, T. Qin, S. Zhao et al., “FastSpeech 2: Fast and high-quality end-to-end text to speech,” 2020. [Online]. Available: https://arxiv.org/abs/2006.04558 [Google Scholar]

16. J. Shen, R. Pang, R. J. Weiss, M. Schuster, N. Jaitly et al., “Natural TTS synthesis by conditioning WaveNet on Mel spectrogram predictions,” in 2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Calgary, AB, Canada, pp. 4779–4783, 2018. [Google Scholar]

17. J. Devlin, M. W. Chang, K. Lee and K. Toutanova, “BERT: Pre-training of deep bidirectional transformers for language understanding,” in Proc. 2019 Conf. of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Minneapolis, Minnesota, USA, vol. 1, pp. 4171–4186, 2019. [Google Scholar]

18. A. Adhikari, A. Ram, R. Tang and J. Lin, “DocBERT: BERT for document classification,” 2019. [Online]. Available: http://arxiv.org/abs/1904.08398 [Google Scholar]

19. I. Beltagy, K. Lo and A. Cohan, “SciBERT: A pretrained language model for scientific text,” in Proc. 2019 Conf. on Empirical Methods in Natural Language Processing and the 9th Int. Joint Conf. on Natural Language Processing (EMNLP-IJCNLP), Hong Kong, China, pp. 3615–3620, 2019. [Google Scholar]

20. A. K. Das, D. Mishra, K. Das, A. K. Mohanty, M. A. Mohammed et al., “A deep network-based trade and trend analysis system to observe entry and exit points in the forex market,” Mathematics, vol. 10, no. 19, pp. 3632, 2022. [Google Scholar]

21. A. Iliev, N. Kyurkchiev and S. Markov, “On the approximation of the step function by some sigmoid functions,” Mathematics and Computers in Simulation, vol. 133, pp. 223–234, 2017. [Google Scholar]

22. A. Hamidoglu, “On general form of the tanh method and its application to nonlinear partial differential equations,” Numerical Algebra Control and Optimization, vol. 6, no. 2, pp. 175–181, 2016. [Google Scholar]

23. V. Nair and G. E. Hinton, “Rectified linear units improve restricted boltzmann machines,” in Proc. 27th Int. Conf. on Machine Learning (ICML), Haifa, Israel, pp. 1–8, 2010. [Google Scholar]

24. K. He, X. Zhang, S. Ren and J. Sun, “Delving deep into rectifiers: Surpassing human-level performance on imagenet classification,” in Proc. IEEE Int. Conf. on Computer Vision, Santiago, Chile, pp. 1026–1034, 2015. [Google Scholar]

25. B. Xu, N. Wang, T. Chen and M. Li, “Empirical evaluation of rectified activations in convolutional network,” 2015. [Online]. Available: https://arxiv.org/abs/1505.00853 [Google Scholar]

26. M. Anthimopoulos, S. Christodoulidis, L. Ebner, A. Christe and S. Mougiakakou, “Lung pattern classification for interstitial lung diseases using a deep convolutional neural network,” IEEE Transactions on Medical Imaging, vol. 35, no. 5, pp. 1207–1216, 2016. [Google Scholar] [PubMed]

27. S. Scardapane, S. Van Vaerenbergh, A. Hussain and A. Uncini, “Complex-valued neural networks with nonparametric activation functions,” IEEE Transactions on Emerging Topics in Computational Intelligence, vol. 4, no. 2, pp. 140–150, 2018. [Google Scholar]

28. D. A. Clevert, T. Unterthiner and S. Hochreiter, “Fast and accurate deep network learning by exponential linear units (ELUs),” 2015. [Online]. Available: https://arxiv.org/abs/1511.07289 [Google Scholar]

29. Y. Yu, K. Adu, N. Tashi, P. Anokye, X. Wang et al., “RMAF: Relu-memristor-like activation function for deep learning,” IEEE Access, vol. 8, pp. 72727–72741, 2020. [Google Scholar]

30. Z. Qiumei, T. Dan and W. Fenghua, “Improved convolutional neural network based on fast exponentially linear unit activation function,” IEEE Access, vol. 7, pp. 151359–151367, 2019. [Google Scholar]

31. H. Zhao, F. Liu, L. Li and C. Luo, “A novel softplus linear unit for deep convolutional neural networks,” Applied Intelligence, vol. 48, no. 7, pp. 1707–1720, 2018. [Google Scholar]

32. F. Godin, J. Degrave, J. Dambre and W. De Neve, “Dual rectified linear units (DReLUsA replacement for tanh activation functions in quasi-recurrent neural networks,” Pattern Recognition Letters, vol. 116, pp. 8–14, 2018. [Google Scholar]

33. A. Krizhevsky and G. Hinton, “Learning multiple layers of features from tiny images,” 2009. [Online]. Available: http://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.222.9220&rep=rep1&type=pdf [Google Scholar]

34. D. P. Kingma and J. Ba, “Adam: A method for stochastic optimization,” 2014. [Online]. Available: https://arxiv.org/abs/1412.6980 [Google Scholar]