Meta-Learning Multi-Scale Radiology Medical Image Super-Resolution

1  Introduction

High-quality and high-resolution medical images are very important in medical clinical and diagnostic applications. For example, the diagnosis of mild bone fractures or bone spurs, the detection of early lymphomas or hemangiomas, automatic classification of pneumothorax [1], etc., are essential. In addition to clinical diagnostic applications, high-resolution imaging data are necessary for alignment, segmentation, and fusion operations. However, direct access to high-resolution medical images is challenging due to inter-city medical resource allocation and hardware equipment limitations, and the problem that high-dose radiation can cause severe secondary damage to patients. Therefore, it is valuable to introduce super-resolution (SR) technology into the medical field to enhance the resolution of the obtained medical images through technical means. This means of secondary processing can improve the quality of medical images without increasing the cost and reducing the harm to the patient [2]. The SR method is to establish feature mapping between low-resolution (LR) images and high-resolution (HR) images by technical means and to expand LR images into SR images by filling the low-resolution images with pixels that conform to the logical relationships through functions that simulate the mapping relationships [3–5]. The SR image thus obtained retains all the known details in the LR image and has an image quality approximating the HR image. SR methods are generally divided into single-image super-resolution (SISR) and multi-image super-resolution. Since medical images require image details to be as realistic as possible, we focus on the SISR method. The traditional SR method is to artificially create an appropriate function by which the mapping relationship between LR images and HR images is simulated. This method relies on manual selection of parameters and has low generalizability and poor structure. With the development of deep learning, the field of SR started to use a lot of deep learning methods to simulate the mapping relationship between LR images and HR images by themselves. These SR methods using convolutional neural networks (CNNs) and generative adversarial networks (GANs) have achieved good results [6–9]. However, the current SR methods are all capable of super-resolution work on only one scale. Obtaining SR results at different scales would require training networks at multiple scales. Most of the current methods can only work on SR at integer multiples of scales, and cannot handle non-integer multiples of scales.

In this work, we propose a multi-scale network model using meta-learning. This model allows for training a single network weight to perform SR tasks at multiple scales. Meanwhile, the meta-learning module incorporated into the network can reduce the network complexity, making the network lightweight and consuming fewer computer resources. This work has important implications for acquiring high-resolution medical images with limited hardware devices. This work has important implications for acquiring high-resolution medical images with limited hardware devices. It also has an extremely important role in improving the quality of low-dose radiological images and preventing secondary patient harm.

2  Related Work

2.1 Single-Scale Super-Resolution of a Single Image

Traditionally, SISR methods improve the resolution of the input LR image by various interpolations [10], reconstruction [11], neighborhood embedding [12], and sparse coding [13]. However, these methods cannot simulate the nonlinear transformation from LR image features to HR image features, and the quality of the generated super-resolution images is poor. With the rapid development of deep learning, many researchers began to introduce deep learning into the field of super-resolution. The large number of applications to neural networks makes it possible to establish a nonlinear relationship from LR images to HR images. Dong et al. [14] pioneered the use of SRCNN to solve the SR problem with natural images, achieving better performance than traditional methods. The performance was further improved by using residual blocks to deepen the number of network layers for super-resolution using very deep convolutional networks (VDSR) [15]. After the introduction of generative adversarial networks (GANs) [16], Ledig et al. continued the idea of VDSR combined with a combination of GANs to propose SRGAN [17], trained using visual geometry group (VGG)-based perceptual losses [18] and GANs. This approach is different from the CNN-based super-resolution approach, where the GAN-based approach generates a new image directly from the noise information. The new image seeks to retain the stylistic features of the original image. Although the GAN-based super-resolution method obtains a high mean opinion score (MOS), the generated image is hardly guaranteed to retain all the detailed information in the original image, especially for large-scale super-resolution operations. In contrast, the super-resolution approach of the CNN-base generates a high-resolution image directly from a low-resolution image after interpolation, which can retain the true details of the original image to a greater extent. The enhanced deep residual networks for super-resolution (EDSR) proposed by Lim et al. [19] based on the idea of VDSR has better performance by removing the BN blocks that can affect the super-resolution effect. Zhang et al. designed the Residual Dense Network for Image Super-Resolution (RDN) [20] using dense feature fusion (DFF) to take full advantage of common features between levels. Tong et al. proposed Super-Resolution Using Dense Skip Connections (SRDenseNet) [21], which combines low-level features with high-level features by introducing dense skip connections in a very deep network. All of these methods have achieved good SR results, but all of them can be implemented at only one magnification scale, so improved RDN using meta-learning (MetaRDN) [22] is proposed for free-scale SR tasks. It introduces a meta-upscale module that predicts a weight matrix and replaces the upper sample convolution layer with a matrix multiplication. Instead of learning the up-sampling transformation from a specific scale, this new advanced module learns the interrelationship between up-sampling and different scales, and by establishing this relational equation the new module is able to perform super-resolution tasks at different scales. And Zhu et al. used the meta-upscaling module in combination with GAN in Arbitrary Scale Super-Resolution for Medical Images (MIASSR) [23] to get excellent results on magnetic resonance imaging (MRI) images.

2.2 Medical Image Super-Resolution

With the development of deep learning super-resolution algorithms, the use of SR algorithms in the medical field has started to increase [2]. Compared with the super-resolution task for natural images, medical images have a larger threshold interval, and this characteristic determines that medical images have richer edge information. Therefore, medical image SR requires higher sensitivity and restoration of high-frequency information, focuses more on the preservation of organ structures, and does not need to process the image’s color information due to the image’s single-channel characteristics. Due to the difficulty of access and privacy protection, medical images are difficult to obtain a large number of learning samples, which is disastrous for GAN-based super-resolution algorithms. Therefore, CNN-based super-resolution methods are more widely used in the medical field, especially when used as a pre-processing process for operations such as alignment, segmentation, and fusion. However, the current medical alignment methods are mostly fixed-scale, and obtaining images at different scales requires training network weights at multiple scales. Even non-integer magnification scales cannot be obtained with the existing medical SR algorithms, which is unfavorable for subsequent medical tasks. So we introduce meta-learning into the field of medical SR and propose an arbitrary-scale super-resolution method, which attempts to apply meta-learning to the CNN-base super-resolution method to handle arbitrary-scale SR tasks. The specific contributions of this paper are as follows.

1)   We apply meta-learning to the SR task of medical images for the first time and propose a free-scale algorithm for medical image super-resolution. The algorithm in the paper performs only the highest x4 scale magnification, but the algorithm can also be applied to higher magnifications if appropriate data can be prepared.

2)   In the super-resolution training phase, we use a training strategy that combines traditional learning with meta-learning. This allows our algorithm to have a smaller network weight volume and a lighter network architecture compared to current medical SR algorithms.

3)   Due to the high sensitivity of meta-learning to small samples, the generalizability of the network is greatly improved after multi-source and multi-site data participate in the training set. The covariate sample network has good super-resolution results on cone beam computed tomography (CBCT), plan-computed tomography (pCT), and MRI that good generalization results on the head, neck, pelvis, and liver.

3  Method

The purpose of SISR is to recover the detailed features Ihr of HR images from the image features Ilr of LR. In general, LR images are modeled as follows [4].

Ilr=(Ihr⊗κ)↓s+n(1)

Ihr⊗κ denotes the convolution between the blur kernel κ and the HR image Ihr. ↓s denotes the down-sampling operation with scale s and n represents the noise. In the SISR task, we tried to reverse the degeneracy equation in Eq. (1) to obtain a new super-resolution image Isr from Ilr.

Isr=G(Ilr,s;θG)(2)

G is a fitting function to obtain the SR image and θG represents the parameter weights that can be trained in the function. During each iterative training step, the similarity difference between Isr and Ihr is measured by a loss function ℒSR. This similarity difference is back-propagated to calculate the gradient value and update the network weights θG [5].

θG^=arg minθG⁡ℒSR(G(Ilr),Ihr)(3)

3.1 Enhanced Deep Residual Networks for Super-Resolution (EDSR)

EDSR retains the use of a residual network and the extraction of high-frequency information using SRGAN, but removes the original batch normalization (BN) blocks in the residual network to avoid the loss of high-frequency information and improves the recovery of high-frequency information from the hyper-segmented images [19]. As a widely verified method in the CNN series of super-division methods, its recovery of high-frequency image details and the universality and stability of the code are suitable for medical images.

Referring to the training set preparation method for general super-resolution training and Ma et al. [24] LMISR-GAN study, we used the pCT image group with high-frequency information and precise edges as the EDSR training set, and the bicubic image set obtained by bicubic interpolation as the low-resolution set (LR). The original pCT image set was taken as the high-resolution set (HR). The 0-bit bias module in the original EDSR network was adjusted for medical images, and a super-resolution weight model suitable for medical images was obtained after training. However, the model trained by this method retains the original noise and light spots after super-resolution CBCT processing, which interferes with the alignment process. The EDSR network architecture is shown in Fig. 1.

Figure 1: Meta-learning multi-scale super-resolution network based on EDSR (MESR) feature extraction design. (a) Shows the underlying architecture of the MESR network. (b) Shows the EDSR-lite module used for network feature extraction. (c) Shows the composite loss function used by the network. (d) Shows the design architecture of the network meta-upscaling module

The meta-learning multi-scale super-resolution network, which is improved on the basis of EDSR, mainly lies in the increase of sampling module on meta-learning. Replacing the original single-scale upscale module, the new meta-learning upscale module can utilize the weight prediction property of meta-learning itself to store the trend of weight changes at multiple scales in the module. In this way, the weight data of the scale can be quickly obtained based on the input scale data only when used, and the network size is reduced without taking up additional storage space. Meanwhile, the meta-learning multi-scale super-resolution network adopts a compound loss function to improve the accuracy of super-resolution results as much as possible while ensuring the rapidity.

3.2 Multi-Upscale Module

To generate HR outputs from LR inputs at different scales, the extraction formula for the low-dimensional feature mapping can be defined as:

Isr=𝒰s(Flr;φs)(4)

Isr denotes the pixel values in the SR image, 𝒰s represents the up-sampler of the super-resolution network, Flr denotes the pixel features in the LR image, and φs denotes a set of parameters at the s scale. The up-sampler in a regular super-resolution network [25] can only learn a set of parameters at a specific SR scale.

The meta-upscaling module [22] used in our approach learns the weight parameters at all training scales and performs the corresponding tuning. For a single pixel (i,j) on the SR image, the values are determined by the feature mapping of the corresponding point (i′,j′) on the LR image. For each scale the pixel mapping parameters νi,j can be expressed as:

νi,j=W(is−⌊is⌋,js−⌊js⌋,1s),(i,j)∈Isr(5)

W is the weight prediction network for the meta-upscaling module. ⌊∗⌋ is floor function. Each pixel value ISR(i,j) in the SR image can be obtained by Eq. (6).

Isr(i,j)=νi,j×Flr(i′,j′)(6)

And for the meta-up sampling module, the whole mapping relation equation can be expressed as:

Isr(i,j)=W(i,j;s)×Flr(i′,j′)(7)

Based on the Eq. (7) meta-upscaling module, a single network model can be implemented for multi-scale super-resolution processing by predicting the network weight values at different scales. Fig. 2 shows the mapping relationship between images at different scales.

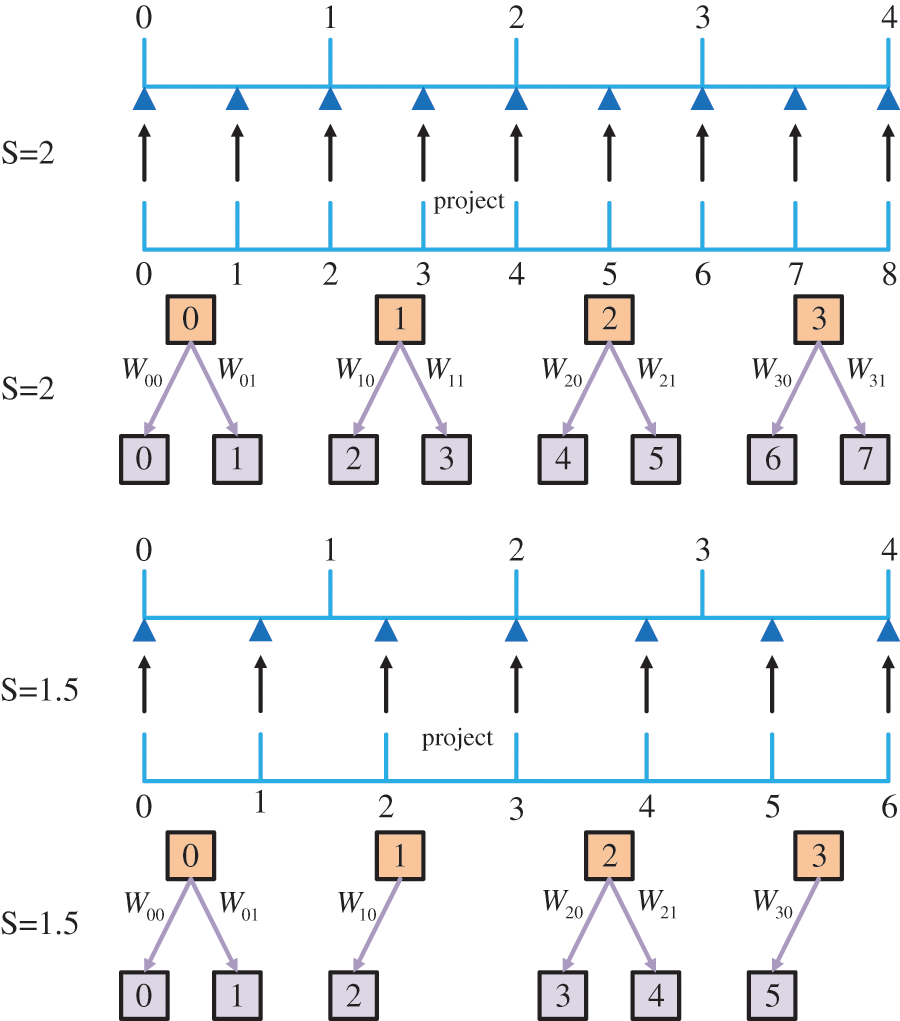
Figure 2: Process demonstration using non-integer multiplicative scale factor s = *.5 upscaled feature maps. For the sake of simplicity, here we only show the upscaling of the one-dimensional features

3.3 Loss Functions

There are three commonly used loss functions for CNN-based super-resolution networks, L1 loss, VGG loss, and GAN loss. To ensure rapidity while improving accuracy in multi-scale model training, we choose a compound loss of three losses as the loss function feedback for the network.

3.3.1 L1 Loss

The SISR task requires calculating the similarity difference between SR images and HR images and iterating the network weights by the similarity difference. Therefore, the pixel-level error calculation is essential for the training and testing of SR networks. We chose the L1 loss as the error loss function, which is based on the principle of calculating the mean absolute error (MAE), a loss function that has the advantage of being computed quickly and has excellent fast performance. It can be defined as:

ℒ1(Isr,Ihr)=1Spix∑(i,j)∈I||Ihr(i,j)−Isr(i,j)||(8)

Spix represents the total number of pixels in the image. The L1 loss function is used more often in super-resolution networks. However, this function is relatively smooth and does not restore the real texture details well, while the real texture details are very important in medical images. Therefore, we introduced perceptual loss and adversarial loss into the training.

3.3.2 VGG-Based Perceptual Loss

The perceptual loss function of the VGG-base was first proposed by Johnson et al. [18] in 2016 and has since been widely used in super-resolution tasks [8–9,26]. It gives the root mean square error (MSE) between the feature domains of the SR image and the HR image. It can be defined as:

ℒperc (Fsr,Fhr)=E(||𝒱l(Fhr)−𝒱l(Fsr)||2)(9)

𝒱 is a pre-trained VGG19 model and F denotes the feature maps of the specific layer 𝒱. Our feature map F was generated by U-shaped network layers, and by hopping together convolutional layers of different depths, richer texture details can be obtained.

3.3.3 Adversarial Loss

We apply Wasserstein GAN-based adversarial loss to generate more perceptually realistic images in our method. GAN mainly contains a generator and a discriminator, and the generator has to generate as realistic an image as possible to pass the discriminator’s judgment [26]. However, this general GAN architecture suffers from the problems of unstable training and crash-prone patterns. Therefore, Arjovsky et al. proposed Wasserstein GAN to solve these problems. They introduced the Wasserstein distance as a counteracting loss to reflect the difference between the generated image and the real image.

ℒWGAN=EIlr[D(G(Ilr))]−EIhr[D(Ihr)](10)

An essential trick of the Wasserstein algorithm is to clip the ownership values of the discriminator to a constant range that satisfies the conditions for the derivable Wasserstein distance. However, when using shearing methods to restrict the discriminator’s weights, it tends to focus on the maximum and minimum values. This makes the discriminator approximate a binary network and reduces the nonlinear simulation capability of GANs. Therefore, a gradient penalty is used instead of the shearing operation. This approach allows the gradient of the discriminator not to jump, and the adversarial loss function using this approach is expressed as:

ℒadv=ℒWGAN+EI[||∇ID(I)||p−1]2(11)

||||p is the p-norm. In summary, the total loss function can be defined as:

ℒSR=λ×ℒ1+γ×ℒadv+η×ℒperc(12)

λ, γ, and η are scale factors to balance each part of the loss function.

4  Experiment and Result

In our experimental arrangement, data sets from three different sources and different sites were selected for validation. The SR task arranged six scales with magnifications between (1,4]. To evaluate our method, three metrics, Peak Signal-to-Noise Ratio (PSNR), Structure Similarity Index Measure (SSIM), and Normalized Root Mean Square Error (NRMSE), were chosen to determine the similarity differences between SR images and HR images and to compare them with four SR algorithms.

4.1 Data and Pre-Processing

The network architecture was obtained based on a pelvic clinical dataset trained from CBCT and pCT images of 18 patients at different time periods. Since the study focused on two-dimensional orientation, the data were selected for cross-sectional slices, where pCT was approximately 130 sized 512 × 512 per patient and CBCT was approximately 80 sized 384 × 384 per patient. The pixel thresholds for all images were constrained to be between [0-2000 Hounsfiled Unit (HU)]. The HR images were obtained by segmenting the background of the original slices and removing the information. Too much background information is worthless for training and slows down the training time, so the background was removed as much as possible during segmentation. The LR images were not obtained by downsampling the corresponding HR according to the traditional method [23], but by selecting the pre-collimated low-dose CBCT slices corresponding to the pCT slices as the LR images. In our experiments, we fixed all pCT images to 384 × 384 and made training sets at different scales by Bicubic interpolation of CBCT images. one HR image set with 622 slices, and six LR image sets with 3732 slices corresponding to six scales. The test set was set to 200 CBCT slices, derived from randomly selected CBCT slices from patient data that did not participate in the training set.

4.2 Metrics

In our experiments, we chose three quality assessment functions to evaluate the image quality of SR images after super-resolution processing. We used PSNR, SSIM, and NRMSE to evaluate the results. PSNR measures the ratio between effective image information and noise and reflects whether an image is distorted. SSIM uses windowed values to compare the differences in brightness, contrast, and structure between the two images and uses normalized data to show the degree of similarity between them. NRMSE is the normalization algorithm of RMSE, which measures the deviation between the super-resolution image and the original image. It is sensitive to outliers in the data and reflects whether there is noise in the super-resolution image.

RMSE=1pix∑x,ypix⁡(HR(x,y)−SR(x,y))2(13)

NRMSE=RMSESR(x,y)max−SR(x,y)min(14)

(x,y) is the image pixel coordinates, HR(x,y) is the pixel value of the original high-definition image, SR(x,y) is the pixel value in the image obtained after over-division, and pix is the total number of pixels in the image.

PSNR=10×log⁡(MAX2RMSE)(15)

MAX is the maximum pixel intensity in the image.

SSIM=(2μHRμSR+c1)(2σHRSR+c2)(μHR2+μSR2+c1)(σHR2+σSR2+c2)(16)

μHR and μSR are the average values of the high-definition image and the super-resolution image, σHR and σSR are the standard deviations of the two images, σHRSR is the covariance of the high-definition image and the super-resolution image.

4.3 Implementation Details

We use PyTorch to build the entire network, process the Dicom format data, and transform it into ‘.npy’ format data for training and testing. We divided the data of 18 patients into training and test sets in the ratio of 5:1. 4354 paired slices were produced in the training set, corresponding to 622 HR image sets and 3732 LR data sets with six different scales. We used 600 slices for training and 22 slices for testing and set the patch size to 96 and the batch size to 8 to reduce the video memory consumption. All experiments were performed with NVIDIA RTX 2080Ti.

Due to the direct processing of medical image data matrices with large thresholds, the hyperparameter configuration under the general common format images cannot be used. We cancel the bias setting in the convolutional layer and set the number of feature maps to 64. Due to the experimental equipment limitation, we limit the training input batch size to 8 and the original patch size is set to 96 × 96. The learning rate is set to 0.0004 and the learning rate decay coefficient for step decay is set to 0.5.

4.4 Multi-Scale Results Analysis

In this section of experiments, we focus on testing the processing effect and network performance of the proposed multi-scale super-resolution network. This section does not involve the comparative study with other publicly available models and the generalizability test of the proposed network in different parts. Therefore, this section mainly uses a single CT dataset of pelvic sites for testing, with three test patient samples and 200 test slices. This section evaluates the super-resolution performance at different scales, using three evaluation metrics with pixel-level visualization difference maps in terms of both numerical and visualization effects, respectively. The visualization effect of super-resolution processing at different scales is shown in Fig. 3.

Figure 3: Results of pCT 6-scale SR images of the pelvis

Table 1 shows the performance of the six scales of SR processing results under three evaluation metrics tested at 200 slices. The table reflects the general trend that the larger the scale, the lower the quality of the super-resolution processing results. However, based on the general analysis of the above graphs, it can be seen that, concerning the results obtained so far, the single-model multi-scale super-resolution processing network has undoubtedly met the requirements for image augmentation and guaranteed image quality. Even the 4x SR processing with the lowest performance can still guarantee a PSNR of about 33 and an SSIM index above 0.95, which has met the requirements of multiple processing methods for image quality. For example, alignment, segmentation, fusion, diagnosis, etc. This shows that our proposed network has an excellent application on a single source with a single site.

4.5 Performance Comparison with Different Methods

The validation of the sample using only our proposed net is unreliable, and the lack of comparative experiments on other methods of the same type is difficult to argue for the novelty and superiority of our method. In this section, we choose some SR methods that have been widely used and some new ones that have been proposed in recent years to compare with our whole network. Since our network is modeled on a private dataset, validation is performed on a public dataset. So we reconstructed all the comparison network models and trained them using our private dataset to achieve the fair comparison condition, which may be slightly different from the data in the original paper on the comparison model. The specific experimental data table is shown in Table 2. By comparing the data in Table 2, we can see that our method performs the best under all three performance indicators for the same SR task at the same scale in the same part. In particular, under the SSIM, which is a crucial structural evaluation metric for medical imaging, our method has the highest 15% improvement over the conventional SR methods in the same field.

Even for the MetaRDN method, which has been the best performing method in recent years, we have about a 2% improvement. Regarding network lightweighting, we still have a particular gap in the MIASSR method, which has done the best lightweighting in recent years. However, with only a 5.1 M complete weight model, we still have an advantage over other networks in the same field in network lightweighting. The experiments in this section prove that our proposed multi-scale SR method is a high-performance, lightweight SR processing algorithm with high practical value.

4.6 Generalizability of Different Sites

In this section, we will test the generalizability of the network using CT slices from three locations: pelvis, chest, and liver. Testing whether the network can have large enough adaptability that a single set of training for but one site can meet the SR requirements for multiple sites, allowing the network to have higher convenience without needing repeated training operations for different site intervals. The experimental results are shown in Figs. 4 and 5. The specific experimental data are shown in Table 3.

Figure 4: Generalization results of multiscale SR on lung images

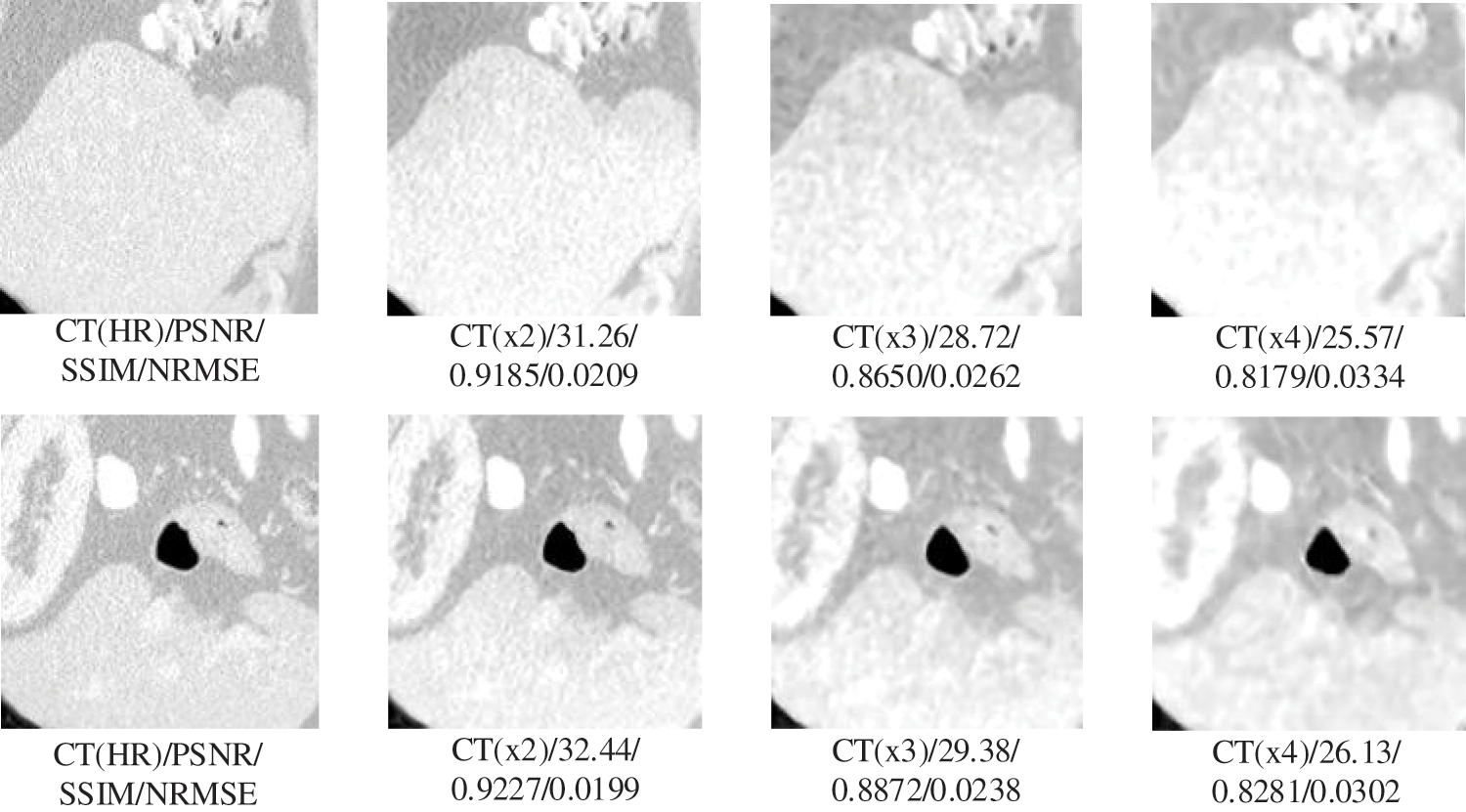
Figure 5: Generalization results of multiscale SR on liver images

The results in Table 3 show that our proposed SR algorithm is superior in terms of generalization to different parts compared to the two deep learning SR methods. The test sample used in the lung visualization results in Fig. 4 is a 512 × 512 slice, while the liver test sample in Fig. 5 is a 160 × 192 slice. Comparing the SR results of the two figures shows that the SR processing results are better at high magnification when the LR image contains more information. Although the 4x SR results are not ideal in the liver, the quality of the results of 2x SR is sufficient for use. Therefore, it can be verified that the generalizability of our proposed method to different sites is also excellent.

5  Discussion

We propose a multi-scale medical super-resolution network in the present work using meta-learning. It uses a meta-learning module in both the training and up-sampling parts. It can not only accomplish the single-model multi-scale SR task, but also significantly reduce the model size to make the network lightweight, and has good generalizability.

We tested the amplification performance of the multi-scale SR network at six scales using 200 slices from the pelvic region, which included amplification ratios with non-integer multiples. With the experimental results in Section 4.4, it can be demonstrated that our multi-scale SR network has good performance on both integer-fold and non-integer-fold amplification. Even with the highest 4-fold SR test, our network can achieve an average SSIM value of 0.96 or higher, which has high practicality. We used seven algorithms from the SR domain to compare with our proposed network. Among them, Bicubic, SRGAN [17], EDSR [19], and RDN [20] are well-established algorithms that have been widely validated, and SRDenseNet [21], MetaRDN [22], and MIASSR [23] are novel SR algorithms that have been proposed in recent years. The experimental comparison in Section 4.5 demonstrates that our network achieves excellent SR results while achieving network lightweighting. The improvement is 15% compared to the earlier SRGAN algorithm and 2% compared to the best-performing MetaRDN algorithm. We also performed generalizability tests on the chest and liver datasets using the model obtained from pelvic training. Although there is a slight shortfall in the 4-fold SR metric, the excellent performance in the 2-fold and 3-fold metrics is sufficient to demonstrate the good generalizability of the model. In future studies, we will improve the model to address the shortcomings of the high-fold SR operation. And we will extend the algorithm to the 3D direction to avoid the extra cost when converting the real-harvested images to 2D slices. The three experiments are sufficient to demonstrate that our proposed multi-scale SR algorithm has a high practical value. This method can compensate for the hardware device deficiency and reduce patient harm while obtaining high-resolution medical images by post-algorithms. It has an essential role in the radiological examination of elderly patients and the practical application of radiological imaging in small cities.

6  Conclusion

This work proposes a multi-scale super-resolution algorithm with meta-learning. The problem that the current SR algorithm only works for a single scale is solved. A network lightweighting improvement is accomplished to reduce the occupation of hardware resources. It can compensate for hardware defects, reduce extra harm to patients, and obtain high-resolution medical images. It has an essential medical clinical value.

Funding Statement: This work is supported by the National Science Foundation for Young Scientists of China (Grant No. 61806060), 2019–2021, and the Natural Science Foundation of Heilongjiang Province (LH2019F024), China, 2019–2021. We also acknowledge support from the Basic and Applied Basic Research Foundation of Guangdong Province (2021A1515220140) and the Youth Innovation Project of Sun Yat-sen University Cancer Center (QNYCPY32).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. S. Feng, Q. Liu, A. Patel, S. U. Bazai, C. K. Jin et al., “Automated pneumothorax triaging in chest X-rays in the New Zealand population using deep-learning algorithms,” Journal of Medical Imaging and Radiation Oncology, Early View, vol. 66, no. 8, pp. 1035–1043, 2022. [Google Scholar] [PubMed]

2. Y. Li, B. Sixou and F. Peyrin, “A review of the deep learning methods for medical images super resolution problems,” Irbm, vol. 42, no. 2, pp. 120–133, 2021. [Google Scholar]

3. L. Schermelleh, R. Heintzmann and H. Leonhardt, “A guide to super-resolution fluorescence microscopy,” Journal of Cell Biology, vol. 190, no. 2, pp. 165–175, 2010. [Google Scholar] [PubMed]

4. W. Yang, X. Zhang, Y. Tian, W. Wang, J. -H. Xue et al., “Deep learning for single image super-resolution: A brief review,” IEEE Transactions on Multimedia, vol. 21, no. 12, pp. 3106–3121, 2019. [Google Scholar]

5. Z. Wang, J. Chen and S. C. Hoi, “Deep learning for image super-resolution: A survey,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 43, no. 10, pp. 3365–3387, 2020. [Google Scholar]

6. C. You, G. Li, Y. Zhang, X. Zhang, H. Shan et al., “CT Super-resolution GAN constrained by the identical, residual, and cycle learning ensemble (GAN-CIRCLE),” IEEE Transactions on Medical Imaging, vol. 39, no. 1, pp. 188–203, 2019. [Google Scholar] [PubMed]

7. J. Park, D. Hwang, K. Y. Kim, S. K. Kang, Y. K. Kim et al., “Computed tomography super-resolution using deep convolutional neural network,” Physics in Medicine & Biology, vol. 63, no. 14, pp. 145011, 2018. [Google Scholar]

8. J. Zhu, G. Yang and P. Lio, “How can we make GAN perform better in single medical image super-resolution? A lesion focused multi-scale approach,” in 2019 IEEE 16th Int. Symp. on Biomedical Imaging (ISBI 2019), San Diego, California, USA, pp. 1669–1673, 2019. [Google Scholar]

9. J. Zhu, G. Yang and P. Lio, “Lesion focused super-resolution,” in Medical Imaging 2019: Image Processing, vol. 10949. Venice, Italy, SPIE, pp. 401–406, 2019. [Google Scholar]

10. R. Keys, “Cubic convolution interpolation for digital image processing,” IEEE Transactions on Acoustics, Speech, and Signal Processing, vol. 29, no. 6, pp. 1153–1160, 1981. [Google Scholar]

11. H. Ji and C. Fermüller, “Wavelet-based super-resolution reconstruction: Theory and algorithm,” in European Conf. on Computer Vision, Berlin, Heidelberg, Springer, pp. 295–307, 2006. [Google Scholar]

12. R. Timofte, V. De Smet and L. Van Gool, “A+: Adjusted anchored neighborhood regression for fast super-resolution,” in Asian Conf. on Computer Vision, Singapore, Springer, pp. 111–126, 2014. [Google Scholar]

13. R. Zeyde, M. Elad and M. Protter, “On single image scale-up using sparse-representations,” in Int. Conf. on Curves and Surfaces, Avignon, France, Springer, pp. 711–730, 2010. [Google Scholar]

14. C. Dong, C. C. Loy, K. He and X. Tang, “Image super-resolution using deep convolutional networks,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 38, no. 2, pp. 295–307, 2015. [Google Scholar]

15. J. Kim, J. K. Lee and K. M. Lee, “Accurate image super-resolution using very deep convolutional networks,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, Las Vegas, Nevada, pp. 1646–1654, 2016. [Google Scholar]

16. I. Goodfellow, J. Pouget-Abadie, M. Mirza, B. Xu, D. Warde-Farley et al., “Generative adversarial nets,” in The 27th Int. Conf. on Neural Information Processing Systems(NIPS), Montreal Canada, vol. 27, pp. 2672–2680, 2014. [Google Scholar]

17. C. Ledig, L. Theis, F. Huszár, J. Caballero, A. Cunningham et al., “Photo-realistic single image super-resolution using a generative adversarial network,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, Honolulu, HI, USA, pp. 4681–4690, 2017. [Google Scholar]

18. J. Johnson, A. Alahi and L. Fei-Fei, “Perceptual losses for real-time style transfer and super-resolution,” in European Conf. on Computer Vision, Amsterdam, The Netherlands, Springer, pp. 694–711, 2016. [Google Scholar]

19. B. Lim, S. Son, H. Kim, S. Nah and K. Mu Lee, “Enhanced deep residual networks for single image super-resolution,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition Workshops, Honolulu, HI, USA, pp. 136–144, 2017. [Google Scholar]

20. Y. Zhang, Y. Tian, Y. Kong, B. Zhong and Y. Fu, “Residual dense network for image super-resolution,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, pp. 2472–2481, 2018. [Google Scholar]

21. T. Tong, G. Li, X. Liu and Q. Gao, “Image super-resolution using dense skip connections,” in Proc. of the IEEE Int. Conf. on Computer Vision, Venice, Italy, pp. 4799–4807, 2017. [Google Scholar]

22. X. Hu, H. Mu, X. Zhang, Z. Wang, T. Tan et al., “Meta-SR: A magnification-arbitrary network for super-resolution,” in Proc. of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Long Beach, CA, USA, pp. 1575–1584, 2019. [Google Scholar]

23. J. Zhu, C. Tan, J. Yang, G. Yang and P. Lio’, “Arbitrary scale super-resolution for medical images,” International Journal of Neural Systems, vol. 31, no. 10, pp. 2150037, 2021. [Google Scholar] [PubMed]

24. Y. Ma, K. Liu, H. Xiong, P. Fang, X. Li et al., “Medical image super-resolution using a relativistic average generative adversarial network,” Nuclear Instruments and Methods in Physics Research Section A: Accelerators, Spectrometers, Detectors and Associated Equipment, vol. 992, pp. 165053, 2021. [Google Scholar]

25. W. Shi, J. Caballero, F. Huszár, J. Totz, A. P. Aitken et al., “Real-time single image and video super-resolution using an efficient sub-pixel convolutional neural network,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, Las Vegas, Nevada, pp. 1874–1883, 2016. [Google Scholar]

26. X. Wang, K. Yu, S. Wu, J. Gu, Y. Liu et al., “ESRGAN: Enhanced super-resolution generative adversarial networks,” in European Conf. on Computer Vision, Munich, Germany, Springer, pp. 63–79, 2018. [Google Scholar]