A Secure and Effective Energy-Aware Fixed-Point Quantization Scheme for Asynchronous Federated Learning

1  Introduction

Machine learning (ML) has been in rapid development in the last decade, constantly evolving and innovating in academia and industry. Several state-of-the-art ML algorithms have emerged, which are utilized in the industrial internet-of-things (IoT), 5G communication, chemical molecular research, and other fields, and drive these fields to a further study level. The wide application of big data technology brings new opportunities and challenges for ML. On the one hand, big data provides massive amounts of information in the training phase of ML, which improves the accuracy and applicability of model training. On the other hand, with the further development of 5G IoT technology, privacy and security have become critical points for the industry to consider [1]. FL [2] dramatically guarantees data privacy in the model training process [3] and provides an effective solution to the islanding effect in ML. Based on securing the data privacy of industrial devices, FL can incorporate numerous industrial devices into the ML training process, saving communication resources during model training [4] and improving the training convergence rate and learning accuracy [5].

However, FL for IoT networks faces several challenges in its implementation. First, IoT devices are diverse in real-world applications and have heterogeneous computing resources (e.g., smartphones vs. smart watches). The slowest nodes maybe become the bottleneck and delay the entire training process [6–10]. Second, synchronous uploading of large amounts of local model updates by edge nodes can lead to congestion in the communication channel and decrease communication efficiency.

In order to handle the above challenges, an AsynFL framework is proposed, which could provide a more flexible global update and alleviate the instantaneous communication load [11]. AsynFL allows model aggregation without waiting for stale devices [12,13] in the way that the central server conducts global model aggregation as soon as it collects a local model [14].

In spite of these advantages, in such AsynFL, the flexible model update generates more communication rounds for the faster edge nodes, which leads to more communication energy consumption. Meanwhile, both in academia and industry, deep learning models are gradually becoming larger and more complex to provide more powerful model training capabilities and more accurate model prediction capabilities. Such large and complex models can be deployed in the cloud in centralized ML frameworks, where computational resources are abundant [15]. However, in applying AsynFL to industrial IoT, such complex models pose a severe challenge to industrial devices’ computing power and battery capacity during computation and communication. Therefore, breaking resource constraints becomes an important research direction for applying FL in industrial IoT.

Model compression is a proven method to reduce edge nodes’ computation and communication consumption. Currently, popular model compression methods are low-rank decomposition [16,17], knowledge distillation [18,19], network pruning [20,21], and fixed-point quantization [22]. Low-rank decomposition can improve inference speed but has a lower compression effect than network pruning and fixed-point quantization [17]. Federated Distillation (FDD) algorithm based on knowledge distillation method is more demanding and has the risk of user privacy leakage [22]. The main idea of network pruning is to remove the smaller elements from the weights matrix and retain only the more important part of the weights [20].

Fixed-point quantization can improve the effect of model training while ensuring a small error. Fixed-point quantization can significantly reduce the representation cost of neural network parameters [23] and thus reduce storage pressure. Due to its architectural characteristics, neural network computation has a low demand for high precision and high dynamic range in digital storage [22,24]. The moderate noise in neural network parameters even could improve the training performance [25,26]. However, the quantization noise tolerance is not boundless in the utilization of fixed-point quantization. When the quantization bit-width is set as an extreme situation, the training accuracy would deteriorate dramatically. Thus, it is important to find a balance between the quantization scale and energy consumption in the fixed-point quantization utilization.

Considering the above challenge in AsynFL and fixed-point quantization, this paper has made the following contributions to the paper:

1) This paper proposes an AsynFL algorithm based on fixed-point quantization. Introducing fixed-point quantization in FL and reducing the model size to a suitable scale can effectively reduce the upstream and downstream communication loss during federated training. At the same time, maintaining the model at a smaller bit-width can also effectively reduce the computation consumption during inference and improve the applicability of neural networks on computationally sensitive devices.

2) This paper proposes a quantization scale selection mechanism based on optimal energy consumption. The bit-width that minimizes the communication energy consumption and the computation energy consumption is calculated while ensuring that the quantization error is within a specific range.

3) This paper applies the FixedAsynFL algorithm to Convolutional Neural Network (CNN), and the results show that the training accuracy loss is in an acceptable state and the energy consumption reduction is significant.

The main structure of this paper is as follows. Section 2 shows some recent work on fixed-point quantization and CNN energy consumption. Section 3 will briefly introduce the basic principles of AsynFL and fixed-point quantization. Section 4 will give a detailed description of the proposed FL algorithm model based on fixed-point quantization. Section 5 will show the experimental simulation results to support the proposed FixedAsynFL algorithm.

It is shown in Table 1 that the utilized key notations in this paper. In order to clearly represent mathematical symbols, this paper uses regular letters, boldface lowercase letters, and boldface uppercase letters to denote scalars, vectors, and matrices respectively.

2  Related Work

After the proposal of the Asynchronous Federated Optimization (FedAsync) algorithm [13], there have been some efforts toward optimizing AsynFL. Y. Chen et al. designed an asynchronous online FL framework, where multiple user equipment (UEs) with continuously arriving samples learn an effective shared model collaboratively [27]. M. Chen et al. proposed a novel FL algorithm that dynamically adjusts the number of local iterations on stragglers to reduce the impact of staleness on the convergence of the global model [28]. All of the above work absorbs the asynchronous aggregation in order to mitigate the heterogeneity of devices in the FL training. These researches paid more attention to the slow edge node in the AsynFL but did not concern with the frequency of communication between the central node and fast edge nodes, which could result in high energy consumption.

Fixed-point quantization could effectively reduce this high energy consumption and optimize the effect of neural network training [29]. There have been many recent studies focusing on fixed-point quantization [22,30–35], which is summarized in Table 2.

Gupta S et al. trained a deep network based on 16-bit fixed-point representation with almost no loss of accuracy for the classification task [22]. Jacob B et al. proposed a quantized inference framework, which could quantize both the weights and activations in the neural network [31]. Based on the first two works, a lightweight INT8 training method was proposed, in which both forward and backward stages were optimized by fixed point quantization [32]. The above researches deeply discuss the problems encountered when fixed-point quantization is applied to neural network training and give effective solutions. However, these articles lack the consideration of the quantization scale on training accuracy and energy consumption.

Several researchers have combined FL with the quantization method [36–40]. However, these works only focus on model training mechanisms and lack attention to the energy consumption of network quantization in the training process. Chen R [41] combined fixed-point quantization with synchronous FL (SynFL) to reduce energy consumption during both the training process and communication process. This paper does not consider the limitations of SynFL.

In view of the advantages and disadvantages of the related works, this paper applies the fixed-point quantization theory in AsynFL, aiming at reducing the energy consumption and communication consumption of edge nodes, and optimizing the quantization scale selection based on the consideration of energy consumption and quantization error.

3  Preliminary Knowledge

3.1 Asynchronous Federated Learning

In AsynFL, wgr denotes the global model on the central node at the rth communication round, which are the weights and bias parameters in the network. Furthermore, wir denotes the local model trained on the ith edge node.

At the beginning of the FL training, the central node distributes the initial global model to all edge nodes participating in the first round of training. As shown in the Fig. 1, the central node in the SynFL mode would not start aggregating uploaded models and generating a new global model wgr until it has received the local models of all participating edge nodes. On the contrary, in the AsynFL, the server immediately updates the global model whenever it receives an uploaded model from any participating edge nodes by weighted averaging, which is shown in the following equation:

Figure 1: Synchronous federated learning and asynchronous federated learning

wgr+1=(1−α)wgr+αwir+1,(1)

where α∈(0,1) is a hyperparameter.

As a comparison, in SynFL, the aggregated update formula for the global model is

wgr+1=1N∑i=1Nwir,(2)

3.2 Fixed-Point Quantization Method

In computer science, the floating-point format is commonly used for computing and storing binary numbers, which is based on scientific notation and is the best way to store huge and tiny numbers [42]. The 4-byte single-precision floating-point number could be taken as an example, which is also named the FP32 format. However, the massive parameters in neural networks pose a more significant challenge to the edge nodes’ computational power and battery capacity [43]. After quantizing the network parameters in fixed-point format, the communication consumption in the FL and the computing energy in the CNN inference process could be reduced.

The fixed-point format of numbers fixes the number's decimal point at a specific location during the storage and computation of the data. This paper use B to denote the bit-width of the fixed-point numbers, BIL to denote the bit-width of the integer part, and BFL to denote the fractional part. Clearly, there is B=BIL+BFL. Unlike floating-point format, there is a particular data range for fixed-point numbers: 1) for signed numbers, the fixed-point format sets the range of the data to [−2BIL−1,2BIL−1−2−BFL], 2) while for unsigned numbers, after quantizing them as fixed-point format, the range of the data is [−2BIL,2BIL−2−BFL]. 2−BFL is the smallest positive number that can be represented by a fixed-point number, also known as step size or quantization step. In the following, δ denotes this number.

This paper defines xf as a floating-point format data and xq as its corresponding fixed-point format and uses round(⋅) to denote the round half-up method. Then the mapping of the floating-point data xf to the signed fixed-point data xq is as follows [25]:

xq={−2BIL−1,xf<−2BIL−1δ⋅round(xfδ),xf∈[−2BIL,2BIL−2−BFL]2BIL−1−δ,xf>2BIL−1−2−BFL,(3)

When mapping a set of data xf in floating-point format to fixed-point data, the decimal point position is determined by the range of the data set. For data of signed type, BIL=1+⌈log2[max{|xf|}]⌉; and for data of unsigned type, BIL=⌈log2[max{|xf|}]⌉. And the quantization noise can be expressed as ϵ=max{|xf|}⋅δ.

3.3 Convolutional Neural Networks

The layers in a CNN can be divided into three categories: convolutional layer, fully connected layer, and pooling layer. Furthermore, among them, it is the convolutional layer and the fully connected layer that occupy more computational energy consumption. The fully connected layer has a similar structure to Multilayer Perceptron (MLP). Thus, the main layers that need to be quantized are convolutional layers and fully connected layers.

4  Fixed-Point Quantization in the Asynchronous Federated Learning

This section will briefly introduce the FixedAsynFL algorithm, including the model training process, quantization method, and the derivation of two kinds of energy consumption. Furthermore, the optimization objective is given at the end: the most suitable quantization scale is selected within the exhaustive method to achieve the minimum value of communication energy consumption and inference energy consumption.

4.1 System Model

In AsynFL, the weight parameters are carried out in the uplink and downlink communication between the edge nodes and the central node. Thus, the objects of fixed-point quantization are the weights in the neural network, which is quantized to the bit-width of BW. A pseudo-code of our FixedAsynFL algorithm is presented in Algorithm 1.

At the beginning of the proposed FixedAsynFL algorithm, the central node generates an initialized global model wg0 and broadcasts this initialized global model to all of the edge nodes. Then, the edge nodes in different computing and communication capability would start their first round of asynchronous local training.

4.1.1 Quantization and Local Model Update

The main procedure on the edge node is fixed-point quantization and local training by the mini-batch gradient descent method. As shown in Fig. 2 and the 3th to 11th lines in Algorithm 1, the ith edge node firstly downloads the latest global model wgr0 from the central node in the r0th round of global training. Then, the global model wgr0 would be quantized into a BW-bit fixed-point model w~gr0 based on Eq. (3) and is also seen as the initialized local model wi(0),r0. Just to be clear in advance, the value of bit-width BW is determined by considering the computation and communication energy consumption of edge nodes, which will be described later.

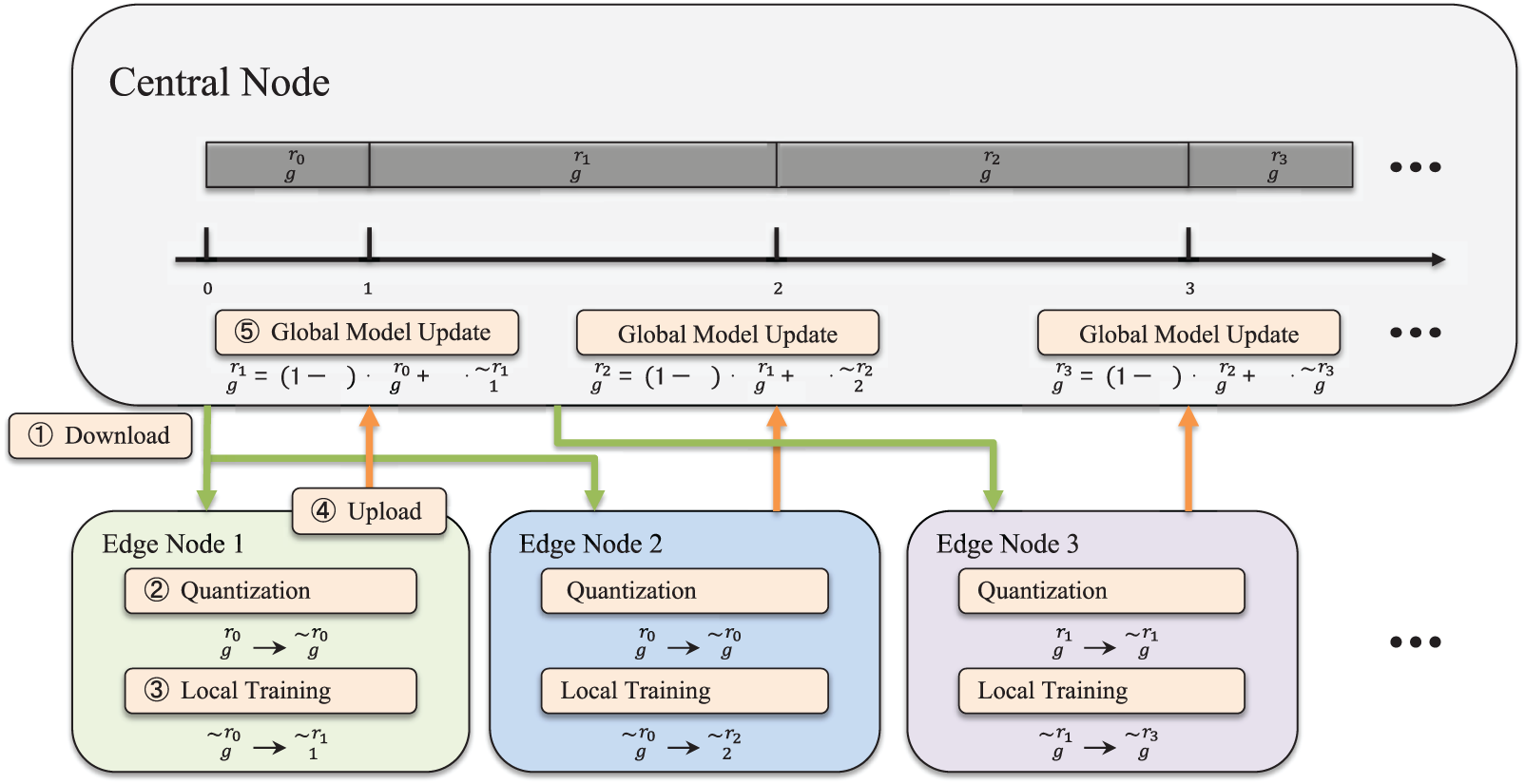
Figure 2: Fixed-point quantization asynchronous federated learning

With finishing fixed-point quantization, the edge nodes perform the weights update process by BW-bit mini-batch gradient descent (mini-batch GD) method. The dataset of the ith edge node is denoted by Di with a size of |Di|. In the mini-batch GD, the local dataset is divided into |Di|/M batches, and the sampled mini-batch data is represented by dik={xm,ym}m=1M, where M is batch size and {xm,ym} are input feature and output label respectively.

In the r0th round, the objective of the ith edge node’s local training is given as follows:

minw~ir0F(w~ir0)=∑k=1Kir0|dik||Di|f(w~ir0;dik),(4)

where Kir is the number of local training iterations; f(w~ir0;dik) denotes the loss function with respect to the fixed-point model and sampled data dik. In each iteration of local training, with the learning rate η, the local model is updated by equation w~i(k+1),r0←w~i(k),r0−η∇f(w~i(k),r0;dik).

After Kir local iterations, the local training of this global round is finished and the local model update of the ith edge node is w~ir1=wi(Kir),r0, which will be immediately transmitted to the central server. It should be clear that the global round r0 and r1 are not adjacent. Because of the characteristic of AsynFL, there might be another edge node uploading its local model w~jr∗ to the central node before the global round r1 (r0<r∗<r1).

4.1.2 Global Model Aggregation

Unlike synchronous aggregation of SynFL, AsynFL updates the global model as soon as it receives local model update wir+1 from the ith edge node by Eq. (1). Then central node will transmit the new global model back to the ith edge node. Since the central node has sufficient computing power, the parameters in the aggregation process are not necessary to be quantized to fixed-point format.

During the global model aggregation, other edge nodes are also performing their own local training and do not conflict with each other.

The detailed proposed FixedAsynFL algorithm flow can be referred to the Algorithm 1.

4.2 Computation Energy Consumption

The computation energy consumption is the required energy for performing arithmetic operations such as addition and multiplication in the local training process, which can be obtained by multiplying the runtime power of the edge nodes’ processors and the local training time delay in a training iteration.

The runtime power pirun of the ith edge node is:

pirun=ciproc(Viproc)2fiproc+pi0,(5)

where Viproc and fiproc denote core voltage and core frequency of the ith edge node’s processor respectively. And ciproc is a constant coefficient that is related to the computing power and hardware configuration of edge nodes ith. pi0 is the power consumption unrelated to the processor’s core voltage/frequency.

The local training time of edge nodes can be expressed by the following equation:

Ticmp(Bw)=k(Bw)γiprocfiproc+ti0.(6)

In the Eq. (4), γiproc denotes the number of cycles for the data fetching and data computing of the ith edge node’s processor, which would be reduced with a linear function k(Bw) because of the fixed-point quantization. Besides, this paper use ti0 to represent the other component unrelated to the training task.

Therefore, the computation energy consumption of the edge node ith could be obtained by calculating the product of processor runtime power and local training time delay.

Eicmp(Bw)=pirun⋅Ticmp(Bw).(7)

4.3 Communication Energy Consumption

In the FixedAsynFL algorithm, this paper sets the uplink communication of edge nodes as a frequency division multiplexer protocol. A Hr-Hz frequency band is equally divided for all edge nodes in the rth round. In AsynFL, the number of edge nodes in the global training would alter in the different communication rounds. Thus, the optimal value of Hr would not be a constant number. For the ith edge node, the uplink communication rate is denoted as

ξi=Hi,rlog2(1+hipitranN0Hi,r).(8)

Hi,r denotes the uplink bandwidth of edge node ith in the rth round. This paper uses hi to denote channel gain and pitran to denote the transmission power of the ith edge node. N0 is the Gaussian white noise. The channel gain hi is assumed as a constant and deterministic value during the training process.

The uplink communication time delay of the ith edge node is defined as Ticom and the communication data size as si. The communication data of the edge node is the local model update, i.e., si=‖wi‖0⋅Bw. The ||⋅||0 denotes the l0 norm, which indicates the number of non-zero elements in the vector.

Thus, the uplink communication delay Ticom can be calculated as follow:

Ticom=siξi=||wi||0⋅BwHrlog2(1+hipitN0Hr).(9)

And the communication energy consumption of edge nodes can be calculated as the product of communication delay and communication transmission power.

Eicom(Hi,r,Bw)=Ticom⋅pitran=||wi||0⋅BwBi,rlog2(1+hipitranN0Hi,r)⋅pitran.(10)

4.4 Problem Formulation

The optimization objective of this paper is to reduce the uplink communication energy consumption and the local training energy consumption of the edge nodes while maintaining the quantization error within a specific range. This paper uses N to denote the number of edge nodes and Ri to denote the number of global training rounds that the ith edge node has participated. Based on what is discussed in this paper, the following optimization objectives are constructed as follows:

minBw,Hr∑i=1N∑r=1Ri{Ei,rcmp(Bw)+Ei,rcom(Bw,Hr)},(11)

subject to,

1N∑i=1Nϵi2≤E,(12)

∑r=1Ri(Ticmp+Ti,tcom)≤Tmax,∀i,(13)

Hi,r=HrN,(14)

Hr∈[1.5×108,2.5×108],(15)

Bw∈[2,10],(16)

where the variables are the quantized bit-width BW and the total frequency band Hr. E is the acceptable upper limit of quantization noise. In this paper, the sum of local training time and communication time of any edge node cannot exceed Tmax.

5  Performance Evaluation

In this section, we conduct abound experiments on the physical platform and the simulated environment to evaluate the effectiveness of our proposed algorithms. We first discuss the experimental settings in detail, and then present the experimental results on the prototype system and simulated environment, respectively. Finally, we provide a brief summary of those results.

5.1 Experiment Settings

In this section, we perform extensive experiments on the simulated environment to evaluate the effectiveness of our proposed algorithms. This section introduces the experiment settings in detail, and then discusses and analyses the experiment results in the simulated environment.

5.1.1 Experiment Environment

Our team deployed the proposed FixedAsynFL algorithm on a GPU Server named Supermicro SuperServer 4029GP-TRT. This server is carrying a 40-core Intel(R) Xeon(R) Silver 4210R CPU and one NVIDIA GeForce RTX 3090 GPU with 24GB RAM. The operation system (OS) is Ubuntu 18.04.6 LTS. We simulate the actual FL training environment which includes the central node and edge node on this server at the code level. Meanwhile, to reflect the heterogeneity of clients, we set different local training delays for each edge node.

As for the communication environment parameters, the total frequency band is set to 200 MHz, and the transmission power of edge nodes is set to 0.2W. The channel gain is 1 and the power spectral density is −174 dBm.

5.1.2 Model and Dataset

To test the proposed algorithm, we choose a commonly-used neural network: LeNet-5 [44]. LeNet-5 is a simple CNN model with one input layer, two convolutional layers, two pooling layers, and three fully connected layers, with the last fully connected layer being the output layer. The network structure is 6C5-MP2-16C5-MP2-120FC-84FC-10, where C5 means 5×5 kernels, MP2 means 2×2 max pooling, and FC means fully connected components. In the local training, we set the batch size and learning rate as 10 and 0.01, respectively. The global training epoch is set as 150.

The dataset is the well-known Modified National Institute of Standards and Technology (MNIST) database [44], which is composed of 60,000 handwritten digits for training and 10,000 for testing. The training set is gathered from 250 people. Half of them are senior high school students and the other staff from the USA Census Bureau. The data distribution of the testing set is the same as the training set. Each image in the MNIST is 256 grayscale images and is represented by a matrix whose size is 28×28.

5.2 Experimental Results on the FixedAsynFL

As shown in Fig. 3, this paper compares the proposed algorithm with two FL algorithms for performance evaluation. The red line in Fig. 3 is the first FL algorithm, FedAsync [13], which is a well-known AsynFL scheme. The global model and local model in this scheme are both in floating-point format, e.g., FP32. The purpose of comparing FedAsync with the proposed FixedAsynFL is to see how much fixed-point quantization affects AsynFL in terms of both training accuracy and energy consumption. The two kinds of blue lines in Fig. 3 are the second FL algorithm, Federated Learning with Quantization (FLQ) [27], which performs synchronous aggregation and quantization compression in global training. The blue solid line is the training accuracy of the FLQ algorithm with the bit-width Bw of 8-bit, e.g., INT8. And the sky-blue dash-dot line is the FLQ algorithm in the INT4 fixed-point quantization format. The purpose of comparing FLQ with the proposed algorithm is to demonstrate the benefits of the asynchronous aggregation mode in training performance while using fixed-point quantization. The two kinds of green lines are the proposed algorithm, FixedAsynFL. Just like the FLQ algorithm, the green solid line, dash-dot line, and dotted line represent the FixedAsynFL algorithm in the INT8, INT6, and INT4 fixed-point quantization respectively.

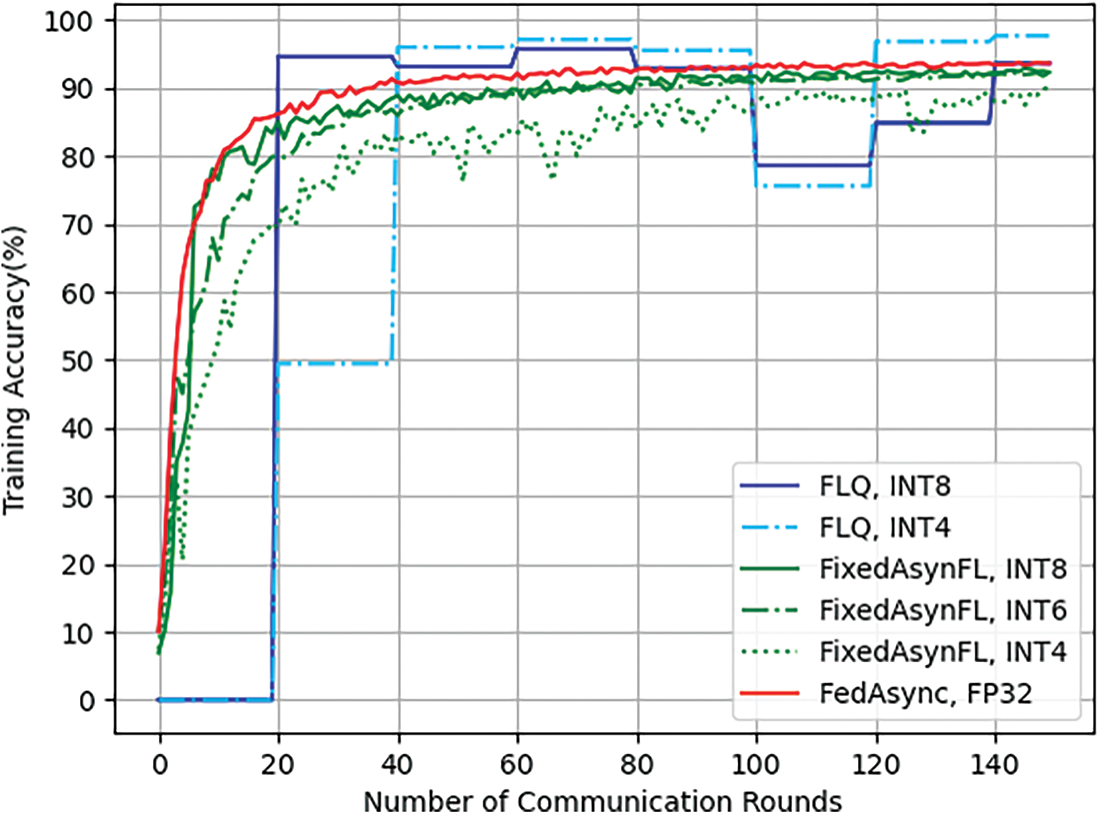
Figure 3: Training accuracy in different FL mechanisms and the different quantization scale

In the comparing experiment, the number of edge nodes is set as 20. Looking at Fig. 3, it is apparent that without the asynchronous aggregation in the central node, the straggler effects of FLQ seriously affect training efficiency. The aggregation can’t be performed in the central node until the lowest edge node has uploaded the local model. Therefore, after the training accuracy of FedAsync and FixedAsynFL is in a trend of smooth and steady, the accuracy of FLQ has not converged yet because of its limited global rounds.

Besides, from Fig. 3 we can also find that the introduction of fixed-point quantization does not cause a significant drop in training accuracy. At the end of the training, the green and red solid lines are not far apart, and the distance between them is perfectly acceptable. According to the comparison of the different quantization scales, the FixedAsynFL with INT4 quantization represented by the green dotted line has a visible impact on the training accuracy situation. When Bw is set to 6-bit and 8-bit, the loss of training accuracy is in a small interval, which demonstrates that a certain amount of model compression can guarantee the accuracy of neural network training.

Fig. 4 shows the growing trend of average energy consumption per edge node in the proposed FixedAsynFL algorithm and FedAsync algorithm. The reason for the absence of the FLQ algorithm is that when the two AsynFL algorithms complete global training, the FLQ algorithm has not completed global convergence and the local training rounds of edge nodes are quite limited. The prominent red polyline belongs to FedAsync, where both computing and communication are based on FP32 format data. It is clear that the fixed-point quantization could retrench much energy consumption in the FixedAsynFL. Besides, it could be found that the energy consumption of FixedAsynFL decreases significantly as the selected fixed-point quantization bit width is reduced. However, this trend is not linearly rising, but oscillating rising. The reason is that due to the heterogeneity of the computational power and hardware level of the edge node devices, the edge nodes involved in the asynchronous model aggregation are not the same in different global rounds, thus leading to variable energy consumption for each global model aggregation.

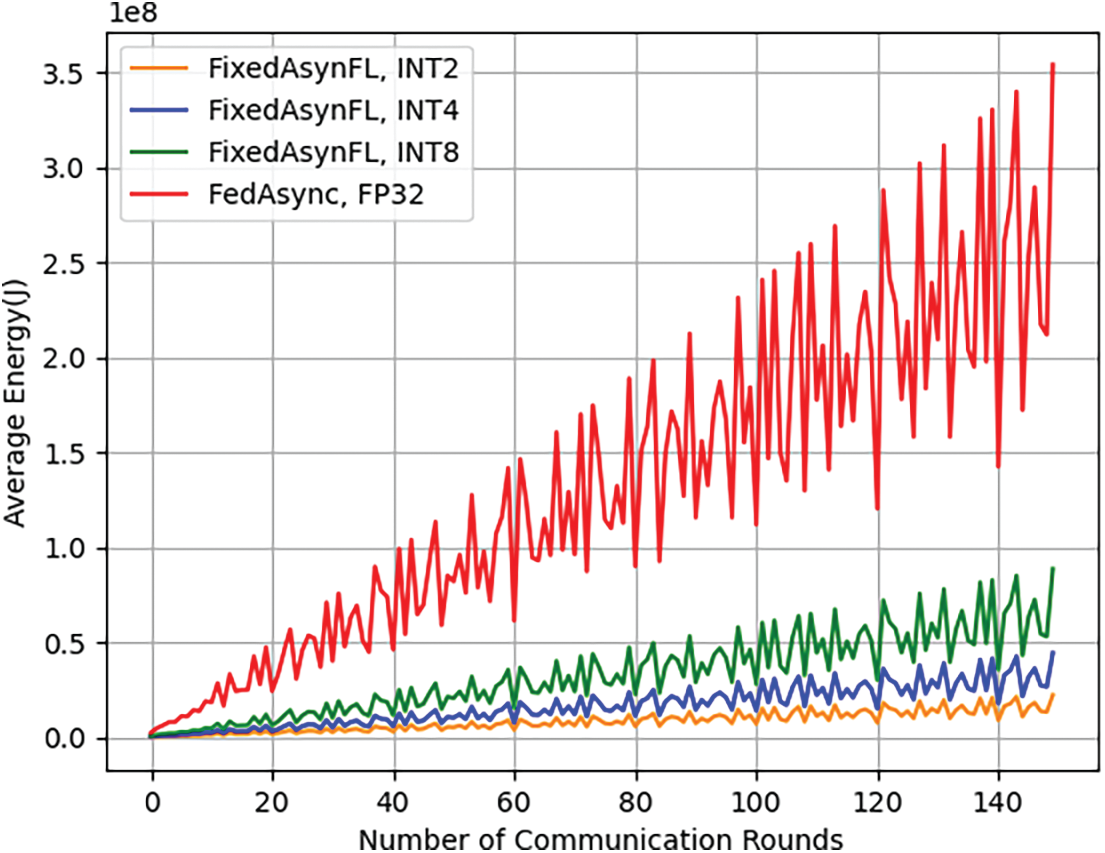
Figure 4: Energy consumption of FixedAsynFL vs. energy consumption of FedAsync

Table 3 indicates the average uplink communication data size in different quantization bit-width. The data size results show that the size of the communication package is linearly related to the quantization scale. And this result is consistent with the principle of fixed-point quantification that has been described in the previous section.

Besides the above experiments, another simulation is also performed which focuses on the number of edge nodes attending the AsynFL. The quantity of edge nodes is varied from 10 to 35. As Figs. 5a and 5b show, the training accuracy of both the FixedAsynFL algorithm and baseline algorithms is better when more edge nodes are involved in the training. This is because as the number of edge nodes involved in training increases, the training dataset used for AsynFL increases accordingly.

Figure 5: (a) Training accuracy with different numbers of edge nodes in the FixedAsynFL algorithm; (b) Training accuracy with different numbers of edge nodes in the three FL algorithms

As depicted in Fig. 6a, the impact of this change on the training accuracy by modifying the hyperparameter α in the proposed FixedAsynFL algorithms and thus adjusting the weight of the local model in the global model update. It can be seen that the training accuracy decreases when the α is larger, which means when the local model takes up a higher weight. This is because there is a staleness effect in AsynFL, i.e., some edge nodes take longer to train locally due to their lack of computing power, and the local model trained by such edge nodes lags behind the current latest global model, which eventually causes a loss in training accuracy. A similar comparison experiment is depicted in Fig. 6b. The hyperparameter α is adjusted in three values, and we could see the effect of hyperparameter α on the proposed FixedAsynFL and the FedAsync algorithm. The results show that different α leads to obvious differences in the training accuracy of the FedAsync algorithm. However, for FixedAsynFL, the final training results are more similar except in the case of larger α, which proves that AsynFL can rely more on the new local model after adopting the fixed-point quantization algorithm.

Figure 6: (a) Training accuracy with different α in FixedAsynFL; (b) Training accuracy with different α in two kinds of AsynFL algorithm

6  Conclusion

In this paper, we have proposed a secure and effective energy-aware FL mechanism, FixedAsynFL. The main goal of the proposed algorithm was to mitigate the influence of massive communication and devices heterogeneous to the FL deployment in industrial IoT. Experimental results show that the fusion of asynchronous aggregation and fixed-point quantization can effectively reduce the energy consumption for ML training and communication data size in FL while ensuring that the error is within a certain range. Thus, deep integration of fixed-point quantization and neural network will improve industrial IoT development. However, there is abundant room for further progress in deploying the proposed FixedAsynFL algorithm in the physical platform and actual industrial IoT scenario in order to further highlight the applicability of the FixedAsynFL algorithm.

The findings of this study have a number of important implications for future practice. Additionally, a further study could assess the restrictions of the large-scale FL from the communication resources supplied by the FL server, which is usually deployed in the BS. In large-scale FL, massive edge nodes would bring great challenges to the limited spectrum resources of BS. We will theoretically analyze it in future work.

Funding Statement: This work was funded by National Key R&D Program of China (Grant No. 2020YFB0906003).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. M. Hosseinzadeh, A. Hemmati and A. M. Rahmani, “6G-enabled internet of things: Vision, techniques, and open issues,” CMES-Computer Modeling in Engineering & Sciences, vol. 133, no. 3, pp. 509–556, 2022. [Google Scholar]

2. B. McMahan, E. Moore, D. Ramage, S. Hampson and B. A. Arcas, “Communication-efficient learning of deep networks from decentralized data,” in Proc. of the 20th Int. Conf. on Artificial Intelligence and Statistics, Fort Lauderdale, FL, USA, pp. 1273–1282, 2017. [Google Scholar]

3. N. N. Thilakarathne, G. Muneeswari, V. Parthasarathy, F. Alassery, H. Hamam et al., “Federated learning for privacy-preserved medical internet of things,” Intelligent Automation & Soft Computing, vol. 33, no. 1, pp. 157–172, 2022. [Google Scholar]

4. D. C. Nguyen, M. Ding, P. N. Pathirana, A. Seneviratne, J. Li et al., “Federated learning for internet of things: A comprehensive survey,” IEEE Communications Surveys & Tutorials, vol. 23, no. 3, pp. 1622–1658, 2021. [Google Scholar]

5. D. C. Nguyen, M. Ding, Q. V. Pham, P. N. Pathirana, L. B. Le et al., “Federated learning meets blockchain in edge computing: Opportunities and challenges,” IEEE Internet of Things Journal, vol. 8, no. 16, pp. 12806–12825, 2021. [Google Scholar]

6. Z. Chen, W. Liao, K. Hua, C. Lu and W. Yu, “Towards asynchronous federated learning for heterogeneous edge-powered internet of things,” Digital Communications and Networks, vol. 7, no. 3, pp. 317–326, 2021. [Google Scholar]

7. K. Yang, T. Jiang, Y. Shi and Z. Ding, “Federated learning via over-the-air computation,” IEEE Transactions on Wireless Communications, vol. 19, no. 3, pp. 2022–2035, 2020. [Google Scholar]

8. S. Wang, T. Tuor, T. Salonidis, K. K. Leung, C. Makaya et al., “Adaptive federated learning in resource constrained edge computing systems,” IEEE Journal on Selected Areas in Communications, vol. 37, no. 6, pp. 1205–1221, 2019. [Google Scholar]

9. G. Zhu, D. Liu, Y. Du, C. You, J. Zhang et al., “Toward an intelligent edge: Wireless communication meets machine learning,” IEEE Communications Magazine, vol. 58, no. 1, pp. 19–25, 2020. [Google Scholar]

10. M. S. H. Abad, E. Ozfatura, D. Gündüz and O. Ercetin, “Hierarchical federated learning across heterogeneous cellular networks,” in IEEE Int. Conf. on Acoustics, Speech and Signal Processing (ICASSP), Barcelona, Spain, pp. 8866–8870, 2020. [Google Scholar]

11. Z. Wang, Z. Zhang, Y. Tian, Q. Yang, H. Shan et al., “Asynchronous federated learning over wireless communication networks,” IEEE Transactions on Wireless Communications, vol. 21, no. 9, pp. 6961–6978, 2022. [Google Scholar]

12. S. Samarakoon, M. Bennis, W. Saad and M. Debbah, “Distributed federated learning for ultra-reliable low-latency vehicular communications,” IEEE Transactions on Communications, vol. 68, no. 2, pp. 1146–1159, 2019. [Google Scholar]

13. C. Xie, S. Koyejo and I. Gupta, “Asynchronous federated optimization,” arXiv preprint arXiv:1903.03934, 2019. [Google Scholar]

14. C. Xu, Y. Qu, Y. Xiang and L. Gao, “Asynchronous federated learning on heterogeneous devices: A survey,” arXiv preprint arXiv:2109.04269, 2021. [Google Scholar]

15. N. P. Jouppi, C. Young, N. Patil, D. Patterson, G. Agrawal et al., “In-datacenter performance analysis of a tensor processing unit,” in Proc. of the 44th Annual Int. Symp. on Computer Architecture, New York, NY, USA, pp. 1–12, 2017. [Google Scholar]

16. M. Denil, B. Shakibi, L. Dinh, M. Ranzato and N. Freitas, “Predicting parameters in deep learning,” Advances in Neural Information Processing Systems, vol. 26, pp. 2148–2156, 2013. [Google Scholar]

17. Y. Idelbayev and M. A. Carreira-Perpinán, “Low-rank compression of neural nets: Learning the rank of each layer,” in Proc. of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Seattle, WA, USA, pp. 8049–8059, 2020. [Google Scholar]

18. G. Hinton, O. Vinyals and J. Dean, “Distilling the knowledge in a neural network,” arXiv preprint arXiv:1503.02531, vol.2, no. 7, 2015. [Google Scholar]

19. E. Jeong, S. Oh, H. Kim, J. Park, M. Bennis et al., “Communication-efficient on-device machine learning: Federated distillation and augmentation under non-iid private data,” arXiv preprint arXiv:1811.11479, 2018. [Google Scholar]

20. S. Han, H. Mao and W. J. Dally, “Deep compression: Compressing deep neural networks with pruning, trained quantization and huffman coding,” arXiv preprint arXiv:1510.00149, 2015. [Google Scholar]

21. X. Qiu, Z. Ye, X. Cei and Z. Gao, “Survey of communication overhead of federated learning,” Journal of Computer Applications, vol. 42, no. 2, pp. 333–342, 2022. [Google Scholar]

22. S. Gupta, A. Agrawal, K. Gopalakrishnan and P. Narayanan, “Deep learning with limited numerical precision,” in Proc. of the 32nd Int. Conf. on Machine Learning. PMLR, Lille, France, pp. 1737–1746, 2015. [Google Scholar]

23. C. Sakr, Y. Kim and N. Shanbhag, “Analytical guarantees on numerical precision of deep neural networks,” in Int. Conf. on Machine Learning, Sydney, Australia, PMLR, pp. 3007–3016, 2017. [Google Scholar]

24. L. Bottou and O. Bousquet, “The tradeoffs of large scale learning,” in Advances in Neural Information Processing Systems. Vol. 20. Vancouver, B.C., Canada, 161–168, 2007. [Google Scholar]

25. A. F. Murray and P. J. Edwards, “Enhanced MLP performance and fault tolerance resulting from synaptic weight noise during training,” IEEE Transactions on Neural Networks, vol. 5, no. 5, pp. 792–802, 1994. [Google Scholar] [PubMed]

26. K. Audhkhasi, O. Osoba and B. Kosko, “Noise benefits in backpropagation and deep bidirectional pre-training,” in The 2013 Int. Joint Conf. on Neural Networks (IJCNN), Dallas, TX, USA, IEEE, pp. 1–8, 2013. [Google Scholar]

27. Y. Chen, Y. Ning, M. Slawski and H. Rangwala, “Asynchronous online federated learning for edge devices with non-iid data,” in 2020 IEEE Int. Conf. on Big Data (Big Data), Atlanta, GA, USA, IEEE, pp. 15–24, 2020. [Google Scholar]

28. M. Chen, B. Mao and T. Ma, “Efficient and robust asynchronous federated learning with stragglers,” in Submitted to Int. Conf. on Learning Representations, Addis Ababa, Ethiopia, pp. 1–14, 2019. [Google Scholar]

29. V. Vanhoucke, A. Senior and M. Z. Mao, “Improving the speed of neural networks on CPUs,” in Deep Learning and Unsupervised Feature Learning Workshop, NIPS 2011, Granada, Spain, pp. 4, 2011. [Google Scholar]

30. D. Lin, S. Talathi and S. Annapureddy, “Fixed point quantization of deep convolutional networks,” in Int. conf. on machine learning, PMLR, New York, NY, USA, pp. 2849–2858, 2016. [Google Scholar]

31. B. Jacob, S. Kligys, B. Chen, M. Zhu, M. Tang et al., “Quantization and training of neural networks for efficient integer-arithmetic-only inference,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, pp. 2704–2713, 2018. [Google Scholar]

32. Q. Zhou, S. Guo, Z. Qu, J. Guo, Z. Xu et al., “Octo: {INT8} training with loss-aware compensation and backward quantization for tiny on-device learning,” in 2021 USENIX Annual Technical Conf. (USENIX ATC 21), Virtual Online, pp. 177–191, 2021. [Google Scholar]

33. C. Louizos, M. Reisser, T. Blankevoort, E. Gavves and M. Welling, “Relaxed quantization for discretized neural networks,” in Int. Conf. on Learning Representations (ICLR), New Orleans, LA, USA, pp. 1–15, 2019. [Google Scholar]

34. S. Jung, C. Son, S. Lee, J. Son, J. Han et al., “Learning to quantize deep networks by optimizing quantization intervals with task loss,” in Proc. of the IEEE/CVF Conf. on Computer Vision and Pattern Recognition, Long Beach, CA, USA, pp. 4350–4359, 2019. [Google Scholar]

35. M. Nagel, M. Baalen, T. Blankevoort and M. Welling, “Data-free quantization through weight equalization and bias correction,” in Proc. of the IEEE/CVF Int. Conf. on Computer Vision, Seoul, Korea, pp. 1325–1334, 2019. [Google Scholar]

36. S. Chen, C. Shen, L. Zhang and Y. Tang, “Dynamic aggregation for heterogeneous quantization in federated learning,” IEEE Transactions on Wireless Communications, vol. 20, no. 10, pp. 6804–6819, 2021. [Google Scholar]

37. M. M. Amiri, D. Gunduz, S. R. Kulkarni and H. V. Poor, “Federated learning with quantized global model updates,” arXiv preprint arXiv:2006.10672, 2020. [Google Scholar]

38. N. Shlezinger, M. Chen, Y. C. Eldar and S. Cui, “UVeQFed: Universal vector quantization for federated learning,” IEEE Transactions on Signal Processing, vol. 69, pp. 500–514, 2020. [Google Scholar]

39. N. Tonellotto, A. Gotta, F. M. Nardini, D. Gadler and F. Silvestri, “Neural network quantization in federated learning at the edge,” Information Sciences, vol. 575, no. 4, pp. 417–436, 2021. [Google Scholar]

40. T. Ma, H. Wang and C. Li, “Quantized distributed federated learning for industrial internet of things,” IEEE Internet of Things Journal, early access, pp. 1, 2021. https://doi.org/10.1109/JIOT.2021.3139772 [Google Scholar] [CrossRef]

41. R. Chen, L. Li, K. Xue, C. Zhang, M. Pan et al., “To talk or to work: Energy efficient federated learning over mobile devices via the weight quantization and 5G transmission co-design,” arXiv preprint arXiv:2012.11070, 2012. [Google Scholar]

42. C. Petzold, Code: The Hidden Language of Computer Hardware and Software. Redmond, WA, USA: Microsoft Press, 2000. [Google Scholar]

43. G. E. Dahl, D. Yu, L. Deng and A. Acero, “Context-dependent pre-trained deep neural networks for large-vocabulary speech recognition,” IEEE Transactions on Audio, Speech, and Language Processing, vol. 20, no. 1, pp. 30–42, 2011. [Google Scholar]

44. Y. LeCun, L. Bottou, Y. Bengio and P. Haffner, “Gradient-based learning applied to document recognition,” Proceedings of the IEEE, vol. 86, no. 11, pp. 2278–2324, 1998. [Google Scholar]