Asymmetric Consortium Blockchain and Homomorphically Polynomial-Based PIR for Secured Smart Parking Systems

1  Introduction

Smart parking is one of the most viable solutions for reducing traffic congestion, which in turn will improve air quality and people’s lives. Smart parking is made possible by connecting, analyzing, and automating the data collection process through the Internet of Things (IoT). For parking slot allocation, low-cost sensors are employed for the data collection process which enables the availability of parking slots to the end users. During data collection, some of the sensitive information needs to be shared across the network. Using IoT-enabled smart parking, data can be shared among the devices using a cloud-enabled centralized server. With a cloud-based centralized server, the performance of the applications increases with quick response time, easy-to-deploy business-oriented solutions, multi-server setup, and reliable backup capabilities. However, the cloud-based centralized server suffers many limitations, including vulnerability to attacks, total reliance on network connectivity, lack of access control, redundancy of data, data loss or leakage, insecure Application Program Interface (API), denial of service attacks, and security and privacy concerns with some service providers. Thus, an automated parking system is needed to optimize the parking slots and to reduce the time it takes to search parking lots by sharing secured information with the customer and the parking slot provider. Some solutions will encompass a complete suite of services such as online payments, parking time notifications, and even car searching functionalities for very large lots. A parking solution can greatly benefit both the user and the lot owner. Here are some of the top benefits such as reduced traffic, optimized parking, reduced pollution, increased safety, and enhanced user experience. IoT devices can link to each other and the data can be centralized with the help of an IoT cloud-based system. The availability of on-street parking spaces or spaces in public and private parking facilities is then determined using big data analysis. In the recent decade, the problem of parking has attracted a lot of attention as the number of motor vehicles is identified to be rapidly increasing globally [1]. The rapid growth in the vehicle rate poses a herculean challenge in determining a vacant slot of parking in a densely populated area specifically during the peak hours of traffic. Therefore, it is necessary to plan for parking appropriately to build facilities using traditional centralized methods of parking slots [2]. Parking vehicles in an unauthorized area has its own legal and security issues and can be handled by giving a proper guidance system.

Smart parking systems (SPS) can be approached using various methodologies such as Wireless sensor networks, multi-agent systems, vehicular Ad-hoc networks, IoT-enabled SPS, Machine learning bases SPS, Global position-based SPS, and various sensors of parking systems [3]. There is a growing need for a smart parking system due to the increase in the number of vehicles available on the market and people’s increasing tendency to shop. Various research directions are provided regarding smart parking slot allocation. The related works are categorized into IoT-based smart parking systems, and block-chain-based smart parking systems to examine the emerging technologies to implement the proposed direction by the researchers to facilitate comfortable living.

1.1 Approach to Smart Parking Systems Using the Internet of Things

Canli et al. [4] utilized Deep-Long Short-Term memory (DLSTM) and cloud computing to connect the vehicles in a more integrated way to allocate the parking slots based on the nearest location of the drivers to save time and energy. Migabo et al. [5] proposed an integrated narrowband-IoT technology for smart parking solutions using radio communications to reduce congestion and improve the allocation by displaying the status of parking lots. Saharan et al. [6] suggested a machine learning-based parking slot prediction process by sharing the secured information among the parties such as owners, agencies, and other stakeholders. Floris et al. [7] discussed the sensor-based parking slot allocation to detect the parking slot for the arriving vehicles automatically using a magnetometer, which helps to protect the drivers and vehicle information to be shared among the network. Buldakov et al. [8] introduced an open-source solution using a smart contract-based parking system in highly urbanized areas. They proposed a trust management scheme to handle security during the parking lot allocation process. Bock et al. [9] proposed a Parking Guidance and Information (PGI) city-wide scale to avoid on-street parking and crowding. They used sensors and windshield cameras for identifying the crowds and parking availabilities. Ke et al. [10] investigated the feasibility of using edge computing using real-time video feed to enable efficient online parking occupancy detection. Ghorpade et al. [11] discussed that the IoT-enabled sensor nodes used in parking areas in particular create a multi-objective grey wolf optimization-based model for the best positioning of wireless sensor nodes to determine smart parking.

Using the IoT-based smart parking system, even though the models work better with better parking slot allocation using sensors and some devices for information exchange, it has its limitations on privacy preservation, authentication, and transparency and it is centralized concerning the data received over the devices through sensors and venerable to attacks. In this situation, Tyagi et al. [12] discussed the technology of blockchain as a promising solution in contrast to the existing centralized solutions as they possess the merits of trust, security, and decentralization during its employment in smart parking applications. The blockchain is a distributed ledger that is immutable, transparent, and managed by several validations in the form of chain blocks.

1.2 Blockchain-Based Smart Parking System

Zhang et al. [13] utilized a blockchain-based privacy-preserving public key query strategy and a Least Recently Used (LRU) optimization mechanism in a fog environment to reduce computation and communication costs. Anitha et al. [14] facilitate security breaches based on various blockchain features in a smart city environment for the enhancement of future directions. Huang et al. [15] utilized the IoT–cloud platform and fog-based blockchain for smart autonomous vehicle parking (SAVP) system to improve the cost-effective solution in smart parking. Ibrahim et al. [16] designed a blockchain framework for data verification and role-based access control for securing the parking service data and checking the performance of the model using mean testing time, response time, throughput, and latency. Badr et al. [17] adopted a consortium blockchain and short randomizable signature to reserve the availability of parking slots, constructed transparency, and security. Jennath et al. [18] developed a non-fungible token system and smart contracts representing the parking lots with maximized financial transparency and agreement between users and lot owners during the process of smart parking. Ni et al. [19] utilized a privacy preservation approach that confirmed better audibility and transparency and pointcheval sanders group signature for a privacy information retrieval process. Balzano et al. [20] constructed an automatic parking system in which vehicles are allocated among several competitive parking areas (called competitors), through a blockchain-based approach, by applying a consensus mechanism to manage the system modifications. Singh et al. [21] adopted an Elliptic Curve Cryptography (ECC) algorithm for attaining secure communication between the smart park allocation and roadside unit (RSU)-based blockchain network for facilitating data verification and authentication at the layer of security in a more distributed manner. It explored the data of parking zone using deep long short-term memory (LSTM) networks for achieving superior parking space for the drivers with better timing and location. Li et al. [22] developed a lattice-based blind signature scheme enabled for a blockchain system. To enhance the security against quantum attacks, and also constructed cryptography algorithms for efficiency. Chaoyang et al. [23] developed secure keyword-searchable attribute-based encryption (KS-ABE) scheme based on lattice cryptography to enhance the security of data sharing against various attacks.

From the previous literature review, the interoperability, traffic congestion control, and parking slot with some security algorithms and communication costs are dealt with. But they fail to have a mechanism for information retrieval securely along with an energy-efficient privacy preservation system to enhance the scalability of the users. This motivates us to propose a model to enhance privacy preservation with a secured information retrieval process that can handle the ‘n’ of users with transparency in the parking slot allocation. Thus, we propose Asymmetric Consortium Blockchain and Homomorphically Computing Univariate Polynomial-based private information retrieval (IACB-HCUPPIR) scheme to ensure the parking slot allocation to the users with privacy preservation and secured information retrieval process.

The objective of the paper is as follows:

•   To ensure the availability of the parking lots with secured privacy preservation using Improved Asymmetric Consortium Blockchain and Homomorphically Computing Univariate Polynomial-based private information retrieval (IACB-HCUPPIR) scheme.

•   To facilitate secure transactions between the users using enhanced Asymmetric Consortium Blockchain.

•   To preserve the location of the drivers, the Homomorphically Computing Univariate Polynomial-based private information retrieval (HCUPPIR) scheme was utilized.

•   To check the performance of the proposed model using the performance metrics such as average response retrieval time and processing rate (PR) and transaction per second (TPS) interns of throughput and latency are benchmarked against the existing blockchain-based secured transaction models.

The succeeding sections of this paper are organized as follows. Section 2 provides background fundamentals of the proposed work. The full description of the enhanced IACB-HCUP-based private information retrieval is presented in Section 3 and HCUPPIR which are essential for implementing the suggested smart parking systems. The benchmark approaches examined based on the degree of privacy preservation, communication, computation overhead, and related metrics are shown in Section 4 along with the outcomes of the proposed IACB-HCUPPIR system. The suggested performance evaluation is discussed in Section 5 of the study. Finally, the conclusion and future directions of the study are mentioned in Section 6.

2  Background Fundamentals

2.1 Consortium Blockchain

A type of blockchain that exists between the public blockchain and the private blockchain is called the consortium blockchain. Due to its limitations and rules, the consortium blockchain’s security has been enhanced. The blockchain network, which processes and records all parking offer transactions, is the brain of our system. The consortium blockchain is managed by authorized parking lots. The advantages of a consortium blockchain are built by several parking lot owners to verify the accessibility, transparency, and security of the parking offers provided by the service providers. To protect the privacy of drivers’ locations, it adopted a private informational retrieval technique to privately retrieve parking allocations from the blockchain nodes.

2.2 Asymmetric Cryptography

Blockchain technology relies on asymmetric cryptography, sometimes referred to as public-key cryptography. Asymmetric cryptography uses various techniques such as Ron Rivest, Adi Shamir, and Leonard Adleman (RSA) technique, secure shell, Diffie Hellman, and secure socket layer. Based on our proposed work widely used RSA technique employs two keys—a private key and a public key. Communication is encrypted using the public key, which is visible to everyone. The message is decrypted using the private key. Asymmetrical techniques are effectively optimized. Furthermore, effectively addressing the problem of key distribution in this case, asymmetric techniques are better suited for the local and distributed solution in parking allocation slots.

2.3 Homomorphic Encryption

In general, homomorphic encryption is considered to be an essential method for resolving database query issues based on encrypted data. The requirements for privacy protection and the algorithms used to handle more complex forms have grown exponentially, which is just in with the growth of communication networks, infrastructure, and capacity. Thus, homomorphic encryption enables accurate analysis of vehicle data by an untrusted third party while protecting the privacy of users. Finally, the user receives the encrypted result. With their private key, the user can access the results. Building a reliable and effective homomorphic encryption technique is essential for safely analyzing vehicle data. these aspects consist of homomorphic encryption, the overview of parking allocation, and secure computation based on these encryption techniques.

3  Proposed Scheme of Smart Parking System

The proposed model is the combination of two algorithms: homomorphically Computing Univariate Polynomial is used for Private Information Retrieval of the users whereas Asymmetric Consortium Blockchain to establish secured transactions using the Homomorphic Encryption (FHE) algorithm. One of the signification benefits of using FHE is encryption mechanism ensures that sensitive information remains secure at all times. Preserves data privacy without sacrificing usability: No features need to be masked or dropped to preserve data privacy. This section deals with private information retrieval and the secure parking slot allocation process.

3.1 Homomorphically Computing Univariate Polynomial-Based Private Information Retrieval (HCUPPIR)

In this section, the system and security models utilized for implementing the private information scheme are designed, and the goals are identified as follows.

3.1.1 System Model-HCUPPIR

A classic Private Information retrieval (PIR) protocol is considered with a single server that includes 2 entities namely, the user and the Database (DB) server.

•   D Server: It is efficient in maintaining as well as computing data. The server saves and handles D ={(j,DB[j]),0≤j≤n−1} containing ‘n’ items. It is assumed that every DB[j] is positive and not a bit alone. Further, the server offers a response to the user’s query with unrestrained computations.

•   User: In the system model, a user makes a query to the server and gets the required outcome. The user desires to conceal the enquired value ‘j’ from the server when requesting the conforming data ‘DB[j]’ and anticipates that the communication is efficient.

Officially, the protocol with a single server includes 3 stages:

•   Query Generation Stage (Qj=QGj): By considering index (j) as input, the query ‘Qj’ is sent to the server by the user

•   Response Production Stage  (Rj=RG(Qj, DB)): Using ‘Qj’ along with DB, ‘Rj’ is returned to the user

•   Response Retrieval Stage (DB[j]=RRRj): On getting a response ‘Rj’, the user sends DB[j] related to index ‘j’

The PIR protocol with a server is correct for a DB of size ‘n’ with index ‘j’ for DB[j]=

RR(DB,j,Qj,Rj),0≤j≤n−1 holds, where ‘Qj=QGj’  and ‘Rj=RG(Qj,DB)’.

3.1.2 Security Model

The server is considered candid but inquisitive. There is no collusion between DB servers as well as third parties. The server loyally follows the protocol. Nevertheless, it is inquisitive about the demanded value of the user. If the server is compromised, the user is unable to confirm because the server launches active attacks and provides a reply that contains errors.

3.1.3 Design Goal

A communication-effective protocol is essential for the user to deal with the demands mentioned above. The protocol is the main focus. Assume that the server has limited capacity, while the server’s computation burden is less important. Precisely, the ensuring goals are considered:

•   The protocol must be capable of preserving privacy. The index (j) must be kept private, and only the user can find ‘j’. Only the user can obtain ‘DB[j]’ after getting the response ‘Rj’ from the server.

•   The protocol should be communication effective. To ensure privacy, added communication costs are incurred. It is essential that communication must be efficient by involving reduced communication costs. Fig. 1 depicts the overview of the Integrated Smart parking system.

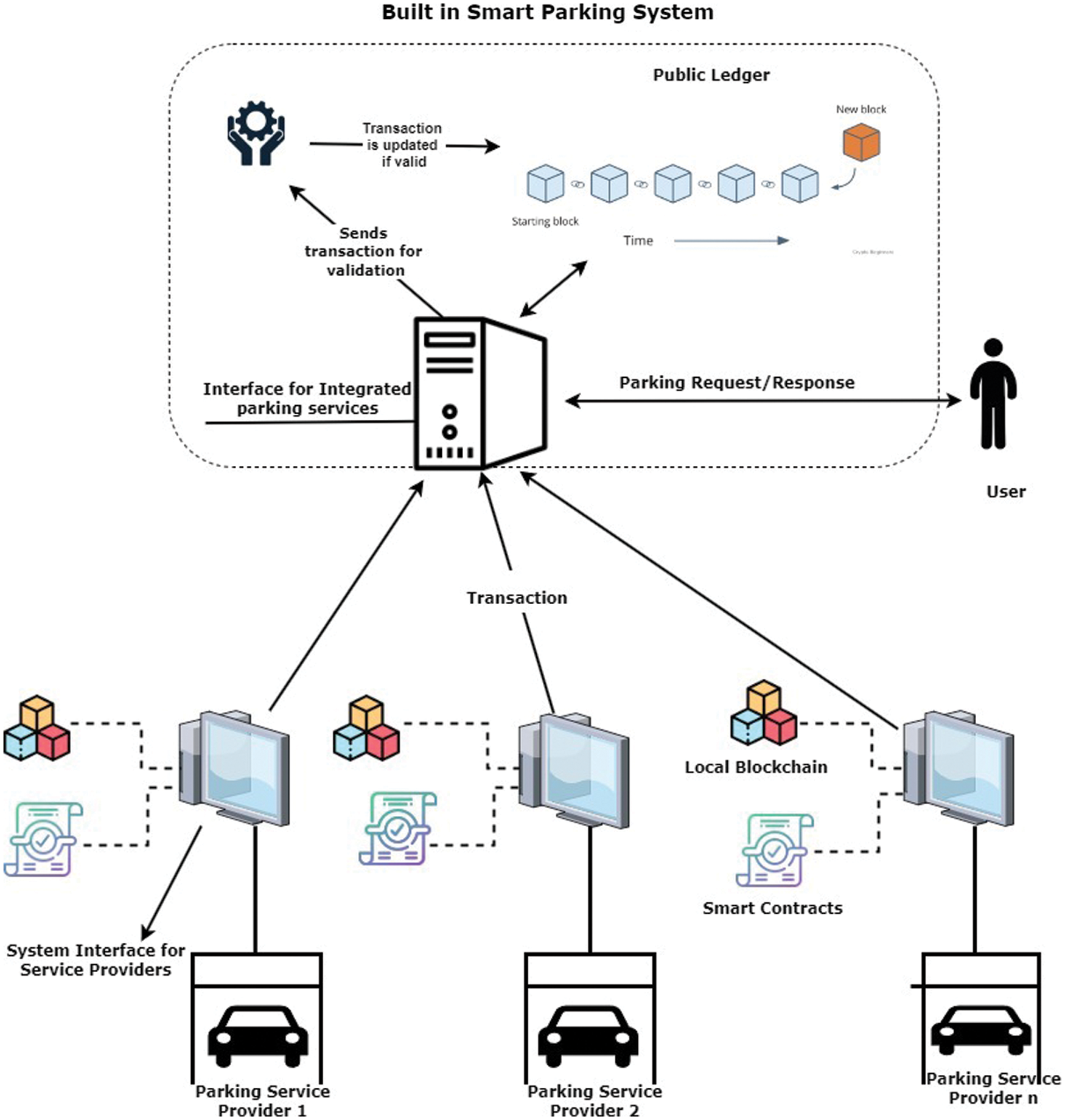
Figure 1: Integrated smart parking systems

3.2 Secured Transaction Using Single-Ciphertext Fully Homomorphic Encryption (FHE)

Single-Ciphertext Fully Homomorphic Encryption (FHE) mechanism using Truncated Polynomial Rings (TPRs) is presented with various steps are follows:

3.2.1 Single-Ciphertext FHE Mechanism

It includes the following algorithms called, Keygen, Encryption (Encr), Decryption (Decr), and Evaluation (Eval). They are detailed in this section.

•   Keygen (α): The security parameter (α) is taken as input, and 2 ‘α2’ bit primes ‘a’ and ‘b’ that satisfy the conditions GCD (a − 1, 3) = GCD (b − 1, 3) = 1 are generated.

n =ab,ϑ(n)=(a−1)(b−1)

The inverse(d) of 3.mod(ϑ(n)), 3.d ≡ 1(mod ϑ(n)) is computed

Modulus(n) is the public key (KeyPub=n)

‘KeyAss=n’ is the assessment key, ‘d’ is the secret key (KeySec=d)

•   Encr (m, KeyPub): Consider plaintext, m ∈M=Zn, p,q∈Zn  is chosen and x ≡ p3(mod n) and y ≡ q3(mod n) is computed. Nine integers for pij ∈Zn  for i,j∈{0,1,2} are arbitrarily chosen with a polynomial f(s,t)=∑i=02∑j=02aijsitj. ‘F(s,t)≡f(s,t)−f(p,q)(mod n)’ is set, and ‘C (s, t) ≡ F (s, t) + m. mod n’ is determined. The Ciphertext is given by ‘C = Enc (m, n) = (x, y, C (s, t))’.

•   Decr (C,  KeySec): After receiving ‘C’, p ≡xd .mod n and q ≡yd .mod n with ‘d’ to obtain the random numbers ‘p, q’. The Plaintext is recovered by replacing ‘p, q’ with ‘C (s, t)’.

C(p,q)≡F(p,q)+m ≡m.mod n

F(p,q)≡f(p,q)–f(p,q)≡0.modn

•   Eval (f^, C, KeyAss)): The assessment algorithm shown in Algorithm 1 includes the given ‘C’ and a univariate polynomial f(s)=∑i=0φδisi ∈Zn[s]. The additions, as well as multiplications, are applied to the TPR ‘Zn[s,t]s3−x,t3−y’. In every iteration, ‘Cf^(s,t)’ is truncated to the TPR using reduction modulo ‘s3−x’ and ‘t3−y’. The outcome of ‘Cf^(s,t)’ is seen in the TPR. It is a bi-variate polynomial in ‘S’.

To guarantee the one-way security of a Ciphertext FHE mechanism, the size (α) of modulus (n) must be more than 2048 bits.

Validating the Generated One-way security Key:

To illustrate the precision of the homomorphic assessment algorithm, it is essential to indicate that,

Decr(Cf^(s,t),d)=f^(m)

It is easy to verify that

Cf^(s,t)≡f^(C(s,t))≡∑i=0φδiC(s,t)i(mod n,s3−x,t3−y)(1)

Two bi-variate polynomials A(s,t),B(s,t)∈Zn[s,t] 

Cf^(s,t)≡f^(C(s,t))+A(s,t) (s3−x)+B(s,t) (t3−y)(mod n)(2)

p3≡x.mod n andq3≡y.mod n

Decr(Cf^(s,t),d≡Cf^(p,q)≡f^(C(p,q))+A(p,q) (p3–x)+B(p,q) (q3−y)mod n(3)

C(p,q)≡m(mod n);p3−u≡0(mod n);q3−v≡0(mod n);

Decr(Cf^(s,t),d)≡Cf^(p,q)≡f^(m).mod n showed in Algorithm 2.

The ‘eth’ RSA problem is that: Given RSA public key n = ab and e, and ciphertext (π) to determine the plaintext (ω), wherein π ≡ωe(mod n). The 3rd RSA problem has e = 3.

3.3 Computational Complexity

The cost involved in the computation of a Ciphertext FHE scheme is shown below.

In the Encryption stage, 2 modular multiplications are performed to find ‘u’ and ‘v’. Finding polynomial F (s, t) demands 18 multiplications along with a few additions, as ‘i + j’ multiplications are involved in computing the monomial pijsitj,i,j=0−2∈F(s,t). In contrast to modular multiplications, the cost involved in modular addition is negligible. There are a total of 22 multiplications with insignificant modular additions during the encryption stage. The complexity of the encryption stage is the complexity of multiplication taken as ‘O (α2)’.

In the Decryption stage, ‘p, q’ is to be obtained from ‘x, y’ by 2 modular exponentiations of exponentiation ‘d’. The complexity of this stage is that of modular exponentiation considered as ‘O(α3)’. A few modular additions are ignored.

In the assessment stage, the output ‘Cf^(s, t)’ is a truncated bi-variable polynomial. It involves φ-iteration, wherein every iteration involves a modular multiplication in addition to an insignificant addition. There are φ-modular multiplications with trivial additions. The complexity of this stage is ‘O(φα2)’, where ‘φ’ is used in ciphertext assessments Fig. 2. Shows the validation process of the user.

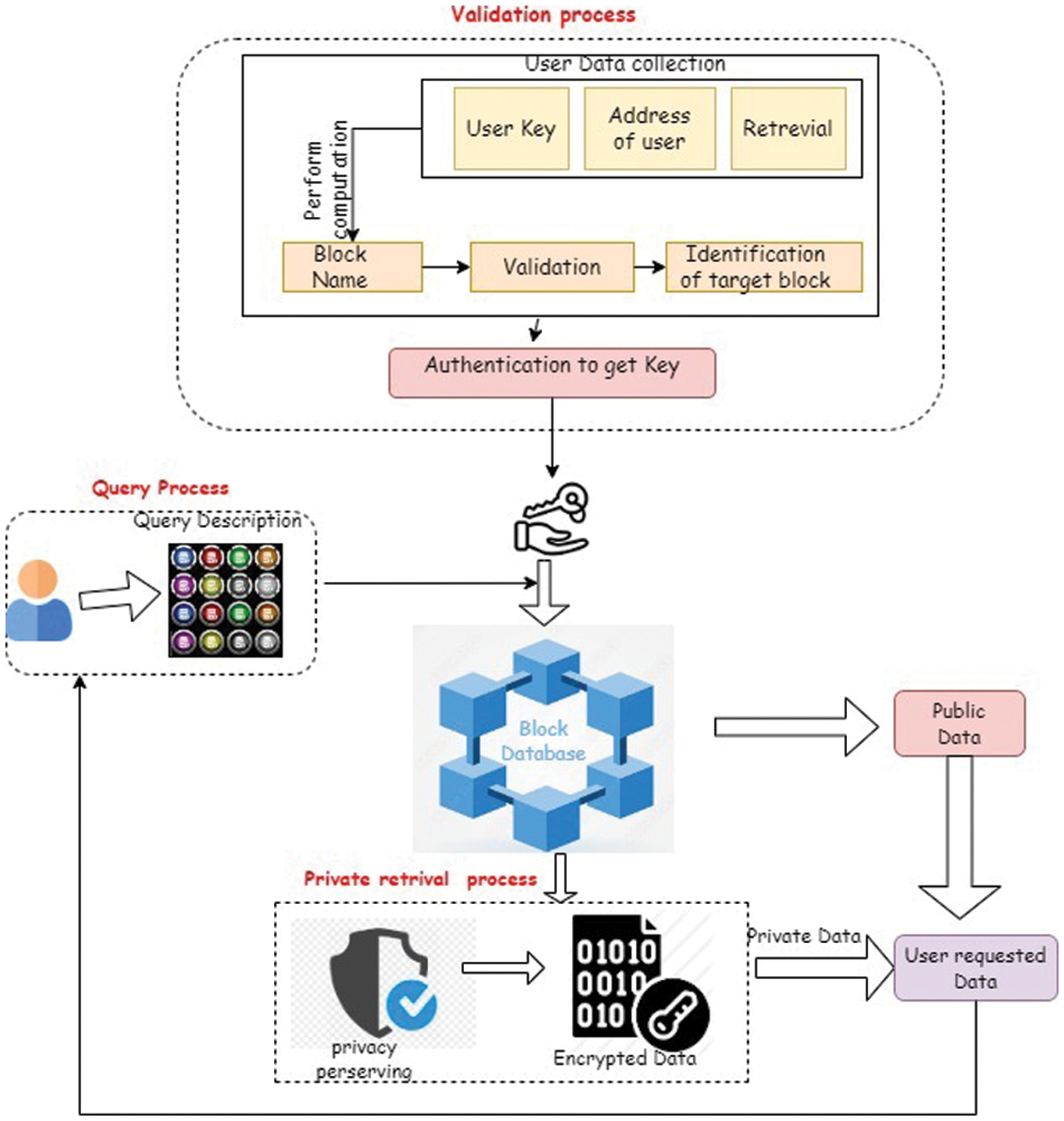
Figure 2: Validation process for the user

The complexity of encryption is O (α2), decryption is O (α3) and assessment is O (φα2) correspondingly, where the length of RSA modulus ‘n’ is ‘α≥2048’.

3.4 Propounded Communication-Effective Protocol

Before investigating the communication-effectual protocol, an outline of how a single-ciphertext FHE mechanism is used to build a single-server protocol is given.

•   The protocol with a single server focuses on aiding the user to get the ‘jth’ data from the server holding the entire database deprived of leaking ‘j’ to the server. The server executes an assessment algorithm on a ciphertext conforming to enquired index. This FHE mechanism is appropriate for the protocol.

•   The user encrypts ‘j’ using the single-ciphertext FHE mechanism and forwards the ciphertext to the server. The index is encrypted using symmetric encryption to ensure efficiency. Parameters ‘p, q’ link the restricted ciphertext C (s, t) and the related plaintext. The parameters ‘p, q’ call a polynomial which is used in encrypting the enquired index; C (s, t) is decrypted using ‘a, b’ disregarding parameters ‘x, y’ as additional information. The server gives a function about ‘jth’ data ‘aj’ related to polynomial ciphertext. The function is decrypted by the user using ‘p, q’ and will precisely get the ‘jth’ data ‘pj’ relating to ‘j’. The server offers computation as well as storage space. It is incapable of obtaining information about ‘j’. Therefore, the protocol attains the goal.

•   Rather than the server, the user should determine the communication complexity. The trade-off overheads of communication, as well as computation between user and server, are to be attained.

•   Single-ciphertext FHE mechanism and Lagrange interpolating polynomial are employed to build the communication-effective protocol with a single-server.

The Symmetric key (p, q) is maintained privately by the user unknown to the DB server.

The algorithms are detailed below:

•   Query Generation Stage: By considering ‘j’ as input, the user forwards Query (Qj) to the server (Algorithm 3).

•   Response Production Stage: On obtaining ‘Qj’, the server gives ‘Rj=g(s,t)’ as output to user. If (x, y) is obtained in the query ‘Qj=(n,x,y,C(s,t))’, the server will not be able to recover ‘j’ owing to the unawareness of Symmetric key (p, q) (Algorithm 4).

•   Response Retrieval Stage: On getting the response ‘Rj= g(s, t)’, the user gets the data DB[j] ≡ g (p, q).mod n conforming to ‘j’ using Symmetric key (p, q) (Algorithm 5).

4  Comparative Analysis and Results Discussion

The potential of the proposed model (IACB-HCUPPIR) scheme and the existing models secure blockchain-based smart parking mechanisms such as Ring signature and improved multi-transaction mode consortium blockchain-based private information retrieval (RSIMBPIR), Elliptic-Curve cryptography-based parking system (ECCBPS), and PARK CHAIN are evaluated based on essential cryptographic operations which are implemented over Raspberry Pi 3 equipment by inheriting Python charm cryptographic library in the system configuration of 1 GB RAM and 1.2 GHz Processor. In specific, the process of implementing HCUPPIR-based blockchain is implemented over the blockchain framework.

4.1 Comparative Analysis of Communication Overhead

The proposed model is compared with the metrics of communication overhead while information is exchanged between the drivers and service providers from the blockchain nodes in the smart parking system. Here, the amount of information exchange was carried out to the packet size (in bytes) and the transaction per second. The proposed IACB-HCUPPIR is compared against the RSIMBPIR [24], ECCBPS [21], and PARK CHAIN [18] for the block nodes from 15 increases by 5 to 45. The number of bytes utilized for the proposed and other models is depicted in Fig. 3.

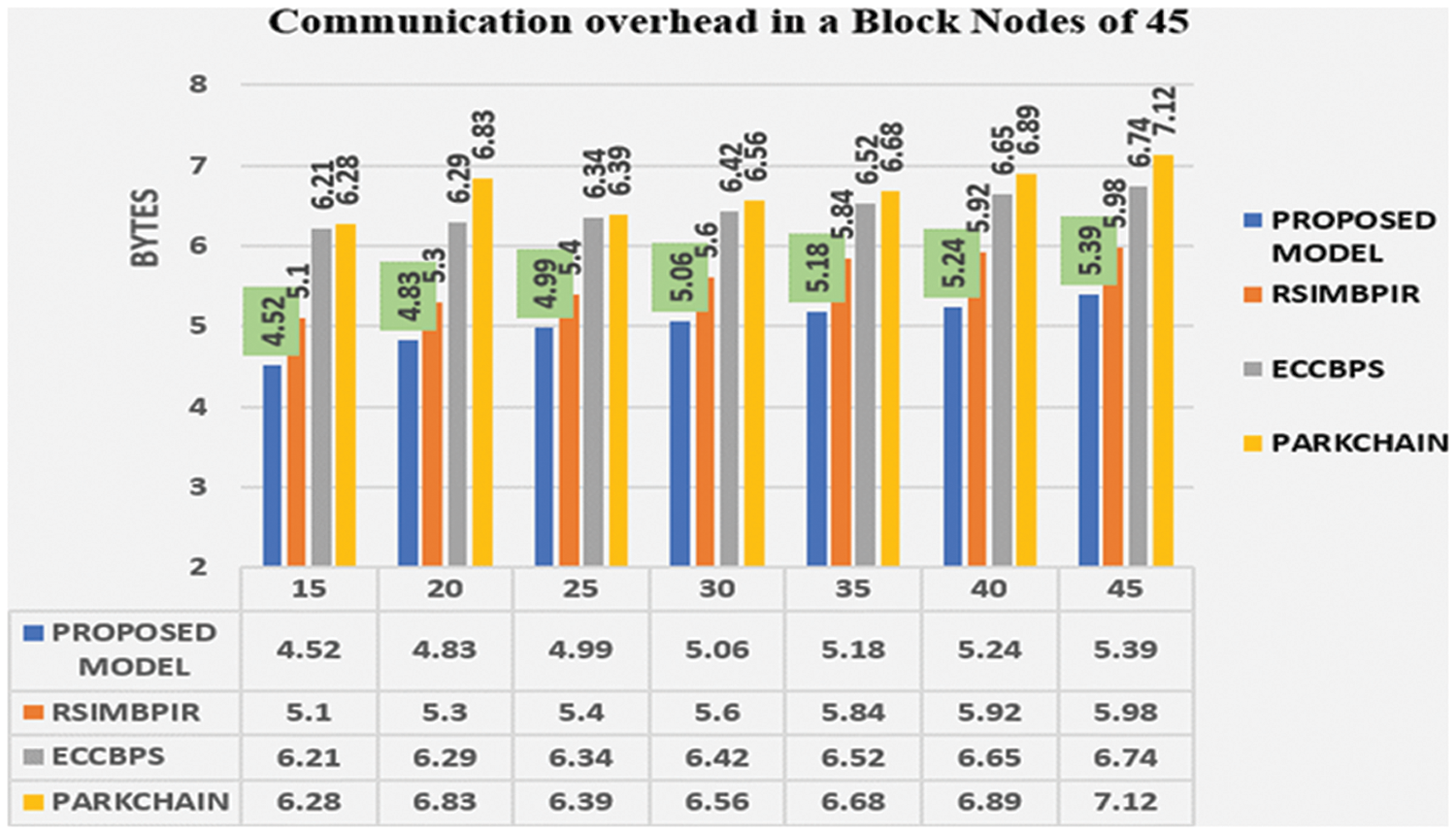
Figure 3: Communication overhead in a block node of 45

Based on the overlapping transactions, the parking slot allocation for various vehicles is allocated based on the unit cell. The proposed model handles the communication overhead based on the number of transactions (in bytes) against the allocated parking lots from various nodes from 20 increased by 20 blocks to 200 blocks along with other existing smart parking models are provided in Fig. 4.

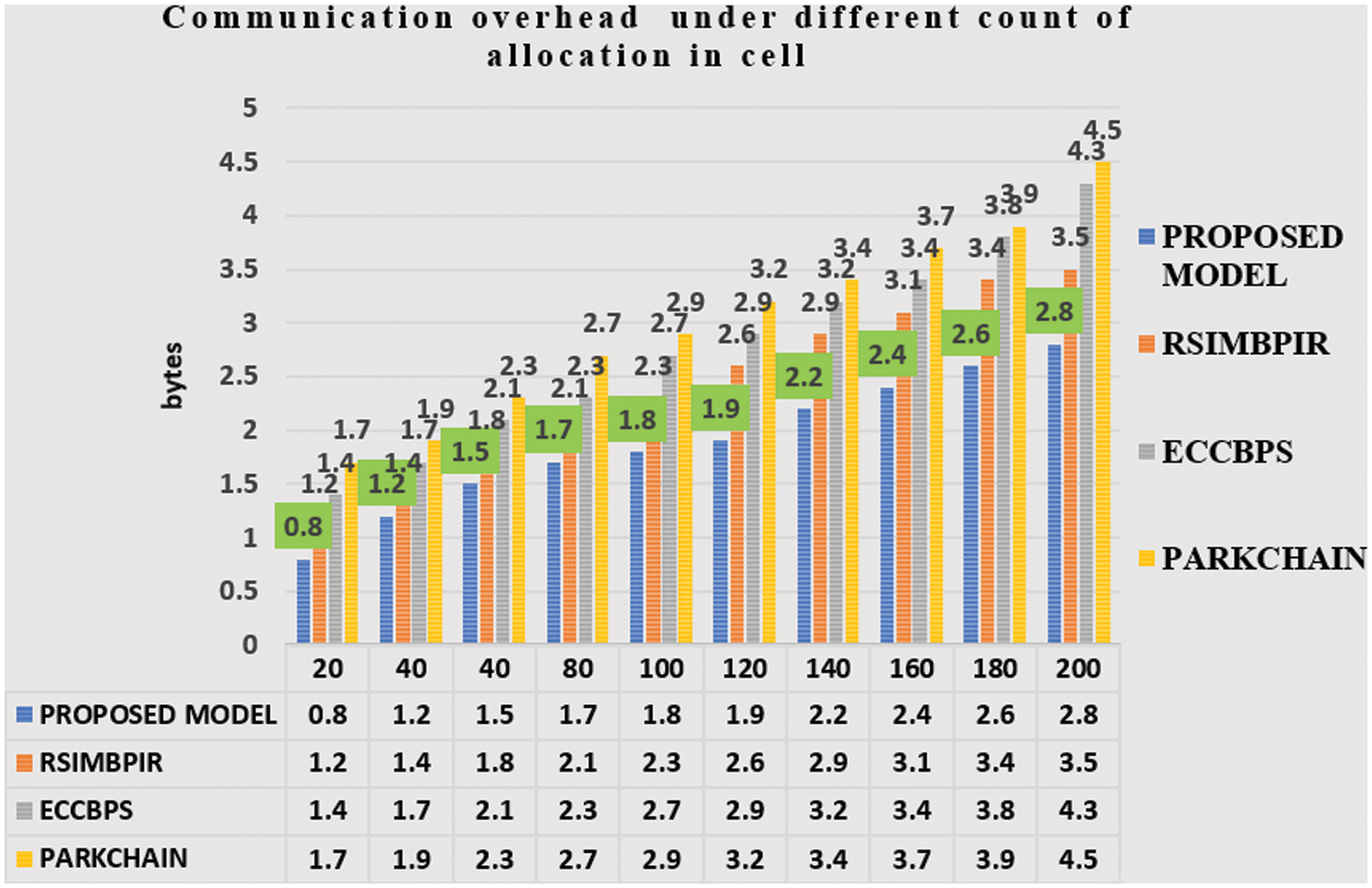
Figure 4: Communication overhead under different counts of allocation in a unit cell

4.2 Comparative Using Retrieval Time (RT) and Processing Rate (PR)

The comparison of the proposed model was evaluated with the other existing models for various block sizes such as 2000, 4000, 6000, 8000, and 10000 blocks. On considering the length of the paper the block size of 8000 and 10000 are provided in Fig. 5. The retrieval time (RT) and the processing time (PR) help in identifying the performance of the proposed model. The retrieval time is calculated as the time taken based on transactions in the network over the blockchain nodes shown in Fig. 5.

Figure 5: Comparison between retrieval response time and users

Based on the response retrieval time of users, the processing rate is calculated as the amount of information transmitted during a specified time period over a network using block sizes 8000 and 10000 in Fig. 6.

processing rate(PR)=Amount of dataTimeperiod in a network(4)

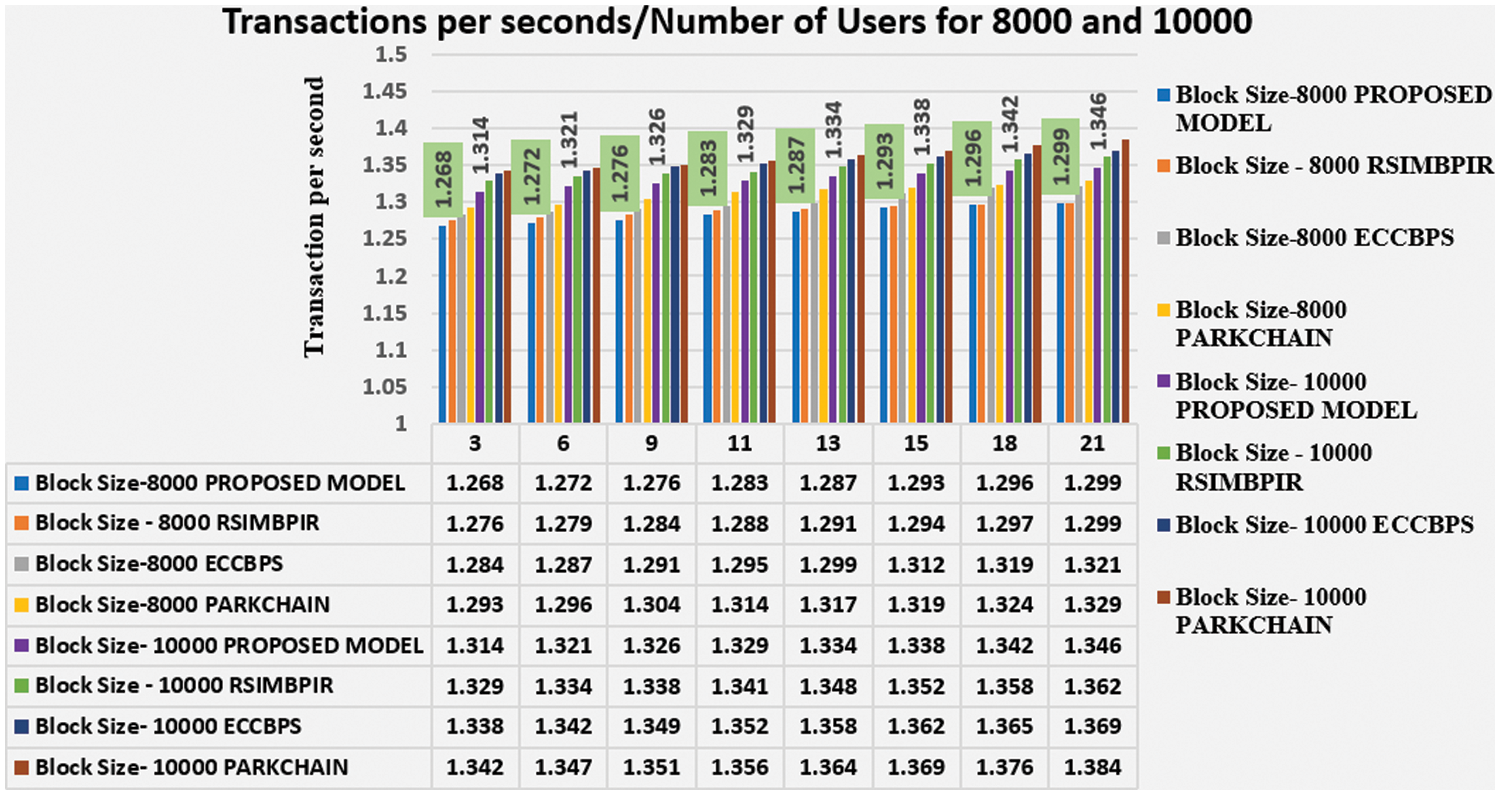
Figure 6: Comparison between processing rate and transaction per second

4.3 Comparative Analysis Based on Throughput

Further, the proposed model can be evaluated the throughput of the various block sizes such as 8000 and 10000 against existing models shown in Fig. 7. This metric is used to measure sending rate of the valid blocks added and the total amount of time takes for those records as in Eq. (5).

Throughput=Total no of records added in blocksTotal no of time taken(5)

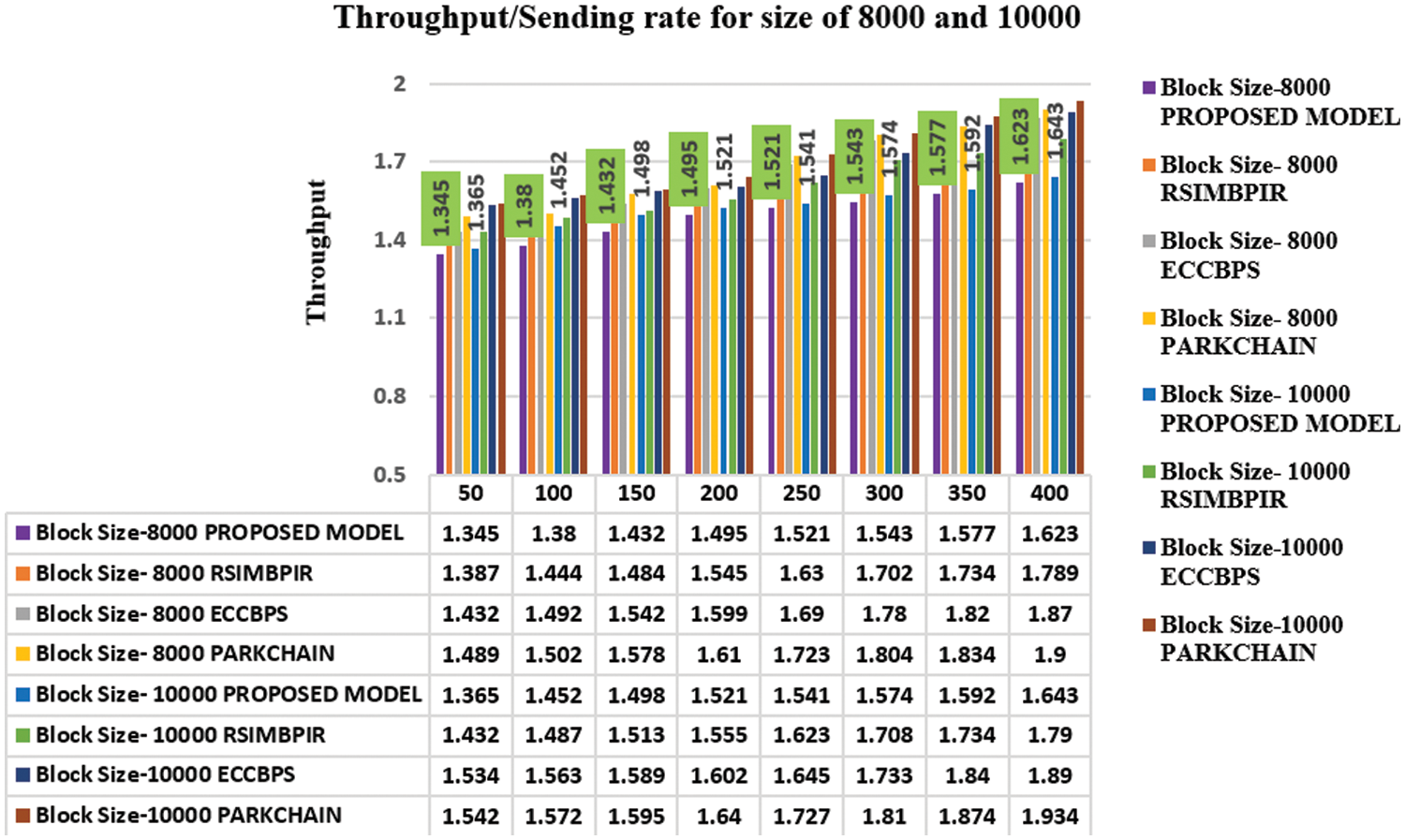
Figure 7: Throughput comparison with block size

4.4 Comparative Analysis Based on Latency

Based on the proposed model the latency is evaluated against various existing models shown in Fig. 8. It is calculated by the number of transactions per second along with transactions submitted to the network are shown in Eq. (6).

latency=number of transactions per secondsnetwork(6)

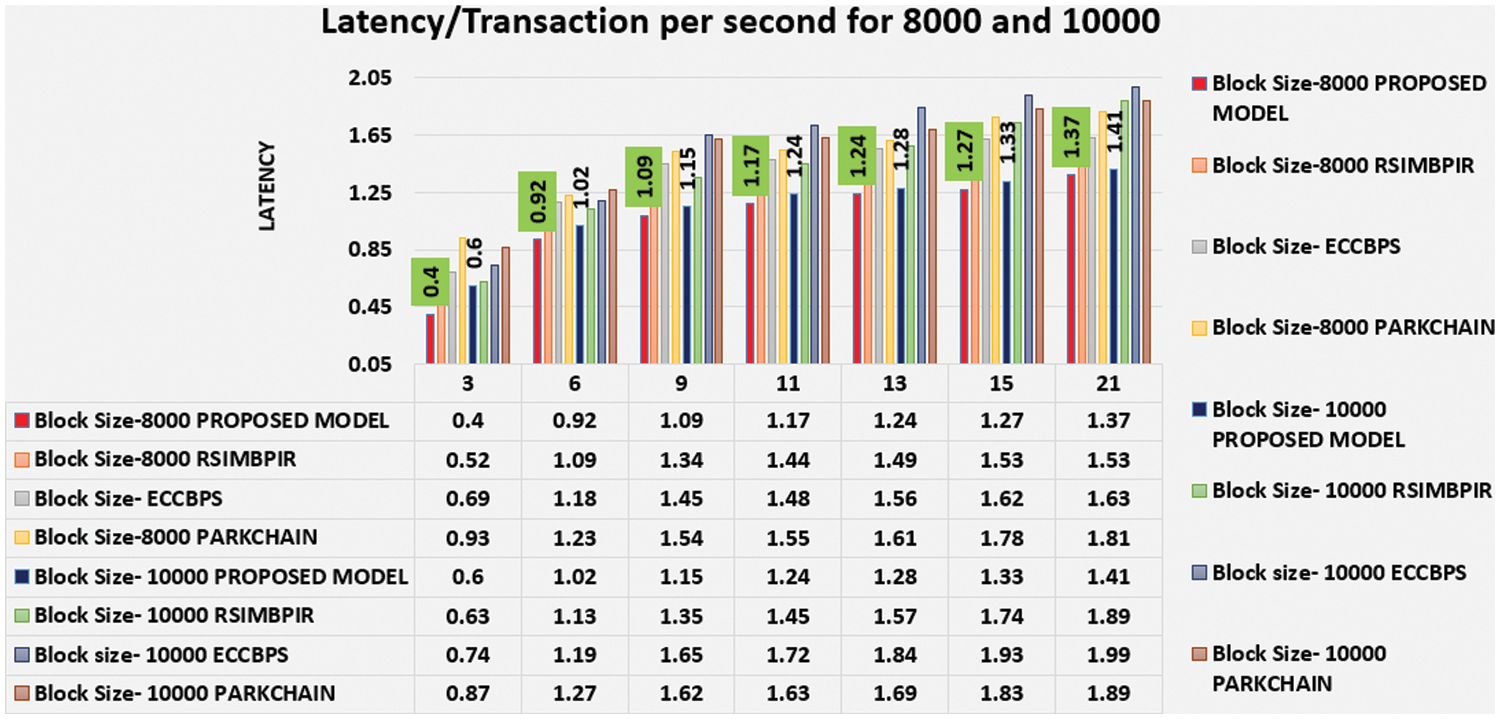
Figure 8: Comparison of latency for block sizes 8000 and 10000

5  Performance Analysis of the Proposed Encryption Algorithms with Existing Algorithms

The simulations were performed at the time of the development environment of the simulator—on a Windows OS Intel Core, 16 GB 1866 MHz RAM, AMD OpenCV using Tenseal and seal libraries. The encryption service as well as the plain text aggregation resided on an external server, so that differences in the overall topology can be neglected in the comparison. It was run on a single 2.7 GHz Intel Core. The simulation and the encryption service communicated through ethernet. This setup with a separate simulation and encryption service also ensured that there is no computation power for the simulation lost to the encryption service. The proposed model used a fully homomorphic encryption technique for privacy preservation. Similarly, Singh et al. [25] utilized privacy preservation using attribute and homomorphic encryption techniques. Also, Alkenazan et al. [26] utilized the parking slot framework without encryption techniques. Having these two works as a benchmark the proposed model is stimulated on the above-said environment on the number of cars against the communication time and the algorithms response time as shown in Fig. 9.

Figure 9: Comparison of proposed algorithm with existing algorithms

6  Conclusion

Improved Asymmetric Consortium Blockchain and Homomorphically Computing Univariate Polynomial-based private information retrieval (IACB-HCUPPIR) scheme are proposed for ensuring the availability of parking lots with transparency and security in a privacy-preserving smart parking system. In specific, an improved Asymmetric Consortium Blockchain is used for achieving secure transactions between different parties interacting in the smart parking environment. It further adopted the method of Homomorphically Computing Univariate Polynomial-based private information retrieval (HCUPPIR) scheme for preserving the location privacy of drivers. The results of IACB-HCUPPIR confirmed better results in terms of minimized computation and communication overload with maximized drivers’ privacy preservation. As one of the limitations of performance measures of blockchain is the transaction throughput and confirmation latency which was measured for the proposed model against the RSIMBPIR [24], ECCBPS [21], and PARKCHAIN [18] and found that the proposed model obtains better parking slot allocation with less time. One of the limitations of homomorphic encryption requires modification in the client-server application to make it functional, which may increase the cost for practical implementation. Even though the performance measures show the betterment of the proposed model, the model can be further extended with online payment, vehicle guidance, better parking supervision with the smart contract, and proof of work using digital signature algorithms. Thus, we ensure the proposed model performs well in allocating parking slots with less time and high security with privacy preservation.

Funding Statement: The research was funded by the School of Information Technology and Engineering, Vellore Institute of Technology, Vellore 632014, Tamil Nadu, India.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. K. K. Kumar, S. Karimunnisa, A. Krishna, N. Cherukuri and C. Z. Basha, “An advanced approach for smart parking solution based on ethereum blockchain system,” in 2021 Second Int. Conf. on Electronics and Sustainable Communication Systems (ICESC), Coimbatore, India, pp. 942–948, 2021. [Google Scholar]

2. M. Mojarad, M. Sedighizadeh and M. Dosaranian-Moghadam, “Optimal allocation of intelligent parking lots in distribution system: A robust two-stage optimization model,” IET Electrical Systems in Transportation, vol. 12, no. 2, pp. 102–127, 2022. [Google Scholar]

3. C. Biyik, Z. Allam, G. Pieri, D. Moroni, O. Fraifer et al., “Smart parking systems: Reviewing the literature, architecture and ways forward,” Smart Cities, vol. 4, no. 2, pp. 623–642, 2021. [Google Scholar]

4. H. Canli and S. Toklu, “Deep learning-based mobile application design for smart parking,” IEEE Access, vol. 9, pp. 61171–61183, 2021. [Google Scholar]

5. E. M. Migabo, K. D. Djouani and A. M. Kurien, “The narrowband internet of things (NB-IoT) resources management performance state of art, challenges, and opportunities,” IEEE Access, vol. 8, pp. 97658–97675, 2020. [Google Scholar]

6. S. Saharan, N. Kumar and S. Bawa, “An efficient smart parking pricing system for smart city environment: A machine-learning based approach,” Future Generation Computer Systems, vol. 106, pp. 622–640, 2020. [Google Scholar]

7. A. Floris, R. Girau, S. Porcu, G. Pettorru and L. Atzori, “Implementation of a magnetometer-based vehicle detection system for smart parking applications,” in 2020 IEEE Int. Smart Cities Conf. (ISC2), Piscataway, NJ, USA, pp. 1–7, 2020. [Google Scholar]

8. N. Buldakov, T. Khalilev, S. Distefano and M. Mazzara, “An open-source solution for smart contract-based parking management,” in IFIP Int. Conf. on Open-Source Systems, Cham, Springer, pp. 55–69, 2020. [Google Scholar]

9. F. Bock, S. Di Martino and A. Origlia, “Smart parking: Using a crowd of taxis to sense on-street parking space availability,” IEEE Transactions on Intelligent Transportation Systems, vol. 21, no. 2, pp. 496–508, 2019. [Google Scholar]

10. R. Ke, Y. Zhuang, Z. Pu and Y. Wang, “A smart, efficient, and reliable parking surveillance system with edge artificial intelligence on IoT devices,” IEEE Transactions on Intelligent Transportation Systems, vol. 22, no. 8, pp. 4962–4974, 2020. [Google Scholar]

11. S. N. Ghorpade, M. Zennaro and B. S. Chaudhari, “GWO model for optimal localization of IoT-enabled sensor nodes in smart parking systems,” IEEE Transactions on Intelligent Transportation Systems, vol. 22, no. 2, pp. 1217–1224, 2020. [Google Scholar]

12. A. K. Tyagi, S. Kumari, T. F. Fernandez and C. Aravindan, “P3 block: Privacy preserved, trusted smart parking allotment for future vehicles of tomorrow,” in Computational Science and Its Applications–ICCSA 2020: 20th International Conference, Cagliari, Italy, July 1–4, Proceedings, Part VI 20, Springer International Publishing, pp. 783–796, 2020. [Google Scholar]

13. C. Zhang, L. Zhu and C. Xu, “BPAF: Blockchain-enabled reliable and privacy-preserving authentication for fog-based IoT devices,” IEEE Consumer Electronics Magazine, vol. 11, no. 2, pp. 88–96, 2021. [Google Scholar]

14. A. Anitha and T. Haritha, “The integration of blockchain with IoT in smart appliances: A systematic review,” Blockchain Technologies for Sustainable Development in Smart Cities, pp. 223–246, 2022. https://www.igi-global.com/chapter/the-integration-of-blockchain-with-iot-in-smartappliances/297436 [Google Scholar]

15. X. Huang, D. Ye, R. Yu and L. Shu, “Securing parked vehicle assisted fog computing with blockchain and optimal smart contract design,” IEEE/CAA Journal of Automatica Sinica, vol. 7, no. 2, pp. 426–441, 2020. [Google Scholar]

16. M. Ibrahim, Y. Lee, H. K. Kahng, S. Kim and D. H. Kim, “Blockchain-based parking sharing service for smart city development,” Computers and Electrical Engineering, vol. 3, pp. 108267, 2022. [Google Scholar]

17. M. M. Badr, W. Al Amiri, M. M. Fouda, M. M. Mahmoud, A. J. Aljohani et al., “Smart parking system with privacy preservation and reputation management using blockchain,” IEEE Access, vol. 8, pp. 150823–150843, 2020. [Google Scholar]

18. H. S. Jennath, S. Adarsh, N. V. Chandran, R. Ananthan, A. Sabir et al., “Park chain: A blockchain-powered parking solution for smart cities,” Frontiers in Blockchain, vol. 2, pp. 6, 2019. [Google Scholar]

19. J. Ni, X. Lin and X. Shen, “Toward privacy-preserving valet parking in autonomous driving era,” IEEE Transactions on Vehicular Technology, vol. 68, no. 3, pp. 2893–2905, 2019. [Google Scholar]

20. W. Balzano, M. Lapegna, S. Stranieri and F. Vitale, “Competitive-blockchain-based parking system with fairness constraints,” Soft Computing, vol. 26, no. 9, pp. 4151–4162, 2022. [Google Scholar]

21. S. K. Singh, Y. Pan and J. H. Park, “Blockchain-enabled secure framework for energy-efficient smart parking in sustainable city environment,” Sustainable Cities and Society, vol. 76, pp. 103364, 2022. [Google Scholar]

22. C. Li, Y. Tian, X. Chen and J. Li. “An efficient anti-quantum lattice-based blind signature for blockchain-enabled systems,” Information Sciences, vol. 546, pp. 253–264, 2021. [Google Scholar]

23. L. Chaoyang, M. Dong, J. Li, G. Xu, X. Chen et al., “Efficient medical big data management with keyword-searchable encryption in healthchain,” IEEE Systems Journal, vol. 16, no. 4, pp. 1–12, 2022. [Google Scholar]

24. S. Singh, D. Satish and S. R. Lakshmi, “Ring signature and improved multi-transaction mode consortium blockchain-based private information retrieval for privacy-preserving smart parking system,” International Journal of Communication Systems, vol. 34, no. 14, pp. e4911, 2021. [Google Scholar]

25. P. Singh, M. Masud, M. S. Hossain and A. Kaur, “Blockchain and homomorphic encryption-based privacy-preserving data aggregation model in smart grid,” Computers & Electrical Engineering, vol. 93, pp. 107209, 2021. [Google Scholar]

26. W. A. Alkenazan, A. A. Taha, M. J. Alenazi and W. Abdul, “An enhanced framework for secure smart parking management systems,” International Transaction Journal of Engineering, Management, & Applied Sciences & Technologies, vol. 12, no. 7, pp. 1–13, 2021. [Google Scholar]