Feature Selection with Deep Belief Network for Epileptic Seizure Detection on EEG Signals

1  Introduction

Epilepsy is a severe and persistent neurological disorder affecting the human brain. Over 50 million people of distinct ages globally, with around 450,000 people below 17 in the US out of almost 3 million people, are detected with such disorders [1]. Its recurring unprovoked seizure acknowledges epileptic seizure (ES). Epilepsy is a phase of synchronous, anomalous innervation of a population of neurons that might last a few minutes [2]. While Epilepsy happens, a person has fleeting instances of involuntary, abnormal body movements, either all at once or in spurts, and may or may not be aware of what is happening. Although ES is uncommon, its consequences on patients’ emotions, relationships, and ability to express themselves physically make diagnosing and treating Epilepsy crucial and comprehensive [3]. The EEG signals are most preferable for detecting Epilepsy since they are portable, economical, and depict precise rhythm from the frequency domain [4]. The EEG gives the voltage variation generated by the ionic presence of neurons from the brain that characterizes the brain’s bioelectric activities. It should be recorded for a longer duration to diagnose ESs. Moreover, this signal is recorded in the number of channels, which makes the analysis complex [5]. Also, the EEG signal is prone to artefacts generated by muscle tremors, main power supply, and electrode movements. This might challenge physicians to detect ESs through noisy EEG signals [6]. Several studies have been carried out to predict and diagnose ESs depending upon EEG modalities and other technologies like MRI coupled with AI methods to overcome this problem. AI techniques like traditional DL and machine learning algorithms were applied for ES diagnosis [7].

Several ML approaches have been introduced based on time, statistical and frequency domains for diagnosing ESs [8]. A trial-and-error methodology could create the classification model and feature selection in ML techniques. To suggest a suitable approach, one must have a solid understanding of signal processing and data mining methodologies [9]. Currently, with enhanced accessibility of data, ML techniques might not perform well. Therefore, the DL technique, a state-of-the-art algorithm, is used. Unlike traditional ML approaches, DL models need enormous amounts of data from the trained stage [10]. Because the model has massive feature spaces, it could face the problem of overfitting in case of insufficient data. Here, the author provided a method for detecting epileptic seizures from EEG data using an Oppositional Aquila Optimizer-based Feature Selection with Deep Belief Network (OAOFS-DBNECD). The primary objective of the presented OAOFS-DBNECD algorithm is to categorize and classify the presence of ESs. The OAOFS technique selects an optimal subset of features using the pre-processed data. For seizure classification, the presented OAOFS-DBNECD technique applies an artificial ecosystem optimizer (AEO) with a deep belief network (DBN) model for seizure classification purposes. An extensive range of simulations is accomplished on the benchmark dataset to ensure the enhanced performance of the presented OAOFS-DBNECD approach.

The remainder of this paper is divided into five sections. Section 2 presents the literature review results. Section 3 lays out the methodology proposed for data pre-processing, extracting the features and categorizing, class labelling, hyperparameter tweaking, design architecture, optimization strategies, and mathematical and conceptual framework. Section 4 compares the suggested technique to the various approaches by portraying the simulated outcomes. Finally, Section 5 highlights the conclusion.

2  Literature Survey

Usman et al. [11] proposed a DL-related ensemble learning technique for predicting ESs. In the presented approach, EEG signals were pre-processed through empirical mode decomposition, and bandpass filtering was applied to remove noise. With synthetic preictal segments generated by utilizing GAN, the class imbalance problem was mitigated. Hilal et al. [12] introduced an intelligent deep canonical sparse AE-related ES detection and classification (DCSAE-ESDC) method using an EEG signal. In the end, the parameter tuning of a DSCAE process is carried out through the krill herd algorithm (KHA). Anter et al. [13] modelled a novel technique for distinctly recognizing seizure conditions (for instance, interictal, ictal, and preictal) from EEG from the IoT structure to monitor patients. Divya et al. [14] devised a fully automatic system similar to Hybrid GWO-Improved Sine Cosine Algorithm (HGWOISCA) with improved SVM called HGWOISCA-SVM for classifying EEG signals. Bhandari et al. [15] devised the new ES recognition utilizing the Improved Ensemble Learning Model (I-ELM). A novel meta-heuristic technique named Modified Tunicate Swarm Algorithm (M-TSA) was implemented to reduce the feature length, manage the training difficulty, and improve detection performance for precise FS.

In [16], a technique for classifying EEG data utilizing DNN structure was presented. Bi-LSTM, a type of RNN, has been used in this technique. In [17], a projected hybrid cuckoo finch optimizer tuned DCNN classifier for predicting and recognizing the incidence of ES using EEG signal data gained by IoT. The author [18] explained each component’s detailed explanation and an overview of the many diagnostic approaches used for epilepsy. In conclusion, the study proposed several novel ideas for seizure detection using DL methods, which are gaining popularity. In [19], medical professionals in the field of neurology have a time-consuming challenge when they must visually examine long-term electroencephalography (EEG). The suggested seizure detection approach was tested using the CHB-MIT scalp EEG database, which achieved a sensitivity of 93.89 per cent and a specificity of 98.49 per cent. In the article [20], to alleviate the burden of data labelling, the author presented a hybrid system that combines unsupervised learning (UL) with traditional supervised learning (SL). Through testing on the CHB-MIT scalp EEG dataset, the proposed seizure detection system is shown to have an overall accuracy of 92.62%, a sensitivity of 95.55%, and a specificity of 92.57%. An improved evolutionary approach is suggested to extract the same features from many networks with different numbers of layers (IGA) [21]. Results for ACC, SPE, SEN, and F1 on the Siena scalp database are 99.13%, 98.36%, and 98.75%, respectively.

In [22], the author presented a unique approach to the few-shot issue by reducing the need for vast data: an automated system based on Deep Metric Learning (DML) for identifying epileptic episodes. Based on the Bonn dataset, the most challenging classification of interictal vs. ictal, an impressive accuracy of 98.60% and specificity of 100% was attained. Because of an unacceptable amount of false alarms [23] produced by cutting-edge technology, automated long-term detection of focal seizures remains one of the most pressing concerns in epilepsy. To speed up the diagnosis of epilepsy, automatic seizure identification from an electroencephalogram (EEG) is crucial [24]. In this study [25], the author implemented an automated learning framework for EEG seizure detection based on the Fourier-Bessel expansion-based empirical wavelet transform (FBSE-EWT) technique. The models were trained and tested using a 10-fold cross-validation procedure. To improve the feature embedding of raw EEG signals throughout seizure and non-seizure periods, a new seizure detection model based on a linear graph convolution network (LGCN) was developed [26].

The authors offered CW-SRNet, a complete epilepsy detection model [27]. The proposed model outperformed other methods with a sensitivity of 96.84% and an absolute specificity of 99.66% on the CHB-MIT dataset. In this work [28], the author presented two innovative strategies for extracting features from EEG data and classifying them using Convolutional Neural Networks (CNNs). The results of the studies showed that the suggested technique outperforms the others in terms of sensitivity, specificity, classification accuracy, and runtime. In this study [29], the author presents the creation of a neural network in software for seizure detection using EEG data. With custom CNN’s built-in software, the author performed training and inference on the CHBMIT dataset and obtained an accuracy of 96.74%. In this research [30], the author presents a two-stage process for identifying epileptic seizures and diagnosing epilepsy. In this study [31], the author contributed a reliable automated seizure detection system that may provide a reliable diagnosis of these disorders. The obtained results proved the effectiveness of the proposed technique, which delivers up to 100% classification results and surpasses similar state-of-the-art methods. To define the dynamic behaviour of juvenile seizure occurrences, the author suggested a novel approach [32], in addition to a comprehensive system for identifying the nullclines on the dimensional space in situations when the governing differential equations are unavailable.

In this study [33], the author discussed a seizure detection system that combines frequency-domain data with a k-means closest neighbour (NL-kNN) classifier based on the principles of neutrosophic logic. Classification accuracies of 98.16%, 100% and 89.06% were attained, respectively. The author of this article [34] built a convolutional neural network (CNN) that automatically detects seizure activity in EEG spectral analysis and assesses their performance. To prevent overfitting, each CNNs was constructed on the VGG-net architecture.

This work aims to assist neurologists in their diagnosis of epilepsy by automating the identification of epileptic seizures from EEG data using machine learning methods. Two ways were used to predict the likelihood of an epileptic seizure [35] occurring inside a windowed EEG recording of 18 channels, which purely depends on convolutional neural networks (CNNs). In addition, a channel dropout technique is presented [36] to gather subtle features from all channels of a specific EEG signal during the model training phase. This research developed an automated method to distinguish seizure signals from background noise. Before feature extraction, raw EEG signals were first preprocessed to eliminate unwanted noise and artefacts [37]. To examine the EEG signal, the author [38] rebuilt the time series EEG signal in High dimensional Phase Space. When calculating features, it is helpful to record where PCs and the Poincare section overlap.

In previous researches, with enhanced accessibility of data, ML techniques might not perform well. Therefore, the DL technique, with specific optimization algorithms are proposed. Unlike traditional ML approaches, DL models need enormous amounts of data from the trained stage, the reason behind is the DL model has massive feature spaces, it could face the problem of overfitting in case of insufficient data. With this, we have devised our objective to classify the seizure using OAOFS-DBNECD model.

3  The Proposed Model

A novel OAOFS-DBNECD methodology was formulated for seizure classification using EEG signals. The major purpose of the presented OAOFS-DBNECD system is to categorize and classify the presence of ESs. To accomplish this, the OAOFS-DBNECD technique uses OAOFS for data preprocessing, feature selection, DBN classification, and AEO hyperparameter tuning. The block diagram of OAOFS-DBNECD system is demonstrated in Fig. 1.

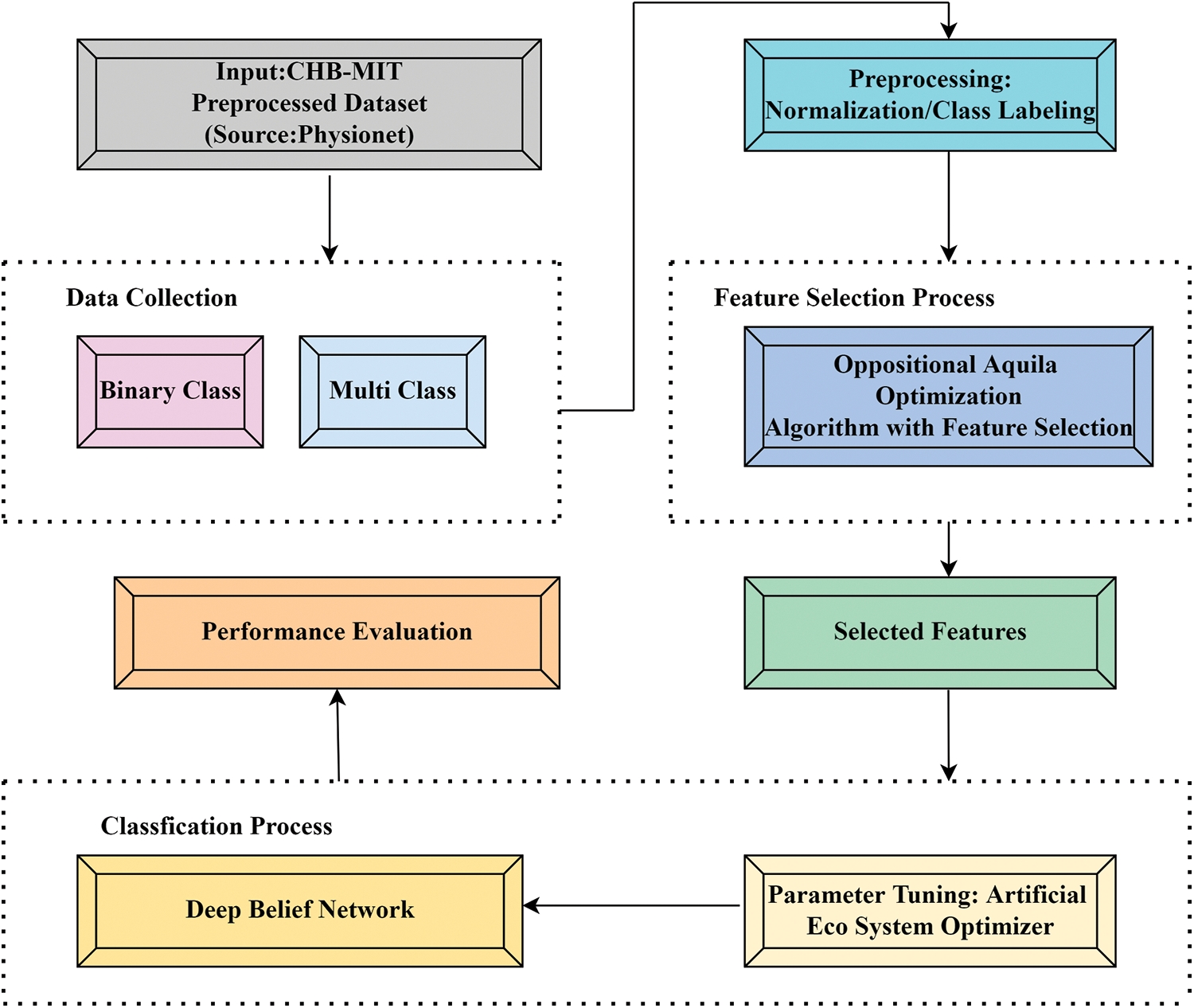
Figure 1: Schematic diagram of OAOFS-DBNECD system

3.1 Data Pre-Processing

Initially, the presented OAOFS-DBNECD technique transforms the EEG signals into .csv format to make it compatible with further processing. Followed by, the min-max scaler for normalizing the input data. Min-Max scaling is a normalized approach which allows us to scale data from the database to particular range utilizing all the feature’s minimal and maximal values as shown in Fig. 2.

Figure 2: Input data

3.2 Design of OAOFS Technique

Following the data preprocessing stage, the OAOFS technique selects an optimal subset of features using the pre-processed data. Abualigah et al. [39] proposed the Aquila Optimizer which is a typical SI technique. The approach can be enhanced by mimicking four behaviors of predator prey of the Aquila based on: exploring within different search spaces by contour flight with short glide attack; swooping, walking, and grabbing prey; High soar and a vertical stoop choose the search space, whereas a low fly and a leisurely descending attack take advantage of a converging search space.

The following are short discussions of the AO’s four approaches:

Strategy1: Expanded exploration (X1).

The Aquila searches for the state space by using high soar and vertical stoop to determine the hunting zone, which may be described mathematically as:

X1(t+1)=Xbest(t)×(1−tT)+(XM(t)−Xbest(t)⋅R1)(1)

XM(t)=1N∑i=1NXi(t),∀j=1,2,3, …, Dim(2)

From the expression, Xbest(t) signifies the better location in the present iteration, X(t) indicates the average value of the position, R1 represents a random value between [0, 1], Dim indicates the dimensional weight of problems, N characterizes the amount of Aquila population, t and T represents the existing iteration and the maximal amount of iterations, correspondingly.

Strategy2: Narrowed exploration (X2).

The Aquila uses spiral flight over prey and hunts over a brief glide, as shown below.

X2(t+1)=Xbest(t)×Ly(D)+XR(t)+(y−x)⋅R2(3)

In Eq. (3), R2 refers to a random value ranging from zero to one, X(t) indicates a random value chosen from Aquila population, D denotes dimensionality, and Ly(D) signifies the Levy flight function as in below equation [40]:

{Ly(D)=s×u×σ|v|1βσ=Γ(1+β)×sine(πβ2)Γ(1+β2)(β_1_)×β×2(4)

In Eq. (4), s refers to constant equivalent to 0.01, β is equivalent to 1.5, u and v represent random number ranges from zero to one, y and χ indicate the spiral flight path in the solution space as:

{y=r× cos (θ)x=r× sin (θ)r=R3+0.00565×D1θ=−0.005×D1+3π2(5)

In Eq. (5), D1 indicates an integer value from 1 to D dimensionality length and R3 is an integer which indicates the search cycles [1,41].

Strategy 3: Expanded exploitation (X3).

The Aquila’s technique, which comprises a vertical drop while seeking solution space through lower flight before striking the target, is mathematically expressed as follows:

X3(t+1)=(Xbest(t)−XM(t))×α−R4+((UB−LB)×R5+LB)×δ(6)

In Eq. (6), α and δ indicate integer number equivalent to 0.1 that is utilized for adjusting exploitation, R4 and R5 shows random values in (0, 1), LB and UB represent upper and lower limits of the problem, correspondingly.

Strategy 4: Narrowed exploitation (X4).

The Aquila pursues prey while taking into account the stochastic escape path and attacks the victim on the ground. This behavior may be mathematically expressed in terms:

{X4(t+1)=QF×Xbest(t)−(G1×X(t)×rand)−G2×Ly(D)+rand×G1QF(t)=t2×rand−1(1−T)2G1=2×rand−1G2=2×(1−tT)(7)

In Eq. (7), QP indicates a quality function parameter that is employed for tuning the search strategy, rand refers to a random number ranges between [0, 1], G1takes a random value within [−1, 1] indicating the Prey monitoring habit, and G2 denotes the flight slope while hunting prey that is reduced from two to zero.

The OAO is derived by the use of oppositional based learning (OBL) approach that stems from the concurrent estimation of opposite pairs of the base agent for improving the probability of meeting an equivalent agent [41]. Contrary to real number N∈[jL,jU] is offered by N→ as:

N→=jL+jU−N(8)

Whereas jL and jU are recognized as the lower as well as upper limits of real number. But the multidimension space, Nis formulated as Nk = {Nk1, Nk2, Nk3, Nk4 … Nkt} and Nkt∈ [jLt, jUt], where t = 1, 2, 3, 4,…, n and the equivalent opposite point is shown below:

N¯={N¯k1,N¯k2,N¯k3,…N¯kt}

N¯kt=jLt+jUt−Nkt(9)

The optimized method changes opposite points by equivalent solution N dependent upon optimum fitness values.

In OAOFS, the continual values in the search space are mapped to binary values utilizing this devised technique for deriving binary position vectors for the solutions. Every location dimension is considered by applying a specific S-shaped transfer operation for computing the solution for movement in binary space. In Eq. (10), the S-shaped function is presented for generating probability values.

S(Xid(iter+1))=11+e(−Xid(iter)3)(10)

The value of S (Xj^d (iter + 1)) indicates the possibility of altering the ith solution’s binary position value in the dth dimension. The binary value is computed as probability, and the threshold values are compared as presented in Eq. (11), whereas rand denotes a random value between 0 and 1.

Xid(iter+1)={1, if rand≤S(Xid(iter+1))0, otherwise(11)

3.3 Epileptic Seizure Classification

For seizure classification, the presented OAOFS-DBNECD technique utilizes AEO with the DBN model. A DBN model comprises two processes: fine-tuning the weight parameter of the whole network through backpropagation (BP) and training RBM layer-wise to create the deep network [42] initially. The architecture of DBN is tuned to the features of the input dataset. Invariably, the number of regions in the brain corresponds to the number of neurons in the output layer. The pre-training procedure has as its goal the achievement of an appropriate value for the whole network. DBN uses RBM as its learning module, an advancement of the DL method. It is a 2-layer network for the accessible neurons and the hidden ones. The Energy function of RBM is expressed below:

E(v, h)=−∑inaivi−∑jmbjhj−∑ijnmWijvihj(12)

In Eq. (12), wij (i = 1, 2,…, m; j = 1, 2,…, n) refers to the weight among vi and hj; m indicates the number of hidden neurons and n indicates the number of visible neurons, correspondingly; ai and bj represents biases of vi and hj, correspondingly. RBM is trained for recreating the input and minimizing the reconstructed errors among the reconstructed and original inputs. Furthermore, a technique named contrastive divergence (CD) takes k iteration to accomplish an estimated convergence state for training the RBM that could decrease the reconstructed error efficiently. During the training phase, the prior RBM’s feature input is used as feed to the succeeding RBM. Independent tests are conducted on each RBM structure to guarantee that feature information is maintained when feature variables are moved to other feature areas. Fig. 3 demonstrates the architecture of DBN. The hyperparameters related to the DBN model are fine-tuned via the AEO algorithm. The AEO algorithm depends on the energy transfer model between living organisms that assist in maintaining the stability of species [43]. For this purpose, three operators namely, decomposition, production, and consumption, are used to accomplish the solution.

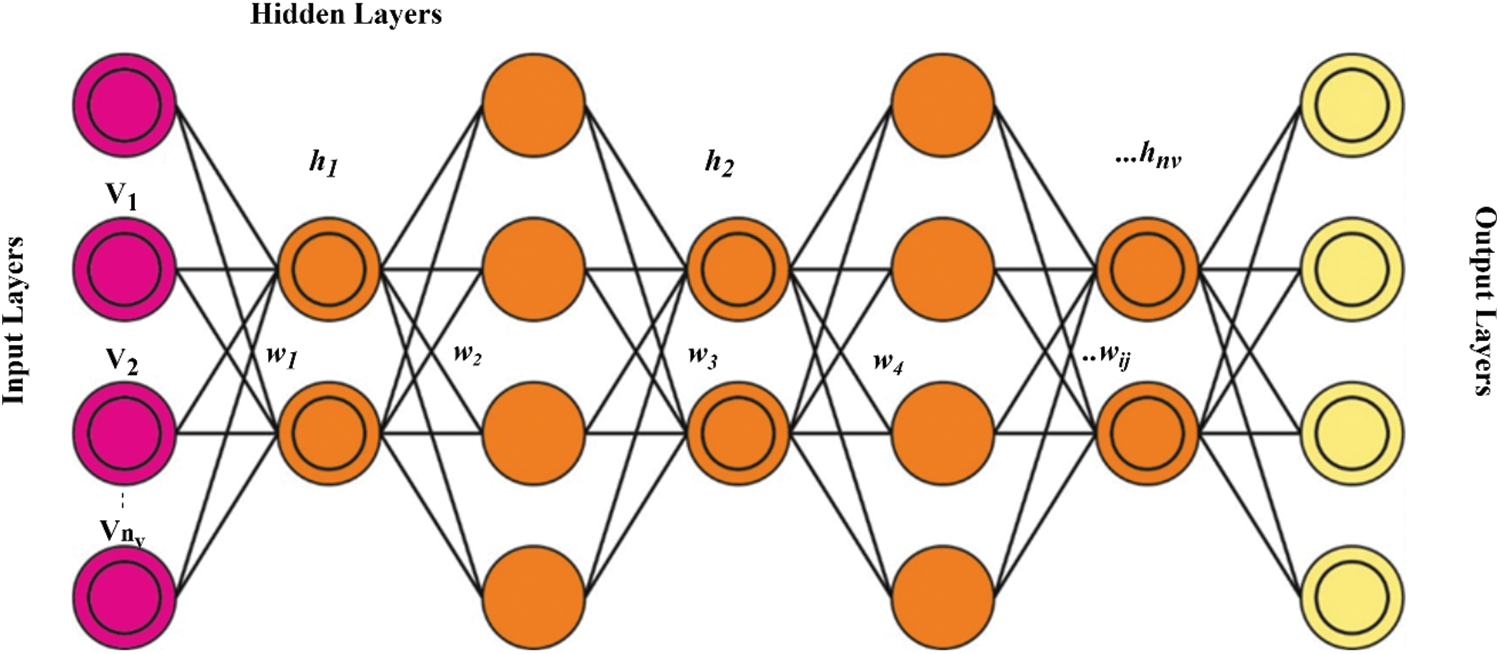
Figure 3: DBN structure

In AEO, producers are characterized as the worst individuals in the population. The production operator between randomly generated produces a new individual. (xrand) and the best (x) individuals by replacing the preceding one and it is shown below:

x1(t+1)=(1−α)xn(t)+αxrand(t)(13)

α=(1−tT)r1(14)

xrand=r¯(Ub−Lb)+Lb(15)

where n represents the size of population, T indicates maximal iteration count, Ub and Lb indicate the upper and lower limits, and r1 random numbers between zero and one.α and r¯ are the linear weight coefficient and random vector value within zero and one, correspondingly. The α coefficient provided in Eq. (13) assists in drifting the individual linearly from the random location towards the better individual through iteration. The consumption operator could be implemented using the consumer after the production operator finishes the producer. A Lévy flight-like random walk called consumption factor (C) is determined for enhancing the exploration ability:

C=12v1|v2|(16)

v1∼N(O, 1),v2∼N(O, 1)(17)

where N(O, 1) characterizes a standard distribution so that the values of mean and standard deviation are equivalent to 0 and 1, and diverse consumers adopt different strategies. A consumer eats only the producer if it is arbitrarily selected as a herbivore (1-x2 and x5 are herbivore consumers, therefore, eat only the producer x_1).

xi(t+1)=xi(t)+C⋅(xi(t)−x1(t)), i∈[2, ⋯ , n](18)

A consumer eats other consumers only with the highest level of energy in case of being selected as a carnivore (consumers from individual of x2 to x5 are eaten by the consumer x_6 as carnivore and has the lowest energy level when compared to the individuals of x2 to x5):

xi(t+1)=xi(t)+C⋅(xi(t)−xi(t)),i∈[3, ⋯, n]

j=randi([2i−1])(19)

xj(t+1)=xj(t)+C⋅(r2⋅(xj(t)−x1(t)))+(1−r2)(xj(t)−xj(t)), i∈[3, ⋯ , n]

j=randi([2i−1])(20)

Whereas r2 represents a random value between 0and 1. A movement is made to a search person’s location based on the worst or a randomly picked member of the general population. Thus, it enables to perform a global search. The decomposer chemically breaks down the residues of died individuals in the population to provide essential nutrients for the growth of the producer. The weight coefficient of h and e along with the decomposition factor of D are intended for mathematically modelling these behaviors. This parameter helps to update the location of xj (i-th individuals) by the location of xn (the decomposer location). Likewise, every individual’s next location is permissible to spread around the decomposers (better individuals):

xi(t+1)=xn(t)+D⋅(e⋅xn(t)−h⋅xj(t)), i∈1,⋯,n(21)

D=3u,u∼N(0, 1)(22)

e=r3⋅rand i ([ 12 ])−1(23)

h=2⋅r3−1(24)

The AEO algorithm will derive a fitness function (FF) for estimating the enhanced classifier performance. It would assign a positive value for indicating the superior performance of the candidate solutions. This method can take the reduced classifier error rate as the fitness function in Eq. (25).

fitness(xi)=ClassifierErrorRate(xi)=number of misclassified samplesTotal number of samples∗100(25)

3.4 Dataset Description

EEG datasets that may be used for training and testing models are either freely accessible to the public or need a paid membership to access. The accessibility of datasets has kicked off the transition phase from the conventional component of learning by trial and error to the patient-centric part of precision care. The CHB-MIT scalp EEG dataset is well-known due to the fact that it is both extensive and annotated. The approach that was used in the preparation of the CHB-MIT scalp EEG database is going to be presented in the following subsections. The pre-processed dataset has been uploaded to IEEE Dataport for public use. In their studies, the researchers who came before you used data from a very small number of patients who were included in the initial EEG database. In order to provide a concise summary of the data, the authors of this study compiled a total of 168 complete minutes of epileptic seizure durations from all of the patients, as well as 68 whole minutes of preictal time.

4  Results and Discussion

The proposed model is simulated using Python 3.6.5 tool. In this section, the seizure classification outcomes of the OAOFS-DBNECD technique are examined on a benchmark dataset [44,45] discussed in earlier section. The dataset holds samples under two classes: seizure and no seizure. In addition, the OAOFS system has chosen a sum of ten features out of 23 total features.

Ten selected features are FP1-F7, C4-P4, CZ-PZ, F4-C4, F7-T7, FP2-F4, FT9-FT10, FZ-CZ, P4-O2, and P8-O2. Fig. 4 shows the convergence graph of the OAOFS technique. The figure implied that the OAOFS technique had attained optimal convergence over several iterations. Fig. 5 portrays the combination of loss and accuracy graph examination of the OAOFS-DBNECD algorithm with and without feature selection. The outcomes displayed the accuracy value has increased, and the loss value decreased with a rise in the count of epochs. It is worth noting that the training loss is lower, and the validation accuracy is higher.

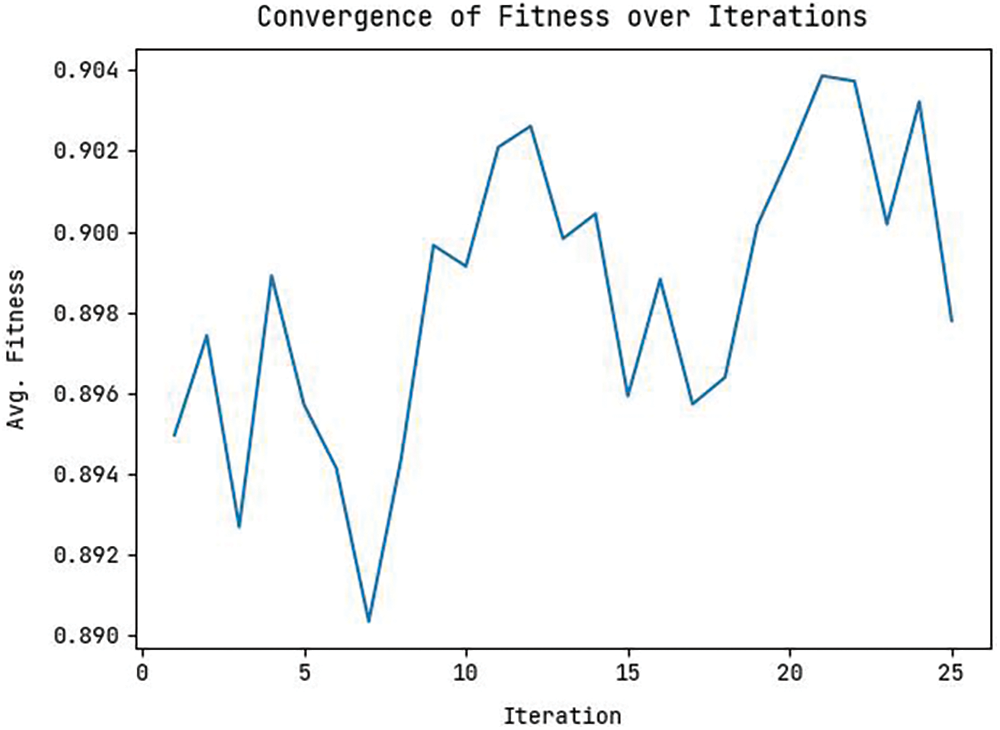
Figure 4: Convergence graph of feature selection model

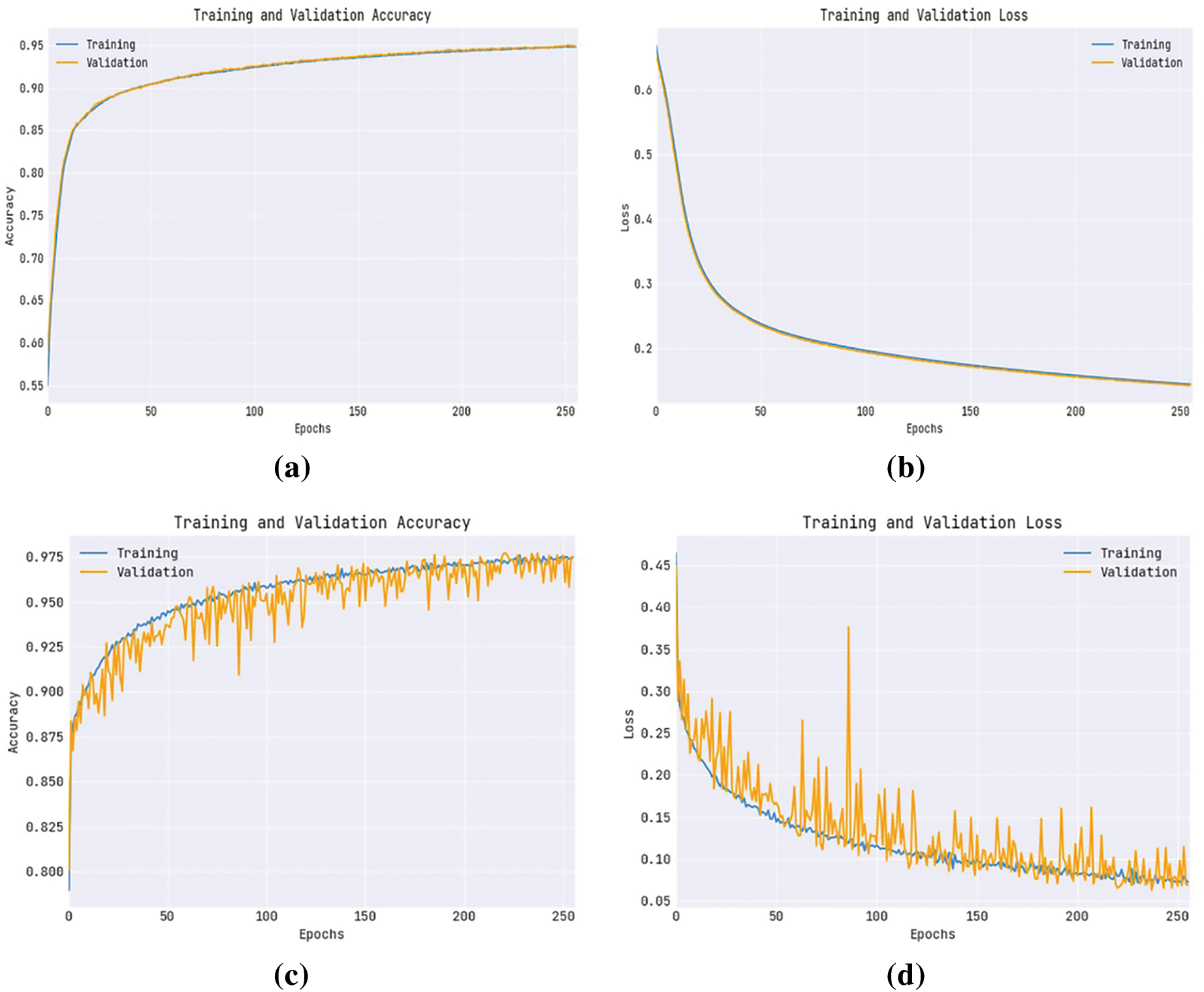
Figure 5: Without feature selection (a) Training accuracy (b) Training loss, with feature selection (c) Training _Accuracy (d) Training_Loss

Fig. 6 establishes a detailed analysis of the OAOFS-DBNECD method without feature selection. Fig. 6a shows the confusion matrix presented by the OAOFS-DBNECD approach under the training set. The figure signified the OAOFS-DBNECD approach had identified 13522 instances under No Seizure and 13033 samples under Seizure.

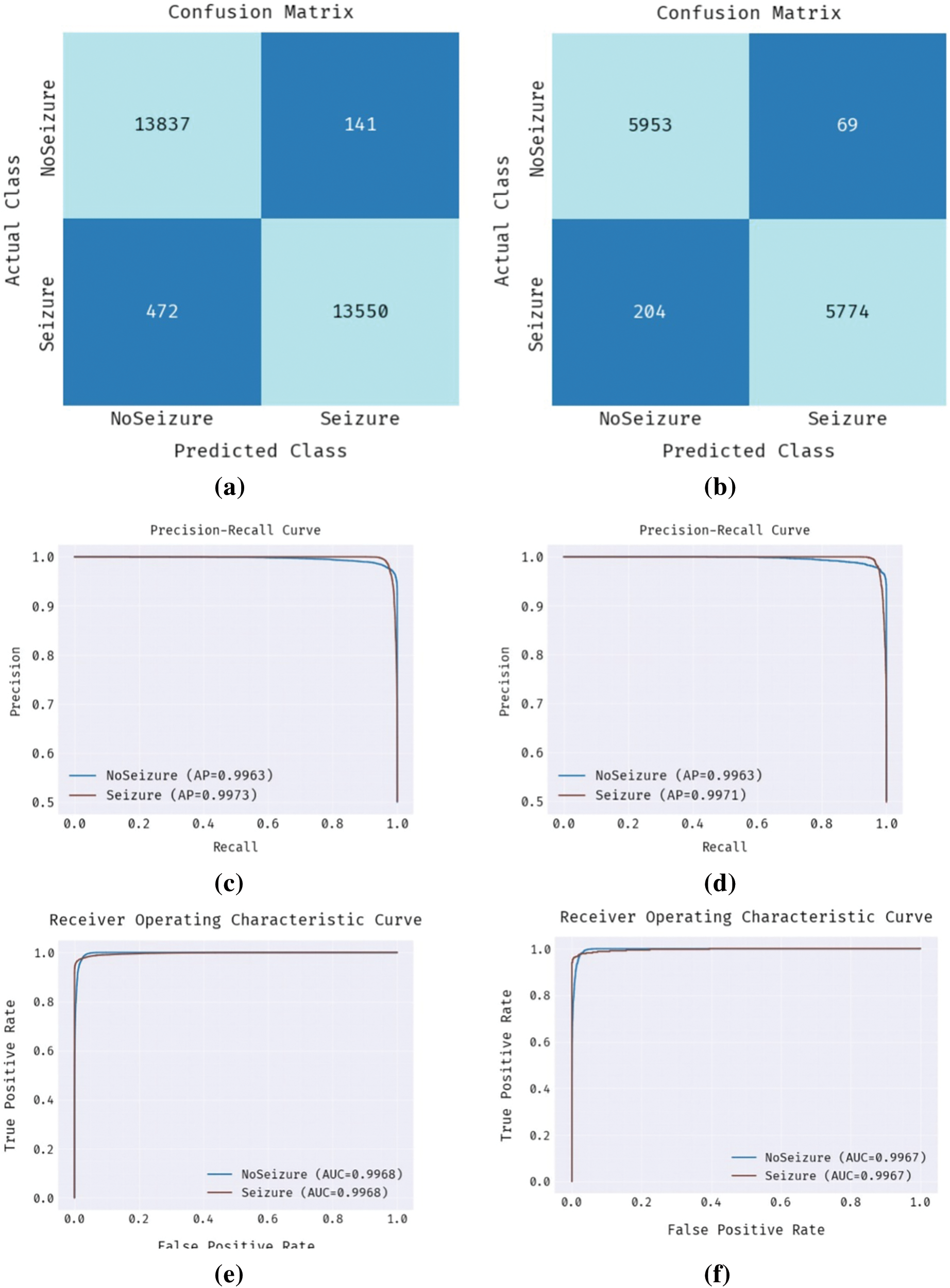
Figure 6: Without feature selection (a) Confusion matrix-training set (b) Confusion matrix-testing set (c) PR-curve-training set (d) PR-curve-testing set (e) ROC-training set (f) ROC-testing set

Likewise, Fig. 6b shows the confusion matrix rendered by OAOFS-DBNECD techniques under the testing set. The figure signified that the OAOFS-DBNECD approach had identified 5852 instances under NoSeizure and 5548 samples under Seizure. Then, Figs. 6c and 6d illustrate the precision-recall analysis of the OAOFS-DBNECD algorithm under the training and testing set. By seeing the figure, it is clear that the OAOFS-DBNECD approach has exhibited maximal precision-recall performance in all classes. Last, Figs. 6e and 6f exemplify the ROC analysis of the OAOFS-DBNECD method in the training and testing set. Maximum ROC values in various class labels showed that the OAOFS-DBNECD method had produced desirable results.

Fig. 7 signifies a comprehensive analysis of the OAOFS-DBNECD methodology under feature selection. Fig. 7a depicts the confusion matrix presented by the OAOFS-DBNECD method under the training set. The figure denoted that the OAOFS-DBNECD technique has identified 13837 instances under NoSeizure and 13550 samples under Seizure. Also, Fig. 7b depicts the confusion matrix provided by the OAOFS-DBNECD algorithm under the testing set. The figure indicated that the OAOFS-DBNECD approach had identified 5953 instances under NoSeizure and 5774 samples under Seizure. Then, Figs. 7c and 7d illustrate the precision-recall analysis of the OAOFS-DBNECD approach under the training and testing set. By seeing the figure, it is clear that the OAOFS-DBNECD approach has established maximal precision-recall performance in all classes. At last, Figs. 7e and 7f exemplify the ROC analysis of the OAOFS-DBNECD algorithm under training and testing. The figure depicted that the OAOFS-DBNECD approach has resulted in practical outcomes with maximal ROC values in different Class labels.

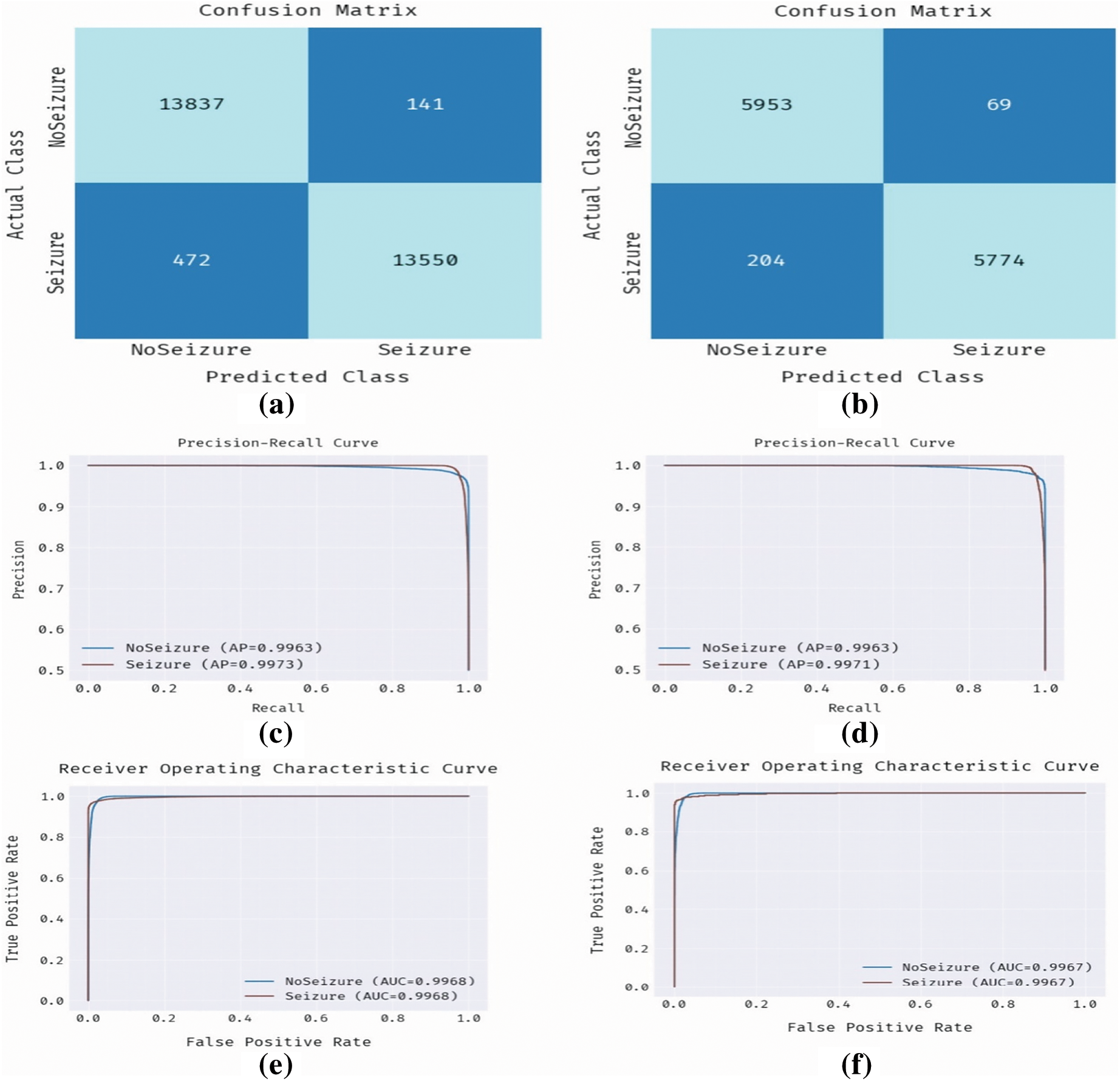
Figure 7: With feature selection training set (a) Confusion matrix-training set (b) Confusion matrix-testing set (c) PR-curve-training set (d) PR-curve-testing set (e) ROC-training set (f) ROC-testing set

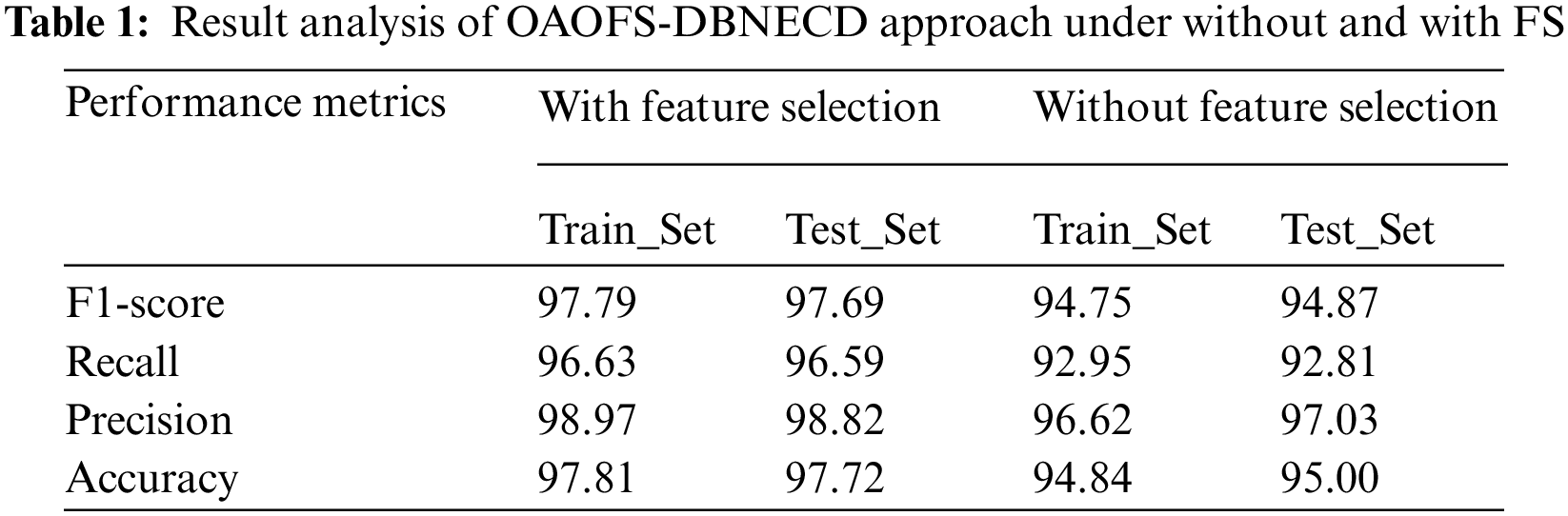
Table 1 provides the overall classification results of the OAOFS-DBNECD model without FS and with FS processes. The OAOFS-DBNECD system has resulted in improved outcomes under both TR and TS sets. For sample, on TR database, the OAOFS-DBNECD technique has attained accuy of 94.84%, precn of 96.62%, recal of 92.95%, and F1_score of 94.75%. Also, on TS data, the OAOFS-DBNECD model has attained accuy of 95%, precn of 97.03%, recal of 92.81%, and F1score of 94.87%. For example, on the TR dataset, the OAOFS-DBNECD approach has reached accuy of 97.81%, precn of 98.97%, recal of 96.63%, and F1score of 97.79%. Similarly, on TS data, the OAOFS-DBNECD technique has reached accuy of 97.72%, precn of 98.82%, recal of 96.59%, and F1score of 97.69%.

A brief comparative study [12] is provided in Table 2 to ensure the enhanced seizure classification outcomes of the OAOFS-DBNECD approach. The results indicated that the SVM and LR models achieved lower accuy of 82.39% and 81.32%, respectively. Additionally, the ResNet-152, Inception-v3, and EESC models have obtained somewhat closer accuy of 90.63%, 91.89%, and 93.92%, correspondingly.

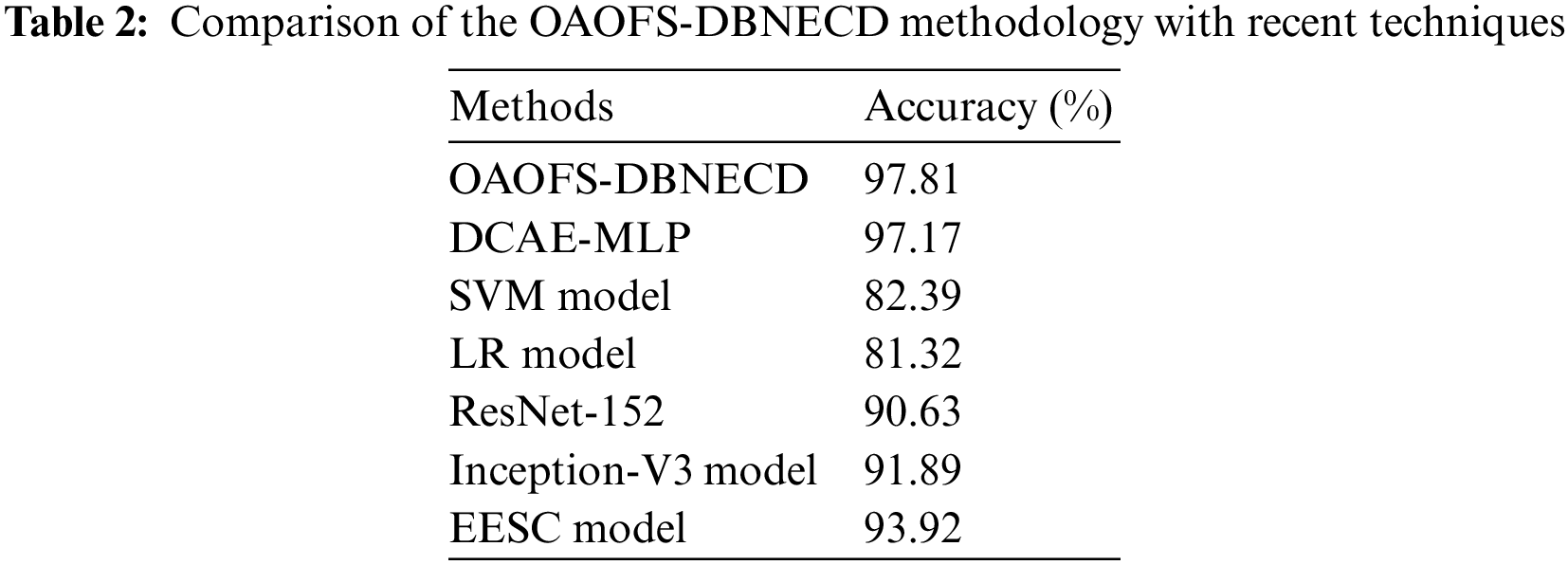
Moreover, the DCAE-MLP model has gained a reasonable accuy of 97.17%. But the presented OAOFS-DBNECD model has shown a maximum accuy of 97.81%. These results affirmed the maximum seizure classification performance on the applied EEG signals. The error rate of the classification is 2.19%.

4.1 Impact of Result

The proposed research OAOFS-DBNECD model has shown maximum accuracy of 97.81%. Based on the results, it is understand that the proposed model confirms the best seizure categorization performance on the used EEG data.

4.2 Limitations

Although we have received 97.81% accuracy over proposed model, still there is a room to improve the accuracy of detection. Since the domain of research is medical, not even single error will lead to big mistakes.

5  Conclusion

In this article, a new OAOFS-DBNECD algorithm was formulated for seizure classification by utilizing EEG signals. The primary objective of the presented OAOFS-DBNECD technique is to categorize and classify the presence of ESs. The proposed OAOFS-DBNECD technique transforms the EEG signals into .csv format at the initial stage. Next, the OAOFS technique selects an optimal subset of features using the pre-processed data. For seizure classification, the presented OAOFS-DBNECD technique utilized AEO with the DBN model for seizure classification purposes. An extensive range of simulations can be accomplished on the benchmark dataset to ensure the enhanced performance of the presented OAOFS-DBNECD approach. The comparison study shows the significant outcomes of the OAOFS-DBNECD technique over other algorithms. The proposed OAOFS-DBNECD model has shown maximum accuracy of 97.81%. These findings confirmed the best seizure categorization performance on the used EEG data. Therefore, in reality, the presented OAOFS-DBNECD technique was utilized for automated seizure classification. Improved classification accuracies from OAOFS-DBNECD may be achieved primarily in the future by deriving a hybrid DL classifier.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. S. Dhull and K. K. Singh, “ESIMD: Epileptic seizure identification using metaheuristic deep learning technique,” Expert Systems, vol. 39, no. 4, pp. 1–15, 2022. [Google Scholar]

2. D. Moldovan, “Crow search algorithm based ensemble of machine learning classifiers for epileptic seizures detection,” in Proc. Int. Conf. on e-Health and Bioengineering (EHB), IEEE, Iasi, Romania, pp. 1–4, 2020. [Google Scholar]

3. N. Darjani and H. Omranpour, “Phase space elliptic density feature for epileptic EEG signals classification using metaheuristic optimization method,” Knowledge-Based Systems, vol. 205, pp. 1–10, 2020. [Google Scholar]

4. A. Malekzadeh, A. Zare, M. Yaghoubi and R. Alizadehsani, “A method for epileptic seizure detection in EEG signals based on tunable q-factor wavelet transform method using grasshopper optimization algorithm with support vector machine classifier,” Internal Medicine Today, vol. 28, no. 1, pp. 98–127, 2021. [Google Scholar]

5. M. Chalaki and H. Omranpour, “Epileptic seizure classification using ConvLSTM deep classifier and rotation short-time Fourier transform,” Journal of Ambient Intelligence and Humanized Computing, vol. Early Acess, pp. 1–17, 2022. [Google Scholar]

6. A. Anuragi, D. S. Sisodia and R. B. Pachori, “Epileptic-seizure classification using phase-space representation of FBSE-EWT based EEG sub-band signals and ensemble learners,” Biomedical Signal Processing and Control, vol. 71, pp. 1–11, 2022. [Google Scholar]

7. V. Patel, J. Tailor and A. Ganatra, “Essentials of predicting epileptic seizures based on EEG using machine learning: A review,” The Open Biomedical Engineering Journal, vol. 15, pp. 1–15, 2021. [Google Scholar]

8. A. Subasi, T. Tuncer, S. Dogan and D. Tanko, “Local binary pattern based feature extraction and machine learning for epileptic seizure prediction and detection,” Modelling and Analysis of Active Biopotential Signals in Healthcare, IOP Publishing, Bristol, England, vol. 2, pp. 1–31, 2020. [Google Scholar]

9. A. Saday and I. A. Ozkan, “Classification of epileptic EEG signals using DWT-based feature extraction and machine learning methods,” International Journal of Applied Mathematics Electronics and Computers, vol. 9, no. 4, pp. 122–129, 2021. [Google Scholar]

10. A. Humairani, B. S. Atmojo, I. Wijayanto and S. Hadiyoso, “Fractal based feature extraction method for epileptic seizure detection in long-term EEG recording,” in Proc. of the Journal of Physics: Conf. Series, IOP Publishing, Yogyakarta, Indonesia, vol. 1844, no. 1, pp. 1–11, 2021. [Google Scholar]

11. S. M. Usman, S. Khalid and S. Bashir, “A deep learning based ensemble learning method for epileptic seizure prediction,” Computers in Biology and Medicine, vol. 136, pp. 104710, 2021. [Google Scholar]

12. A. M. Hilal, A. A. Albraikan, S. Dhahbi, M. K. Nour, A. Mohamed et al., “Intelligentepileptic seizure detection and classification model using optimal deep canonical sparse autoencoder,” Biology, vol. 11, no. 8, pp. 1–18, 2022. [Google Scholar]

13. A. M. Anter, M. Abd Elaziz and Z. Zhang, “Real-time epileptic seizure recognition using Bayesian genetic whale optimizer and adaptive machine learning,” Future Generation Computer Systems, vol. 127, pp. 426–434, 2022. [Google Scholar]

14. P. Divya and B. A. Devi, “Hybrid metaheuristic algorithm enhanced support vector machine for epileptic seizure detection,” Biomedical Signal Processing and Control, vol. 78, pp. 1–19, 2022. [Google Scholar]

15. V. Bhandari and D. H. Manjaiah, “Improved ensemble learning model with optimal feature selection for automated epileptic seizure detection,” Computer Methods in Biomechanics and Biomedical Engineering: Imaging & Visualization, vol. Early Acess, pp. 1–31, 2022. [Google Scholar]

16. E. Tuncer and E. D. Bolat, “Classification of epileptic seizures from electroencephalogram (EEG) data using bidirectional short-term memory (Bi-LSTM) network architecture,” Biomedical Signal Processing and Control, vol. 73, pp. 1–10, 2022. [Google Scholar]

17. B. Kapoor and B. Nagpal, “Hybrid cuckoo finch optimization based machine learning classifier for seizure prediction using EEG signals in IoT network,” Research Square, vol. preprint, pp. 1–28, 2022. [Google Scholar]

18. C. h. Srikanth and R. Kayalvizhi, “A review on EEG based epileptic seizures detection using deep learning techniques,” in Proc. of the 4th Int. Conf. on Smart Systems and Inventive Technology (ICSSIT), IEEE, Tirunelveli, India, pp. 966–973, 2022. [Google Scholar]

19. Y. Zhang, S. Yao, R. Yang, X. Liu, W. Qiu et al., “Epileptic seizure detection based on bidirectional gated recurrent unit network,” IEEE Transactions on Neural Systems and Rehabilitation Engineering, vol. 30, pp. 135–145, 2022. [Google Scholar] [PubMed]

20. Y. Guo, X. Jiang, L. Tao, L. Meng, C. Dai et al., “Epileptic seizure detection by cascading isolation forest-based anomaly screening and easy ensemble,” Transactions on Neural Systems and Rehabilitation Engineering, IEEE, vol. 30, pp. 915–924, 2022. [Google Scholar]

21. Y. Xiong, F. Dong, D. Wu, L. Jiang, J. Liu et al., “Seizure detection based on improved genetic algorithm optimized multilayer network,” IEEE Access, vol. 10, pp. 81343–81354, 2022. [Google Scholar]

22. L. Duan, Z. Wang, Y. Qiao, Y. Wang, Z. Huang et al., “An automatic method for epileptic seizure detection based on deep metric learning,” Journal of Biomedical and Health Informatics, IEEE, vol. 26, no. 5, pp. 2147–2157, 2021. [Google Scholar]

23. D. Sopic, T. Teijeiro, D. Atienza, A. Aminifar and P. Ryvlin, “Personalized seizure signature: An interpretable approach to false alarm reduction for long-term epileptic seizure detection,” Epilepsia, vol. Early Acess, pp. 1–11, 2022. [Google Scholar]

24. Y. Zhao, G. Zhang, C. Dong, Q. Yuan, F. Xu et al., “Graph attention network with focal loss for seizure detection on electroencephalography signals,” International Journal of Neural Systems, vol. 31, no. 7, pp. 1–14, 2021. [Google Scholar]

25. A. Anuragi, D. S. Sisodia and R. B. Pachori, “Automated FBSE-EWT based learning framework for detection of epileptic seizures using time-segmented EEG signals,” Computers in Biology and Medicine, vol. 136, pp. 1–16, 2021. [Google Scholar]

26. Y. Zhao, C. Dong, G. Zhang, Y. Wang, X. Chen et al., “EEG-Based seizure detection using linear graph convolution network with focal loss,” Computer Methods and Programs in Biomedicine, vol. 208, pp. 1–8, 2021. [Google Scholar]

27. N. Ke, T. Lin and Z. Lin, “Channel-weighted squeeze-and-excitation networks for epileptic seizure detection,” in Proc. of the 33rd Int. Conf. on Tools with Artificial Intelligence (ICTAI), Washington, USA, pp. 666–673, 2021. [Google Scholar]

28. S. Ramakrishnan, A. M. Murugavel, P. Sathiyamurthi and J. Ramprasath, “Seizure detection with local binary pattern and CNN classifier,” in Proc. of the Journal of Physics: Conf. Series, IOP Publishing, Washington, USA, vol. 1767, no. 1, pp. 1–12, 2021. [Google Scholar]

29. O. Kaziha and T. Bonny, “A convolutional neural network for seizure detection,” in Proc. of the 2020 Advances in Science and Engineering Technology Int. Conf. (ASET), Dubai, United Arab Emirates, pp. 1–5, 2020. [Google Scholar]

30. Z. Chen, G. Lu, Z. Xie and W. Shang, “A unified framework and method for EEG-based early epileptic seizure detection and epilepsy diagnosis,” IEEE Access, vol. 8, pp. 20080–20092, 2020. [Google Scholar]

31. I. B. Slimen, L. Boubchir, Z. Mbarki and H. Seddik, “EEG epileptic seizure detection and classification based on dual-tree complex wavelet transform and machine learning algorithms,” Journal of Biomedical Research, vol. 34, no. 3, pp. 151–161, 2020. [Google Scholar] [PubMed]

32. M. Zabihi, S. Kiranyaz, V. Jäntti, T. Lipping and M. Gabbouj, “Patient-specific seizure detection using nonlinear dynamics and nullclines,” IEEE Journal of Biomedical and Health Informatics, vol. 24, no. 2, pp. 543–555, 2019. [Google Scholar] [PubMed]

33. A. Q. Ansari, P. Sharma and M. Tripathi, “Automatic seizure detection using neutrosophic classifier,” Physical and Engineering Sciences in Medicine, vol. 43, no. 3, pp. 1019–1028, 2020. [Google Scholar] [PubMed]

34. P. Z. Yan, F. Wang, N. Kwok, B. B. Allen, S. Keros et al., “Automated spectrographic seizure detection using convolutional neural networks,” Seizure, vol. 71, pp. 124–131, 2019. [Google Scholar] [PubMed]

35. P. Boonyakitanont, A. Lek-uthai, K. Chomtho and J. Songsiri, “A comparison of deep neural networks for seizure detection in EEG signals,” bioRxiv, Vol. First Online, pp. 1–6, 2019. [Google Scholar]

36. C. Huang, W. Chen and G. Cao, “Automatic epileptic seizure detection via attention-based CNN-BiRNN,” in Proc. Int. Conf. on Bioinformatics and Biomedicine (BIBM), IEEE, San Diego, CA, USA, pp. 660–663, 2019. [Google Scholar]

37. A. Nandy, M. A. Alahe, S. N. Uddin, S. Alam, A. A. Nahid et al., “Feature extraction and classification of EEG signals for seizure detection,” in Proc. of the Int. Conf. on Robotics, Electrical and Signal Processing Techniques (ICREST), IEEE, Dhaka, Bangladesh, pp. 480–485, 2019. [Google Scholar]

38. R. S. Selvakumari, M. Mahalakshmi and P. Prashalee, “Patient-specific seizure detection method using hybrid classifier with optimized electrodes,” Journal of Medical Systems, vol. 43, no. 5, pp. 1–7, 2019. [Google Scholar]

39. L. Abualigah, D. Yousri, M. Abd Elaziz, A. A. Ewees, M. A. Al-Qaness et al., “Aquila optimizer: A novel meta-heuristic optimization algorithm,” Computers and Industrial Engineering, vol. 157, pp. 1–37, 2021. [Google Scholar]

40. S. Mahajan, L. Abualigah, A. K. Pandit and M. Altalhi, “Hybrid aquila optimizer with arithmetic optimization algorithm for global optimization tasks,” Soft Computing, vol. 26, no. 10, pp. 4863–4881, 2021. [Google Scholar]

41. A. Kumar and G. Shankar, “Dynamic stability enhancement of TCSC-based tidal power generation using quasi-oppositional harmony search algorithm,” IET Generation, Transmission & Distribution, vol. 12, no. 10, pp. 2288–2298, 2018. [Google Scholar]

42. J. Chen, X. Zhang, Y. Cheng and N. Xi, “Surface EMG based continuous estimation of human lower limb joint angles by using deep belief networks,” Biomedical Signal Processing and Control, vol. 40, pp. 335–342, 2018. [Google Scholar]

43. R. M. Rizk-Allah and A. A. El-Fergany, “Artificial ecosystem optimizer for parameters identification of proton exchange membrane fuel cells mode,” International Journal of Hydrogen Energy, vol. 46, no. 75, pp. 37612–37627, 2021. [Google Scholar]

44. A. Goldberger, L. Amaral, L. Glass, J. Hausdorff, P. C. Ivanov et al., “Physio bank, PhysioToolkit, and PhysioNet: Components of a new research resource for complex physiologic signals,” Circulation, vol. 101, no. 23, pp. 215–220, 2000. [Google Scholar]

45. B. Deepa and K. Ramesh, “Epileptic seizure detection using deep learning through min max scaler normalization,” International Journal of Health Sciences, vol. 6, no. S1, pp. 10981–10996, 2022. [Google Scholar]