Subspace Clustering in High-Dimensional Data Streams: A Systematic Literature Review

1  Introduction

The digital revolution has resulted in a continuous stream of data arriving sequentially from sensors and devices at time-varying intervals. In practice, many data stream mining applications deal with unlabeled streaming data because there are few true class labels and the number of classes is often unknown [1]. Moreover, obtaining the labels requires expert knowledge, making it time-consuming and expensive, and in certain cases is not possible at all. Clustering can be considered as a concise model when specific labeled information is not available. Clustering groups related objects in such a way that members of the same cluster are more similar to each other than members of different clusters. Clustering is particularly difficult in the high-dimensional scenario because the behavior of features varies greatly across different parts of the data. A data object is considered high-dimensional if it contains ten or more features [2,3]. When clustering high-dimensional data, the distance between two objects becomes more and more similar across all dimensions until all objects are equidistant and no proper clusters can be formed. This problem, known as the “curse of dimensionality”, causes distance or density-based conventional clustering algorithms to fail to accurately compute the similarity between objects. The “curse of dimensionality” can be viewed from two aspects. First, not all features contribute to the definition of a cluster. Traditional clustering algorithms perform clustering in a full-dimensional space; therefore, the presence of irrelevant features complicates the similarity calculation during the clustering process. Second, the subsets of features that define one cluster may be different from those that define another. For this reason, a global feature reduction approach may not be able to find a subspace that includes all clusters in the dataset. These problems can be solved by using subspace clustering, which can identify meaningful clusters in subspaces formed by different combinations of features. Conventional subspace clustering algorithms are suitable for static environments where the size of data is known, and the discovered patterns do not change. However, the constant arrival of data streams from different dynamic systems further complicate subspace clustering in high-dimensional data. Data streams have several special properties that exceed the capabilities of a typical subspace clustering algorithm designed for static data sets. They are continuous and potentially unbounded. Therefore, it is impossible to keep the entire data stream in main memory. A common approach to overcome this limitation is to store information about the data streams in compact form using synopsis structures. Unlike static data, data streams evolve, leading to changes in the corresponding data model over time. This phenomenon is known in the literature as concept drift, where a clustering model created at time t may be obsolete at time t + δ, leading to poor performance on the new data [4]. A data stream clustering algorithm typically includes a cluster maintenance mechanism to manage these changes. The characteristics of data streams require a subspace clustering algorithm capable of handling high-dimensional data and adapting to the unbounded and evolving nature of data streams.

Several authors have contributed to the literature reviews on data stream clustering. Recent reviews include Zubaroğlu et al. [1], who compared the basic clustering techniques, computational complexity, and accuracy of several recent algorithms for data stream clustering. Fahy et al. [5] studied techniques for handling changes in data streams with limited labels, including clustering. Bahri et al. [6] thoroughly investigated the basic algorithms for various data stream mining tasks, including clustering. Tareq et al. [7] conducted a systematic literature review on density and grid-based algorithms for clustering data streams by identifying their strengths and weaknesses and investigating how these algorithms address the problems of evolving data streams. Al-Khamees et al. [8] classified data stream clustering algorithms into five categories: Partition-based, Hierarchical-based, Grid-based, Density-based, and Model-based. Batool et al. [9] focused on clustering algorithms that can handle evolving data streams, while Mahdi et al. [10] compared clustering algorithms for large data sets. Mansalis et al. [11] studied state-of-the-art algorithms for clustering data streams and evaluated their performance for different datasets and parameter settings. Carnein et al. [12] provided a very detailed survey of algorithms for clustering data streams, while several other articles [13–15] studied algorithms for clustering data streams specifically for grid and density-based approaches. A few articles [11–12,14,16] discussed algorithms for dealing with high-dimensional data streams. However, the explanations are brief, and no article explicitly focused on how to perform clustering in high-dimensional data streams. Although [17–20] have published surveys on clustering high-dimensional data, these articles do not focus on data streams. Due to the lack of systematic reviews on clustering of high-dimensional data streams, this article conducts a literature review that focuses on clustering in high-dimensional data streams and fills the gaps of previous reviews. This article contributes to finding, evaluating, and interpreting existing research on subspace clustering algorithms for high-dimensional data streams. The work provides a detailed description of clustering methods, subspace clustering approaches, synopsis structures, cluster maintenance mechanisms, and a discussion of the essential elements in this research area that form the basis for future research. This article uses a systematic methodology to review the literature. Section 2 defines the research questions and describes the review processes. Section 3 provides a detailed description of the findings, which are divided into general and main findings that address the research questions. Section 4 interprets the findings, while Section 5 concludes the article with recommendations for future research.

2  Methodology

In this article, we adopted the Preferred Reporting Items for Systematic reviews and Meta-Analyses (PRISMA) method [21], an established standard for reporting systematic reviews and meta-analyses. The PRISMA method consists of four phases: identification, screening, eligibility, and inclusion. The identification phase identifies the keywords used in the extraction of records from academic research databases. The selected keywords are usually synonyms related to the topic of interest and are combined with Boolean operators. Once the keywords are identified, the next step is to search and merge records from multiple databases. Since records may appear in multiple databases, duplicates can be removed using an appropriate software. In the screening phase, records are narrowed down by establishing inclusion and exclusion criteria. Criteria may include year, country, study area, publication type, and language, which can be filtered during the database search. In the eligibility phase, the number of datasets is further reduced by performing a quality assessment for each dataset. This process is illustrated in Fig. 1 and aims to answer the following research questions: 1) How is subspace clustering performed in the high-dimensional data streams? and 2) How are the unbounded and evolving characteristics handled in the high-dimensional data streams?

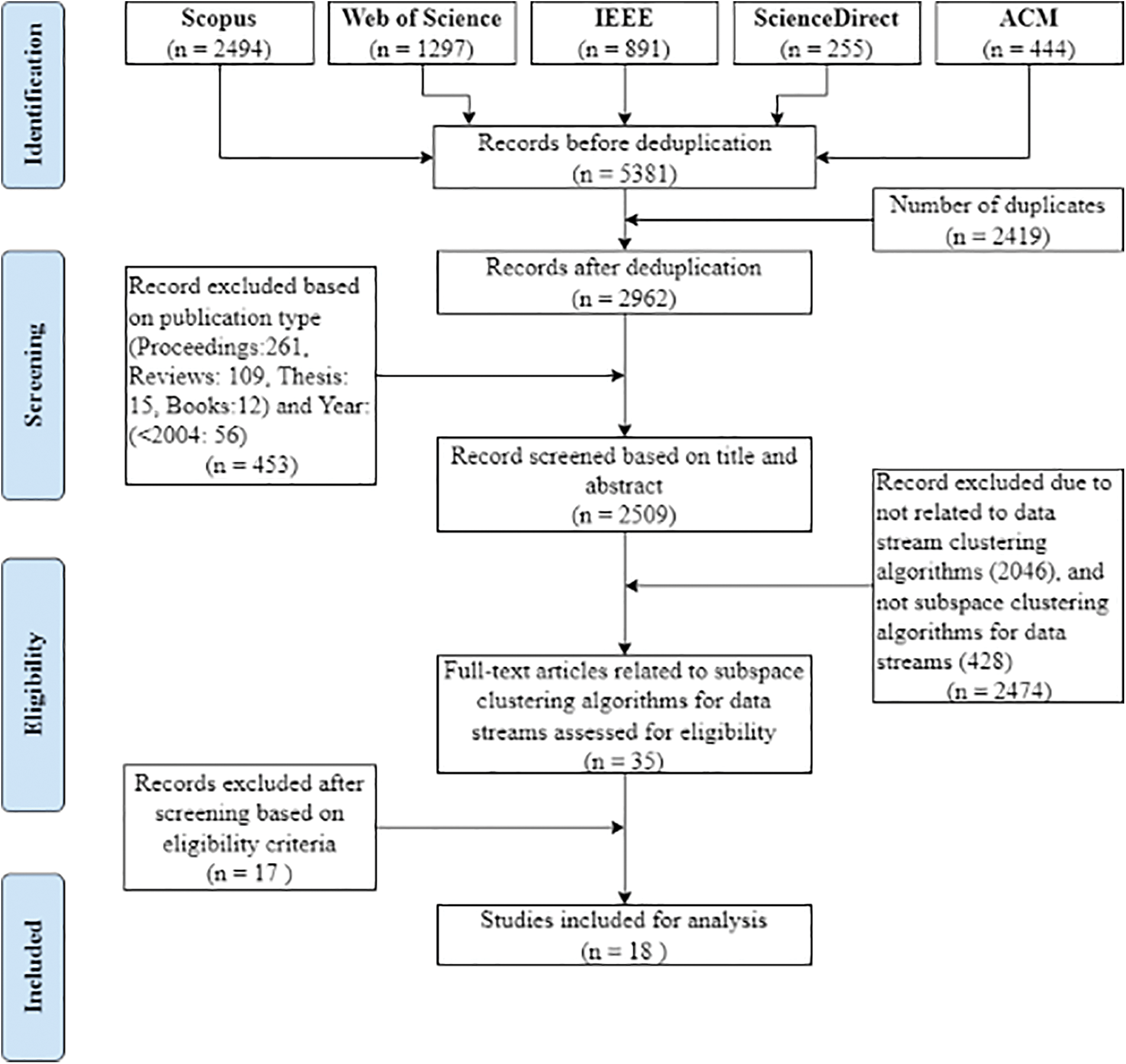
Figure 1: Systematic review process of subspace clustering algorithms for high-dimensional data streams

2.1 Identification

The initial review was conducted in July 2021 and revisited in July 2022 to incorporate the most recent and relevant research. Five major databases were selected for this review: Scopus, Web of Science, Institute of Electrical and Electronics Engineers (IEEE), ScienceDirect, and Association for Computing Machinery (ACM). After all relevant keywords were considered, search terms were developed based on two keywords: “data stream” and “clustering”. These keywords were selected for two reasons: 1) the article is limited to data streams and clustering as a primary data type and data mining approach.; 2) since high-dimensional clustering of data streams is a subset of data stream clustering, a broader search was conducted to increase the likelihood of finding relevant articles. Therefore, the Boolean operators ‘AND’ and a wildcard containing the keywords were used in the search for relevant articles based on the title, abstract, or keyword. As a result, 5381 articles were retrieved from all databases: Scopus (2494), Web of Science (1297), IEEE (891), ScienceDirect (255), and ACM (444). The article list was downloaded from the respective databases in ‘.bib’, ‘.enw’ and ‘.ris’ formats.

2.2 Screening

The deduplication process was performed automatically using Rayyan, a web-based platform for systematic reviews, and manually using Microsoft Excel. Of the 5381 articles, 2419 were found to be identical and subsequently removed. A total of 2962 articles were screened using several inclusion and exclusion criteria. The first criterion was the type of literature. We focused on peer-reviewed journal and conference articles and excluded articles in the form of systematic reviews, surveys, workshop reports, technical reports, books, and dissertations. We also focused only on articles published in English. In addition, a time period of 18 years (2005–2022) was chosen for the timeline. According to Kraus et al. [22], researchers can rely on the concept of maturity of a study to determine the best range of publication for their review. They explained that for a mature study, where a good number of articles can be tracked, the timeframe for publication could be shorter than that for a less mature study. They further explained that for a less mature study, a longer publication timeframe is needed because there are a limited number of articles and many research questions are still unanswered. In our review, a shorter publication timeframe resulted in very few articles that were relevant to our scope of study, making them insufficient for analysis. In our selected timeline, important articles are the predecessors of many subsequent algorithms and therefore have an important methodological concept for our analysis. A total of 453 articles were excluded based on these criteria. Then, the remaining articles were screened based on their title and abstract. This removed 2046 articles that were not related to data stream clustering and 428 articles that were not related to subspace clustering algorithms for high-dimensional data streams. Thus, the screening left us with 35 articles eligible for quality evaluation.

2.3 Eligibility

The quality of the 35 articles was evaluated based on three criteria: 1) Is there a clear description of the subspace clustering process?; 2) Is there a clear synopsis structure to handle the unbounded constraint of data streams?; and 3) Is there a clear description of the cluster maintenance mechanism to handle evolving data streams? Next, the full texts were analyzed to identify articles with detailed descriptions of the clustering process, synopsis structure, and cluster maintenance mechanism. As a result, 17 articles were excluded, leaving 18 articles for analysis.

3  Results

3.1 General Findings

The inclusion phase yielded a total of 18 articles for synthesis. About 33% of these were journal articles, while the rest were published in conference proceedings. The general findings of these articles are presented in Table 1 in terms of experimental datasets, parameters, and evaluation metrics. Aggarwal et al. [23] introduced a partition-based algorithm that establishes subspace clustering for high-dimensional data streams. The algorithm stores the cluster synopsis in a fading cluster structure and the significant dimensions in a dimensional bit vector. It outperforms previous clustering algorithms by its clustering quality and efficiency. However, the dimensional bit vector assigns equal non-zero weights to cluster dimensions and zero weights to non-cluster dimensions, which is insufficient for tracking the evolution of data streams. Therefore, Ren et al. [24] proposed a dimensional weight matrix that assigns a different non-zero weight to each dimension associated with a cluster. Meanwhile, Liu et al. [25] and Ren et al. [26] adapted the synopsis structure of Aggarwal et al. [23] by using an exponential histogram of the cluster feature to store the distribution of data points and capture the evolution of each cluster. Similarly, Chairukwattana et al. [27] adopted the dimensional bit vector of Aggarwal et al. [23] to support high-dimensional clustering in evolution-based algorithms for clustering data streams. Subsequently, Waiyamai et al. [28] proposed discriminative dimension selection to identify the most significant and distinguishable dimensions for each cluster, while Waiyamai et al. [29] improved their cluster splitting process by using background or domain knowledge. Most of these algorithms are sensitive to the predefined average number of dimensions and clusters and prefer spherical clusters that can be confounded with noise and outliers.

In a prior work, Ntoutsi et al. [30] pioneered a density-based subspace clustering algorithm for high-dimensional data streams that can find arbitrarily shaped clusters and does not require a predefined number of clusters. The algorithm stores the cluster synopsis in a projected micro-cluster and the significant dimensions in a dimension preference vector. The synopsis structure of the algorithm is improved in Ahmed et al. [31] by using exponential moving averages to reduce the memory size and speed up the clustering process. Meanwhile, the work of Hassani et al. [32] focused on the optimization of the algorithm, while Huang et al. [33] proposed an Euler kernel function as a new similarity metric to reduce the sensitivity to outliers. Lu et al. [34] established a grid-based subspace clustering algorithm that can also find clusters of arbitrary shapes. The algorithm uses a grid structure to cluster incoming data streams and analyze the data distribution of each dimension for subspace construction. The algorithm produces clusters that lie in the same subspace. Therefore, a recursive region partition technique is proposed in Sun et al. [35] to find clusters in different subspaces. The synopsis structure of Lu et al. [34] is also improved by Wang et al. [36], Zhang et al. [37], and Ren et al. [38] to provide quick access to cluster information. In contrast to other works that cluster in the axis-parallel subspace, Borutta et al. [39] and Borutta et al. [40] performed high-dimensional clustering in an arbitrarily oriented subspace.

The algorithms in Table 1 were tested on several real-world datasets, selecting only numerical attributes. The Knowledge Discovery and Data Mining Competition 1999 (KDDCUP’99) network intrusion dataset addresses the cyberattack detection problem and includes 494,020 connection records with 42 attributes. Each record is labeled as either a normal connection or an intrusion. The Forest Cover Type dataset corresponds to the forest cover type prediction problem with 591,012 records and 54 attributes. Each record is labeled as a class of forest cover. Knowledge Discovery and Data Mining Competition 1998 (KDDCUP’98) Charitable Donation refers to a direct marketing campaign with 191,779 records and 481 attributes. Each record is labeled either as a donor or otherwise, as a result of the marketing campaign. The clustering quality is evaluated using several metrics: accuracy, cross-entropy, purity, f-measure, normalized mutual information, precision, recall, adjusted Rand index, and adjusted mutual information. Clustering efficiency is evaluated based on algorithm runtime and memory usage.

3.2 Main Findings

3.2.1 Subspace Clustering Process in High-Dimensional Data Streams

When performing subspace clustering, an infinite number of subspaces may exist, so testing all possible subspaces is computationally infeasible. Therefore, the usual assumption in subspace clustering over static data is to restrict the search space to either an axis-parallel subspace or an arbitrarily oriented subspace. In the axis-parallel subspace, the cluster points form an axis-parallel hyperplane in which they are widely scattered along the irrelevant axes but densely clustered along the relevant features. The method for finding axis-parallel clusters can be divided into top-down and bottom-up approaches. In the top-down approach, the subspace of the cluster is defined starting from the full-dimensional space. The bottom-up approach identifies the subspaces that contain clusters by starting with all one-dimensional subspaces that contain at least one cluster. In an arbitrarily oriented subspace, the points with correlated features are distributed along an orthogonal hyperplane on which they are closely aligned regardless of the variance of the correlated features. Algorithms capable of discovering arbitrarily oriented correlated clusters can be classified as Principal Component Analysis (PCA) or Hough transform algorithms. PCA-based clustering algorithms use PCA to detect low-dimensional subspaces defined by correlations between attributes. Hough transform-based clustering algorithms do not rely on the locality assumption, and thus can be used for global subspace clustering [3,18,40].

Subspace clustering algorithms for high-dimensional data streams can be similarly categorized according to the above concept. High-Dimensional Projected Stream Algorithm (HPStream) [23] finds clusters in an axis-parallel subspace by adopting a top-down approach. At the beginning of the clustering process, the data points are normalized to equalize the standard deviation of each dimension. From an initial sample, a set of initial clusters is created based on k-means clustering and assigned to the dimensions in which they have the smallest radius. The cluster assignment is then updated by considering only the dimensions associated with each cluster. This is repeated until both the clusters and the dimensions converge. Each cluster statistic is stored in the form of a fading cluster structure and its projected dimensions are stored in a d-dimensional bit vector. At each new data point, the projected dimensions for each cluster are updated and the distance between each cluster centroid and the new data point is calculated using only the appropriate set of projected dimensions. If the new data point is within the boundary radius of the cluster, it is assigned to the corresponding cluster, otherwise it is assigned to a new cluster. Periodically, when the number of clusters reaches a maximum value or their timestamp exceeds the last N observed timestamps, the oldest cluster with the least recent update is removed. The standard deviation of each dimension is also recalculated, and the corresponding cluster statistics are modified. Similar procedures are adopted by Weighted Subspace Clustering Algorithm for High-Dimensional Data Stream (WSCStream) [24] and High-Dimensional Data Stream Clustering Algorithm over Sliding Window (HSWStream) [25] with corresponding improvements to the dimension selection method and synopsis structure.

Likewise, Evolution-based Clustering Algorithm of High-Dimensional Data Streams (SE-Stream) [27] uses the dimension selection method of HPStream [23] and a hierarchical approach to form clusters. The algorithm initially treats the data points as isolated clusters and forms an active cluster once a sufficiently dense region is present. A cluster is considered active if the weight is greater than or equal to a predefined threshold. Then, a dimensional projection is performed on the active cluster and the cluster synopsis is stored in a fading cluster structure with a histogram. When a data point arrives, it is assigned to the nearest cluster if the radius of the new data point is smaller than a predefined threshold; otherwise, it is an isolated data point. All existing clusters whose weight is lower than a predefined threshold are deleted. Additionally, a cluster is split if the data distribution is different. A dimensional projection is performed again when a cluster is divided, or a new cluster is created. If the number of clusters exceeds the threshold, the closest pair of clusters is merged. Evolution-based Clustering of High-Dimensional Data Streams using Discriminative Dimension Algorithm (SED-Stream) [28] and Evolution-based Clustering of High-Dimensional Data Streams using Constraint-based Discriminative Dimension Algorithm (SEDC-Stream) [29] use similar hierarchical approaches with corresponding improvements to the dimension selection method and cluster splitting mechanism.

Density-based Projected Clustering Algorithm over High-Dimensional Data Streams (HDDStream) [30] also uses a top-down approach to find clusters in an axis-parallel subspace. It initializes clusters from a collection of points based on the previous conventional algorithm by computing the subspace preference vector of each density-connected set of points to generate potential projected micro-clusters. The new data point is temporarily added to each micro-cluster, and its new projected subspaces are calculated. The new data point is assigned to the nearest micro-cluster with a radius below the maximum radius threshold; otherwise, a new outlier micro-cluster is created, and vice versa. A projected micro-cluster is demoted to an outlier micro-cluster if it exceeds the dimensionality threshold, or its weight is below the weight threshold. When a clustering request arrives, an offline procedure is applied to the micro-clusters. High-Dimensional and High-Speed Data Streams Algorithm (HSDStream) [31], Density-Based Projected Clustering Algorithm of Data Streams (PreDeConStream) [32] and High-Dimensional Stream Clustering Algorithm using Euler Kernel (HEStream) [33] adapt similar clustering processes with corresponding improvements to the synopsis structure, optimization method, and similarity metric.

In contrast, Grid-based Clustering Algorithm for High-dimensional Data Streams (GCHDS) [34] performs subspace clustering based on a bottom-up approach in an axis-parallel subspace. It starts by constructing a uniformly partitioned initial grid structure from a set of data points, where each grid cell contains a list of statistical parameters. A new data point is assigned to the nearest cell; otherwise, the grid cell is expanded to accommodate the new data point. After some time, all data in the grid structure are faded by a fading factor. When a clustering request arrives, the distribution of each dimension is analyzed and only the significant dimensions are selected for clustering. Each cell in the grid structure is projected onto the selected subspace, and connected cells are called clusters. A fading function is used to eliminate the influence of old data. Grid-based Subspace Clustering Algorithm for High-dimensional Data Streams (GSCDS) [35] applies a similar procedure to improve subspace identification. Subspace Clustering Algorithm of High-Dimensional Online Data Streams (SOStream) [36] divides each dimension of the data space into grid intervals, with each unit classified as potentially dense or insignificant. A monitoring lattice structure is used to hold all possible dense units in a prefix-tree lattice structure. When a new data point is received, the associated node is updated and a new unit with a high probability of becoming a dense unit is determined. When the size of the monitoring lattice reaches a predefined threshold, pruning operations are performed at regular intervals. When a new clustering request is received, the Apriori principle determines the subspaces that contain clusters. Subspace Partition Clustering Algorithm for High-Dimensional Data Streams (SPDStream) [37] extends SOStream [36] by classifying each unit as dense, potentially dense, or adjacent and keeping all non-empty units in a CD-Tree lattice. High-dimensional Dense Grid Tree for Clustering High-Dimensional Data Streams Algorithm (HGStream) [38] is also an extension of SOStream [36] that finds dense units based on a grid density threshold and maintains all non-empty units in an HDG-Tree lattice. Moreover, Density-based Data Streams Subspace Clustering Algorithm over Weighted Sliding Windows (SDSStream) [26] uses a preceding conventional algorithm in its initialization stage to generate potential and outlier micro-clusters in the form of an exponential histogram of cluster features. Incoming data points are assigned to the nearest or new micro-clusters. When a clustering request arrives, the conventional algorithm is applied to the potential micro-clusters to obtain the final clustering result.

PCA-based Correlation Clustering Algorithm for Data Streams (CorrStream) [39] and Clustering Algorithm in Arbitrary Subspaces based on the Hough Transform for Data Streams (CashStream) [40] perform clustering in an arbitrarily oriented subspace based on the Hough transform and PCA. CorrStream [39] is a hybrid of partition and density-based clustering algorithms that forms micro-clusters from a set of initial data points using two distance measures, Euclidean and correlation distance. The eigenvector of each micro-cluster is initialized based on PCA, resulting in the dimensionality of the subspace for each micro-cluster. When a new data point arrives, it is assigned to its nearest micro-cluster. Otherwise, a new micro-cluster is created, and updated or new eigenvectors are generated. A cluster model describing the correlation subspaces is created when there is a request for final clustering based on a density-based correlation cluster model. CashStream [40] is a grid-based clustering algorithm that converts a batch of objects from the data space into a Hough space to identify intersections of a given set of object functions. The Hough space is divided into grid cells and searched for dense regions. Clusters are represented as dense regions in the subspace, and the object functions that form the clusters are transformed back into the data space to identify subspace clusters in lower dimensions. Information about the clusters is stored in a synopsis structure called Concept. Once a new Concept is created, the importance score of all existing Concepts is recalculated using a weighting factor. The existing Concepts are then merged if they are identical in terms of similarity to the newly created Concept.

3.2.2 Synopsis Structure and Cluster Maintenance Mechanism in High-Dimensional Data Streams

The development of appropriate synopsis structures for storing statistical summaries of data streams is a crucial step in developing algorithms for clustering data streams, especially considering that data stream applications involve unbounded constraints. Since it is impractical to store the entire data stream in memory, special synopsis structures must be used to summarize the data stream. Synopsis structures for subspace clustering algorithms in high-dimensional data streams include the fading cluster structure (FCS) [22,23,31], the fading temporal cluster feature (FTCF) [24,25], the fading cluster structure with histogram (FCH) [26–28], the projected micro-cluster (PMC) [30], exponential moving average micro-cluster (EAMC) [31], shared nearest-neighbour projection micro-cluster (SNN-PMC) [33], grid structure (GS) [33,34], monitoring lattice (ML) [36], CD-Tree lattice (CDTL) [37], HDG-Tree lattice (HDGTL) [38], micro-cluster (CCMicro) [39] and Concept [40]. These synopsis structures can be divided into two main categories: micro-cluster and grid structure. The FCS is a micro-cluster that consists of a condensed representation of the cluster’s statistics. It integrates historical and current data with a user-defined fading factor that can perform updates and temporarily remove outdated data. Given a set of d-dimensional points 𝒞={Xi1… Xin} at time t with timestamps Ti1… Tin, the FCS is a (2.d + 1) tuple defined as follows:

ℱ𝒞(𝒞, t)=(FC2x(𝒞, t)¯, FC1x(𝒞, t)¯, W(t))(1)

where the FC2x(𝒞, t)¯ and FC1x(𝒞, t) ¯ are vectors with d entries. For each dimension j, FC2x(𝒞, t)¯ is the weighted sum of squares of the corresponding data values in that dimension. The j-th entry of FC2x(𝒞, t)¯ is equal to ∑k=1nf(t− Tik).(xikj)2. For each dimension j, FC1x(𝒞, t) ¯ is the weighted sum of the corresponding data values in that dimension. The j-th entry of FC1x(𝒞, t)¯ is equal to ∑k=1nf(t− Tik).(xikj). W(t) is a single entry of the sum of all weights of the data points at time t, where W(t) is equal to ∑k=1nf(t− Tik). The FCS has additivity and temporal multiplicity properties where the additive property specifies the union of two cluster structures, 𝒞1 ∪𝒞2 by ℱ𝒞(𝒞1 ∪𝒞2, t)= ℱ𝒞(𝒞1, t)+ ℱ𝒞(𝒞2, t). The temporal multiplicity specifies the cluster structure at time ℱ𝒞(𝒞, t). If no points are added to 𝒞 in the time interval (t, t+ δt), then ℱ𝒞(𝒞, t+ δt)= e−λδt.ℱ𝒞(𝒞, t).

The FTCF extends FCS with an exponential histogram of cluster feature (EHCF) to store data at different levels of granularity. Each bucket in the EHCF represents an FCTF associated with a collection of data points. The FTCF is a (2.d + 3) tuple defined as follows:

FTCF(𝒞, t)=(FC2x(𝒞, t)¯, FC1x(𝒞, t)¯, W(t), t, n)(2)

where FC2x(𝒞, t)¯, FC1x(𝒞, t)¯, and W(t) are defined similarly as in Eq. (1), t is the timestamp of the latest point and n is the total number of data points. Based on the timestamp, the EHCF can store the most recent observation individually, while older observations are merged and summarized.

The FCH extends FCS to detect the change of cluster structure through a histogram and store the information of relevant dimensions for each cluster. The FCH is defined as follows:

FCH=(FC2x(𝒞, t)¯, FC1x(𝒞, t)¯, W(t), H(t), BS(t))(3)

where FC2x(𝒞, t)¯, FC1x(𝒞, t)¯, and W(t) are defined similarly as in Eq. (1). H(t) is an α-bin histogram of data values with α equal width intervals. For the l-th bin histogram of the j-th dimension at time t, the elements of Hj are given as Hij(t)= ∑i=1Nf(t− Ti).(xij).(yilj), where yil is the weight of xi in the lth bin and BS(t) is a bit vector of projected dimensions at time t.

The PMC extends FCS to distinguish between core micro-cluster, potential core micro-cluster, and outlier micro-cluster. A micro-cluster that is assigned a dimension preference vector is referred to as a PMC. The term ‘projected’ means that the micro-cluster is defined over a projected subspace of the feature space. The PMC is defined as follows:

PMC=(FC2x(𝒞, t)¯, FC1x(𝒞, t)¯, W(t), VAR¯, Φ(mc) ¯)(4)

where FC2x(𝒞, t)¯, FC1x(𝒞, t)¯, and W(t) are defined similarly as in Eq. (1). VAR¯ is a variance vector of the projected micro-cluster, defined by a variance threshold parameter δ that indicates whether a dimension should be considered preferred or not. Φ(mc) ¯ is a dimension preference vector of the projected micro-cluster.

The EAMC redefines PMC to reduce memory usage and speed up the processing of projected subspace data streams using exponential moving average. The EAMC is defined as follows:

EAMC(t)=(EA1(t),EA2(t), W(t))(5)

where EA1(t) is the d-dimensional vector of exponential weighted moving average of points along each dimension, such that for dimension j: EA1j(t)=αpj(t)+(1−α)EA1j(t−1), where α=21+N is a smoothing factor controlled by the size of time window; and pj(t) is the latest point in time window. EA2(t) is the d-dimensional vector of exponential weighted average of points along each dimension, such that for dimension j: EA2j(t)=αp2j(t)+(1−α)EA2j(t−1). W(t) is the sum of the of data points at time t.

The SNN-PMC redefines PMC to select subspaces of different micro-clusters based on shared nearest-neighbour density information. The SNN-PMC is defined as follows:

SNN−PMC=(CF1¯, CF2¯, N, VAR¯, B¯,P,W)(6)

where CF1¯ is the linear sum of the projection micro-cluster, i.e., CF1 ¯= ⟨CF1¯1, CF1¯2,…,CF1¯d⟩, CF1¯j=∑i=1nxij, xij represents the value of data point xi on dimension j. CF2¯ is the linear sum of squares vector of the projection micro-cluster, i.e., CF2 ¯= ⟨CF2¯1, CF2¯2,…,CF2¯d⟩, CF2¯j=∑i=1n(xij)2. N is the total number of data points contained in the projection micro-cluster, i.e., N=∑i=1n|xi|. VAR¯ is a variance vector of the projection micro-cluster, B¯ is a preference dimension vector of the projection micro-cluster, P is the shared nearest-neighbor density of the projection micro-cluster, and W is the weight of the projection micro-cluster.

The CCMicro is a micro-cluster generated as result of a PCA-based subspace clustering on an arbitrarily oriented subspace. The micro-cluster at time t for a set of d-dimensional points C={p1, p2,…, pn} arriving at different time points is defined as follows:

CCMicro(C, t)=(V(t), E(t), μ(t), ts)(7)

where V(t) is the eigenvector matrix of the covariance matrix of C at time t, E(t) is the corresponding eigenvalues of the eigenvectors in V(t), μ(t) is the mean of the data points contained in C at time t, and ts is the timestamp of the update of this micro-cluster.

A Concept is a micro-cluster, which represents a cluster resulting from a Hough transform-based subspace clustering on an arbitrarily oriented subspace. In a data space 𝒟∈Rd, a Concept of dimensionality l<d captures an l-dimensional hyperplane in parameter space P  with aggregated information of data objects. A Concept consists of the following attributes:

Concept=(E, μ, N, t, P)(8)

where E is a set containing d−l equations in Hessian normal form (HNF), μ is the mean of all data objects associated with the cluster, N is the number of data objects associated with the cluster, t is the timestamp of the last update, and P is the reference to the parent Concept of dimensionality l+1, if l<d−1.

The GS is a grid structure that stores the statistical information for each cell with a total number of points greater than zero. The GS is defined as follows:

GS=(ci1,ci2,…,cid,countu)(9)

where cij is an open right interval in the partitioning of a dimension and counti is the total number of points. ML is a prefix-tree lattice structure that extends GS by using a delayed insertion and pruning technique to minimize memory consumption. All potential dense units are stored in ML where a node in ML corresponds to a cell unit. Each node maintains:

ML=(UI, Cnt, maxMissed, UTt)(10)

where UI is the cell unit associated with the node, Cnt is the number of data points contained in the unit, maxMissed is the maximum number of data points contained in the unit, and UTt is the most recent data point contained in the unit. The CDTL structure was introduced to maintain the connection between dense units and adjacent units. All non-empty units are inserted into the CDTL, where each leaf node is denoted as follows:

CDTL=(CNO, id, selectivity, tlast)(11)

where CNO is the serial number of the micro-cluster, id is the unit identifier, selectivity is the total number of objects contained in the unit, and tlast is the time of the last update of the unit. The HDGTL structure improves the ML structure by allowing the reuse of inner nodes, thereby reducing the number of middle nodes and memory consumption. It is a network structure tree consisting of root, inner, and leaf nodes.

In most data stream scenarios, more recent data may reveal new trends or changes (i.e., concept drift) in the data distribution. These data can be used to explain how the observed process evolved. Systems that evaluate both old and new data equally do not capture the evolving characteristics of data streams and therefore cannot deal with concept drift. Moving window methods have been proposed to account for concept drift in data streams. Most selected algorithms use the time fading window to assign a weight to each object depending on its arrival time. A new object is assigned the highest possible weight, which decreases exponentially over time and is generally defined by a fading function:

ω(t)=β−λ(t−t0)(12)

where λ is the decay rate that determines how much new objects are preferred over old ones, t is the current time, and t0 is the timestamp of the data object. The fading function has a value in the range (0, 1). The constant β is usually set to 2, while the decay rate λ is user-defined depending on the application. Another type of moving window called a sliding window can also be used. This window considers only the most recent data. The window keeps its size w and slides over time, starting at the current time t. Thus, each window contains only objects in the interval [tw+1, t], discarding older objects. The window can be specified in terms of time points (i.e., the last 100 time points) or objects (i.e., the last 1000 objects).

4  Discussion

The clustering process, cluster search, subspace search, synopsis structure, cluster maintenance, and evaluation measures are among the important elements for subspace clustering in high-dimensional data streams. Based on the findings, the clustering process can be divided into two main categories: 1) single-phase approach, and 2) two-phase approach. The single-phase approach runs completely online and consists of three stages—initialization, refinement, and maintenance. Initialization starts with clustering the initial data streams and searching for significant subspaces of the clusters. Then, the cluster information is stored in the form of a specific synopsis structure. The refinement stage is performed iteratively as new data streams become available. In this process, new data points are assigned to the cluster synopsis and subspaces closest to them. Periodically, cluster maintenance is performed when a predefined threshold is reached to ensure that only accurate information is considered for clustering. The two-phase approach, on the other hand, has an additional offline phase to perform the final clustering. As with the single-phase approach, an initial cluster synopsis is created, and a new data point is assigned to the closest cluster. Then, cluster maintenance is performed when a predefined threshold condition is met. In addition, the final clustering phase is activated at the user’s request. The two-phase approach can be further divided depending on the stage in which the subspace search is performed. The first approach performs the subspace search during both the online and offline phases, while the second approach performs the subspace search only during the offline phase. The two-phase approach is more widely used than the single-phase approach because it allows the generation of macro-clusters by merging overlapping micro-clusters based on user-defined parameters [12,13,15,41,42].

The cluster search approach can be divided into four categories based on the taxonomy of conventional clustering algorithms: partition-based, hierarchical-based, grid-based, and density-based approaches. In general, the partition-based subspace clustering algorithms produce higher quality clusters, support high stream speeds, and consume less memory than their predecessors. Nevertheless, their clustering quality depends on the given maximum number of clusters and average projected dimensions. Moreover, they can only identify spherical clusters, which may contain noise and outliers. The hierarchical-based subspace clustering algorithms allow the monitoring and detection of changes in the cluster structure, including cluster appearance, disappearance, self-evolution, merging, and splitting. The agglomerative hierarchical strategy makes the algorithms less sensitive to outliers, but the susceptibility decreases as the dimension increases. In addition to the maximum number of clusters and the average projected dimensions, other thresholds are required to detect cluster evolution, and these thresholds vary by application domain. The grid-based subspace clustering algorithm is robust against noise and outliers and can locate clusters of any shape due to the use of the grid structure. Moreover, it does not require a predefined number of clusters and projected dimensions. Nevertheless, the quality of clustering depends on the size and position of the grid cell in the feature space. Density-based subspace clustering algorithms can filter out noise or outliers by forming clusters of dense regions and finding clusters with variable shapes, and do not require a predefined number of clusters and projected dimensions. Nevertheless, several parameters are required to form the micro-clusters. The density-based approach is superior to other clustering approaches in the literature because it is able to generate multiple micro-clusters that distinguish true clusters from outliers [43–46].

The approach to subspace search is chosen based on the goal of examining an axis-parallel subspace or an arbitrarily oriented subspace. The approach for an axis-parallel subspace search depends on the application domain and whether the clusters are allowed to be in overlapping or non-overlapping subspaces. If it is the former, the top-down approach is chosen; if the latter, the bottom-up approach is chosen. Most algorithms for clustering subspaces in high-dimensional data streams weigh each dimension equally to determine how much it contributes to the subspace. Within a given cluster, feature dimensions do not necessarily contribute equally to the formation of the subspace. Assigning different weights to each dimension is beneficial to show the relative importance of each dimension to the cluster [47,48]. In addition, most algorithms depend on conventional subspace clustering algorithms when searching for subspaces. Conventional algorithms use traditional distance metrics (i.e., Euclidean distance, weighted Euclidean distance, Manhattan distance, k-nearest neighbor distance) that may lose their qualitative meaning in a high-dimensional space. Investigating the distance metrics for subspace clustering in high-dimensional data streams will further the understanding of their impact on clustering and subspace search results.

The unbounded constraint imposed by data streams is overcome by storing a synopsis of that data in the form of micro-clusters or a grid structure. A micro-cluster is a common synopsis structure for partition-based, hierarchical-based, and density-based clustering algorithms, while a grid structure is for grid-based clustering algorithms. Among all types of micro-clusters found in the literature on subspace clustering for high-dimensional data streams, the projected micro-cluster (PMC) is the most efficient choice due to its ability to handle outliers [11]. The PMC defines three types of micro-clusters: projected core micro-clusters, potential projected core micro-clusters and outlier micro-clusters. The PMC has properties of additivity and temporal multiplicity, which can be used to add new data points to an existing PMC and downgrade an existing PMC if no points are added to it within a certain time interval.

The time fading window which gives more weight to the most recent data is often applied to ensure that the clustering model is always updated. The moving window methods partially address the challenges posed by the evolving nature of data streams. However, there is a need to develop a more robust algorithm for clustering data streams to detect concept drift [14]. Concept drift can generally be handled in two ways: implicit approach and explicit approach [49,50]. The implicit approach is a proactive mechanism that internally adapts to changes in data streams without any mechanism to detect the changes. The learning algorithm is periodically retrained with the latest data to represent the current model while discarding the older data. This method is often referred to in the literature as a forgetting mechanism, where the old data elements can be discarded using the time fading window or a sliding window. However, the implicit approach is limited by its slow response to changes, and the high cost of regular updates, even when no changes occur. The explicit approach, on the other hand, is a reactive mechanism with an external change detection mechanism that sends a trigger to the learning algorithm, which then revises its model to reflect the current change. The explicit method helps the learning model deal with the change immediately and recover quickly from the performance degradation. It is time saving and cost effective because the learning model is updated only when a drift is signaled.

Evaluation is another essential element of subspace clustering algorithms in high-dimensional data streams. Clustering algorithms are usually evaluated using external evaluation metrics for class-labeled data. Most algorithms have used clustering purity to evaluate clustering quality. However, clustering is different from classification, and mapping between classes and clusters is not always possible [11]. Unlike external metrics, internal metrics aim to evaluate clustering quality without having access to ground truth labels. Clustering quality is evaluated in terms of the structure of clusters and their relationship to each other. The internal evaluation metrics for data stream clustering algorithms have been well studied in [51].

5  Conclusion

Clusters in high-dimensional space can be formed from a small number of significant and distinct dimensions called subspaces. Subspace clustering helps mitigate problems with clustering in high-dimensional space because it can identify meaningful clusters in subspaces formed by different feature combinations. It is a complicated process even when considering static data. The problem becomes much more complex when considering data streams that are unbounded and evolving. This article reviewed a total of 18 algorithms for subspace clustering in high-dimensional data streams. The algorithms are interpreted based on their subspace clustering approach, how the cluster information is stored as synopsis structures, and how the clusters are updated.

Currently, most algorithms use a two-phase clustering framework, where data are summarized into micro-clusters or grid cells in the online phase and the final clusters are generated in the offline phase. The algorithms first create subspace clusters from a collection of raw data streams. The subspace clustering process deals with two separate problems: Cluster Search and Subspace Search. Cluster search relies on a basic cluster model, with the density-based cluster model providing better performance. Subspace search starts from a specific search space and applies specific search techniques to find relevant dimensions for the clusters. Some algorithms assign a data point to exactly one cluster, removing possible important information about the data from other dimensions. In some cases, an object may belong to multiple clusters, especially if the clusters are formed from completely different dimensions. Several algorithms find clusters with overlapping subspaces but interpreting the clustering result can be difficult. Due to the unbounded nature of data streams, clustering of incoming data streams is performed on the cluster synopsis rather than on the raw data. Many forms of synopsis structures have been used, with projected micro-clusters being the most suitable due to their ability to handle noise and outliers. As the data streams evolve, the concept drift of the clustering result is implicitly managed through window models that assign different weights depending on the timeliness of the data.

Future work can focus on multiple research topics. The clustering framework can be modified to run fully online to more accurately detect changes in data streams. Although the density-based approach is superior to the other approaches, it includes several user-defined parameters that can be optimized for a more efficient cluster search. The traditional similarity metrics can be improved for a more efficient subspace search. Since most current algorithms weigh the subspace dimensions of the clusters equally, techniques for weighting the dimensions differently can also be explored. These techniques are known in the literature as soft subspace clustering. The synopsis structure and the explicit aspects of detecting concept drift in data streams can be further investigated to achieve a more efficient online clustering performance. Finally, future work can experiment with intrinsic evaluations of subspace clustering algorithm performance, especially in an environment where ground truth labels are not available.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. A. Zubaroğlu and V. Atalay, “Data stream clustering: A review,” Artificial Intelligence Review, vol. 54,no. 2, pp. 1201–1236, 2021. [Google Scholar]

2. X. Wen and H. Juan, “PSubCLUS: A parallel subspace clustering algorithm based on spark,” IEEE Access, vol. 9, pp. 2535–2544, 2021. [Google Scholar]

3. A. Kelkar, S. F. Rodd and U. P. Kulkarni, “Estimating distance threshold for greedy subspace clustering,” Expert Systems with Applications, vol. 135, pp. 219–236, 2019. [Google Scholar]

4. L. Rutkowski, M. Jaworski and P. Duda, “Basic concepts of data stream mining,” in Stream Data Mining: Algorithms and Their Probabilistic Properties, vol. 56. Cham, Switzerland: Springer Nature Switzerland AG, pp. 13–33, 2020. [Google Scholar]

5. C. Fahy, S. Yang and M. Gongora, “Scarcity of labels in non-stationary data streams: A survey,” ACM Computing Surveys (CSUR), vol. 55, no. 2, pp. 1–39, 2022. [Google Scholar]

6. M. Bahri, A. Bifet, J. Gama, H. M. Gomes and S. Maniu, “Data stream analysis: Foundations, major tasks and tools,” Wiley Interdisciplinary Reviews: Data Mining and Knowledge Discovery, vol. 11, no. 3, pp. 1–17, 2021. [Google Scholar]

7. M. Tareq, E. A. Sundararajan, A. Harwood and A. A. Bakar, “A systematic review of density grid-based clustering for data streams,” IEEE Access, vol. 10, pp. 579–596, 2022. [Google Scholar]

8. H. A. Al-Khamees and E. S. Al-Shamery, “Survey: Clustering techniques of data stream,” in 2021 First Babylon Int. Conf. on Information Technology and Science, Babil, Iraq, pp. 113–119, 2021. [Google Scholar]

9. K. Batool and G. Abbas, “A comprehensive review on evolving data stream clustering,” in 2021 Int. Conf. on Communication Technologies, Rawalpindi, Pakistan, pp. 138–143, 2021. [Google Scholar]

10. M. A. Mahdi, K. M. Hosny and I. Elhenawy, “Scalable clustering algorithms for big data: A review,” IEEE Access, vol. 9, pp. 80015–82019, 2021. [Google Scholar]

11. S. Mansalis, E. Ntoutsi, N. Pelekis and Y. Theodoridis, “An evaluation of data stream clustering algorithms,” Statistical Analysis and Data Mining: The ASA Data Science Journal, vol. 11, no. 4, pp. 167–187, 2018. [Google Scholar]

12. M. Carnein and H. Trautmann, “Optimizing data stream representation: An extensive survey on stream clustering algorithms,” Business & Information Systems Engineering, vol. 61, no. 3, pp. 277–297, 2019. [Google Scholar]

13. A. Haneen, A. Noraziah and M. H. Abd Wahab, “A review on data stream classification,” Journal of Physics: Conference Series, vol. 1018, no. 1, pp. 1–8, 2018. [Google Scholar]

14. U. Kokate, A. Deshpande, P. Mahalle and P. Patil, “Data stream clustering techniques, applications, and models: Comparative analysis and discussion,” Big Data and Cognitive Computing, vol. 2, no. 4, pp. 1–30, 2018. [Google Scholar]

15. T. Keshvani and M. Shukla, “A comparative study on data stream clustering algorithms,” in Proceeding of the Int. Conf. on Computer Networks, Big Data and IoT, Madurai, India, pp. 219–230, 2018. [Google Scholar]

16. E. Alothali, H. Alashwal and S. Harous, “Data stream mining techniques: A review,” Telecommunication Computing Electronics and Control, vol. 17, no. 2, pp. 728–737, 2019. [Google Scholar]

17. M. J. Lesot, “Subspace clustering and some soft variants,” in Thirteenth Int. Conf. on Scalable Uncertainty Management, Compiègne, France, pp. 433–443, 2019. [Google Scholar]

18. B. A. Kelkar and S. F. Rodd, “Subspace clustering—A survey,” Data Management, Analytics and Innovation, vol. 808, pp. 209–220, 2019. [Google Scholar]

19. D. Pandove, S. Goel and R. Rani, “Systematic review of clustering high-dimensional and large datasets,” ACM Transactions on Knowledge Discovery from Data, vol. 12, no. 2, pp. 1–68, 2018. [Google Scholar]

20. H. P. Kriegel, P. Kröger and A. Zimek, “Clustering high-dimensional data: A survey on subspace clustering, pattern-based clustering, and correlation clustering,” ACM Transactions on Knowledge Discovery from Data, vol. 3, no. 1, pp. 1–58, 2009. [Google Scholar]

21. S. F. Mohamed Shaffril, H. A. Samsuddin and A. Abu Samah, “The ABC of systematic literature review: The basic methodological guidance for beginners,” Quality & Quantity, vol. 55, no. 4, pp. 1319–1346, 2021. [Google Scholar]

22. S. Kraus, M. Breier and S. Dasí-Rodríguez, “The art of crafting a systematic literature review in entrepreneurship research,” International Entrepreneurship and Management Journal, vol. 16, no. 3, pp. 1023–1042, 2020. [Google Scholar]

23. C. C. Aggarwal, J. Han, J. Wang and P. S. Yu, “On high dimensional projected clustering of data streams,” Data Mining and Knowledge Discovery, vol. 10, no. 3, pp. 251–273, 2005. [Google Scholar]

24. J. Ren, L. Li and C. Hu, “A weighted subspace clustering algorithm in high-dimensional data streams,” in 2009 Fourth Int. Conf. on Innovative Computing, Information and Control, Kaohsiung, Taiwan, pp. 631–634, 2009. [Google Scholar]

25. W. Liu and J. OuYang, “Clustering algorithm for high dimensional data stream over sliding windows,” in 2011 IEEE Tenth Int. Conf. on Trust, Security and Privacy in Computing and Communications, Changsha, Hunan Province, China, pp. 1537–1542, 2011. [Google Scholar]

26. J. Ren, S. Cao and C. Hu, “Density-based data streams subspace clustering over weighted sliding windows,” in 2010 First ACIS Int. Symp. on Cryptography, and Network Security, Data Mining and Knowledge Discovery, E-Commerce and Its Applications, and Embedded Systems, Qinhuangdao, Hebei, China, pp. 212–216, 2010. [Google Scholar]

27. R. Chairukwattana, T. Kangkachit, T. Rakthanmanon and K. Waiyamai, “SE-stream: Dimension projection for evolution-based clustering of high dimensional data streams,” in Proc. of the Fifth Int. Conf. on Knowledge and Systems Engineering, Hanoi, Vietnam, pp. 365–376, 2014. [Google Scholar]

28. K. Waiyamai, T. Kangkachit, R. Rakthanmanon and T. Chairukwattana, “SED-stream: Discriminative dimension selection for evolution-based clustering of high dimensional data streams,” International Journal of Intelligent Systems Technologies and Applications, vol. 13, no. 3, pp. 187–201, 2014. [Google Scholar]

29. K. Waiyamai and T. Kangkachit, “Constraint-based discriminative dimension selection for high-dimensional stream clustering,” International Journal of Advances in Intelligent Informatics, vol. 4, no. 3, pp. 167–179, 2018. [Google Scholar]

30. I. Ntoutsi, A. Zimek, T. Palpanas, P. Kröger and H. P. Kriegel, “Density-based projected clustering over high dimensional data streams,” in Proc. of the 2012 SIAM Int. Conf. on Data Mining, Anaheim, California, USA, pp. 987–998, 2012. [Google Scholar]

31. A. Ahmed, I. Ahmed and W. Shahzad, “A novel high dimensional and high speed data streams algorithm: HSDStream,” International Journal of Advanced Computer Science and Applications, vol. 7, no. 9, pp. 381–392, 2016. [Google Scholar]

32. M. Hassani, P. Spaus, M. M. Gaber and T. Seidl, “Density-based projected clustering of data streams,” in Sixth Int. Conf. on Scalable Uncertainty Management, Marburg, Germany, pp. 311–324, 2012. [Google Scholar]

33. R. Huang, R. Xiao, W. Zhu, P. Gong, J. Chen et al., “Towards an efficient real-time kernel function stream clustering method via shared nearest-neighbor density for the IIoT,” Information Sciences, vol. 566, pp. 364–378, 2021. [Google Scholar]

34. Y. Lu, Y. Sun, G. Xu and G. Liu, “A grid-based clustering algorithm for high-dimensional data streams,” in First Int. Conf. on Advanced Data Mining and Applications, Wuhan, China, pp. 824–831, 2005. [Google Scholar]

35. Y. Sun and Y. Lu, “A grid-based subspace clustering algorithm for high-dimensional data streams,” in Int. Conf. on Web Information Systems Engineering, Wuhan, China, pp. 37–48, 2006. [Google Scholar]

36. S. Wang, Y. Fan, C. Zhang, H. Xu, X. Hao et al., “Subspace clustering of high dimensional data streams,” in Seventh IEEE/ACIS Int. Conf. on Computer and Information Science, Portland, Oregon, pp. 165–170, 2008. [Google Scholar]

37. Z. Zhang and H. Wang, “A fast subspace partition clustering algorithm for high dimensional data streams,” in 2009 IEEE Int. Conf. on Intelligent Computing and Intelligent Systems, Shanghai, China, vol. 1, pp. 491–495, 2009. [Google Scholar]

38. L. Ren, J. Li and Y. Xia, “HDG-Tree: A structure for clustering high-dimensional data streams,” in 2009 Third Int. Symp. on Intelligent Information Technology Application, Nanchang, China, vol. 2, pp. 594–597, 2009. [Google Scholar]

39. F. Borutta, P. Kröger and T. Hubauer, “A generic summary structure for arbitrarily oriented subspace clustering in data streams,” in Twelfth Int. Conf. on Similarity Search and Applications, Newark, USA, pp. 203–211, 2019. [Google Scholar]

40. F. Borutta, D. Kazempour, F. Mathy, P. Kröger and T. Seidl, “Detecting arbitrarily oriented subspace clusters in data streams using hough transform,” in Twenty-Fourth Pacific-Asia Conf. on Knowledge Discovery and Data Mining, Singapore, vol. 12084, pp. 356–368, 2020. [Google Scholar]

41. K. Fatehi, M. Rezvani and M. Fateh, “ASCRClu: An adaptive subspace combination and reduction algorithm for clustering of high-dimensional data,” Pattern Analysis and Applications, vol. 23, no. 4, pp. 1651–1663, 2020. [Google Scholar]

42. C. Nixon, M. Sedky and M. Hassan, “Reviews in online data stream and active learning for cyber intrusion detection-A systematic literature review,” in 2021 Sixth Int. Conf. on Fog and Mobile Edge Computing, Gandia, Spain, pp. 1–6, 2021. [Google Scholar]

43. E. Ezugwu, A. M. Ikotun, O. O. Oyelade, L. Abualigah, J. O. Agushaka et al., “A comprehensive survey of clustering algorithms: State-of-the-art machine learning applications, taxonomy, challenges, and future research prospects,” Engineering Applications of Artificial Intelligence, vol. 110, pp. 1–43, 2022. [Google Scholar]

44. T. Kolajo, O. Daramola and A. Adebiyi, “Big data stream analysis: A systematic literature review,” Journal of Big Data, vol. 6, no. 1, pp. 1–30, 2019. [Google Scholar]

45. S. S. Reddy, “A review on data stream clustering algorithms over sliding windows,” International Journal of Research and Analytical Reviews, vol. 6, no. 2, pp. 386–393, 2019. [Google Scholar]

46. E. Ezugwu, A. K. Shukla, M. B. Agbaje, O. N. Oyelade, A. José-García et al., “Automatic clustering algorithms: A systematic review and bibliometric analysis of relevant literature,” Neural Computing and Applications, vol. 33, no. 11, pp. 6247–6306, 2021. [Google Scholar]

47. M. Li and L. Wang, “Soft subspace clustering with entropy constraints,” in 2020 Thirteenth Int. Congress on Image and Signal Processing, BioMedical Engineering and Informatics, Chengdu, China, pp. 920–925, 2020. [Google Scholar]

48. C. Liu, Y. Li, Q. Zhao and C. Liu, “Reference vector-based multi-objective clustering for high-dimensional data,” Applied Soft Computing, vol. 78, pp. 614–629, 2019. [Google Scholar]

49. S. Iwashita and J. P. Papa, “An overview on concept drift learning,” IEEE Access, no. 7, pp. 1532–1547, 2018. [Google Scholar]

50. S. Agrahari and A. K. Singh, “Concept drift detection in data stream mining: A literature review,” Journal of King Saud University-Computer and Information Sciences, 2021. Advance online publication. https://doi.org/10.1016/j.jksuci.2021.11.006 [Google Scholar] [CrossRef]

51. M. Hassani and T. Seidl, “Using internal evaluation measures to validate the quality of diverse stream clustering algorithms,” Vietnam Journal of Computer Science, vol. 4, no. 3, pp. 171–183, 2017. [Google Scholar]