An Efficient Color-Image Encryption Method Using DNA Sequence and Chaos Cipher

1  Introduction

In the Internet and advanced technological era, digital images have become vital to communication, military, medicine, and other fields in which these images contain crucial information. Hence, digital image encryption is one of the measures to prevent unauthorized access to these images, and finding a method of encrypting that is both safe and efficient is significant. Due to the large data capacity, the redundancy is high, and pixels are correlated strongly, rendering the conventional encryption schemes, such as Data Encryption Standard (DES), Advanced Encryption Standard (AES), and Rivest–Shamir–Adleman (RSA), no longer valid to deal with images. Therefore, chaos-based encryption algorithms have been introduced to deal with images as it has strong sensitivity to control factors and initial parameters, high unpredictability, and convoluted behavior [1]. DNA-based encryption algorithms are becoming more popular and considered ideal nowadays. DNA-based algorithms are highly preferred because of their vast storage and extensive parallelism.

Currently, researchers are highly interested in experimenting with Chaos and DNA to strengthen encryption algorithms and provide a more active way to secure images [2,3]. Liu et al. [4] proposed a bit-level algorithm using a DNA computation and a double-chaos system to encrypt color images. They used the Arnold algorithm to scramble the plaintext image’s three-color components. After that, an enhanced double chaos system comprised of Rossler and Lorenz chaotic maps was used. Wang et al. [5] developed a new method based on the classic scrambling-diffusion process. In the scrambling process, the original image is confused twice using the hyper-chaotic Chen system’s two chaotic sequences. Those chaotic sequences are employed to determine DNA coding and decoding rules and substitution rules throughout the diffusion process. Wang et al. [6] suggested a novel RGB image encoding system based on the Lorenz system and DNA permutation. Amani et al. [7] proposed a new adaptive RGB image encoding system based on hyper-chaotic dynamics and DNA sequence operation. They explained how the combination of DNA sequence, the Chen hyper-chaotic system, and the adaptive approach increase the algorithm’s complexity and security. Wang et al. [8] suggested a novel chaotic image encryption method. The first stage of encryption at the pixel level is carried out using Coupled Map Lattice (CML) and DNA diffusion sequences. Then, using a chaotic method to select the DNA encoding rules and generate a DNA matrix; finally, the second round of encryption is performed using Hamming distance at the DNA level, DNA complementary rule, cyclic shift function, DNA operation rule, as well as other activities.

According to the above literature review, the existing color image encryption algorithms have the following flaws: The DNA diffusion-based encryption algorithm employs a single calculation method, resulting in low security and complexity. There is no disruption in the correlation between a color image’s channels, which makes it vulnerable to statistical attacks. The encryption method has flaws in its resistance to conventional attacks and low security. In order to address the issues mentioned above, this paper proposes a color image encryption scheme that combines image hashing, 4D hyperchaotic systems, and dynamic DNA addition operations. This paper makes the following significant contributions:

•   The plain image’s SHA-256 hash is utilized to produce secret keys. Even a slight change to the original image will significantly change the SHA-256 hash value [9], which not only increases the key’s sensitivity to resist plaintext attacks but can also detect and analyze the location of image tampering.

•   Image security is improved at the cost of increased system complexity. The randomness and complexity of the chaotic sequences are increased by high-dimensional chaotic systems, making the encryption method more secure.

•   The algorithm usage of a hyper-chaotic system to scramble each pixel causes each pixel in each channel to be scrambled into a new position chaotically. This technique is repeated four times using sequences generated from the 4D Lorenz hyper-chaotic system.

•   The algorithm uses DNA operation methods by exploiting the excellent characteristics of a hyper-chaotic system, such as randomness, to determine the DNA operation methods randomly.

The remainder of this paper is organized as follows: Section 2 presents the background of the suggested technique, containing chaotic systems and DNA encoding. Section 3 illustrates the proposed encryption method in this work, followed by the discussion of the experiment results in Section 4. Finally, the conclusion is given in Section 5.

2  Background

This paper integrated a range of strategies and procedures to obtain favorable outcomes. This section explains the fundamental notions behind these strategies and procedures.

2.1 4D Lorenz Chaotic System

This work employs the chaotic sequences created by the Lorenz hyper-chaotic system to encrypt the image in this paper due to its greater randomness and unpredictable nature. The following equation is a mathematical representation of the Lorenz hyper-chaotic [10].

{x¯=w+a(y−x)y¯=−xz−y+cx z¯=xy− bz w¯= rw−yz (1)

where (a, b, c, and r) are the system’s control parameters, while (x, y, z, and w) are the system’s state variables. The system Eq. (1) enters a hyper-chaotic state when we set (a = 10, b = 8/3, c = 35, and r = −1).

2.2 4D Rossler Chaotic System

Hyper-chaotic functions have higher security because they have a large space of keys. One of the hyper-chaotic systems is the 4D Rossler system, which is described by the following equation [11].

{A^=−B−CB^=A+αB+DC^=β+CA D^=γD−δC (2)

where (A, B, C, and D) are the state variables, while (α, β, γ, and δ) are the control parameters. When (α = 0.25, β = 3, γ = 0.05, and δ = 0.5), the above system is in a hyper-chaotic state.

2.3 DNA Sequence

In today’s world, DNA computing is permeating the sphere of cryptography. In DNA cryptograms, information is transmitted through DNA based on biological technology.

2.3.1 DNA Encoding

A DNA molecule comprises four nucleotides: A, T, C, and G. There is a complementary relationship between these nucleotides; if the value ‘00’ is assigned to A, then the value ‘11’ should be assigned to T. Likewise, if the value ‘01’ is assigned to C, then the value ‘10’ should be assigned to G. Thus, there are 24 types of DNA coding rules, but only eight of them meet the complementary relationship [12]. As shown in Table 1, there are eight rules for encoding and decoding the binary sequence. For example, imagine an image with a pixel value of 38. The binary expression for this pixel is ‘00100110’. The DNA strand is created as ‘AGCG’ by applying Rule0. We can recover the binary sequence by decoding with Rule4 ‘10110011’ and obtain 179, which is a different pixel value.

2.3.2 DNA Operations

As with binary numbers, the DNA sequences can be added, subtracted, and XORed in the same way, and the results are influenced by the rule used to perform these operations.

3  Proposed Encryption Method

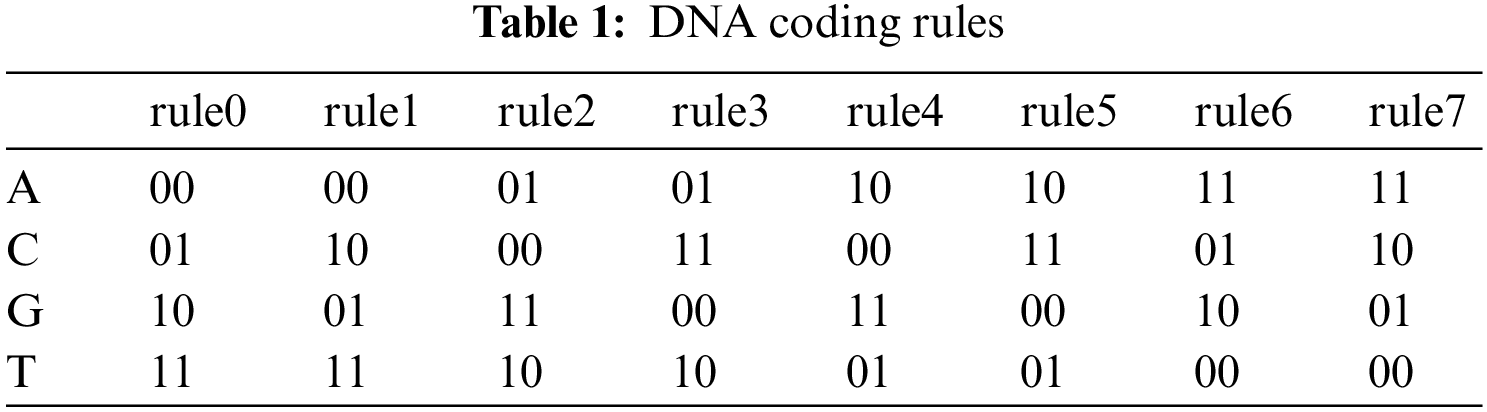
The proposed encryption method comprises three steps: Primary Keys Generation, Confusion procedure, and Diffusion procedure. Fig. 1 depicts the encryption algorithm as a flow chart. In addition, the decryption algorithm works in the reverse direction from the encryption algorithm, allowing identical restoration of the original color image.

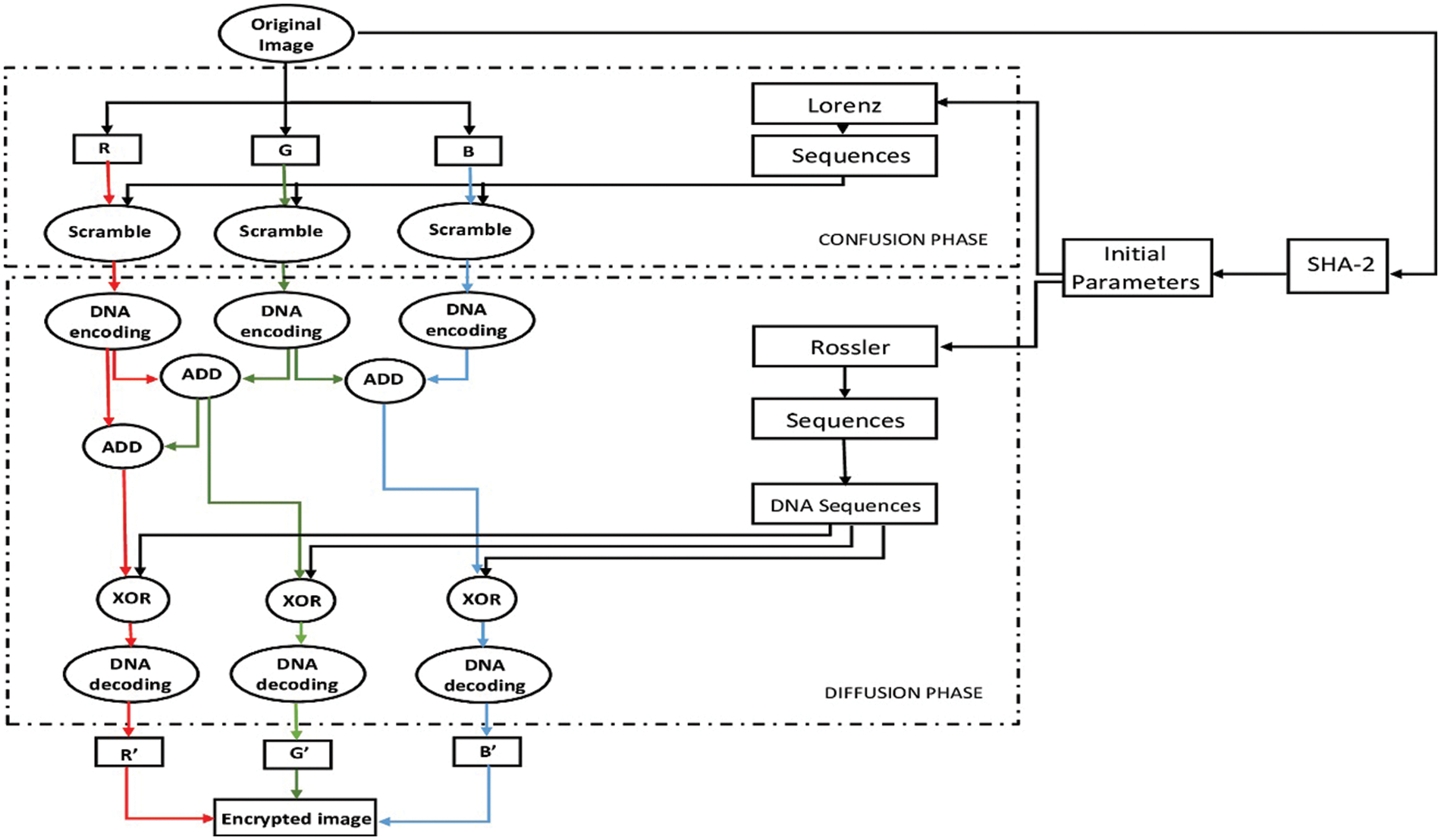
Figure 1: The flow chart of the proposed encryption method

3.1 Primary Keys Generation

Hyper-chaotic maps are used in the proposed encryption method. As the generation of the primary key plays a significant role in the encryption process, the key space of the primary key is paramount to the security of hyper-chaotic maps. Following are the steps of primary keys generation:

Step 1: The original key is generated by SHA-256, which is a hashing algorithm. The matrix I0 represents the original image pixels. By hashing with SHA-256, we can obtain K0. A key characteristic of K0 is that it is a one-time-key that varies depending on the image.

K0=fSHA−256(I0)(3)

Step 2: The initial key is generated by hashing K0, which consists of 32 bytes with SHA-384. We can get K1 contain 48 bytes.

K1=fSHA−384(K0)(4)

Step 3: Once the initial key has been generated, it can be utilized to obtain the chaotic system’s initial parameters. A 384-bit K1 is divided into 8-bit blocks, and we get 48 blocks b1, b2,…, b48. After that, every four blocks are grouped, resulting in 12 groups, G1, G2, …, G12.

Gi={b4i−3;b4i−2;b4i−1;b4i},(1≤i≤12)(5)

Step 4: According to chaotic system, seeds S1, S2, …, S12 are determined as follows:

Si=∑m=03b4i−m26,(1≤i≤12)(6)

Step 5: The following are the initial parameters for our chaotic systems that are generated from the random seeds:

X0=A0=S1+S2+S3(7)

Y0=B0=S4+S5+S6(8)

Z0=C0=S7+S8+S9(9)

W0=D0=S10+S11+S12(10)

3.2 Confusion Procedure

In the following steps, the positions of the pixels on the original image have been scrambled based on the sequences created by using the Lorenz hyper-chaotic system:

Step 1: Suppose that a color image has the dimensions m × n, where m and n are the image’s rows (height) and columns (width), respectively.

Step 2: Decompose the color image into its R (m, n), G (m, n), and B (m, n) components matrices.

Step 3: Generation of the Xi, Yi, Zi, and Wi chaotic sequences via Lorenz hyper-chaotic map using the initial parameters X0, Y0, Z0, and W0, as described in Section 3.1.

Step 4: Choose an array for each chaotic sequence that is identical to the original matrix in terms of size.

Step 5: Sort the sequences as follows:

{[∼,Index_x]=sort(X,′ascend′)[∼,Index_y]=sort(Y,′descend′)[∼,Index_z]=sort(Z,′ascend′)[∼,Index_w]=sort(W,′descend′)(11)

where Index_x, Index_y, Index_z, and Index_w are the X, Y, Z, and W index sequences, respectively.

Step 6: Scrambling the positions of pixels using the X, Y, Z, and W index sequences sequentially for each component and obtaining RGB scrambled matrices Rs, Gs, and Bs.

3.3 Diffusion Procedure

Step 1: Three different matrices Rbinary, Gbinary, and Bbinary can be generated, which are all of (m, n, 8) size, by transforming the RGB scrambled matrices into an 8-bit binary representation.

Step 2: Each binary pixel in the three matrices is encoded into DNA; so that Rbinary, Gbinary, and Bbinary are encoded using rules 5, 6, and 7, respectively. We can get RDNA, GDNA, and BDNA, and their size is (m, n, 4).

Step 3: Generation of four chaotic sequences, A, B, C, and D, via Rossler hyper-chaotic map using the initial parameters A0, B0, C0, and D0, as described in Section 3.1.

Step 4: Choose an array for each chaotic sequence that is the same size as the original matrix.

Step 5: The first chaotic sequence A is converted into a range from 0 to 7 according to the following equation:

A=mod(round(A * 10∧4),8)(12)

Step 6: The addition operation between the three matrices is done according to Eq. (13), and the addition rule is chosen dynamically depending on sequence A.

{GDNA′=RDNA+GDNABDNA′=GDNA+BDNARDNA′=RDNA+GDNA′(13)

Step 7: The rest of the chaotic sequences B, C, and D are converted into a range from 0 to 255 according to Eq. (14). Then, they are converted into matrices of binary numbers, then converted to DNA coding using the rules 5, 6, and 7 to get BDNA, CDNA, DDNA, respectively.

{B=mod(round(B∗10∧4),256)C=mod(round(C∗10∧4),256)D=mod(round(D∗10∧4),256)(14)

Step 8: Xor operation is applied between the chaotic sequences, BDNA with RDNA′, to get RDNA″, CDNA with GDNA′, to get GDNA″, and DDNA with BDNA′, to get BDNA″.

Step 9: DNA sequences are decoded to binary representation by using the rules 0, 1, and 2 with the ciphered matrices obtained from Step 8, respectively. Then, the binary matrices converted into the pixel matrices R′, G′, and B′.

Step 10: Finally, the encrypted image is created by combining the three components.

3.4 Decryption Method

The encrypted image generated through the encryption algorithm is sent by insecure channel. As the proposed image cryptosystem is symmetric, therefore, the decryption can also be carried out by using the similar steps in the opposite direction. After receiving the color (RGB) encrypted image, the recipient acquires the encryption's private keys which have been transformed through insecure channel. These keys can be employed in hyper-chaotic systems for the creation of random values for encryption. The pixel value is restored to its original value prior to encryption by first executing the diffusion step and then doing the confusion step to restore pixels to their original places in the image before encryption. The decryption process of images is shown in Fig. 2.

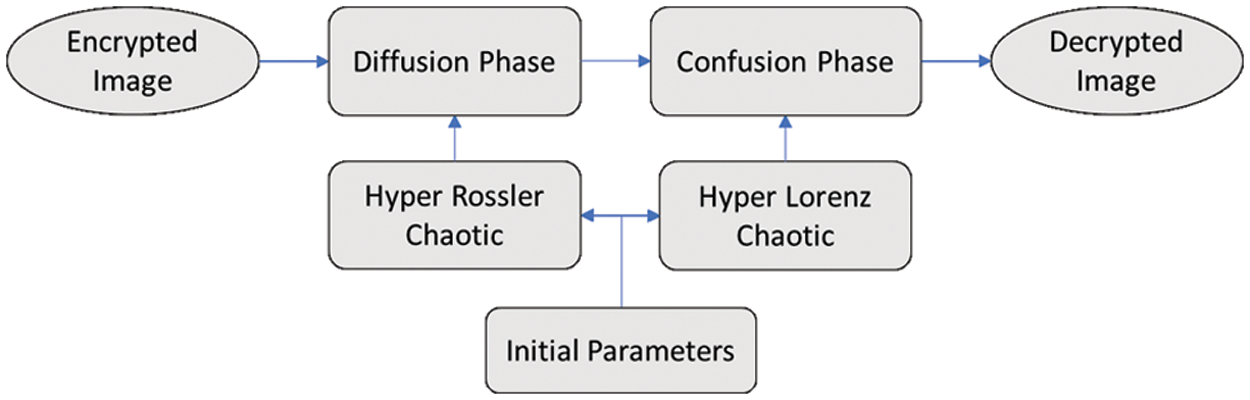
Figure 2: Block diagram of image decryption process

4  Experimental Results

This section aims to assess the robustness of the developed scheme using various analyses, including statistics, key space, chosen, and known plaintext. This algorithm is performed in MATLAB R2013a with 8 GB RAM and Intel(R) Core (TM) i5-4310U processor and 32-bit Windows 8. We used six RGB images with dimensions 256 × 256 pixels in png format to perform the efficacy test. Fig. 3 shows the six test images with their corresponding encrypted images.

Figure 3: (a–f) Plain images, (g–l) Encrypted images

4.1 Key Space

An image encryption method must have a vast key space to prevent brute-force assaults. However, the encryption speed may slow down when the space of secret keys is huge. A key space with a size greater than 2100 is required to provide high levels of protection from malicious attacks [13]. The key in the proposed encryption method is composed primarily of the initial parameters X0, Y0, Z0, and W0 composed of hyper Lorenz and hyper Rossler maps. Thus, if precision is set at 10−15, there are four keys in total, meaning the total key space is 1060 ≈ 2200, much larger than 2100. As a result, we have implemented an encryption algorithm with enough key space to withstand various brute-force attacks.

4.2 Histogram Analysis

Statistically, a histogram is a graphical representation that illustrates a visual representation of the data distribution. By plotting the number of pixels in an image at each color intensity level, a histogram illustrates the distribution of pixels within the image. Fig. 4 shows the color histogram for the Lena image before (a) and after (b) encryption. The encrypted image histogram and the probability distribution in the interval are uniformly distributed when comparing the encrypted and plaintext color images. In this way, the statistical analysis makes it difficult for attackers to guess the original image. The results indicate that the algorithm prevents statistical attacks effectively.

Figure 4: (a) Red, Green, and Blue histograms for a plain image, (b) Red, Green, and Blue histograms for a cipher image

4.3 Correlation Analysis

Correlation analysis determines the similarity between the cipher and the original image [14]. There should be no correlation between the immediate pixels in the cipher image to protect against statistical attacks. The key to assessing encryption method performance is reducing the correlation between pixels next to each other. From the plaintext and ciphertext images’ three components, from the vertical, horizontal, and diagonal directions, 50,000 pairs of neighboring pixels are randomly picked. Fig. 5 illustrates the distribution of pixel pairs for the Lena image. The correlation coefficient is defined as follows:

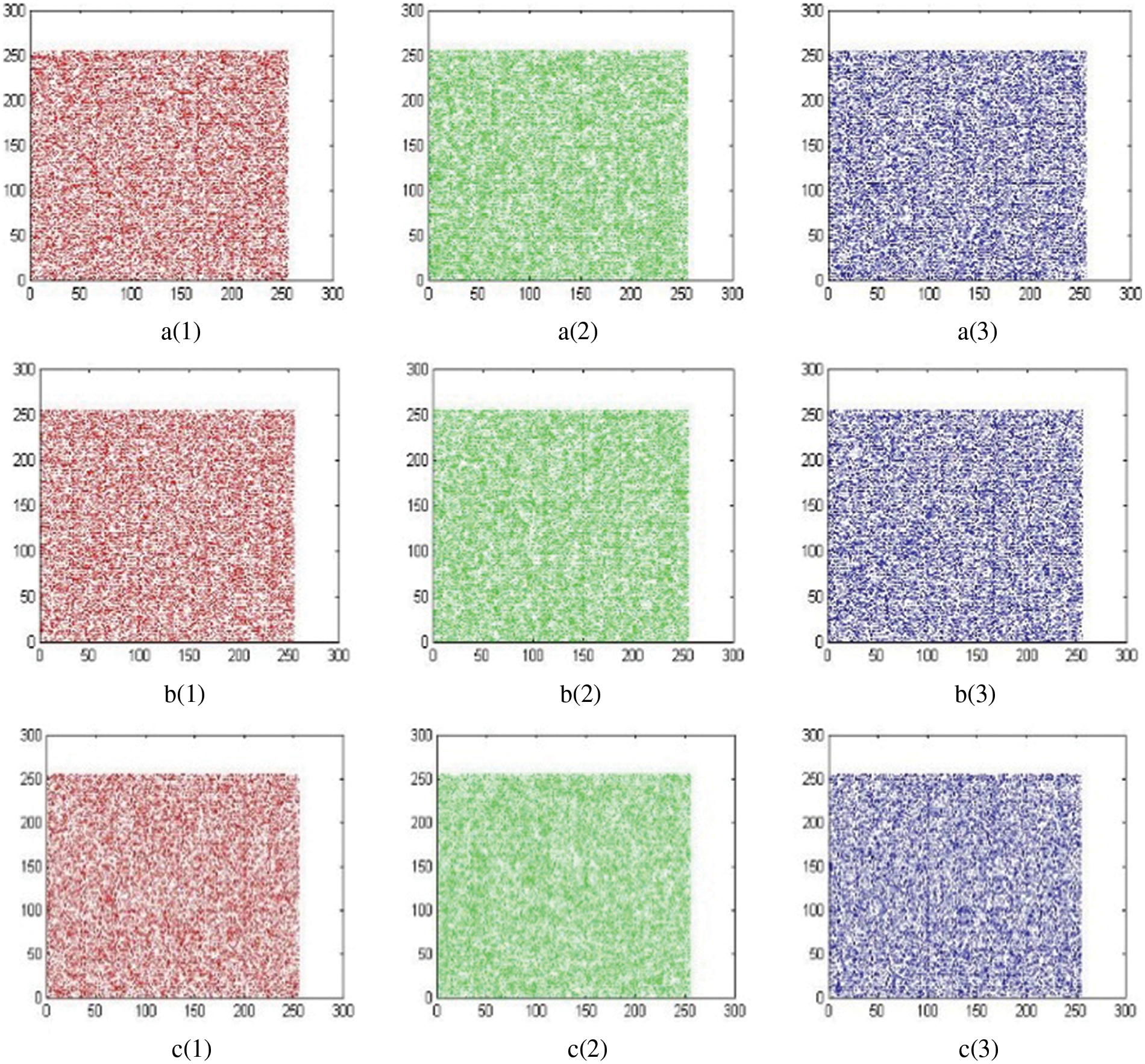
Figure 5: Correlation analysis: Horizontal cipher image correlation of a(1) for r, a(2) for g, and a(3) for b planes; Vertical cipher image correlation of b(1) for r, b(2) for g, and b(3) for b planes; Diagonal cipher image correlation of c(1) for r, c(2) for g, and c(3) for b planes

rxy=cov(x,y)σxσy(15)

cov(x,y)=1N∑i=1N(xi−x¯)(yi−y¯)(16)

σx=1N∑i=1N(xi−x¯)2,and∑y=1N∑i=1N(yi−y¯)2(17)

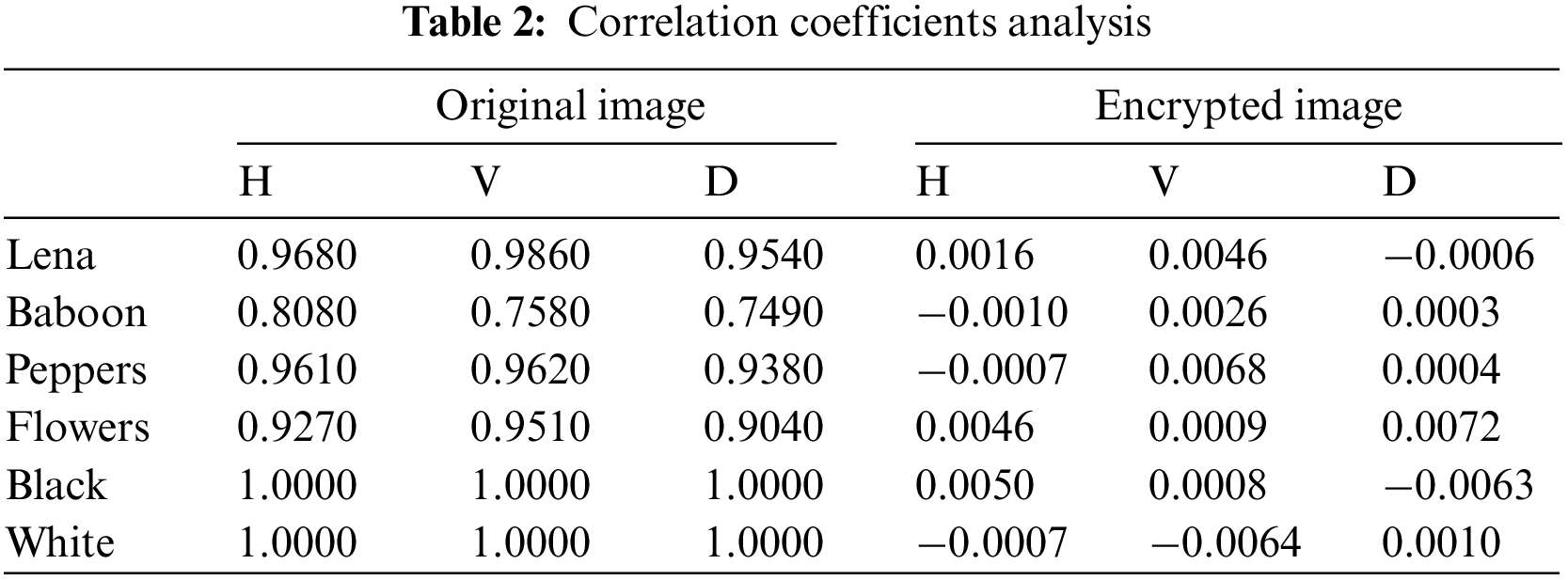
where x and y are two neighboring grayscale values and N is the total number of pixels in the image. In Table 2, we display the correlation coefficients between the original and encrypted images. Based on the results, the suggested approach successfully removes the close association between neighboring pixels in the original image. Using an encrypted image, an attacker cannot gather useful information.

4.4 Information Entropy Analysis

Entropy identifies the texture of an image by measuring its randomness. The formula below calculates the entropy (H) for a message source (s).

H(s)=∑i=12l−1⁡p(si)log2⁡(1p(si))(18)

The entropy is expressed in bits, and H(s) represents the probability of a symbol si. In order to achieve the best encryption, the entropy value should be as close to 8 as possible.

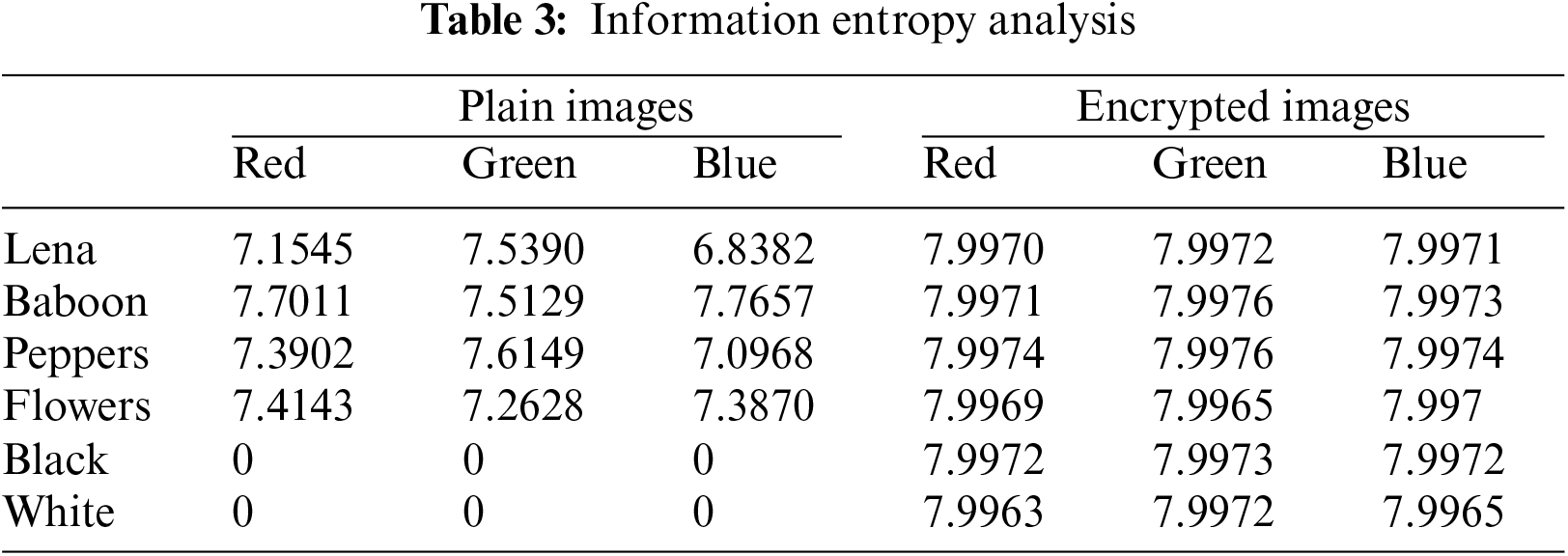
Table 3 computes and tabulates the entropy of the six plain images and their associated encrypted images. The encrypted image’s entropy value is closer to the theoretical value, according to Table 3. This proves that the proposed encryption method can withstand statistical attacks.

4.5 Differential Attacks Analysis

Generally, minor modifications in the plain image should not affect an encryption algorithm (for example, changing only one pixel). It is possible to observe changes in the input image by making small changes. This method can find the relationship between the encrypted and original images. The number of pixel change rate (NPCR) and unified average changing intensity (UACI) were used to assess how one-pixel change affects the entire encrypted images with the proposed encryption method. The following formulas calculate NPCR and UACI:

NPCR=∑i,jD(i.j)L×100% (19)

UACI=1L[∑i,j|C1(i,j)−C2(i,j)|255]×100% (20)

Table 4 displays the outcomes for six images. The result shows that the proposed encryption technique is immune to differential attacks and has a high level of security.

4.6 Robustness Analysis

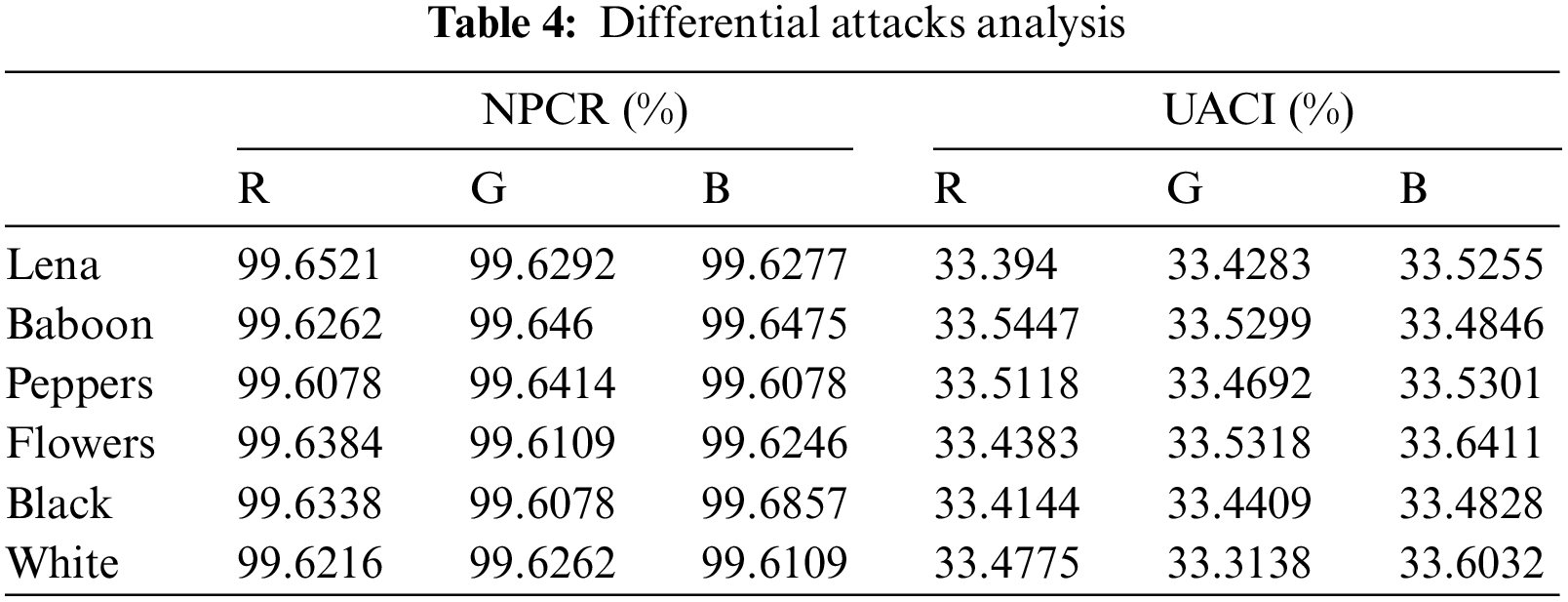
Image encryption algorithms should be evaluated on their robustness as well. Information security comprises three elements: confidentiality, integrity, and availability. Confidentiality can be guaranteed via statistical randomness, while integrity and availability can be guaranteed via robustness. In order to check the robustness of the encryption algorithm with changing data, the encrypted image is given a salt-and-pepper effect. Figs. 6a and 6b demonstrate that the algorithm resists salt-and-pepper noise in a certain way. Although we cannot retrieve the plain image from the decrypted image with added noise, the information of the plain image can still be seen. Then, to check the robustness of the encryption algorithm in the event of data loss, we removed part of the image’s data. Based on the results in Figs. 6c and 6d, the algorithm can still resist an attack in case data is lost.

Figure 6: Robustness analysis: (a) 0.1 salt and pepper noise in encrypted image; (b) 0.1 percent salt and pepper noise in decrypted image; (c) ¼ Loss of data in encrypted image; (d) ¼ Loss of data in decrypted image

4.7 Security Comparison Analysis

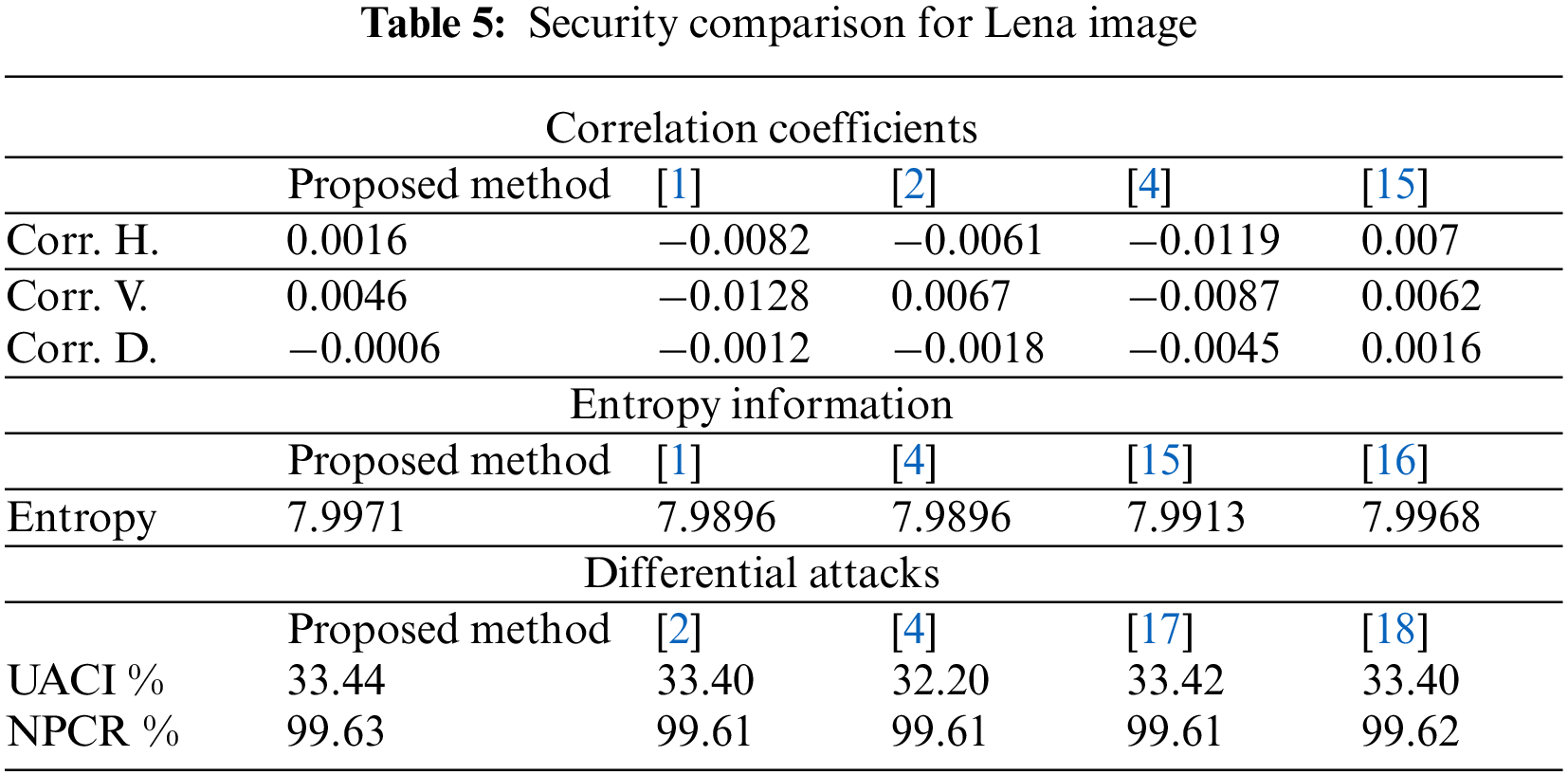
The suggested image encryption strategy is compared to the security of competing systems based on various parameters. For simplicity, we use the image of Lena for comparison. Table 5 lists the findings of the correlation comparison (Colored images are calculated by averaging horizontal, vertical, and diagonal directions), information entropy, UACI, and NPCR. The results showed that the proposed encryption method outperforms other systems in terms of security.

5  Conclusions

In this paper, we proposed a method of encrypting color images that uses chaotic maps and DNA. This paper has analyzed an image cryptosystem that used hyper-chaotic systems and a variety of technologies. We properly utilized hyper-chaotic systems to generate eight sequences, of which four scramble the pixel locations and break up the correlations between them (confusion process). The other four change the value of pixels (diffusion process). Additional techniques, such as SHA-256 and SHA-384, are used as a source of strength for plain image sensitivity by confounding the relationship between the plain image and the initial conditions values of hyper-chaotic systems. The technique of DNA coding is employed to improve the cryptosystem’s security. Confusion and diffusion have yielded an entropy value of 7.997 bit and 2200 key space, and the correlation coefficient is nearly zero. The efficacy of the method utilized has been verified through numerous evaluations, and the results show that it is resistant and effective against attacks like statistical and brute-force attacks. Furthermore, the proposed encryption method is more efficient than several existing color image encryption algorithms.

Funding Statement: This research is funded by Universiti Sains Malaysia (USM) via an external Grant Number (304/PNAV/650958/U154).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

1. X. Wu, K. Wang, X. Wang, H. Kan and J. Kurths, “Color image DNA encryption using NCA map-based CML and one-time keys,” Signal Processing, vol. 148, no. 9, pp. 272–287, 2018. [Google Scholar]

2. N. Iqbal, R. A. Naqvi, M. Atif, M. A. Khan, M. Hanif et al., “On the image encryption algorithm based on the chaotic system, DNA encoding, and castle,” IEEE Access, vol. 9, pp. 118253–118270, 2021. [Google Scholar]

3. J. Wu, X. Liao and B. Yang, “Image encryption using 2D Hénon-Sine map and DNA approach,” Signal Processing, vol. 153, no. 7, pp. 11–23, 2018. [Google Scholar]

4. Q. Liu and L. Liu, “Color image encryption algorithm based on DNA coding and double chaos system,” IEEE Access, vol. 8, pp. 83596–83610, 2020. [Google Scholar]

5. X. Wang and L. Liu, “Image encryption based on hash table scrambling and DNA substitution,” IEEE Access, vol. 8, pp. 68533–68547, 2020. [Google Scholar]

6. X. Y. Wang, P. Li, Y. Q. Zhang, L. Y. Liu, H. Zhang et al., “A novel color image encryption scheme using DNA permutation based on the lorenz system,” Multimedia Tools Applications, vol. 77, no. 5, pp. 6243–6265, 2018. [Google Scholar]

7. H. R. Amani and M. Yaghoobi, “A new approach in adaptive encryption algorithm for color images based on DNA sequence operation and hyper-chaotic system,” Multimedia Tools Applications, vol. 78, no. 15, pp. 21537–21556, 2019. [Google Scholar]

8. X. Wang, Y. Wang, X. Zhu and C. Luo, “A novel chaotic algorithm for image encryption utilizing one-time pad based on pixel level and DNA level,” Optics and Lasers in Engineering, vol. 125, no. 2, pp. 105851, 2020. [Google Scholar]

9. L. A. Shihab, “Technological tools for data security in the treatment of data reliability in big data environments,” International Transaction Journal of Engineering, Management, & Applied Sciences & Technologies, vol. 11, no. 9, pp. 1–13, 2020. [Google Scholar]

10. X. Wang and M. Wang, “A hyperchaos generated from lorenz system,” Physica A: Statistical Mechanics and its Applications, vol. 387, no. 14, pp. 3751–3758, 2008. [Google Scholar]

11. O. E. Rossler, “An equation for hyperchaos o.e. rossler,” Physics Letters A, vol. 71, no. 2, pp. 155–157, 1979. [Google Scholar]

12. S. M. Abdullah and I. Q. Abduljaleel, “Speech encryption technique using S-box based on multi chaotic maps,” TEM Journal, vol. 10, no. 3, pp. 1429–1434, 2021. [Google Scholar]

13. T. S. Ali and R. Ali, “A new chaos based color image encryption algorithm using permutation substitution and boolean operation,” Multimedia Tools Applications, vol. 79, no. 27–28, pp. 19853–19873, 2020. [Google Scholar]

14. H. A. Yoirnis and T. Y. Abdalla, “Hiding processing approaches for digital images encryption using wavelet transform,” Basrah Journal for Engineering Science, vol. 8, no. 1, pp. 1–12, 2008. [Google Scholar]

15. P. Liu, T. Zhang and X. Li, “A new color image encryption algorithm based on DNA and spatial chaotic map,” Multimedia Tools Applications, vol. 78, no. 11, pp. 14823–14835, 2019. [Google Scholar]

16. A. Rehman, X. Liao, R. Ashraf, S. Ullah and H. Wang, “A color image encryption technique using exclusive-OR with DNA complementary rules based on chaos theory and SHA-2,” Optik, vol. 159, no. Supplement C (May), pp. 348–367, 2018. [Google Scholar]

17. H. G. Mohamed, D. H. ElKamchouchi and K. H. Moussa, “A novel color image encryption algorithm based on hyperchaotic maps and mitochondrial DNA sequences,” Entropy, vol. 22, no. 2, pp. 158, 2020. [Google Scholar] [PubMed]

18. M. Samiullah, W. Aslam, H. Nazir, M. I. Lali, B. Shahzad et al., “An image encryption scheme based on DNA computing and multiple chaotic systems,” IEEE Access, vol. 8, pp. 25650–25663, 2020. [Google Scholar]