Identifying Counterexamples Without Variability in Software Product Line Model Checking

1  Introduction

A software product line is defined as a “set of software-intensive systems that share a common, managed set of features satisfying the specific needs of a particular market segment or mission and that are developed from a standard set of core assets in a prescribed way” [1]. It is essential in developing any product using software that requires a communication infrastructure. SPL is widely used in embedded and critical systems [2], such as automobiles or avionics. Critical systems require high quality, security, formal verification and proper analysis techniques. Model checking is an automatic technique to verify the behaviour model of a system against a property expressed in temporal logic [3].

However, the main challenge in model checking is the state explosion problem that may occur when the system under verification has parallel components, which is even harder for SPL. In the worst case, as an SPL with ‘n’ features yields up to ‘2n’ individual systems to verify, variability dramatically exacerbates state explosion. It is also not feasible to apply single-system model checking to the thousands of variants that can compose real-world SPL [4].

There have been many variability-aware techniques to address the SPL model-checking problem [5–7]. However, these techniques verify the standard behavior of several products only once. Abstraction technology is a powerful technique used in single-system model checking, such as CEGAR (Counterexample Guided Abstraction-Refinement)-based [8–10] model checker SLAM [11,12] and Basic Linear Algebra Subprograms Technical (BLAST) [13]. One of the main challenges of adopting the abstraction technique in model checking lies in identifying whether a reported counterexample is spurious or authentic. Doyen et al. [8] proposed an approach to check whether a counterexample is spurious. A combination of 0–1 Integer Linear Programming (ILP) and machine learning models is used for refining the abstraction. Tian et al. [14] proposed a new definition of “failure state”, called the “false state”. The failure state depends only on its previous and successor state, thus enabling the search to be naturally parallelized. Such approaches make the identification of spurious counterexamples more efficient in single-system model checking. However, this approach cannot be directly applied to SPL model checking, as they didn’t consider the variability.

To the best of our knowledge, Cordy et al. [4,15] were the first to introduce abstraction technology into SPL model checking, which set nicely as the basis for abstraction-based SPL model checking. Identification of reported counterexamples utilizing abstraction technologies in SPL is exacerbated because the variability constitutes a new source of complexity. The counterexample may be valid for some products but spurious for others. σ=s^0α0s^1α1…sn Set as a counterexample, a feature expression characterizes the products to execute it. The counterexample ‘σ’ corresponds to the actual paths explored in the original model step by step. The feature expression σb′(i) represents the products that can execute the counterexample in the concrete model in the current phase. Compared with ‘σb’, it is easy to detect spurious products and decide it needs refinement at the current step. The significant advantage of the method is that it can analyze spurious products at each step. The computation of reachable relations is essential for identifying the violated products. It represents the sets of features visiting each state. However, the comparison of feature expressions is tedious. In the worst case, the analysis will reach the last state in the counterexample with no product violating the property since the aim of detection was not to identify the spurious products, but the violated products. Furthermore, the frequent refinement-abstraction process will lead to the non-prominent performance of their approach.

This paper focuses on efficiently identifying genuine counterexamples when using state abstraction in SPL model checking. Here, we check whether the counterexamples are spurious or genuine. Also, we analyze whether there exists any violated products by the genuine counterexamples. The spurious counterexamples are for guiding the refinement. By analyzing counterexamples in the abstract model, we observed that spurious products are due to the failure state (Section 3 describes the approach). Thus, we can transpose the check of whether a counterexample is spurious or genuine to check whether there exists a failure state in the counterexample. Any violated product must correspond to some genuine counterexamples with no failure state. Initially, we check whether there exist any failure states in the counterexamples. Then we extract violated products by the genuine counterexamples with no failure state. Identifying whether a failure state exists in the counterexample relies on the merging of corresponding concrete states, rather than the feature expression in the transition. The feature expressions can have ignored during the process of identifying counterexamples in the abstract model. Our approach is similar to the method proposed by the authors in [14]. However, it is only suitable for single-system. It is also easier to identify counterexamples. Our proposed approach applies to SPL.

Furthermore, we propose a new strategy, which performs the refinement after discovering all spurious counterexamples and proves its correctness.

Our main contributions are summarized as follows.

•   Instead of identifying spurious products through tedious feature comparison expressions along the path for determining reachable relations, we only check whether there exist failure states with less memory space while checking the counterexamples.

•   We adopt a parallel detection algorithm to check failure states, which can improve the efficiency of checking counterexamples with thousands of millions of states in great examples in SPL.

•   We evaluate the benefits of our approach. Compared with the existing approaches, it has shown a significant improvement in verifying the products varying with the growth of the system scale.

The rest of the paper is organized as follows: Section 2 surveys related work, Section 3 introduces the background, and Section 4 describes IsSpurious-I. Section 5 describes the genuine counterexamples in detail. Section 6 presents the algorithm for checking counterexamples and Section 7 describes the experimental results. Finally, Section 8 concludes the findings and discusses future work.

2  Related Work

This section briefly presents relevant work related to the SPL model checking. The most intuitive method in SPL model checking relies on checking each product independently. In this case, off-the-shelf abstraction technologies of a single system are applied directly. Still, the number of products is vast, and it does not take the commonality among them into consideration. Benduhn et al. [16] divides the SPL model into annotation-based and composition-based from the viewpoint of modeling techniques, and the commonality is that they all modeled SPL as a whole.

Beckert et al. [17] discussed how features could be modeled in Calculus of Communicating Systems (CCS) [18] and integrated into SPL. The SPL method is represented as a labeled transition system whose transitions are annotated with feature combinations, and the result is a set of products that satisfy a property. Frank et al. [19] showed how product lines could have been modeled as an extension to I/O automata, who adapted the algorithm of Nouri et al. [20] to verify an SPL model. The variability model specifies the legal products of the product line to ensure that the model checker only explores legal products. Abbas [21] discussed an approach as Family-TS, which includes all transitions of all products into a single TS. As there is no explicit information about the mapping between transitions and products, it only can be used to reason about a limited set of properties. To include more information about the mapping between transitions and products of the product line, Ter Beek et al. [22] proposed to use “Modal Transition Systems (MTS).” An MTS is a TS in which a transition can be either mandatory or optional.

Classen et al. [7,23,24] proposed a behavior model called FTS, which can link a given execution to the same set of products that produce this execution. Here, all the products are modeled in one system, and each transition is labeled with a feature expression. Hence, the details regarding the mapping between transitions and products are completely revealed. Cordy et al. [4,19,25–27] set the basis of F-abstraction, which we recapitulated in Section 2. The authors present two abstraction strategies and three abstraction methods based on FTS. One of the fundamental differences between their approach and our approach is that the former is based on variability and considers features throughout the whole checking process. Our approach identifies the real counterexamples in an efficient manner. The approach considers variability only when it finds the real counterexamples. Dimovski et al. [28,29] presents a variability-specific abstraction refinement (with a low number of variants) and then uses a single-system model checker to check the SPL.

3  Background

In this section, we introduce the basic concepts and definitions of featured transition systems (FTS), along with the verification and abstraction of SPL behavior model.

3.1 Featured Transition Systems

In model checking, Transition System (TS) [3] represents the behavior of individual products. TS is a form of Kripke structure that is suitable for modeling the behavior of individual products. However, it can neither represent the behavior of an SPL nor link each behavior to the same set of products that can execute it. Classen et al. [7] proposed a Featured Transition System (FTS) to overcome this problem by describing the combined behavior of an entire system family.

In FTS, an additional feature expression labels each transition. The additional feature expression specifies which combinations of features are required to trigger the change that will form an FTS. A feature model (FM) [19] is a tree-like hierarchy of features/components, representing the information on all possible products of SPL in terms of features and relationships among them. The FM consists of a feature diagram and additional constraints. The semantics of an FM ‘d’ defined over a set of features ‘F’ is the set of all valid products, denoted by [[d]]FM⊆2F [20]. Four structural and semantic relationships exist between the parent and child features. The relationships correspond to alternative, mandatory, or optional. Consider the FM of an online payments SPL sample as shown in Fig. 1. There are seven features in which Unionpay (U), Alipay (A), and Wechat (W) are optional. At the same time, QR-code (Q) and Account (I) are or-decomposable.

Figure 1: A spurious counterexample

An FTS is defined as follows.

Definition 1. An FTS is defined as a tuple (S,Act,trans,I,AP,L,d,η). ‘S’ correspond to a set of states and ‘Act’ a set of actions. trans⊆S×ACT×S is the transition relation. I⊆S is a set of initial states. AP is a set of atomic propositions. L:S→2AP is a labeling function that associates every state with the set of atomic propositions. d is an FM over feature F, and η:trans→B(F) is a total function labeling each transition with a feature expression, i.e., Boolean function over the set of features. The set of products that satisfy the criteria is denoted by [[η(t)]].

3.2 Abstraction in SPL Model Checking

Abstraction technologies are used to solve the state explosion problem of single-system model checking. The disadvantage of the abstraction technique is that the counterexamples may be spurious, as the abstract model may introduce more behaviors that are not present in the original model [30]. Thus, if a property is valid on the abstract model, it is also valid on the original one. If a property is invalid on the abstract model (obtain a counterexample), it may be valid on the original model (the counterexample is spurious). That means the abstraction function is too coarse to validate the property, and the abstract model needs refinement. This process repeats until it finds a real counterexample and no counterexample. In the latter case, the property is satisfied in the original model.

The concept of abstraction is utilized in SPL model checking in such a way that the abstract model preserves the behavior of all valid products modeled by the FTS. The abstraction function of FTS must add a requirement [4,31]. If a product can execute a concrete transition, it must be able to run the corresponding abstract transition too. The F-abstraction is a surjection, h: S→S^, h(s)=h(s′)⇒L(s)=L(s′). An abstraction of an FTS under ‘h’ is FTSh=(S^,Act,transh,Ih,AP,Lh,d,ηh), S^={h(s)|s∈S}, Ih={h(s0)|s0∈I}, Lh(h(s))=L(s), transh is defined as s→αs′⇒h(s)→αh(s′) and ηh.

(∨s∈h−(s^),s′∈h−(s′^)⋅s→αs′η(s,α,s′))⇒ηh(s^,α,s^′)

or equivalently

(∪s∈h−(s^),s′∈h−(s′^)⋅s→αs′[[η(s,α,s′)]])⊆ηh(s^,α,s^′)(1)

There are two fundamental differences between SPL and single-system model checking: Firstly, it is different in obtaining the abstract model. In SPL, all the feature expressions between h−(s^i) and h−(s^i+1) should be made in disjunction to ensure that (1) is satisfied. While in a single system, one transition between h−(s^i) and h−(s^i+1) is enough to construct a relation between s^i and s^i+1. Secondly, they are different in searching counterexamples. As it is essential to identify all the violated products in an SPL, the process cannot stop as soon as it finds one real counter-example, except that this counterexample is executable by all products. The model checker will ignore the violations performed by other products. Thus, an SPL-specific model-checking algorithm should search for all the valid counterexamples in the model. However, in a single system, one real counterexample is enough to demonstrate this violation.

4  Exposition of IsSpurious-I

In this section, we will illustrate the process of identifying counterexamples proposed by Cordy et al. [4]. To the best of our knowledge, it is the state-of-the-art approach in SPL model checking. The FTS model checker may return several counterexamples. The authors propose two refinement strategies. 1. Find All Before Refining (FABR) is in the model checker to find all the counterexamples, then check themselves, and refine the model. 2. Refine When Found One (FWFO) where, as soon as the model checker finds one counterexample, it checks the example, and refines the model [32]. The underlying causes of spurious products are then analyzed by formally demonstrating their algorithm, which is called as the “IsSpurious-I”, when using state abstraction in SPL model checking.

σ=s^0α0s^1α1…s^n is set as a finite counterexample in a state abstraction model, and σb∈B(F). σ∈Prefix ([[(FTSh)|p]])TS is used for all p∈[[σb]]. σb represents the products that violate the property FTSh, and have not been discovered to be spurious. σb′ represents the products that can execute the counterexample in FTS up to the current step, it initializes the feature expression λ. All the detected products can reach the initial states.

Si is a set of binary tuples that include reachable states in each h−(s^i)(0≤i≤n) from I (the set of initial states). It then helps to find out the corresponding feature expressions labeling each state. For the sake of simplicity, we use the reachable state set Si. bi denotes the corresponding feature expressions. Si is then computed under the following conditions:

1)   for state s∈Si(0≤i≤n), it is reachable from Sk(0≤k≤i−1).

2)   for state s∈Si(0≤i≤n), if (s′,s)∈trans, it has either s′∈Si or s′∈Si−1.

3)   for state s, the corresponding feature expressions are labelled with feature expression. s can be reached by products in [[b]].

ℜ(s) is used to denote the set of direct successors state s∈S. ℜ(S) represents the set of direct successors of all states in S. S0k,k≥0, is computed as follows:

S00={(i,λ)|i∈I∩h−(s^0)}

S01={(s,b)|s∈ℜ(S00)∩h−(s^0),b=∨(s′,b′)∈S00,(s′,s)∈transb′∧η(s′,s)}

S02={(s,b)|s∈ℜ(S01)∩h−(s^0),b=∨(s′,b′)∈S01,(s′,s)∈transb′∧η(s′,s)}…

S0k={(s,b)|s∈ℜ(S0k−1)∩h−(s^0),b=∨(s′,b′)∈S0k−1,(s′,s)∈transb′∧η(s′,s)}

So, S0=∪k=0∞S0k, S0={s|(s,b)∈S0}, b0=∨(s,b)∈S0b. Likewise, for each i(0≤i≤n), Sik(k≥0) can be computed by:

Si0={(s,b)|s∈ℜ(Si−1)∩h−(s^i),b=∨(s′,b′)∈Si−1,(s′,s)∈transb′∧η(s′,s)}

Si1={(s,b)|s∈ℜ(Si0)∩h−(s^i),b=∨(s′,b′)∈Si0,(s′,s)∈transb′∧η(s′,s)}

Si2={(s,b)|s∈ℜ(Si1)∩h−(s^i),b=∨(s′,b′)∈Si1,(s′,s)∈transb′∧η(s′,s)}…

Sik={(s,b)|s∈ℜ(Sik−1)∩h−(s^i),b=∨(s′,b′)∈Sik−1,(s′,s)∈transb′∧η(s′,s)} Consequently,Si=∪k=0∞Sik,Si={s|(s,b)∈Si}, bi=∨(s,b)∈Sib. h−(s^i) is finite, there must exist a natural number m, ∪k=0m+1Sik=∪k=0mSik. Each state s in Si is reachable from I,S0,…,Si−1 in the original model. To check the spurious products, bi is added to σb′, that is

σb′←σb′∧bi

Compared to the result with σb, if σb⇏σb′ is satisfied, it means that any product in [[σb]]∖[[σb′]] is a spurious product, and a refinement should be performed to eliminate it.

Fig. 1 represents a simulated FTS with its state abstraction, and the counterexample is ⟨s^0,s^1,s^2,s^3,s^4⟩. In the abstract model, we can obtain σb=λ∧f4∧f13∧(f24∨f25)∧f32. For convenience, we ignore the action on the transition. The label fi simulates the feature expression on the transition. In this example, I={0}.

S00={(i,λ)|i∈I∩h−(s^0)}={(0,λ)}

S01={(s,b)|s∈ℜ(S00)∩h−(s^0),b=∨(s′,b′)∈S00,(s′,s)∈transb′∧η(s′,s)}={(1,λ∧f1),(2,λ∧f2)}

S02={(s,b)|s∈ℜ(S01)∩h−(s^0),b=∨(s′,b′)∈S01,(s′,s)∈transb′∧η(s′,s)}={(3,λ∧f1∧f3)}

S03={(s,b)|s∈ℜ(S02)∩h−(s^0),b=∨(s′,b′)∈S02,(s′,s)∈transb′∧η(s′,s)}=∅.

Thus, S0=S00∪S01∪S02={(0,λ),(1,λ∧f1),(2,λ∧f2),(3,λ∧f1∧f3)}. Then, there have:

S0={0,1,2,3},B0=λ∨(λ∧f1)∨(λ∧f2)∨(λ∧f1∧f3)=λ.

Similarly, it has:

S1={6,8},B1=λ∧f4;

S2={10,11,12},B2=λ∧f4∧f13;

S3={22,23,24},B3=λ∧f4∧f13∧(f24∨f25);

S4=∅,B4=∅.

Fig. 1 shows the spurious products caused by the merging of states in h−(s^3). To eliminate it, we need to decompose states in h−(s^3) into two separate state sets {22, 23, 24} and {21}.

To sum up, variability is the basis of IsSpurious-I. To identify the spurious products, each Bj(0≤j≤i−1) should be computed sequentially, as the value Bj relies on the complete prefix ⟨B0,B1,…,Bj−1⟩.

5  Real Counterexample

The ultimate goal of abstraction-based SPL model checking is to identify all the violated products. The focus is not on the spurious products [33]. Two cases may occur while checking the abstract model: 1) no counterexample is returned, which means all the products that are currently being checked satisfy the property. 2) Several counterexamples are returned, where they will be further checked to identify whether it is spurious. The violated product must correspond to a real path in the original model. Only genuine counterexamples can help in the identification of the violated products.

Fig. 1 presents the derivation of the spurious products. For example, the spurious products contain feature f32, which is derived from the merging of concrete states of the original model corresponding to h−(s^3). Feature f32 triggers the transition from abstract state s^3 to s^4, which does not exist in the corresponding concrete state set from S3 to S4, in which the abstract state s^3 is failure state. We can eliminate the spurious products by identifying failure states s^3 and splitting the corresponding concrete state set h−(s^3), which results in theorem 1.

Theorem 1. FTSh is an abstract model of FTS, and σ=s^0α0…s^n be a counterexample. If there is at least one failure state in σ, then counterexample σ is spurious.

Proof 1 follows from the definition of failure state.

While checking for the counterexamples, we need to identify whether a failure state exists in the counterexample without variability. Consequently, the computation of feature expression σb′, and the computation of reachability relation sets Si mentioned in section III should be avoided.

In this way, detecting failure states in SPL is analogous to a single system, but differs significantly from the case where the counterexample is accurate. The approach then extracts the absolute executable paths. Our proposed approach is inspired by the approach proposed by Kusano et al. [11]. We propose a novel approach to check counterexamples in abstraction-based SPL model checking.

Initially, we formally define the failure state. Sini0,Sini1,⋯, and Sinin,0<i≤n, are defined as given below:

Sini0={s|s∈h−(s^i),s′∈h−(s^i−1)and(s′,s)∈trans}

Sini1={s|s∈h−(s^i),s′∈Sini0and(s′,s)∈trans}

Sini2={s|s∈h−(s^i),s′∈Sini1and(s′,s)∈trans}

…

Sinin={s|s∈h−(s^i),s′∈Sinin−1and(s′,s)∈trans}

Sini=∪j=0∞Sinij. Since h−(s^i) is finite, there must exist a natural number n, such that ∪j=0n+1Sinij=∪j=0nSinij. Here,Sini0 denotes the set of states h−(s^i) with inputting edges from the states in h−(s^i−1), and Sini1 denotes the set of states h−(s^i) with inputting edges from the states Sini0, and so on.

Sin00={s|s∈h−(s^0)∩I}

Sin01={s|s∈h−(s^0),s′∈Sin00and(s′,s)∈trans}

Sin02={s|s∈h−(s^0),s′∈Sin01and(s′,s)∈trans}

…

Sin0n={s|s∈h−(s^0),s′∈Sin0n−1and(s′,s)∈trans}

Here, Sin00 is the intersection of initial states I and h−(s^0). Symmetrically,Souti0,Souti1,⋯ and Soutin,0≤i<n are also defined.

Souti0={s|s∈h−(s^i),s′∈h−(s^i+1)and(s,s′)∈trans}

Souti1={s|s∈h−(s^i),s′∈Souti0and(s,s′)∈trans}

Souti2={s|s∈h−(s^i),s′∈Souti1and(s,s′)∈trans}

…

Soutin={s|s∈h−(s^i),s′∈Soutin−1and(s,s′)∈trans}

Then we have Souti=∪j=0∞Soutij. Similar to Sini, a natural number ‘n’ should exist. ∪j=0n+1Soutij=∪j=0nSoutij. Here Souti0 denotes the states h−(s^i) with outputting edges to the states h−(s^i+1), and Souti1 denotes the states h−(s^i) with outputting edges to the states Souti0, and so on. We also noted that, for the last state s^n in the counterexample,

Soutn0={s|s∈h−(s^n)∩F}

Soutn1={s|s∈h−(s^n),s′∈Soutn0and(s,s′)∈trans}

Soutn2={s|s∈h−(s^n),s′∈Soutn1and(s,s′)∈trans}

…

Soutnn={s|s∈h−(s^n),s′∈Soutnn−1and(s,s′)∈trans}

F is the set of acceptable states in the original model.

Si=Sini∩Souti, if Si=∅, σ is spurious. Since Si−1 cannot reach Si+1 through Si in the original model. However, for each counterexample σ,Si≠=∅, σ may still be spurious.

The counterexample without a failure state is a real counterexample. There are three differences in identifying counterexamples between a single system and SPL. Firstly, the number of counterexamples identified is different. In a single system model checking, one real counterexample is enough. In SPL, the objective is to identify all products that violate the property. All the counterexamples that exist in the abstract model are found out for ensuring completeness. Secondly, the transitions along the counterexample path are different. In SPL, all feature expressions should make a disjunction for ensuring that (1) is satisfied. In a single system, one transition is enough to construct a transition between s^i and s^i+1. Thirdly, if a real counterexample is found in a single system, the property is violated and the checking process will be terminated. In SPL, all the genuine counterexamples are then analyzed to discern violated products in the original model.

Fig. 2 shows our abstraction-refinement strategy, called New-FABR. Firstly, we apply an initial state abstraction to obtain an abstract FTS given to the model checker along with the FM and a formula [λ]φ, which represents the detected products, and φ is a formula. The model checker may return two impossible cases: 1) no counterexamples, implying that all checked products at the current loop satisfy the property. The model checker then terminates the checking. 2) Several counterexamples. For the real counterexamples that have no failure states, we will further discern the violated products from the absolute paths. It is then updated to avoid the violated products, so that the same can be detected again in the next loop. Otherwise, we refine the model to build a new abstract model after all the spurious counterexamples are detected. The system repeats the process until no counterexamples are returned, or the updated feature quantifier is unsatisfied.

Figure 2: Overview of New-FABR

Theorem 2. The New-FABR strategy is terminable and correct in state abstraction-based SPL model checking.

Proof 2. At the end of verification, the New-FABR procedure can have three possibilities: 1) no counterexample is found in the current loop and the procedure is terminated. 2) Some genuine counterexamples have been found, and the feature quantifier λ is updated into λ′. 3) Several failure states have been found, and it triggers a refinement. Here, λ′ is a subset of λ, and the number of updates is finite. Hence, the number of refinements is also finite, thus making the strategy terminable.

p is set as a valid product. After verification, any of the three cases may occur: 1) The system finds no counterexample, and all products satisfy the property. ‘p’ also satisfies the property; 2) ‘p’ is associated with a real counterexample, thus violating the property; 3) ‘p’ is associated with spurious counterexamples. Hence, ‘p’ is a spurious product. In this case, p will have to be rechecked after a refinement, thus making it a correct strategy.

Similar to the FABR, the New-FABR waits for the model checker to find all the counterexamples and checks them. The differences are: 1) the FABR considers feature throughout the checking process, while the New-FABR considers it only when it finds the real counterexamples; 2) the New-FABR only returns the violated products. Other products that are not mentioned implicitly satisfy the property. The FABR returns both the satisfied and violated products explicitly.

6  Checking Counterexamples

In this section, we present an algorithm for checking counterexamples in SPL. The abstract model FTS works by selecting a set of variables insensitive to the desired property to be invisible [8]. The set of variables involved in the FTSV is separated into two disjoint parts: VV and VI. V=VV∪VI. A set of values ‘V’ indicate the state of the system. In the original FTS model, all variables are visible. In order to obtain an abstract model FTSh, some variables are selected to be invisible. Therefore, an original model FTS=(S,Act,transh,I,AP,L,d,η), a selected set of visible variables VV, and an abstract model FTSh=(S^,Act,trans,Ih,AP,L^,d,ηh) can be obtained by algorithm F-ABSTRACTION as shown below.

It is similar to a single system’s abstract algorithm except that in step 5, the feature expressions label ηh between abstract state s^ and abstract state s′^ should be assigned as the disjunction of feature expressions between h−(s^) and h−(s′^) in the original FTS. Any product that can trigger a concrete transition in the original mode must be able to trigger the corresponding abstract transition in the abstract model as well. Once the system obtains the abstraction model from the original model, a model checker will check whether the property is satisfied on the abstract model. If the system doesn’t return any counterexamples, it means that it satisfies the property, and is valid for all the products. If the system returns several counterexamples, it calls a function to verify the same.

7  Evaluation

To simulate the state space of SPL and make the results more general, we designed our experiments in the following aspects: 1) preprocessing, where we construct the feature models manually. These feature models are used to simulate the constraint of products. SPL can detect them by providing the number of features. The structural and semantic relationship between a parent feature and its child features is alternative, mandatory, or optional; 2) randomly generate the original models by providing the numbers of states, transitions and label each transition with a random feature from the corresponding feature model. 3) achieve the abstract models by selecting a set of variables from V to the abstract state [8]. 4) select several paths (i.e., counterexample) randomly in the abstract model by providing the number of counterexamples. We implement algorithms IsSpurious-I and CheckFailure on the same selected paths and record the time consumed.

Fig. 3 presents the curves depicting the average time consumed by the two algorithms on different models. The horizontal axis (s, t, f) represents the size of the model and the number of features, and the vertical axis describes the average time (ms) used for checking counterexamples.

Figure 3: Comparison between algorithm CheckFailure and IsSpurious-I

To mitigate the effect of randomness, we generated five models for each size and the test is run for ten times for each model, and the average time is computed. Table 1 shows the model size and the experimental results. We performed the experiments on a 4-core PC. We randomly generate models with the size (s, t, v, f, c) being (10, 50, 2, 2, 2), (50, 1250, 4, 4, 5), (100, 5000, 8, 8, 10), (500, 125000, 12, 10, 15), (1000, 500000, 16, 12, 20), (5000, 13000000, 20, 14, 25), (10000, 50000000, 24, 16, 30) and (50000, 180000000, 28, 18, 35) respectively. s denotes the number of states, t denotes the number of transitions, v denotes the number of variables, f denotes the number of features in the original model and c denotes the number of counterexamples in the abstract model. Algorithm IsSpurious-I is then compared with the CheckFailure.

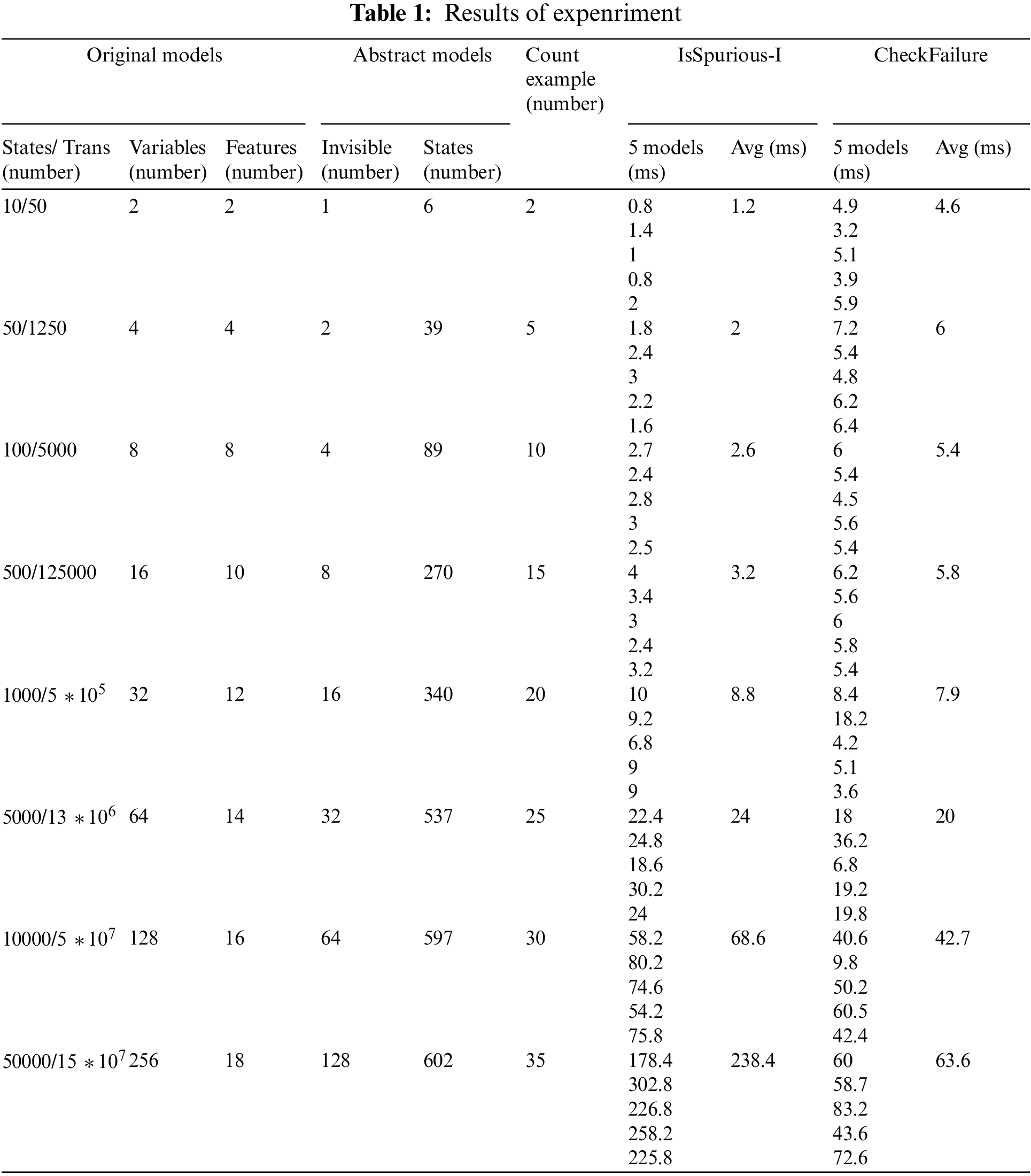
As the scale of the model grows, our algorithm proves to outperform other methods. Our approach is particularly suitable for SPL model checking, which has a super large scale. The time difference between identifying genuine and spurious counterexamples is significant in algorithm IsSpurious-I, while it is close in algorithm PEIC [34]. This is because the algorithm “IsSpurious-I” needs to traverse the entire path to identify a real counterexample. Also, it requires finding the first failure state only to identify a spurious counterexample. We theoretically prove the feasibility of applying the rebate-guided model detection method to the product line. This idea is also verified experimentally.

8  Conclusions

We have presented a novel approach to separate the identification of the counterexamples from the search of the violated products in abstraction-based SPL model checking. This approach proves that it could not only avoid the time-consuming verification of spurious products, but also can make use of the most advanced single-system counterexample searching and identification method. To prove our method, we present a PEIC approach that modifies the state-of-the-art single-system counterexample identification technology [14], where the counterexample identification deals with expanding the reachable state sets in parallel. In addition, we design an FTDR strategy and integrate it with PEIC to reduce the number of refinements to only once at each refinement-abstraction loop. The experimental result shows that our algorithm performs better than IsSpurious-I, as the model size increases. The FTDR strategy combined with the PEIC algorithm can solve the problems of large-scale SPL model checking. In the future, we will integrate other advanced single-system model checking technologies into the SPL in the Internet of Things environment through ambient intelligence [35].

Acknowledgement: The authors would like to thank the anonymous reviewers for their selfless reviews and valuable comments, which have improved the quality of our original manuscript.

Funding Statement: The research in this paper was supported by the Fund of Excellent Youth Scientific and Technological Innovation Team of Hubei’s Universities (Project No: T201818); Science and Technology Research Program of Hubei Provincial Education Department (Project No: Q20143005); Guiding project of scientific research plan of Hubei Provincial Department of Education (Project No: B2021261).

Conflicts of Interest: The authors declare they have no conflicts of interest to report regarding the present study.

References

1. S. Gill, “A review of research and innovation in garment sizing,” Prototyping and Fitting, Textile Progress, vol. 47, no. 1, pp. 1–85, 2015. [Google Scholar]

2. S. Demissie, F. Keenan, and F. McCaffery, “Investigating the suitability of using agile for medical embedded software development,” in Proc. SPICE, Dublin, Ireland, vol. 29, pp. 409–416, 2016. [Google Scholar]

3. B. Woźna-Szcześniak, “Checking EMTLK properties of timed interpreted systems via bounded model checking,” in Proc. of the 2014 Int. Conf. on Autonomous Agents and Multi-Agent Systems, Paris, France, pp. 1477–1478, 2014. [Google Scholar]

4. M. Cordy, P. Heymans, A. Legay, P. -Y. Schobbens, B. Dawagne et al., “Counterexample guided abstraction refinement of product-line behavioural models,” in Proc. FSE, Hong Kong, China, pp. 190–201, 2014. [Google Scholar]

5. M. Varshosaz, L. Luthmann, P. Mohr, M. Lochau and M. Mousavi, “Modal transition system encoding of featured transition systems,” Journal of Logical and Algebraic Methods in Programming, vol. 106, pp. 1–28, 2019. [Google Scholar]

6. P. Asirelli, M. H. Ter Beek, S. Gnesi and A. Fantechi, “Formal description of variability in product families,” in 15th Int. Software Product Line Conf., Munich, Germany, pp. 130–139, 2011. [Google Scholar]

7. A. Classen, P. Heymans, P. -Y. Schobbens, A. Legay and J. -F. Raskin. “Model checking lots of systems: Efficient verification of temporal properties in software product lines,” in Proc. of the 32nd ACM/IEEE Int. Conf. on Software Engineering, Cape Town, South Africa, vol. 1, pp. 335–344, 2010. [Google Scholar]

8. L. Doyen, G. Frehse, G. J. Pappas and A. Platzer, “Verification of hybrid systems,” in Handbook of Model Checking, Springer Press, Springer, Cham, pp. 1047–1110, 2018. [Google Scholar]

9. E. Althaus, B. Beber, W. Damm, S. Disch, W. Hagemann et al., “Verification of linear hybrid systems with large discrete state spaces using counterexample-guided abstraction refinement,” Science of Computer Programming, vol. 148, pp. 123–160, 2017. [Google Scholar]

10. L. Ferretti, J. Kwon, G. Ansaloni, G. D. Guglielmo, L. P. Carloni et al., “Leveraging prior knowledge for effective design-space exploration in high-level synthesis,” IEEE Transactions on Computer-Aided Design of Integrated Circuits and Systems, vol. 39, no. 11, pp. 3736–3747, 2020. [Google Scholar]

11. Kusano M. and C. Wang, “Flow-sensitive composition of thread-modular abstract interpretation,” in Proc. of the 24th ACM SIGSOFT, Seattle, Washington, USA, vol. 1, pp. 799–809, 2016. [Google Scholar]

12. C. Iwendi, Z. Jalil, A. R. Javed, T. Reddy G and R. Kaluri, “KeySplitwatermark: Zero watermarking algorithm for software protection against cyber-attacks,” IEEE Access, vol. 8, pp. 72650–72660, 2020. [Google Scholar]

13. P. A. Abdulla and G. Delzanno, “Parameterized verification,” International Journal on Software Tools for Technology Transfer, vol. 18, no. 5, pp. 1–5, 2016. [Google Scholar]

14. C. Tian and Z. Duan., “Detecting spurious counterexamples efficiently in abstract model checking,” in Proc. of the 2013 Int. Conf. on Software Engineering, San Francisco, CA, USA, pp. 202–211, 2013. [Google Scholar]

15. M. Cordy, A. Classen, G. Perrouin, P. Y. Schobbens, P. Heymans et al., “Simulation-based abstractions for software product-line model checking,” in Proc. of the 34th Int. Conf. on Software Engineering, Zurich, Switzerland, pp. 672–682, 2012. [Google Scholar]

16. F. Benduhn, T. Thüm, M. Lochau, T. Leich and G. Saake, “A survey on modeling techniques for formal behavioral verification of software product lines,” in Proc. of the Ninth Int. Workshop on Variability Modelling of Software-Intensive Systems, Pisa, Italy, pp. 80–87, 2015. [Google Scholar]

17. B. Beckert, T. Bormer and D. Grahl, “Deductive verification of legacy code,” in Int. Symp. on Leveraging Applications of Formal Methods, Karlsruhe, Germany, pp. 749–765, 2016. [Google Scholar]

18. R. Sassioui, M. Jabi, L. Szczecinski, L. Le, M. Benjillali et al., “HARQ and AMC: Friends or foes?,” IEEE Transactions on Communications, vol. 65, no. 2, pp. 635–650, 2016. [Google Scholar]

19. A. Frank, A. Kleidon, and M. Alberti, “Earth as a hybrid planet: The anthropocene in an evolutionary astrobiological context.,” Anthropocene, vol. 19, no. 1, pp. 13–21, 2017. [Google Scholar]

20. A. Nouri, S. Bensalem, M. Bozga, B. Delahaye, C. Jegourel et al., “Statistical model checking QoS properties of systems with SBIP,” International Journal on Software Tools for Technology Transfer, vol. 17, no. 2, pp. 171–185, 2015. [Google Scholar]

21. A. K. Abbas, S. Qassim and H. H. Safi, “Systematic mapping study on managing variability in software product line engineering,” Diyala Journal of Engineering Sciences, vol. 8, no. 4, pp. 511–520, 2015. [Google Scholar]

22. M. H. Ter Beek, A. Fantechi, S. Gnesi and F. Mazzanti, “Modelling and analysing variability in product families: Model checking of modal transition systems with variability constraints,” The Journal of Logical and Algebraic Methods in Programming, vol. 85, no. 2, pp. 287–315, 2016. [Google Scholar]

23. C. Mattarei, “Scalable safety and reliability analysis via symbolic model checking”, Ph.D. dissertation, University of Trento, Trento, 2016. [Google Scholar]

24. A. S. Dimovski, A. S. Al-Sibahi, C. Brabrand and A. Wąsowski, “Efficient family-based model checking via variability abstractions,” International Journal on Software Tools for Technology Transfer, vol. 19, no. 5, pp. 585–603, 2017. [Google Scholar]

25. H. Mao, Y. Chen, M. Jaeger, T. D. Nielsen, K. G. Larsen et al., “Learning deterministic probabilistic automata from a model checking perspective,” Machine Learning, vol. 105, no. 2, pp. 255–299, 2016. [Google Scholar]

26. B. K. Aichernig and M. Tappler, “Efficient active automata learning via mutation testing,” Journal of Automated Reasoning, vol. 63, no. 4, pp. 1103–1134, 2019. [Google Scholar]

27. M. Narendhar and K. Anuradha, “An efficient design model validation for the quality software development,” Journal of Theoretical and Applied Information Technology, vol. 95, no. 11, pp. 2406–2416, 2017. [Google Scholar]

28. A. S. Dimovski, A. S. Al-Sibahi, C. Brabrand and A. Wąsowski, “Family-based model checking without a family-based model checker,” in Int. SPIN Workshop on Model Checking of Software, Stellenbosch, South Africa, pp. 282–299, 2015. [Google Scholar]

29. A. S. Dimovski and A. Wąsowski, “Variability-specific abstraction refinement for family-based model checking,” in Int. Conf. on Fundamental Approaches to Software Engineering, Berlin, Heidelberg, pp. 406–423, 2017. [Google Scholar]

30. C. Aiswarya, B. Bollig and P. Gastin, “An automata-theoretic approach to the verification of distributed algorithms,” Information and Computation, vol. 259, no. 1, pp. 305–327, 2018. [Google Scholar]

31. J. Ma and G. L. Kremer, “A systematic literature review of modular product design (MPD) from the perspective of sustainability,” International Journal of Advanced Manufacturing Technology, vol. 86, no. 5, pp. 1509–1539, 2016. [Google Scholar]

32. A. Pranugrahaning, J. D. Donovan, C. Topple and E. K. Masli, “Corporate sustainability assessments: A systematic literature review and conceptual framework,” Journal of Cleaner Production, vol. 295, no. 6, pp. 126385, 2021. [Google Scholar]

33. G. T. Reddy, M. P. K. Reddy, K. Lakshmana, R. Kaluri, D. S. Rajput et al., “Analysis of dimensionality reduction techniques on big data,” IEEE Access, vol. 8, pp. 54776–54788, 2020. [Google Scholar]

34. G. T. Reddy, M. Reddy, K. Lakshmana, D. S. Rajput, R. Kaluri et al., “Hybrid genetic algorithm and a fuzzy logic classifier for heart disease diagnosis,” Evolutionary Intelligence, vol. 13, no. 2, pp. 185–196, 2020. [Google Scholar]

35. P. K. Donta, T. Amgoth and C. S. R. Annavarapu, “An extended ACO-based mobile sink path determination in wireless sensor networks,” Journal of Ambient Intelligence and Humanized Computing, vol. 12, no. 10, pp. 8991–9006, 2021. [Google Scholar]