A Novel Lightweight Image Encryption Scheme

1  Introduction

Recent technological advances have profusely altered global communication, where One of the most pivotal advancements of this century is the frequent use of small computing devices. These devices are becoming essential for both individual customers and global organizations. Hence, these technological advances led to immersing the general public in wired and wireless communication routes. The widespread use of such devices compels cryptographers to devise methods for safeguarding the data transmission process. Correspondence is used to transmit official and private communication between organizations and individuals. The sensitivity of some of these data makes a secure transmission form necessary due to concerns about unauthorized access to data [1]. Recently, image-based communication has become increasingly popular in private and public scenarios. This connection can be seen in money transactions, medical reports, and military exercises. Images transferred between parties without a secure connection are constantly at risk of stealing or losing their data. Therefore image encrypting has of major importance [2].

Salsa20 appears to be an appropriate candidate for image encoding due to its intriguing structure [3].

The chaotic encryption technique has been used extensively for image encryption due to its properties (initial conditions sensitivity, pseudo-randomness, and non-periodicity). These properties conform to the required encryption characteristics, which can be found in the chaotic encryption technique [4,5]. DNA cryptography techniques are becoming a viable network method. They provide a high level of parallelism, which helps regulate computational speed. Its capacity for storing information via DNA molecules is very large. This capacity is accompanied by low power consumption. Compared to standard encryption algorithms like data encryption standard (DES) and advanced encryption standard (AES), DNA cryptography is a new method for unbroken data that provides exceptional network security. Scientists exploit the benefits of DNA coding and chaotic systems by combining them into image cryptosystems to create more powerful and secure systems that are difficult to access or break [6]. Since the 2010s, many image encryption schemes have been proposed, but many of them have not been effective due to their lower key space and computational complexity. According to previous literature [7,8], a secure cryptosystem must contain confusion and diffusion. Some schemes in the literature [9,10] do not fulfill the abovementioned requirements. Some schemes are also unsuitable for Internet of Things (IoT) devices and real-time applications.

In this paper, a novel lightweight image encryption approach is suggested. This approach integrates the chaotic system with Salsa20 and DNA. This integration improves the security and efficiency of image encryption by utilizing the high diffusion supplied by the XOR operation and the Lorenz system. It also incorporates the high confusion provided by a new S-Box. The contributions of this research are as follows:

•   Present a new lightweight image encryption/decryption scheme that requires less time and less memory and has high efficiency. The scheme is also designed to be more secure and ensure lower correlation coefficients between adjacent pixels of the encrypted image.

•   Creating a highly sensitive key for encrypting and decrypting images based on the innovative 5D Lorenz map system has more advantages than the simple chaotic system. A greater parameter, space, high randomizations, and a vast number of chaotic sequences are among the many advantages of this system.

•   Significantly increase the key space with a proposed novel 5D Lorenz map system; this will protect images from unauthorized access (Henon map, sin map, ten maps, etc.).

•   Propose new S-Boxes to synthesize efficient 16 ×16 S-Boxes based on the 2D Henon map. These boxes are compared with recent methods.

•   Evaluating the proposed scheme with many metrics, such as entropy, correlation, and differential attack.

The rest of the paper consists of the following sections: literature review, theoretical background, and proposed encryption and decryption scheme. The practical system performance is evaluated; the last section concludes the paper.

2  Literature Review

Images are a key part of communication. The general public and organizations both rely on transmitting a massive amount of data in the form of images. Some sensitive and important images necessitate a secure way of transmission. Numerous encryption algorithms are available in the literature to obtain security and confidentiality. A concise literature review is provided hereafter. Alireza et al. [9] proposed an efficient digital image encryption based on Salsa20. The results and analysis demonstrate that the algorithm has an acceptable level of security. Zheng et al. [10] proposed a lightweight authenticated encryption scheme for railway cloud service based on a novel discrete chaotic S-Box coupled map lattice (SCML). Zhang et al. [11] an image encryption scheme based on bit permutation and dynamic DNA encoding. Security analysis indicated that the algorithm could withstand attack operations such as statistical analysis and exhaustive analysis. Janakiraman et al. [12] proposed a chaotic lightweight algorithm and its implementation on a 32-bit microcontroller to encrypt grayscale images. The scheme’s performance is sufficient for real-time applications, but it is not robust because it is based on spatial domain techniques. Patro et al. [13] proposed a combined hyper-chaos and chaos-based encryption technique to secure images. One round of diffusion and multi-stage bit-plane permutation operations are performed to obtain better encryption results, but this method is insecure due to the limited key space. Qasim et al. [3] proposed a hybrid encryption algorithm that consisted of modified Salsa20 and chaos theory; it has been applied by encrypting medical information. Most tests demonstrate that the messy Salsa proposed is faster than the original. An improved algorithm was designed by Lin [14]. Its purpose was to analyze the existing cryptographic methods based on chaotic maps and resist the chosen plaintext attack (CPA). In this scenario, an improved CIES-UBPRPD (chaotic map-based image encryption system employing both plaintext-related permutation and diffusion) approach is used to achieve higher plaintext sensitivity than the original CIES-UBPRPD method. Despite its resilience and high security, it is more time-consuming than the original CIES-UBPRPD method. Guan et al. [15] developed image encryption in the frequency domain by combining the techniques of 4D hyper chaotic maps and DNA encoding. Dagadu et al. [16] proposed an image encryption scheme based on a pseudo-randomly enhanced logistic map, random permutation, and DNA. Zheng et al. [17] proposed an image encryption scheme based on a multi-chaotic system and DNA coding. This method has high security, but it is not suitable for color images. Liu et al. [18] designed a cost-effective, lightweight image encryption scheme regarding time and storage, which was based on message passing (MP) and chaotic maps. Gupta et al. [19] proposed a fast, secure, and lightweight symmetric image cryptographic algorithm based on the session key. Ravichandran et al. [20] Suggested using integer wavelet transforms (IWT), DNA computing, and chaos to form an effective medical image encryption method. This plan is impervious to CPA, but it is not used for color images. Ferdush et al. [21] presented a standard framework and algorithm based on two chaotic maps, such as Arnold and logistic, for lightweight image encryption. This scheme is implemented for a grayscale image only. Abdallah et al. [22] suggested incorporating numerous shuffling operations based on the 3D-Lornez chaos theory, the initial permutation (IP) and S-Box ideas, and the confusion and diffusion operations in the key process.

State-of-the-art research indicates that some encryption algorithms are slow or unsuitable for color images, and those others are less resistant to plaintext and differential assaults. Some encryption algorithms are also unsuitable for Internet of Things devices and real-time applications. The cryptosystem must be resistant to statistical and differential assaults as a result. The cryptosystem must also be extremely sensitive to its secret keys and use a larger key space to prevent data from being retrieved by an unauthorized user.

3  Theoretical Background

3.1 Chaos System

Chaos theory is a mathematical discipline that includes the study of complex systems. The main components of chaos theory are sensitivity to the initial value, parameters, and randomness. Applying minor input adjustments lead to greatly alters the systems’ outputs. Systems based on chaos theory are more secure for image encryption; unauthorized individuals cannot predict the chaos sequence if they are unaware of the proper control parameters and initial values [23].

3.1.1 Lorenz Chaotic Mapping

Lorenz mapping is a typical example of chaotic mapping in chaotic systems, and the system dynamic equations are:

x=α(y−x)(1)

y=xz+βx−y(2)

z=xy−γz(3)

System parameters are part of the mapping; their typical values are 10, 28, and 8/3. When they remain constant, the system collapses when the criterion of 24.74 is met. The Lorenz system generates chaotic sequences with a more complicated system structure than the low-dimensional one, which can combine chaotic sequences with either one or more variables. The sequence design is highly flexible [24].

3.1.2 H’enon map

The term Hénon-Pomeau attractor/map is frequently used to refer to a discrete-time dynamic system. It is among the most studied models of chaotic behavior in dynamic systems. The H’enon system maps a point in the plane (Xn,Yn) to a new point [25]. The H’enon map is a 2D discrete chaotic map, which is defined by the following equation:

Xn+1=1−aXn2+Yn(4)

Yn+1=bxn(5)

When parameter b = 0.3 and a ∈ [1.06,1.22]∪ [1.27,1.29] ∪ [1.31,1.42], the H’enon map is chaotic [26].

3.2 Salsa20 Algorithm

The stream cipher Salsa(20) uses a counter mode for encryption. Salsa(20) initial seed is an array (4, 4) with 512 bits. Edition, XOR, and rotation are the fundamental operations of Salsa(20), and they are used on an array of Salsa(20) for 10 cycles. Salsa(20) refers to the fact that its array is altered twice in each round. At the end of the Salsa(20), the final adjustment of the array and its initial seed are added [27].

3.3 DNA Rules

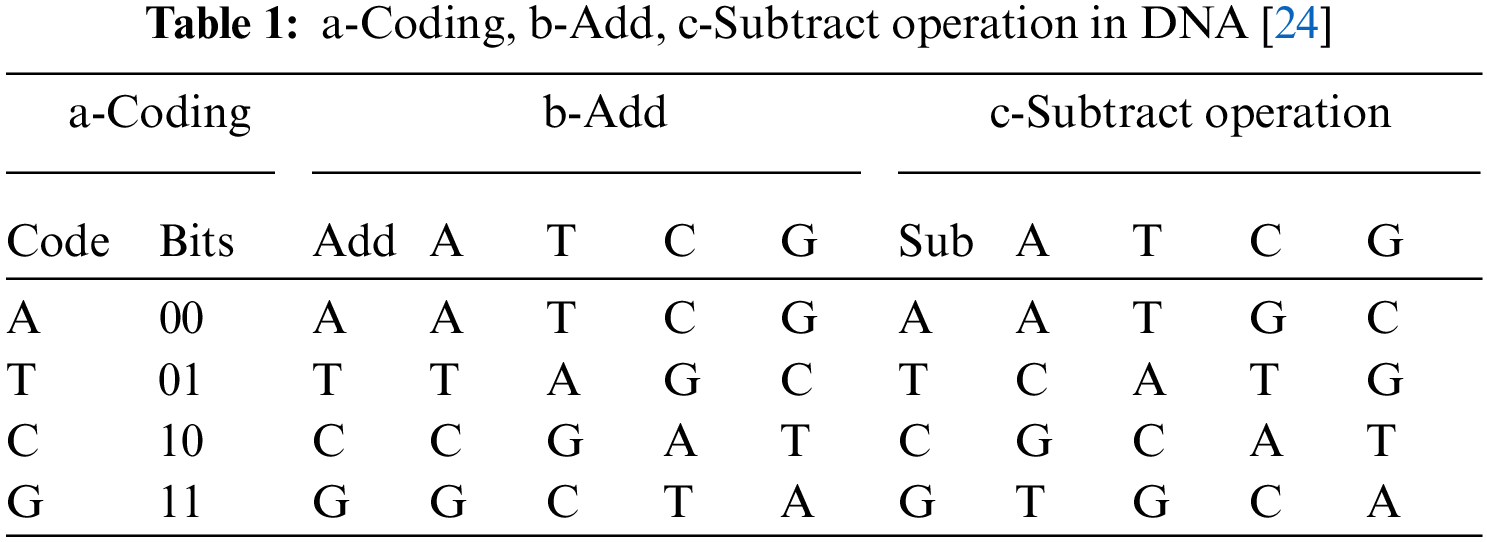
The nucleic acid bases that make up a DNA sequence are broken down into four categories: adenine (A), cytosine (C), thymine (T), and guanine (G). The letter A and the letter T, as well as the letters G and C, are complementary. Because the binary numbers 0 and 1 are complimentary to one another, the binary numbers 00 and 11 and 01 and 10 are also complementary. A total of 24 possible coding combinations may be achieved by encoding the numerals 00, 01, 10, and 11 using the four bases A, T, C, and G. Only eight of these combinations can satisfy the Watson-Crick complement requirement [24]. Those combinations are shown in Table 1.

4  Proposed S-Box Algorithm and its Performance

4.1 Construction of S-Box

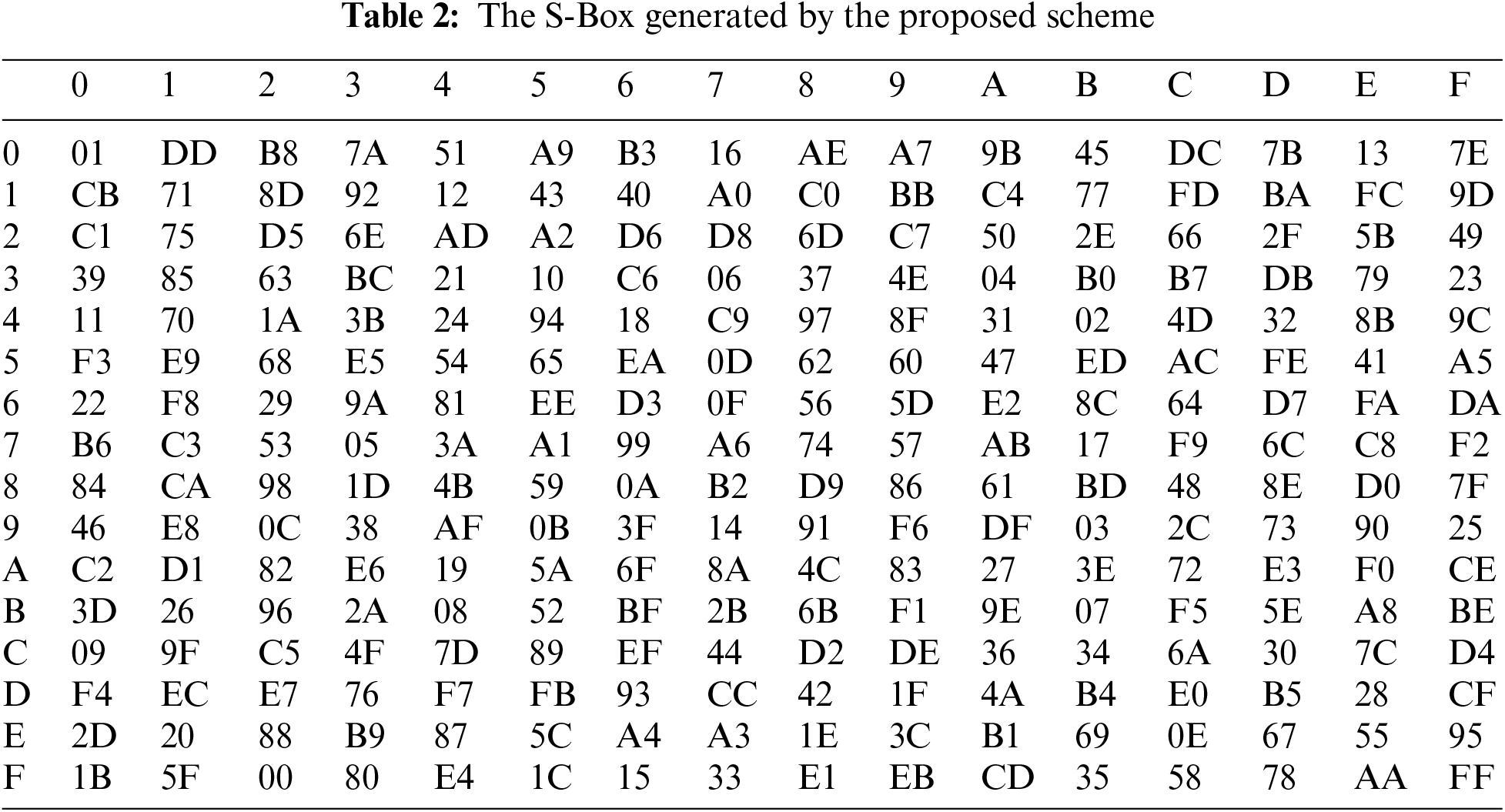
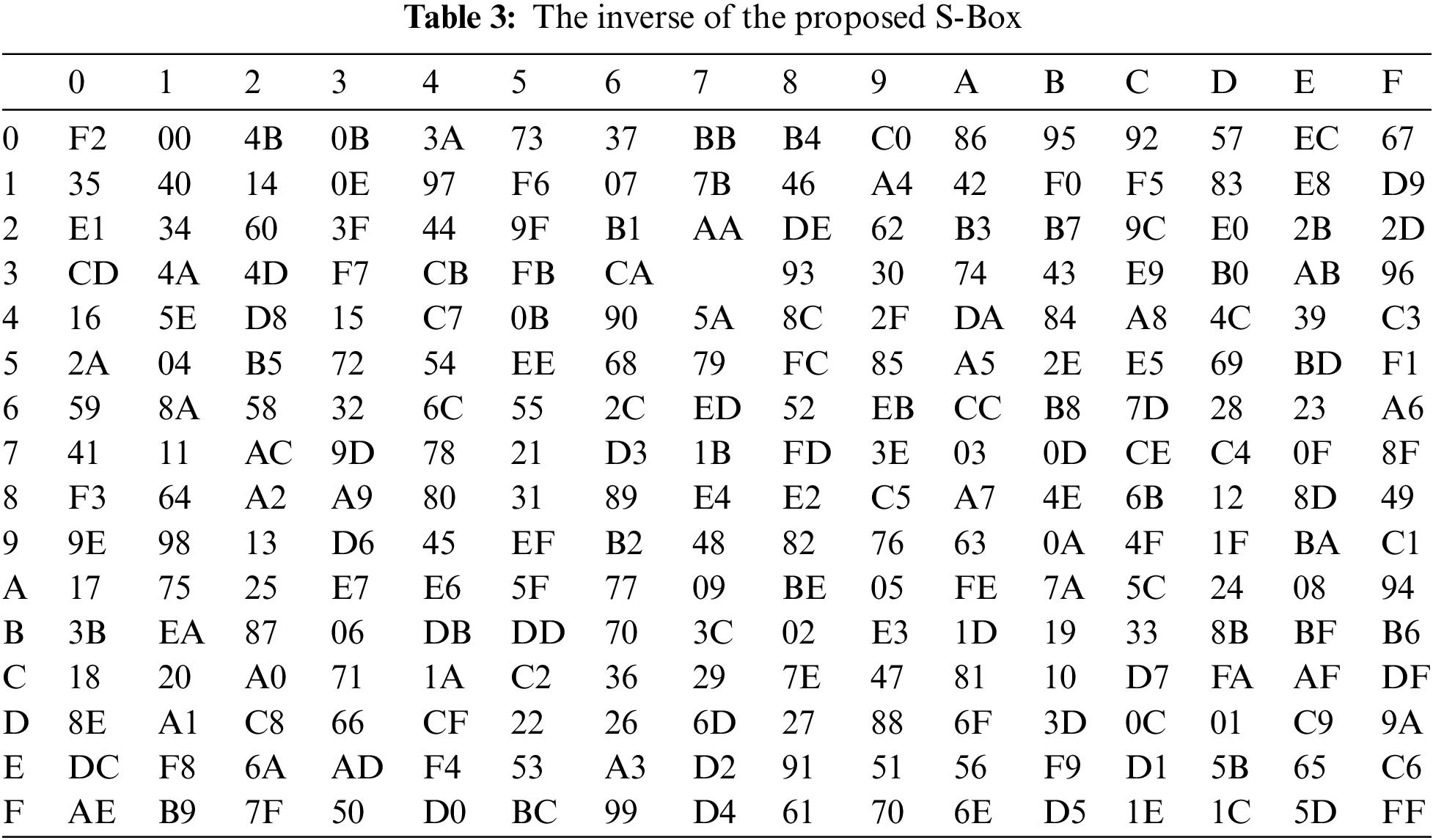
There is a viable theory about the construction of a superior S-Box. According to the outcomes of the final operation of the supplied scheme requirements for creating a new dynamic S-Box based on chaos theory principles, an S-Box that satisfies this criterion is resistant to differential cryptanalysis. This operation provides increased protection and complexity based on the two-dimensional chaotic H’enon system. Using the H’enon chaotic map (2D) and the initial value X0 for the chaotic system and numbers created, one can generate a big 1616 S-Box. It similarly consists of a range of numbers (0–255) and uses the S-Box output method to produce the H’enon system values. All values contained within the S-Box must be distinct and not repeated. The responsive dependency on the initial State with chaos theory changes the construction of the S-Box, and the result of the dynamic S-Box is inversed with every slight change in the initial value. S-Box and its inversed form are listed in Tables 2 and 3.

4.2 Performance Analysis of Proposed S-Box

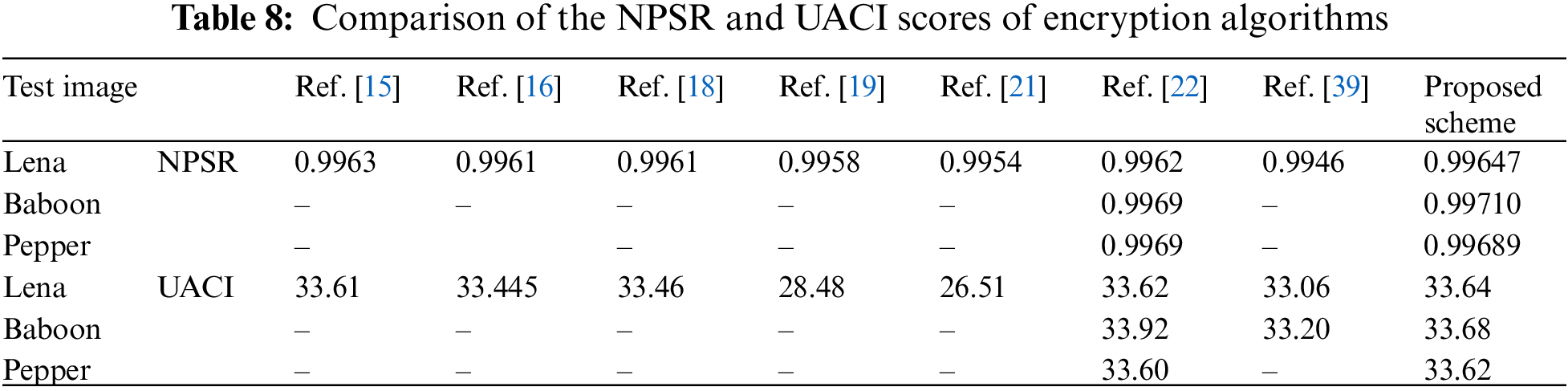
The strength of the suggested S-Box is assessed using multiple conventional performance analyses. The assessments in this work include the following criteria: balanced criterion (BC), completeness criterion (CC), avalanche criteria (AC), strict avalanche criteria (SAC), nonlinearity, and bijective properties.

4.2.1 BC

One of the most critical S-Box tests is to ensure that the distribution of 0s and 1s in the output sequences is balanced. The results of this test (which employed two words with the new S-Box) reveal that the new S-Box is balanced, as presented in Table 3.

4.2.2 CC

This standard ensures comprehensiveness. When something is complete, every bit of output is tested against every bit of input [28]. As seen in Tables 1 and 2, the created S-Box passes this test.

4.2.3 AC

The non-relationship between input bits and the output sequence is essential to a good block cipher. A block cipher is evaluated using the avalanche criterion. In the avalanche criterion, a small change in plaintext results in a large change in cipher text. A small change may include flipping a single bit from 0 to 1 or vice versa, which causes a large change in output. The value of this criterion is calculated using Eq. (6) and should be in the range of 0–1, with 0.5 being the best value.

AC=Number of Flipped Bits in Cipher TextNumber of All Bits in Cipher Text (6)

To test the proposed S-Box, a single bit is changed from the letter “L” to the letter “M” Both are then replaced with data from the proposed S-Box. In five of the original eight bits, the result of “L” differed from “M” As a result of Eq. (6), the AC is 0.625. The formed S-Box meets the avalanche condition. The results of this test were compared to the findings of other relevant studies, as presented in Table 4.

4.2.4 SAC

Whenever the AC and CC are obtained, the SAC is obtained. The S-Box meets the SAC when switching one bit from the input results in a 50% change in the output bits [28]. Our proposal meets the requirements AC, CC, and SAC.

4.2.5 Nonlinearity Property

To resist linear cryptographic attacks, the nonlinearity of the Boolean function must be large [32]. The nonlinearity scores of the S-Box obtained via H’enon chaotic map are 110, 106, 106, 108, 108, 106, and 106, with an average of 107.25. This average was the objective function’s goal .When compared to other techniques, the H’enon chaotic map method is considered. acceptable outcomes for achieving high nonlinearity.

4.2.6 Bijective Property

Generated S-Boxes for the H’enon chaotic map have different output values from the interval [0,255] with no repetition. Both S-Boxes satisfy the bijectivity property.

5  The Proposed Lightweight Scheme

This work aims to design a Lightweight Image Encryption/Decryption Scheme that can be used to transfer a secure image in an untrusted channel. This scheme is inspired by a combination of some functions from Salsa20 and DNA algorithms. This scheme involves breaking the link between the pixels and is mostly concentrated on concepts such as confusion and dispersion. This scheme was developed to achieve high encryption efficiency, resistance to various assaults with an appropriate execution time, memory savings, and complexity reduction. Fig. 1 presents the structure of the proposed scheme.

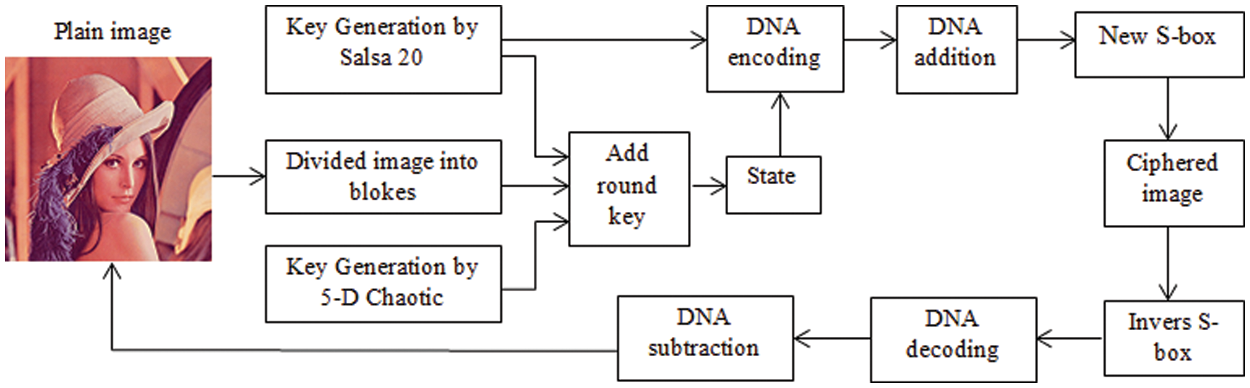
Figure 1: General structure of the proposed scheme

5.1 The Proposed Encryption Scheme

The step-by-step proposed lightweight image encryption scheme is presented in Fig. 2.

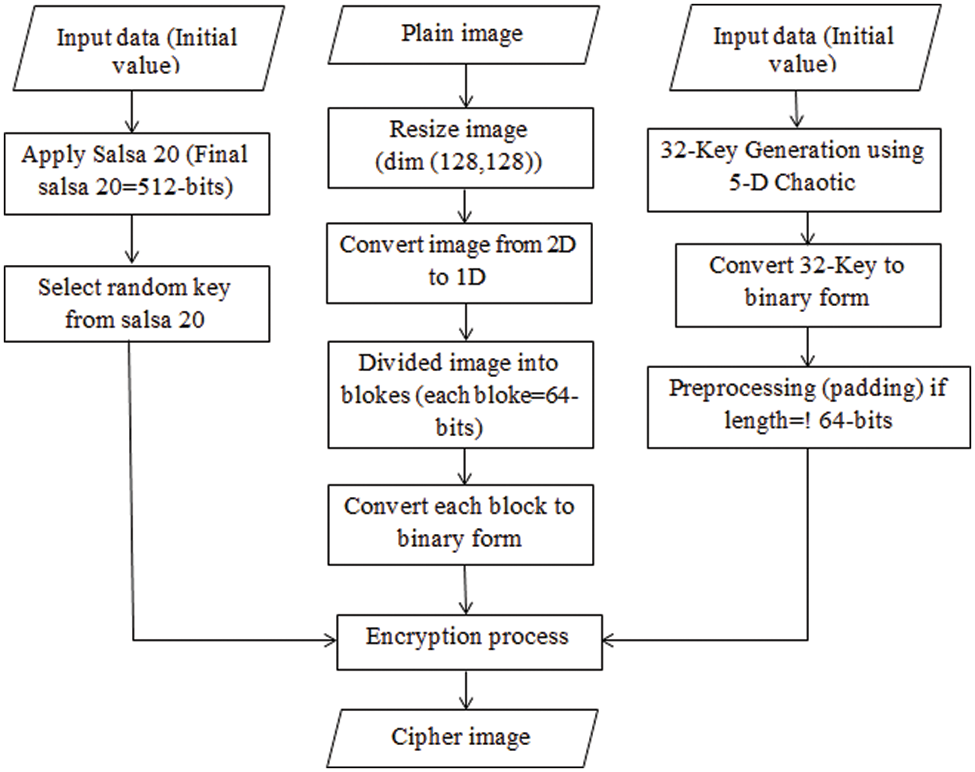
Figure 2: The proposed lightweight image encryption scheme

5.1.1 Key generation using 5D chaotic system

A new 5D chaotic system of differential dynamic, chaotic equations has been proposed to examine chaotic properties and produce a series of numerical output sequences. The proposed innovative 5D chaotic system equations are:

X[i+1]=x[i]+(−s×x[i]+y[i]×k[i]−r×p[i])×dt (7)

Y[i+1]=y[i]+(−y[i]−x[i]×z[i]+r×x[i]−u×p[i])×dt(8)

Z[i+1]=z[i]+(z[i]×x[i]×y[i]−1.5×s×p[i]−k[i])×dt (9)

K[i+1]=k[i]+(s×x[i]+(u×y[i]−r×k[i])×dt (10)

P[i+1]=p[i]+(b×(x[i]+k[i])/z[i]+y[i])×dt(11)

where b, r, s,u, and dt comprise the chaos parameter, andx, y , z , k, and p comprise the initial conditions for the chaos map. The proposed 5D chaotic system was implemented and evaluated, and the Lyapunov exponents for the initials and parameters were calculated. With the maximal Lyapunov values (x = 2.1, y = 0.5, z = 1.1, k = 1.1, and p = 0.1) and parameters (b = 0.01, r = 0.5, s = 0.95, u = 1.1, and dt = 0.01), the suggested novel 5D chaotic system possesses super chaotic Lyapunov values that include five positive values. All proposed systems use the generated chaos keys (K1, K2… K5), which are then placed in the file for ease of use and referenced in subsequent operations. Fig. 3 displays the chaotic attractors of each plane of the 5D Lorenz chaotic map.

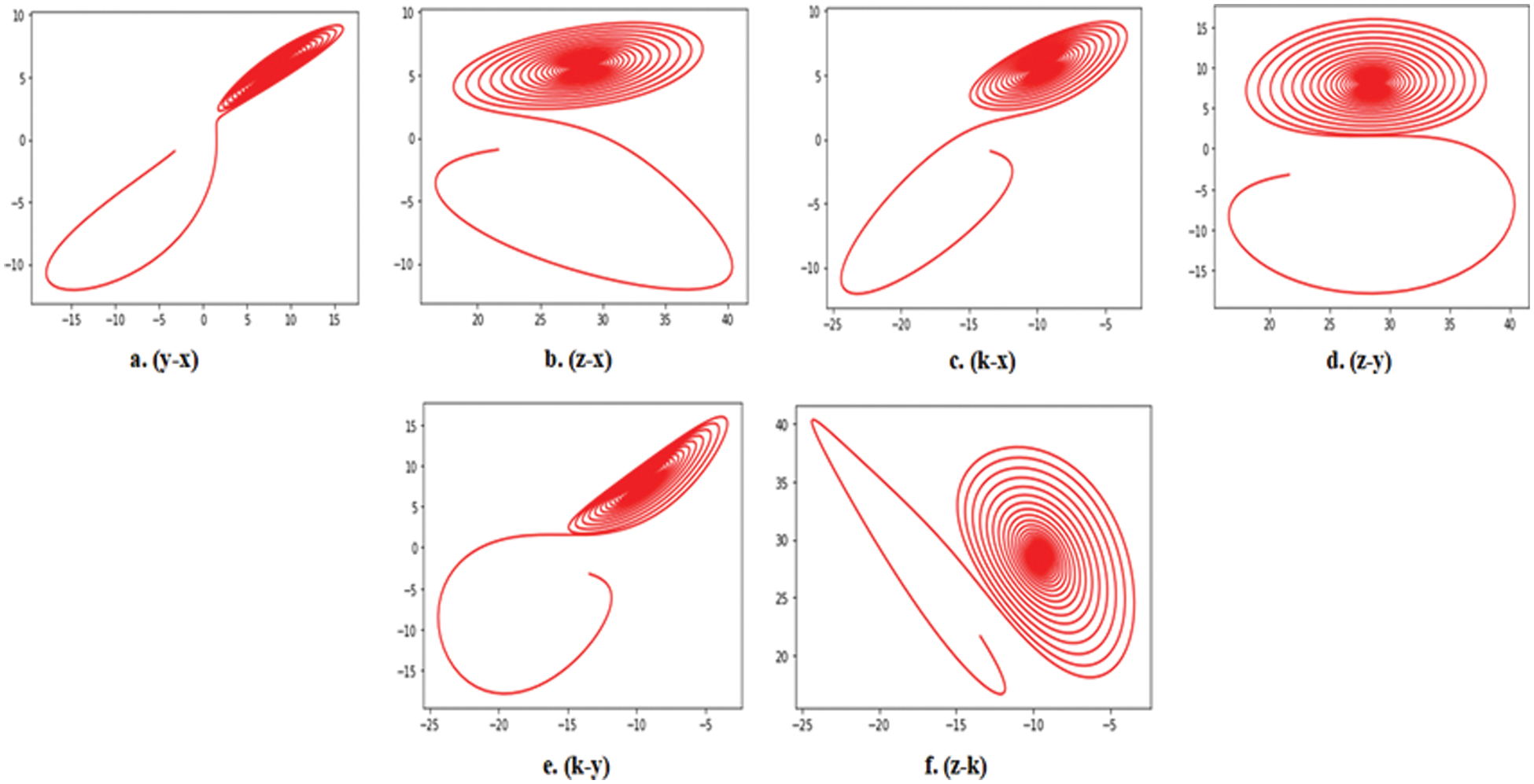
Figure 3: Chaotic attractors of each plane of the 5D Lorenz chaotic map

5.1.2 Salsa20

In the proposed scheme, Salsa20 was applied to generate 512 bits block of keystream (Matrix 4 * 4; 16 words). The first four numbers are selected from the initial values of keys to k [0], the second set of four numbers from the initial keys to k [1], and the third set of four numbers from the initial keys to k [2], and this pattern is repeated. The final four numbers were selected from the initial keys to k [7]. The first four numbers are selected from the initial values of the nonce to n [0], and the second set of four numbers from the initial values of the nonce to n [1]. The first four numbers are selected from the initial values of block counters to b [0], and the second set of four numbers from the initial values of block counters to b [1]. For Constants, c [0] = 61707865, c [1] = 3320646e, c [2] = 79622d32, and c [3] = 6b206574. We applied a Little-endian Function to keys (k [0], k [1]… k [7]), nonce (n [0] and n [1]), and block counters (b [0], b [1]). To generate the initial matrix (S), 512 bits, the block of keystream (Matrix 4 * 4; 16 words) is ordered as follows:

S=(c0k0k1k2k3c1v0v1i0i1c3k4k5k6k7c4)

In each iteration, 20 rounds came next (r-value), and S was selected as the input (only for the first iteration). Quarter rounds equations were applied in Salsa20. The columns round equation was then applied. Every row is transposed as a column to generate (S1) distinct 512 bits, the keystream block. Note that S1 is the next iteration’s input until the twenty rounds are completed. The Adding operation is also applied between S1 (after 20 rounds) and S for every word; the result is the Final Salsa. The inputs in the Add Round Process are State (block of image = 46-bits) and 32 Chaotic keys. Final Salsa20 has the initial values i = 0 and j = 0. The State is converted from integer to binary for 32 rounds. If the number of the round (i) is even: first, XOR is applied between keys (Z [i] and K [i]) into (CK). Then, the XOR operation is applied between (State and CK) into (State). After this, the XOR operation applies between keys (X [i] and Y [i]) into (CK). Next, the XOR operation is applied between (State and CK) into (State). We apply XOR between key P [i] and Final Salsa20 [j] into (CK) and j = j + 1. Finally, the XOR operation is applied between (State and CK) into State and i = i +1. If the number of the round (i) is odd, XOR is applied between keys (Z [i] and K [i]) into (CK). Then, the XOR operation is applied between (State and CK) into (State). The XOR operation is applied between keys (X [i] and Y [i]) into (CK). Next, XOR is applied between (State and CK) into (State). Finally, if the value of iis less than or equal to 32, then i = i + 1 or the Final State equals the State.

State1 and a random key from salsa20 are the initial values for DNA encryption. A random key is selected from Final Salsa20 and converted to the binary form. Padding was applied to ensure the length of the key was exactly 64 bits. Zeros are added on the left of the key in case the length must be adjusted. Next, every two-bit block is split and encoded with DNA code using Table 1a. Finally, the result is named the DNA key. The Final State was also encoded with DNA using Table 1a. The result is named DNA State. Subsequently, the DNA-Addition operation is applied to the DNA state and DNA key using Table 1b. The output from this stage is Final State. The Final State input is added to the new S-Box, where the values replace the pixel values of the Final State matrix in the proposed S-Box.

5.2 The Proposed Decryption Scheme

The decryption process is the inverse of its encryption process of (LIES). The five-dimension randomness chaotic system generates 32 keys, and the Salsa20 algorithm generates 512 bits blocks of keystream. Also, the sub-DNA operation is used, as presented in Table 1c. Add Round is used to decrypt data to avoid threats. The inverse of each previous process was completed; Fig. 4 presents the decryption process of the proposed scheme.

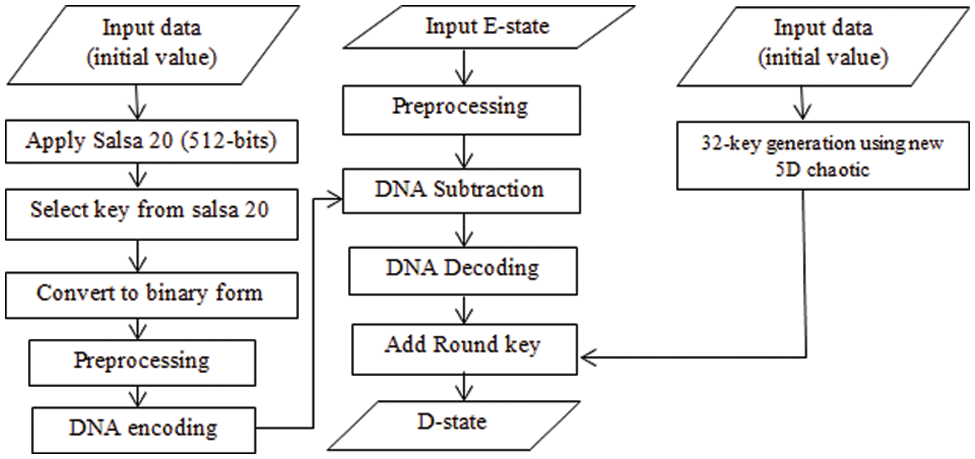
Figure 4: The proposed lightweight image decryption scheme

6  Simulation Experiments and Performance Analysis

The experiment was carried out on a personal computer with Intel core i5, 2.40 GHz CPU, 8 GB memory, windows 10, and Python 3.7.4. The test images (Lena, Baboon, and Pepper) have dimensions of 128 × 128 with 24-bit color. Fig. 5 shows that some of the cipher images are noise-like images, which makes it impossible to infer anything valuable from them. A key space analysis, histogram analysis, correlation coefficient analysis, information entropy analysis, and differential analysis are all included in the performance evaluation of the suggested design.

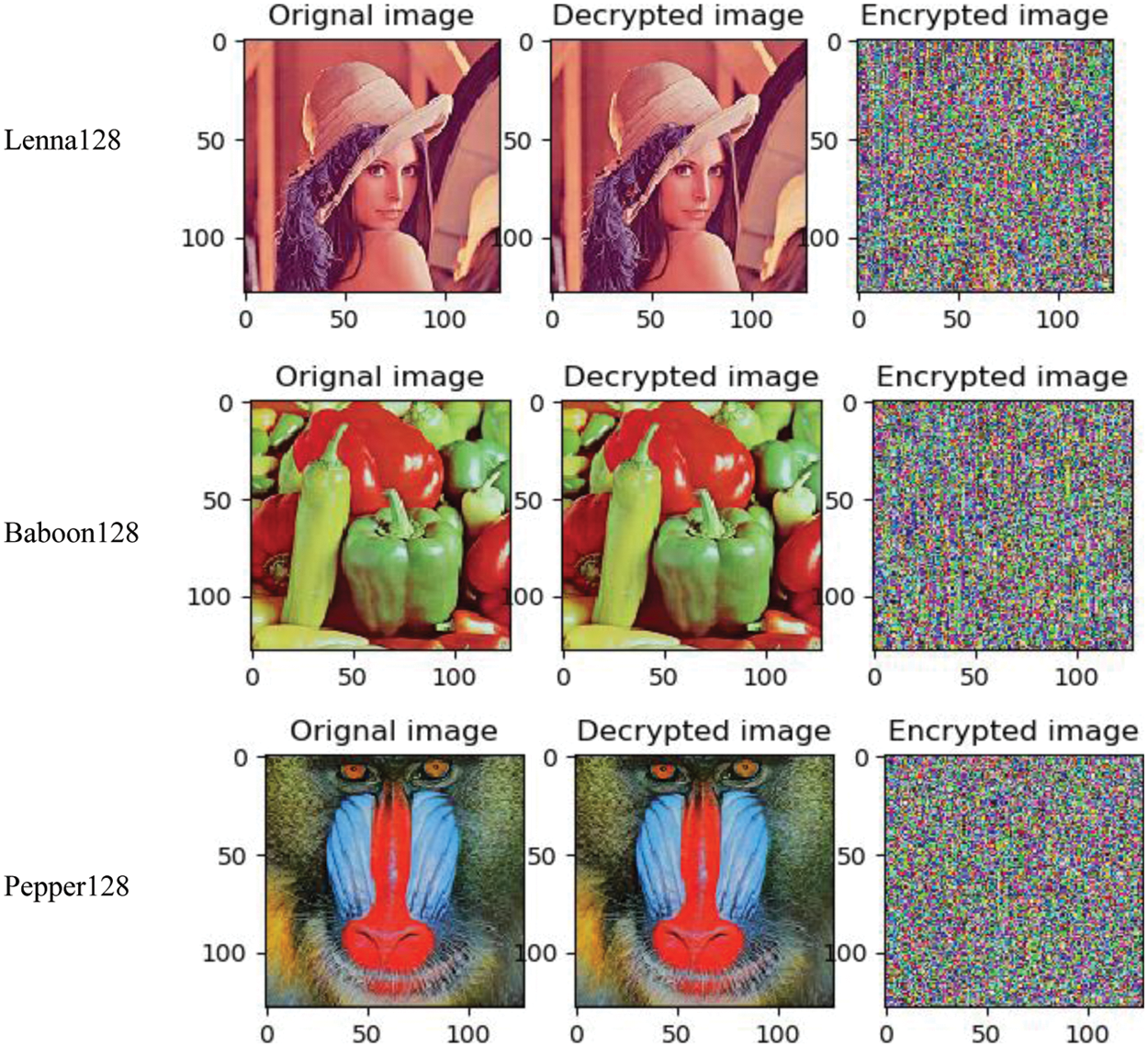
Figure 5: Simulation results of the proposed encryption/decryption scheme

6.1 Key Space

The key space volume can ensure that the proposed scheme resists the attack. The encryption method must have a wide key space to withstand an extensive attack. A key space over 2100 enables a high level of protection [33]. The secret keys used in the proposed algorithm can be summarized as follows: the five initial values of the 5D chaos system are denoted; iteration time N0 is used as the secret key in the proposed scheme; the number of keys is 32; the ranges of these keys are key-x0 (−40, 40), key- y0 (−40, 40), key- z0 (1, 81), key- k0 (−250, 250), and key− p0 (1000, 2500). If all the initial values have the precision of 1015, the key space can calculate as key space = 80 × 1015 × 80 × 1015 × 80 × 1015 × 500 × 1015 ×1500 ≈ 2 237 > 2 128.

6.2 Histogram Analysis

A histogram displays the distribution of an image’s pixel intensity. A safe encryption system must include an encrypted image with a uniform histogram to withstand statistical attacks [34]. Fig. 6 presents the histograms of the plain image (Lena) and the encrypted image (b, d). In Fig. 6, the values of the encrypted image have equal distribution (d). As a result, the distribution of the plain image Lena in Fig. 6a differs significantly.

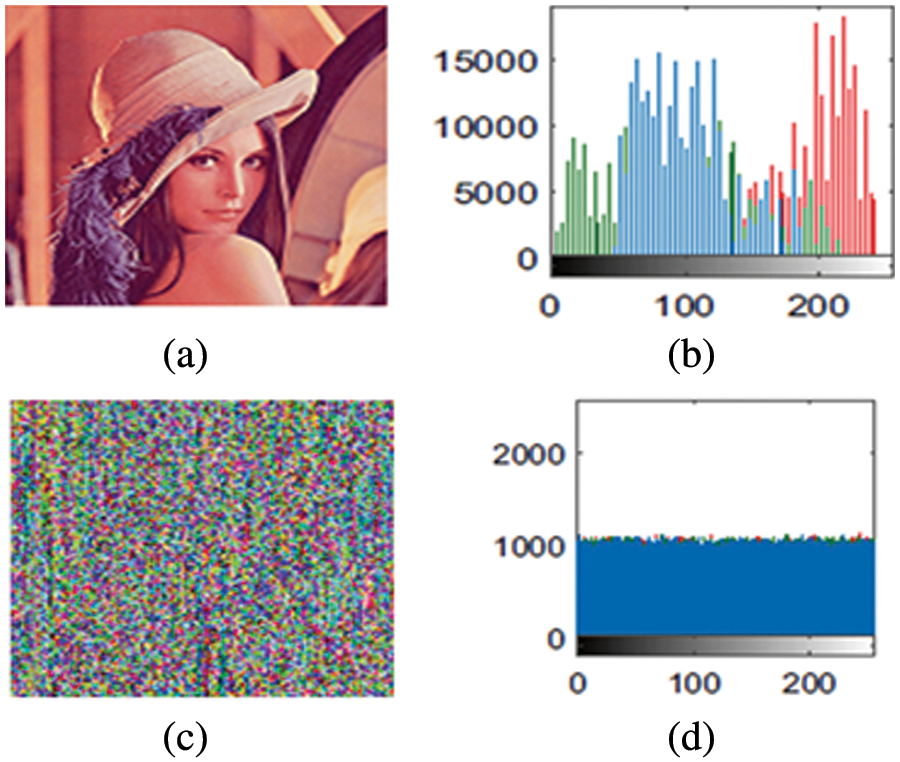
Figure 6: Results of the proposed scheme. (a) Original a plain image. (b) Histogram of plain image. (c) The complete encrypted image. (d) Histogram of the encrypted image.

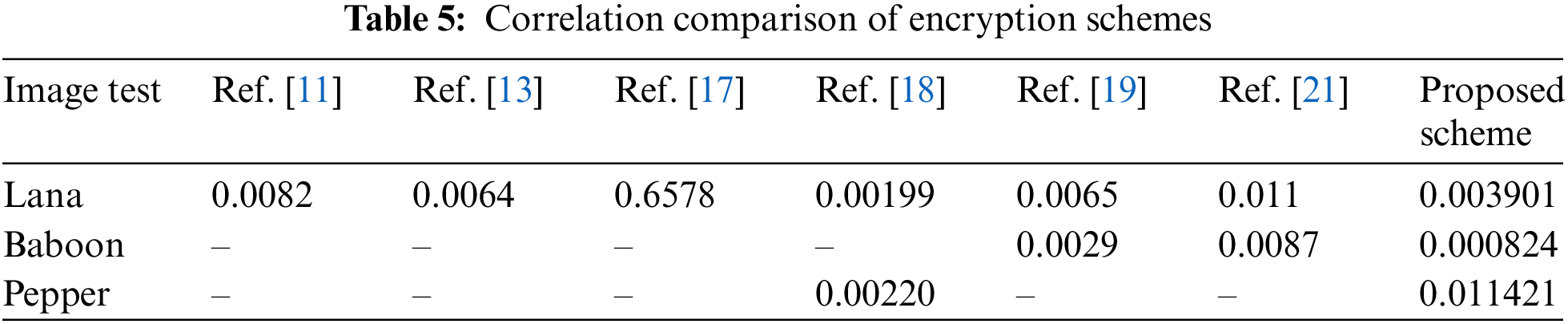
6.3 Correlation between Plain and Ciphered Images

Within this portion, an examination of the association between plain and encrypted images is carried out. The calculation of the correlation coefficient follows the format of Eq. (12) [34].

r=∑i(xi−xm)(yi−ym)∑i(∑i(xi−xm)2(∑i(yi−ym)2(12)

Both xm and ym averages plain and ciphered images. Because the correlation coefficients between the plain and ciphered images are so close to zero, it may be deduced that the suggested encryption scheme possesses the correlation quality sought after. Table 5 lists the findings of the comparison of the correlations.

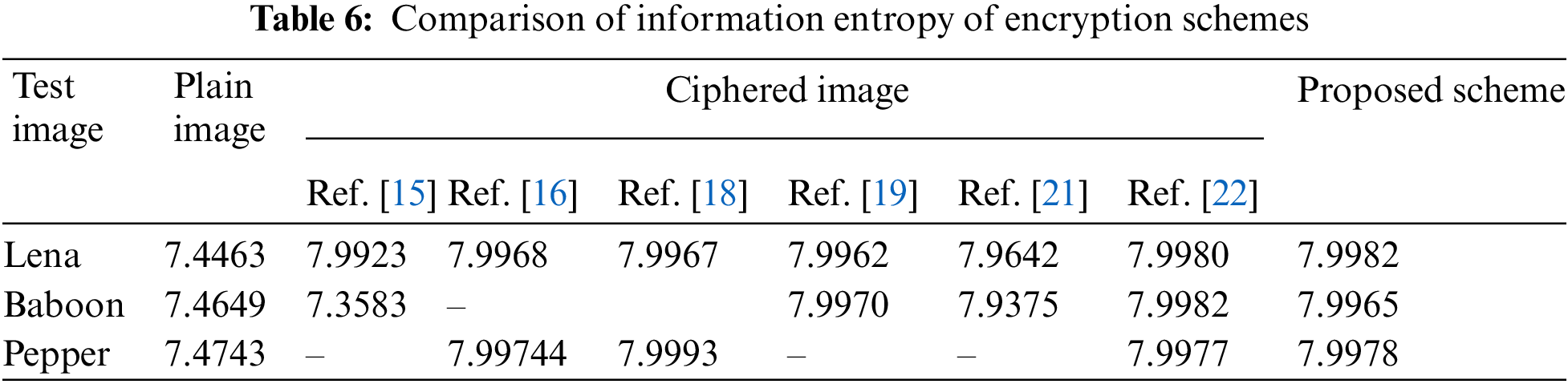
6.4 Information Entropy Analysis

Information entropy (IE) is an important index for measuring randomness [35]. The information entropy is calculated according to the following formula [36]:

H(e)=−∑i=0m−1⁡P(ei)log2⁡P(ei)(13)

where e is the origin of the information, m is the number of bits that must be present for the symbol mi and p (ei) is the probability that the symbol ei Will be present. The entropy of a 24-bit color image can reach its maximum value when all of the pixels are laid out in an even distribution. This maximum entropy value means that the information is random. The information entropy must be near eight in a ciphered image because it decreases the chance of an attacker decrypting it. Because the entropies of the encrypted images are quite close to the ideal value of eight, it can be deduced that the suggested method possesses the required information entropy properties. Calculating the information entropies of both the plain and the cipher images can be accomplished using Eq. (13). Table 6 presents the findings.

6.5 Differential Analysis

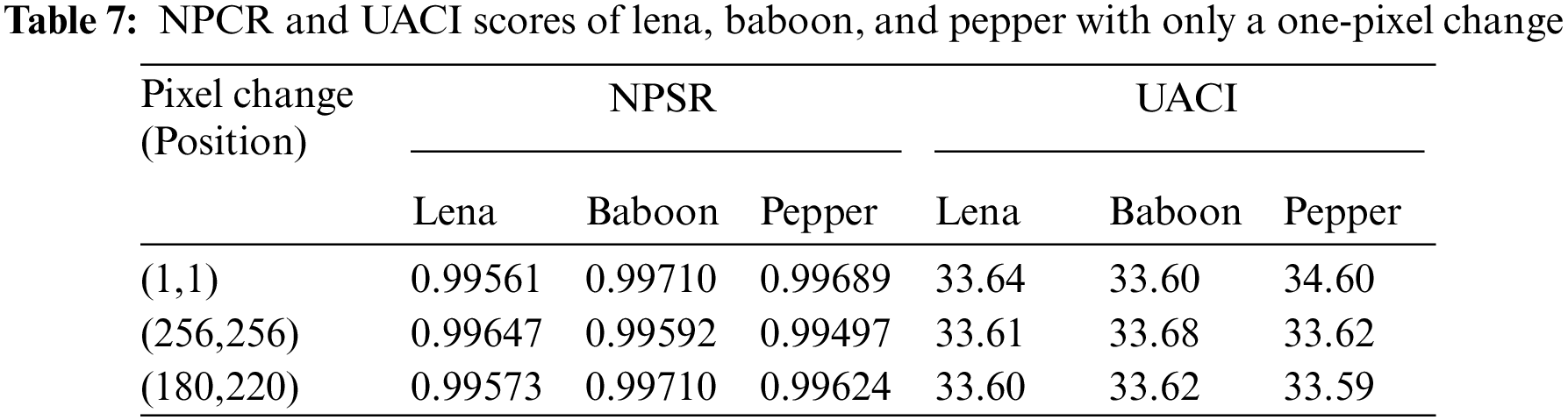
An effective encryption strategy must ensure that each slight change to the plain image results in a considerable difference in the encrypted images to protect against a differential attack. The suggested encryption approach can make two ciphered images completely distinct, even if their plain images differ by one pixel. Let C1 and C2 be the two encrypting images, and compute the measured value of the plain image’s sensitivity to a slight modification using Eqs. (14) and (15) [37,38]:

NPCR=∑i=1N⁡∑j=1M⁡[D(i,j)M×N]×100%(14)

UACI=∑i=1N⁡∑j=1M⁡[absC1(i,j)−C2(i,j)255×M×N]×100%(15)

where D(i,j) = 0 if C1(i,j) = C2 (i,j). Otherwise, D(i,j) = 1. NPCR focuses on the total number of pixels, which fluctuates during a differential attack. Table 8 presents an NPSR comparison of differential schemes. The Lena, Baboon, and Pepper images were chosen as the test images, and the NPCR and UACI values were computed. Table 7 presents the NPCR and UACI results. The suggested algorithm achieves high NPCR and UACI scores, with an NPCR of 0.99710 and a UACI of 33.68. These scores indicate that the suggested encryption method is resistant to a differential attack.

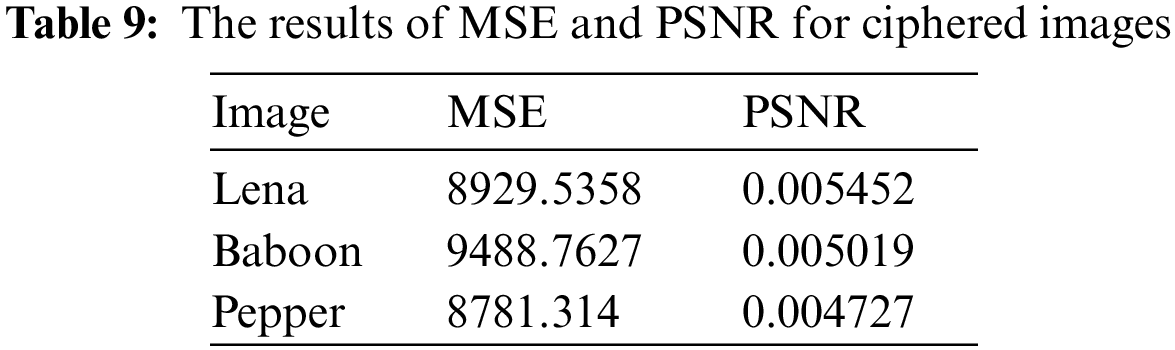
6.6 Mean Square Error and Peak Signal-to-Noise Ratio

MSE can calculate the difference in pixel values between two pictures. MSE values between these plaintext and encrypting images are most likely sufficient for a reliable encryption system. The peak signal-to-noise ratio (PSNR) quantifies the difference in peak error between plain and encrypted pictures. The PSNR of plain and ciphered images should be low due to their large disparity. The MSE and PSNR values are obtained from Eqs. (16) and (17) [40].

MSE=∑i=1M∑j=1N(Pij−Cij)2M×N(16)

PSNR=20log10⁡[ImaxMSE](17)

Both Pij and Cij Are the pixels of plain and ciphered images at the position (i,j), and Imax , the maximum pixel estimation of the image. Table 9 presents the results of MSE and PSNR for the ciphered images. The proposed encryption scheme achieves the desired effect.

6.7 Encryption and Decryption Time

The main evaluation criterion is how long the cryptographic strategy takes to encrypt and decrypt any image. A slight discrepancy between encrypting and decryption time is discovered. As a result, decrypting the photos takes longer than encrypting them. Table 10 compares our proposed solution with existing lightweight image encryption methods. As a result, our approach takes less overall time in seconds (s) to execute than current methods.

7  Conclusions

A large amount of communication is in the form of images. A fast, secure, and lightweight encryption technique is required for this communication. This paper proposes LIES. The proposed method is a unique, fast, safe, and lightweight encryption/decryption technique that exploits confusion and diffusion principles. We not only provide an effective S-Box building approach developed using the Hénon system, but also an image encryption scheme has been discussed that uses a unique 5D chaotic system, Salsa20, and S-Box.

S-Box modeling and experimental data demonstrate that the proposed S-Boxes have more desired features. The building approach of the suggested S-Boxes and the proposed image encryption method are more efficient because LIES has a high peak signal-to-noise ratio and is highly sensitive to the secret key. The encrypted image provides the attacker with no information. The suggested approach is resistant to heavy attacks and takes less time to execute than previously discussed methods, making it an efficient, lightweight image encryption scheme. The method provides lower correlation coefficients than other methods, another indicator of an efficient image encryption system.

Even though the proposed scheme has useful applications in image transmission, it still requires profound improvement in implementing the high-intelligence scheme and verifying its feasibility on devices with the Internet of Things (IoT) enabled.

Funding Statement: The authors received no funding for this study.

Conflicts of Interest: The authors declare they have no conflicts of interest to report regarding the present study.

References

    1. C. Paar and J. Pelzl, Understanding cryptography: A textbook for students and practitioners, Midtown Manhattan, New York City: Springer Publishing Company, 2010. [Online]. Available: https://link.springer.com/book/10.1007/978-3-642-04101-3. [Google Scholar]

    2. A. Javeed, T. Shah and A. Attaullah, “Lightweight secure image encryption scheme based on chaotic differential equation,” Chinese Journal of Physics, vol. 66, no. 2, pp. 645–659, 2020. [Google Scholar]

    3. K. R. Qasim and S. S. Qasim, “Encrypt medical image using CSalsa20 stream algorithm,” Medico-Legal Update, vol. 20, no. 3, pp. 1248–1256, 2020. [Google Scholar]

    4. G. Alvarez and S. Li, “Some basic cryptographic requirements for chaos-based cryptosystems,” International Journal of Bifurcation and Chaos, vol. 16, no. 8, pp. 2129–2151, 2006. [Google Scholar]

    5. A. N. Telem, C. Segning, G. Kenne and H. B. Fotsin, “Image encryption using multi-scroll attractor and chaotic logistic map,” Computers, Materials & Continua, vol. 72, no. 2, pp. 3448–3463, 2022. [Google Scholar]

    6. S. Paul, P. Dasgupta, P. K. Naskar and A. Chaudhuri, “Secure image encryption scheme based on DNA and new multi chaotic map,” Journal of Physics, vol. 1447, no. 1, pp. 1–12, 2020. [Google Scholar]

    7. M. Khan and F. Masood, “A novel chaotic image encryption technique based on multiple discrete dynamical maps,” Multimedia Tools and Applications, vol. 78, no. 18, pp. 26203–26222, 2019. [Google Scholar]

    8. J. Ahmad and S. O. Hwang, “A secure image encryption scheme based on chaotic maps and affine transformation,” Multimedia Tools and Applications, vol. 75, no. 21, pp. 13951–13976, 2015. [Google Scholar]

    9. A. Jolfaei and A. Mirghadri, “Survey: Image encryption using Salsa20,” IJCSI International Journal of Computer Science Issues, vol. 7, no. 5, pp. 213, 2010. [Google Scholar]

  10. Q. Zheng, X. Wang, M. K. Khan, W. Zhang, B. B. Gupta et al., “A lightweight authenticated encryption scheme based on chaotic SCML for railway cloud service,” IEEE Access, vol. 6, pp. 711– 722, 2017. [Google Scholar]

  11. X. Zhang, F. Han and Y. Niu, “Chaotic image encryption algorithm based on bit permutation and dynamic DNA encoding,” Computational Intelligence and Neuroscience, vol. 2017, no. 10, pp. 1–11, 2017. [Google Scholar]

  12. S. Janakiraman, K. Thenmozhi, J. B. Rayappan and R. Amirtharajan, “Lightweight chaotic image encryption algorithm for real-time embedded system: Implementation and analysis on 32-bit microcontroller,” Microprocessors and Microsystems, vol. 56, no. 1, pp. 1–12, 2018. [Google Scholar]

  13. K. A. Patro, B. Acharya and V. Nath, “A secure multi-stage one-round bit-plane permutation operation based chaotic image encryption,” Microsystem Technologies, vol. 25, no. 7, pp. 2331–2338, 2019. [Google Scholar]

  14. C. Lin, “Cryptanalysis and improvement of a chaotic map-based image encryption system using both plaintext related permutation and diffusion,” Entropy, vol. 22, no. 589, pp. 1–23, 2020. [Google Scholar]

  15. M. Guan, X. Yang and W. Hu, “Chaotic image encryption algorithm using frequency-domain DNA encoding,” IET Image Processing, vol. 13, no. 9, pp. 1535–1539, 2019. [Google Scholar]

  16. J. Dagadu, J. P. Li and P. C. Addo, “An image cryptosystem based on pseudorandomly enhanced chaotic DNA and random permutation,” Multimedia Tools and Applications, vol. 78, no. 17, pp. 24979–25000, 2019. [Google Scholar]

  17. J. Zheng, Z. Luo and Z. Tang, “An image encryption algorithm based on multichaotic system and DNA coding,” Discrete Dynamics in Nature and Society, vol. 2020, no. 10, pp. 1–16, 2020. [Google Scholar]

  18. H. Liu, B. Zhao, J. Zou, L. Huang and Y. Liu, “A lightweight image encryption algorithm based on message passing and chaotic map,” Security and Communication Networks, vol. 1, no. 7151836, pp. 1–12, 2020. [Google Scholar]

  19. M. Gupta, K. K. Gupta and P. K. Shukla, “Session key based fast, secure and lightweight image encryption algorithm,” Multimedia Tools and Applications, vol. 80, no. 7, pp. 10391–10416, 2021. [Google Scholar]

  20. D. Ravichandran, A. Banu, S. B. Murthy, V. Balasubramanian, S. Fathima et al., “An efficient medical image encryption using hybrid DNA computing and chaos in transform domain,” Medical & Biological Engineering & Computing, vol. 59, no. 3, pp. 589–605, 2021. [Google Scholar]

  21. J. Ferdush, M. Begum and M. S. Uddin, “Chaotic lightweight cryptosystem for image encryption,” Advances in Multimedia, vol. 2021, no. 5, pp. 16, 2021. [Google Scholar]

  22. A. A. Abdallah and A. K. Farhan, “A new image encryption algorithm based on multi chaotic system,” Iraqi Journal of Science, vol. 63, no. 1, pp. 324–337, 2022. [Google Scholar]

  23. A. Arab, M. J. Rostami and B. Ghavami, “An image encryption method based on chaos system and AES algorithm,” The Journal of Supercomputing, vol. 75, no. 10, pp. 6663–6682, 2019. [Google Scholar]

  24. Y. Niu, X. Zhang and F. Han, “Image encryption algorithm based on hyperchaotic maps and nucleotide sequences database,” Computational Intelligence and Neuroscience, vol. 2017, no. 40, pp. 9, 2017. [Google Scholar]

  25. M. Li, M. Xu, J. Luo and H. Fan, “Cryptanalysis of an image encryption using 2D Henon-Sine Map and DNA approach,” IEEE Access, vol. 7, pp. 63336–63345, 2019. [Google Scholar]

  26. Z. Hua and Y. Zhou, “Image encryption using 2D Logistic-adjusted-Sine map,” Information Sciences, vol. 339, no. 8, pp. 237–253, 2016. [Google Scholar]

  27. D. P. Schmid and A. Biryukov, “Slid pairs in Salsa20 and Trivium,” Mathematics, Computer Science, vol. 22, no. 2, pp. 1–17, 2014. [Google Scholar]

  28. R. S. Salman, A. K. Farhan and A. Shakir, “Creation of S-Box based one-dimensional chaotic logistic map: Colour image encryption approach,” International Journal of Intelligent Engineering and Systems, vol. 15, no. 5, pp. 378–389, 2022. [Google Scholar]

A. A. Alzaidi, M. Ahmad, M. N. Doja, E. Al Solami, M. M. Sufyan et al., “A new 1D chaotic map and β-hill climbing for generating Substitution-Boxes,” IEEE Access, vol. 6, no. 10, pp. 55405–55418, 2018. [Google Scholar]

  30. Q. Lu, C. Zhu and G. Wang, “A novel S-Box design algorithm based on a new compound chaotic system,” Entropy, vol. 21, no. 10, pp. 1004, 2019. [Google Scholar]

  31. G. Hanchinamani, D. G. Narayan and R. Savakknavar, “Construction of S-Box based on parametric mixing of chaotic maps,” in Proc. ICAECT, Bhilai, India, pp. 1–4, 2021. [Google Scholar]

  32. A. H. AL-Wattar, “A review of block cipher’s S-Boxes tests criteria,” Iraqi Journal of Statistical Sciences, vol. 16, no. 29, pp. 91–104, 2019. [Google Scholar]

  33. S. Mohammad Seyedzadeh and S. Mirzakuchaki, “A fast color image encryption algorithm based on coupled two-dimensional piecewise chaotic map,” Signal Processing, vol. 92, no. 5, pp. 1202–1215, 2012. [Google Scholar]

  34. M. A. Khodher, A. Alabaichi and A. S. Abbas, “Dual method cryptography image by two force secure and steganography secret message in IoT,” Telecommunication, Computing, Electronics and Control, vol. 18, no. 6, pp. 2928–2938, 2020. [Google Scholar]

  35. M. Ragab and E. B. Ashary, “Metaheuristic lightweight cryptography for security enhancement in Internet of Things,” Computers, Materials & Continua, vol. 72, no. 2, pp. 3010–3023, 2022. [Google Scholar]

  36. A. M. Alabaichi, “True color image encryption based on dna sequence, 3D chaotic map, and key-dependent DNA S-Box of AES,” Journal of Theoretical and Applied Information Technology, vol. 96, no. 2, pp. 304–321, 2019. [Google Scholar]

  37. H. Liu and X. Wang, “Colour image encryption based on one-time keys and robust chaotic maps,” Computers & Mathematics with Applications, vol. 59, no. 10, pp. 3320–3327, 2010. [Google Scholar]

  38. M. Ahmad, M. N. Doja and M. M. S. Beg, “Security analysis and enhancements of an image cryptosystem based on hyperchaotic system,” Journal of King Saud University–Computer and Information Sciences, vol. 33, no. 1, pp. 77–85, 2021. [Google Scholar]

  39. B. Yousif, F. Khalifa, A. Makram, A. Takieldeen, “A novel image encryption/decryption scheme based on integrating multiple chaotic maps,” AIP Advances, vol. 10, no. 7, pp. 1–9, 2020. [Google Scholar]

  40. Y. Q. Zhang, J. L. Hao and X. Y. Wang, “An efficient image encryption scheme based on S-Boxes and fractional-order differe der differential logistic map,” IEEE Access, vol. 8, pp. 54175–54188, 2020. [Google Scholar]