Lattice-Based Authentication Scheme to Prevent Quantum Attack in Public Cloud Environment

1  Introduction

Recently, cloud computing has become very popular among corporations, individuals, and government organizations for its ability to provide low-cost services via the internet. Due to the availability of high-speed internet connections, these services can be accessed easily for numerous purposes. Cloud computing offers various services, and storage is considered one of the most important services for various architectures and applications. Annually, billions of devices outsource massive amounts of data, which are stored in cloud computing globally. However, security is a significant concern for these outsourced stored data in cloud computing environments because of advanced computing devices and strong adversaries. Therefore, cryptographic techniques such as Elliptic-curve cryptography (ECC), Symmetric, Asymmetric, Identity-based, Hashing, and many more techniques are used to protect outsourced data in the cloud computing environment. The ECC authentication protocols are based on discrete logarithm problems, whereas RSA (Rivest–Shamir–Adleman) is based on large numbers of factorizations. RSA-based cryptography techniques are slower because of the exponentiation and heavy computation and communication costs.

Recently, the world has seen a race among countries and organizations to build superior quantum computers. These quantum computers are so strong that they can break the traditional cryptographic algorithms, add more attacks on authentication protocols, and open a way to easily access the stored data on the public cloud. On the other hand, lattice-based cryptography provides excellent efficiency and simplicity in the post-quantum cryptographic era. For this purpose, we have proposed a lattice-based authentication scheme for public cloud computing in this study. So far, the lattice-based cryptography protocols resist quantum attacks.

1.1 Motivation and Contributions

The Lattice-based cryptographic authentication technique gives hope for the post-quantum era. A lattice is a set of all the integer’s linear combinations of base vectors, such as 𝒷1,𝒷2,𝒷2,…𝒷n∈Zn, A = {∑𝒶i∗𝒷i:𝒶i∈Zn}. The lattice is based on a base vector and can only be scaled by integers; no fractions are involved. Even quantum computers cannot solve the lattice-based problem in polynomial time. The lattice that only two basis vectors are defined 𝓋1=(0,1) and 𝓋2=(1,0). Here, the lattice is a set of all values that can be reached by any scale and combination of basis vectors. There is no point to reach 𝓋1=(0,1) and 𝓋2=(1,0) without fractional scalars, and the scale is only possible with whole integers. However, traditional cryptographic techniques, such as RSA, are based on mathematical problems that can be easily verified but are hard to compute. RSA is based on prime factorization and works excellently with traditional computers but failed in the quantum computing era. Therefore, the lattice shortest vector problem is a major cryptographic algorithm that can prevent quantum attacks excellently. According to our knowledge, in the quantum computing era, the 𝒜 can use Shor’s technique and easily break traditional authentication protocols. The following are our contributions.

•   We have utilized the lattice-based Ring with errors (RLWE) technique for the design of our protocol.

•   Our proposed protocol is secure under the RLWE problematic assumptions.

•   We have utilized the Gaussian probability distribution, also known as the discrete gaussian, which plays a vital role in lattice-based cryptography algorithms.

•   The formal security analysis of our proposed scheme shows that it can fulfill the security requirements in public cloud environments in the post-quantum era.

•   Our scheme is secure against all known traditional attacks in the informal security analysis.

•   The protocol performance analysis section demonstrates that the proposed protocol is efficient as compared to the existing lattice-based techniques.

1.2 Network Model

Our protocol consists of two entities, a user and a public cloud server. The user uses portable devices to access the public cloud server. In contrast, public cloud servers provide various services to the user using high-speed internet, such as storage space, access to shared data and private data space, and many more. The detailed diagram of the proposed model is shown in Fig. 1.

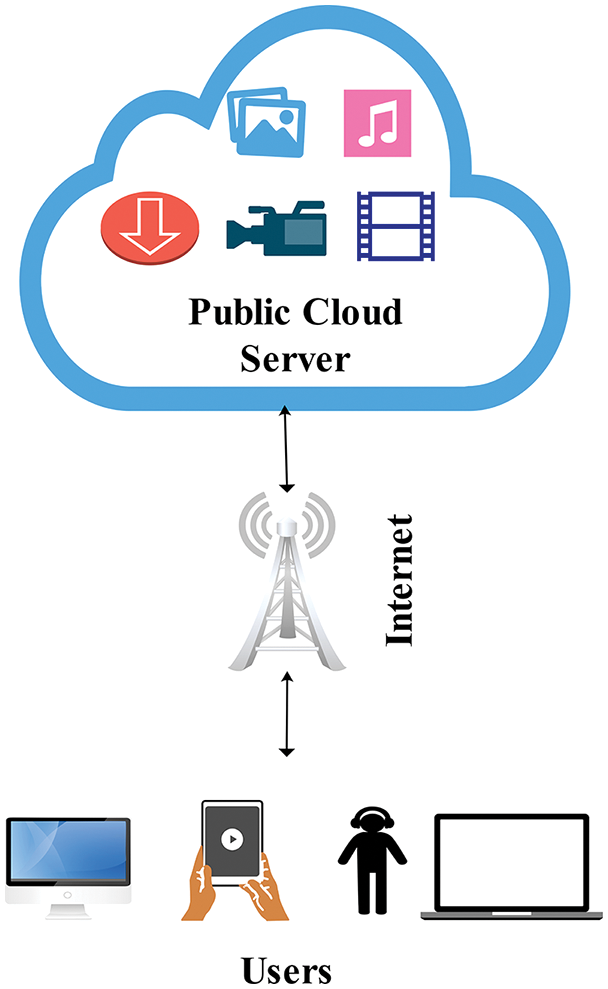
Figure 1: Proposed network model

2  Literature Review

In this portion of the paper, we will discuss and analyze the limitations of existing authentication techniques.

Different cryptographic techniques have been used to authenticate different peers in different environments, Hashing, Bilinear pairing, Identity-based, Elliptic curve (ECC), Chaotic maps, Code-based, and Lattice-based. However, some of these cryptographic techniques are not secure against quantum attacks. The authors of [1] proposed an authentication scheme for a public cloud server environment that achieved all known security goals but was not much feasible for the quantum computing era. Some existing proposed schemes are not efficient against quantum attacks and are vulnerable to known security attacks, for example, the schemes [2–13] suffer from offline password attacks, while the schemes [5,6,10,13–21] cannot provide anonymity. As a result, the protocols [4,9,21–24] are vulnerable to insider attacks. Furthermore, the schemes [5–9,13,16–19,24–27] are not secure enough against impersonation attacks, and the protocols [18,19,28] are vulnerable to replay attacks.

The increasing competition to build high-performance quantum computers among organizations will potentially threaten these cryptographic techniques. However, the lattice-based cryptography method is the most secure against quantum attacks. Therefore, the researchers are trying to utilize the lattice-based cryptography technique to propose an authentication scheme for various environments. For example, an ideal lattice-based authentication scheme for mobile devices is proposed in [29]. The authors of [30] proposed a lattice-based authentication protocol for Internet of Things (IoT) devices. In [29], the authors claimed that their scheme is the first ever lattice-based scheme for mobile devices. However, the communication and computation costs were much higher than our proposed scheme.

Furthermore, the authors utilized a Radio Frequency Identification (RFID) system for an IoT environment to secure communications and resist quantum attacks, and the author used the lattice-based cryptography technique. Another scheme is proposed in [31] for IoT-enabled smart devices under the ring LWE problem using a lattice-based cryptography technique. Although the scheme is proposed for IoT devices, but the communication and computation costs are very high as compared to our proposed scheme. Finally, the authors of [32] proposed an authentication scheme for the internet of vehicles, where the authors utilized the identity-based technique in lattice-based cryptography. In this scheme, the edge nodes first gets private keys from the private key generator (PKG) and later communicate with each other using these keys. Furthermore, the author uses identity-based cryptography (IBC) to reduce the overhead of certificate management.

The distribution of quantum keys using fuzzy logic is presented in [33]. The scheme is intended for nuclear command and control centers (NCCC) and has management, rigor, self-learning, inherent security, and authentication capabilities. The distribution of quantum keys based on fuzzy logic guarantees the user’s identity. In [34], the authors utilize the edge and fog computing through deep learning in a quantum computing framework, where the edge node has the capacity for processing, communication, caching, and storage. The scheme used an intelligent quantum computing framework coupled with deep learning for updating edge caching contents in a fog-computing radio access network.

3  Proposed Scheme

In this section of our research study, we present an authentication strategy for public cloud environments based on lattice cryptography.

3.1 Setup Procedure

■   The public cloud server selects random number rS ∈Zqixi Where q is an odd prime number, and i is an integer that satisfies q mod 2i = 1.

■   The public cloud server selects secure hash function h(.).

■   The public cloud server selects the secret value S that belongs e←χβ⇒f(x) = 12πσe−12(x−μσ)2.

■   The Public cloud server Select ∂⇒χβ, where χβ is the Gaussian distribution

■   The public cloud server calculates public key PKS = rS. S + 2.e

■   The public cloud server published {q, i, rS, PKS, h(.)} and saved S as a secret key.

3.2 Registration Procedure

•   Select IDU and send it to the public cloud server.

•   The public cloud server then selects the random number rS ∈Zqixi, choose γ,ρ←χβ and calculates the user secret key SU = h (IDU|| S), and S1 = h (IDu|| rS) ⊕ SU. After calculation, the public cloud server sends {rS1, S1} to the user.

•   The user then selects the password PWU and calculates S2 = h (rS|| IDU) ⊕ h (PWu|| IDU) ⊕ S1, and S3 = h (IDu|| PWu|| S2). The user store {S2, S3, ρ,∂ }.

________________________________________________________________________________________________________________________________________________________

User                                                Public Cloud Server

________________________________________________________________________________________________________________________________________________________

Select IDU

                                {IDU}⟶

                                                rS ∈Zqixi

                                                γ,ρ←χβ,

                                                SU = h (IDU||S)

                                                S1 = h (IDu||rS1) ⊕ SU

                                                Store { γ,∂}

                                {rS,S1,ρ,∂}⟵

selects the password PWU

S2 = h (rS||IDU) ⊕ h (PWu|| IDU) ⊕ S1

S3 = h (IDu||PWu||S2)

Store {S2, S3, ρ,∂ }

________________________________________________________________________________________________________________________________________________________

         Module 1: User registration procedure

3.3 Login and Registration Procedure

•   The user input IDU* and PWU* and calculate the S3* = h (IDu*|| PWu*|| S2) and check S3*? = S3 if true, then the system proceeds further; otherwise, connection is terminated. The user selects a random number rU ∈Zqixi and calculates further. M = rS. rU + 2.ρ and forward {M} towards the public cloud server.

•   The public cloud server selects the random number rS1∈Zqixi and calculates further M1 = rS. rS1 + 2. γ, M2 = (M||S), M3 = ∂(M2), M4 = (M2||M3), M5 = h (M|| M1|| M3|| M4) and sends {M1, M3, M5} to user.

•   The user calculates M2/ = (rU . PKS), M4/ = (M2/|| M3), M5/? = h(M|| M1|| M3|| M4) if the value matches, then proceed further otherwise, terminate the connection. The user further calculates M6 = h (IDU|| PWU) ⊕ S2, M7 = (M1|| rU), M8 = ∂ (M7), M9 = (M7|| M8), M10 = h (M|| M8|| M9|| M1|| M3|| M4|| M2) ⊕ IDU, M11 = h (IDU|| M6|| M10|| M|| M8|| M9|| M1|| M3|| M2/|| M5), SKU = h (IDU|| M10|| M|| M8|| M9|| M11|| M1|| M3|| M2/|| M5) and sends {M10, M8, M11} towards public cloud server.

•   The public cloud server calculates further M7/ = (M|| rS1), M9/ = (M7/||M8), IDU = h (M|| M8|| M9/|| M1|| M3|| M4|| M2) ⊕ M10, M6/ = h (IDU||S), M11/ = h (IDU ||M6/|| M10|| M|| M8|| M9/|| M1|| M3|| M2|| M5) and check M11/? = M11 if true, proceed further; otherwise, terminate the connection. The public cloud server calculates the session key SKS = h (IDU|| M10|| M|| M8|| M9/|| M11|| M1|| M3|| M2|| M5).

________________________________________________________________________________________________________________________________________________________

User                                                Public Cloud Server

________________________________________________________________________________________________________________________________________________________

IDU* and PWU*

Calculate

S3* = h (IDu*||PWu*||S2)

Check S3*? = S3

random number rU ∈Zqixi

M = rS. rU + 2.ρ

                                   {M}⟶

                                                     random number rS1∈Zqixi

                                                     Calculates

                                                     M1 = rS. rS1 + 2. γ

                                                     M2 = (M.S)

                                                     M3 = ∂(M2)

                                                     M4 = (M2.M3)

                                                     M5 = h(M||M1||M3||M4)

                                   {M1,M3,M5}⟵

Calculates

M2/ = (rU . PKS)

M4/ = (M2/||M3)

M5/? = h(M||M1||M3||M4)

M6 = h(IDU||PWU) ⊕ S2

M7 = (M1. rU)

M8 = ∂ (M7)

M9 = (M7||M8)

M10 = h(M||M8||M9||M1||M3||M4||M2) ⊕ IDU

M11 = h(IDU||M6||M10||M||M8||M9||M1||M3||M2/||M5)

SKU = h(IDU||M10||M||M8||M9||M11||M1||M3||M2/||M5)

                                   {M10,M8,M11}⟶

                                                     Calculates

                                                     M7/ = (M . rS1)

                                                     M9/ = (M7/. M8)

                                                     IDU = h(M||M8||M9/||M1||M3||

                                                           M4||M2) ⊕ M10

                                                     M6/ = h(IDU.S)

                                                     M11/ = h(IDU||M6/||M10||M||M8||

                                                           M9/||M1||M3||M2||M5)

                                                     M11/? = M11

                                                     SKS = h(IDU, M10||M||M8||M9/||

                                                           M11||M1||M3||M2||M5)

                                    SKU=SK⟷

________________________________________________________________________________________________________________________________________________________

         Module 2: Login and authentication procedure

4  Security Analysis

In this section, we will explain and validate our scheme against various attacks. We have proposed a lattice-based authentication scheme for the public cloud environment and used the Real-or-Random (ROR) model to check whether our proposed scheme is secure enough. With informal security analysis, we have further discussed the possible attacks on our proposed scheme.

4.1 Formal Security Analysis Using ProVerif

We have used ProVerif to check whether the session secret is secured, the session key exchanged between the communicating parties is confidential, and the attacker can access the session key at the start of the session. Fig. 2 is the ProVerif simulation results, showing that our protocol is secure.

Figure 2: ProVerif code result

4.2 Formal Security Analysis Using ROR Model

In this section, we have tested our proposed scheme in the ROR model against a strong adversary 𝒜. In the ROR model, five queries have been defined that show the capabilities of 𝒜. We let the 𝒜 launch various attacks on our protocol. The five queries are defined in Table 2.

Two participants are involved in our scenario, i.e., the user PU𝒯 and public cloud server PP𝓈𝒯.

Theorem. The 𝒶𝒶𝒹𝓋 can violate the session key of our proposed scheme

𝒶𝒹𝓋𝒶=|P𝓇(Succ)−12|

P𝓇(Succ) means the probability of success. Our proposed scheme is secure if

𝒶𝒹𝓋𝒶≤𝓆𝓀22+(𝕢ℯ+𝕢𝓈𝕢)2+(𝕢ℯ+𝕢𝓈)𝒶𝒹𝓋𝒶RE

where Execute query is denoted with 𝕢ℯ. The Send query is denoted by 𝕢𝓈 and Ring learning with errors denoted by 𝒶𝒹𝓋𝒶RE.

Proof. In this section, we will play Games with 𝒜 to check whether our scheme is secure.

G𝒜Mε0. The 𝒜 launch an actual attack on the proposed scheme in this game and tries to win the game.

𝒶𝒹𝓋𝒶=|P𝓇(Succ0)−12|

=|P𝓇(Succ0)−P𝓇(Succ4)+P𝓇(Succ4)−12|

=|∑𝒶=14𝒶𝒹𝓋𝒶+P𝓇(Succ4)−12|

G𝒜Mε1. The 𝒜 intercept transmitted message in the login & authentication phase and try to launch an eavesdropping attack by using Execute query. But ρ and γ are a sample from the Gaussian distribution χβ. Therefore, we obtain

𝒶𝒹𝓋𝒶=|P𝓇(Succ0)−P𝓇(Succ1)|=0

G𝒶Mε2. If collision occurs among transmitted messages {M}, {M1, M3, M4} and {M10, M8, M11}. However, the random number is generated using ∈Zqixi. Therefore, we obtained the following:

𝒶𝒹𝓋𝒶=|P𝓇(Succ1)−P𝓇(Succ2)|≤𝕕𝓀22+(𝕢ε+𝕢𝓈𝕢)2

G𝒜Mε3. The 𝒜 guesses the session key SK in this game. According to our proposed scheme, the session key is calculated SK = h (IDU, M10, M, M8, M9, M11, M1, M3, M2, M5), and the values of each instance belong to ∈Zqixi and χβ. Hence,

𝒶𝒹𝓋𝒶=|P𝓇(Succ2)−P𝓇(Succ3)|≤(𝕢ε+𝕢𝓈)𝒶𝒹𝓋𝒶RE

G𝒜Mε4. In this game, the 𝒜 used a Test query in order to get the secret values. Thus, we obtain

𝒶𝒹𝓋𝒶=|P𝓇(Succ3)−P𝓇(Succ4)|≤𝕕𝓀22

Therefore, the 𝒜 cannot construct the session key SK.

|P𝓇(Succ4)|=12

Hence, our proposed scheme is secure under the assumption of lattice-based Ring learning with errors method.

4.3 Informal Security Analysis

The proposed scheme is based on Lattice-based cryptography, where the users and public cloud servers register themselves using a secure channel. However, if the 𝒜 by any chance captures transmitted messages in the login & authentication phase, it still cannot extract secret values. Furthermore, our scheme resists all known attacks, and more details are given below.

1.    Provide anonymity. Our scheme provides anonymity to users and public cloud servers. The user’s identity is secured using a one-way hash function and public cloud server secret key. The messages that include identity are M6 = h (IDU|| PWU) ⊕ S2, and M11 = h (IDU|| M6|| M10|| M|| M8|| M9|| M1|| M3|| M2/|| M5). Therefore, it is challenging for 𝒶 to break or guess the secret key and random numbers of a public cloud server. Hence, our proposed scheme provides anonymity.

2.    Secure against replay attack. If 𝒜 tries to impersonate any communicating peers and try to send a previous session key SK capture message. However, in our scheme, random numbers are generated randomly and fresh for each session. Therefore, the 𝒶 cannot launch a replay attack on our scheme. Hence, the proposed scheme is secure against replay attacks.

3.    Provide mutual authentication. In our proposed scheme, the communicating parties mutually authenticate each other using S3*? = S3, M5/? = M5, and M11/? = M11. If these values are tempered or modified, the connection gets terminated. Thus, our scheme provides mutual authentication.

4.    Provide session key. The user and public cloud server calculate the session key SKU = SKS. The connection will be terminated if any value is tempered or modified in the session key contraction phase. Therefore, our scheme provides a session key for secure communications.

5.    Provide message integrity. The user and public cloud server check the message integrity in the login and authentication phase. The user side checks the messages S3*? = S3, M2/ = (rU ||PKS), M4/ = (M2/|| M3), M5/? = h (M|| M1|| M3|| M4), and confirms whether these messages are from a public cloud server, while the public cloud server also checks the messages received from a user, such as M7/ = (M || rS1), M9/ = (M7/ || M8), M6/ = h(IDU||S), and M11/ = h(IDU|| M6/|| M10|| M|| M8|| M9/|| M1|| M3|| M2|| M5). The connection is terminated if any of these messages are modified or tempered. Hence, our scheme provides message integrity.

6.    Secure against impersonation attack. In our proposed scheme, the random numbers are generated randomly, and the identity is secured using a one-way hash function and public cloud secret key. Therefore, the 𝒜 cannot get any information from the transmitted messages. Hence, our proposed scheme is secure against impersonation attacks.

7.    Secure against stolen verifier attack. In the registration phase, the public cloud server did not store any values. Therefore, our scheme is secure against stolen verifier attacks.

8.    Secure against offline password attack. Let’s suppose that 𝒜 extracts all the secret values from the stored data on the user side. However, 𝒜 will need a user identity, a public cloud server secret key, and a random number to get the password. Therefore, our scheme is secure against offline password-guessing attacks.

9.    Secure against modification attack. In our proposed scheme login and authentication phase, the transmitted messages are verified by both communicating peers. For example, the user side verifies S3*? = S3, M5/? = h(M|| M1|| M3|| M4), while the public cloud server-side verifies M11/? = M11. If any of these values are modified, the connection will be terminated. Hence, our scheme is secure against modification attacks.

10.   Secure against MITM attack. As we prove that our scheme is secure against impersonation and provide message integrity. Hence, our scheme is secure against a man-in-the-middle attack.

5  Performance Analysis

In this part of our research article, we have calculated our protocol’s computation and communication costs. After calculating the communication and computation costs, we compare our scheme with the existing protocols.

5.1 Computation Cost

We have considered the work done in [29]. The TSM represents the time taken for multiplication with the scalar operation, and TGD means the time taken for Gaussian distribution samples. In contrast, TM represents the time consumed during multiplication, and TMA is the time taken during multiplication with addition, while T∂ the time taken during characteristic function and the execution time taken by different operations are listed in Table 3. Considering the execution times shown in Table 3, our proposed scheme’s total computation cost is ≅0.003888463 ms. We further calculated the user-side and server-side costs separately in Table 3 and combined them at the end. Fig. 3 shows the comparison of our proposed scheme with the recent existing scheme in terms of computation cost. The results show that our scheme computation cost is lower than the existing schemes.

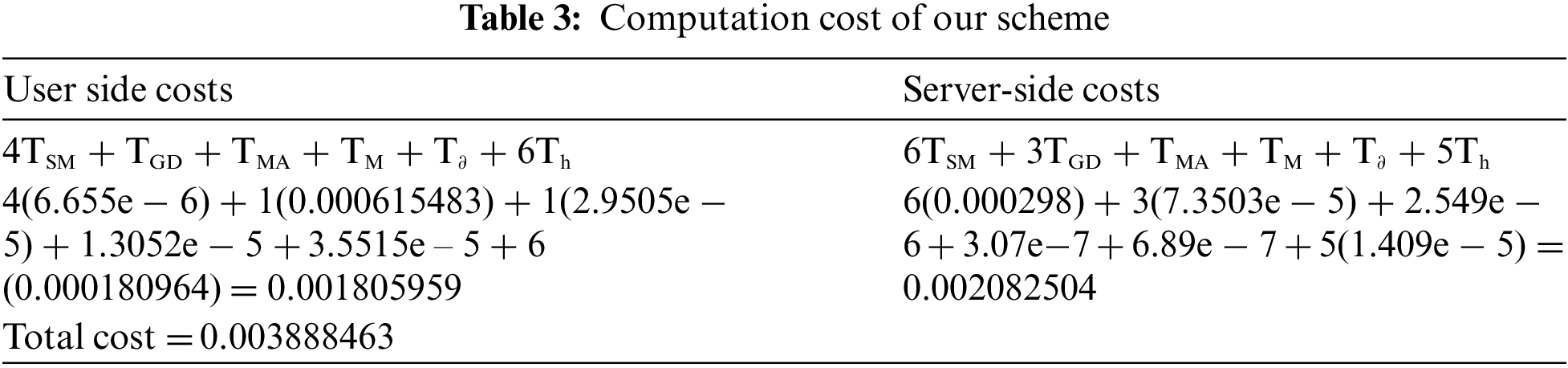
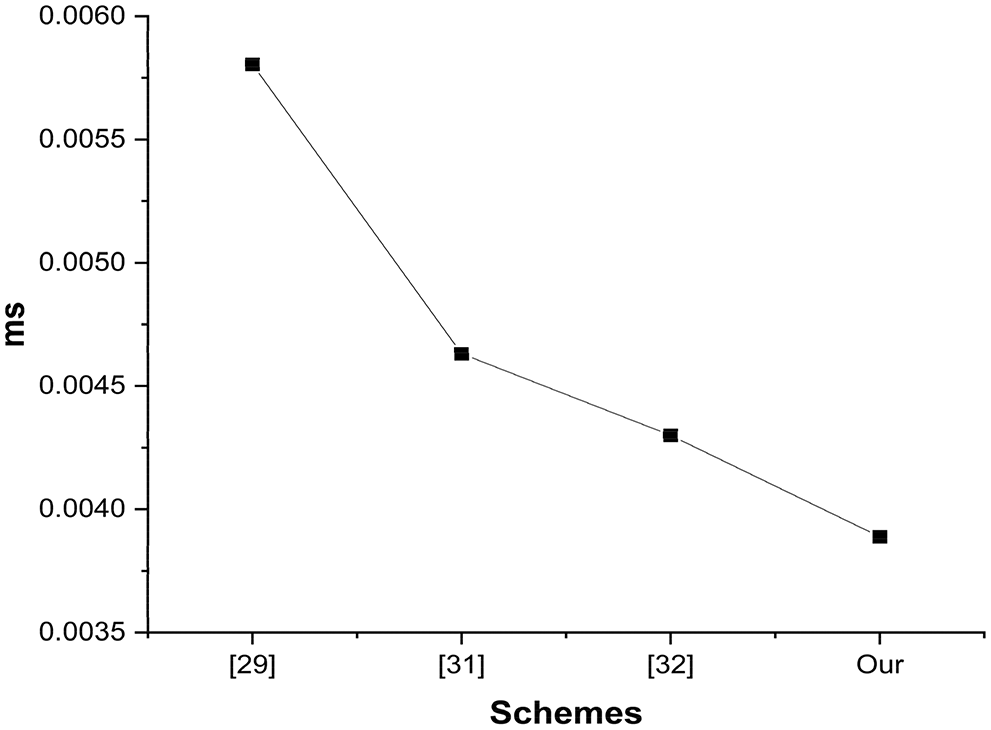
Figure 3: Computation cost

5.2 Communication Cost

We have computed the communication cost in this part of our lattice-based authentication protocol. We have considered the work [29] and calculated our communication cost. In our proposed scheme, the user and public cloud server exchange messages in the login and authentication phase. From these transmitted messages, we calculate our total communications cost. The one-way hash function fixed output is 512 bits, the identity is 32 bits, the timestamp is 64 bits, the random number is 256 bits, and the secret value is 256 bits. Therefore, the user-side transmitted messages are [{M} + {M10, M8, M11}] and the user-side communication cost equals to {1024} + {544} + {1536} ≅ 3104 bits. Whereas the public cloud server-side transmitted messages are [{M1, M3, M4}] and the communication cost is equal to [{1024} + {1536} + {3072} ≅ 5632] bits. Hence, the total communication cost is equal to 8736 bits. Fig. 4 shows the comparison of our proposed scheme with other existing schemes. The results in Fig. 4 show that our scheme is much more lightweight than the existing protocols.

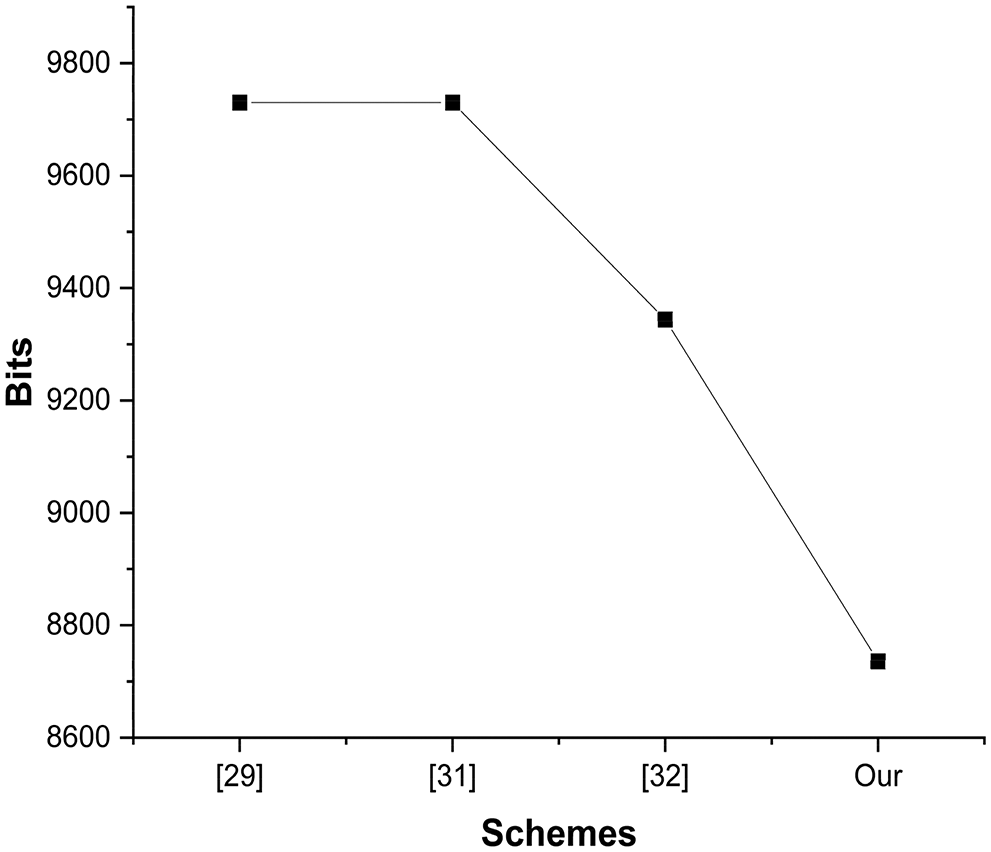
Figure 4: Communication cost

5.3 Security Comparison Analysis

Here, we have examined some contemporary and established authentication systems, both lattice-based and more conventional, and compared them with our approach. Existing lattice-based techniques offer the same level of security as our proposed scheme, but at substantially higher costs in terms of computation and communication. Furthermore, quantum attacks can compromise conventional authentication methods. Table 4 displays the comparative analysis in terms of the security of our system with existing schemes.

6  Conclusion

The traditional cryptographic algorithms work great with classical computers. However, things will change once quantum computers come to reality. Shor’s technique can easily break traditional cryptographic techniques using quantum computing. Keeping this in mind, we have proposed a lattice-based cryptography technique to authenticate peers in public cloud computing. The security of the proposed scenario has been conducted using the ROR model, while the performance analysis section considers two aspects, communication and computation costs. Both analysis showed that the proposed mechanism is robust, lightweight, efficient, and can easily be implemented for practical use.

In future work, we intend to modify and reduce the proposed scheme’s computation and communication costs. Furthermore, we will also try to use the proposed scheme for IoT-enabled devices in a public cloud environment.

Funding Statement: The authors wish to thank the Korean Government (Ministry of Science and ICT) through the National Research Foundation of Korea (NRF) Grant 2021R1A2C1010481.

Conflicts of Interest: The authors declare they have no conflicts of interest to report regarding the present study.

References

    1. N. Khan, J. Zhang and S. U. Jan, “A robust and privacy-preserving anonymous user authentication scheme for public cloud server,” Security and Communication Networks, vol. 2022, pp. 1–14, 2022. [Google Scholar]

    2. S. Roy, S. Chatterjee, A. K. Das, S. Chattopadhyay, S. Kumari et al., “Chaotic map-based anonymous user authentication scheme with user biometrics and fuzzy extractor for crowdsourcing internet of things,” IEEE Internet of Things Journal, vol. 5, no. 4, pp. 2884–2895, 2017. [Google Scholar]

    3. S. Qiu, D. Wang, G. Xu and S. Kumari, “Practical and provably secure three-factor authentication protocol based on extended chaotic-maps for mobile lightweight devices,” IEEE Transactions on Dependable and Secure Computing, vol. 19, no. 2, pp. 1338–1351, 2020. [Google Scholar]

    4. M. Fakroon, M. Alshahrani, F. Gebali and I. Traore, “Secure remote anonymous user authentication scheme for smart home environment,” Internet of Things, vol. 9, pp. 100158, 2020. [Google Scholar]

    5. B. Ying and A. Nayak, “Lightweight remote user authentication protocol for multi-server 5G networks using self-certified public key cryptography,” Journal of Network and Computer Applications, vol. 131, pp. 66–74, 2019. [Google Scholar]

    6. M. Nikooghadam, R. Jahantigh and H. Arshad, “A lightweight authentication and key agreement protocol preserving user anonymity,” Multimedia Tools and Applications, vol. 76, no. 11, pp. 13401–13423, 2017. [Google Scholar]

    7. R. Amin, T. Maitra, D. Giri and P. Srivastava, “Cryptanalysis and improvement of an RSA based remote user authentication scheme using smart card,” Wireless Personal Communications, vol. 96, no. 3, pp. 4629–4659, 2017. [Google Scholar]

    8. M. Luo, Y. Zhang, M. K. Khan and D. He, “A secure and efficient identity-based mutual authentication scheme with smart card using elliptic curve cryptography,” International Journal of Communication Systems, vol. 30, no. 16, pp. e3333, 2017. [Google Scholar]

    9. T. Maitra, M. S. Obaidat, R. Amin, S. H. Islam, S. A. Chaudhry et al., “A robust ElGamal-based password-authentication protocol using smart card for client-server communication,” International Journal of Communication Systems, vol. 30, no. 11, pp. e3242, 2017. [Google Scholar]

  10. S. H. Islam, “Design and analysis of an improved smartcard-based remote user password authentication scheme,” International Journal of Communication Systems, vol. 29, no. 11, pp. 1708–1719, 2016. [Google Scholar]

  11. T. Maitra, M. S. Obaidat, S. H. Islam, D. Giri and R. Amin, “Security analysis and design of an efficient ECC-based two-factor password authentication scheme,” Security and Communication Networks, vol. 9, no. 17, pp. 4166–4181, 2016. [Google Scholar]

  12. S. D. Kaul and A. K. Awasthi, “Security enhancement of an improved remote user authentication scheme with key agreement,” Wireless Personal Communications, vol. 89, no. 2, pp. 621–637, 2016. [Google Scholar]

  13. M. Qi and J. Chen, “New robust biometrics-based mutual authentication scheme with key agreement using elliptic curve cryptography,” Multimedia Tools and Applications, vol. 77, no. 18, pp. 23335–23351, 2018. [Google Scholar]

  14. A. Hassan, N. Eltayieb, R. Elhabob and F. Li, “An efficient certificateless user authentication and key exchange protocol for client-server environment,” Journal of Ambient Intelligence and Humanized Computing, vol. 9, no. 6, pp. 1713–1727, 2018. [Google Scholar]

  15. Q. Jiang, N. Zhang, J. Ni, J. Ma, X. Ma et al., “Unified biometric privacy preserving three-factor authentication and key agreement for cloud-assisted autonomous vehicles,” IEEE Transactions on Vehicular Technology, vol. 69, no. 9, pp. 9390–9401, 2020. [Google Scholar]

  16. W. -i. Bae and J. Kwak, “Smart card-based secure authentication protocol in multi-server IoT environment,” Multimedia Tools and Applications, vol. 79, no. 23, pp. 15793–15811, 2020. [Google Scholar]

  17. S. Banerjee, V. Odelu, A. K. Das, S. Chattopadhyay and Y. Park, “An efficient, anonymous and robust authentication scheme for smart home environments,” Sensors, vol. 20, no. 4, pp. 1215, 2020. [Google Scholar]

  18. L. Zhou, X. Li, K. -H. Yeh, C. Su and W. Chiu, “Lightweight IoT-based authentication scheme in cloud computing circumstance,” Future Generation Computer Systems, vol. 91, pp. 244–251, 2019. [Google Scholar]

  19. R. Martínez-Peláez, H. Toral-Cruz, J. R. Parra-Michel, V. García, L. J. Mena et al., “An enhanced lightweight IoT-based authentication scheme in cloud computing circumstances,” Sensors, vol. 19, no. 9, pp. 2098, 2019. [Google Scholar]

  20. S. Kumari, X. Li, F. Wu, A. K. Das, K. -K. R. Choo et al., “Design of a provably secure biometrics-based multi-cloud-server authentication scheme,” Future Generation Computer Systems, vol. 68, pp. 320–330, 2017. [Google Scholar]

  21. S. S. Sahoo, S. Mohanty and B. Majhi, “A secure three factor based authentication scheme for health care systems using IoT enabled devices,” Journal of Ambient Intelligence and Humanized Computing, vol. 12, no. 1, pp. 1419–1434, 2021. [Google Scholar]

  22. A. G. Reddy, E. -J. Yoon, A. K. Das, V. Odelu and K. -Y. Yoo, “Design of mutually authenticated key agreement protocol resistant to impersonation attacks for multi-server environment,” IEEE Access, vol. 5, pp. 3622–3639, 2017. [Google Scholar]

  23. R. Amin and G. Biswas, “Design and analysis of bilinear pairing based mutual authentication and key agreement protocol usable in multi-server environment,” Wireless Personal Communications, vol. 84, no. 1, pp. 439–462, 2015. [Google Scholar]

  24. R. Ali and A. K. Pal, “An efficient three factor–based authentication scheme in multiserver environment using ECC,” International Journal of Communication Systems, vol. 31, no. 4, pp. e3484, 2018. [Google Scholar]

  25. F. Wang, G. Xu, C. Wang and J. Peng, “A provably secure biometrics-based authentication scheme for multiserver environment,” Security and Communication Networks, vol. 2019, pp. 1–15, 2019. [Google Scholar]

  26. R. Amin, S. H. Islam, N. Kumar and K. -K. R. Choo, “An untraceable and anonymous password authentication protocol for heterogeneous wireless sensor networks,” Journal of Network and Computer Applications, vol. 104, pp. 133–144, 2018. [Google Scholar]

  27. A. H. Moon, U. Iqbal and G. M. Bhat, “Mutual entity authentication protocol based on ECDSA for WSN,” Procedia Computer Science, vol. 89, pp. 187–192, 2016. [Google Scholar]

  28. P. Chandrakar and H. Om, “An extended ECC-based anonymity-preserving 3-factor remote authentication scheme usable in TMIS,” International Journal of Communication Systems, vol. 31, no. 8, pp. e3540, 2018. [Google Scholar]

  29. Q. Feng, D. He, S. Zeadally, N. Kumar and K. Liang, “Ideal lattice-based anonymous authentication protocol for mobile devices,” IEEE Systems Journal, vol. 13, no. 3, pp. 2775–2785, 2018. [Google Scholar]

  30. S. Akleylek and M. Soysaldı, “A new lattice-based authentication scheme for IoT,” Journal of Information Security and Applications, vol. 64, pp. 103053, 2022. [Google Scholar]

  31. S. Rana and D. Mishra, “Lattice-based key agreement protocol under ring-LWE problem for IoT-enabled smart devices,” Sādhanā, vol. 46, no. 2, pp. 1–11, 2021. [Google Scholar]

  32. D. S. Gupta, S. Ray, T. Singh and M. Kumari, “Post-quantum lightweight identity-based two-party authenticated key exchange protocol for internet of vehicles with probable security,” Computer Communications, vol. 181, pp. 69–79, 2022. [Google Scholar]

  33. M. Shabbir, F. Ahmad, A. Shabbir and S. A. Alanazi, “Cognitively managed multi-level authentication for security using fuzzy logic based quantum key distribution,” Journal of King Saud University-Computer and Information Sciences, vol. 34, no. 4, pp. 1468–1485, 2022. [Google Scholar]

  34. T. Hasan, F. Ahmad, M. Rizwan, N. Alshammari, S. A. Alanazi et al., “Edge caching in fog-based sensor networks through deep learning-associated quantum computing framework,” Computational Intelligence and Neuroscience, vol. 2022, pp. 1–17, 2022. [Google Scholar]

  35. B. Bera, D. Chattaraj and A. K. Das, “Designing secure blockchain-based access control scheme in IoT-enabled internet of drones deployment,” Computer Communications, vol. 153, pp. 229–249, 2020. [Google Scholar]

  36. J. Srinivas, A. K. Das, N. Kumar and J. J. Rodrigues, “TCALAS: Temporal credential-based anonymous lightweight authentication scheme for internet of drones environment,” IEEE Transactions on Vehicular Technology, vol. 68, no. 7, pp. 6903–6916, 2019. [Google Scholar]

  37. Z. Ali, S. Hussain, R. H. U. Rehman, A. Munshi, M. Liaqat et al., “ITSSAKA-MS: An improved three-factor symmetric-key based secure AKA scheme for multi-server environments,” IEEE Access, vol. 8, pp. 107993–108003, 2020. [Google Scholar]