An Efficient EMD-Based Reversible Data Hiding Technique Using Dual Stego Images

1  Introduction

In the era of the internet, the internet of things (IoT), and mobile communications, the interchange of vast amounts of digital data has become an easy task. Some of this information includes some secret data. Unintended recipients can easily access this data. Thus, there is a need for the development of means to protect the transmitted data. Thus far, researchers have developed two main methods to achieve data protection: Data encryption [1] and Data hiding [2–43]. Data encryption techniques share the data in a meaningless form and can be easily identified as confidential data, making it vulnerable to attacks [2]. DHTs conceal the secret data in meaningful digital media (usually a digital image called a cover image). Depending on the nature of the hidden message, one can classify DHTs into two main categories: Digital watermarking, when the message is concerned with the cover, and steganography, otherwise [2]. Steganographic techniques transparently conceal the secret message into a cover object such as a digital image. The main objective of these techniques is to hide the mere existence of the secret message in the cover object. However, the concealment of the secret message in the cover object produces a distorted stego object with reduced visual quality. Steganographic techniques should keep the distortion minimal and transparent so it cannot be detected. Another important objective in steganography is to increase the data hiding capacity, defined as the number of secret message bits embedded in the cover object. However, increasing data hiding capacity introduces more distortions in the cover image, reducing visual quality and destroying transparency. Thus, there is a need for a tradeoff between transparency and data-hiding capacity [3]. DHTs may also be classified as irreversible [3–23] and reversible [24–43]. In irreversible DHTs, the distortions to the cover object are permanent, and one can’t restore the original cover object after extracting the secret message. In reversible DHTs, the distortions to the cover image are not permanent, and one can restore the original cover image after extracting the secret message. The reversibility of DHTs is necessary for some applications, such as military, law enforcement, and medical applications. DHTs are numerous and may be carried out in the spatial or transform domains [3]. In the spatial domain, one can find several methods, such as Image interpolation, Difference expansion (D.E.), Histogram shifting (H.S.), Least significant bit substitution (LSB), and EMD-based methods [3].

The EMD-based methods have some attractive features: They provide high-quality stego images and can attain relatively high embedding rates. EMD-based techniques have witnessed extensive research efforts [4–36]. Reference [8] introduced the first EMD-based technique, partitioning the cover image into groups of n-pixels; they embedded a (2n+1)−ary secret digit into each group of n-pixels by increasing or decreasing the value of only one pixel in the group by one. The stego image quality is relatively low. Reference [9] proposed an Improved EMD (IEMD) method in which they were able to increase the embedding rate up to 1.5 bits per pixel (bpp) while maintaining good-quality stego images. Reference [10] introduced the diamond encoding technique in which they embed a (2k2+2k+1)−ary secret digit into a pair of cover pixels. The embedding parameter k controls the embedding rate. The image quality becomes low as k goes high. Reference [12] proposed a fully EMD technique (FEMD), in which they utilized a new extraction function and increased the data hiding capacity up to 4.5 bpp. However, the image quality is low. Reference [13] proposed a formula FEMD (FFEMD) in which they eliminated the need for the 256×256 matrix function table needed in the FEMD method. However, numerical complexity is increased. Reference [14] combined difference expansion and FFEMD to improve the data hiding capacity and image quality. They have also proposed a solution to the overflow problem in EMD-based techniques. Reference [15] proposed a method to embed an n2−ary secret digit into each group of n pixels obtaining up to a four bpp embedding rate. This method is similar to the IEMD scheme, with a slight improvement in image quality. The above-mentioned EMD-based algorithms are irreversible and numerically demanding. Due to the extraction function’s cyclic nature, most EMD-based DHTs are irreversible, and one can find a few reversible EMD-based DHTs [24–43]. Reference [24] proposed the first reversible EMD-based DHT using two stego images. They insert A 5−ary secret digit into two consecutive pixels of the two cover images. The algorithm is somewhat numerically demanding, provides an embedding rate of one bpp, and high-quality stego images of 45 dB PSNR values. Reference [25] proposed an EMD-based reversible DHT using two stego images. They insert A 5−ary secret digit into one pixel in the first cover image and its dual image in the second cover image. The algorithm is numerically demanding and provides an embedding rate of 1.55 bpp and stego images of 38 dB PSNR values. Reference [27] proposed an adaptive EMD-based reversible DHT using two stego images. Using a 9−ary numeral system, they inserted two secret digits into two adjacent pixels in the first and second cover images. The algorithm is numerically demanding, provides an embedding rate of 1.55 bpp, and stego images quality of 43 dB PSNR values. Reference [28] proposed an EMD-based reversible DHT using two stego images. They insert a 9−ary secret digit into one pixel in the first cover image and its dual image in the second cover image. The algorithm is numerically demanding and provides an embedding rate of 1.55 bpp and stego images of 38 dB PSNR values. Reference [29] proposed an EMD-based reversible DHT using two stego images. Using a 9−ary numeral system, they inserted two secret digits into two adjacent pixels in the first and second cover images. The algorithm is numerically demanding and provides an embedding rate of 1.55 bpp and stego image quality of 43 dB PSNR values. Reference [30] proposed a reversible DHT using an orientation combination of dual stego images. Using a 25−ary numeral system, they inserted a secret digit into two adjacent pixels in each stego image. The algorithm is numerically demanding and provides an embedding rate of 1.14 bpp and stego image quality of 50 dB PSNR values. Reference [31] proposed an adaptive EMD-based reversible DHT using two stego images. Using a 5−ary numeral system, they inserted two secret digits into two adjacent pixels in the first and second cover images. The algorithm is numerically demanding and provides an embedding rate of 1 bpp and stego image quality of 50 dB PSNR values. Reference [32] proposed an RDHT using an orientation combination of dual stego images. Using a 52−ary numeral system, they inserted two secret digits into two adjacent pixels in the two stego images. The algorithm is numerically demanding and provides an embedding rate of 1.58 bpp and stego images quality of 45 dB PSNR values. Reference [38] proposed a numerically efficient RDHT using two shadow images. Using a combination of 2−ary and 5−ary numeral systems, they obtained an embedding rate of 1.56 bpp and stego images quality of 43 dB PSNR values. However, the algorithm needs the 256×256 reference matrix. Reference [40] proposed an RDHT using three shadow images. Using a combination of 5−ary and 6−ary numeral systems, they obtained an embedding rate of 1.13 bpp and stego images quality of 48 dB PSNR values. However, the algorithm is somewhat complex and requires the transmission of side information to achieve reversibility. Reference [42] proposed an adaptive turtle-shell-based RDHT using dual images. Using an 8−ary numeral system, they obtained an embedding rate of 1.25 bpp and stego images quality of 45 and 49 dB PSNR values. Again, the algorithm is numerically demanding. All these methods use two or more cover images and improve security via secret key sharing [44].

We summarize our findings by the following points:

•   Due to the cyclic nature of the extraction function and the overflow problem, EMD-based DHTs are not directly reversible

•   EMD-based DHTs can provide high embedding rates. However, increasing the embedding rate decreases the stego image quality

•   In general, increasing embedding rates above two bpp results in significant distortions in the stego image, making it vulnerable to detection

•   Researchers proposed the use of dual images to develop reversible EMD-based DHTs

•   The use of dual images increases the security of the secret data via secret key sharing

•   Thus far, existing dual image-based EMD-based reversible DHTs are numerically demanding, require complex search algorithms, and need to generate a 256×256 reference matrix

This paper presents an EMD-based reversible DHT using dual stego images. The contributions of our technique are:

•   Simple and numerically efficient embedding and extraction algorithms

•   Relatively high data-hiding capacity

•   Direct and numerically efficient conversion of the binary secret message to 4−ary and vice versa

•   Elimination of the need for the 256×256 reference matrix used in similar techniques by replacing it with novel two 2×4 lookup tables, and elimination of the need for the complex and numerically demanding search step required by similar techniques

•   An embedding strategy that enables straightforward reversibility with almost zero computational cost

•   Increased Security by using secret key sharing and the equal high-quality of the two stego images

The rest of this paper proceeds as follows. In Section 2, we give a summary of some related work. Section 3 outlines the proposed algorithm, the data-hiding step, and the data extraction and image recovery step. Section 4 gives experimental simulation results. Finally, Section 5 presents the discussion, conclusion, and future work.

2  Background

This section presents the fundamentals of EMD-based DHTs and gives details of some related techniques.

2.1 Fundamentals of EMD-Based DHTs

These schemes conceal an l−ary secret digit in a group of n-pixels of the M×N cover image I. The first step in these schemes is to segment I into groups of n-pixels. The extraction function takes the form fe(x1,x2,…,xn)=(∑i=1nai×xi)modl where ais and l are positive integers. The extraction function fe(x1,x2,…,xn) is cyclic and has a range of 0 to l−1 values. We refer to these values as characteristic values. Using the vector of pixels v(x1,x2,…,xn) as the origin of an n-coordinate system, we search for a vector v′=[x1′,x2′,…,xn′] within a neighborhood-set ψ(x1,x2,…,xn). The new vector (stego vector) v′ should satisfy the condition fe(x1′,x2′,..,xs,.,xn′)=sl; where sl is the secret digit in the l−ary number system. We define the neighborhood-set ψ(x1,x2,…,xn) as the set of vectors vψ=[p1,p2,…,pn] that satisfy a distance condition of the form ∑i|pi−xi|≤k;k=1,2,3,…,l−1, or minimize a cost function J=|vvT−v′Tv′|. We choose k such that each characteristic value occurs at least once over the set ψ(x1,x2,…,xn). The distortion in ψ(x1,x2,…,xn) should be minimal. Thus, we pick a small neighborhood set ψl(x1,x2,…,xn) to satisfy: 1) There are precisely l elements in ψl(x1,x2,…,xn), and 2) The values of fe(x1,x2,…,xn) over ψl(x1,x2,…,xn) are mutually exclusive. Increasing n usually decreases the distortion and data hiding capacity. For this, the most commonly used value is n=2. Fig. 1 shows some examples (patterns) of the neighborhood set ψl and the corresponding characteristic values. The second step is to embed an l−ary secret digit into the vector [x1,x2,…,xn] so that the distance between the original cover vector [x1,x2,…,xn] and the resulting stego vector [x1′,x2′,..,xs,.,xn′] is minimal. In the extraction step, the stego image pixels are segmented into a group of vectors v′=[x1′,x2′,…,xn′] in the same order as that in the embedding step. The resulting secret message is: sl=fe(x1′,x2′,..,xs,.,xn′) [11].

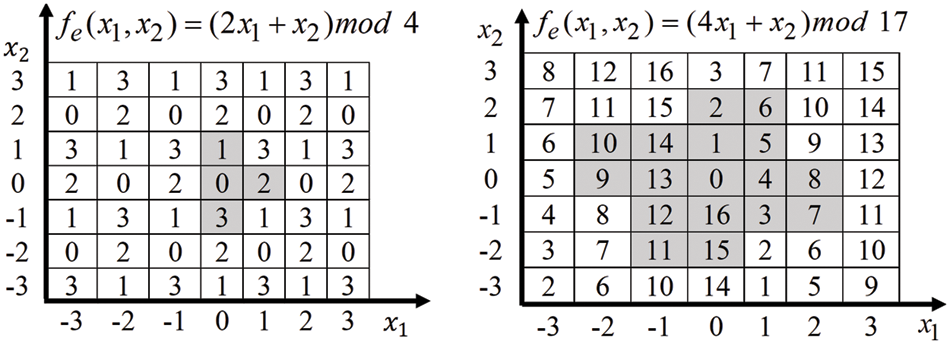
Figure 1: Neighborhood set for different extraction functions

2.2 Related Work

This section presents two closely related DHTs proposed by [8,31].

2.2.1 EMD Algorithm [8]

This scheme is the basis of EMD-based DHTs. It embeds a (2n+1)−ary secret digit in a sequence of n-cover pixels. The algorithm starts by segmenting the cover image into blocks of n-non-overlapping pixels. In order to conceal the secret digit, only one of the n-pixels is increased or decreased by one. The extraction function used in the embedding and extraction phases is:

fe(x1,x2,…,xn)=(∑i=1ni×xi)mod (2n+1); where xi represents the ith pixel value, n is the number of pixels, and mod is the modulus operation. To embed a secret digit into a group of pixels (x1,x2,…,xn), we find the difference d=(s−fe(x1,x2,…,xn))mod(2n+1) and obtain the modified Block as follows:

If d=0

  Set (x1′,x2′,…,xn′)=(x1,x2,…,xn)

ElseIf d≤n

  Set (x1′,x2′,..,xs,.,xn′)=(x1,x2,..,xs+1,..,xn),

Else

  Set (x1′,x2′,..,x2n+1−s,.,xn′)=(x1,x2,..,x2n+1−s−1,..,xn)

End.

At the receiver end, we extract the secret digit as s=fe(x1′,x2′,…,xn′)=(∑i=1ni×xi)mod (2n+1). The hiding capacity for this scheme is (log2⁡(2n+1))/n bpp. The maximum hiding capacity occurs when n=2 with a 1.161 bpp embedding rate. This scheme is irreversible.

2.2.2 Reversibility Data Hiding [31]

Reference [31] proposed an EMD-based reversible DHT scheme using dual images. The extraction function is: fe(x1,x2)=(x1+2x2)mod5, where (x1,x2) are two adjacent pixels in the original cover image I. Fig. 2a shows the 256×256 reference matrix M. Fig. 2b shows a 3×3 block centered at pixel pair (x1,x2). They divide the block pixels into two distinct groups: G1 and G2. Each block contains nine positions labeled as: l1,l2,…,l9, as shown in Fig. 2b. G1 consists of the positions (l2,l4,l5,l6,l8), while G2 consists of the locations (l1,l3,l5,l7,l9). The algorithm embeds two 5−ary secret digits (S1,S2) into each pair of pixels (x1,x2), resulting in two stego images (x1′,x2′) and (x1″,x2″). The algorithm starts by scanning the reference matrix M and obtaining the 3×3 block corresponding to the pixel pair (x1,x2). Then it locates the position of S1 in G1 and the position of S2 in G2. Denote the pixel values in these locations as (x1p1,x2p1) and (x1p2,x2p2). Let Sd=(x2p1−x1p1)2+(x2p2−x1p2)2 be the square of the length of the line connecting these positions and find the stego pixels values using the following algorithm:

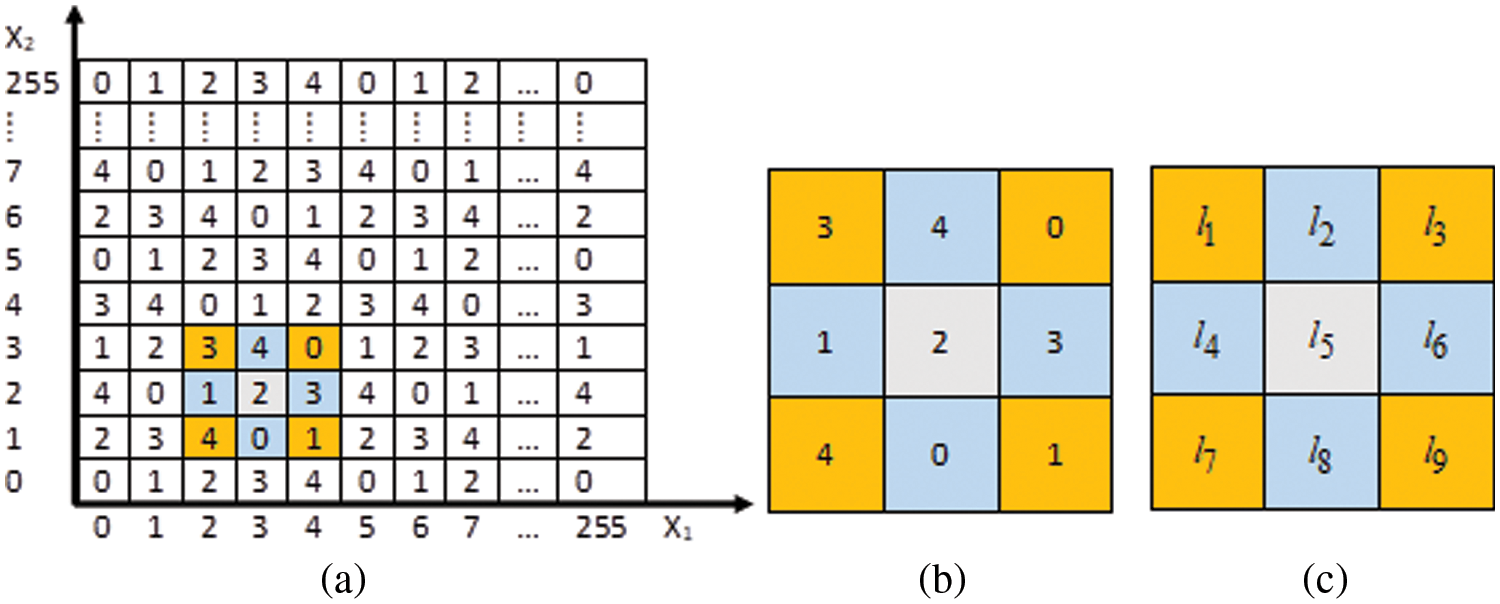
Figure 2: (a) Reference matrix (b) 3 × 3 block (c) 9 positions labeling

Embedding Algorithm [31]

If (x1=0) or (x1=255) or (x2=0) or (x2=255), then

      Do not embed the secret message. Set (x1′,x2′)=(x1,x2) and (x1″,x1″)=(x1,x2)

ElseIf (Sd=0) or (Sd=2) or (Sd=5), then

      Set (x1′,x2′)=(x1p1,x2p1) and (x1″,x2″)=(x1p2,x2p2)

ElseIf Sd=1, then Set (x1″,x2″)=(x1p2,x2p2).

     If (x1″,x2″)=(x1,x2), then

           Set (x1′,x2′)=(x1p1,x2p1)

     ElseIf the line segment from (x1p1,x2p1) to (x1p2,x2p2) is clockwise, then

         Set (x1′,x2′)=(2x1p1−x1p2,2x2p1−x2p2)

     Else

         Set (x1′,x2′)=(2x1−x1p2,2x2−x2p2)

     End

End

Secret message extraction and original image recovery [31]

Given the two stego pixel pairs (x1′,x2′) and (x1″,x2″), resulting from the embedding step, find the distance Sd=(x2p1′−x1p1′)2+(x2p2″−x1p2″)2. Next, recover the original pixel pair (x1,x2) and extract the secret digits (S1,S2) according to the following cases:

Case 1: Sd=0;

       If (x1=0) or x1=255, or x2=0, or x2=255), then

         Set (x1new′,x2new′)=(x1′,x2′) and (x1,x2)=(x1′,x2′). Do not extract any secret digits.

       Else

         Set (x1new′,x2new′)=(x1′,x2′) and (x1,x2)=(x1′,x2′). Extract the two secret digits from the reference matrix M corresponding to (x1new′,x2new′) and (x1′,x2′).

       End

Case 2 Sd=1;

       Set (x1new′,x2new′)=(x1′,x2′) and (x1,x2)=(x1″,x2″). Extract the two secret digits from the reference matrix M corresponding to (x1new′,x2new′) and (x1′,x2′)

Case 3 Sd=2;

       Set (x1new′,x2new′)=(x1′,x2′) and (x1,x2)=(x1′,x2′). Extract the two secret digits from the reference matrix M corresponding to (x1new′,x2new′) and (x1′,x2′).

Case 4 Sd=5;

       Set (x1new′,x2new′)=(x1′,x2′).

       If |x1′−x1″|=2, then

          (x1,x2)=((x1′+x1″)/2,x2′),

       Else

           Set (x1,x2)=(x1′,(x1″+x2′)/2).

           Extract the two secret digits from the reference matrix M corresponding to (x1new′,x2new′) and (x1′,x2′).

       End

Case 5 Sd=4;

       Set (x1new′,x2new′)=(x1′−(x1′−x1″)/2,x2′−(x2′−x2″)/2). Set (x1,x2) equal the center pixel that forms a clockwise rotation with the line segment from (x1′,x2′) to (x1″,x2″). Extract the two secret digits from the reference matrix M corresponding to (x1new′,x2new′) and (x1′,x2′).

Case 6 Sd=8;

       Set (x1,x2)=((x1′+x1″)/2,(x2′+x2″)/2) Set the pixels (x1new′,x2new′) equal to the pixel that is adjacent to pixels (x1,x2) and ((x1″,x2″). The line segment connecting the points (x1new′,x2new′) and (x1″,x2″) forms a counterclockwise rotation around (x1,x2). Extract the two secret digits from the reference matrix M corresponding to (x1new′,x2new′) and (x1′,x2′).

3  The Proposed Scheme

The proposed algorithm is a reversible EMD-based algorithm that uses the general extraction function: fe(x,y)=(x+cy)modm. In this paper, we set c=3 and m=4. Choosing m=4 means we need to convert the message into the 4−ary number system, which requires almost zero computational cost because we can convert two or eight bits of the binary message stream instead of converting the whole message. Thus, the proposed scheme uses the extraction function fe(x,y)=(x+3y)mod4. The neighborhood-set ψ(0,0) in Fig. 3 shows how the extraction function generates the complete 4−ary number system set. The shaded row in Fig. 3 results from decrementing x by one and incrementing it by 0, 1, or 2 while keeping y intact. The shaded column in Fig. 3 results from decrementing y by one and incrementing it by 0, 1, or 2 while preserving the value of x. To understand the proposed algorithm, consider a cover image IC consisting of two neighboring pixels (x1,x2); we generate two cover images IC1=IC2=IC, as shown in Fig. 4. A secret message digit S1 is embedded by substituting x1 and y1 in the extraction function and modifying x1. The embedding process finds the distance d1=(S1−fe(x1,y1))mod4, locates this value in the shaded row of the neighborhood set ψ(0,0) and adjusts x1 in the first cover image accordingly to obtain the first stego image IC1′. Another secret message digit S2 is embedded using x2 and y2. To do this: find the value fe(x2,y2)=(x2+3y2)mod4 and the distance d2=(S2−fe(x2,y2))mod4, locate this value in the shaded column of the neighborhood set ψ(0,0), and modify y2 in the second cover image accordingly to obtain the second stego image IC2′. Note that the shaded pixels remain intact and can be combined to recover the original cover image achieving reversibility.

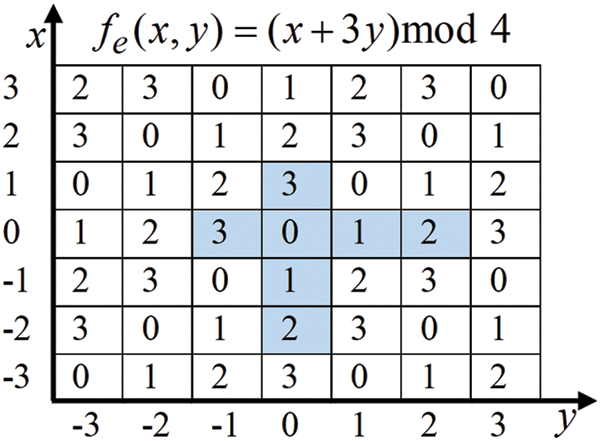
Figure 3: Neighborhood set

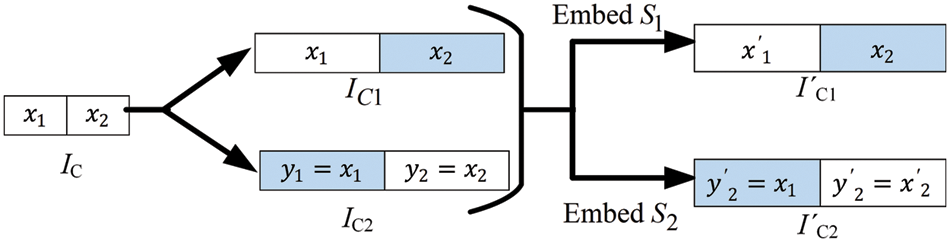
Figure 4: Flow of proposed dual images embedding

In the proposed algorithm, we facilitate the embedding process by defining two novel modification tables to eliminate the search step in the neighborhood set and modify the cover images systematically in a numerically efficient manner. In Fig. 4, the changes to pixels (x1,x2) needed to embed the differences d1 and d2 are given in the first modification matrix mm1 given by Eqs. (1) and (2) below.

mm1=[012−10000](1)

mm2=[00000−1−21](2)

Eq. (3) finds the stego pixels (x1′,y1′):

[x1′y1′]=[x1y1]+mm1(:,d1)(3)

We calculate the stego pixels (x2′,y2′) using Eq. (4).

[x2′y2′]=[x2y2]+mm2(:,d2)(4)

For extraction, we find the two secret digits S1=(x1′+3y1′)mod4 and S2=(x2′+3y2′)mod4. One should notice that the embedding step may change the original embeddable pixel value by a maximum absolute value δ=2. The change in pixel value may result in overflow or underflow. As outlined in the following subsection, we adjust the border embeddable pixels’ values to prevent this problem.

3.1 The Proposed Data Embedding Algorithm

Given the N×M gray level original cover image IC and a binary secret message W with length lW; the embedding procedure consists of the following steps:

Step 1: Obtain the dual cover images IC1 and IC2 as: IC1=IC2=IC.

Step 2: Classify the dual cover images’ pixels into two classes: embeddable pixels and non-embeddable pixels. Embeddable pixels in the first cover image IC1 are the pixels p(i,j);imod(2)=1,i=1,2,3…M and j=1,2,3…N. Embeddable pixels in the second cover image IC2 consist of pixels p(i,j);jmod(2)=0,i=1,2,3…M andj=1,2,3…N. The White pixels (even columns in IC1 and odd columns in IC2) in Fig. 5 show the embeddable pixels for the dual cover images, while the shaded pixels (even columns in IC1 and odd columns in IC2) are the non-embeddable pixels. The union of the non-embeddable pixels in the two stego images gives the original cover image IC.

Step 3: Prevent overflow and underflow problems by modifying each embeddable pixel p(i,j) in the cover images IC1 and IC2 using Eq. (5).

p(i,j)={255−δ,if p(i,j)>255−δδ,if p(i,j)<δ(5)

where δ denotes the absolute maximum change to any embeddable pixel. In our algorithm, δ=2.

Step 4: Sequentially scan the cover images from left to right and top to bottom and embed one 4−ary secret digit using steps 5–8.

Step 5: Get two bits from the binary secret message and find its 4−ary value Sd.

Step 6: Let the current decimal values of the pixels in the preprocessed cover images be: IC1(i,j)=x and IC2(i,j)=y. Use Eq. (6) to find the value of the extraction function as:

fe(x,y)=(x+3y) mod4(6)

Step 7: Use Eq. (7) to find the distance d as:

d=(Sd−fe(x,y)) mod4(7)

Step 8: Find mm1 and mm2 as defined by Eqs. (1) and (2), and use Eq. (8) to find the new values of the stego pixels IC1′(i,j) and IC2′(i,j).

[IC1′(i,j)IC2′(i,j)]={[xy]+mm1(:,d);ifIC1′(i,j)isembeddable[xy]+mm2(:,d);ifIC2′(i,j)isembeddable(8)

The result of this process is the two stego images IC1′ and IC2′. We repeat steps 4–8 until all secret message bits are embedded.

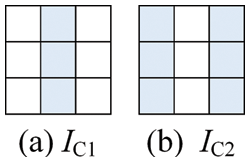
Figure 5: Embeddable pixels selection

3.2 The Proposed Data Extraction and Image Recovery Algorithm

Given the dual stego images IC1′ and IC2′ we recover the original cover image and extract the secret message using the following steps:

Step 1: Classify the stego images’ pixels into two classes: embeddable and non-embeddable pixels, in the same manner as in the embedding step. Fig. 6 shows this classification where the white pixels are the embeddable pixels while the shaded pixels are the non-embeddable pixels.

Step 2: Recover the original cover image IC by combining the non-embeddable pixels in the two stego images IC1′ and IC2′.

Step 3: Refer to Fig. 6 and let the current decimal values of the stego images’ pixels in IC1′ and IC2′ be pC1′(i,j)=x′ and pC2′(i,j)=y′. Extract the secret message digit using Eq. (9).

Sd=(x′+3y′)mod4(9)

Step 4: Find the binary value of Sd and concatenate it to the extracted binary message. Extract all secret message digits by repeating steps 3 and 4.

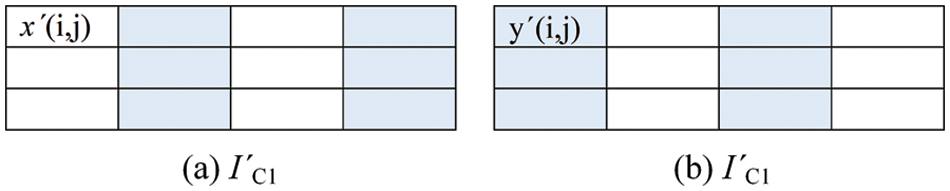
Figure 6: Embeddable pixels classification

3.3 Numerical Example

We conclude this section by giving a numerical example to illustrate the operational steps of the proposed reversible DHT. Fig. 7 shows a 1 × 2 original cover image IC and the corresponding dual cover images IC1 and IC2. The shaded pixels in Fig. 7 are non-embeddable, while the white pixels are embeddable. The preprocessing step replaces the value 255 in the cover image IC1 by 253. Fig. 8 shows the resulting preprocessed cover images.

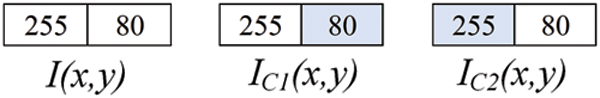
Figure 7: Original and dual cover images

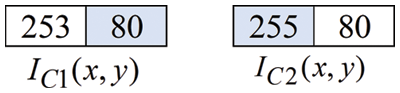
Figure 8: Preprocessed dual cover images

Given the binary secret message W = [1011], convert every two binary bits into its 4−ary format. The resulting secret message is S = [23]. The digits of the secret message S are embedded in the dual cover images as follows:

Assign the value of the first pixel in IC1 as: x=pC1(1,1)=253 and assign the value of the first pixel in IC2 as:y=pC2(1,1)=255 → Use Eq. (6) to find the value of the extraction function, fe=(x+3y)mod4=2 → Get the first secret digit S1=2→ Use Eq. (7) to find the distance d=(S1−fe)mod4=0. → use Eq. (8) to find the stego images pixels as:

[pC1′(1,1)pC2′(1,1)]=[xy]+mm1(:,d)=[253255]+[00]=[253255].

Assign the value of the next pixel in IC1 as: x=pC1(1,2)=80 → assign the value of the first pixel in IC2 as: y=pC2(1,2)=80.→ use Eq. (6) to find the value of the extraction function fe=(x+3y)mod4=0→ Get the next secret digit S2=3→ Use Eq. (7) to find the distance d=(S2−fe)mod4=3. → use Eq. (8) to find the stego images pixels as:

[pC1′(1,2)pC2′(1,2)]=[xy]+mm2(:,d)=[8080]+[01]=[8080]+[01]=[8081].

Fig. 9 shows the resulting dual stego images.

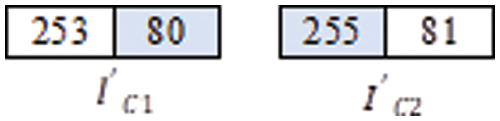
Figure 9: Dual stego images

For extraction, starting with dual stego images in Fig. 9, the original cover image is obtained by combining the shaded columns in IC1′, and IC2′. We extract the hidden message as follows: Assign the value of the first pixel in IC1′ as: x=pC1′(1,1)=253 and assign the value of the first pixel in IC2′ as: y=pC2(1,1)=255. → Use Eq. (9) to find the value of the first hidden digit as S1=(x+3y)mod4=2 → Convert S1 to its two bits binary equivalent S1d=10→ Concatenate this to the extracted binary message. Assign the value of the next pixel in IC1′ as: x=pC1′(1,2)=80 and assign the value of the next pixel in IC2′ as: y=pC2′(1,2)=81. → use Eq. (9) to find the value of the next hidden digit as S2=(x+3y)mod4=3 → Convert S2 to its two-bit binary equivalent S2d=11→ Concatenate this to the extracted binary message. The resulting extracted message: Sext = [S1dS2d] = [1011] is equivalent to the embedded message W.

4  Experimental Results

This section presents the simulation results of the proposed technique. To measure the quality of the stego images, we use the PSNR values of the stego images. The PSNR between an M×N original cover image I and the stego image I′, is given by Eq. (10) [45]:

PSNR(I,I′)=10 log10⁡M×N×(255)2∑i=1M∑j=1N(X(i,j)−Is(i,j))2dB(10)

We use the embedding rate as a measure of the data hiding capacity. The embedding rate R is given by Eq. (11).

R=EB/(2×M×N)(11)

where EB represents the total number of the embedded binary bits.

We used the CPU time as a measure to evaluate the numerical efficiency. In our simulations, we used twelve 512×512 grayscale cover images. The secret message is a randomly generated binary secret message using MatLab. Fig. 10 shows the twelve test images. We performed our simulations on a personal computer with an Intel(R) Core(T.M.) i7-6700 CPU @ 3.40 GHz and 8 G.B. memory.

Figure 10: Test images

4.1 Performance Evaluation of the Proposed Technique

Fig. 11 shows the stego images at the maximum embedding rate. The high quality of the stego images is clear, and the human eye can detect no traces of any artifacts.

Figure 11: Stego images

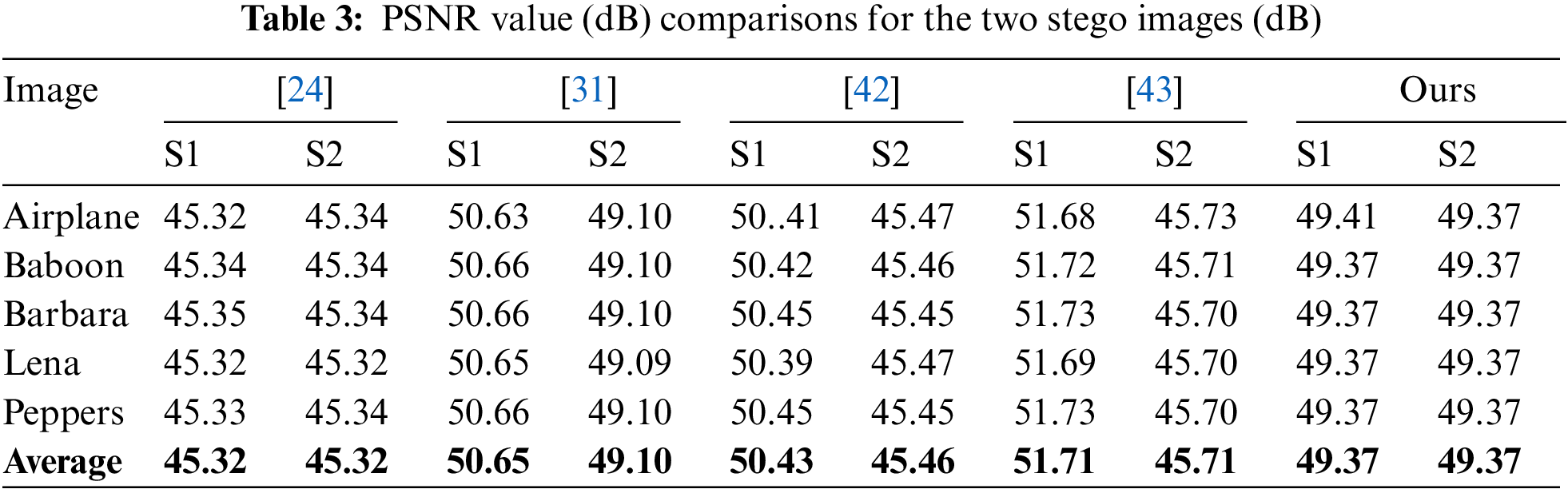
Table 1 gives the main features of our technique. The high quality of the stego images is evident via an average PSNR value of more than 49 dB. In addition, Table 1 also shows that the average absolute distortion in the pixels is about 0.5/pixel. Moreover, Table 1 also shows that, at the maximum embedding rate, our algorithm achieved a high average PSNR value of 49 dB. We conducted another experiment to investigate the PSNR values of the stego images against different embedding rates. Fig. 12 shows the results for the Lena image, where the PSNR values for both stego images ranged from 80 dB when the embedding rate is 1/16 bpp to 49 dB when the embedding rate is one bpp. An essential feature of our algorithm is that the PSNR values are practically identical for both stego images. This feature improves security. In addition, the PSNR values are almost identical for all test images. This shows that the performance of our technique does not depend on the cover image. Our technique embeds one 4−ary digit (two binary bits) in each pixel pair in the cover images resulting in an embedding rate of one bpp, as Table 1 shows. Table 2 demonstrates the numerical efficiency of our technique. The numerical efficiency of our technique resulting from using the modification tables and eliminating the search step is evident in the short embedding and extraction times shown in Table 2.

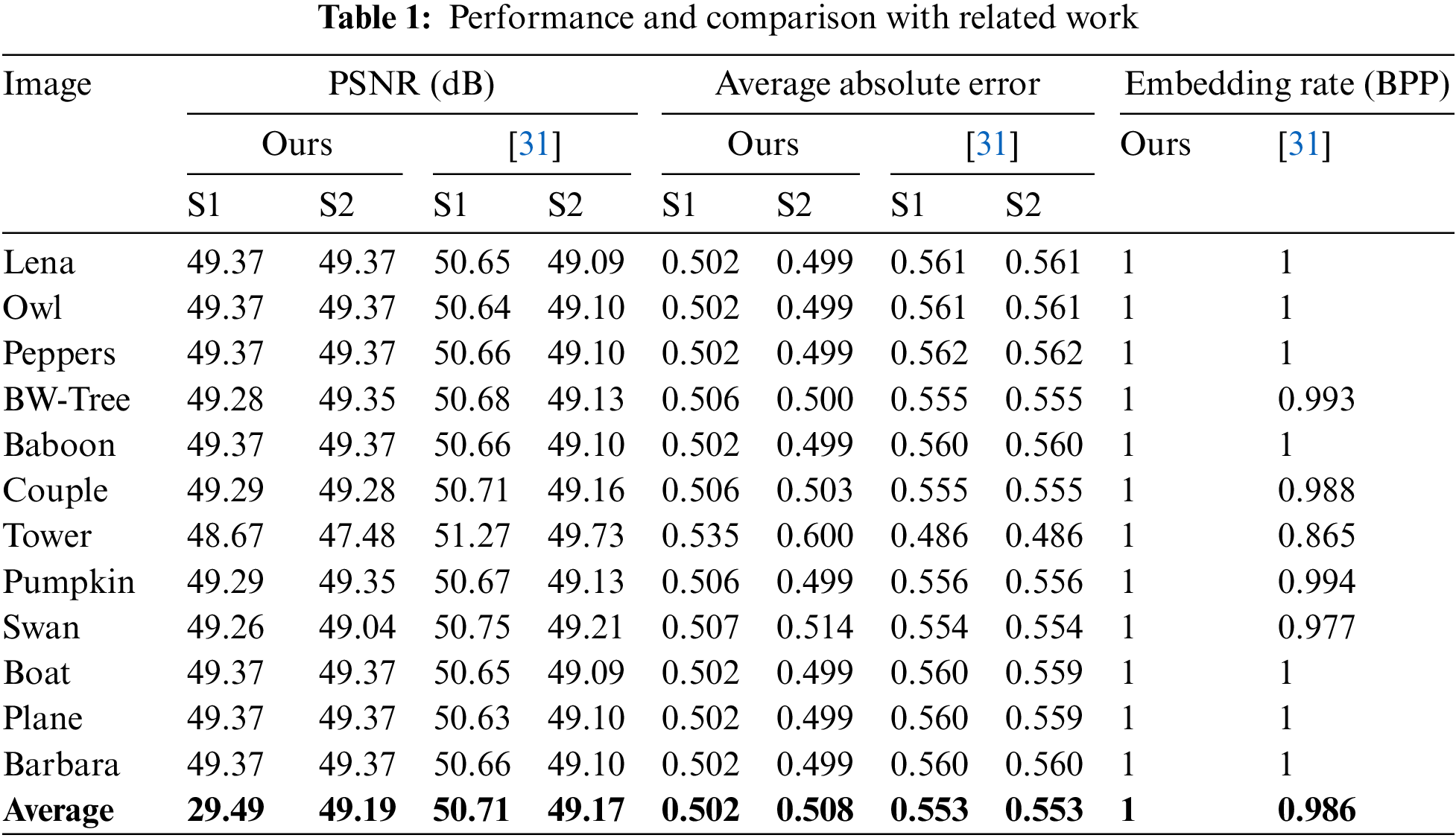
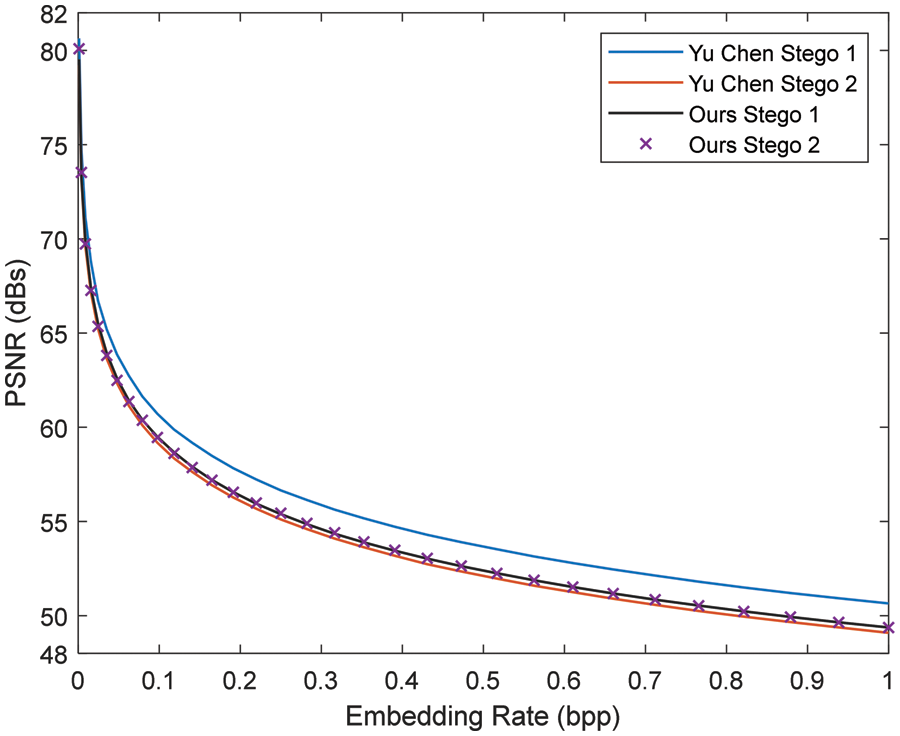
Figure 12: PSNR vs. embedding rate performance lena image

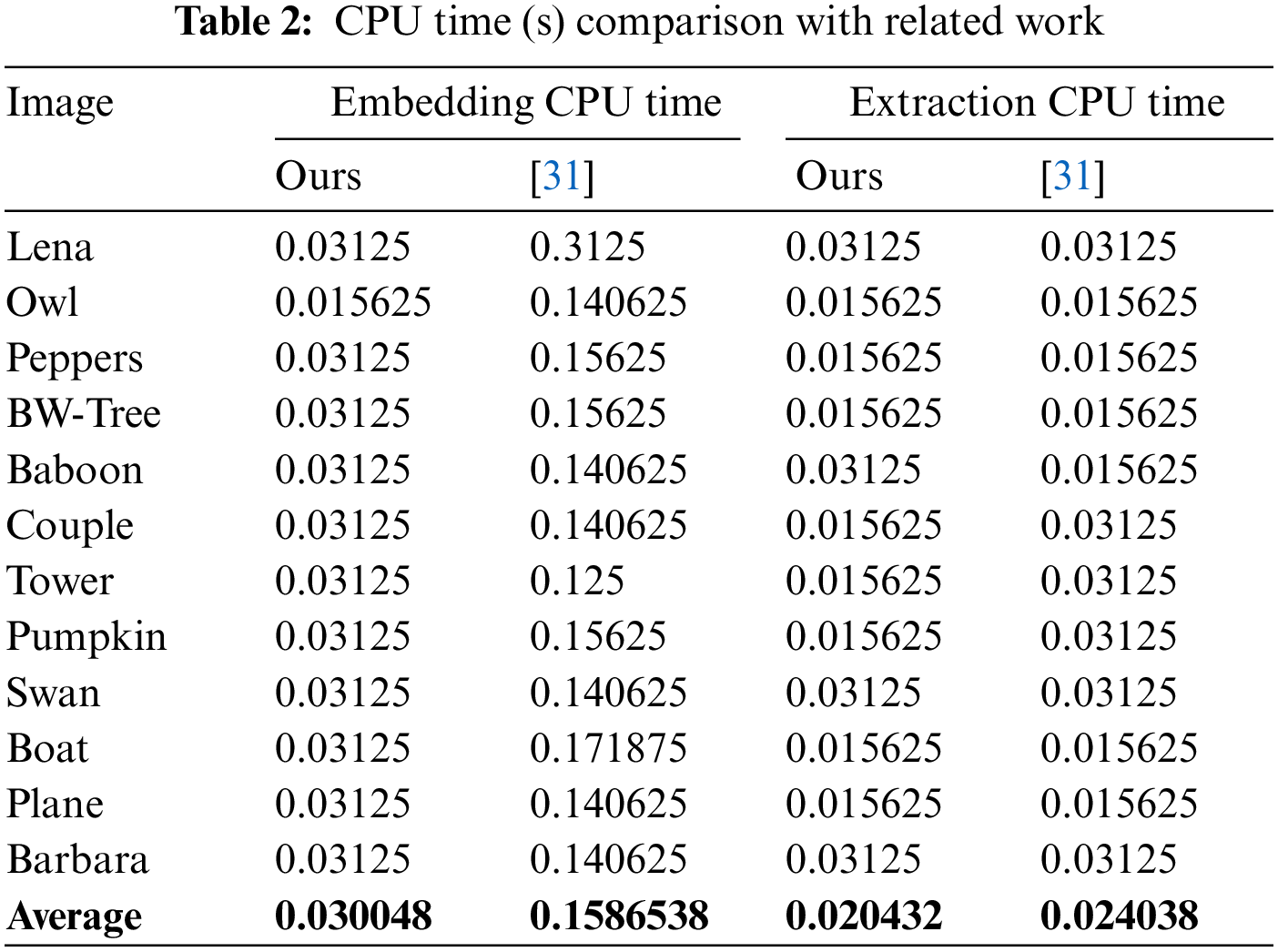
4.2 Performance Comparisons with Related Work

Table 1 also compares our technique with [31] in terms of PSNR values, average absolute error, and embedding rates. The average embedding rate of our technique is one bpp, while that of [31] is 0.9859 bpp. In obtaining these results, we converted each byte of the binary message to its 5−ary value in [31] and 4−ary value in our technique. The PSNR values for both techniques are close. However, The PSNR values of our two stego images are almost identical, while that of [31] are slightly different. Fig. 12 gives the PSNR values vs. Embedding rate for both techniques and shows that the PSNR values of our two stego images lie between the two stego images’ PSNR values in [31]. Another feature of our technique is numerical efficiency and simplicity. Instead of using a 256×256 neighborhood matrix in the embedding and extraction phases in [31], we only need two 2×4 lookup tables, resulting in significant savings in storage and numerical calculations. Although the execution time depends on the status of the operating system and may vary from one run to another, Table 2 shows that the embedding CPU time of our technique is one-fifth of that of [31]. Table 2 also shows that the extraction CPU time of our technique is 0.8 that of [31]. Table 3 compares the PSNR values of our technique with that of [24,31,42,43]. These techniques have maximum embedding rates of 1, 1, 1.25, and 1 bpp, respectively. For a fair comparison, Table 3 gives PSNR values at the same embedding rate of 1 bpp. Our technique and [24] give equal PSNR values for both stego images making them less susceptible to detection by intruders. The PSNR value of the two stego images in [31,42,43] by 1, 5, and 5 dB, respectively, making it more vulnerable to detection. Overall, our technique outperforms other techniques in terms of image quality, simplicity, and numerical efficiency.

5  Conclusion

This paper presented a new reversible RDHT based on EMD. The proposed technique is simple and numerically efficient. It limits image distortions and increases stego image quality and transparency. Each pixel pair of the two stego images (one pixel from each stego image) hides one 4−ary secret digit by modifying only one pixel with a maximum distortion of two resulting in an embedding rate of one bpp. Using the two novel 2×4 lookup tables highly reduces numerical calculations by eliminating the numerically demanding search step in similar techniques. The embedding strategy enabled direct reversibility at almost zero computational cost. Increased security is achieved by transmitting the two stego images on separate channels so that only the receiver with both stego images and the embedding sequence can extract the secret message. Experimental results demonstrate the high quality of the two stego images with more than 49 dB average PSNR values. Experimental results also show that the embedding CPU time of our technique is one-fifth of that of [31]. The extraction CPU time of our technique is 0.8 that of [31].

Funding Statement: The author received no funding for this study.

Conflicts of Interest: The author declares that he has no conflicts of interest to report regarding the present study.

References

    1. Z. Yin, Y. Peng and Y. Xiang, “Reversible data hiding in encrypted images based on pixel prediction and bit-plane compression,” IEEE Transactions on Dependable and Secure Computing, vol. 19, no. 2, pp. 992–1002, 2022. [Google Scholar]

    2. I. J. Cox, M. L. Miller, J. A. Bloom, J. Fridrich and T. Kalker, “Chapter 1-Introduction,” in The Morgan Kaufmann Series in Multimedia Information and Systems, 2nd edition, Morgan Kaufmann, Amsterdam, Netherlands: Elsevier Publishing company, pp. 1–13, 2008. [Google Scholar]

    3. A. A. Mohammad, A. Al-Haj and M. Farfoura, “An improved capacity data hiding technique based on image interpolation,” Multimedia Tools and Applications, vol. 78, no. 6, pp. 7181–7205, 2018. [Google Scholar]

    4. Z. S. Younus and M. K. Hussain, “Image steganography using exploiting modification direction for compressed encrypted data,” Journal of King Saud University-Computer and Information Sciences, vol. 34, no. 6, pp. 2951–2963, 2022. [Google Scholar]

    5. C. -M. Wang, N. -I. Wu, C. -S. Tsai and M. -S. Hwang, “A high quality steganographic method with pixel-value differencing and modulus function,” Journal of Systems and Software, vol. 81, no. 1, pp. 150–158, 2008. [Google Scholar]

    6. K. -H. Jung and K. -Y. Yoo, “Improved exploiting modification direction method by modulus operation,” International Journal of Signal Processing Image Processing and Pattern Recognition, vol. 2, no. 3, pp. 79–87, 2009. [Google Scholar]

    7. W. Kou, “Image hiding by square fully exploiting modification directions,” Journal of Information Hiding and Multimedia Signal Processing, vol. 4, no. 1, pp. 128–137, 2013. [Google Scholar]

    8. X. Zhang and S. Wang, “Efficient steganographic embedding by exploiting modification direction,” IEEE Communications Letters, vol. 10, no. 11, pp. 781–783, 2006. [Google Scholar]

    9. C. -F. Lee, Y. -R. Wang and C. -C. Chang, “A steganographic method with high embedding capacity by improving exploiting modification direction,” in Third Int. Conf. on Intelligent Information Hiding and Multimedia Signal Processing (IIH-MSP 2007), Kaohsiung, Taiwan, pp. 497–500, 2007. [Google Scholar]

  10. R. -M. Chao, H. -C. Wu, C. -C. Lee and Y. -P. Chu, “A novel image data hiding scheme with diamond encoding,” EURASIP Journal on Information Security, vol. 2009, pp. 1–9, 2009. [Google Scholar]

  11. R. Rasiyath, “Data embedding and extracting using pixel pair matching with potential masking,” Indian Journal of Applied Research, vol. 3, no. 7, pp. 272–276, 2011. [Google Scholar]

  12. T. D. Kieu and C. -C. Chang, “A steganographic scheme by fully exploiting modification directions,” Expert Systems with Applications, vol. 38, no. 8, pp. 10648–10657, 2011. [Google Scholar]

  13. W. -C. Kuo and M. -C. Kao, “A steganographic scheme based on formula fully exploiting modification directions,” IEICE Transactions on Fundamentals of Electronics, Communications and Computer Sciences, vol. E96.A, no. 11, pp. 2235–2243, 2013. [Google Scholar]

  14. S. -Y. Shen and L. -H. Huang, “A data hiding scheme using pixel value differencing and improving exploiting modification directions,” Computers & Security, vol. 48, pp. 131–141, 2015. [Google Scholar]

  15. T. D. Sairam and K. Boopathybagan, “An improved high capacity data hiding scheme using pixel value adjustment and modulus operation,” Multimedia Tools and Applications, vol. 79, no. 23–24, pp. 17003–17013, 2019. [Google Scholar]

  16. S. Atawneh, A. Almomani, H. Al Bazar, P. Sumari and B. Gupta, “Secure and imperceptible digital image steganographic algorithm based on diamond encoding in DWT domain,” Multimedia Tools and Applications, vol. 76, no. 18, pp. 18451–18472, 2016. [Google Scholar]

  17. Z. Li and Y. He, “Steganography with pixel-value differencing and modulus function based on PSO,” Journal of Information Security and Applications, vol. 43, pp. 47–52, 2018. [Google Scholar]

  18. S. Saha, A. Chakraborty, A. Chatterjee, S. Dhargupta, S. K. Ghosal et al., “Extended exploiting modification direction based steganography using hashed-weightage array,” Multimedia Tools and Applications, vol. 79, no. 29–30, pp. 20973–20993, 2020. [Google Scholar]

  19. J. -H. Horng, S. Xu, C. -C. Chang and C. -C. Chang, “An efficient data-hiding scheme based on multidimensional mini-sudoku,” Sensors, vol. 20, no. 9, pp. 2739, 2020. [Google Scholar]

  20. H. -H. Liu, P. -C. Su and M. -H. Hsu, “An improved steganography method based on least-significant-bit substitution and pixel-value differencing,” KSII Transactions on Internet and Information Systems, vol. 14, no. 11, pp. 4537–4556, 2020. [Google Scholar]

  21. C. -F. Lee, J. -J. Shen, S. Agrawal, Y. -X. Wang and Y. -H. Lee, “Data hiding method based on 3D magic cube,” IEEE Access, vol. 8, pp. 39445–39453, 2020. [Google Scholar]

  22. R. Atta, M. Ghanbari and I. Elnahry, “Advanced image steganography based on exploiting modification direction and neutrosophic set,” Multimedia Tools and Applications, vol. 80, no. 14, pp. 21751–21769, 2021. [Google Scholar]

  23. J. J. Ranjani and F. Zaid, “Pseudo magic cubes: A multidimensional data hiding scheme exploiting modification directions for large payloads,” Computers & Electrical Engineering, vol. 89, pp. 106928, 2021. [Google Scholar]

  24. C. -C. Chang, T. Kieu and Y. -C. Chou, “Reversible data hiding scheme using two steganographic images,” in Proc. of TENCON 2007-2007 IEEE Region 10 Conf., Taipei, Taiwan, pp. 1–4, 2007. [Google Scholar]

  25. C. -C. Chang, T. -C. Lu, G. Horng, Y. -H. Huang and Y. -M. Hsu, “A high payload data embedding scheme using dual stego-images with reversibility,” in Proc. of 2013 9th Int. Conf. on Information, Communications & Signal Processing, Tainan, Taiwan, pp. 1–5, 2013. [Google Scholar]

  26. C. Qin, C. -C. Chang and T. -J. Hsu, “Reversible data hiding scheme based on exploiting modification direction with two steganographic images,” Multimedia Tools and Applications, vol. 74, no. 15, pp. 5861–5872, 2014. [Google Scholar]

  27. J. -Y. Hsiao, A. -C. Pan and P. -Y. Chen, “An adaptive reversible data hiding scheme using dual stego-image,” International Journal of Computers and Applications, vol. 43, no. 3, pp. 282–291, 2018. [Google Scholar]

  28. C. -F. Lee, C. -Y. Weng and K. -C. Chen, “An efficient reversible data hiding with reduplicated exploiting modification direction using image interpolation and edge detection,” Multimedia Tools and Applications, vol. 76, no. 7, pp. 9993–10016, 2016. [Google Scholar]

  29. J. -Y. Lin, Y. Chen, C. -C. Chang and Y. -C. Hu, “Dual-image-based reversible data hiding scheme with integrity verification using exploiting modification direction,” Multimedia Tools and Applications, vol. 78, no. 18, pp. 25855–25872, 2019. [Google Scholar]

  30. X. Chen and W. Guo, “Reversible data hiding scheme based on fully exploiting the orientation combinations of dual stego-images,” International Journal of Network Security, vol. 22, no. 1, pp. 126–135, 2020. [Google Scholar]

  31. Y. Chen, J. Lin, C. C. Chang and Y. C. Hu, “Reversibly hiding data using dual images scheme based on EMD data hiding method,” International Journal of Computational Science and Engineering, vol. 21, no. 4, pp. 583, 2020. [Google Scholar]

  32. J. -Y. Lin, J. -H. Horng, C. -C. Chang and Y. -H. Li, “Asymmetric orientation combination for reversible and authenticable data hiding of dual stego-images,” Symmetry, vol. 14, no. 4, pp. 819, 2022. [Google Scholar]

  33. S. Subburam, S. Selvakumar and S. Geetha, “High performance reversible data hiding scheme through multilevel histogram modification in lifting integer wavelet transform,” Multimedia Tools and Applications, vol. 77, no. 6, pp. 7071–7095, 2017. [Google Scholar]

  34. S. Kim, X. Qu, V. Sachnev and H. J. Kim, “Skewed histogram shifting for reversible data hiding using a pair of extreme predictions,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 29, no. 11, pp. 3236–3246, 2019. [Google Scholar]

  35. L. -C. Huang, S. -F. Chiou and M. -S. Hwang, “A reversible data hiding based on histogram shifting of prediction errors for two-tier medical images,” Informatica, vol. 32, no. 1, pp. 69–84, 2021. [Google Scholar]

  36. J. -Y. Lin, Y. Liu and C. -C. Chang, “A real-time dual-image-based reversible data hiding scheme using turtle shells,” Journal of Real-Time Image Processing, vol. 16, no. 3, pp. 673–684, 2019. [Google Scholar]

  37. H. Yu, R. Wang, L. Dong, D. Yan, Y. Gong et al., “A high-capacity reversible data hiding scheme using dual-channel audio,” IEEE Access, vol. 8, pp. 162271–162278, 2020. [Google Scholar]

  38. X. Chen and C. Hong, “An efficient dual-image reversible data hiding scheme based on exploiting modification direction,” Journal of Information Security and Applications, vol. 58, pp. 102702, 2021. [Google Scholar]

  39. X. -Z. Xie and C. -C. Chang, “Hiding data in dual images based on turtle shell matrix with high embedding capacity and reversibility,” Multimedia Tools and Applications, vol. 80, no. 30, pp. 36567–36584, 2021. [Google Scholar]

  40. S. Chen and C. -C. Chang, “Reversible data hiding based on three shadow images using rhombus magic matrix,” Journal of Visual Communication and Image Representation, vol. 76, pp. 103064, 2021. [Google Scholar]

  41. J. -Y. Lin, J. -H. Horng and C. -C. Chang, “A reversible and authenticable secret sharing scheme using dual images,” Multimedia Tools and Applications, vol. 81, no. 13, pp. 17527–17545, 2022. [Google Scholar]

  42. C. -C. Chang, G. -D. Su, C. -C. Lin and Y. -H. Li, “Position-aware guided hiding data scheme with reversibility and adaptivity for dual images,” Symmetry, vol. 14, no. 3, pp. 509, 2022. [Google Scholar]

  43. Y. Liu and C. C. Chang, “A turtle shell-based visual secret sharing scheme with reversibility and authentication,” Multimedia Tools and Applications, vol. 19, no. 3, pp. 25295–25310, 2018. [Google Scholar]

  44. A. Shamir and M. -S. Hwang, “How to share a secret,” Communications of the ACM, vol. 22, no. 11, pp. 612–613, 1979. [Google Scholar]

  45. D. R. Setiadi, “PSNR vs. SSIM: Imperceptibility quality assessment for image steganography,” Multimedia Tools and Applications, vol. 80, no. 6, pp. 8423–8444, 2020. [Google Scholar]