Federated Feature Concatenate Method for Heterogeneous Computing in Federated Learning

1  Introduction

Machine learning technologies have been widely applied to various applications with artificial intelligence. In the Internet-of-Things (IoT) applications [1,2], cloud service providers have introduced intelligent and customized personal services for each client by analyzing the sensing data collected from IoT devices. In medicine and healthcare applications, machine learning models help doctors provide suggestions for diagnosis and treatment decision-making (e.g., blurry retinal disorder [3], cancer [4,5], and COVID-19 [6,7]). To train a model from scratch, the features are extracted and learned from a dataset usually labeled with a set of known classes. According to a large amount of training data, the training process of an entire deep learning model may be heavily loaded for a centralized server. Distributed machine learning [8] approaches have been presented to enable model training among multiple servers and reduce the training time. However, the consensus on data privacy is rising [9,10], and raw data collected from clients are usually sensitive. Clients are concerned about data upload to a remote training server. The challenge for deep learning applications is to accomplish model training with a sensitive dataset residing at the participant client.

Federated learning (FL) [11,12] is an emerging technology for distributed machine learning. FL enables collaborative learning among clients to locally train the resident data. In addition to uploading the raw data, each client in FL only uploads the extracted features to the remote server. The server then aggregates the collected parameters on average and produces a new global model. The gradient values are calculated and sent back to the participant clients for the model parameter update. Therefore, the server accomplishes the model training and prevents clients from violating the data privacy during the training process. However, the time for model training could be varied when the computing capabilities of the participant clients are heterogeneous. In this case, the server must wait for the client with a lower computation to accomplish its local training and upload the results for aggregation. The local training may also fail for the client because of the constrained resource for an out-of-memory. Hence, FL faces the new challenge of accomplishing the model training among heterogeneous clients while reducing the training time and retaining the test accuracy.

Split learning techniques [13,14] are applied to FL to overcome a client’s limited computation. Using split learning, each client only takes a few layers of a deep neural network (DNN) model to train the local data. The remaining model layers are offloaded to the server to concatenate the training. In most of the previous works [15–18], each client in FL splits the DNN model at the same layer. The cutting layer borderline must be set according to the less computing capability of a client. When clients have heterogeneous computing capabilities, a powerful client only takes a few layers for the model training, despite being equipped with a high computing resource. Consequently, computing resources are wasted if the client cannot contribute its powerful computation to train more layers of a DNN model. Therefore, FL faces another challenge of concatenating the training process when the computing capabilities of clients are heterogeneous.

In view of this, previous works improved the FL efficiency with innovative methods [19–22]. A few studies considered distinct clients, and rare ones explored the effect of different cutting layers. The motivation of the present study is to accomplish FL considering heterogeneous computing for participant clients. A novel approach involving the federated feature concatenate (FedFC) training in FL is proposed. FedFC not only adopts the synergy of model splitting and feature concatenation into FL, but also considers the heterogeneity of the computing capabilities among participant clients. Each distinct client in FedFC can take different cutting layers of a DNN model for collaborative training. In other words, a client with a lower computing capability takes fewer model layers, while a powerful one takes more for training. The FedFC server concatenates the intermediate model parameters from different clients and takes the remaining model layers for federated training and aggregation.

In this way, FedFC accomplishes synchronous model training without any raw data uploads from distinct clients. Heterogeneous clients in FedFC are responsible for different model layers according to the local computing capability. To evaluate the effectiveness of FedFC, this study not only explores the performance impacts of splitting different layers on a model training, but also examines different non-independent and identically distributed (non-IID) cases of data and class imbalance among participant clients in horizontal FL. The results show that FedFC outperforms other approaches in terms of the test accuracy while reducing the computation loading for the constrained client and accelerating the convergence speed. Overall, the major contributions of this work are threefold:

•   The FedFC method is proposed for collaborative training in FL.

•   The performance impacts of splitting different model layers for the participant clients are investigated.

•   The proposed FedFC is applied to shorten the overall training time while improving the test accuracy.

The remainder of this paper is organized as follows: Section 2 discusses the most relevant works; Section 3 introduces the proposed FedFC method and the corresponding algorithms in FL; Section 4 presents the performance evaluations and the empirical results; and Section 5 provides the concluding remarks and future works.

2  Background and Related Works

This section presents the basis of technologies relevant to the proposed FedFC in terms of FL, split learning (SL), and splitfed learning (SFL). The state-of-the-art works related to this study will also be discussed.

2.1 Federated Learning

FL was first proposed by Google in 2017 and applied in the G-board application among mobile devices [23–25]. The proposed solution enables collaborative training without uploading raw data from clients. Each client in FL trains an entire ML model, with the raw data residing at the local. Only the model parameters are uploaded from each client to a centralized server for the aggregation of the model parameters on average (i.e., FedAvg). In the case of heterogeneous computing on different clients, each client may be equipped with various hardware resources, resulting in time variants for the model training among clients. The lowest computing capability of a client, called a straggler, generally limits the complete time for model training in FL [26–28].

Many solutions have been proposed to overcome the abovementioned challenge via asynchronous mechanism, client selection, grouping strategy, and neuron masking. Xie et al. [29] proposed the asynchronous mechanism that enables the server to immediately aggregate the model parameters without waiting for all uploads from constrained clients. However, the model of a constrained client could be stale to prolong the time for the model convergence. Nishio et al. [30] proposed a client selection strategy using collected information from the client (e.g., network bandwidth). To reduce the training time, clients who are stragglers cannot participate in FL training. However, a straggler may have a large amount of training data. The training model accuracy will be affected without the participation of an informative straggler.

Chai et al. [31] adopted the idea of grouping clients and proposed the adaptive selection mechanism for when stragglers have a large amount of training data. The adaptive selection mechanism enabled each group of clients to take turns in joining the FL training to alleviate the impact of the training time from stragglers. The authors further combined the idea of grouping clients and the asynchronous mechanism in [32]. The clients in the same group adopted synchronous FL training, while multiple groups adopted asynchronous FL training. When the server aggregates the model parameters, the server only considers recent model parameter updates from each group. However, the model may not be converged when the model parameters from the slower group are out-of-date. Previous works did not consider a practical situation, in which the clients may not train an entire model due to hardware resource limitations.

Meanwhile, Xu et al. [33] profiled the model training time for the hardware resource of each client and exploited neuron masking to skip the partial neurons of the model and reduce the computational cost for a client. However, the client still needs to have a complete model for the client-side training. The training may fail if the memory space is insufficient for the client. In contrast, FedFC splits an entire model into two parts. The client only needs to train a few layers of the DNN model. The remaining layers are offloaded to the server.

2.2 Split Learning

SL [14,34] was first proposed to consider the hardware resource of a constrained client. The idea behind splitting a model is to divide a DNN model into two sub-models allocated with different portions of model layers. One sub-model, called the client-side model, is used to train the local data on a client with the first few model layers. The other is the server-side model used to sequentially train the remaining layers for the constrained client. In each iteration, each client trains the model parameters with local data and uploads the smashed data, including the activation values of the cut layer, to the server. The server then takes the remaining training of the server-side model with the smashed data and computes the gradient value for the global model. The updated values for the smashed data gradient are sent back to the client to update the client-side model.

During the SL training process, the data privacy is protected by the client because raw data are transformed into smashed data after training on a client. The loading of training the deep learning model is eliminated on a client because each client only takes the client-side model for local training instead of training all layers of the entire model. However, traditional SL adopts sequential training, resulting in only one client participating in the SL training at the same time. The training time becomes longer when the number of participant clients increases [17,35,36].

Jeon et al. [37] adopted a parallel strategy for participant clients to accelerate the SL training time. However, the server still sequentially inputs the smashed data from each client to train the server-side model. When the number of clients becomes larger in training, the worst case is that it will be the same as the traditional SL and result in a longer training time. Zhang et al. [38] also adopted the parallel training strategy and trained the server-side model with the feature concatenate method. When the server-side model training is finished, the server splits the gradient according to the smashed data size of each client. The corresponding gradient is sent back to the client to update the client-side model. However, each client in the previous works was allocated with the same model layers, resulting in the wastage of computing resources for the client with a powerful computing capability.

2.3 Splitfed Learning

Thapa et al. [18] introduced SFL to leverage the FL and SL advantages for training splitting models to reduce the training time and computing loads on clients. SFL includes two kinds of training processes: SFLv1 and SFLv2. All SFLv1 clients simultaneously train the client-side model and upload the smashed data to the corresponding server-side models. The main server trains the server-side models and averages the gradients of all server-side models. After finishing the client-side model training, the client then uploads the parameters of the client-side model to another fed server. The fed server aggregates the parameters of all client-side models and generates updated global parameters. SFLv2 is similar to SFLv1, but with only one server-side model adopted in the main server. The main server exploits institutional incremental learning [39] to train the server-side model. The training proceeds until all of the smashed data of the participant clients had been input to the server-side model for training. After finishing the server-side model training, the main server then updates the gradient of the smashed data back to the client. Accordingly, the client can update the client-side model.

Based on the SFL solutions, many works have proposed enhanced methods to improve the training communication in-between clients and servers. He et al. [16] adopted a similar model between the client and the server. The client-side model was responsible for the shallower layers of the ResNet [40] architecture, while the server-side model was responsible for the deeper layers. Both the client- and server-side models output their predicted results. Subsequently, the client and the server exchange results with each other. In this way, the client- and server-side models can learn from each other through knowledge distillation [41]. However, the server trains the server-side model in a sequential order. The training time will be longer when many clients join the training.

In the work of Pal et al. [17], the server-side model in SFL was updated with the smashed data of all clients, while the client-side model was updated with the smashed data of the client itself. An updating imbalance occurred between the client- and server-side models when they were set to the same learning rate. The authors revealed that the learning rate for the server-side model training must be adjusted according to the number of clients. Han et al. [15] claimed that the client-side model of existing SFL architecture must wait for the server to calculate the gradient of the smashed data before updating the client-side models. Massive data transmissions were involved during the SFL training procedures, resulting in an increase in communication loadings. Therefore, the authors proposed locally generated losses to add an auxiliary network layer to the client-side model. The smashed data are input to the auxiliary network for prediction and uploaded to a server for the server-side model training. After the local training completion, the client uploads the client-side model parameters to the fed server, which then aggregates the parameters from the participant clients and updates the result back to each client.

State-of-the-art works have achieved some improvements in SFL; however, only a few have considered the heterogeneous computing of participant clients [42,43]. The effect of splitting different model layers on the training performance is rarely explored. This study intends to conduct a collaborative training of participant clients assigned with different cutting layers of the client-side model. A novel FedFC method is proposed herein to concatenate the output features of different layers from distinct clients. Compared to SFL, FedFC only facilitates a single server-side model to concatenate the learning features. A mixed layer approach is presented for FL among heterogeneous clients. Each client can participate in the collaborative training with different model layers; therefore, clients can make good use of their computing resources. Other works have not considered the solution for heterogeneous clients. The results show that FedFC reduces the computation loading for the constrained client while improving the convergence speed and the test accuracy.

3  Federated Feature Concatenate

In the image segmentation task, the deep layer output in a model classifies each image pixel to a specific class. However, the classification result may not be identical because the deep layer output lose information from the shallow layer. To solve this problem, U-Net [44] is applied to the image segmentation task. The U-Net model adopts an encoder–decoder architecture. The input of each decoder block refers to not only the output of the previous layer in the model, but also to that of the corresponding encoder block. These two features are concatenated at the channel dimension. The concatenated result is then finally input into the decoder block, forming a U-shape architecture. FedFC is inspired by U-Net and adopts the feature concatenate method in the training procedure. Therefore, it collaborates with each client, which may be split with different model layers in FL.

3.1 Overview of the FedFC Method

For the effective utilization of the computing resource of each client, FedFC enables clients to determine the number of model layers according to their computing capability. It also leverages the split model and tfeatures concatenate methods to reduce the training time on the local client. In FedFC, only a server-side model is necessary to process the smashed data from each client-side model. Therefore, the server storage maintenance is alleviated. Fig. 1 depicts the workflow for detailing the training processes of an FL model using FedFC.

•   At the initial stage, each client requests for an initial training model from the server.

•   Step 1: Each client starts training the client-side model using local data and uploads the smashed data to the server.

•   Step 2: Before training each layer of the server-side model, the server checks if smashed data have been uploaded from a client. Through the training process for the server-side model, the server executes the feature concatenate if any layer has uploaded with the smashed data from a client; otherwise, the server keeps training the next layer of the server-side model.

•   Step 3: After finishing the server-side model training, the server sends the gradients back to the client who uploaded the smashed data, such that the client-side model can be updated accordingly.

•   Step 4: After finishing a round of local training, each client uploads its local parameters of the client-side model to the server and waits for the model parameter aggregation in FL.

•   Step 5: Upon receiving all the model parameters from the participant clients, the server records the in-place parameters of the client- and server-side models within an original model. To this end, the server adopts FedAvg algorithms to generate a new global model. Both of the parameters collected from the client- and server-side models are aggregated on average.

•   Step 6: The server updates its server-side model with the new global parameters and sends out the new global parameters back to each client for the client-side model update.

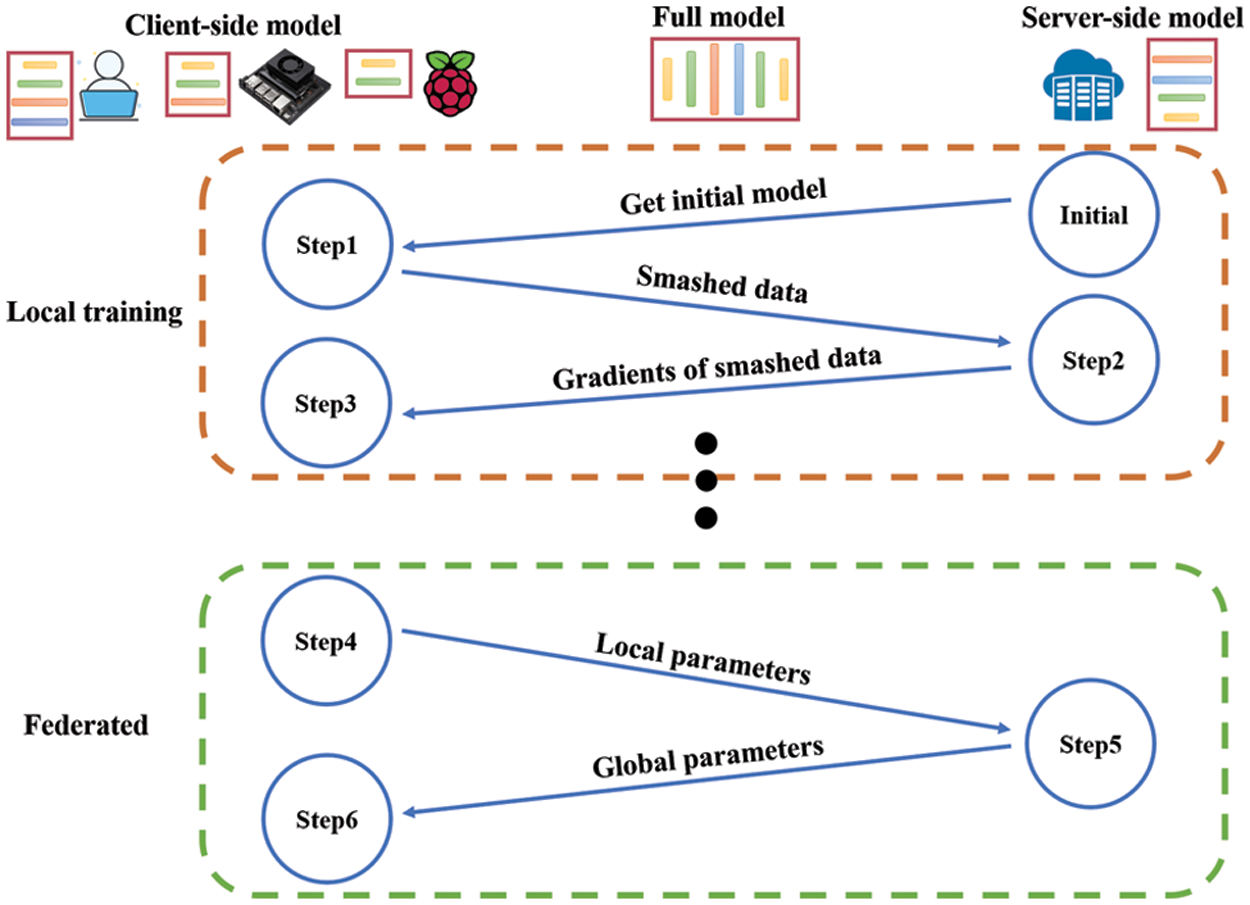
Figure 1: FedFC training workflow

3.2 Model Training in FedFC

This section elaborates on the training processes in FedFC from the perspectives of forward and back propagation. Fig. 2 illustrates the forward propagation procedures for the server-side model, where the 4-tuple of (B, C, H, W) represents the values of the batch size, channel, height, and width of the smashed data, respectively.

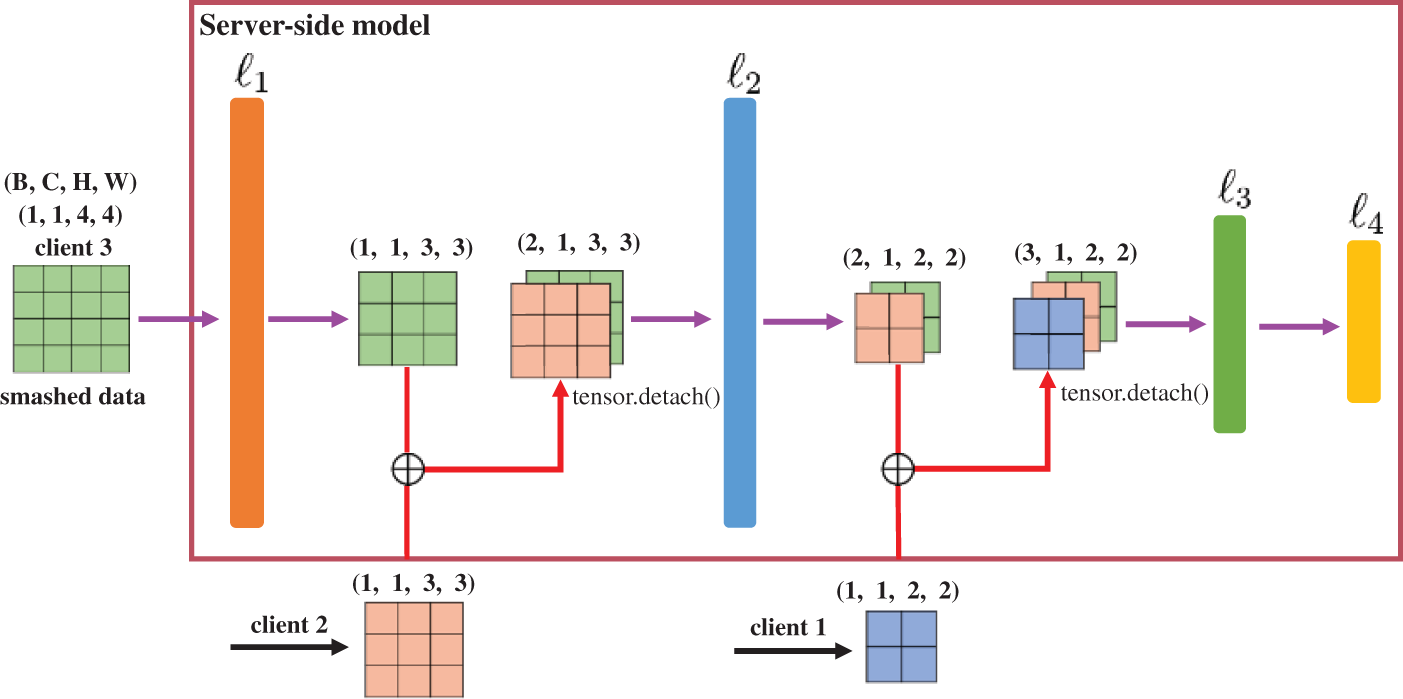
Figure 2: Forward propagation for the server-side model in FedFC

Let us assume that the input of the server-side model is the smashed data of Client 3. After the ℓ1 layer calculation, new smashed data are generated with the values of (1, 1, 3, 3). At this time, the server checks that the values of the smashed data from Client 2 are the same as (1, 1, 3, 3). It then concatenates the ℓ1 layer output with the smashed data of Client 2. New values of (2, 1, 3, 3) are generated, and a tensor.detach() attribute is added at this step. The attribute is noted for stopping the gradient calculation when the server performs the backpropagation at this step. Next, the server inputs the values of the smashed data with (2, 1, 3, 3) for the ℓ2 layer calculation. After the calculation, new smashed data are generated with the values of (2, 1, 2, 2). At this time, the server checks that the value of the smashed data from Client 1 is also (1, 1, 2, 2). It then concatenates the ℓ2 layer output with the smashed data of Client 1. The new value of (3, 1, 2, 2) is generated, and a tensor.detach() attribute is added at this step. Hereafter, the server inputs the values of the smashed data with (3, 1, 2, 2) to the ℓ3 layer and so on until the forward propagation of the server-side model is finished.

After completing a forward propagation to train the server-side model, the server must calculate the loss value between the predicted results and the actual labels. The gradient is calculated, and the server-side model parameters are updated throughout the backpropagation. Fig. 3 illustrates the backpropagation for the server-side model. When the server executes the backpropagation to calculate the ℓ3 layer gradient, the procedure stops because the attribute of this step is noted with a tensor.detach(). The server must split the gradient value of (3, 1, 2, 2) into two portions, namely (2, 1, 2, 2) and (1, 1, 2, 2). The gradient value of (1, 1, 2, 2) will be sent back to the smashed data of Client 1, while the other (2, 1, 2, 2) is used to proceed with the backpropagation. When calculating the ℓ2 layer gradient, the server also detects that the attribute is noted with a tensor.detach(). The server splits the gradient value of (2, 1, 3, 3) into two portions similar to (1, 1, 3, 3). One portion of the gradient values is sent back to the smashed data of Client 2. The other is used to proceed with the backpropagation until that of the server-side model is finished. Finally, the server sends the gradients of the corresponding smashed data to each client for the client-side model update. The subsequent section will introduce detailed FedFC algorithms for the participant client and the server. The model parameter aggregation in FedFC is presented hereafter.

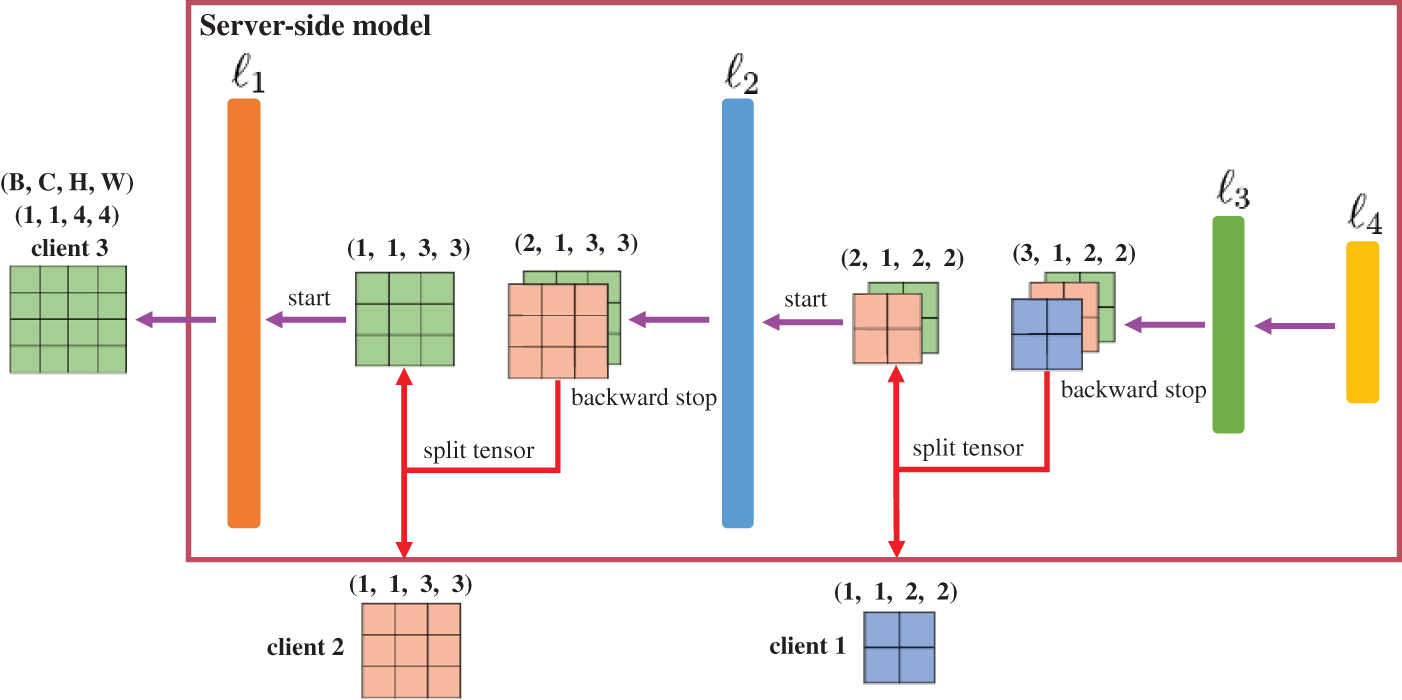
Figure 3: Backpropagation for the server-side model in FedFC

In view of this, FedFC can alleviate the computing loads for distinct clients to train the client-side model. Let Ph,weight denote the weight parameters of the h layer and Ph,bias denote the bias parameters of the h layer. The total parameter Ptotal of a DNN model with L layers is calculated as follows:

Ptotal=∑h=1L(ph,weight+ph,bias)

Therefore, a client with fewer layers of a DNN model represents fewer calculations for the client-side model training. The overall computing load is lower for the client with a constrained resource.

3.3 FedFC Algorithms

Assume the total number of the K clients participating in a round of FedFC training, and that each client k trains a single local epoch. The server splits the initial model into the client- (wc) and server-side (ws) models, where wc has a different number of layers for each client k. Clients are responsible for training the client-side models wc, whereas the server is responsible for training the server-side model ws. Algorithm 1 depicts the training procedures for the participant clients.

First, each client k requests an initial model wc from the server. Next, each client uses the local data xk and actual labelsyk to train the client-side model until a specified local epoch E is finished. In each iteration, each client uploads the smashed data Sk and the correspondingyk to the server to train the server-side model. After receiving the corresponding gradients of Sk from the server, each client updates the client-side model with the learning rate η and the gradient gc,k. When each client approaches the specified local epoch E, all clients upload their model parameters wc,k to the server and wait for the new parameters wc∗ after applying Algorithm 3. To this end, a single training round is completed in FedFC.

Algorithm 2 shows the procedures for each iteration to train the server-side model on a server. The server initially splits the initial model into wc and ws, in which the number of layers in ws is determined according to the last layer of wc. The server must process the smashed data for different layers of the participant clients. The forward propagation procedures are presented from lines 5 to 15. At each layer, the server first checks if any client uploads the smashed data before the server-side model training. If a client uploads the smashed data, and the input feature Xsm of the current layer is null, the server concatenates the smashed data S and assigns the result to Xsm; otherwise, the server concatenates the feature Xsm of a previous layer with the smashed data S of the client. Subsequently, the server assigns the result to Xsm and adds the attribute with a tensor.detach(). The addition of the tensor.detach() attribute to Xsm is a note for the server to identify that the client has uploaded the smashed data at this step. Next, the server inputs the new Xsm to the current layer for training. If none of the clients upload the smashed data, the output feature of the previous layer will be input to the next layer for training. When the forward propagation is finished, the server concatenates the actual labels y1,y2,…,yK to form Y and proceeds with the backpropagation updates in the next procedures.

The backpropagation procedures are presented from lines 17 to 28. First, the server calculates the loss value between Y^ and Y for the updated gradients of the model parameters throughout the backpropagation. When updating the gradient gsm for each layer of the server-side model, the server checks if the tensor.detach() attribute is added at the current layer. If the attribute exists, the server must split the gradients into gs′m and g′ according to the number of clients. If it does not, the server proceeds with updating the backpropagation. After the backpropagation, the server updates the server-side model parameters ws∗ and sends the gradients of the smashed data back to the corresponding clients for the client-side model update.

After each client k completes its local training, all clients must upload the model parameters wc,k from the client to the server. The server aggregates the model parameters from the participant clients and sends the updated global parameters back to the clients. During this time, FedFC completes the model training for one round. Algorithm 3 shows the FedAvg algorithm used in FedFC. After each client uploads the model parameters, the server checks if the amount of parameters of each wc,k is equal. If it is, then the numbers of the layers of the distinct client-side models are similar with each other. As a result, the server can average the model parameters from all clients to generate new global parameters wc∗ for the client-side model. The updated wc∗ will be sent back to the participant clients. Each client then proceeds with the model training with the updated parameters of the client-side model at the next round.

If the amount of parameters of each client-side model is not equal, which means that the numbers of the layers of the distinct client-side model are different, the server must average the parameters per layer of the client-side models. In this case, the server must exploit the smashed data of different layers to train the server-side model. Therefore, the server averages the partial parameters of the server-side model with those of the client-side models overlapped at each layer, as shown in Line 6. Next, the server checks if the ws parameters are intersected with the client-side model. If this is the case, it averages Set A and the partial parameters of the server-side model at the current layer and updates the overlapped server- and client-side model parameters; otherwise, it only averages Set A and updates the client-side model parameters. Finally, the server generates the global parameters wc∗ for the client-side model and the parameters ws∗ for the server-side model. wc∗ is sent back to the participant clients according to the corresponding layers of the client-side model.

4  Performance Evaluations

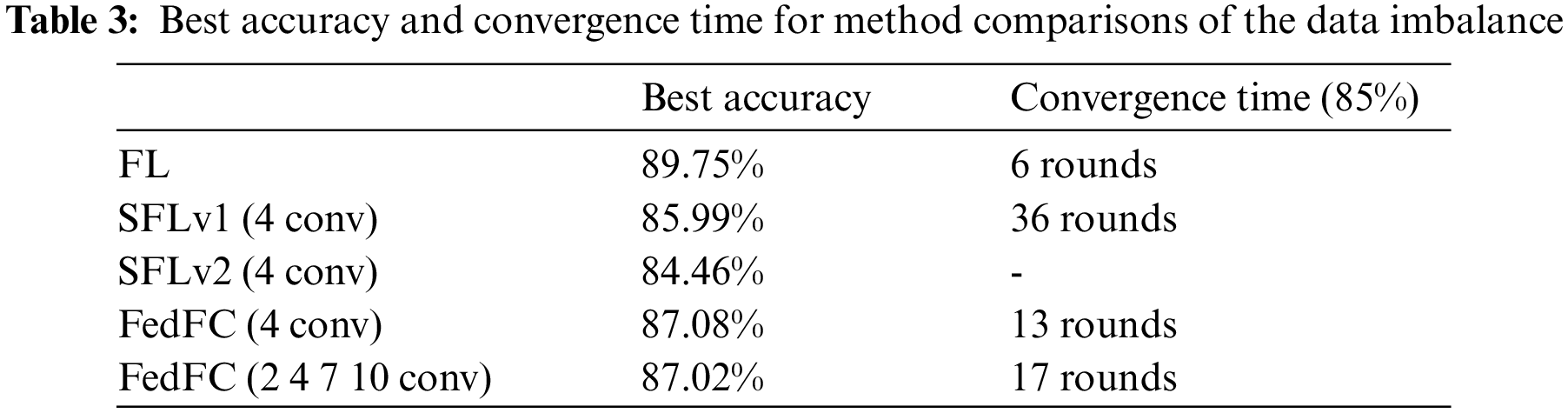
The experiments were conducted on a workstation with GTX 1080 GPUs for emulating four clients and one server. The VGG16 [45] model used for FL was composed of 13 convolution layers and three fully connected layers, each with a kernel size of 3 × 3. The programs were written in Python 3.6 with PyTorch 1.5, cudatoolkit 10.2, and flask 2.0. CIFAR-10 was adopted for the dataset, where 50,000 images were categorized for training, and the other 10,000 images were used for testing. The batch size was 32. The learning rate was 0.001. The optimizer adopted stochastic gradient descent and momentum. The experiments also considered different dataset scenarios, including the data and class imbalance for the participant clients. In the data imbalance experiment, four clients were allocated 40%, 30%, 20%, and 10% of the training data. For the class imbalance case, classes 0–2 were dispatched to Client 1; classes 2–4 were dispatched for Client 2; classes 4–6 were dispatched for Client 3; and classes 7–9 were dispatched for Client 4. The compared methods included centralized learning (CL), FL, SFLv1, SFLv2, and FedFC. The performance metrics were the test accuracy and the convergence time required to achieve a specified test accuracy. All experiments were performed for 200 rounds, with an epoch of 10 per round.

4.1 Effect of the Model Cutting Layer

This experiment evaluated the effects of the model cutting layers and compared the best test accuracy with CL. In FedFC, the model was split into different model layers (i.e., second, fourth, seventh, and 10th layers). Fig. 4 shows the training results of the data imbalance case. The training result of FedFC was closer to the that of CL when the cutting layer was two for each client-side model. The test accuracy gradually decreased as the number of layers of the client-side model increased. It exceeded the result of the seventh layer when the number of layers of the client-side model was assigned with the 10th layer.

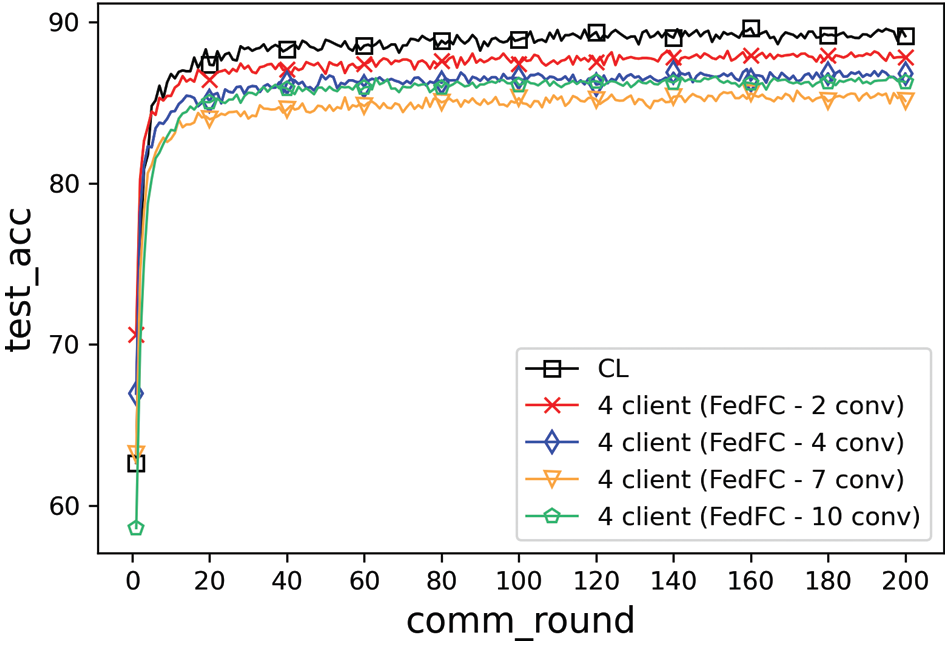
Figure 4: Model layer effect of the data imbalance

Table 1 records the best accuracy and convergence time for the data imbalance case. The best accuracy decreased when the client-side model increased from the second to seventh layer. It increased to 86.63% when the client-side model had 10 layers. The performance of different cutting layers in FedFC was slightly degraded when compared to CL. Similar trends were found in the perspective of the convergence time. The number of training rounds became longer when the number of layers of the client-side model increased, but significantly reduced again for the 10th layer. The phenomenon only occurred when the features were extracted before and after the middle layer of the DNN model.

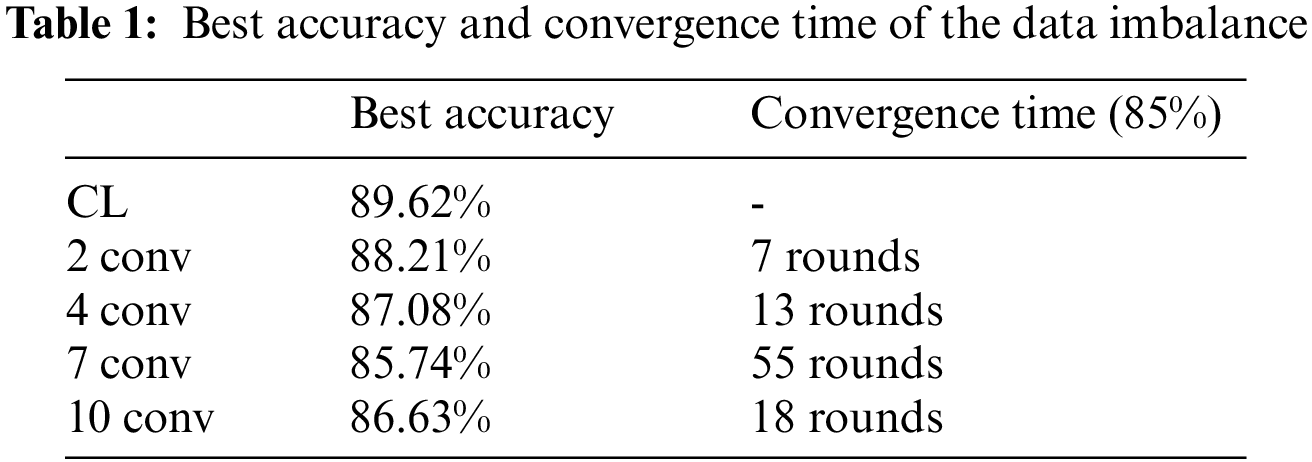
This study referred to the work of [46] to explore the reason behind the phenomenon and expose its critical impact. The shallow layers in the model generally learned the general features suitable for the distinct learning tasks. For example, the features of the shallow layers of the model were extracted for the edge features in the images. These general features are expected to be applicable to other image classification tasks. The deep layers in the model also learned specific features to identify specific data classes. Finally, the middle layers in the model learned the co-adaptation of features affected by the general and specific features. Hence, the co-adapted features were the key point to the accurate classification of the DNN model. In our experiments, feature co-adaptation occurred in the seventh layer, while specific features occurred in the 10th layer. Accordingly, the test accuracy in the 10th layer increased because a few co-adapted features were extracted while growing from the seventh to the 10th layer. Consequently, the features learned by the server-side model were more specific in improving the test accuracy.

Fig. 5 shows the training result for the class imbalance case. The best accuracy of the second layer was 77.3%. A total of 122 rounds were needed to achieve the test accuracy of 75%; however, that of the 10th layer reached 78.1% and took a shorter convergence time. Table 2 lists the best accuracy and convergence time for achieving 75% test accuracy. When the number of layers of the client-side model increased, the test accuracy increased, while the convergence time decreased. The gap in the convergence speed between the seventh and 10th layers was significant in this experiment. The model started to learn feature co-adaptation since the seventh layer. Meanwhile, the client-side model tended to identify the local data by the client itself. The output features became more specific when the number of layers of the client-side model increased. Therefore, the test accuracy gradually increased when fewer parameters were offloaded to the server-side model.

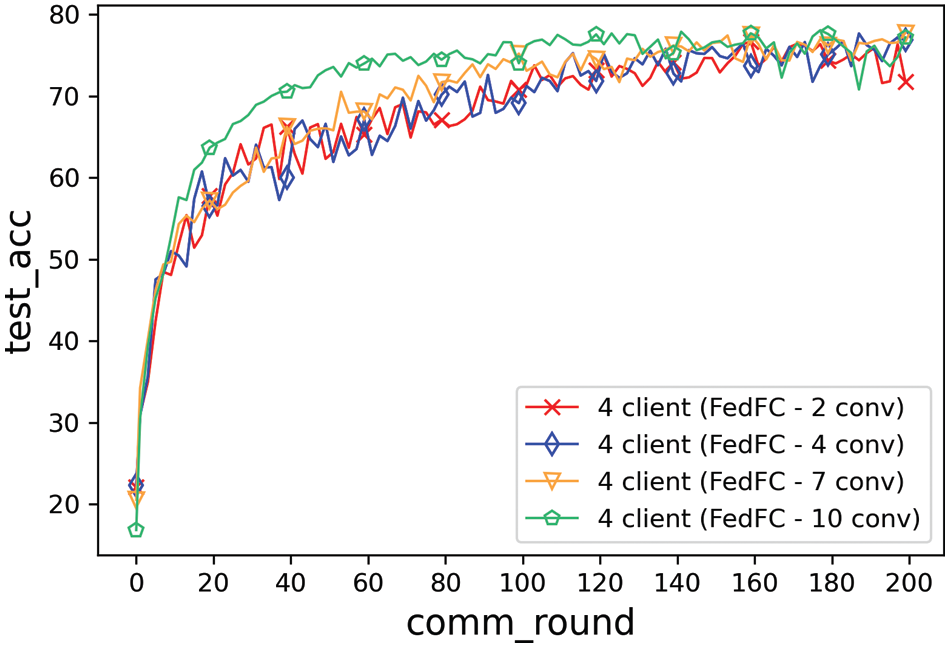
Figure 5: Model layer effect of the class imbalance

Overall, the cutting layer (10th layer) in this experiment performed better than the others in terms of the test accuracy and convergence time. However, not all the participant clients can train a DNN model for 10 layers on the client-side. The proposed approach must complete the model training according to different cutting layers of the client-side model. Hence, FL can be accomplished considering heterogeneous computing and class imbalance among the participant clients in FedFC.

4.2 Method Comparisons

This section compares the test accuracies of FL, SFLv1, SFLv2, FedFC, and mixed of the client-side model for FedFC (FedFC-mixed layer). According to the configuration in SFL [18], SFLv1, SFLv2, and FedFC split at the fourth layer. The FedFC-mixed layer considered the mixing of the training layers of (2, 4, 7, 10), in which the second, fourth, seventh, and 10th layers were allocated to distinct clients. Fig. 6 illustrates the experimental results of the data imbalance case. Table 3 highlights the best accuracy and convergence time of FL, SFLv1, SFLv2, FedFC, and FedFC-mixed layer. The test accuracies of FedFC and FedFC-mixed layer were improved by 1.09% and 1.03%, respectively, compared to that of SFLv1. Compared to SFLv2, FedFC and FedFC-mixed layer showed improved test accuracies of 2.62% and 2.56%, respectively. In terms of the convergence time, FL took six rounds to achieve 85% of test accuracy. By contrast, SFLv2 did not achieve 85% test accuracy in 200 training rounds. Compared to SFLv1, FedFC and FedFC-mixed layer outperformed SFLv1 by 63.89% and 52.78%, respectively.

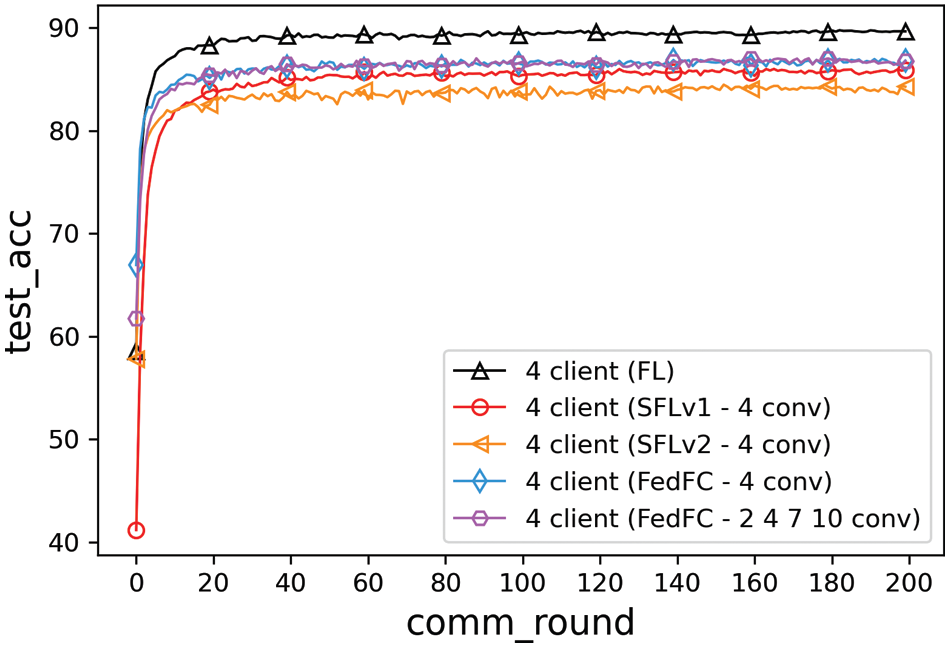
Figure 6: Method comparisons of the data imbalance

The abovementioned results can be attributed to each client uploading the smashed data to the corresponding server-side model for each SFLv1 iteration. SFLv1 must maintain multiple server-side models and adopt an oversampling method to ensure that each iteration can obtain the smashed data from the client-side model. In addition, SFLv2 exploited a sequential approach to train the server-side model, which resulted in a high probability for the server-side model to a local optimum. In other words, in an unbalanced data distribution, clients with a few training data only oversampled the limited training data and uploaded similar smashed data for the server-side for model training. The server repeatedly learned the same features from the client; hence, the gradient should be a very small value. Consequently, the small gradient slowed down the update ratio of the server-side model. FL needed the least number of rounds to achieve a specified test accuracy of 85%, but it assumed that all clients should be homogeneous and affordable for the entire model training on the client-side. In contrast, FedFC proposed the feature concatenate method to concatenate the smashed data uploaded from the distinct clients before inputting the features to the server-side model for training. Hereafter, the server calculated the loss values according to the smashed data and updated the gradients of the model parameters throughout the backpropagation.

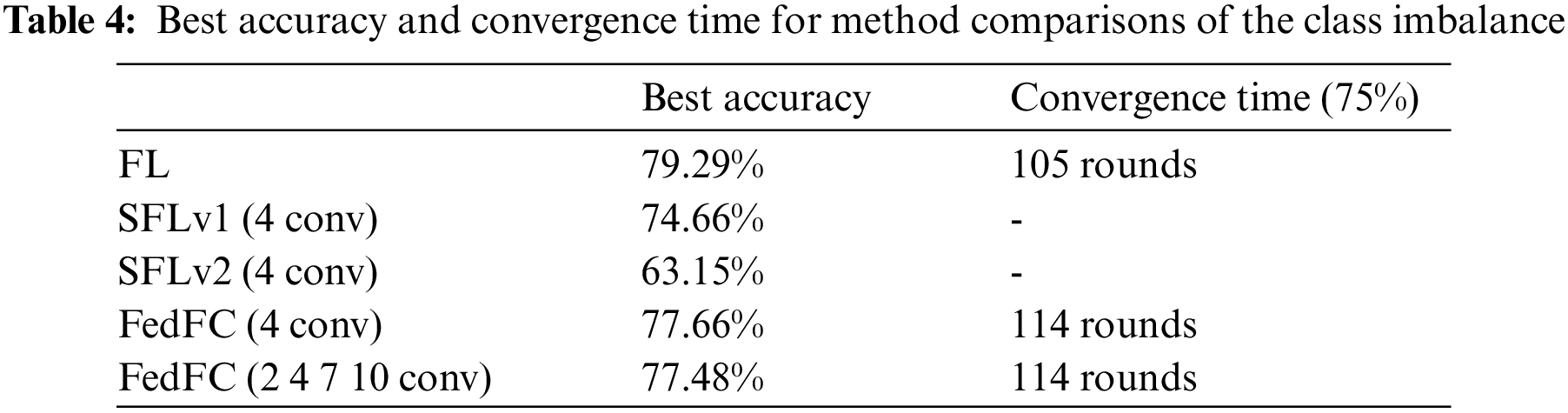
Fig. 7 depicts the results of the class imbalance case. The best accuracies of FL, SFLv1, SFLv2, FedFC, and FedFC-mixed layer were 79.29%, 74.66%, 63.15%, 77.66%, and 77.48%, respectively. Compared to SFLv1, the test accuracies of FedFC and FedFC-mixed layer increased by 3% and 2.82%, respectively. Even FedFC outperformed SFLv2 by up to 14.5% in the test accuracy. Table 4 presents the best accuracy and convergence time for achieving a specified test accuracy for each method. FL took 105 rounds to achieve 75% test accuracy, while FedFC and FedFC-mixed layer must train for 114 rounds. SFLv1 and SFLv2 did not reach the desired test accuracy in 200 rounds because FedFC used a feature concatenate method to train the server-side model.

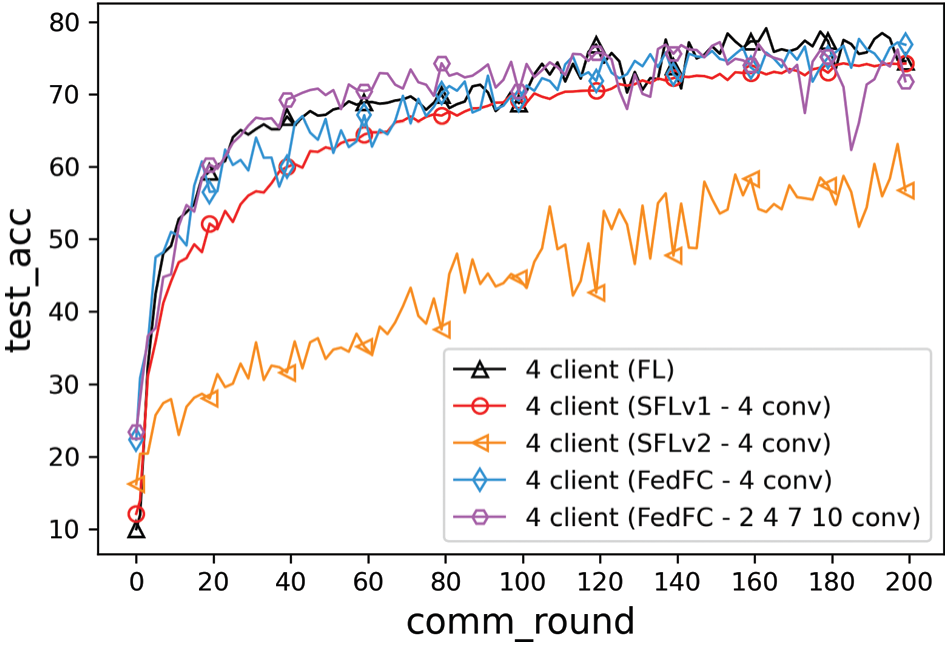
Figure 7: Method comparisons of the class imbalance

To update the server-side model in FedFC, the input of the server-side model was concatenated with the smashed data uploaded from the participant clients. However, SFLv1 maintained multiple server-side models, and each client-side model corresponded to a server-side model. When all the server-side models in SFLv1 accomplished the training in one iteration, the server averaged the gradients of all server-side models and updated the gradient values to all server-side models. In the class imbalance case, the gradient value calculated by SFLv1 was biased toward the training data of the client itself, resulting in a deviation of the server-side model update. Meanwhile, SFLv2 exploited the sequential approach to train the server-side model with the smashed data uploaded from the clients. In the class imbalance case, SFLv2 suffered from a catastrophic forgetting problem [47]; hence, the server-side model only remembered the smashed data from the latest client and forgot the previously learned features. Overall, FedFC enabled heterogeneous clients for collaborative training with constrained resources on the client-side and offloaded the training burden to the server-side model.

4.3 Extreme Class Imbalance

In the previous experiments, the data classes assigned to the participant clients were overlapped in the class imbalance case. This section further considers an extreme data class imbalance among the participant clients to train an FL model. The data classes were allocated without an intersection between any two clients. The experiment was configured with five clients, with each client being responsible for training the first four layers of VGG16. The data classes in CIFAR-10 were equally allocated to these five clients, in which classes 0 and 1 were allocated to Client 1; classes 2 and 3 were allocated to Client 2; classes 4 and 5 were allocated to Client 3; classes 6 and 7 were allocated to Client 4; and classes 8 and 9 were allocated to Client 5.

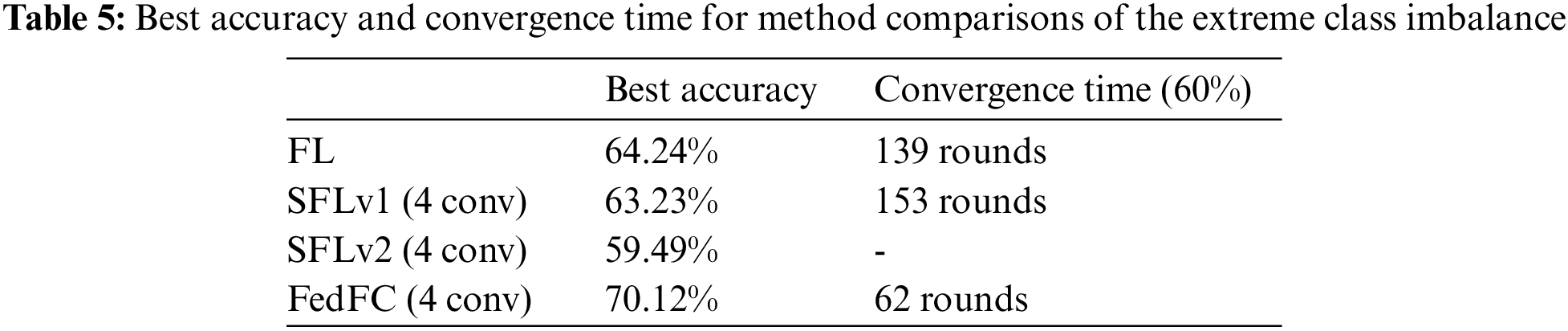
Fig. 8 shows the experimental results for the extreme class imbalance case. In terms of the best accuracy, FedFC outperformed SFLv1 and SFLv2 by up to 6.89% and 10.63%, respectively. FedFC also enhanced the test accuracy by 5.88% when compared to FL. Table 5 shows the best accuracy and convergence time for achieving 60% test accuracy for each method. The results show that SFLv2 cannot reach the desired 60% accuracy within 200 training rounds. On the contrary, FedFC only spent 62 rounds to achieve the specified test accuracy, saving 55.39% and 59.47% of the convergence time compared to FL and SFLv1, respectively.

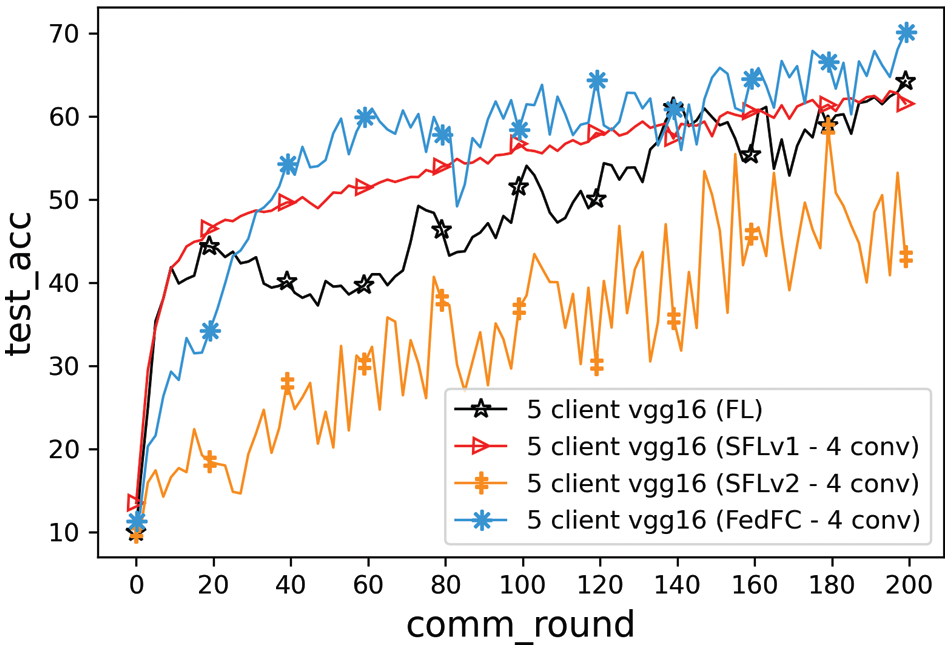
Figure 8: Method comparisons of the extreme class imbalance

FedFC outperformed the others because the proposed approach adopted a feature concatenate method for the heterogeneous clients to retain a better test accuracy with a shorter convergence time. By contrast, SFLv1 averaged the gradients of all the server-side models before updating the model parameters. In this case, the gradient calculations were more fitting to the training data of the client itself, such that the bias value of the model update was increased. SFLv2 dramatically suffered from catastrophic forgetting in the extreme class imbalance case. More local epochs were training in FL; hence, the client-side model will head toward only identifying the data classes residing at the client. The test accuracy also dramatically decreased in the extreme class imbalance case.

4.4 Training Time Evaluations

This experiment considered four clients with different computing capabilities of CPU i7-8700, GPU 1080, GPU 1660ti, and GPU 2080ti to evaluate the performance in a more practical environment. Client 1 equipped with CPU i7-8700 was assigned with the second layer for the client-side model training. Client 2 equipped with GPU 1080 was responsible for the fourth layer. Client 3 with GPU 1660ti was responsible for the seventh layer. Lastly, Client 4 equipped with GPU 2080ti was responsible for the 10th layer. The model was trained for 200 rounds. The local epoch was set to five for each round. The data distribution was allocated as class imbalance. The SFL approached were not comparable in this experiment because the released codes were only targeted to the simulation on a single machine, rather than a real deployment on multiple machines. Therefore, this experiment compared only FL, FedFC, and FedFC-mixed layer. FedFC was split at the fourth layer for each client-side model. The FedFC-mixed layer considered the mixed layers of (2, 4, 7, 10).

Fig. 9 shows the practical results of the realistic training time in seconds. The best accuracies of FedFC and FedFC-mixed layer were found as 76.6% and 77.47%, respectively, whereas that of FL was only 70.47%. The results illustrate that the proposed FedFC approaches outperformed FL by up to 7% when the computing capabilities of the participant clients were heterogeneous. For FL, each client must train an entire model, and the server must wait until all clients have uploaded the model parameters before the aggregation. In this practical training, the client equipped with the CPU-only resource spent the longest time training the model when compared to other clients with GPU resources. Regarding the convergence time for achieving 75% test accuracy, FL failed to converge the model within the training time of 120,000 s. By contrast, FedFC and FedFC-mixed layer trained the server-side model by concatenating the smashed data uploaded from the clients. The server-side model can learn all client features and reduce the computation cost of the client-side model by splitting the entire model. The FedFC-mixed layer performed better than FedFC because each client provided empirical features for the different layers of the client-side model. The server-side model can learn not only the smashed data from the current client, but also other feature information learned from the previous layers of the other clients. Consequently, the specific features learned in the deeper layer of the server-side model were clearer when identifying the data classes. Therefore, FedFC can accelerate the convergence speed while improving the test accuracy for the heterogeneous computing in FL.

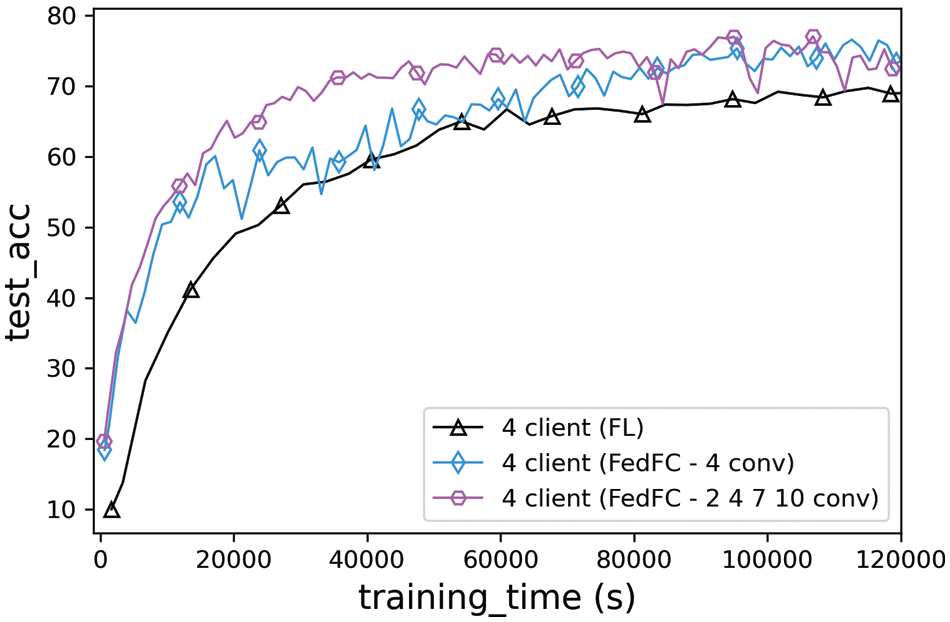
Figure 9: Training time of the heterogeneous clients with CIFAR-10

5  Conclusion

In federated learning, the client with limited computing resources may prolong the convergence time for model training. The model may not even finish due to being out-of-memory on the constrained client. This study proposed the FedFC method for heterogeneous clients in FL by using the split model. The participant client took a few model layers for training on the client-side. The other model layers were offloaded to the server for the remaining training. This study not only investigated the impact of different cutting layers in FedFC, but also introduced a mixed layer approach for FL among heterogeneous clients. Beneficial from the split model and the feature concatenate methods, the specific features learned in the deeper layer of the server-side model were more identical for the data class classification. Therefore, FedFC can reduce the computation loading for the constrained client and accelerate the convergence speed. The experiment results showed that FedFC showed an improved best accuracy of approximately 1% and 2.6% when compared to SFLv1 and SFLv2, respectively, when the data volume distribution was unbalanced among the participant clients. The convergence time of FedFC was also shortened better compared to that of SFLv1 when achieving the specified test accuracy of 85%. In the case of a class unbalanced distribution, FedFC improved its best accuracy by up to 3% and 14.5% compared to SFLv1 and SFLv2, respectively. Moreover, in the extreme class imbalance experiment, it outperformed the best accuracies of FL, SFLv1, and SFLv2 by 5.88%, 6.89%, and 10.63%, respectively.

In conclusion, the proposed approach is suitable for heterogeneous clients in FL because it shortens the convergence time and improves the test accuracy. The co-adapted features play a critical role in the adequate classification of the deep learning model. The client with powerful computing resources may take half of the model layers, while the constrained client should consider fewer layers based on the capability of its local resources. An interesting topic for future research would be how to determine the minimum required layers for a client according to the capability of its computing resources, dataset data distributions, and its network connectivity. The limitation of the current FedFC is the resource consumption of server resources suitable for the linear model [48] in deep training. How to adapt FedFC with varied training loads and dynamically allocate the memory for the DNN in FL are also interesting topics for future works. The privacy issue of the smashed data in secure federated learning [49–51] remains an open topic for research directions.

Funding Statement: This work is financially supported by the National Science and Technology Council (NSTC) of Taiwan under Grants 108-2218-E-033-008-MY3, 110-2634-F-A49-005, 111-2221-E-033-033, and the Veterans General Hospitals and University System of Taiwan Joint Research Program under Grant VGHUST111-G6-5-1.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

    1. Z. Zhou, X. Chen, E. Li, L. Zeng, K. Luo et al., “Edge intelligence: Paving the last mile of artificial intelligence with edge computing,” in Proc. of the IEEE, vol. 107, no. 8, pp. 1738–1762, 2019. [Google Scholar]

    2. B. Qian, J. Su, Z. Wen, D. N. Jha, Y. Li et al., “Orchestrating the development lifecycle of machine learning-based IoT applications: A taxonomy and survey,” ACM Computing Surveys, vol. 53, no. 4, pp. 1–47, 2020. [Google Scholar]

    3. H. Zhao, B. Yang, L. Cao and H. Li, “Data-driven enhancement of blurry retinal images via generative adversarial networks,” in Int. Conf. on Medical Image Computing and Computer-Assisted Intervention, Shenzhen, China, pp. 75–83, 2019. [Google Scholar]

    4. K. Clark, B. Vendt, K. Smith, J. Freymann, J. Kirby et al., “The cancer imaging archive (TCIAMaintaining and operating a public information repository,” Journal of Digital Imaging, vol. 26, no. 6, pp. 1045–1057, 2013. [Google Scholar]

    5. V. Tresp, J. M. Overhage, M. Bundschus, S. Rabizadeh, P. A. Fasching et al., “Going digital: A survey on digitalization and large-scale data analytics in healthcare,” in Proc. of the IEEE, vol. 104, no. 11, pp. 2180–2206, 2016. [Google Scholar]

    6. B. Yan, J. Wang, J. Cheng, Y. Zhou, Y. Zhang et al., “Experiments of federated learning for COVID-19 chest x-ray images,” in Int. Conf. on Artificial Intelligence and Security, Dublin, Ireland, pp. 41–53, 2021. [Google Scholar]

    7. I. Feki, S. Ammar, Y. Kessentini and K. Muhammad, “Federated learning for COVID-19 screening from chest x-ray images,” Applied Soft Computing, vol. 106, pp. 1–9, 2021. [Google Scholar]

    8. J. Verbraeken, M. Wolting, J. Katzy, J. Kloppenburg, T. Verbelen et al., “A survey on distributed machine learning,” ACM Computing Surveys, vol. 53, no. 2, pp. 1–33, 2020. [Google Scholar]

    9. C. Tankard, “What the GDPR means for businesses,” Network Security, vol. 2016, no. 6, pp. 5–8, 2016. [Google Scholar]

  10. J. K. O’herrin, N. Fost and K. A. Kudsk, “Health insurance portability accountability act (HIPAA) regulations: Effect on medical record research,” Annals of Surgery, vol. 239, no. 6, pp. 772–778, 2004. [Google Scholar]

  11. K. Bonawitz, H. Eichner, W. Grieskamp, D. Huba, A. Ingerman et al., “Towards federated learning at scale: System design,” in Proc. of the 2nd Machine Learning and Systems, Stanford, CA, USA, pp. 374–388, 2019. [Google Scholar]

  12. B. McMahan, E. Moore, D. Ramage, S. Hampson and B. A. y Arcas, “Communication-efficient learning of deep networks from decentralized data,” in Proc. of the 20th Int. Conf. on Artificial Intelligence and Statistics, Fort Lauderdale, Florida, USA, pp. 1273–1282, 2017. [Google Scholar]

  13. C. Thapa, M. A. P. Chamikara and S. A. Camtepe, “Advancements of federated learning towards privacy preservation: From federated learning to split learning,” Federated Learning Systems, vol. 965, pp. 79–109, 2021. [Google Scholar]

  14. P. Vepakomma, O. Gupta, T. Swedish and R. Raskar, “Split learning for health: Distributed deep learning without sharing raw patient data,” arXiv:1812.00564, pp. 1–7, 2018. [Online]. Available: https://doi.org/10.48550/arXiv.1812.00564. [Google Scholar]

  15. D. -J. Han, H. I. Bhatti, J. Lee and J. Moon, “Accelerating federated learning with split learning on locally generated losses,” in Int. Workshop on Federated Learning for User Privacy and Data Confidentiality, Vienna, Austria, pp. 1–12, 2021. [Google Scholar]

  16. C. He, M. Annavaram and S. Avestimehr, “Group knowledge transfer: Federated learning of large CNNs at the edge,” in The 34th Conf. on Neural Information Processing Systems, Vancouver, BC, Canada, pp. 14068–14080, 2020. [Google Scholar]

  17. S. Pal, M. Uniyal, J. Park, P. Vepakomma, R. Raskar et al., “Server-side local gradient averaging and learning rate acceleration for scalable split learning,” in Int. Workshop on Trustable, Verifiable and Auditable Federated Learning, Vancouver, BC, Canada, pp. 1–9, 2022. [Google Scholar]

  18. C. Thapa, P. C. M. Arachchige, S. Camtepe and L. Sun, “Splitfed: When federated learning meets split learning,” in Proc. of the AAAI Conf. on Artificial Intelligence, vol. 36, no. 8, pp. 8485–8493, 2022. [Google Scholar]

  19. Q. Yang, Y. Liu, T. Chen and Y. Tong, “Federated machine learning: Concept and applications,” ACM Transactions on Intelligent Systems and Technology, vol. 10, no. 2, pp. 1–19, 2019. [Google Scholar]

  20. T. Li, A. K. Sahu, A. Talwalkar and V. Smith, “Federated learning: Challenges, methods, and future directions,” IEEE Signal Processing Magazine, vol. 37, no. 3, pp. 50–60, 2020. [Google Scholar]

  21. O. A. Wahab, A. Mourad, H. Otrok and T. Taleb, “Federated machine learning: Survey, multi-level classification, desirable criteria and future directions in communication and networking systems,” IEEE Communications Surveys & Tutorials, vol. 23, no. 2, pp. 1342–1397, 2021. [Google Scholar]

  22. C. Xu, Y. Qu, Y. Xiang and L. Gao, “Asynchronous federated learning on heterogeneous devices: A survey,” arXiv:2109.04269, 2021. [Online]. Available: https://doi.org/10.48550/arXiv.2109.04269. [Google Scholar]

  23. T. Yang, G. Andrew, H. Eichner, H. Sun, W. Li et al., “Applied federated learning: Improving google keyboard query suggestions,” arXiv:1812.02903, 2018. [Online]. Available: https://doi.org/10.48550/arXiv.1812.02903. [Google Scholar]

  24. S. Ramaswamy, R. Mathews, K. Rao and F. Beaufays, “Federated learning for emoji prediction in a mobile keyboard,” arXiv:1906.04329, 2019. [Online]. Available: https://doi.org/10.48550/arXiv.1906.04329. [Google Scholar]

  25. A. Hard, K. Rao, R. Mathews, S. Ramaswamy, F. Beaufays et al., “Federated learning for mobile keyboard prediction,” arXiv:1811.03604, 2018. [Online]. Available: https://doi.org/10.48550/arXiv.1811.03604. [Google Scholar]

  26. Y. Chen, Y. Ning, M. Slawski and H. Rangwala, “Asynchronous online federated learning for edge devices with non-iid data,” in IEEE Int. Conf. on Big Data, Atlanta, GA, USA, pp. 15–24, 2020. [Google Scholar]

  27. S. Dhakal, S. Prakash, Y. Yona, S. Talwar and N. Himayat, “Coded federated learning,” in IEEE Globecom Workshops, Waikoloa, HI, USA, pp. 1–6, 2019. [Google Scholar]

  28. L. Li, H. Xiong, Z. Guo, J. Wang and C. -Z. Xu, “Smartpc: Hierarchical pace control in real-time federated learning system,” in IEEE Real-Time Systems Symp., Hong Kong, China, pp. 406–418, 2019. [Google Scholar]

  29. C. Xie, S. Koyejo and I. Gupta, “Asynchronous federated optimization,” arXiv:1903.03934, 2020. [Online]. Available: https://arxiv.org/abs/1903.03934. [Google Scholar]

  30. T. Nishio and R. Yonetani, “Client selection for federated learning with heterogeneous resources in mobile edge,” in IEEE Int. Conf. on Communications, Shanghai, China, pp. 1–7, 2019. [Google Scholar]

  31. Z. Chai, A. Ali, S. Zawad, S. Truex, A. Anwar et al., “Tifl: A tier-based federated learning system,” in Int. Symp. on High-Performance Parallel and Distributed Computing, Stockholm, Sweden, pp. 125–136, 2020. [Google Scholar]

  32. Z. Chai, Y. Chen, A. Anwar, L. Zhao, Y. Cheng et al., “Fedat: A high-performance and communication-efficient federated learning system with asynchronous tiers,” in Proc. of the Int. Conf. for High Performance Computing, Networking, Storage and Analysis, St. Louis, Missouri, USA, pp. 1–16, 2021. [Google Scholar]

  33. Z. Xu, F. Yu, J. Xiong and X. Chen, “Helios: Heterogeneity-aware federated learning with dynamically balanced collaboration,” in ACM/IEEE Design Automation Conf., San Francisco, CA, USA, pp. 997–1002, 2021. [Google Scholar]

  34. O. Gupta and R. Raskar, “Distributed learning of deep neural network over multiple agents,” Journal of Network and Computer Applications, vol. 116, pp. 1–8, 2018. [Google Scholar]

  35. S. Oh, J. Park, P. Vepakomma, S. Baek, R. Raskar et al., “Locfedmix-sl: Localize, federate, and mix for improved scalability, convergence, and latency in split learning,” in Proc. of the ACM Web Conf., Lyon, France, pp. 3347–3357, 2022. [Google Scholar]

  36. W. Wu, M. Li, K. Qu, C. Zhou, W. Zhuang et al., “Split learning over wireless networks: Parallel design and resource management,” arXiv:2204.08119, 2022. [Online]. Available: https://doi.org/10.48550/arXiv.2204.08119. [Google Scholar]

  37. J. Jeon and J. Kim, “Privacy-sensitive parallel split learning,” in Int. Conf. on Information Networking, Barcelona, Spain, pp. 7–9, 2020. [Google Scholar]

  38. M. Zhang, L. Qu, P. Singh, J. Kalpathy-Cramer and D. L. Rubin, “Splitavg: A heterogeneity-aware federated deep learning method for medical imaging,” IEEE Journal of Biomedical and Health Informatics, vol. 26, no. 9, pp. 4635–4644, 2022. [Google Scholar]

  39. K. Chang, N. Balachandar, C. Lam, D. Yi, J. Brown et al., “Distributed deep learning networks among institutions for medical imaging,” Journal of the American Medical Informatics Association, vol. 25, no. 8, pp. 945–954, 2018. [Google Scholar]

  40. K. He, X. Zhang, S. Ren and J. Sun, “Deep residual learning for image recognition,” in Proc. of the IEEE Conf. on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, pp. 770–778, 2016. [Google Scholar]

  41. G. Hinton, O. Vinyals and J. Dean, “Distilling the knowledge in a neural network,” in NIPS Deep Learning Workshop, Montreal, Canada, pp. 1–9, 2014. [Google Scholar]

  42. D. Wu, R. Ullah, P. Harvey, P. Kilpatrick, I. Spence et al., “Fedadapt: Adaptive offloading for IoT devices in federated learning,” IEEE Internet of Things Journal, vol. 9, no. 21, pp. 20889–20901, 2022. [Google Scholar]

  43. P. Joshi, C. Thapa, S. Camtepe, M. Hasanuzzamana, T. Scully et al., “Splitfed learning without client-side synchronization: Analyzing client-side split network portion size to overall performance,” in Collaborative European Research Conf., Cork, Ireland, pp. 1–7, 2021. [Google Scholar]

  44. O. Ronneberger, P. Fischer and T. Brox, “U-net: Convolutional networks for biomedical image segmentation,” in Int. Conf. on Medical Image Computing and Computer-Assisted Intervention, Munich, Germany, pp. 234–241, 2015. [Google Scholar]

  45. K. Simonyan and A. Zisserman, “Very deep convolutional networks for large-scale image recognition,” in Int. Conf. on Learning Representations, San Diego, CA, USA, pp. 1–14, 2015. [Google Scholar]

  46. J. Yosinski, J. Clune, Y. Bengio and H. Lipson, “How transferable are features in deep neural networks?,” in Int. Conf. on Neural Information Processing Systems, Montreal, Canada, pp. 3320–3328, 2014. [Google Scholar]

  47. M. J. Sheller, B. Edwards, G. A. Reina, J. Martin, S. Pati et al., “Federated learning in medicine: Facilitating multi-institutional collaborations without sharing patient data,” Scientific Reports, vol. 10, no. 1, pp. 1–12, 2020. [Google Scholar]

  48. L. Wang, J. Ye, Y. Zhao, W. Wu, A. Li et al., “SuperNeurons: Dynamic GPU memory management for training deep neural networks,” in Symp. on Principles and Practice of Parallel Programming, Vienna, Austria, pp. 41–53, 2018. [Google Scholar]

  49. C. Dwork and A. Roth, “The algorithmic foundations of differential privacy,” Foundations and Trends in Theoretical Computer Science, vol. 9, no. 3–4, pp. 211–407, 2014. [Google Scholar]

  50. P. Kairouz, H. B. McMahan, B. Avent, A. Bellet and M. Bennis, “Advances and open problems in federated learning,” Foundations and Trends in Machine Learning, vol. 14, no. 1–2, pp. 1–210, 2021. [Google Scholar]

  51. K. Zhang, X. Song, C. Zhang and S. Yu, “Challenges and future directions of secure federated learning: A survey,” Frontiers of Computer Science, vol. 16, no. 5, pp. 1–8, 2022. [Google Scholar]