Connected Vehicles Computation Task Offloading Based on Opportunism in Cooperative Edge Computing

1  Introduction

Multi-access edge computing (MEC) has attracted more attention than ever before because it can handle the computation tasks of connected vehicles (CVs) with limited resources by computing offloading [1]. However, CVs encountered computation-intensive and delay-critical computation tasks. In this case, only relying on the fixed edge servers (FESs) deployed near the roadside units (RSUs) may cause the computation congestion of some FESs and the load imbalance of computation resources between them. In urban congested areas or areas with inadequate infrastructures, the density and computation resource capacity of FESs will affect the offloading performance.

Recently, the MEC architectures of task offloading have undergone extensive design work to augment the task-processing capabilities of edge servers (ESs). Some research works [2–4] suggested MEC/Fog computing (FC)-based architectures for task offloading in vehicular networks. These architectures deploy ESs/fog servers (FSs) at fixed wireless infrastructures, enabling the exchange of information between vehicles and ESs/FSs through vehicle-to-infrastructure (V2I) communication with low latency. However, it is unable to handle all the computation-intensive tasks in urban areas’ hot spots because each ES/FS only has a limited-service area and finite computing power. Some existing approaches [5–7] attempted to adaptively offload excessive computation-intensive tasks to the ESs/FSs and alleviate and balance the load of the ESs/FSs by optimizing the computation offloading strategy. However, unanticipated latency and task failure may occur because of vehicular mobility, dynamic vehicular density distribution, and time-varying computation resources of ESs/FSs. To sum up, the task offloading problem in vehicular networks has not been completely addressed.

Ad-hoc edge clouds, which can use mobile vehicles with high-performance computation capacities and idle scattered in the traffic network as opportunistic CVs, have emerged as an effective approach to tackle these complications [8]. These clouds can form an ad-hoc local resource pool and offer opportunistic computing services. Ad-hoc edge cloud can be created anytime and anywhere according to the availability of opportunistic CVs and cooperate with the fixed edge cloud to form a novel hybrid cloud, allowing resources and computation sharing. Furthermore, this hybrid cloud can convert the idle resources due to congestion into valuable and useful computation capacities and further alleviate the resource limitation of MEC. Although vehicle or unmanned aerial vehicle (UAV) assisted MEC provides chances for computation offloading to vehicles with restricted local processing capabilities [9,10], they did not effectively schedule resources, assign tasks in MEC, and establish load balance between opportunistic CVs and FESs.

On the basis of the foregoing backdrop, the task offloading and resource allocation problem in a novel hybrid cloud are examined in this paper. There are still some crucial challenges in realizing the opportunistic ad-hoc edge cloud to balance the efficient joint offloading decision and resource allocation of the fixed edge cloud: (1) how to select the appropriate edge computing node; (2) how to reasonably allocate resources. However, offloading decisions are extremely dynamic ascribed to the mobility of CVs. More sophisticated edge computing node selection schemes and resource allocation strategies should be created to improve the task offloading effectiveness of CVs in distributed systems. Particularly, our proposed scheme considers the mobility of CVs when deciding the offloading to the edge computing nodes and handles the potential trade-offs between communication and computation latency. The contributions of this study are outlined as follows,

(1)   A scalable opportunistic CV-assisted MEC framework, which offloads tasks through opportunistic CVs cooperating with FESs, is proposed. Furthermore, the joint offloading decision and resource allocation problem for opportunistic ad-hoc edge cloud-assisted MEC is formulated as a Mixed Integer Nonlinear Programming (MINLP) problem with minimum task response latency.

(2)   The formulated MINLP problem is decomposed into two subproblems: 1) a distributed method based on duality theory is proposed to optimize the resource allocation subproblem with the fixed task offloading strategy; 2) a satisfaction-driven method is proposed to solve the subproblem of edge computing node selection based on the resource allocation strategy.

(3)   A comprehensive series of experiments based on real city maps are conducted to verify that our suggested scheme improves the conventional approaches in load balancing, average response latency, task completion rate, and offloading rate.

The structure of the paper is organized as follows. Section 2 overviews the related literature. In Section 3, the system framework and the optimization model are described. Section 4 details the specific solution algorithm. Section 5 presents the simulation results of our scheme. Finally, conclusions are drawn in Section 6.

2  Related Works

Many researchers have studied the offloading strategies, task scheduling strategies, and resource allocation schemes in the MEC environment. Afsar et al. [11] maximized the computation resources of a cluster of nearby MEC through the cooperative game approach to reduce the task response latency. In a FiWi-enhanced vehicular edge computing (VEC) network, Zhang et al. [12] suggested a software-defined network load-balancing task offloading technique. To assure a better task offloading scheme, users must bargain with one another, which necessitates constant information exchange between them. Zhang et al. [13] placed small cloud server infrastructure with limited resources, such as a cloudlet near the network’s edge, and provided context-aware services based on network information. This method requires centralized frequent communication among controllers, cloudlet, and mobile devices. Al-Khafajiy et al. [14] presented a task offloading scheme with load balancing, where FSs of the Fog layer form a service group to provide services for the outside world. An FS with a heavier load can also redistribute its tasks to the lightly loaded FSs to achieve load balancing. Using a finite power budget, server computational capability, and wireless network coverage, Song et al. [15] proposed a method for offloading tasks to ESs to maximize the reward for each server. Tang et al. [16] constructed the VEC model in the form of a frame and designed a dynamic framing offloading algorithm based on Double Depth Q-Network (DFO-DDQN) to minimize the total delay and waiting time of tasks from mobile vehicles. Dai et al. [17] established a fog-based architecture to facilitate low-latency information interchange between vehicular users and FSs via V2I communication. Since each FS is limited to a specific service area, it cannot meet the demand for vehicles outside of that area. Additionally, the FS only serves a small number of users and has finite computational capacities, making it impossible for them to complete all the computation-intensive tasks in urban areas’ hotspots. The computing architectures for supporting CVs considered in the works above are computation-aided architectures, in which CVs only produce computation tasks and offload their tasks to ESs deployed on a static infrastructure. However, the uncertainty driven by the mobility of CVs makes the decision-making of task offloading more complicated [18], causing insufficient computation resources of ESs and a decrease in task offloading performance with the increase in task requests.

The architectures studied for supporting CVs in certain works are computation-enabled architectures, in which CVs can perform computation and generate computation tasks. In other words, the tasks of CVs will be completed independently, in conjunction with other adjacent vehicle clusters, or with the assistance of edge clouds. Wang et al. [19] summarized the existing computing architecture design in MEC/FC for CVs in detail and analyzed the service demands and design considerations of MEC architecture from both academic and commercial viewpoints, providing a novel perspective for mobile vehicles as fog nodes. Nonetheless, this is just an idea. Tang et al. [20] proposed a task scheduling strategy based on the greedy heuristic algorithm in the architecture based on FC. Specifically, vehicles form vehicle ad-hoc networks (VANETs) and contribute their computation resources to supplement vehicular fog computing (VFC), so as to effectively handle tasks offloaded from mobile device. Besides, RSU acts as a cloud center and is responsible for scheduling vehicles within its communication range. Lin et al. [21] proposed a contextual clustering of bandits based online vehicular task offloading solution, where the target vehicular user equipment learns the unknown environment during offloading, to minimize the overall offloading energy while meeting offloading delay of each task under an unknown environment. Zhang et al. [22] offloaded partial computation tasks to other devices and enhanced service quality by optimizing resource allocation, lowering latency, and using less energy. Fatemidokht et al. [23] suggested a novel secure and cost-effective method based on an AI algorithm with UAV-assisted for urban VANET (VRU) protocol. This method significantly reduced the packet delivery ratio and delay time. In vehicle-to-vehicle (V2V) communication, Dai et al. [24] fully utilized the computation capacity of numerous surrounding vehicles and processed tasks for close-by vehicles. However, the computation resources of ESs are time varying owing to the dynamic joining and departing of vehicles, resulting in an unforeseen delay or task failure. Ma et al. [25] designed a unique task scheduling mode for resource allocation management and computing edge server choice in addition to proposing an edge computing solution based on outside parked vehicles. However, this idea is only aimed at static vehicular cloud, neglecting the dynamic environment. The path of task offloading is long, accompanied by optimization variables such as selection decisions and resource allocation. Considering that these optimization variables require task offloading to meet task processing delay and resource constraints, it is comparatively challenging.

3  System Model and Problem Analysis

3.1 Scenario Description

In this study, a scalable opportunistic CVs assisted-MEC (SOMEC) scenario is proposed, as illustrated in Fig. 1. The system framework consists of three layers: (1) CV layer; (2) scalable edge computing layer with fixed edge cloud and opportunistic ad-hoc edge cloud, where the fixed edge cloud is deployed on the RSUs. Opportunistic ad-hoc edge cloud is temporarily created by mobile vehicles with high-performance computational capacities scattered in the traffic road network but not fully utilized as opportunistic CVs; (3) application layer. User CVs and opportunistic CVs are identified as 𝒩={1,2,⋯,N} and ℳ={1,2,⋯,M}, respectively. The set of RSU is ℛ={1,2,⋯,R}; the set of all computing nodes is represented as ℒ={0,1,2,…,M,M+1,M+2,…,M+R}, a computing node k∈ℒ, where k=0 denotes user CV locally, 1≤k≤M indicates opportunistic ES (OES), and k>M represents FES. Y={yik|i∈𝒩,k∈ℒ} implies edge computing node selection file profile, where yik=1 indicates that the task is placed on the edge computing node k∈ℒ for execution, otherwise yik=0. The notation TAi={ϑi,γi,ξi,oi} can be used to represent the task of the user CV i, which comprises the task input-data size ϑi and computation intensity γi. Specifically, maximum latency tolerance is ξi, and the output/input ratio oi is related to the properties of the task. Afterward, the time is discretized into the form of non-overlapping time slots of equal length with time intervals of t~ to determine the computation offloading process of the dynamics of vehicles. The amount of time slots is mostly determined by the maximum latency tolerance, i.e., G=max{⌊ξi/t~⌋}i∈𝒩.

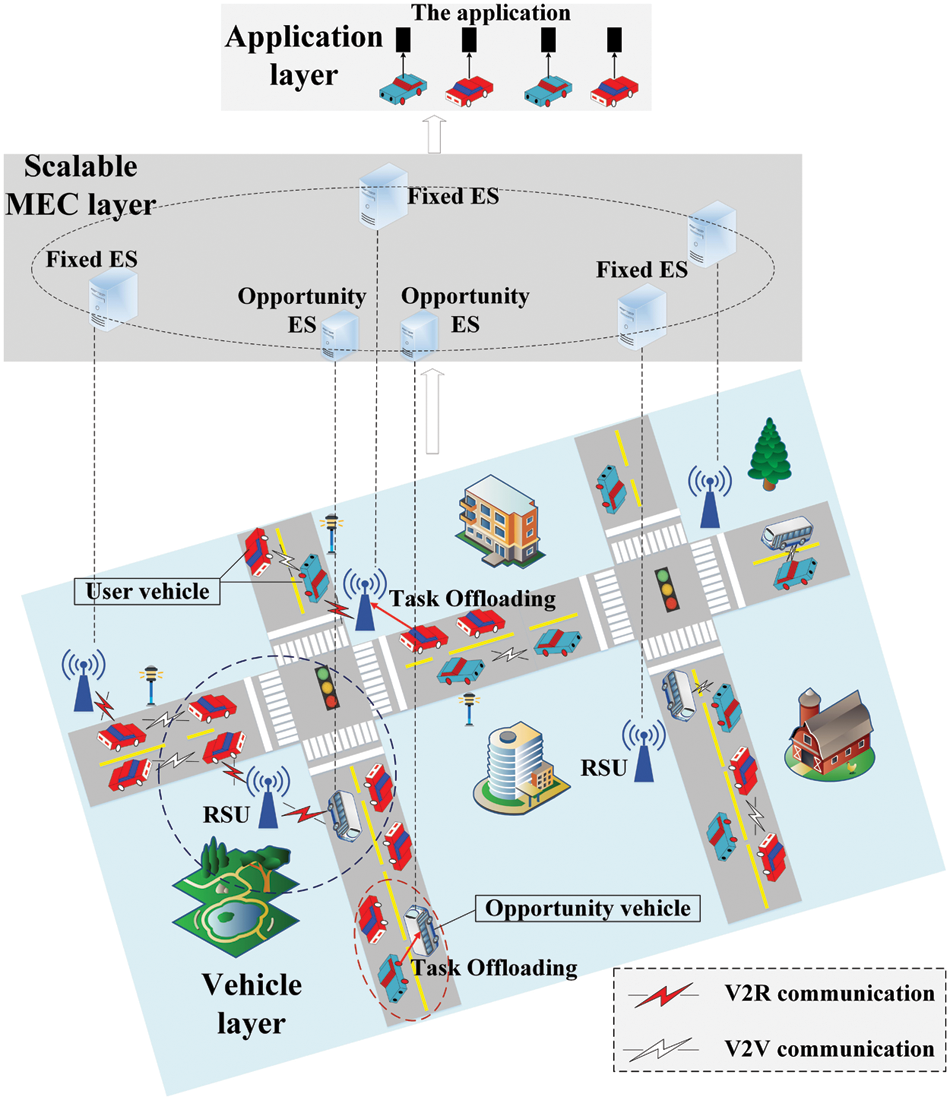
Figure 1: Framework of scalable opportunistic CV-assisted MEC

3.2 System Model

3.2.1 Vehicular Mobility Model

In most cases, the vehicular velocity follows a Gaussian distribution. A reduced version of this distribution can be used [26] to make the research more applicable to the real scenes. The truncated Gaussian probability density function (PDF) is additionally written as:

f~v(v)=fv(v)∫VminVmaxfv(s)ds=2fv(v)erf(Vmax−μσ2)−erf(Vmin−μσ2),(1)

where fv(v)=1σ2πexp⁡(−(v−μ)22σ2) indicates the Gaussian PDF, μ denotes the average velocity, σ represents the standard deviation of the velocity, and erf(⋅) is an error function. The velocity of each vehicle is defined as v∈[Vmin,Vmax], where Vmax=μ+3σ and Vmin=μ−3σ are the maximal and minimal vehicular velocity, respectively.

As a result, Eq. (1) provides the following equation for an equivalent velocity:

uv=1∫VminVmaxf~v(v)vdv=erf(Vmax−μσ2)−erf(Vmin−μσ2)2σ2π∫VminVmaxexp⁡(−(v−μ)22σ2)vdv.(2)

For the angle α∈{0,π}, both user CVs and opportunistic CVs maintain uniform linear motion during computation offloading. Suppose that the initial position of user CV i and opportunistic CV s are pi=(xi,yi) and ps=(xs,ys), respectively, their positions in the g−th time slot can be written as pig=(xig,yig) and psg=(xsg,ysg), where xig=xi+vigt~cos⁡α and yig=yi+vigt~sin⁡α, xsg and ysg are calculated the same. The deployment location of the FES j is generally fixed and designated as pj=(xj,yj).

3.2.2 Communication Model

The orthogonal frequency-division multiple access (OFDMA) system is used in our situation [27]. Based on the Shannon-Haley theorem, the communication link’s transmission rate is expressed in the g−th time slot as:

Ri,kg,m=Wikℓklog2⁡(1+Ptmhi,kgk0||pig−pkg||−θIik+σ2),(3)

where m=up and m=down for uplink and downlink, respectively. Wik represents the channel bandwidth, σ2 denotes the noise spectral density, Ptm signifies the transmission power, Iik indicates the interference caused by more CVs following the same channel, θ stands for the path loss exponent, k0 refers to a proportional constant coefficient that depends on (λ/4π)2, hi,kg reflects the small-scale fading channel power gain between computing node k and user CV i in the g−th time slot. The number of tasks running on computing node k at the same time is expressed as ℓk:

ℓk=∑i∈𝒩yik.(4)

3.2.3 Task Offloading Model

For each user CV to finish its task, there are three offloading decisions: running locally in the vehicle (k=0), offloading to the OES (1≤k≤M), and offloading to the FES (k>M).

1)   Local computing on the vehicle: In this scenario, the computation capability determines the task’s response latency, estimated as:

ti,0=γi/filocal,(5)

2)   Offloading to the FES: In this scenario, the task’s response latency is composed of the execution time, the time it takes for input data to be transmitted and the time it takes for output data to be transmitted. These three times can be estimated as:

ti,j=tijexe+tijup+tijdown.(6)

The execution time of the task is expressed as:

ti,jexe=γifjes,(7)

where fjes expresses the computation capacity of the FES j.

In the g−th time slot, the wireless transmission latency of the uplink for the task of the user CV i is:

ti,jg,up=ϑiRi,jg,up,(8)

where Ri,jg,up denotes the transmission rate of uplink for user CV i and FES j in the g−th time slot.

Since the task has the maximum latency tolerance, the variable ϑi,jg,down is introduced to represent the size of the downlink output data from FES j to the user CV i in the g−th time slot. The wireless transmission latency of the downlink for the user CV i is:

ti,jg,down=ϑi,jg,downRi,jg,down+hmudRSUV+ϑi,jg,downB¯,(9)

where, in the wireless backhauls, hmu represents the number of hops that need to transmit output data between RSUs to reach the vehicle, dRSU indicates the average distance between two neighboring RSUs, V denotes the data delivery speed, B¯ refers to the equivalent bandwidth between two neighboring RSUs.

In heterogeneous networks, the equivalent bandwidth is determined by the bandwidth on each of the selected communication links, expressed as:

B¯=11/B1+1/B2+⋯+1/Bhmu=B1×B2×⋯×BhmuB1+B2+⋯+Bhmu.(10)

3)   Offloading to the OES: In this scenario, the task’s response latency is composed of the execution time, the time it takes for input data to be transmitted, waiting time, and the time it takes for output data to be transmitted:

ti,s=tisexe+tisup+tiswait+tisdown,(11)

Tasks assigned to the OES s before task TAi should be known to compute tiswait. Let wqis denote all tasks assigned to the OES s before task TAi. Then, the waiting response latency of TAi is the total execution response latency of tasks in wqis, expressed as:

tiswait=∑TAi′∈wqisγi′fsov,(12)

where TAi′ denotes the task assigned to the OES s before TAi, γi′ represents the computation amount of task TAi′, and fsov indicates the computation capacity of OES s.

If the user CV i is still in the coverage range of the OES s after TAi is completed, the output results can be directly transmitted to the user CV i through V2V communication through wireless backhaul. In this case, the response latency of the output data of task TAi in the g−th time slot is:

ti,sg,down=ϑi,sg,downRi,sg,down.(13)

If the user CV i is not within the coverage of the OES s after TAi is completed, the output data should be transmitted to the user CV i through the wireless backhaul and vehicle-to-RSU (V2R) and V2V communications. In this case, the response latency of the output data of task TAi in the g−th time slot is:

ti,sg,down=ϑi,sg,downRi,sg,down+ϑi,sg,downRi,lg,down+hmu′dRSUV+ϑi,sg,downB¯′,(14)

where hmu′ represents the number of hops required for the nearest RSU of the OES s to reach the nearest RSU of user CV i after the task TAi is completed, B¯′ signifies the equivalent bandwidth between the origin RSU and the destination RSU on the wireless backhaul link.

3.3 Problem Formulation

Multiple vehicular tasks will simultaneously compete for edge computation resources. Unreasonable resource allocation may provoke network link congestion, low task completion rate, and low edge computation resource utilization. The file profiles of edge computing node selection and resource allocation are defined as Y={yik|i∈𝒩,k∈ℒ} and X={xik|i∈𝒩,k∈ℒ}, respectively. Further, our optimization problem can be expressed as:

P1​:argxik,yikminTtotal=∑i∈N∑k∈ℒyiktiks.t. C1​:yik∈{ 0,1 } C2​:∑k∈ℒyik=1,∀i∈N C3​:∑i∈Nyik≤1,∀k∈ℒ C4​:∑i∈Nyiktik≤ξi,∀k∈ℒ C5​:∑i∈Nkxik≤fkmax,∀k∈ℒ.(15)

C1 denotes a binary vector. C2 ensures that each task can only be executed by one computing node. C3 implies that a task is only executed once. C3 and C4 assure the maximum tolerance latency for each task. C5 guarantees that the overall computation resources of the edge computing node assigned to its tasks do not exceed its maximum capacity fkmax, where 𝒩k={i∈𝒩|yik=1} represents the set of tasks assigned to the edge computing node.

4  Design and Analysis of Resource Scheduling Algorithm

An algorithm with exponential computational complexity is usually required to find the best edge computing node and resource allocation strategy for problem P1. This problem is a MINLP problem since the edge computing node selection profile Y is binary and the resource allocation profile X is a continuous vector. This problem is obviously an NP-hard problem [28]. Therefore, problem P1 is decomposed into two subproblems: 1) the resource allocation, which achieves the optimal computation resource allocation with the fixed offloading decision via the Lagrange dual method; 2) the offloading decision (i.e., computing node selection), which optimizes the offloading decision adopted the satisfaction-driven method based on TE learning.

4.1 Based on Duality Theory for Resource Allocation

Assume that the edge computing node has been given, namely, Y=Y0. Then, P1 is a convex problem concerning X. P1 can be rewritten as:

P2:argxikminTtotal=∑i∈𝒩k∑k∈ℒγixiks.t.C5.(16)

Theorem 1. Given Y=Y0, problem P2 is a convex problem with respect to X.

Proof: See Appendix A.

The Lagrange multiplier v={vk,k∈ℒ} is employed to address problem P2. Then, the problem can be converted into a Lagrange function:

L(x,v)=∑i∈𝒩k∑k∈ℒγixik+∑k∈ℒvk(∑i∈𝒩kxik−fkmax).(17)

The optimization problem is converted into a dual problem:

D¯(v)=minL(x,v)=minxik∑k∈ℒ(∑i∈𝒩kγixik+vk(∑i∈𝒩kxik−fkmax)).(18)

The aforementioned problem demonstrates that this is a convex optimization problem and is connected to vk. The optimization problem should satisfy the dual property:

xik∗=argxikmin{∑i∈𝒩kγixik+vk(∑i∈𝒩kxik−fkmax)}.(19)

Each iteration is updated in the following way:

vk(n+1)=[vk(n)+ε(∑i∈𝒩kxik−fkmax)]+,(20)

where n represents the iteration index, and ε denotes the update operation step.

Since the high-speed movement of vehicles will cause dynamic changes in computation resources on the ES, an adequate constant step size must be chosen to guarantee the convergence of the optimization problem and speed up the convergence rate. The algorithm is described in Algorithm 1. The initial value of v is set to v(0) to obtain the ideal value of xik. The value of xik can be calculated according to Eq. (19). Then, the initial value of vk can be obtained and updated in conjunction with Eq. (20). The above steps are iterated until the value of xik is fixed or the value of vk is 0. The convergence analysis of the algorithm is detailed as follows.

Theorem 2. Assume that ||ε||2 is small enough, v≥0. Then, the suggested algorithm can converge to the optimal solution.

Proof: See Appendix B.

4.2 Satisfaction-Driven Method for Offloading Strategy

The best edge computing node for the task is chosen once the best resource allocation has been determined by lessening the overall response latency constraint of all offload tasks. After the determination of the optimal resource allocation X∗, the following step is to choose the optimal edge computing node by curtailing the response latency. The problem is rephrased per Section 4.1 as:

P3​:argyikminTtotal=∑i∈N∑k∈ℒyiktik,s.t. C1,C2,C3,C4(21)

where tik can be written as:

tik={ti,0,if k=0ti,s,if1≤k≤Mti,j,if k>M.(22)

Owing to the dynamic mobility of vehicles, the selection of edge computing nodes for the user CV i can be regarded as an exploration and exploitation process. Under the inspiration of TE learning, a satisfaction-driven method is proposed for edge computing node selection. Moreover, it has been verified that this method can make the distributed system stay at the optimal Nash equilibrium point with high probability [29]. Edge computing nodes with higher probability can be better explored when the task response latency of the user CV i is large or tends to increase. The user CV i can maintain the currently selected edge computing node with a high probability and explore other edge computing nodes with a low probability when the task response latency of the user CV i is small or tends to decrease. Consequently, the task response latency of the vehicle changes to a decreasing trend. The state of each vehicle consists of three parts: emotion value, benchmark edge computing node, and benchmark response latency. For the user CV i, its state in the time slot g is expressed as:

ξi(g)={mi(g),e¯i(g),t¯i(g)},(23)

where mi(g) denotes the satisfaction value, e¯i(g) indicates the benchmark edge computing node, and t¯i(g) represents the benchmark response latency.

Similar to TE-learning, satisfaction value is defined as content (c), discontent (d), watchful (c−), and hopeful (c+). Among them, c indicates that user CV is satisfied with the current task response latency, d implies that user CV is dissatisfied with the current task response latency, c− suggests that the current task response delay may increase, and c+ reflects that the current task response latency may decrease.

Each time slot is divided into three mini-slots, and the selection and status of edge computing nodes of a vehicle are updated once during each time slot. The first of them is used for executing actions, while edge computing nodes are selected. The second of them is utilized for offloading tasks and exploring response latency, and the third is used for status updates. The second mini-slot lasts substantially longer than the first and third mini-slots.

The user CV i first determines its available set of edge computing nodes at the start of the time slot g. If the response latency of the edge computing node k to complete the task is less than the latency tolerance of the task, the edge computing node k is an available computing node for the user CV i. In the first mini-slot, the edge computing node k is selected for the user CV i according to the current emotion value degree. The edge computing node selected by the user CV i in the time slot g is recorded as e¯i(g). The method of selecting edge computing nodes for vehicles in the first mini-slot is described as follows, and the specific process is illuminated in Algorithm 2.

(1)   If mi(g)=c, the user CV i will select the benchmark edge computing node, i.e., ei(g)=e¯i(g), with probability Φ. Meanwhile, the user CV i will explore other available edge computing nodes with probability 1−Φ.

(2)   If mi(g)=d, the current response latency is not acceptable to the user CV i, then other edge computing nodes with probability 1 will be explored.

(3)   If mi(g)=c−, it shows that the response latency of the user CV i will tend to increase, but further confirmation is required. Thus, the user CV i will select the benchmark edge computing node, i.e., ei(g)=e¯i(g) with probability 1.

(4)   If mi(g)=c+, it shows that the response latency of the user CV i will tend to decrease, but further confirmation is required. Thus, the user CV i will select the benchmark edge computing node, i.e., ei(g)=e¯i(g) with probability 1.

The user CV i offloads the task and explores the edge computing node in the second mini-slot, and the response latency is recorded as ti(g).

After selecting the edge computing node, the user CV i updates the state in the third mini-slot following the current state and the detected response latency. The specific method is detailed as follows, and the specific process is illustrated in Algorithm 3.

(1)   If mi(g)=c and the user CV i has selected the benchmark edge computing node, i.e., ei(g)=e¯i(g), then the status of the user CV i is updated as:

ςi(g+1)={{c+,e¯i(g),t¯i(g)},ti(g)−t¯i(g)<tth{c−,e¯i(g),t¯i(g)},ti(g)−t¯i(g)>tth{c,e¯i(g),t¯i(g)},|ti(g)−t¯i(g)|≤tth,(24)

(2)   If mi(g)=c and the user CV i has explored other edge computing nodes, its state update can be divided into the following two situations:If ti(g)−t¯i(g)>tth, then,

ςi(g+1)={c,e¯i(g),t¯i(g)}.(25)

In other words, the user CV’s state is unaltered.If ti(g)−t¯i(g)<tth, then,

ςi(g+1)={{c,ei(g),ti(g)},w.p.P(Δt){c,e¯i(g),t¯i(g)},w.p.1−P(Δt),(26)

where w.p. indicates “with probability”, P(Δt) denotes the increasing function of Δt, where Δt=t¯i(g)−ti(g).

(3)   If mi(g)=d and the user CV i has explored other edge computing nodes with probability 1, the status of the user CV i is updated as follows:

ςi(g+1)={{c,ei(g),ti(g)},w.p.P′(ti(g)){c,e¯i(g),t¯i(g)},w.p.1−P′(ti(g)),(27)

where P′(ti(g)) represents a decreasing function of response latency ti(g). Eq. (27) suggests that the larger the response latency ti(g) of exploration, the smaller the probability that the user CV i selects the edge computing node ei(g) of exploration.

(4)   If mi(g)=c− and the user CV i has selected the benchmark edge computing node with probability 1, then the status of the user CV i is updated as:

ςi(g+1)={{c,e¯i(g),t¯i(g)},t¯i(g)−ti(g)>tth{d,e¯i(g),t¯i(g)},t¯i(g)−ti(g)<tth,(28)

where t¯i(g)−ti(g)>tth implies that the task response latency of the user CV i has no clear tendency of increasing, and thus its satisfaction value becomes c again; t¯i(g)−ti(g)<tth demonstrates that the task response latency of the user CV i has a tendency of increasing, and thus its satisfaction value becomes d.

(5)   If mi(g)=c+ and the user CV i has selected the benchmark edge computing node with probability 1, then the status of the user CV i is updated as:

ςi(g+1)={{c,e¯i(g),ti(g)},t¯i(g)−ti(g)>tth{c−,e¯i(g),t¯i(g)},ti(g)−t¯i(g)>tth{c,e¯i(g),t¯i(g)},|ti(g)−t¯i(g)|≤tth,(29)

4.3 Algorithm Complexity Analysis

The computational complexity of the joint optimization algorithm is primarily caused by two factors: computing node selection and resource allocation. Since CVs need to perform N calculations locally first, the complexity is O(N). Concerning Algorithm 1, the complexity of Step 5 is O(MN), the complexity of updating the Lagrange multiplier in step 9 is O(M)+O(N), and O(1/ε2) iterations are required to converge. Therefore, the complexity of Algorithm 1 is (O(N)+O(M)+O(N)+O(MN))⋅O(1/ε2)=O(MN/ε2). Each mini-slot in the edge computing node selection scheme has a computational complexity of O(MN). Therefore, the total complexity of the joint optimization Algorithm is 3×O(MN)+O(MN/ε2)=O(MN/ε2).

5  Experimental Simulation

5.1 Experiment Setup

MATLAB and simulation of urban mobility (SUMO) were utilized as two main platforms. MATLAB software is employed as an interface with TraCI. Some reduced urban areas of Lishui District, Nanjing in China and Jing’an District, Shanghai in China were downloaded from OpenStreetMap. The GPS locations of these two urban areas are shown in Table 1. Both areas of these regions are approximately 25km2. Besides, SUMO was adopted with OpenStreetMap to generate realistic vehicular mobility. In MATLAB, the suggested algorithm and the following comparison algorithms were implemented, and their performances were analyzed.

(1)   Local computing on the vehicle (LC): The tasks are executed locally by the user CVs.

(2)   Fixed edge server only scheme (FESO): The task is offloaded to the FESs to satisfy the maximum tolerance latency of the task when the LC latency exceeds the task’s latency tolerance. The proposed task allocation approach is employed to select edge computing nodes and allocate resources.

(3)   Random offloading of local, FESs and OESs (RO_LFO): Computing nodes include user CVs local, FESs, and OESs, and each task is randomly assigned with equal probability to one computing node.

(4)   Genetic algorithm (GA): GA is a meta-heuristic algorithm, which mainly grapples with the NP-hard global optimization problems. X and Y are encoded into chromosomes, and the population is expressed as the size or number of chromosomes. The fitness function is consistent with the objective function. In the selection part, the stochastic tournament method is adopted to select parents, and it stops when GA reaches the maximum number of iterations set.

(5)   Block successful upper-bound minimization (BSUM) algorithm [30]: BSUM is a distributed selection strategy optimization algorithm. Each coordinate computing node is selected using the cyclic rule as a task is transmitted to the vehicle first. Moreover, the task will be offloaded to the server only when the vehicle cannot meet the maximum delay of the task or achieve a lower system benefit.

In the simulation scenario, 8 RSUs are deployed, and it is assumed that the communication coverage of each RSU and opportunistic CV is 500 and 200 m, respectively. Vehicles enter the traffic network following the Poisson distribution process, with an average velocity ranging from 10 to 20 m/s. Each vehicle is provided with a pair of origin and destination that are randomly assigned to each vehicle based on the normal distribution. The default number of the user CVs and opportunistic CVs is 500 and 50, respectively. The bandwidth is divided into a total of 20 equal sub-bands, each of which is equal to 20 MHz. Table 2 provides the other relevant parameters involved in the simulation.

5.2 Performance Analysis

The experiments mainly evaluate the performance of the algorithm from five metrics:

(1)   Average response latency: Average task response latency for all user CVs.

(2)   Task completion rate: The valid return data of ES divided by the total amount of demand output data of the vehicular tasks, i.e., CR=∑i=1N∑g=1Gϑig,down/∑i=1Nϑi⋅oi, where the variable ϑig,down represents the actual received downlink output data of the user CV i in the g−th time slot.

(3)   Offloading rate of edge computing nodes: The ratio of the number of offloaded user CVs to the number of all user CVs.

(4)   Load balancing of the algorithm: The variance s2 of the average resource utilization efficiency, expressed as ρk=1ℒk∑i=1ℒkγifik, is utilized to better evaluate load balancing. fik indicates the computation resource allocated by the edge computing node k to user CV i. Therefore, s2 is expressed as s2=1k∑k∈ℒ(ρk−ρk¯).

(5)   Running time of the algorithm: The running time is used to verify the performance of computational complexity.

5.2.1 Analysis of the Impact of Two Different Regional Topologies

The results of the average response latency of tasks were compared under two different regional topologies by setting the experimental parameters such as the size of the task input data, the computation load, and the density of OESs. Fig. 2 illustrates that our proposed scheme can obtain similar results in different regional topologies. It is inferred that our proposed scheme may be suitable for vehicular task offloading in most real scenes.

Figure 2: The results of the average response latency under two different regional topologies. The charts corresponding to the default experimental parameters are N=500, ϑi=2.5MB, and γi=1500cycles/bit, for (a) size of the task input data, (b) computation load, and (c) density of OESs

5.2.2 Analysis of the Impact of the Size of the Task Input Data

Fig. 3 compares the performance of all the schemes by changing the size of the task input data. Fig. 3a suggests that the average response latency is constant and largest for LC execution of the user CV when the task input data increases owing to the limited computation capacities of the user CVs and no computation offloading. The average response latency of the other schemes will increase with the increase in the task input data. This can be explained as follows. The data transmission latency will increase because when each edge computing node executes the task, and the computation resources of each edge computing node used to execute the task will also decrease with the increase in the task input data. However, the average response latency of our proposed scheme is better than other schemes since OESs with abundant computation resources are used to balance the computing load of FESs in our proposed scheme. From another perspective, OESs also make the optimal offloading strategy according to the size of the task input data, so as to effectively select the edge computing nodes.

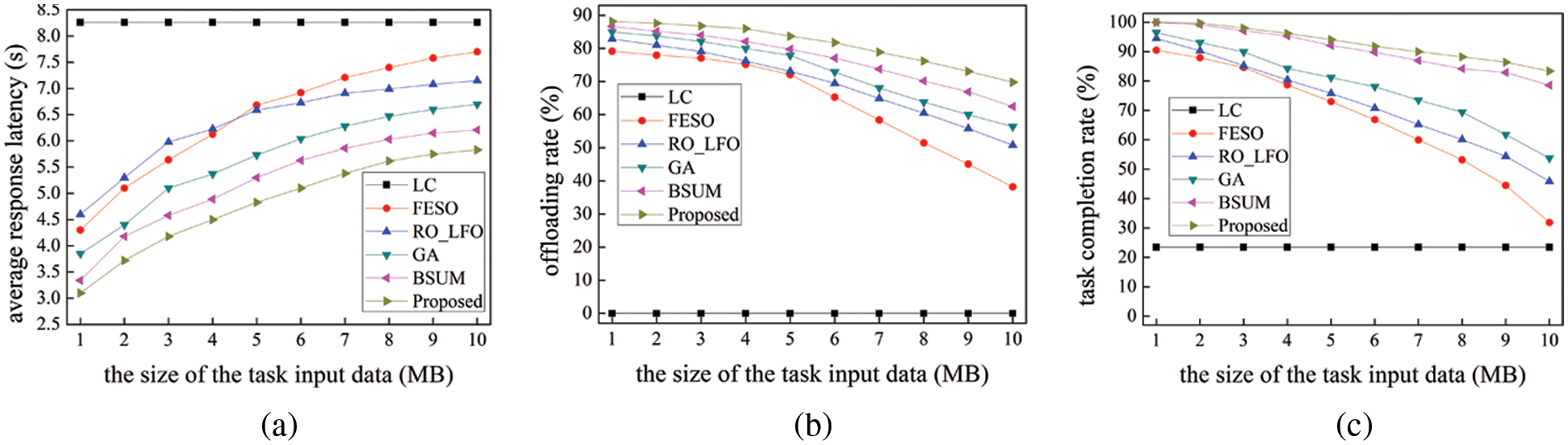
Figure 3: Comparisons of the impact of the size of the task input data. The charts corresponding to N=500, M=50, γi=1500cycles/bit, and ϑi changes from 1 to 10 MB, for (a) average response latency, (b) offloading rate, and (c) task completion rate

5.2.3 Analysis of the Impact of the Computation Load

Then, the performance of our suggested scheme and other schemes are discussed while changing the computation load of each task. In Fig. 4a, the average response latency for all the schemes increases with the increase in the computation load for each task. Compared with the LC execution of user CVs, other schemes have a smaller slope. The average response latency of our proposed scheme is about half of the LC since OESs can effectively balance the computation load of FESs. In Fig. 4b, the offloading rate first rises and subsequently decreases with the increase in the computation load of each task. The tasks that can be executed locally on the user CVs are set within the maximum tolerable latency. Thus, the computation load of the initial tasks is relatively small, and most tasks can be executed locally. However, the required computation resources increase as the computation load of tasks increases, and it must be offloaded to the nearby edge computing nodes for execution. The offloading rate decreases as the computation load of each task increases to a certain extent. Additionally, our proposed scheme successfully balances the computation load of OESs and FESs, and the offloading rate is higher than other schemes. In Fig. 4c, the task completion rates of all schemes significantly decrease as the computation load for each task increases. This is in that an increasing number of tasks cannot be finished within the maximum tolerable latency of tasks using the allocated computation resources of edge computing nodes. Nonetheless, our proposed scheme reaches a higher task completion rate than that of other schemes.

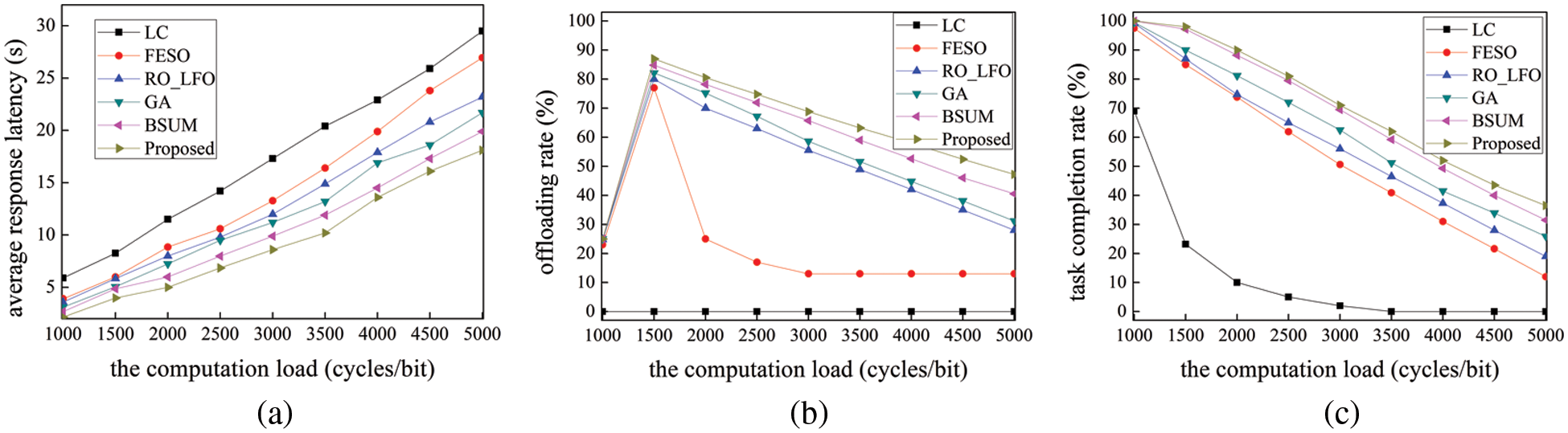
Figure 4: Comparisons of the impact of the computation load. The charts corresponding to N=500, M=50, ϑi=2.5MB, and γi changes from 1500 to 5000 cycles/bit, for (a) average response latency, (b) offloading rate, and (c) task completion rate

5.2.4 Analysis of the Impact of the Density of OESs

Fig. 5 displays the results of our performance evaluation of all the schemes using different densities of OESs. Notably, the performance of the schemes is impacted by the density of OESs rather than the number of OESs. Fig. 5a suggests that the average response latency for all the schemes decreases with the increasing density of OESs as OESs are also computation resources to reduce the average response latency. The higher the density, the more OESs for user CVs to select the best edge computing node for task offloading. As the density of OESs increases, our proposed scheme has enough opportunity for user CVs to offload tasks to edge computing nodes, or to transmit data through a relay mechanism with fewer hops, leading to a higher offloading rate and task completion rate.

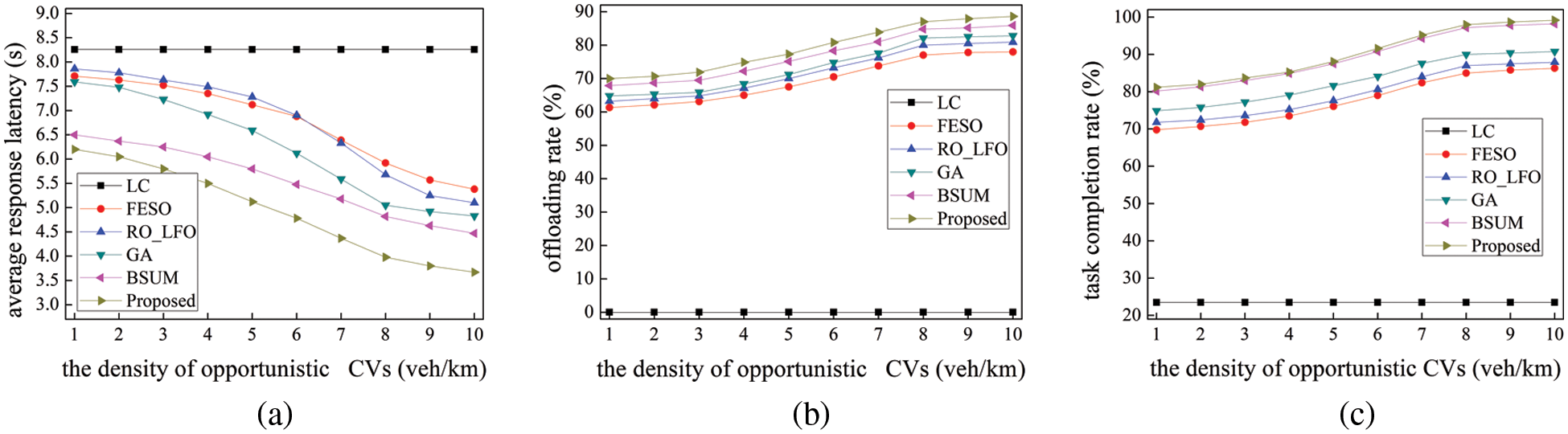
Figure 5: Comparisons of the impact of the density of opportunistic CVs. The charts corresponding to N=500, ϑi=2.5MB, γi=1500cycles/bit, and the density of opportunistic CVs changes from 1 to 10 veh/km, for (a) average response latency, (b) offloading rate, and (c) task completion rate

5.2.5 Analysis of Load Balancing Among the FESs

Our proposed scheme integrates load balancing into the task offloading problem for effectively balancing the server load. The performance comparison results of our proposed scheme and other schemes in load balancing are illustrated in Fig. 6 for the utilization efficiency of computation resources of FESs. Each component contains the load status of FESs. As revealed in Fig. 6, s2 of FESO, RO_LFO, GA, BSUM, and our proposed scheme are 0.3992, 0.5486, 0.3108, 0.1474, and 0.0548, respectively. Our proposed scheme performs the fairest load, enabling the variance to be the smallest and decrease by 34.44%, 49.38%, 25.6%, and 9.26% compared with the comparison schemes, respectively. Due to this occurrence, certain FESs will have computational congestion, while others will remain idle. If there is no suitable vehicle relay, only nearby servers are selected, though BSUM and GA also optimize the selection of computing nodes and resource allocation, and both of them perform unbalanced load allocation. As a result, the load balancing of server computation resources must be considered in the process of selecting the appropriate computing nodes.

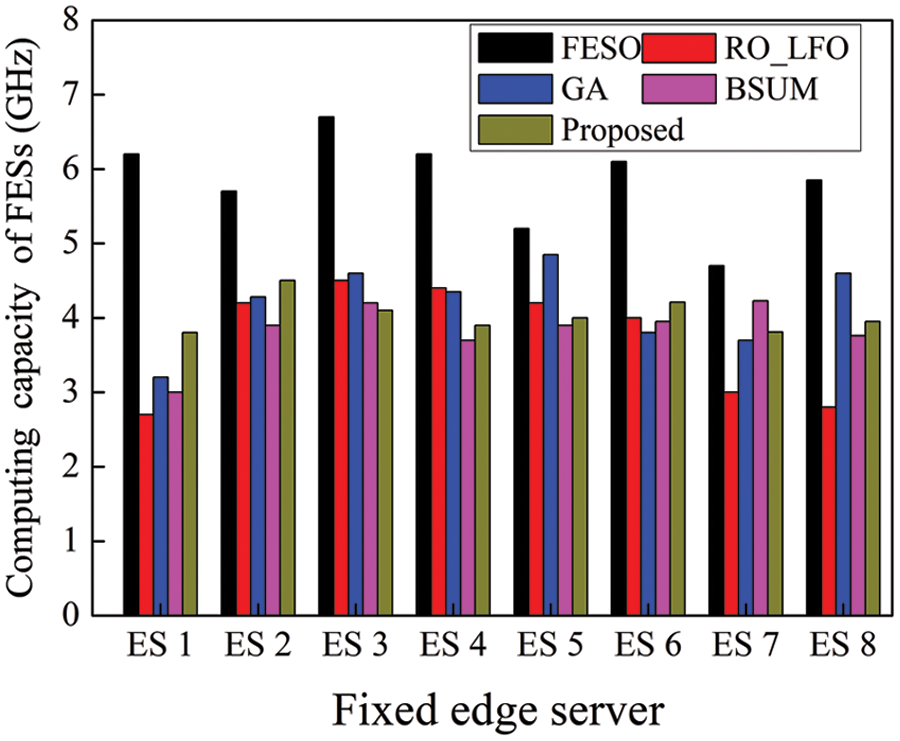
Figure 6: Comparison of load balancing among the FESs under five schemes. The charts corresponding to N=500, M=50, ϑi=2.5MB, and γi=1500cycles/bit

5.2.6 Analysis of Running Time

Fig. 7 exhibits the average running time of each iteration of all the schemes under different user CVs. Due to the global search, GA runs longer than other schemes since it converges to the local optimal value of the fitness function more quickly. Then, it becomes stuck close to this local optimal value, indicating that GA is not appropriate for online scheduling in the context of vehicular edge computing. Although the running time of LC, FESO, and RO_LFO is relatively short, their system performance is relatively poor because our proposed scheme can generate better offloading decision than these three schemes. Besides, our proposed scheme provides the best selection of computing nodes in most vehicular edge computing scenarios. It not only can achieve an approximate optimal solution but also has higher computing efficiency than BSUM.

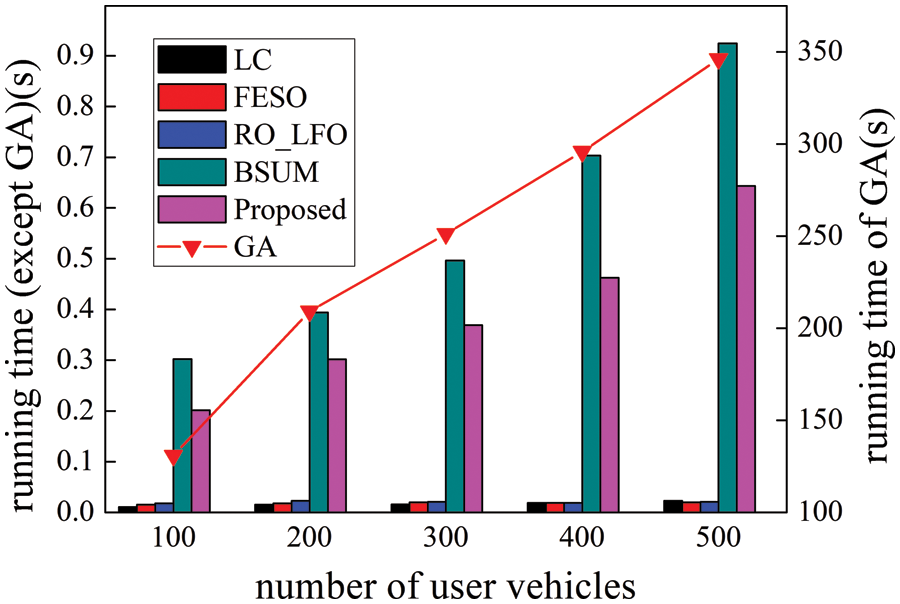
Figure 7: Running time comparison of all schemes under different user CVs. The charts corresponding to M=50, ϑi=2.5MB, γi=1500cycles/bit, and user CVs change from 100 to 500

5.2.7 Analysis of Multi-Hop Transmission

User CVs may not have the same edge computing nodes when offloading tasks and waiting for downloading output results. Thus, it is necessary to perform multi-hop transmission of data results through RSUs or relays between vehicles. Fig. 8 renders the number of hops required to send the task output back to the user CVs for our proposed scheme. It is observed that about 66.3% of user CVs are still in the RSU of offloading tasks or the direct communication coverage of OESs after completing computation tasks. However, about 22.8% of user CVs temporarily change their traveling routes ascribed to the influence of real-time traffic flow, while they can only connect with other vehicles or RSU through the one-hop relay to receive the output results. However, some user CVs will pass through remote suburbs in the actual traffic scene. In this case, the number of deployed RSUs or OESs is relatively small, the user CVs are disconnected from the network of these edge computing nodes, and other vehicles or RSUs in the network can be used as relay nodes. Therefore, a multi-hop relay mechanism is required to transmit data through these relay nodes.

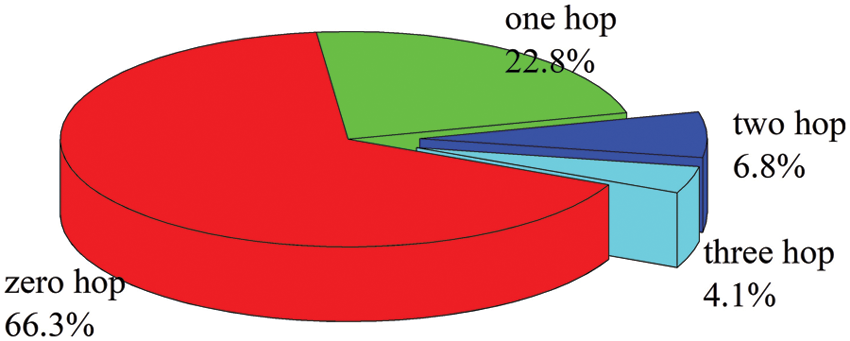
Figure 8: Multi-hop transmission of our proposed scheme. The charts corresponding to N=500, M=50, ϑi=2.5MB, and γi=1500cycles/bit

6  Conclusions and Future Work

In this paper, a novel scalable system framework was proposed for computation task offloading in opportunistic CV-assisted MEC. A tremendous number of resource-rich and underutilized CVs in the traffic road network were generated as opportunistic ad-hoc edge cloud to alleviate the resource constraints of MEC by providing opportunistic computing services. The problem of joint offloading decision and resource allocation was described as a MINLP problem to achieve load balancing between FESs and OESs. The original problem was decomposed into two sub-problems (offloading decision and resource allocation) to realize load balancing between FESs and OESs and continuously curtail task response latency of user CVs under various constraints. Finally, a comprehensive series of experiments were conducted to verify that our proposed scheme reduced load balancing by 34.44%, 49.38%, 25.6%, and 9.26% compared with other comparative schemes, and effectively lessened the task delay response, increased the completion rate of vehicular tasks, and demonstrated high reliability.

In future work, the impact of lower communication concerns, such as communication resources and channel allocation, will be included to make the system model more realistic and robust. Additionally, a small-scale test bench will be considered to investigate how well the suggested model performs in real-world traffic situations.

Funding Statement: This research was supported by the National Natural Science Foundation of China (61871400), Natural Science Foundation of Jiangsu Province (BK20211227) and Scientific Research Project of Liupanshui Normal University (LPSSYYBZK202207).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

    1. S. R. Pokhrel and J. Choi, “Improving tcp performance over Wi-Fi for internet of vehicles: A federated learning approach,” IEEE Transactions on Vehicular Technology, vol. 69, no. 6, pp. 6798–6802, 2020. [Google Scholar]

    2. Z. Ning, J. Huang and X. Wang, “Vehicular fog computing: Enabling real-time traffic management for smart cities,” IEEE Wireless Communications, vol. 26, no. 1, pp. 87–93, 2019. [Google Scholar]

    3. T. K. Rodrigues, J. Liu and N. Kato, “Offloading decision for mobile multi-access edge computing in a multi-tiered 6G network,” IEEE Transactions on Emerging Topics in Computing, vol. 10, no. 3, pp. 1414–1427, 2022. [Google Scholar]

    4. Q. Wu, Y. Zeng and R. Zhang, “Joint trajectory and communication design for multi-UAV enabled wireless networks,” IEEE Transactions on Wireless Communications, vol. 17, no. 3, pp. 2109–2121, 2018. [Google Scholar]

    5. H. Wu, L. Chen, C. Shen, W. Wen and J. Xu, “Online geographical load balancing for energy-harvesting mobile edge computing,” in 2018 IEEE Int. Conf. on Communications (ICC), Kansas City, MO, USA, pp. 1–6, 2018. [Google Scholar]

    6. G. Qu, H. Wu, R. Li and P. Jiao, “DMRO: A deep meta reinforcement learning-based task offloading framework for edge-cloud computing,” IEEE Transactions on Network and Service Management, vol. 18, no. 3, pp. 3448–3459, 2021. [Google Scholar]

    7. H. Wu, K. Wolter, P. Jiao, Y. Deng, Y. Zhao et al., “EEDTO: An energy-efficient dynamic task offloading algorithm for blockchain-enabled IoT-edge-cloud orchestrated computing,” IEEE Internet of Things Journal, vol. 8, no. 4, pp. 2163–2176, 2021. [Google Scholar]

    8. T. Dbouk, A. Mourad, H. Otrok, H. Tout and C. Talhi, “A novel ad-hoc mobile edge cloud offering security services through intelligent resource-aware offloading,” IEEE Transactions on Network and Service Management, vol. 16, no. 4, pp. 1665–1680, 2019. [Google Scholar]

    9. N. Cha, C. Wu, T. Yoshinaga, Y. Ji and K. -L. A. Yau, “Virtual edge: Exploring computation offloading in collaborative vehicular edge computing,” IEEE Access, vol. 9, pp. 37739–37751, 2021. [Google Scholar]

  10. X. Huang, X. Yang, Q. Chen and J. Zhang, “Task offloading optimization for UAV assisted fog-enabled internet of things networks,” IEEE Internet of Things Journal, vol. 9, no. 2, pp. 1082–1094, 2022. [Google Scholar]

  11. M. M. Afsar, R. T. Crump and B. H. Far, “Energy-efficient coalition formation in sensor networks: A game-theoretic approach,” in 2019 IEEE Canadian Conf. of Electrical and Computer Engineering (CCECE), Edmonton, AB, Canada, pp. 1–6, 2019. [Google Scholar]

  12. X. Zhang, J. Zhang, Z. Liu, Q. Cui, X. Tao et al., “MDP-based task offloading for vehicular edge computing under certain and uncertain transition probabilities,” IEEE Transactions on Vehicular Technology, vol. 69, no. 3, pp. 3296–3309, 2020. [Google Scholar]

  13. F. Zhang and M. M. Wang, “Stochastic congestion game for load balancing in mobile-edge computing,” IEEE Internet of Things Journal, vol. 8, no. 2, pp. 778–790, 2021. [Google Scholar]

  14. M. Al-Khafajiy, T. Baker, M. Asim, Z. Guo, R. Ranjan et al., “Comitment: A fog computing trust management approach,” Journal of Parallel and Distributed Computing, vol. 137, pp. 1–16, 2020. [Google Scholar]

  15. M. Song, Y. Lee and K. Kim, “Reward-oriented task offloading under limited edge server power for multi-access edge computing,” IEEE Internet of Things Journal, vol. 8, no. 17, pp. 13425–13438, 2021. [Google Scholar]

  16. H. Tang, H. Wu, G. Qu and R. Li, “Double deep Q-network based dynamic framing offloading in vehicular edge computing,” IEEE Transactions on Network Science and Engineering, 2022. https://doi.org/10.1109/TNSE.2022.3172794. [Google Scholar]

  17. P. Dai, K. Hu, X. Wu, H. Xing, F. Teng et al., “A probabilistic approach for cooperative computation offloading in MEC-assisted vehicular networks,” IEEE Transactions on Intelligent Transportation Systems, vol. 23, no. 2, pp. 899–911, 2022. [Google Scholar]

  18. Y. Mao, C. You, J. Zhang, K. Huang and K. B. Letaief, “A survey on mobile edge computing: The communication perspective,” IEEE Communications Surveys & Tutorials, vol. 19, no. 4, pp. 2322–2358, 2017. [Google Scholar]

  19. H. Wang, T. Liu, X. Du, B. Kim, C. Lin et al., “Architectural design alternatives based on cloud/edge/fog computing for connected vehicles,” IEEE Communications Surveys & Tutorials, vol. 22, no. 4, pp. 2349–2377, 2020. [Google Scholar]

  20. C. Tang, X. Wei, C. Zhu, Y. Wang and W. Jia, “Mobile vehicles as fog nodes for latency optimization in smart cities,” IEEE Transactions on Vehicular Technology, vol. 69, no. 9, pp. 9364–9375, 2020. [Google Scholar]

  21. Y. Lin, Y. Zhang, J. Li, F. Shu and C. Li, “Popularity-aware online task offloading for heterogeneous vehicular edge computing using contextual clustering of bandits,” IEEE Internet of Things Journal, vol. 9, no. 7, pp. 5422–5433, 2022. [Google Scholar]

  22. L. Zhang, Z. Zhao, Q. Wu, H. Zhao, H. Xu et al., “Energy-aware dynamic resource allocation in UAV assisted mobile edge computing over social internet of vehicles,” IEEE Access, vol. 6, pp. 56700–56715, 2018. [Google Scholar]

  23. H. Fatemidokht, M. K. Rafsanjani, B. B. Gupta and C. -H. Hsu, “Efficient and secure routing protocol based on artificial intelligence algorithms with UAV-assisted for vehicular ad hoc networks in intelligent transportation systems,” IEEE Transactions on Intelligent Transportation Systems, vol. 22, no. 7, pp. 4757–4769, 2021. [Google Scholar]

  24. P. Dai, Z. H. Huang, K. Liu, X. Wu, H. L. Xing et al., “Multi-armed bandit learning for computation-intensive services in MEC-empowered vehicular networks,” IEEE Transactions on Vehicular Technology, vol. 69, no. 7, pp. 7821–7834, 2020. [Google Scholar]

  25. C. Ma, J. Zhu, M. Liu, H. Zhao, N. Liu et al., “Parking edge computing: Parked-vehicle-assisted task offloading for urban VANETs,” IEEE Internet of Things Journal, vol. 8, no. 11, pp. 9344–9358, 2021. [Google Scholar]

  26. S. Yousefi, E. Altman, R. El-Azouzi and M. Fathy, “Analytical model for connectivity in vehicular ad hoc networks,” IEEE Transactions on Vehicular Technology, vol. 57, no. 6, pp. 3341–3356, 2008. [Google Scholar]

  27. Y. Mao, J. Zhang, S. H. Song and K. B. Letaief, “Stochastic joint radio and computational resource management for multi-user mobile edge computing systems,” IEEE Transactions on Wireless Communications, vol. 16, no. 9, pp. 5994–6009, 2017. [Google Scholar]

  28. U. Saleem, Y. Liu, S. Jangsher Y. Li and T. Jiang, “Mobility-aware joint task scheduling and resource allocation for cooperative mobile edge computing,” IEEE Transactions on Wireless Communications, vol. 20, no. 1, pp. 360–374, 2020. [Google Scholar]

  29. B. S. R. Pradelski and H. P. Young, “Learning efficient nash equilibria in distributed systems,” Games and Economic Behavior, vol. 75, no. 2, pp. 882–897, 2012. [Google Scholar]

  30. Y. K. Tun, Y. M. Park, N. H. Tran, W. Saad, S. R. Pandey et al., “Energy-efficient resource management in UAV-assisted mobile edge computing,” IEEE Communications Letters, vol. 25, no. 1, pp. 249–253, 2021. [Google Scholar]

Appendix

Appendix A

Given Y=Y0, the objective function in P1 becomes a function about X. If the objective function in problem P2 is defined as Ψ(X), then the second-order Hessian matrix is ∇2Ψ(X). Thus,

∂2Ψ(X)∂xik2=2γixik3,∀i∈𝒩k,k∈ℒ,(30)

∂2Ψ(X)∂xik∂xpq=0,∀(i,k)≠(p,q).(31)

Since the Hessian matrix is a positive semi-definite matrix and it is simple to determine that ∇2Ψ(X)≥0, so the problem P2 is a convex optimization problem.

Appendix B

The following equation can be obtained using the update operation of v in conjunction with the assumption that Φ={v∗} represents the dual problem’s solution and the introduction of adjustment parameter a so that aε′=ε.

Q(n+1)=∑k∈ℒvk(n+1)−vk∗ε′≤∑k∈ℒ[vk(n)+ε(∑i∈𝒩kxik(n)−fkmax)−vk∗]2ε′=∑k∈ℒ(vk(n)−vk∗)+2a∑k∈ℒ(vk(n)−vk∗)(∑i∈𝒩kxik(n)−fkmax)+a2∑k∈ℒε′(∑i∈𝒩kxik(n)−fkmax)2.(32)

The following dual problem can be reformulated when the Lagrange multiplier is optimal:

D(v∗)=minxik∑k∈ℒ(∑i∈𝒩kγixik+vk(∑i∈𝒩kxik−fkmax))≤∑k∈ℒ(∑i∈𝒩kγixik+vk∗(∑i∈𝒩kxik−fkmax)).(33)

The following dual problem is obtained when the Lagrange function changes with the update operation:

D(v(n))=∑k∈ℒ(∑i∈𝒩kγixik+vk(n)(∑i∈𝒩kxik−fkmax)).(34)

Therefore,

D(v(n))−D(v∗)≥∑k∈ℒ(vk(n)−vk∗)(∑i∈𝒩kxik−fkmax).(35)

Then,

Q(n+1)≤Q(n)+2a(D(v(n))−D(v∗))+a2∑k∈ℒε′(∑i∈𝒩kxik(n)−fkmax)2.(36)

The following inequality is true as long as xik(n) and fkmax are bounded, where Z is a constant,

∑k∈ℒε′(∑i∈𝒩kxik(n)−fkmax)2≤Z.(37)

As a result,

Q(n+1)≤Q(n)+2a(D(v(n))−D(v∗))+a2Z.(38)

Then, Φφ is defined as the following form, where φ>0,

Ψφ={v|D(v)≤D(v∗)≤D(v)+φ}.(39)

Set the parameter a to a≤φ/Φ. Thus, Q(n+1)≤Q(n)+φ2. Let Q(v)=∑k∈ℒ(vk−vk∗)/ε′ is bounded and Λ(φ,Φ) represents the upper bound. Hence, Q(n)≤Λ(φ,Φ)+φ2. Q(n) becomes closer to 0 as φ approaches 0, and then v approaches the optimal value.