A Dynamic Multi-Attribute Resource Bidding Mechanism with Privacy Protection in Edge Computing

1  Introduction

With the development of the Internet of Things (IoT), computation-intensive applications (e.g., virtual reality, face recognition, and online games) are developing rapidly. The continuous improvement of quality of service (QoS) for users and the development of related applications have resulted in high computing performance and low latency requirements for the IoT [1]. Edge computing is a distributed architecture that is close to users and therefore provides faster service than cloud computing [2]. Edge providers are rich in resources with low latency and widely rented by IoT users [3]. Therefore, how to rent edge resources at a reasonable price has become a computational economic problem [4].

Resource bidding is the first problem to be resolved in the edge resource transaction. Generally, multiple providers are competitive, because edge users can choose various combinations of edge providers according to different edge resource attributes. For edge providers, the benefits are determined by the bidding price and the number of edge resources that are traded. For edge users, their benefits are related to their tasks with different complexity, size, and latency [5]. Hence, how to price reasonably to maximize the benefits for edge users and providers is challenging. The bidding problem of edge providers is similar to the bin packing problem [6], which is NP-hard and cannot get an optimal solution in polynomial time. So, the edge resource transaction between multiple providers and users can be regarded as a typical non-cooperative game [7]. A price equilibrium point lies in the non-cooperative game model to maximize the benefits for edge providers and users.

Another important issue to be aware of in edge resource transactions is the potential disclosure of commercially sensitive information, such as provider costs and previous transaction data. The transaction information of edge resources is collected by third-party agents that are reliable and won’t leak the participants’ private information [8,9]. However, these agents are honest-but-curious about their users [10]. They may snoop on the privacy of transaction participants and might obtain such private information. Most of the existing privacy protection models used by third-party agents for data publishing are vulnerable to attacks [11,12]. Therefore, it is necessary to establish a new secure edge resource bidding system to effectively combine information protection and benefit optimization in the resource transaction process.

To overcome the above issues, this paper constructs a secure edge resource bidding mechanism named Dynamic Multi-attribute Resources Bidding Mechanism (DMRBM). It not only protects the sensitive information of edge users and providers, but also helps edge providers price appropriately. As a result, both edge providers and users can maximize the benefits while meeting the users’ needs.

The DMRBM consists of a privacy protection part and a dynamic multi-attribute edge resource bidding part. On the one hand, the privacy protection part combines sampling [13] and differential privacy [14] to protect the information of edge providers and users. Compared to the existing resource bidding mechanism [8,15], our proposed mechanism reduces the computational complexity with the sampling strategy, and improves the privacy protection level as well as the performance with the differential privacy strategy. On the other hand, on the premise that the sensitive data of both providers and users are protected, the prices of providers fluctuate within a certain range. Therefore, a dynamic pricing strategy for multi-attribute resources is proposed in this paper. First, in order to normalize the QoS of providers, multi-attribute values are mapped into the same dimension and combined these values according to the user’s preferences. Second, since the price of one edge provider changes dynamically with the prices of users and other edge providers, two evaluation functions are proposed, i.e., PPR and LPR. These two evaluation functions maximize for users and edge providers by selecting appropriate edge providers in resource transactions. Then, the users combine the results of two evaluation functions by a weighted method, according to their preferences. Finally, the approximate optimal solution is calculated based on the game theory [16,17].

Our main contributions are listed as follows:

•   Based on the dynamic characteristics of prices of different edge providers and different user demands, a dynamic multi-attribute edge resource bidding mechanism is designed to achieve reasonable prices. Furthermore, this paper approximately computes the maximum benefits based on game theory by conducting the evaluation functions of providers, including PPR and LPR.

•   Differential privacy method is used to prevent information leaks. The average benefits of the privacy protection mechanism are 12% higher than that without the protection mechanism.

•   Non-cooperative game is constructed between providers and users. It proves that the generated prices sequence from our resource bidding mechanism is convergent and it approaches the Nash equilibrium solution.

The rest of the paper is organized as follows. Section 2 introduces some related work. Section 3 analyzes the system model and the problem that should be solved. Section 4 designs the details of the proposed DMRBM. In Section 5, we list extensive experiments and make comparisons. Finally, our conclusions are discussed in Section 6.

2  Related Work

We make a brief summary and analysis of the work related to two topics: (1) the edge computing resource bidding; (2) the security issues in edge computing.

As for resource bidding, there are many game models to get the maximum benefits for both edge providers and users, such as Bilateral market game [18,19], Stackelberg game [20], Maximize game [21], etc. When it comes to competitions, the models can be divided into the following three categories. Zhang et al. [20] used a multi-provider single user model, aiming at increasing the demand and the benefit for a single user, and multiple providers bid to achieve a price equilibrium. Begam et al. [22] considered a multi-user pricing model for revenue generation. In view of the inappropriate behaviors in bidding, Xie et al. [19] employed a method of increasing the punitive function to adjust the price, so as to improve the fairness and trustworthiness of the game. Guo et al. [23] proposed a novel trust evaluation method by integrating the comparison of true utility and expected utility in auction mechanism. However, a common shortcoming of the aforementioned work is that they failed to cope with the information security issue, e.g., price protection by edge providers and information leaks by a third-party agent. Therefore, these models remain vulnerable to opponents. From a practical point of view, it is increasingly insecure about releasing real information.

The information security problem attracts many researchers. Some encryption algorithms are indeed very popular in the field of information security. You et al. [24] made a summary of some common security protection models. Ram et al. [25] protected data through data encryption and distribution. Gu et al. [26] studied the privacy of data transmission between multi-edge nodes and end-users. But in the field of big data, encryption and decryption methods face long delays. Their computational complexity cannot meet the demand of real-time performance. Approximate computing can reduce design complications with an increase in performance and efficiency for error-resilient applications [27]. A trust-based multi-agent imitation learning (T-MAIL) scheme was proposed in [28]. To avoid encryption/decryption delays, an approximate computing method was introduced [29]. Lei et al. [30] used approximate dynamic programming techniques to solve joint computing offload and multi-user scheduling problems. Derbeko et al. [31] suggested the sampling of an approximate computing as a method of improving computational performance. Wang et al. [32] proposed a novel verifiable multi-dimensional (t,n) threshold quantum state sharing scheme to overcome the shadow attack.

Apart from encryption algorithms, other approaches are explored in the field of information security. Blockchain technology can be used for privacy protection in [33]. Huo et al. [34] summarized the privacy issues in a cloud/edge-based industrial IoT system. An efficient and privacy-protected VANETs data offload scheme based on the concept of edge computing is proposed in [35]. They explored certain approaches to ensure information security in the process of edge resource reservation. But they failed to take the numerical characteristics of information into consideration and the operation was complicated. A mechanism is heuristically introduced to ensure information security by differential privacy [36].

3  System Model and Problem Formulation

In this section, the entities of the resource bidding system in edge computing are initially described. Then, this paper analyzes the way of bidding information leakage in edge computing. Finally, this paper integrates the optimization objectives of edge resource bidding.

3.1 System Model

The edge providers have many types of resources and each provider’s resource capacity is limited. Since the user requirements tend to be met by multiple edge providers, to simplify the model complexity, this paper first considers the system with only transactions among a single user and multiple providers.

Edge Providers: The resource attributes are represented by matrix K:

K=[k1,1⋯k1,K⋮⋱⋮kn,1⋯kn,K](1)

n denotes the total number of providers and K represents the total number of the edge resources’ attributes. This paper assumes that p={p1,⋯,pn,⋯,pN}, where pn represents the n-th edge provider’s initial prices. h={h1,⋯,hn,⋯,hN} is regarded as the costs of all edge providers, where hn stands for the cost of n-th edge provider. It is easy to know that the prices must be higher than the costs of edge providers, i.e., pn≥hn,∀n∈N. Q={Q1,⋯,Qn,⋯,QN} refers to the QoS of the edge providers.

Aggregator: Each aggregator corresponds to a single user and E edge providers. The process in the aggregator is as follows. First, the edge providers deliver their information (e.g., price, QoS, and cost) into the aggregator. Second, these providers compete in the aggregator in the non-cooperation game theory. Then the aggregator will choose the appropriate providers aiming to maximize the benefits for the user and the providers when these providers meet the user’s requirements. Finally, the aggregator returns the competition results to the user and providers.

User: The user chooses edge resources from N providers, considering K attributes of the resources. p¯,t and Z represent the maximum acceptable prices for the user and the user’s benefits when it has accomplished its jobs and its QoS demand, respectively. The user can purchase multiple attributes of multiple edge providers in combination.

Fig. 1 depicts a user’s resource combination process based on multiple edge providers. Each provider has different resources in practice. For the convenience of drawing and describing, this paper supposes that each provider has only one unique resource, e.g., the edge provider EP1 has a unique resource S1. Depending on whether the provider is selected or not, there are 256 ways to combine providers’ resources, and the user chooses the most beneficial one. For example, there are 5 selected edge providers, each provider has 3 different attribute resources, different costs, and different prices. The user will choose the combination of edge providers to meet its requirement and keep costs as low as possible. It may cause privacy leakage in the bidding process of edge resources. For example, when the aggregators make requests to edge providers and users, the edge providers and users can be attacked, resulting in privacy leakages. Besides, the aggregators receive responses from edge providers and users, and may share information about edge providers and users with other users or aggregators for monetary purposes (e.g., advertising). Similarity attacks and knowledge background attacks are often encountered in bidding. The attackers can infer the private information that can affect the result of resource bidding through unimportant information.

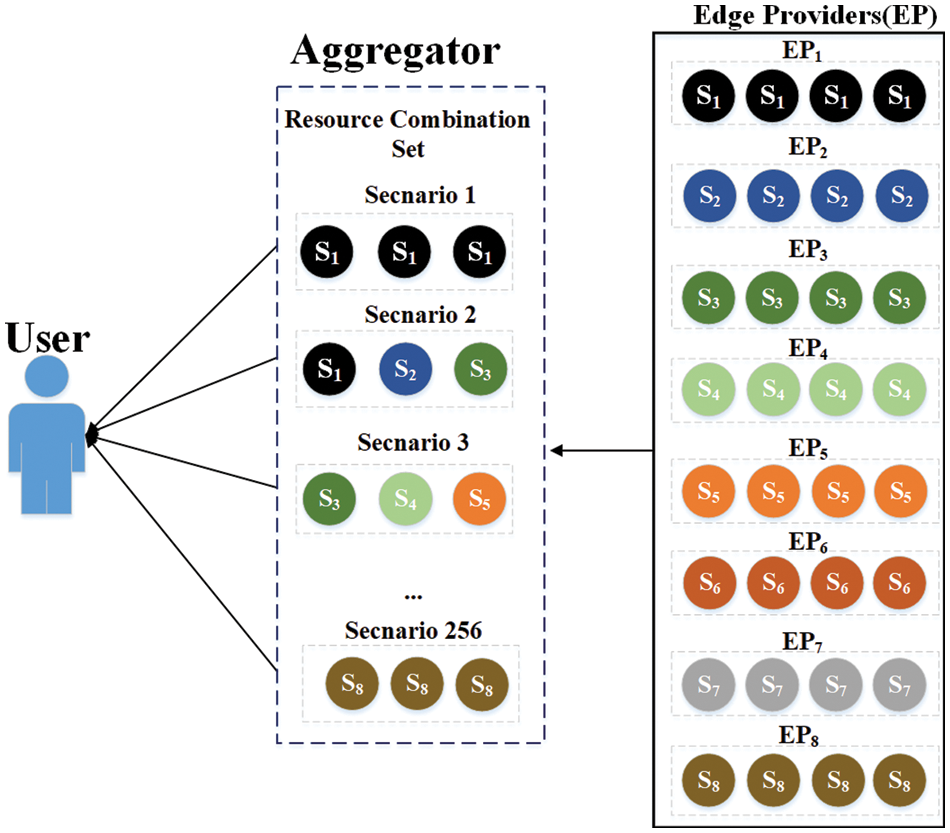
Figure 1: Combination process of multiple edge providers’ resources

3.2 Problem Formulation

The total benefits for the user are determined by the benefits from completing tasks and the cost of purchasing resources from edge providers. So, this paper detects the total benefits for the user by:

U=t−∑n=1NynWnpn∗(2)

where yn, Wn and pn∗ respectively represent the decision of whether the EPn is purchased by the user, the QoS which is provided by EPn and the optimal price of EPn when it is purchased by the user.

The benefit for the edge provider EPn is defined as:

πn=ynWn(pn∗−hn)(3)

The optimization objectives could be expressed as:

max U

max πn,∀n

s.t. C1:pn∗>hn

C2:Wn≤Qn

C3:yn∈{0,1}(4)

The restrictions C1, C2, and C3 represent the price restriction, the resource restriction, and the decision restriction, respectively.

4  Algorithm Design

In this section, this paper considers the whole process of creating a fair resource bidding mechanism with privacy protection. Since it is NP-hard to directly solve the maximum benefit problem, the approximate maximum benefit for edge providers and the user is calculated by approximate computing. This paper first designs a DMRBM based on a game theory in 4.1. It is noticed that when edge providers and users trade with third-party agents, their sensitive information is easy to be leaked. Therefore, in the bidding mechanism, this paper adopts the privacy protection algorithm which is composed of sampling and differential privacy to prevent sensitive information leakage caused by third-party agents. The privacy protection algorithm is depicted in 4.2.

The architecture of DMRBM is shown in Fig. 2. First, this paper calculates the QoS of edge providers through expert preference. Afterward, this paper designs a privacy protection algorithm. Next, the initial provider combination is selected according to the user’s preference for resource attributes. Each provider adjusts the optimal price through the non-cooperative game. Finally, when all the prices of providers tend to be stable, the user makes the final purchase decision and the providers set the prices according to the purchase decision.

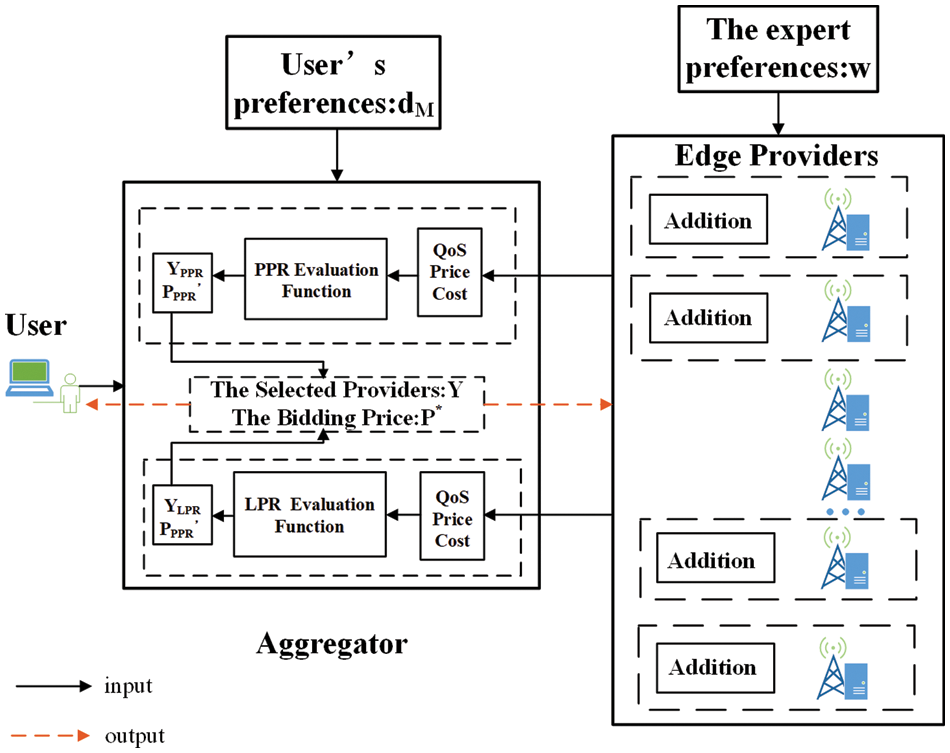
Figure 2: Architecture of DMRBM

4.1 Dynamic Multi-Attribute Resource Bidding Mechanism

The QoS value of the edge provided to the user is determined by the values and the expert preference of multiple attributes. This paper normalizes the attributes using feature scaling, and all the values lie into [0,M]:

ki,j′=M⋅ki,j−min{k⋅,j}max{k⋅,j}−min{k⋅,j}(5)

min{k⋅,j} and max{k⋅,j} are minimum and maximum of all providers’ j-th attribute values, respectively. This paper uses simple addition weighting (SAW) [37] to perform the comparison of quality attributes. The QoS that the provider EPn can provide to the user is:

Qn=∑k∈Kωk⋅kn,k′(6)

ω=(ω1,⋯,ωK) is a K-dimension vector of the attribute preferences for edge resources. This vector meets the condition that ∑k∈Kωk=1,ωk∈[0,1].

To select providers effectively and reasonably, while maximizing the benefits for both providers and the user, the following two evaluation functions are introduced: (1) Price-Performance Ratio (PPR) evaluation function; (2) Lower Price based on Rewards (LPR) evaluation function. It is apparent that choosing the edge provider with the highest cost performance ratio (i.e., PPR) for transaction will bring maximum benefits for the user. To maintain a reasonable and fair competition environment for resources, a better solution is to combine multiple edge providers to conduct transactions while maintaining benefits. Therefore, LPR is proposed for edge providers. First, this paper assumes that the user has a preference dM=⟨i,j⟩, i and j respectively indicating the probability that the user chooses the providers based on the PPR and LPR. Meanwhile, i+j=1. The PPR and LPR evaluation functions are defined as:

PPRe=Qepe(7)

LPRe=μ1pe+(1−μ)ree,μ∈(0,1)(8)

where ree represents the reward given by the system and is determined by the PPR of all selected providers. In detail, ren is directly proportional to its PPR. Thus, the reward of provider n is:

ren=Re⋅PPRn∑e=1NPPRe(9)

where Re is the total reward given by the system. The two evaluation functions evaluate providers from different perspectives, and they are also correlated. The LPR evaluation function focuses on selecting edge providers with a low price but relatively high PPR. The higher the PPR evaluation function value of edge provider n is, the higher the reward ren will be. The higher PPR or LPR is, the more likely the provider will be selected. After determining the evaluation functions, the providers should enhance their competitiveness by adjusting their prices. Here this paper elaborates form the perspective of game theory.

There are E players in the game and each participating provider can be seen as a player. Each player has three elements, i.e., price, QoS, and cost. pE′={p1′,⋯,pe′,⋯,pE′}, QE′={Q1′,⋯Qe′,⋯,QE′} and hE′={h1′,⋯,he′,⋯,hE′} respectively refer to the prices, QoS and costs of all participating providers. Furthermore, this paper lets Yr1={Y1r1,⋯,YEr1} and Yr2={Y1r2,⋯,YEr2}, where Y1r1 and Y1r2∈{0,1}. They indicate the decision sets in the r1-th round and r2-th round of the providers in PPR and LPR respectively. In the two functions, pPPR,e∗ and pLPR,e∗ mean two final prices of providers EPe. If Y1r1=0 and Y1r2=0, the provider EPe does not provide any resources to the user. Otherwise, the provider can provide resources to the user. The game runs by the following steps:

Step 1: Initialize the game. Initialize the price pe′, QoS Qe′, the cost he′ by Algorithm 2 for privacy protection and set the initial Ye0=1 for each provider EPe.

Step 2: Calculate the critical price. Calculate the PPR value by Eq. (7). The critical price is the optimal price for providers in the current state and it refers to the price at which a provider can get the maximum benefit when the price and QoS of other providers are determined. If the price performance of the provider is at an average level of the price performance of all alternative providers, the price of the provider is at a critical price. The provider EPe adjusts the price according to the average PPR value of other providers. Then, the critical value pPPR,er1 for PPR function in the r1-th round of EPe is defined by:

pPPR,er1={p¯,pPPR,er1>p¯|Yr1−1∖{e}|Qe′∑yϵYr1−1∖{e}PPRy,he′≤pPPR,er1≤p¯0,Yer1=0(10)

If pPPR,er1>p¯ or he′>pPPR,er1, EPe will be withdrawn from the PPR game and Yer1=0. If not, Yer1=1. For example, there are 5 edge providers, these providers’ QoS, prices, and costs are Q′={10,20,25,30,15}, p′={10,10,20,10,20}, h′={5,3,10,20,8}. This paper calculates the critical price pPPR,11 in the first round. The average PPR of other providers ∑e∈{2,3,4,5}PPRe4=1.75. Thus, pPPR,11=Q1′1.75=5.71. Due to pPPR,11>h1′, this paper considers the critical price to be feasible.

Since the reward ree can be fixed according to PPRe, this paper regards the reward as a fixed amount. If the price of a provider is at an average level of the prices of all optional providers, the price of this provider is also at a critical price. To reasonably improve the LPR value and get more benefits, EPe alters the price pLPR,er2 based on the prices of other providers. Calculate the critical price pLPR,er2 by:

pPPR,er2={p¯,pPPR,er2 > p¯∑y∈Yr2−1\{e}pLPR,yr2−1'|Yr2−1\{e}|,he '−ree≤pLPR,er2≤p¯0,Yer2=0(11)

If the price he′−ree>pLPR,er2 or pLPR,er2>p¯, the player EPe will be withdrawn from the game and Yer2=0. In neither cases, Yer2=1.

Step 3: Make the final price and strategy. Compute all the players’ prices iteratively. This process will not end until the prices pPPR,er1 and pPPR,er2 no longer change with each EPe and the players no longer change in the nearest two iterations. In each iteration, compute the critical price by Eqs. (10) and (11) separately. The iteration will end when Yr1=Yr1−1, ||pYr1−pYr1−1||≤G, Yr2=Yr2−1 and ||pYr2−pYr2−1||≤G are met. The solutions pPPR,er1 and pLPR,er2 are unique, and the user can choose multiple providers to purchase resources and complete the tasks.

After circling the three steps, the aggregator will get the results Yr1,Yr2,pPPR∗ and pLPR∗. In the bidding process, this paper comes up with a method to calculate the proper price pE∗, as the combination of pPPR,e∗ and pLPR,e∗ for EPe. A final decision profile Y={Y1,⋯,YE} for the user is defined as:

Ye={1,Yer1=1orYer2=10,otherwise(12)

where We is composed of WPPR,e and WLPR,e. They represent QoS transactions between the user and the provider EPe based on PPR and LPR. WPPR,e and WLPR,e are defined as:

WPPR,e=Yer1Qe′ZpPPR,e∗∑y∈Yr1PPRy⋅i

WLPR,e=Yer2Qe′ZPLPR,e∗∑y∈Yr2PPRy⋅j(13)

where Z means the user’s QoS demand. Since the strategy Y has been determined, this paper can measure the synthetical prices of the providers with the user’s preference by:

pe∗={i⋅pPPR,e∗+j⋅pLPR,e∗,Ye=10,otherwise(14)

where i and j indicate the probability that the user chooses the providers based on PPR and LPR. The total benefits of the player EPe are composed of π(Yer1,Y(−e)r1) and π(Yer2,Y(−e)r2), which represents the benefits of the two evaluation functions respectively. The benefits of the two evaluation functions are denoted as:

π(Yer1,Y(−e)r1)=WPPR,e(pPPR,e∗−he′)

π(Yer2,Y(−e)r2)=WLPR,e(pPPR,e∗−he′+ree)(15)

:

This paper designs Algorithm 1 to solve the resource transaction problem in dynamic multi-attribute resource bidding. In this algorithm, the critical prices pPPR∗ and pLPR∗ are first calculated based on the game theory. Then, the decision Y, We and the benefits can also be calculated. The original data of edge providers and the user in Algorithm 1 is the output of Algorithm 2 after privacy protection processing.

4.2 Privacy Protection Algorithm

As a secure design, this paper takes some measures to protect private information during the bidding process. The edge providers’ cost is taken as an example for detailing privacy protection operations.

4.2.1 Sampling Edge Providers

There are many combinations of providers and their resource attributes. This paper chooses providers that respond to user requirements through sampling. Sampling is an approximate computing method. The reasons for sampling are threefold: (1) The sampling protects the information of providers who are not sampled. (2) Too many providers participating in the bidding would lead to high complexity and long computing time. The sampling of providers can help avoid this issue. (3) The sampling proportion of providers can be changed according to the demand. One important feature of simple random sampling (SRS) is that each sample has the same probability of being picked. SRS is fair, so this paper applies it to N edge providers to select E providers that will participate in the next process according to the sampling parameter s. This paper sets up a response group in EPn,resn=⟨pn,Qn,hn⟩and defines the SRS decision profile x={xn},n∈N,xn∈{0,1}.EPn is chosen by the user if and only if xn=1. The information of these selected providers will be stored locally.

4.2.2 Differential Privacy

Edge providers selected though the SRS process adopts the differential privacy technology to protect their privacy. Normally, people do not want to answer sensitive questions. In cases where necessary information must be provided, vague items may be employed. Differential privacy is a method to protect information privacy by increasing noise. Considering the trade-off between data privacy and players’ benefits, the parameter p can be calculated by uniform noise mechanism and discrete Laplacian mechanism [38]. The process of differential privacy works for one of the elements of resn, such as pn, which is as follows. First, generate a parameter p∈(0,1). Then, add the “noise”. If the number is less than p, the provider responds with the true answer to the sensitive question, i.e., the price pn. Otherwise, the provider offers a wrong answer which adds a noise value vn to pn. v is subject to Laplace distribution with scale parameter Sf/ε where Sf is the query sensitivity function:

pn′=pn+vn(16)

pn′ means the response price of EPn. It is proved that the privacy mechanism has achieved ε-differential privacy [39]. Consider that a database produces transcript U on the set of queries G={G1,⋯,Gq}, and let ε>0 be an arbitrarily small real constant. Transcript U satisfies ε-differential privacy that every pair of sibling datasets (D1,D2) meets |D1|=|D2|, while D1 and D2 differ in only one record, which holds that:

lnPr[GD1=U]Pr[GD2=U]≤ε(17)

The privacy budget ε specifies the amount of protection required, with smaller values corresponding to stricter protection. More importantly, after sampling and differential privacy processing, a higher degree of privacy protection can be achieved, named Zero-Knowledge privacy [40]. Meanwhile, as more data are collected, it can statistically eliminate the impact of probabilistic perturbations on overall. This privacy mechanism using probability s achieves εZK privacy, which means that:

εZK=ln(s⋅ε2−s1−s+1−s)(18)

To protect the privacy of the user and edge providers, this paper designs Algorithm 2. Its input is {N,KN,IK∗,ωK,s,p,λ}, where N represents the set of all the providers, KN is the set of all the providers’ attributes, IK suggests the importance of the attributes, s indicates the sampling proportion of the providers, p embodies the degree of differential privacy, and λ is the Laplace parameter. We can see that the complexity of Algorithms 1 and 2 are O(αE2) and O(N), respectively.

5  Experiments

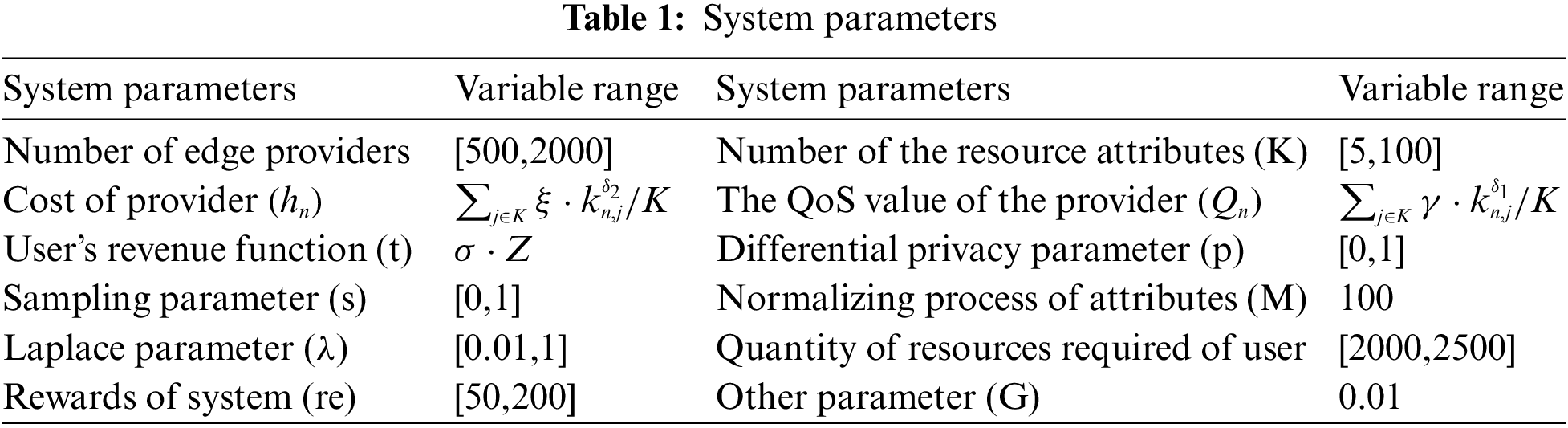
In the simulation, this paper considers the scenario in which a user can jointly purchase resources from hundreds of edge providers deployed in various network infrastructures. The idle resources’ types and numbers of the edge providers are limited. The benefit of the user to complete the tasks is fixed. The unit price of resources provided by each edge provider cannot exceed its cost. However, the unit cost of the same attribute resources may differ among edge providers. Each provider has idle resources, where the maximum value of idle resources owned by each provider varies from 0 to 100. Table 1 depicts the parameters of our secure edge resource bidding mechanism, and parts of them are referred to [41].

5.1 Effect of DMRBM

This paper evaluates the algorithm from three aspects: convergence, benefits of edge providers and the user, and the influence of privacy protection. Our experiment is based on the parameters in Table 2.

5.1.1 Convergence of DMRBM

The experiment is based on the 100 providers selected from 1000 providers through the privacy protection process. This paper describes how the prices of 10 edge providers change with the number of iterations and the results based on the PPR and LPR corresponding to Fig. 3 are not correlated.

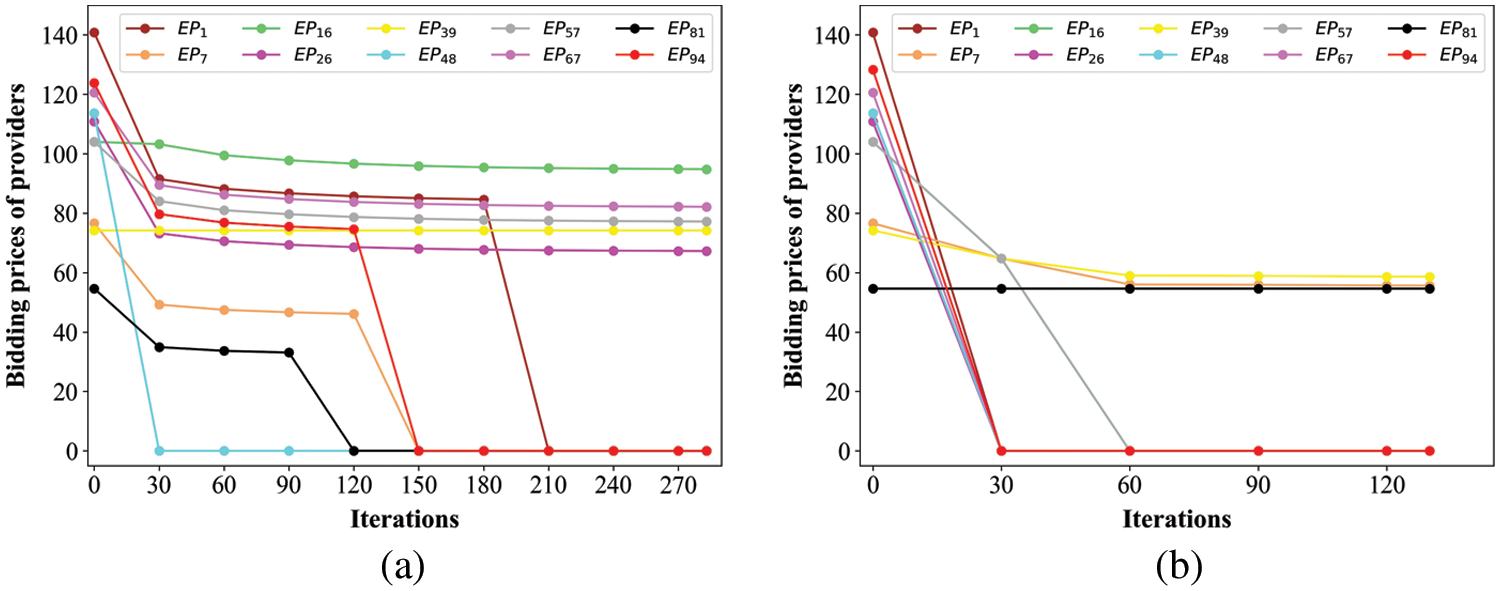
Figure 3: (a) Prices with PPR and (b) prices with LPR

Fig. 3 shows the convergence process of bidding prices by the PPR and LPR evaluation functions in Algorithm 1. As the number of iterations increases, the bidding price decreases. Interestingly, these figures indicate that the providers’ prices will reach a stable state, either 0 or the critical price pe∗. Furthermore, some providers withdraw the bidding when the condition satisfies pe∗<he in PPR and pe∗<he−ree in LPR. In Fig. 3b, we can find that the final prices of different providers are very close, but not exactly equivalent. This is due to the different rewards ree of each edge provider. And the sublinear convergence of pE∗ and sequence pE.

5.1.2 Benefit Analysis between the User and N Edge Providers

The sums of the providers’ and user’s benefits are depicted in Fig. 4. It is most surprising that comparing the results of different sampling parameters (s = 0.9 and s = 1), there is a large increase in the user and a large decrease in the edge providers. There is a greater chance for the bidding based on all the providers to choose the better provider for the user than the bidding based on part providers.

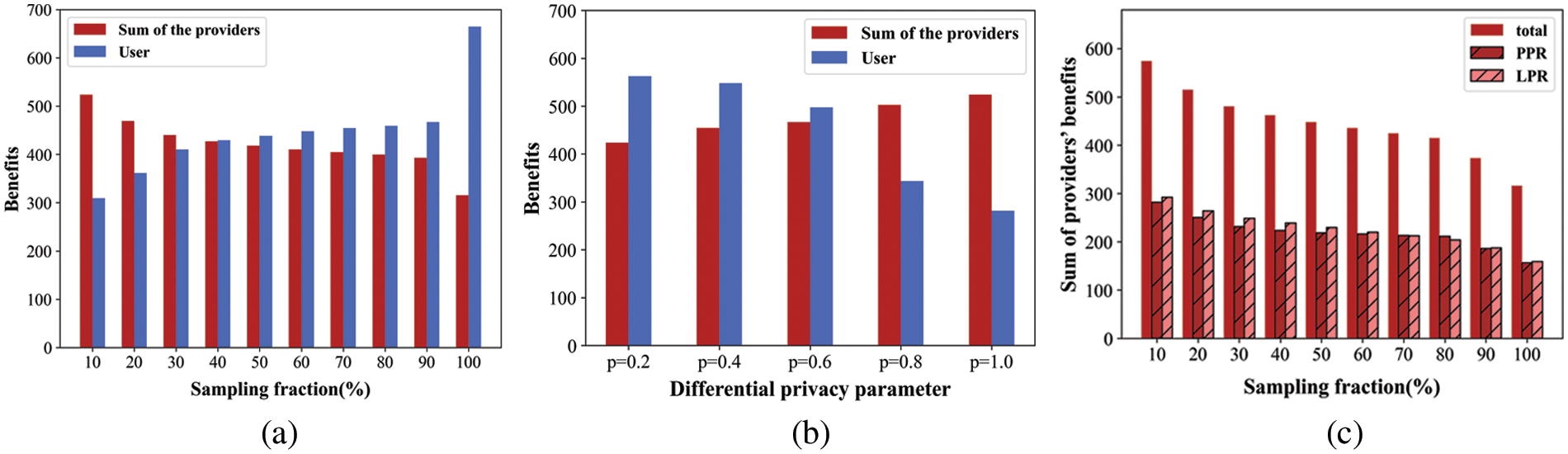
Figure 4: (a) Benefits of providers and user by different sampling fractions, (b) benefits of providers and user by differential privacy parameter p with s = 10%, and (c) benefits of two evaluate functions

Fig. 4a analyzes the influence of the number of providers on the total benefits. We can see that as the number of edge providers increases, the gross benefits of the providers decline and the user’s benefit increases. Fig. 4b illustrates that the differential privacy parameter p has a significant impact on the total benefits. The lower p means that the information used to compete deviates more from the initial information, and the larger p means that the information used to compete deviates less from the initial information. More surprisingly, when p is lower, the prices of the information after sampling will be closer to those before sampling. Fig. 4c demonstrates the sums of the providers and the benefits of the game based on the two evaluation functions separately. The user has the same preferences, which means i = j = 0.5. The benefits of the game based on LPR evaluation function are composed of two parts: the benefits of lower prices and the benefits of rewards. It is indicated that the benefits of only the pricing game are less than the benefits of a game based on PPR.

5.1.3 Performance Comparison of the Benefits

For fairly comparison, this paper uses two common resource pricing algorithms, CTOPD and PG-RL, respectively. The centralized task offloading and payment determination mechanism (CTOPD) is proposed by [42], which designs a centralized stable matching algorithm to make decisions on task offloading and the payment, but it only considers the stability of task offloading. The policy gradient (PG)-based reinforcement learning (RL) algorithm is proposed by [43], which enables continuous pricing, but it may overfit.

In the first simulation, this paper fixes the number of providers, N = 100. As shown in Fig. 5a, it is observed that the average benefits achieved by DMRBM are always higher than those achieved by the two comparison algorithms. Particularly, CTOPD only considers the match stability, it achieves the lowest benefits. In addition, PG-RL relies too much on historical information, which causes the average benefits to be lower than those of DMRBM. In the second simulation, this paper investigates the benefits that can be achieved by users and providers. Specifically, this paper fixes the number of users, while varying the number of providers from 20 to 100. As shown in Fig. 5b, this paper presents the system’s user benefits. It is shown that with the increase in the number of providers, the average benefits of the users increase. This is reasonable. With more providers in the system, the users have more chances to buy the resources to gain higher benefits.

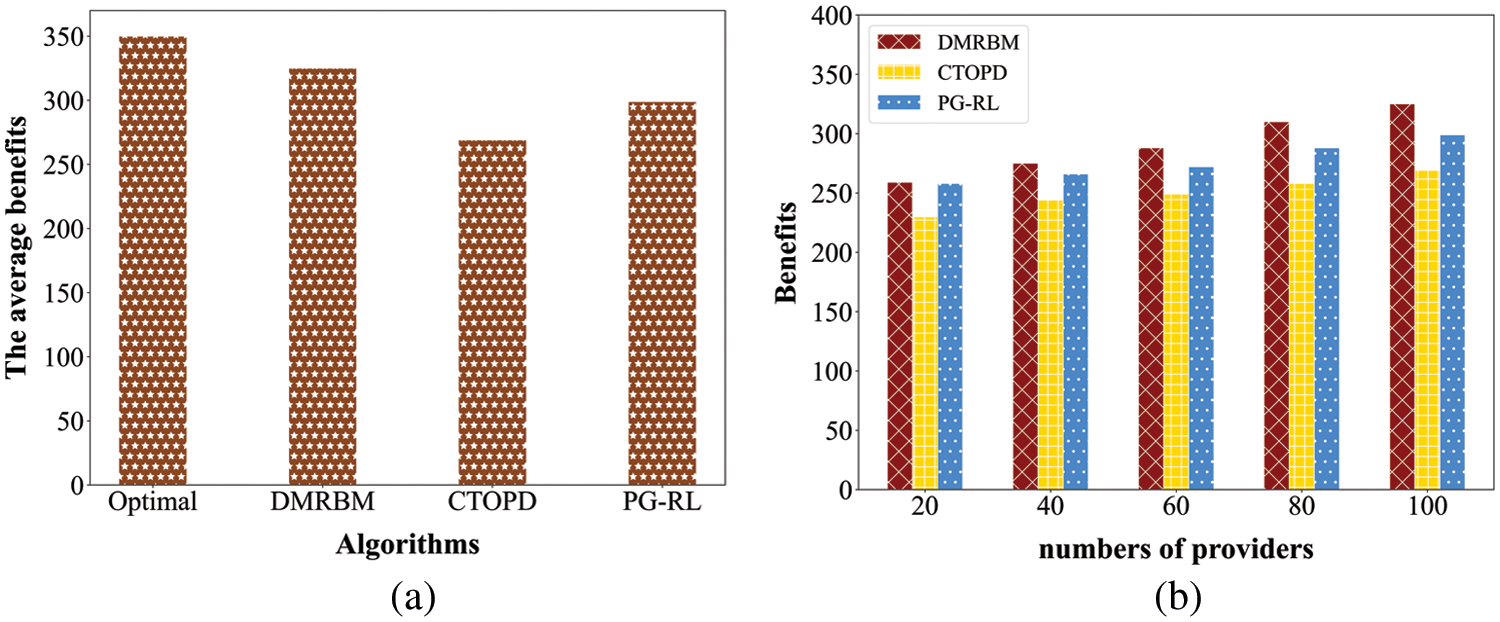
Figure 5: (a) The comparison on benefits and (b) benefits with numbers of providers

5.1.4 The Rewards of LPR

As mentioned above, we know that for the same QoS demands, the game based on PPR can get the highest benefits, so this paper needs to consider the benefits bought by a lower price and a reward respectively in the game based on LPR. As we can see from Fig. 6a, the benefits of a game based on lower prices outweigh those based on the rewards. Their benefits tend to be stable as the sample fractions increase. Although the total benefits decrease, the number of providers increases greatly, which corresponds to the expectations. As we can see from Fig. 6b, DMRBM increases the number of selected providers on the condition that the benefits of edge providers and users are maximized. The number of selected providers is greater than that of selected providers based on the PPR game or based on LPR game alone. Additionally, this paper finds that there are no inescapable links between the number of selected providers and the growth of sample fractions, nor do they inevitably increase one another.

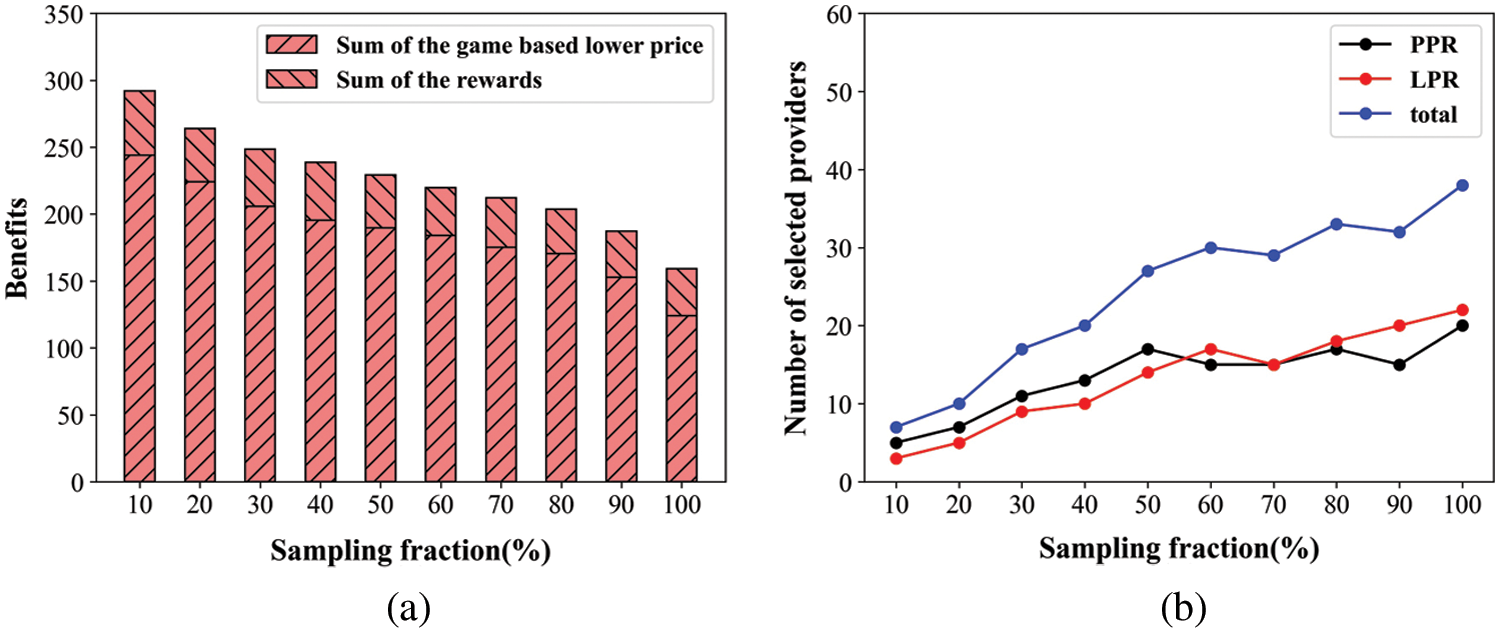
Figure 6: (a) Rewards of LPR with sampling fraction and (b) Number of optimal providers by PPR, LPR

5.2 Effect of Privacy Protection Algorithm

This paper evaluates the effectiveness of the privacy protection process from two aspects: the accuracy loss of bidding caused by privacy protection and the degree of privacy protection.

5.2.1 Accuracy Loss of the Sampling and Differential Privacy

There could be a deviation since this paper estimates the total information based on the selected one. This paper calculates this deviation η1=∑n=1Npn−xnpn⋅NE∑i=1Epi′. The accuracy loss η2 represents the proportion of noise in the real value and is then defined as η2=∑i=1E(pi′−pi)2∑i=1Epi′. This paper estimates the impact of the sampling parameter s and differential privacy parameter p on the accuracy loss η1 and η2 respectively in Fig. 7. It depicts the total accuracy loss in the scenario of the ensured s and p in Fig. 7c. Because the total accuracy loss is caused by the sampling and differential privacy, this paper makes separate analyses in line with the losses caused by each step. In Fig. 7a, it first decreases noticeably as the sampling parameter s is gradually increased. This figure shows a steady decrease in the gradual increase of s. Fig. 7b also describes the trend that the more p increases, the less accuracy loss η2 will present. In terms of total accuracy loss, we can see in Fig. 7c that as p increases, the total accuracy loss decreases first and then tends to be stable. The reason is that when the sampling parameter s is relatively small, the sampling accuracy loss is greater. When s is large, the factor that affects the accuracy loss is the operation of differential privacy. Only when the sampling fraction s approaches 1, p has a great impact on the accuracy loss. Fig. 7c is a lateral reflection of Figs. 7a and 7b.

Figure 7: (a) Accuracy loss η1 with sampling parameter s, (b) Accuracy loss η2 with the s, and (c) accuracy loss with sampling and differential privacy parameters

5.2.2 The Privacy Level of the Privacy Protection

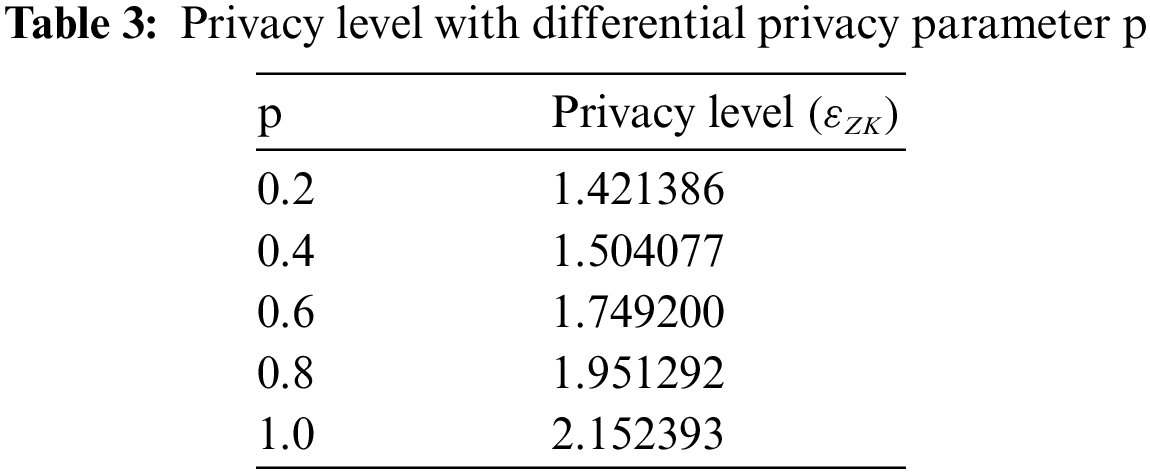
This paper measures the degree of privacy protection εZK after performing sampling and differential privacy. The privacy is measured by the level of achieved zero-knowledge privacy by Eq. (18). In this case, this paper uses the same sampling parameter s = 0.5 to calculate the privacy level of the differential privacy parameter p. Table 3 shows how different p parameter settings affect privacy. The smaller εZK is, the higher the degree of privacy protection will be. This result also fits into the definition of privacy level, which decreases as the probability of truthful answers increases.

6  Conclusion

Our study focuses on edge providers’ resource bidding and privacy security issues in the bidding process. Our aims are to protect the privacy of the edge providers and users and to find reasonable prices in the resource bidding for more diverse edge providers. This paper proposes a secure edge resource bidding mechanism based on approximate computing, differential privacy, and game theory. The combination of these methods makes the competition result of sampled data and differential privacy information become as close as possible to the competition result of real information. At the same time, it can not only protect the edge providers’ private information but also choose the proper providers and reasonable prices through the providers’ two evaluation functions (namely PPR and LPR) in the DMRBM. The feasibility of this mechanism is verified by a large number of simulation results and comparisons with the existing technologies and benchmark schemes.

Funding Statement: This work was supported in part by National Natural Science Foundation of China under Grant No. 62172349, 62032020, and 62172350, the Research Foundation of Education Bureau of Hunan Province under Grant No. 21B0139, the National Key Research and Development Program of China under Grant 2021YFB3101200, Hunan Science and Technology Planning Project under Grant No. 2019RS3019.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

    1. L. He, K. Ota and M. Dong, “Learning IoT in edge: Deep learning for the internet of things with edge computing,” IEEE Network, vol. 32, no. 1, pp. 96–101, 2018. [Google Scholar]

    2. Y. Mao, C. You, J. Zhang, K. Huang and K. B. Letaief, “A survey on mobile edge computing: The communication perspective,” IEEE Communications Surveys & Tutorials, vol. 19, no. 4, pp. 2322–2358, 2017. [Google Scholar]

    3. J. Wang, L. Zhao, J. Liu and N. Kato, “Smart resource allocation for mobile edge computing: A deep reinforcement learning approach,” IEEE Transactions on Emerging Topics in Computing, vol. 9, no. 3, pp. 1529–1541, 2021. [Google Scholar]

    4. F. Li, H. Yao, J. Du, C. Jiang, Z. Han et al., “Auction design for edge computation offloading in SDN-based ultra dense networks,” IEEE Transactions on Mobile Computing, vol. 21, no. 5, pp. 1580–1595, 2020. [Google Scholar]

    5. T. Liu, S. Ni, X. Li, Y. Zhu, L. Kong et al., “Deep reinforcement learning based approach for online service placement and computation resource allocation in edge computing,” IEEE Transactions on Mobile Computing, 2022. https://doi.org/10.1109/TMC.2022.3148254. [Google Scholar]

    6. Y. Nakamura, T. Mizumoto, H. Suwa, Y. Arakawa, H. Yamaguchi et al., “In-situ resource provisioning with adaptive scale-out for regional IoT services,” in 2018 IEEE/ACM Symp. on Edge Computing (SEC), Seattle, USA, pp. 203–213, 2018. [Google Scholar]

    7. Z. Junhui, Y. Tao, G. Yi, W. Jiao and F. Lei, “Power control algorithm of cognitive radio based on non-cooperative game theory,” China Communications, vol. 10, no. 11, pp. 143–154, 2013. [Google Scholar]

    8. W. Lu, S. Zhang, J. Xu, D. Yang and L. Xu, “Truthful multi-resource transaction mechanism for P2P task offloading based on edge computing,” IEEE Transactions on Vehicular Technology, vol. 70, no. 6, pp. 6122–6135, 2021. [Google Scholar]

    9. K. Xiao, W. Shi, Z. Gao, C. Yao and X. Qiu, “DAER: A resource preallocation algorithm of edge computing server by using blockchain in intelligent driving,” IEEE Internet of Things Journal, vol. 7, no. 10, pp. 9291–9302, 2020. [Google Scholar]

  10. T. Liu, H. Guo, C. Danilov and K. Nahrstedt, “A privacy-preserving data collection and processing framework for third-party UAV services,” in 2020 IEEE 19th Int. Conf. on Trust, Security and Privacy in Computing and Communications (TrustCom), Guangzhou, China, pp. 683–690, 2020. [Google Scholar]

  11. C. Piao, Y. Shi, J. Yan, C. Zhang and L. Liu, “Privacy-preserving governmental data publishing: A fog-computing-based differential privacy approach,” Future Generations Computer Systems: FGCS, vol. 90, no. 1, pp. 158–174, 2019. [Google Scholar]

  12. L. Hartmann, “Bounded privacy: Formalising the trade-off between privacy and quality of service,” in Lecture Notes in Informatics (LNI), Bonn: Gesellschaft für Informatik, pp. 267–272, 2018. [Google Scholar]

  13. J. Zhang, S. Pourazarm, C. G. Cassandras and I. C. Paschalidis, “The price of anarchy in transportation networks: Data-driven evaluation and reduction strategies,” Proceedings of the IEEE, vol. 106, no. 4, pp. 538–553, 2018. [Google Scholar]

  14. W. Huang, S. Zhou, T. Zhu and Y. Liao, “Privately publishing internet of things data: Bring personalized sampling into differentially private mechanisms,” IEEE Internet of Things Journal, vol. 9, no. 1, pp. 80–91, 2022. [Google Scholar]

  15. B. Baek, J. Lee, Y. Peng and S. Park, “Three dynamic pricing schemes for resource allocation of edge computing for IoT environment,” IEEE Internet of Things Journal, vol. 7, no. 5, pp. 4292–4303, 2020. [Google Scholar]

  16. W. Sun, J. Liu, Y. Yue and H. Zhang, “Double auction-based resource allocation for mobile edge computing in industrial internet of things,” IEEE Transactions on Industrial Informatics, vol. 14, no. 10, pp. 4692–4701, 2018. [Google Scholar]

  17. R. Berardo and M. Lubell, “The ecology of games as a theory of polycentricity: Recent advances and future challenges,” Policy Studies Journal, vol. 47, no. 1, pp. 6–26, 2019. [Google Scholar]

  18. G. Benita Nancy and J. J. V. Nayahi, “Bidirectional bidding for efficient allocation of multiple resources in clouds,” in 2016 Int. Conf. on Recent Trends in Information Technology (ICRTIT), Chennai, India, pp. 1–8, 2016. [Google Scholar]

  19. K. Xie, X. Wang, G. Xie, D. Xie, J. Cao et al., “Distributed multi-dimensional pricing for efficient application offloading in mobile cloud computing,” IEEE Transactions on Services Computing, vol. 12, no. 6, pp. 925–940, 2019. [Google Scholar]

  20. H. Zhang, Y. Xiao, S. Bu, D. Niyato, F. R. Yu et al., “Computing resource allocation in three-tier IoT fog networks: A joint optimization approach combining stackelberg game and matching,” IEEE Internet of Things Journal, vol. 4, no. 5, pp. 1204–1215, 2017. [Google Scholar]

  21. M. Yu, A. Liu, N. N. Xiong and T. Wang, “An intelligent game-based offloading scheme for maximizing benefits of IoT-edge-cloud ecosystems,” IEEE Internet of Things Journal, vol. 9, no. 8, pp. 5600–5616, 2022. [Google Scholar]

  22. R. Begam, W. Wang and D. Zhu, “TIMER-Cloud: Time-sensitive VM provisioning in resource-constrained clouds,” IEEE Transactions on Cloud Computing, vol. 8, no. 1, pp. 297–311, 2020. [Google Scholar]

  23. J. Guo, G. Huang, Q. Li, N. N. Xiong and S. Zhang, “STMTO: A smart and trust multi-UAV task offloading system,” Information Sciences, vol. 573, no. 1, pp. 519–540, 2021. [Google Scholar]

  24. X. Z. You and S. Zhang, “A kind of network security behavior model based on game theory,” in Int. Conf. on Parallel & Distributed Computing, Chengdu, China, pp. 950–954, 2003. [Google Scholar]

  25. C. P. Ram and G. Sreenivaasan, “Security as a Service (SasSSecuring user data by coprocessor and distributing the data,” in Trendz in Information Sciences & Computing (TISC2010), Chennai, India, pp. 152–155, 2010. [Google Scholar]

  26. B. Gu, L. Gao, X. Wang, Y. Qu, J. Jin et al., “Privacy on the edge: Customizable privacy-preserving context sharing in hierarchical edge computing,” IEEE Transactions on Network Science and Engineering, vol. 7, no. 4, pp. 2298–2309, 2020. [Google Scholar]

  27. M. Ramasamy, G. Narmadha and S. Deivasigamani, “Carry based approximate full adder for low power approximate computing,” in 7th Int. Conf. on Smart Computing & Communications (ICSCC), Harbin, China, pp. 1–4, 2019. [Google Scholar]

  28. P. Zeng, A. Liu, C. Zhu, T. Wang and S. Zhang, “Trust-based multi-agent imitation learning for green edge computing in smart cities,” IEEE Transactions on Green Communications and Networking, vol. 6, no. 3, pp. 1635–1648, 2022. [Google Scholar]

  29. W. Yang and H. Thapliyal, “Approximate adiabatic logic for low-power and secure edge computing,” IEEE Consumer Electronics Magazine, vol. 11, no. 1, pp. 88–94, 2022. [Google Scholar]

  30. L. Lei, H. Xu, X. Xiong, K. Zheng and W. Xiang, “Joint computation offloading and multiuser scheduling using approximate dynamic programming in NB-IoT edge computing system,” IEEE Internet of Things Journal, vol. 6, no. 3, pp. 5345–5362, 2019. [Google Scholar]

  31. P. Derbeko, S. Dolev, E. Gudes and J. D. Ullman, “Efficient and privacy preserving approximation of distributed statistical queries,” IEEE Transactions on Big Data, vol. 8, no. 5, pp. 1399–1413, 2022. [Google Scholar]

  32. Y. Wang, X. Lou, Z. Fan, S. Wang and G. Huang, “Verifiable multi-dimensional (t,n) threshold quantum secret sharing based on quantum walk,” International Journal of Theoretical Physics, vol. 61, no. 2, pp. 1–17, 2022. [Google Scholar]

  33. M. Dabbagh, K. K. R. Choo, A. Beheshti, M. Tahir and N. S. Safa, “A survey of empirical performance evaluation of permissioned blockchain platforms: Challenges and opportunities,” Computers & Security, vol. 100, no. 1, pp. 102078, 2021. [Google Scholar]

  34. Y. Huo, C. Meng, R. Li and T. Jing, “An overview of privacy preserving schemes for industrial internet of things,” China Communications, vol. 17, no. 10, pp. 1–18, 2020. [Google Scholar]

  35. J. Cui, L. Wei, H. Zhong, J. Zhang, Y. Xu et al., “Edge computing in VANETs-An efficient and privacy-preserving cooperative downloading scheme,” IEEE Journal on Selected Areas in Communications, vol. 38, no. 6, pp. 1191–1204, 2020. [Google Scholar]

  36. L. Gao, S. Deng and W. Ren, “Differentially private consensus with an event-triggered mechanism,” IEEE Transactions on Control of Network Systems, vol. 6, no. 1, pp. 60–71, 2019. [Google Scholar]

  37. G. V. Prasad, A. S. Prasad and S. Rao, “A combinatorial auction mechanism for multiple resource procurement in cloud computing,” IEEE Transactions on Cloud Computing, vol. 6, no. 4, pp. 904–914, 2018. [Google Scholar]

  38. Q. Geng and P. Viswanath, “Optimal noise adding mechanisms for approximate differential privacy,” IEEE Transactions on Information Theory, vol. 62, no. 2, pp. 952–969, 2016. [Google Scholar]

  39. F. Mcsherry, K. Nissim and A. Smith, “Calibrating noise to sensitivity in private data analysis,” Lecture Notes in Computer Science, vol. 3876, no. 8, pp. 265–284, 2012. [Google Scholar]

  40. J. L. Rrushi, “DNIC architectural developments for 0-Knowledge detection of OPC malware,” IEEE Transactions on Dependable and Secure Computing, vol. 18, no. 1, pp. 30–44, 2021. [Google Scholar]

  41. J. Hu, K. Li, C. Liu and K. Li, “A game-based price bidding algorithm for multi-attribute cloud resource Provision,” IEEE Transactions on Services Computing, vol. 14, no. 4, pp. 1111–1122, 2021. [Google Scholar]

  42. X. Wang, J. Wang, X. Zhang, X. Chen and P. Zhou, “Joint task offloading and payment determination for mobile edge computing: A stable matching based approach,” IEEE Transactions on Vehicular Technology, vol. 69, no. 10, pp. 12148–12161, 2020. [Google Scholar]

  43. S. Chen, L. Li, Z. Chen and S. Li, “Dynamic pricing for smart mobile edge computing: A reinforcement learning approach,” IEEE Wireless Communications Letters, vol. 10, no. 4, pp. 700–704, 2021. [Google Scholar]