Numerical Computation of SEIR Model for the Zika Virus Spreading

1  Introduction

The coronavirus is known as one of the quickly spreading diseases. Adequate and appropriate processes and proper treatment are required to avoid its spread and control. To manage the affected population’s probability, the epidemic with the function of therapy is displayed. Prospects reveal how many individuals based on the afflicted classes have gone for the cure. Few of the traditional samples provide the treatment ratios, which are proportional to the affected number of patients [1]. The medical possessions indicate the treatment of such viruses, which are moderately controlled in the whole world [2]. Concludingly, the lack of preparedness and resources for any unexpected outbreak reasons the deaths. The Zika virus was discovered by the Uganda Rhesus macaques group in the mid of the last century [3]. The vectors of the mosquito are responsible for the Zika transmission using the “Aedes”. The clinical indications of the Zika-based virus are familiar to individuals suffering from dengue fever. The progression ratio of dengue fever in the humans between 3 to 12 days. Almost 1/4 individuals suffer a Zika virus infection with the use of its common symptoms [4,5]. The human infection is dangerous during the transplacental transmission or child transfer through mother to kids [6]. Few features of the Zika virus are linked to the Chikungunya virus and dengue [7].

Currently, there is no definitive treatment for the Zika virus with the exclusion of controlling the vectors by using insecticide spray along with the extinguishing habitats of the larval breeds. In recent investigations, pregnant women, particularly present vulnerable to the infection of Zika virus infection [8–10]. The mathematical form of the models has become a growing factor in this work by using disease epidemiology and its control [11–15]. Lee et al. [16] designed a Zika virus model to consider human and vector population dynamics. He concluded the digital investigations to reduce the disease spreading. Sun et al. [17] proposed and discovered a mathematical system based on sheep brucellosis, which is used in the process of proportion and immigration. Li et al. [18] suggested that cattle and sheep use the multiple groups of the brucellosis system to avoid cross-infection with a better way to evade the undulant fever.

Moreover, the researchers considered indirect/direct transmission forms through diseased animals and environmental viruses. The best control policies are vaccination, elimination, reduction in migration, and disinfection. Xing et al. [19] proposed a mathematical model for the avian influenza spread dynamics. Temperature cycling is the primary reason for the sickness and dealers. Alternatively, Sun et al. [20] established the transmission cholera system to highlight the virus dynamics in China. The researcher’s community investigated the increasing immunization coverage rate and the managing environment to prevent disease spreading. Yu et al. [21] presented the sophisticated behavior based on the biological systems due to the numerous limit cycle bifurcation along with the predictor-prey simple system. Li et al. [22] proposed the SIR nonlinear system using the recovery and incidence rates.

The performances of computations are based on the SEIR nonlinear system using the Zika virus spreading through the computational artificial neural networks (ANNs) and the scaled conjugate gradient (SCG), ANNs-SCG scheme. Recently, stochastic solvers have been famous due to the variety of stiff-natured problems [23–25]. The computing solvers have been used to present the solutions of various complicated models, e.g., food supply systems [26], dynamical HIV nonlinear systems [27,28], periodic differential models [29–31], thermal explosion networks [32], a corneal form of the eye surgery model [33,34], smoking dynamical nonlinear system [35] and singular stiff models [36]. The authors are motivated to present the stochastic applications for the SEIR nonlinear system based on the Zika virus spreading. The computing numerical performances are examined in this study using the ANNs-SCG to solve the SEIR nonlinear system of the Zika virus spreading.

1.1 Motivation and Innovative Contributions

A few motivational aspects and novel features of the SEIR nonlinear system based on the Zika virus spreading using the artificial neural networks (ANNs) enhanced by the scaled conjugate gradient (SCG), ANNs-SCG approach are presented:

•   The numerical representations of the SEIR nonlinear system based on the spreading of the Zika virus have been described/presented/analyzed using the ANNs-SCG stochastic solver.

•   Different cases and scenarios of the spreading of the Zika virus have been numerically simulated using the ANNs-SCG stochastic solver for a better understanding of the dynamics.

•   The stochastic solver’s exactness is authenticated by comparing the obtained reference solutions.

•   The values based on the absolute error for each dynamic of the SEIR nonlinear system of the Zika virus spreading have been observed in good negligible ranges by using the ANNs-SCG scheme.

•   The constancy of the scheme is authenticated through the values of state transitions, error histograms measures, correlation, and regression analysis.

1.2 Organization

The other paper parts are presented: Section 2 provides the mathematical model. Section 3 shows the proposed stochastic methodology. Section 4 designates the results and discussions of the model. The conclusions along with future research studies are presented in the final Section.

2  System Model: Nonlinear Zika Virus Dynamics

This section performs both forms of infection based on vector-to-human and human-to-human transmission. This model is categorized based on the total population of the human (NH(y)), vulnerable humans SH(y), exposed humans EH(y), infected humans IH(y), and recovered humans RH(y), i.e., NH(y) = SH(y) + EH(y) + IH(y) + RH(y). The mosquito total population is represented by NV(y), which is given in three vector classes: susceptible SV(y), exposed EV(y), and infected IV(y), i.e., NV(y)= SV(y)+ EV(y) + IV(y). The mathematical form of the model is provided as follows in Eq. (1), while the SEIR nonlinear system based on the Zika virus spreading is tabulated in Table 1 as [37]:

{dSH(y)dy=AH−SH(y)βH(IV(y)+ρIH(y))−μHSH(y),(SH)0=k1,dEH(y)dy=βH(ρIH(y)+IV(y))SH(y)−(χH+μH)EH(y),(EH)0=k2,dIH(y)dy=χHEH(y)−(η+μH+γ)IH(y),(IH)0=k3,dRH(y)dy=−μHRH(y)+γIH(y),(RH)0=k4,dSV(y)dy=AV−βVIH(y)SV(y)−μHSV(y),(SV)0=k5,dEV(y)dy=βVIH(y)SV(y)−(μV+δH)EV(y),(EV)0=k6,dIV(y)dy=EV(x)δV−μVIV(x),(IV)0=k7.(1)

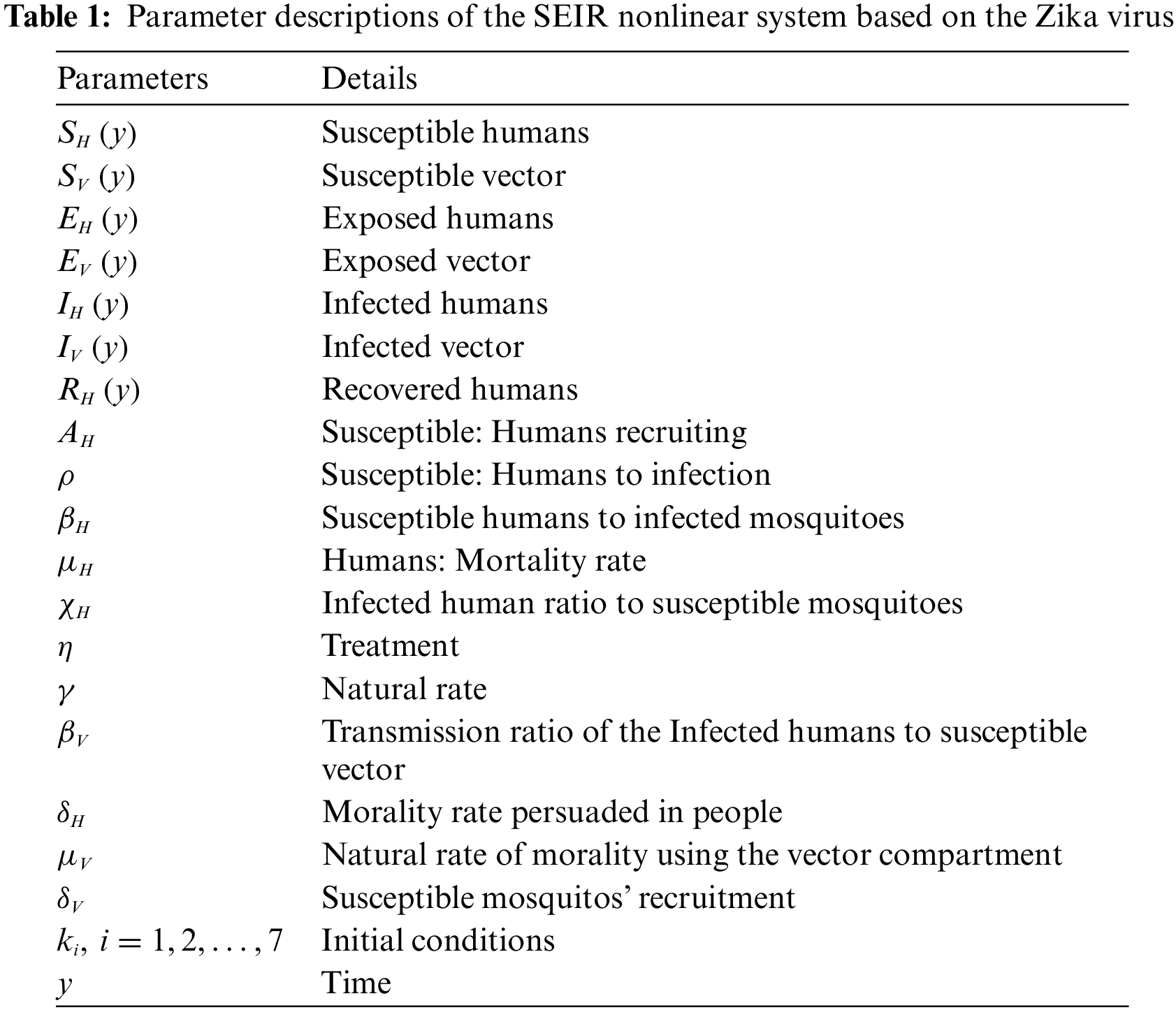
The necessary definitions of the terms in the SEIR nonlinear system (1) based on the Zika virus spreading are tabulated in Table 1 as reported in [37].

While theoretical convergence and further descriptions based on the parametric values using the global and local stability can be seen in the reported study [37] for interested readers.

3  Methodology

The proposed computing scheme for solving the SEIR nonlinear system based on the Zika virus spreading is presented in two phases.

•   The process of the artificial neural networks (ANNs) and the scaled conjugate gradient (SCG), ANNs-SCG computing scheme is provided along with extensive and critical explanations.

•   The numerical representations through the ANNs-SCG computing scheme for the SEIR nonlinear system based on the Zika virus spreading are provided.

A suitable procedure based on the flow structure for the ANNs-SCG computing scheme for the SEIR nonlinear system using the Zika virus spreading is described in Fig. 1. The ANNs-SCG computing scheme is applied through the ‘nftool’ ‘MATLAB’ build-in command with a single hidden layer, single input, and output layer structure, 12 hidden neurons, activation/kernel function of log-sigmoid, n-fold cross authentication with n = 0, 1000 iterations and optimization of the scaled conjugate gradient algorithm for training/learning of ANNs weights. The default stoppage limits, step size, and tolerances are applied to label the data, training for targets and inputs through the standard numerical results. The dataset selection is divided into three parts, 11% for testing, 72% for training, and 17% for validation. The hidden layers and output/input layers are presented for the SEIR nonlinear system based on the Zika virus through the ANNs-SCG shown in Fig. 2.

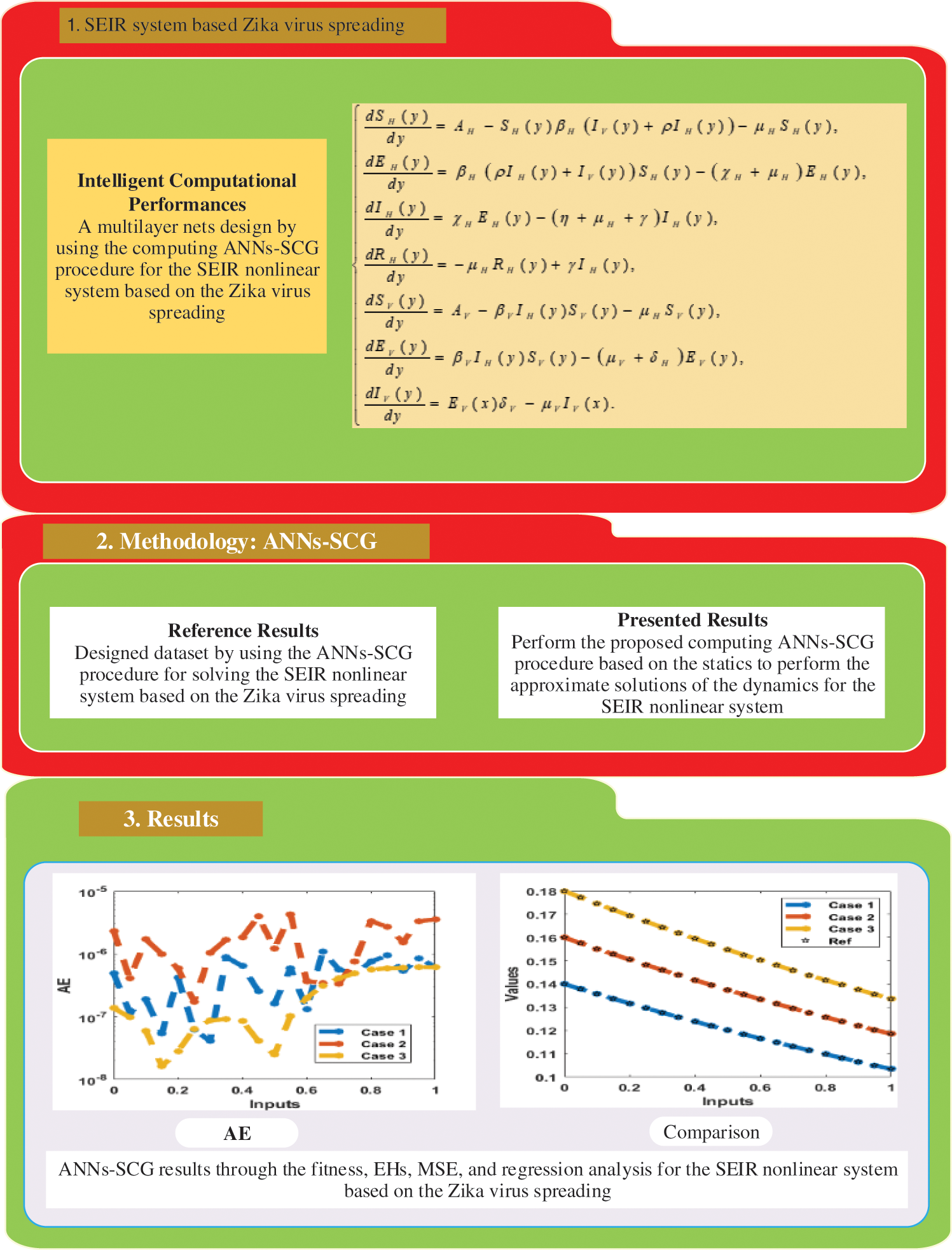
Figure 1: Designed ANNs-SCG procedure for the SEIR nonlinear system based on the Zika virus

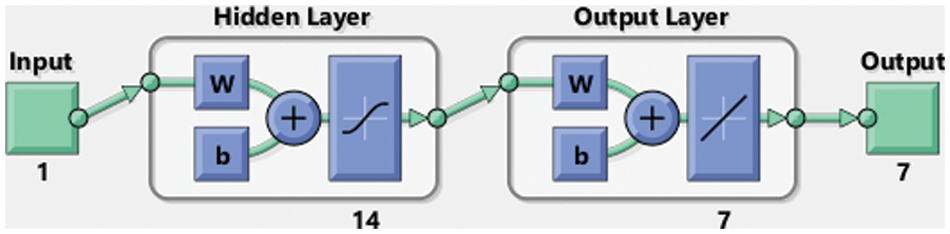
Figure 2: Layer structure of the SEIR nonlinear system based on the Zika virus

4  Numerical Simulations

The numerical explanations are provided for solving the SEIR nonlinear system based on the Zika virus using the stochastic scheme. The mathematical form of the SEIR nonlinear systems is presented in three cases with different sets of initial conditions:

Case 1: Consider the SEIR nonlinear system based on the Zika virus with βH=0.12, AH=0.1, μH=0.1, χH=0.13, ρ=0.14, η=0.15, βV=0.2, γ=0.17, δH=0.22, δV=0.3, μV=0.25, k1=0.1, k2=0.12, k3=0.14, k4=0.16, k5=0.18, k6=0.2 and k7=0.22 is presented as:

Case 2: Consider the SEIR nonlinear system based on the Zika virus with βH=0.12, AH=0.1, μH=0.1, χH=0.13, ρ=0.14, η=0.15, βV=0.2, γ=0.17, δH=0.22, δV=0.3, μV=0.25, k1=0.12, k2=0.14, k3=0.16, k4=0.18, k5=0.20, k6=0.22 and k7=0.24 is presented as:

Case 3: Consider the SEIR nonlinear system based on the Zika virus with βH=0.12, AH=0.1, μH=0.1, χH=0.13, ρ=0.14, η=0.15, βV=0.2, γ=0.17, δH=0.22, δV=0.3, μV=0.25, k1=0.14, k2=0.16, k3=0.18, k4=0.20, k5=0.22, k6=0.24 and k7=0.26 is presented as:

The numerical solutions of the SEIR nonlinear system based on the Zika virus are presented by using the artificial neural networks (ANNs) and the scaled conjugate gradient (SCG), ANNs-SCG with input intervals 0 and 1. Figs. 3 to 7 indicate the graphical performances of the SEIR nonlinear system based on the Zika virus spreading through the ANNs-SCG approach. The capable performances of each dynamic based on the SEIR nonlinear system based on the Zika virus are presented in Fig. 3 by taking the states of transitions and performances. The obtained measures based on mean square error (MSE) using the performances of best curves, authentication, testing, and training are presented in Figs. 3a–3c. The state transitions measures are derived in Figs. 3d–3f for the SEIR nonlinear system based on the Zika virus. The best measures based on different performances to present the solutions of the SEIR nonlinear system of the Zika virus at iterations 23, 30, and 28 were found as 3.60328 × 10−12, 7.17372 × 10−11, and 2.13257 × 10−12. The gradient measures of the SEIR nonlinear system based on the Zika virus, are calculated as 7.7856 × 10−08, 9.0585 × 10−08, and 6.7981 × 10−08. These graphical plots provide the convergence measures, exactness, and accuracy performances of the designed ANNs-SCG approach to solving the SEIR nonlinear system of the Zika virus spreading. The fitting curve performances are presented in Figs. 5a–5c for each dynamic of the SEIR nonlinear system of the Zika virus spreading through the ANNs-SCG. The values based on the maximum error are derived based on the training, authentication, and testing for the Zika virus spreading through the ANNs-SCG. Fig. 4d–4f is provided the SEIR nonlinear system based on the Zika virus spreading using the ANNs-SCG. The EHs performances for respective cases are performed as 2.82 × 10-07, 2.27×10-06, and 2.86×10-07, respectively.

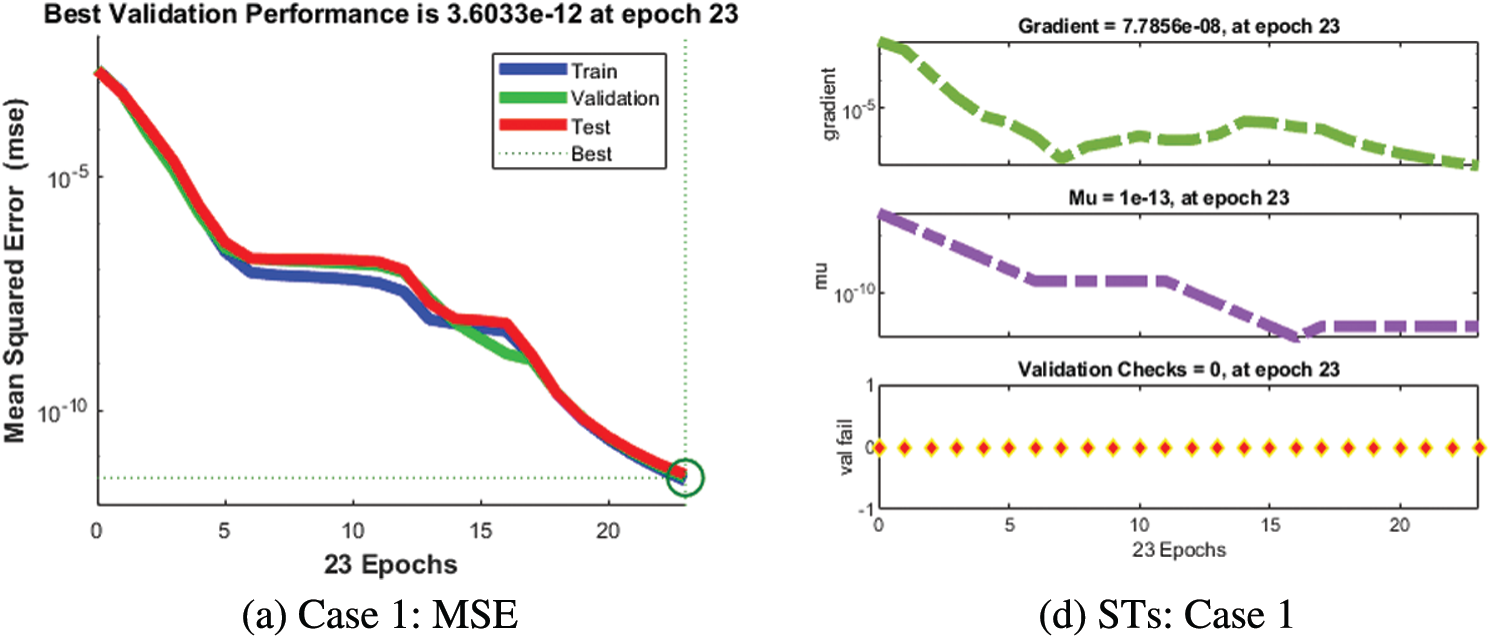
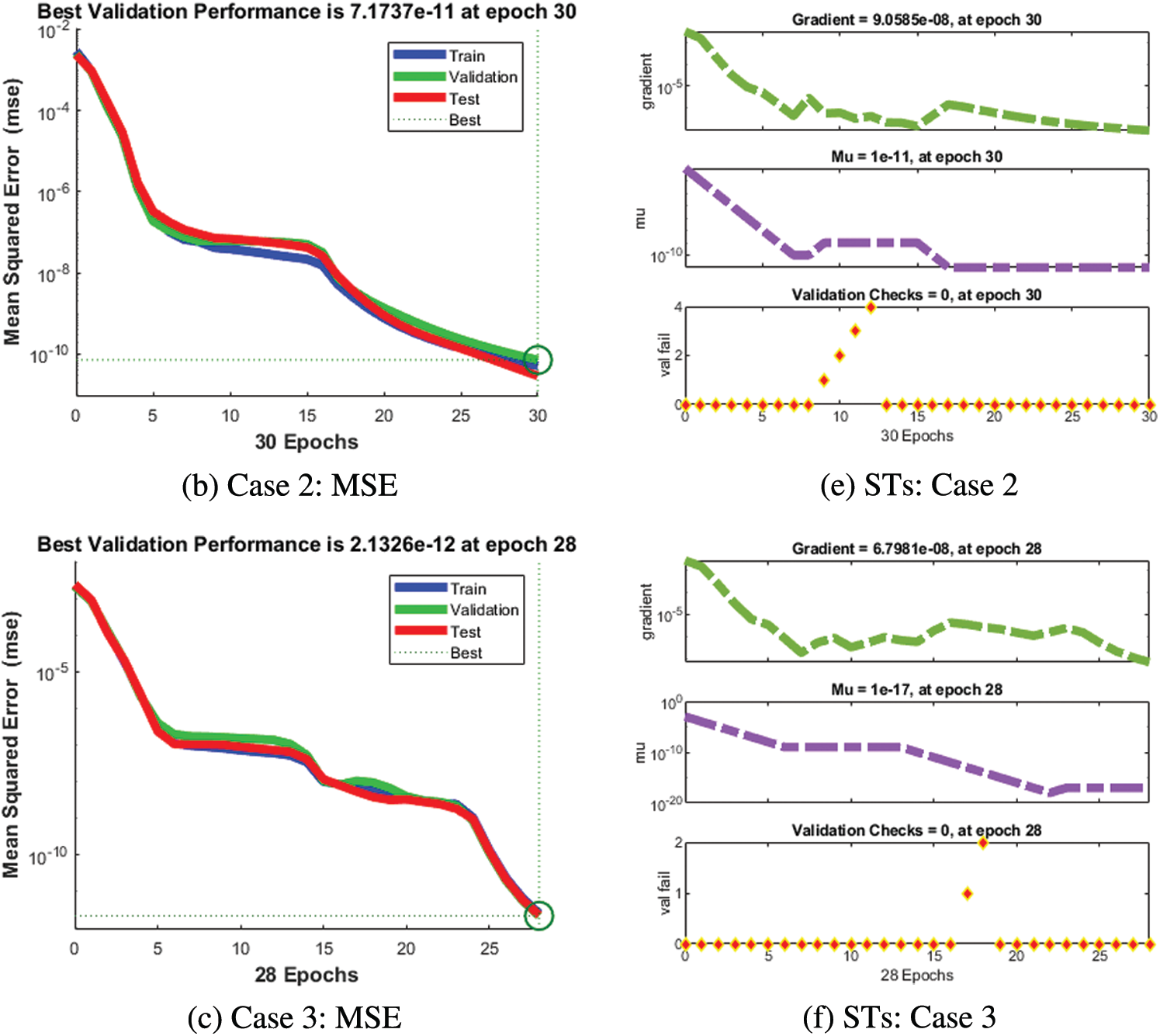
Figure 3: MSE and STs of the SEIR nonlinear system based on the Zika virus spreading

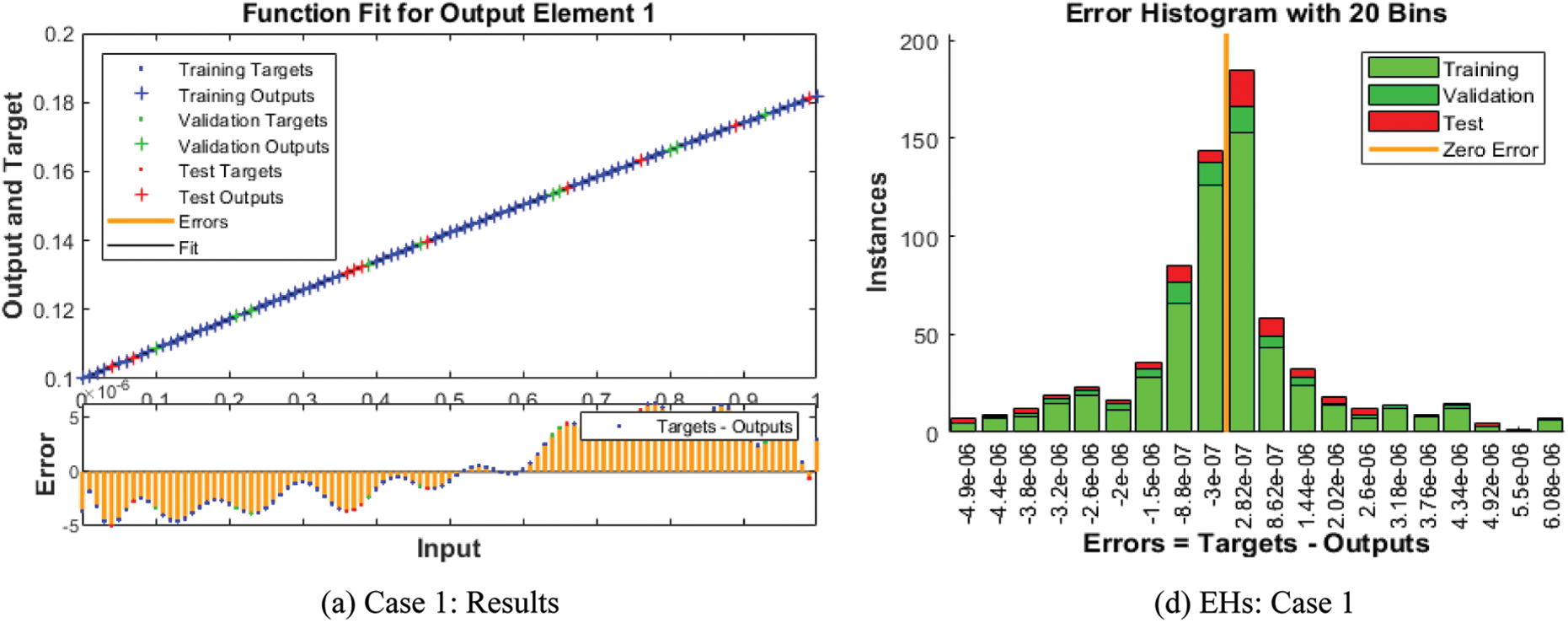
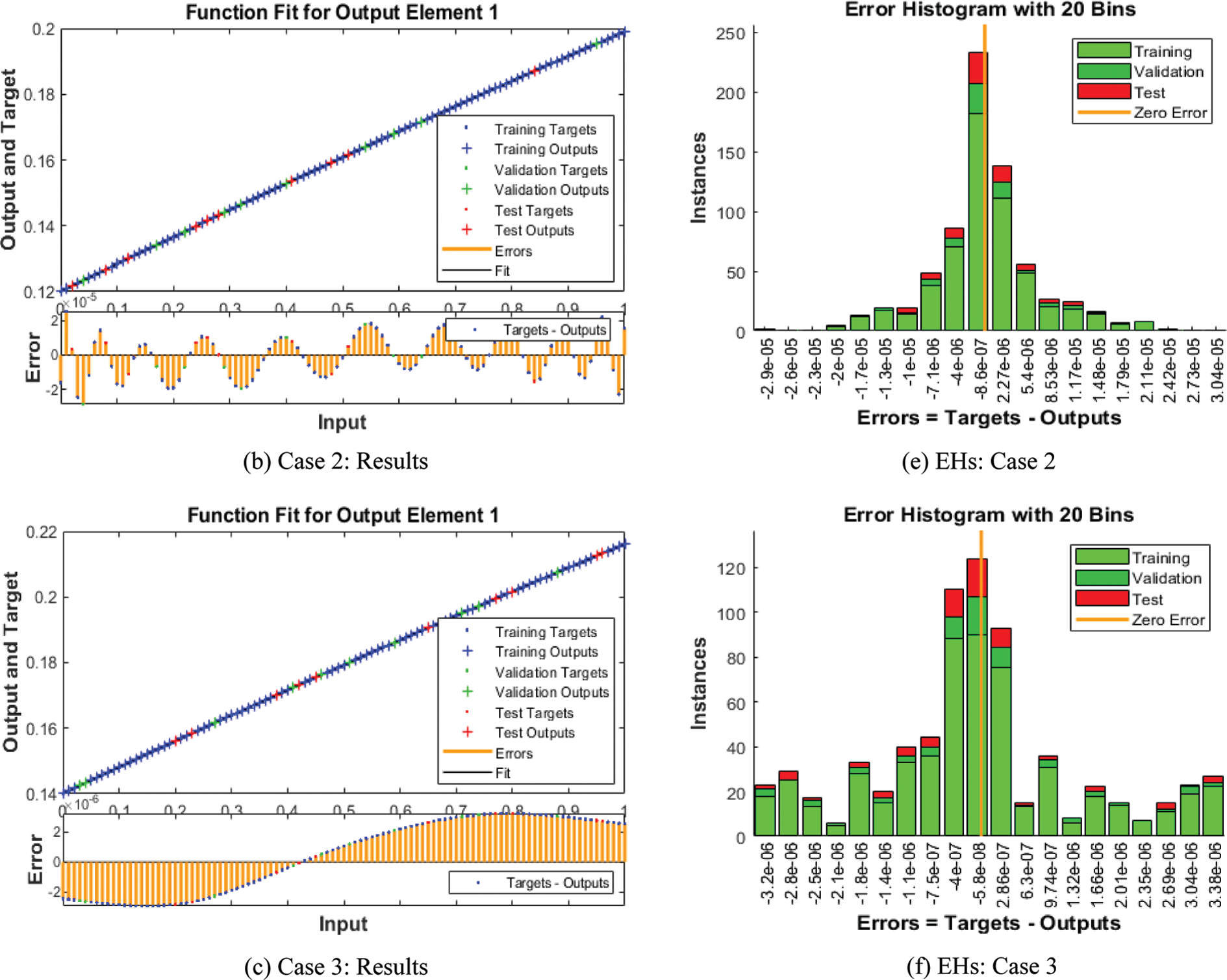
Figure 4: Result performances and EHs based on the SEIR nonlinear system of the Zika virus spreading

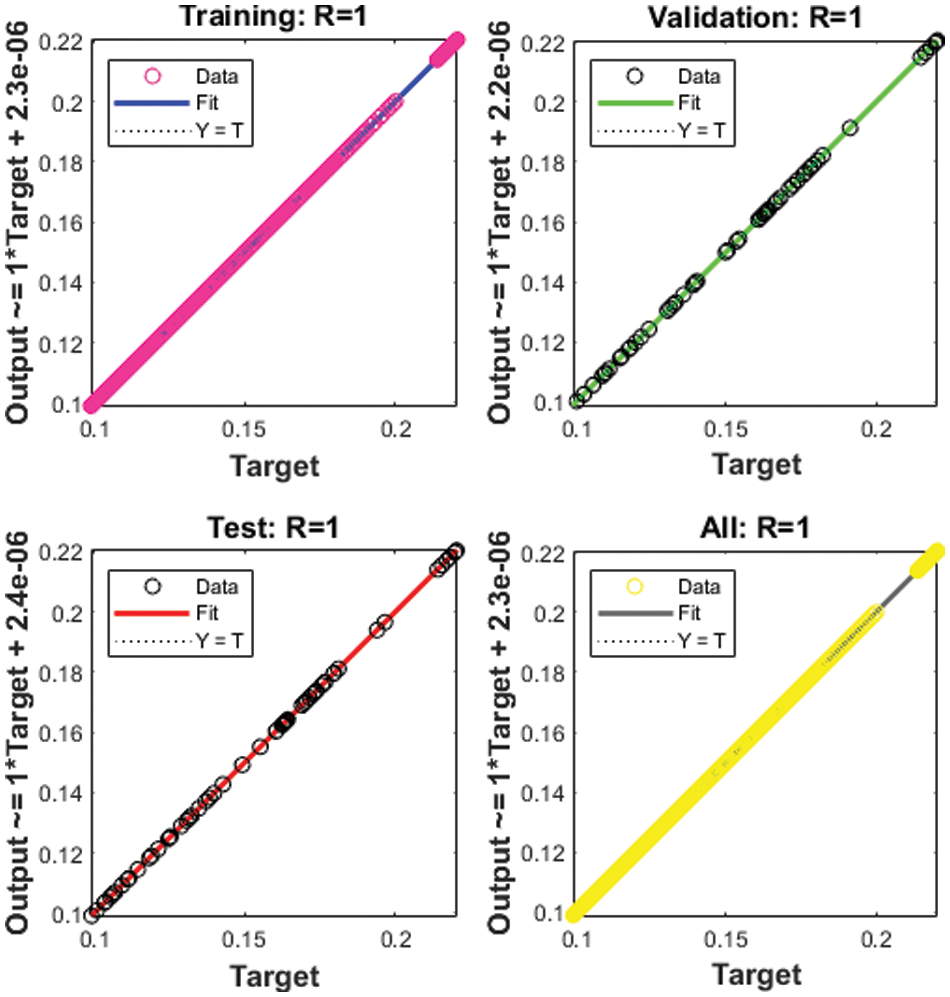
Figure 5: Regression for Case 1

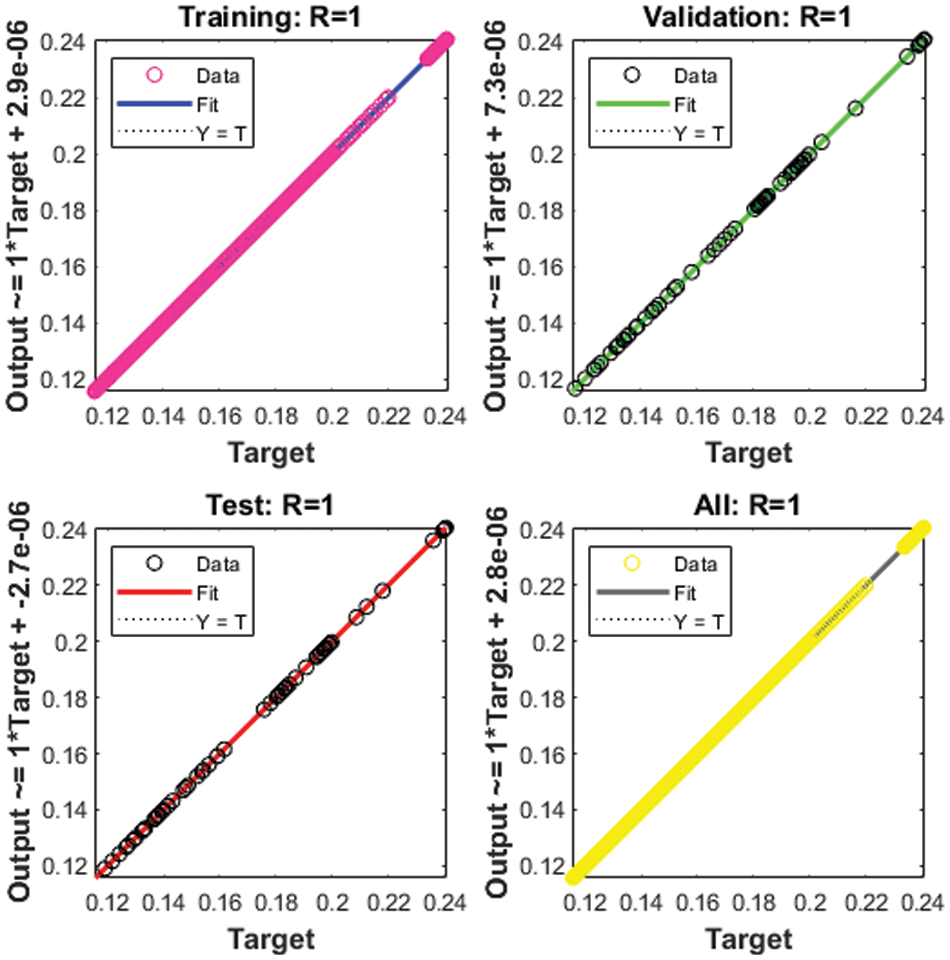
Figure 6: Regression for Case 2

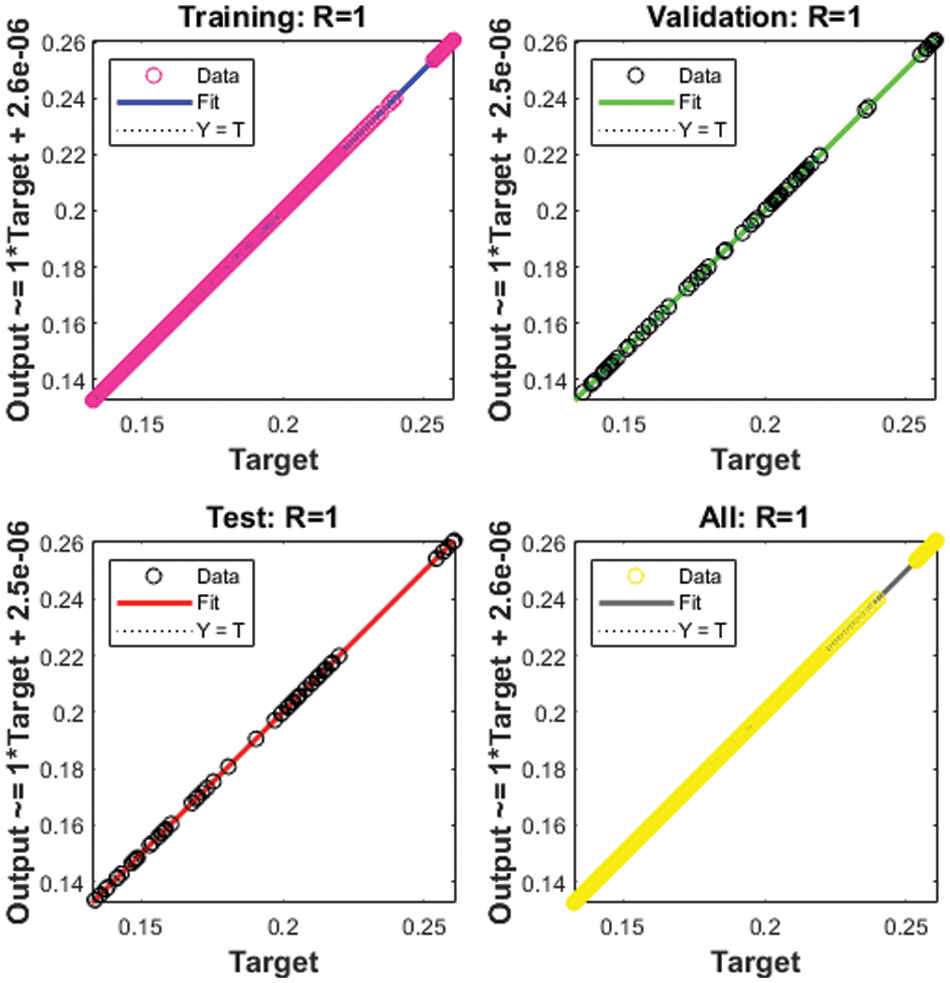
Figure 7: Regression for Case 3

The correlation plots are provided in Figs 5–7, which authenticates the performances of the regression. The correlations based on the determination coefficient, i.e., performances of R2 found as 1 to solve the SEIR nonlinear system of the Zika virus spreading using the ANNs-SCG. The best plots of the training, testing, and corroboration authenticate the performances of the ANNs-SCG and are found correct for the SEIR nonlinear system of the Zika virus spreading. Table 2 represents the SEIR nonlinear system based on the Zika virus spreading through the MSE convergence of training, iterations, substantiation, testing and complexity measures. The complexity performances of the ANNs-SCG scheme are provided for the training of the systems, i.e., execution cost based on the 1000 iterations and SEIR nonlinear system based on the Zika virus spreading. The complexity is presented in Table 2 based on the ANNs-SCG approach, which takes around 5 ± 2 s in each case of the SEIR nonlinear system.

The result comparison plots and AE (obtained and reference results) to solve the SEIR nonlinear system based on the Zika virus spreading are illustrated in Figs. 8 and 9. The derived and reference outputs for each class of the SEIR nonlinear system based on the Zika virus spreading are overlapped. The excellence, and perfection of the proposed ANNs-SCG are observed with the overlapping of the results. Fig. 9 authenticates the AE measures for each variation of the SEIR nonlinear system of the Zika virus spreading. The AE results are performed as 10−05 to 10−07, 10−05 to 10−06 and 10−04 to 10−06 for the category SH(y), 10−06 to 10−08, 10−05 to 10−06 and 10−06 to 10−07 for class EH(y), 10−06 to 10−07, 10−05 to 10−06 and 10−05 to 10−07 for class IH(y), 10−07 to 10−09, 10−05 to 10−07 and 10−06 to 10−08 for class RH(y), 10−06 to 10−09, 10−05 to 10−07 and 10−06 to 10−07 for class SV(y), 10−05 to 10−07, 10−04 to 10−06 and 10−05 to 10−06 for class EV(y) and 10−06 to 10−07, 10−05 to 10−07 and 10−07 to 10−08 for class EH(y) of the SEIR nonlinear system. These performances of the SEIR nonlinear system of the Zika virus spreading are performed exactly and accurately.

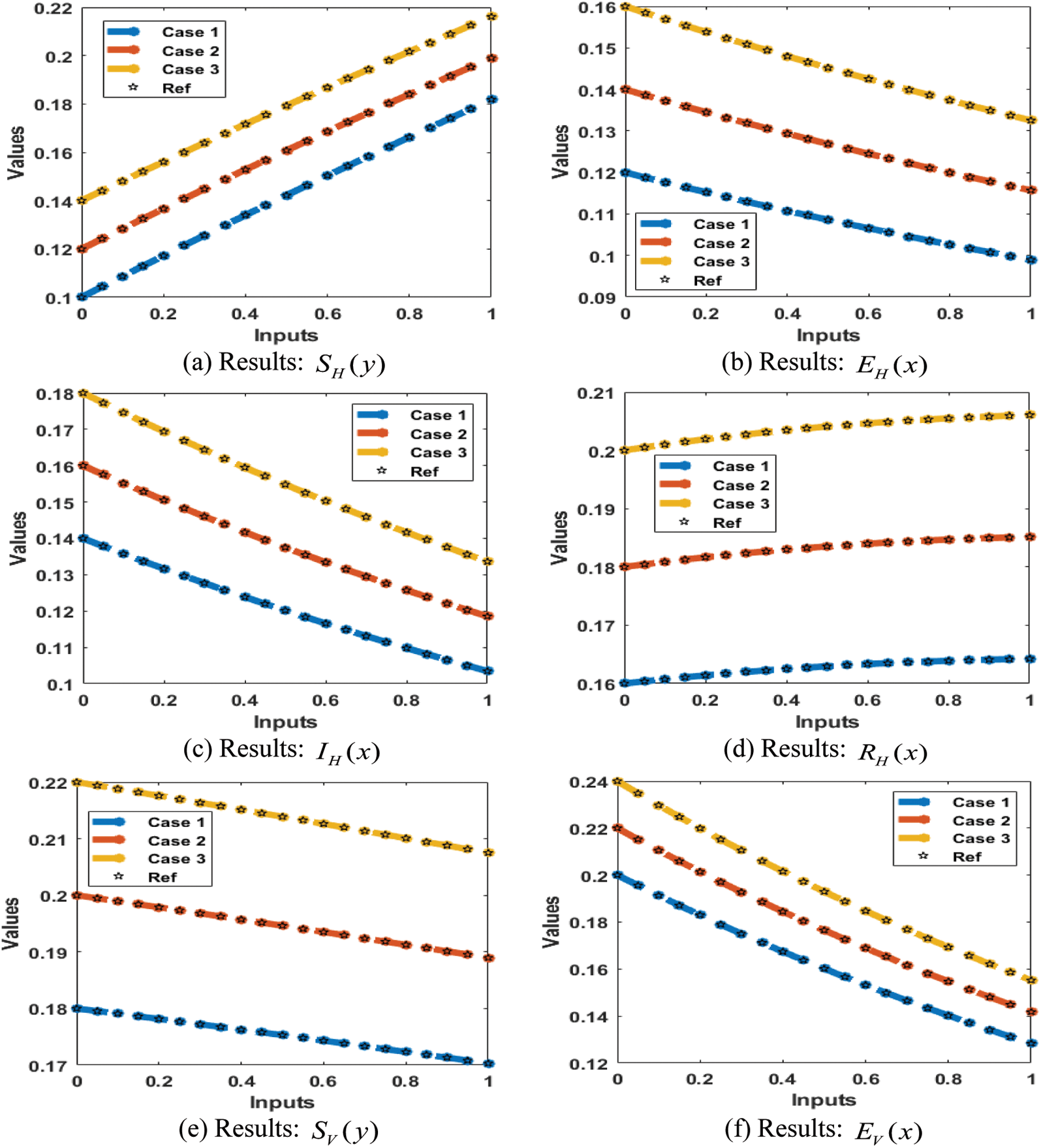
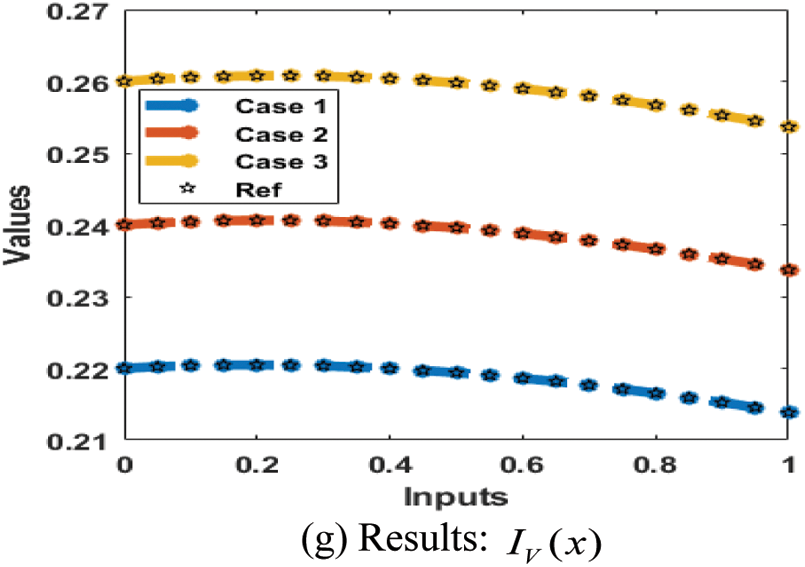
Figure 8: Results for the SEIR nonlinear system based on the Zika virus spreading

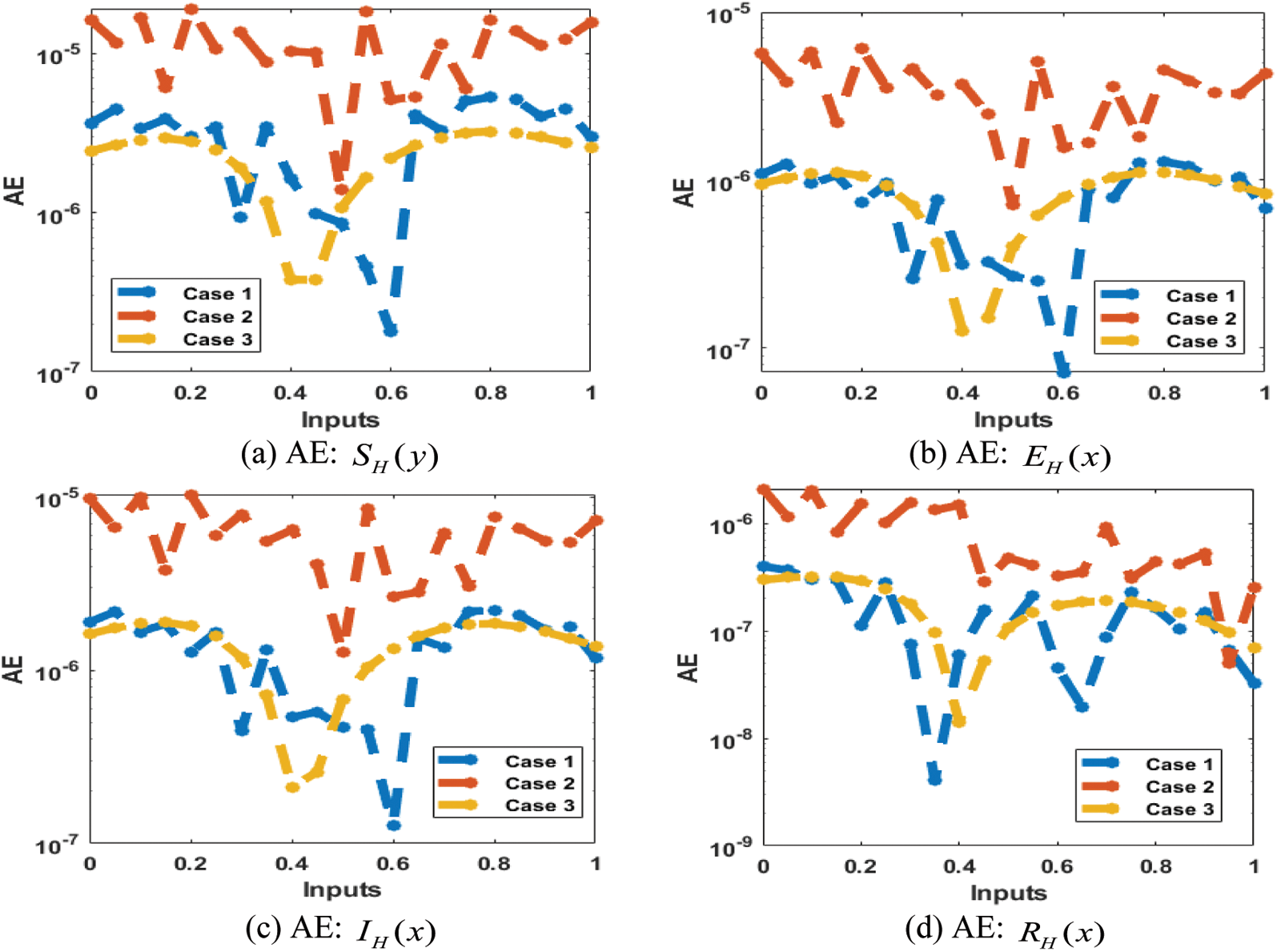
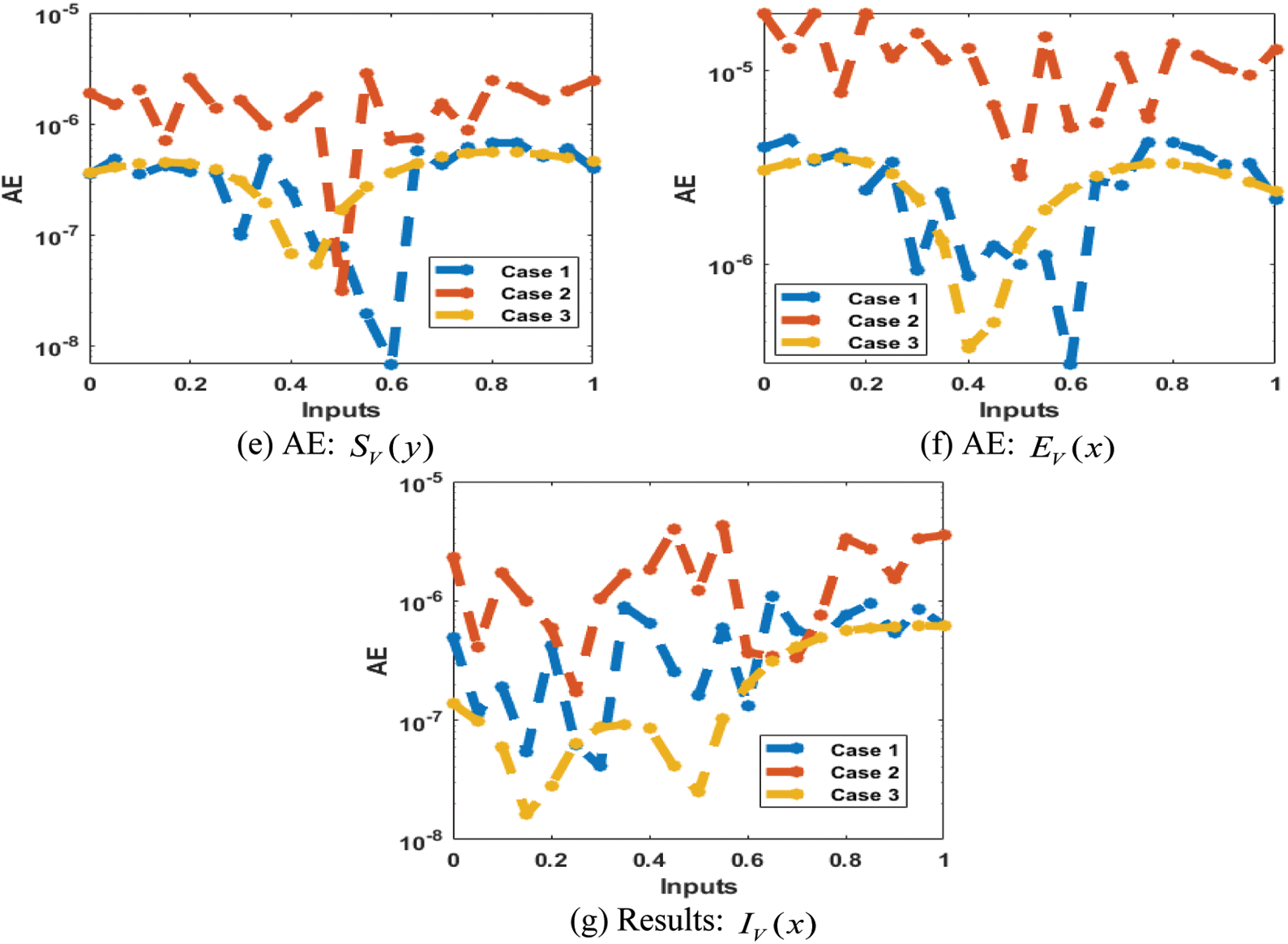
Figure 9: AE for the SEIR nonlinear system based on the Zika virus spreading

5  Conclusion

The purpose of the current work is to present the numerical performances of the SEIR nonlinear system based on the Zika virus spreading by using stochastic procedures. The epidemic form of the SEIR nonlinear system is divided into four dynamics of the patients, susceptible patients S(y), exposed patients hospitalized E(y), infected patients I(y) and recovered patients R(y). The system’s computing numerical performances are examined using artificial neural networks along with the scaled conjugate gradient. Few concluding remarks of this study are presented as:

•   The numerical presentations based on the SEIR nonlinear system of the Zika virus spreading have been described through the stochastic scheme.

•   Three variations of the Zika virus spreading have been described through the stochastic procedure and numerically stimulated using the designed computational approach.

•   The exactness of the scheme is verified by using the comparison procedures of the obtained reference solutions.

•   The default stoppage limits, step size, and tolerances are applied to label the data, training targets, and inputs, which have been accessed using the standard numerical result performances.

•   The AE values of each dynamic of the SEIR nonlinear system of the spreading Zika virus have been performed accurately using the proposed scheme.

•   The statics of the dataset has been divided into three parts, 11% for testing, 72% for measures for training and 17% for validation.

•   The constancy of the computing scheme has been authenticated through the different statistical performances.

In the future, the suggested schemes can be applied to propose the numerical performances of the computational dynamics based on fluidic systems, computer virus systems, fractional kinds of systems, and biological models [38–47].

Acknowledgement: This research has received funding support from the NSRF via the program anagement Unit for Human Resources & Institutional Development, Research and Innovation [Grant number B05F640183] and Chiang Mai University. Watcharaporn Cholamjiak would like to thank National Research Council of Thailand (N42A650334) and Thailand Science Research and Innovation, the University of Phayao (Grant No. FF66-UoE).

Funding Statement: This work was supported by Chiang Mai University and NSRF [Grant No. B05F640183].

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

    1. W. Wang, “Backward bifurcation of an epidemic model with treatment,” Mathematical Biosciences, vol. 201, no. 1–2, pp. 58–71, 2006. [Google Scholar]

    2. L. Liu, “A delayed SIR model with general nonlinear incidence rate,” Advances in Difference Equations, vol. 1, no. 1, pp. 1–11, 2015. [Google Scholar]

    3. D. I. Simpson, “Zika virus infection in man,” Transactions of the Royal Society of Tropical Medicine and Hygiene, vol. 58, no. 4, pp. 335–338, 1964. [Google Scholar]

    4. D. Musso, A. I. Ko and D. Baud, “Zika virus infection—After the pandemic,” New England Journal of Medicine, vol. 381, no. 15, pp. 1444–1457, 2019. [Google Scholar]

    5. A. R. Yadav and S. K. Mohite, “A review on zika virus infection,” Research Journal of Pharmaceutical Dosage Forms and Technology, vol. 12, no. 4, pp. 295–297, 2020. [Google Scholar]

    6. M. R. Duffy, T. H. Chen, W. T. Hancock, A. M. Powers, J. L. Kool et al., “Zika virus outbreak on Yap Island, federated states of Micronesia,” New England Journal of Medicine, vol. 360, no. 24, pp. 2536–2543, 2009. [Google Scholar]

    7. D. Musso, T. Nhan, E. Robin, C. Roche, D. Bierlaire et al., “Potential for Zika virus transmission through blood transfusion demonstrated during an outbreak in French Polynesia,” Eurosurveillance, vol. 19, no. 14, pp. 20761, 2014. [Google Scholar]

    8. I. I. Bogoch, O. J. Brady, M. U. Kraemer, M. German, M. I. Creatore et al., “Anticipating the international spread of Zika virus from Brazil,” The Lancet, vol. 387, no. 10016, pp. 335–336, 2016. [Google Scholar]

    9. E. Marbán-Castro, A. Goncé, V. Fumadó, L. Romero-Acevedo and A. Bardají, “Zika virus infection in pregnant women and their children: A review,” European Journal of Obstetrics & Gynecology and Reproductive Biology, vol. 265, no. 3, pp. 162–168, 2021. [Google Scholar]

  10. P. Ferraris, H. Yssel and D. Missé, “Zika virus infection: An update,” Microbes and Infection, vol. 21, no. 8–9, pp. 353–360, 2019. [Google Scholar]

  11. K. O. Okosun and O. D. Makinde, “A co-infection model of malaria and cholera diseases with optimal control,” Mathematical Biosciences, vol. 258, no. 1, pp. 19–32, 2015. [Google Scholar]

  12. Y. Guerrero Sánchez, Z. Sabir, H. Günerhan and H. M. Baskonus, “Analytical and approximate solutions of a novel nervous stomach mathematical model,” Discrete Dynamics in Nature and Society, vol. 2020, Article ID 5063271, 2020. [Google Scholar]

  13. A. K. Kiani, W. U. Khan, M. A. Z. Raja, Y. He, Z. Sabir et al., “Intelligent backpropagation networks with bayesian regularization for mathematical models of environmental economic systems,” Sustainability, vol. 13, no. 17, pp. 9537, 2021. [Google Scholar]

  14. Z. Sabir, J. L. Guirao, T. Saeed and F. Erdoğan, “Design of a novel second-order prediction differential model solved by using adams and explicit Runge-Kutta numerical methods,” Mathematical Problems in Engineering, vol. 2020, no. 3, pp. 1–7, 2020. [Google Scholar]

  15. Z. Sabir, M. G. Sakar, M. Yeskindirova and O. Saldir, “Numerical investigations to design a novel model based on the fifth order system of Emden-Fowler equations,” Theoretical and Applied Mechanics Letters, vol. 10, no. 5, pp. 333–342, 2020. [Google Scholar]

  16. E. K. Lee, Y. Liu and F. H. Pietz, “A compartmental model for Zika virus with dynamic human and vector populations,” in AMIA Annual Symp. Proc.,vol. 2016, pp. 743–752, 2016. [Google Scholar]

  17. G. Q. Sun and Z. K. Zhang, “Global stability for a sheep brucellosis model with immigration,” Applied Mathematics and Computation, vol. 246, pp. 336–345, 2014. [Google Scholar]

  18. M. T. Li, G. Q. Sun, Y. F. Wu, J. Zhang and Z. Jin, “Transmission dynamics of a multi-group brucellosis model with mixed cross infection in public farm,” Applied Mathematics and Computation, vol. 237, pp. 582–594, 2014. [Google Scholar]

  19. Y. Xing, L. Song, G. Q. Sun, Z. Jin, J. Zhang et al., “Assessing reappearance factors of H7N9 avian influenza in China,” Applied Mathematics and Computation, vol. 309, no. 20, pp. 192–204, 2017. [Google Scholar]

  20. G. Q. Sun, J. H. Xie, S. H. Huang, Z. Jin, M. T. Li et al., “Transmission dynamics of cholera: Mathematical modeling and control strategies,” Communications in Nonlinear Science and Numerical Simulation, vol. 45, pp. 235–244, 2017. [Google Scholar]

  21. P. Yu and W. Lin, “Complex dynamics in biological systems arising from multiple limit cycle bifurcation,” Journal of Biological Dynamics, vol. 10, no. 1, pp. 263–285, 2016. [Google Scholar]

  22. G. H. Li and Y. X. Zhang, “Dynamic behaviors of a modified SIR model in epidemic diseases using nonlinear incidence and recovery rates,” PLoS One, vol. 12, no. 4, pp. e0175789, 2017. [Google Scholar]

  23. Z. Sabir, M. A. Z. Raja, A. S. Alnahdi, M. B. Jeelani and M. A. Abdelkawy, “Numerical investigations of the nonlinear smoke model using the Gudermannian neural networks,” Mathematical Biosciences and Engineering, vol. 19, no. 1, pp. 351–370, 2022. [Google Scholar]

  24. Z. Sabir, H. A. Wahab, S. Javeed and H. M. Baskonus, “An efficient stochastic numerical computing framework for the nonlinear higher order singular models,” Fractal and Fractional, vol. 5, no. 4, pp. 1–14, 2021. [Google Scholar]

  25. Z. Sabir, K. Nisar, M. A. Z. Raja, A. A. B. A. Ibrahim, J. J. P. C. Rodrigues et al., “Design of Morlet wavelet neural network for solving the higher order singular nonlinear differential equations,” Alexandria Engineering Journal, vol. 60, no. 6, pp. 5935–5947, 2021. [Google Scholar]

  26. Z. Sabir, “Stochastic numerical investigations for nonlinear three-species food chain system,” International Journal of Biomathematics, vol. 15, no. 4, pp. 1–17, 2022. [Google Scholar]

  27. M. Umar, Z. Sabir, F. Amin, J. L. Guirao and M. A. Z. Raja, “Stochastic numerical technique for solving HIV infection model of CD4+ T cells,” The European Physical Journal Plus, vol. 135, no. 5, pp. 1–19, 2020. [Google Scholar]

  28. M. Umar, Z. Sabir, M. A. Z. Raja, H. M. Baskonus, S. W. Yao et al., “A novel study of Morlet neural networks to solve the nonlinear HIV infection system of latently infected cells,” Results in Physics, vol. 25, no. 6803, pp. 104235, 2021. [Google Scholar]

  29. W. Weera and P. Niamsup, “Robust stability criteria for uncertain neutral systems with interval nondifferentiable time-varying delay and nonlinear perturbations,” Journal of Applied Mathematics, vol. 2011, pp. 1–21, 2011. [Google Scholar]

  30. Z. Sabir, M. A. Z. Raja, T. Botmart and W. Weera, “A neuro-evolution heuristic using active-set techniques to solve a novel nonlinear singular prediction differential model,” Fractal and Fractional, vol. 6, no. 29, pp. 1–14, 2022. [Google Scholar]

  31. Z. Sabir, C. M. Khalique, M. A. Z. Raja and D. Baleanu, “Evolutionary computing for nonlinear singular boundary value problems using neural network, genetic algorithm and active-set algorithm,” The European Physical Journal Plus, vol. 136, no. 2, pp. 1–19, 2021. [Google Scholar]

  32. Z. Sabir, “Neuron analysis through the swarming procedures for the singular two-point boundary value problems arising in the theory of thermal explosion,” The European Physical Journal Plus, vol. 137, no. 5, pp. 1–19, 2022. [Google Scholar]

  33. B. Wang, J. F. Gomez-Aguilar, Z. Sabir, M. A. Z. Raja, W. F. Xia et al., “Numerical computing to solve the nonlinear corneal system of eye surgery using the capability of morlet wavelet artificial neural networks,” Fractals-An Interdisciplinary Journal on the Complex Geometry of Nature, vol. 30, no. 5, pp. 1–19, 2022. [Google Scholar]

  34. M. Umar, F. Amin, H. A. Wahab and D. Baleanu, “Unsupervised constrained neural network modeling of boundary value corneal model for eye surgery,” Applied Soft Computing, vol. 85, no. 1, pp. 1–16, 2019. [Google Scholar]

  35. T. Saeed, Z. Sabir, M. S. Alhodaly, H. H. Alsulami and Y. G. Sánchez, “An advanced heuristic approach for a nonlinear mathematical based medical smoking model,” Results in Physics, vol. 32, no. 8, pp. 1–13, 2022. [Google Scholar]

  36. Z. Sabir and H. A. Wahab, “Evolutionary heuristic with Gudermannian neural networks for the nonlinear singular models of third kind,” Physica Scripta, vol. 96, no. 12, pp. 125261, 2021. [Google Scholar]

  37. S. Rezapour, H. Mohammadi and A. Jajarmi, “A new mathematical model for Zika virus transmission,” Advances in Difference Equations, vol. 2020, no. 1, pp.1–15, 2020. [Google Scholar]

  38. Z. Sabir, M. A. Z. Raja, M. Shoaib and J. F. Aguilar, “FMNEICS: Fractional Meyer neuro-evolution-based intelligent computing solver for doubly singular multi-fractional order Lane-Emden system,” Computational and Applied Mathematics, vol. 39, no. 4, pp. 1–18, 2020. [Google Scholar]

  39. K. A. Touchent, Z. Hammouch and T. Mekkaoui, “A modified invariant subspace method for solving partial differential equations with non-singular kernel fractional derivatives,” Applied Mathematics and Nonlinear Sciences, vol. 5, no. 2, pp. 35–48, 2020. [Google Scholar]

  40. H. Günerhan and E. Çelik, “Analytical and approximate solutions of fractional partial differential-algebraic equations,” Applied Mathematics and Nonlinear Sciences, vol. 5, no. 1, pp. 109–120, 2020. [Google Scholar]

  41. Z. Sabir, M. A. Z. Raja, J. L. Guirao and T. Saeed, “Meyer wavelet neural networks to solve a novel design of fractional order pantograph Lane-Emden differential model,” Chaos Solitons & Fractals, vol. 152, no. 2, pp. 1–14, 2021. [Google Scholar]

  42. E. İlhan and İ.O. Kıymaz, “A generalization of truncated M-fractional derivative and applications to fractional differential equations,” Applied Mathematics and Nonlinear Sciences, vol. 5, no. 1, pp. 171–188, 2020. [Google Scholar]

  43. P. Lakshminarayana, K. Vajravelu, G. Sucharitha and S. Sreenadh, “Peristaltic slip flow of a Bingham fluid in an inclined porous conduit with Joule heating,” Applied Mathematics and Nonlinear Sciences, vol. 3, no. 1, pp. 41–54, 2018. [Google Scholar]

  44. T. Sajid, S. Tanveer, Z. Sabir and J. L. G. Guirao, “Impact of activation energy and temperature-dependent heat source/sink on maxwell-sutterby fluid,” Mathematical Problems in Engineering, vol. 2020, pp. 1–15, 2020. [Google Scholar]

  45. R. Ahmad, A. Farooqi, J. Zhang and N. Ali, “Steady flow of a power law fluid through a tapered non-symmetric stenotic tube,” Applied Mathematics and Nonlinear Sciences, vol. 4, no. 1, pp. 255–266, 2019. [Google Scholar]

  46. Z. Sabir, A. Imran, M. Umar, M. Zeb, M. Shoaib et al., “A numerical approach for 2-D Sutterby fluid-flow bounded at a stagnation point with an inclined magnetic field and thermal radiation impacts,” Thermal Science, vol. 25, no. 3, pp. 1975–1987, 2021. [Google Scholar]

  47. M. Shoaib, M. A. Z. Raja, M. T. Sabir, S. Islam, Z. Shah et al., “Numerical investigation for rotating flow of MHD hybrid nanofluid with thermal radiation over a stretching sheet,” Scientific Reports, vol. 10, no. 1, pp. 1–15, 2020. [Google Scholar]