An Optimal Algorithm for Resource Allocation in D2D Communication

1  Introduction

With the development of the Internet of Things (IoTs) and Artificial Intelligence (AI) [1], emerging technologies [2,3] and applications such as autonomous driving [4–7], smart medical care [8,9], industrial automation [10], virtual reality [11] and augmented reality [12] have sprung up. The effective implementation of these intelligent applications depends on the rapid acquisition, transmission and summary processing of environmental information by different types of IoT nodes such as sensors. How to support large-scale data transmission and rapid processing of massive wireless nodes has become a huge challenge for future wireless networks. The traditional mobile cloud computing technology transfers the data at the edge of the network to the cloud server center for processing. With the geometric growth of the data volume, the mobile cloud computing technology faces communication network congestion, long end-to-end delay, user data privacy protection, and other problems. In order to effectively solve the problems existing in cloud computing technology, mobile edge computing (MEC) technology came into being [13]. This technology utilizes the communication, computing and storage capabilities of terminal equipment such as base stations, access points, and IoT nodes at the edge of the wireless network to process data information and computing tasks at the edge, which can effectively reduce the communication traffic of the backbone network and reduce the end-to-end communication and computing delay, improve the data privacy protection capabilities, and further stimulate various localized application innovations [14,15].

At the same time, various intelligent applications in the future rely on artificial intelligence technology (such as deep learning, etc.), and use locally obtained data samples for artificial intelligence model training and intelligent deduction [16,17]. In order to meet the low-latency requirements of various intelligent applications, edge intelligence technology has become an important research direction and has received extensive attention from academia and industry [18,19]. This technology effectively combines MEC and artificial intelligence to support AI model training and intelligent deduction at the edge of the network. By endowing network edge nodes with human-like real-time response capabilities, edge intelligence technology can effectively support emerging intelligent application scenarios and provide high-quality, low-latency service experience.

In edge intelligence technology, federated learning [20] is an important branch. Different from the traditional centralized machine learning technology, the federated learning aims to distribute the machine learning model training process to multiple edge nodes (such as wireless terminals such as IoT nodes) in the MEC network, and conduct machine learning under the coordination of edge servers. The edge nodes participating in federated learning can directly use data stored locally for model training without sharing their user data. Specifically, the federated learning iteratively proceeds as follows: 1) In each iteration, the edge server sends the current global AI model parameters to all edge nodes participating in joint learning; 2) According to the received model parameters, each edge node uses the locally stored data samples to update the local model, such as calculating the gradient according to the loss function and updating the parameters; 3) Each edge node uploads the updated model parameters to the edge server; 4) The edge server performs a global aggregation operation, and performs a weighted average of the local model parameters sent by each edge node to obtain new global model parameters. The above operations are iteratively performed until the model training converges. In general, the federated learning can be divided into two ways: synchronous [21] and asynchronous [22]. That is, the local model parameter update and global aggregation of different edge nodes need to be fully synchronous, or can be done asynchronously. Reference [23] compares synchronous federated learning and asynchronous federated learning. The research in this paper focuses on synchronous federated learning.

Efficient implementation of federated learning faces a series of technical challenges. On the one hand, the computing resources of edge nodes are relatively limited. On the other hand, the implementation of federated learning relies on frequent parameter update and aggregation between edge nodes and edge servers, and as the number of edge nodes increases and the dimension of AI models increases, the above parameter update and aggregation will lead to communication overhead very large. Therefore, the limited computing and communication resources are the main bottlenecks for the improvement of joint learning performance. In the actual network, different edge nodes have heterogeneity in computing power, and the data sample sizes that different edge nodes need to process are also different. Therefore, the calculation execution time for local model update will be different. At the same time, due to the differences in deployment locations and the fading characteristics of wireless channels, the channel states between different edge nodes and edge servers are also different, resulting in differences in the performance of model parameters during upload and download. Therefore, how to optimize the communication and computing resource allocation of the network is an important means to improve the performance of joint learning. In the existing work, reference [24] studied how to efficiently utilize the limited resources to achieve adaptive joint learning in a resource-constrained MEC system. However, it only considers the resources consumed by the two processes of local model update and global aggregation, while ignoring the communication resources consumed by the model parameter update process. Reference [25] proposed a ternary gradient method to reduce the communication time of joint learning. Reference [26] proposed two methods to reduce the communication cost of the model parameter upload link to improve the communication efficiency of joint learning. Reference [27] proposed a new multiple access method to achieve fast aggregation of global model parameters. However, the above existing studies have ignored the influence of the heterogeneity of computing and communication capabilities of edge nodes on the training of federated learning models. Due to this heterogeneity, in the joint learning process, the time it takes for different edge nodes to complete the local model update and parameter upload will be different, and the node that first completes the model parameter upload needs to wait for other nodes to upload the model parameters, resulting in computational problems and the waste of communication resources, resulting in a decrease in the performance of joint learning. Therefore, this paper proposes to utilize offloading technology to solve this problem.

In the MEC system, offloading is an important technology, which can effectively improve the computing power of edge nodes and alleviate the situation that the computing and communication capabilities of edge nodes do not match the task load. Generally, according to different offloading objects, offloading techniques can be divided into two types, namely offloading between devices and infrastructure (such as base stations) [28] and D2D offloading [29]. Offloading between devices and infrastructure means that devices with weak computing power or shortage of computing resources offload some or all computing tasks to infrastructures (such as base stations) that are closer to them for processing. D2D offloading refers to devices with weak computing power or shortage of computing resources, using D2D communication and other technologies to offload some computing tasks to nearby devices with strong computing power or idle for processing. At present, the solution of how to apply offloading technology to federated learning has not been proposed yet.

This paper studies federated learning in MEC networks. The D2D computing task offloading for federated learning in the MEC network is shown in Fig. 1. The system includes an edge server and multiple heterogeneous edge nodes, and each node stores its own user data. In order to solve the problem of efficient joint learning in the heterogeneous scene of nodes, this paper proposes a D2D computing task offloading scheme for joint learning. In view of the heterogeneity of computing and communication capabilities of edge nodes, before the joint learning model training starts, the edge nodes use D2D communication to offload the tasks. It matches the communication ability, thereby minimizing the total time of D2D computing task offloading and joint learning model training, and improving the efficiency of joint learning.

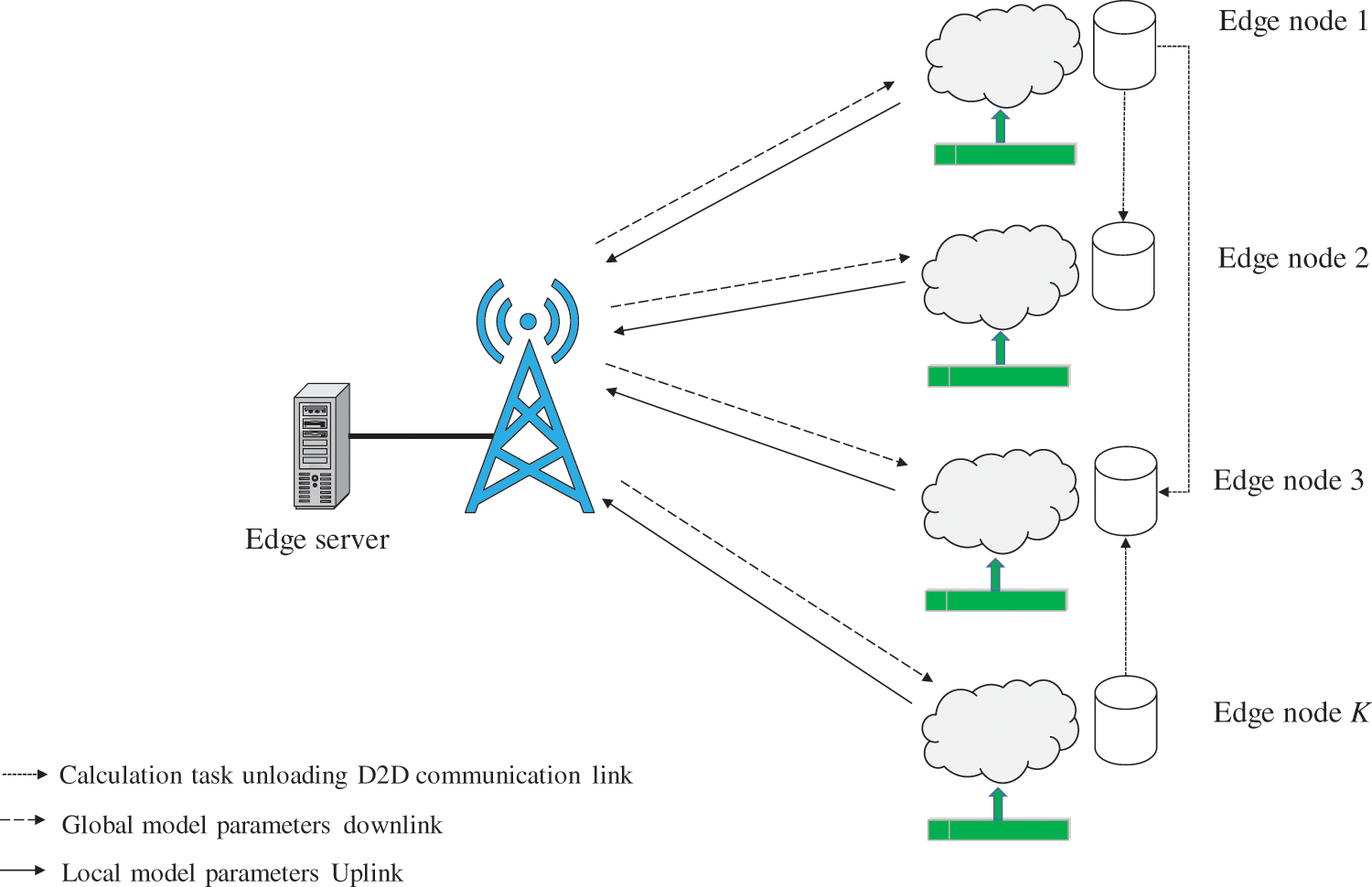
Figure 1: Proposed system model

In this paper, it is assumed that the D2D task offloading between different edge nodes and the uploading of the model parameters of the uplink adopts the frequency division multiple access (FDMA) protocol to avoid the mutual interference of different edge nodes in the transmission process. Based on this, the goal of this paper is to optimize the amount of computing tasks offloaded by all edge nodes, so as to minimize the total time consumed by the offloading process of computing tasks and the training process of the joint learning model. However, since the computational task offload of edge nodes is a discrete variable, this problem is a non-convex optimization problem that is difficult to solve. In order to facilitate the solution, this paper converts the non-convex optimization problem into a convex optimization problem by means of continuous discrete variables, and then rounds the obtained continuous solution to obtain the original problem. The simulation results show that the proposed D2D computing task offloading scheme can reduce the impact of the heterogeneity of computing and communication capabilities of edge nodes on the training of the joint learning model. It greatly reduces the time consumed by the joint learning model training and improve the training efficiency of the joint learning model. At the same time, it reduces the impact of the non-IID characteristics of the data, and improve the accuracy of model training.

2  Federated Learning

This paper studies the federated learning system based on MEC. As shown in Fig. 1, the system includes an edge server and K edge nodes, and the set of edge nodes is represented as k = {1, 2, …, K}. Any edge node i ∈ K owns a local dataset Di consisting of all data samples stored locally. For any data sample d in any local data set Di, it usually consists of two parts, the feature vector xd of the data sample and the label yd. A machine learning model is described by a model parameter w, and the accuracy of the model is often evaluated by a loss function. For the model parameter w and the feature vector xd and label yd of the data sample d, the loss function is defined as f(w,xd,yd), abbreviated as fd(w). This paper mainly studies the machine learning model of smooth support vector machine (SSVM), and its loss function is shown in Eq. (1).

fd(w)=λ2||w||+12max(0,1−ydwTxd)2(1)

The research method in this paper can also be extended to other machine learning models. On edge node i, its local loss function is defined as:

Fi(wi)=∑d∈Difd(wi)|Di|(2)

Among them, wi is the local model parameter of edge node i, and |Di| is the size of the dataset Di.

On edge servers, the global loss function is defined as:

F(wserver)=∑i=1K|Di|Fi(wi)∑i=1K|Di|(3)

Among them, wserver is a global model parameter, generally there are:

wserver=∑i=1K|Di|wi∑i=1K|Di|(4)

Finding the global model parameter wserver∗ that minimizes the global loss function F(wserver) is the objective of the joint learning model, which is expressed as:

wserver∗=argminF(wserver)(5)

Eq. (5) typically employs a synchronous distributed gradient descent technique to minimize the global loss function F(wserver). The synchronous distributed gradient descent algorithm has four steps: global model parameter download, local model update, local model parameter upload, and global aggregation. The joint learning model training process is a cycle of the above four steps until the model training is completed. For the convenience of description, this paper will complete these four steps in sequence as a frame of joint learning. Model training consists of several frames. The frame structure of joint learning is shown in Fig. 2.

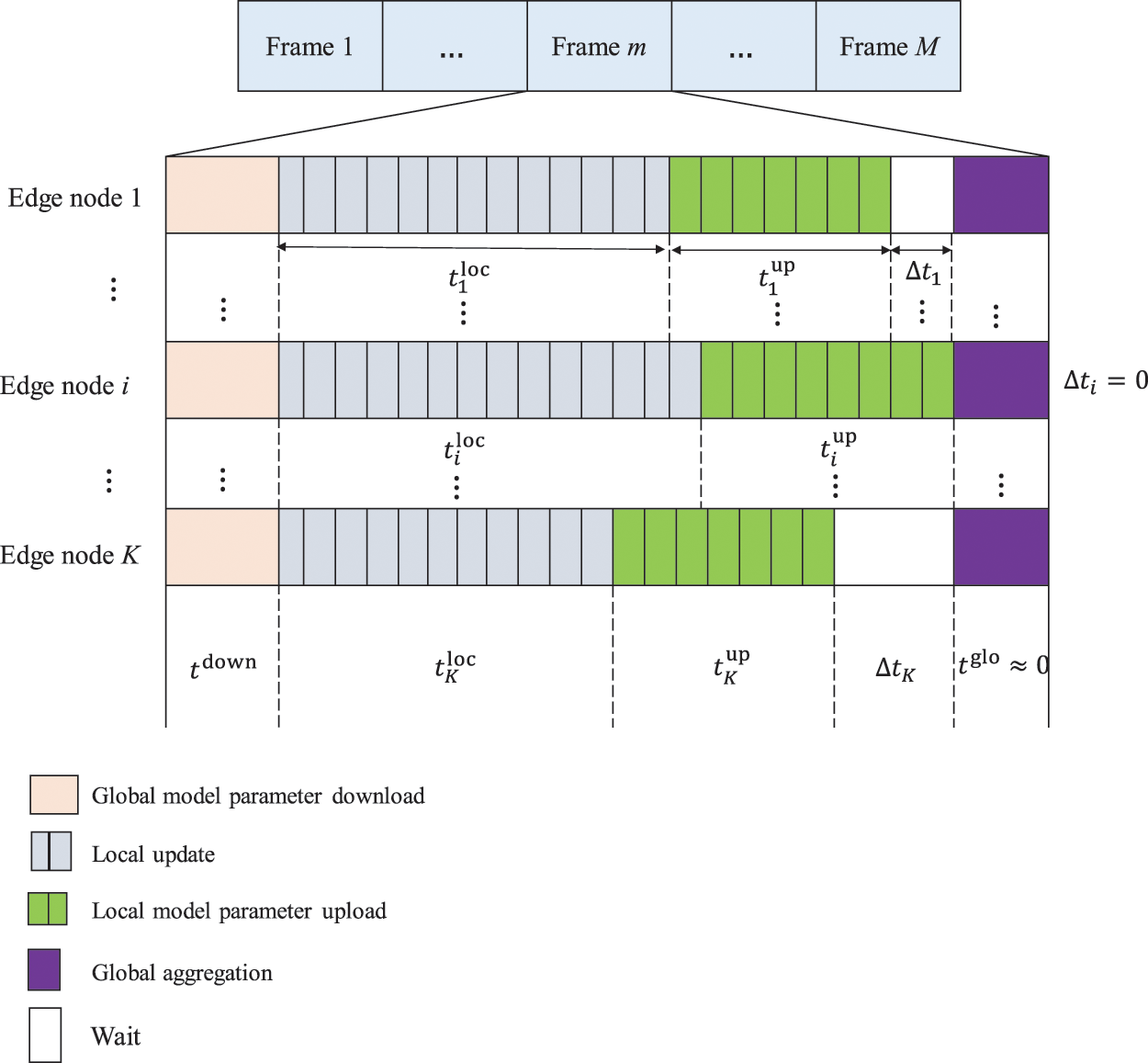
Figure 2: Schematic diagram of the frame structure of joint learning

It is assumed that the FDMA access protocol is used when uploading model parameters between edge nodes and edge servers, and different edge nodes use different frequency bands, so there is no mutual interference between edge nodes. In addition, the uplink/downlink for model parameter transmission uses Time Division Duplex (TDD) technology. Due to the reciprocity of the channel, the channel state information of the uplink/downlink is consistent. This paper assumes that the wireless channel during the training of the federated learning model is static and does not change.

2.1 Global Model Parameters

At the beginning of each frame, that is, when the federated learning model training starts or after the edge server completes the global aggregation operation, the edge server needs to send the global model parameters to each edge node. The information transfer rate for global model parameter download is determined by the user with the worst channel gain [30]. Let Pserver be the transmit power of the edge server, then the information transmission rate for downloading global model parameters is:

rdown=Blog2⁡(1+mini∈K(gi)PserverΓn0B)(6)

Among them, gi is the channel power gain between the edge node i and the edge server, n0 is the noise power spectral density, B is the channel bandwidth, Γ≥1 is the signal-to-noise ratio (SNR) gap under the actual modulation and coding method, which describes the actual transmission constant of the gap between the rate and the channel capacity. For simplicity, this paper assumes Γ=1.

Therefore, the time it takes for the edge server to send the global model parameters to each edge node is:

tdown=qrdown(7)

Among them, q is the number of bits corresponding to the model parameter w.

2.2 Local Model Update

After receiving the global model parameters, all edge nodes overwrite the original local model parameters with the global model parameters. The process that edge nodes use their local datasets to update local model parameters using gradient descent method is called local model update operation. All edge nodes can perform one or more local model update operations. In this paper, all edge nodes are set to use batch gradient descent (BGD) method to train the model [31]. That is, gradient update is performed using all data samples in one local model update operation.

For any edge node i, when the n∈{1,2,…,N}th local model update is performed in the m∈{1,2,…,M}th frame of joint learning, its local model parameters wi(m,n). Gradient update according to the following rules:

wi(m,n)={wserver(m)−η∇Fi(wserver(m)),n=1wi(m,n−1)−η∇Fi(wi(m,n−1)),n>1(8)

where η is the learning rate. In the mth frame of joint learning, when n=1, each edge node performs gradient update on the global model parameter wserver(m) issued by the edge server, specifically when m=1, wserver(m) is the system initialized global model parameters. When m>1, wserver(m) is the global model parameter obtained by performing the weighted average operation on the local model parameters of all edge nodes. When n>1, each edge node performs gradient update on the local model parameters wserver(m,n−1) obtained by the (n−1)th local model update.

In order to analyze the latency performance of the local model update, it is assumed that any edge node uses a data sample to perform a local model update operation that requires a floating-point operation. loss function decision. This paper uses the machine model SSVM to find the gradient of the loss function of SSVM, and we can get:

∇f(w)={λw+(1−ydwTxd)xd,ydwxd<1λw,ydwxd>1(9)

During the training process of the joint learning model, it is difficult to count the number of floating-point operations of the piecewise function in Eq. (9). Therefore, in this paper, the maximum number of floating-point operations required for a data sample to perform a local model update operation in Eq. (9) is taken as the number of floating-point operations actually performed. The number of floating-point operations required for the inner product of two vectors of dimension u is 2u − 1. Let the dimension of the data sample feature be u, so the dimension of the model parameters is also u. For any data sample of any edge node, the maximum number of floating-point operations required to derive any element of the model parameter vector is (2u − 1) + 4. Therefore, for the derivation of the model parameters of dimension u number of floating-point operations required is u((2u − 1) + 4) = 2u2 + 3u. Therefore, the number of floating-point operations a required by any edge node to perform a local model update operation using any data sample is 2u2 + 3u + 2u = 2u2 + 5u, when u is large enough, a ≈ 2u2.

Edge node i can perform ci floating-point operations in one CPU clock cycle, and its CPU clock frequency is fi. Assuming that all edge nodes upload the local model parameters to the edge server after performing N≥1 local model update operations, the time consumed by edge node i to perform N local model update operations using the batch gradient descent method is:

tiloc(Si)=NaSici1fi(10)

Among them, Si is the number of data samples stored locally by edge node i.

2.3 Uploading Local Model Parameters

When each edge node completes N local model update operations, it needs to upload its local model parameters to the edge server. In order to avoid mutual interference between different edge nodes, the FDMA access technology is used in the process of uploading local model parameters, and the system bandwidth is evenly distributed to all edge nodes participating in joint learning, and each edge node performs local model in the allocated frequency band. parameter transfer.

Each edge node uploads local model parameters according to the FDMA access protocol, and the transmission bandwidth allocated by all edge nodes is B/K. Therefore, the information transmission rate at which the edge server receives the local model parameters uploaded by the edge node i is:

riup=BKlog2⁡[1+giPin0B/K](11)

Among them, Pi is the transmit power of edge node i.

Since the number of bits of the local model parameters is the same as the number of bits of the global model parameters, the time consumed by the edge node i to upload the local model parameters to the edge server is:

tiup=qriup(12)

2.4 Global Aggregation

After receiving the local model parameters uploaded by all edge nodes participating in the joint learning, the edge server performs a weighted average operation on all the local model parameters, and the process of obtaining new global model parameters is called global aggregation.

Since the computing power of the edge server is strong enough, and the global aggregation operation only performs a weighted average operation on all the received local model parameters, which requires less computation, the time tglo consumed by the global aggregation will be very small. Therefore, the time consumed by global aggregation is negligible, i.e., tglo≈0.

After completing the model training of M-frame joint learning, the total time consumed by the system is:

ttotal=M(tdown+maxi∈K{tloc(Si)+tiup})(13)

Among them, M is the number of frames trained by the joint learning model.

Due to the heterogeneity of edge nodes, that is, the difference in CPU clock frequency of different edge nodes, the difference in the number of floating-point operations that can be performed in one CPU clock cycle, the difference in the number of stored data samples, and the difference in transmit power. There is a difference in the time taken to complete the local model update operation process and the local model parameter upload process in one frame.

It can be seen from Eq. (13) that the time consumed to complete the training of a frame of joint learning model is limited by the edge node that finally completes the upload of local model parameters. Because the edge server needs to receive the local model parameters uploaded by all edge nodes to perform the global aggregation operation, and the edge node that completes the local model parameter upload first needs to wait for the edge node that completes the local model parameter upload last before it can get the global aggregation of the edge server and then send new data of global model parameters to start the next frame. As shown in Fig. 2, the edge node i is the last edge node that completes the upload of local model parameters. Therefore, the waiting time Δti of edge node i is zero, and at this time, other edge nodes j that complete the upload of local model parameters before edge node i waiting time of Δtj (j≠i) will be greater than or equal to zero.

The greater the heterogeneity of different edge nodes, the longer the edge nodes with stronger computing and communication capabilities (or smaller data samples) need to wait, which will cause the computing and communication resources of edge nodes with strong computing and communication capabilities. At the same time, it prolongs the time consumed by the joint learning model training process and reduces the training efficiency of the joint learning model.

3  Problem Modeling

3.1 Computational Task Offloading for Federated Learning

In order to reduce the impact of the heterogeneity of computing and communication capabilities of edge nodes on the training efficiency of the joint learning model, this paper proposes a D2D computing task offloading scheme for joint learning. The process of performing D2D computing task offloading is defined as the 0th frame of joint learning. The D2D computing task offloading for joint learning is shown in Fig. 3. The D2D computing task offload is realized by D2D communication technology, and a D2D communication link is directly established between edge nodes, without the need for communication through base station services. By allocating the amount of computing tasks of edge nodes participating in joint learning, the optimal compromise between the time consumed by computing task offloading and the time consumed by joint learning model training is achieved, which reduces the computing and communication capabilities of edge nodes. The effect of heterogeneity on the training efficiency of the federated learning model.

Figure 3: Computational task offloading for federated learning

In machine learning, the number of data samples reflects the amount of computing tasks required for model training. Therefore, the offloading of computing tasks for D2D is actually the offloading of data samples between edge nodes.

The number of data samples unloaded from edge node i to j is sij. Then, after completing the unloading of D2D computing tasks, the number of data samples owned by edge node i is:

Si′=Si+∑j≠isji−∑j≠isij(14)

The FDMA access protocol is used when computing tasks are offloaded between edge nodes to avoid mutual interference between different links. Since there is no task transfer between two edge nodes in the process of offloading computing tasks between edge nodes, the bandwidth allocated to the communication link between any two edge nodes is

BW=BK(K−1)/2(15)

Let Pij be the transmission power of edge node i unloading data samples to edge node j, then the information transmission rate of edge node i unloading data samples to edge node j is:

rijoffl=BK(K−1)/2log2⁡[1+hijPijn0BK(K−1)/2](16)

Among them, hij is the channel gain between edge node i and j.

Therefore, the time it takes for edge node i to unload data samples to edge node j is:

tijoffl(sij)=bsijrijoffl(17)

Among them, b is the number of bits of a training data sample.

After the D2D computing task is unloaded, the time consumed by the edge node i to perform the local model update operation is:

tiloc(Si′)=NaSi′ci1fi(18)

Substituting Eq. (14) into Eq. (18), we can get:

tiloc({sij})=Na(Si+∑j≠isji−∑j≠isij)ci1fi(19)

3.2 Problem Modeling and Optimization

Based on the above D2D computing task offloading scheme, this paper considers the problem of computing task distribution among different edge nodes, minimizes the total time consumed by the computing task offloading process and the joint learning model training process, and realizes the task offloading process time consumption and model training process time consumption is the optimal compromise between the them. Therefore, the goal of this paper is to minimize the total latency consumed by the joint learning training process by optimizing the amount of data sample unloading {sij}. The problem can be modeled as (P1).

(P1):min{sij}maxi,j∈K{tijoffl(sij)}+M(tdown+maxi∈K{tiloc({sij})+tiup})(20)

s.t.∑j≠isij≤Si,∀i∈K

sij≥0,∀i,j∈K,j≠i(21)

Among them, Eq. (20) indicates that the total amount of data samples unloaded by edge node i cannot exceed the number of data samples it has, and Eq. (21) indicates that the amount of data sample unloading is a non-negative number.

Although the D2D computing task offloading scheme for federated learning increases the time consumed by the D2D computing task offloading process, it can effectively reduce the impact caused by the heterogeneity of computing and communication capabilities between different edge nodes, making each edge node more efficient. The amount of computing tasks is matched with its computing power, reducing the time consumed in the training process of the joint learning model, thereby achieving the goal of minimizing the total time consumed by the entire system. This scheme can achieve the optimal compromise between the time consumption of the computing task unloading process and the time consumption of the model training process.

Since the variables {sij} are discrete variables, problem (P1) is not a convex optimization problem, which makes it difficult to solve.

To facilitate the solution, first relax {sij} to a continuous variable. At the same time, the auxiliary variables Toffl and Tloc_up are introduced. Therefore, the problem (P1) can be transformed into a convex optimization problem, namely (P1.1).

(P1.1):min{sij},Toffl,Tloc_upToffl+M(Tloc_up+Tdown)

s.t.tijoffl(sij)≤Toffl,∀i,j∈K,j≠i(22)

tiloc({sij})+tiup≤Tloc_up,∀i,j∈K,j≠i(23)

∑j≠isij≤Si,∀i∈K(24)

sij≥0,∀i,j∈K,j≠i(25)

Since the problem (P1.1) is a convex optimization problem, the mature convex optimization tool CVX can be used to solve the problem (P1.1), and the continuous solution {sij} can be obtained. On this basis, the continuous solution {sij} is rounded up and down at the same time. By traversing and comparing all the rounding combinations of {sij}, the solution that minimizes the value of the problem is found. The corresponding {sij} is the integer solution of the obtained problem (P1).

4  Simulation Results

In this section, simulation experiments are used to verify that the D2D computing task offloading scheme proposed in this paper achieves a large performance gain for the time consumption of the joint learning process.

4.1 Experimental Configuration

This paper simulates a MEC environment on a cellular network consisting of an edge server and several edge devices. The distribution of edge nodes in the MEC system is shown in Fig. 4, where the transmit power of the edge server is 50 W. The total bandwidth B of the system is 100 MHz, and the noise power spectral density 0 n is −174 dBm/Hz.

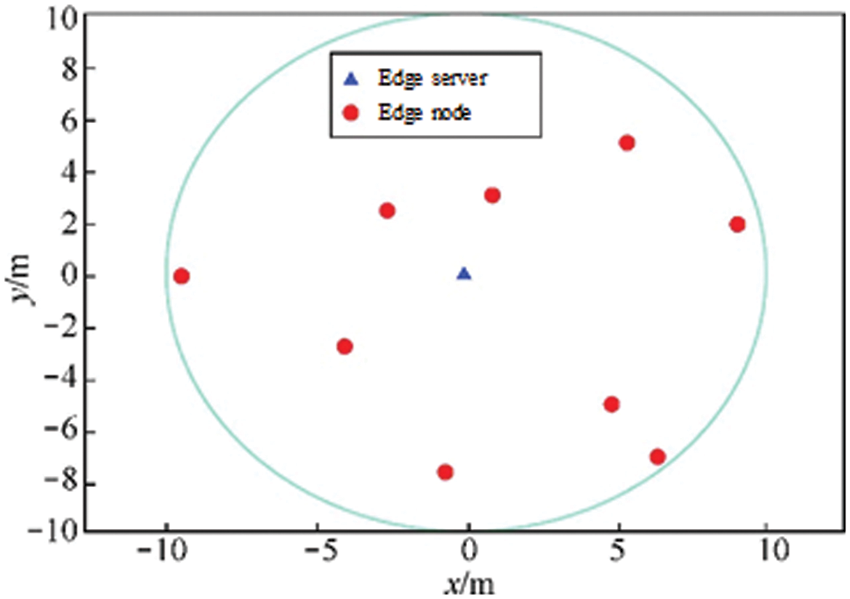
Figure 4: Distribution of edge nodes in the MEC system

In the MEC system, there are three heterogeneous edge nodes for three different types of smartphones to participate in the joint learning model training, which are named as edge node I, edge node II and edge node III. The CPU clock frequency If of the edge node I is 1.5 GHz, the number of floating-point operations cI that can be performed in one CPU clock cycle is 8, and the transmit power PI is 2 W. The CPU clock frequency fII of edge node II is 1.95 GHz, the number of floating-point operations cII that can be performed in one CPU clock cycle is 12, and the transmit power PII is 2 W. The CPU clock frequency fIII of edge node III is 2.6 GHz, the number of floating-point operations cIII that can be performed in one CPU clock cycle is 16, and the transmit power PIII is 2 W. In this paper, it is assumed that edge node I, edge node II and edge node III each have three edge nodes to participate in joint learning, that is, a total of nine edge nodes participate in joint learning.

The public data set used for joint learning model training is the MNIST data set, with a total of 70,000 images of handwritten digits with white characters on a black background, of which 60,000 pictures are training data samples and 10,000 pictures are test data samples [17]. The number of bits b owned by a data sample is 6136 bits. Each data sample has a total of 784 pixels as the characteristics of the data sample, so there are 784 model parameters in total. Assuming that each model parameter has 8 bits, the total number of bits q owned by all model parameters is 6272 bits. There are a total of 10 labels in the MNIST dataset, which are numbers 0 to 9. In this experiment, the joint learning model is used to classify whether the handwritten digits are odd or even.

Before the start of the experiment, all edge nodes have 4500 data samples, and the data set owned by each edge node is assumed to be non-IID. That is, the labels of the data samples owned by each edge node only have the MNIST data set labels.

The training model used in the experiment in this paper is SSVM, and a data sample can be obtained to perform a local model update operation, which requires 2 × 7842 = 1229312 floating-point operations, that is, a = 1229312.

4.2 Results

Given the number of global aggregations M = 40 and the number of local model updates N = 5, Fig. 5 compared the global loss function and model training accuracy of joint learning model training over time before and after D2D computing task offloading, D2D computing task offloading before and after, the global loss function of the joint learning model.

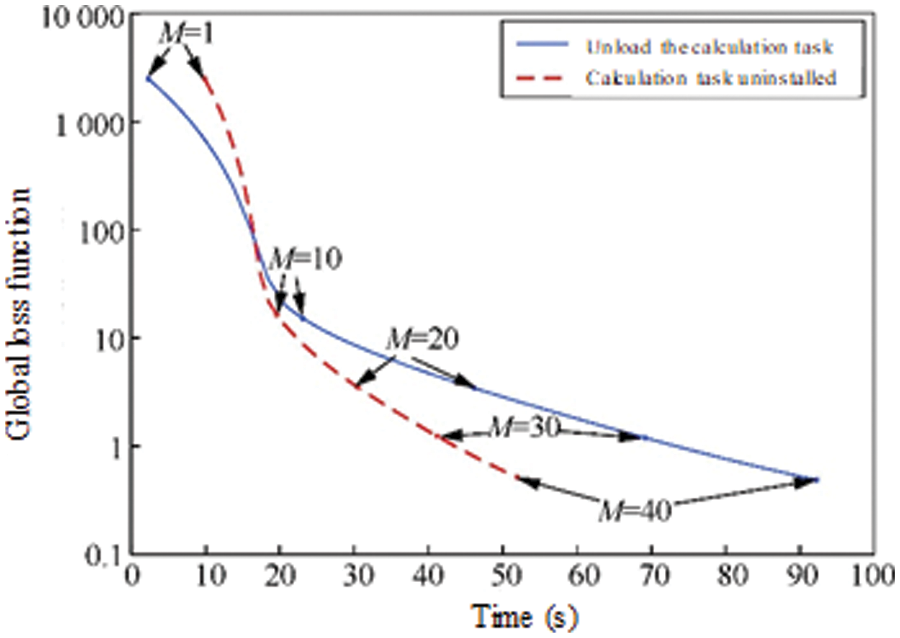
Figure 5: The global loss function of the joint learning model before and after the D2D computing task is unloaded

It can be seen from Fig. 5 that the global loss function of the joint learning model before and after the D2D computing task is unloaded shows a significant downward trend during the training process. Although in the early stage of joint learning model training, the joint learning after D2D computing task unloading needs to consume extra time in the process of computing task unloading, but in the process of model training, its global loss function decline rate per unit time is greater than that without D2D. The decline rate of the global loss function per unit time in the joint learning of computing task offloading shows that the D2D computing task offloading scheme for joint learning not only does not affect the training of the joint learning model, but also can significantly improve the training efficiency of the joint learning model.

The training accuracy of the joint learning model before and after the D2D computing task is unloaded is shown in Fig. 6, which also verifies that the joint learning-oriented D2D computing task offloading scheme can significantly improve the training efficiency of the joint learning model. After completing 40 global aggregations, the training accuracy of the joint learning model before and after D2D computing task unloading is about 0.85 and 0.86, respectively, and the training accuracy of the joint learning model after D2D computing task unloading is higher than that without D2D computing task unloading. The model training accuracy is improved by 0.01, because D2D offloads computing tasks (actually D2D data sample offloading), which weakens the non-IID characteristics of data samples, thereby improving the training accuracy of the joint learning model.

Figure 6: The training accuracy of the federated learning model before and after the D2D computing task is unloaded

Fig. 7 shows the relationship between the time consumption of the system and the accuracy of the model under different global aggregation times before and after the D2D computing task is unloaded. There are five points on each line, which are the points corresponding to the time consumption of the system and the accuracy of the model when M is 10, 20, 30, 40 and 50.

Figure 7: The relationship between system time consumption and model accuracy under different global aggregation times before and after D2D computing task unloading

It can be seen from Fig. 7 that when M is small, the difference in total time consumed by the system before and after D2D computing task unloading is not large, but its accuracy is low. However, with the increase of M, the training accuracy of the joint learning model before and after the offloading of D2D computing tasks continues to improve, but the gap of the total time consumed by the system continues to increase, and the total time consumed by the system for offloading D2D computing tasks Significantly less than the total time consumed by a system without D2D computational task offloading. In practice, joint learning model training often requires a large number of global aggregations to make the joint learning model perform better. Therefore, in practical applications, the D2D computing task offloading scheme for joint learning proposed in this paper can effectively reduce the time consumed by the joint learning model training and significantly improve the training efficiency of the joint learning model. Given the same M, the training accuracy of the joint learning model after D2D computing task offloading is higher than the training accuracy of the joint learning model without D2D computing task offloading. The computing task offloading scheme can also reduce the influence of the non-IID characteristics of the data and improve the accuracy of model training.

5  Conclusion

This paper considers the joint learning model of joint edge server and multiple edge nodes in the MEC system, studies the influence of edge node communication and computing heterogeneity on the training efficiency of joint learning model, and proposes a D2D computing task for joint learning. The unloading scheme, by allocating the number of data samples of edge nodes participating in joint learning, realizes the optimal compromise between the time consumed by data sample unloading and the time consumed by joint learning model training, so as to minimize the time consumed by the system. The simulation results verify that the D2D computing task offloading scheme for joint learning proposed in this paper can effectively reduce the impact of the heterogeneity of edge node computing and communication capabilities, significantly improve the training efficiency of the joint learning model, and at the same time, it can reduce the non-independence of data. The influence of the same distribution characteristic improves the training accuracy of the joint learning model. The future work is to consider different other parameters and evaluate the proposed method.

Acknowledgement: The authors would like to thanks the editors and reviewers for their review and recommendations.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

    1. O. Hamid, R. Abduljabbar and N. Alhyani, “Fast and robust approach for data security in communication channel using pascal matrix,” Indonesian Journal of Electrical Engineering and Computer Science, vol. 19, no. 1, pp. 248–256, 2020. [Google Scholar]

    2. S. Khodhair, M. Nagmash, R. B. Abduljabbar and A. Alrawi, “Minimum delay congestion control in differentiated service communication networks,” The Open Electrical & Electronic Engineering Journal, vol. 12, no. 3, pp. 42–51, 2018. [Google Scholar]

    3. S. Bashir, M. H. Alsharif, I. Khan, M. A. Albreem, A. Sali et al., “MIMO-Terahertz in 6G nano-communications: Channel modeling and analysis,” Computers, Materials & Continua, vol. 66, no. 1, pp. 263–274, 2020. [Google Scholar]

    4. A. Amin, X. Liu, I. Khan, P. Uthansakul, M. Forsat et al., “A robust resource allocation scheme for device-to-device communications based on Q-learning,” Computers, Materials & Continua, vol. 65, no. 2, pp. 1487–1505, 2020. [Google Scholar]

    5. S. Alemaishat, O. A. Saraereh, I. Khan, S. H. Affes, X. Li et al., “An efficient precoding scheme for millimeter-wave massive MIMO systems,” Electronics, vol. 8, no. 9, pp. 1–15, 2019. [Google Scholar]

    6. A. Al-Nimrat, M. Smadi, O. A. Saraereh and I. Khan, “An efficient channel estimation scheme for mmwave massive MIMO systems,” in Proc. IEEE Int. Conf. on Communication, Networks and Satellite (ComNetSat), Makassar, Indonesia, pp. 1–8, 2019. [Google Scholar]

    7. I. Khan and D. Singh, “Efficient compressive sensing based sparse channel estimation for 5G massive MIMO systems,” AEU-International Journal of Electronics and Communications, vol. 89, pp. 181–190, 2018. [Google Scholar]

    8. A. Amin, X. H. Liu, M. A. Saleem, S. Henna, T. Islam et al., “Collaborative wireless power transfer in wireless rechargeable sensor networks,” Wireless Communications and Mobile Computing, vol. 9701531, pp. 1–13, 2020. [Google Scholar]

    9. F. Jameel, T. Ristaniemi, I. Khan and B. M. Lee, “Simultaneous harvest-and-transmit ambient backscatter communications under Rayleigh fading,” EURASIP Journal on Wireless Communications and Networking, vol. 19, no. 1, pp. 1–9, 2019. [Google Scholar]

  10. W. Shahjehan, S. Bashir, S. L. Mohammed, A. B. Fakhri, A. A. Isaiah et al., “Efficient modulation scheme for intermediate relay-aided IoT networks,” Applied Sciences, vol. 10, no. 6, pp. 1–12, 2020. [Google Scholar]

  11. O. A. Saraereh, A. Alsaraira, I. Khan and B. J. Choi, “A hybrid energy harvesting design for on-body internet-of-things (IoT) networks,” Sensors, vol. 20, no. 2, pp. 1–14, 2020. [Google Scholar]

  12. T. Jabeen, Z. Ali, W. U. Khan, F. Jameel, I. Khan et al., “Joint power allocation and link selection for multi-carrier buffer aided relay network,” Electronics, vol. 8, no. 6, pp. 1–15, 2019. [Google Scholar]

  13. S. Alemaishat, O. A. Saraereh, I. Khan and B. J. Choi, “An efficient resource allocation algorithm for D2D communications based on noma,” IEEE Access, vol. 7, pp. 120238–120247, 2019. [Google Scholar]

  14. R. A. Alhameed, I. Elfergani and I. Rodriguez, “Recent technical developments in energy-efficient 5G mobile cells: Present and future,” Electronics, vol. 9, no. 4, pp. 1–4, 2020. [Google Scholar]

  15. S. Safavat, N. Sapavath and D. Rawat, “Recent advances in mobile edge computing and content caching,” Digital Communications and Networks, vol. 6, no. 2, pp. 189–194, 2020. [Google Scholar]

  16. M. Mehrabi, S. Shen, Y. Hai, V. Latzko, G. Koudouridis et al., “Mobility- and energy-aware cooperative edge offloading for dependent computation tasks,” Network Journal, vol. 1, no. 2, pp. 1–12, 2020. [Google Scholar]

  17. Z. Abbas, Z. Ali, G. Abbas, L. Jiao, M. Bilal et al., “Computational offloading in mobile edge with comprehensive and energy efficient cost function: A deep learning approach,” Sensors, vol. 21, no. 10, pp. 1–18, 2021. [Google Scholar]

  18. B. Letaief, W. Chen and Y. Shi, “The roadmap to 6G: AI empowered wireless networks,” IEEE Communications Magazine, vol. 57, no. 8, pp. 84–90, 2019. [Google Scholar]

  19. M. Chen, Y. Miao, H. Gharavi, L. Hu and I. Humar, “Intelligent traffic adaptive resource allocation for edge computing-based 5G networks,” IEEE Transactions on Cognitive Communications and Networking, vol. 6, no. 2, pp. 499–508, 2020. [Google Scholar]

  20. J. Konecny, M. Brendan and D. Ramage, “Federated machine learning: Concept and applications,” ACM Transactions on Intelligent Systems and Technology, vol. 10, no. 2, pp. 1–17, 2019. [Google Scholar]

  21. J. Zhang, H. Tu and Y. Ren, “An adaptive synchronous parallel strategy for distributed machine learning,” IEEE Access, vol. 18, no. 6, pp. 19222–19230, 2018. [Google Scholar]

  22. M. Hosseinzadeh, A. Hemmati and A. Rahmani, “Federated learning-based IoT: A systematic literature review,” International Journal of Communication Systems, vol. 35, no. 11, pp. 518–533, 2022. [Google Scholar]

  23. C. Xie, O. Koyejo and I. Gupta, “ZenoPS: A distributed learning system integrating communication efficiency and security,” Algorithms Journal, vol. 15, no. 7, pp. 1–18, 2022. [Google Scholar]

  24. S. Wang, T. Tuor and T. Salonidis, “Adaptive federated learning in resource constrained edge computing systems,” IEEE Journal on Selected Areas in Communications, vol. 37, no. 6, pp. 1205–1221, 2019. [Google Scholar]

  25. B. Guo, Y. Liu and C. Zhang, “A partition based gradient compression algorithm for distributed training in AIoT,” Sensors Journal, vol. 21, no. 6, pp. 1–19, 2021. [Google Scholar]

  26. X. Li, G. Zhu and Y. Cong, “Wirelessly powered data aggregation for IoT via over-the-air function computation: Beamforming and power control,” IEEE Transactions on Wireless Communications, vol. 18, no. 7, pp. 3437–3452, 2019. [Google Scholar]

  27. M. Liyanage, P. Porambage, A. Ding and A. Kalla, “Driving forces for multi-access edge computing (MEC) IoT integration in 5G,” ICT Express, vol. 7, no. 2, pp. 127–137, 2021. [Google Scholar]

  28. J. Xu, L. Chen and K. Liu, “Designing security-aware incentives for computation offloading via device-to-device communication,” IEEE Transactions on Wireless Communications, vol. 17, no. 9, pp. 6053–6066, 2018. [Google Scholar]

  29. S. Lee, Y. Tcha and S. Seo, “Efficient use of multicast and unicast channels for multicast service transmission,” IEEE Transactions on Communications, vol. 59, no. 5, pp. 1264–1267, 2019. [Google Scholar]

  30. J. Ibanez, J. Alonso, P. Jorda, E. Defez and J. Sastre, “Two taylor algorithms for computing the action of the matrix exponential on a vector,” Algorithms Journal, vol. 15, no. 2, pp. 1–19, 2022. [Google Scholar]

  31. J. Park, S. Lee, H. Kim, S. Song and S. Kang, “System invariant method for ultrasonic flaw classification in weldments using residual neural network,” Applied Sciences, vol. 12, no. 3, pp. 1–17, 2022. [Google Scholar]