Combined Effect of Concept Drift and Class Imbalance on Model Performance During Stream Classification

1  Introduction

In recent years, with the development of technology and high-speed internet, the internet of things (IoT) based applications generate huge amounts of data, which are called data streams. Electricity price prediction, smart health systems, credit card transactions, social websites, and telecommunications are common examples of applications that generate data streams. Classification of these data streams is very challenging because the data streams are characterized as high-speed, non-stationary data distribution, the number of classes is not fixed, and it is infinite in length [1]. Due to such characteristics, the data streams contain inbuilt problems of concept drift and class imbalance. The concept drift is a situation where statistical properties of the target variable, which the model is attempting to forecast change in unexpected ways over the period of time [2,3]. Hence, the efficiency of the classifiers learned from previous data degrades due to the change in target concepts in new data [4]. Class imbalance is a problem where the data distribution among the classes is not the same. Instances in one class are significantly underrepresented known as minority class in comparison to instances in another class having a huge amount of data samples known as majority class [5]. If a classifier is trained on imbalanced data it becomes biased toward majority class instances and misclassifies the minority class instances [6]. When class imbalance and concept drift arise concurrently, the problem becomes much more difficult to solve [7]. Many real-world applications are affected by both class imbalance and concept drift in various domains such as software engineering [8], social media mining [9], risk management [10], and anomaly detection [11]. The difficulty comes from the fact that the solution of one problem may have an impact on the treatment of another. The conventional classification and drift detection algorithms can be sensitive to the class imbalance issue and become less accurate. Similarly, class imbalance strategies can be inaccurate in properly balancing the data if they do not consider the changing class imbalance ratio and change in data distribution among different classes [12].

Efforts have been made in the literature to cope with the joint problem of concept drift and class imbalance. The existing studies are dealing with both the problems individually without further understanding and addressing the impact of one problem on the other. We refer to [3,5] for more details about techniques for concept drift and class imbalance. To identify the effects of the concept drift on classifier’s performance few experimental studies are conducted such as [13,14]. The study [13] was limited to identifying the challenges of concept drift detection when data is imbalanced. Whereas the focus of the study [14] was to compare the performance of a single classifier with the ensemble approach (multiple classifiers) in handling concept drift. Another recent experimental study [15] analyzed the effect of class imbalance ratio on classifier’s performance, but it did not consider the concept drift problem, also, the drift adaptation in presence of class imbalance was not properly addressed. Moreover, the study used datasets with different predefined class imbalance ratios. In contrast to data streams where the class imbalance ratio is not known, and it can change drastically resulting shift from minority class to majority and vice versa [16]. In [17] authors investigated the effect of concept drift on the single-class results of online models using three distinct forms of classifiers in different scenarios involving class imbalance. Their focus was to find how concept drift impacts each class’s output when the data is skewed and does a shift in the class composition have an impact on the identification of concept drift. The authors track the current recall of the online model for each class. The study demonstrates that identifying drift in unbalanced data streams is more challenging than it is in balanced data streams. The study was limited to monitor the recall only which is not enough. For a better understanding of the problem, other performance measures like precision, F1 score, and geometric mean should also be considered.

1.1 Motivation

The concept drift and class imbalance are inbuilt problems of data streams; therefore, it is very necessary to understand their correlation before proposing any solution to address both issues at a time. To the best of our knowledge, none of the existing studies focused on identifying the correlation between concept drift and class imbalance and their effect on minority and majority classes on different performance measures. Therefore, the current study aims to fill this gap.

We present an experimental insight to answer the two research questions. 1) Does class imbalance further contribute to performance degradation if it occurs concurrently with the concept drift? The answer to this question will help in identifying the impact of the joint problem and the correlation between class imbalance and concept drift. 2) What is the effect of change in class imbalance ratio on the minority as well as majority class in presence of concept drift? Does it equally affect precision and recall?

Addressing the class imbalance problem research community mostly focuses on the minority class. In the case of data stream learning due to a change in imbalance ratio majority class may also be affected. Therefore, identifying the effect of change in class imbalance ratio on both minority as well as majority classes will help in understanding the problem in depth. When the data is skewed, achieving high accuracy is not sufficient. The aim is to achieve more correct (precision) and more complete (recall) results. Achieving high precision may sometimes decrease recall and vice versa. To achieve high values for precision and recall it is necessary to understand the impact of concept drift and class imbalance on these performance measures. The outcome of these research questions will help in designing better solutions for addressing the joint problem of concept drift and class imbalance for learning from nonstationary data streams.

1.2 Contribution

In this paper, we perform experimental analysis on the classification performance of state-of-the-art algorithms proposed for the classification of non-stationary data streams. The experiments are performed on benchmark binary class datasets containing class imbalance and concept drift issues. The contribution of our work is summarized as follows:

1.    This work analyzed the correlation between concept drift and class imbalance for streaming data

2.    The study experimentally evaluated the impact of concept drift and change in class imbalance ratio on each class (minority and majority) using precision and recall

3.    The classification was performed using four different classifiers and the class imbalance was addressed using three different data balancing approaches to get more generalized outcomes of the study.

We discuss existing approaches proposed for addressing the issues of class imbalance and concept drift in Section 2. Section 3 describes the methodology applied to perform the experiments. Results are discussed in Section 4. In Section 5 we conclude our work and suggest some guidelines based on our experimental results which can help in designing better solutions for addressing the joint problem for non-stationary data stream classification.

2  Literature Review

Most of the existing approaches proposed for dealing with class imbalance and concept drift work independently. The class imbalance handling approaches are generally categorized into three groups: data-based, algorithm-based, and ensemble-based systems [6,18]. Most of the approaches are proposed for static data where the class imbalance ratio for minority and majority classes is known. The most common approaches to deal with class imbalance are Random Oversampling (ROS), Random Under Sampling (RUS), and Synthetic Minority Oversampling Technique (SMOTE). The approaches proposed for the dynamic environment such as Adaptive synthetic sampling (ADASYN) which identifies nearest neighbors for each minority instance, and then count the number of majority examples in these neighbor instances to calculate the ratio which is ultimately used for deciding the number of instances generated for each instance. The selectively recursive approach (SERA) [19] suggested chunk-based learning for dealing with class imbalance. It balances minority classes in the current chunk by selecting the most appropriate minority samples using Mahalanobis distance from the previous chunk. The recursive ensemble approach (REA) [20], employs the k-nearest neighbor theory to pick minority examples from the previous chunk that have trends close to those of the most recent chunk to balance the data.

Concept drift handling approaches on the other hand can be classified in many forms, including online learning algorithms [17,21,22] vs. batch learning algorithms [23,24]; single classifier [25] vs. ensemble-based or multiple classifiers approaches [26–29]; and active [30] vs. passive [31] approaches. The active learning approaches use a drift detection system only in the presence of drift. Whereas the passive learning approaches presume possible continuing drift and constantly refresh the model with new data (set). While online learning algorithms learn one example at a time, batch learning algorithms involve blocks of instances. Online learners exhibit greater plasticity but less flexibility. Additionally, they are more susceptible to noise and the order in which data are delivered. Although batch learners profit from the existence of large volumes of data and have superior reliability properties, they may be inefficient when the batch size is too limited or when data from different environments are used in the batch.

Some studies address the joint problem of concept drift and class imbalance such as the Dynamic Weighted Majority (DWM) based ensemble approach proposed in [32] to deal with concept drift in online learning, it maintains a weighted pool of classifiers (experts), when any classifier produces wrong results its weights are decreased, the weights are normalized and ranged in 0 to 1 (0 = poor performance, 1 = high performance) and after reaching to the specified threshold the classifier is removed from the ensemble and a new classifier is added to the ensemble with weight = 1 and trained on the new data. The DWM uses the classifier’s prediction and its weights to calculate a weighted sum of each class, and the class with the height weight is considered a global prediction.

Ensemble-based algorithm for nonstationary environments (NSE) proposed in [31] as an extension of learn++ called Learn++.NSE. Initially, the ensemble is initialized with a single classifier created on the first available data batch. The ensemble is tested on new data and the misclassified data examples are identified and a new classifier is added to the ensemble. Each new and old classifier of the ensemble is evaluated on the training data. The classifiers which identify the previously misclassified examples are given more credit and those which misclassify such data are penalized. The final output is achieved using weighted majority voting of the current members of the ensemble. Wang et al. [33] introduced an online class imbalance learning system consisting of class imbalance identification, drift detection, and adaptive online learning. They regarded a shift in the ratio of class imbalance as a kind of drift. They suggested bagging-based methods for oversampling and under sampling to deal with evolving class imbalances and class swapping. Based on this work, a modified version named Weighted Ensemble Online Begging (WEOB) [34] was proposed, which employs adaptive weights and models dynamic relationships between groups using definitions of multi-minority and multi-majority classes. Ghazikhani et al. [35] developed a neural network-based two-layer online ensemble model to deal with concept drift and class imbalance in data streams. Cost-sensitive learning is incorporated during the learning process to address the class disparity. They suggested a Window Based Weighting solution for dealing with concept drift. The window-based weighting strategy increases the weight of the applicant classifier when it forecasts correctly and reduces it when it predicts wrong results.

Mirza et al. suggested an ensemble of an online sequential extreme learning machine (ESOS-ELM) [36] to deal with a class disparity of concept drifting data streams. Based on the balance data, the model was educated. It detects abrupt drift as model output falls below a threshold, and they used statistical decision theory to detect gradual drift. It incorporates both short and long memory to store historical data to retrain the model in the event of drift, as well as two distinct lists of classifiers educated on minority and majority class samples. The system provided no provision for minority class drift. The study [9] suggested a class-based ensemble approach to class evolution (CBCE) for identifying emerging, fading, and reappearing classes in online learning. For every new class, it retains a separate model and upgrades it when new examples are introduced. If an instance of a class does not exist after an extended period, the class is known to be fading. If a class disappeared historically and any instances reappeared, it is known to be reoccurring. The model’s final output is determined by the highest output among the outputs of CB classifiers. To address the dynamic class imbalance dilemma, a new method was created based on under-sampling. The CBCE has difficulty dealing with multiple and diverse groups.

Gomes et al. [37] presented an adaptive version of the Random Forest Classifier (ARFC) by using the online bagging-based resampling and updated adaptive approach to deal with different types of concept drifts in evolving data streams. The adaptive approach they proposed is to train the background tree for each tree for which a warning signal is generated. When the actual drift has been detected the tree which generated the warning is replaced with its respective background tree (which was trained in the background after the detection of the warning). The ARFC can work as instance based as well as chunk based. The online bagging-based resampling is used to handle the class imbalance issue in input data streams. The proposed method is not suitable in environments where true labels of data are not available or delayed.

Lin et al. [38] introduced an ensemble learning paradigm to address the concept drift. The hierarchical AdaBoost.NC was used to train the model in conjunction with SMOTE to oversample the minority class to address the data imbalance issue. The Linear Four Rates (LFR) [39] technique was used in the second stage to identify concept drift. The final stage involves creating a new classifier by merging stage one (pre-drift) and stage two classifiers (after the drift). The study [40] proposed Drift Detector and Resampling Ensemble (CDRE) method for resolving concept drift and multiclass imbalance issues. It stores minority samples from current data streams to perform resampling if new data streams contain insufficient minority samples. Additionally, by comparing the number of classes in the current and the previous data stream block, new classes and incomplete classes are detected, or what is known as concept drift. If none of the examples are associated with the stored samples, it produces an alert signal. The CDRE is tasked with detecting the emergence of a new class as a result of concept drift. In [41], the researchers recommend a hierarchical sampling method and an ensemble methodology to resolve class imbalance and concept drift. They measured the difference between minority and majority groups using minority and majority class statistical means. If the measured mean is greater than the given threshold, they consider the arrival of class imbalance and concept drift. They picked characteristics from the majority class that were more like those of the minority class to balance the data. The balancing module was often used to train the candidate classifier on fresh data and to substitute the less reliable candidate classifier with the newly trained classifier using the ensemble technique.

Li et al. [42] suggested Dynamic Updated Ensemble (DUE) as a chunk-based ensemble approach that generates multiple candidate classifiers for each block and weights them using a piece-wise process. The weights of previous ensemble participants are determined by their results on the most recent examples and their consistency rating, and when the ensemble size approaches a predefined threshold, the ensemble’s worst-performing classifiers are eliminated. They employ bagging as a mechanism for responding to the new situation created when the minority and majority classes are swapped. To deal with extremely skewed data streams, the research carried out by [43] proposes a framework that combines Dynamic Ensemble Selection with preprocessing approaches (including both oversampling and undersampling). A strategy that uses bagging classifiers that are diversified via the use of stratified bagging and that executes sampling with replacement independently from the minority class and the majority class was suggested. Bagging-based approaches require a significant amount of time and are, as a result, not recommended for continuously streaming data. This strategy can only be used for problems involving binary classes; nevertheless, most applications in the actual world create multi-class data streams. Online updating of the best predictor is accomplished using a segment-based drift adaptation approach (SEGA) by [44]. The drift-gradient is defined on a portion of the training set. It measures the widening of the gap between the oldest and newest segments. In other words, if the drift-gradient on the old segment is smaller, then the new instance’s distribution is more closely aligned with that of the old segment. SEGA retrains predictors using just a portion of the training data instead of the whole dataset, which is prevalent in current research on concept drift adaptability. Segments in SEGA are defined by the time frames of instances. It’s difficult to choose the appropriate ensemble predictor, the training set size, and the number of segments for real-world data streams, hence this segment is not applicable. An optimized two-sided Cusum churn detector (OTCCD) was suggested in study [45] that combines rising and dropping mean averages to identify drift. Based on Cumulative Sum Drift Method (CusumDM) [46] and motivated by concerns of class imbalance left out while dealing with higher accuracies, OTCCD is an innovative approach for identifying concept drift and addressing the class imbalance in data streams. The fundamental goal of this research was to provide a solution for data stream mining that addresses concept drift and class imbalance while also outperforming its predecessors. SMOTE was utilized to balance the data accessible in the sliding window using a sliding window-based technique. To determine whether there had been any drift, they used the Cusum test. The data in the current window was first balanced, and then a drift detector was applied. This is a poor method for identifying drift. Disturbance data should be able to tell the drift detector apart. Synthetic data generated with SMOTE might confuse the drift detection process. Passive drift detection ensembles with the smartness of G-mean maximization and aging-based adaptive learning have recently been suggested by researchers in [47]. It consists of a core group of five foundational ensembles. In this way, it creates smart pools of data that map to the same region of feature space. These pools lead to the sub-ensembles with the most local competence in that feature area that are most likely to produce the best outcomes. It follows the test-and-learn model of online learning. As data changes over time, it uses an aging-based method to ignore the older data and place a greater emphasis on the more current data. G-mean maximization is the goal when dealing with data stream skewness. It may be difficult to use this strategy in situations when previous notions reappear.

All these studies deal with class imbalance and concept drift separately without identifying the impact of one problem on the solution of another problem. Hence there is a need of identifying the correlation between concept drift and different factors of class imbalance and the impact of one problem on the solution of the other.

3  Methodology

The core aim of the experiments is to identify the correlation among factors of class imbalance and concept drift and the effect of change in class imbalance ratio on classifier performance in terms of precision and recall. We also aim to identify the effect of the joint problem on individual classes. The evaluation is performed on the prequential method where incoming samples are used for testing first and then used for training. Hence, we incrementally track the performance at each data chunk. Experiments are performed with four state-of-the-art classifiers on two synthetic and one real benchmark dataset. Details of datasets and classifiers are given in Section 3.1. We performed experiments based on the following two scenarios which are also presented in Fig. 1.

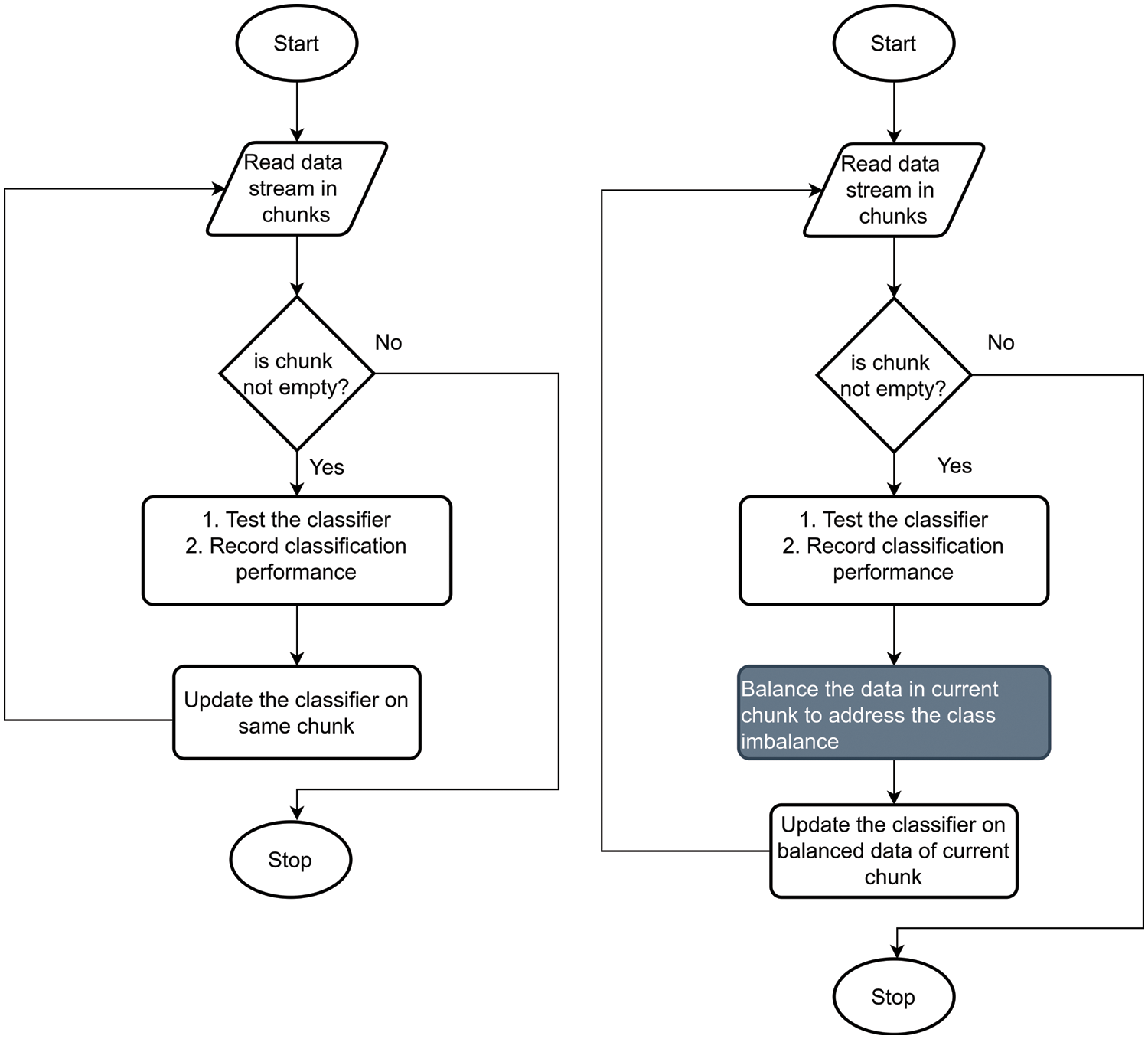
Figure 1: Flow diagram of experimental methodology

Scenario-1: Data streams are classified as received and performance is recorded. The classifier is updated without externally balancing the data.

Scenario-2: Data streams are classified as received and performance is recorded. The classifier is updated by balancing the data using ROS, RUS, and SMOTE before the classifier adaptation phase

We perform a separate experiment for both scenarios. For the first experiment, data streams are classified as received without externally balancing the data, and the performance scores are recorded for the current chunk. We calculate the class imbalance ratio at each chunk and the same chunk is then used to update the classifier so that classifier can adapt to the changes. In the second experiment we followed the same method but with one difference that is we addressed the class imbalance problem by balancing the data using ROS, RUS, and SMOTE before the classifier adaptation phase. The flow diagram of the methodology followed to perform both experiments is presented in Fig. 1. The Scikit-Multiflow and imbalance-learn python libraries were used in the experiment. The Scikit-Multiflow provides an implementation of ensemble and tree-based classifiers to learn from the data streams. Whereas, imbalance-learn provides implementations of data balancing techniques. In this study, the performance of four state-of-the-art classifiers namely Adaptive Random Forest Classifier (ARFC) [37], Learn++.NSE [27], Dynamic Weighted Majority Classifier (DWMC) [36], and Hoeffding Adaptive Tree Classifier (HATC) [38] were evaluated in the above-mentioned scenarios. In this study we will refer Learn++.NSE as LPPNSEC. These classifiers are specially designed for classifying the non-stationary data streams. The ARFC uses Adaptive Window (ADWIN) for drift detection and uses online bagging to handle the class imbalance in evolving data streams. The LPPNSEC creates a new classifier for each new batch of data and adds to an ensemble using a dynamic weighted majority vote to address the changes in data distribution. DWMC Ensemble approach adds and removes the experts (classifiers) from the ensemble based on its performance (weights) to address the concept drift. Hoeffding Tree is a Tree-based incremental approach to deal with the drifting data streams.

3.1 Datasets

The datasets used in current experimental study are explained below.

3.1.1 Similarity Ensemble Approach (SEA)

There are four different blocks of data in SEA dataset. The three-dimensional feature space of each block contains 15000 random points. The three characteristics have randomly generated values in the range [0; 10), and only the first two are pertinent. In each block, a data point belongs to class 1, if f1 + f2 ≤ θ and class 0 otherwise, where f1 and f2 represent the first two features, and θ is a threshold value for the two classes. Threshold values for the four data blocks are 8, 9, 7, and 9.5 in sequence. The experiment is set up as follows: We randomly selected 1000 samples from the first block for training and 2500 samples from every four blocks for testing. The window size is chosen as 500 points, hence after the first five chunks from block 1 concept changes to block 2, similarly after the next five chunks (10th chunk) concept changes to block 3 and after the next 5 chunks (15th chunk) concept changes to block 4.

3.1.2 SINE1

In SINE1 dataset there are 5 blocks of data with different concepts. Each block contains 20000 random points of two-dimensional feature space (x1, and x2) with equal data distribution. The classification function y = sin(x), if the data instances are under the curve they are considered positive and considered negative otherwise. Like the SEA dataset, we randomly selected 1000 samples from the first block for training and 2500 samples from every five blocks for testing. The window size is chosen as 500 points, hence after the first five chunks from block 1 concept changes to block 2, similarly after the next five chunks (10th chunk) concept changes to block 3, and so on.

3.1.3 Electricity Dataset 2 (ELEC2)

The electricity pricing dataset Elec2 [48] is used in our experiment to simulate the concept drift and class imbalance environment, which originally contains 45312 samples drawn from 7 May 1996 to 5 December 1998 with one sample for every half an hour (48 samples per day) from the electricity market in New South Wales, Australia. This dataset provides time and demand fluctuations in the price of electricity in New South Wales, Australia. The day, period, New South Wales electricity demand, Victoria electricity demand, and the scheduled electricity transfer between the two states are used as the input features to predict whether the price of New South Wales will be higher or lower than that of Victoria as in a 24-h period (or 48 instances). Usually, a data chunk consists of seven days (7*48) of data which is 336 instances.

For the experiment, we used 20 days of historical data (20 * 48 = 960) for training as done by [49] and the remaining data 44352 samples for testing. Testing data is converted into 132 chunks (weeks), each chunk contains 336 samples i.e., 48 * 7.

3.2 Evaluation Metrics

The most used performance measure metrics in the past have been total accuracy and error rate. When data is imbalanced, however, they are heavily skewed in favor of the majority class. To avoid this, the performance of the classifiers is also measured on Precision, Recall, F1 score, and geometric mean. The evaluation is performed on the prequential method where incoming samples are used for testing first and then used for training. Hence, we incrementally track the performance at each data chunk.

4  Results & Discussions

We discuss results one by one as per our research questions, so the results of each question are discussed below:

4.1 Effect of Change in Class Imbalance Ratio and Concept Drift on Model Performance

In this section we answer Question One by performing experiments on two different scenarios which are discussed below:

4.1.1 Scenario–1

In the first scenario, all four classifiers are tested on the SEA and ELEC2 datasets to observe their performance in presence of class imbalance and concept drift. Both the datasets are imbalanced in nature and contain concept drift. For the SEA dataset, the drift location is known whereas, for the ELEC2 dataset drift locations are unknown. For the SEA dataset, it can be observed in Fig. 2, that the performance (in terms of accuracy and G-mean) of all the classifiers was decreased especially at the point where concept drift has occurred such as at points 5, 10 and 15. It can be observed that the performance of all the classifiers has decreased from around 5% to 12%. The LPPNSEC produced the lowest accuracy and g-mean as compared to the other three classifiers. It can also be observed that there is a drastic change in class imbalance ratio mostly at the same locations where the concept drift has occurred. So, it is not very clear whether the performance of classifiers is affected by only concept drift, or it was because of class imbalance. To get more understanding of the results we addressed the class imbalance issue and then performed the experiments which are discussed in Sub-Section 4.1.2.

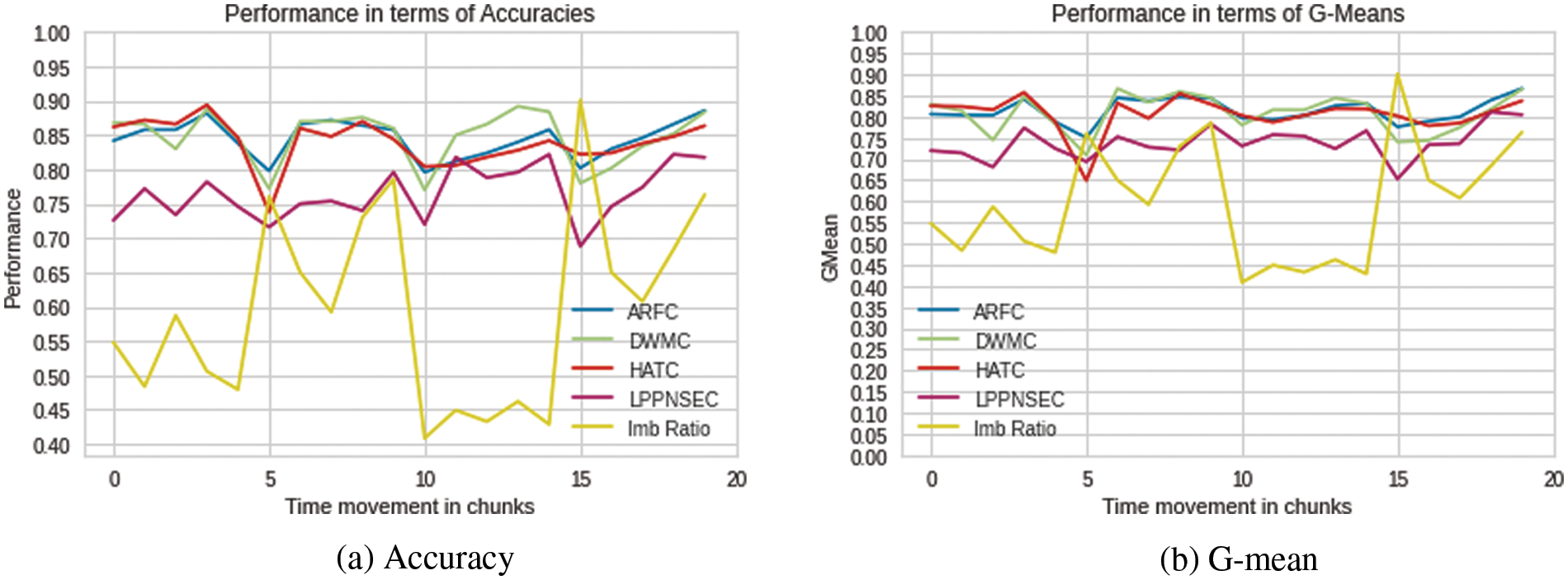
Figure 2: Performance of classifiers on SEA dataset

Figs. 3a–3d shows the performance of all four classifiers on the ELEC2 dataset. Although the concept drift positions are unknown in the ELEC2 dataset, the change in class imbalance ratio can be observed. According to a study [4], in the electricity dataset, the change in class imbalance ratio is declared as concept drift. The results of all the four classifiers on the ELEC2 dataset also show that in most of the times when there is a change in class imbalance the performance of the classifier is decreased from 10% to 60% depending on the change in imbalance ratio. The data is balanced when the imbalance ratio is 1 and the imbalance otherwise. The data is highly imbalanced if the imbalance ratio is far from 1.

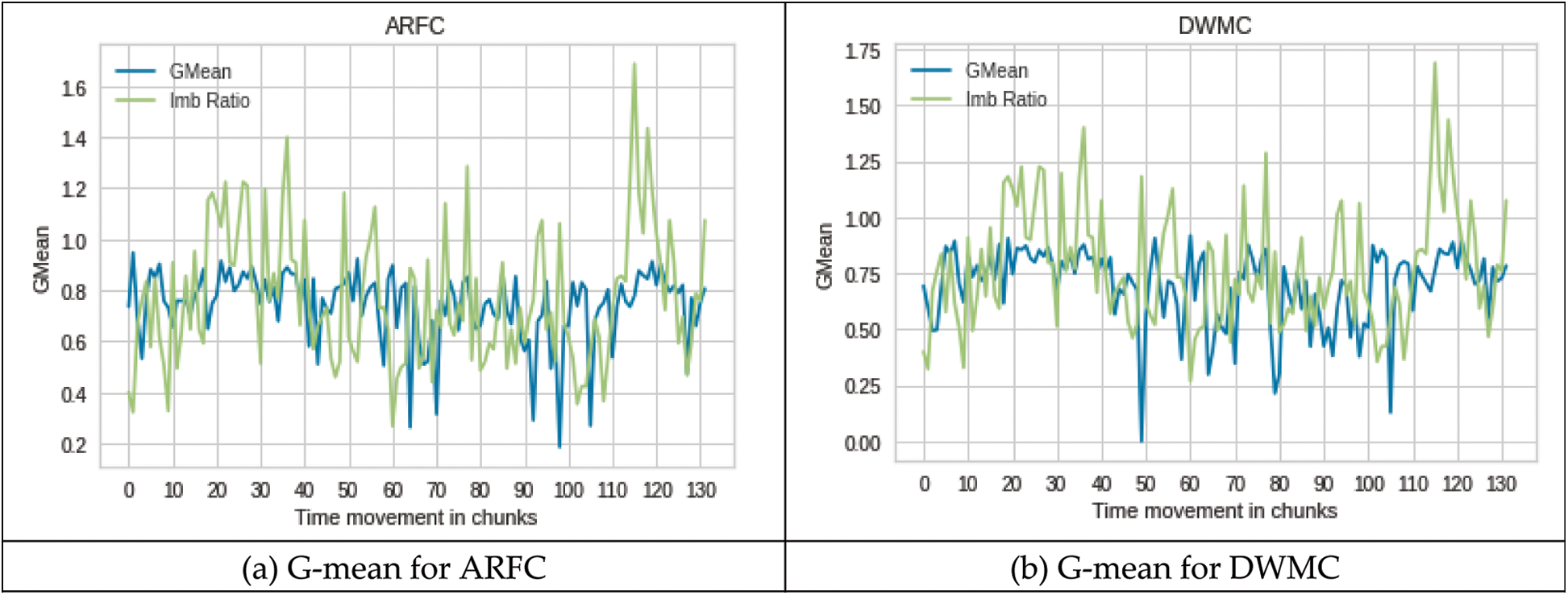
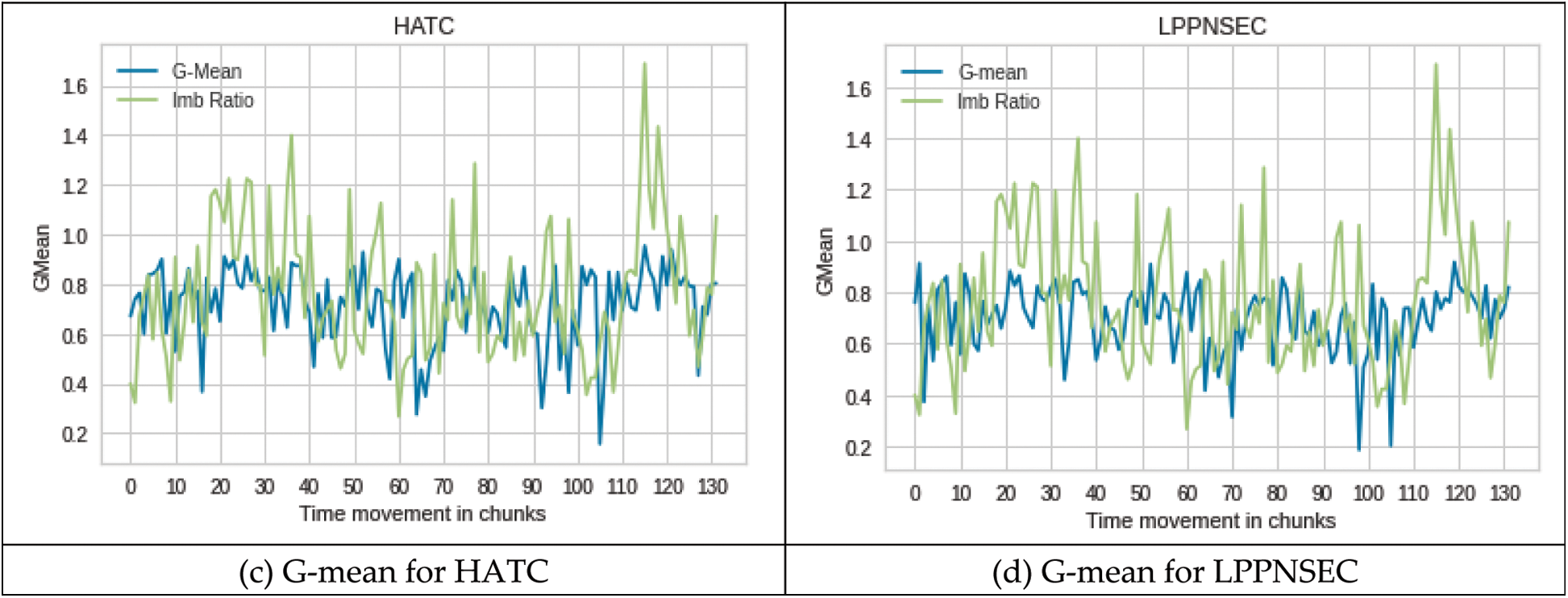
Figure 3: Performance on ELEC2 dataset

4.1.2 Scenario–2

To further analyze whether the decrease in performance is because of concept drift or change in class imbalance ratio we used the most well-known and simplest data balancing approaches i.e., Random Over sampling, Random Under sampling and SMOTE to balance the data before retraining the classifiers to see the effect on balance data for scenario-2. Here we assume that if performance is fully improved after balancing the data that means a decrease in performance was because of class imbalance, if the performance is partially improved then we consider that both class imbalance and concept drift contributed to the performance decrease. If the performance is not improved at all then we consider the performance was decreased because of concept drift only. After applying data balancing approaches the performance of each classifier is tested and the result is compared with the actual results i.e., without applying data balancing approaches. The performance of each classifier is discussed separately below.

ARFC: The decrease in performance of ARFC when concept drift and class imbalance occurred together, has now partially improved its performance after retraining the classifier on balanced data. Figs. 4b and 4c shows that performance was improved at chunk position 5 after training the ARFC on balanced data using ROS and SMOTE, which proves that the concept drift was not the only factor to decrease the performance. The change in class imbalance also contributed to performance degradation which was recovered by balancing the data. At chunk 10 where second drift occurred with a change in class imbalance ratio, RUS showed slightly improved performance whereas ROS and SMOTE decreased the performance as compared to the performance on normal (imbalance) data. At chunk 15, balancing the data with SMOTE and RUS showed an increase in performance. However, RUS produced zero g-mean for initial chunks. In general, ARFC produced better results when data was balanced with SMOTE compared to ROS and RUS as shown in Fig. 4.

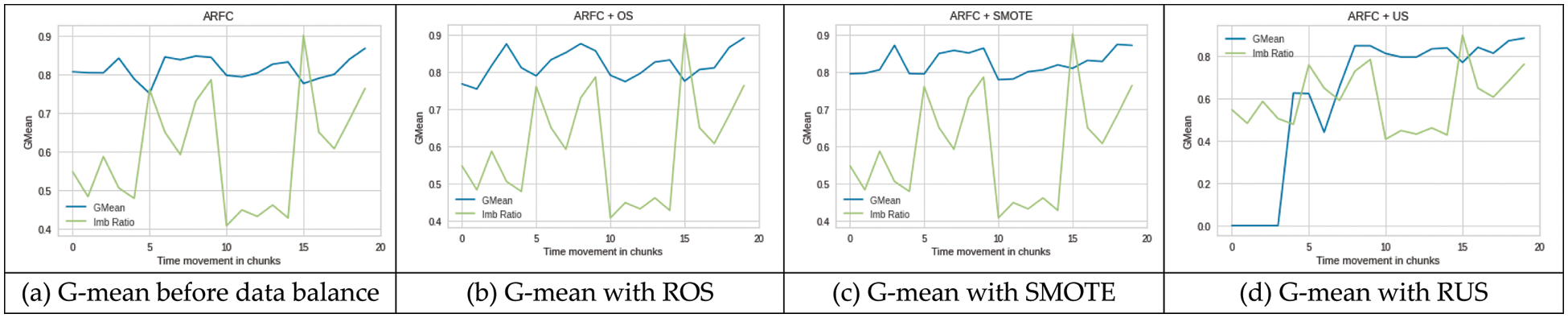
Figure 4: Performance ARFC on imbalance (a) and balanced (b–d) SEA dataset

DWMC: Like ARFC, the performance of DWMC has also improved after addressing the class imbalance issue as can be seen in Fig. 5. The DWMC produced almost similar results when the class imbalance issue was solved with ROS and SMOTE. Using both techniques, the performance of DWMC has improved at chunk 5 and chunk 15. Also, both ROS and SMOTE showed an extreme decrease in performance in chunks 12 and 13 as shown in Figs. 5b and 5c. Remember there is no concept drift at chunk 12 or 13, hence we assume that because the data was highly imbalanced and generating synthetic instances for oversampling did not produce good results for DWMC. Although there was no such impact with ARFC at the same stage. The RUS produced an increase in g-mean at all drift locations and relatively constant performance. But it produced a very low g-mean for a few initial and last chunks Fig. 5d. In general, we can say DWMC performed better using under-sampling the data instead of oversampling the data while addressing the class imbalance issue.

Figure 5: Performance DWMC on imbalance (a) and balanced (b–d) SEA dataset

HATC: The performance of HATC was decreased at the positions where concept drift and class imbalance occurred together, but as compared to positions 10 and 15, the effect is much higher at position 5 as can be seen in Fig. 6a. Again, All three approaches i.e., ROS, SMOTE, and RUS produced improved results at chunk positions 5 and 15 and produced slightly low g-mean at chunk 10 Figs. 6b–6d. The ROS and SMOTE produced a sudden decrease in g-mean at chunk 3. We assume that synthetic data generated for oversampling might not truly represent actual data that result in performance degradation. In general, ROS produced a stable performance for HATC except for that one chunk (chunk 3). Although the drift type is the same at all three points, its effect is not the same as shown in Fig. 6c.

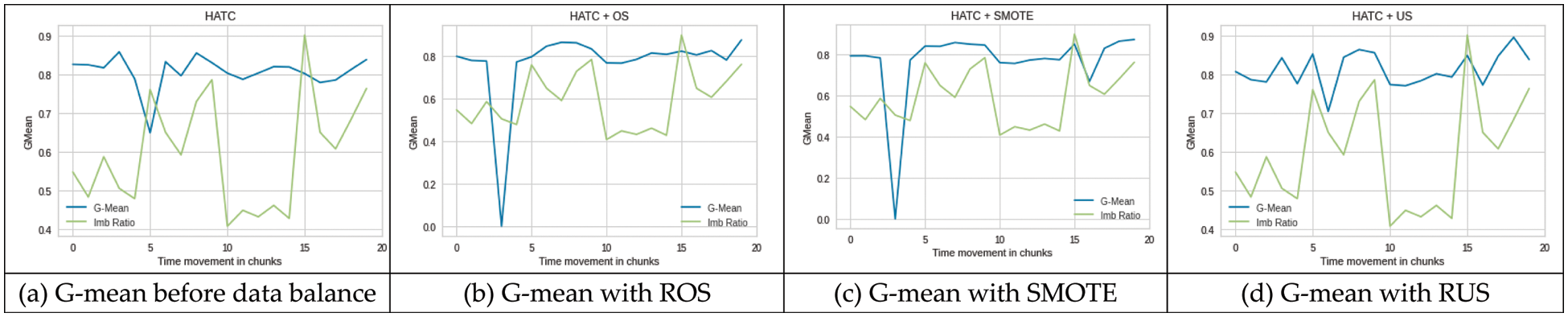
Figure 6: Performance HATC on imbalance (a) and balanced (b–d) SEA dataset

LPPNSEC: It produced poor performance in terms of g-mean as compared to other classifiers. Also, its performance has fluctuated throughout the process but still can be observed that at the drift position its performance is decreased showing the highest decrease at chunk 15 which is improved after balancing the data with all ROS, SMOTE, and RUS approaches shown in Figs. 7a–7d. There was not much difference in performance with all these data balancing approaches but still ROS and SMOTE performed slightly better together with LPPNSEC than RUS is shown in Fig. 7d.

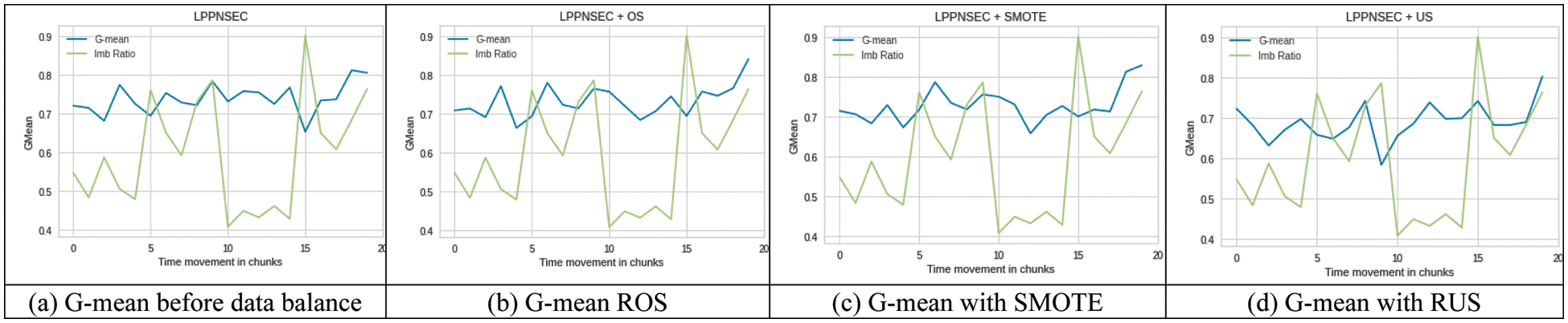
Figure 7: Performance LPPNSEC on imbalance (a) and balanced (b–d) SEA dataset

In general, for scenario-2 we conclude that the classifier performance degradation was not only because of concept drift. When the classifier was retrained on balanced data it produced improved performance, this shows that the change in class imbalance also contributed to a decrease in performance.

4.2 Effect of Change in Class Imbalance Ratio on Individual Classes and Performance Measures

In Section 4.1 we saw the effect of concept drift and change in class imbalance ratio on classifier performance in terms of accuracy and g-mean. It is still not clear whether the effect of change in class imbalance ratio is the same on the minority as well as majority classes or it affects only the minority class. Generally, due to class imbalance, the classifier misclassifies the instances of minority class which causes poor performance in terms of precision and recall for the minority class. Therefore, the objective of most classifiers is to achieve higher precision and recall for the minority class. In this experiment, we examine the effect of change in class imbalance ratio on both minority and majority classes because the change in class imbalance may affect both minority and majority classes. We also measure the performance of the classifier for both classes on different performance metrics to answer question number two. We used built-in precision, recall, and f1_score functions available in the python library. We calculated all these values for every chunk and the results are visualized in Figs. 8a to 8h. The class-0 (% of samples) and class-1 (% of samples) in these figures represent the percentage of samples of the particular class available in any chunk. If the percentage of samples in a class is closer to 50%, it shows the data is more balanced and imbalanced otherwise.

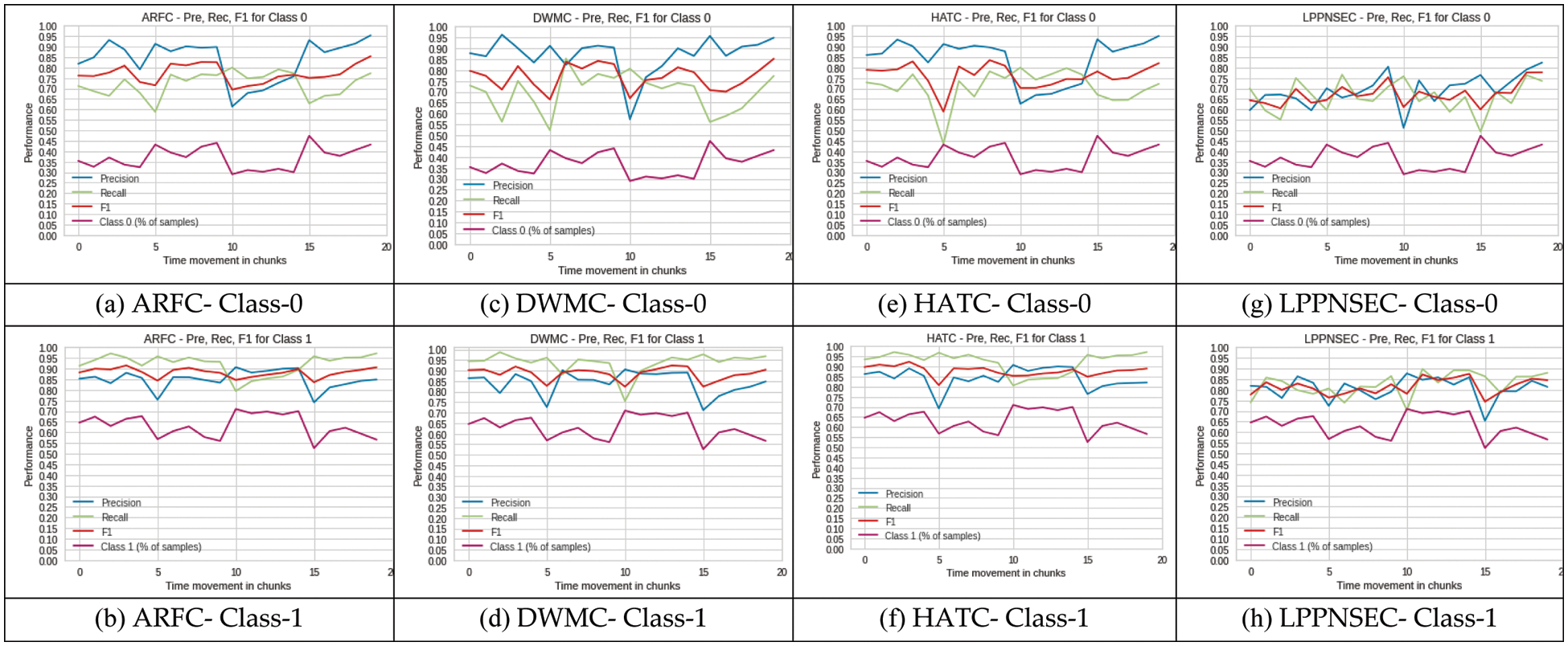
Figure 8: Class-wise performance of ARFC, DWMC, HATC, and LPPNSEC in terms of precision, recall, F1 score

4.2.1 Minority Class (Class-0)

In the case of ARFC, the change in class imbalance ratio shows direct relation to precision Fig. 8a. In other words, an increase in the number of samples for class-0 improves the precision of class-0 and a decrease in the number of samples for class-0 causes a decrease in precision for the same class. Similar results are achieved for class-0 with DWMC, HATC, and LPPNSEC Figs. 8c, 8e and 8g. Whereas the change in the number of samples in class-0 showed a reverse effect on recall. The increase in the number of samples in class-0 causes a decrease in recall and vice versa. Our results show the effect of drift cannot be the same on both precision and recall if it occurs together with class imbalance especially when the class imbalance ratio suddenly changes. As can be seen in Figs. 8a, 8c, 8e, and 8g, at positions 5 and 15 recall has decreased and precision has increased whereas at position 10 results are the opposite. Keep in mind these results are achieved on four different classifiers (ARFC, DWMC, HAT, and LPPNSEC) but still show the same patterns. Another thing to notice here is, that when there is an incremental change in the number of samples in minority and majority classes precision and recall move in the same direction which can be seen in the same diagrams, especially for the last few chunks where the change in class imbalance is incremental.

4.2.2 Majority Class (Class-1)

For the majority class i.e., class-1, the impact of a sudden change in class imbalance ratio has the same as the minority class which is precision and recall move in opposite directions. But there are a few differences as well. Let’s take the case of ARFC for both class-0 and class-1, at drift positions 5 and 15 precision is decreased and recall is increased for class-1 which is opposite to class-0. Similarly for drift position 10, precision is increased but recall is decreased for class-1 which is also opposite of class-0 as can be seen in Figs. 8a and 8b. The same pattern can be seen in results from DWMC, HATC, and LPPNSEC Figs. 8c to 8h. As we discussed due to increment change in class imbalance precision and recall move in the same direction. If you notice for the last few chunks, the number of samples in the minority class is increasing and the number of samples in the majority class is decreasing as a result the precision and recall both are increasing so as the F1 score Figs. 8a to 8h. The reason is data becoming more balanced i.e., the percentage of samples in each class is going closer to 50 which is a sign of equal data distribution in each class (50% in each class).

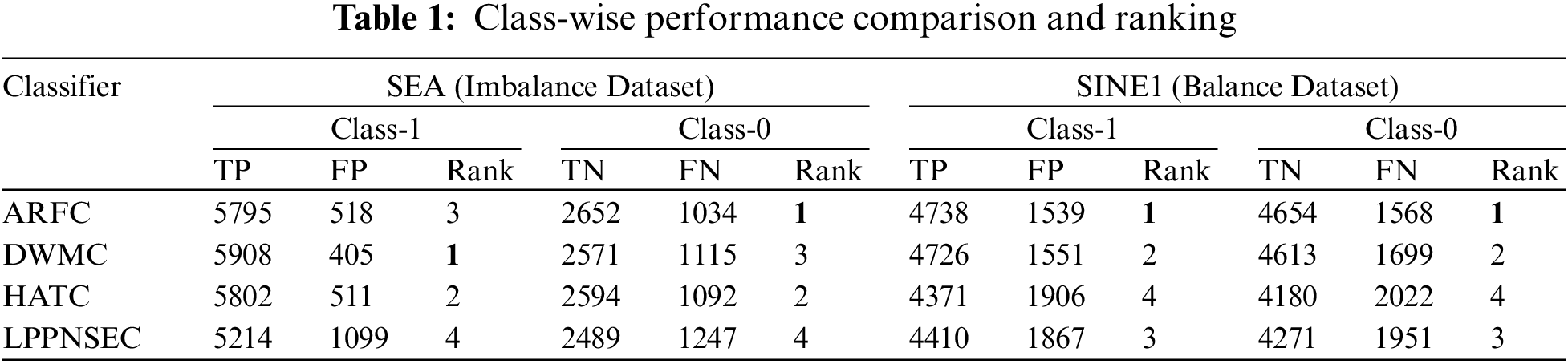
According to [6], when data is skewed the classifiers become biased towards the majority class or true positive (TP) and misclassify the minority class or true negative (TN) which results in increasing the false positive (FP). Any classifier which gives more focus on the minority class may misclassify the majority class and considers TP as TN which results in increasing false negative (FN). Therefore, the classifier is considered best if it produced a low value for FP and FN and a high value for TP and TN. Hence, we compared the performance of the selected classifiers and recorded the result of all the chunks. The summary of the results is given in Table 1 for the SEA and SINE1 datasets. For the SEA dataset, in terms of correctly identifying the majority class (class-1), the DWMC produced a high rate of TP and a low rate for FP which is in bold letters. HATC was on second and produced slightly better results than ARFC in terms of TP rate and FP. The LPPNSEC produced a very low rate for TP and high FP hence its performance was poor for the majority class. For the minority class (class-0), ARFC produced better results among all and produced high value for TN and low value for FN, whereas HATC again produced second best. The DWMC which produced the best results for the majority class produced poor results for the minority class. The LPPNSEC is again at last which shows it performed poorly for both majority and minority classes. HATC gives constant performance for both minority class as well as majority class. Whereas, for the SINE1 dataset which has balanced data, ARFC outperformed the other three classifiers on both class-1 and class-0, while DWMC remains second. HATC performed well on imbalance data and was third but did not perform well on balance data hence comes forth in performance whereas LPPNSEC performed better on balanced data, the results can be seen in Table 1.

5  Conclusion

Class imbalance and concept drift are the key issues in applications such as smart grid and sensor-based industrial applications which generate non-stationary data streams. Machine learning algorithms focus on dealing with both issues separately without understating the correlation of both the problems. As a result, when both problems occur together at the same time the existing techniques suffer in handling the joint issue properly. To address the joint issue, we believe, we must have in-depth knowledge of the problem and the relationship of concept drift with the class imbalance and vice versa. To overcome this gap, in this paper we performed experimental analysis on balanced and imbalanced datasets containing concept drift using four state-of-the-art classifiers. To remove the class imbalance effect, we used ROS, RUS, and SMOTE methods. We identified the effect of concept drift and class imbalance problems on classifier performance and individual classes. We further analyzed the effect of the joint issue on the precision and recall of each class to better understand the problem. Experimental results showed that:

•   The classification performance of the classifier severely affected when data face the joint issue of concept drift and class imbalance.

•   The change in class imbalance ratio directly affects the precision and recall of both minority and majority classes.

•   The precision of each class (minority and majority) increased when the number of samples increased and decreased otherwise.

•   Whereas recall decreased when the number of samples increased and increased otherwise.

•   Results also showed that when there is a constant change in class imbalance, the precision and recall move in the same direction i.e., if the number of samples increases the precision and recall also increase, and if the number of samples decreases the precision and recall also decrease.

•   The performance of the ARFC, DWMC, HATC, and LPPNSEC classifiers were tested on minority and majority classes for an imbalanced dataset and the result showed ARFC performed better on minority classes and DWMC on majority classes. The HATC showed consistent performance in both classes.

•   On a balanced dataset, ARFC performed better than DWMC, HATC, and LPPNSEC far both classes (class-0 and class-1).

•   The performance of data balancing techniques is not constant with all classifiers; they performed good for certain classifiers and worse for other classifiers even on the same dataset.

Our results also show that change in class imbalance ratio can affect both minority and majority classes. Therefore, the focus should be given to improve the performance of both classes instead of targeting only the minority class. We also recommend that both precision and recall should be monitored, and the classifier should produce a high performance for both precision and recall which will give the best results for TP, FP, TN, and FN. Applications such as electricity price prediction, smart health systems, predicting the remaining useful life of a machine, fault diagnosis, and spam filtering face the issue of concept drift and class imbalance. Considering the findings of this study will help in designing intelligent and adaptive solutions that can cope with the combined challenge of concept drift and class imbalance in these applications. Our current work is limited to the binary class problem only. The effect of other factors of class imbalance like rare examples and borderline examples are not considered too. In the future, we will work on the limitations of this study and will extend our work for multi-class data streams. Identification of the correlation between concept drift and class imbalance in presence of multiple minority classes and multiple majority classes along with other factors of class imbalance will be a great challenge.

Acknowledgement: The authors of this research acknowledge the services and support of Center for Research in Data Science and High-Performance Cloud Computing Centre (HPC3), Universiti Teknologi PETRONAS to complete this research study. The authors also acknowledge Dr. Syed Muslim Jameel (Assistant Professor, Sir Syed University, Pakistan) for his technical support in the implementation of the experiment.

Funding Statement: The authors would like to extend their gratitude to Universiti Teknologi PETRONAS (Malaysia) for funding this research through grant number (015LA0–037).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

    1. A. Margara and T. Rabl, “Definition of data streams,” In :Encyclopedia of Big Data Technologies, S. Sakr and A. Y. Zomaya, (Eds.Cham: Springer International Publishing, pp. 648–652, 2019. [Google Scholar]

    2. S. M. Jameel, M. A. Hashmani, H. Alhussain, M. Rehman and A. Budiman, “A critical review on adverse effects of concept drift over machine learning classification models,” International Journal of Advanced Computer Science and Applications (IJACSA), vol. 11, no. 1, pp. 206–211, 2020. [Google Scholar]

    3. J. Lu, A. Liu, F. Dong, F. Gu, J. Gama et al., “Learning under concept drift: A review,” IEEE Transactions on Knowledge and Data Engineering, vol. 31, no. 12, pp. 2346–2363, 2019. [Google Scholar]

    4. W. W. Y. Ng, J. Zhang, C. S. Lai, W. Pedrycz, L. L. Lai et al., “Cost-sensitive weighting and imbalance-reversed bagging for streaming imbalanced and concept drifting in electricity pricing classification,” IEEE Transactions on Industrial Informatics, vol. 15, no. 3, pp. 1588–1597, 2018. [Google Scholar]

    5. G. Haixiang, L. Yijing, J. Shang, G. Mingyun, H. Yuanyue et al., “Learning from class-imbalanced data: Review of methods and applications,” Expert Systems with Applications, vol. 73, pp. 220–239, 2017. [Google Scholar]

    6. B. Zhu, B. Baesens and S. K. vanden Broucke, “An empirical comparison of techniques for the class imbalance problem in churn prediction,” Information Sciences, vol. 408, pp. 84–99, 2017. [Google Scholar]

    7. Y. Lu, Y. M. Cheung and Y. Y. Tang, “Adaptive chunk-based dynamic weighted majority for imbalanced data streams with concept drift,” IEEE Transactions on Neural Networks and Learning Systems, vol. 31, no. 8, pp. 2764–2778, 2020. [Google Scholar]

    8. S. Wang, L. L. Minku and X. Yao, “Online class imbalance learning and its applications in fault detection,” International Journal of Computational Intelligence and Applications, vol. 12, no. 4, pp. 1340001–13400020, 2013. [Google Scholar]

    9. Y. Sun, K. Tang, L. L. Minku, S. Wang and X. Yao, “Online ensemble learning of data streams with gradually evolved classes,” IEEE Transactions on Knowledge and Data Engineering, vol. 28, no. 6, pp. 1532–1545, 2016. [Google Scholar]

  10. M. R. Sousa, J. Gama and E. Brandão, “A new dynamic modeling framework for credit risk assessment,” Expert Systems with Applications, vol. 45, pp. 341–351, 2016. [Google Scholar]

  11. J. Meseguer, V. Puig and T. Escobet, “Fault diagnosis using a timed discrete-event approach based on interval observers: Application to sewer networks,” IEEE Transactions on Systems, Man, and Cybernetics-Part A: Systems and Humans, vol. 40, no. 5, pp. 900–916, 2010. [Google Scholar]

  12. B. Krawczyk, “Learning from imbalanced data: Open challenges and future directions,” Progress in Artificial Intelligence, vol. 5, no. 4, pp. 221–232, 2016. [Google Scholar]

  13. S. Wang, L. L. Minku and X. Yao, “A systematic study of online class imbalance learning with concept drift,” IEEE Transactions on Neural Networks and Learning Systems, vol. 29, no. 10, pp. 4802–4821, 2018. [Google Scholar]

  14. S. Priya and R. A. Uthra, “Comprehensive analysis for class imbalance data with concept drift using ensemble based classification,” Journal of Ambient Intelligence and Humanized Computing, vol. 12, no. 5, pp. 4943–4956, 2021. [Google Scholar]

  15. F. Thabtah, S. Hammoud, F. Kamalov and A. Gonsalves, “Data imbalance in classification: Experimental evaluation,” Information Sciences, vol. 513, pp. 429–441, 2020. [Google Scholar]

  16. Ł Korycki and B. Krawczyk, “Concept drift detection from multi-class imbalanced data streams,” in 2021 IEEE 37th Int. Conf. on Data Engineering (ICDE), Chania, Crete, Greece, pp. 1068–1079, 2021. [Google Scholar]

  17. S. Wang, L. L. Minku, D. Ghezzi, D. Caltabiano, P. Tino et al., “Concept drift detection for online class imbalance learning,” in Proc. of the 2013 Int. Joint Conf. on Neural Networks (IJCNN), Fairmont Hotel. Dallas, Texas, USA, pp. 1–10, 2013. [Google Scholar]

  18. B. Pal, A. K. Tarafder and M. S. Rahman, “Synthetic samples generation for imbalance class distribution with LSTM recurrent neural networks,” in Proc. of the Int. Conf. on Computing Advancements, New York, NY, USA, pp. 1–5, 2020. [Google Scholar]

  19. M. Kubat and S. Matwin, “Addressing the curse of imbalanced training sets: One-sided selection,” in Int. Conf. on Machine Learning, Nashville, Tennessee, USA, vol. 97, pp. 179–186, 1997. [Google Scholar]

  20. S. Yen and Y. Lee, “Cluster-based under-sampling approaches for imbalanced data distributions,” Expert Systems with Applications, vol. 36, no. 3, pp. 5718–5727, 2009. [Google Scholar]

  21. A. Budiman, M. I. Fanany and C. Basaruddin, “Adaptive online sequential ELM for concept drift tackling,” Computational Intelligence and Neuroscience, vol. 2016, pp. 20–37, 2016. [Google Scholar]

  22. H. Zhang and Q. Liu, “Online learning method for drift and imbalance problem in client credit assessment,” Symmetry, vol. 11, no. 7, pp. 890–908, 2019. [Google Scholar]

  23. A. Bifet and R. Gavalda, “Learning from time-changing data with adaptive windowing,” in Proc. of the 2007 SIAM Int. Conf. on Data Mining, Minneapolis, Minnesota, USA, pp. 443–448, 2007. [Google Scholar]

  24. A. Pesaranghader and H. L. Viktor, “Fast hoeffding drift detection method for evolving data streams,” in Joint European Conf. on Machine Learning and Knowledge Discovery in Databases, Riva del Garda, Italy, pp. 96–111, 2016. [Google Scholar]

  25. Ö. Gözüaçık and F. Can, “Concept learning using one-class classifiers for implicit drift detection in evolving data streams,” Artificial Intelligence Review, vol. 54, no. 5, pp. 3725–3747, 2021. [Google Scholar]

  26. W. N. Street and Y. Kim, “A streaming ensemble algorithm (SEA) for large-scale classification,” in Proc. of the Seventh ACM SIGKDD Int. Conf. on Knowledge Discovery and Data Mining, San Francisco, CA, USA, pp. 377–382, 2001. [Google Scholar]

  27. T. Al-Khateeb, M. Masud, K. Al-Naami, S. E. Seker, A. Mustafa et al., “Recurring and novel class detection using class-based ensemble for evolving data stream,” IEEE Transactions on Knowledge and Data Engineering, vol. 28, no. 10, pp. 2752–2764, 2016. [Google Scholar]

  28. D. Brzezinski and J. Stefanowski, “Reacting to different types of concept drift: The accuracy updated ensemble algorithm,” IEEE Transactions on Neural Networks and Learning Systems, vol. 25, no. 1, pp. 81–94, 2014. [Google Scholar]

  29. D. M. Farid, L. Zhang, A. Hossain, C. M. Rahman, R. Strachan et al., “An adaptive ensemble classifier for mining concept drifting data streams,” Expert Systems with Applications, vol. 40, no. 15, pp. 5895–5906, 2013. [Google Scholar]

  30. B. Kurlej and M. Wozniak, “Active learning approach to concept drift problem,” Logic Journal of IGPL, vol. 20, no. 3, pp. 550–559, 2012. [Google Scholar]

  31. R. Elwell and R. Polikar, “Incremental learning of concept drift in nonstationary environments,” IEEE Transactions on Neural Networks, vol. 22, no. 10, pp. 1517–1531, 2011. [Google Scholar]

  32. J. Z. Kolter and M. A. Maloof, “Dynamic weighted majority: An ensemble method for drifting concepts,” Journal of Machine Learning Research, vol. 8, pp. 2755–2790, 2007. [Google Scholar]

  33. S. Wang, L. L. Minku and X. Yao, “A learning framework for online class imbalance learning,” in 2013 IEEE Symp. on Computational Intelligence and Ensemble Learning (CIEL), Orlando, FL, USA, pp. 36–45, 2013. [Google Scholar]

  34. S. Wang, L. L. Minku and X. Yao, “Resampling-based ensemble methods for online class imbalance learning,” IEEE Transactions on Knowledge and Data Engineering, vol. 27, no. 5, pp. 1356–1368, 2015. [Google Scholar]

  35. A. Ghazikhani, R. Monsefi and H. S. Yazdi, “Ensemble of online neural networks for non-stationary and imbalanced data streams,” Neurocomputing, vol. 122, pp. 535–544, 2013. [Google Scholar]

  36. B. Mirza, Z. Lin and N. Liu, “Ensemble of subset online sequential extreme learning machine for class imbalance and concept drift,” Neurocomputing, vol. 149, pp. 316–329, 2015. [Google Scholar]

  37. H. M. Gomes, A. Bifet, J. Read, J. P. Barddal, F. Enembreck et al., “Adaptive random forests for evolving data stream classification,” Machine Learning, vol. 106, no. 9–10, pp. 1469–1495, 2017. [Google Scholar]

  38. C. -C. Lin, D. -J. Deng, C. -H. Kuo and L. Chen, “Concept drift detection and adaption in big imbalance industrial IoT data using an ensemble learning method of offline classifiers,” IEEE Access, vol. 7, pp. 56198–56207, 2019. [Google Scholar]

  39. M. F. A. M. Fauzi, I. A. Aziz and A. Amiruddin, “The prediction of remaining useful life (RUL) in Oil and Gas industry using artificial neural network (ANN) algorithm,” in 2019 IEEE Conf. on Big Data and Analytics (ICBDA), Suzhou, China, pp. 7–11, 2019. [Google Scholar]

  40. K. V. Kokilam, D. P. P. Latha and D. J. P. Raj, “Learning of concept drift and multi class imbalanced dataset using resampling ensemble methods,” International Journal of Recent Technology and Engineering, vol. 8, no. 1, pp. 1332–1340, 2019. [Google Scholar]

  41. S. Ancy and D. Paulraj, “Handling imbalanced data with concept drift by applying dynamic sampling and ensemble classification model,” Computer Communications, vol. 153, pp. 553–560, 2020. [Google Scholar]

  42. Z. Li, W. Huang, Y. Xiong, S. Ren and T. Zhu, “Incremental learning imbalanced data streams with concept drift: The dynamic updated ensemble algorithm,” Knowledge-Based Systems, vol. 95, pp. 105694–105711, 2020. [Google Scholar]

  43. P. Zyblewski, R. Sabourin and M. Woźniak, “Preprocessed dynamic classifier ensemble selection for highly imbalanced drifted data streams,” Information Fusion, vol. 66, pp. 138–154, 2021. [Google Scholar]

  44. Y. Song, J. Lu, A. Liu, H. Lu and G. Zhang, “A Segment-based drift adaptation method for data streams,” IEEE Transactions on Neural Networks and Learning Systems, vol. 33, no. 9, pp. 1–14, 2021. [Google Scholar]

  45. A. A. Toor and M. Usman, “Adaptive telecom churn prediction for concept-sensitive imbalance data streams,” The Journal of Supercomputing, vol. 78, no. 3, pp. 3746–3774, 2022. [Google Scholar]

  46. M. Basseville and I. V. Nikiforov, Detection of Abrupt Changes: Theory and Application. vol. 104. Englewood Cliffs: prentice Hall, 1993. [Google Scholar]

  47. R. V. Kulkarni, S. Revathy and S. H. Patil, “Smart pools of data with ensembles for adaptive learning in dynamic data streams with class imbalance,” IAES International Journal of Artificial Intelligence, vol. 11, no. 1, pp. 310–318, 2022. [Google Scholar]

  48. M. Harries and N. S. Wales, “Splice-2 comparative evaluation: Electricity pricing,” Technical report, The University of South Wales, 1999. [Google Scholar]

  49. D. Huang, H. Zareipour, W. D. Rosehart and N. Amjady, “Data mining for electricity price classification and the application to demand-side management,” IEEE Transactions on Smart Grid, vol. 3, no. 2, pp. 808–817, 2012. [Google Scholar]