Accelerating Falcon Post-Quantum Digital Signature Algorithm on Graphic Processing Units

1  Introduction

Shor’s algorithm [1] running on a quantum computer can break the current public key cryptosystems including Rivest–Shamir–Adleman (RSA), digital signature algorithm (DSA), and elliptic curve Diffie–Hellman (ECDH). After 2016, the National Institute of Standards and Technology (NIST) has been organizing a competition to standardize post-quantum cryptography (PQC) to provide reasonable security in the era of quantum computing [2]. There are four algorithms (Classical McEliece [3], CRYSTALS-Kyber [4], NTRU [5], and Saber [6]) in the key encapsulation mechanism (KEM), and three algorithms (CRYSTALS-Dilithium [7], Falcon [8], and Rainbow [9]) in the digital signature algorithm (DSA) in the Round 3 finalists. Among the Round 3 DSA algorithms, Falcon has advantages of shortest key length and fastest signature verification speed. Thus, Falcon can be seamlessly integrated into current security protocols (e.g., transport layer security (TLS) and domain name server security (DNSSEC)) and applications. Consequently, Falcon has recently been selected as one of the standard algorithms in the NIST competition. The advent of Internet of Things (IoT) and cloud environments has significantly increased the number of clients that servers must process. Therefore, servers have the burden of processing high volume cryptographic operations or cryptographic protocol executions for secure communication with clients. For example, servers should concurrently confirm the authenticity of certificates from clients; in a particular situation, they should generate multiple key pairs and sign messages with Signature as a Service (SaS) [10,11]. Graphics processing units (GPUs) can be used as cryptographic accelerators. Many studies [10–12] demonstrated that optimized cryptographic software with GPUs can achieve an impressive throughput enhancement compared with conventional software operating on the central processing unit (CPU). Certain studies [13–18] have been conducted on PQC to improve its performance using GPUs.

This study presents the first Falcon software optimized on an NVIDIA GPU. Although the Falcon team [8] opened the CPU environment and embedded environments source codes, it did not provide the GPU environment software. Furthermore, on the GPU side, Falcon source codes are related to recursive function inefficiency. Thus, in this study, the gap is filled by developing an efficient GPU Falcon software. When Falcon source codes for CPU execution are converted in an efficient GPU side software, multiple limitations such as warp divergence related to using branch instructions and the heavy use of recursive functions require to be solved. First, a fine-grained execution model is applied to implement the introduced Falcon and identify the optimal number of threads in a thread block. Second, dummy-based polynomial operation methods that alleviate the warp divergence effect and an iterative version of Falcon sampling are proposed. Furthermore, the introduced Falcon software is optimized by considering the GPU advantage on chip memory (registers, shared memory, and constant memory) and by implementing polynomial multiplications using number theoretic transform (NTT)-based method and fast Fourier transform (FFT)-based method.

The contributions of this study can be summarized as follows:

• This is the first study on Falcon implementation in a GPU environment

This study is the first to present GPU Falcon software, which was developed with a fine-grained execution model where n threads (n = 32 is selected for optimal performance) cooperate to compute a Falcon operation: Keygen for generating a pair of public and private keys, Sign for generating a signature, and Verify for signature verification. Furthermore, the introduced Falcon software on an NVIDIA RTX 3090 GPU can execute 256 concurrent Falcon operations. It was observed that its throughput with Falcon-512 and Falcon-1024 parameters outperforms at 35.14, 28.84, and 34.64 times and 33.31, 27.45, and 34.40 times, respectively, better than the CPU reference implementation using the AVX2 instructions on a Ryzen 9 5900X CPU running at 3.7 GHz for Keygen, Sign, and Verify.

• The proposed additional optimization implementation plan

This study introduced a dummy-based parallel execution method to alleviate the divergence effect from branch instructions, as well as an effective, economical approach to convert the ffSampling recursive version into an iterative one because the GPU recursive function execution is inefficient. Furthermore, the polynomial multiplication operations in the integer number and complex number domains were optimized using the NTT-based and FFT-based methods; the fine-grained execution model parallelized both the NTT-based and FFT-based methods.

The remainder of this study is structured as follows: Section 2 presents works of literature review on GPU cryptographic algorithms optimization and introduces research trends for Falcon; Section 3 provides a brief description of Falcon and GPU; Section 4 introduces implementation methods for operating GPU Falcon and optimization implementation methods to improve performance; Section 5 evaluates the implementation performance results; and Section 6 is the conclusion.

2  Related Work

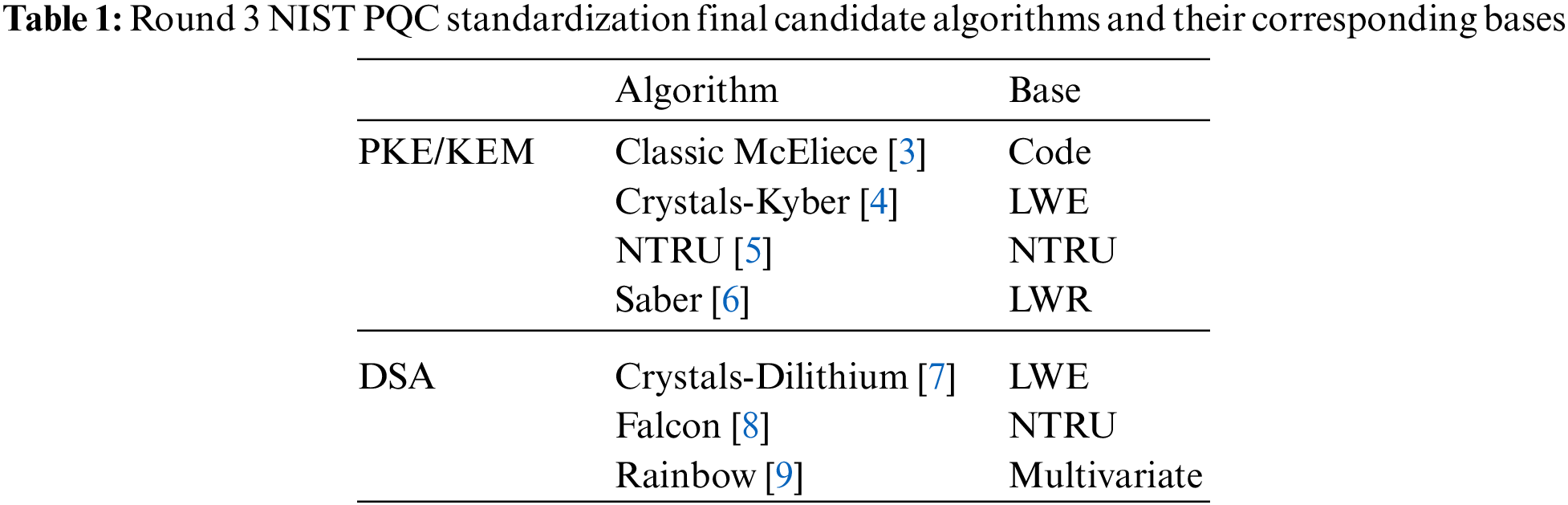
Since 2016, NIST has organized a contest for standardizing PQC algorithms as a response to PQC demand. In July 2020, the third round of the project was started; Table 1 shows the round’s competition algorithms. The candidate algorithms were classified into public key encryption (PKE)/ KEM and DSA. Information on the final candidate algorithms are presented on the PQClean [19]. In June 2022, four algorithms were selected as the final standard algorithms: Crystals-Kyber for KEM, Crystals-Dilithium, Falcon, and Sphincs+ for DSA.

There have been multiple pieces of research on PQC implementation in a GPU environment [13–18]. Gupta et al. (2020) [13] proposed the techniques that allow PQC-based KEM algorithms such as FrodoKEM, NewHope, and CRYSTALS-Kyber to run fast on GPU. For NewHope, Gao et al. (2021) [14] proposed a computational structure that maximizes GPU computational efficiency by improving its implementation. Furthermore, Seong et al. (2021) [15] introduced a parallel operation structure for the server to efficiently process the key exchange protocol in a multi-client environment via the NTRU algorithm. Moreover, PQC-based KEM algorithms such as Saber, SIKE, and NTRU have been examined on GPU [16–18]. Although certain studies have implemented lattice-based PQC in GPU environments, these only focused on the optimization of polynomial multiplication such as parallelizing the NTT-based polynomial multiplications [13,14], and [16]. However, in addition to polynomial multiplication optimization, this study focuses on minimizing divergence effects and converting recursive-based sampling into an iterative version.

For PQC-based DSA, the final candidates were CRYSTALS-Dilithium [20], Falcon, and the Rainbow [21] algorithms. Dilithium and Falcon were selected as the final standard algorithms. Furthermore, CRYSTALS-Dilithium and Falcon are lattice-based cryptographic algorithms and polynomial operations are considered their primary computation methods [22]. To date, the primary concern of GPU lattice-based PQC implementation was to optimize polynomial multiplication by parallelizing the NTT-based method [23,24]. However, reference codes for Falcon are not directly converted into the software on the GPU side because of the heavy use of recursive functions and their branch instructions. To our knowledge, this is the first result of Falcon implementation on a GPU environment.

3  Backgrounds

3.1 Falcon Overview

Falcon [25] is a post-quantum DSA algorithm based on the lattice NTRU problem. Falcon uses the operation in the field of Q[x]/(ϕ), where ϕ=xn+1, and is divided into Falcon-512 and Falcon-1024 depending on whether n = 512 or 1024. The necessary notation for the algorithm description is shown in Table 2. For example, Falcon-512 and Falcon-1024 uses polynomials of 512 terms and 1024 terms, respectively. Table 3 describes the Falcon-512 and Falcon-1024 parameters. Falcon-512 and Falcon-1024 provide NIST Security Levels 1 and 5, respectively. Falcon comprises three primary functions: Keygen generates a pair of public and private keys, Sign generates a signature, and Verify verifies the signature.

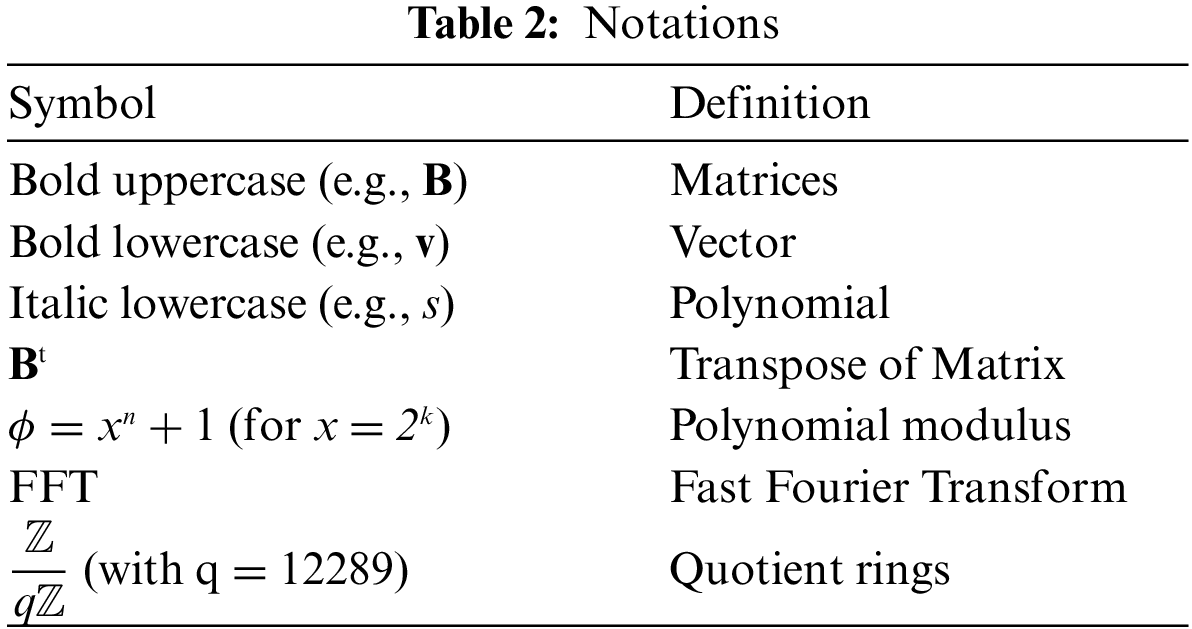
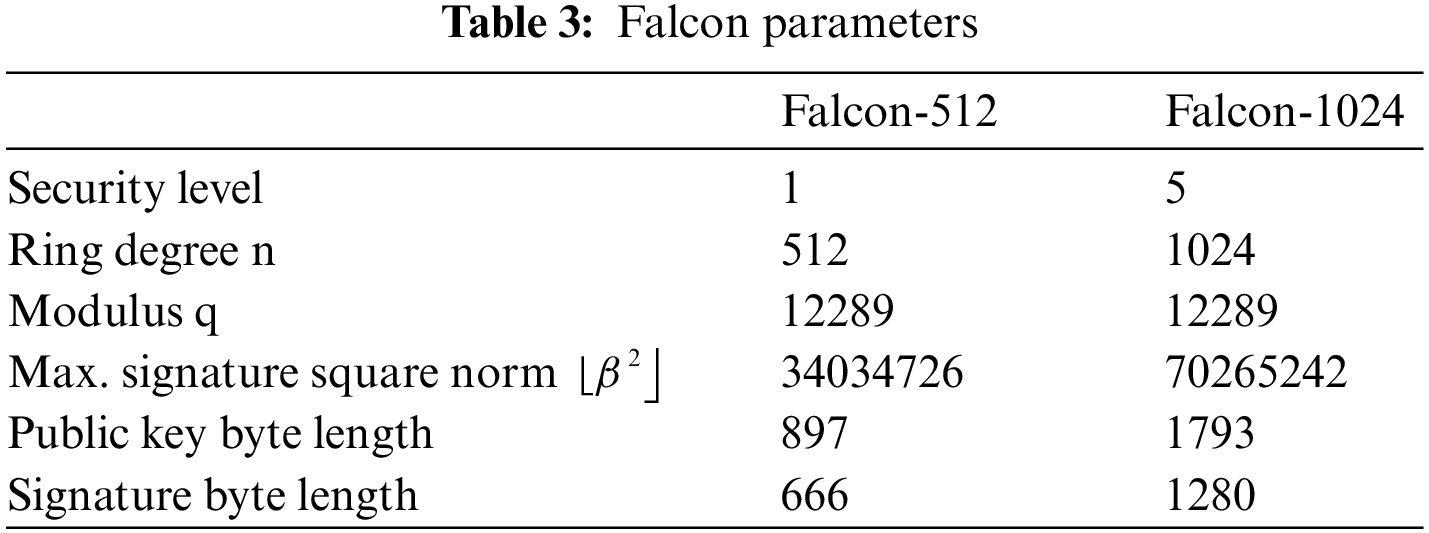
In the Keygen step, the private key F and G components, which satisfies the NTRU equation, are obtained via random polynomials f and g (refer to Algorithm 1). The Sign phase involves hashing the message to a value modular ϕ (refer to Algorithm 2). Next, the signer creates a polynomial-based signature pair (s1, s2) using (f, g, F, G), which is the signer’s secret information. The signature value is obtained as s2. In Verify (refer to Algorithm 3), s1 is calculated using the hashed message and signature s2; moreover, it is determined whether the signature is correct based on whether (s1, s2) satisfies the shortest vector in a lattice.

The Sign generates s1 and s2 by satisfying s1 + s2h = c mod (ϕ, q) using the message m, the random seed r, and the private key sk. The ffSampling function is repeatedly called (refer to Algorithm 4) to calculate s that meets the condition. In Verify, s1 and s2 are recalculated and verified if ‖s1,s2‖2≤⌊β2⌋ is satisfied. Falcon uses multiple methods to perform efficient polynomial operations for signature generation and verification process.

A FFT-based discrete Gaussian sampling is used to efficiently generate polynomial matrices. Moreover, FFT-based [26] and NTT-based [27] methods are used for polynomial multiplication on the complex number domain and integer number domains, respectively. The FFT and NTT are known as efficient methods that can reduce the computational complexity of the existing school book-based polynomial multiplication from O(n2) to O(nlogn). In FFT and NTT-based polynomial multiplication, two polynomials are converted into either the FFT or NTT domain. Then, point-wise multiplication is computed using the two converted polynomials. After completing the point-wise multiplication process, the final result is obtained by applying either the inverse FFT or NTT. In addition to the NTT-based method that uses integer numbers, the FFT-based method coefficients of polynomials are complex numbers (comprising a real part and an imaginary part) and thus floating-point type is used in representing them.

Complex number-based operations are included in the Keygen and Sign processes. From the Falcon implementation perspective, complex numbers are represented using an IEEE 754 64-bit floating-point representation [28] known as double precision. FFT-related functions operate on double precision. For NTT, the operation is implemented on a 16-bit integer representation because an integer operation is performed on modular q on the finite field Zq. The modular multiplication over Zq is performed using the Montgomery multiplication [29,30].

In the DSA, different signature values are generated using a random value generator function that is performed even for the same message. Generally, multiple functions are used to generate random values. However, to extract a value that satisfies a specific range or distribution, it is important to perform a sampling process. In Falcon, a function called ffSampling is used when generating a signature value. The ffSampling process can be reported in Algorithm 4 [31]. The splitfft and mergefft inside ffSampling perform the domain transformation, and DZ (SamplerZ) accepts only the desired value by rejection sampling. As per the rejection sampling, each value is subject to acceptance–rejection evaluation and only those values that satisfy the condition can be accepted. Values determined acceptable by SamplerZ follow a distribution like the discrete Gaussian distribution.

In addition to the primary functions, Falcon uses additional ones. The Sign phase HashToPoint function replaces the message hash value with a polynomial. Moreover, the Compress function compresses the generated signature value. However, the Decompress function called during the Verify process restores the output value generated by the Compress function in the Sign phase.

3.2 Graphic Processing Units

GPUs are devices developed to process graphics operations. Currently, their usage is extended to general purpose applications such as machine learning and accelerating cryptographic operations. Although GPU has a higher number of cores than CPU, a GPU core is slower than that of the CPU. For example, NVIDIA RTX 3090 GPU has 10,496 computational cores. GPUs are known for parallel computation rather than sequential execution. NVIDIA GPUs contain multiple independent streaming multiprocessors (SMs) in which each has multiple computational cores. For example, RTX 3090 has 82 SMs that each have 128 cores. Moreover, each SM has an instruction cache, a data cache, and a shared memory space.

Generally, libraries such as compute unified device architecture (CUDA) [32] or open computing language (OpenCL) [33] are used to operate general purpose computing on graphics processing units (GPGPU). The CUDA library enables GPU parallel programming via the NVCC compiler. In GPU implementation, tasks are processed in parallel by threads that are computation units. Typically, all 32 threads are grouped into an instruction execution unit known as warp. The threads of the same warp perform the same operation without a separate synchronization procedure. Moreover, the bundles of thread blocks composed of multiple threads are distributed to streaming multiprocessor cores. To maximize GPU resource utilization, identifying the optimal number of threads and thread blocks is important.

The proper usage of GPU memory is an important efficiency factor. A GPU is composed of multiple types of memory, and their characteristics are as follows:

•   Global memory is the dynamic random access memory (DRAM) that occupies the largest capacity of the GPU. However, memory reference speed is slow because data must be copied between the CPU and GPU via a PCIe interface to share data between the CPU and GPU.

•   Shared memory is the memory shared by threads in the same block. It is on-chip memory that has faster access speed than global memory. Shared memory is divided into equally sized memory banks that can be simultaneously accessed.

•   Constant memory is read-only memory. Here, data copying can be performed outside the GPU kernel. When warp threads frequently access data in constant memory, the data are cached to enable fast memory access.

•   Texture memory has the fastest memory access speed for graphic work but is small in size. Therefore, local memory requires to be allocated when multiple local variables are used.

The GPU is operated by the CPU-launched kernel function. Before using external data in GPU operation, the data require to be copied from the CPU to GPU. Moreover, it is important to perform a memory copy from the GPU to the CPU to use the computed data on the GPU in the CPU. Each thread running inside the kernel receives a unique identification.

4  Proposed Falcon GPU Implementation

4.1 Difficulties and Solutions

Many errors are generated when converting Falcon reference codes to GPU. This is because certain operation functions are implemented in a form that is unsuitable for the GPU environment (i.e., the original Falcon reference codes do not fit the GPU’s single instruction multiple threads (SIMT) execution model). Therefore, the study introduces multiple implementation methods that can handle the difficulties that arise during Falcon’s reference code conversion to GPU efficient codes.

4.1.1 CPU to GPU Data Porting Difficulties and Solutions

Falcon uses multiple variables and constant data to generate and confirm signatures. There are declared and used variables inside the function (e.g., temporary variables that store intermediate computation values, flags, and counters) as well as predefined data values (e.g., RC table for SHA-3, max_sig_bits for decoding, GMb for NTT conversion, and iGMb for inverse NTT conversion) that are used in the reference table form. In processes, certain data (e.g., message, signature, and key materials) consume memory from start to finish. Generally, variables declared inside a function can be similarly used on the GPU. However, if the variable size increases beyond a certain level, the stack memory may become insufficient, e.g., in Falcon-1024, the size of one public key is 1,793 bytes while the size of one signature is 1,280 bytes. Since the latest GPU register capacity per block is 256 KB, if the number of available threads per block increases, the register runs out and slow local memory is used instead. Therefore, the CPU dynamically allocates and uses memory for the variable. However, performing dynamic memory allocation in the middle of GPU kernel execution reduces the overall computationally intensive efficiency of the GPU. The size of multiple polynomial data used to solve the NTRU equation in Falcon reference codes may be difficult for each thread to independently declare and use. Therefore, the study has dynamically allocated the memory required to store polynomials before launching kernel execution. To prevent the declaration of variables during a function execution or a change in memory size through the memory reallocation function that results in a performance decrease, the variables are defined in advance as the largest size. Falcon structure variables containing the primary data (i.e., signature, signature length, public key, public key length, message, and message length) are predefined and used in a GPU.

For reference tables having constant data used in Falcon, table values are copied in advance via constant memory and are cached on the GPU. During Verify, five constant tables are stored (RC table used in SHA-3 function, max_sig_bits used in Falcon decoding function, GMb table used in NTT conversion, iGMb table used for inverse NTT conversion, and l2bound table for verifying length condition in the signing and verification processes) in a constant memory area wherein the total amount is ~4 kB.

Moreover, standard memory copy functions such as memcpy, which are frequently used in the original Falcon reference codes, have limited usage on the GPU. Accordingly, the value is copied via a deep copy with a for-loop.

4.1.2 Solution for GPU Double Recursive Function Difficulties

In cryptography, sampling is a method that extracts random values in a specific distribution. Falcon has a function known as SamplerZ that performs discrete Gaussian sampling. Moreover, the entire sampling function of Falcon is ffSampling (refer to Algorithm 4) and its structure is similar to FFT. The ffSampling function is called in a double recursive manner in which a parent function recursively calls two child functions for log2n times for the polynomial dimension n. As the operation proceeds, ffSampling recursively calls itself twice. At this time, the input parameter n is halved. For example, if ffSampling n input is 1024, the total number of ffSampling functions recursively called via the double recursive manner becomes 2047 times (= 1 + 2 + 4 + … + 1024). Fig. 1 shows the simplified expressions of the functions before and after the recursive functions. The code block performed in the conditional statement is substituted using the X symbol. The code block before the first recursive function is substituted with the F symbol. The code block after the second recursive function is substituted with the H symbol while the block between two recursive functions is substituted with the G symbol. The block related to X, F, H, and G symbols can include normal function calls (not recursive functions).

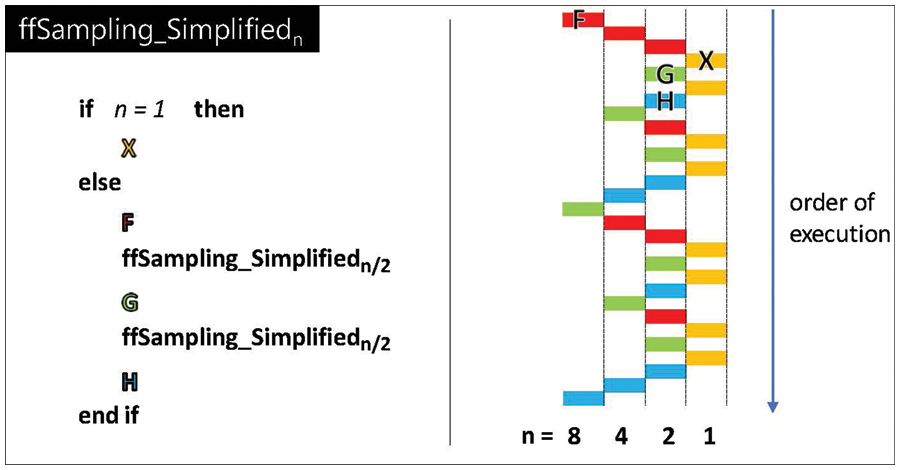
Figure 1: Illustration of a simplified ffSampling when n = 8 (red, yellow, green, and blue-sky rectangles denote codes related to F, X, G, and H symbols, respectively)

In GPUs where multiple threads perform simultaneous operations, the use of recursive functions is extremely limited because of the function call stacks problem. Therefore, to efficiently process the ffSampling function on the GPU, the double recursive function requires to be replaced with an iterative version. First, Fig. 1 shows that the F and H blocks are always continuously executed at the beginning and end of ffSampling. After a repeated execution of the first F, the next is X when n is 1, and G and X are executed only before the last H is consecutively executed. Because the number of iterations continuously executed is repeated log2n times as per the first input n, the following rules are derived for the iterative version of ffSampling by borrowing the concept of the ruler function [34] which defines the order of execution and the execution times for each code block (F, X, G, and H):

•   In the middle part, the primary iteration is repeated a total of n/2–1 times; within the main loop, there are two extra loops with the sequence following the derived ruler function as the number of repetitions are executed further. Fig. 2 shows the derived ruler function graph for the ffSampling iterative version.

•   G and X are first executed in the middle loop and H is executed RF[i] times where the RF function is a predefined table in constant memory and RF[i] is the i-th result of the ruler function for the index i that is the counter to the primary loop repetitions. Then, G is performed once and then F is performed RF[i] times. Then, X is executed to complete the series of primary loops.

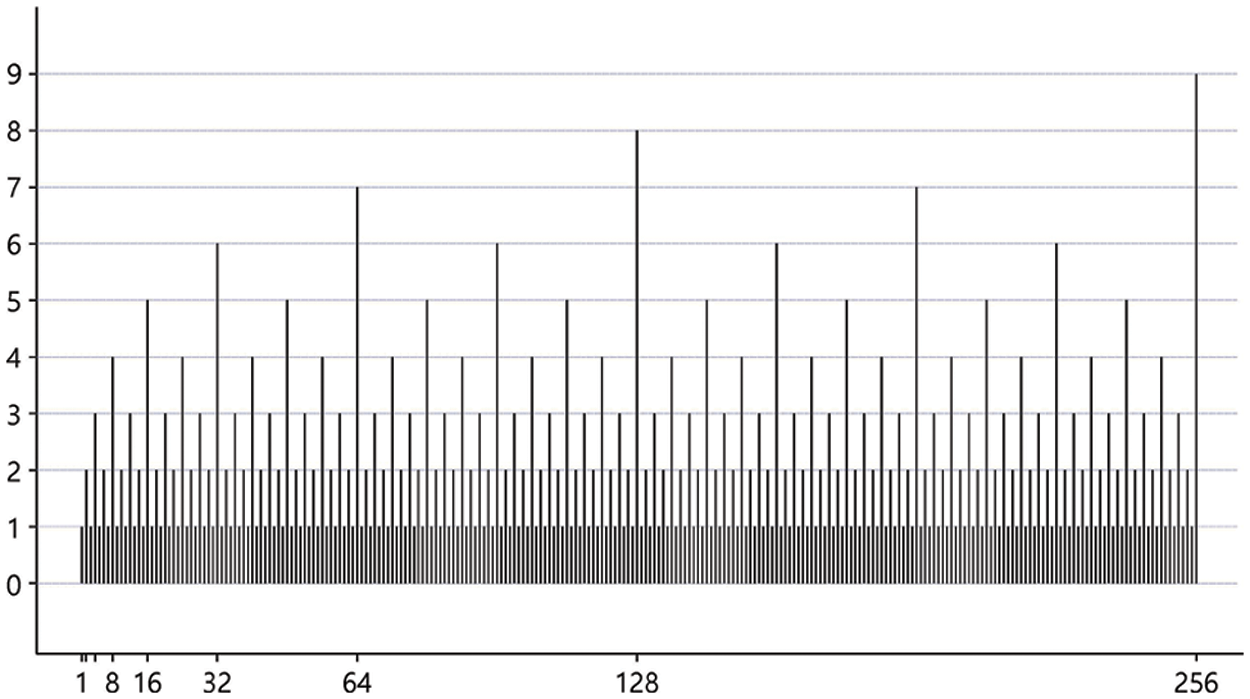
Figure 2: Ruler function graph

Algorithm 5 is the proposed ffSampling iterative version corresponding to the ruler function recursive execution shown in Fig. 1. While the process of replacing a recursive function with an iterative execution model improves efficiency, one other problem still remains. Because the existing ffSampling uses a Falcon tree, each time ffSampling is recursively called, another child of the tree is called. To use different parameters in the same function, even when using the iterative version, the address of each child of the tree is stored as an address pointer array and passed as a function argument. Then, the address pointer array stores the variable addresses used at each tree level.

4.2 Proposed Functionalities and Overall Software Structure

4.2.1 Software Functionalities

The introduced software provides key generation (Keygen), signing (Sign), and verification (Verify) functions. For Keygen, it is assumed that multiple and independent keys are generated and can be used in the future, whereas for Verify, each multiple signatures should be confirmed with its related public key. Unlike the abovementioned two operations, it is assumed for Sign that a single key or multiple keys can be used to sign multiple messages. For example, a typical application server must sign multiple messages with its private key. However, each key in an outsourced signature server [10,11] should sign certain messages. To summarize, the Falcon software provides three functions: Keygen for multiple keys, Sign for single key and multiple keys, and Verify for multiple keys. Thus, in Section 5, the Falcon software performance based on the aforementioned functionalities is presented.

4.2.2 Overall Structure

There are two primary execution models when implementing GPU applications: coarse-grained execution (CGE) model and fine-grained execution (FGE) model. In CGE, the thread processes one complete task. For example, a CGE thread computes a single Keygen, Sign, or Verify. It has two important advantages: ease of implementation and provision of maximum throughput. However, there is latency in completing the assigned operation because the computational power of each GPU core is considerably lower than that of the CPU.

FGE can reduce latency to complete the assigned operation by making multiple threads operate together. A single Keygen, Sign, or Verify can be processed using multiple threads in the FGE model. The Falcon software lowers operation latency while providing reasonable throughput by following the FGE model.

In the NVIDIA GPU, the maximum number of threads that reside in each thread block is 1,024. However, because there are limited resources per block, it is necessary to adjust the number of threads by considering the required resource (registers) in each thread within the block. When selecting the optimal number of threads in a block, it should be a multiple of Warp size, which is typically 32. Because Warp is the unit of scheduling in GPU, the CUDA manual suggests that the number of threads in a block should be a multiple of Warp size [32]. The study tested GPU Falcon implementation on a target GPU (RTX 3090) with multiple numbers of threads per block and reported that using 32 threads per block provided the best performance in terms of latency. Thus, in the implementation, 32 threads in a block can compute a single Keygen, Sign, or Verify. To simultaneously process multiple operations, the study’s software launches multiple thread blocks. Fig. 3 shows the software overall structure.

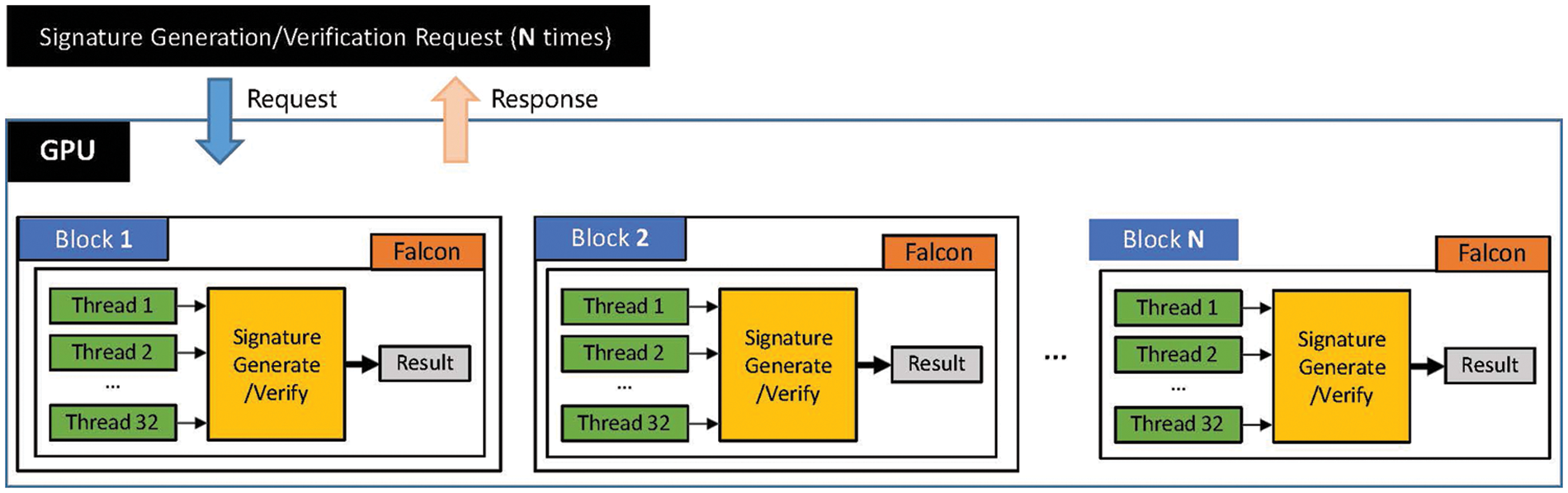
Figure 3: Overall structure of the Falcon GPU software

In the introduced software, 16 and 32 terms are assigned in the polynomial operation of each thread in a thread block for Falcon-512 and Falcon-1024, respectively, with the applied FGE model. Moreover, multiple Keygen, Sign, or Verify can be computed by launching multiple thread blocks. Several techniques are proposed to minimize warp divergence and for efficient cooperation among block threads, including parallel implementation of polynomial multiplication in the Falcon software.

4.3 Specific Parallel Optimization Strategy

4.3.1 Optimization Method for Common Polynomial Functions

General polynomial-based operation functions operate on each term belonging to a polynomial. For example, when two polynomials are added, each term of the two polynomials should be added based on the position. If the number of terms in the polynomial is 512 (Falcon-512), then 512 addition operations are performed. Therefore, if the GPU optimizes the addition operation using 32 threads, each thread can operate on 16 terms such that the addition of all 512 terms can be processed in parallel. For Falcon-1024, each thread in a block comprising 32 threads should process 32 polynomial operation terms.

4.3.2 Optimization Method for NTT and FFT Functions

In the study FGE model, each thread of a block cooperates to process polynomial operations such as addition and multiplication. The same number of terms belonging to a polynomial is allocated to and processed by each thread. For example, when adding two polynomials with 512 terms, each of the 32 threads compute different 16 terms, i.e., the i-th thread adds 16 terms of the two polynomials from 16×i to 16×i+15 indexes where 0≤i≤31. However, polynomial multiplication is more complex than simple polynomial addition. Falcon uses NTT- and FFT-based methods for efficient polynomial multiplications in the integer and complex domains. Because NTT is an integer domain analog of FFT, the process is similar. Thus, only the NTT-based polynomial multiplication method is explained. NTT-based polynomial multiplication comprises three parts: conversion to the NTT domain, point-wise multiplication, and inverse NTT conversion (which is conversion back to the original). In the NTT process, the Zq[X]/<ϕ>(ϕ=Xn+1), which is the ring of Falcon, is factored to n different sub-Rings of degree 1, and a polynomial in Zq[X]/<ϕ> is converted into n polynomials over the factored sub-Rings. Thus, the NTT process can be considered to repeatedly reduce the intermediate polynomials by the sub-Rings of Zq[X]/<ϕ> until it reaches degree 1.

Butterfly operation is the primary NTT conversion computation that is responsible for reducing coefficients in degrees higher than the factored sub-Ring’s degree to a lesser degree. Because one Butterfly operation reduces the coefficient, n/2 times of Butterfly operations are executed in log2n layers where n = 512 or 1024. For example, at the first layer, a coefficient in the range of 511-th degree and 256-th degree is reduced to the range of 255-th degree and 0-th degree with 256 Butterfly operations for n = 512. Butterfly operation multiplies a coefficient to be reduced with a twiddle factor and adds/subtracts it with a coefficient in a lower degree. Twiddle factors are predefined values stored in constant memory. After converting two polynomials over Zq[X]/<ϕ> into the NTT domain, n coefficients in the NTT domain are multiplied by each other in a point-wise manner. The i-th coefficient of the first polynomial is multiplied by the i-th coefficient of the second polynomial and then stored in the i-th position. After computing point-wise multiplication, n coefficients are converted into a polynomial over Zq[X]/<ϕ> with inverse NTT (iNTT). Note that iNTT is almost the same as the NTT process except that the inverse twiddle factors are used.

In the parallel NTT and FFT implementation, because 32 threads cooperatively process a Falcon operation such as Keygen, Sign, and Verify, these compute an NTT operation in cooperation. For n = 512, there are eight layers in NTT conversion where each layer computes 256 Butterfly operations. Thus, each thread computes eight Butterfly operations in each layer. When a thread processes a Butterfly, it accesses two coefficients: one to be multiplied with a twiddle factor and the other to be added/subtracted with the multiplied result. Because each thread simultaneously accesses a different coefficient, it is important to determine the coefficients that are accessed by the threads. For efficient position calculation, section_number and index_number are first defined. The section_number and index_number are computed with section_number = offset/interval_size and index_number = offset mod interval_size, respectively. The initial value of interval_size is 256 which decreases by half for each layer such that the final layer becomes 1. Moreover, in a Butterfly operation, term_number is the first operand index and the second operand is indexed with term_number + interval_size; these two operands are in the same polynomial. At the i-th layer, two operands in a Butterfly operation are located (512≤i) apart in the polynomial. Fig. 4 shows how term_number is computed and how each thread accesses two operands for the Butterfly operation. Because 32 threads cooperatively execute NTT conversion, each thread executes eight Butterfly operations in each layer. Although their operational structures are similar, the difference between NTT and FFT is that each uses 16-bit and 64-bit integers double-precision float-point, respectively, for expressing polynomial coefficients. Algorithm 6 shows the proposed parallel NTT algorithm. Note that in-place indicates the resulting sub-polynomials are stored in the output storage memory. Each thread in a block executes Algorithm 6 for a complete NTT conversion operation. The n in the inner loop (Step 5–15) is the number of threads in a block. It is divided by the thread per block (TPB).

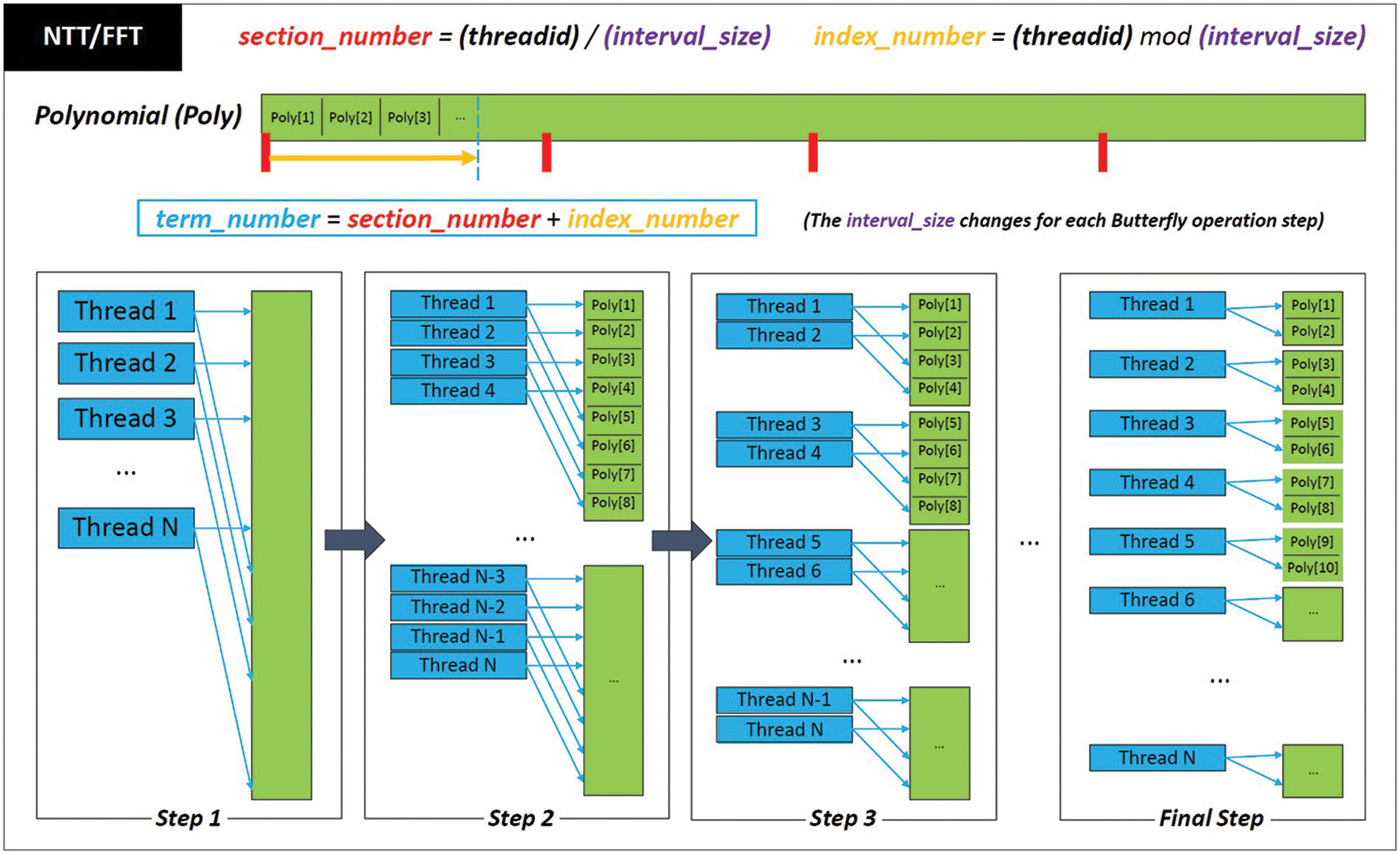
Figure 4: Parallel implementation techniques for NTT and FFT

Remarks The CUDA platform provides a cuFFT library for FFT conversion operations. However, it requires certain rules to use the library, i.e., the data should be stored in the cufftComplex structure before converting it to the FFT domain. The cufftComplex data memory should be allocated before launching a kernel function. However, in the Falcon software, the FFT conversion process is performed in the middle of Keygen, Sign, and Verify. Thus, allocating memory to the cufftComplex data is difficult. Furthermore, the original data should be converted to cufftComplex data format, which results in overhead because Falcon codes use only an array format to express complex numbers. Thus, the study implemented its own FFT-based polynomial multiplication method.

4.3.3 Reducing Divergence Effects with Dummy Operations

Synchronization should always be considered when multiple threads concurrently perform operations. If threads perform different operations because of branch-like statements, even within the same warp, a divergence problem occurs. This is when the first branch threads execute the corresponding statement as per the branch statement while the other branch threads enter the idle state without performing other operations until all operations on the first branch are performed.

Warp divergence occurs if the threads cannot perform the same operation because of branch instructions. Thus, the functions containing branch instructions with dummy operation-based parallel codes are redesigned. Moreover, the additional memory of a precomputation table must be applied in the dummy operation-based model, i.e., additional memory or a table to exclude the result of a dummy operation can be used such that it does not affect the final result. Fig. 5 shows the basic approach to dummy operation-based parallel codes where the left side shows the original codes including branch instructions, i.e., thread i in a block executes either R[i] = f(A[i]) op g(A[i]) or R[i] = f(A[i]) where f and g are a type of simple function, and op means operations such as addition and multiplication. Furthermore, the right side of the figure shows the revised codes. Moreover, f and g are redefined as table operations with f′ and g′. For example, f′(A [3]) and g′(A [1]) return zero value, which does not affect the final result.

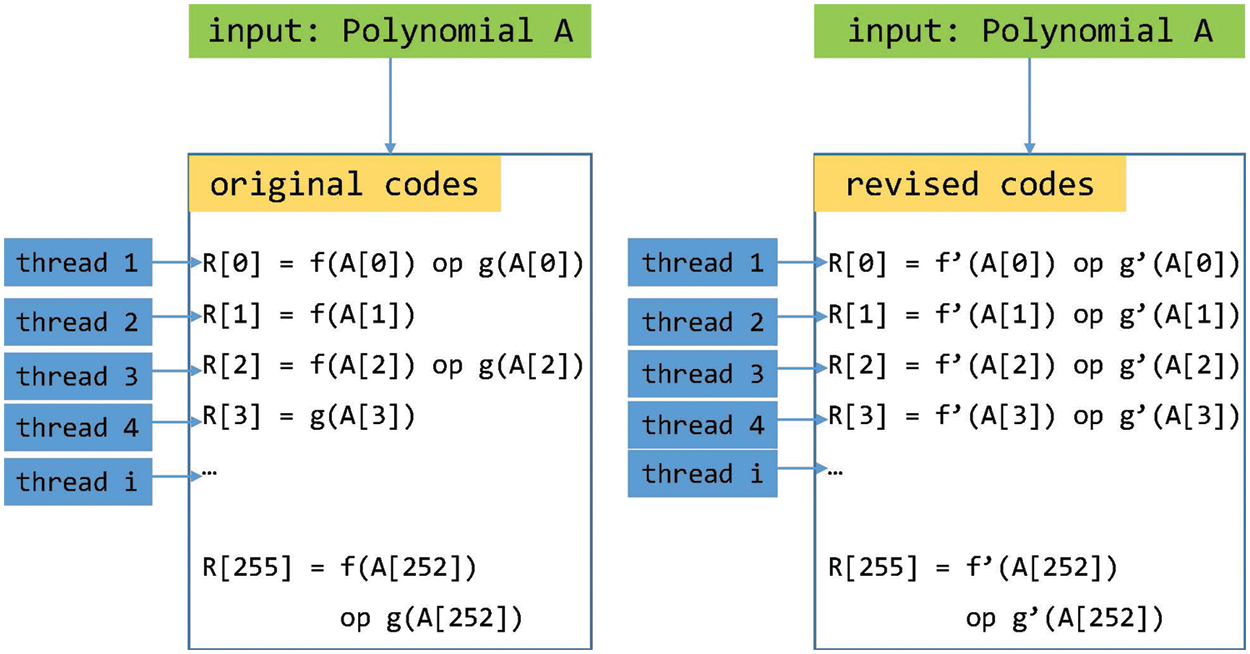
Figure 5: A basic approach for dummy operation-based parallel codes

4.3.4 Reducing Latency for Memory Copy

To reduce the idle time of GPU kernel execution because of memory copy between CPU and GPU, the CUDA stream technique [32] is further exploited, which can asynchronously execute memory copy while the kernel executes Falcon operation. From the experimental result, the 32 CUDA stream provides the best performance.

5  Results

This section discusses the evaluation of the Falcon performance running successfully on the GPU and confirms its implementation by comparing output results through the test vector. Table 4 shows the performance comparison between the proposed implementation on a GPU and the latest Falcon implementation on a CPU running AVX2. The Falcon result of the CPU used for performance comparison is referenced by Pornin (2019) [35].

The performance evaluation environment was as follows: the operating system was Windows and the AMD Ryzen 9 5900X CPU and NVIDIA GeForce RTX 3090 GPU were used. The performance evaluation was measured based on the time required to process a certain amount of key generation/signature generation/signature verification workload and measured based on the average of 1,000 repetitions of the same operation. The GPU-side software was implemented such that 32 threads for each block cooperatively performed one Falcon operation, and the number of blocks available was set to 256, which corresponded to the performance threshold. The time calculation for performance measurement was conducted based on the operation time, including the memory copy time between the CPU and GPU.

The values in Table 2 are the throughput per second. In the table, Sign1 and Sign2 are the throughput of the signing operation when using multiple keys and a single key, respectively. For CPU implementations, there is no difference between using multiple keys and a single key because the CPU software’s serial execution only uses a single key. For example, Pornin (2019) [35] used Falcon-512 to generate 7,692.9 signatures per second. The study proposed implementation uses a GPU to simultaneously perform more operations. In Falcon-512, it has a 52 times faster throughput for key generation, 58 times speed for signature generation, and 72 times faster signature verification compared with those in the study by Prest et al. (2022) [31]. When using AVX2 instructions, Falcon-512 shows 44/45/45 times faster performance for Keygen/Sign1/Verify, respectively, than those in the Pornin (2019) study [35]. For Falcon-1024, this study confirmed that its implementation was about 43/43/44 times faster than those of Pornin (2019) [35] for Keygen/Sign1/Verify, respectively. For Sign2, using a single signing key, the proposed implementation outperforms the CPU implementation [35] with the AVX2 by 50 and 47 times for Falcon-512 and Falcon-1024, respectively.

Compared with Falcon CPU software (Software4) using AVX2 on the latest AMD Ryzen 9 5900X CPU, the study’s Falcon-512 software demonstrated 35/28/34 times better performance in Keygen/Sign1/Verify, respectively. Moreover, the study’s Falcon-1024 software demonstrated 33/27/34 times better performance in Keygen/Sign1/Verify, respectively.

6  Conclusion

In this study, it was suggested that PQC can operate on GPU by considering the Falcon as an example which is the final selected algorithm by NIST’s PQC standardization competition. Multiple methods were proposed to successfully help the existing functions operate on the GPU. Moreover, optimization techniques that can be quickly processed using the GPU features were introduced. To our knowledge, this is the first result of implementing Falcon on a GPU. By operating PQC on a GPU, the possibility of replacing the existing algorithm with PQC in multiple server environments using the GPU is proposed. Furthermore, in this study, the proposed implementation techniques have potential use for other lattice-based PQCs.

Funding Statement: This work was partly supported by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MSIT) (No. 2022R1C1C1013368). This was partly supported in part by Korea University Grant and in part by the Institute of Information and Communications Technology Planning and Evaluation (IITP) Grant through the Korean Government [Ministry of Science and ICT (MSIT)], Development of Physical Channel Vulnerability-Based Attacks and its Countermeasures for Reliable On-Device Deep Learning Accelerator Design, under Grant 2021-0-00903.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

    1. P. W. Shor, “Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer,” SIAM Journal on Scientific Computing, vol. 26, no. 5, pp. 1484–1509, 1997. [Google Scholar]

    2. D. Moody, “Round 2 of nist PQC competition.” In Invited Talk at PQCrypto, ChongQing, China, 2019. [Google Scholar]

    3. M. R. Albrecht, D. J. Bernstein, T. Chou, C. Cid, J. Gilcher et al., “For classic mceliece,” 2022. [Online]. Available: https://classic.mceliece.org. [Google Scholar]

    4. P. Schwabe, R. Avanzi, J. Bos, L. Ducas, E. Kiltz et al., “For Crystals-Kyber,” 2022. [Online]. Available: https://pq-crystals.org/kyber/index.shtml. [Google Scholar]

    5. C. Chen, O. Danba, J. Hoffstein, A. Hulsing, J. Rijneveld et al., “For NTRU,” 2022. [Online]. Available: https://ntru.org/. [Google Scholar]

    6. J. -P. D’Anvers, A. Karmakar, S. S. Roy, F. Vercauteren, J. M. B. Mera et al., “For Saber,” 2022. [Online]. Available: https://www.esat.kuleuven.be/cosic/pqcrypto/saber/. [Google Scholar]

    7. V. Lyubashevsky, L. Ducas, E. Kiltz, T. Lepoint, P. Schwabe et al., “For Crystals-Dillithium,” 2022. [Online]. Available: https://pq-crystals.org/dilithium/index.shtml. [Google Scholar]

    8. T. Prest, P. -A. Fouque, J. Hoffstein, P. Kirchner, V. Lyubashevsky et al., “For Falcon,” 2022. [Online]. Available: https://falcon-sign.info. [Google Scholar]

    9. J. Ding, M. -S. Chen, A. Petzoldt, D. Schmidt, B. -Y. Yang et al., “For Rainbow,” 2022. [Online]. Available: https://www.pqcrainbow.org. [Google Scholar]

  10. S. C. Seo, T. Kim and S. Hong, “Accelerating elliptic curve scalar multi- plication over GF(2m),” Journal of Parallel and Distributed Computing, vol. 75, pp. 152–167, 2015. [Google Scholar]

  11. W. Pan, F. Zheng, Y. Zhao, W. T. Zhu and J. Jing, “An efficient elliptic curve cryptography signature server with GPU acceleration,” IEEE Transactions on Information Forensics and Security, vol. 12, no. 1, pp. 111–122, 2017. [Google Scholar]

  12. L. Gao, F. Zheng, R. Wei, J. Dong, N. Emmart et al., “DPF-ECC: A framework for efficient ECC with double precision floating-point computing power,” IEEE Transactions on Information Forensics and Security, vol. 16, pp. 3988–4002, 2021. [Google Scholar]

  13. N. Gupta, A. Jati, A. K. Chauhan and A. Chattopadhyay, “PQC acceleration using GPUs: FrodoKEM, NewHope, and Kyber,” IEEE Transactions on Parallel and Distributed Systems, vol. 32, no. 3, pp. 575–586, 2020. [Google Scholar]

  14. Y. Gao, J. Xu and H. Wang, “CUNH: Efficient GPU implementations of post-quantum KEM NewHope,” IEEE Transactions on Parallel and Distributed Systems, vol. 33, no. 3, pp. 551–568, 2021. [Google Scholar]

  15. H. Seong, Y. Kim, Y. Yeom and J. -S. Kang, “Accelerated implementation of NTRU on GPU for efficient key exchange in multi-client environment,” Journal of the Korea Institute of Information Security & Cryptology, vol. 31, no. 3, pp. 481–496, 2021. [Google Scholar]

  16. K. Lee, M. Gowanlock and B. Cambou, “Saber-GPU: A response-based cryptography algorithm for saber on the GPU,” in Proc. Pacific Rim Int. Symp. on Dependable Computing, Perth, Australia, pp. 123–132, 2021. [Google Scholar]

  17. S. C. Seo, “SIKE on GPU: Accelerating Supersingular isogeny-based key encapsulation mechanism on graphic processing units,” IEEE Access, vol. 9, pp. 116731–116744, 2021. [Google Scholar]

  18. W. -K. Lee, H. Seo, Z. Zhang and S. O. Hwang, “Tensorcrypto: High throughput acceleration of lattice-based cryptography using tensor core on GPU,” IEEE Access, vol. 10, pp. 20616–20632, 2022. [Google Scholar]

  19. PQClean Project, 2022. [Online]. Available: https://github.com/PQClean/PQClean. [Google Scholar]

  20. L. Ducas, E. Kiltz, T. Lepoint, V. Lyubashevsky, P. Schwabe et al., “Crystals-dilithium: A lattice-based digital signature scheme,” IACR Transactions on Cryptographic Hardware and Embedded Systems, vol. 2018, pp. 238–268, 2018. [Google Scholar]

  21. J. Ding, M. -S. Chen, A. Petzoldt, D. Schmidt, B. -Y. Yang et al., “Rainbow specifications and supporting documentation,” 2022. [Online]. Available: https://csrc.nist.gov/projects/post-quantum-cryptography/round-3-submissions. [Google Scholar]

  22. H. Nejatollahi, N. Dutt, S. Ray, F. Regazzoni, I. Banerjee et al., “Post-quantum lattice-based cryptography implementations: A survey,” ACM Computing Survey, vol. 51, no. 6, pp. 1–41, 2019. [Google Scholar]

  23. W. -K. Lee, S. Akleylek, D. C. -K. Wong, W. -S. Yap, B-M. Goi et al., “Parallel implementation of Nussbaumer algorithm and number theoretic transform on a GPU platform: Application to qTESLA,” The Journal of Supercomputing, vol. 77, no. 4, pp. 3289–3314, 2021. [Google Scholar]

  24. Ö Özerk, C. Elgezen, A. C. Mert, E. Öztürk and E. Savas, “Efficient number theoretic transform implementation on GPU for homomorphic encryption,” The Journal of Supercomputing, vol. 78, no. 2, pp. 2840–2872, 2022. [Google Scholar]

  25. P. -A. Fouque, J. Hoffstein, P. Kirchner, V. Lyubashevsky, T. Pornin et al., “Falcon: Fast-Fourier lattice-based compact signatures over NTRU,” 2022. [Online]. Available: https://www.di.ens.fr/~prest/Publications/falcon.pdf. [Google Scholar]

  26. W. M. Gentleman and G. Sande, “Fast fourier transforms: For fun and profit,” in Proc. AFIPS, New York, NY, USA, pp. 563–578, 1966. [Google Scholar]

  27. R. Agarwal and C. Burrus, “Fast convolution using Fermat number trans-forms with applications to digital filtering,” IEEE Transactions on Acoustics, Speech, and Signal Processing, vol. 22, no. 2, pp. 87–97, 1974. [Google Scholar]

  28. I. C. Society, “IEEE standard for floating-point arithmetic,” IEEE STD 754-2019, 2019. [Online]. Available: https://ieeexplore.ieee.org/document/8766229. [Google Scholar]

  29. P. Montgomery, “Modular multiplication without trial division,” Mathematics of Computation, vol. 44, no. 170, pp. 519–521, 1985. [Google Scholar]

  30. G. Seiler, “Faster AVX2 optimized NTT multiplication for ring-LWE lattice cryptography,” IACR Cryptololgy ePrint Archive, Report 2018/039, 2018. [Google Scholar]

  31. T. Prest, P. -A. Fouque, J. Hoffstein, P. Kirchner, V. Lyubashevsky et al., “Falcon specifications and supporting documentation,” 2022. [Online]. Available: https://csrc.nist.gov/projects/post-quantum-cryptography/round-3-submissions. [Google Scholar]

  32. NVIDIA. P. Vingelmann and F. H. Fitzek, “CUDA, release: 10.2.89,” 2022. [Online]. Available: https://developer.nvidia.com/cuda-toolkit. [Google Scholar]

  33. J. E. Stone, D. Gohara and G. Shi, “OpenCL: A parallel programming standard for heterogeneous computing systems,” Computing in Science Engineering, vol. 12, no. 3, pp. 66–73, 2010. [Google Scholar]

  34. O. F. Inc, “The ruler function, entry a001511 in the on-line encyclopedia of integer sequences,” 2022. [Online]. Available: http://oeis.org/A001511. [Google Scholar]

  35. T. Pornin, “New efficient, constant-time implementations of falcon,” Cryptology ePrint Archive, Report 2019/893, 2019. [Google Scholar]