Efficient Certificateless Authenticated Key Agreement for Blockchain-Enabled Internet of Medical Things

1  Introduction

IoMT is a newly developed healthcare service system with the increase of smart medical devices [1], which helps to manage medical devices, collect electronic medical records (EMR), and then realize the connection between things and things, things and people. Especially with the increasing of wearable health devices and smart medical devices, IoMT takes essential responsibility for collecting and managing medical data from these wireless body area devices [2]. However, a traditional centralized healthcare service system easily causes data tampering, information loss, and privacy leakage problems, which cause much damage to patients’ privacy, even worse, the country’s security.

Blockchain technology takes a new vision to solve the centralized problem in the traditional healthcare service systems and support medical data cross-agency sharing between different medical institutions [3,4]. Many blockchain-enabled healthcare service systems have been proposed, such as Healthchain [5,6], Medichain [7], and Blockchain-based data sharing (BBDS) [8], which establish distributed medical data management and sharing platforms for IoMT. The medical devices can become the data collection nodes in the Blockchain-enabled IoMT systems and transform medical data between different medical institutions and healthcare systems. When medical data transform into the IoMT network, the security of these data and personal privacy are the major concerns for patients and medical institutions [9,10]. Especially with the increasing of wearable health devices and smart medical devices, the privacy security in the cross-device sharing processes between these devices becomes the main challenge for the utilization of medical data.

Symmetric encryption can provide more efficient encryption and decryption, which is widely used in many healthcare service systems, especially the wireless medical network [11]. The secret key in symmetric encryption is most important for two parties, and it generally needs a KA protocol to pre-share a secret key for the new issue. KA protocol can construct a secret key between two or more strange parties to ensure that the parties communicate securely [12]. For wearable health devices and smart medical devices in the blockchain-enabled IoMT systems, the fragmented medical data collected from different wireless medical devices need to be shared and transmitted to the personal medical app, then established as an integrated medical data record [13,14]. Meanwhile, these devices need low latency, high security, and location awareness to satisfy the user’s experience. Therefore, a secure and efficient KA protocol is needed for medical data sharing between wireless medical devices and mobile medical apps.

To strengthen the medical data sharing security, this paper designs a cross-device key agreement model for blockchain-enabled IoMT and proposes a certificateless authenticated KA protocol. The contributions of this work are summarized as follows:

•   A cross-device key agreement model for the blockchain-enabled IoMT system is designed, which can help to establish a secure key agreement mechanism between wireless medical devices and mobile medical apps. The operating records will be uploaded and recorded in Healthchain ledger as immutable records, which can decrease the ledger redundancy and guarantee data traceability.

•   A certificateless authenticated KA protocol has been proposed, and this protocol only needs message transfer between the two parties once. The certificateless mechanism can avoid the key escrow problem and improve the efficiency of key agreement. Meanwhile, the security proof shows that the proposed KA protocol can resist the standard key-compromise impersonation attack.

•   The security analysis and performance analysis have been given, which show that the proposed KA protocol can satisfy the security attributes of know key security, unknown key share, random number compromise security, and sender’s forward security. Meanwhile, the efficiency comparison shows that the proposed KA protocol is more efficient than other protocols in similar literature.

The rest of this paper is organized as follows. Section 2 presents the related work of blockchain-enabled IoMT and key agreement protocols. Section 3 describes some preliminaries. Section 4 provides the proposed certificateless authenticated KA protocol. Section 5 and Section 6 present security analysis and performance analysis results. Section 7 summarizes this paper and describes future work.

2  Related Works

2.1 Blockchain-enabled IoMT

In order to break the monopolies and silos of medical data, researchers put efforts into exploring distributed IoMT systems with blockchain technology. Xu et al. proposed a double chain Healthchain system for large-scale EMR data management, which contains the userchain and doctorchain [5]. Our former work established a novel peer-to-peer platform for EMR management and proposed a Stackelberg pricing algorithm to promote medical data sharing between different medical institutions [6]. Rouhani et al. introduced a decentralized medical data asset management system called MediChain, which can help patients manage their medical data and obtain their own EMR ownership [7]. Xia et al. utilized blockchain technology to establish a medical data sharing system for cloud environments [8]. Moreover, Hylock et al. presented a Healthchain system around the patient, which can help patients take part in the EMR curation and dissemination [15]. Rahoof et al. utilized the private and consortium blockchain technology to establish a Healthchain system, as the former serves for intra-regional communication, and the latter serves for inter-regional communication [16]. These works mainly focus on constructing the privacy and data security management framework which solve traditional medical service system problems such as centralization, information loss, and privacy disclosure.

Some KA protocols have been proposed for electronic medical record management and sharing. For the traditional IoMT system. Mir et al. proposed a KA protocol based on biometrics authentication, which can improve the system security for telemedicine health services [17]. Zhang et al. presented a three-factor KA protocol for privacy-preserving in e-health systems, which can realize dynamic authentication [18]. Ravanbakhsh et al. gave a new remote user mutual authentication method based KA protocol for the e-health systems [19]. These KA protocols can improve the key security in the traditional centralized system, but they do not suitable for a distributed system based on blockchain technology. Then, for the blockchain-enabled IoMT systems. Mwitende et al., Mwitende et al. presented two KA protocols, one is the authenticated KA protocol, and the other is the certificateless authenticated KA protocol [20,21]. These two protocols are proposed to improve health data security in wireless body area networks. Chen et al. introduced a group KA protocol for blockchain-based Internet of things, which was also suitable for medical data protection in blockchain-enabled IoMT systems [22]. Wu et al. presented an authenticated KA protocol that can improve the medical data’s security in fog-driven IoT healthcare systems [23]. These protocols also have some problems, such as key escrow, certificate management, and identity leakage, which will lead the protocol more inefficient and insecure.

2.2 Key Agreement Protocols

The Diffie-Hellman protocol is the first public-key agreement protocol [24]. But this protocol lacks the authentication of communication entities, and it cannot resist the hacking attack, which has abilities to control the communication channel [25]. Authenticated KA protocols can resist attacks from active adversaries in the traditional public-key cryptosystem. However, there appeared to be a new problem with certificate management for those KA protocols under the traditional public-key cryptosystem. Then, to simplify the key management, Shamir first gave the idea of public-key cryptography with personal identity, which was called ID-PKC [26]. There existed a key generation centre (KGC) which served as the trusted third party to generate the private key relating to the user’s identity, and the identity was the user’s public key. Although ID-PKC can efficiently solve the problem of certificate management, it can also suffer attacks from the KGC, which possesses all the user’s secret keys. The malicious KGC can simulate any user to deceive others, which is known as the private key escrow problem [27]. In addition, certificateless public key cryptography (CL-PKC) has been introduced to weaken the influence of the key escrow problem in ID-PKC [28].

Some CL-PKC-based KA protocols have been presented in recent years. Zhang proposed a modified certificateless pairing-based KA protocol with formal security analysis, which only needed to transmit the message one time between two parties [29]. Islam et al. proposed a certificateless multi-receiver encryption-based elliptic curve cryptography without bilinear pairings [30]. Bala et al. summarized the impersonation attacks on the certificateless KA protocol and introduced some possible solutions [31]. Xie et al. gave a certificateless authenticated KA protocol based on the Diffie-Hellman assumption [32]. Meanwhile, Tedeschi et al. presented a certificateless KA protocol, claiming this scheme is lightweight for IoT communication [33]. Deng et al. proposed a two-party certificateless authenticated KA for a smart grid [34]. Hosseini et al. introduced a lightweight authentication scheme with KA protocol to improve the security of patient privacy in IoMT [35]. Alzahrani et al. proposed a secure KA scheme for a UAV-based crowd monitoring system [36]. Pu et al. introduced a KA protocol for wireless body area networks, which satisfied the properties of lightweight and anonymity [37]. These protocols have strong application ability, but they do not suitable for blockchain-enabled IoMT systems. Moreover, the traditional large integer decomposition, and discrete logarithm cannot resist quantum attacks. Therefore, with the development of quantum computers and quantum computing, lattice-based encryption and similar anti-quantum protocols have caused many considerations for future information security [38–40].

This paper focuses on medical data security, and a cross-device key agreement model for blockchain-enabled IoMT is introduced first. This model can guarantee the security of key agreement processes between different users and improve data transmission security in traditional IoMT systems. Meanwhile, a KA protocol has been proposed to support the proposed model. Compared with former protocols in similar literature, this KA protocol is more secure and efficient based on the discrete logarithm hard problem on elliptic curves.

3  Some Mathematical Problems

Let E be an elliptic curve over a prime finite field Fp, where p > 3 is an odd number. For simplification of computation, the curve is defined by equation

y2=x3+ax+b,

where a, b ∈ Fp are constants, such that

△=4a3+27b2≠0.

All points on E and the infinity point O form a cyclic additive group G with order n based on the operation of point addition R = P + Q.

Some hard problems are given below which are the security bases of the proposed KA scheme [30].

The elliptic curve discrete logarithm problem (ECDLP): If E is an elliptic curve over a prime finite field Fp, and P is a point with order n and Q is a point in group G generated by P, then it is hard to find an integer t such that Q = tP.

The Computational Diffie-Hellman (CDH) problem: Given a generator P of G and (aP, bP) for unknown a, b ∈ Zn * , the task of the CDH problem is to compute abP.

The Decisional Diffie-Hellman (DDH) problem: Given a generator P of G and (aP, bP, cP) for unknown a, b, c ∈ Zn * , the task of the DDH problem is to decide whether the equation abP = cP holds.

4  The Proposed Certificateless Authenticated KA Protocol

This section first presents a cross-device key agreement model for medical data sharing in blockchain-enabled IoMT. Then, an efficient pair-free certificateless KA protocol has been proposed for secure key establishment between different medical parties in blockchain-enabled IoMT.

4.1 The Cross-device Key Agreement Model

The cross-device key agreement model in the blockchain-enabled IoMT is shown in Fig. 1. This model mainly contains three parts: wireless medical device, mobile medical app, and Healthchain ledger. The wireless medical devices are the medical data collectors which can record and upload the patient’s health data; The mobile medical apps are the medical data management terminal that can bring and share personal data in different medical institutions; The Healthchain ledger is the online public recordation which can record all the data transactions and operations. However, how to establish a secure key between these three parts and how to guarantee privacy security in the transfer processes between different devices are important problems that should be considered.

•   Key agreement: Around the patient or doctor node, the wireless medical devices take responsibility for collecting and transmitting daily medical data, and the mobile medical apps take responsibility for storing and managing medical data. When medical data are transmitted between these devices or apps, there needs a secure session key for data encryption and decryption. The KA protocol can help establish this session key and guarantee medical data security and personal privacy. It will generally reset the session key after a certain period or when some new devices are added. This secure key agreement mechanism can efficiently create a new session key for medical data transmission. Then, certificateless KA protocol can improve the efficiency of KA protocol, as it does not contain the time consumption algorithm of bilinear pairings and discrete logarithms. It also makes the KA protocol more suitable for medical data transmitting among wireless medical devices and mobile medical apps in IoMT.

•   Healthchain ledger: This Healthchain ledger only contains the lightweight message, such as the unified ledger for the whole network, the data operation records, and the data storage addresses. In this cross-device agreement model, the agreed keys, the management record of old or new wireless medical devices and mobile medical apps, and the operations of medical data storage, sharing, encryption, and decryption should all be uploaded and recorded into the Healthchain ledger. It can provide the tracing mechanism for medical data authentication and establish a verification path for a medical data audit.

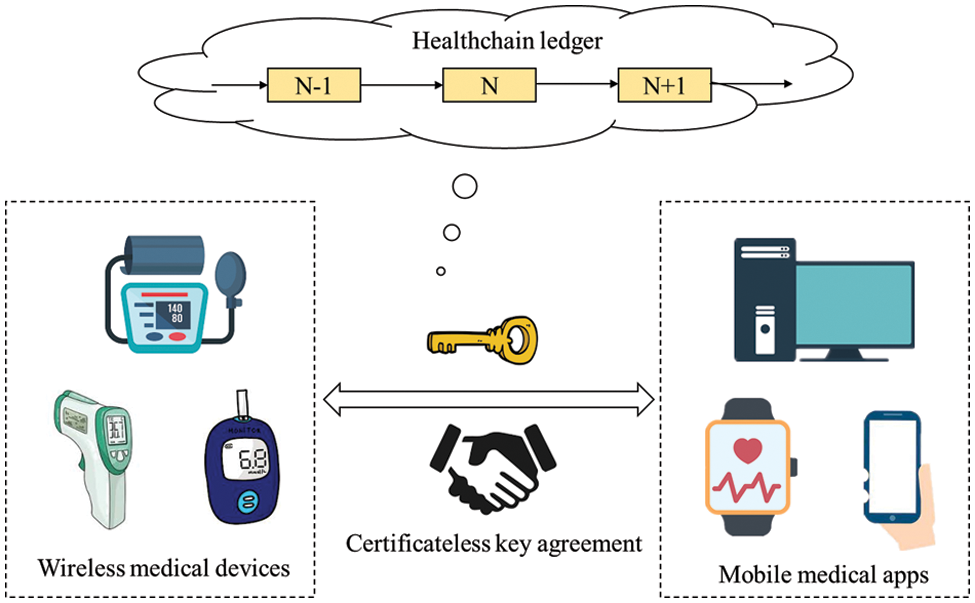
Figure 1: Cross-device key agreement model

4.2 The Proposed Certificateless KA Protocol

This section presents a new certificateless authenticated KA protocol. The simple workflow of the proposed KA protocol is shown in Fig. 2, and the detail descriptions of every step are as following.

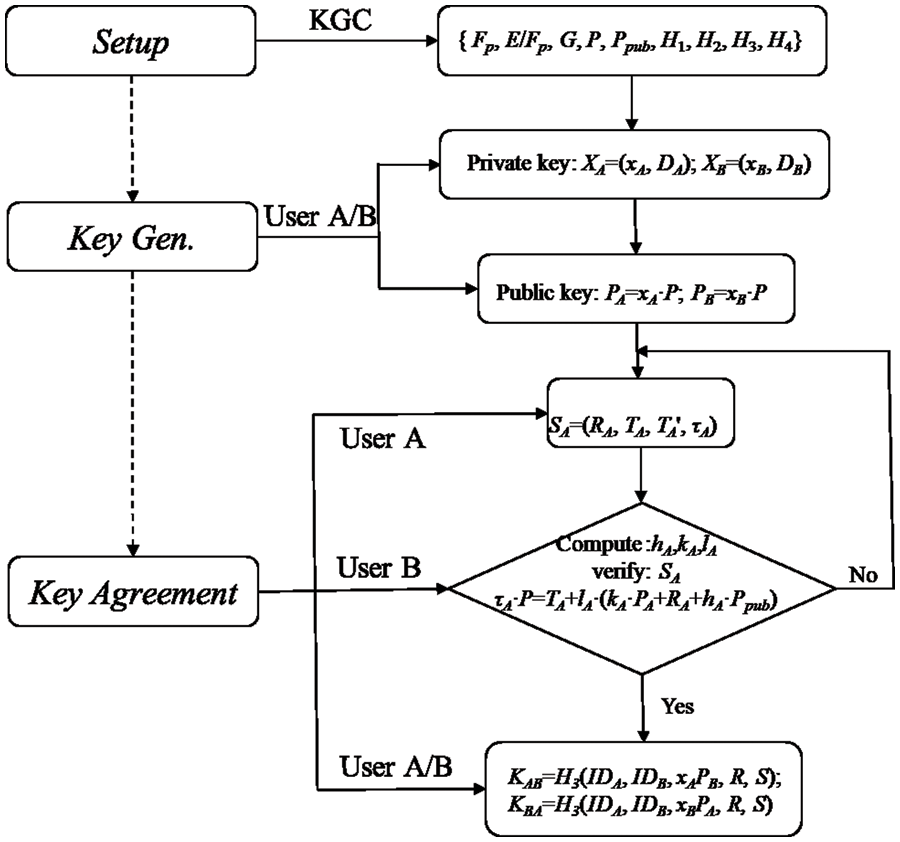
Figure 2: The workflow of KA protocol

Setup: Given the security parameter ζ, and KGC generates the other system parameters and master key.

(1)   Selects a k-bit prime p, and creates the parameters {Fp, E/Fp, G, P};

(2)   Selects y ∈ Zn * as the master private key mk, and calculates the master public key Ppub = y⋅P;

(3)   Selects some hash functions: H1: {0, 1}* × G→ Zn* , H2: G × {0, 1}* × G  G × G × G→ Zn*, H3: {0, 1}* × G × {0, 1}* × G × G × G × G→ Zn* and H4: {0, 1}* × {0, 1}* × G × G × G × G × {0, 1}* × {0, 1}*→{0, 1}l which are cryptographic secure;

(4)   Publishes the system parameters params = {Fp, E/Fp, G, P, Ppub, H1, H2, H3, H4}, and stores the master key y secretly.

Partial private key extract: Given params, mk, and a user with identity IDi, KGC generates the user’s partial private key by following steps.

(1)   Chooses a random number ri ∈ Zn*, and calculates Ri = ri⋅P and hi = H1(IDi, Ri);

(2)   Calculates si = ri + hiy mod n, and sends Di = {si, Ri} to the user through a secret channel.

Here, si is valid as the equation si⋅P = Ri + hi⋅Ppub holds.

Set secret value: Given params, user IDi randomly picks xi ∈ Zn*, and keeps xi as his/her secret value.

Set private key: Given params, Di and xi, user keeps Xi = (xi, Di) as his/her private key.

Set public key: Given params, user IDi calculates Pi = xi⋅P, and keeps Pi as his/her public key.

Key agreement: Two entities sender A and receiver B plan to negotiate a session key. A’s identity is IDA, private key is XA = (xA, DA), and the related public key is PA = xA⋅P . B’s identity is IDB, private key is XB = (xB, DB), and the related public key is PB = xB⋅P . Then, the session key will be established by next three steps:

Step 1: Given params, IDA, DA, and xA, the sender A selects a random number tA ∈ Zn*, tA′ ∈ Zn* and calculates:

TA=tA⋅P,TA′=tA′⋅P,

kA=H2(TA,IDA,PA,PB,RA,Ppub),

lA=H3(TA′,IDA,PA,PB,RA,Ppub),

and τA = tA + lA(kAxA + sA). SA = (RA, TA, TA′, τA) is a YTF signature. A sends signature SA to the receiver B.

Step 2: Given params, IDA, PA, and the signature SA, the receiver B examines the validation of the signature SA. The receiver B calculates

hA=H1(IDA,RA),kA=H2(TA,IDA,PA,PB,RA,Ppub)

and

lA=H3(TA′,IDA,PA,PB,RA,Ppub).

If the equation τA⋅P = TA + lA⋅(kA⋅PA + RA + hA⋅Ppub) holds, B believes that the signature SA is valid and sent by A. Otherwise, B refuses and aborts.

Step 3: A and B can generate the session key by calculating kAB and kBA, respectively.

kAB=H4(IDA,IDB,PA,PB,tA′PB,xAPB,SA)

kBA=H4(IDA,IDB,PA,PB,xBTA′,xBPA,SA)

Then, the session key is sk = kAB = kBA.

5  Security Analysis

5.1 The Security Proof

Now, e the security proof has been given in this section.

Lemma 1: The proposed certificateless authenticated KA protocol based on DDH problem can resist the type I adversary A in the random oracle model. In other words, if A can forge a valid session key with advantage ε by at most qH2 times H2 queries, qH3 times H3 queries, qs times Secret value queries, qc times Corrupt queries, qsr times Session-Key-Reveal queries, there exists another algorithm C which can solve the DDHP instance with advantage ε′≥(qs+qc)−2e^−1ε(e^ is the base of the natural logarithm).

Proof: Given an arbitrary random triple {aP, bP, cP}. C plans to solve the DDH problem by querying the key agreement algorithms with adversary A. Here, C will decide whether abP = cP, or a2P = cP, or b2P = cP holds. Then, following query-respond game shows that how C can solve DDH problem.

To setup the system parameters, C randomly selects e ∈ Zn* and sets Ppub = eP, then he sets the system parameters params = {Fp, E/Fp, G, P, Ppub, H1, H2, H3, H4} and sends them to A.

H1 query: C initializes an empty list listH1 storing (IDi, Ri, hi). Upon receiving a H1 query from A, C first checks the query history. If this query already exists, C finds the storing (IDi, Ri, hi) on listH1 and returns hi back. Otherwise, he selects hi ∈ Zn* at random and adds the corresponding storing to listH1, then he returns hi as the response.

H2 query: C initializes an empty list listH2 storing (Ti, IDi, Pi, Pj, Ri, Ppub, ki). Upon receiving a H2 query from A, C first checks the query history. If this query already exists, C finds the storing (Ti, IDi, Pi, Pj, Ri, Ppub, ki) on listH2 and returns ki back. Otherwise, he selects ki ∈ Zn* at random and adds the corresponding storing to listH2, then he returns ki as the response.

H3 query: C initializes an empty list listH3 storing (Ti′, IDi, Pi, Pj, Ri, Ppub, li). Upon receiving a H3 query from A, C first checks the query history. If this query already exists, C finds the storing (Ti′, IDi, Pi, Pj, Ri, Ppub, li) on listH3 and returns li back. Otherwise, he selects li ∈ Zn* at random and adds the corresponding storing to listH3, then he returns li as the response.

H4 query: C initializes an empty list listH4 storing (IDi, IDj, Pi, Pj, Ui, Vi, Si, hi′). Upon receiving a H4 query from A, C first checks the query history. If this query already exists, C finds the storing (IDi, IDj, Pi, Pj, Ui, Vi, Si, hi′) on listH4 and returns hi′ back. Otherwise, C selects randomly hi′ ∈ {0, 1}l and adds the corresponding storing to listH4, then he returns hi′ as the response.

Create queries: C initializes an empty list listC. For user IDi, C does not do any operation if IDi has been submitted previously. Otherwise, C flips a coini ∈ {0, 1, 2} that yields 0, 1, and 2 with probability δ, (1−δ)/2 and (1−δ)/2, respectively.

If coini = 0, C randomly chooses a number xi ∈ Zn*, calculates the public key Pi = xiP. Then, C randomly chooses a number ri ∈ Zn* and calculates Ri = ri⋅P. Then he submits Ri and IDi to H1 query and recovers the storing (IDi, Ri, hi) from listH1. And C calculates si = ri + hie mod n and takes Di = (si, Ri) as the partial private key and adds (coini, IDi, ri, xi, Di, Pi) into listC.

If coini = 1, C randomly chooses a number xi ∈ Zn* and calculates the public key Pi = xiaP. Then, C sets xi: = ⊥, randomly chooses a number ri ∈ Zn* and calculates Ri = ri⋅P. Then he submits Ri and IDi to H1 query and recovers the storing (IDi, Ri, hi) from listH1. And C calculates si = ri + hie mod n and takes Di = (si, Ri) as the partial private key and adds (coini, IDi, ri ,⊥, Di, Pi) into listC.

If coini = 2, C randomly chooses a number xi ∈ Zn*, calculates the public key Pi = xibP. Then, C sets xi: = ⊥, randomly chooses a number ri ∈ Zn* and calculates Ri = ri⋅P. Then he submits Ri and IDi to H1 query and recovers the storing (IDi, Ri, hi) from listH1. And C calculates si = ri + hie mod n and takes Di = (si, Ri) as the partial private key and adds (coini, IDi, ri, ⊥, Di, Pi) into listC.

Public key queries: For identity IDi, C first performs the Create oracle, and finds out the storing (coini, IDi, ri, *i , Di, Pi) from listC , where *i may be xi or ⊥. Then, he returns Pi as the response.

Secret value queries: For identity IDi, C first performs the Create oracle, and finds out the storing (coini, IDi, ri, *i, Di, Pi) from listC. If *I = ⊥, C reports failure and aborts (Event 1). If *I = xi and Pi≠xiP, C returns ⊥ (If a Public key replacement query on IDi, has been made by A, Pi≠xiP). Otherwise, C returns xi as the answer.

Corrupt queries: On inputting an identity IDi, C submits IDi to the Create oracle, then finds out the storing (coini, IDi, ri, *i, Di, Pi) from listC. If *i = ⊥, C reports failure and aborts (Event 2); else if Pi≠xiP, returns (⊥, Di) as the answer; Else returns (xi, Di) as the response.

Partial private key queries: For identity IDi, C first performs the Create oracle, and finds out the storing (coini, IDi, ri, *i, Di, Pi) from listC. Then he returns Di as the response.

Public-Key-Replacement queries: For (IDi, Pi′), C first performs the Create oracle, and finds out the storing (coini, IDi, ri, *i, Di, Pi) from listC and then sets Pi = Pi′.

Send queries: To respond to A’s queries, C initializes an empty list listS storing (IDi, Pi, Pj, Ri, Si). On input a query ∏ijn from A, C first checks whether this query has been queried. If so, C finds the corresponding storing on listS and returns Si to A.

Otherwise, C performs the Create oracle with IDi, and finds out the storing (coini, IDi, ri, *i, Di, Pi) from listC and (IDi, Ri, hi) from listH1. Then, C randomly selects τi, ki and li in Zn*, and calculates ti = τi−li(ki + ri + hie) and Ti = tiP. Next, C sets

H2(Ti,IDi,Pi,Pj,Ri,Ppub):=ki,

H3(Ti′,IDi,Pi,Pj,Ri,Ppub):=li,

Si:=(Ri,Ti,τi),

Then, he adds (Ti, IDi, Pi, Pj, Ri, Ppub, ki), (Ti′, IDi, Pi, Pj, Ri, Ppub, li) and (IDi, Pi, Pj, Ri, ti, Si) to listH2, listH3 and listS, respectively. At last, he returns Si as the response.

Session key reveal queries: When receives the Session key reveal query on ∏ijn, C performs the Create oracle with IDi, and recovers the storing (coini, IDi, ri, *i, Di, Pi) and (coinj, IDj, rj, *j, Dj, Pj) from listC. Also, C submits ∏ijn to the send oracle and recovers (IDi, Pi, Pj, Ri, ti, Mi) from listS. Then, he calculates Ui and Vi according to coini and coinj. The values of Ui and Vi are listed in Table 1 as following.

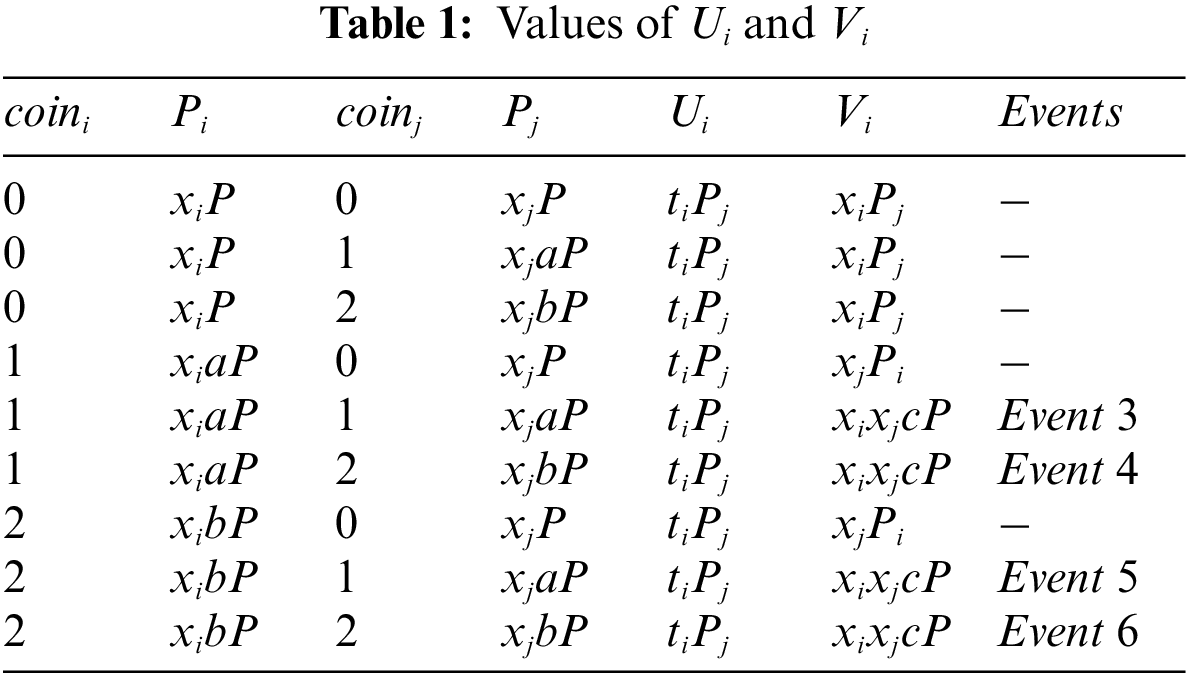
In Table 1, if Event 3, or Event 4, or Event 5, or Event 6 occurs, C randomly selects a string w ∈ {0, 1}l and returns w as the session key. Otherwise, C submits (IDi, IDj, Pi, Pj, Ui, Vi, Si) to H4 oracle and recovers (IDi, IDj, Pi, Pj, Ui, Vi, Si, hi′) from listH4, then he returns hi′ as the response.

Random number reveal queries: When receives a random number reveal query on ∏ijn, C finds out storing (IDi, Pi, Pj, Ri, ti, Si) on listS and returns ti as the response.

Test queries: When A asks a Test query on ∏ijn. C queries the Session key reveal oracle and gets ψ, where ψ=w or ψ=hi′. It can compute that ψ=w with a probability (1−δ)2, while ψ=hi′ with a probability 1−(1−δ)2. C outputs ψ as the answer.

The former query-respond operations are all in the message space, which are uniformly distributed. Therefore, A cannot distinguish the difference between this simulation and the real word before C aborts. In this case, when the Event 3, or Event 4, Event 5 and Event 6 happen, A can find a solution of the DDHP (Pixi,Pjxj,Vixixj) = (aP, aP, cP) or (aP, bP, cP) or (bP, aP, cP) or (bP, bP, cP) with advantage ε. Therefore, A wins out in this query-respond game with an advantage ε.

C will abort if Event 1 or Event 2 happens. Then, it can derive

Pr[¬Event2]≥δqs,Pr[¬Event2]≥δqc

Because Event 1 is independent to Event 2, it can derive

Pr[¬abort]=Pr[¬Event1∧¬Event2]≥δ(qs+qc)

On the other hand, Pr[Event3]=Pr[coini=1∧coinj=1]=(1−δ2)2. Similarly,

Pr[Event4]=Pr[Event5]=Pr[Event6]=(1−δ2)2

Therefore, Pr[Event3∨Event4∨Event5∨Event6]=(1−δ)2.

It can derive the probability that C finds a salutation for DDH problem.

ε′=Pr[¬Event1∧¬Event2∧(Event3∨Event4∨Event5∨Event6)]≥δ(qs+qc)(1−δ)2ε≥(qs+qc)−2e^−1ε

here e^ is the base of the natural logarithm. This completes the proof of lemma 1.

Lemma 2: The proposed certificateless authenticated protocol based on DDH problem can resist the type II adversary A in the random oracle model. In other words, if A can forge a valid session key with advantage ε by at most qH2 times H2 queries, qH3 times H3 queries, qs times Secret value queries, qc times Corrupt queries, qsr times Session-Key-Reveal queries, there exists another algorithm C which can solve the DDH problem with advantage ε′≥(qs+qc)−2e^−1ε.

Proof: Given an arbitrary random triple {aP, bP, cP}. C plans to solve the DDH problem. That is, C will decide whether abP = cP, or a2P = cP, or b2P = cP holds. Then, following query-respond game shows how C can solve DDH problem.

To setup the system parameters, C randomly selects e ∈ Zn* and sets Ppub = eP, then he sets the system parameters params = {Fp, E/Fp, G, P, Ppub, H1, H2, H3, H4} and gives params and e to A.

A can query all the oracles as that described in Lemma 1 except that he cannot make Public-Key-Replacement queries.

By using the computation technique similar like lemma 2, it can prove that C may solve the DDH problem with advantage at least (qs+qc)−2e^−1ε.

Theorem 1. The proposed certificateless authenticated KA protocol can resist type I adversary and type II adversary in the random oracle model depending on the hardness of DDH problem.

Proof: The theorem proof follows directly from lemma 1–2.

5.2 Security Attributes Analysis

The former security proof has shown that the proposed KA protocol is secure against common attacks. This section provides analyses of security attributes that the proposed certificateless KA protocol can capture.

(1)   Unknown key share: The sender A computes his/her session key with the identity IDB and public key PB of receiver B. So, sender A knows whom the target entity communicated. If one adversary impersonates B to receive and verify the ephemeral secret sent by A. He/she cannot compute a correct session key without sender A’s or receiver B’s private key. In addition, the ephemeral secret will be verified by receiver B. If someone impersonates A to create the session key with B, B can find he/she is not A and abort. Then, entity A (Here, A may be the sender or the receiver) cannot be coerced to share a key with the unidentified entity that is not the target entity B.

(2)   Known key security: In the key agreement phase, the ephemeral secret is the signature of a message. The adversary cannot obtain any information from this signature and derive any information about former session keys even if he compromises the session key of sender A or receiver B. If the adversary compromises A’s session key, he/she cannot obtain any information about other former session keys. With random number tA, the session key computed by sender A is fresh. If the adversary compromises receiver B’s session key, he/she cannot obtain any information about other former session keys. Because of the unique signature message, the session key computed by receiver B is unique. Hence, the proposed scheme can capture Known key security.

(3)   Random number compromise security: Sender A’s private key is constructed by the partial private key and A’s secret value. Although the adversary intercepts the random number in the partial private key generated phase, he/she cannot know sender A’s private key. In Step 1 of the session key phase, with the random number used, once the performance of KA protocol will produce a new signature and generate an exclusive session key. Therefore, the compromise of a random number cannot obtain any information about A’s private key and session key.

(4)   Key forward security: Every session key of the once-key agreement is unique in the proposed KA protocol. With a random number used, the adversary cannot capture the session key even though he/she intercepts sender A’s private key. Therefore, the proposed KA can capture key forward security as compromising A’s private key cannot influence the former constructed session.

(5)   Standard key compromise impersonation: In the proposed KA protocol, if A’s (Here A can be either a sender or a receiver) private key has been compromised, the adversary only can impersonate A. He/she cannot generate a valid signature without knowing entity’s private key. So he/she cannot impersonate any other entity in the presence of A. Then, the proposed KA protocol can capture standard key compromise impersonation.

In particular, this paper adds a certificateless signature to the proposed KA protocol. When receiver B receives the ephemeral secret sent by A, B first verifies validation of the information. Then, B knows that the ephemeral secret comes from A and calculates the session key. The adversary cannot impersonate any entity to communicate with B even if he obtains B’s private key, as he cannot create a valid signature with only one entity’s private key. Therefore, the adversary cannot impersonate the sender and other entities to B with a valid ephemeral secret, and the proposed KA protocol can achieve standard key compromise impersonation.

6  Performance Analysis

6.1 Efficiency Comparison

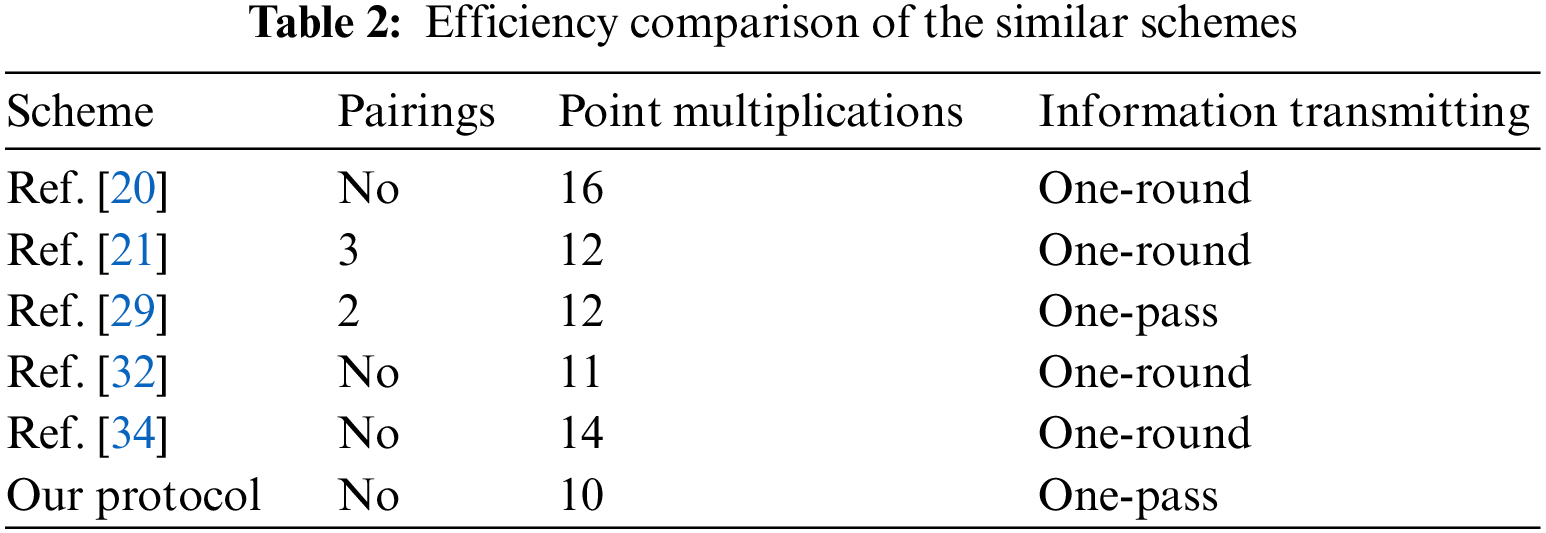
Compared with similar KA protocols, the proposed KA protocol in this paper has many advantages. The comparison results are shown in Table 2. The protocols in Refs. [21,29] are based on bilinear pairings, which are time consumption as one pairing operation is about 11110 multiplications in finite field F3163. Then, the main operation in these protocols is point multiplication, and the proposed KA protocol utilizes the least point multiplication computation. Moreover, the proposed KA protocol only needs one-time information transmission, which can save half the time burden of the information authenticated in the session key agreement phase compared with one-round protocols. Although the KA protocol in Ref. [29] is also one-pass, it needs bilinear pairings, which are the time consumption operations.

Then, this paper performs the proposed KA scheme on a Windows 10 desktop with Intel(R) Core (TM) i7 central processing unit (CPU) 3.0 GHz and 16G random access memory (RAM). The parameters setting is according to the principle in [41], pairing operation takes 1.9 s, and point multiplication takes 0.81 s for 128-bit security. Therefore, the time consumption of the proposed KA protocol is 10 * 0.81 = 8.1 s, and the performance comparisons of this time consumption are shown in Fig. 3a. Then, considering the energy consumption of the wireless medical device, the proposed KA protocol has been performed with some wireless sensor nodes, generally 3.0 V and 8.0 mA, with the power level of MICA 2. The energy consumption of the proposed KA protocol is 3.0 * 8.0 * 0.81 * 10 = 194.4 mJ, and performance comparisons with the other similar literature are shown in Fig. 3b. From simulation results, the proposed KA protocol is more time and energy-saving than other protocols in similar literature. It also shows that this protocol is economical and practical for medical data sharing between different parties through blockchain-enabled IoMT.

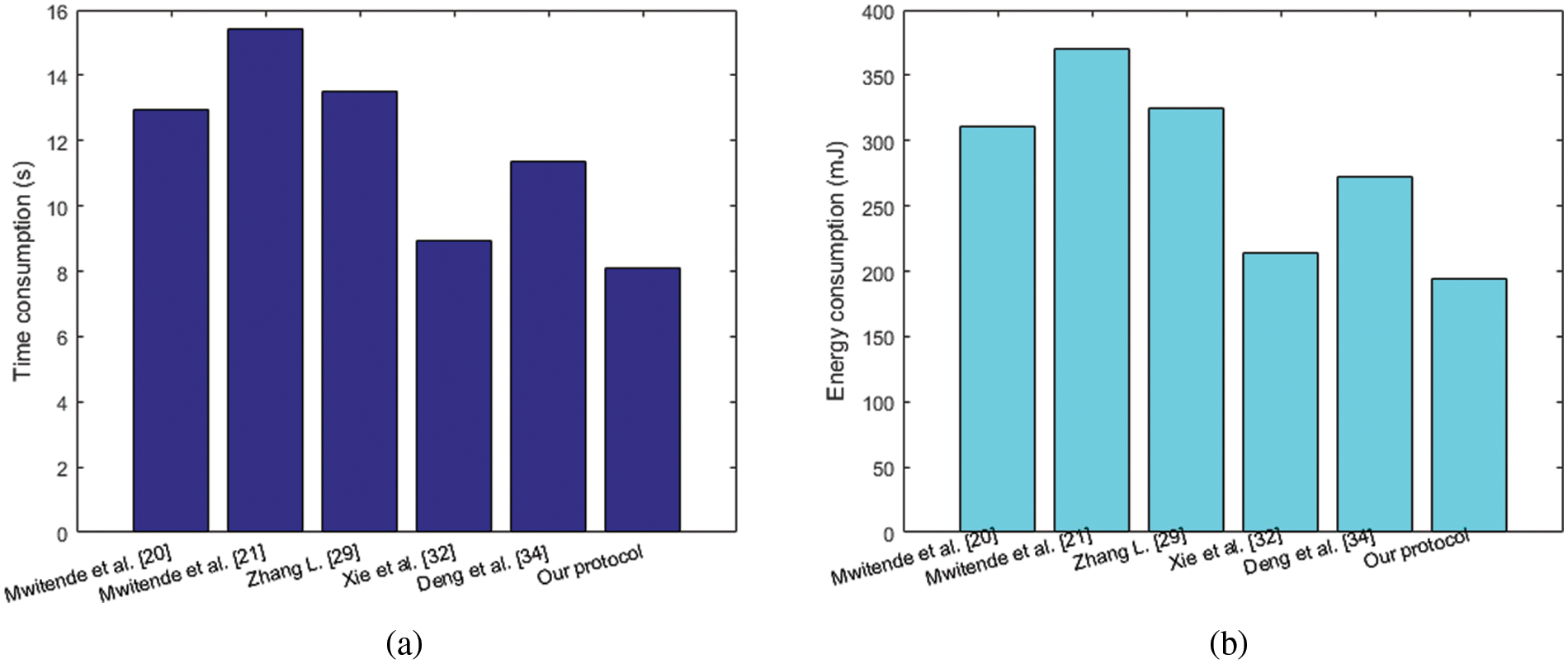
Figure 3: Performance comparisons: (a) Time consumption; (b) Energy consumption

6.2 Transaction Performance in Blockchain-enabled IoMT

To check the practicability of the proposed cross-device key agreement model in blockchain-enabled IoMT system, the transaction of medical data sharing has been performed on the Hyperledger Fabric concerning the transaction throughput (TSP) and transaction latency (TL). Here, we perform it with the transaction number increasing from 200 to 1600 and present the simulation results. It selects 5 nodes to simulate the medical data sharing transaction, ‘peer 1’, and ‘peer 2’ are common nodes that only can participate in the transaction; ‘peer 3’, ‘peer 4’ and ‘peer 5’ are management nodes which can participate the general transaction and manage blockchain ledger. The average CPU consumption for these five nodes is shown in Fig. 4a. So, common nodes do not consume many resources, and management nodes consume a few more. The results also show that resource consumption is growing slowly with the increase in transaction numbers. Meanwhile, transaction success rate always keeps 100% which is shown in Fig. 4b. This result illustrates that the blockchain-enabled IoMT system is stable and reliable, and the cross-device key agreement model can support the medical data sharing to guarantee data security.

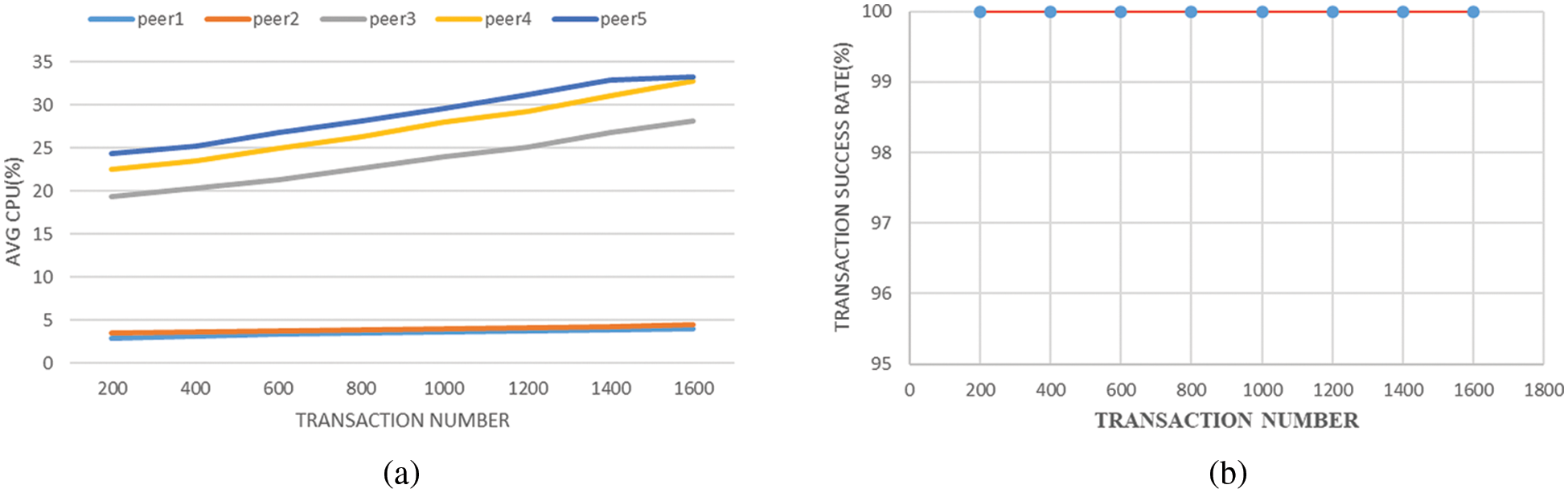
Figure 4: The medical data sharing processing in blockchain-enabled IoMT: (a) Average CPU consumption; (b) Transaction success rate

Then, there select three items, such as “CreateAccount”, “Query”, and “Transaction”, to describe the variation of TSP and TL with the increase of the transaction number from 200 to 1600. For the simulation results, Fig. 5a shows the trend chart of transaction throughput, and Fig. 5b shows the trend chart of average transaction latency. As transaction throughput, the items “CreateAccount” and “Transaction” keep stable, and the “Query” increases slightly with the increase of transaction number. As the transaction latency, the items “CreateAccount” and “Query” keep stable, and the “Transaction” increases slightly with the increase of transaction number. Therefore, it can derive that TSP and TL are less affected by the test environment, and the proposed data privacy preserving model is practical for health data sharing in the Blockchain-enabled IoMT system.

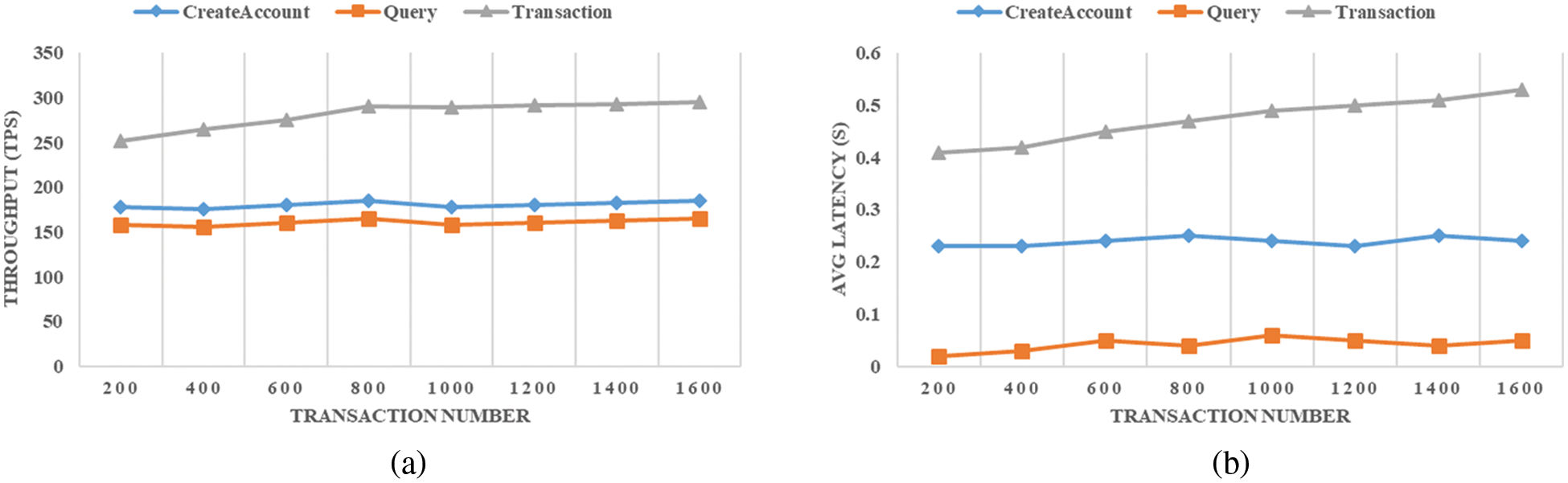
Figure 5: The medical data sharing processing in blockchain-enabled IoMT: (a) Transaction throughput; (b) Transaction latency

7  Conclusion

This paper presents a cross-device key agreement model for the blockchain-enabled IoMT system, which can improve information transfer security between wireless medical devices and mobile medical apps. Then, a pairing-free certificateless authenticated KA protocol has been given, which can help to establish a secure session key for medical sharing among blockchain-enabled IoMT system. Based on the CDH and DDH hard problems, the proposed KA protocol can resist the attack of standard key-compromise impersonation and achieve the sender’s forward security property. This research can protect the security of patients’ privacy and strength the system security for secure data sharing in blockchain-enabled IoMT system.

In the future, our team will continue to put efforts on the research of security issues in blockchain-enabled IoMT system, such as secure secret sharing between different wireless medical devices, medical data anonymous authentication, and anti-quantum attack signature scheme.

Funding Statement: This work was supported by the National Natural Science Foundation of China under Grant 92046001, 61962009, the JSPS KAKENHI Grant Numbers JP19K20250, JP20H04174, JP22K11989, Leading Initiative for Excellent Young Researchers (LEADER), MEXT, Japan, and JST, PRESTO Grant Number JPMJPR21P3, Japan. Mianxiong Dong is the corresponding author, the Doctor Scientific Research Fund of Zhengzhou University of Light Industry under Grant 2021BSJJ033, Key Scientific Research Project of Colleges and Universities in Henan Province (CN) under Grant No. 22A413010.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

    1. G. J. Joyia, R. M. Liaqat, A. Farooq and S. Rehman, “Internet of medical things (IoMTApplications, benefits and future challenges in healthcare domain,” Journal of Communications, vol. 12, no. 4, pp. 240–247, 2017. [Google Scholar]

    2. G. Yang, Z. Pang, M. J. Deen, M. Dong, Y. T. Zhang et al., “Homecare robotic systems for healthcare 4.0: Visions and enabling technologies,” IEEE Journal of Biomedical and Health Informatics, vol. 24, no. 9, pp. 2535–2549, 2020. [Google Scholar]

    3. M. Mettler, “Blockchain technology in healthcare: The revolution starts here,” in Proc. IEEE 18th Int. Conf. on E-Health Networking, Applications and Services (Healthcom), Munich, Germany, pp. 1–3, 2016. [Google Scholar]

    4. C. Li, M. Dong, J. Li, G. Xu, X. B. Chen et al., “Efficient medical big data management with keyword-searchable encryption in healthchain,” IEEE System Journal, vol. 16, no. 4, pp. 5521–5532, 2022. [Google Scholar]

    5. J. Xu, K. Xue, S. Li, H. Tian, J. Hong et al., “Healthchain: A blockchain-based privacy preserving scheme for large-scale health data,” IEEE Internet of Things Journal, vol. 6, no. 5, pp. 8770–8781, 2019. [Google Scholar]

    6. C. Li, M. Dong, J. Li, G. Xu, X. B. Chen et al., “Healthchain: Secure EMRs management and trading in distributed healthcare service system,” IEEE Internet of Things Journal, vol. 8, no. 9, pp. 7192–7202, 2021. [Google Scholar]

    7. S. Rouhani, L. Butterworth, A. D. Simmons, D. G. Humphery and R. Deters, “MediChain TM: A secure decentralized medical data asset management system,” in Proc. IEEE Int. Conf. on Internet of Things (iThings) and IEEE Green Computing and Communications (GreenCom) and IEEE Cyber, Physical and Social Computing (CPSCom) and IEEE Smart Data (SmartData), Halifax, NS, Canada, pp. 1533–1538, 2018. [Google Scholar]

    8. Q. Xia, E. B. Sifah, A. Smahi, S. Amofa and X. Zhang, “BBDS: Blockchain-based data sharing for electronic medical records in cloud environments,” Information, vol. 8, no. 2, pp. 44, 2017. [Google Scholar]

    9. G. Hatzivasilis, O. Soultatos, S. Ioannidis, C. Verikoukis, G. Demetriou et al., “Review of security and privacy for the internet of medical things (IoMT),” in Proc. 15th Int. Conf. on Distributed Computing in Sensor Systems (DCOSS), Santorini Island, Greece, pp. 457–464, 2019. [Google Scholar]

  10. F. Alsubaei, A. Abuhussein and S. Shiva, “Security and privacy in the internet of medical things: Taxonomy and risk assessment,” in Proc. IEEE 42nd Conf. on Local Computer Networks Workshops (LCN Workshops), Singapore, pp. 112–120, 2017. [Google Scholar]

  11. P. Kumar and H. J. Lee, “Security issues in healthcare applications using wireless medical sensor networks: A survey,” Sensors, vol. 12, no. 1, pp. 55–91, 2012. [Google Scholar]

  12. S. Blake-Wilson, D. Johnson and A. Menezes, “Key agreement protocols and their security analysis,” in IMA Int. Conf. on Cryptography and Coding, Berlin, Heidelberg, Springer, pp. 30–45, 1997. [Google Scholar]

  13. G. Srivastava, J. Crichigno and S. Dhar, “A light and secure healthcare blockchain for IoT medical devices,” in Proc. IEEE Canadian Conf. of Electrical and Computer Engineering (CCECE), Edmonton, AB, Canada, pp. 1–5, 2019. [Google Scholar]

  14. S. Shi, D. He, L. Li, N. Kumar, M. K. Khan et al., “Applications of blockchain in ensuring the security and privacy of electronic health record systems: A survey,” Computers & Security, vol. 97, no. 101966, pp. 1–20, 2020. [Google Scholar]

  15. R. H. Hylock and X. Zeng, “A blockchain framework for patient-centered health records and exchange (HealthChainEvaluation and proof-of-concept study,” Journal of Medical Internet Research, vol. 21, no. 8, pp. 1–30, 2019. [Google Scholar]

  16. T. P. A. Rahoof and V. R. Deepthi, “HealthChain: A secure scalable health care data management system using blockchain,” in Proc. Int. Conf. on Distributed Computing and Internet Technology, Bhubaneswar, OSFC, India, pp. 380–391, 2020. [Google Scholar]

  17. O. Mir and M. Nikooghadam, “A secure biometrics based authentication with key agreement scheme in telemedicine networks for e-health services,” Wireless Personal Communications, vol. 83, no. 4, pp. 2439–2461, 2015. [Google Scholar]

  18. L. Zhang, Y. Zhang, S. Tang and H. Luo, “Privacy protection for e-health systems by means of dynamic authentication and three-factor key agreement,” IEEE Transactions on Industrial Electronics, vol. 65, no. 3, pp. 2795–2805, 2017. [Google Scholar]

  19. N. Ravanbakhsh and M. Nazari, “An efficient improvement remote user mutual authentication and session key agreement scheme for E-health care systems,” Multimedia Tools and Applications, vol. 77, no. 1, pp. 55–88, 2018. [Google Scholar]

  20. G. Mwitende, Y. Ye, I. Ali and F. Li, “Certificateless authenticated key agreement for blockchain-based WBANs,” Journal of Systems Architecture, vol. 110, no. 101777, pp. 1–20, 2020. [Google Scholar]

  21. G. Mwitende, I. Ali, N. Eltayieb, N. Wang and F. Li, “Authenticated key agreement for blockchain-based WBAN,” Telecommunication Systems, vol. 74, no. 3, pp. 347–365, 2020. [Google Scholar]

  22. C. M. Chen, X. Deng, W. Gan, J. Chen and S. K. Islam, “A secure blockchain-based group key agreement protocol for IoT,” The Journal of Supercomputing, vol. 77, no. 8, pp. 9046–9068, 2021. [Google Scholar]

  23. T. Y. Wu, T. Wang, Y. Q. Lee, W. Zheng, S. Kumari et al., “Improved authenticated key agreement scheme for fog-driven IoT healthcare system,” Security and Communication Networks, vol. 2021, no. 6658041, pp. 1–16, 2021. [Google Scholar]

  24. W. Diffie and M. E. Hellman, “New directions in cryptography,” IEEE Transactions on Information Theory, vol. 22, no. 6, pp. 644–654, 1976. [Google Scholar]

  25. G. Lowe, “An attack on the needham-schroeder public-key authentication protocol,” Information Processing Letters, vol. 56, no. 3, pp. 131–133, 1995. [Google Scholar]

  26. A. Shamir, “Identity-based cryptosystems and signature schemes,” in CRYPTO’84, LNCS, vol. 196, pp. 47–53, 1984. [Google Scholar]

  27. T. H. Yuen, W. Susilo and Y. Mu, “How to construct identity-based signatures without the key escrow problem,” International Journal of Information Security, vol. 9, no. 4, pp. 297–311, 2010. [Google Scholar]

  28. S. Al-Riyami and K. G. Paterson, “Certificateless public key cryptography,” Proceedings of ASIACRYPT, LNCS, vol. 2894, pp. 452–473, 2003. [Google Scholar]

  29. L. Zhang, “Ceritificateless one-pass and two-party authenticated key agreement protocol and its extensions,” Information Sciences, vol. 293, pp. 182–195, 2015. [Google Scholar]

  30. S. K. H. Islam, M. K. Khan and A. M. Al-Khouri, “Anonymous and provably secure certificateless multireceiver encryption without bilinear pairing,” Security and Communication Networks, vol. 8, no. 13, pp. 2214–2231, 2015. [Google Scholar]

  31. S. Bala, G. Sharma and A. K. Verma, “Impersonation attack on certificateless key agreement protocol,” International Journal of Ad Hoc and Ubiquitous Computing, vol. 27, no. 2, pp. 108–120, 2018. [Google Scholar]

  32. Y. Xie, L. Wu, J. Shen and L. Li, “Efficient two-party certificateless authenticated key agreement protocol under GDH assumption,” International Journal of Ad Hoc and Ubiquitous Computing, vol. 30, no. 1, pp. 11–25, 2019. [Google Scholar]

  33. P. Tedeschi, S. Sciancalepore, A. Eliyan and R. Di Pietro, “LiKe: Lightweight certificateless key agreement for secure IoT communications,” IEEE Internet of Things Journal, vol. 7, no. 1, pp. 621–638, 2019. [Google Scholar]

  34. L. Deng and R. Gao, “Certificateless two-party authenticated key agreement scheme for smart grid,” Information Sciences, vol. 543, pp. 143–156, 2021. [Google Scholar]

  35. S. A. Hosseini Seno and R. Budiarto, “An efficient lightweight authentication and key agreement protocol for patient privacy,” Computers, Materials & Continua, vol. 69, no. 3, pp. 3495–3512, 2021. [Google Scholar]

  36. B. Alzahrani, A. Barnawi, A. Irshad, A. Alhothali, R. Alotaibi et al., “A secure key agreement scheme for unmanned aerial vehicles-based crowd monitoring system,” Computers, Materials & Continua, vol. 70, no. 3, pp. 6141–6158, 2022. [Google Scholar]

  37. C. Pu, H. Zerkle, A. Wall, S. Lim, K. K. R. Choo et al., “A lightweight and anonymous authentication and key agreement protocol for wireless body area networks,” IEEE Internet of Things Journal, vol. 9, no. 21, pp. 21136–21146, 2022. [Google Scholar]

  38. C. Li, Y. Tian, X. B. Chen and J. Li, “An efficient anti-quantum lattice-based blind signature for blockchain-enabled systems,” Information Sciences, vol. 546, pp. 253–264, 2021. [Google Scholar]

  39. C. Li, G. Xu, Y. Chen, H. Ahmad and J. Li, “A new anti-quantum proxy blind signature for blockchain-enabled internet of things,” Computers, Materials & Continua, vol. 61, no. 2, pp. 711–726, 2019. [Google Scholar]

  40. S. Choudhary and A. Gupta, “AKAME: A post-quantum authenticated key-agreement and message encryption scheme based on ring-LWE,” International Journal of Information Technology, vol. 14, no. 3, pp. 1669–1676, 2022. [Google Scholar]

  41. N. Gura, A. Patel, A. Wander, H. Eberle and S. C. Shantz, “Comparing elliptic curve cryptography and RSA on 8-bit CPUs,” in Proc. Int. Workshop on Cryptographic Hardware and Embedded Systems, Cambridge, MA, USA, pp. 119–132, 2004. [Google Scholar]