Improved Whale Optimization with Local-Search Method for Feature Selection

1  Introduction

Data mining has become an increasingly popular research subject in the information sector in recent years [1]. In Knowledge Discovery in Databases (KDD), the preprocessing step precedes that of data mining, and yet, it significantly affects the performance of the data mining technique [2]. This can be observed either in the running time or the quality of the retrieved patterns needed in analyzing the whole dataset. Feature selection is an essential step of preprocessing to remove redundant data from a dataset. There are two methods associated with feature selection: filters and wrappers [3]. The filter model evaluates the feature subsets based on the data using selected techniques [4].

Meanwhile, a learning algorithm like a classification uses wrapper methods to assess the selected subset of features during the search [5]. In general, the performance of filters is faster when compared to that of wrappers. This owes to the fact that filters gauge the information gain, the distance between features, and feature dependency, and all of these are less costly computationally than measuring a classifier’s accuracy [3]. Due to their ability to discover subsets that fit the pre-determined classifier, wrappers were explored in classification studies, particularly regarding accuracy [6]. In applying a wrapper feature selection model, 3 factors are usually determined: a classifier, a subset of feature measures, and a search method for identifying the optimum features [7].

Getting a (near) optimum subset from the original set of features is challenging. Metaheuristics have proven their reliability in the solution of countless problems of optimization in the past twenty years [8,9], as can be observed in production problems, engineering design, machine learning, and data mining scheduling, to name a few [10]. The investigations of metaheuristics can be observed in the feature selection context. As opposed to the fundamental mechanisms of search, metaheuristics show better performance. This is because the complete search tends to lead to the formation of all potential solutions for the issue [11]. As can be found in the literature, many different metaheuristics can be applied in the search for feature subset space in selecting (sub) optimal feature sets. Among them are Differential Evolution (DE) [12], Tabu Search (TS) [13], Simulated Annealing (SA) [14], Record-to-Record Travel (RRT) Algorithm [15,16], Genetic Algorithm (GA) [17–19], Particle Swarm Optimization (PSO) [20–22], Ant Colony Optimization (ACO) [23], as well as Artificial Bee Colony (ABC) [24].

In the design or utilization of metaheuristics, the two opposing criteria to be considered including exploration of the search space (diversification) and the exploitation of the found best solutions (intensification) [10]. In this regard, metaheuristics algorithms are classable into two families, namely population-based and single solution-based algorithms. Population-based methods are exploration-oriented examples of these algorithms are Swarm Intelligence and Evolutionary algorithms. Meanwhile, single solution-based methods focus on exploiting a single solution, Great Deluge (GD) and simulated annealing are examples of these algorithms.

The Great Deluge (GD) algorithm by Dueck [25] encompasses a single-solution-based meta-heuristic. There is a similarity between GD and Simulated Annealing (SA) to a certain degree. In particular, both accept poorer solutions following an acceptance rule throughout the solution search procedure for local optima escape. A variable known as level governs the inferior solution acceptance rule. In this regard, all imperfect solutions with a value of penalty cost less than that of level are acceptable.

For this reason, GD is competent in exploring a more significant solution search region in the solution search process. Initially, the assignment of the level value generally follows the initial solution cost. Furthermore, the computed decay rate during the search progress will reduce the value. Only one parameter is needed in GD, which encompasses the expected cost of the sought-after solution. The GD algorithm will investigate the possible search regions. Here, the solution quality is nearly comparable to the projected quality. GD’s effectiveness has been extensively scrutinized.

A recent optimization algorithm called Whale Optimization Algorithm (WOA) [26] models the intelligent behavior of foraging humpback whales. The WOA algorithm is simple in terms of implementation with fewer parameters. In addition, a logarithmic spiral function is applied. (therefore, it covers the border area in the search space), many scholars in diverse domains have shown a preference towards the use of this algorithm in their obtained solution of countless problems of optimization, including the problem of IEEE 30-Bus economic dispatch [27], truss sizing optimization issues, and frame structures [28] and the solution of unit commitment issue [29]. Accordingly, when WOA and GD algorithms are merged, they can result in a hybrid model, producing superior outcomes (as opposed to their discrete usage). The hybridization improves the WOA algorithm’s property of exploitation.

Furthermore, the disruptive selection mechanism is employed in place of random selection to improve exploration. This article suggests combining the WOA algorithm and GD algorithm for feature selection to improve the WOA algorithm in terms of exploitation. To achieve improved exploitation, the GD algorithm is applied in two hybridization models: The first model involves the application of GD as a constituent within the WOA algorithm, and here, GD searches in the neighboring solutions of the best solution order to reach the local optimum solution. The second model involves using GD within a pipeline mode following the termination of WOA to improve the best-found solution. The search agents from the population are selected using disruptive selection. This preserves the algorithm in terms of its diversity. The use of disruptive selection provides all individuals equal opportunity to be chosen.

The remaining portion of this paper is structured as follows: Section 2 discusses the associated works, while Section 3 highlights the fundamentals of the WOA and the GD algorithms. Section 4 explains the proposed technique, while Section 5 displays and analyses the overall results of each proposed method. The conclusion to this paper and suggestions for the subsequent work is shown in Section 6.

2  Related Works

The application of hybrid metaheuristics in optimization can be observed among many scholars [10]. In determining many practical or academic problems, the performance of hybrid algorithms appears to be better than those of other comparable algorithms [30]. In the feature selection domain, a hybrid metaheuristic algorithm first occurred in 2004 [31]. This approach embeds local search techniques into the GA algorithm to control the search process. A hybrid algorithm from the combination of simulated annealing and Markov chain was proposed by Martin and Otto [32] in solving the problem of travel salesman. The application of Tabu search (TS) combined with simulated annealing (SA) algorithms was demonstrated in solving the problem of reactive power [33] and the Symmetrical Problem of Traveling Salesman [34]. This hybridized algorithm applies the Markov chain in the local optima exploration. Within the area of feature selection, the use of hybrid metaheuristic algorithms has been generally fruitful. Accordingly, in Mafarja et al. [35], a filter feature selection hybrid method with SA was applied to improve the competency of the local search of the genetic algorithm. A total of 8 UCI datasets were employed in the algorithm testing. As opposed to the state-of-the-art methods, the performance shown was good, particularly concerning the number of chosen attributes. The application of the hybrid method based on genetic algorithm (GA) & SA was demonstrated and assessed on the “hand-printed Farsi” characters in [36]. In [37], a hybrid algorithm of wrapper feature selection was presented. Here, GA’s crossover operator integrated the metropolis acceptance criteria for simulated annealing. In generating a hybrid wrapper feature selection algorithm, GA and SA were hybridized [37]. This new hybrid was applied in the classification of the power disturbance in the problem of the Power Quality (PQ) and also in the optimization of the Support Vector Machine (SVM) parameters for similar issues [38].

A method proposed for feature selection problem that combines the WOA&SA algorithm for feature selection problem [39]. A hybrid GA&SA metaheuristic method was presented by Olabiyisi Stephen et al. [40] to extract features in timetabling issue. Using this approach, the selection procedure for GA and SA has been substituted by the selection process. This was to prevent load-up at the local optima. In a wrapper feature selection, GA was hybridized with TS. The FUZZY ARTMAP Neural Network classifier was applied for evaluation purposes [41]. In their study, Majdi et al. [42] proposed two filter feature selection memetic techniques involving fuzzy logic in controlling the primary factors in two selected local search-based methods, including record-to-record and GA algorithms later merged with GA. A local search algorithm was presented in Moradi et al. [43] in guiding the process of search in the particle swarm optimization (PSO) algorithm to choose the least reduces following their information of correlation. The hybridized GA and PSO algorithms with an SVM classifier (GPSO) were employed in [44] for microarray data classification.

Similarly, a hybrid mutation operator with a multi-objective PSO was presented in [45], whereas [46] proposed a novel blend between GA and PSO to optimize the feature set for the datasets of Digital Mammograms. Further, from the mix between Ant Colony Optimization (ACO) and GA, two-hybrid wrapper feature selection algorithms were established [47,48]. ACO and CS (Cuckoo Search) algorithms were used in [49]. In [50], SLS (“Stochastic Local Search”) and HSA (“Harmony Search Algorithm”) were combined for the feature selection method as a wrapper method.

In presenting a novel wrapper feature selection technique, a study [12] combined Artificial Bee Colony with a differential evolution algorithm (DE). Furthermore, two studies [51,52] presented a survey involving metaheuristics and feature selection. Memetic algorithms for feature selection are available; therefore, justifiable to contemplate not creating new ones. Notably, the No-Free-Lunch (NFL) theorem has reasonably evidenced that an algorithm that can resolve all optimization problems does not exist. For the context of this study, the presumption is that there seems to be no single heuristic as wrapper feature selection that has the capacity in resolving all problems associated with feature selection. This implies the possibility of improving the presently available techniques to better resolve the currently emerging problems of feature selection. As recently, several feature selection methods have been proposed as wrapper-based methods [53–57]. Hence, a method for the feature selection is discussed in the following section.

3  Materials and Approaches

3.1 The Original Whale Optimization Algorithm (WOA)

A metaheuristic approach, namely WOA, was suggested by Mirjalili et al. [26], and it encompasses a population-based stochastic algorithm. The operation of this algorithm is akin to the foraging humpback whales’ behavior. The humpback whales hunt schools of small fishes or krill that swim nearby the surface. These whales would swim around these krill and fishes within a decreasing circle, generating different bubbles in a circle or ‘9’ formed path. Accordingly, the operation in the algorithm’s initial phase (exploitation phase) mimics the encircling of prey and the assault by spiral bubble-net. The next step, the exploration phase, involves an operation like the random prey search. The mathematical model for each stage is accordingly detailed in the following section.

3.1.1 The WOA Exploitation Phase

Humpback whales would first encircle their prey during hunting. This behavior can be mathematically modeled by Eqs. (1) and (2) [26].

D=|C . X∗→(t)−X→(t)|(1)

X→(t+1)=X∗→(t)−A→ . D(2)

From the above: t signifies the present iteration, X∗ signifies the most attained optimum solution, the X denotes a vector for the position. Further, vectors of the coefficient are represented by A and C. The computation of these vectors is respectively expressed in Eqs. (3) and (4):

A→=2a→.r→−a→(3)

C→=2.r→(4)

From the above, over the iterations passage (exploration and exploitation phases), a linearly declines from 2 to 0, while r denotes a random vector formed by uniform distribution within [0, 1]. As expressed in Eq. (2), the whales (agents) have their positions updated based on the prey (best solution) position. The modification of A and C vector values control the regions where a whale is locatable within the prey neighborhood. The shrinking encircling behavior can be attained through the reduction of a value in Eq. (3), as depicted in Eq. (5):

a=2−t 2MaxIter(5)

Computation is made to ascertain the distance between the best-known search agent X* and the search agent X. The computation is made to mimic the spiral-shaped path. In Eq. (5), MaxIter signifies the highest permissible iterations. This is followed using a spiral equation in the generation of the neighbor search agent position as expressed by Eq. (6):

X→(t+1)=D′.ebl.cos⁡(2πl)+X∗→(t)(6)

where, D′=|X∗→(t)−X→(t)| And denotes the distance between the ith whale and the prey; b is a constant in delineating the logarithmic spiral form. At the same time, l represents a randomly generated number in the range [−1, 1]. This study used a 50 percent probability-making selection between the two procedures, reduction encircling and spiral-shaped path, throughout the optimization process. Eq. (7) below can be referred to. p signifies a randomly generated number in [0, 1].

X→(t+1)={Shrinking Encircling (Eq. (2))if(p<0.5)Spiral−Shaped path (Eq. (6))if(p≥0.5)(7)

3.1.2 The WOA Exploration Phase

The exploration of WOA was improved by selecting a random search agent to guide the search. In other words, the search agents’ positions are not changed based on the best position. As such, a vector A with randomly generated numbers higher than 1 or lower than −1 is applied to force the search agent to detach itself from the best agent. The modeling of the present process is expressed in Eqs. (8) and (9) below:

D→=|C→.Xrand→−X→|(8)

X→(t+1)=Xrand→−A→.D→(9)

From the above: Xrand→ It encompasses a randomly selected whale that is selected from the present population.

Being a population-based stochastic algorithm, WOA’s convergence is assured by applying the best-attained solution so far to allow updating the position of the remaining solutions. The WOA algorithm’s pseudo-code is displayed in Fig. 1; as observed, WOA generates a random initial population. When the optimization process initiates, WOA evaluates the process by applying the objective function. After identifying the best solution, the algorithm repetitively executes the following steps. The execution of the steps will end once the satisfaction of an end criterion is reached. Accordingly, there are four steps: 1) Updating the main coefficients, 2) Formation of a random value which is used when the algorithm updates the solution position with the application of either Eqs. (2)/(9) or (6), 3) Involves preventing the solutions from moving beyond the site of search, and 4) Returning the best-obtained solution as a guesstimate of the global optimum.

Figure 1: The WOA algorithm pseudo-code (The original algorithm)

Nonetheless, this may cause solutions to become trapped in local optima. The application of random variables enables switching between three equations, allowing the solutions’ position to be updated. Meanwhile, the adaptive parameter a is employed to balance local convergence (exploitation) and optima avoidance (exploration). With the application of this parameter, the magnitude of the changes within the solutions is efficiently reduced. Besides that, it stimulates convergence/exploitation proportionate to the iteration number.

3.2 Great Deluge (GD) Algorithm

The GD algorithm by Dueck [25] carries a deterministic acceptance function for the neighboring solutions, distinguishing it from SA. The mechanism of GD mimics the analogy of a hill climber’s direction in a great deluge to maintain his feet dry. Identifying the global optimal of the optimization problem can be viewed as identifying the uppermost point within a landscape. The non-stop occurrence of precipitation increases the water level, but GD does not move outside the water level. To attain the global optimum, GD will explore the uncovered landscape region.

The summarized GD design can be viewed in Fig. 2. Here, a produced neighbor solution is tolerated providing that the objective function’s absolute value is lower than the present boundary value (Level). The level’s initial value is equivalent to the initial target function. In the search process, the level value is monotonically reduced. The decrease decrement denotes the algorithm’s parameter (i.e., rain speed). This parameter (i.e., level) dictates the quality of the results gained and search time. The high rain speed parameter (decay rate) produces a fast algorithm, but the results would have poor quality.

Figure 2: A generic pseudo-code of the great deluge metaheuristic algorithm [59]

The degraded Ceiling algorithm, a variant of GD, was presented in [58]. This algorithm’s use maximizes the algorithm’s intrinsic capability to escape from local optima while a simple set of neighborhood moves is preserved. Such an attribute reduces the needed time for an iterative search process. On the other hand, the attainment of a small value of rain speeds (decay rate (or β)) allows the algorithm to produce better results, but the computation time will be longer.

3.3 Disruptive Selection

Disruptive selection (DS) is among the popular selection mechanisms applied in evolutionary algorithms [60]. In the application of this mechanism, solutions are randomly chosen from the population. Then, a comparison was made between these solutions, and a tournament would ascertain the best solution. In particular, the tournament generates a random number in the range [0, 1]. Next, the generated value would be evaluated with a selection probability which furnishes a process that facilitates the adjustment of the selection pressure, which is set to 0.5 usually. Higher random would require selecting the solution with the greatest fitness value. Else, the weak solution would be chosen. As a result, most solutions could be chosen, and the diversity of the selected solutions could be retained [61]. The DS focuses on poorer and greatest fitness levels, trying to maintain population variety by enhancing worse fitness solutions in conjunction with fitness solutions. Therefore, all solutions will be as excellent as feasible for the population [62]. DS transforms the fitness value of all individuals (fiti) into an absolute value of the variation between fitness (fi) and means fitness of all individuals (ft). The DS tends to preserve variety longer since it is better to maintain the highest and lowest solutions. Eq. (10) measures the function of fitness [63].

pi=fiti∑i=0nfiti,wherefiti=|fi−ft¯|(10)

4  Proposed Method

The Feature selection solution can be represented with a binary value. Hence, the binary version of the WOA algorithm needs to be constructed to be employed with the feature selection issue. Accordingly, a solution is signified within the 1D vector. Here, the vector length follows the number of features within the initial dataset. Each value within the vector is denoted by 0 or 1, whereby 1 indicates that the conforming attribute is chosen or the value is set to 0. It is performed to accomplish two clashing objectives: the lowest number of selected features and higher classification precision. As such, it entails a multi-objective optimization problem. A smaller feature number in the solution with greater classification accuracy will generate a superior solution. For the solutions, each is assessed using the suggested fitness function. To obtain classification accuracy and the smallest number of selected features in the solution, the fitness function relies on applying the K-nearest neighbor (KNN) classifier [61]. Notably, the number of selected features (lowest) and the accuracy (highest) must be balanced in evaluating the search agents. For this purpose, the objective function (Fitness) in Eq. (11) is applied in this work for evaluation.

Fitness=αγr(D)+β|RN|,(11)

From the above: γr(D) Signifies the error rate of classification of a classier in question, in this context, the KNN classifier. Meanwhile, |R| denotes the cardinality of the subset chosen, whereas |N| signifies the overall number of attributes within the dataset; α and β entail the two parameters corresponding to the significance of classification quality and length of the subset. Further, α ∈ [0, 1] & β = (1 − α) are based on [64]. Exploitation in the WOA algorithm is based on the distance computation between the search agent and the best so far recognized whale. This study uses an efficient local search method to search for the neighborhood across the best-known solution, anticipating that the resulting outcomes would be superior. Also, considering that the exploration in the WOA algorithm (see Eq. (9)) is dictated by the position change of every agent following a random solution, the utilization of a different mechanism of selection (e.g., Disruptive selection) may lead to better ability of exploration in the algorithm. Notably, based on the selection pressure, disruptive selection allows the weak solutions more chance to be chosen during the search process. This makes WOA superior in terms of its diversity competency.

Hybrid Methods

WOA is a population-based metaheuristic that introduces diversity in the exploration of search space by enhancing numerous solutions concurrently and iteratively and selecting the best solution from them. Local search algorithms (i.e., Great Deluge (GD) algorithm) can intensify the search in local areas, where a single solution is iteratively enhanced till a satisfactory solution is acquired. GD algorithms have been hybridized with WOA to balance the intensification and diversification. In addition, the exploitation can be introduced by an algorithm that accepts a worse solution, as keeping accepting the only improved solution will get stuck in local optima [10]. So, we included another way for whales to hunt prey where humpback whales first encircle, to attack and back (by accepting the worst solution). Then the GD algorithm will occur in Fig. 1, lines #9 and #15. This hybridization is called in this paper WOAGD1. Instead, after the process of the WOA algorithm, The GD is used to improve the best solution; this hybridization is called WOAGD2.

GD provides a high level of exploitation using perturbation solutions for candidates. The idea of the GD metaheuristic [25,62] is to guide the diversification of search by using a boundary value (water level) to accept worse neighboring solutions. The value of the level is gradually reduced linearly (specified decay rate) throughout the search. A decrease in the level value forces the current solution as an evaluation function to decrease correspondingly until convergence. In each iteration, a new neighboring solution of the neighborhood method will be generated from the current solution (line# 8, Fig. 2). The neighborhood method used here is based on the threshold for selecting and deselecting a set of k random features. The new neighboring solution will always be accepted if its quality evaluation value is better or poorer than the current best solution. A solution worse than the current best solution will only be obtained if its quality evaluation value is equal to or lower than the boundary value. In brief, The GD algorithm always accepts a move that increases solution quality and a poorer solution if the solution quality is below or equal to a boundary (level) to avoid local Optima.

Fig. 2 shows the pseudo-code for great deluge algorithms. GD follows the analogy that occasionally, an individual who climbs a hill goes down before reaching a new maximum height to avoid becoming moist when the water level increases from the bottom. We may take the objective function (formula (11)) to be hills. The fitness value indicates the height of the hills, and the top of the hills are the best values. The more the height, the more accuracy. When the WOA solution has reached a particular hilltop, we may claim that it reaches a local minimum, but it may not be the global minimum. The solution should drop from the hilltop and search the neighboring region further to reach the hill with a minimum height. Also, using the Disruptive selection method by WOA provides GD with initial candidate solutions for further improvement. Finally, the WOA and the two hybridization methods (i.e., WOAGD1, WOAGD2) are evaluated when the disruptive selection method is used. In this work, these methods are WOA_DS, WOAGD1_DS, and WOAGD2_DS.

5  Experiments

5.1 Datasets

The algorithm suggested is applied in this study using python. A total of 15 benchmark datasets furnished by the UCI data repository were utilized to analyze the proposed methods’ performance through the execution of experiments [65]. The employed datasets are accordingly detailed in Table 1.

5.2 Parameter Settings

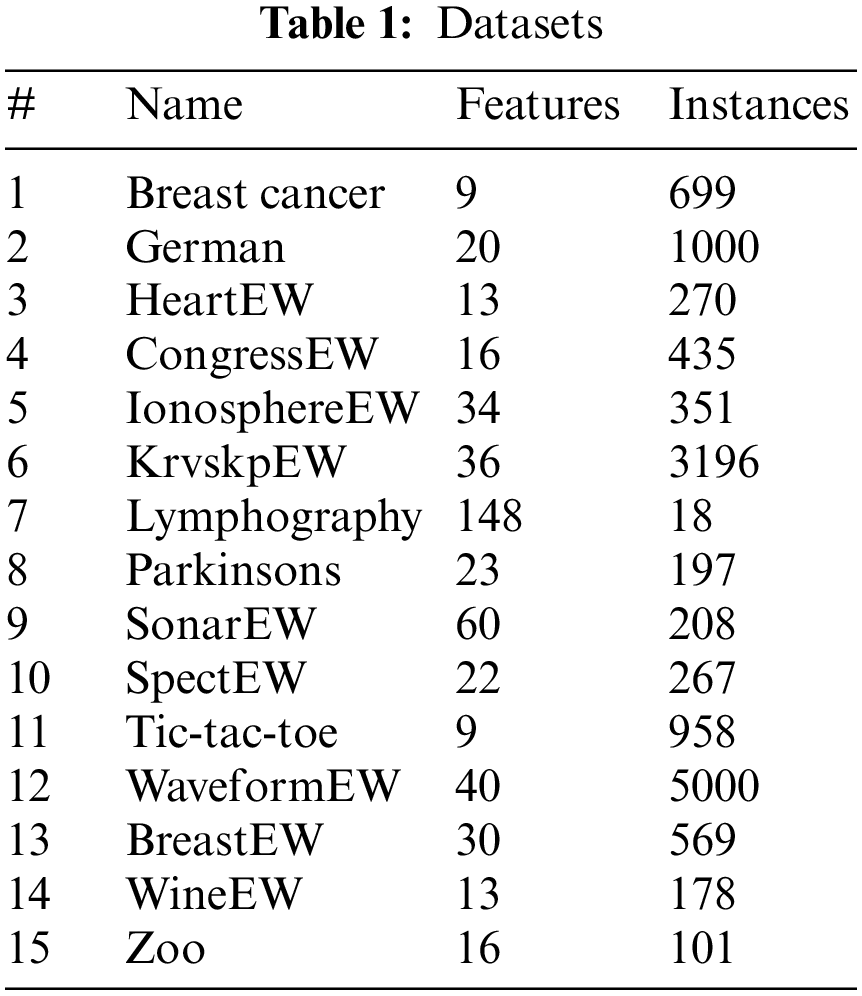
The best results were generated using a wrapper method grounded upon the KNN classifier (where K = 5 [64]) with the “Euclidean distance matric.” For evaluation purposes, the proposed approach splits all datasets in cross-validation following [66]. In cross-validation of K-fold, folds of K−1 are employed for validation & training while the rest of the fold is utilized for testing, reiterating this mechanism M times. As such, for each dataset, the evaluation of the individual optimizer is carried out K∗M times. The size of data for validation and training are of the same size. The parameters in the experiments’ details are as follows: the highest number of iterations is 100 while the population size is 10 and α = 0.99. Besides that, the algorithms are each run 5 times, applying random seed. For this purpose, an “Intel Core i5 machine”, equipped with 8 GB of RAM and a 2.3 GHz CPU is used.

5.3 Results and Discussion

The present section presents the results attained. Accordingly, a comparison was made between the WOA, WOAGD1, and WOAGD2. The comparison was to evaluate the impact of hybridizing the GD algorithm with the native WOA. To assess the impact of Disruptive selection usage (instead of utilizing the random mechanism), a comparison was then made among the 3 approaches that employ Disruptive selection (DS) (WOA_DS, WOAGD1_DS, and WOAGD2_DS). Besides that, a comparison was also made between the proposed approaches and the advanced methods of feature selection, such as PSO, Multi-Verse Optimizer (MVO), Grey Wolf Optimizer (GWO), and GA algorithms [31,45,57,67]. In the comparison, the criteria used are accuracy and the average selection size. The selected attributes on the test dataset were applied for the classification accuracy comparison, and the average accurateness obtained from 5 runs was computed.

5.3.1 Comparison of the Two Hybridization Methods of WOA

The present section discusses WOA, WOAGD1, and WOAGD2 in terms of their performance concerning the two goals of achieving average selection size, classification accuracy, and computational time. As mentioned, in WOAGD1, the GD algorithm is an internal operator, and in WOAGD2, the GD algorithm is operated on the final solution following the termination of the WOA algorithm. Table 2 demonstrates the superiority of the hybrid algorithms to the native ones regarding accuracy with several selected features.

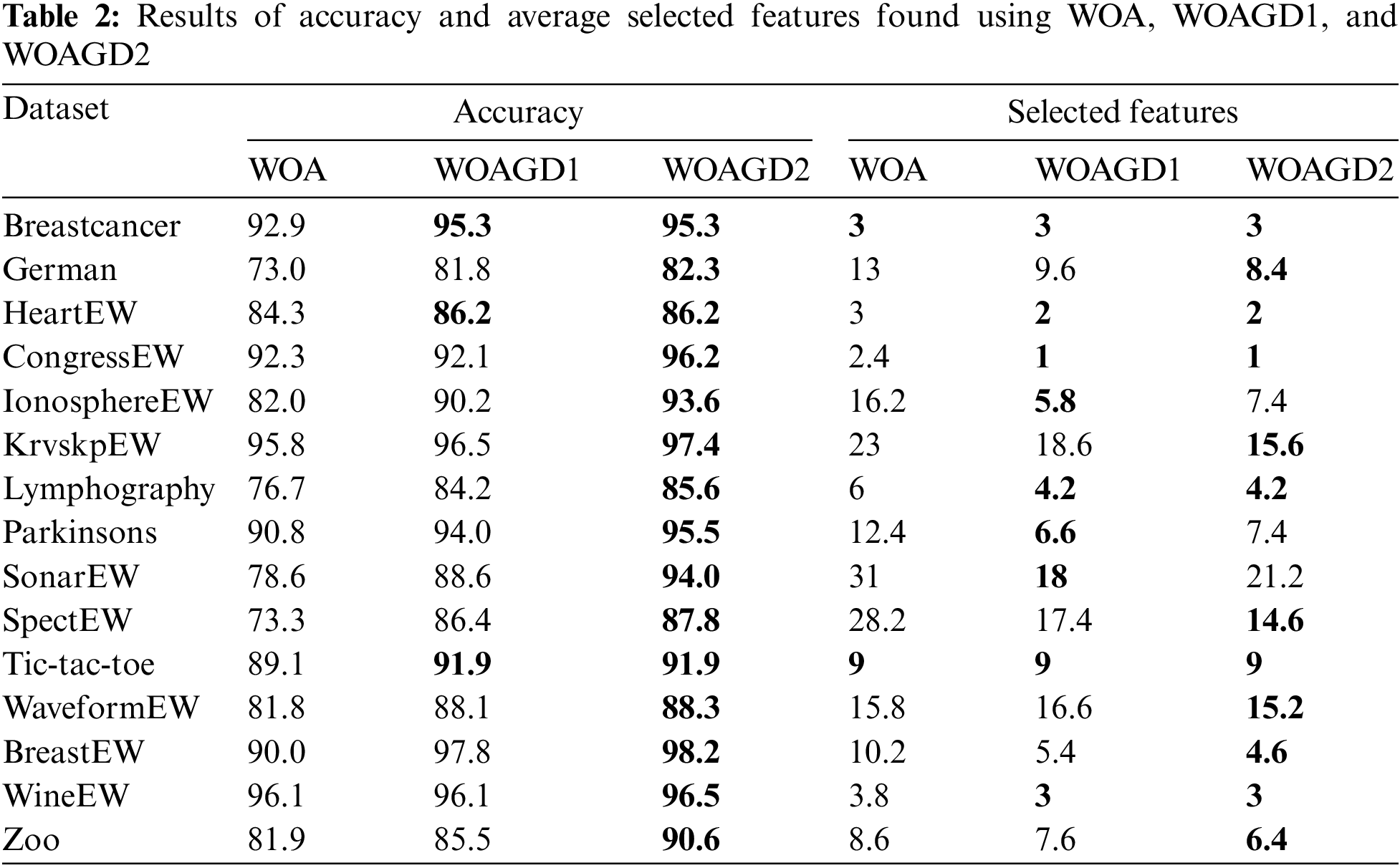
From Table 2, for the exact dataset, WOAGD1 is better than WOA in the accuracy of a classification and the chosen attributes. For all datasets, the hybrid approaches appear to be better than the native algorithm, especially regarding the number of selected features. In fact, in the classification accuracy and number of selected attributes, WOAGD1 outperforms other methods in three and seven datasets, respectively.

The results obtained for WOAGD2 show an identical pattern. In nearly all datasets, the performance of WOAGD2 appears to supersede that of WOA. For classification accuracy, the comparison between WOAGD1 and WOAGD2 shows the superior performance of WOAGD2 to that of WOAGD1 over 12 datasets. For 3 datasets, WOAGD1 also achieved classification accuracy the same as WOAGD2. Concerning the number of selected attributes, WOAGD2 beats WOAGD1 in 6 datasets. Meanwhile, on 3 datasets, WOAGD1 shows performance superior to WOAGD2, and both algorithms achieved the same number of selected attributes in 6 datasets.

Fig. 3 presents the convergence behavior of WOA, WOAGD1, and WOAGD2 algorithms, where four datasets (Krvskp EW, IonosphereEW, German, and SonarEW) are considered, the values of the fitness attained from each approach were supposed to show the convergence, WOAGD2 shows better convergence behavior among others, also WOA unable to further improve the fitness at an early stage, which shows the essence of the proposed hybrid approaches.

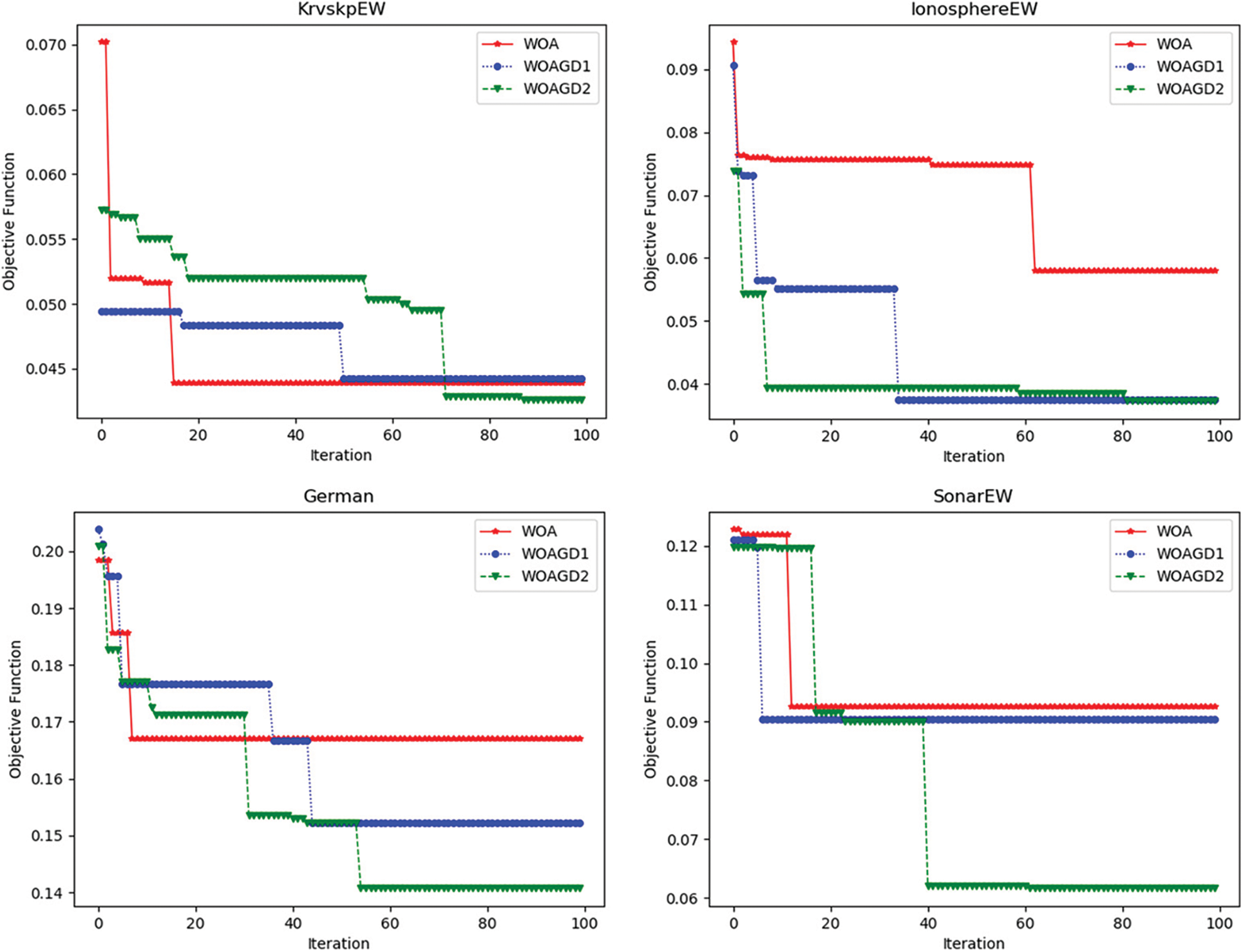
Figure 3: Convergence of WOA, WOAGD1, and WOAGD2 algorithms from four datasets (KrvskpEW, IonosphereEW, German, and SonarEW)

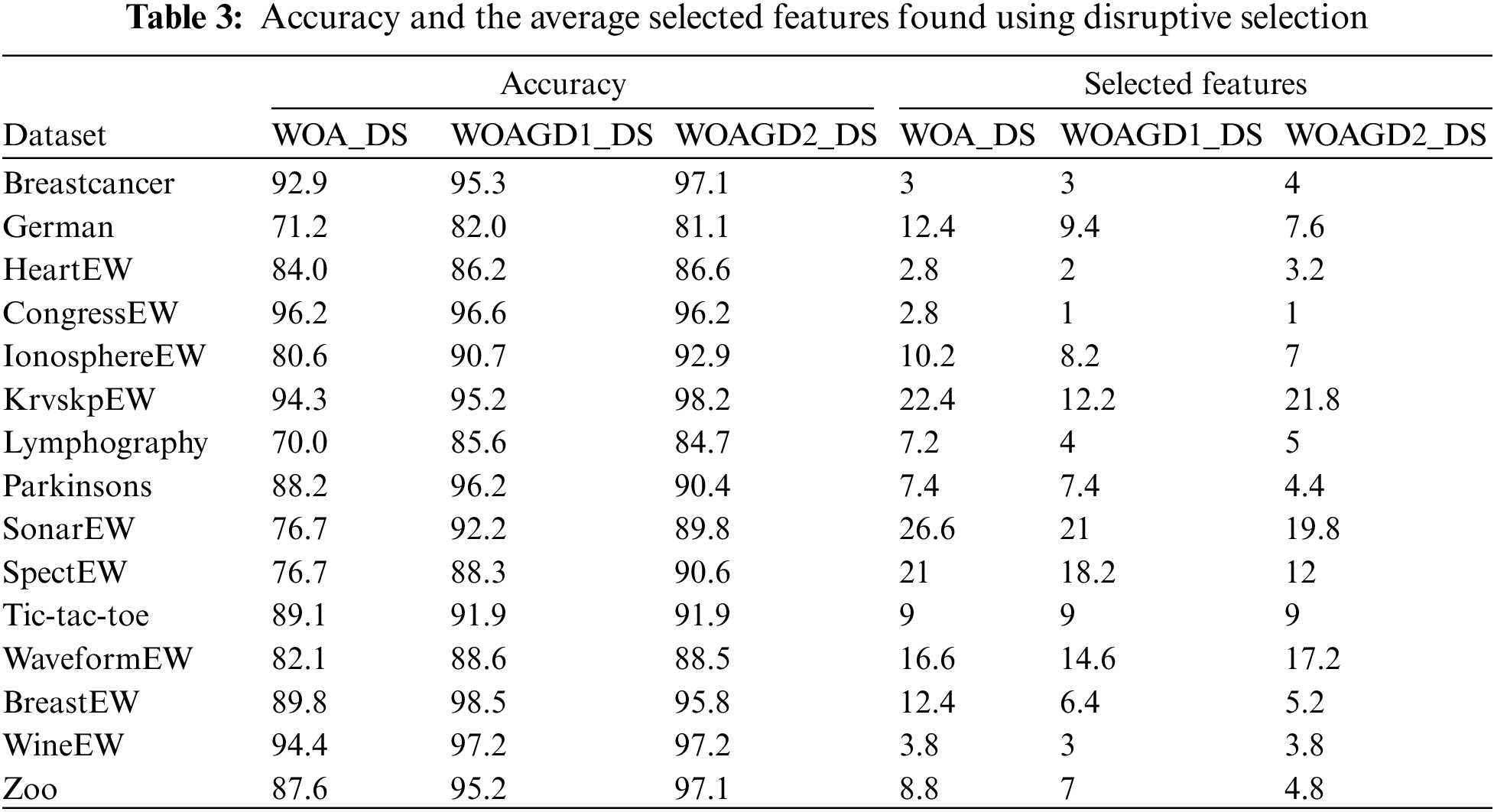
5.3.2 Comparison of the Disruptive Selection Applied to the Three Versions (WOA_DS, WOAGD1_DS, and WOAGD2_DS)

The proposed approaches’ performance appears to be nearing the attainment of both objectives. Also, both methods show performance superior to that demonstrated by the native algorithm. The results prove that both hybrid models considerably improved the native algorithm, particularly in terms of performance. Nonetheless, between the two proposed models, no considerable difference was detected. For this reason, the proposed approaches are retained in this study. Besides that, the effect of improving the exploration property through applying the mechanism of Disruptive selection to balance the exploration and exploitation. Table 3 displays the consequences of Disruptive selection utilization. Table 3 demonstrates the performance of the selection method, and as can be observed, WOAGD2_DS performs better on all datasets, especially in terms of accuracy. On specific datasets, WOAGD2_DS appears competent for the 2nd objective concerning the number of chosen features. Notably, for any dataset, the performance of the WOA algorithm does not supersede that of the hybrid methods.

5.3.3 Results Produced by the Proposed Approaches

In the present subsection, the 6 suggested methods are compared. Accordingly, the effect of the improvement of exploitation, exploration, and combination is analyzed. As can be referred to in Tables 2 and 3, the application of DS facilitates the advancement of exploration in the WOA algorithm, while using GD leads to better exploitation. For the proposed approaches, their performance is progressively improved as follows: WOA < WOA_DS < WOAGD1 < WOAGD1_DS < WOAGD2 < WOAGD2_DS. WOA is a robust algorithm that can balance exploitation and exploration in the global optimum search.

Meanwhile, the use of GD enhances the WOA algorithm exploitation. Disruptive selection enhances the exploration of the WOA algorithm, and Disruptive selection is complementary to the GD role. As may be observed, in terms of classification accuracy, the approaches of WOAGD2_DS beat the rest of the tested techniques on nearly all datasets. Regarding the number of selected features, the results generated by WOAGD2_DS approaches also appear to be better on numerous datasets. These findings imply the appropriateness and efficiency of WOAGD2_DS regarding exploration and exploitation. The appropriateness and efficiency of WOAGD2_DS are factored in using a local search and selection mechanism. The obtained results show that the use of GD following the execution of the WOA algorithm generates better performance than having GD embedded within WOA. WOA can locate the high-performance areas in the problem’s feature space. Furthermore, the sequential hybrid GD and WOA do not adversely impact WOA exploration. This is crucial when the issue at hand is hard to resolve.

The average running time used for all datasets that each method requires in reaching the final solution is as follows: WOA requires 2.82 s,WOAGD1 requires 17.88 s, WOAGD2 requires 13.36 s, WOA_DS requires 2.64 s, WOAGD1_DS requires 18.10 s, and WOAGD2_DS requires 14.55 s, where the exact settings of parameters and datasets were employed on all approaches during testing. For performance comparison purposes, the computational time was used, and the average running time proves the superiority of WOA_DS over other approaches. The WOA is ranked second in computational time. Additionally, the comparison between the two hybrid models shows that the (WOAGD1 and WOAGD1_DS) need more computational time than WOAGD2 and WOAGD2_DS to identify the best results due to the local search method used during the search process.

5.3.4 Results Evaluation Against State-of-the-Art Methods

As mentioned in the proceeding section, the approach of WOAGD2_DS’s classification accuracy is better than others, which is proven in all datasets. Besides that, the approach is also more competitive than others regarding the number of selected attributes. The present section elaborates on the efficiency comparison of the best method among the suggested with other comparable approaches documented in the literature of feature selection. The results comparisons of WOAGD2_DS, PSO, MVO, GWO, and GA algorithms in Accuracy (ACC) and the average number of selected features (Avg.SF) can be observed in Table 4.

Table 4 shows that the accuracies obtained by WOAGD2_DS outperform other algorithms in 13 datasets out of 15, while in the CongressEW dataset MVO algorithm produces higher accuracy, and in the WineEW dataset, GWO outperforms different algorithms. However, the associated accuracies of MVO and GWO algorithms using other datasets showed to be lower than other algorithms. In terms of the average number of selected features, comparing WOAGD2_DS with other optimizers, it appears that the performance of WOAGD2_DS is superior in 10 datasets. Finally, Fig. 4 shows the box and whisker plot for WOAGD2_DS; the whisker and box plot indicates the distribution of the precision values for each solution acquired from the WOAGD2_DS algorithm for 10 datasets, displaying the distribution of the outcomes.

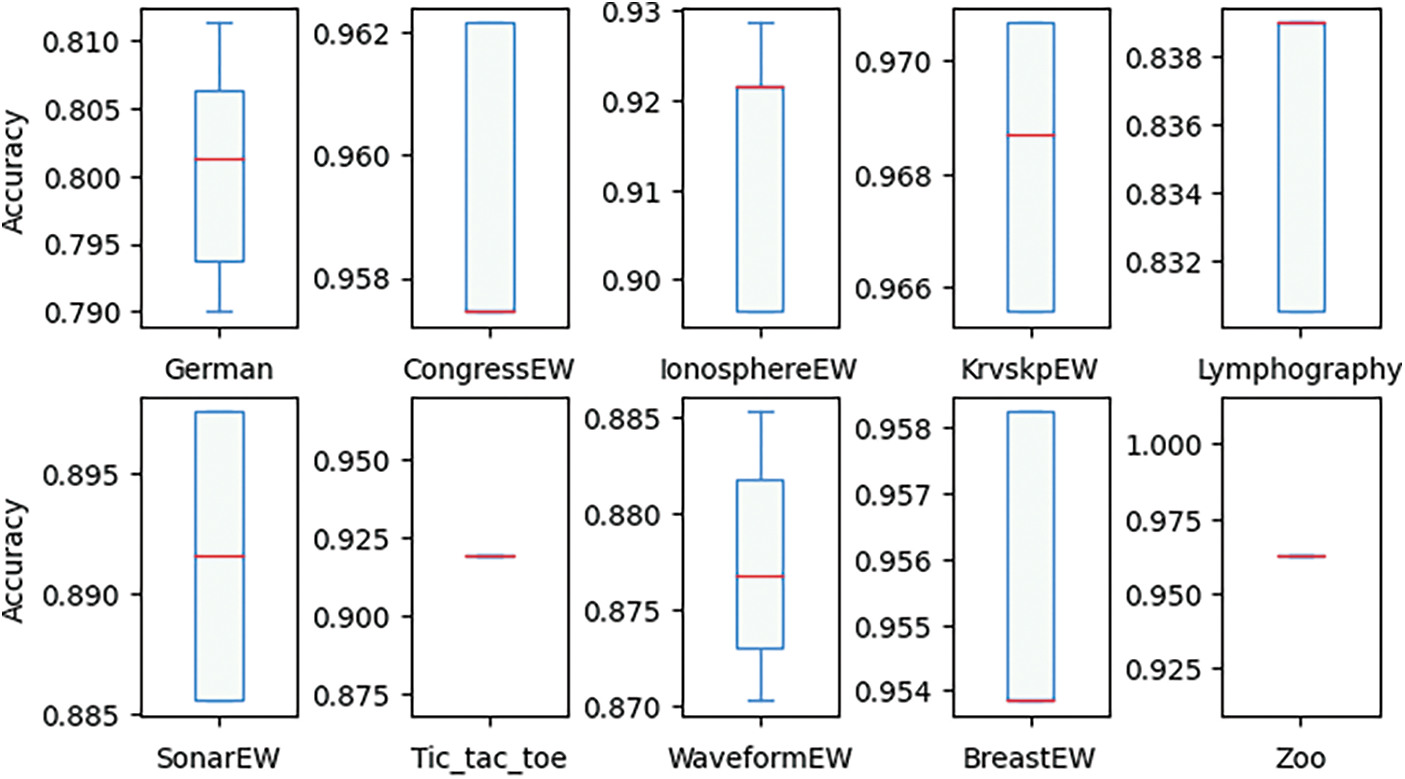
Figure 4: Box and whisker plot for all datasets using the WOAGD2_DS algorithm

In Fig. 4 the line separating the box into two horizontal parts shows the median of the 5 runs, and the results seem to be generally distributed in most of the tested datasets. The results show that the WOAGD2_DS algorithm appears stable, as indicated by the upper and lower bounds. In addition, the WOAGD2_DS algorithm is superior in selecting the lower number of attributes. This is because this approach employs a disruptive selection mechanism that allows weak and reasonable solutions to give more potential to be chosen, then all solutions in the population will get the chance to be enhanced and exploited by the local search method. The feature selection method, with the proposed wrapper approach, shows better accuracy and reduces the dimensions of the datasets. This process enables the algorithm to broadly investigate areas within the feature space and apply GD in increasing these regions. This method leverages the worth of utilizing a global search algorithm that has proven its efficiency in exploration and a local search, which has proven its efficiency in exploiting the solution of feature selection problems.

6  Conclusion

The Feature selection problem is among the main elements in the improvement of the capacity of the classifier in dealing with the problem of classification. The present work presented 4 variant hybrid metaheuristic algorithms grounded on the WOA algorithm. In the proposed approach, the GD algorithm is combined to exploit the solutions provided by WOA. The inclusion of GD is based on two hybrid models. In the first model, the application of GD as a local search operator to the search agents was chosen. Therefore, two methods were used, namely WOAGD1 and WOAGD1_DS. Contrariwise, the search in the neighboring best-discovered solution following every WOA iteration in the second model (WOAGD2 and WOAGD2_DS) involved the application of GD. The mechanism of Disruptive selection was applied in the search agents’ section (rather than using the mechanism of random selection), namely WOAGD1_DS and WOAGD2_DS. Such usage allows more opportunities for selecting weak and reasonable solutions, improving WOA diversity. This study employed four wrapper feature selection methods (PSO, MVO, GWO, and GA) to compare and evaluate the proposed approaches’ performances. The results appear that WOAGD2_DS demonstrated the best performance with GD and Disruptive selection; it can be deduced that the approaches presented in this study can balance the exploration and exploitation of a metaheuristic algorithm. Notably, exploration and exploitation are the two primary objectives of this algorithm. Our future work direction focuses on the hybridization of the WOA algorithm with other population-based metaheuristic algorithms that may generate interesting and worthy outcomes, and for this reason, it should be considered in future works. Further potential research is on using a hybrid WOA algorithm to solve actual life problems, for instance, medical data.

Acknowledgement: Many thanks to the Deanship of Scientific Research at the Imam Abdulrahman Bin Faisal University. Where this research is part of a project funded by Imam Abdulrahman Bin Faisal University, under Grant Number 2020-083-BASRC.

Funding Statement: This research is part of a project funded by Imam Abdulrahman Bin Faisal University, under Grant Number 2020-083-BASRC.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

    1. J. Han, M. Kamber and J. Pei, Data mining: Concepts and techniques, 3rd ed., San Francisco, CA, USA: Morgan Kaufmann Publishers Inc., pp. 111–118, 2011. [Google Scholar]

    2. S. F. Crone, S. Lessmann and R. Stahlbock, “The impact of preprocessing on data mining: An evaluation of classifier sensitivity in direct marketing,” European Journal of Operational Research, vol. 173, pp. 781–800, 2006. [Google Scholar]

    3. H. Liu and H. Motoda, “Feature selection for knowledge discovery and data mining,” in The Springer International Series in Engineering and Computer Science, 1st ed., vol. 454. New York, NY: Springer Science and Business Media, pp. 151–181, 2012. [Google Scholar]

    4. Z. Zhu, Y. Ong and M. Dash, “Wrapper–filter feature selection algorithm using a memetic framework,” IEEE Transactions on Systems, Man, and Cybernetics, Part B (Cybernetics), vol. 37, no. 1, pp. 70–76, 2007. [Google Scholar]

    5. R. Kohavi and G. H. John, “Wrappers for feature subset selection,” Artificial Intelligence, vol. 97, pp. 273–324, 1997. [Google Scholar]

    6. H. Liu and L. Yu, “Toward integrating feature selection algorithms for classification and clustering,” IEEE Transactions on Knowledge and Data Engineering, vol. 17, no. 4, pp. 491–502, 2005. [Google Scholar]

    7. A. Zarshenas and K. Suzuki, “Binary coordinate ascent: An efficient optimization technique for feature subset selection for machine learning,” Knowledge-Based Systems, vol. 110, pp. 191–201, 2016. [Google Scholar]

    8. A. Abuhamdah, W. Boulila, G. M. Jaradat, A. M. Quteishat, M. K. Alsmadi et al., “A novel population-based local search for nurse rostering problem,” International Journal of Electrical and Computer Engineering (2088-8708), vol. 11, pp. 471–480, 2021. [Google Scholar]

    9. M. Alzaqebah, S. Jawarneh, M. Alwohaibi, M. K. Alsmadi, I. Almarashdeh et al., “Hybrid brain storm optimization algorithm and late acceptance hill climbing to solve the flexible job-shop scheduling problem,” Journal of King Saud University-Computer and Information Sciences, vol. 34, no. 6, pp. 2926–2937, 2022. [Google Scholar]

  10. E. -G. Talbi, Metaheuristics: From Design to Implementation, 1st ed., vol. 74. New Jersey, USA: John Wiley & Sons Inc., pp. 23–33, 2009. [Google Scholar]

  11. I. Guyon and A. Elisseeff, “An introduction to variable and feature selection,” Journal of Machine Learning Research, vol. 3, pp. 1157–1182, 2003. [Google Scholar]

  12. E. Zorarpacı and S. A. Özel, “A hybrid approach of differential evolution and artificial bee colony for feature selection,” Expert Systems with Applications, vol. 62, pp. 91–103, 2016. [Google Scholar]

  13. A. -R. Hedar, J. Wang and M. Fukushima, “Tabu search for attribute reduction in rough set theory,” Soft Computing, vol. 12, pp. 909–918, 2008. [Google Scholar]

  14. R. Jensen and Q. Shen, “Semantics-preserving dimensionality reduction: Rough and fuzzy-rough-based approaches,” IEEE Transactions on Knowledge and Data Engineering, vol. 16, pp. 1457–1471, 2004. [Google Scholar]

  15. M. Mafarja and S. Abdullah, “A fuzzy record-to-record travel algorithm for solving rough set attribute reduction,” International Journal of Systems Science, vol. 46, pp. 503–512, 2015. [Google Scholar]

  16. M. Mafarja and S. Abdullah, “Record-to-record travel algorithm for attribute reduction in rough set theory,” Journal of Theoretical and Applied Information Technology, vol. 49, pp. 507–513, 2013. [Google Scholar]

  17. M. M. Kabir, M. Shahjahan and K. Murase, “A new local search based hybrid genetic algorithm for feature selection,” Neurocomputing, vol. 74, pp. 2914–2928, 2011. [Google Scholar]

  18. M. K. Alsmadi and I. Almarashdeh, “A survey on fish classification techniques,” Journal of King Saud University-Computer and Information Sciences, 2020. https://doi.org/10.1016/j.jksuci.2020.07.005. [Google Scholar]

  19. M. K. Alsmadi, “Content-based image retrieval using color, shape and texture descriptors and features,” Arabian Journal for Science and Engineering, vol. 45, pp. 3317–3330, 2020. https://doi.org/10.1007/s13369-020-04384-y. [Google Scholar]

  20. R. Bello, Y. Gomez, A. Nowe and M. M. Garcia, “Two-step particle swarm optimization to solve the feature selection problem,” in Seventh Int. Conf. on Intelligent Systems Design and Applications (ISDA 2007), Rio de Janeiro, Brazil, pp. 691–696, 2007. [Google Scholar]

  21. M. K. Al smadi, G. M. Jaradat, M. Alzaqebah, I. ALmarashdeh, F. A. Alghamdi et al., “An enhanced particle swarm optimization for itc2021 sports timetabling,” Computers, Materials & Continua, vol. 72, pp. 1995–2014, 2022. https://doi.org/10.32604/cmc.2022.025077. [Google Scholar]

  22. A. Adamu, M. Abdullahi, S. B. Junaidu and I. H. Hassan, “An hybrid particle swarm optimization with crow search algorithm for feature selection,” Machine Learning with Applications, vol. 6, pp. 100–108, 2021. [Google Scholar]

  23. S. Kashef and H. Nezamabadi-pour, “An advanced ACO algorithm for feature subset selection,” Neurocomputing, vol. 147, pp. 271–279, 2015. [Google Scholar]

  24. J. Wang, T. Li and R. Ren, “A real time IDSs based on artificial bee colony-support vector machine algorithm,” in Third Int. Workshop on Advanced Computational Intelligence, Suzhou, Jiangsu, China, pp. 91–96, 2010. [Google Scholar]

  25. G. Dueck, “New optimization heuristics,” Journal of Computational Physics, vol. 104, no. 1, pp. 86–92, 1993. [Google Scholar]

  26. S. Mirjalili and A. Lewis, “The whale optimization algorithm,” Advances in Engineering Software, vol. 95, pp. 51–67, 2016. [Google Scholar]

  27. H. J. Touma, “Study of the economic dispatch problem on IEEE 30-bus system using whale optimization algorithm,” International Journal of Engineering Technology and Sciences (IJETS), vol. 5, pp. 11–18, 2016. [Google Scholar]

  28. A. Kaveh and M. I. Ghazaan, “Enhanced whale optimization algorithm for sizing optimization of skeletal structures,” Mechanics Based Design of Structures and Machines, vol. 45, pp. 345–362, 2017. [Google Scholar]

  29. D. P. Ladumor, I. N. Trivedi, P. Jangir and A. Kumar, “A whale optimization algorithm approach for unit commitment problem solution,” in Proc. National Conf. Advancement in Electrical and Power Electronics Engineering (AEPEE 2016), Morbi, India, 2016. [Google Scholar]

  30. E. -G. Talbi, “A taxonomy of hybrid metaheuristics,” Journal of Heuristics, vol. 8, pp. 541–564, 2002. [Google Scholar]

  31. I. -S. Oh, J. -S. Lee and B. -R. Moon, “Hybrid genetic algorithms for feature selection,” IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 26, pp. 1424–1437, 2004. [Google Scholar]

  32. O. C. Martin and S. W. Otto, “Combining simulated annealing with local search heuristics,” Annals of Operations Research, vol. 63, pp. 57–75, 1996. [Google Scholar]

  33. K. Lenin, B. R. Reddy and M. Suryakalavathi, “Hybrid tabu search-simulated annealing method to solve optimal reactive power problem,” International Journal of Electrical Power and Energy Systems, vol. 82, pp. 87–91, 2016. [Google Scholar]

  34. Y. Lin, Z. Bian and X. Liu, “Developing a dynamic neighborhood structure for an adaptive hybrid simulated annealing–tabu search algorithm to solve the symmetrical traveling salesman problem,” Applied Soft Computing, vol. 49, pp. 937–952, 2016. [Google Scholar]

  35. M. Mafarja and S. Abdullah, “Investigating memetic algorithm in solving rough set attribute reduction,” International Journal of Computer Applications in Technology, vol. 48, pp. 195–202, 2013. [Google Scholar]

  36. R. Azmi, B. Pishgoo, N. Norozi, M. Koohzadi and F. Baesi, “A hybrid GA and SA algorithms for feature selection in recognition of hand-printed farsi characters,” in 2010 IEEE Int. Conf. on Intelligent Computing and Intelligent Systems, Xiamen, China, pp. 384–387, 2010. [Google Scholar]

  37. J. Wu, Z. Lu and L. Jin, “A novel hybrid genetic algorithm and simulated annealing for feature selection and kernel optimization in support vector regression,” in 2012 IEEE 13th Int. Conf. on Information Reuse & Integration (IRI), Las Vegas, NV, USA, pp. 401–406, 2012. [Google Scholar]

  38. K. Manimala, K. Selvi and R. Ahila, “Hybrid soft computing techniques for feature selection and parameter optimization in power quality data mining,” Applied Soft Computing, vol. 11, pp. 5485–5497, 2011. [Google Scholar]

  39. M. M. Mafarja and S. Mirjalili, “Hybrid whale optimization algorithm with simulated annealing for feature selection,” Neurocomputing, vol. 260, pp. 302–312, 2017. [Google Scholar]

  40. O. Olabiyisi Stephen, M. Fagbola Temitayo, O. Omidiora Elijah and C. Oyeleye Akin, “Hybrid metaheuristic feature extraction technique for solving timetabling problem,” International Journal of Scientific and Engineering Research, vol. 3, no. 8, pp. 1–6, 2012. [Google Scholar]

  41. T. W. Chin, “Feature selection for the fuzzy artmap neural network using a hybrid genetic algorithm and tabu search,” Master’s Dissertation, Universiti Sains Malaysia, Malaysia, 2007. [Google Scholar]

  42. M. Majdi, S. Abdullah and N. S. Jaddi, “Fuzzy population-based meta-heuristic approaches for attribute reduction in rough set theory,” World Academy of Science, Engineering and Technology, International Journal of Computer, Electrical, Automation, Control and Information Engineering, vol. 9, pp. 2462–2470, 2015. [Google Scholar]

  43. P. Moradi and M. Gholampour, “A hybrid particle swarm optimization for feature subset selection by integrating a novel local search strategy,” Applied Soft Computing, vol. 43, pp. 117–130, 2016. [Google Scholar]

  44. E. -G. Talbi, L. Jourdan, J. Garcia-Nieto and E. Alba, “Comparison of population based metaheuristics for feature selection: Application to microarray data classification,” in 2008 IEEE/ACS Int. Conf. on Computer Systems and Applications, Doha, Qatar, pp. 45–52, 2008. [Google Scholar]

  45. Z. Yong, G. Dun-Wei and Z. Wan-Qiu, “Feature selection of unreliable data using an improved multi-objective PSO algorithm,” Neurocomputing, vol. 171, pp. 1281–1290, 2016. [Google Scholar]

  46. J. Jona and N. Nagaveni, “A hybrid swarm optimization approach for feature set reduction in digital mammograms,” WSEAS Transactions on Information Science and Applications, vol. 9, pp. 340–349, 2012. [Google Scholar]

  47. M. E. Basiri and S. Nemati, “A novel hybrid ACO-GA algorithm for text feature selection,” in 2009 IEEE Congress on Evolutionary Computation, Trondheim, Norway, pp. 2561–2568, 2009. [Google Scholar]

  48. R. Babatunde, S. Olabiyisi and E. Omidiora, “Feature dimensionality reduction using a dual level metaheuristic algorithm,” Optimization, vol. 7, pp. 49–52, 2014. [Google Scholar]

  49. J. Jona and N. Nagaveni, “Ant-cuckoo colony optimization for feature selection in digital mammogram,” Pakistan Journal of Biological Sciences: PJBS, vol. 17, pp. 266–271, 2014. [Google Scholar]

  50. M. Nekkaa and D. Boughaci, “Hybrid harmony search combined with stochastic local search for feature selection,” Neural Processing Letters, vol. 44, pp. 199–220, 2016. [Google Scholar]

  51. I. Boussaïd, J. Lepagnot and P. Siarry, “A survey on optimization metaheuristics,” Information Sciences, vol. 237, pp. 82–117, 2013. [Google Scholar]

  52. G. Chandrashekar and F. Sahin, “A survey on feature selection methods,” Computers and Electrical Engineering, vol. 40, pp. 16–28, 2014. [Google Scholar]

  53. P. Agrawal, H. F. Abutarboush, T. Ganesh and A. W. Mohamed, “Metaheuristic algorithms on feature selection: A survey of one decade of research (2009–2019),” IEEE Access, vol. 9, pp. 26766–26791, 2021. [Google Scholar]

  54. M. Alwohaibi, M. Alzaqebah, N. M. Alotaibi, A. M. Alzahrani and M. Zouch, “A hybrid multi-stage learning technique based on brain storming optimization algorithm for breast cancer recurrence prediction,” Journal of King Saud University-Computer and Information Sciences, vol. 34, no. 8, pp. 5192–5203, 2022. [Google Scholar]

  55. R. Abu Khurma, I. Aljarah, A. Sharieh, M. Abd Elaziz, R. Damaševičius et al., “A review of the modification strategies of the nature inspired algorithms for feature selection problem,” Mathematics, vol. 10, pp. 464, 2022. [Google Scholar]

  56. S. Taghian and M. H. Nadimi-Shahraki, “A binary metaheuristic algorithm for wrapper feature selection,” International Journal of Computer Science Engineering, vol. 8, no. 5, pp. 168–172, 2019. [Google Scholar]

  57. M. Ghosh, R. Guha, R. Sarkar and A. Abraham, “A wrapper-filter feature selection technique based on ant colony optimization,” Neural Computing and Applications, vol. 32, no. 12, pp. 7839–7857, 2020. [Google Scholar]

  58. B. McCollum, P. McMullan, A. J. Parkes, E. K. Burke and S. Abdullah, “An extended great deluge approach to the examination timetabling problem,” in Proc. of the 4th Multidisciplinary Int. Scheduling: Theory and Applications 2009 (MISTA 2009), Dublin, Ireland, pp. 424–434, 2009. [Google Scholar]

  59. El. -G. Talbi, Metaheuristics: From Design to Implementation. John Wiley & Sons, Hoboken, N.J, New Jersey and canada, 2009. [Google Scholar]

  60. M. Alzaqebah and S. Abdullah, “Comparison on the selection strategies in the artificial bee colony algorithm for examination timetabling problem,” International Journal of Soft Computing and Engineering (IJSCE), vol. 1, pp. 158–163, 2011. [Google Scholar]

  61. N. S. Altman, “An introduction to kernel and nearest-neighbor nonparametric regression,” The American Statistician, vol. 46, no. 3, pp. 175–185, 1992. [Google Scholar]

  62. G. Dueck, “New optimization heuristics: The great deluge algorithm and the record-to-record travel,” Journal of Computational Physics, vol. 104, pp. 86–92, 1993. [Google Scholar]

  63. T. Kuo and S. -Y. Hwang, “Using disruptive selection to maintain diversity in genetic algorithms,” Applied Intelligence, vol. 7, pp. 257–267, 1997. [Google Scholar]

  64. E. Emary, H. M. Zawbaa and A. E. Hassanien, “Binary ant lion approaches for feature selection,” Neurocomputing, vol. 213, pp. 54–65, 2016. [Google Scholar]

  65. D. Dua and C. Graff, “UCI Machine Learning Repository,” Irvine, CA: The University of California, School of Information and Computer Science, 2019. [Online]. Available: http://archive.ics.uci.edu/ml. [Google Scholar]

  66. T. Hastie, R. Tibshirani and J. Friedman, “Model assessment and selection,” in The Elements of Statistical Learning, New York, NY: Springer, pp. 219–259, 2009. [Google Scholar]

  67. Q. Al-Tashi, S. J. A. Kadir, H. M. Rais, S. Mirjalili and H. Alhussian, “Binary optimization using hybrid grey wolf optimization for feature selection,” IEEE Access, vol. 7, pp. 39496–39508, 2019. [Google Scholar]