 Open Access
Open Access
ARTICLE
One-Class Arabic Signature Verification: A Progressive Fusion of Optimal Features
1 Centre of Artificial Intelligence, Faculty of Information Sciences and Technology, University Kebangsaan Malaysia, Bangi, 43600, Malaysia
2 Information Technology Center, Iraqi Commission for Computers and Informatics, Baghdad, 10009, Iraq
3 Institute of Graduate Studies and Research, University of Alexandria, 163 Horreya Avenue, El Shatby, 21526, P.O. Box 832, Alexandria, Egypt
* Corresponding Author: Ansam A. Abdulhussien. Email:
Computers, Materials & Continua 2023, 75(1), 219-242. https://doi.org/10.32604/cmc.2023.033331
Received 14 June 2022; Accepted 01 August 2022; Issue published 06 February 2023
Abstract
Signature verification is regarded as the most beneficial behavioral characteristic-based biometric feature in security and fraud protection. It is also a popular biometric authentication technology in forensic and commercial transactions due to its various advantages, including noninvasiveness, user-friendliness, and social and legal acceptability. According to the literature, extensive research has been conducted on signature verification systems in a variety of languages, including English, Hindi, Bangla, and Chinese. However, the Arabic Offline Signature Verification (OSV) system is still a challenging issue that has not been investigated as much by researchers due to the Arabic script being distinguished by changing letter shapes, diacritics, ligatures, and overlapping, making verification more difficult. Recently, signature verification systems have shown promising results for recognizing signatures that are genuine or forgeries; however, performance on skilled forgery detection is still unsatisfactory. Most existing methods require many learning samples to improve verification accuracy, which is a major drawback because the number of available signature samples is often limited in the practical application of signature verification systems. This study addresses these issues by presenting an OSV system based on multifeature fusion and discriminant feature selection using a genetic algorithm (GA). In contrast to existing methods, which use multiclass learning approaches, this study uses a one-class learning strategy to address imbalanced signature data in the practical application of a signature verification system. The proposed approach is tested on three signature databases (SID-Arabic handwriting signatures, CEDAR (Center of Excellence for Document Analysis and Recognition), and UTSIG (University of Tehran Persian Signature), and experimental results show that the proposed system outperforms existing systems in terms of reducing the False Acceptance Rate (FAR), False Rejection Rate (FRR), and Equal Error Rate (ERR). The proposed system achieved 5% improvement.Keywords
As a result of increased security requirements in authenticating applications, biometric systems have developed as revolutionary security systems in pattern recognition and E-Systems. Biometric systems are security solutions that use physiological attributes to identify or validate an individual. Fingerprints, thumb imprints, palm prints, nerves, iris recognition, face recognition, and deoxyribonucleic acid (DNA) are characteristics of physiological characteristics [1], while handwriting, voice, keyboards, signatures, and other modalities are instances of behavioral characteristics [2]. The signature of an individual is one of the most widely used and legally recognized behavioral biometrics, providing a means of verification and personal identity in a variety of applications, including financial, commercial, and legal operations. A verification system aims to distinguish between authentic and counterfeit signatures, which are frequently linked to intrapersonal and interpersonal variability. Genuine and forged signatures are the two distinct types of signatures. A genuine signature belongs to the person who signed it, and a forged signature is a copy or imitation of a person’s signature made by an illegitimate person that can be classified into three categories: random forging, unskilled forging (sample forgery), and skilled forging. The most difficult forgery to detect is skilled forgery, in which the forger has a thorough knowledge of the claimed identity’s signature and has practiced the signatures several times before the forging attempt [3].
Signature verification methods have two remarkable types: online and offline. An online signature verification device measures the sequential details by collecting the signature image on tablets, Personal Digital Assistant (PDAs), iPads, and smartphones. An offline verification checks signatures using an optical detector to capture signatures on a piece of paper. However, offline signatures are more complex than online signatures because offline signatures lack a dynamic nature and contains static data such as slant, bounding box, signature length and height, baseline, bold pen, and size, which vary from one person to another. Online signatures have a dynamic nature and operate on features such as writing orientation, pen tip positions, momentum, velocity, and pressure. These features is easy to distinguish.
Offline handwritten signature verification consists of three major processes: preprocessing, feature extraction, and feature verification [4]. The process of extracting data from a signature image based on feature categories, including shape features, geometric characteristics, grid attributes, textural features, wavelet transforms, chord moments, and the fusion of local and global features is known as feature extraction. Feature fusion is the process of integrating the patterns of multiple features into a single matrix, which improves error rates when compared to separate descriptors [5], including score-level fusion and high-priority index feature fusion.
According to the literature, extensive research has been conducted on signature verification systems in various languages, including English, Hindi, Bangla, and Chinese. However, studies of Arabic signatures are restricted, and progress is slow because it is more challenging to master than other languages. Arabic script is distinguished by its cursive form, changing letter shapes, joining and non-joining characters, delayed strokes, and ligatures [6,7]. Systems for Arabic script cannot discriminate between extracted features in skilled forgeries and genuine signatures. The problem with existing techniques is that they typically use combination features without considering correlation and discriminant such that the generated feature vector is unable to recognize a skilled forgery. In addition, fusion techniques were used to increase the computational time of the system.
Similarly, features extracted by the modern deep learning approach are far from perfect. Training models requires many samples and a lot of effort in selecting images appropriate to construct training sets [8]. Deep learning also requires a lot of computational resources during training, including expensive GPUs [9,10]. This paper’s primary purpose is to propose an offline Arabic signature verification system using hybrid features to add another dimension that can recognize skilled forgery and genuine signatures at a highly accurate rate. A simple concatenated fusion strategy is used to combine multiple features and GA for selecting optimal feature sets.
A GA is used to select the optimal features and has become a convenient method to solve complex optimization problems with several local optima. Many researchers have asserted success forces in a variety of applications. They discovered that GAs’ crossover operation, a characteristic not found in other optimization approaches, can form the basis for a generic strategy that can improve a set of suboptimal solutions [11]. As the search progresses, the solutions to any evolutionary method progressively cluster around one or more “good” solutions. This clustering might be the population’s convergence toward a certain solution. If the population clusters quickly, the population may become stagnant, making potential development unlikely. Although it is frequently discovered that the top section of the population may appear identical, reinitialization can also introduce randomness into the population to improve diversity [12]. As a result, GA is a better choice compared with metaheuristic algorithms.
This paper is organized as follows. Motivations and contributions of this study are described in Section 2. Related work is reviewed in Section 3. The proposed signature verification system’s design is described in Section 4, and experimental data and a comparison of the proposed method to related work are shown in Section 5. The results of these experiments are discussed in Sections 6, and 7 summarizes and outlines conclusions and suggested directions of future work.
Signatures are part of the essential behavioral human attributes and widely used as proof of identification for legal purposes on a variety of documents in everyday life, including bank checks, credit cards, and wills. The design of an effective automatic system to manage such a high volume of signatures offers many potential benefits for signature authentication to prevent fraud and other crimes, particularly given the large number of signatures processed daily through visual examination by authorized persons. Many signature verification methods have been explored and are still being studied, particularly among offline methods, primarily because a handwritten signature is the output of a complex process that is dependent on the signer’s psychophysical status and the circumstances under which the signature is made.
Results may show a large variability between samples from the same individual and a high degree of closeness to skilled forgeries. In addition, offline signatures lack dynamic information such as writing speed and pressure. Another challenge is that the size of the available signature databases is often restricted, particularly in terms of the number of genuine signatures per writer. For a practical application of the signature verification system, no forgery data are typically available for training. This disadvantage is severe, particularly for deep learning techniques that require a large amount of training data. This study focuses on improving the OSV system for Arabic scripts. The contributions of this study include the following:
• The proposed method improves signature verification using effective preprocessing processes such as image scaling, denoising, binarization and eliminating stray isolated pixels to balance noise reduction and loss of data.
• Multiple features are fused based on local and global feature extraction approaches.
• Fused features are fed to GA to select robust features.
• A one-class learning approach is used to manage unbalanced data because this approach uses less computing time and memory.
Feature extraction is a critical stage in OSV and is often regarded as one of the most challenging operations. Feature extraction strongly relies on a writer’s intrapersonal variability because it is related to uniqueness. Thus, signature discriminative power fluctuates depending on distribution, scarcity, and dissimilarity factors. Researchers have used several types of features to improve models’ performances. Based on the literature, three primary features exist: statistical features, structural features, and model-based features or automated features [13,14]. This study focuses on statistical features, which are statistical and mathematical measurements that can be used to classify pertinent information into different classes. Statistical features can be split into two categories: global and local. Global features describe the global traits of the entire image. In local feature extraction, the signature image is separated into several units or parts, and features are extracted from each segment of the image [15]. Statistical features might be represented in shape, geometric data, grid, textural data, wavelet transform, or chord moments.
The authors in [16] presented a new textural element for offline handwritten signature verification. A local difference feature (LDF) is a texture description that is similar to local binary patterns (LBPs). The LDF computes the differences between a center pixel and eight neighbors within a certain radius. Before assessing the histogram of codes, differences were coded into binary threshold values. A support vector machine (SVM) classifier trained on real signatures was used for verification. The GPDS (Grupo de Procesado Digital de Senales) and CEDAR datasets were used in the experiments, and the best accuracy was obtained using 10 reference signatures with 6.10% FRR, 8.26% FAR, and 7.18% AER (Average Error Rate) for the GPDS dataset and 5.81% FRR, 10.00% FAR, and 7.90% AER for the CEDAR dataset, respectively.
In [17], the authors used an extension of LBP called multiscale local binary patterns (MSLBPs) to capture local and global features from the signature image. The LBP features were extracted from signature images at different radii and stored in histograms. The fusion of histogram features at various scales was used to form a single feature vector. The results obtained by that approach were 4.0% FAR and 5.6% FRR on the CEDAR dataset, and 0.8% FAR and 2.0% FRR on the MUKOS (Mangalore University Kannada Off-line Signature) dataset.
The authors in [18] presented a feature fusion and optimum feature selection (FS)-based automated approach. Preprocessing signature samples yielded 22 gray-level cooccurrence matrices (GLCMs) and 8 geometric features. A parallel method was used to combine both characteristics based on a high-priority index feature. A skewness-kurtosis-based FS technique (skewness-kurtosis controlled PCA) was also used to select optimal features for signature classification. Validation using the MCYT (Ministerio de Ciencia Y Tecnologia), GPDS synthetic and CEDAR datasets showed FARs of 2.66%, 9.17% and 3.34%, respectively.
The authors in [19] used Taylor series expansion to extract the characteristics and applied SVM as a classifier on the CEDAR and MUKOS datasets. They obtained 95.25% on the CEDAR dataset and 98.93% on the MUKOS dataset. In [20], the authors presented a novel feature extraction approach based on static image splitting using the density center. A new feature called pixel length was mentioned in the proposed system. This feature was combined with three additional features (pixel density, cell angle, and pixel angle), all of which were standard features in the signature verification procedure. The classification was performed using the Euclidean distance method. When the system was tested on the GPDS database, the performance was 18.94% FAR, 8.81% FRR, and 13.87% AER.
The authors in [21] modeled offline handwritten signature verification by concentrating on grid-based ordered lattices of simple and compound events of pixel assortments. They proposed a method for assessing signature qualitative properties using complexity, stability, and overall quality in a quantitative fashion. They used the same features that were used in the verification. The proposed quality measures, particularly complexity and overall quality, were validated using the CEDAR, GPDS, and MCYT signature databases and achieved EERs of 4.12%, 9.42%, and 9.2%, respectively.
In [22], the authors provided a collection of characteristics based on the distribution of quasi-straight-line segments for OSV. The 8-N chain codes were used to detect the collection of quasi-straight-line segments that define the signature border. The orientations of the line segments were used to create 12 classes of quasi-straight-line segments. The feature set was then derived from those 12 classes. For verification, an SVM classifier was used. The results were 3.72% FAR, 2.65% FRR and 3.18% AER for the CEDAR standard signature dataset, and 13.35% FAR, 7.0% FRR and 11.4% AER for the GPDS-100 dataset.
The authors in [23] suggested a crowdsourcing experiment to develop a human baseline for signature recognition and a new attribute-based automated signature verification system based on forensic document examiner analysis. This system combines the dynamic time-wrapping algorithm with an attribute-based approach to improve accuracy with a 5% EER. The authors in [24] presented the Hadamard transform-based approach and tested it on the SUSIG (Sabanci University Signature) dataset. The Hadamard matrix was created from the extracted features, and then Euclidean and Manhattan distances were used for feature comparison and verification. In [25], the authors introduced a novel offline Arabic signature verification technique that uses two-level fuzzy-set related verification. The difference between the features retrieved from the test signature and the mean values of each corresponding feature in the training signatures were used for level-one verification for the same signature. Level-two verification was the output of the fuzzy logic module, which is based on membership functions derived from signature attributes in the training dataset for a given signer. The authors used the ratio of the signature’s width to height and the ratio of the area filled by signature pixels to the size of the bounding box as global features for feature extraction. Local characteristics include pixel density dispersion and gravity center distance. The suggested technique achieved 2% FRR, 5% FAR, and 98% accuracy on a dataset that included genuine and forgery signatures picked by individuals. The system’s capacity to detect skilled forging signatures in Arabic script was considerably lower than that achieved in a Western script because the system could not distinguish between the extracted characteristics in both skilled forgery and authentic signatures.
In [26], the authors presented an OSV mechanism for the Arabic and Persian languages. Preprocessing, image registration, feature extraction, and signature verification were the four processes used in their approach. DWT was used to extract characteristics from the signature picture, and signatures were verified using logical operations and mathematical equations. The experimental outcomes were FRR 10.9%, FAR 1.56%, and AER 6.23%. Convolutional neural networks (CNNs) [27], recurrent neural networks [28], deep metric learning [29] and some other deep machine learning have been used to extract and learn automatic features from raw data (e.g., pixels in images). Statistical and model-based features were not used in this case. The authors in [30] introduced a solution that used deep CNNs to learn features from data (signature images) in a writer-independent format; the proposed system obtained an ERR of 2.74% on the GPDS-160 dataset. However, the overall quality of the genuine signature was not properly captured and rendered these features less discriminatory against slow-traced skilled forgeries.
Although, the significant of existing verification methods, the problems and the weak points of recent the offline signature verification techniques are the complexity of the proposed feature fusion strategies, which may result in data loss and affect computing time. Moreover, the conflicting nature of data produces counter-intuitive results, and high-dimension characteristics from several approaches may be noisy and influence verification accuracy in recognizing a skilled forgery. Secondly, the disadvantage of the proposed deep learning approach is the inability to simulate the lack of signatures datasets in practical applications due to the need for enormous amounts of data for learning and a considerable amount of effort in selecting images adequate for constructing training sets. For more information, see [31–34].
In general, the issue of skilled forgery is a challenge that must be addressed. Signatures are not physiological or behavioral and may be acquired and easily imitated by a skilled forger [35]. Several characteristics can identify a signature at the stroke level, and signatures may have poor creativity and do not precisely match the usual writing style. The position of the writer and the instruments used for writing, injury, illness, age, psychological condition, and external influences such as alcohol and drugs can all affect signatures. They may cause inconveniences in the letters’ design, aberrant movements, and a lack of rhythm. The following are several of the differences between authentic signatures and forged signatures: (1) a forger slows down writing and scrutinizes the genuine signature with additional care, while a genuine writer trusts his or her work and signs without hesitation; (2) a forger creates a line with angularity and directional variation but are not necessarily disconnected; (3) forgers may expose their writing style because they rely on memory and may not recall all the details; and (4) forgeries typically have poor line quality because lines or strokes represent the quality of speed, the continuity of motion, and the degree of physical proficiency. The stroke’s edges are visible to highlight the angle between the writing instrument and the stroke, even if a forger attempts to imitate the angle at which the authentic writer drew. Finally, (5) after the initial stroke, forgers hesitate to make their work unsteady or appear to be done differently. Although it is not critical to the genuine writer, the last stroke is also treated with self-consciousness.
The suggested signature verification model consists of four phases: preprocessing, hybrid feature fusion, feature extraction, and classification based on one-class learning, as shown in Fig. 1.
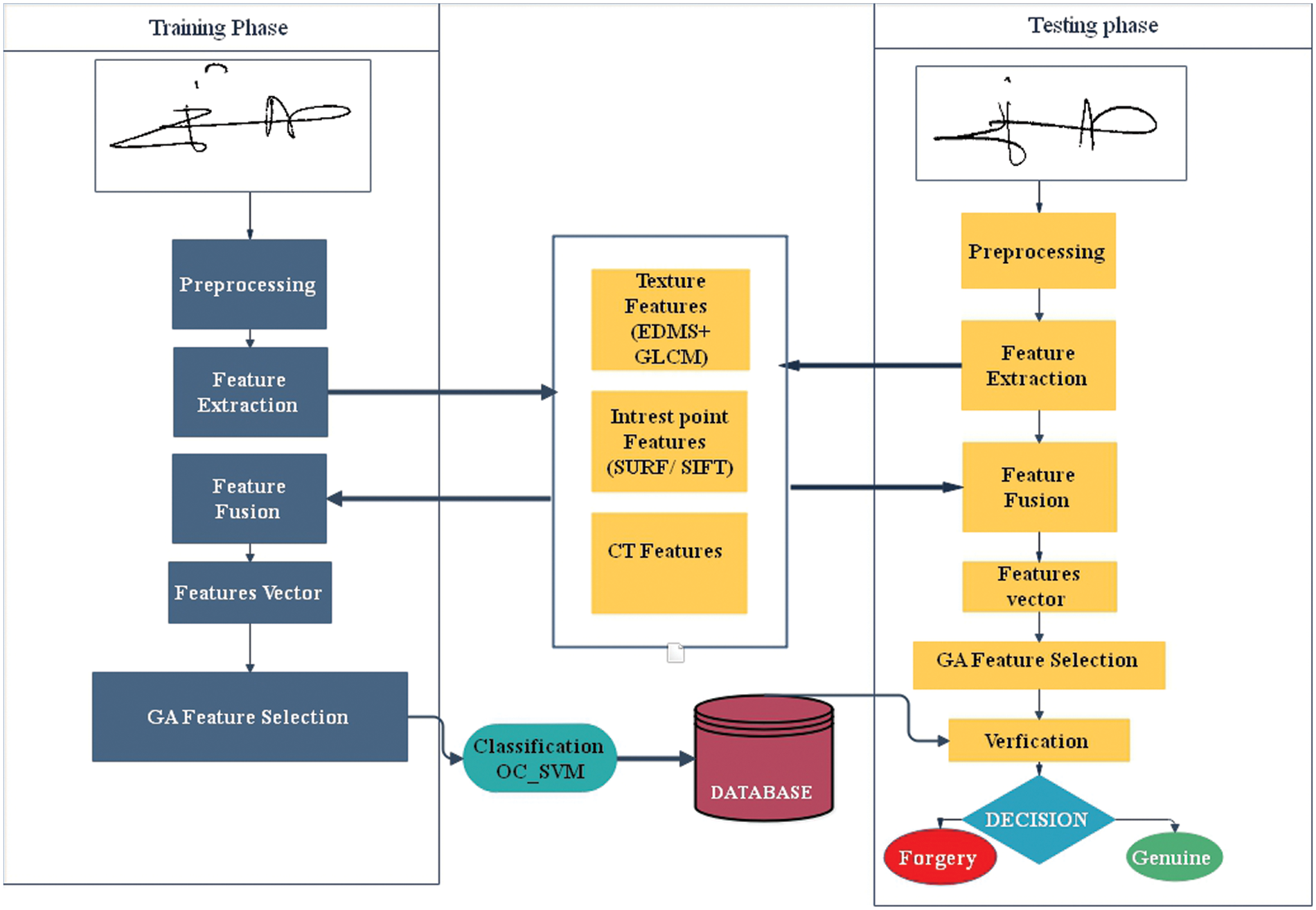
Figure 1: Flowchart of proposed system
Preprocessing is a critical component of this system and is required to modify raw data either to address the data collection process due to the limitations of the capturing device sensor or to prepare the data for subsequent system processes [36]. Spurious noise in a scanned signature image must be removed to avoid errors and make the signatures suitable for feature extraction in both the training and testing phases. However, achieving a balance between noise reduction and data loss is a challenge because some critical information is lost during preprocessing, possibly harming the system’s performance in later phases [15]. The following processes are used to provide effective preprocessing of the signature image without decreasing model performance. Prepossessing includes the following stages:
1. Grayscale: Verification only focuses on the signature’s pattern, not color. As a result, a color signature image is converted into a grayscale image, which makes computations easier.
2. Binarization: Histogram-based binarization is used to transform the grayscale signature into a binary image
where T = 0.5216 is the threshold.
3. Image denoising: After binarization of the reference image, the A two-dimensional window (3 × 3) median filtering technique is used to remove noise from the binary image
where
4. Cropping: The image is isolated from the backdrop using a vertical and horizontal projection segmentation method to eliminate the signature’s white space.
5. Stray isolated pixel elimination: Any blob with less than 30 pixels is deleted using the MATLAB function
6. Skeletonization and thinning: An image is reduced to single-pixel width. Thinning is an iterative process that results in skeleton production. This procedure minimizes the number of character characteristics to aid feature extraction and classification by erasing the pen’s width fluctuations. The stages of preprocessing are shown in Fig. 2.

Figure 2: Preprocessing steps (a) grayscale image (b) image denoising (c) cropping (d) isolated remove
Feature extraction is a technique that is used to describe specific signature properties that can be used to classify signatures. In this study, the characteristics of a signature image are extracted using a multistatistical feature extraction approach.
Edge Direction Matrix (EDMs) is the texture feature extraction technique manages the edge of a binary image [37] and is based on statistical analyses of the relationships between pixels in the immediate vicinity by determining the first-order relationship ED1 and second-order relationship ED2, as shown in Fig. 3b. This method uses a (3 × 3) Laplacian filter kernel matrix [38] to extract edge pictures, and the resulting image is known as an edge (x, y) based on Eq. (3):
where:
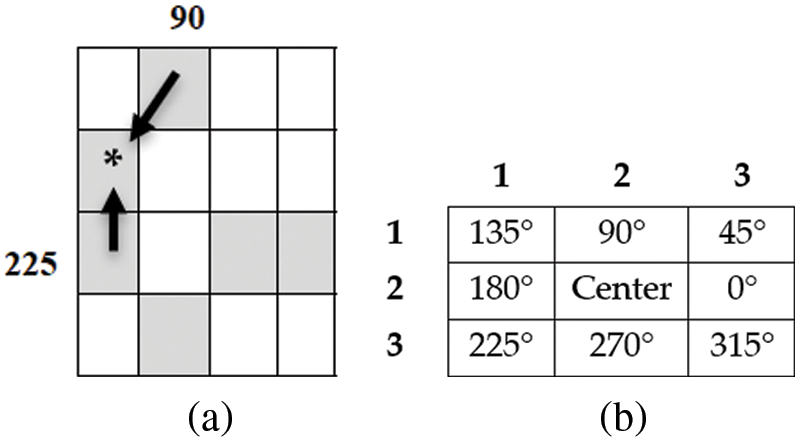
Figure 3: (a) Two edge neighboring pixels, (b) EDMs principal
Every edge image pixel is connected to a (3 × 3) kernel matrix, and each of the eight neighboring pixels directly relates to the center pixel. The equations in Algorithms 1 and 2 are used to obtain critical statistical properties, including data attributes and distribution descriptions.
The total number of occurrences is computed and saved in a relevant cell in ED1. As shown in Fig. 3a, each pixel on ED1 is associated with two pixels. Only the numbers 0° to 135° are used to extract the features in this study.

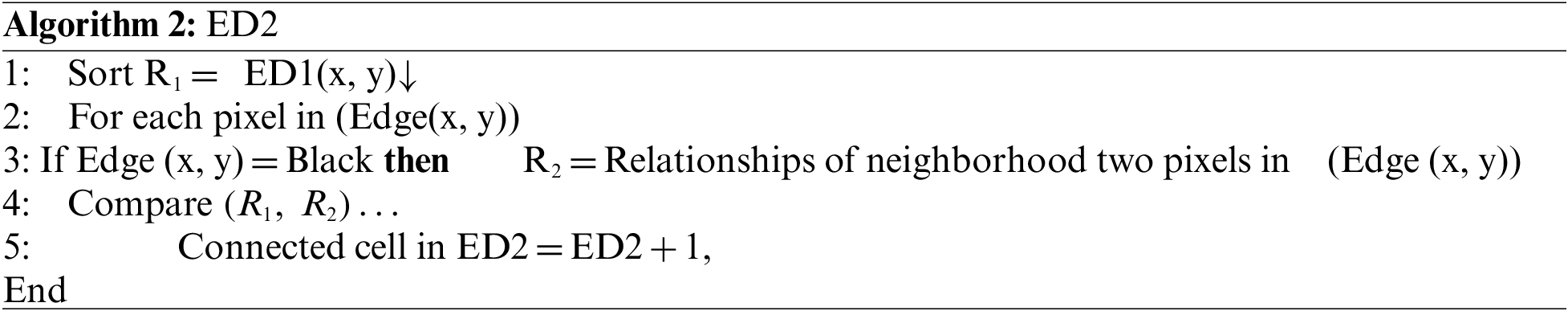
ED1 and ED2 are used in statistical approaches to extract various features. The characteristics analyzed in this study include correlation, homogeneity, pixel regularity, weights, edge direction, and edge regularity.
4.2.2 Gray Level Co-Occurrence Matrix
Local texture information is extracted using the GLCM features and depicts the frequency of a pixel value known as the reference pixel with intensity i occurring in a particular relationship to the neighborhood of a pixel with intensity j. Each element
• Contrast returns a measure of the intensity contrast between a pixel and its neighbor over the entire image, as in Eq. (6):
• Energy yields the sum of the squared items in the GLCM of Eq. (7):
• Homogeneity exhibits the homogeneity properties of image size or the size of the neighborhood of each occurrence matrix element as in Eq. (8):
• Correlation shows the magnitude of the linear relationship of the neighbor pixel gray level in Eq. (9):
4.2.3 Speeded Up Robust Features
The Speeded Up Robust Feature (SURF) method is fast and dependable at describing and comparing images in a local similarity-invariance manner. The integral image is used to compute the sum of the pixel values of the binary image. The integral image
Determining the sum of pixels contributes to boosting the speed of convolutions performed by the Hessian blob detector to find interest points. The Hessian matrix H (p, σ) at point
where
4.2.4 Scale Invariant Feature Transform
The scale invariant feature transform (SIFT) descriptor captures invariant features: persistent image domain translations, rotations, scaling transformations, minor perspective transformations and illumination variations. The scale-space extrema of Differences-of-Gaussians (DoG) within a difference-of-Gaussian pyramid provide these interest points. A (DoG) pyramid is constructed using the differences between contiguous levels in the Gaussian pyramid produced from the input image employing recurrent smoothing and subsampling.
The point at which (DoG) values approach exceeds the spatial coordinates in the image domain, and the scale level in the pyramid is used to generate interest points. The DoG
where
The curvelet transform (CT) is used to capture curves on the handwritten signature with limited coefficients [24]. The CT is described in Eqs. (14) and (15):
where
Different feature vectors are combined to create the final feature vector for classification. The primary goal of this phase is to merge all of the information from multiple descriptors into a single feature matrix, which can assist in reducing error rates compared to separate descriptors. In this study, the early concatenation fusion strategy combines features to create a new vector of dimension
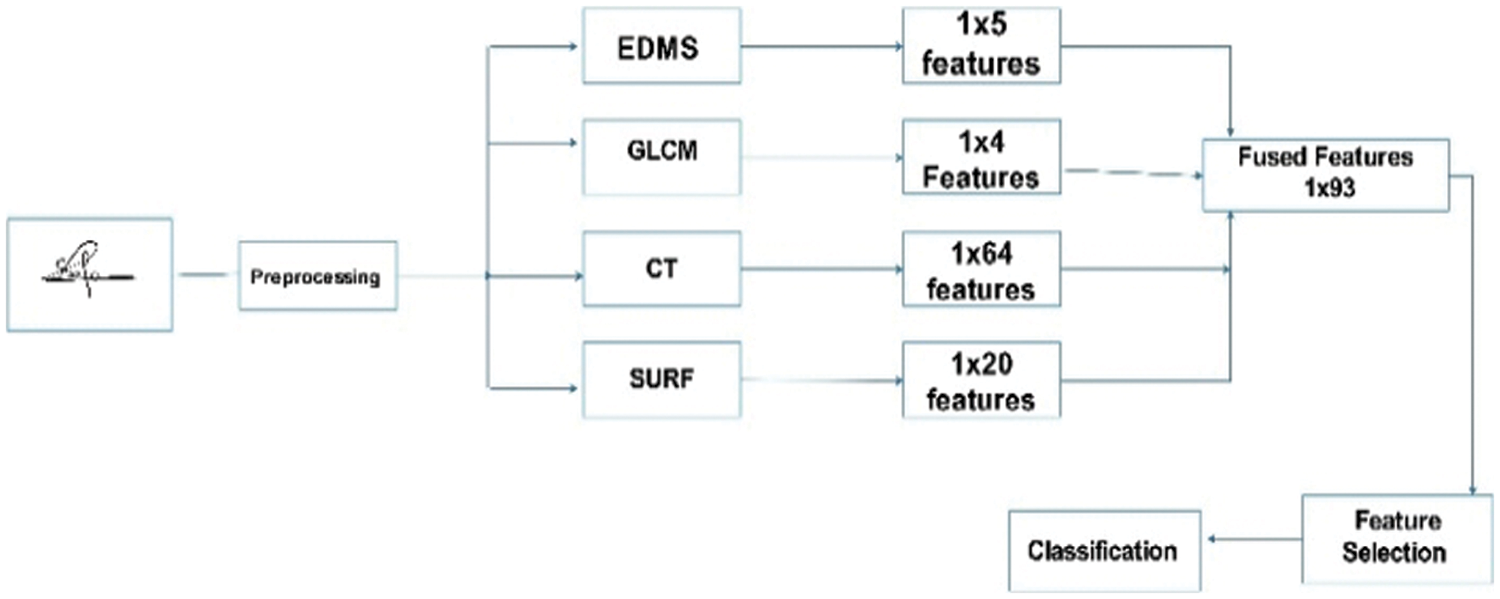
Figure 4: Strategy of feature fusion
4.4 Genetic Algorithm Feature Selection
In intelligent algorithms and machine learning, FS is an essential operation to select a subset of data to obtain the best solution [39]. Validating the authenticity of a personal signature is a challenging task in signature verification due to variations in the person’s signatures, such as slant, strokes and alignment. A fused number of characteristics increases correlation and reduces FRR but increases FAR. As a result, consistency assessment is critical for determining the system’s performance. To test the consistency of these features, choosing the best feature set is necessary.
However, minimum research has been done to assess the consistency of these characteristics [40]. Thus, these methods underperform with a small number of features. Thus, a feature selection method is required to select a subset of features from many features to represent precise, compact data; this also encourages us to suggest a metaheuristic technique for verifying handwritten signatures. In this study, a GA is used to select distinct features.
GA is an adaptive heuristic search technique that can select features based on modulation classification. GA can manage more complexity than neural networks and performs well when identifying a good feature for a specific category that causes the most visible issues. GA is a complete approach to problem-solving or teaching a computer to respond to certain situations in a certain way [41]. Fig. 5 shows the GA flow chart.
• Initial population: The population size is initialized in this study and set to 10. Following the selection of population size, each population’s position is assigned randomly, and the populations are ranked according to their fitness function. Finally, the best population’s cost is calculated and saved for further steps.
• Crossover: This step is essential in a GA. A crossover point is selected randomly from the genes for each pair of parents to be mated. Parents’ genes are exchanged to make offspring until the crossover point is achieved, as shown in Fig. 6a. Uniform crossover is used, having a crossover rate of 0.8.
• Mutation: This process is performed on new offspring, in which several genes have a low random frequency, as shown in Fig. 6b. Certain bits in the bit string are inverted. A uniform mutation strategy with a mutation rate of 0.3 is selected.
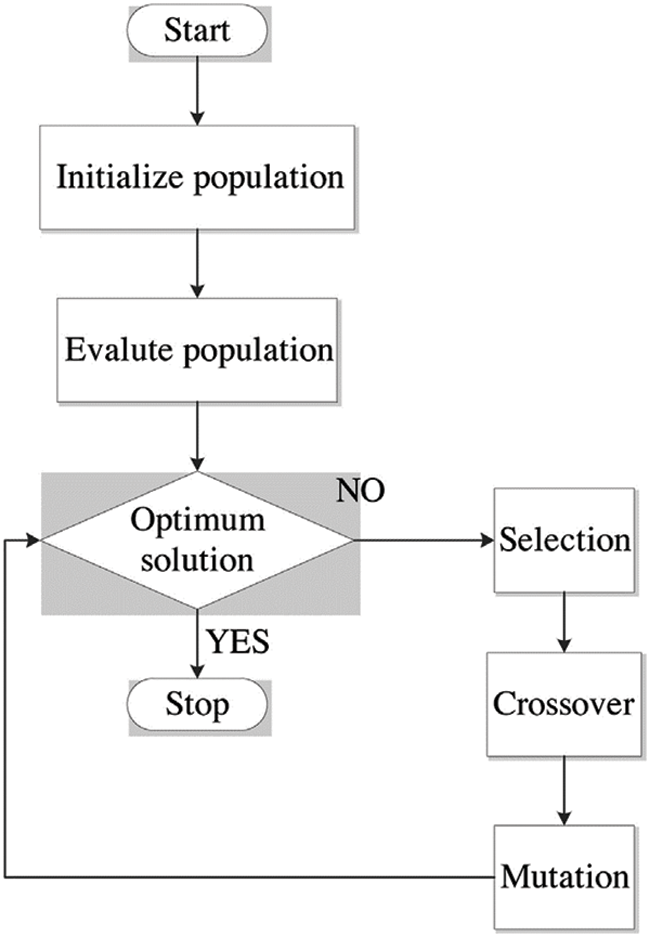
Figure 5: GA flowchart
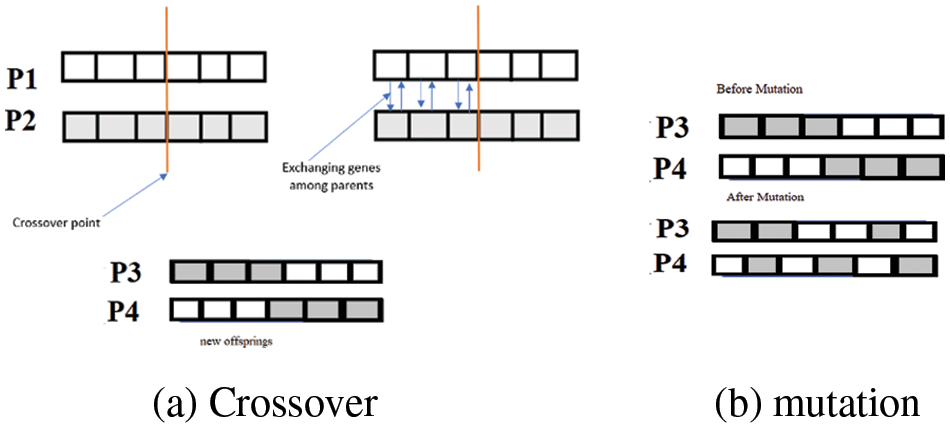
Figure 6: Crossover and mutation process
Chromosomes are selected using a roulette wheel selection algorithm that uses crossover and mutation procedures to maintain the selective pressure in the middle rather than high or low. The circular wheel is split into n pies in a roulette wheel selection, where n equals the number of individuals. Each individual receives a corresponding circle piece based on their fitness level. The wheel is turned around at a fixed point on its circumference. The portion of the wheel immediately ahead of the setpoint is designated as the parent. The identical procedure is used for the second parent. The probability
where
• Selection: The concept of the selection phase is choosing the fittest individuals and letting them pass their genes along to the following generations. A couple of individuals (parents) are selected based on their fitness scores. Individuals with high fitness have a better probability of being chosen for reproduction, as shown in Algorithm 3.
The size of the optimum features is

4.5 One_Class Support Vector Machine
One of the most commonly used one-class classifiers is the one-class support vector machine (OC_SVM), which can effectively manage a training set that contains negative samples [42]. The origin in the feature space is the only nontarget sample used by OC_SVM. Additionally, in the feature space, the ideal hyperplane may be found by maximizing the distance between the images of the target (negative or positive) samples and the origin. The hyperplane is defined by Eq. (18):
where
where N is the number of training writer samples, ρ defines the distance of the hyperplane from the origin, and
5 Experiment Results and Analysis
The primary objective of this study uses the proposed method to distinguish between forged (F) and genuine (G) signatures. The experiments were performed on three handwritten signature databases (SID-Signature in Arabic script) and two public databases (CEDAR and University of Tehran Persian Signature UTSig), as shown in Fig. 7. The proposed approaches were assessed on each database by calculating FRR, FAR, which considers skilled forgeries, and EER, as defined in Eqs. (21)–(23). Performance was compared with previous related signature verification approaches to assess the verification accuracy of the proposed approach. The model was run in MATLAB R2021a on an Intel Core i5 computer with a 2.30 GHz processor with 8 GB RAM:

Figure 7: Databases samples
5.1 Validation with the SID-Signature Database
SID-Signature is a dataset that was developed to study signatures of Tunisian origin. This dataset contains signatures from 100 writers of various ages and cultural and scientific backgrounds. The collected signatures were digitized at a 300-dpi resolution using three scanners: HP 3200C, HP G2710, and EPSON DX4400 [43]. The database includes 4000 genuine signatures divided randomly into 70% for training and 30% for testing. Samples of 2000 skilled forgery signatures and 2000 simple forgery signatures were used only for testing. The different experiments performed to validate the proposed method were performed on a training set containing only genuine data.
The first experiment fused texture features using EDMs, GLCM, the interest point feature SURF, and CT. GA was used for feature selection with 10 for population size, 0.3 mutations, and 0.8 crossovers. The experiment yielded 6.81% FRR on genuine, 4.76 FAR skilled forgeries, and 4.20% FAR simple forgeries. The EER was 5.65%.
In the second experiment, SIFT was used instead of SURF to extract the interest point feature, GA with the same parameter, and OC-SVM. The result was a 3.91% FAR for simple forgery, 4.81% for skilled forgery, 6.80% for FFR, and 5.58% for EER. The results from Experiments 1 and 2 are shown in Table 1.

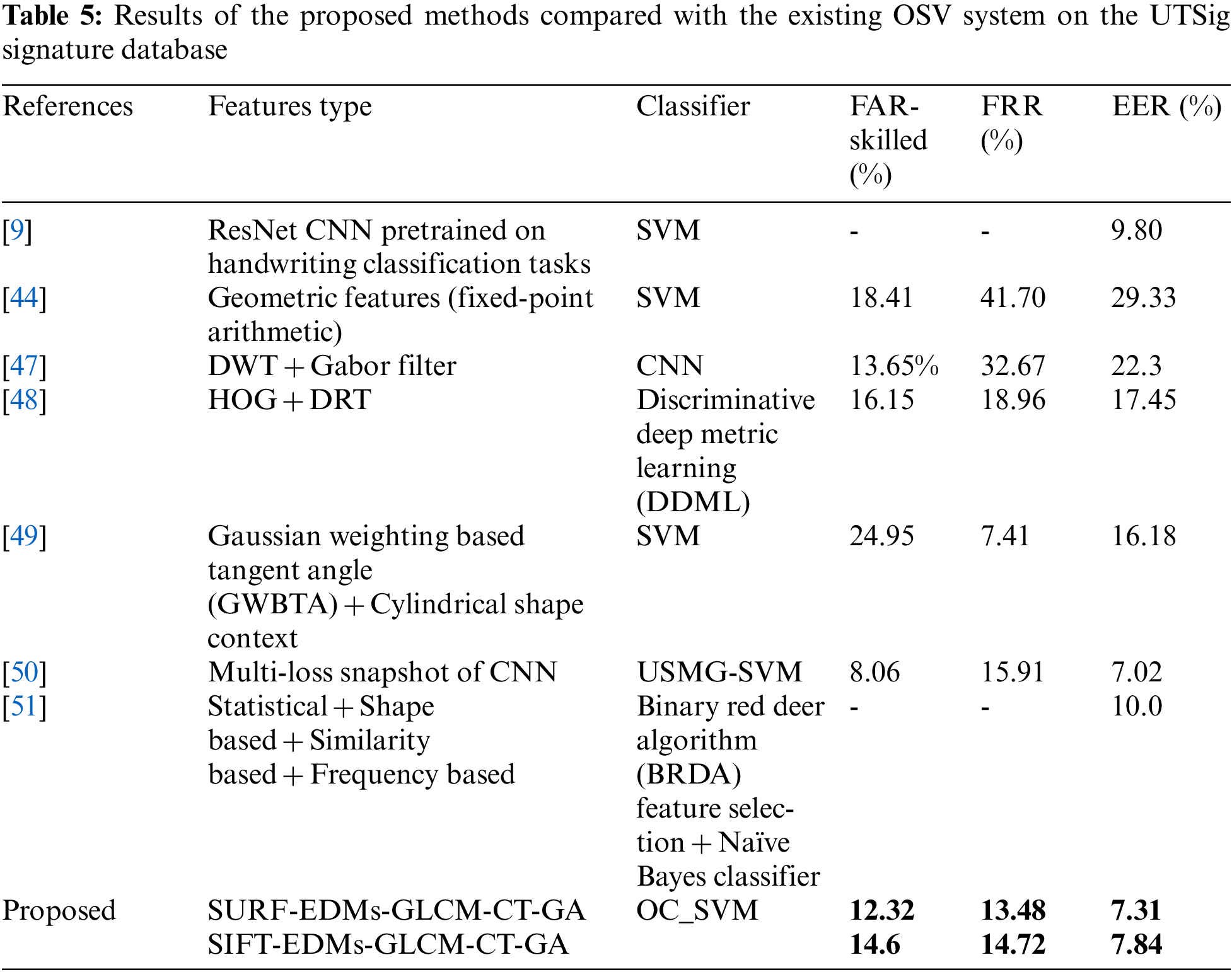
5.2 Validation with the CEDAR Database
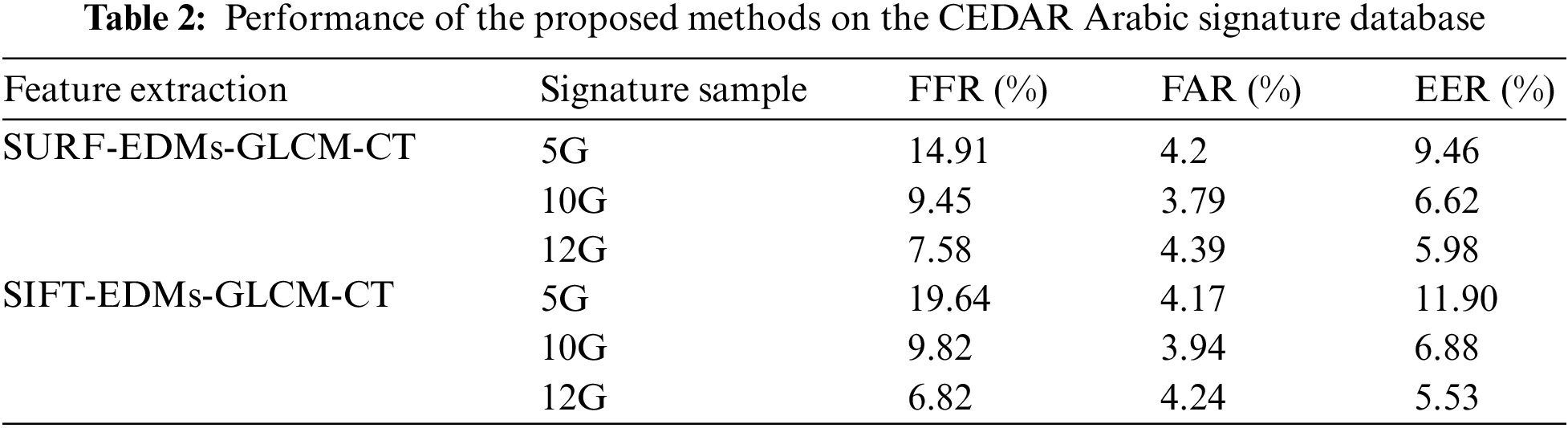
The CEDAR dataset is most commonly used for signature verification and contains 55 signature sample sets from 55 signers, which are all relevant to educational experiences, with 1320 samples of genuine signatures and 1320 samples of forgeries. Only genuine signatures were selected at random for training with three sets of signatures: 5 genuine, 10 genuine, and 12 genuine. The system was tested with all forged signatures and authentic signatures.
Similar to the previous experiment, two feature sets were compared, and GA was used to select the best feature set. The FRR, FAR and EER are determined to measure the accuracy of the proposed system. The results of the experiments are summarized in Table 2.
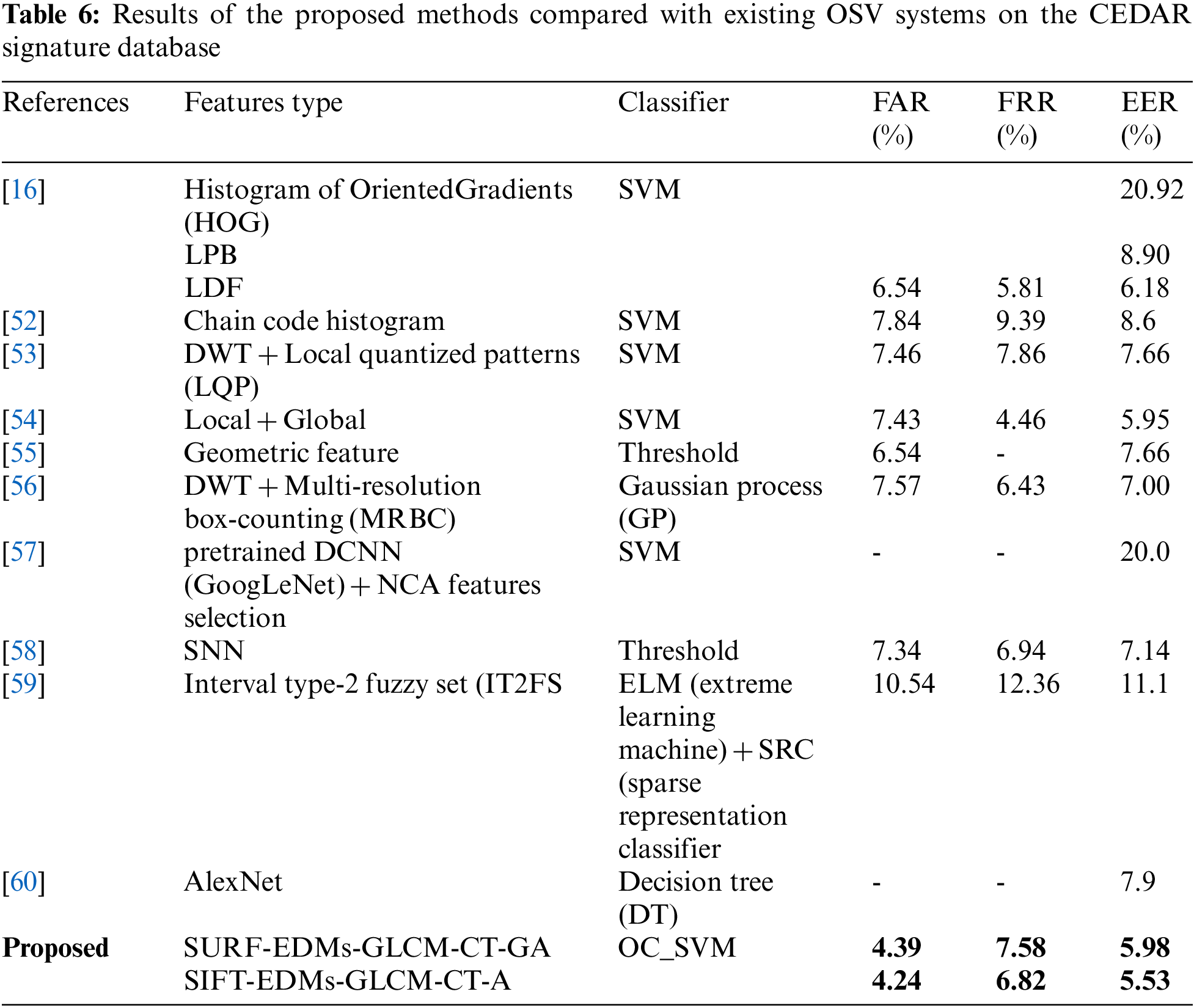
5.3 Validation with the UTSig Database
UTSig is a collection of 8280 images from 115 University of Tehran classes [44]. Each class has 27 genuine signatures, 6 skilled forgeries and 36 simple forgeries. For training, 70% of genuine signatures were selected randomly, and 30% of genuine signatures with all sample forgeries were chosen randomly for testing. The results of the experiments are shown in Table 3.

The proposed system’s performance compared to those of existing approaches are described using FAR, FRR, and EER, as shown in Tables 4–6.
This section includes analyses of the proposed offline verification system in FAR, FRR, and AER. As shown in Figs. 1 and 3, the proposed method consists of three primary phases: feature extraction and fusion; feature selection, where the results of fused hybrid features are improved using the GA feature selection approach; and finally, forged and genuine signatures are verified using OC-SVM.
This study investigated three public datasets: SID signature, CEDAR, and UTSig. Tables 1–3 show that the proposed approach obtained superior FAR, FRR, and ERR on the three databases compared with existing approaches, particularly for skilled forgeries, which is this study’s essential contribution. The verification system’s accuracy improved due to features and GA feature selection. The proposed feature extraction is advantageous because it combines texture features, interest point features, and CT features to address the low interclass between skilled forgery and genuine and high interclass of genuine for each writer.
This combination aims to make the most of each technique by complementing other advantages, thus enhancing verification capability. EDMs is a global feature for texture features that specifies the entire signature image. Thus, EDMs has not achieved a high level of accuracy for skilled forgeries, although it has been adequate for simple forgeries. Otherwise, GLCM is a local feature that characterizes a small portion of the signature image and extracts additional information. GLCM has been more effective than EDMs for skilled forgeries and is more accurate.
SURF is another method of extracting local features that has been previously used to acquire keypoints. Under various viewing conditions, SURF can accurately locate the interest points. SURF was similar to SIFT in terms of performance but was faster. In addition, curves in the Arabic signature are captured using a CT, which is more effective at representing curved discontinuities than a wavelet. The proposed one class classification approach simulated the practical application in the real world that includes unbalanced data between genuine and forgery such as database used SID-Arabic signature, the model was trained only genuine signatures without forgery in training phase.
Verification accuracy increased by excluding non-instructive features via the feature selection process (EER), as shown in Fig. 8. In this study, the complexity of the proposed model is measured based on computation time. In experimental Section 7, each signature is processed in 0.01, 0.0227 and 0.021 s. for the CEDAR, SID, and UTSIG databases, respectively.
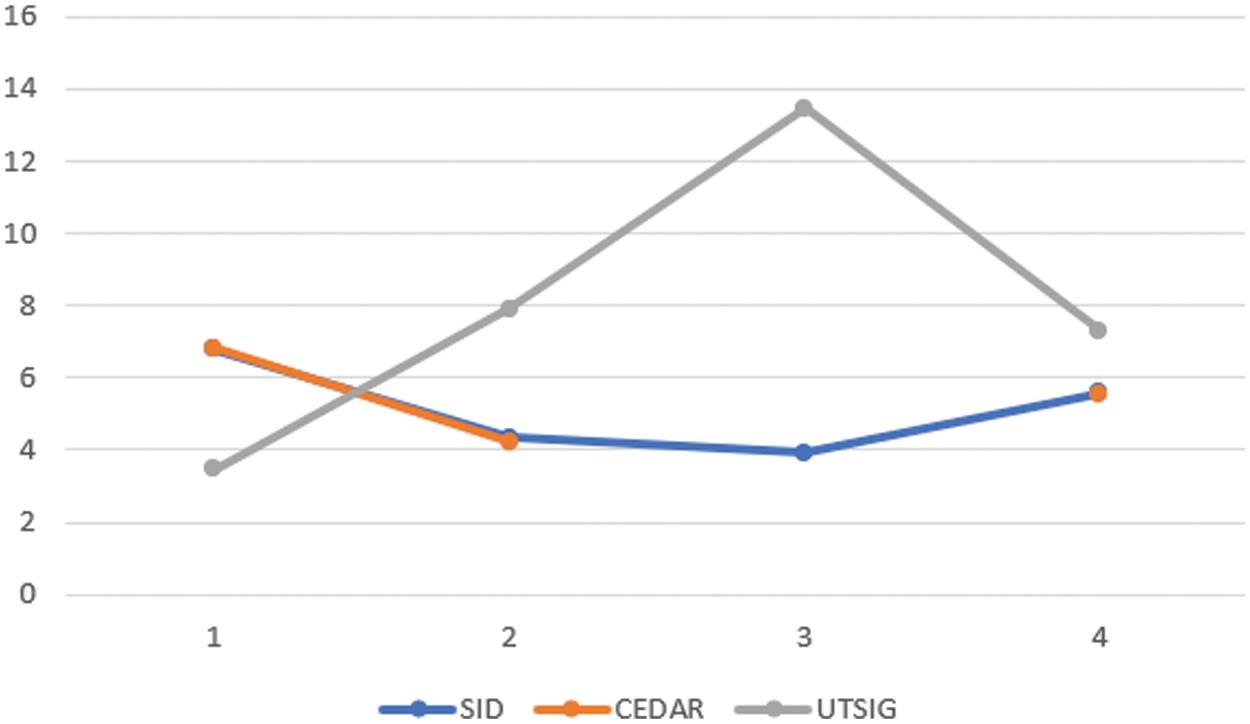
Figure 8: Comparative of database (CEDAR, SID, UTSIG) on plot curve
A new method is introduced for Arabic OSV based on hybrid features and GA-based optimal feature selection. The proposed technique computes and fuses four different types of statistical approaches. The finest GA-based features are then selected for final verification. On the SID-Arabic signature database, the combination of features and feature selection enhanced the 5%–10% FAR of Arabic signature verification without affecting computation time, which yielded 6.81% FRR, 4.76% FAR skilled, 4.20% FAR simple, and 5.65% EER. To simulate a signature verification system in the real world where only genuine signatures are available, OC-SVM is used for the classification phase. The proposed system handled the limitation of existing Arabic signature verification systems on skilled forgery.
Also, two public databases, UTSig and CEDAR, are used, and the proposed approach yields EERs of 7.31% and 5.53%, respectively. Results show that the proposed system outperforms existing approaches for one-class learning. However, the proposed system’s performance can be affected by an increase in the variety of features. In the future, accuracy can be enhanced through feature selection by improving crossover and mutation. Also, current feature extraction approaches can be developed to create new features.
Acknowledgement: I would like to thank CAIT of the research group Faculty of Information Science and Technology, University of Kebangsaan Malaysia.
Funding Statement: The authors received no specific funding for this study.
Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.
References
1. A. Parnandi and R. Gutierrez-Osuna, “Physiological modalities for relaxation skill transfer in biofeedback games,” IEEE Journal of Biomedical and Health Informatics, vol. 21, no. 2, pp. 361–371, 2015. [Google Scholar]
2. V. B. Semwal and G. C. Nandi, “Generation of joint trajectories using hybrid automate-based model: A rocking block-based approach,” IEEE Sensors Journal, vol. 16, no. 14, pp. 5805–5816, 2016. [Google Scholar]
3. K. Kumari and V. K. Shrivastava, “A review of automatic signature verification,” in Proc. the Second Int. Conf. on Information and Communication Technology for Competitive Strategies (ICTCS), New York, NY, USA, pp. 1–5, 2016. [Google Scholar]
4. Y. M. Al-Omari, S. N. H. S. Abdullah and K. Omar, “State-of-the-art in offline signature verification system,” in Proc. Int. Conf. on Pattern Analysis and Intelligence Robotics (ICPAIR), Kuala Lumpur, KL, Malaysia, pp. 59–64, 2011. [Google Scholar]
5. A. Majid, M. A. Khan, M. Yasmin, A. Rehman, A. Yousafzai et al., “Classification of stomach infections: A paradigm of convolutional neural network along with classical features fusion and selection,” Microscopy Research and Technique, vol. 83, no. 5, pp. 562–576, 2020. [Google Scholar]
6. I. S. Al-Sheikh, M. Mohd and L. Warlina, “A review of arabic text recognition dataset,” Asia-Pacific Journal of Information Technology and Multimedia, vol. 9, no. 1, pp. 69–81, 2020. [Google Scholar]
7. D. Wilson-Nunn, T. Lyons, A. Papavasiliou and H. Ni, “A path signature approach to online Arabic handwriting recognition,” in Proc. IEEE 2nd Int. Workshop on Arabic and Derived Script Analysis and Recognition (ASAR), London, UK, pp. 135–139, 2018. [Google Scholar]
8. A. Abdullah and W. E. Ting, “Orientation and scale based weights initialization scheme for deep convolutional neural networks,” Asia-Pacific Journal of Information Technology and Multimedia, vol. 9, no. 2, pp. 103–112, 2020. [Google Scholar]
9. O. Mersa, F. Etaati, S. Masoudnia and B. N. Araabi, “Learning representations from Persian handwriting for offline signature verification, a deep transfer learning approach,” in Proc. 4th Int. Conf. on Pattern Recognition and Image Analysis (IPRIA), Tehran, Iran, pp. 268–273, 2019. [Google Scholar]
10. H. Sun and R. Grishman, “Lexicalized dependency paths based supervised learning for relation extraction,” Computer Systems Science and Engineering, vol. 43, no. 3, pp. 861–870, 2022. [Google Scholar]
11. X. Yang, “Genetic algorithms,” in Nature-Inspired Optimization Algorithms, 1st ed., chapter 5, London, UK: Elsevier, pp. 77–87, 2014. [Google Scholar]
12. R. Guha, M. Ghosh, S. Kapri, S. Shaw, S. Mutsuddi et al., “Deluge based genetic algorithm for feature selection,” Evolutionary Intelligence, vol. 14, no. 2, pp. 357–367, 2021. [Google Scholar]
13. A. Rehman, S. Naz and M. I. Razzak, “Writer identification using machine learning approaches: A comprehensive review,” Multimedia Tools and Applications, vol. 78, no. 8, pp. 10889–10931, 2019. [Google Scholar]
14. H. Sun and R. Grishman, “Employing lexicalized dependency paths for active learning of relation extraction,” Intelligent Automation & Soft Computing, vol. 34, no. 3, pp. 1415–1423, 2022. [Google Scholar]
15. M. Stauffer, P. Maergner, A. Fischer and K. Riesen, “A survey of state of the art methods employed in the offline signature verification process,” in New Trends in Business Information Systems and Technology, 1st ed., vol. 294. Switzerland, AG: Springer, Cham, pp. 17–30, 2021. [Google Scholar]
16. N. Arab, H. Nemmour and Y. Chibani, “New local difference feature for off-line handwritten signature verification,” in Proc. Int. Conf. on Advanced Electrical Engineering (ICAEE), Algiers, Algeria, pp. 1–5, 2019. [Google Scholar]
17. B. Pilar, B. H. Shekar and D. S. Sunil Kumar, “Multi-scale local binary patterns-a novel feature extraction technique for offline signature verification,” in Proc. Recent Trends in Image Processing and Pattern Recognition (RTIP2R), Singapore, pp. 140–148, 2019. [Google Scholar]
18. F. E. Batool, M. Attique, M. Sharif, K. Javed, M. Nazir et al., “Offline signature verification system: A novel technique of fusion of GLCM and geometric features using SVM,” Multimedia Tools and Applications, vol. 79, no. 13, pp. 1–20, 2020. [Google Scholar]
19. B. H. Shekar, B. Pilar and D. S. Sunil Kumar, “Offline signature verification based on partial sum of second-order Taylor series expansion,” in Lecture Notes in Networks and Systems, 1st ed., vol. 43. Singapore: Springer, pp. 359–367, 2018. [Google Scholar]
20. B. M. Al-Maqaleh and A. M. Q. Musleh, “An efficient offline signature verification system using local features,” International Journal of Computer Applications, vol. 131, no. 10, pp. 39–44, 2015. [Google Scholar]
21. E. N. Zois, L. Alewijnse and G. Economou, “Offline signature verification and quality characterization using poset-oriented grid features,” Pattern Recognition, vol. 54, no. 7, pp. 162–177, 2016. [Google Scholar]
22. M. Ajij and S. Pratihar, “Quasi-straightness based features for offline verification of signatures,” in Proc. IEEE Int. Conf. on Identity, Security and Behavior Analysis (ISBA), New Delhi, India, pp. 1–7, 2017. [Google Scholar]
23. D. Morocho, A. Morales, J. Fierrez and R. Vera-Rodriguez, “Towards human-assisted signature recognition: Improving biometric systems through attribute-based recognition,” in Proc. IEEE Int. Conf. on Identity, Security and Behavior Analysis (ISBA), Sendai, Japan, pp. 1–6, 2016. [Google Scholar]
24. H. Kaur and E. R. Kansa, “Distance based online signature verification with enhanced security,” International Journal of Engineering Development and Research (IJEDR), vol. 5, no. 2, pp. 1703–1710, 2017. [Google Scholar]
25. S. M. Darwish and Z. H. Noori, “Distance and fuzzy classifiers alliance: The solution to off-line Arabic signature verification system for forensic science,” International Journal of Artificial Intelligence Research, vol. 2, no. 2, pp. 71–81, 2018. [Google Scholar]
26. H. Hiary, R. Alomari, T. Kobbaey, R. Z. Al-Khatib, M. A. Al-Zu’Bi et al., “Off-line signature verification system based on DWT and common features extraction,” Journal of Theoretical and Applied Information Technology, vol. 51, no. 2, pp. 165–174, 2013. [Google Scholar]
27. J. Jahandad, S. M. Sam, K. Kamardin, N. N. A. Sjarif and N. Mohamed, “Offline signature verification using deep learning convolutional neural network (CNN) architectures GoogLeNet inception-v1 and inception-v3,” in Proc. the Fifth Information Systems Int. Conf., Surabay, Indonesia, pp. 475–483, 2019. [Google Scholar]
28. S. Lai, L. Jin and W. Yang, “Online signature verification using recurrent neural network and length-normalized path signature descriptor,” in Proc. Int. Conf. on Document Analysis and Recognition, (ICDAR), Kyoto, Japan, pp. 400–405, 2017. [Google Scholar]
29. H. Rantzsch, H. Yang and C. Meinel, “Signature embedding: Writer independent offline signature verification with deep metric learning,” in Advances in Visual Computing (ISVC), 1st ed., vol. 10073. Las Vegas, NV, USA: Springer, Cham, pp. 616–625, 2016. [Google Scholar]
30. L. G. Hafemann, R. Sabourin and L. S. Oliveira, “Analyzing features learned for offline signature verification using deep CNNs,” in Proc. Int. Conf. on Pattern Recognition (ICPR), Cancun, Mexico, pp. 2989–2994, 2016. [Google Scholar]
31. S. Manna, S. Chattopadhyay, S. Bhattacharya and U. Pal, “SWIS: Self-supervised representation learning for writer independent offline signature verification,” in Proc. IEEE Int. Conf. on Image Processing (IEEE ICIP), Bordeaux, France, pp. 1–7, 2022. [Google Scholar]
32. D. Tsourounis, I. Theodorakopoulos, E. N. Zois and G. Economou, “From text to signatures: Knowledge transfer for efficient deep feature learning in offline signature verification,” Expert Systems with Applications, vol. 189, no. 3, pp. 116–136, 2022. [Google Scholar]
33. N. Xamxidin, M. Muhammat, Z. Yao, A. Aysa and K. Ubul, “Multilingual offline signature verification based on improved inverse discriminator network,” Information, vol. 13, no. 6, pp. 293, 2022. [Google Scholar]
34. T. Tuncer, E. Aydemir, F. Ozyurt and S. Dogan, “A deep feature warehouse and iterative MRMR based handwritten signature verification method,” Multimedia Tools and Applications, vol. 81, no. 3, pp. 3899–3913, 2022. [Google Scholar]
35. V. K. Jha, “Hand written signature verification using principal componenet algorthim,” B.Sc. dissertation, Galgotias University, India, 2020. [Google Scholar]
36. H. J. Jeong, K. S. Park and Y. G. Ha, “Image preprocessing for efficient training of YOLO deep learning networks,” in Proc. IEEE Int. Conf. on Big Data and Smart Computing (BigComp), Shanghai, China, pp. 635–637, 2018. [Google Scholar]
37. B. Bataineh, S. N. H. S. Abdullah and K. Omar, “Arabic calligraphy recognition based on binarization methods and degraded images,” in Proc. Int. Conf. on Pattern Analysis and Intelligent Robotics (ICPAIR), Kuala Lumpur, Malaysia, pp. 65–70, 2011. [Google Scholar]
38. H. Uoosefian, K. Navi, R. Faghih Mirzaee and M. Hosseinzadeh, “High-performance CML approximate full adders for image processing application of laplace transform,” Circuit World, vol. 46, no. 4, pp. 285–299, 2020. [Google Scholar]
39. A. Ihsan and E. Rainarli, “Optimization of k-nearest neighbour to categorize Indonesian news articals,” Asia-Pacific Journal of Information Technology and Multimedia, vol. 10, no. 1, pp. 43–51, 2021. [Google Scholar]
40. A. Y. Ebrahim, H. Kolivand, A. Rehman, M. S. M. Rahim and T. Saba, “Features selection for offline handwritten signature verification: State of the art,” International Journal of Computational Vision and Robotics, vol. 8, no. 6, pp. 606–622, 2018. [Google Scholar]
41. M. Brezocnik, M. Kovacic and L. Gusel, “Comparison between genetic algorithm and genetic programming approach for modeling the stress distribution,” Materials and Manufacturing Processes, vol. 20, no. 3, pp. 497–508, 2005. [Google Scholar]
42. Y. Chen, X. S. Zhou and T. S. Huang, “One-class SVM for learning in image retrieval,” in Proc. Int. Conf. on Image Processing, Thessaloniki, Greece, pp. 34–37, 2001. [Google Scholar]
43. I. A. Ben Abdelghani and N. E. Ben Amara, “SID signature database: A Tunisian off-line handwritten signature database,” in Proc. Int. Conf. on Image Analysis and Processing (ICIAP), Naples, Italy, pp. 131–139, 2013. [Google Scholar]
44. A. Soleimani, K. Fouladi and B. N. Araabi, “UTSig: A Persian offline signature dataset,” IET Biometrics, vol. 6, no. 1, pp. 1–8, 2017. [Google Scholar]
45. I. A. B. Abdelghani and N. E. B. Amara, “Planar multi-classifier modelling-NN/SVM: Application to off-line handwritten signature verification,” in Proc. Computational Intelligence in Security for Information Systems Conf. (CISIS), Burgos, Spain, pp. 87–97, 2015. [Google Scholar]
46. I. Abroug and N. E. B. Amara, “Off-line signature verification systems: Recent advances,” in Proc. Int. Image Processing, Applications and Systems Conf. (IPAS), Sfax, Tunisia, pp. 1–6, 2014. [Google Scholar]
47. K. Vohra and S. V. Kedar, “Signature verification using support vector machine and convolution neural network,” Turkish Journal of Computer and Mathematics Education, vol. 12, no. 1S, pp. 80–89, 2021. [Google Scholar]
48. A. Soleimani, B. N. Araabi and K. Fouladi, “Deep multitask metric learning for offline signature verification,” Pattern Recognition Letters, vol. 80, no. 12, pp. 84–90, 2016. [Google Scholar]
49. P. N. Narwade, R. R. Sawant and S. V. Bonde, “Offline handwritten signature verification using cylindrical shape context,” 3D Research, vol. 9, no. 4, pp. 48, 2018. [Google Scholar]
50. S. Masoudnia, O. Mersa, B. N. Araabi, A. H. Vahabie, M. A. Sadeghi et al., “Multi-representational learning for offline signature verification using multi-loss snapshot ensemble of CNNs,” Expert Systems with Applications, vol. 133, no. 19, pp. 317–330, 2019. [Google Scholar]
51. D. Banerjee, B. Chatterjee, P. Bhowal, T. Bhattacharyya, S. Malakar et al., “A new wrapper feature selection method for language-invariant offline signature verification,” Expert Systems with Applications, vol. 186, no. 24, p. 115756, 2021. [Google Scholar]
52. R. K. Bharathi and B. H. Shekar, “Off-line signature verification based on chain code histogram and support vector machine,” in Proc. Int. Conf. on Advances in Computing, Communications and Informatics(ICACCI), Mysore, India, pp. 2063–2068, 2013. [Google Scholar]
53. A. K. Bhunia, A. Alaei and P. P. Roy, “Signature verification approach using fusion of hybrid texture features,” Neural Computing and Applications, vol. 31, no. 12, pp. 8737–8748, 2019. [Google Scholar]
54. M. Sharif, M. A. Khan, M. Faisal, M. Yasmin and S. L. Fernandes, “A framework for offline signature verification system: Best features selection approach,” Pattern Recognition Letters, vol. 139, no. 11, pp. 50–59, 2020. [Google Scholar]
55. K. S. Manjunatha, D. S. Guru and H. Annapurna, “Interval-valued writer-dependent global features for off-line signature verification,” in Proc. Int. Conf. on Mining Intelligence and Knowledge Exploration (MIKE), Hyderabad, India, pp. 133–143, 2017. [Google Scholar]
56. S. Shariatmadari, S. Emadi and Y. Akbari, “Nonlinear dynamics tools for offline signature verification using one-class Gaussian process,” International Journal of Pattern Recognition and Artificial Intelligence, vol. 34, no. 1, pp. 2053001, 2020. [Google Scholar]
57. K. Kumari and S. Rana, “Offline signature recognition using deep features,” in Machine Learning for Predictive Analysis, 1st ed., vol. 141. Ahmedabad, India: Springer, pp. 405–421, 2021. [Google Scholar]
58. A. B. Jagtap, D. D. Sawat, R. S. Hegadi and R. S. Hegadi, “Verification of genuine and forged offline signatures using siamese neural network (SNN),” Multimedia Tools and Applications, vol. 79, no. 47–48, pp. 35109–35123, 2020. [Google Scholar]
59. S. Qiu, F. Fei and Y. Cui, “Offline signature authentication algorithm based on the fuzzy set,” Mathematical Problems in Engineering, vol. 2021, no. 1, pp. 5554341, 2021. [Google Scholar]
60. C. Wencheng, G. Xiaopeng, S. Hong and Z. Limin, “Offline Chinese signature verification based on AlexNet,” in Proc. Int. Conf. on Advanced Hybrid Information Processing (ADHIP), Harbin, China, pp. 33–37, 2017. [Google Scholar]
Cite This Article
 Copyright © 2023 The Author(s). Published by Tech Science Press.
Copyright © 2023 The Author(s). Published by Tech Science Press.This work is licensed under a Creative Commons Attribution 4.0 International License , which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.


 Submit a Paper
Submit a Paper Propose a Special lssue
Propose a Special lssue View Full Text
View Full Text Download PDF
Download PDF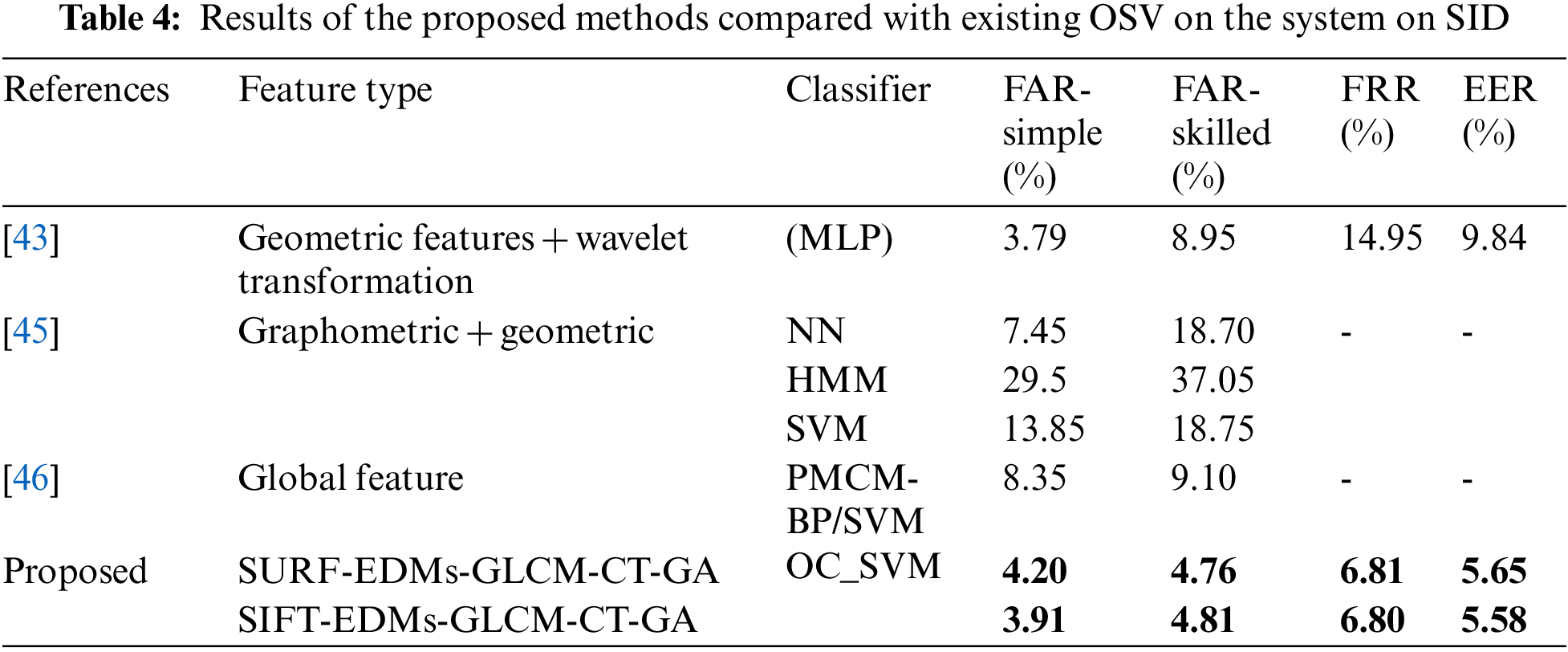
 Downloads
Downloads
 Citation Tools
Citation Tools