Multi-Objective Optimization of External Louvers in Buildings

1  Introduction

Energy consumption is a challenge for global contemporary architecture in general, and for developing-country contemporary architecture in particular [1,2]. Modern attention to climate and its role in the architectural design process is associated with significant changes [3,4]. Today, outstanding architecture has been considered [5], which is the result of estimating and measuring a wide range of variables. The importance of paying attention to the position of daylight in intelligent energy consumption is growing [6]. It has become necessary due to rising energy demand, scarcity of fossil resources, pollution, global warming and the greenhouse effect, and the need to limit fossil fuel consumption and focus on renewable energy. Today, removing heat from lighting systems and lighting residential and commercial spaces both require significant amounts of energy. Using sunlight as a source of illumination has numerous advantages, both economically and environmentally.

Improving the comfort and convenience of interior space by optimizing natural light levels is now one of the most important issues in space reconstruction and improvement, particularly in office buildings [7]. With rising energy consumption, the need for multi-objective optimization and efforts to reduce consumption is growing, particularly in developing countries, prompting architects to excel in architecture and make the best use of renewable energy [8]. It not only provides a favorable environment for users, but it also reduces energy consumption for cooling and heating the environment [9]. Fluorescent lamps emit approximately 75 lm/W of light, whereas incandescent bulbs emit approximately 20 lm/W of light. As a result, when compared to equivalent electric lighting, daylighting generates only half to a fifth of the heat, significantly reducing the building′s cooling burden [10]. Lighting energy consumption can be reduced by up to 65 percent by utilizing active and passive systems that utilize natural light and electronic controls [11]. Because electric lighting can account for 25%–40% of a commercial building’s energy requirements, the combined savings from reduced lighting and cooling loads can be significant. As a result, controlling the amount of light entering the space is an important factor in improving energy efficiency in the building, and since the only part of the building that directly enters the sun is the window, the use of louvers to control the penetration is recommended. The passage of sunlight into space is critical [12]. The use of daylight in a wide range of Indonesian cities, including Jakarta, is noteworthy due to its convenient geographical location and having many sunny hours throughout the year [13]. The effects of the reflection coefficient of skylights were investigated using computer simulation with radiance, and the light coefficients in nearby spaces were reported in the form of formulas with varying reflection coefficients.

In this study, Ant Colony Optimization (ACO) and algorithmic programming will be utilized in order to make an estimate of the dimensions and technical specifications of external louvers, as well as to propose a model for designing the southern openings of educational space in order to maximize energy efficiency and consumption, as well as to provide the necessary light level for indoor space. In order to attain this purpose, there are three crucial actions that must first be taken: first, the background of the subject must be evaluated; second, effective parameters must be retrieved; and third, these parameters must be simulated and optimized.

2  Materials and Methods

In this research, the ACO algorithm was designed. The problem is defined and structured in the form of a graph in the first step, and the amount of initial pheromone that must be placed on each graph in order to start the algorithm is evaluated in the second step. Ants defined the mechanism of graph navigation in the third step, which is known as path selection [14]. The suitability of the ants’ paths was evaluated in the fourth step, and the pheromones of all the ants’ pathways were updated based on their competence. Finally, the convergence condition was added to bring the algorithm to a halt.

2.1 Structuring Solutions in Graphs

The multi-objective optimization method was created using the approach of archives to the dominant solutions, while taking into account the fundamental structure of the ants optimization algorithms. The main solution in this technique is to assign an ant society to each of the goals of an optimization problem. What matters is how the communities relate to the aforementioned goals. At each computing step in the current method, all of the solutions developed in one society are transferred to the opposite community, where the ants of that community attempt to improve the answers based on their criteria. The first step in using the ACO metaheuristic algorithm to solve problems is to graph the existing solutions. Each column in the graph represents a cube block. In fact, a node that the ant must pass through [15,16]. As previously stated, our goal is to reverse the density model’s achievement at various depths. According to the graph generated by this algorithm, the ants construct a variety of models by traversing each cube block and assigning a value as a density difference to that cube. He finally selects the best model as the final answer after examining each of the models in each iteration.

2.2 Primary Pheromone

To begin the algorithm, consider the pheromone value as the initial value () on each node of the graph. To increase the level of exploratory search at the start of the algorithm, the path's initial pheromones are assumed to be superimposed. As a result, the initial search phase will be very exploratory, preventing the algorithm from achieving early or local convergence, because, despite the high pheromone, the algorithm will have enough time to search for a wider area of probability space.

2.3 Select the Path and Navigate the Graph

To decide on the different density values for each cube block, a relation that not only works on the basis of probability but also has random choices must be designed. Four relations were created for this purpose based on the intended purpose [17]. Using this relationship, the ants can decide which node to go to next based on probability or chance.

Gi={Max{phi(t)} if q0>qiJ Otherwise (1)

{phi(t)} is the amount of pheromone on the nth node in the t-th iteration, and Max{phi(t)} indicates the selection of the node that has the most pheromone accumulated on it. In the above relation, J is a random function, in fact, it is a vector function with dimensions of the number of rows of graphs, each of which is attributed to one of the nodes of a column of the graph [18]. This vector’s numbers are filled at random, so that all of its numbers are zero and only one of its assets is one. The ants should visit the node to which the number one is assigned as the next node. In the preceding relationship, qi is a random value in the interval [0,1] that is generated for each cube block in each iteration and is compared to q0, which is the problem parameter. Each ant traverses the entire graph to generate a matrix, which can be computed by putting this matrix in the relation of three anomalies for all stations.

2.4 Fit Calculation (Value Function)

The fit function is obtained by applying an appropriate conversion to the target function, which is the function to be optimized. This function assigns a numerical value to each ant solution to determine its quality. The higher the quality of the answer, the more suitable it is, and the more likely its nodes will participate in the paths made by the ants in subsequent repetitions. Greater fit will be synonymous with maximization or minimization of the objective function, depending on whether the problem is maximization or minimization. Because determining the density of each cube block follows the maximization of the function, the minimization problems must be converted to maximization. That is, the maximum pheromone (maximum fit) attributed to the nodes present (density of each block) in the matrix structure should be the minimum sum of the absolute magnitude of errors (sum of the absolute magnitude of the anomalous difference calculated from the measured anomaly) at all observation stations on the ground be pertinent Finally, the fitness function used in this study was designed using Eq. (2) by performing various tests and examining the relationship between the sum of the absolute magnitude of errors and the amount of pheromones attributed to the nodes [19].

Δphik=1(eSum of Erorr )0.5

Sum of Error =∑i=1N|gobservation −gCalculate |(2)

In the above relation, N indicates the number of observation stations and Δphik the amount of pheromone (suitability) attributed to the density selected for the cube blocks by the second ant. gobservation  is an anomaly of gravity measured by a gravimeter that enters the algorithm as an observation. gCalculate  shows the anomaly of gravity calculated from Eq. (3). Using the high fit function, the lower the total value of the absolute error of the path traversed by an ant, the higher the amount of pheromone calculated to belong to the path traversed by that ant, and vice versa. The advantage of using this function over the other methods mentioned is that the fit function with an exponential behavior leads the ants to navigate through nodes that give us high accuracy, the relationship between the sum of the absolute magnitude of the errors. The amount of pheromone calculated by Eq. (4) is not a linear relationship but an exponential relationship, and the closer the absolute value of the error is to zero, the more strongly the amount of competency calculated [20].

2.5 Evaporation of Pheromones

Evaporation of pheromones in this algorithm, in proportion to the pheromone on each node, is done from all nodes, Eq. (3):

phi(t)=(1−v)phi(t−1),∀i∈G(3)

In the above relation, phi(t) of the pheromone of node i in the repetition of t th and phi(t−1) of the pheromone of the node i in the repetition of t − 1. M May i < 1 Parameter v is used to prevent the unlimited accumulation of pheromones on a node and enables the algorithm to forget past bad decisions. Using such a procedure to evaporate pheromones will make the algorithm more exploratory, because by using this method, evaporation from nodes that have more pheromones will occur more than from nodes that have less pheromones [21].

2.6 Pheromone Update

After the pheromone evaporates from all nodes, it is time to update the pheromone in the nodes surveyed by the ants.

phi(t)=phi(t−1)+∑k=1mδphik,∀i∈G(4)

In the above relation Δphik is the amount of pheromones that the km ant leaves on the nodes that it has passed along its path, and this value is adopted by the km ant in proportion to the degree of competence of the selected solution. Using the equation for evaporation and pheromone 7 and 6 will cause more pheromones to accumulate on the optimal nodes after a while and as a result they will have a better chance of being selected by the next ants and the non-optimal nodes will have less pheromones and vice versa. They also have less to choose from next ants [22].

2.7 Convergence Condition

Very different modes can be considered for the algorithm’s convergence condition in meta-heuristic algorithms, and this condition varies depending on the problem conditions. Again, the algorithm’s convergence condition is such that, in each iteration, if 60% of the ants follow a single path, and we do not have the result of improvements over previous iterations, the path chosen by at least 1% of the ants is accepted as a convergence path. As a result, the algorithm will continue until this condition is met, and it will stop as soon as this condition is met. Fig. 1 depicts the algorithm's implementation process [23].

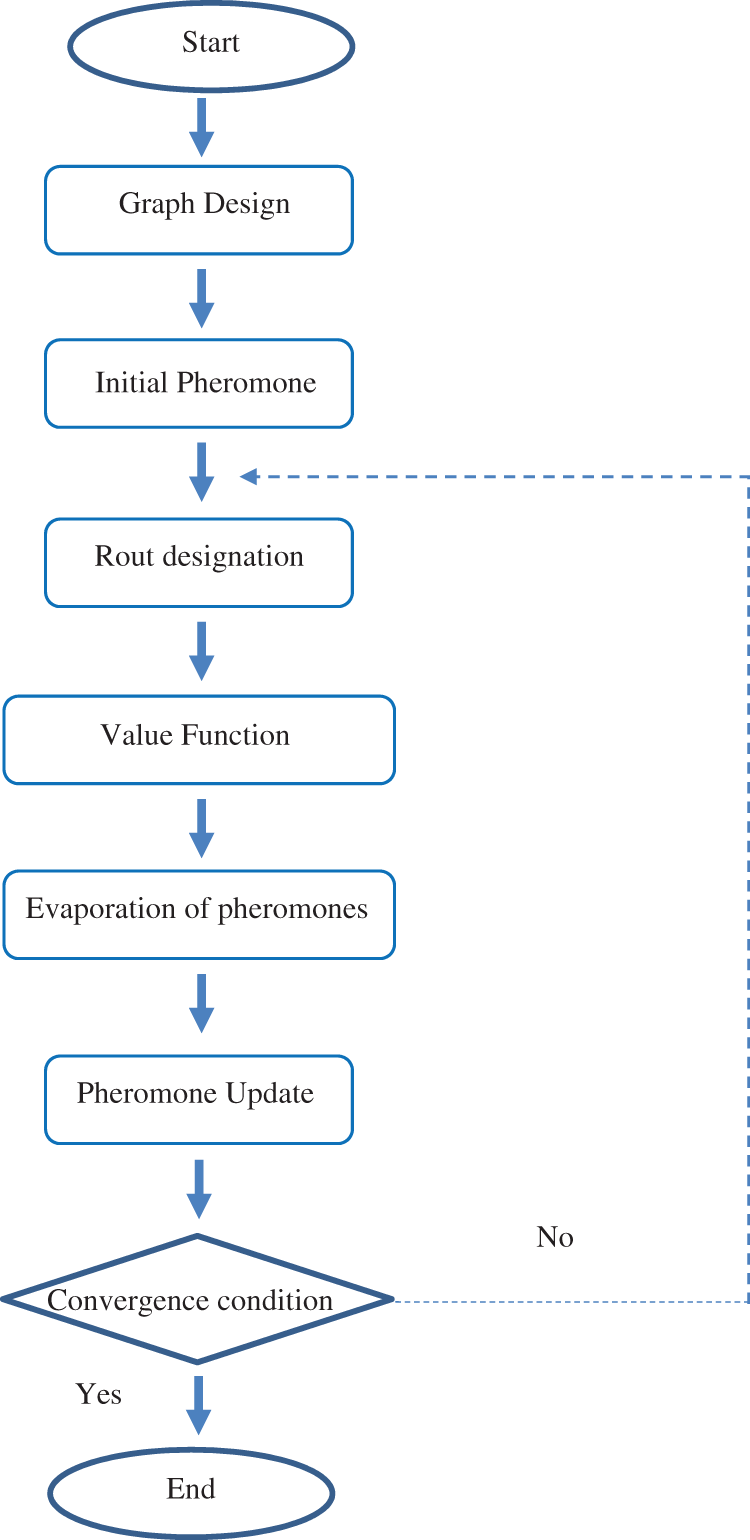
Figure 1: AOC designed for inverse modeling

2.8 Simulated Space Specifications

All simulations are run for all days of the year and from 8:00 AM to 1:00 PM for various states of variables in a specific period. Simulations that produce the desired outcome are examined. It should be noted that the amount of light in the simulations is also measured at a height of 85 cm (the height of the study surface in class) and under Jakarta, Indonesian climatic conditions.

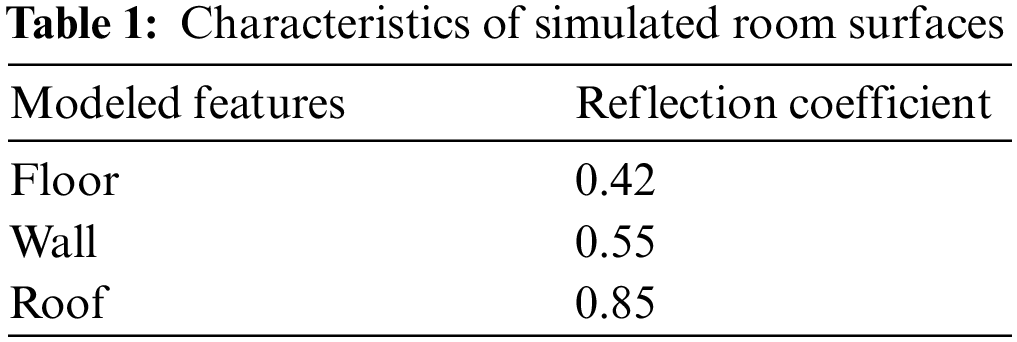
For Revit simulation, use a class with dimensions of 800 cm × 600 cm and a height of 300 cm, as well as windows with dimensions of 160 cm × 160 cm (35% of the wall area) that are 85 cm from the floor on the south wall (Fig. 2). The window’s dimensions to the external wall have been estimated to be 30% to 40%. In this case, the window can minimize energy exchange while still providing adequate lighting. As a result, the window area accounts for 35% of the wall area. The interior walls and ceiling were simulated with materials that were very white in wall texture, and the space floor was made of materials that were close to ceramic and white. The reflection coefficient of this room's interior surfaces is as follows: (Table 1).

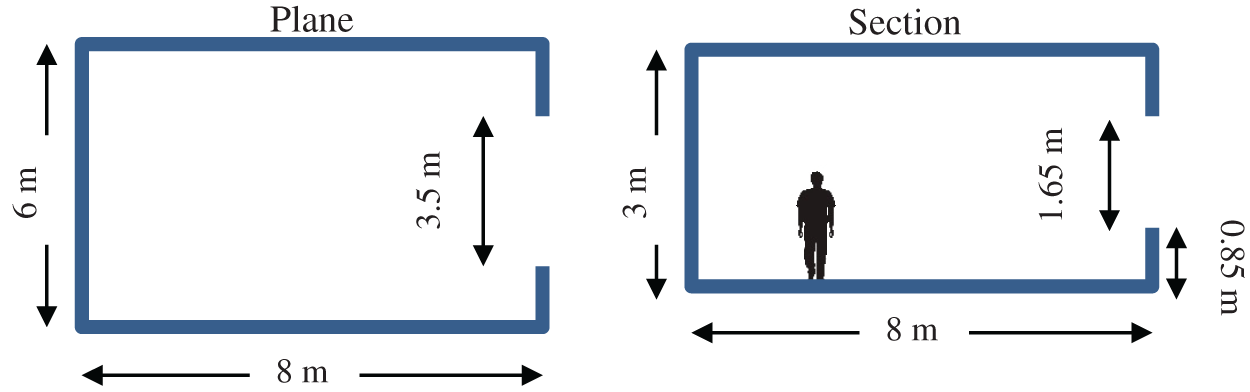
Figure 2: Characteristics of the simulated space in plane and section of room

Jakarta weather information is available on the website of the Office of Energy Efficiency and Renewable Energy, which has been used for simulation. The location of the shutters in the external state and the amount of light required in the spaces with different uses, the amount of light in the space is 350–550 lux. It should be noted that the type of shutter adjustment is based on climate. In this study, the climate of Jakarta with a longitude of 106.8 and a latitude of −6.2 is examined. Since the working hours in Jakarta class are from 8:00 AM–01:00 PM, in the simulation, the same time range is considered for working hours. Therefore, in the ACO algorithms, the objective function (brightness) is considered according to the educational space use of 350–550 lux space in the horizontal level 85 cm above the floor level (studding level). This surface is divided into 30 by 30 cm squares. The goal is to find the optimal amount of variables for the design of louvers that have a brightness level of 350–500 lux in 65% of the time of desk and work surface productivity.

2.9 Specifications of the Simulated Louvre System

The angle of rotation, number, depth, distance of the louvers from the window, and reflection of the louvers were extracted after testing the sensitivity of the parameters. These five parameters comprise a design algorithm in which the shape of the Louvre changes as the parameters are changed. The following parameters and the range of their changes are defined (Fig. 3):

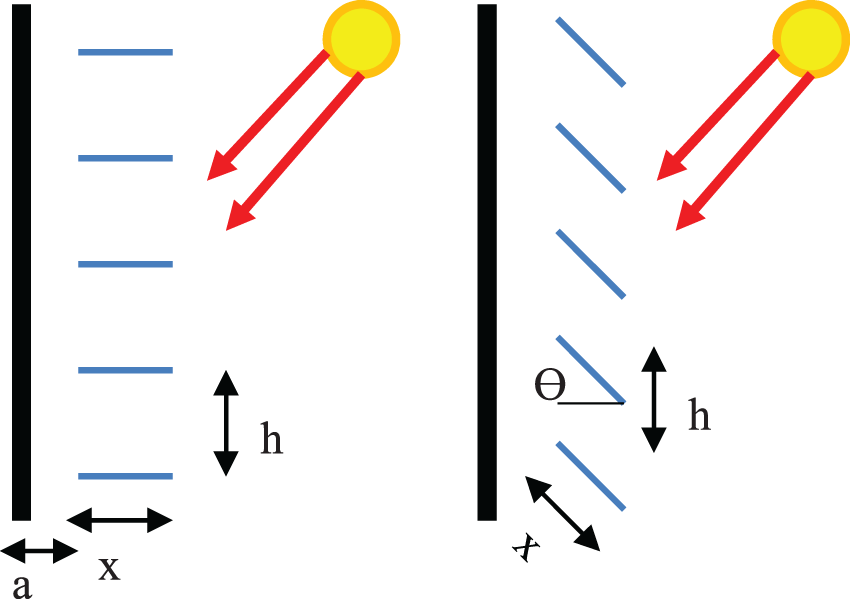
Figure 3: Effective parameters in the design of louvers

The distance of the louvers from the glass surface (a), which in this study varies between 0–40 cm with distances of 15 cm. Depth of louvers (x) which in this study is defined according to the degree of overlap of louvers between 15–45 cm with distances of 15 cm. The angle of rotation of the louvers (ϴ) varies between 0–90 degrees with distances of 10 degrees. The number of louvers (n) in this study is defined between 2 to 10 according to the dimensions of the window, which also determines the distance between the louvers (h). The reflection of the Louvres (R) varies in the range between 0%–100%.

3  Results and Discussion

The origin of AOC algorithm is inspired by the effect that ants have on movement. Pass. Many species of ants leave a substance called a pheromone on the ground in their path of motion, creating an effect that is used to mark the path taken. This effect is their communication tool, and in fact, by sensing the effects of the pheromone, other food-seeking ants can find their way to the food source that others have discovered [24].

The ability of ants to adapt to changes in their environment is an important aspect of ant colony life. For instance, when the shortest path is blocked by an obstacle. They can no longer track the pheromone’s effect. As a result, some ants choose to turn right while others choose to turn left at random. Ants that take the shorter path at random amplify the previous pheromone faster than ants that take the longer path. As a result, more ants choose the shorter path with more pheromones. Most ants quickly choose a new shorter path as a result of this positive feedback [25,26].

The optimization problems in the ACO algorithm are organized as a graph with vertices and edges. In this graph, problem states are the sum of all possible ants to navigate. In the ACO algorithm, each possible solution is represented as a graph with edges and nodes. The amount of pheromones attributed to a node determines how many times it is selected by ants. The amount of pheromones on each node is proportional to the degree of competence of that node, and thus the number of times it is selected by ants is determined. Furthermore, the pheromone from each node evaporates from all nodes [27,28].

The window without the Louvre is tested first as a base, and then the various dimensions and angles of the Louvre are examined in various conditions. At this stage, the simulation space is tested and simulated as a base mode without the Louvre light control system, and the brightness of the space at the working level (85 cm above the ground) is determined during the summer revolution, winter solstice, and equinox.

It is demonstrated by Fig. 4 that an excessive amount of light enters the room, which, in addition to producing glare, also causes the room’s temperature to rise, while certain areas of the room do not receive an adequate amount of light. This pattern was modeled for all four seasons, and each simulation showed the same effect in terms of the light quality in space (glare and a lack of light in certain areas of the space). After that, the solution of putting louvers was incorporated into the simulation, and its many configurations were examined for their effectiveness. As a result, the test area was replicated in the Revite environment at the beginning without taking into account the Louvre system as the starting point. After that, the simulation volume is loaded so that the parametric louvers can be designed and the parameters that are defined in the Grasshopper plugin may be determined. For each of the variables, a particular interval has been created; this period shifts depending on the Louvres′ shape and the amount of effect they have. The Galapagos plugin is introduced to the algorithm so that evolutionary calculations may be used to find the most effective ways for variables to interact with one another. This allows the variables that have been defined to be optimized. The simulation and optimization procedure is depicted in a concise manner in Fig. 5. With the assistance of parametric simulation of daylight and optimization of effective parameters utilizing ACO algorithm, the goals of this study were to optimize the daylight control system (Louvre) and to determine the design requirements of this type of system. Both of these goals were to be accomplished with the help of this study. As a result, numerous distinct parameters are altered all at once, and the outcomes are utilized. The ultimate goal of enhancing the performance of this kind of system is to reduce energy consumption while simultaneously maximizing the amount of natural light that is let in.

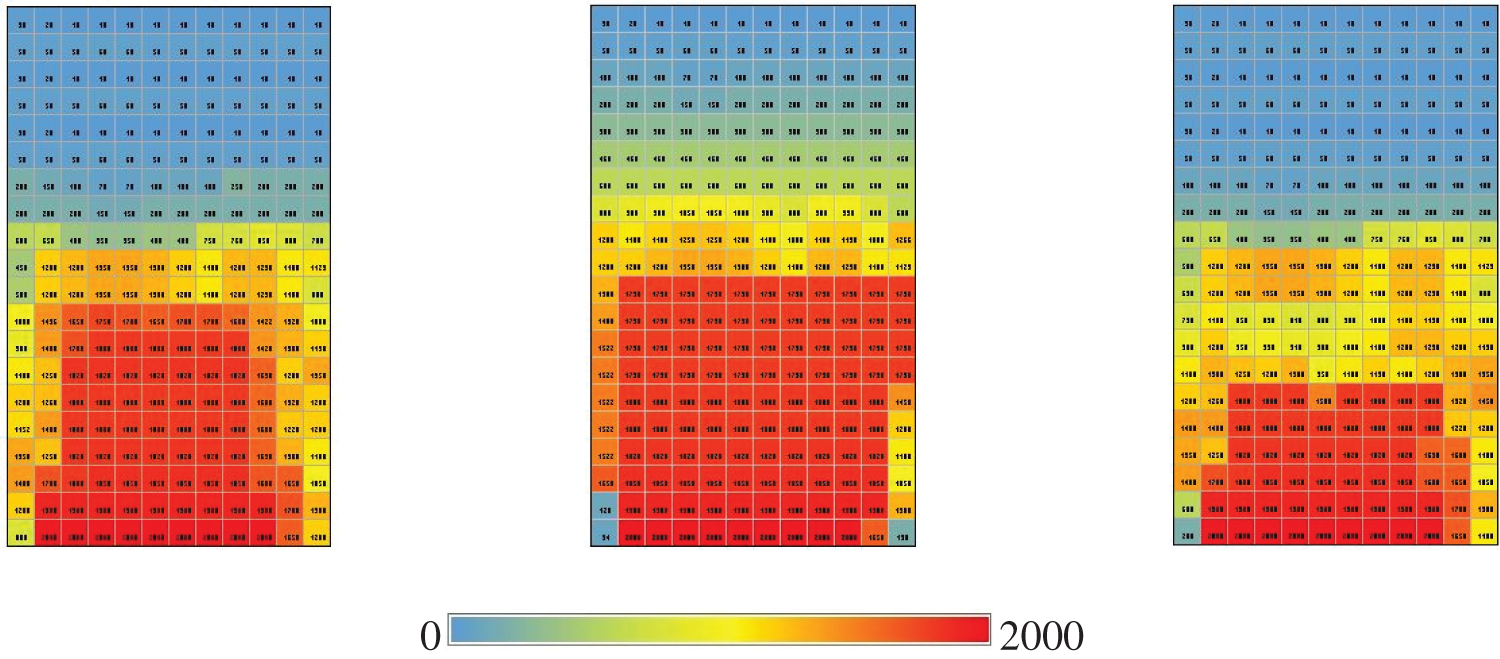
Figure 4: The average brightness of the simulated sample across each of the four seasons

Figure 5: The processes while highlighting a variety of simulation and optimization tools explaination

Although the number of variables and the large number of cases make it impossible to study all compounds in a multivariate function, metric simulation allows the study of daylight performance by changing the parameters. In this study, complex geometry models T and L with different densities were used to further evaluate the efficiency of the ACO algorithm designed for inverse linear modeling. 0 (ACO algorithm regulatory parameters), q0 (ACO algorithm regulatory parameters), and are 0.5, 0.6, and 0.08, respectively. According to the use of the simulated space, the intervals between 350 to 550 have been selected as optimal conditions, in order to achieve the most optimal states, the intervals between 360–440, including 50 modes, were selected as optimal conditions (Fig. 6).

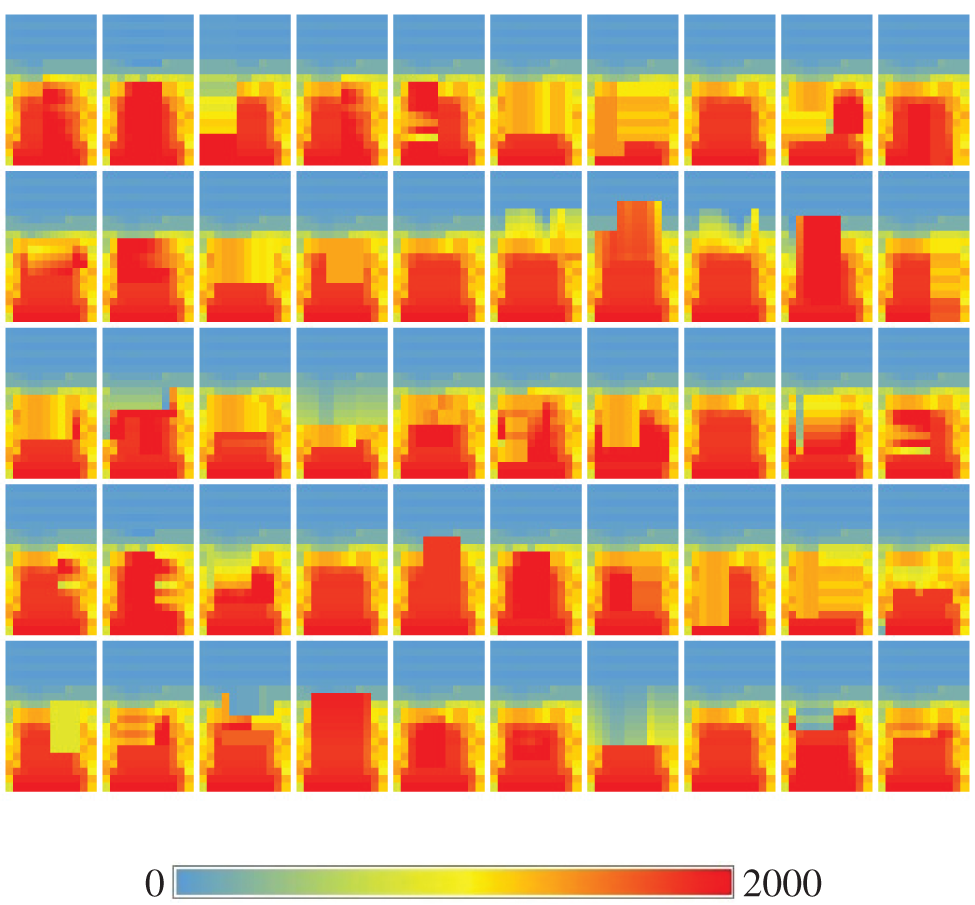
Figure 6: The results of applying the brightness optimization to the simulated sample

The distance of the louvers from the glass surface (a) in the simulation performed in the intervals between 0–50 cm with distances of 10 cm has changed. Among the 53 final optimal samples, the distance of the louvers from the window was 0 in 38.8% of cases and 10 cm in 38.4% and 20 cm in 25.5% of the samples. In none of the desirable cases, a distance of 40 and 50 cm has been recorded. Depth of louvers (x) which in this study is defined according to the degree of overlap of louvers between 10–50 cm with distances of 10 cm. Among the 53 optimal final samples, in 37.9% of the cases, the depth of the louvers was 2.13 in, 30 cm in 1.30 in, 20 cm in 10 cm, in 13.3% in 40 cm and 11.9% in 50 cm have been registered. The angle of rotation of the Louvres (ϴ) in the simulation varied between 0–90 degrees with distances of 15 degrees. Cases of 60 degrees were recorded in 14.6% of 45 degrees, in 16.1% of 30 degrees and in 12.2% of cases of 15 degrees; other angles were repeated in less than 10 samples. The number of louvers (n) is defined between 2 and 10 according to the dimensions of the window. The results of the analysis of 53 simulated favorable conditions show that in 20.7% of cases the number of Louvres is 4, in 17.9% of cases 5, in 11.2% of cases 6, in 14.2% of cases 3 and other items are small. The reflection coefficient of the Louvres (R) varies between 0%–100%. The results of the analysis of 53 simulated favorable conditions show that in 77.3% of cases 0%, in 18.8% of cases 10% and in 3.9% of cases the reflection rate of 20% was recorded. The number of louvers (n) is defined between 2 and 10 according to the dimensions of the window. The results of the analysis of 53 simulated favorable conditions show that in 20.7% of cases the number of louvers is 4, in 16.9% of cases 5, in 13.2% of cases 6, in 13.2% of Items 3 and other items are small. The reflection coefficient of the Louvres (R) varies between 0%–100%. The results of the analysis of 53 simulated favorable conditions show that in 77.3% of cases 0%, in 18.8% of cases 10% and in 3.7% of cases the reflection rate of 20% was recorded. In none of the cases was the reflection rate 30% to 100% recorded.

Table 2 represents the correlation between five independent variables and dependent variables using Kendall Tau test. The highest correlation is related to the two independent variables of louver reflection coefficient (R) and louver rotation angle (ϴ) with a confidence coefficient of 0.81 and a direct correlation coefficient of 0.59 Between the two independent variables, the depth of the louvers (x) and the distance of the louvers from the window (a) with a confidence coefficient of 0.99, a direct correlation coefficient of 0.48 was recorded. Between two independent variables, the distance of the Louvres from the window (a) and the angle of rotation of the Louvres (ϴ), a correlation coefficient of −0.55 has been recorded indirectly with a confidence coefficient of 0.98, and between the two independent variables, the depth of the Louvres (x) and the angle of rotation of the Louvres (ϴ) With a reliability coefficient of 0.99, a correlation coefficient of −0.4 has been recorded indirectly. Regarding the correlation between the independent variables and the dependent variable, shows that the average correlation of the brightness level in terms of lux (dependent variable) with the number of louvers (n) has a correlation coefficient of 0.052 and a direct relationship with the depth of the louvers (x). The correlation coefficient is 0.59 and the indirect relationship with the distance of the Louvre from the window (a) is the correlation coefficient of 0.32 and the indirect relationship.

4  Conclusion

According to the simulations that were carried out during the summer revolution, the winter revolution, the spring equinox, and the autumn equinox in the city of Jakarta, the amount of lighting was greater than what was required for educational space (−400). This results in an increase in the amount of energy required to cool the environment. As a result, the application of light control systems like louvers plays a vital part in the process of controlling and improving the quality of the light that is available within. The results of both the simulation and the installation of external louvers show that the installation of this system in the southern wall of the building in the city of Jakarta has a significant effect on controlling the amount of incoming light and lighting level of educational space for energy efficiency and intelligent consumption, as well as providing the required light level inside the building. It has quite a few. According to the findings of this research, there are five key considerations that need to be made when designing external louvers. These include the number of louvers, the depth of the louvers, the angle of rotation of the louvers, the distance of the louvers from the window, and the reflection coefficient of the louvers. The results of the study that simulated 2000 different modes in the city of Jakarta show that the best reflection from the louvers is between 0 and 15 percent, and the optimal distance between the louvers and the window is in the range of 0 to 18 centimeters. These findings are based on the findings of the study that was conducted in Jakarta.

Funding Statement: The authors received no funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

    1. A. Eltaweel, M. A. Mandour, Q. Lv and Y. Su, “Daylight distribution improvement using automated prismatic louvre,” Journal of Daylighting, vol. 7, no. 1, pp. 84–92, 2020. [Google Scholar]

    2. A. Arslanyilmaz, “Book review: Task-based language learning and teaching with technology,” The EuroCALL Review, vol. 31, no. 1, pp. 134–136, 2014. [Google Scholar]

    3. K. C. Chu, D. J. Horng and K. C. Chang, “Numerical optimization of the energy consumption for wireless sensor networks based on an improved ant colony algorithm,” IEEE Access, vol. 7, pp. 105562–105571, 2019. [Google Scholar]

    4. F. Dahan, K. El Hindi, H. Mathkour and H. Alsalman, “Dynamic flying ant colony optimization (DFACO) for solving the traveling salesman problem,” Sensors (Switzerland), vol. 19, no. 8, pp. 1837, 2019. [Google Scholar]

    5. X. Dai, S. Long, Z. Zhang and D. Gong, “Mobile robot path planning based on ant colony algorithm with a∗ heuristic method,” Frontiers in neurorobotics, vol. 13, pp. 15, 2019. [Google Scholar]

    6. D. A. Friedman and E. Søvik, “The ant colony as a test for scientific theories of consciousness,” Synthese, vol. 198, no. 2, pp. 1457–1480, 2021. [Google Scholar]

    7. K. Kosutova, T. van Hooff, C. Vanderwel, B. Blocken and J. Hensen, “Cross-ventilation in a generic isolated building equipped with louvers: Wind-tunnel experiments and CFD simulations,” Building and Environment, vol. 154, no. 9, pp. 263–280, 2019. [Google Scholar]

    8. N. A. Kyriakakis, M. Marinaki and Y. Marinakis, “A hybrid ant colony optimization-variable neighborhood descent approach for the cumulative capacitated vehicle routing problem,” Computers & Operations Research, vol. 134, pp. 105397, 2021. [Google Scholar]

    9. Q. Li, Y. Wang, L. Ma, M. Arici, D. Li et al., “Effect of sunspace and PCM louver combination on the energy saving of rural residences: Case study in a severe cold region of China,” Sustainable Energy Technologies and Assessmentss, vol. 45, no. 3, pp. 101126, 2021. [Google Scholar]

  10. Y. Liu and B. Cao, “A novel ant colony optimization algorithm with levy flight,” IEEE Access, vol. 8, pp. 67205–67213, 2020. [Google Scholar]

  11. Z. Liu, X. Wang, K. Lu and D. Su, “Retraction: Automatic arrhythmia detection based on convolutional neural networks,” Computers, Materials & Continua, vol. 63, no. 2, pp. 1079, 2020. [Google Scholar]

  12. Z. Liu, X. Wang, C. Sun and K. Lu, “Retraction: Implementation system of human eye tracking algorithm based on FPGA,” Computers, Materials & Continua, vol. 62, no. 3, pp. 1487, 2020. [Google Scholar]

  13. H. Lloyd and M. Amos, “Solving sudoku with ant colony optimization,” IEEE Trans. Games, vol. 12, no. 3, pp. 302–311, 2020. [Google Scholar]

  14. T. H. Nguyen and R. Grishman, “Graph convolutional networks with argument-aware pooling for event detection,” 32nd AAAI Conference on Artificial Intelligence, AAAI 2018, vol. 32, no. 1, pp. 5900–5907, 2018. [Google Scholar]

  15. Q. Luo, H. Wang, Y. Zheng and J. He, “Research on path planning of mobile robot based on improved ant colony algorithm,” Neural Computing and Applications, vol. 32, no. 6, pp. 1555–1566, 2020. [Google Scholar]

  16. M. Neroni, “Ant colony optimization with warm-up,” Algorithms, vol. 14, no. 10, pp. 295, 2021. [Google Scholar]

  17. T. Nurcahyadi and C. Blum, “Adding negative learning to ant colony optimization: A comprehensive study,” Mathematics, vol. 9, no. 4, pp. 1–23, 2021. [Google Scholar]

  18. A. I. Palmero-Marrero and A. C. Oliveira, “Effect of louver shading devices on building energy requirements,” Applied energy, vol. 87, no. 6, pp. 2040–2049, 2010. [Google Scholar]

  19. Z. Ruan, H. Luo, W. Lin and J. Wang, “Erratum: Mitigating content caching attack in NDN,” Computers Materials & Continua, vol. 56, no. 3, pp. 483–499, 2018. [Google Scholar]

  20. A. Sadeghianjahromi, S. Kheradmand, H. Nemati and C. C. Wang, “Optimization of the louver fin-and-tube heat exchangers↔a parametric approach,” Journal of Enhanced Heat Transfer, vol. 27, no. 4, pp. 289–312, 2020. [Google Scholar]

  21. P. Sriromreun and P. Sriromreun, “An optimum design for air filter housing-louver: Enhancing filter life-time,” Case Studies in Thermal Engineering, vol. 21, no. 9, pp. 100701, 2020. [Google Scholar]

  22. Y. Tao, X. Fang, S. Setunge, J. Tu, J. Liu et al., “Naturally ventilated double-skin façade with adjustable louvers,” Solar Energy, vol. 225, pp. 33–43, 2021. [Google Scholar]

  23. L. Vinet and A. Zhedanov, “A ‘missing’ family of classical orthogonal polynomials,” Journal of Physics A: Mathematical and Theoretical, vol. 44, no. 8, pp. 085201, 2011. [Google Scholar]

  24. A. Molajou, P. Pouladi and A. Afshar, “Incorporating social system into water-food-energy nexus,” Water Resources Management, vol. 35, no. 13, pp. 4561–4580, 2021. [Google Scholar]

  25. M. Sadeghzadeh, M. H. Ahmadi, M. Kahani, H. Sakhaeinia, H. Chaji et al., “Smart modeling by using artificial intelligent techniques on thermal performance of flat-plate solar collector using nanofluid,” Energy Science & Engineering, vol. 7, no. 5, pp. 1649–1658, 2019. [Google Scholar]

  26. M. Zamen, A. Baghban, S. M. Pourkiaei and M. H. Ahmadi, “Optimization methods using artificial intelligence algorithms to estimate thermal efficiency of PV/T system,” Energy Science & Engineering, vol. 7, no. 3, pp. 821–834, 2019. [Google Scholar]

  27. M. Sheikholeslami, M. Jafaryar, E. Abohamzeh, A. Shafee and H. Babazadeh, “Energy and entropy evaluation and two-phase simulation of nanoparticles within a solar unit with impose of new turbulator,” Sustainable Energy Technologies and Assessments, vol. 39, no. 6, pp. 100727, 2020. [Google Scholar]

  28. A. Molajou, V. Nourani, A. Afshar, M. Khosravi and A. Brysiewicz, “Optimal design and feature selection by genetic algorithm for emotional artificial neural network (EANN) in rainfall-runoff modeling,” Water Resources Management, vol. 35, no. 8, pp. 2369–2384, 2021. [Google Scholar]