Weighted De-Synchronization Based Resource Allocation in Wireless Networks

1  Introduction

Over the last decade, mobile wireless communication technology has undergone spectacular development globally. The upcoming wireless communication systems are expected to produce artificial intelligence fusing applications which will provide high-quality services ranging from wireless multimedia to autonomous applications [1]. In particular, the ongoing demand for wireless devices and tremendous growth in the installation of data-consuming internet of things (IoT) services will additionally reduce the limited wireless resources [2]. Thus, methods for efficiently managing wireless resources are required to address the ever-fast changing and growing number of devices in the network. The essential considerations in designing a resource allocation method include fairness in QoS, scalability, and decentralization [3].

Fairness is a significant factor for resource allocation in wireless networks because consumers use radio wireless resources in diverse applications such as intelligent transportation, smart environment monitoring, fuel station, health care unit, water management, or smart rural village [4,5], and therefore the consumers have different demands for wireless resources [6]. Algorithms for fair resource allocation can be categorized into two broad types: centralized and distributed. Centralized algorithms require at least a central node as a coordinator to manage the resources, whereas distributed algorithms can work without relying on any particular central node as long as all nodes maintain a connection in the same network [7]. In resource allocation, weight generally refers to priorities based on criteria such as the willingness to pay for resources, importance of the task or service. In many circumstances, the appropriate notion of fairness is something other than the uniform sharing of resources. In wireless networks, the importance of weighted resource allocation is emphasized when nodes in a network require a different QoS. Weighted resource allocation provides resources proportional to the node requirements to alleviate QoS issues because assigning an equal amount of resources in a weighted network can degrade QoS or cause unfair QoS. The consequence of unfair QoS levels is unbalanced service provision and potential service suspension due to resource starvation. Therefore, by allocating resources according to the users’ needs, a fair QoS can be achieved [8].

With a large network environment, the number of nodes can vary rapidly according to the network dynamics, such as channel conditions, node mobility, and services, requiring a careful architecture and management of the network and resources [9,10]. In such a scenario, it is more efficient to run the resource allocation algorithm in a distributed manner rather than in a centralized way. Distributed resource allocation allows each node to use the needed resource while reserving some resources for the rest of the nodes in the network. Plus, distributed resource allocation reduces the network overhead and complexity. Many researchers have conducted studies on weighted and non-weighted resource allocation in wireless networks. To accomplish weighted fairness in a distributed network environment, the authors in [11] proposed a weighted de-synchronization-based link scheduling mechanism (WDESYNC-TDMA), in which the concept of traffic weight is additionally applied to the conventional DESYNC [12]. Through simulation, WDESYNC-TDMA can achieve self-scheduling task according to the traffic load. In [13], the authors applied the Kuramoto synchronization model to address load balancing in base stations (BS). The proposed method involves transferring the load from BS and offloading it to access points (AP). The simulation results show a quick reduction in difference load level among BS and the excessive load is offloaded to AP. The authors in [14] applied an altered Kuramoto model to desynchronize the resource in wireless network. The study focuses on using the desynchronization of the Kuramto model and map it to time division multiple access (TDMA) timeslot. The results suggest short convergence time and fairly allocated resources among users. In [15], to avoid congestion and provide weighted fairness, the authors developed an adaptive rate-based congestion control. The method involves flexibly determining the utilisation factors based on gradient method such that the lower rate is determined by the source with smaller value of round trip time. According to [16], a novel decentralized rate control-based congestion avoidance protocol was proposed to achieve weighted fairness along with energy efficiency. The protocol adaptively calibrates the total rate of the data entering nodes while achieving global weighted fairness. In [17], the authors studied weighted fairness in a caching system using Markov chain. The proposed method is called weighted fair caching which provides owners fairness or enables them to manage the resource allocation among the content.

With recent rapid increases in the number of devices connected to wireless networks, the importance of scalable radio resource management operating in a distributed manner and the role of fairness among nodes are critical aspects in ensuring reliable services to numerous nodes in such network environments. In this paper, we consider the Kuramoto model for achieving fair and distributed radio resource allocation in a wireless network. Because the conventional Kuramoto model is designed for synchronization only and is thus not suitable for fair resource allocation, we propose a modified Kuramoto-Desync model, whose purpose is to achieve fair resource allocation among nodes in a distributed manner. The proposed Kuramoto-Desync model evenly spaces the phases of all the nodes in the network. By mapping the evenly spaced phase interval of each node to the time-division multiple access or TDMA-based data time slot, we achieve fair resource allocation among contending nodes in a distributed way. The necessary condition for the convergence of the Kuramoto-Desync model is analyzed. The simulation results show that the proposed model successfully performs fair resource allocation even in dynamic network topology and that the convergence speed of the proposed model is quite stable compared to that of the comparison model.

Fairness can be achieved when the amount of resources allocated to users is the same. Likewise, leveraging a synchronization model such as Kuramoto model in resource allocation can lead to improvement in fairness. Achieving fairness can result in improved throughput and reducing packet collision [18].

The Kuramoto model can be described as nonlinear self-sustained phase oscillators spinning at varying intrinsic frequencies connected through the sine of their phase differences. The model displays a phase transition at a specific coupling strength, in which a mutual behavior is accomplished. Hence, the Kuramoto model is only applicable for fair resource allocation, where all allocated resources are equal.

In this paper, we study the wireless resource allocation algorithm based on the Kuramoto model. The original Kuramoto model is the synchronization model; thus, we propose a modified version of the model to achieve weighted de-synchronization according to the weight of each node, so that it is applicable to resource allocation for network users with different QoS. The simulation results present scalability in dense network environment and better convergence speed compared to the previous algorithm.

2  Weighted Kuramoto De-Synchronization Model

2.1 The Kuramoto Model

The Kuramoto model represents oscillators of firm natural frequencies and non-adjustable coupling constants connected via all-to-all coupling. The first work was proposed by Winfree [19], and was later extended and expressed in simpler mathematical terms by Kuramoto [20]. The Kuramoto model consists of a population of N phase oscillators which are governed as follows:

dθidt=ωi+λN∑j=1Nsin⁡(θj−θi),j=1,2,…,N,(1)

where θi,ωi, and λ are the phase angle, the intrinsic frequency, and the coupling strength, respectively. The set of the phase oscillators exhibits the collective behavior at a specific critical coupling strength value. Consider the discrete-time model as follows:

θi(t+1)=θi(t)+λN∑j=1Nsin⁡(θj(t)−θi(t)).(2)

Many studies ranging from physical and chemical to biological and social systems, have used of Kuramoto model to synchronize a large population of interrelated elements [21].

2.2 The Proposed Weighted Kuramoto Model

We know that the Kuramoto model is a synchronization procedure that models chaotic oscillator-like systems to behave in an orderly fashion where the oscillator operates at the same rate. Accordingly, to solve the resource allocation problem in an unfair wireless network system, we propose a modified Kuramoto model, the weighted Kuramoto desynchronization model. The weighted Kuramoto desynchronization model can achieve weighted fairness by allocating the resource (phase angle spacing) according to the needs of different nodes. The proposed weighted Kuramoto de-synchronization model can be expressed as follows:

θi(t+1)=θi(t)−λN∑n=1Ne(ϕni(t)−π)2sin⁡ϕni(t),(3)

where ϕni(t) is the two-phase differences between nodes i and n, respectively. Let γji(t) be the two-phase differences between nodes j and i. Let L={li∣i=1,…,N} be the set of weight for all nodes, where li is the weight of node i. With this assumption, the weight of node i can be calculated as follows:

wi=2πli∑j=1Nli(4)

Before computing ϕji(t), each node is required to sort the two-phase difference γji(t) in ascending order and arrange its weight wj accordingly. The sorted output is denoted by (γ~ji(t),w~j(t)), which satisfies the inequality as follows: γ~1i(t)<γ~2i(t)<⋯<γ~Ni(t). For instance, we have a pair of (γ1:4,i(t),w1:4)={(5,1),(1,2),(3,3),(0,4)}. Therefore, the sorted output is (γ~1:4,i(t),w~1:4(t))=(0,4),(1,2),(3,3),(5,1). Afterward, ϕni(t) can be defined as follows:

ϕni(t)=mod((γ~ni(t)+wi−∑j=1nw~j+2π(n−1)N),2π).(5)

3  Analysis on Convergence

In this section, we prove the convergence condition of the proposed weighted Kuramoto model. A useful metric in the study of the phase coupling oscillators model is the phase centroid that can be defined as follows:

R(t)=1N[cos⁡θn(t)sin⁡θn(t)].(6)

The magnitude of the phase centroid, ρ(t)≡∥R(t)∥∈[0,1], measures the order in the system: ρ(t)=0 for desynchronization, and ρ(t)=1 for synchronization. The phase centroid can be defined as θ¯(t)≡∠R(t). It is noted that the magnitude of the phase centroid varies from 0 to 1 when the weight of all nodes are different to each other because the phase coupling oscillators will not converge to a strict de-synchronization. In this context, it is imperative to obtain a certain range of learning rates λ when we prove the system convergence considering various weight directly. For this purpose, we first consider that the weight of all nodes are equal to each other (w1=⋯=wN), and prove that the phase coupling oscillator model converges to strict desynchronization with a certain range of λ at some time t. With this assumption, the updating rule can be rewritten as follows:

θi(t+1)=θi(t)−λN∑n=1Ne(γni(t)−π)2sin⁡(γni(t)).(7)

In the next part we will prove the condition of learning rate λ that causes the system to converge.

Theorem 1. Assume there are N oscillators in the network that update their phases according to (3). When λ is uniformly initialized in the range of (0,πe(ϕmax−π)2sin⁡ϕmax], the phases of all oscillators are spaced equally as of θn=2πnN. In addition, the phase coupling oscillators converge to a stable state by spacing with reference to their weight.

Proof. Let the Lyapunov candidate at time step t be given by

V(t)=ρ(t)=R(t)Tμθ¯(t),(8)

where μθ¯(t)≡[cos⁡θ¯(t)sin⁡θ¯(t)]T is the unit vector in the direction of θ(t). Here, we will prove that V(t) is equal to zero at some time t, which means the system converges to strict de-synchronization. The difference between two consecutive time-steps can be expressed by:

∇V(t)=V(t+1)−V(t)=R(t+1)Tμθ¯(t+1)−R(t)Tμθ¯(t)≤R(t+1)Tμθ¯(t)−R(t)Tμθ¯(t)≤0(9)

where ∇R(t)=R(t+1)T−R(t)T. Then ∇V(t) can be written as

∇V(t)≤∇R(t)μθ¯(t)=1N∑n=1N[cos⁡θn(t+1)−cos⁡θn(t)sin⁡θn(t+1)−sin⁡θn(t)]T[cos⁡θ¯(t)sinθ¯n(t)]T=1N∑n=1N(cos⁡(θ¯(t)−θn(t+1))−cos⁡(θ¯n(t)−θn(t)))=1N∑n=1N(cos(θ¯(t)−θn(t)+λN∑j=1Ne(γjn(t)−π)2sin⁡(γjn(t)))−cos⁡(θ¯(t)−θn(t))).(10)

To study ∇V(t), we examine two cases:

Case 1,γjn(t) and θ¯(t)−θn(t)∈(0,π],

Case 2, γjn(t) and θ¯(t)−θn(t)∈(π,2π].

In Case 1 ,∇V(t)≤0 when θ¯(t)−θ(t)<θ¯(t)−θn(t)+λN∑j=1Ne(γjn(t)−π)2sin⁡(γjn(t))≤π,

⇒0<λN∑j=1Ne(γjn(t)−π)2sin⁡(γjn(t))≤π−(θ¯(t)−θn(t)).(11)

Let f(ϕ¯jn(t))=∑j=1Ne(γjn(t)−π)2sin⁡(γjn(t)) be the shifting function, and f(ϕmax) be the maximum value of f. Then (11) can be rewritten as 0<λNf(ϕmax)≤π. After that we can find ϕmax using first order derivative.

ddγjn(t)(∑j=1Ne(γjn(t)−π)2sin⁡(γjn(t)))=(2(γjn(t)−π)sin⁡γjn(t)+cos⁡γjn(t))e(γjn(t)−π)2(12)

⇒2(ϕmax−π)sin⁡(ϕmax)+cos⁡ϕmax=0.(13)

By approximation, sin⁡ϕmax≈ϕmax and cos⁡ϕmax≈1−ϕmax22. Then (13) can be rewritten as 2(ϕmax−π)ϕmax+1−ϕmax22=0⇒ϕmax=0.1657.

Therefore, ∀λ∈(0,π/e(ϕmax−π)2sin⁡ϕmax],∇V(t)≤0. In Case 2, ∇V(t)≤0 when π≤θ¯(t)−θn(t)+λN∑j=1Ne(γjn(t)−π)2sin⁡(γjn(t))<θ¯(t)−θ(t),

⇒0<−λN∑j=1Ne(γjn(t)−π)2sin⁡(γjn(t))≤θ¯(t)−θn(t)−π.(14)

Let αkn(t)=2π−γjn(t)∈(0,π]. Then (14) can be rewritten as

0<−λN∑j=1Ne(2π−αkn(t)−π)2sin⁡(2π−αkn(t))≤θ¯(t)−θn(t)−π,⇒0<−λN∑j=1Ne(γjn(t)−π)2sin⁡(αkn(t))≤θ¯(t)−θ(t)−π.(15)

where (15) can be rewritten as 0<λNf(αmax)≤π. From the solution in Case 1, we derived αmax=ϕmax. Therefore, for all λ∈(0,π/e(ϕmax−π)2sin⁡(ϕmax)],∇V(t)≤0. With varying weight, the phase coupling oscillators converge to a stable state by spacing from its nearest neighbor with reference to its weight when it satisfies γ~ni(t)=wi−∑j=1nw~j. Since γ~ni(t) is sorted in ascending order, the phase will be arranged as follow: γ~1i(t)<γ~2i(t)<⋯<γ~Ni(t). Furthermore, the weight of node i, denoting as wi, is equal to w~1. Therefore, we can rewrite γ~ni(t) as γ~ni(t)=∑j=2nw~j. The phase oscillator reaches a strict de-synchronization for all λ∈(0,π/e(ϕmax−π)2sin⁡(ϕmax)]. It results in equally spaced phases, which is given by θn=2πnN. Therefore, two-phase difference between node i to node n is derived as γ~ni=2π(n−1)N. From (5), two-phase difference is given by

ϕni=γ~ni(t)+wi−∑j=1nw~j+2π(n−1)N.(16)

Therefore, γ~ni(t) is equal to ∑j=2nw~j, which proves that the condition for all λ∈(0,πe(ϕmax−π)2sin⁡(ϕmax)] is true. For that reason, the phase coupling oscillators converge to a stable state by spacing from its nearest neighbor with reference to its weight.

4  Application of Weighted Kuramoto De-Synchronization in Wireless Networks

This section explains how the proposed weighted Kuramoto model is applied to TDMA-based networks to achieve fair resource allocation. Suppose N nodes are in a network, which fires periodically with a period of TDMA frame size. Fundamentally, the action of firing denotes broadcasting a firing message that all the other nodes can hear. A node in the network identifies phase information of its neighboring nodes by overhearing their firing action. A node updates its phase according to the weighted Kuramoto model. When a node phase becomes 2π, it computes a new phase using (3), transmitting this calculated phase to all nodes via a broadcasting message, and adjusting its phase according to the calculated phase. All nodes update their phase in succession correspondingly until convergence is achieved, where all nodes are spaced equally or fairly according to their weight.

The proposed weighted Kuramoto de-synchronization model allows nodes to automatically manage the slot sizes for fully utilizing bandwidth without incurring any collisions. The mapping relation between the phase of a node and resource allocation in a TDMA frame is described as follows. First, we split the phase circle into a line segment. At time t=τ for a non-negative integer τ, node i is allocated TDMA time slots by mapping the two consecutive phase differences from θi(τ) to θj(τ). If S time slots are in a TDMA frame, a node i occupies the data time slots ranging ⌊(θi(τ))⋅S⌋ to ⌊(θj(τ))⋅S⌋−1, where the ⌊⋅⌋ notation is the floor function. We used this operation to ensure the mutually exclusive and collectively exhaustive resource allocation among nodes in a network, although de-synchronization has not yet been reached.

5  Performance Evaluation

In this section, we analyze the performance of the proposed algorithm under different environment. In Fig. 1, five nodes are randomly initialized in the network in the range of [0,2π). In this figure, we use equal weight for all nodes. As a result, the nodes converge to equally spaced intervals which can be verified by the Lyapunov differential reaching zero at around 30 iterations, as can be seen in the Fig. 2. In Fig. 3, we set the value of L={3,2,5,2,1} for node 1 to 5 respectively. We confirmed that the Lyapunov differential converges to a value greater than zero because the weight inputs are different as in presented Fig. 4. To further evaluate the performance of the proposed model, we configured the network as initially starting with only four random nodes. At 100 iterations, we added two more nodes to the network, and at 200 iterations we remove one node. The result illustrated in Fig. 5 displays all the nodes adjusting their phases as the number of nodes changes, with equal weight for all nodes. In Fig. 6, we can verify the network convergence when the Lyapunov differential reaches zero. It is also noticeable that the fewer the nodes in the network, the longer it takes for the system to converge. This outcome is due to the need for each node to shift phase. With more nodes in the network, the phase shifting of each node decreases. In Fig. 7, we set the weight L={1,2,3,4,5,6} for each node, respectively. To evaluate the model flexibility, we add two nodes and remove one node at 100 and 200 iteration, respectively. We can verify that the nodes adjust to the change. As can be seen in Fig. 8, the Lyapunov differential no longer approaches zero, but rather some arbitrary value at a constant state when convergence is reached. This is due the weighted desynchronization.

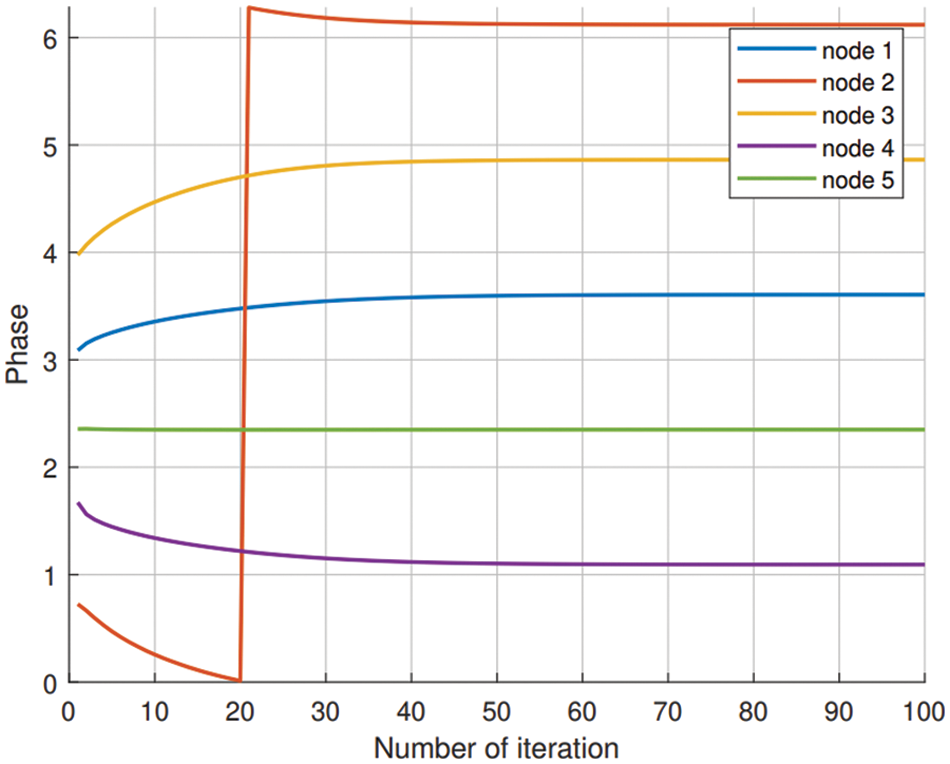
Figure 1: De-synchronization using weighted Kuramoto model

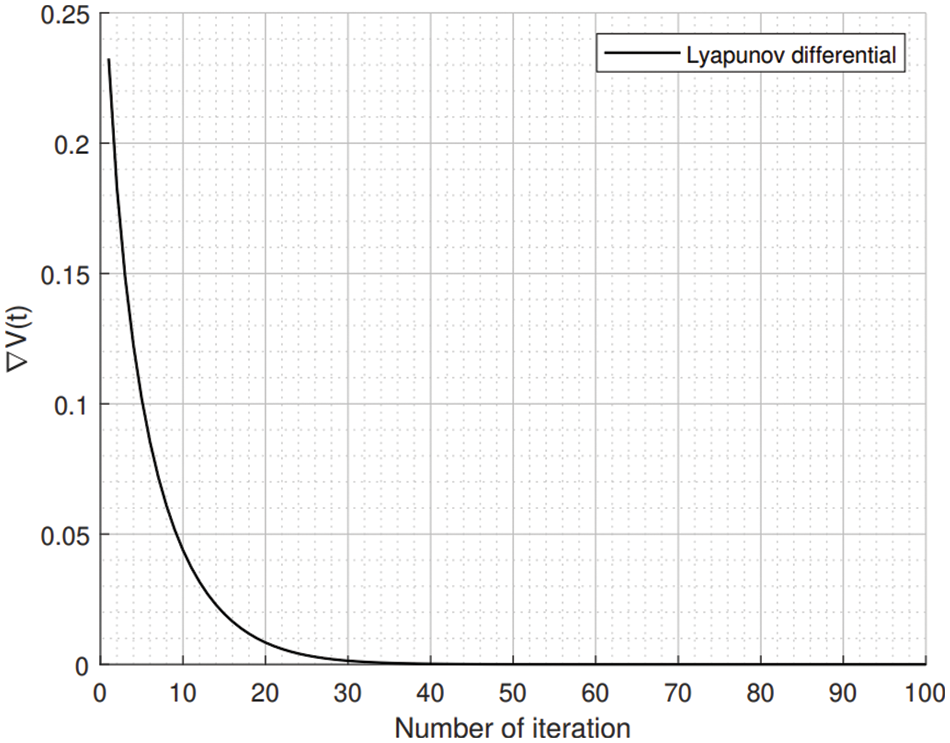
Figure 2: Lyapunov differential under the same environment to Fig. 1

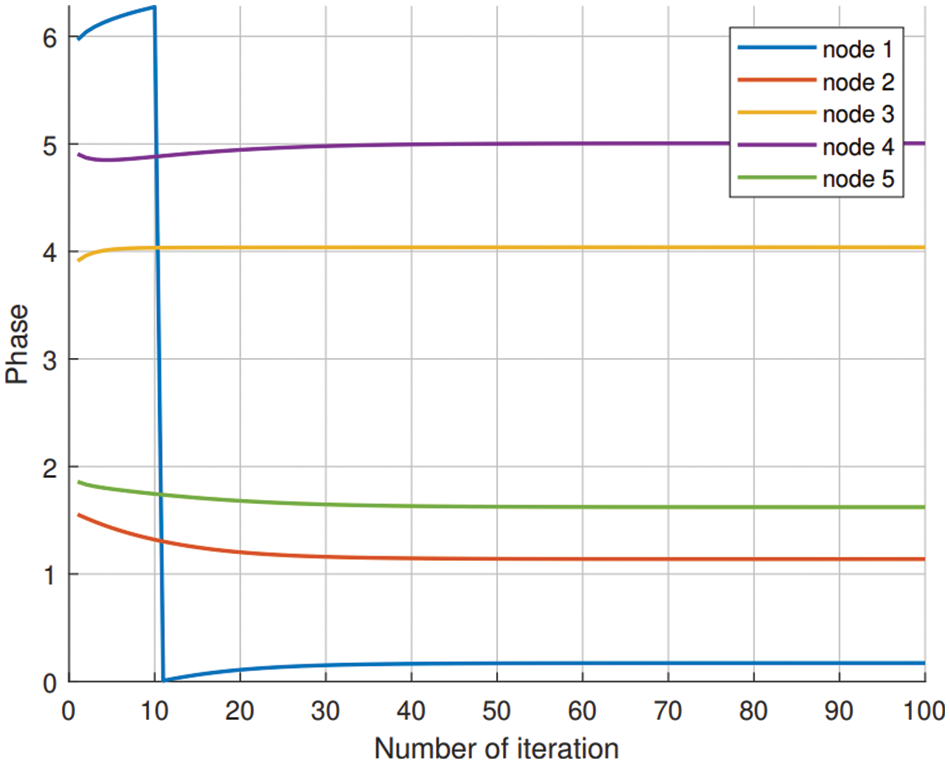
Figure 3: Weighted de-synchronization using weighted Kuramoto model

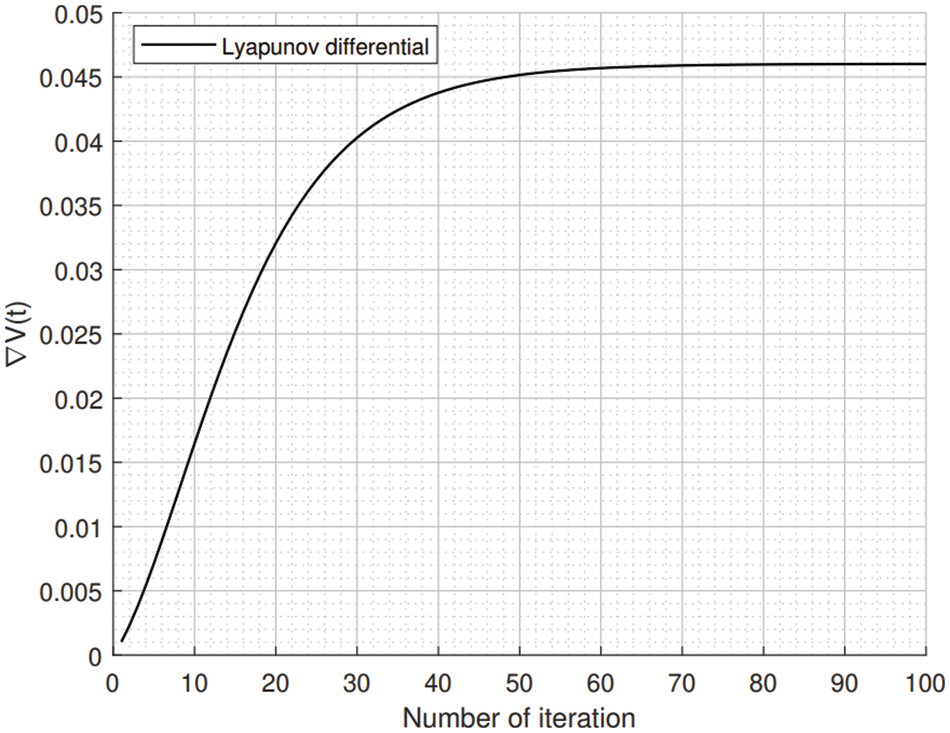
Figure 4: Lyapunov differential under the same environment to Fig. 3

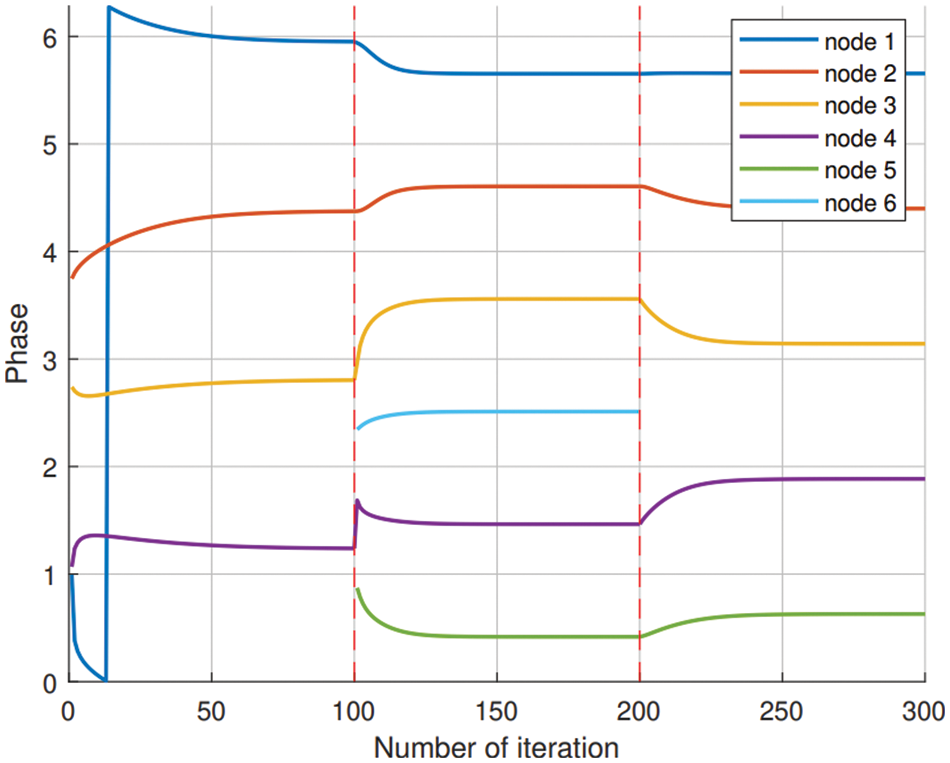
Figure 5: De-synchronization using weighted Kuramoto model with varied number of nodes and the number of iteration

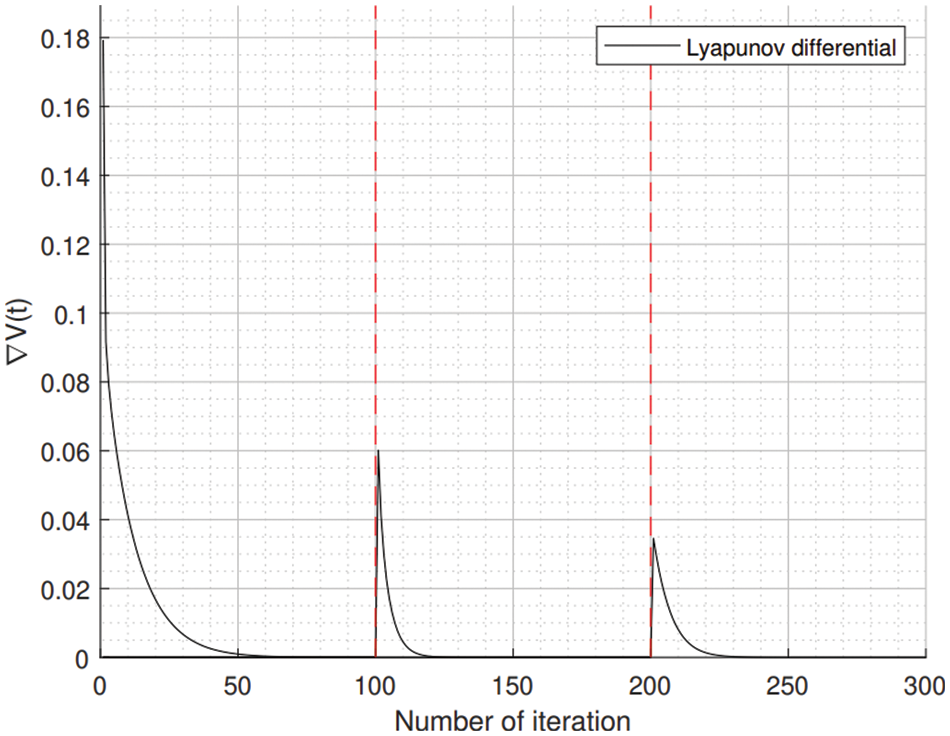
Figure 6: Lyapunov differential under the same environment to Fig. 5

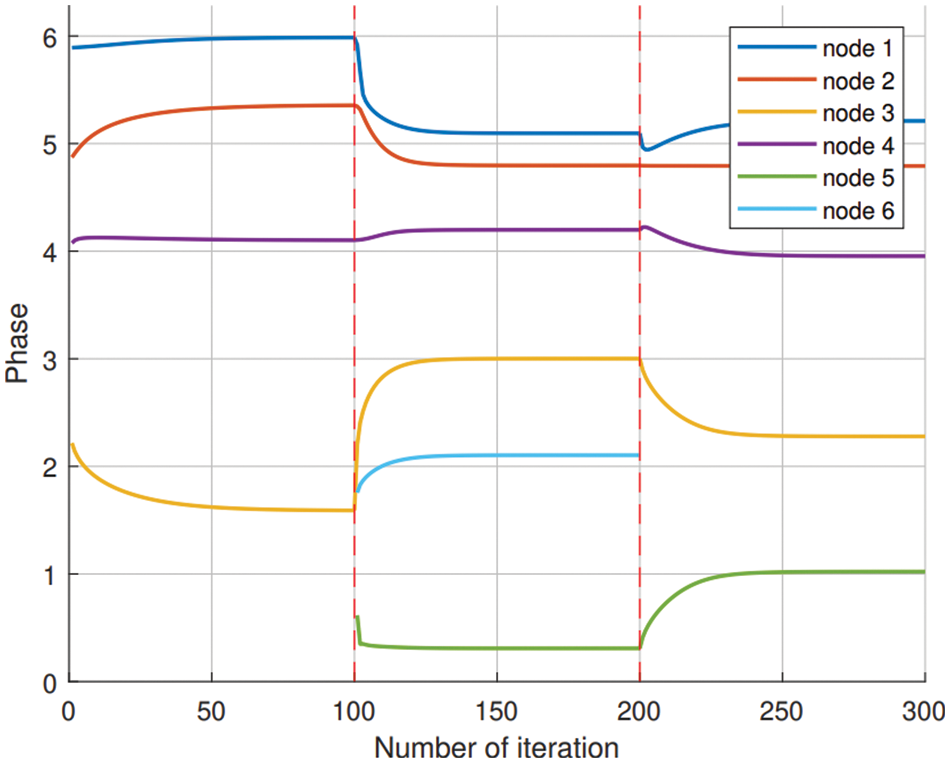
Figure 7: De-synchronization using weighted Kuramoto model with varied number of nodes and the number of iteration

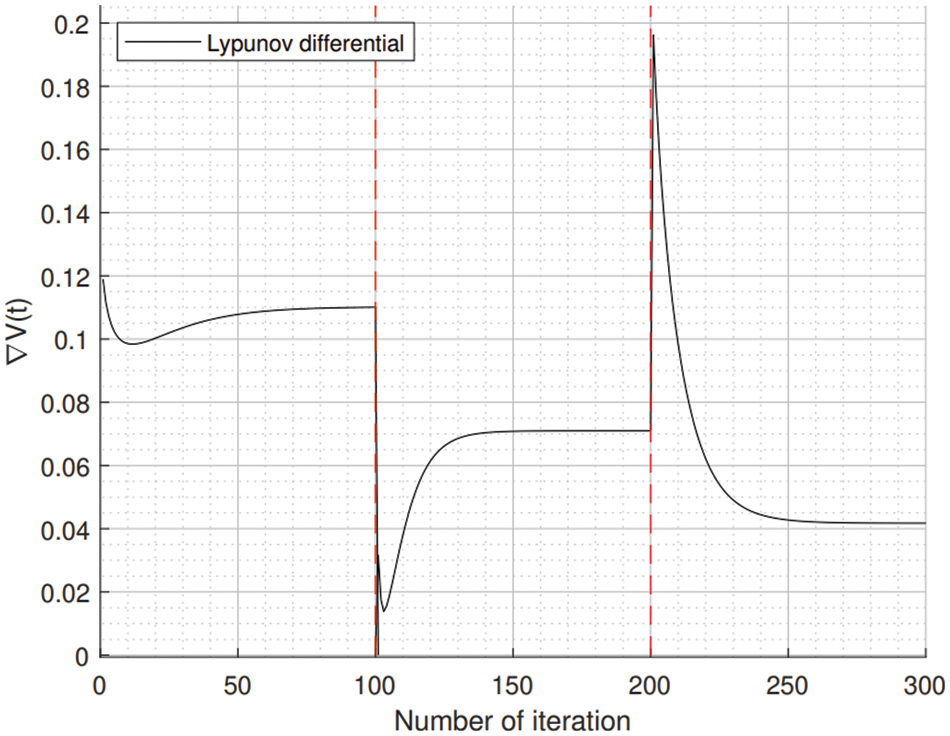
Figure 8: Lyapunov differential under the same environment to Fig. 7

In Fig. 9, we compare the convergence speed of the proposed to WDESYNC-TDMA [11]. In this simulation, we compare the number of rounds that are taken to a given number of nodes in the network for the algorithm to converge. It can be seen that the proposed model achieves a noticeable faster convergence speed (lower number of iteration) compared to that of the WDESYNC-TDMA. As the number of nodes grows the convergence speed of the WDESYNC-TDMA also increases whereas the proposed model maintains a stable rate, highlighting the potential scalability of the proposed algorithm within dense network environment.

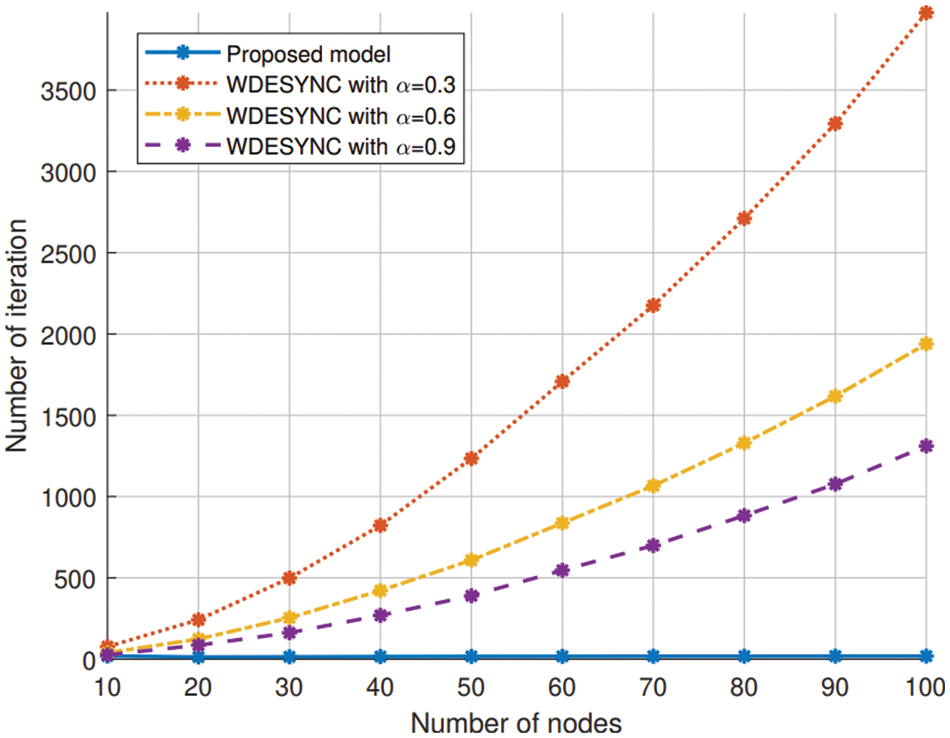
Figure 9: The average number of iteration required to attain convergence under the proposed model and WDESYNCE-TMDA with various learning rate

6  Conclusion

This paper provides insight into weighted wireless networks, where each user has different resource requirements. We propose a weighted Kuramoto de-synchronization model to allocate resources to each user according to their network traffic weight to achieve fair resource allocation and to utilize resources efficiently. Furthermore, we analytically derive the required conditions for convergence. In the simulation results, we assess the performance of the weighted Kuramoto model in various scenarios. In addition, the proposed model exhibits fast convergence, which demonstrates flexibility and high adaptability in the dense network environment.

Due to the nature of multi-hop network, in the weighted Kuramoto de-synchronization model, one node cannot relay its information to the other nodes across the network. Hence, in the future, we plan to study the weighted Kuramoto de-synchronization model in a multi-hop network. In addition, overhearing neighboring nodes and phase updating can cause energy consumption issue. For this reason, we plan to study the application of sleep mode in the Kuramoto model to increase the energy efficiency of the network.

Funding Statement: This research was supported by the MSIT (Ministry of Science and ICT), Korea, under the ITRC support program (IITP-2021-2018-0-01799) supervised by the IITP (Institute for Information & communications Technology Planning & Evaluation), by the Korea Institute of Energy Technology Evaluation and Planning (KETEP) and the Ministry of Trade, Industry & Energy (MOTIE) of the Republic of Korea (No. 20214000000280), and by the National Research Foundation of Korea (NRF) grant funded by the Korea government (MEST) (No.NRF-2020R1A2C1010929).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present research work.

References

    1. C. Wang, M. D. Renzo, S. Stanczak, S. Wang and E. G. Larsson, “Artificial intelligence enabled wireless networking for 5G and beyond: Recent advances and future challenges,” IEEE Wireless Communications, vol. 27, no. 1, pp. 16–23, 2020. [Google Scholar]

    2. W. Saad, M. Bennis and M. Chen, “A vision of 6G wireless systems: Applications, trends, technologies, and open research problems,” IEEE Network, vol. 34, no. 3, pp. 134–142, 2020. [Google Scholar]

    3. L. D. Xu, W. He and S. Li, “Internet of things in industries: A survey,” IEEE Transactions on Industrial Informatics, vol. 10, no. 4, pp. 2233–2243, 2014. [Google Scholar]

    4. H. Mohapatra and A. K. Rath, “Survey on fault tolerance-based clustering evolution in WSN,” IET Networks, vol. 9, no. 4, pp. 145–155, 2020. [Google Scholar]

    5. H. Mohapatra and A. K. Rath, “Detection and avoidance of water loss through municipality taps in India by using smart taps and ICT,” IET Wireless Sensor Systems, vol. 9, no. 6, pp. 447–457, 2019. [Google Scholar]

    6. NTT. DoCoMo Inc., “White Paper: 5G radio access: Requirements, concept and technologies,” 2014. [Online]. Available: https://www.docomo.ne.jp/english/binary/pdf/corporate/technology/whitepaper_5g/DOCOMO_5G_White_Paper.pdf. [Google Scholar]

    7. D. Baker and A. Ephremides, “The architectural organization of a mobile radio network via a distributed algorithm,” IEEE Transactions on Communications, vol. 29, no. 11, pp. 1694–1701, 1981. [Google Scholar]

    8. F. Harada, T. Ushio and Y. Nakamoto, “Adaptive resource allocation control for fair qos management,” IEEE Transactions on Computers, vol. 56, no. 3, pp. 344–357, 2007. [Google Scholar]

    9. H. Mohapatra and A. K. Rath, “Fault-tolerant mechanism for wireless sensor network,” IET Wireless Sensor Systems, vol. 10, no. 1, pp. 23–30, 2020. [Google Scholar]

  10. H. Mohapatra and A. K. Rath, “Fault tolerance in WSN through pe-leach protocol,” IET Wireless Sensor Systems, vol. 9, no. 6, pp. 358–365, 2019. [Google Scholar]

  11. Y. Taniguchi, “De-synchronization-based weighted scheduling adaptive to traffic load for wireless networks,” in Int. Conf. on Computer, Communications, and Control Technology (I4CT), Langkawi, pp. 130–134, 2014. [Google Scholar]

  12. J. Degesys, I. Rose, A. Patel and R. Nagpal, “DESYNC: Self-organizing de-synchronization and tdma on wireless sensor networks,” in Proc. of ACM/IEEE Int. Conf. on Information Processing in Sensor Networks, Toronto, Ontario, Canada, pp. 11–20, 2007. [Google Scholar]

  13. Q. Wang, S. Wang, M. Zhu, M. Ma and H. Chen, “A Bio-inspired and user-experience preferred load-balance algorithm for heterogeneous networks,” in IEEE/CIC Int. Conf. on Communications in China (ICCC), Beijing, China, pp. 335–340, 2018. [Google Scholar]

  14. U. -S. Yu, H. -H. Choi and J. -R. Lee, “Kuramoto-desync: Distributed and fair resource allocation in a wireless network,” IEEE Access, vol. 7, pp. 104769–104776, 2019. [Google Scholar]

  15. L. Khoshnevisan and F. R. Salmasi, “Adaptive rate-based congestion control with weighted fairness through multi-loop gradient projection internal model controller,” IET Control Theory Applications, vol. 9, no. 18, pp. 2641–2647, 2015. [Google Scholar]

  16. G. Li and J. Li, “Global weighted fairness guaranteed congestion avoidance protocol for wireless sensor networks,” in 2011 Proc. IEEE Int. Conf. on Computer Communications (INFOCOM), Shanghai, China, pp. 601–605, 2011. [Google Scholar]

  17. L. Shi, X. Wang, R. T. B. Ma and Y. C. Tay, “Weighted fair caching: Occupancy-centric allocation for space-shared resources,” Performance Evaluation, vol. 127–128, pp. 194–211, 2018. [Google Scholar]

  18. H. Obata, R. Hamamoto, C. Takano and K. Ishida, “SP-MAC: A media access control method based on the synchronization phenomena of coupled oscillators over WLAN,” IEICE Transactions on Information and Systems, vol. E98.D, no. 12, pp. 2060–2070, 2015. [Google Scholar]

  19. A. T. Winfree, “Biological rhythms and the behavior of populations of coupled oscillators,” Journal of Theoretical Biology, vol. 16, no. 1, pp. 15–42, 1967. [Google Scholar]

  20. Y. Kuramoto, “Self-entrainment of a population of coupled non-linear oscillators,” in Proc. Int. Symp. Mathematical Problems in Theorical Physics, in Lecture Notes in Physics. Berlin, Germany, Springer, pp. 420–422, 1975. [Google Scholar]

  21. J. A. Acebrón, L. L. Bonilla, C. J. Pérez Vicente, F. Ritort and R. Spigler, “The kuramoto model: A simple paradigm for synchronization phenomena,” Reviews of Modern Physics, vol. 77, no. 1, pp. 137–185, 2005. [Google Scholar]