Detecting Double JPEG Compressed Color Images via an Improved Approach

1  Introduction

With the rapid development of the Internet, the network has undoubtedly become the most convenient way to transmit information. Furthermore, with the advancement of image processing technology particularly the emergence of the JPEG format, digital images have become an important container for social networking on the Internet. Due to the ingenious design of the JPEG format, images can be rapidly distributed, stored and transmitted. Today, the existing JPEG standard has been generic enough to support a wide variety of applications for continuous-tone image [1]. However, technological advances has also made information security an increasingly serious problem. Therefore, the originality, reality and integrity of the images may be questioned, which overturns the common perception that if there is a picture, there is the truth. The appearance of faked images in our lives has drawn much of the researchers’ attention to the study of image forensics such as JPEG image forensics [2–7], JPEG image-splicing [8–11], JPEG image-resampling [12–15], JPEG image steganography [16,17] and double JPEG image detection [18–33].

Detecting double JPEG compression in the color images plays a significant role in digital forensics. Double JPEG compressed color images often lead to image forgery. The reason is that double JPEG compression is inevitable when the images are manipulated by tampers. Double JPEG compression can be classified by different standards. For instance, based on whether the quality factors are the same, double JPEG compression is divided into two categories: one of them is with different quantization matrices and the other is with the same quantization matrix [19–35]. Fig.1 demonstrates the process of double JPEG compression with the same quantization matrix. For another instance, based on whether the grids of the block-wise discrete cosine transform (DCT) are aligned or not, double JPEG compression can be divided into the aligned ones [20] and the non-aligned ones [21]. The aligned double JPEG compressed images with the same quantization matrix have unique characteristics that are more obscure and thus make it difficult to distinguish features effectively. For the sake of making detection more difficult, tampers prefer aligned double JPEG compression, which helps to achieve a more indiscernible effect.

Figure 1: Double JPEG compression with the same quantization matrix

Currently, the studies on double JPEG compression in the color images mainly adopt traditional manual methods to extract features. However, the extracted features may not be comprehensive. In addition, the detection of double JPEG compressed color images with the same quantization matrix is more problematic because the compression traces are more hidden in this case. Particularly, when the compression quality factor is low, it is more challenging to distinguish between singly compressed images and doubly ones by the extracted features. This paper aims to extract more comprehensive and subtle features by CNN. The main contributions of this paper are:

•   The numbers of nonzero pixels and the sum of pixel values of color space conversion error can be applied as features to detect double JPEG compression on color images. These features were found to be valid by conducting experiments and analyzing the results.

•   Through analyzing the three types of error, different feature extraction methods are adopted according to the characteristics of the errors. For the color space conversion error, we use manual method to extract image features. For the rounding error and the truncation error, we use CNN to extract image features. A combination of traditional handcraft extraction and CNN is used to extract features more efficiently. Unlike CNN within computer vision, this paper adopts averaging pooling to focus on local features, and employs 1×1 convolutional kernels and Dropout layers to prevent model overfitting. In addition, adopting SVM helps to obtain valid classification results when the sample size is not massive.

•   The proposed method remains valid when self-defined quality factors are involved. In other words, the proposed method has potential to detect double JPEG compression on color images with the same self-defined quantization matrix.

The rest of this paper is organized as follows. In Section 2, relevant studies and the main methods used for double JPEG compression detection are described. Four kinds of error in double JPEG compressed color images are introduced in Section 3. Section 4 mainly presents analysis of the errors and the framework for detecting double JPEG compressed color images in detail. The experiment for the proposed method is depicted and analyzed in Section 5. In the final section, some conclusions are given.

2  Related Work

There are already many approaches for the double JPEG compression detection with different quantization matrices. However, they are not applicable to double JPEG detection with the same quantization matrix. In [22], a regulation that the number of different JPEG coefficients monotonically decreases with the increase in the number of compression was obtained by experiments. In the same paper, this regulation was used to design an algorithm for detecting double JPEG compression with the same quantization matrix, and a new random perturbation strategy was proposed. However, the algorithm also has its limitations: first, it is sophisticated and requires constant compression and decompression of JPEG images; second, it only achieves high detection accuracy for cases with high compression quality factors. In [23], Niu et al. made a further study on the basis of [22] and achieved relatively good detection results for low compression quality factors.

In [24], Yang et al. extracted the error images from gray images, and presented a method that utilizes error-based statistical features (EBSF). Then, the extracted features were used in the SVM for the detection of double JPEG compression with the same quantization matrix. Nevertheless, due to the nonlinearity of rounding truncation operations and the variety of image statistics, it is still an open problem to make a thorough analysis on the difference of error blocks between two consecutive JPEG compressions with the same quantization matrix [24]. Recently, deep learning technique, which develops at a very quick pace, has been used extensively in the field of image forensics. In [25], a CNN framework was proposed, which mainly consists of a preprocessing layer and a feature proposal layer. In [26], Wang et al. built a multi-column CNN framework for the classification of 8×8 identifiable blocks. In [27], Huang et al. proposed a dense CNN framework to detect double JPEG with the same quantization matrix.

Nowadays, faked color images may have negative impacts on our daily life, so it is of necessity and importance to study the double JPEG detection for color images with the same quantization matrix. In [22], a color image was approximately regarded as multiple grayscale images. However, such an approximation may cause the incompleteness of the extraction of features. Recently, the following studies on color images have been conducted. In [28], Wang et al. extracted the color space conversion error in color images first, then extracted the relevant features by mapping the truncation error and the rounding error of the three channels to spherical coordinates. In [29], Wang et al. proposed the convergence error and the transposition error for the first time by analyzing the stability of color images. Under particular conditions, some existing methods may produce better results since they were designed with a specific application [30]. The above methods can be used to detect double JPEG compression. Nevertheless, how to extract more comprehensive and subtle features still needs to be investigated in the future. In this paper, based on the proposed error in [28], research is further conducted to detect double JPEG compressed color images. We focus on aligned double JPEG compression detection with the same quantization matrix in color images. Throughout this paper, the double JPEG compressed color images refer to the aligned compressed color images with the same quantization matrix, unless otherwise specified.

3  Error in Double JPEG Compressed Color Images

Fig. 2 illustrates the procedures of the JPEG compression and decompression. From the primitive color images to the JPEG compressed color images, the JPEG compression is running for color images during this process, and a JPEG decompression process is operated for color images from the color images JPEG compression to the recomposed color images. The JPEG compression for color images mainly involves color space conversion, block separation, DCT, quantization, and entropy encoding. In contrast, the JPEG decompression is the opposite process, which primarily includes entropy decoding, inverse quantization, inverse discrete cosine transform (IDCT) and inverse color space conversion to yield reconstructed color images.

Figure 2: Four sources of error in JPEG compression and decompression

Four types of error in double JPEG compressed color images are also described in Fig. 2. The first one is the quantization error, which occurs in the quantitative procedure and is irreversible. The quantitative procedure mainly includes a rounding operation. The second one is the truncation error and the third one is the rounding error. Followed by the IDCT in the process of the JPEG decompression, the truncation and the rounding operations are carried out to make preparations for the inverse color space conversion. When the inverse color space conversion is performed, YCbCr color model is conversed to RGB color model. The Y channel indicates the luminance, the Cb channel and the Cr channel represent the chrominance-blue and the chrominance-red respectively. Besides, since the range of the three channel values of RGB are all [0,255], the range of Y, Cb, Cr channel values are also all [0,255]. The value of the truncation error is defined as 255 when the value of the IDCT transformation is higher than 255, and the value of truncation operation is defined as 0 when the value of the IDCT transformation is lower than 0. The rounding operation is conducted by rounding the value after the IDCT transformation. For example, the pixel value is initially set to be 257.7, then it turns into 255 after RTO, which means that the value of the truncation error at this pixel is −2.7. Likewise, when the pixel value is initially set to be 214.6, it will turn into 215 after RTO, here the value of the rounding error at this pixel is 0.4. Moreover, the value of the rounding error is found to be in the range of [−0.5,0.5], while the value of the truncation error is uncertain. The fourth type of the errors is the color space conversion error, which is obtained after RTO. Start from the Begin button in Fig. 2, the rounding and truncation operations are carried out. Then, the operation of inverse color space conversion, RTO, and the reconstruction of color image are carried out successively for color images. This is how the double JPEG compression is done, as depicted by the blue arrow in Fig. 2.

3.1 Color Space Conversion Error

The research objects in this paper are color images. The previous researches mainly focused on grayscale images, and color images were assumed to be multiple gray images. However, some features in color images are neglected. Therefore, our research is based on color images, and the color space conversion error is applied to extract features.

The notations used in this paper and their meanings are listed as shown in Table 1.

From Fig. 2, we know that JPEG compression and decompression include the procedure of color space conversion and inverse color space conversion. Color space conversion is designed by exploiting the characteristics that like different abilities of the human eye to recognize colors. The conversion of the RGB color model to the YCbCr color model is implemented through the process represented by the following equations.

{Y=0.299R+0.587G+0.114BCb=−0.169R−0.331G+0.5B+128Cr=0.5R−0.419G−0.081B+128(1)

By Eq. (1), color conversion can be conducted and the first step of JPEG compression is accomplished. In turn, the conversion process from the YCbCr color model to the RGB color model can be performed according to the following Eq. (2), and the inverse color space conversion is fulfilled.

{R=Y+0(Cb−128)+1.402(Cr−128)G=Y−0.344(Cb−128)−0.714(Cr−128)B=Y+1.772(Cb−128)+0(Cr−128)(2)

The occurrence of the quantization error, the rounding error and the truncation error leads to the deviation of pixel values and consequently results in color space conversion error. Y = 75, Cb = 45 and Cr = 112 may be initially set for a pixel. According to Eq. (2), we get R = 53, G = 115 and B = 0. After substituting the values into Eq. (1), Y = 83, Cb = 81 and Cr = 106 can be obtained. Hence, the color space conversion error is 8, 36 and −6 on the three channels. Furthermore, no matter what the quantization error, the rounding error and the truncation error are, the color space conversion error is 8, 36 and −6 when Y = 75, Cb = 45 and Cr = 112. Thus, it is not easy to ascertain the association among the quantization error, the rounding error and the truncation error.

3.2 The Rounding Error and the Truncation Error

For convenience, this paper assumes that an n-times compressed image is an image compressed n-times with the same quantization matrix. In the JPEG decompression process, the sources of the truncation error and the rounding error has been analyzed. Defined TREn as:

TREn=RTO(IDCT(IDn))−IDCT(IDn)(3)

where IDn refers to the de-quantized JPEG coefficient in the n-th decompression process and is obtained from Eq. (4):

IDn=Kn×Q(4)

where Kn is the JPEG coefficient matrix of the n-th color compressed image and Q is the quantization matrix. When a JPEG image is given, Q is obtained by the software JPEGsnoop. Then, the truncation error and the rounding error are manipulated to obtain the quantization coefficient matrix M. The main procedure is shown in Fig. 3 below.

Figure 3: The procedure to obtain the quantization coefficient matrix

Compare Fig. 2 with Fig. 3, it is obvious that the operation to get the quantization coefficient matrix is similar to the JPEG compression for images, including the block separation for the truncation error and the rounding error, the DCT transform and the quantization. Eventually, the quantization coefficient matrix is got by Eq. (5).

M=DCT(TREn)./Q(5)

where DCT denotes the discrete cosine transform, ‘. /’ signifies the division operation between the corresponding elements of TREn and Q. Here, the quantization operation uses the quantization table obtained from the header file.

The significant difference between the above operation and JPEG compression is that the quantization operation in JPEG compression is irreversible, including the quantization of floating-point data and the nearest-neighbor rounding operation of the quantized floating-point data. The quantization operation is merely the quantization of the floating-point data and does not involve the rounding operation of the quantized floating-point data. Therefore, when the quantization operation is performed, the resulting matrix with quantized coefficients is a floating-point matrix and contains negative coefficients.

4  The Proposed Method

The method proposed in this paper utilizes the three types of error mentioned above: the color space conversion error, the rounding error and the truncation error. In the process of analyzing the error, different feature extraction methods are adopted according to the characteristics of the error, i.e., traditional manual feature extraction is used for the color space conversion error, and CNN is used to extract image features from the rounding error and the truncation error. Also, SVM is applied to detect double JPEG compression with the same quantization matrix.

Unlike the processing for gray images, JPEG compression for color images needs a procedure for color space conversion. The color space conversion error is initiated by two continuous color space conversions due to the reconstruction of the image and preparing for the next compression [27]. Considering the source of the color space conversion error, traditional methods are used to extract features in this paper. As for the rounding error and the truncation error, they are produced at one time in the process of decomposition. In the light of specific conditions of the rounding error and the truncation error, this paper uses a designed CNN model to extract as more detailed features as possible.

4.1 Analysis of the Color Space Conversion Error

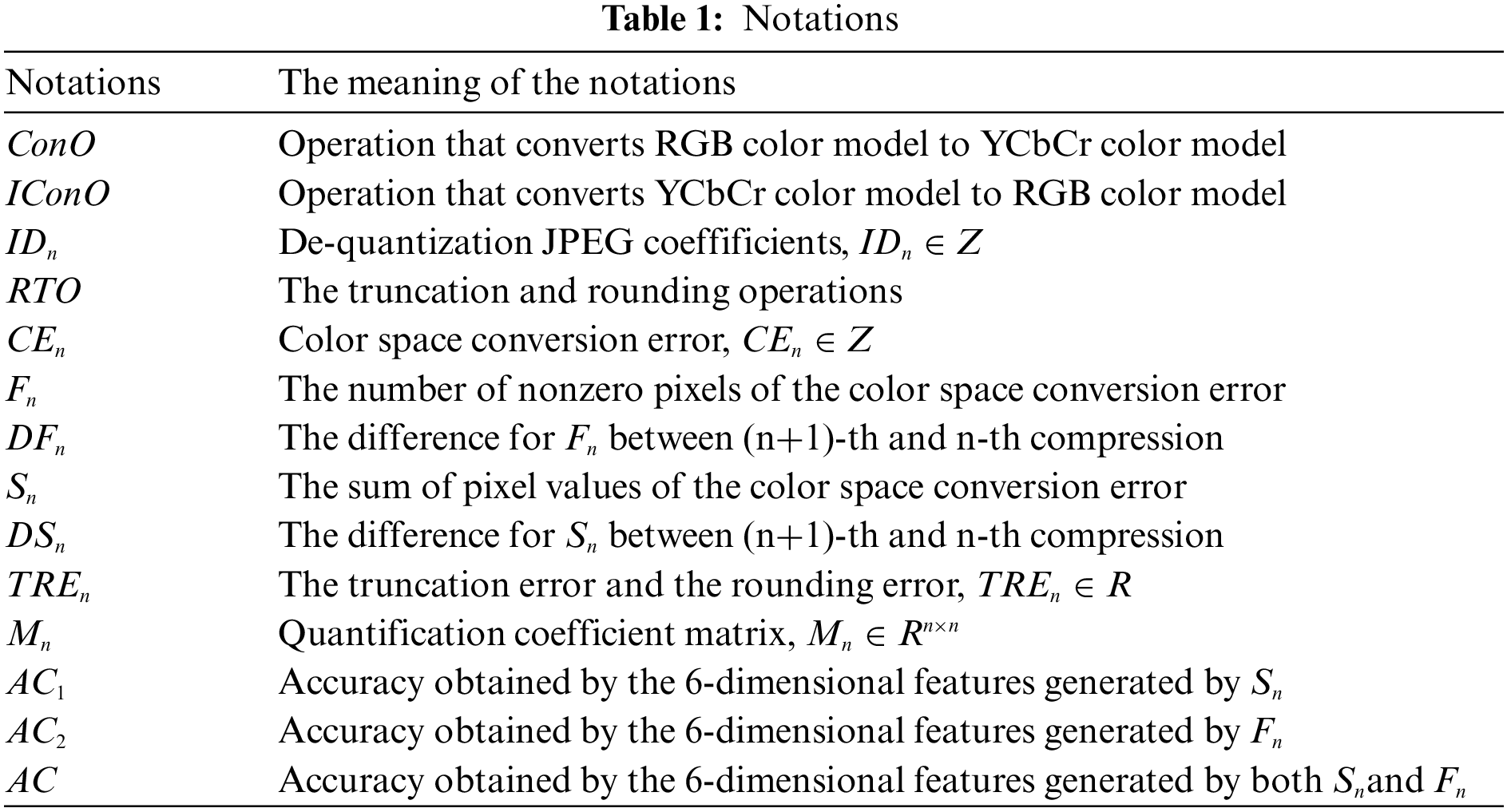
The following Fig. 4 demonstrates that the number of nonzero pixels and the sum of pixel values in the color space conversion error can be regarded as features for extraction. In this case, regulations on the variation of the average of F and the average of S can be obtained by analyzing the color space conversion error, which in turn provides a solid foundation for the next step of feature extraction. According to the sources of the color space conversion error, define CEn as:

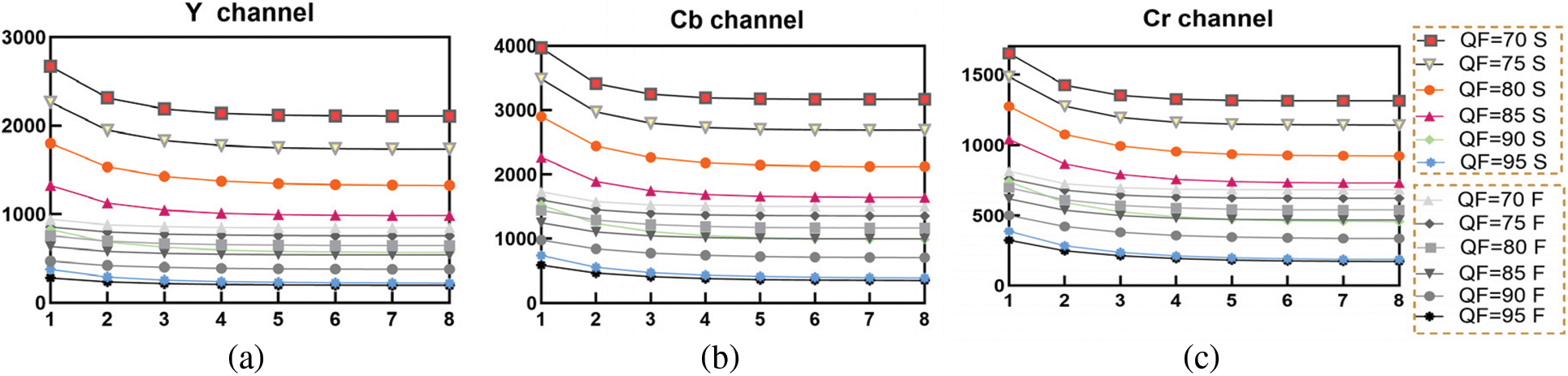
Figure 4: Variation tendency of the average of the number of nonzero pixel and the sum of pixel values of color space conversion error with different quality factors, where the horizontal axis represents compression times, and the vertical axis represents the average of F and the average of S for all of the images on Uncompressed Color Image Database (UCID) dataset. (a) the Y channel with quality factors 70 to 95; (b) the Cb channel with quality factors 70 to 95; (c) the Cr channel with quality factors 70 to 95

CEn=ConO(IConO(RTO(IDCT(IDn))))−RTO(IDCT(IDn))(6)

where IDCD means the inverse discrete cosine transform, IConO means the operation of converting YCbCr to RGB color model, and ConO denotes the operation that converts RGB to YCbCr color model. CEn is with the same dimension as the original image.

As already given in Table 1, the number of nonzero pixels for CEn is denoted by Fn, and the sum of pixel values for CEn is represented as Sn.

Quality factors Q1 and Q2 can be arbitrarily chosen at {20,40,60,70,75,80,85,90,95}. To illustrate the regularity more conveniently, this paper prefers to set the quality factor as Q1∈{70,75,…,95} and Q2=95 respectively. As seen in Fig. 4a, the variations of the average of F and the average of S under the Y channel at Q1are portrayed as compression times increases. Both the average of the number of nonzero pixel and the sum of pixel values of color space conversion error decrease monotonically. Furthermore, the sum of pixel values of the color space conversion error is generally greater than the average of the number of nonzero pixel of conversion error. On the whole, with a quality factor Q1, the average of the number of nonzero pixel is a value between [0, 3000]. Similarly, with a certain quality factor, the averages of the number of nonzero pixel in Figs. 4b and 4c are a value between [0, 4000] and a value between [0, 1700] respectively.

These experimental results demonstrate that when JPEG image is compressed over and over again with the same quantization matrix, both the average of F and the average of S decrease monotonically. This intrinsic property of JPEG image can be utilized to discriminate between the singly compressed images and the doubly ones.

In Fig. 5, how the average of DS and the average of DF in the three channels with a quality factor of 95 change as compression times increase are presented. It is obvious from Figs. 4 and 5 that the average of the number of nonzero pixel and the sum of pixel values of the conversion error is decreasing monotonically and eventually stabilizing as compression times increases, no matter in which channel and with which compression quality factor. Moreover, Fig. 5 clearly illustrates that in all of the three channels, both the average of DS and the average of DF decline slower and slower as compression time increases. Therefore, Sn, DSn, Fn and DFn could be adopted as features to detect double JPEG compression by the above analysis.

Figure 5: Variation tendency of the difference of the number of nonzero pixel and the sum of pixel values of conversion error between single and double compression with quality factors 95, where the horizontal axis represents compression times, and the vertical axis represents the average of DS and the average of DF for all of the images on UCID dataset. (a) the Y channel with quality factor 95; (b) the Cb channel with quality factor 95; (c) the Cr channel with quality factor 95

It is clear from Fig. 6a that as the quality factor increases, the average of F1 decreases monotonically in the three channels of Y, Cb and Cr. Fig. 6b illustrates the changing situation of the average of S1 with quality factors {20,40,…,95}. Likewise, as the quality factors increases, both the average of F1 and S1 decreases monotonically in all of the three channels. This intrinsic property of JPEG image is beneficial for us to make an explanation for the classification results. In addition, experimental results indicate that for any given quality factor, the color space conversion error in Cb channel is the biggest contributor to classification. Moreover, it can also be seen from Fig. 6 that the value of Cb channel is usually larger than that of Y channel, while the value of Y channel is usually larger than that of Cr channel.

Figure 6: The tendency of the average of F1 and the average of S1 in the three channels, where the horizontal coordinate indicates the quality factor {20,40,60,70,75,80,85,90,95}, the vertical coordinate indicates the average of F1 and the average of S1. (a) the average of F1 with different quality factors; (b) the average of S1 with different quality factors

According to the analysis above, the color conversion error cannot be adopted directly as a feature to distinguish primary compression from secondary compression. However, Tables 2 and 3 show that Sn and DSn can be chosen as features with the desired functions. Therefore, each channel has two-dimensional features, and a total of 6-dimensional features can be obtained in the three channels.

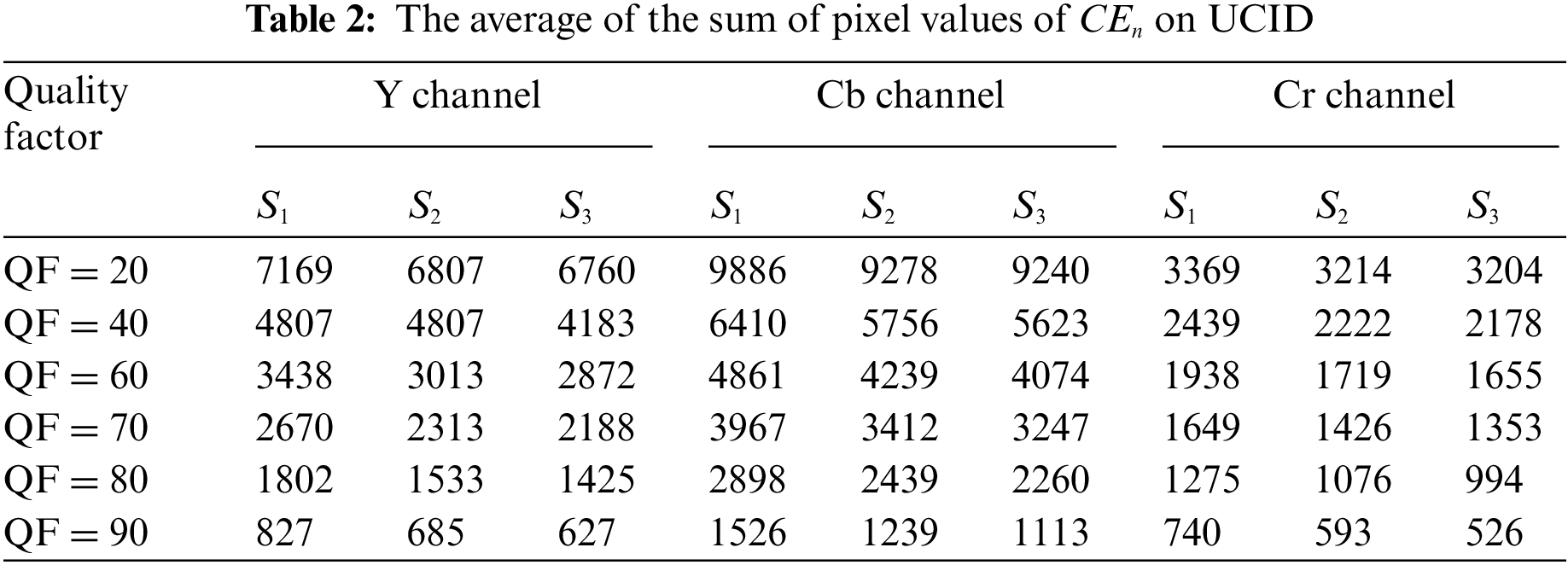
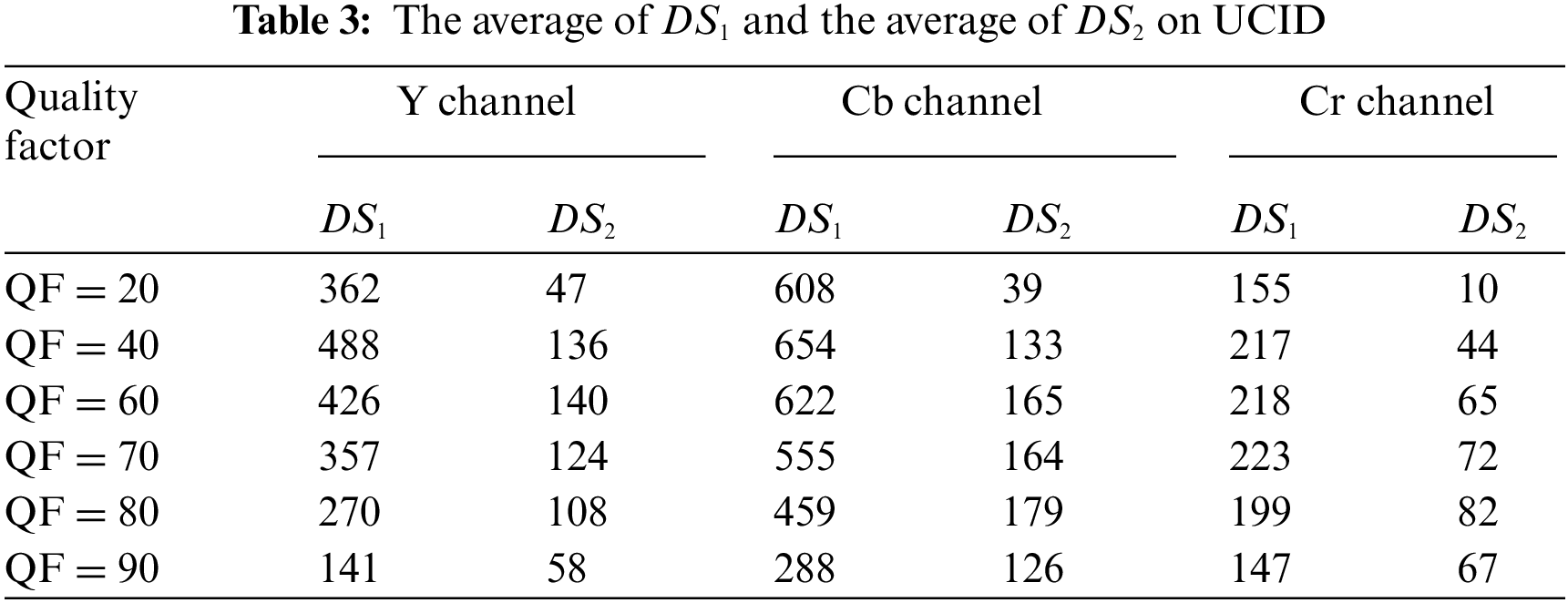
In addition, Tables 4 and 5 present the average of Fn and the average of DFn with different quality factors. Sn and DSncan be adopted as features to distinguish primary compression from secondary compression. Therefore, each channel can be seen as having 2-dimensional features, and a total of 6-dimensional features can be obtained in the three channels. Thus, a total of 12-dimensional features about the color space conversion error are extracted as in Tables 2–5.

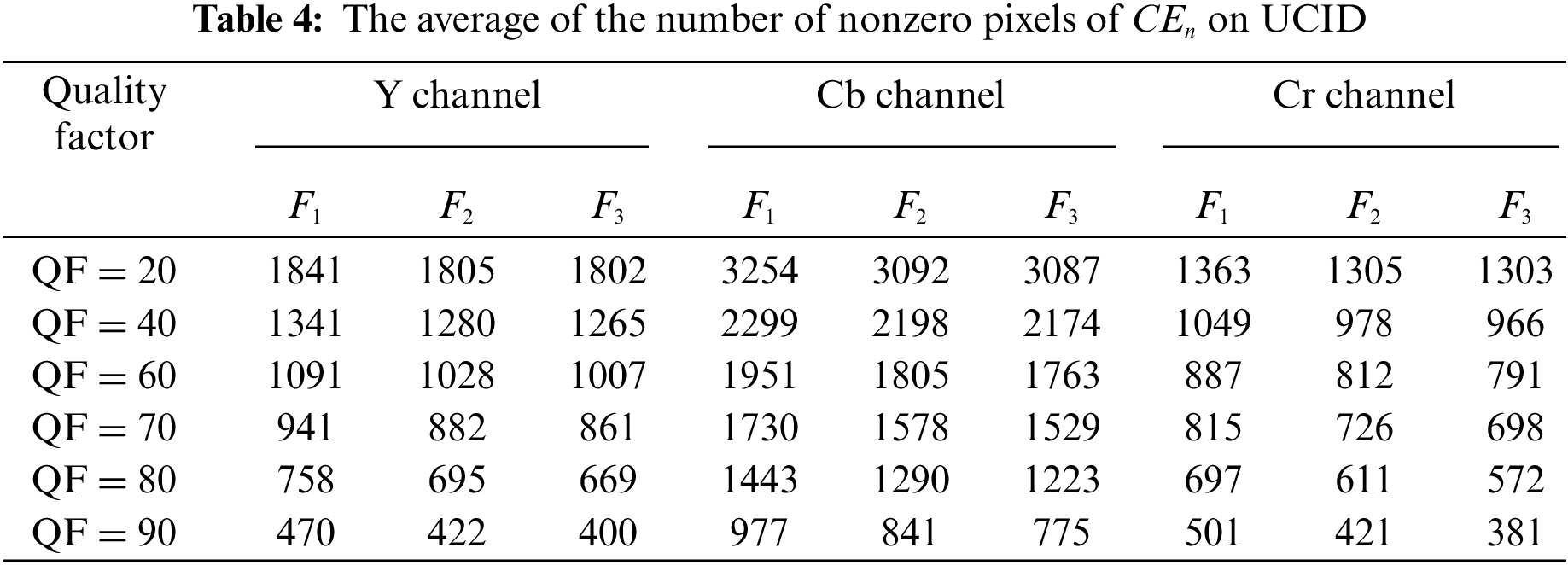
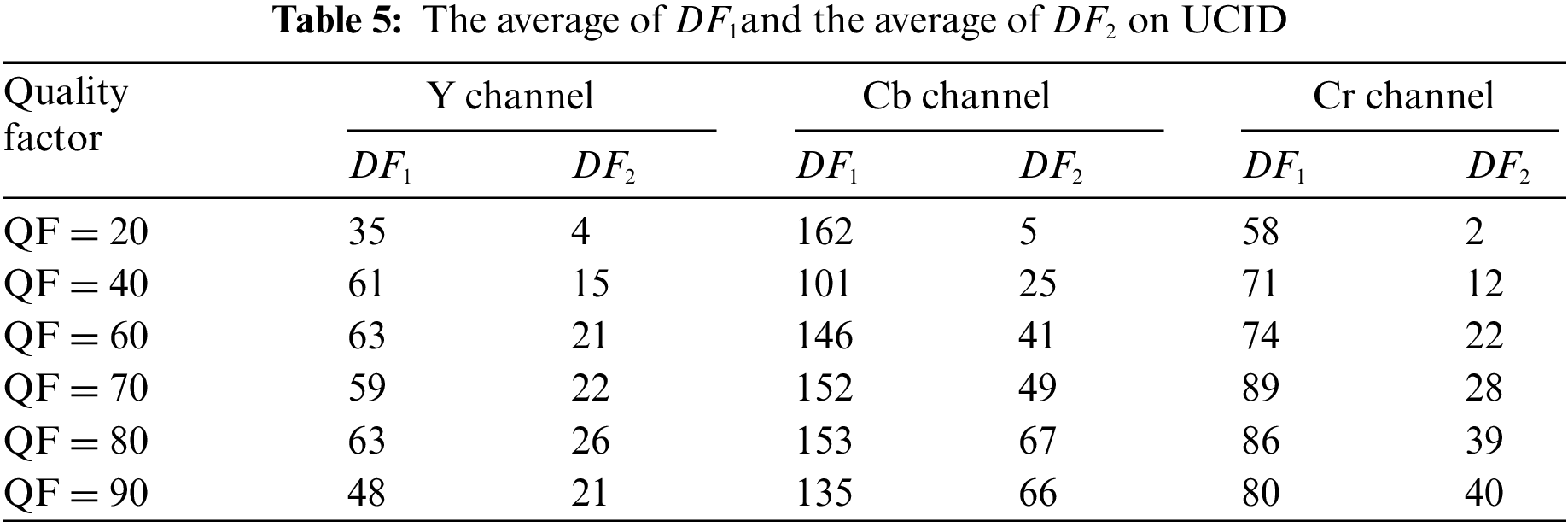
4.2 Analysis of the Rounding Error and the Truncation Error

By the above description, the rounding error, the truncation error and the quantization coefficient matrix are derived. To extract features from the rounding error and the truncation error, a specific CNN will be applied in our experiment. Although many models can be applied [34–35], there are three advantages of CNN. Firstly, owing to the properties of the convolution and pooling computations, it is possible that the translation of the image has no effect on the final feature vector. In this sense, the extracted features are less likely to be over-fitted. Moreover, it is meaningless to transform the translation characters because of the translation invariance, and the process of transforming the samples again is eliminated. Secondly, extracting features by CNN is more fitting than that by simple projection, orientation, or center of gravity, since by CNN feature extraction will not hit a bottleneck when improving the accuracy of double JPEG compression. Thirdly, the fitting ability of the whole model can be controlled by using different convolutions, pooling and the size of the final output feature vector. The dimensionality of the feature vector can be reduced by CNN when the model is overfitting, while the output dimensionality of the convolution layer can be increased by CNN when the model is underfitting. CNN is more flexible than other feature extraction methods. There are also 1×1 convolutional kernel and Dropout layers to reduce model overfitting. Each matrix extracts 64-dimensional features, hence 128-dimensional features are extracted by two matrices. The extraction method is as shown in Fig. 7.

Figure 7: The framework for detection

4.3 The Framework of Detection

In the experiment, the UCID [36] with size 512×384×3 is chosen as the experimental object, and first RTEn and M are extracted from it. This is followed by four times of convolution, Batch Normalization (BN) [37], Rectified Linear Unit (ReLU) and average pooling. Then UCID goes through two convolutions, BN, ReLU and average pooling, and passes through 2 layers of Dropout, 2 layers of Linear, and 1 layer of ReLU. Finally, the 128-dimensional features can be obtained as is shown in Fig. 7. The purpose of using the 1×1 convolutional kernel [37] and Dropout layers is to prevent the model from overfitting, and the function of BN and ReLU layers is to prevent the disappearance of the gradient and to maintain the convergence rate of the model in a stable state. Traditional CNN models generally adopt maximum pooling, which is intended to focus on the main feature information. The average pooling is used in our model because it is able to focus on local features, which is a useful function for us. Furthermore, the reason for using only error images rather than the entire content of the image as the input to the feature network, is to avoid extracting the features that may influence the classification results.

As can be seen from Fig. 7, 12-dimensi1onal features are extracted from the color space conversion error, and 128-dimensional features are extracted from the rounding error and the truncation error. Therefore, a total of 140-dimensional features are extracted from each image. According to different quality factors, two buttons are set as shown in Fig. 7. The first one is for the case that 12-dimensional features and 128-dimensional features are beneficial for classification, i.e., they provide effective features. The second one is for the case that one or two types of the features are not very useful for classification, they will be removed from the 140-dimensional features. Besides, SVM is applied, which has high classification accuracy and a good generalization ability when the sample is not huge in size. In this way, a subtle framework is established as depicted in Fig. 7, which combines the advantages of CNN and SVM to ensure that the valid features are extracted and the invalid ones are eliminated, and thus achieves the effect of increasing the accuracy of classification. The framework is eventually used to detect double JPEG compression.

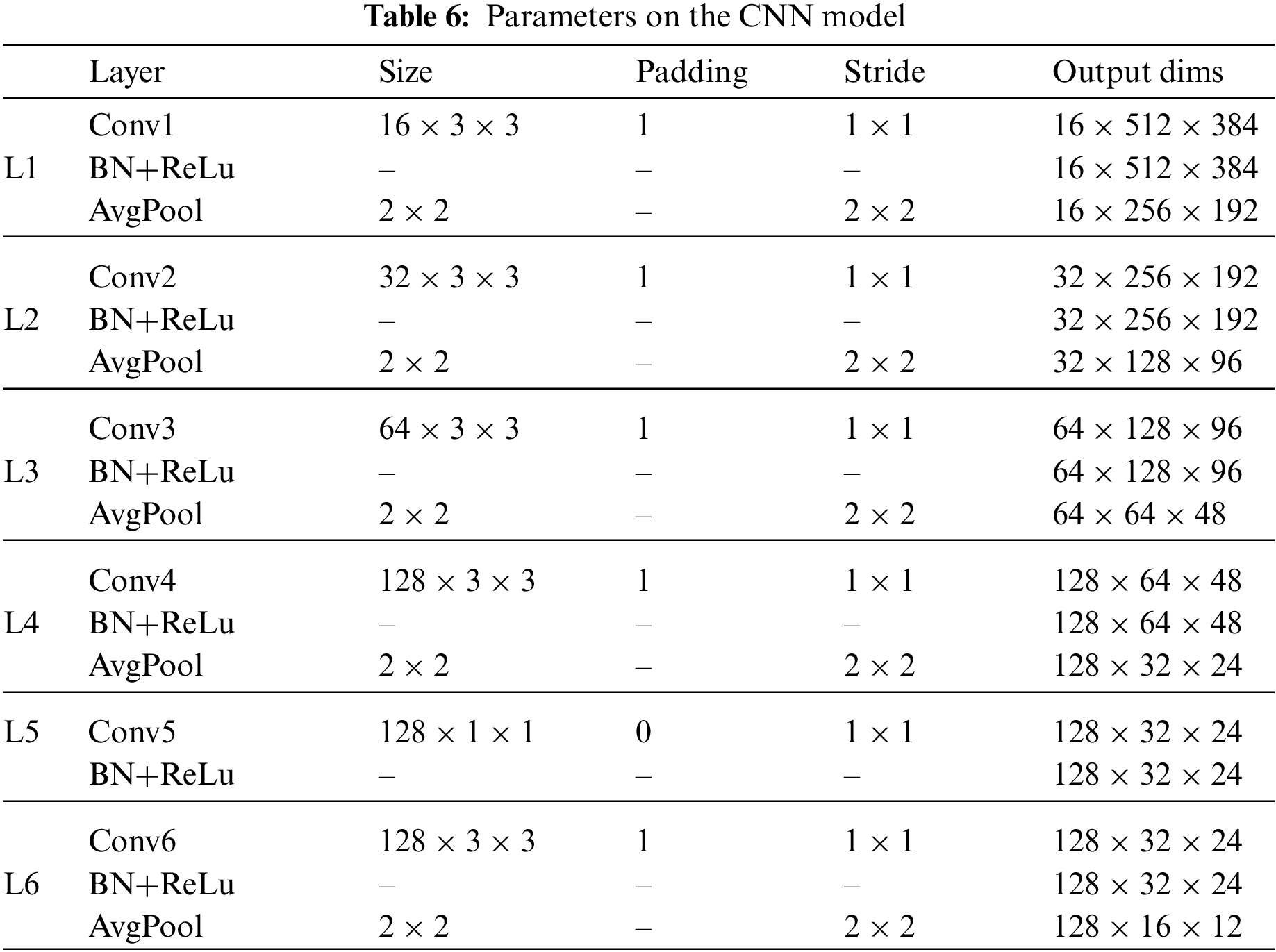
For the CNN model, the rounding error images, the truncation error images and the quantization coefficient images are randomly used, with 80% for training and 20% for testing, respectively. The trained model parameters are saved and the trained model is used to extract the features of each image on the UCID dataset. Table 6 listed the parameters of each layer in the process of feature extraction. To facilitate the description, take a rounding error image and a truncation error image of size 512×384×3 as a set of example for input, then the output dimensions of the error image after it passes through each layer could be obtained as shown in Table 6.

For the classifier, a Gaussian kernel soft-edge SVM is used, and the parameters c and g are defined by a grid-search on the multiplicative grid (c,g)∈{(2i,2j)|i∈{−20,…,0,…,20},j∈{−15,−14,…, 3}}. Each training is repeated 20 times, from which the generalizability of the model is embodied. Finally, the average classification accuracy rate is reported. In addition, Machine learning methods could also be employed for both feature selection and classification [38].

5  Experiment

All experiments are based on the UCID database on which all images are in color instead of being previously converted to grayscale images. Then negative samples are produced from a single compressed image with a specific quality factor, and positive samples are generated by double compression with the same quantization matrix. For each quality factor, half of the positive and negative sample images are randomly selected as training samples, and the remaining ones are used as testing samples.

Table 7 gives the classification accuracy only generated by color space conversion errors, where the first column represents different quality factors, the second column presents the accuracies obtained by the 6-dimensional features extracted from the sum of pixel values of the color space conversion error, and the third column shows the accuracies obtained by the 6-dimensional features extracted from the number of nonzero pixels of the color space conversion error, which are input to the classification results of the SVM. By comparing the second and the third column, we know AC1 outperforms AC2 for any given quality factor. The fourth column indicates the classification result of these 12-dimensional features fed into the SVM together, and it is apparent that this result is the best, which also implies both the two types of features are useful information.

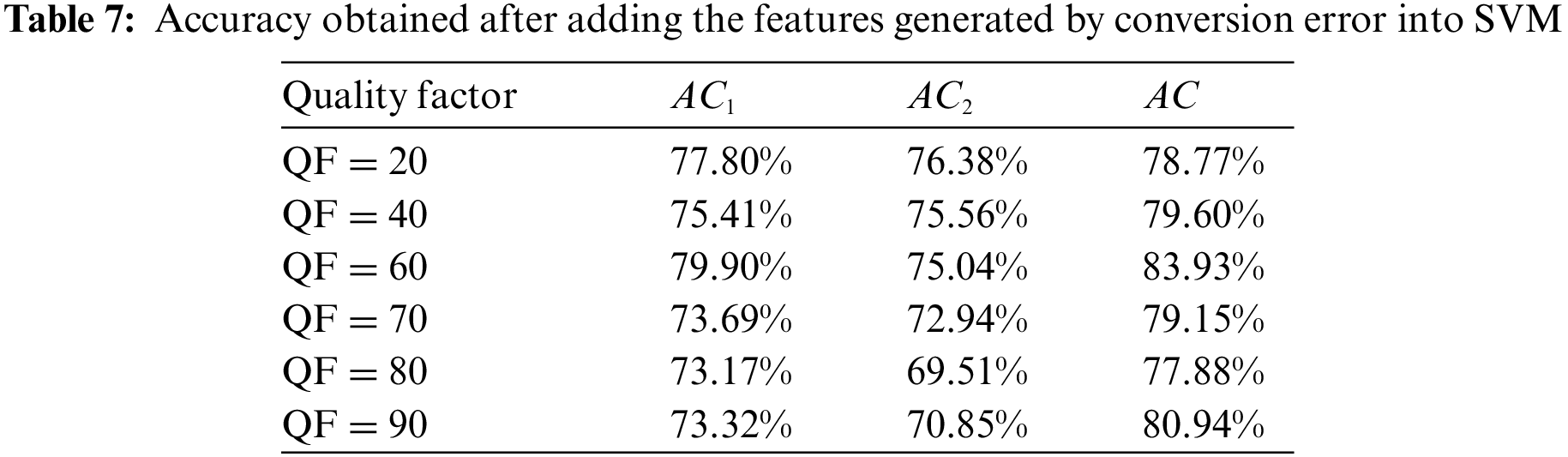
In addition, Table 7 reveals that for high quality factors, the images retain more original information, and features extracted from the color space conversion error are more useful for the classification of singly and doubly compression, which improves the accuracy of double JPEG classification.

Table 8 demonstrates the detection accuracies of the method proposed in this paper and other methods under the UCID dataset. The detection accuracies with quality factors 20, 40 and 60 were not discussed in both [22,26]. We use the symbol ‘-’ to present the missing accuracies. It is demonstrated from Table 8 that the method proposed is superior to the method discussed in [22]. The result of [22] is at least 6% less than that in this paper when the quality factor is less than 80. In [24], the classification performance is better than that in this paper at quality factors 80 and 90, although the difference is not significant. When the quality factor is less than 70, the results of this paper are at least 7% more than those of [27]. As for the results of [26], except for the case that the quality factor is 80, they are not as good as the corresponding results in this paper. Compared with methods in [24,27,28,39], the proposed method exhibits a better improvement in detection accuracy of at least 5% at quality factors less than 70.

Compared to a recent paper [28], the enhancement in accuracy with a lower quality factor in this paper is attributed to the addition of new features from the extraction of color space transformation errors, as well as the use of CNNs to extract more effective features. Current detection algorithms for double JPEG compression with the same quantization matrix have accuracies up to 99% or more for high quality factors, while they are not ideal for the classification of low quality factors. If this phenomenon is utilized by tampers, the detection accuracy results of such algorithms will not be as satisfactory as expected. Accordingly, the method proposed in this paper has practical implications compared to the existing methods.

JPEG images are extensively used on the Internet due to their advantages such as occupying less space, easy for transmission and store. According to the relevant data, around 80% of the images on the Internet have adopted JPEG compression standard. Tampers tend to avoid double JPEG detection intentionally, hence it is of great necessity to increase quality factors of images.

The quantization matrix used in the JPEG compression is not limited to 100 standard Q matrices (represented by the quality factors). And there are different image processing softwares being convenient for users to apply their own customized quantization matrix. Due to the ingenious design of the framework, the extraction process for the input image is used as a direct extraction method using the quantization matrix for compression. Therefore, the classification is still applicable even if the coders use their own customized quality factors for compression. To sum up, the method has a broader applicability than the existing methods.

6  Conclusion

This paper poses the problem of double JPEG detection under the same quantization matrix for color images. We propose a method for features extraction based on a combination of CNN and traditional methods. With the error image being input, a novel framework designed to extract 140-dimensional features starts to work. Based on the extracted features, a SVM classifier is used for classification. The ingenuity of this method is to combine CNN with SVM, which takes advantage of CNN in feature extraction and SVM in classification for small samples with high accuracy. The experimental results demonstrate that the method outperforms the current state-of-the-art methods on double JPEG detection for color images, especially those with low quality factors. When the quality factor is less than 80, the accuracy of the proposed method are at least 3% more than that of the other methods. However, there are still many constraints for double JPEG compression detection of color images with the same quantization matrix. For instance, since the quantization error cannot be obtained by the existing methods, the relationships between the conversion error, the quantization error, the truncation error and the rounding error cannot be well expressed. For another instance, at present the quantization error cannot be used for the detection of double JPEG compression yet. Moreover, though satisfactory performance of our proposed method have been demonstrated by experiment, more factors need to be taken into consideration since the situation may be complicated in most realistic scenarios. Accordingly, further thoughts and studies on solving practical problems are necessary.

Funding Statement: Supported by the Fundamental Research Funds for the Central Universities (No. 500421126).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

    1. G. K. Wallace, “The JPEG still picture compression standard,” IEEE Transactions on Consumer Electronics, vol. 38, no. 1, pp. xviii–xxxiv, 1992. [Google Scholar]

    2. S. Cha, U. Kang and E. Choi, “The image forensics analysis of JPEG image manipulation (Lightning Talk),” in 2018 Int. Conf. on Software Security and Assurance (ICSSA), Seoul, Korea, pp. 82–85, 2018. [Google Scholar]

    3. K. H. Rhee, “Forensic detection of JPEG compressed image,” in 2018 Int. Conf. on Computational Science and Computational Intelligence (CSCI), Las Vegas, Nevada, USA, pp. 485–488, 2018. [Google Scholar]

    4. G. Fahmy, “Nonorthogonal DCT implementation for JPEG forensics,” in 2014 14th Int. Conf. on Hybrid Intelligent Systems, Kuwait, pp. 7–11, 2014. [Google Scholar]

    5. W. Luo, J. Huang and G. Qiu, “JPEG error analysis and its applications to digital image forensics,” IEEE Transactions on Information Forensics and Security, vol. 5, no. 3, pp. 480–491, 2010. [Google Scholar]

    6. V. L. L. Thing, Y. Chen and C. Cheh, “An improved double compression detection method for JPEG image forensics,” in 2012 IEEE Int. Symp. on Multimedia, Irvine, CA, USA, pp. 290–297, 2012. [Google Scholar]

    7. H. Ren and S. Niu, “Separable reversible data hiding in homomorphic encrypted domain using POB number system,” Multimedia Tools and Applications, vol. 81, no. 2, pp. 2161–2187, 2021. [Google Scholar]

    8. M. -J. Kwon, I. -J. Yu, S. -H. Nam and H. -K. Lee, “CAT-Net: Compression artifact tracing network for detection and localization of image splicing,” in 2021 IEEE Winter Conf. on Applications of Computer Vision (WACV), Waikoloa, HI, USA, pp. 375–384, 2021. [Google Scholar]

    9. A. Roy, D. B. Tariang, R. S. Chakraborty and R. Naskar, “Discrete cosine transform residual feature based filtering forgery and splicing detection in JPEG images,” in 2018 IEEE/CVF Conf. on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, Utah, USA, pp. 1552–1560, 2018. [Google Scholar]

  10. W. Wei, S. Wang and Z. Tang, “Estimation of rescaling factor and detection of image splicing,” in 2008 11th IEEE Int. Conf. on Communication Technology, Hangzhou, China, pp. 676–679, 2008. [Google Scholar]

  11. H. R. Kang, “Detection of spliced image forensics using texture analysis of median filter residual,” IEEE Access, vol. PP, no. 99, pp. 1, 2020. [Google Scholar]

  12. S. Li, Z. Han, Y. Chen, B. Fu, C. Lu et al., “Resampling forgery detection in JPEG-compressed images,” in 2010 3rd Int. Congress on Image and Signal Processing, Yantai, China, pp. 1166–1170, 2010. [Google Scholar]

  13. D. Zhu and Z. Zhou, “Resampling tamper detection based on JPEG double compression,” in 2014 Fourth Int. Conf. on Communication Systems and Network Technologies, Bhopal, India, pp. 914–918, 2014. [Google Scholar]

  14. B. Bayar and M. C. Stamm, “On the robustness of constrained convolutional neural networks to JPEG post-compression for image resampling detection,” in 2017 IEEE Int. Conf. on Acoustics, Speech and Signal Processing (ICASSP), New Orleans, LA, USA, pp. 2152–2156, 2017. [Google Scholar]

  15. A. C. Popescu and H. Farid, “Exposing digital forgeries by detecting traces of resampling,” IEEE Transactions on Signal Processing, vol. 53, no. 2, pp. 758–767, 2005. [Google Scholar]

  16. K. Petrowski, M. Kharrazi, H. T. Sencar and N. Memon, “PSTEG: Steganographic embedding through patching [image steganography],” in Proc. (ICASSP ′05). IEEE Int. Conf. on Acoustics, Speech, and Signal Processing, Philadelphia, PA, USA, pp. 537–540, 2005. [Google Scholar]

  17. Q. J. Ji, P. P. Yu and Z. H. Xia, “QDCT encoding-based retrieval for encrypted JPEG images,” Journal on Big Data, vol. 2, no. 1, pp. 32–51, 2020. [Google Scholar]

  18. Z. Liu, X. Wang and J. Chen, “Passive forensics method to detect tampering for double JPEG compression image,” in 2011 IEEE Int. Symp. on Multimedia, Dana Point, CA, USA, pp. 185–189, 2011. [Google Scholar]

  19. Y. Niu, X. Li, Y. Zhao and R. Ni, “Primary quality factor estimation of resized double compressed JPEG images,” in 2020 IEEE Int. Conf. on Image Processing (ICIP), Abu Dhabi, United Arab Emirates, pp. 583–587, 2020. [Google Scholar]

  20. F. Zhao, Z. Yu and S. Li, “Detecting double compressed JPEG images by using moment features of mode based DCT histograms,” in 2010 Int. Conf. on Multimedia Technology, Ningbo, China, pp. 1–4, 2010. [Google Scholar]

  21. J. Wang, W. Huang, X. Luo, Y. -Q. Shi and S. K. Jha, “Non-aligned double JPEG compression detection based on refined Markov features in QDCT domain,” Journal of Real-Time Image Processing, vol. 17, no. 1, pp. 7–16, 2019. [Google Scholar]

  22. F. Huang, J. Huang and Y. Q. Shi, “Detecting double JPEG compression with the same quantization matrix,” IEEE Transactions on Information Forensics and Security, vol. 5, no. 4, pp. 848–856, 2010. [Google Scholar]

  23. Y. Niu, X. Li, Y. Zhao and R. Ni, “An enhanced approach for detecting double JPEG compression with the same quantization matrix,” Signal Processing Image Communication, vol. 76, no. 2, pp. 89–96, 2019. [Google Scholar]

  24. J. Yang, J. Xie, G. Zhu, S. Kwong and Y. -Q. Shi, “An effective method for detecting double JPEG compression with the same quantization matrix,” IEEE Transactions on Information Forensics and Security, vol. 9, no. 11, pp. 1933–1942, 2014. [Google Scholar]

  25. P. Peng, T. Sun, X. Jiang, K. Xu, B. Li et al., “Detection of double JPEG compression with the same quantization matrix based on convolutional neural networks,” in 2018 Asia-Pacific Signal and Information Processing Association Annual Summit and Conf. (APSIPA ASC), Honolulu, Hawaii, USA, pp. 717–721, 2018. [Google Scholar]

  26. Z. Wang and L. Zhu, “Double compression detection based on feature fusion,” in Int. Conf. on Machine Learning and Cybernetics IEEE, Singapore, pp. 379–384, 2017. [Google Scholar]

  27. X. Huang, S. Wang and G. Liu, “Detecting double JPEG compression with same quantization matrix based on dense CNN feature,” in 2018 25th IEEE Int. Conf. on Image Processing (ICIP), Athens, Greece, pp. 3813–3817, 2018. [Google Scholar]

  28. J. Wang, H. Wang, J. Li, X. Luo, Y. -Q. Shi et al., “Detecting double JPEG compressed color images with the same quantization matrix in spherical coordinates,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 30, no. 8, pp. 2736–2749, 2020. [Google Scholar]

  29. H. Wang, J. W. Wang, X. Y. Luo, Y. H. Zheng, B. Ma et al., “Detecting aligned double JPEG compressed color image with same quantization matrix based on the stability of image,” IEEE Transactions on Circuits and Systems for Video Technology, vol. 32, no. 6, pp. 4065–4080, 2022. [Google Scholar]

  30. H. A. Jalab, R. W. Ibrahim, A. M. Hasan, F. K. Karim, A. R. Al-Shamasneh et al., “A new medical image enhancement algorithm based on fractional calculus,” Computers, Materials & Continua, vol. 68, no. 2, pp. 1467–1483, 2021. [Google Scholar]

  31. T. Y. Hang, S. Z. Niu and P. F. Wang, “Multimodal-adaptive hierarchical network for multimedia sequential recommendation,” Pattern Recognition Letters, vol. 152, pp. 10–17, 2021. [Google Scholar]

  32. A. N. Harish, V. Verma and N. Khanna, “Double JPEG compression detection for distinguishable blocks in images compressed with same quantization matrix,” in 2020 IEEE 30th Int. Workshop on Machine Learning for Signal Processing (MLSP), Espoo, Finland, pp. 1–6, 2020. [Google Scholar]

  33. A. U. Deshpande, A. Narayan Harish, S. Singh, V. Verma and N. Khanna, “Neural network based block-level detection of same quality factor double JPEG compression,” in 2020 7th Int. Conf. on Signal Processing and Integrated Networks (SPIN), Zurich, Switzerland, pp. 828–833, 2020. [Google Scholar]

  34. J. W. Zhang, M. Z. A. Bhuiyang, X. Yang, A. K. Singh, D. F. Hsu et al., “Trustworthy target tracking with collaborative deep reinforcement learning in EdgeAI-Aided IoT,” IEEE Transactions on Industrial Informatics, vol. 18, no. 2, pp. 1301–1309, 2022. [Google Scholar]

  35. J. Zhang, X. Yan, Z. Cheng and X. Shen, “A face recognition algorithm based on feature fusion,” Concurrency and Computation: Practice and Experience, vol. 34, no. 14, e5748, 2020. [Google Scholar]

  36. G. Schaefer and M. Stich, “UCID-An uncompressed colour image database,” in Proc. SPIE. Speech, Signal Process, pp. 472–480, San Jose, CA, USA, 2004. [Google Scholar]

  37. G. Xu, H. Z. Wu and Y. Q. Shi, “Structural design of convolutional neural networks for steganalysis,” IEEE Signal Processing Letters, vol. 23, no. 5, pp. 708–712, 2016. [Google Scholar]

  38. O. Bardhi and B. G. Zapirain, “Machine learning techniques applied to electronic healthcare records to predict cancer patient survivability,” Computers, Materials & Continua, vol. 68, no. 2, pp. 1595–1613, 2021. [Google Scholar]

  39. Y. Niu, X. Li, Y. Zhao and R. Ni, “Detection of double JPEG compression with the same quantization matrix via convergence analysis,” IEEE Transactions on Circuits and Systems for Video Technology, pp. 3279–3290, 2021. [Google Scholar]