A Credit Card Fraud Model Prediction Method Based on Penalty Factor Optimization AWTadaboost

1  Introduction

With the rise of the electronic payment era, more and more people are using credit cards to make purchases and transfers. There is no doubt that electronic payment has brought great convenience to people’s daily life and work, but at the same time, the risk of theft of users’ personal information is also increasing, leading to an increase in credit card fraud cases year by year. Therefore, the prevention of credit card fraud has become one of the hot topics of discussion in academia and industry: A deep learning (DL) based problem-solving method for text data has been developed using Kaggle dataset, using an inverse frequency method to input images into CNN structure with class weights to solve class imbalance problem, while applying DL and machine learning (ML) methods to verify the robustness and effectiveness of their system [1]. An ML-based credit card fraud detection engine is proposed by Emmanuel et al. Firstly, the genetic algorithm is used for feature selection, after that various ML classifiers are used to build the fraud detection engine separately. Finally, the method is experimentally proven to be superior to existing systems [2], K et al. designed a multi-classifier framework to address the challenge of credit card fraud detection. At its core is an integrated model with multiple machine learning classification algorithms and uses the behavior-knowledge space (BKS) to combine predictions from multiple classifiers [3]. A novel classifier, the moth-flame earth worm optimisation-based deep belief network (MF-EWA-based DBN) for fraud detection, has also been innovative proposed [4]. Recent advances in machine learning algorithms and deep reinforcement learning for credit card fraud detection systems were studied and evaluated by Khanh et al. [5]. Hussain et al. [6] introduced a new scheme rating mechanism to rate the importance of two-factor authentication for smart cards, which helps to determine good and bad schemes with managers for decision-making. Hsuan et al. [7] proposed an autoencoder with probabilistic random forest (AE-PRF) approach for credit card fraud detection, and showed through experimental results that AE-PRF can be well suited for severely unbalanced classification scenarios. But with the advent of boosting, credit card fraud detection has also started to use this approach extensively: Saleh et al. [8] studied 66 machine learning models based on two-stage evaluation in a real credit card fraud detection dataset and concluded that the AllKNN-CatBoost model outperformed previous models in the evaluation metrics. Some scholars [9] concluded from the experimental results that the decision tree boosting technique is significantly better than the other techniques by comparing the classification results after using several separate different classifiers and using an integrated approach (Boosting).

Boosting is an important class of machine learning algorithms, and his basic idea is to form a strong classifier by integrating a series of weak classifiers together according to different weights [10]. The boosting algorithm needs to know the upper limit of the error rate of the classifier in advance, which is difficult to implement in practical applications. For this reason Freund et al. [11] proposed the Adaboost algorithm. As the superiority of Adaboost algorithm was exploited, some scholars also started to use Adaboost for credit card fraud: Kuldeep et al. [12] applied a hybrid method of Adaboost and majority voting to credit card fraud detection. The experimental results also showed that majority voting method has good accuracy in detecting credit card fraud cases. Karthik et al. [13] constructed a new model for credit card fraud detection by building a hybrid model of bagging and boosting integrated classifier, fusing the key features of both techniques. However, these studies ignore the fact that the traditional Adaboost algorithm is prone to overfitting when there are noisy samples in the sample set, which makes the classification effect poor. In order to solve this problem, the mainstream research direction is to reduce the weight of noisy samples, but how to determine the noisy samples and how to modify the sample weights is still a hot issue. Among them, Fan et al. [14] proposed to use the clustering algorithm in Adaboost to determine the noisy samples dynamically and adopt a new method to update the weights of misclassified samples, and this improvement has been proved to be effective in the final experimental results. And this paper will provide a simpler idea: using the number of consecutive misclassifications to determine the noisy samples, while introducing a penalty factor to reconstruct the weight distribution of the samples. This method is more convenient to implement, and at the same time the accuracy is improved compared with other traditional learning algorithms.

At the same time, considering the large number of samples trained in the actual credit card fraud, it will lead to the long processing time of traditional Adaboost, so it is not appropriate to apply Adaboost directly to the credit card fraud scenario. For the time-consuming improvement of Adaboost algorithm, the research direction is mainly through pruning operation to screen out the data with little value, such as static weight trimming adaboost (SWTAdaboost) [15] and dynamic weight trimming adaboost (DWTAdaboost) [16], while this paper will adopt the Adaboost algorithm with adaptive weight trimming (AWTadaboost) proposed by Bing et al. [17], and then use the penalty factor to reconstruct the sample weight assignment to finally obtain the PF_ AWTAdaboost algorithm. The main innovations of this paper are as follows.

(1)   Systematically analyzed the drawbacks of the traditional Adaboost algorithm in the presence of noisy samples, and proposed a method to optimize the algorithm by constructing penalty factors with the number of successive misclassifications of samples.

(2)   By comparing the penalty strength of the three types of penalty factors constructed in this paper, the best penalty factor is determined. It is then introduced into the AWTAdaboost algorithm to obtain the final optimization algorithm. Final application to credit card fraud detection scenario.

The rest of the paper is organized as follows: chapter 2 provides a theoretical analysis and selection of the introduced penalty factors, then introduces our improved algorithm--the PF_AWTAdaboost algorithm, chapter 3 designs experiments on datasets such as credit card fraud to compare with other algorithms, and finally draws conclusions in chapter 4.

2  PF_AWTAdaboost Algorithm

This section first proposes the concept of penalty factor by analyzing the traditional Adaboost algorithm, and compares the three nonlinear penalty functions proposed in this paper, then migrates the penalty factor to the AWTAdaboost algorithm, introduces the PF_AWTAdaboost algorithm process, and finally analyzes the convergence of the AWTAdaboost algorithm.

2.1 Penalty Factors

2.1.1 Theoretical Analysis of Introducing Penalty Factors

Obviously, in the traditional Adaboost algorithm, if there is noise in the training set, the weight of noisy samples that are difficult to classify correctly will increase with the number of iterations, which will make the base classifier pay too much attention to the noisy samples and thus make a wrong decision, leading to the degradation of the performance of the final strong classifier. Therefore, reducing the weight of noisy samples becomes a mainstream direction for improvement, and this paper proposes to use the number of consecutive misclassifications to distinguish normal samples from noisy samples, because noisy samples are more difficult to classify correctly than normal samples, and the number of misclassifications of noisy samples in the process of iteration is definitely more than the number of misclassifications of normal samples, but in order to avoid treating the occasional misclassified normal samples as noise values. We choose the number of consecutive misclassifications of samples to minimize the misclassification cases. On this basis, we establish the penalty factor A(e), where e is the number of consecutive misclassifications, and A(e) decreases as e grows. After introducing the penalty factor, Eqs. (3) and (4) becomes.

Dn+1(i)′=Dn(i)Zne−αnAn(ei)(5)

(When the classification is correct, let An(ei)=1, and ei Reset to 0)

Dn+1(i)′=Dn(i)ZneαnAn(ei)(6)

By comparison, it is found that the weight of noisy samples under Eq. (6) will be smaller than that under Eq. (4), thus making the weak classification no longer overly concerned with noisy samples, and the following analysis of the changes to the traditional Adaboost performance after the introduction of A(e).

With the introduction of the penalty factor Eqs. (1) and (2) becomes.

εn′=∑Gn(xi)≠yidn(i)An(ei)(7)

αn′=12ln⁡(1−εn′εn′)(8)

Since A(e) ≤ 1, there exists.

dn(i)≥dn(i)An(ei)(9)

Thus making

εn′≤εn(10)

Then by comparing Eqs. (2) and (8) we get.

αn′≥αn(11)

Therefore, in the final classification decision, the classifier will not overlearn noisy samples, while classifiers with lower error rates will receive greater weights in the Adaboost algorithm with the introduction of penalty factors than under the traditional Adaboost algorithm.

2.1.2 Selection of A(e)

Regarding the selection of A(e), three nonlinear continuous penalty functions are proposed under the constraints proposed in this paper. Are 1logc⁡x,c−x,x−c respectively. Where c is a constant value chosen from the actual situation (c > 0) and x is the number of consecutive sample misclassifications. The penalty weight of the penalty function is also related to the value of c. Therefore, in the case of c taking the same value, the penalty weights of the three penalty functions change with the number of consecutive misclassifications as shown in Fig. 1 (here c takes e): with the increase in the number of consecutive misclassifications, the penalty weights of the three penalty factors are rising, but the 1logc⁡x images are smoother and more reasonable, so this paper chooses 1logc⁡x as the penalty factor.

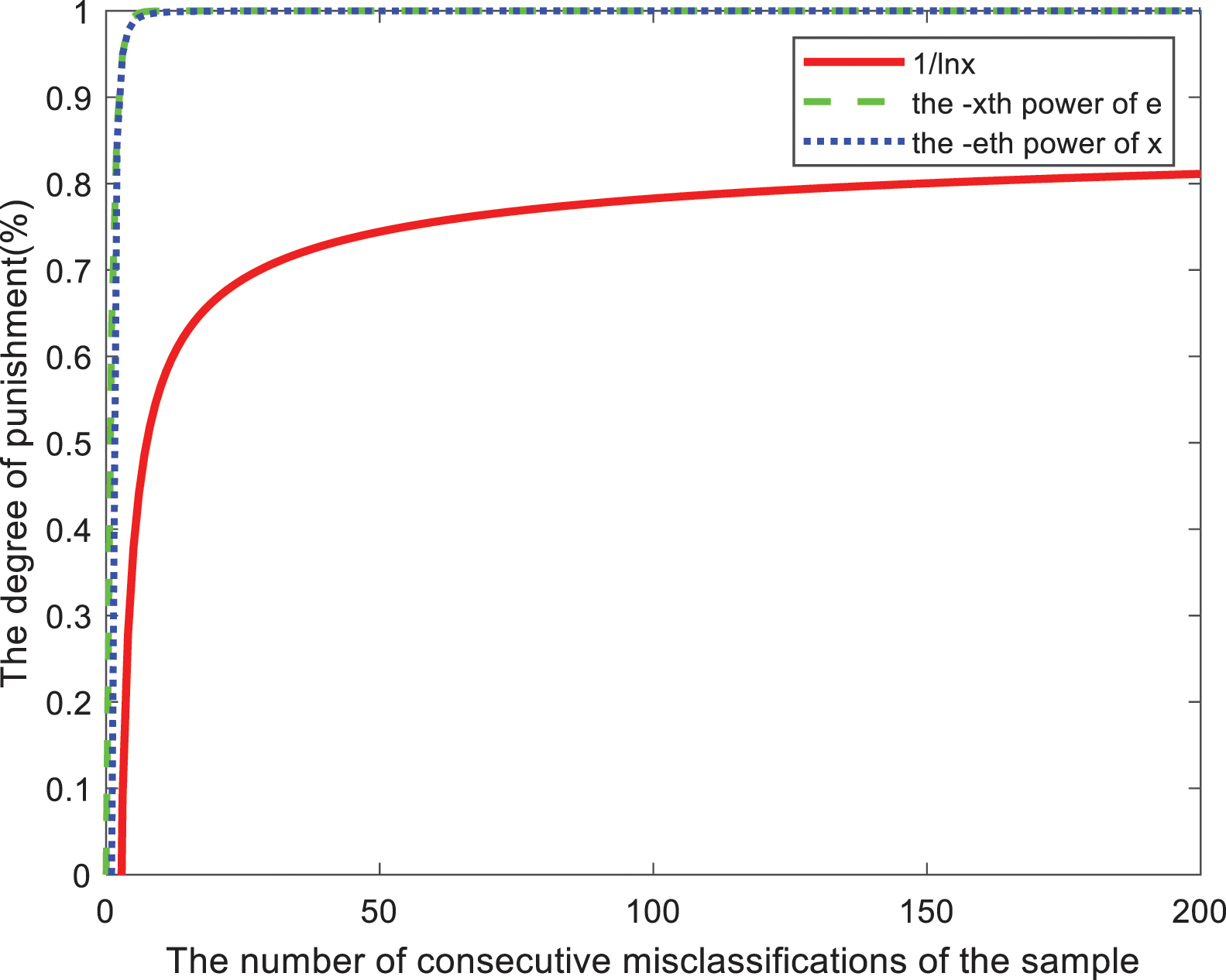
Figure 1: Image of penalty strength for each penalty factor

2.2 PF_AWTAdaboost Algorithm

2.3 Convergence Analysis of the PF_AWTAdaboost Algorithm

The following analysis shows whether the error rate of the AWTAdaboost algorithm still meets the requirements after introducing the penalty factor.

The error rate of the original AWTAdaboost algorithm is

ε=1m∑i=1m||(H′(xi)≠yi)||(14)

Let f(x)=∑n=1Nαn′Gn′(x), we have H′(x)=sign(f(x)), and when H′(x)≠yi, there exists yif(xi)≤0, at this time exp⁡(−yif(xi))≥1, with :

||(H′(xi)≠yi)||≤exp⁡(−yif(xi))(15)

With the introduction of the penalty factor.

Dn+1(i)=Dn(i)exp⁡(−αn′yiGn′(xi)An(ei))Zn=exp⁡(−∑nαn′yiGn′(xi)An(ei))m∏nZn(16)

Due to An(ei)≤1,exp⁡(−∑nαn′yiGn′(xi))>0, therefore.

Dn+1(i)>exp⁡(−yif(xi))m∏nZn(17)

Combining Eqs. (14), (15), and (17), we can see that

ε=1m∑i=1m||(H′(xi)≠yi)||≤1m∑i=1mexp⁡(−yif(xi))<1m∗m∑i=1mDn+1(i)∗∏nZn(18)

And because by the definition of the sample distribution there is ∑i=1Dn+1(i)=1, so

ε<∏nZn(19)

Dn(i) After the update to make Dn+1(i) becomes a new probability distribution there are.

Dn+1(i)=Dn(i)∑i=1NDn(i)(20)

Also according to Eq. (13) we get

Dn(i)∑i=1NDn(i)=Dn(i)exp⁡(−αn′yiGn′(xi)An(ei))Zn(21)

According to Eq. (21) we have

Zn=∑i=1NDn(i)exp⁡(−αn′yiGn′(xi)An(ei))=∑Gn′(xi)≠yieαn′An(ei)+∑Gn′(xi)=yie−αn′An(ei)(22)

Because An(ei)≤1, while linking Eq. (12) can be obtained

Zn≤(1−εn′)e−αn′+εn′eαn′=2εn′(1−εn′)=1+2r(23)

where r=−2(12−εn′)2

Compare 1+2r and e−r the Taylor expansions of

Zn≤1+2r≤e−r(24)

The final error rate of PF_AWTAdaboost algorithm on the training set can be obtained according to Eqs. (19) and (24) ε is

ε=1m∑i=1m||(H′(xi)≠yi)||<∏nZn≤e−nr(25)

Therefore, it can be finally concluded that the error rate of PF_AWTAdaboost algorithm has an upper bound on the training set, and the upper bound on the error rate decreases exponentially when the number of iterations increases, so the AWTAdaboost algorithm still converges after the penalty factor is introduced.

3  Experiment

3.1 Experiment Preparation

3.1.1 Data Set Processing

The dataset used in this paper is the credit card fraud dataset provided by the kaggle platform, which contains transactions made by European cardholders via credit cards in September 2013, showing transactions that occurred over a two-day period. There were 492 fraudulent transactions out of 284, 807 transactions. The dataset has been processed by PCA and the details are shown in Table 1. Since the number of positive and negative categories in the original dataset samples is severely out of proportion as well as the existence of some missing values, etc., in order to enhance the generalization ability of the model and prevent overfitting, feature engineering is performed before training, and after under sampling, the processed dataset is divided randomly according to an approximate 3:1. We obtain the final training set (total number of samples is 831) and the test set (total number of samples is 279).

3.1.2 Evaluation Indicators

Precision and recall are often used as metrics for algorithm performance evaluation when exploring the performance of binary classification algorithms. We divide the class of actual sample value and the class of classifier prediction as follows: when the actual sample value is a positive case and the classifier predicts a positive case as a true case TP; when the actual sample value is a negative case and the classifier predicts a positive case as a false positive case FP; when the actual sample value is a negative case and the classifier predicts a negative case as a true negative case TN; and when the actual sample value is a positive case and the classifier predicts a negative case as a false negative case FN. This defines the precision rate P=TPTP+FP and the recall rate R=TPTP+FN.

In the problem of credit card fraud detection, it is the minority class of samples that is of concern. Therefore, it is very important to identify the few fraudulent transactions or users with high accuracy to avoid financial losses. The traditional classification criteria may focus more on the majority class samples, and the accuracy rate is still high even if all the minority class samples are incorrectly predicted, so the traditional classification metrics are not applicable to the imbalanced classification problem. In order to select metrics for more comprehensive evaluation of classifiers, scholars have summarized and proposed two evaluation criteria for unbalanced classification problems -- F-meature, ROC (Receiver Operating characteristic).

F-meature is an evaluation criterion that combines precision and recall, which is defined as.

F−meature=(1+β2)∗R∗Pβ2∗P+R(26)

where β is the coefficient that balances the precision and recall, and when β F-meature is F1 of the criterion when it is taken as 1. This criterion can take into account both minority and majority classes.

ROC is a graph with FP/(FP + TN) (false positive case rate) as the horizontal axis and TP/(TP + FN) (true case rate) as the vertical axis, which indicates the change of false positive case rate and true case rate when the threshold value is changed, and when the ROC curve is closer to the upper left corner, it means that the classifier gets higher true case rate with lower false positive case rate. However, the ROC curve only reflects the change of false positive rate and true rate, and cannot be used to evaluate the classifier quantitatively [18], so we generally choose the area under the ROC curve (AUC) as the evaluation index, i.e., the area enclosed by the ROC curve, and a larger AUC value indicates a better overall performance of the classifier. Therefore, in this section, we choose F1 value and AUC value as credit card fraud prediction evaluation metrics.

3.2 Parameters

In the PF_AWTAdaboost algorithm model training, there are two independent parameters: the sample trimming threshold k, and the penalty factor c. Since the ln-type penalty factor is selected in this paper, c at this point denotes the true number. First some experiments are performed to find the optimal values of these parameters.

3.2.1 Selection of K-Value

Here we choose 40 classifiers and select k from 5 to 10 for the experiments. Since the k value will determine the number of cropped samples and thus affect the operation time and classification, this paper selects the one with better effect by observing the F1 value of each k value on the test set. The results of the runs for different k values are shown in Fig. 2.

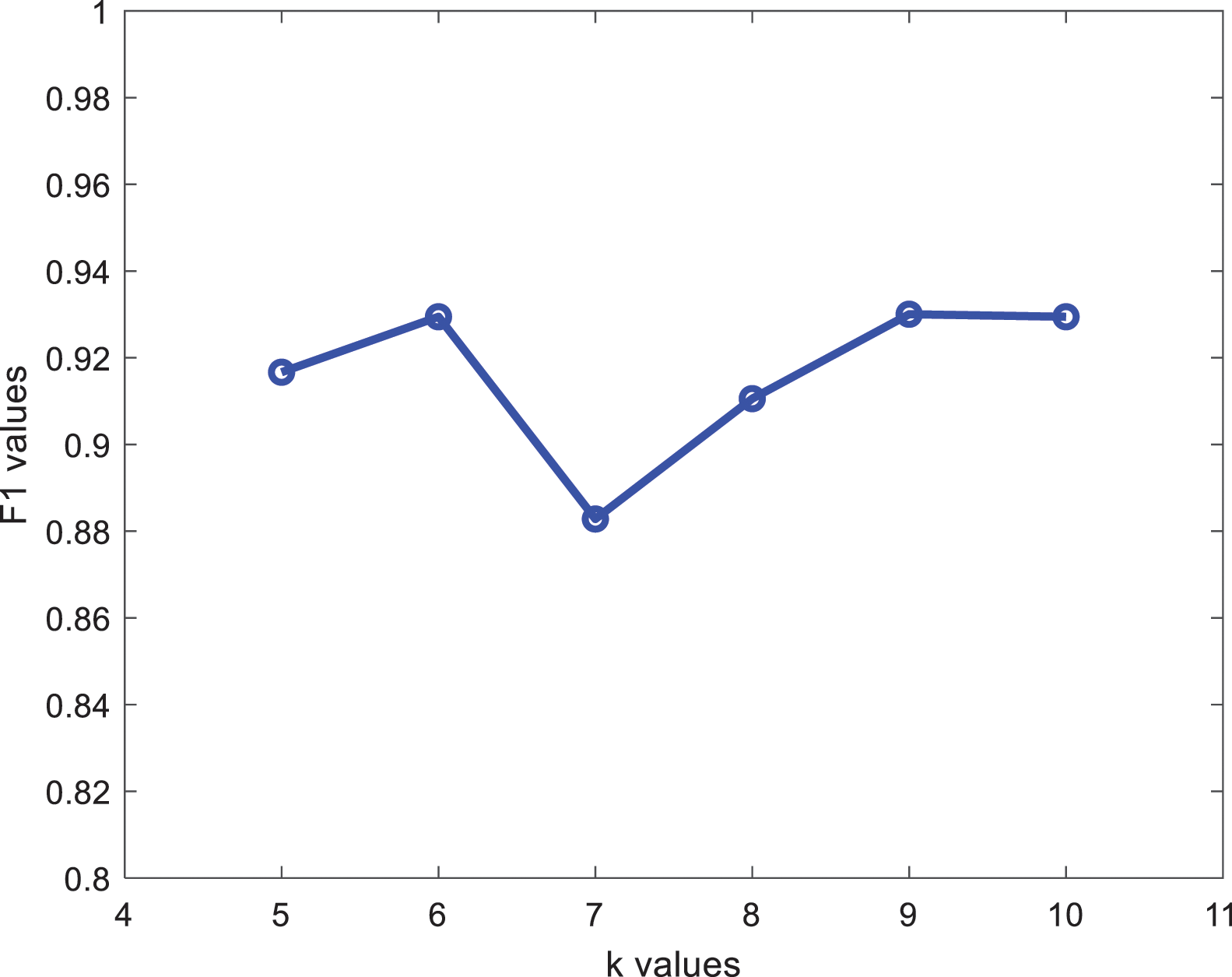
Figure 2: F1 values at different k values

The F1 value is highest for k = 6 and k = 9. However, considering that the higher the value of k, the higher the number of cropped samples, the more likely it is to cause decision errors, k = 9 is discarded and k = 6 is chosen for the experiment.

3.2.2 Selection of C-Value

The penalty factor selected in this paper is 1logc⁡x, where the value of c directly determines the threshold value of the penalty factor to distinguish between normal and noisy samples and the size of the penalty strength, so a better value of c will enhance the comprehensive performance of the classifier, i.e., the F1 value is increased. The results of running with different penalty factors are shown in Fig. 3:

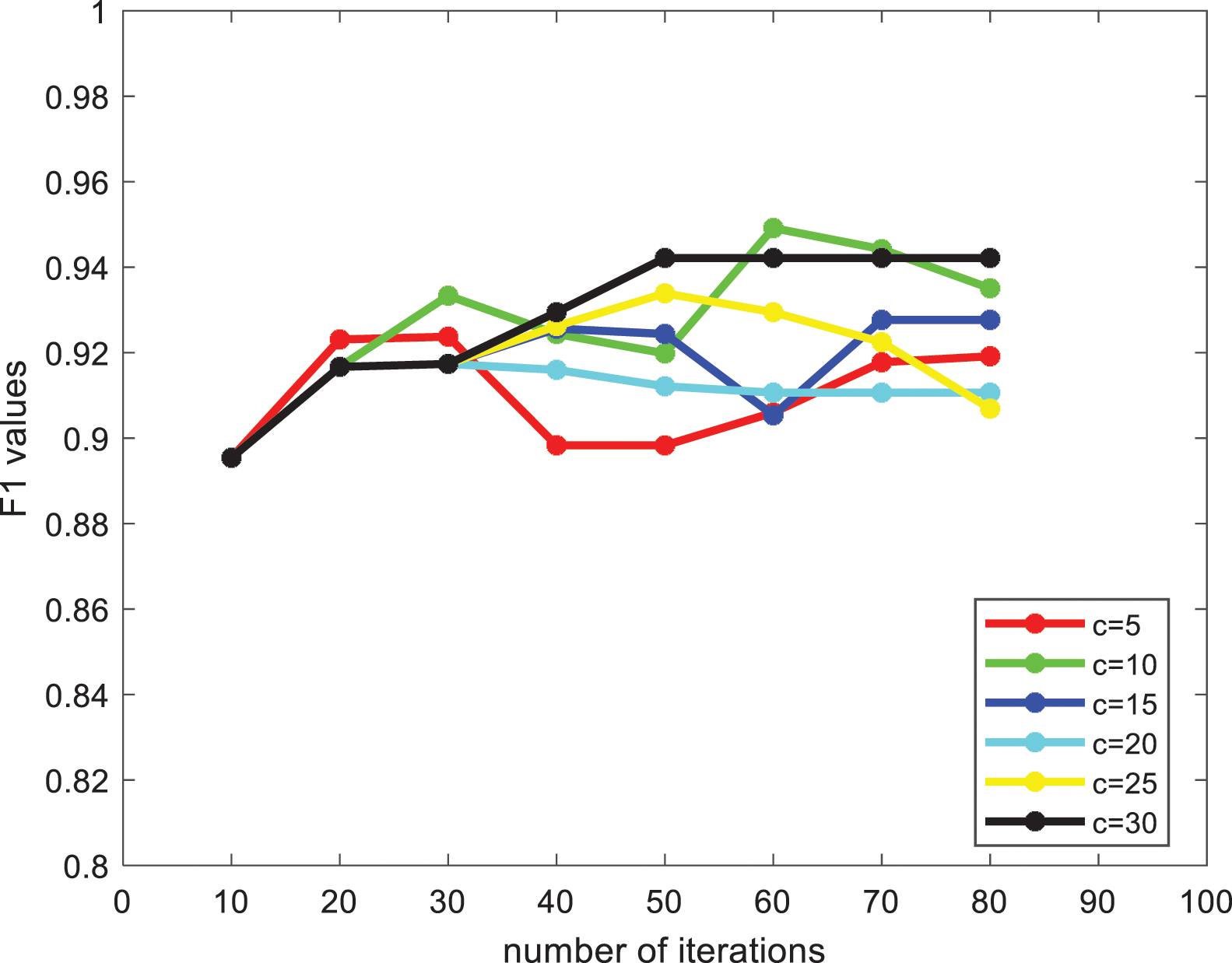
Figure 3: F1 values at different c values

From Fig. 3, it can be found that the F1 value of the algorithm under each penalty factor tends to increase roughly as the number of iterations increases, among which c = 30 is more effective, so we choose a penalty factor of 1log30⁡x.

3.3 Experimental Results of Credit Card Fraud Dataset

From Figs. 4 and 5 shows that: on the credit card fraud dataset, when the number of iterations is between 40 and 80 the F1 value, AUC value of PF_AWTAdaboost algorithm is better than the other algorithms, and the F1 value, AUC value of SVM algorithm is significantly lower than the other algorithms. And when the number of iterations is 10 to 40, the PF_AWTAdaboost algorithm overlaps with the AWTAdaboost algorithm image because the penalty factor selected in this paper is 1log30⁡x, that is, the sample will be penalized when the number of consecutive misjudgments exceeds 30, so the penalty factor will not work when the number of iterations is less than or equal to the misjudgment threshold set by the penalty factor.

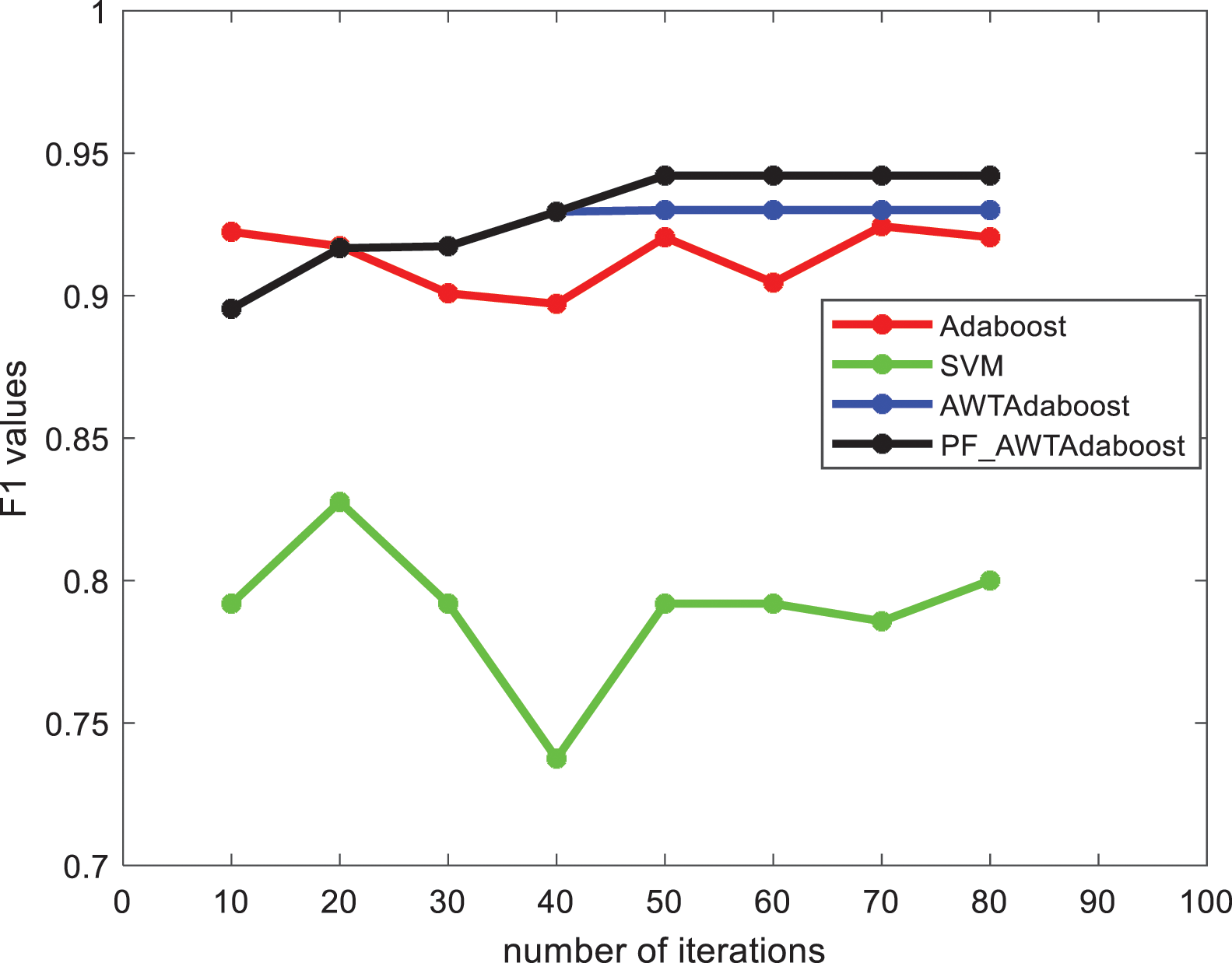
Figure 4: F1 values of each algorithm in the credit card fraud dataset

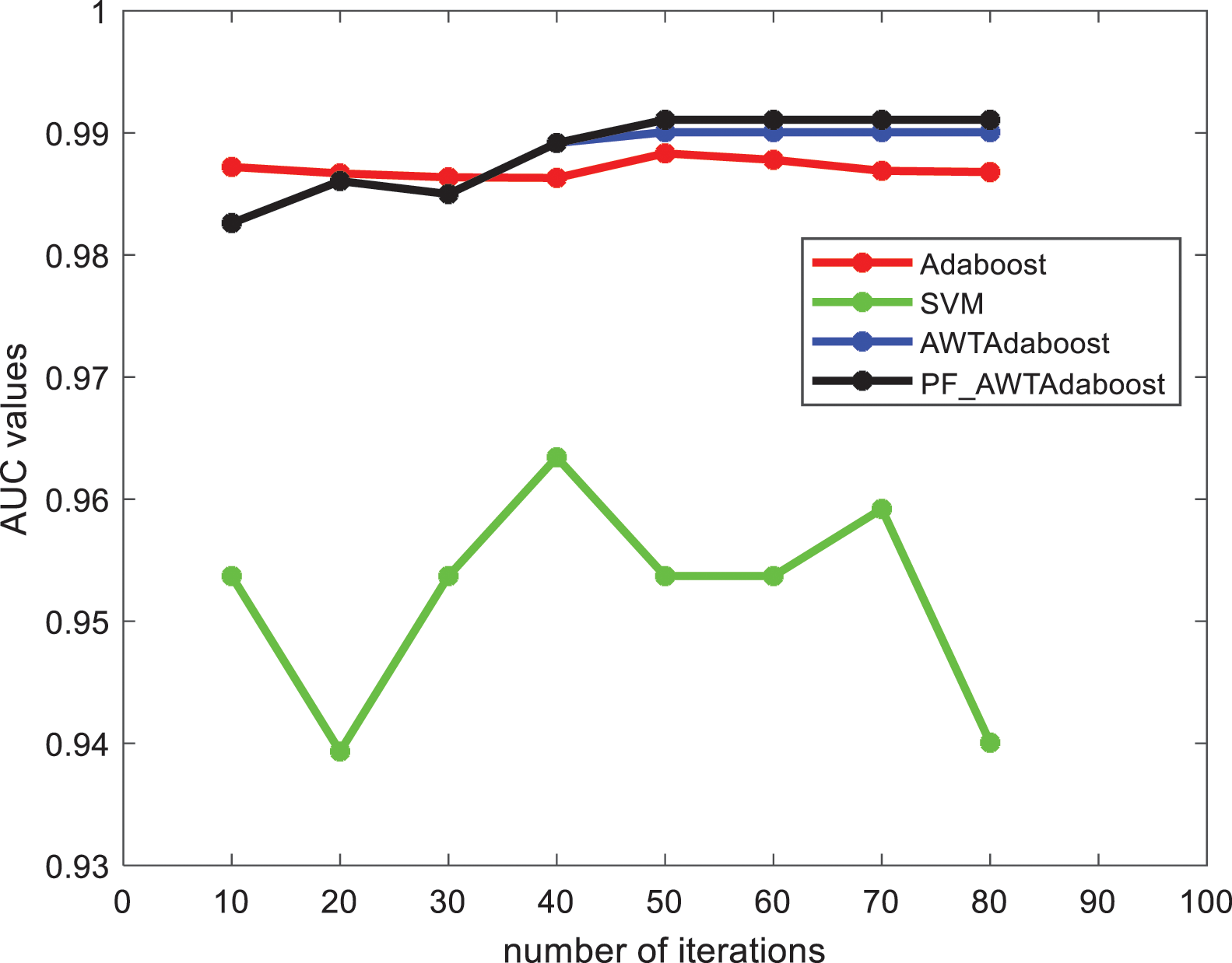
Figure 5: AUC values of each algorithm in the credit card fraud dataset

The highest F1 value of PF_AWTAdaboost algorithm is 0.9421 which is 0.0216 higher than the traditional Adaboost algorithm, 0.0121 higher than the AWTAdaboost algorithm, and 0.1146 higher compared to the SVM algorithm. The highest AUC value of PF_AWTAdaboost algorithm is 0.9910 which is 0.0027 higher than the traditional Adaboost algorithm, 0.0010 higher than the AWTAdaboost algorithm and 0.276 higher than the SVM algorithm.

By comparing the F1 and AUC values of each algorithm, it can be found that the comprehensive performance of the classifier model trained by PF_AWTAdaboost algorithm is better than the traditional Adaboost algorithm and AWTAdaboost algorithm in credit card fraud problem.

3.4 Experimental Results on Other Data Sets

In order to verify the high universality of the algorithm proposed in this paper, the algorithms were tested on Horse, Wisconsin, Breast cancer, Adult, custom datasets, and 10 datasets selected from the kaggle platform. The custom dataset was created to test the gradient ascent algorithm, which has a smaller sample size (only 100 samples in both the training and test sets) and is more prone to classification errors than the other datasets. The same experiments as before were performed on these datasets, and the best values are bolded. Tables 2–4 show the F1 values, AUC values, and accuracy rates of the algorithms on each dataset.

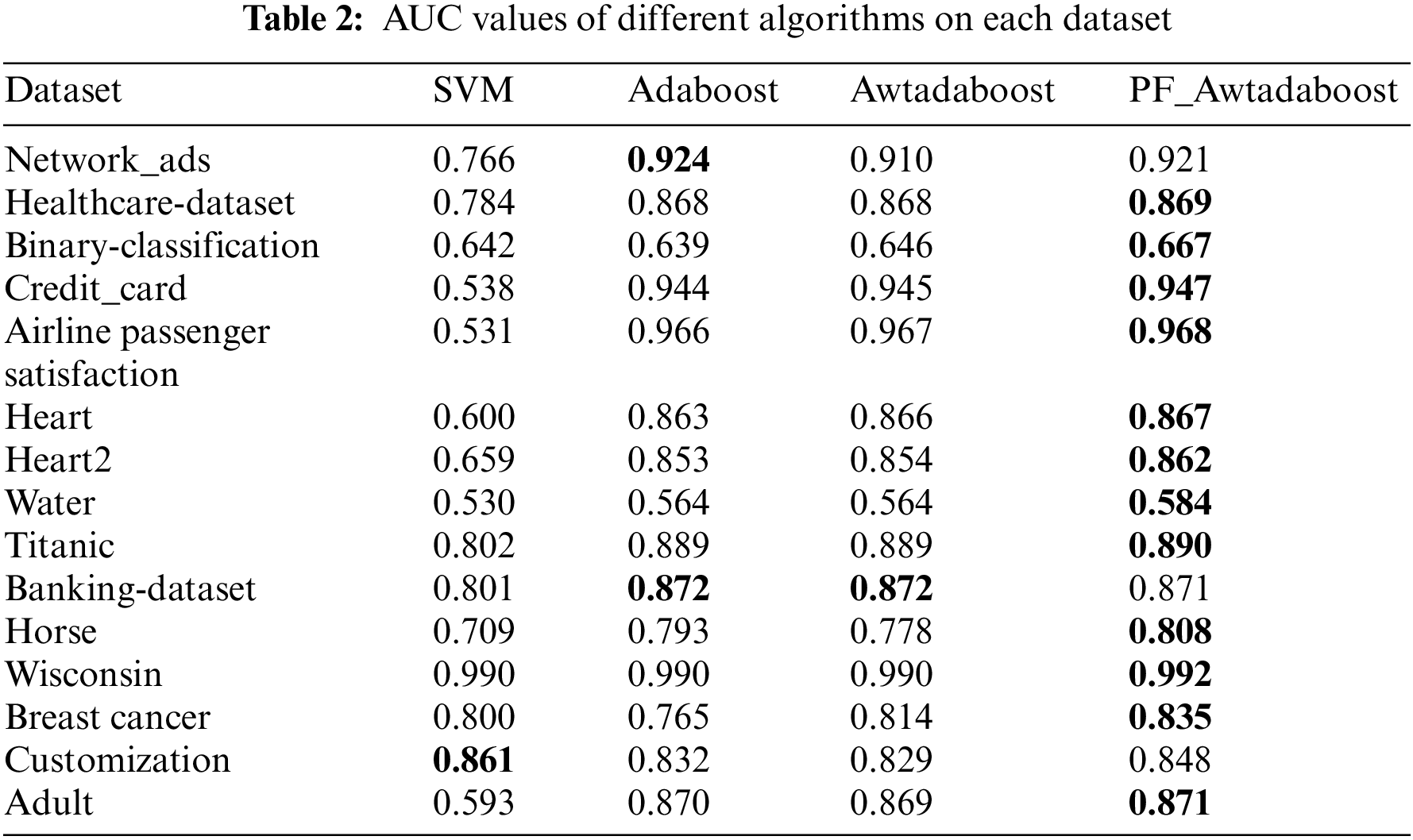
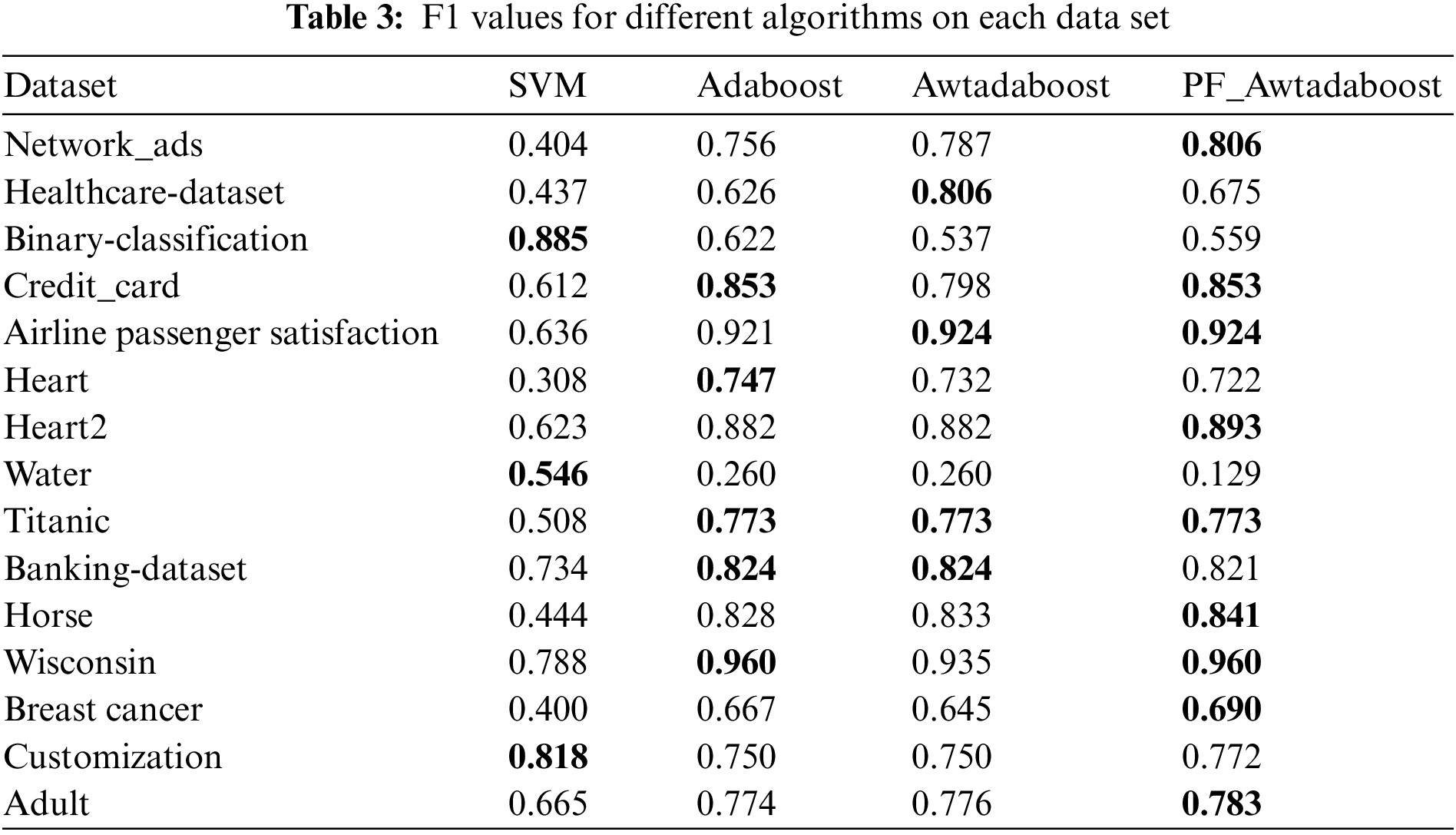
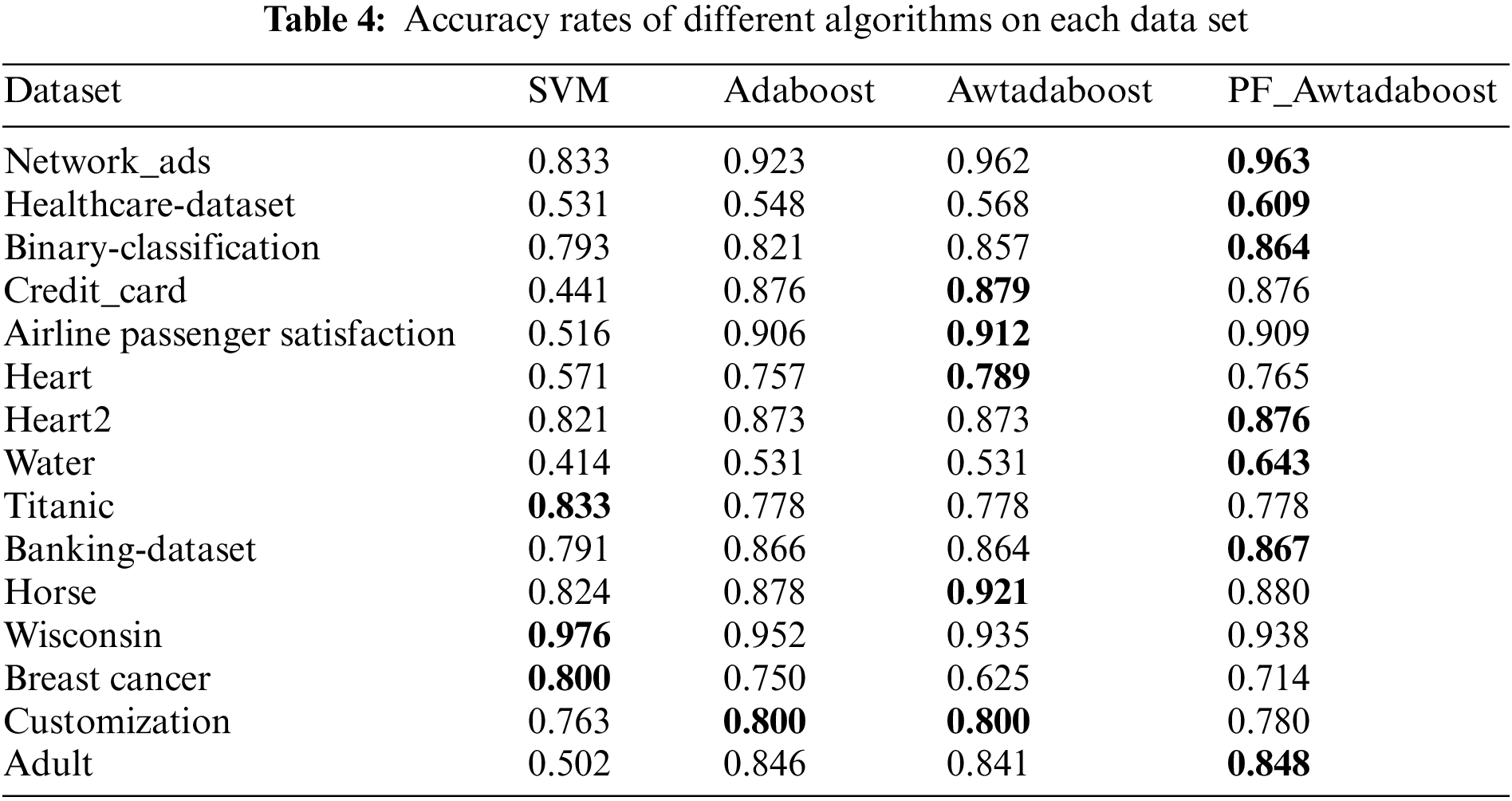
From Table 2, it can be seen that PF_AWTAdaboost performs significantly better than the other three algorithms in terms of AUC values. PF_AWTAdaboost achieved optimal results in 12 out of 15 experiments, with a maximum increase in AUC of 0.07 compared to Adaboost, 0.437 compared to SVM, and 0.03 compared to AWTAdaboost, From Table 3, it can be seen that PF_AWTAdaboost has obtained the highest F1 values in 9 out of 15 experiments. Among them, the F1 value of PF_AWTAdaboost has a maximum improvement of 0.05 compared to Adaboost, 0.414 compared to SVM, and 0.055 compared to AWTAdaboost. As shown in Table 4, PF_AWTAdaboost obtained the highest accuracy rate in 7 out of 15 experiments. The accuracy rate of PF_AWTAdaboost has increased by 0.061 compared to Adaboost, 0.435 compared to SVM, and 0.11 compared to AWTAdaboost.

Therefore, combining these three tables shows that:In these 15 datasets, compared with the other three algorithms, the PF_AWTAdaboost algorithm shows superior generalization ability, especially in improving the AUC value. Therefore, it can be proved that the improvement proposed in this paper is reasonable under different scenarios.

4  Conclusion

In order to reduce the impact of noisy samples on the classification performance of Adaboost algorithm in credit card fraud scenarios, this paper proposes a new method to reduce the impact of noisy samples by determining the number of consecutive misclassifications of samples and constructing penalty factors to change the original Adaboost sample weight assignment. By comparing the penalty strength of three different types of penalty factors proposed in this paper, the best penalty factor is selected. Then the penalty factors were migrated to AWTAdaboost to form PF_AWTAdaboost, which was verified to be still convergent by formula derivation, and finally PF_AWTAdaboost was compared with other three traditional machine learning algorithms in credit card fraud dataset and other datasets respectively. The test results in the credit card fraud dataset show that the F1 and AUC values of PF_AWTAdaboost algorithm are higher than the other algorithms, with an improvement of 0.0121 and 0.0010, respectively, compared to the AWTAdaboost algorithm, and 0.0216 and 0.0027, respectively, compared to the Adaboost algorithm. The PF_AWTAdaboost algorithm also shows excellent generalization performance in UCI dataset and kaggle dataset, which verifies that the proposed improved method is advantageous in both credit card fraud scenarios and other scenarios.

Funding Statement: This research was funded by Innovation and Entrepreneurship Training Program for College Students in Hunan Province in 2022 (3915).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  A. Abdullah, A. Majid, O. O. Dominic, A. Amerah, R. H. Tayyab et al., “A novel text2img mechanism of credit card fraud detection: A deep learning approach,” Electronics, vol. 11, no. 5, pp. 756, 2022. [Google Scholar]

 2.  I. Emmanuel, S. Y. Xia and W. Z. Hui, “A machine learning based credit card fraud detection using the GA algorithm for feature selection,” Journal of Big Data, vol. 9, no. 1, pp. 1–17, 2022. [Google Scholar]

 3.  N. A. K., R. K. Kaur, C. H. Siang, S. Manjeevan and L. C. Peng, “Credit card fraud detection using a hierarchical behavior-knowledge space model,” PLoS ONE, vol. 71, no. 1, pp. e0260579, 2022. [Google Scholar]

 4.  S. Deepika and S. Senthil, “Credit card fraud detection using moth-flame earth worm optimisation algorithm-based deep belief neural network,” International Journal of Electronic Security and Digital Forensics, vol. 14, no. 1, pp. 53–75, 2022. [Google Scholar]

 5.  D. T. Khanh, T. T. Cong, T. L. Minh and T. M. Viet, “Machine learning based on resampling approaches and deep reinforcement learning for credit card fraud detection systems,” Applied Sciences, vol. 11, no. 21, pp. 10004, 2022. [Google Scholar]

 6.  K. Hussain, N. Jhanjhi, H. M. Rahman, J. Hussain and M. H. Islam, “Using a systematic framework to critically analyze proposed smart card based two factor authentication schemes,” Journal of King Saud University-Computer and Information Sciences, vol. 33, no. 4, pp. 417–425, 2019. [Google Scholar]

 7.  L. T. Hsuan and J. J. Ruey, “Credit card fraud detection with autoencoder and probabilistic random forest,” Mathematics, vol. 9, no. 21, pp. 2683, 2021. [Google Scholar]

 8.  A. N. Saleh and F. S. Mohamed, “Enhanced credit card fraud detection model using machine learning,” Electronics, vol. 11, no. 4, pp. 662, 2022. [Google Scholar]

 9.  B. Aisha, A. Amal, A. Norah, A. Nouf, A. Nida et al., “Enhancing the credit card fraud detection through ensemble techniques,” Journal of Computational and Theoretical Nanoscience, vol. 16, no. 11, pp. 4461–4468, 2019. [Google Scholar]

10. R. E. Schapire, “The strength of weak learnability,” Machine Learning, vol. 5, no. 2, pp. 197–227, 1990. [Google Scholar]

11. Y. Freund and R. E. Schapire, “A decision-theoretic generalization of on-line learning and an application to boosting,” Journal of Computer and System Sciences, vol. 55, no. 1, pp. 119–139, 1997. [Google Scholar]

12. R. Kuldeep, L. C. Kiong, S. Manjeevan and N. A. K, “Credit card fraud detection using ADABOOST and majority voting,” IEEE Access, vol. 6, pp. 14277–14284, 2018. [Google Scholar]

13. V. S. S. Karthik, A. Mishra and U. S. Reddy, “Credit card fraud detection by modelling behaviour pattern using hybrid ensemble model,” Arabian Journal for Science and Engineering, vol. 47, no. 2, pp. 1987–1997, 2021. [Google Scholar]

14. Y. C. Fan, L. G. Jun, Y. C. Gang and J. C. Jun, “A clustering-based flexible weighting method in adaboost and its application to transaction fraud detection,” Science China Information Sciences, vol. 64, no. 12, pp. 1–11, 2021. [Google Scholar]

15. J. Friedman, T. Hastie and R. Tibshirani, “Additive logistic regression: A statistical view of boosting (with discussion and a rejoinder by the authors),” The Annals of Statistics, vol. 28, no. 2, pp. 337–407, 2000. [Google Scholar]

16. J. H. Xing and Z. Y. Jin, “Fast adaboost training algorithm by dynamic weight trimming,” Chinese Journal of Computers, vol. 32, no. 2, pp. 336–341, 2009. [Google Scholar]

17. X. L. Bing, D. Q. Liang and T. LFang, “Fast training adaboost algorithm based on adaptive weight trimming,” Journal of Electronics & Information Technology, vol. 42, no. 11, pp. 2742–2748, 2020. [Google Scholar]

18. L. Y. Jing, G. H. Xiang, L. Y. Nan and L. Xiao, “A boosting based ensemble learning algorithm in imbalanced data classification,” Systems Engineering-Theory & Practice, vol. 36, no. 1, pp. 189–199, 2016. [Google Scholar]