Billiards Optimization Algorithm: A New Game-Based Metaheuristic Approach

1  Introduction

Optimization is the process of finding the best solution among all feasible solutions for a problem. In fact, a problem that has more than one “feasible solution” is known as an optimization problem. With advances in science and technology, scientists encounter newer optimization applications that must be addressed using effective optimization methods. Deterministic and stochastic approaches are considered as effective tools for optimization problems. Deterministic approaches perform well in solving linear, convex, continuous, and derivative optimization problems. However, most real-world optimization applications have features such as nonlinear, non-convex, non-derivative, discrete search space, and high dimensions. The weakness of deterministic approaches to handle optimization problems with such features has led to the emergence of stochastic approaches as well as metaheuristic algorithms [1].

Metaheuristic algorithms are stochastic-based approaches that are able to provide optimal solutions to optimization problems through utilizing random search, random operators, and trial and error processes [2]. Due to the random search process of optimization algorithms, there is no guarantee that the solution achieved by these methods is exactly the global optimum [3]. However, these are acceptable candidate solutions known as quasi-optimal solutions [4]. The optimization process in metaheuristic algorithms begins with the production of a number of random candidate solutions. Then, during the iterations of the algorithm, the candidate solutions are improved so that at the end of the algorithm implementation, the best candidate solution is identified as the solution to the problem [5]. Exploration with the concept of global search and exploitation with the concept of local search are two key factors in the optimization process accomplished by metaheuristic algorithms. Balancing these two capabilities during the iterations of the algorithm plays an important role in the algorithm success to achieve the optimal solution.

Metaheuristic algorithms have been used in many scientific applications, including prediction of linear dynamical systems [6], solving systems of singular boundary value problems [7], solutions of Troesch’s and Bratu’s problems [8], deep learning algorithms [9–11], energy carriers [12,13], electrical engineering [14–19], protection [20], and energy management [21–24]. The design of metaheuristic algorithms is inspired by various natural phenomena, animal behavior in nature, physical laws, biological sciences, rules of games, and so on [25]. Particle Swarm Optimization (PSO) is a nature-inspired approach that is modeled based on the search behavior and strategy of fishes and birds for food [26]. Genetic Algorithm (GA) is a well-known metaheuristic algorithm based on mathematical modeling of biological sciences [27]. Gravitational Search Algorithm (GSA) is a metaheuristic algorithm designed based on modeling the laws of physics and the force of gravity [28]. Teaching-Learning Based Optimization (TLBO) is an optimization approach introduced based on the simulation of human activities [29]. Volleyball Premier League (VPL) is an optimization approach developed on the basis of modeling the rules and conditions governing volleyball league competitions [30].

The main research question is that considering various metaheuristic algorithms that have been investigated so far, is there still a need to introduce newer metaheuristic algorithms? In response to this question, No Free Lunch (NFL) theorem [31] explains that there is no guarantee for the same performance of a metaheuristic algorithm in all optimization problems. Based on the NFL theorem, a metaheuristic algorithm may provide very favorable results for a set of objective functions, but it may fail to address some other optimization problems. Hence, based on the NFL theorem, there is no assumption about the success or failure of implementing a metaheuristic algorithm on an optimization problem. The NFL theorem motivates researchers to provide suitable solutions for optimization problems through designing new metaheuristic algorithms.

The innovation and novelty of this paper is the design of a new game-based metaheuristic algorithm called Billiards Optimization Algorithm (BOA) to deal with optimization applications in different fields of science and technology. The contribution of this article is as follows. The basic idea of BOA is the rules of the billiards game and the strategy of the players during this game. Different steps of BOA implementation are described and mathematically modeled. The effectiveness of BOA in solving optimization problems is tested for twenty-three standard benchmark functions of unimodal and multimodal types. The results obtained by BOA are compared with the solutions achieved by ten well-known metaheuristic algorithms.

The rest of the article is as follows: In Section 2, literature review is provided. The proposed BOA is introduced in Section 3. Simulation studies and results are presented in Section 4. Finally, conclusions and some suggestions for future investigations are provided in Section 5.

2  Lecture Review

Metaheuristic algorithms can be divided into five groups based on the source of inspiration in their design: swarm-based, evolutionary-based, physics-based, game-based, and human-based algorithms.

Swarm-based algorithms are inspired by nature, and the swarming behaviors of animals, birds, and other living things. PSO is one of the most popular and one of the first optimization methods, which was developed based on modeling the movement of birds and fishes in search of food. The ability of ants to discover the shortest path between food sources and nests has been a central idea in Ant Colony Optimization (ACO) design [32]. The strategy of grey wolves in hunting and attacking prey is employed in the Grey Wolf Optimizer (GWO) design [33]. The humpback whale net-bubble hunting strategy has been a major source of inspiration in Whale Optimization Algorithm (WOA) [34]. The strategy of pelicans in hunting and trapping prey has been the main inspiration of Pelican Optimization Algorithm (POA) [35]. Some other swarm-based algorithms proposed so far are: Fennec Fox Optimization (FFO) [36], Reptile Search Algorithm (RSA) [37], Cat and Mouse based Optimizer (CMBO) [38], Good Bad Ugly Optimizer (GBUO) [39], Marine Predator Algorithm (MPA) [40], Tasmanian Devil Optimization (TDO) [41], Mutated Leader Algorithm (MLA) [42], Tunicate Search Algorithm (TSA) [43], Northern Goshawk Optimization (NGO) [44], Donkey Theorem Optimizer (DTO) [45], Rat Swarm Optimization (RSO) [46], All Members Based Optimizer (AMBO) [47], Red Fox Optimization (RFO) [48], Mixed Best Members Based Optimizer (MBMBO) [49], and Mixed Leader Based Optimizer (MLBO) [50].

Evolutionary-based algorithms are inspired by the concepts of natural selection, biology, and genetics. GA and Differential Evolution (DE) [51] are among the most widely used and well-known evolutionary algorithms, inspired by the process of reproduction, Darwin’s theory of evolution, and random operators such as selection, crossover, and mutation. Some other evolutionary-based algorithms can be listed as: Average and Subtraction-Based Optimizer (ASBO) [52], Genetic Programming (GP) [53], Search Step Adjustment Based Algorithm (SSABA) [54], Evolutionary Programming (EP) [55], Selecting Some Variables to Update-Based Algorithm (SSVUBA) [56], and Artificial Immune System (AIS) technique [57].

Physics-based algorithms are arisen from simulating processes, laws, and concepts in physics. Simulated Annealing (SA) is one of the most famous optimization algorithms that is inspired by the physical process of melting and cooling metals known as annealing [58]. Simulation of the law of curvature and spring force was the main idea for designing Spring Search Algorithm (SSA) [59], simulation of momentum and collision of objects has been the main inspiration of Momentum Search Algorithm (MSA) [60], simulation of gravitational force and laws of motion between objects at different distances has been the main inspiration of GSA. Some other physics-based algorithms are: Multi-Verse Optimizer (MVO) [61], Binary Spring Search Algorithm (BSSA) [62], Equilibrium Optimizer (EO) [63], and Henry Gas Solubility Optimization (HGSO) [64].

Game-based algorithms are inspired by modeling the rules of various individual and team games, the behavior of players, coaches, and referees, as well as holding competitions. Simulating the organization of the football league as well as the behavior of the players, and the interactions of the clubs with each other has been the main idea in the design of Football Game Based Optimization (FGBO) [65]. The players’ effort to put the puzzle pieces together has been the major inspiration in Puzzle Optimization Algorithm (POA) design [66]. Hide Object Game Optimizer (HOGO) is an optimization approach developed based on modeling players' behavior to find a hidden object in the hide object game [67]. Some other game-based algorithms are: VPL, Darts Game Optimizer (DGO) [68], Binary Orientation Search algorithm (BOSA) [69], Shell Game Optimization (SGO) [70], Orientation Search algorithm (OSA) [71], and Ring Toss Game Based Optimizer (RTGBO) [72].

Human-based algorithms are inspired by human behaviors, the interactions of people in a community with each other, and the relationships between humans. TLBO is one of the most widely used optimization techniques that is designed based on modeling the space of a classroom with the presence of a teacher and a number of students in two phases of teaching and learning. Interactions between doctor and patients for examination, prevention, and treatment have been the main inspiration of Doctor and Patient Optimization (DPO) [73]. Modeling and following the people of a society by the leader in order to develop that society has been the source of inspiration in designing Following Optimization Algorithm (FOA) [74]. Some other human-based algorithms are: Teamwork Optimization Algorithm (TOA) [75], Group Optimization (GO) [76], Archery Algorithm (AA) [77], Poor and Rich Optimization (PRO) technique [78], and Skill Optimization Algorithm (SOA) [79].

Based on the best knowledge gained from the above literature review, the behavior of players in the game of billiards has not been used in the design of any metaheuristic algorithm so far. While billiards players try to place balls in pockets is an intelligence process that has a good potential to design an optimizer. In order to address this research gap, in this study, based on the mathematical modeling of this process, a new metaheuristic algorithm has been designed, which is discussed in the next section.

3  Billiards Optimization Algorithm

In this section, theory of Billiards Optimization Algorithm (BOA) is described and then its mathematical modeling for use in optimization applications is presented.

3.1 Inspiration of BOA

Billiards is a fascinating sport that has become a favorite of many people. However, different games are based on the rules and conditions of billiards. In general, in this game, players try to place the balls inside the pockets of the billiards table. The players’ strategy to perform this activity is an intelligence behavior that has a potential to be designed as an optimizer. BOA is based on the simulation of players’ behavior in this game, which is discussed below.

3.2 Initialization of BOA

The BOA approach is a population-based metaheuristic algorithm whose members are billiards balls. Each BOA member is a candidate solution that assigns values to problem variables based on its position in the search space. BOA members can be mathematically modeled using a matrix according to Eq. (1). BOA members are randomly initialized at the beginning of the algorithm implementation using Eq. (2).

X=[X1⋮Xi⋮XN]N×m=[x1,1⋯x1,d⋯x1,m⋮⋱⋮⋱⋮xi,1⋯xi,d⋯xi,m⋮⋱⋮⋱⋮xN,1⋯xN,d⋯xN,m]N×m,(1)

Xi:xi,d=lbd+r×(ubd−lbd),(2)

Here, X is the population matrix of BOA, Xi indicates ith candidate solution, xi,d represents the value of dth variable proposed by ith population member, N is the number of BOA’s members, m denotes the number of variables, r is a random number in interval [0−1], lbd and ubd are the lower bound and upper bound of dth variable, respectively.

Given that each member of the population is a candidate solution to the problem, a value for the objective function is calculated for each member of the population. The values obtained for the objective function can be represented mathematically using a vector according to Eq. (3).

F=[F1⋮Fi⋮FN]N×1=[F(X1)⋮F(Xi)⋮F(XN)]N×1,(3)

Here, F is the vector of objective function values and Fi represents the obtained value for the objective function based on ith population member.

Considering the values obtained for the objective function, the best value identifies the best member of the population. Given that in each iteration, the positions of the population members are updated and new values are evaluated for the objective function, the best member of the population must be updated in each iteration.

3.3 Mathematical Model of BOA

In BOA, members of the population are updated based on the players’ behavior in placing balls in the pockets of the game table. Since the billiards table has 8 pockets, in each repetition, among the members of the population, 8 better members are considered as the pockets. The rest of the population is considered as balls that have to be moved towards these pockets. The player selects one of these pockets to hit each ball. The BOA design assumes that the pocket is chosen at random. In order to simulate this process, a proposed random position is first calculated according to Eq. (4) for each member of the population. Then, if the value of the objective function is improved in the new position, it replaces the previous position of that member according to Eq. (5).

Xinew:xi,dnew=xi,d+r×(Pi,d−I×xi,d)(4)

Xi={Xinew,Finew<FiXi,else,(5)

Here, Xinew is the new calculated status of ith population member, xi,dnew indicates its dth dimension, Finew represents its corresponding objective function value, Pi is the selected pocket for ith population member, Pi,d denotes its dth dimension, r is a random number in interval [0−1], and I is a random number, which is selected randomly from set of {1,2}.

3.4 Repetition Process, Pseudocode, and Flowchart of BOA

After updating all members of the population, the first iteration of the BOA is completed. The algorithm then enters the next iteration based on the new positions obtained for the population members. The process of updating members of the BOA population is repeated until the end of the algorithm implementation according to Eqs. (4) and (5). After complete implementation of the BOA, the best candidate solution obtained during the algorithm iterations is the output, which is the solution to the problem. The BOA implementation steps are shown through a flowchart in Fig. 1 and the corresponding pseudo-code is presented in Algorithm 1.

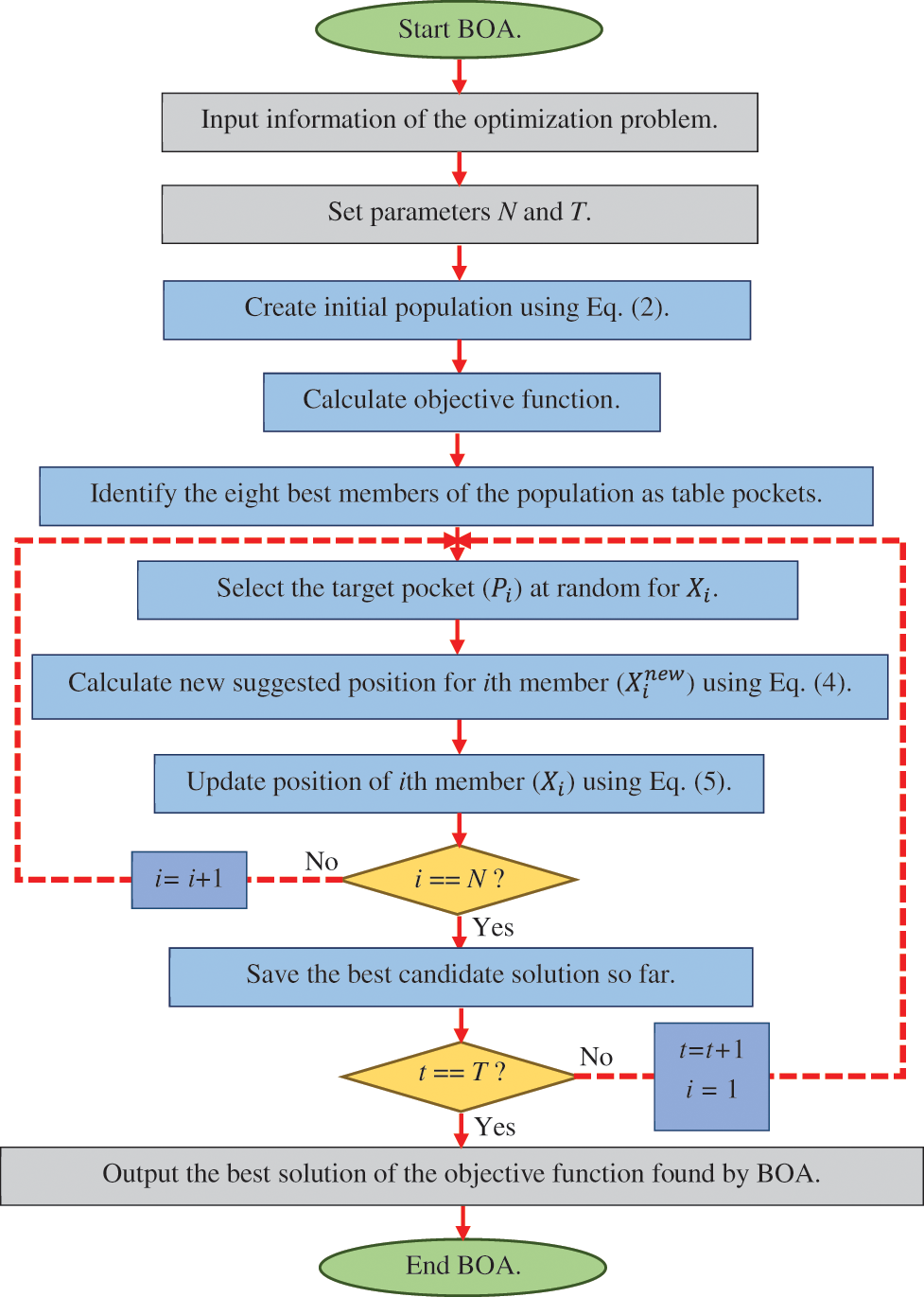
Figure 1: Flowchart of Billiards Optimization Algorithm (BOA)

3.5 Computational Complexity

In this subsection, the computational complexity of the BOA is analyzed. BOA initialization has a computational complexity of O(Nm), where N is the BOA population size and m is the number of problem variables. The process of updating the algorithm population has a computational complexity equal to O(NmT), where T is the number of algorithm iterations. Accordingly, the total computational complexity of BOA is equal to O(Nm(1 + T)).

4  Simulation Studies and Results

In this section, the performance of BOA in solving optimization problems is evaluated. To this end, BOA has been implemented on twenty-three standard objective functions of unimodal, high-dimensional multimodal, and fixed-dimensional multimodal types. Comprehensive information of these test functions including the mathematical model, dimensions, constraints, optimal value of the objective function, and other details has been presented in [80]. The capability of BOA in providing solutions to these functions has been compared with the performance of ten well-known metaheuristic algorithms including GA, WOA, RSA, PSO, GWO, MPA, MVO, GSA, TLBO, and TSA. The proposed BOA approach and ten competitor algorithms are each implemented on F1 to F23 functions in twenty independent implementations, while each implementation contains 1000 iterations. The optimization results are presented using six statistical indicators of mean, best, worst, standard deviation (std), median, and rank.

4.1 Evaluation of Unimodal Functions

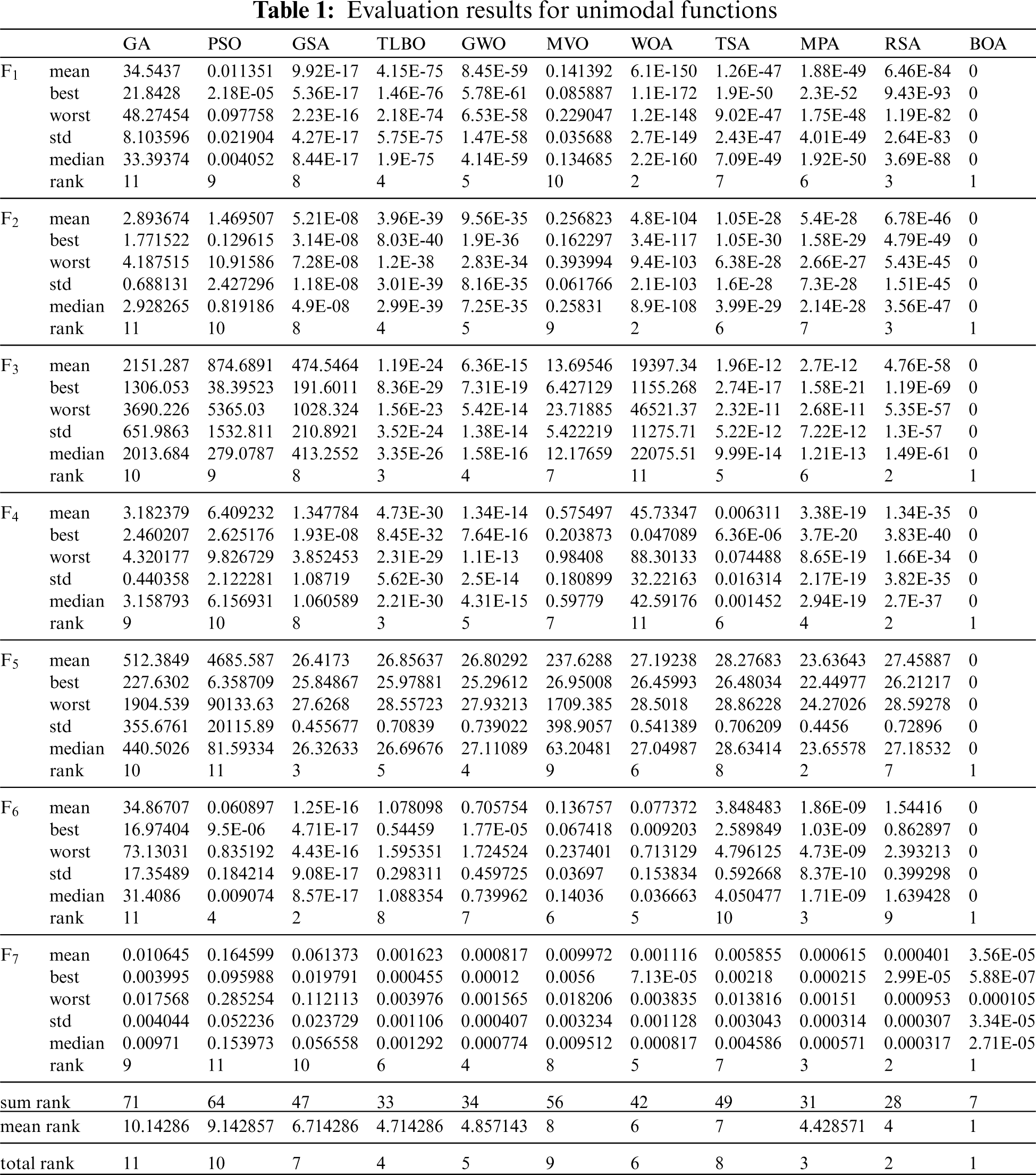
Unimodal functions F1 to F7 are suitable for testing local search capability or the exploitation of metaheuristic algorithms since they have only one optimal solution. The results of optimization of F1 to F7 functions using BOA and the mentioned competitor algorithms are reported in Table 1. The results show that BOA has provided the global optimum for F1 to F6 functions. Also, in solving F7, the BOA approach is the first best optimizer for this function. Based on the presented simulation results, it is clear that BOA has a high capability to solve unimodal problems and its performance is superior to competitor algorithms.

4.2 Evaluation of High-Dimensional Multimodal Functions

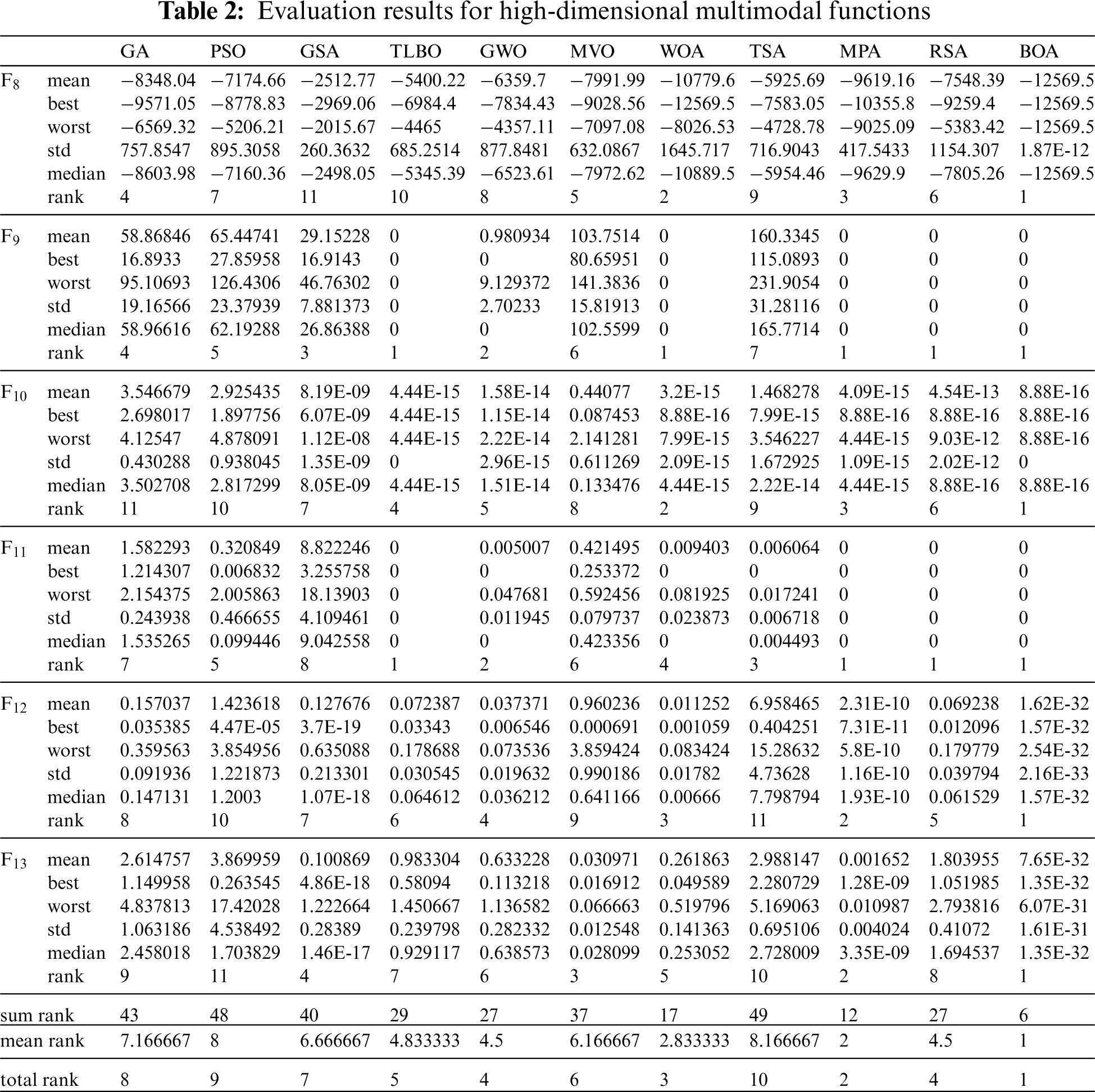
High-dimensional multimodal functions F8 to F13 are appropriate for testing global search capability or exploration of metaheuristic algorithms due to having multiple local optimal solutions. The results of BOA implementation and competitor algorithms on F8 to F13 functions are presented in Table 2. The optimization results show that BOA has provided the global optimum for F9 and F11 functions. In solving the functions F8, F10, F12, and F13, the proposed approach is the first best optimizer. Based on the simulation results, it is concluded that BOA has a high ability to solve high-dimensional multimodal problems and its global search power and exploration capability is superior than the considered competitor algorithms.

4.3 Evaluation of Fixed-Dimensional Multimodal Functions

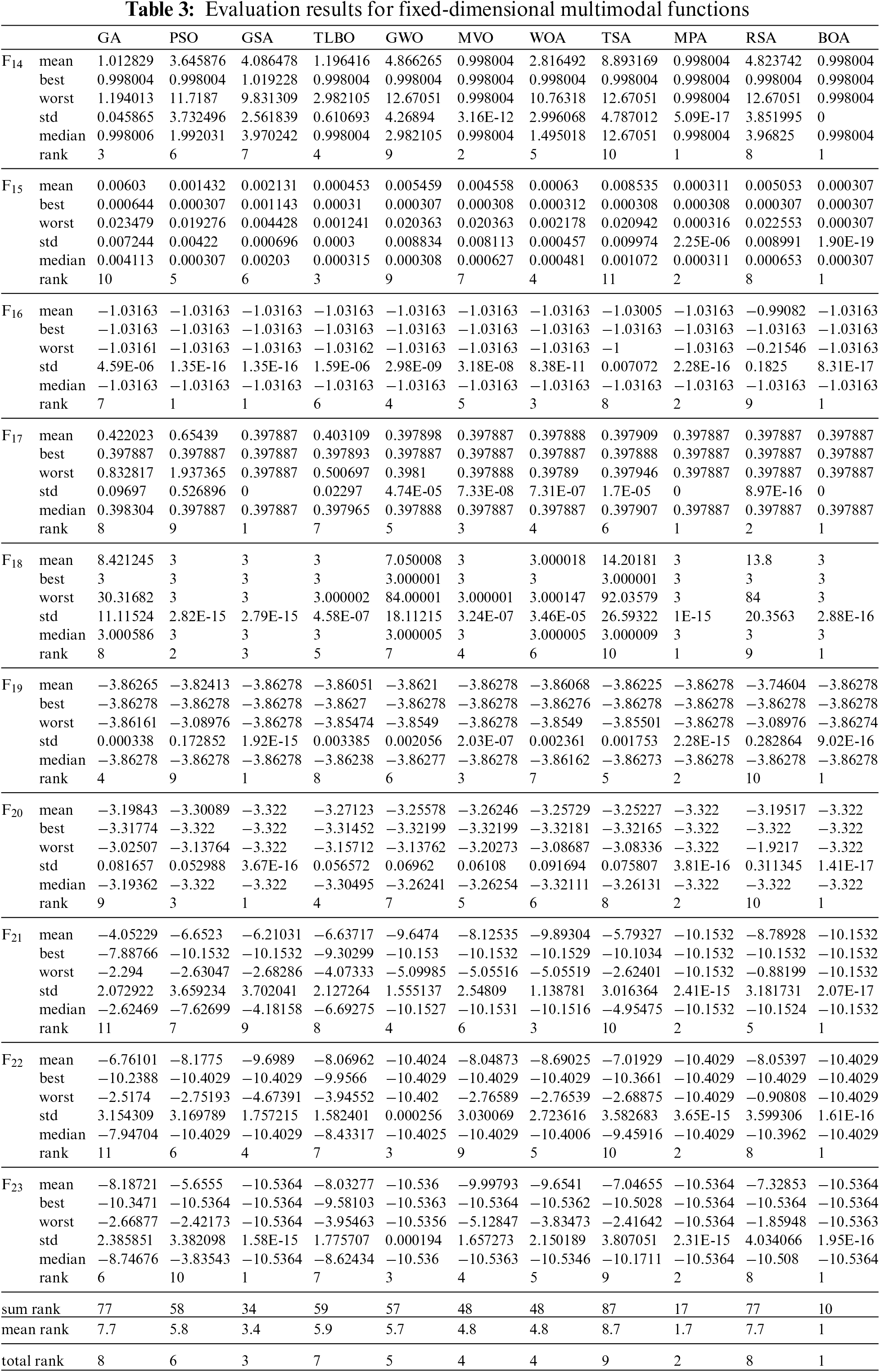
Fixed-dimensional multimodal functions F14 to F23 are suitable for evaluating the ability of metaheuristic algorithms to strike a balance between exploration and exploitation. The results obtained for F14 to F23 functions using BOA and the mentioned competitor algorithms are released in Table 3. BOA approach is the first best optimizer for F15 and F20 functions. Considering other functions of this group, where BOA achieves values similar to some competitor algorithms for the mean index, it provides better values for the std index. Analysis of the simulation results shows that BOA has a superior ability to balance exploration and exploitation characteristics compared to competitor algorithms.

The boxplot diagrams for the performance of BOA and competitor algorithms in optimizing functions F1 to F23 are shown in Fig. 2.

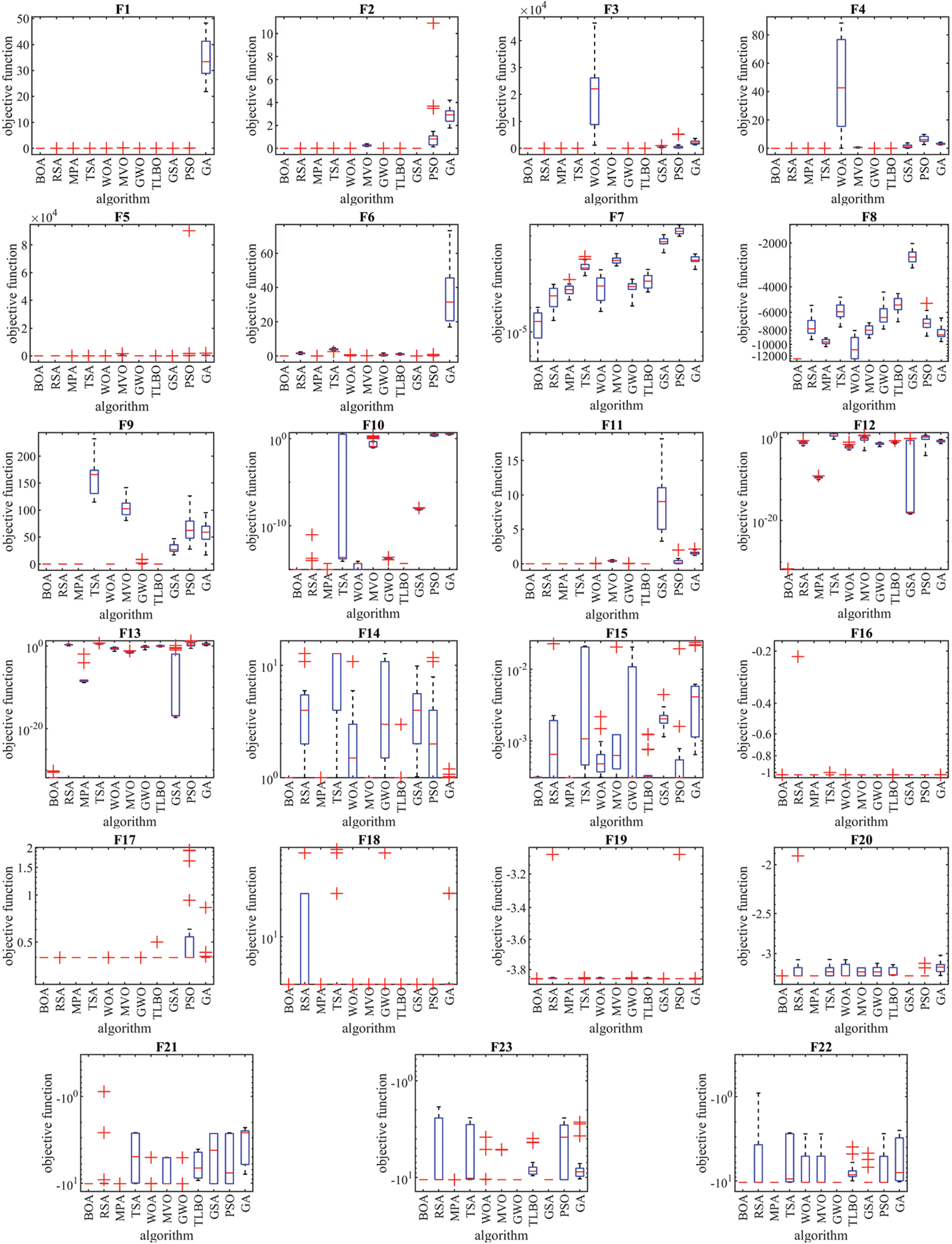
Figure 2: Boxplots of performances for Billiards Optimization Algorithm (BOA) and competitor algorithms

4.4 Statistical Analysis

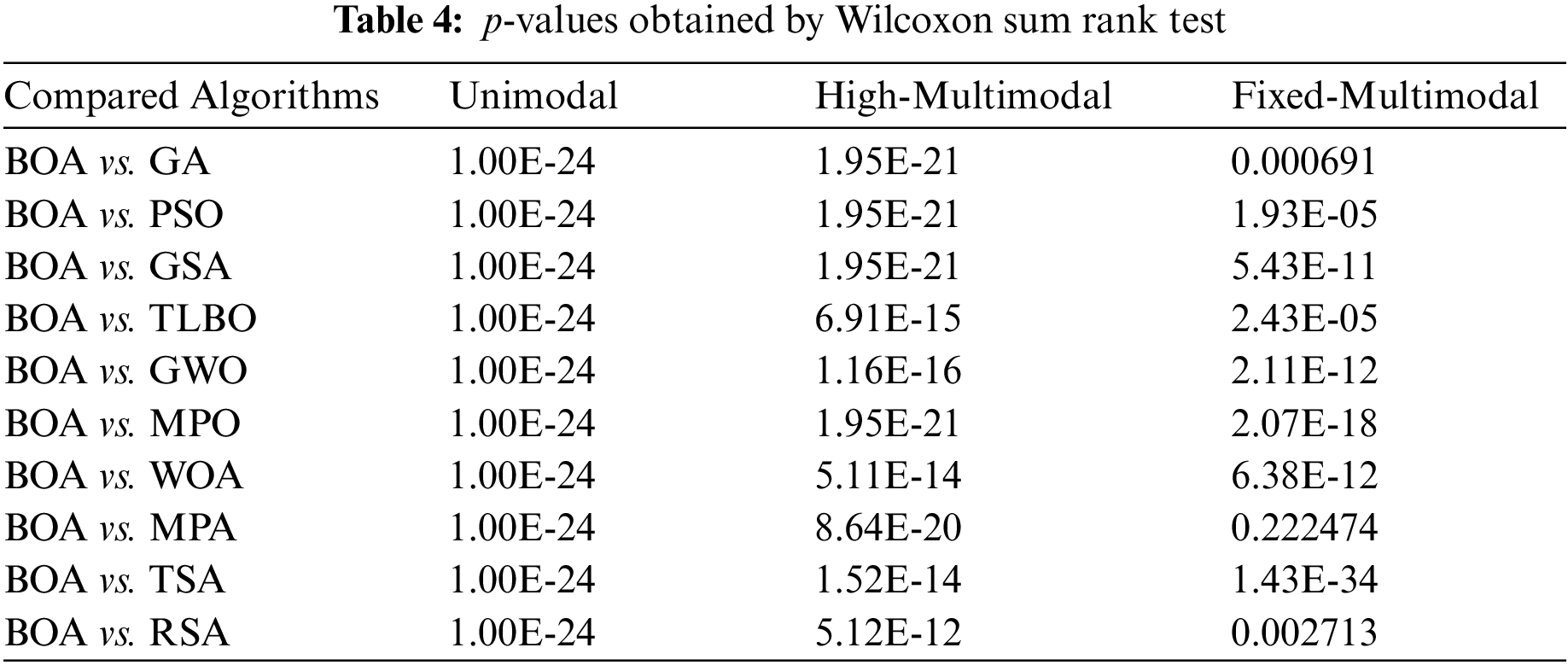
In this subsection, a statistical analysis is presented to evaluate the BOA performance against the considered competitor algorithms. The Wilcoxon rank sum test [81], which is a non-parametric test, is used to accomplish this analysis. In this test, using an index called p-value, it is shown whether there is a significant difference between the mean of the two data samples.

The results of Wilcoxon rank sum test statistical analysis on the outputs of BOA and competitor algorithms are reported in Table 4. It can be seen from the simulation results that in cases where the p-value is less than 0.05, the proposed BOA has a significant statistical superiority over the corresponding competitor algorithm. Considering the obtained p-values and since the value of this index is less than 0.05 in all cases, it is concluded that BOA has a significant statistical superiority over all ten competitor algorithms in optimizing all three types of objective functions including unimodal, high-dimensional multimodal, and fixed-dimensional multimodal functions.

5  Conclusions and Future Works

In this paper, a new game-based metaheuristic algorithm entitled Billiards Optimization Algorithm (BOA) was introduced. The main inspiration in BOA design is the behavior of the players in the billiards game to place the balls in the pockets of the game table. Different steps of BOA were described and mathematically modeled. The performance of the proposed BOA approach was evaluated in solving twenty-three standard benchmark functions of unimodal, high-dimensional multimodal, and fixed-dimensional multimodal types. The optimization results showed that BOA has a high ability in exploration, exploitation, and balancing these features during the optimization process. The performance of BOA was compared with ten well-known metaheuristic algorithms. Analysis of the simulation results showed that the proposed BOA approach has superior performance over the competitor algorithms by providing better results.

The authors also offer some proposals for future research. Design and development of binary and multi-objective versions of BOA is an attractive research topic. Application of BOA for optimization problems in various fields of science and real-world issues is also another research proposal for future investigations.

Funding Statement: The research and article are supported by Specific Research project 2022 Faculty of Education, University of Hradec Králové, Czech Republic.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  M. Dehghani, E. Trojovská and P. Trojovský, “A new human-based metaheuristic algorithm for solving optimization problems on the base of simulation of driving training process,” Scientific Reports, vol. 12, no. 1, pp. 9924, 2022. [Google Scholar]

 2.  M. Dehghani, Z. Montazeri, G. Dhiman, O. P. Malik, R. Morales-Menendez et al., “A spring search algorithm applied to engineering optimization problems,” Applied Sciences, vol. 10, no. 18, pp. 6173, 2020. [Google Scholar]

 3.  G. Dhiman, K. K. Singh, M. Soni, A. Nagar, M. Dehghani et al., “MOSOA: A new multi-objective seagull optimization algorithm,” Expert Systems with Applications, vol. 167, no. 4, pp. 114150, 2021. [Google Scholar]

 4.  F. A. Zeidabadi, M. Dehghani and O. P. Malik, “RSLBO: Random selected leader based optimizer,” International Journal of Intelligent Engineering and Systems, vol. 14, no. 5, pp. 529–538, 2021. [Google Scholar]

 5.  M. Dehghani, Z. Montazeri, A. Dehghani, H. Samet, C. Sotelo et al., “DM: Dehghani method for modifying optimization algorithms,” Applied Sciences, vol. 10, no. 21, pp. 7683, 2020. [Google Scholar]

 6.  Z. Abo-Hammour, O. Alsmadi, S. Momani and O. Abu Arqub, “A genetic algorithm approach for prediction of linear dynamical systems,” Mathematical Problems in Engineering, vol. 2013, no. 4, pp. 831657, 2013. [Google Scholar]

 7.  Z. Abo-Hammour, O. Abu Arqub, O. Alsmadi, S. Momani and A. Alsaedi, “An optimization algorithm for solving systems of singular boundary value problems,” Applied Mathematics & Information Sciences, vol. 8, no. 6, pp. 2809–2821, 2014. [Google Scholar]

 8.  Z. Abo-Hammour, O. Abu Arqub, S. Momani and N. Shawagfeh, “Optimization solution of Troesch’s and Bratu’s problems of ordinary type using novel continuous genetic algorithm,” Discrete Dynamics in Nature and Society, vol. 2014, pp. 401696, 2014. [Google Scholar]

 9.  A. J. Moshayedi, A. S. Roy, A. Kolahdooz and Y. Shuxin, “Deep learning application pros and cons over algorithm,” EAI Endorsed Transactions on AI and Robotics, vol. 1, pp. 1–13, 2022. [Google Scholar]

10. A. J. Moshayedi, A. S. Roy, L. Liao and S. Li, “Raspberry Pi SCADA zonal based system for agricultural plant monitoring,” in Proc. of IEEE 6th Int. Conf. on Information Science and Control Engineering (ICISCE), Shanghai, China, pp. 427–433, 2019. [Google Scholar]

11. A. J. Moshayedi, A. S. Roy, S. K. Sambo, Y. Zhong and L. Liao, “Review on: The service robot mathematical model,” EAI Endorsed Transactions on AI and Robotics, vol. 1, pp. 1–19, 2022. [Google Scholar]

12. M. Dehghani, Z. Montazeri, A. Ehsanifar, A. R. Seifi, M. J. Ebadi et al., “Planning of energy carriers based on final energy consumption using dynamic programming and particle swarm optimization,” Electrical Engineering & Electromechanics, no. 5, pp. 62–71, 2018. [Google Scholar]

13. Z. Montazeri and T. Niknam, “Energy carriers management based on energy consumption,” in Proc. of IEEE 4th Int. Conf. on Knowledge-Based Engineering and Innovation (KBEI), Tehran, Iran, pp. 0539–0543, 2017. [Google Scholar]

14. M. Dehghani, Z. Montazeri and O. P. Malik, “Optimal sizing and placement of capacitor banks and distributed generation in distribution systems using spring search algorithm,” International Journal of Emerging Electric Power Systems, vol. 21, no. 1, pp. 20190217, 2020. [Google Scholar]

15. M. Dehghani, Z. Montazeri, O. P. Malik, K. Al-Haddad, J. M. Guerrero et al., “A new methodology called dice game optimizer for capacitor placement in distribution systems,” Electrical Engineering & Electromechanics, no. 1, pp. 61–64, 2020. [Google Scholar]

16. S. Dehbozorgi, A. Ehsanifar, Z. Montazeri, M. Dehghani and A. Seifi, “Line loss reduction and voltage profile improvement in radial distribution networks using battery energy storage system,” in Proc. of IEEE 4th Int. Conf. on Knowledge-Based Engineering and Innovation (KBEI), Tehran, Iran, pp. 0215–0219, 2017. [Google Scholar]

17. Z. Montazeri and T. Niknam, “Optimal utilization of electrical energy from power plants based on final energy consumption using gravitational search algorithm,” Electrical Engineering & Electromechanics, no. 4, pp. 70–73, 2018. [Google Scholar]

18. M. Dehghani, M. Mardaneh, Z. Montazeri, A. Ehsanifar, M. J. Ebadi et al., “Spring search algorithm for simultaneous placement of distributed generation and capacitors,” Electrical Engineering & Electromechanics, no. 6, pp. 68–73, 2018. [Google Scholar]

19. M. Premkumar, R. Sowmya, P. Jangir, K. S. Nisar and M. Aldhaifallah, “A new metaheuristic optimization algorithms for brushless direct current wheel motor design problem,” Computers, Materials & Continua, vol. 67, no. 2, pp. 2227–2242, 2021. [Google Scholar]

20. A. Ehsanifar, M. Dehghani and M. Allahbakhshi, “Calculating the leakage inductance for transformer inter-turn fault detection using finite element method,” in Proc. of Iranian Conf. on Electrical Engineering (ICEE), Tehran, Iran, pp. 1372–1377, 2017. [Google Scholar]

21. M. Dehghani, Z. Montazeri and O. P. Malik, “Energy commitment: A planning of energy carrier based on energy consumption,” Electrical Engineering & Electromechanics, no. 4, pp. 69–72, 2019. [Google Scholar]

22. M. Dehghani, M. Mardaneh, O. P. Malik, J. M. Guerrero, C. Sotelo et al., “Genetic algorithm for energy commitment in a power system supplied by multiple energy carriers,” Sustainability, vol. 12, no. 23, pp. 10053, 2020. [Google Scholar]

23. M. Dehghani, M. Mardaneh, O. P. Malik, J. M. Guerrero, R. Morales-Menendez et al., “Energy commitment for a power system supplied by multiple energy carriers system using following optimization algorithm,” Applied Sciences, vol. 10, no. 17, pp. 5862, 2020. [Google Scholar]

24. H. Rezk, A. Fathy, M. Aly and M. N. F. Ibrahim, “Energy management control strategy for renewable energy system based on spotted hyena optimizer,” Computers, Materials & Continua, vol. 67, no. 2, pp. 2271–2281, 2021. [Google Scholar]

25. M. Dehghani, Z. Montazeri, A. Dehghani, O. P. Malik, R. Morales-Menendez et al., “Binary spring search algorithm for solving various optimization problems,” Applied Sciences, vol. 11, no. 3, pp. 1286, 2021. [Google Scholar]

26. J. Kennedy and R. Eberhart, “Particle swarm optimization,” in Proc. of ICNN’95-Int. Conf. on Neural Networks, Perth, WA, Australia, pp. 1942–1948, 1995. [Google Scholar]

27. D. E. Goldberg and J. H. Holland, “Genetic algorithms and machine learning,” Machine Learning, vol. 3, no. 2/3, pp. 95–99, 1988. [Google Scholar]

28. E. Rashedi, H. Nezamabadi-Pour and S. Saryazdi, “GSA: A gravitational search algorithm,” Information Sciences, vol. 179, no. 13, pp. 2232–2248, 2009. [Google Scholar]

29. R. V. Rao, V. J. Savsani and D. Vakharia, “Teaching—learning-based optimization: A novel method for constrained mechanical design optimization problems,” Computer-Aided Design, vol. 43, no. 3, pp. 303–315, 2011. [Google Scholar]

30. R. Moghdani and K. Salimifard, “Volleyball premier league algorithm,” Applied Soft Computing, vol. 64, no. 5, pp. 161–185, 2018. [Google Scholar]

31. D. H. Wolpert and W. G. Macready, “No free lunch theorems for optimization,” IEEE Transactions on Evolutionary Computation, vol. 1, no. 1, pp. 67–82, 1997. [Google Scholar]

32. H. Givi, M. A. Noroozi, B. Vahidi, J. S. Moghani and M. A. V. Zand, “A novel approach for optimization of z-matrix building process using ant colony algorithm,” Journal of Basic and Applied Scientific Research, vol. 2, no. 9, pp. 8932–8937, 2012. [Google Scholar]

33. S. Mirjalili, S. M. Mirjalili and A. Lewis, “Grey wolf optimizer,” Advances in Engineering Software, vol. 69, pp. 46–61, 2014. [Google Scholar]

34. S. Mirjalili and A. Lewis, “The whale optimization algorithm,” Advances in Engineering Software, vol. 95, no. 12, pp. 51–67, 2016. [Google Scholar]

35. P. Trojovský and M. Dehghani, “Pelican optimization algorithm: A novel nature-inspired algorithm for engineering applications,” Sensors, vol. 22, no. 3, pp. 855, 2022. [Google Scholar]

36. E. Trojovská, M. Dehghani and P. Trojovský, “Fennec fox optimization: A new nature-inspired optimization algorithm,” IEEE Access, vol. 10, pp. 84417–84443, 2022. [Google Scholar]

37. L. Abualigah, M. Abd Elaziz, P. Sumari, Z. W. Geem and A. H. Gandomi, “Reptile search algorithm (RSAA nature-inspired meta-heuristic optimizer,” Expert Systems with Applications, vol. 191, no. 11, pp. 116158, 2022. [Google Scholar]

38. M. Dehghani, Š. Hubálovský and P. Trojovský, “Cat and mouse based optimizer: A new nature-inspired optimization algorithm,” Sensors, vol. 21, no. 15, pp. 5214, 2021. [Google Scholar]

39. H. Givi, M. Dehghani, Z. Montazeri, R. Morales-Menendez, R. A. Ramirez-Mendoza et al., “The good, the bad, and the ugly optimizer,” Applied Sciences, vol. 11, no. 5, pp. 2042, 2021. [Google Scholar]

40. A. Faramarzi, M. Heidarinejad, S. Mirjalili and A. H. Gandomi, “Marine predators algorithm: A nature-inspired metaheuristic,” Expert Systems with Applications, vol. 152, no. 4, pp. 113377, 2020. [Google Scholar]

41. M. Dehghani, Š. Hubálovský and P. Trojovský, “Tasmanian devil optimization: A new bio-inspired optimization algorithm for solving optimization algorithm,” IEEE Access, vol. 10, pp. 19599–19620, 2022. [Google Scholar]

42. F. A. Zeidabadi, S. A. Doumari, M. Dehghani, Z. Montazeri, P. Trojovský et al., “MLA: A new mutated leader algorithm for solving optimization problems,” Computers, Materials & Continua, vol. 70, no. 3, pp. 5631–5649, 2022. [Google Scholar]

43. S. Kaur, L. K. Awasthi, A. L. Sangal and G. Dhiman, “Tunicate swarm algorithm: A new bio-inspired based metaheuristic paradigm for global optimization,” Engineering Applications of Artificial Intelligence, vol. 90, no. 2, pp. 103541, 2020. [Google Scholar]

44. M. Dehghani, Š. Hubálovský and P. Trojovský, “Northern Goshawk Optimization: A new swarm-based algorithm for solving optimization problems,” IEEE Access, vol. 9, pp. 162059–162080, 2021. [Google Scholar]

45. M. Dehghani, M. Mardaneh, O. P. Malik and S. M. NouraeiPour, “DTO: Donkey theorem optimization,” in Proc. of Iranian Conf. on Electrical Engineering (ICEE), Yazd, Iran, pp. 1855–1859, 2019. [Google Scholar]

46. G. Dhiman, M. Garg, A. Nagar, V. Kumar and M. Dehghani, “A novel algorithm for global optimization: Rat swarm optimizer,” Journal of Ambient Intelligence and Humanized Computing, vol. 12, no. 8, pp. 8457–8482, 2021. [Google Scholar]

47. F. A. Zeidabadi, S. A. Doumari, M. Dehghani, Z. Montazeri, P. Trojovský et al., “AMBO: All members-based optimizer for solving optimization problems,” Computers, Materials & Continua, vol. 70, no. 2, pp. 2905–2921, 2022. [Google Scholar]

48. D. Połap and M. Woźniak, “Red fox optimization algorithm,” Expert Systems with Applications, vol. 166, no. 10, pp. 114107, 2021. [Google Scholar]

49. S. A. Doumari, F. A. Zeidabadi, M. Dehghani and O. P. Malik, “Mixed best members based optimizer for solving various optimization problems,” International Journal of Intelligent Engineering and Systems, vol. 14, no. 4, pp. 384–392, 2021. [Google Scholar]

50. F. A. Zeidabadi, S. A. Doumari, M. Dehghani and O. P. Malik, “MLBO: Mixed leader based optimizer for solving optimization problems,” International Journal of Intelligent Engineering and Systems, vol. 14, no. 4, pp. 472–479, 2021. [Google Scholar]

51. R. Storn and K. Price, “Differential evolution-a simple and efficient heuristic for global optimization over continuous spaces,” Journal of Global Optimization, vol. 11, no. 4, pp. 341–359, 1997. [Google Scholar]

52. M. Dehghani, Š. Hubálovský and P. Trojovský, “A new optimization algorithm based on average and subtraction of the best and worst members of the population for solving various optimization problems,” PeerJ Computer Science, vol. 8, no. 10, pp. e910, 2022. [Google Scholar]

53. W. Banzhaf, P. Nordin, R. E. Keller and F. D. Francone, “Genetic programming: An introduction: On the automatic evolution of computer programs and its applications,” in Library of Congress Cataloging-in-Publication Data, 1st ed., vol. 27, San Francisco, CA, USA: Morgan Kaufmann Publishers, pp. 1–398, 1998. [Google Scholar]

54. F. A. Zeidabadi, A. Dehghani, M. Dehghani, Z. Montazeri and Š. Hubálovský, “SSABA: Search step adjustment based algorithm,” Computers, Materials & Continua, vol. 71, no. 3, pp. 4237–4256, 2022. [Google Scholar]

55. D. B. Fogel, Artificial Intelligence through Simulated Evolution, Hoboken, New Jersey, U.S. United States: Wiley-IEEE Press, pp. 227–296, 1998. [Google Scholar]

56. M. Dehghani and P. Trojovský, “Selecting some variables to update-based algorithm for solving optimization problems,” Sensors, vol. 22, no. 5, pp. 1795, 2022. [Google Scholar]

57. S. A. Hofmeyr and S. Forrest, “Architecture for an artificial immune system,” Evolutionary Computation, vol. 8, no. 4, pp. 443–473, 2000. [Google Scholar]

58. S. Kirkpatrick, C. D. Gelatt and M. P. Vecchi, “Optimization by simulated annealing,” Science, vol. 220, no. 4598, pp. 671–680, 1983. [Google Scholar]

59. M. Dehghani, Z. Montazeri, A. Dehghani and A. Seifi, “Spring search algorithm: A new meta-heuristic optimization algorithm inspired by Hooke’s law,” in Proc. of IEEE 4th Int. Conf. on Knowledge-Based Engineering and Innovation (KBEI), Tehran, Iran, pp. 0210–0214, 2017. [Google Scholar]

60. M. Dehghani and H. Samet, “Momentum search algorithm: A new meta-heuristic optimization algorithm inspired by momentum conservation law,” SN Applied Sciences, vol. 2, no. 10, pp. 1–15, 2020. [Google Scholar]

61. S. Mirjalili, S. M. Mirjalili and A. Hatamlou, “Multi-verse optimizer: A nature-inspired algorithm for global optimization,” Neural Computing and Applications, vol. 27, no. 2, pp. 495–513, 2016. [Google Scholar]

62. M. Dehghani, Z. Montazeri, A. Dehghani, N. Nouri and A. Seifi, “BSSA: Binary spring search algorithm,” in Proc. of IEEE 4th Int. Conf. on Knowledge-Based Engineering and Innovation (KBEI), Tehran, Iran, pp. 0220–0224, 2017. [Google Scholar]

63. A. Faramarzi, M. Heidarinejad, B. Stephens and S. Mirjalili, “Equilibrium optimizer: A novel optimization algorithm,” Knowledge-Based Systems, vol. 191, pp. 105190, 2020. [Google Scholar]

64. F. A. Hashim, E. H. Houssein, M. S. Mabrouk, W. Al-Atabany and S. Mirjalili, “Henry gas solubility optimization: A novel physics-based algorithm,” Future Generation Computer Systems, vol. 101, no. 4, pp. 646–667, 2019. [Google Scholar]

65. M. Dehghani, M. Mardaneh, J. M. Guerrero, O. P. Malik and V. Kumar, “Football game based optimization: An application to solve energy commitment problem,” International Journal of Intelligent Engineering and Systems, vol. 13, no. 5, pp. 514–523, 2020. [Google Scholar]

66. F. A. Zeidabadi and M. Dehghani, “POA: Puzzle optimization algorithm,” International Journal of Intelligent Engineering and Systems, vol. 15, no. 1, pp. 273–281, 2022. [Google Scholar]

67. M. Dehghani, Z. Montazeri, S. Saremi, A. Dehghani, O. P. Malik et al., “HOGO: Hide objects game optimization,” International Journal of Intelligent Engineering and Systems, vol. 13, no. 4, pp. 216–225, 2020. [Google Scholar]

68. M. Dehghani, Z. Montazeri, H. Givi, J. M. Guerrero and G. Dhiman, “Darts game optimizer: A new optimization technique based on darts game,” International Journal of Intelligent Engineering and Systems, vol. 13, no. 5, pp. 286–294, 2020. [Google Scholar]

69. M. Dehghani, Z. Montazeri, O. P. Malik, G. Dhiman and V. Kumar, “BOSA: Binary orientation search algorithm,” International Journal of Innovative Technology and Exploring Engineering, vol. 9, no. 1, pp. 5306–5310, 2019. [Google Scholar]

70. M. Dehghani, Z. Montazeri, O. P. Malik, H. Givi and J. M. Guerrero, “Shell game optimization: A novel game-based algorithm,” International Journal of Intelligent Engineering and Systems, vol. 13, no. 3, pp. 246–255, 2020. [Google Scholar]

71. M. Dehghani, Z. Montazeri, O. P. Malik, A. Ehsanifar and A. Dehghani, “OSA: Orientation search algorithm,” International Journal of Industrial Electronics, Control and Optimization, vol. 2, no. 2, pp. 99–112, 2019. [Google Scholar]

72. S. A. Doumari, H. Givi, M. Dehghani and O. P. Malik, “Ring toss game-based optimization algorithm for solving various optimization problems,” International Journal of Intelligent Engineering and Systems, vol. 14, no. 3, pp. 545–554, 2021. [Google Scholar]

73. M. Dehghani, M. Mardaneh, J. M. Guerrero, O. P. Malik, R. A. Ramirez-Mendoza et al., “A new “doctor and patient” optimization algorithm: An application to energy commitment problem,” Applied Sciences, vol. 10, no. 17, pp. 5791, 2020. [Google Scholar]

74. M. Dehghani, M. Mardaneh and O. P. Malik, “FOA: ‘Following’optimization algorithm for solving power engineering optimization problems,” Journal of Operation and Automation in Power Engineering, vol. 8, no. 1, pp. 57–64, 2020. [Google Scholar]

75. M. Dehghani and P. Trojovský, “Teamwork optimization algorithm: A new optimization approach for function minimization/maximization,” Sensors, vol. 21, no. 13, pp. 4567, 2021. [Google Scholar]

76. M. Dehghani, Z. Montazeri, A. Dehghani and O. P. Malik, “GO: Group optimization,” Gazi University Journal of Science, vol. 33, no. 2, pp. 381–392, 2020. [Google Scholar]

77. F. A. Zeidabadi, M. Dehghani, P. Trojovský, Š. Hubálovský, V. Leiva et al., “Archery nlgorithm: A novel stochastic optimization algorithm for solving optimization problems,” Computers, Materials & Continua, vol. 72, no. 1, pp. 399–416, 2022. [Google Scholar]

78. S. H. S. Moosavi and V. K. Bardsiri, “Poor and rich optimization algorithm: A new human-based and multi populations algorithm,” Engineering Applications of Artificial Intelligence, vol. 86, no. 12, pp. 165–181, 2019. [Google Scholar]

79. H. Givi and M. Hubalovska, “Skill optimization algorithm: A new human-based metaheuristic technique,” Computers, Materials & Continua, vol. 74, no. 1, pp. 179–202, 2023. [Google Scholar]

80. X. Yao, Y. Liu and G. Lin, “Evolutionary programming made faster,” IEEE Transactions on Evolutionary computation, vol. 3, no. 2, pp. 82–102, 1999. [Google Scholar]

81. F. Wilcoxon, “Individual comparisons by ranking methods,” Breakthroughs in Statistics, vol. 1, no. 6, pp. 196–202, 1992. [Google Scholar]