Data Security Storage Mechanism Based on Blockchain Network

1  Introduction

With the continuous evolution of blockchain technology, technologies such as distributed databases, consensus mechanisms, P2P networks, Internet of Things, smart contracts, and cryptography have been gradually integrated [1–3]. Blockchain is a distributed ledger, essentially a decentralized database with decentralization, immutability, traceability, collective maintenance, and openness and transparency. However, while realizing decentralization and de-trust, blockchain will disclose the entire network’s transaction information to achieve the node’s consensus, and the disclosure of information will reduce data privacy [4]. At the same time, with the increase in the number of users, the impact of data expansion is also an urgent problem that blockchain technology needs to solve.

As the supporting technology of digital currency, blockchain essentially uses a chain data structure to verify and store data. It combines with a distributed consensus mechanism to generate and update data to ensure the state consistency of honest nodes in the entire network. Blockchain technology’s basic attributes are decentralization, verifiability, and tamper resistance. The most representative cryptocurrencies are Bitcoin and Ethereum. However, the openness and transparency of the blockchain also bring great pressure and challenges to users’ privacy protection. Cryptography is a powerful tool for constructing and guaranteeing modern information security. Among many modern cryptography technologies, theories such as cryptographic commitment and zero-knowledge proof align with people’s perception of information in the online world because of their distinctive features of reliable proof and high efficiency. The need for authenticity and secrecy has attracted much attention, so it also stands out in many schemes.

In blockchain technology, valuable information is permanently stored in the form of data, and these carriers for storing data information constitute blocks. Technically, a block is a data structure that records a transaction, reflects the flow of funds from the transaction, and cryptographically guarantees that the record is immutable and unforgeable. The decentralization of the blockchain enables scalability, robustness, privacy, and load balancing well, avoiding the risk of a single point of failure in a centralized structure [5]. Therefore, the blockchain has solved some data storage problems from different aspects at the beginning, but it still has its own data expansion problem, leading to low block communication efficiency.

As an important part of modern cryptography, cryptographic commitment technology can play an important role in solving data security, privacy security, regulatory inspection, etc. The perfect combination of cryptographic commitment and blockchain will solve the current dilemma faced by blockchain. On the one hand, the openness and transparency of blockchain make it have many limitations in terms of privacy and data security. On the other hand, how to solve the algorithm performance problem and improving the system’s throughput and response speed is a difficult problem faced by the large-scale implementation of the blockchain.

The contributions of this paper are summarized as follows.

1.    First, this paper analyzes traditional blockchain systems’ current problems and proposes replacing Merkle Tree with polynomial commitments. In this way, we can realize the aggregation verification of multiple proofs and reduce the communication cost of data verification.

2.    Second, we analyze the correctness of the aggregation algorithm and the update algorithm. A security model is established for our scheme through the integration with smart contract technology, and security analysis is performed. Doing so reduces validator storage.

3.    Finally, we compare the proposed schemes. The control variable method uses different methods for comparison in different scenarios. The comparison results show that our scheme can effectively reduce communication consumption when the amount of verification data is relatively large, which has obvious advantages over other schemes.

2  Related Work

The KZG [6] scheme is a commitment scheme specially designed to deal with polynomials. The committer outputs a short commitment to the polynomial, which can then be proved or “opened” at any time by a short evaluation to convince the verifier that the evaluation of the submitted polynomial is correct. Polynomial commitment schemes (PC) have been used to reduce communication and computational costs in a wide range of applications, including proofs of storage and replication, anonymous credentials, verifiable secret sharing, and zero-knowledge arguments. The zero-knowledge proof (ZKP) scheme is a proof system that can solve transaction trust issues, privacy protection issues, data encryption issues, and interaction issues in the blockchain. ZKP [7] was proposed by Goldwasser et al. in the early 1980s and is specifically defined as the prover that can convince the verifier that a certain assertion is correct without providing any useful information to the verifier. Essentially, a ZKP is an agreement involving two or more parties, a series of steps that two or more parties need to take to accomplish a task. The prover proves to the verifier and convinces it that it knows or possesses a certain message, but the proof process cannot reveal any information about the proved message to the verifier.

There are many types of PC solutions, and polynomials play an important role in building ZKP algorithms. The definition of promise is: the promiser provides a public value, which is called commitment, which is bound to the original message and does not expose the Message; The promiser needs to open the promise and send the message to the verifier to verify the correspondence between the promise and the message. The polynomial commitment can be regarded as a commitment to a polynomial. On the premise of not exposing the polynomial, a proof is used to prove the value of the polynomial at a certain point z, satisfying P(z) = a is established. Different entry points will lead to different effects. There are many schemes to achieve polynomial commitment. We have compared the construction of the current polynomial commitment scheme, as shown in Table 1:

Polynomial commitments can be used to construct ZKP algorithms. Different polynomial commitment schemes will lead to different properties of zero-knowledge proof algorithms, and there are obvious differences in efficiency and security. For example, the FRI-based zk-STARKs algorithm, which relies on a few mathematical security assumptions, is quantum-resistant and does not require any trusted setup. Furthermore, in the Supersonic [8] algorithm based on DARK, if the unknown order group is an RSA Group, it needs to be set credibly, relying on the assumption of difficulty in decomposing large numbers. No trusted setting is required if it is a Class Group, depending on the difficulty of calculating the number of Class Group elements.

In Table 2, we compare several mainstream polynomial commitment schemes. Different schemes have different advantages and efficiencies. In the process of practical application, a comprehensive evaluation needs to be made according to the application scenario. Whether you need better efficiency or better security is a question worth weighing.

3  Problem Statement

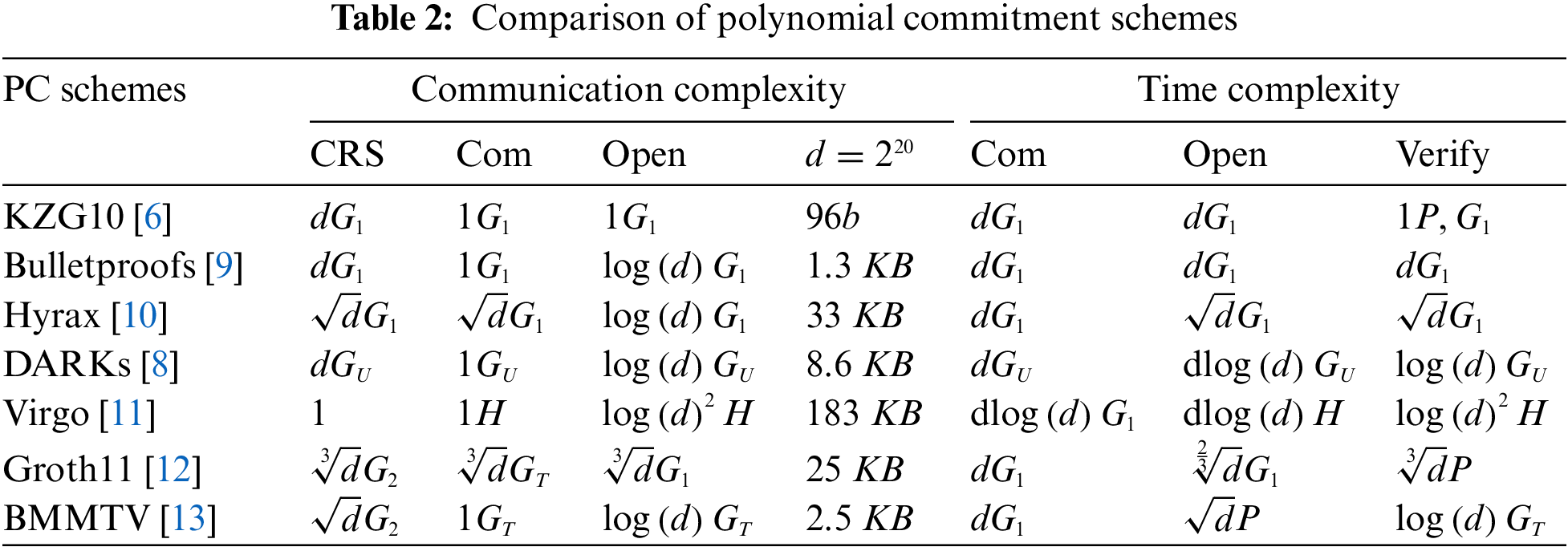
We understand a “blockchain protocol” as a protocol that allows an indeterminate number of computer behaviors to be unified into a single computer. Then, its operation will generate two kinds of data at the computer participating in the relevant protocol: one is block data, which is what we often call the blockchain, which records everything that happened in the network in the past; the other is state data, that is, data representing the current state of the entire network [14]. For Ethereum, the “state” information includes: how much balance the account has, how many transactions there are (not including the content of the transactions that have been issued, that is, the block data), what is the code of the contract, the value of the internal storage item What is, and some data related to the operation of the consensus mechanism. We can refer to Fig. 1 for the transaction process of the blockchain.

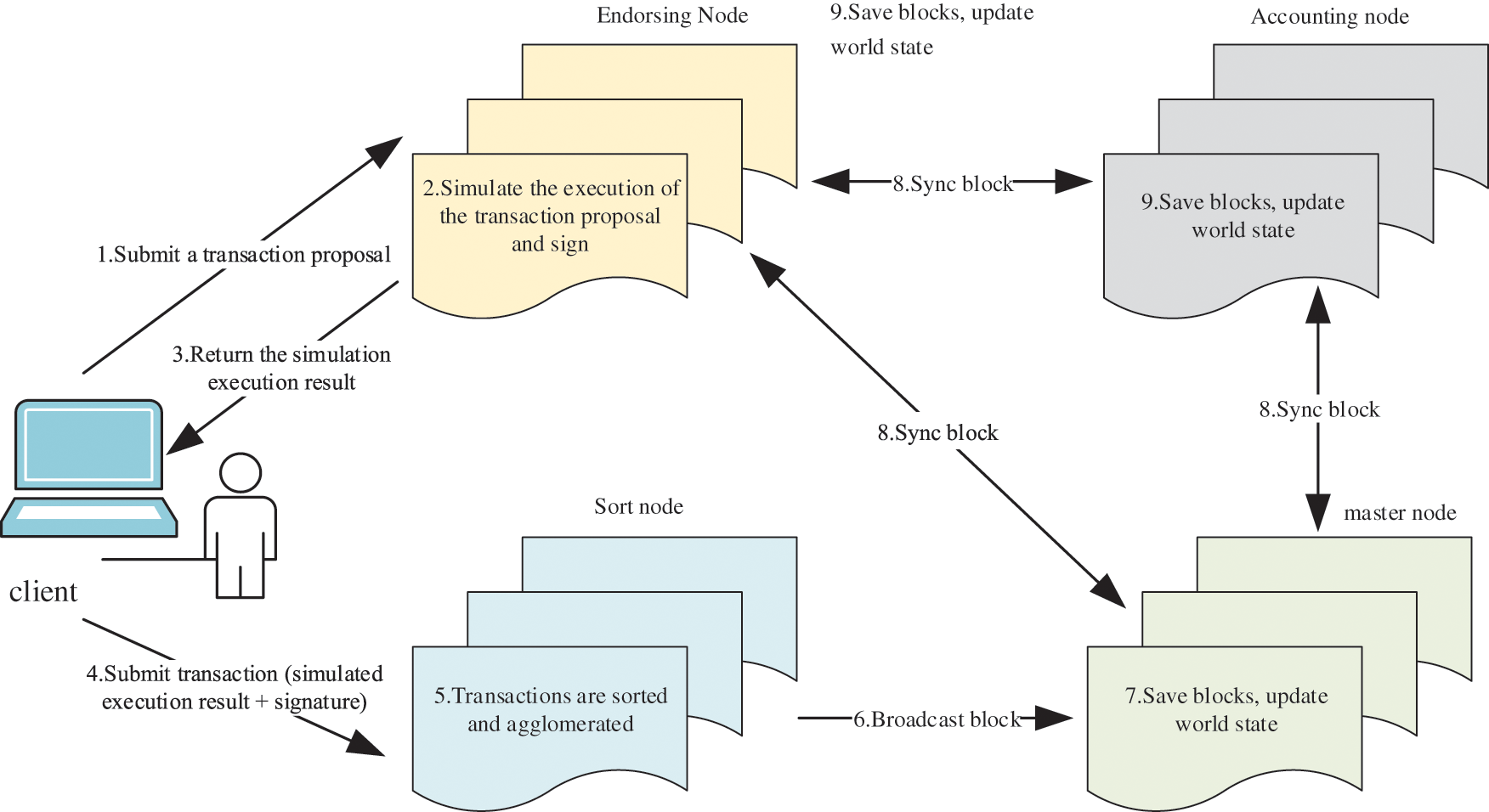
Figure 1: Blockchain transaction process

The particularity of state data is that: on the one hand, state data is the result of the execution of historical blocks (transactions included); on the other hand, it is the premise of executing new blocks. Therefore, on the current Ethereum blockchain, full nodes must save state data so that they can verify the legitimacy of newly received blocks by executing them. As you can imagine, because the number of users and contracts will continue to increase, the size of the state data will continue to grow without some control. This is the state data bloat problem [15].

The impact of the state bloat problem is certain: it makes block verification more and more difficult. Because it is also reading and writing a state object when there are 100,000 state objects, compared to when there are only 1,000 state objects, the overhead resource o increases, it is precise because of this that state expansion will increase the threshold for running a full node (in unit time, the resource overhead, mainly the random read and write of the hard disk will continue to rise). It will also gradually unbalance the proportion of gas overhead of each operation of the Ethereum Virtual Machine (EVM), resulting in increased demand for nodes.

Merkle Tree is the storage method or verification scheme used by the vast majority of cryptocurrencies in blockchain technology [16]. Each block in the blockchain is mainly composed of two parts: the block header and the block body. The block body contains complete transaction information, and the data information contained in a block body may be hundreds or thousands, so this will consume a lot of storage space for users [17,18]. To solve this problem, Satoshi Nakamoto proposed the concept of SPV (Simple Payment Verification), which only saves the block header of each block. SPV can verify payments without running a full node, and users only need to save all block headers. Although users cannot verify transactions by themselves, if they can find a matching transaction from somewhere in the blockchain, they can know that the transaction has been confirmed by the network and can also confirm how many times the network has confirmed the transaction. The data verification process of the Merkle tree is shown in Fig. 2.

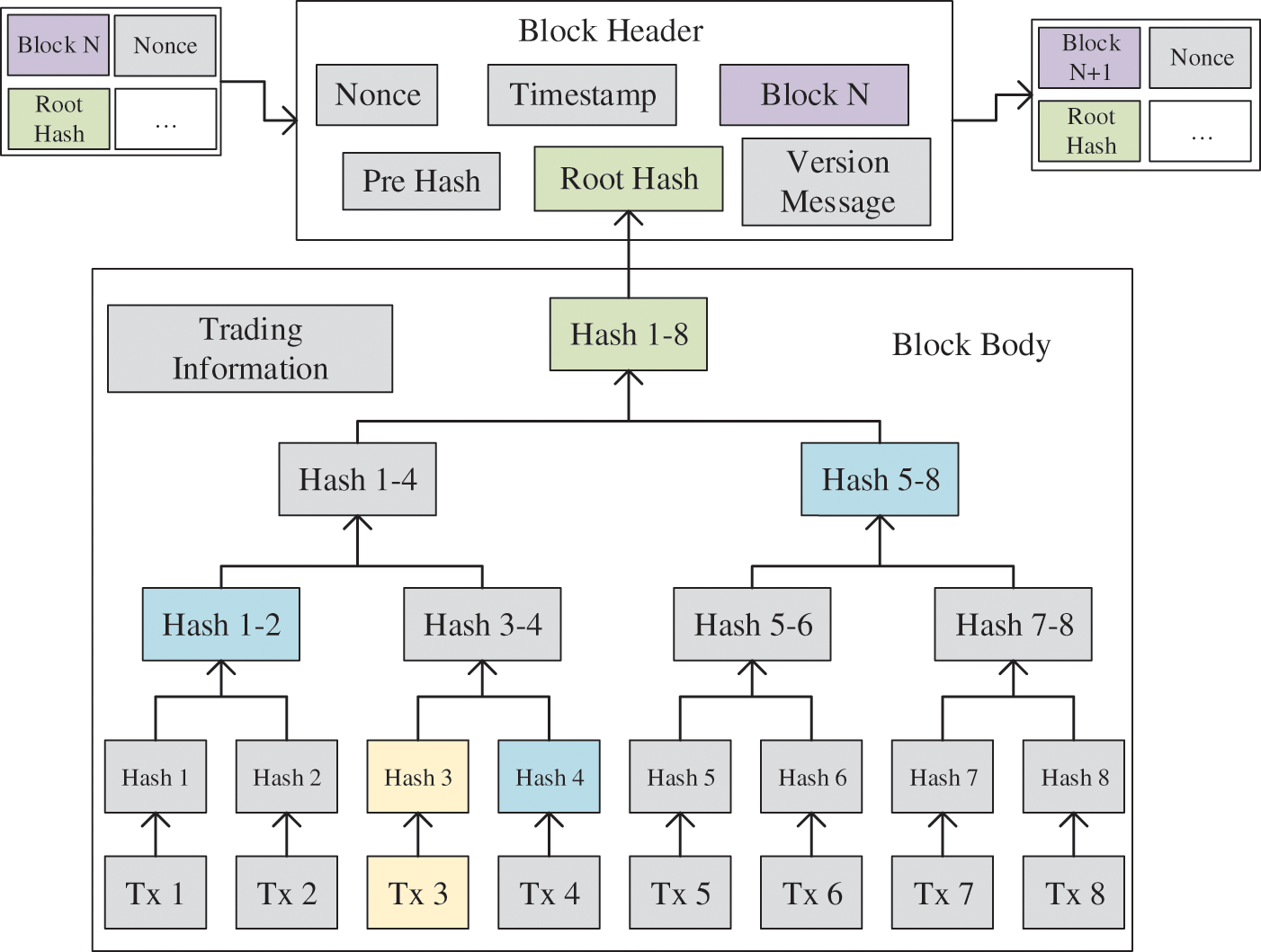
Figure 2: Merkle tree verification process

It should be noted here that SPV emphasizes verifying payments, not transactions, and the two concepts are different.

1)   Verification of payment: It is only necessary to determine whether the transaction used for payment has been verified and how many times the network has confirmed it. (i.e., how many blocks are superimposed).

2)   Verification of transactions: It is necessary to verify whether the account balance is sufficient for expenditure, whether there is double payment, whether the transaction script is passed, etc. Generally, this operation is completed by the miners of the full node. Full node: includes functions of wallet (payment verification), miner, complete blockchain database, and network routing node.

Assuming that numbers 1–8 represent transactions, to verify whether the transaction is fraudulent, we need to know the hash value of the leaf node and the intermediate node that we want to prove, and so on, to get the hash value of the root node finally. In this way, we can verify that the transaction is not fraudulent. In Fig. 2, we can clearly understand that the verification of each transaction needs to calculate the hash from bottom to top, and the existence of intermediate nodes also leads to additional space overhead.

Over time, blocks will continue to increase, and with it comes the issue of block capacity and efficiency. When there are more and more blocks, the data will also accumulate, and more space will be consumed, which will affect the information transmission rate of the entire blockchain. From the user’s point of view, this is unacceptable. We can shorten the verification time, improve the throughput of the system, and improve the overall efficiency by optimizing the consensus mechanism and using new technologies such as cryptography and smart contracts [19,20]. The introduction of smart contracts has brought greater research value to the blockchain. The smart contract itself has the advantages of trustlessness, security, efficiency, and no need for third-party arbitration, and it is just right to combine with blockchain technology. However, if the design is unreasonable, it will not only fail to provide safe and effective technical results but also may be attacked. The operating mechanism of the smart contract is shown in Fig. 3. Therefore, how to design an effective mechanism to improve the efficiency of the blockchain system under the premise of protecting privacy and security is an urgent problem to be solved.

Figure 3: Smart contract operating mechanism

4  Efficient Storage Verification Mechanism for Data in Blockchain

In traditional blockchains, it is difficult to provide proofs for all intermediate nodes using Merkle trees of width d to store data. Merkle trees are hard to do if all proofs are provided to the verifier, which we solve using an efficient multi-validation technique with polynomial commitments. However, we want to replace proofs for the entire Merkle tree with only a small, constant number of polynomial proofs. We aim to provide proof of commitment to intermediate nodes as efficiently as possible. Improve verification time and communication efficiency by generating proofs using proof aggregation and then putting them into smart contracts for verification. For specific algorithm schemes, see Sections 4.2, 4.3, and 4.4. Our overall design is shown in Fig. 4.

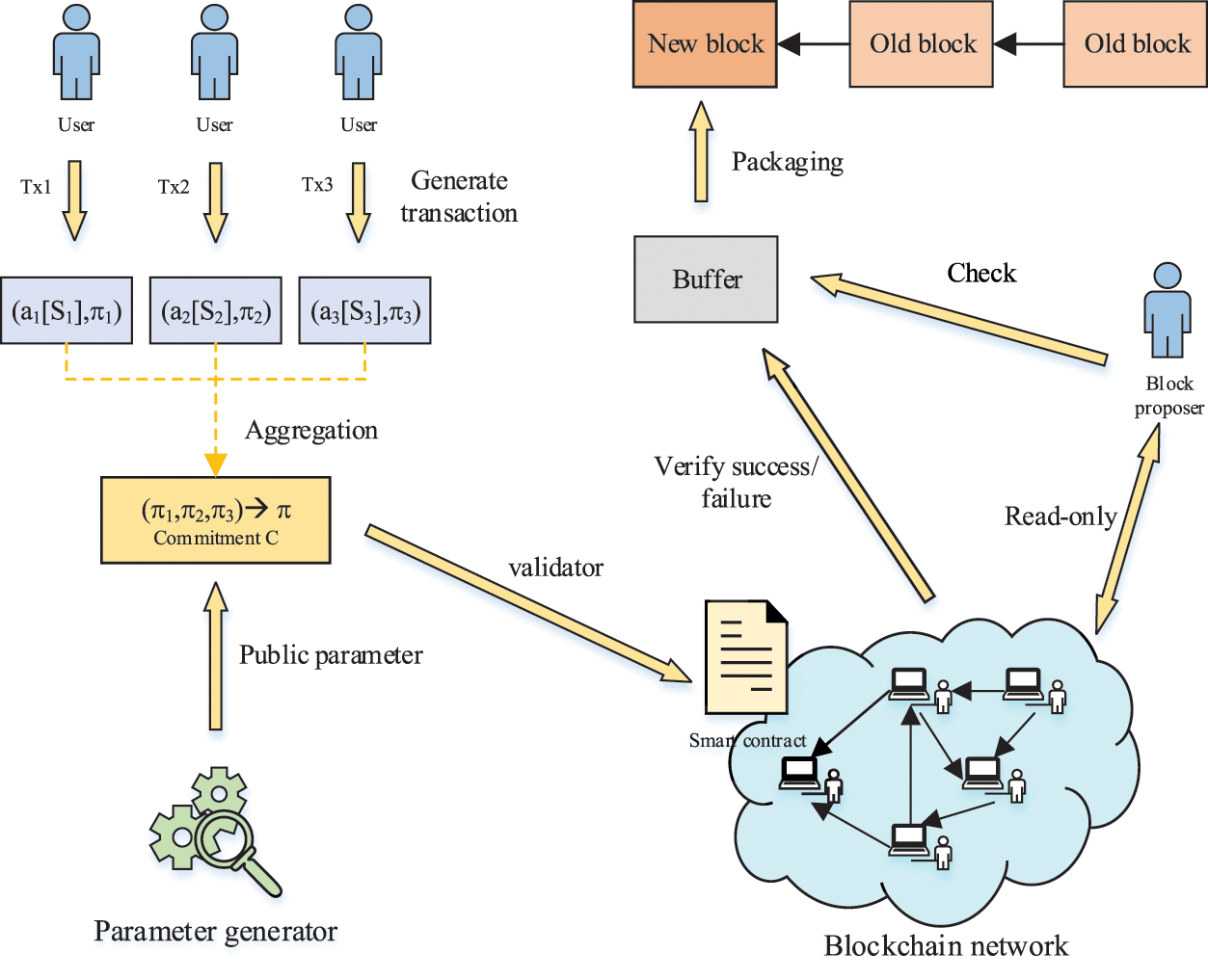
Figure 4: Efficient storage verification mechanism for data in the blockchain

4.1 Preliminary Knowledge

Cryptographic commitments are an important class of cryptographic primitives, and hash commitments are the simplest implementation among many technologies. The cryptographic commitment scheme is a two-phase interactive protocol involving two parties; the two parties are the promiser and the receiver, respectively. The first stage is the commitment-level stage. The promiser selects a message m and sends it to the receiver in the form of ciphertext, which means that it will not change m. The second stage is the opening stage. The committer discloses the message m and the blinding factor (equivalent to the secret key), and the receiver uses this to verify whether it is consistent with the message received in the commitment stage. The secrecy and binding of cryptographic commitments are key features commonly used in the design of privacy protection schemes. While ensuring the confidentiality of private data, it also ensures the uniqueness of interpretation of private data in the ciphertext. Cryptography promises to provide another efficient ciphertext representation for private data.

4.1.1 Pedersen Commitment

Pederson promises, used in conjunction with elliptic curves in cryptography, is a form of ciphertext with strong binding and homomorphic addition properties based on discrete logarithmic hard problems. There are generally two parties involved. We can define the public parameter ck={G,q,g,h}, where g is the generator of the group G, q is the prime order of the group G, h is the element in G, and the discrete logarithm is unknown.

Definition 1. Comck(a,r):=grha is a Pederson commitment to a, where r is a random number and is not public.

Multivariate Pederson commitment is an extension of Pederson commitment, that is, given public parameters ck=(G,q,g,h1,…,hn), where g is the generator of group G, (h1,…,hn)∈Gn, the discrete logarithms of these points are unknown; given a message (m1,…,mn)∈Zqn, the corresponding Pederson commitment is: C=Comck(m1,…,mn,r)=gr∏i=1nhimi. Pederson promises are divided into a promise commit phase and a promise open phase, as follows:

1)   Commitment submission stage: Assuming that there is a multiplicative group G, g0,g1∈G of prime order q as the generator, r∈zq is a random number, for message m, it’s Pederson promises C=g0rg1m, and then the promiser sends (m,r,g0,g1) to the receiver.

2)   Commitment opening stage: After the receiver receives the promised message, it verifies whether the equation c=g0rg1m holds if so, choose to accept, otherwise choose to reject.

Pederson promises to satisfy Hiding and Binding:

Hiddenness: Commitment values and random numbers are computationally indistinguishable. Since r is a random number, C0=grha0 and C1=grha1 are computationally indistinguishable, thus hiding the content.

Binding: After a promise is made, the content of the promise cannot be modified. Assuming that there are r′ and a′≠a such that grha=C=gr′ha′, then there is h=g(r−r′)(a′−a)−1, which shows that the discrete logarithm problem of h has been solved, which contradicts the assumption of the difficulty of the discrete logarithm, so the binding property is satisfied.

4.1.2 Polynomial Commitment

Polynomial expressions include coefficient notation and point value notation, both of which can uniquely determine a polynomial. The two representation methods have their application scenarios. For example, the coefficient representation method is efficient in the case of calculation and addition, while the point value representation method is efficient in the case of calculation and multiplication. Both are essentially expressing the same polynomial, so they can be transformed into each other. The fast Fourier transform (FFT) algorithm is to realize the conversion method of coefficient expression to point value expression, and inverse fast Fourier transform (IFFT) algorithm is just the opposite.

Assuming that the prover has the polynomial P(x)=a0+a1⋅x+a2⋅x2+…+ad−1⋅xd−1, we commit the polynomial P(x) Go out, the specific process is as follows:

1)   The prover calculates C←PloyCommit(P(x)) through the commitment algorithm, that is, a commitment to each coefficient of the polynomial P(x). C=(c1,c2,…,cd), where ci=Comck(ai,ri)=grihai,i=0,1,…,d−1. Here ck={G,q,g,h}, which are public parameters, and then send C to the verifier.

2)   The verifier chooses x at random and sends it to the prover.

3)   The prover computes the evaluation and generates the proof π←PolyEval(x,P(x)), where π=(v,ρ), v=P(x), ρ=∑i=0d−1rixi; and send π to the validator.

4)   The verifier calculates v←PolyVerify(C,π,x), where v={1,Comck(v,ρ)=∑i=1dcixi0,Comck(v,ρ)≠∑i=1dcixi,  1 means the verification passed, and 0 means the verification failed.

Using the well-known Fiat-Shamir [21] method, the interactive commitment protocol can be transformed into a non-interactive one, where x=H(π,ck). The prover publishes the commitment value (π,v,ρ), and the verifier calculates x and calls PolyVerify(C,π,x) to verify whether the commitment is legal.

4.2 Construction of Polynomial Commitment Schemes

Inspired by the Kate et al. [6] scheme and the Bootle et al. [22] scheme, based on the polynomial commitment scheme proposed by them, we use the Same-Commitment Aggregation scheme in the Pointproofs [23] scheme to join the UpdataCommit algorithm and the Aggregate algorithm. We can construct a polynomial of degree d: P(x)=a0+a1⋅x+a2⋅x2+…+ad−1⋅xd−1. The coefficients of the polynomial P(x) are the leaf nodes of the Merkle tree, respectively. The specific algorithm thought steps are as follows:

1)   The information stored in the leaf nodes of the Merkle tree is replaced by the subterms of the polynomial P(x).

2)   The prover commits the polynomial P(x) and sends it to the verifier.

3)   The verifier sends an evaluation point s, requesting the value P(s) of the evaluation point s. And send a random challenge x.

4)   The prover sends the evaluation result z = P(s) and the corresponding proof information.

5)   The verifier opens the promise and verifies the proof against the corresponding information, outputting either acceptance or rejection.

6)   Using Fiat-Shamir transformation to achieve non-interactive zero-knowledge.

7)   Implement Aggregate Validation.

4.2.1 Implementation of Polynomial Commitment Scheme

Polynomial P(x)=a0+a1⋅x+a2⋅x2+…+ad−1⋅xd−1, let a→=(a0,a1,…,ad−1), G→=(G0,G1,⋯,Gd−1). a0,a1,…,ad−1 are the coefficients of the polynomial P(x), and G0,G1,⋯,Gd−1 are independent generators based on discrete logarithmic relationships. We follow the following protocol:

1)   The prover generates a commitment value C to the polynomial P(x) as a commitment to a→, where C=⟨a→,G→⟩.

2)   The verifier sends an evaluation point s and a random challenge x, and requests to evaluate P(s). We let b→=(b1,b2,…,bd)=(1,S,S2,…,Sd−1). s is the location of the evaluation point.

3)   The prover sends the evaluation result z=⟨a→,b→⟩ in the computation, and the corresponding proof π.

4)   The verifier accepts or rejects the output by verifying the proof.

The Bulletproofs scheme in the case of Jonathan Bootle et al. utilizes a polynomial halving operation to achieve a performance improvement. For convenience, we assume that the constant term is zero and that the polynomial degree is highest d. The random number x sent by the validator can be used to implement the halving operation, which can be used to reduce the size of the proof, see Eqs. (1)–(3):

a→′=x−1(a1a2:ad2)+x(ad2+1ad2+2:ad)=(x−1a1+xad2+1x−1a2+xad2+2:x−1ad2+xad)(1)

b→′=x(b1b2:bd2)+x−1(bd2+1bd2+2:bd)=(xb1+x−1bd2+1xb2+x−1bd2+2:xbd2+x−1bd)(2)

G→′=x(G1G2:Gd2)+x−1(Gd2+1Gd2+2:Gd)=(xG1+x−1Gd2+1xG2+x−1Gd2+2:xGd2+x−1Gd)(3)

Now the problem to be proved is simplified by z=⟨a→,b→⟩ to prove z′=⟨a→′,b→′⟩, the prover will a→′,b→′ z′ Sent to the verifier, the verifier only needs to verify whether z′=⟨a→′,b→′⟩ and C′=⟨a→′,G→′⟩ are established.

From Eqs. (1) and (2) we can calculate z′, See Eq. (4):

z′=⟨a→′,b→′⟩

=⟨(x−1a1+xad2+1x−1a2+xad2+2:x−1ad2+xad),(xb1+x−1bd2+1xb2+x−1bd2+2:xbd2+x−1bd)⟩

=(x−1a1+xad2+1)(xb1+x−1bd2+1)+…+(x−1ad2+xad)(xbd2+x−1bd)

=(a1b1+a2b2+…+adbd)+x−2(a1bd2+1+a2bd2+2+…+ad2bd)+x2(b1ad2+1+b2ad2+2+…+bd2ad)

=z+x−2Lz+x2Rz(4)

From Eqs. (1) and (3) we can calculate C′, See Eq. (5):

C′=⟨a→′,G→′⟩

=⟨(x−1a1+xad2+1x−1a2+xad2+2:x−1ad2+xad),(xG1+x−1Gd2+1xG2+x−1Gd2+2:xGd2+x−1Gd)⟩

=(x−1a1+xad2+1)(xG1+x−1Gd2+1)+…+(x−1ad2+xad)(xGd2+x−1Gd)

=(a1G1+a2G2+…+adGd)+x−2(a1Gd2+1+a2Gd2+2+…+ad2Gd)+x2(G1ad2+1+G2ad2+2+…+Gd2ad)

=C+x−2La+x2Ra(5)

The information contained in the proof sent by the final prover is: vector a→′ (half the size of a→), points La, Ra on the elliptic curve, and scalar values Lz, Rz. The Fiat-Shamir method utilized can transform the above protocol into a non-interactive one.

4.2.2 Zero-Knowledge Proof Scheme

The Bulletproofs algorithm is optimized in the Halo [24] article, and the problem C=⟨a→,G→⟩ and z=⟨a→,b→⟩ is transformed into the problem M=C+zU=⟨a→,G→⟩+⟨a→,b→⟩U, where U is the introduced public generator. Similarly, the problem M can be halved, and we can convert the proof into: M′=C′+z′U=⟨a→′,G→′⟩+⟨a→′,b→′⟩U. Similarly, we can obtain the calculation method of M′ as follows, See Eq. (6):

M′=⟨a→′,G→′⟩+⟨a→′,b→′⟩U

     =[C+x−2La+x2Ra]+[z+x−2Lz+x2Rz]U

     =M+x−2(La+LzU)+x2(Ra+RzU)

     =M+x−2L+x2R(6)

L=La+LzU,R=Ra+RzU are all points on the elliptic curve, the verifier only needs to verify M′=M+x−2L+x2R=⟨a→′,G→′⟩+⟨a→′,b→′⟩U can be established. But the information of a→′ will be leaked, a→′ is a linear combination of the original vector a→′. In order to realize zero-knowledge, a generator H needs to be introduced to realize the binding, and the original proof becomes: M=C+zU+rH=⟨a→,G→⟩+⟨a→,b→⟩U+rH, where r is generated by the prover and known only by the prover. In the same way, there will also be information about a→′ in L and R. In order to prevent leakage, it is necessary to introduce random values rL,rR in each round for binding. At this time, L=La+LzU+rLH, R=Ra+RzU+rRH. The final promise we get is: M′=M+x−2L+x2R. The prover only needs to send a→′ and the final bound value r′ (r′ is composed of r,rL,rR in each round), and the verifier can open the commitment M′=⟨a→′,G→′⟩+⟨a→′,b→′⟩U+r′H. In this way, we can hide information. In order to achieve a more general zero-knowledge proof, we can refer to a more general Schnorr protocol proposed in the Halo article. In the case of not needing to send a→′, only need to send r′ Zero-knowledge verification can also be achieved.

4.3 Aggregate Authentication Scheme

The basic algorithms of this program include Setup, Commit, UpdataCommit, Open, Aggregate, and VerifyOpen. We mainly add the UpdataCommit algorithm and Aggregate algorithm. Setup is used to generate public parameters, the Commit algorithm generates commitments to polynomials, the UpdataCommit algorithm is used to update commitments, the Open algorithm is used to open commitments, the Aggregate algorithm implements the aggregation of commitments, and the VerifyOpen algorithm provides verification operations. Now we integrate all the schemes, and the specific algorithm scheme is as follows:

1)   ck←Setup(1λ,d): Given a security parameter λ and a polynomial degree constraint d, output the public parameter ck=(G,Fp,G→,H). G is a group of prime order p, Fp is a finite field, G→ is a linear combination of group element vectors, and H is a generator.

2)   C←Commit(ck,a→,r): Input public parameters ck, vector a→ and binding factor r, a→ is a linear combination of coefficients of polynomial p(x), p(x) degree is at most d−1, and output commitment is C.

3)   C′←UpdataCommit(C,S,a→[S],a→′[S]): Enter the promise C, the location set to be updated S, and after updating the data in the location set to be updated from a→[S] to a→′[S], the corresponding update promise is C′.

4)   πi←Open(i,a→,r): Open the proof πi corresponding to position i, input the position i and (a→,r) of the polynomial p(x) to be opened, and output the proof πi.

5)   π′←Aggregate(C,S,a→[S],{πi:i∈S}): Input commitment C, open position set S, the corresponding proof for each position is {πi:i∈S}, and the output is aggregate proof π′.

6)   0/1←VerifyOpen(C,S,a→[S],π′): The input is promise c, the open position set s, open information a→[S], aggregate proof π′. Output 0 or 1 for “reject” or “accept”.

4.4 Implementation of Smart Contract Design

In the smart contract, we need to verify two issues: the first is the ownership issue. The account operated by the user must be his own when a transaction occurs; this is to prevent malicious users from operating other people’s accounts to conduct transactions. The second is the legal issue. After converting the state information of each account into a polynomial commitment, it needs to be verified in the smart contract. The user account is verified in the smart contract. Only the verified user account will be accepted. Otherwise, the verification will fail.

When the Merkle tree in the blockchain verifies the transaction, it starts from the leaf node, and each layer needs an intermediate node to assist in the verification, which will cause a waste of space and an increase in time overhead. If a smart contract is used to store the leaf nodes or proofs of the Merkle tree, the space consumption is huge, and the space and time overhead cannot be borne. After replacing the Merkle tree with polynomial commitments, we only need to store the commitments in the smart contract. When verification is required, we can directly open the commitment in the smart contract for verification. In the blockchain system, as long as the conditions are met, the contract will be triggered to verify the contract, which can prevent third parties from tampering with the generated commitment information. To a certain extent, the security is strengthened, and at the same time, the introduction of smart contracts can also save our time overhead. The specific contract design is shown in Fig. 5.

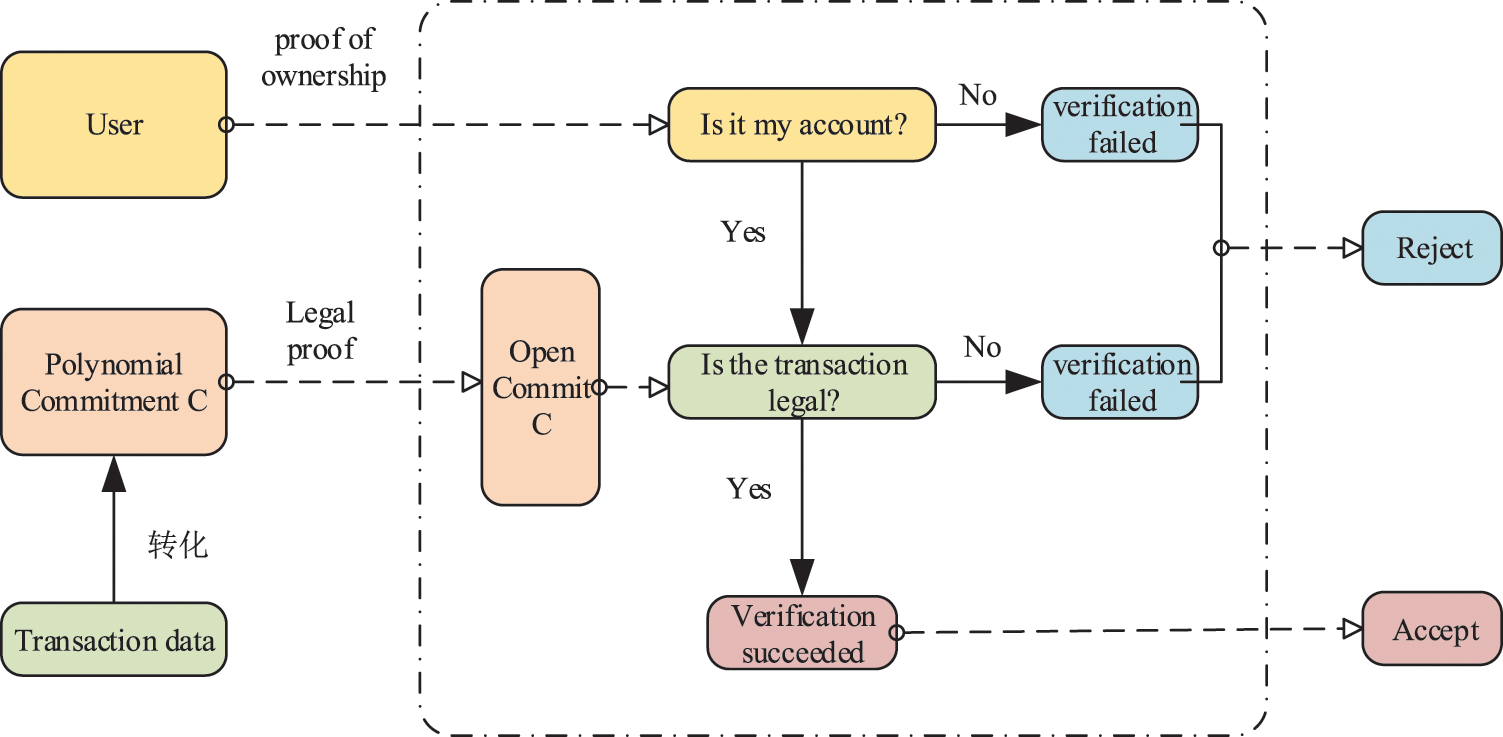
Figure 5: Smart contract design

5  Theoretical Analysis of Scheme

5.1 Preliminaries

Knowledge of bilinear mappings is required in our solution. The following briefly reviews the basic concepts of bilinear maps and groups of bilinear maps. We adopt the notation definition of Boneh et al. [25]:

1)G1 and G2 are two (multiplicative) cyclic groups of prime order p.

2)g1 is a generator of G1 and g2 is a generator of G2;

3)φ is an isomorphism from G2 to G1, with φ(g2)=g1; and

4)e is a bilinear map e: G1×G2→GT.

For simplicity, we can set G1=G2. The proofs of security require an efficiently computable isomorphism φ:G2→G1. When G1=G2 and g1=g2 one could take φ as the identity map. On elliptic curves, we can use the trace map as φ.

Let G1 and G2 be two groups as above, with an additional group GT such that |G1|=|G2|=|GT|. A bilinear map is a map e: G1×G2→GT with the following properties:

1) Bilinear: for all u∈G1,v∈G2 and a,b∈Z,e(ua,vb)=e(u,v)ab.

2) Non-degenerate:e(g1,g2)≠1.

We say that (G1,G2) are bilinear groups if there exists a group GT, an isomorphism φ:G2→G1, and a bilinear map e: G1×G2→GT as above, and e, φ, and the group action in G1,G2, and GT can be computed efficiently.

5.2 Correctness Analysis

Take a random value β←ZP, n→=(β,β2,…,βD), g1n→=(g1β,…,g1βD), g1βDn→[−1]=(g1βD+2,…,g1β2D), g2n→=(g2β,…,g2βN), gTβD+1=e(g1β,g2βD). Now let’s introduce the meaning expressed by the symbol. [D] represents the set of polynomial coefficient vector subscripts. a→ represents a vector of coefficients of the polynomial, ai represents the coefficient of the polynomial. n→ represents a vector of random numbers, consisting of β. S represents the set of positions. The correctness analysis of the UpdataCommit algorithm and Aggregate algorithm is as follows.

For all i∈[D], we have πi=Prove(i,a→)=g1βD+1−ia→[−i]⊤n→[−i] satisfying Eq. (7):

e(C,g2βD+1−i)=e(πi,g2)⋅gTβD+1ai(7)

Multiply both sides of the equation a→⊤n→=a→[−i]⊤n→[−i]+βiai by βD+1−i to get Eq. (8):

(a→⊤n→)βD+1−i=βD+1−ia→[−i]⊤n→[−i]+βD+1ai(8)

Converted to pairing operation, we can get Eq. (9):

e(g1a→⊤n→,g2βD+1−i)=e(g1βD+1−ia→[−i]⊤n→[−i],g2)⋅gTβD+1ai(9)

To prove the correctness of the aggregation algorithm Aggregate, multiply the exponents on both sides of Eq. (7) by ti=H(i,C,S,a→[S]) to get Eq. (10):

e(C,g2βD+1−iti)=e(πiti,g2)⋅gTβD+1aiti(10)

Multiplying the above equation by all i∈S gives Eq. (11):

e(C,g2ΣiϵsβD+1−iti)=e(∏i∈sπiti,g2)⋅gTβD+1Σiϵsaiti(11)

The correctness of the UpdataCommit algorithm is easily derived from Eq. (12):

a→′⊤n→=(a→′[S]−a→[S])⊤n→[S]+a→⊤n→(12)

5.3 Security Analysis

Under the assumption of l−wBDHE, the scheme satisfies the binding based on the same commitment aggregation in the Algebraic Group Model (AGM) + Random Oracle Model (ROM) model. The protocol is secure if the binding is secure and the adversary cannot forge an attack.

Suppose the adversary can compute C=g1z→⊤a→ and provide a proof for(S,a→[S]) that π′ can be accepted by the verifier, where a→[s]≠z→[S]. We have Eq. (13):

e(g1z→⊤a→,g2ΣiϵsβD+1−iti)=e(π′,g2)⋅gTβD+1Σiϵsziti=e(π′,g2)⋅gTβD+1Σiϵsaiti(13)

The parameter g1βD+1 opponent is unknown, that is, the coefficient corresponding to the βD+1 term in logg1⁡π′ is 0. Comparing Σiϵsaiti≡PΣiϵsziti in Eq. (13), expressed as a vector, should satisfy: z→[S]⊤t→≡Pa→[S]⊤t→, where t→=(H(i,C,S,a→[s]),i∈S). Assuming that (S,z→[S],a→[S]) is fixed, we make a uniform choice for t→←ZP[S], then we have Eq. (14):

Prt→(z→[S]≡Pa→[S]andz→[S]⊤t→≡Pa→[S]⊤t→)=1p(14)

It indicates that the corresponding probability can be ignored. Note that the commitment C is generated in the AGM and determines z→ ,C,S,a→[s] as the input H(i,C,S,a→[s]) in the ROM, and the output is ti. If the opponent can find the corresponding ai≠zi value such that Σiϵsaiti≡PΣiϵsziti holds, the binding property does not hold.

5.4 Program Comparison Analysis

The commitment scheme proposed in this paper is asymptotically compared with other commitment schemes in Table 3. We assume each account memory contains N = 1000 variables, each storing a 32-byte value. The schemes we compare include Merkle Tree, pairing-based LM19 [26], and Class Group and RSA-based BBF19 [27]. ck represents public parameters, com represents the size of the promise, open represents the size of the open promise, group represents the group assumption used, and agg represents the aggregate of promises. − Indicates that the function or setting is not available, and √ indicates that the function is available. The complexity in this table is asymptotic in the number of exponential, pairing, and field operations. For class groups, we use a 2048-bit group. For pairing groups, we use BLS12-381. For Merkle Trees, we assume paths of length 10 and 256-bit hashes.

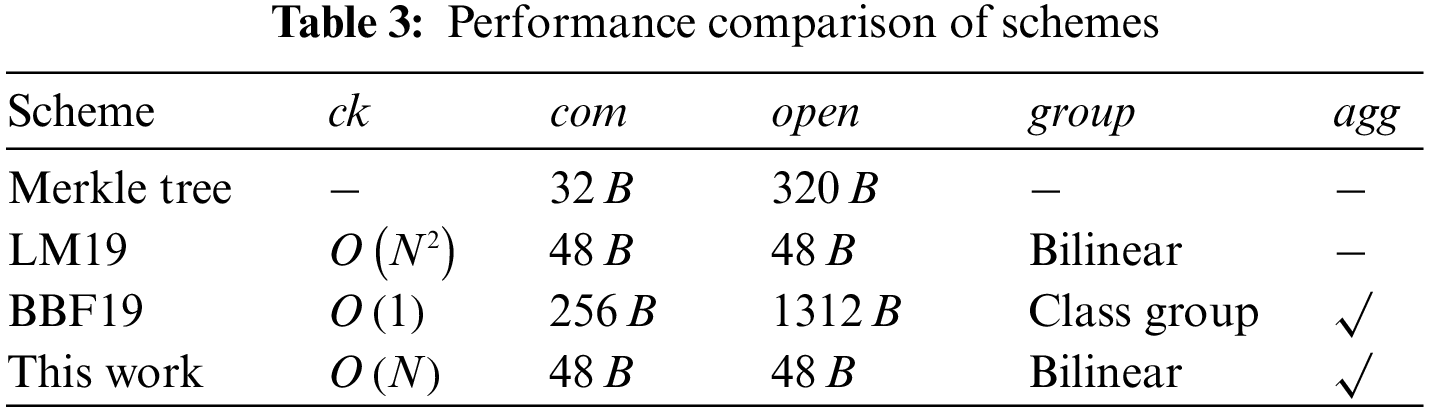
The size of a Merkle proof is affected by the depth of the Merkle tree, so the proof size also grows with the number of transactions stored per block. However, the proof size of a single block of data in a polynomial commitment scheme is not affected by the number of transactions stored in each block. Since the Merkle Tree scheme and the LM19 scheme have no aggregation algorithm, the proof size is not fixed. Both our scheme and the BBF19 scheme have aggregation algorithms. They have fixed-size proofs as traffic increases. However, the scheme in this paper is a bilinear group scheme. It has a smaller proof size at the same level of security.

This scheme, combined with the use of smart contracts, can improve efficiency faster. Opening the proof at a certain point can minimize the overhead because the proofs across transactions can be aggregated into a single proof. This solution is specially designed for smart contracts. When the communication volume is larger, the aggregation solution’s efficiency advantage is more obvious.

6  Conclusion

With the rapid development of blockchain technology, more and more problems are encountered in terms of privacy protection, system stability, data storage, and communication efficiency. We use the scheme of polynomial commitment to improve the blockchain system and use the improved scheme to protect the data security of the blockchain system. The traditional blockchain system uses the Merkle tree to store and verify data. Compared with the traditional Merkle tree, the scheme in this paper has been improved in space and time, which improves the efficiency of block transactions in the blockchain. In this paper, we can better optimize the blockchain system, reduce the time overhead required for verification, and improve communication efficiency by realizing the combined use of proof aggregation verification and smart contracts. However, how to use more advanced technology in blockchain research to ensure efficient data verification and storage while protecting privacy and security is still an issue worth studying in the future.

Funding Statement: This work is supported by the Fundamental Research Funds for the central Universities (Zhejiang University NGICS Platform), Xiaofeng Yu receives the grant and the URLs to sponsors’ websites are https://www.zju.edu.cn/. And the work are supported by China’s National Natural Science Foundation (No. 62072249, 62072056). Jin Wang and Yongjun Ren receive the grant and the URLs to sponsors’ websites are https://www.nsfc.gov.cn/. This work is also funded by the National Science Foundation of Hunan Province (2020JJ2029). Jin Wang receives the grant and the URLs to sponsors’ websites are http://kjt.hunan.gov.cn/.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References:

 1.   Y. Jeon, K. Lee and H. Kim, “Distributed join processing between streaming and stored big data under the micro-batch model,” IEEE Access, vol. 7, pp. 34583–34598, 2019. [Google Scholar]

 2.   J. Wang, Y. Gao, W. Liu, W. Wu and S. J. Lim, “An asynchronous clustering and mobile data gathering schema based on timer mechanism in wireless sensor networks,” Computers, Materials & Continua, vol. 58, no. 3, pp. 711–725, 2019. [Google Scholar]

 3.   Y. J. Ren, F. J. Zhu, P. K. Sharma, T. Wang, J. Wang et al., “Data query mechanism based on hash computing power of blockchain in internet of things,” Sensors, vol. 20, no. 1, pp. 1–22, 2020. [Google Scholar]

 4.   X. R. Zhang, X. Sun, X. M. Sun, W. Sun and S. K. Jha, “Robust reversible audio watermarking scheme for telemedicine and privacy protection,” Computers, Materials & Continua, vol. 71, no. 2, pp. 3035–3050, 2022. [Google Scholar]

 5.   X. R. Zhang, W. F. Zhang, W. Sun, X. M. Sun and S. K. Jha, “A robust 3-D medical watermarking based on wavelet transform for data protection,” Computer Systems Science & Engineering, vol. 41, no. 3, pp. 1043–1056, 2022. [Google Scholar]

 6.   A. Kate, G. M. Zaverucha and I. Goldberg, “Constant-size commitments to polynomials and their applications,” in ASIACRYPT, Singapore: Springer, pp. 177–194, 2010. [Google Scholar]

 7.   G. Shafi, S. Micali and C. Rackoff, “The knowledge complexity of interactive proof-systems (extended abstract),” in Proc. of the 17th Annual ACM Symp. on Theory of Computing, Rhode Island, USA, Providence, pp. 6–8, 1985. [Google Scholar]

 8.   B. Bünz, B. Fisch and A. Szepieniec, “Transparent SNARKs from DARK compilers,” in Proc. EUROCRYPT, Zagreb, Croatia, Springer, pp. 677–706, 2020. [Google Scholar]

 9.   B. Bünz, J. Bootle, D. Boneh, A. Poelstra, P. Wuille et al., “Bulletproofs: Short proofs for confidential transactions and more,” in Proc. IEEE Symp. on Security and Privacy (SP), California, CA, USA, pp. 315–334, 2018. [Google Scholar]

10.  R. S. Wahby, I. Tzialla, A. Shelat, J. Thaler and M. Walfish, “Doubly-efficient zkSNARKs without trusted setup,” in Proc. IEEE Symp. on Security and Privacy (SP), San Francisco, CA, USA, pp. 926–943, 2018. [Google Scholar]

11.  J. Zhang, T. Xie, Y. Zhang and D. Song, “Transparent polynomial delegation and its applications to zero knowledge proof,” in Proc. IEEE Symp. on Security and Privacy (SP), San Francisco, CA, USA, pp. 859–876, 2020. [Google Scholar]

12.  J. Groth, “Efficient zero-knowledge arguments from two-tiered homomorphic commitments,” in Proc. ASIACRYPT, Seoul, South Korea, pp. 431–448, 2011. [Google Scholar]

13.  B. Bünz, M. Maller, P. Mishra, N. Tyagi and P. Vesely, “Proofs for inner pairing products and applications,” in Proc. ASIACRYPT, Singapore, pp. 65–97, 2021. [Google Scholar]

14.  T. Wang, C. Zhao, Q. Yang, S. Zhang and S. C. Liew, “Ethna: Analyzing the underlying peer-to-peer network of ethereum blockchain,” IEEE Transactions on Network Science and Engineering, vol. 8, no. 3, pp. 2131–2146, 2021. [Google Scholar]

15.  J. Wang, Y. Yang, T. Wang, R. S. Sherratt and J. Zhang, “Big data service architecture: A survey,” Journal of Internet Technology, vol. 21, no. 2, pp. 393–405, 2020. [Google Scholar]

16.  M. Muneeb, Z. Raza, I. U. Haq and O. Shafiq, “SmartCon: A blockchain-based framework for smart contracts and transaction management,” IEEE Access, vol. 10, pp. 23687–23699, 2022. [Google Scholar]

17.  C. Ge, W. Susilo, Z. Liu, J. Xia, P. Szalachowski et al., “Secure keyword search and data sharing mechanism for cloud computing,” IEEE Transactions on Dependable and Secure Computing, vol. 18, no. 6, pp. 2787–2800, 2021. [Google Scholar]

18.  C. Ge, Z. Liu, J. Xia and L. Fang, “Revocable identity-based broadcast proxy re-encryption for data sharing in clouds,” IEEE Transactions on Dependable and Secure Computing, vol. 18, no. 3, pp. 1214–1226, 2021. [Google Scholar]

19.  Y. J. Ren, Y. Leng, J. Qi, P. K. Sharma, J. Wang et al., “Multiple cloud storage mechanism based on blockchain in smart homes,” Future Generation Computer Systems, vol. 115, no. 2, pp. 304–313, 2021. [Google Scholar]

20.  Y. J. Ren, Y. Leng, Y. P. Cheng ang J. Wang, “Secure data storage based on blockchain and coding in edge computing,” Mathematical Biosciences and Engineering, vol. 16, no. 4, pp. 1874–1892, 2019. [Google Scholar]

21.  A. Fiat and A. Shamir, “How to prove yourself: Practical solutions to identification and signature problems,” in Proc. Advces Cryptology (Lecture Notes in Computer Science), Santa Barbara, CA, USA, pp. 186–194, 1986. [Google Scholar]

22.  J. Bootle, A. Cerulli, P. Chaidos, J. Groth and C. Petit, “Efficient zero-knowledge arguments for arithmetic circuits in the discrete log setting,” in Proc. EUROCRYPT, Vienna, Austria, pp. 327–357, 2016. [Google Scholar]

23.  S. Gorbunov, L. Reyzin, H. Wee and Z. Zhang, “Pointproofs: Aggregating proofs for multiple vector commitments,” in Proc. ACM SIGSAC Conf. on Computer and Communications Security, Virtual Event, USA, pp. 2007–2023, 2020. [Google Scholar]

24.  S. Bowe, J. Grigg and D. Hopwood, “Halo: Recursive proof composition without a trusted setup,” IACR Cryptol, ePrint Arch, Report 2019/1021, 2019. [Google Scholar]

25.  D. Boneh and X. Boyen, “Short signatures without random oracles,” in Proc. EUROCRYPT, Interlaken, Switzerland, Springer, pp. 56–73, 2004. [Google Scholar]

26.  R. W. F. Lai and G. Malavolta, “Subvector commitments with application to succinct arguments,” in Proc. CRYPTO, Santa Barbara, CA, USA, pp. 530–560, 2019. [Google Scholar]

27.  D. Boneh, B. Bünz and B. Fisch, “Batching techniques for accumulators with applications to IOPs and stateless blockchains,” in Proc. CRYPTO, Santa Barbara, CA, USA, pp. 561–586, 2019. [Google Scholar]