A Novel Wrapper-Based Optimization Algorithm for the Feature Selection and Classification

1  Introduction

Machine Learning (ML) is an interdisciplinary field that relies on ideologies across computer science, stats, cognitive neuroscience, engineering, and a range of other fields. The approaches such as clustering, regression, and classification are well-known ML approaches, however, the classification methods are the most widely used for solving various real-world tasks [1]. Classification falls under the data mining methods that help in extracting meaningful data from datasets and providing classification results. Generally, a classification technique uses the training data to train the developed model. Once the model is well-trained, the testing data is utilized to generate the classification results [2]. Various classifiers such as Support Vector Machine (SVM), K-Nearest Neighbor (KNN), and hybrid deep neuro-fuzzy classifiers [3] have shown a prominent performance for the applications of time-series classification [4], facial expression classification [5], image classification [6], and social media such as Twitter data classification [7].

Even though these algorithms have been effectively used for a range of classification-related tasks, their performance suffers significantly when applied to high-dimensional data. In general, for every n original feature in a dataset, 2n potential feature subset combinations are produced and assessed at a high computing cost [8]. Similarly, when we talk about medical data, it is the most sensitive data that contain numerous aspects linked to disease, and it must be handled with extreme caution to provide the correct diagnosis of disease for quality services. Hence, managing such data is a critical job in the medical industry. Owing to many features, there is always a strong possibility of data having missing values and repetitive and distinct features. Generally, medical data experiences two challenging issues; (i) owing to many features, there is always a strong possibility of data having missing values and repetitive and distinct features, (ii) the majority of the medical datasets contain ultrasound images and various types of lab results. The number of features in such datasets might range between two and thousands. Due to the high dimensionality, processing such datasets on a system with lower specifications is typically a challenging and time-consuming task. These two factors often disturb the results of classification accuracy in the field of medical science. Therefore, before using the data for disease classification in the medical system, it is important to use effective data preparation and data reduction techniques to find the most relevant risk factors [9].

Hence, to address the data high-dimensionality problem in medical data, literature has proposed various feature selection (FS) techniques that help in reducing the feature size [10]. Integrating FS approaches with classification methods doesn’t only assist in enhancing the classification accuracy but also aids in minimizing the computing cost. Generally, the FS practices are classified into filter and wrapper methods. The filter method doesn’t use any classification algorithm. Moreover, it overlooks classification accuracy and instead concentrates on the characteristics of the data such as input and output variables. Wrapper methods, on the other hand, employ classifiers and are tied directly to the data features. However, wrapper methods are known to be computationally intensive, yet they outperform filter approaches in terms of the quality of output [11,12]. Therefore, wrapper methods also known as metaheuristic techniques, are widely used to evaluate the effectiveness of selected features [13]. Metaheuristics use a derivative-free approach, which simplifies implementation while escaping the algorithm from being caught in local optima [14]. Literature regarding metaheuristic optimization algorithms offers a wide variety of methods. Because medical data is classified as complex data, performing data pre-processing using standard metaheuristics as FS techniques reduce the classification accuracy. Moreover, the capacity of any metaheuristic algorithm to locate the best solution is determined by its exploration and exploitation abilities. The proper stability between explorative and exploitative search aids in the achievement of the desired result. Therefore, a growing number of novel metaheuristic techniques with better and enhanced search algorithms are published every year.

Similarly, a novel swarm intelligence-based metaheuristics algorithm called Sand Cat Swarm Optimization (SCSO) has been proposed in 2022 [15]. To validate the efficiency of the algorithm, the original study of SCSO tested the algorithm on various benchmark functions where the algorithm has outperformed by generating effective outcomes compared to well-known metaheuristics algorithms. Moreover, the SCSO algorithm has been successfully implemented on several engineering design problems including welded beam design, tension/compression spring design, pressure vessel design, and three-bar truss design. Besides, the algorithm has also been used to compute the minimum safety factor for earth slopes under static and earthquake situations in [16]. Inspired by the effectiveness of this novel technique for solving high-dimensional global optimization problems, the main goal of the study is to propose the SCSO approach as an FS technique to find out the optimum features from the high-dimensional medical data to generate quality outcomes with high classification accuracy. To the best of our knowledge, this study is the first effort on implementing the novel SCSO algorithm for the task of FS. Moreover, the study’s main contributions are presented as follows:

•   At first, the novel and efficient metaheuristic approach with better search capabilities named SCSO algorithm is proposed to perform FS-related tasks to identify the best features from the complex and high-dimensional medical data.

•   The efficiency of the selected feature subset obtained from the SCSO algorithm is evaluated, classified, and validated using a KNN classifier.

•   The performance of the proposed SCSO-KNN approach is compared with six recent state-of-the-art algorithms using the common evaluation metrics of average feature size, classification accuracy, and computational cost.

•   Additionally, non-parametric statistical tests using Wilcoxon signed-rank test are done to examine the significant difference between the outcomes obtained by the proposed SCSO technique and the compared algorithms.

The remaining study is structured as follows: Section 2 discusses the related works and Section 3 explains the working mechanism of the proposed SCSO method. Section 4 delivers an explanation of the proposed methodology for the task of FS using a novel SCSO technique. Section 5 discusses the obtained results. Finally, Section 6 summarizes the conclusions and provides a future recommendation in the field of optimization.

2  Related Works

Metaheuristics are used to find the best solutions to a given problem of interest. These algorithms are remarkably effective for averting the algorithms from premature convergence and can be easily tailored to the specific problem [17]. A metaheuristic algorithm, in general, employs a number of agents in the search process to build a dynamic system of solutions using a set of rules or mathematical models over multiple iterations until the identified solution fulfills a given criterion [18]. During the search process, the mathematical modeling of a metaheuristic algorithm uses two key components of exploration and exploitation. The effectiveness of an algorithm completely depends on these two search phrases. During the phase of exploitation search, an algorithm broadens its scope to include previously unexplored regions. Whereas, in the exploitation search phase, an algorithm focuses on promising regions to identify a potential solution.

Over the past decades, various metaheuristic algorithms have been introduced in the literature by either improving existing methods, enhancing the performance of one method by hybridizing it with another method, or proposing novel algorithms [14]. Besides, before optimizing a problem, the literature advises selecting a metaheuristic algorithm based on their search mechanisms such as single solution-based algorithms and population-based algorithms. Single solution-based algorithms follow exploitative search mechanisms, while population-based algorithms employ more effective explorative search mechanisms. Moreover, as the name indicates, single solution-based algorithms use one solution on each iteration. The algorithms in this category often fail to explore the solution in a wider search space, therefore, have the probability of falling in local minima. Comparatively, population-based algorithms offer excellent exploratory searches using the number of solutions over several iterations, which protects the algorithms from being stuck in local minima. Hence, the majority of the studies can be witnessed in literature employing population-based algorithms for solving non-linear complex real-world problems [17].

The popular techniques in the category of single solution-based are Tabu Search Algorithm (TSA) [19], Simulated Annealing Algorithm (SAA) [20], Hill Climbing Algorithm (HCA) [21], and Guided Local Search Algorithm (GLSA) [22]. The population-based algorithms are further subdivided into four categories; (i) Swarm intelligence methods replicate the swarm hunting strategy of living species such as insects, fishes, or animals. Although each member of the swarm intelligence method has their own intellect and behavior, the collaboration between the members increases the ability to address highly non-linear problems. (ii) Evolutionary methods are impacted by biological and evolutionary processes. These algorithms use the parameters of mutation, crossover, and selection to produce new solutions by combining the optimum solutions. (iii) Physics-based methods are derived from actual physical laws and usually refer to the conveyance of search solutions based on governing principles inherent in physical practices. Whereas, (iv) Human behavior-based methods are purely inspired by human behavior and the way human interacts with other humans to solve an optimization problem [14]. The following Table 1 summarizes the recent population-based metaheuristic techniques from each category from the year 2019 to the year 2022.

2.1 Metaheuristics for Feature Selection in Medical Sciences

In contrast to other domains, datasets in the field of medical sciences typically contain a greater number of features. The majority of the features in such data are essential for comprehending the illness and guide in developing a machine learning-based prediction model. Generally, a machine learning model needs a substantial amount of data to prevent the risk of over-fitting. The massive amounts of features, however, greatly undermine the efforts of building an effective model due to the curse of dimensionality. Besides, when a dataset’s dimensionality grows significantly, the amount of useful information decreases due to an increase in data sparsity. Likewise, noise is another factor that affects the performance of machine learning and adds to its complexity [59].

To overcome such issues, various metaheuristic-based FS approaches have been introduced in the literature. These techniques primarily work for dimensionality reduction by identifying only relevant features and removing the irrelevant and redundant features from the given dataset. An FS technique requires searching the complete feature space by identifying distinct candidates for feature subsets. This search can be performed in one of three ways: completely, sequentially, or randomly. In the first approach, an extensive search is done to cover all of the feature space and ensures the best solution depending on the chosen evaluation metric. But it has the drawback of being computationally costly when used across a wide feature space. Comparatively, sequential search has a lower computational cost than complete search but it doesn’t guarantee finding the optimum solution because it uses the prior rankings produced by other approaches. Similarly, the random search activates with a random subset of feature space, therefore this approach also does not provide the best solution. The subsequent subset is created at random, and the procedure is repeated until the threshold value is met [60]. All these methods are effective in one way or another way to find the suitable and reduced feature subset from high-dimensional data. Therefore, a decrease in data dimensionality enhances the effectiveness of many machine learning models by lowering the complexity and computational cost. Moreover, a good FS approach helps in increasing the model’s interpretability and classification accuracy [60].

Owing to such advantages, FS approaches have been widely used to solve real-world problems with high data dimensionalities such as image, text, and video classification, image processing, clustering, and industrial applications such as fault detection. In medical science, the goal of FS is to produce a smaller feature subset while still producing higher classification and disease prediction accuracy. Hence, the effectiveness of the FS approaches has been tested in the field of medical science for the applications of medical image processing, biomedical signal processing, and early diagnosis of disease. Table 2 summarizes the most recent metaheuristic algorithms from the literature that has been used in the field of medical sciences for the task of FS.

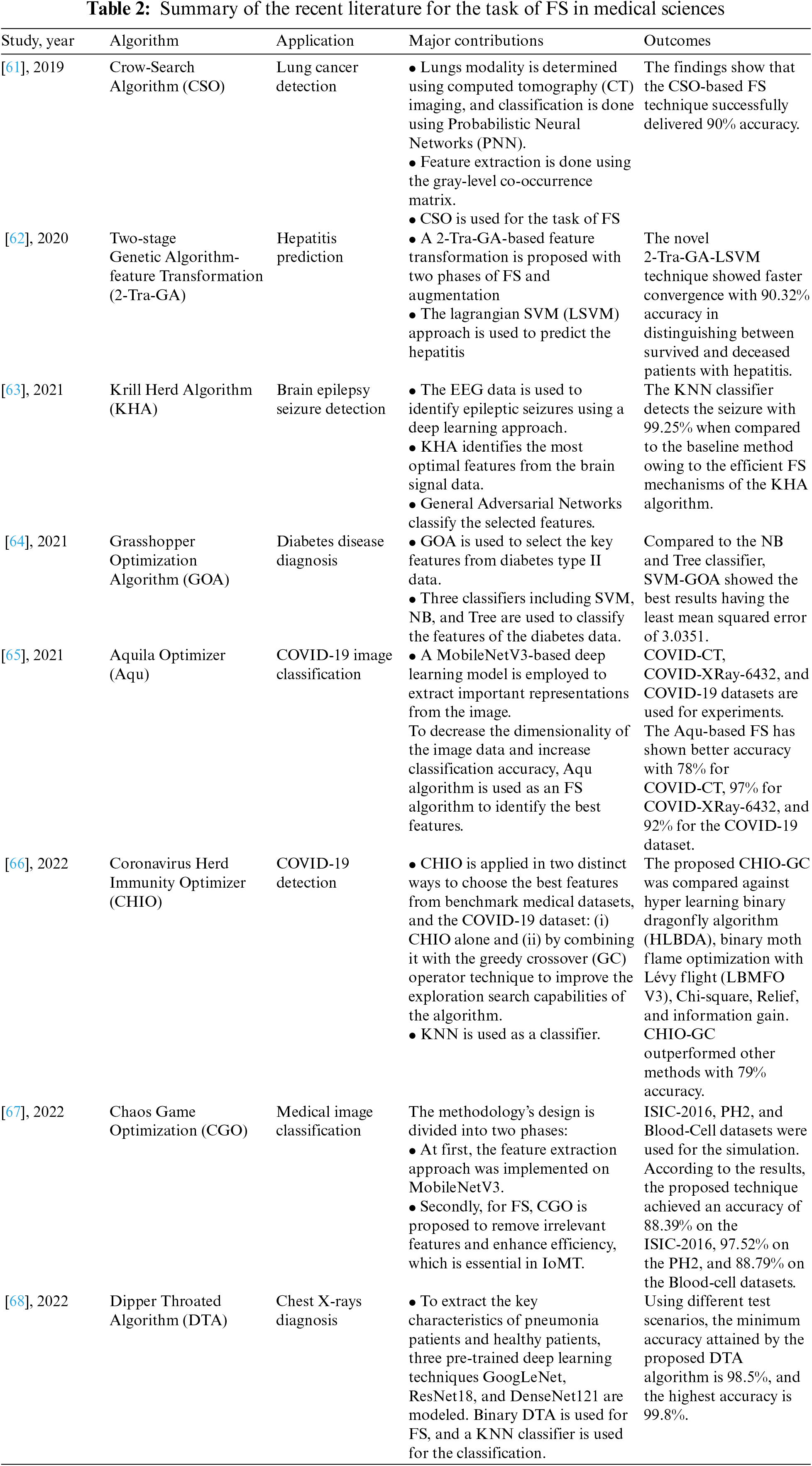
On the one hand, the algorithm mentioned in Table 2 has demonstrated satisfactory performance. On the other hand, most of the algorithms possess serious drawbacks. For example, CSO, GOA, and DTA suffer from slow convergence with being stuck in the local optimum [69,70]. The performance of KHA, CHIO, and Aqu gets disturbed by their poor exploitation search mechanism which prevents the algorithm from reaching the global optimum solution [71,72]. Whereas, GAs are viewed as extremely slow, expensive to implement, and time-consuming [73].

Therefore, this study has proposed a novel SCSO metaheuristic algorithm due to its excellent tradeoff between exploration and exploitation search strategies. The SCSO method aids in finding the direction to the best solution with a faster convergence speed. The next section (Section 3) explains the working mechanism of the proposed SCSO algorithm along with its mathematical modeling.

3  Sand Cat Swarm Optimization Algorithm (SCSO)

Sand Cat Swarm Optimization is a novel nature-inspired algorithm recently introduced by Seyyedabbasi et al. [15]. Sand cats are members of the Felis family of mammals that live in deserts such as Central Asia, Africa, and the Arabian Peninsula Sahara. The sand cat has a hard time finding food in the desert because of the harsh weather. As a result, they prefer to hunt at night with their remarkable ability to sense food using their hearing and detecting low-frequency noises to locate prey moving underground. These distinct qualities assist the sand cat in sensing movement and successfully following and attacking prey. According to the sand cat’s behavior, there are two main steps to hunting: seeking prey and attacking it. Therefore, the original study of the SCSO algorithm has highlighted these steps for solving optimization problems. Furthermore, the SCSO algorithm possesses an excellent explorative and exploitative search mechanism.

Since the SCSO is a population-based technique, the first step is to identify the problem by generating an initial population with the number of sand cats. A sand cat is a 1× d array that represents the answer to a d dimensional optimization problem where x1,x2,…xd are the variables with floating-point numbers and the values for every x need to be assigned among lower bound (LB) and upper bound (UB) such as (∀xi∈[LB,UB]). A candidate matrix containing the sand cat population (s) based on the problem size Ms×Md with s=1,…n is established initially to begin the SCSO process. Furthermore, each sand cat’s fitness cost is determined by calculating a specific objective function to get optimal values of the SCSO algorithm that helps in defining the problem’s most important parameters. To find the optimum solution, the sand cat with the lowest cost is picked as the best solution when the iteration is completed. Following that, in the next iteration, other cats strive to approach the best solution/chosen cat. However, if a fine solution is not discovered in the subsequent iterations, the algorithm ensures memory efficiency by not storing it in the memory unnecessarily.

Exploration strategy in SCSO algorithm: The solutions for every single cat in SCSO are denoted as Xi=(x1i,x2i,x3i,….xdi). Surprisingly, the sand cat can detect frequencies below 2 kHz. As the iterations proceed, the 2 kHz value (kG⟶) will decline linearly from two to zero. To locate prey, it is believed that the sensitivity range of sand cats begins at 2 kHz and ends at 0 kHz, where the algorithm utilizes the value of SCh = 2 (sand cat hearing) to search for prey as shown in the following Eq. (1):

kG⟶=SCh−(2×SCh×CiMi+Mi)(1)

where Ci and Mi defines the current and maximum iterations.

The value of SCh which is set at two, however, can be adjusted to determine the speed of actions in search agents when dealing with different problems. Apart from that, the T vector shown in Eq. (2) is the most important parameter that helps in determining the shift from exploration to exploitation.

T⟶=2×kG⟶×rnd(0,1)−kG⟶,K⟶=kG⟶×rand(0,1)(2)

According to Eq. (2), to avoid the local optimum, each sand cat’s sensitivity range is defined with different values. Therefore, the overall sensitivity range kG⟶ is reduced from two to zero. The range of sensitivity in cats is depicted as K⟶ which is used in global and local search stages and kG⟶ is used to guide the parameter T for transition control during these two phases.

In SCSO, each sand cat’s position is adjusted depending on the three parameters such as the position of the best candidate (Pbest_c⟶), the current position of the candidate (Pcurrent⟶), and the range of sensitivity (K⟶). As a result, the sand cats are able to locate another location of the potential optimal prey as in Eq. (3):

P⟶(i+1)=K⟶.(Pbest_c⟶(i)−rnd(0,1).i))(3)

Exploitation strategy in SCSO algorithm: During the phase of exploitation in SCSO, the distance between the sand cat’s best position Pbest⟶ and current position Cbest⟶ is determined using Eq. (4):

Prnd⟶=|rnd(0,1).Pbest⟶(i)−Cbest⟶(i)|

P⟶(i+1)=Pbest⟶(i)−Prnd⟶.cos⁡(θ)(4)

Besides that, because the sensitivity range of a sand cat is assumed to be a circle, the movement direction is decided by the θ (arbitrary angle) on the circle with its values from −1 and 1. The SCSO uses the Roulette Wheel selection method to choose an arbitrary angle for every sand cat while determining the hunting position. With each iteration, the random location Prnd make certain that the cats are close by their target to help them to approaching the hunt. Moreover, Eq. (5) looks after the location update for all cats during the exploration and exploitation search phases as follows:

X⟶(t+1)={Pbest⟶(i)−Prnd⟶.cos⁡(θ).r⟶|T|≤1;exploitationK⟶.(Cbest(i)⟶)−rnd(0,1).Pcurrent⟶(i)|T|>1;exploration(5)

According to the SCSO method, when |T| is less than or equal to 1, the cats are trained to approach the target (exploitation). But when |T| is greater than 1 they will search for a new viable solution in the broad region (exploration). The proposed SCSO algorithm is beneficial for tackling high-dimensional problems due to its efficiency in finding promising regions in the global search area with a fast rate of convergence. Following Algorithm 1 shows the pseudo-code of the proposed SCSO algorithm [15].

4  Research Methodology

This study has proposed a novel FS technique based on the recently introduced SCSO and KNN classifier for the classification of medical data. Since the algorithm is relatively new, to the best of the authors’ knowledge, this study is the first effort to implement the SCSO algorithm as an FS approach for dimensionality reduction and classification of medical data, specifically. Generally, the FS process involves finding the optimum feature subset from the overall features in the dataset. Fig. 1 illustrates the flow of the complete FS and classification process.

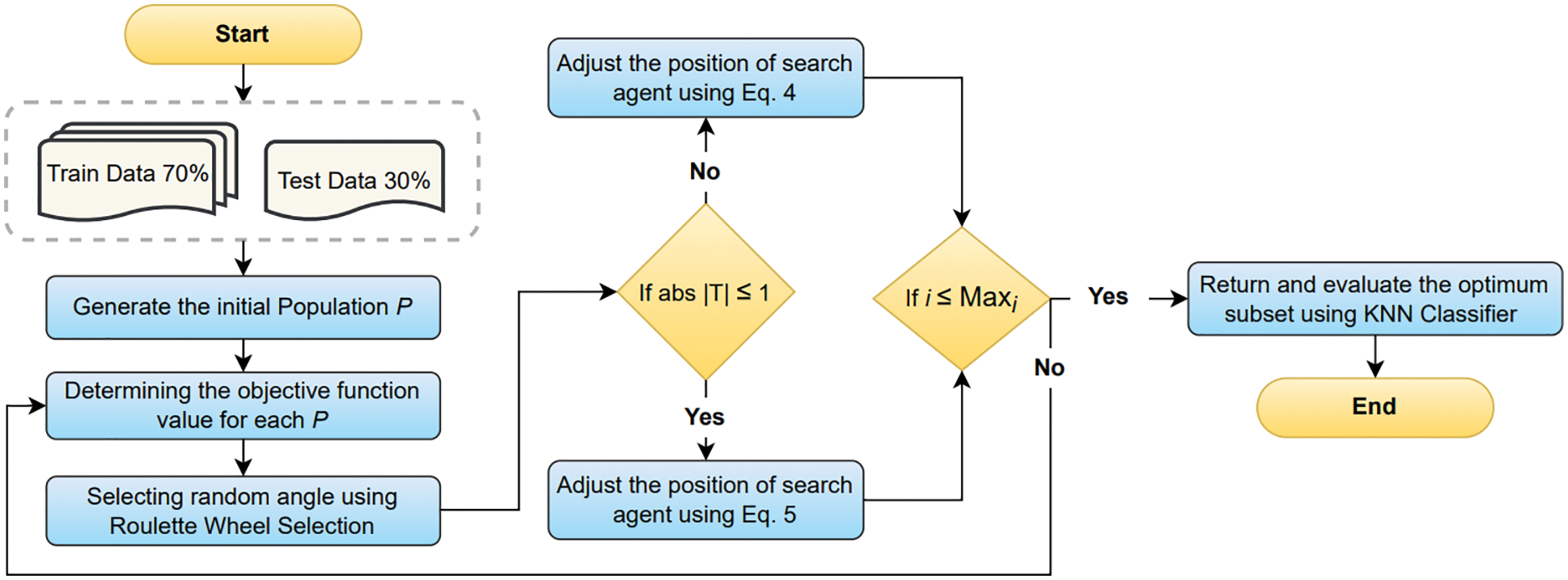
Figure 1: Proposed FS approach based on SCSO and KNN

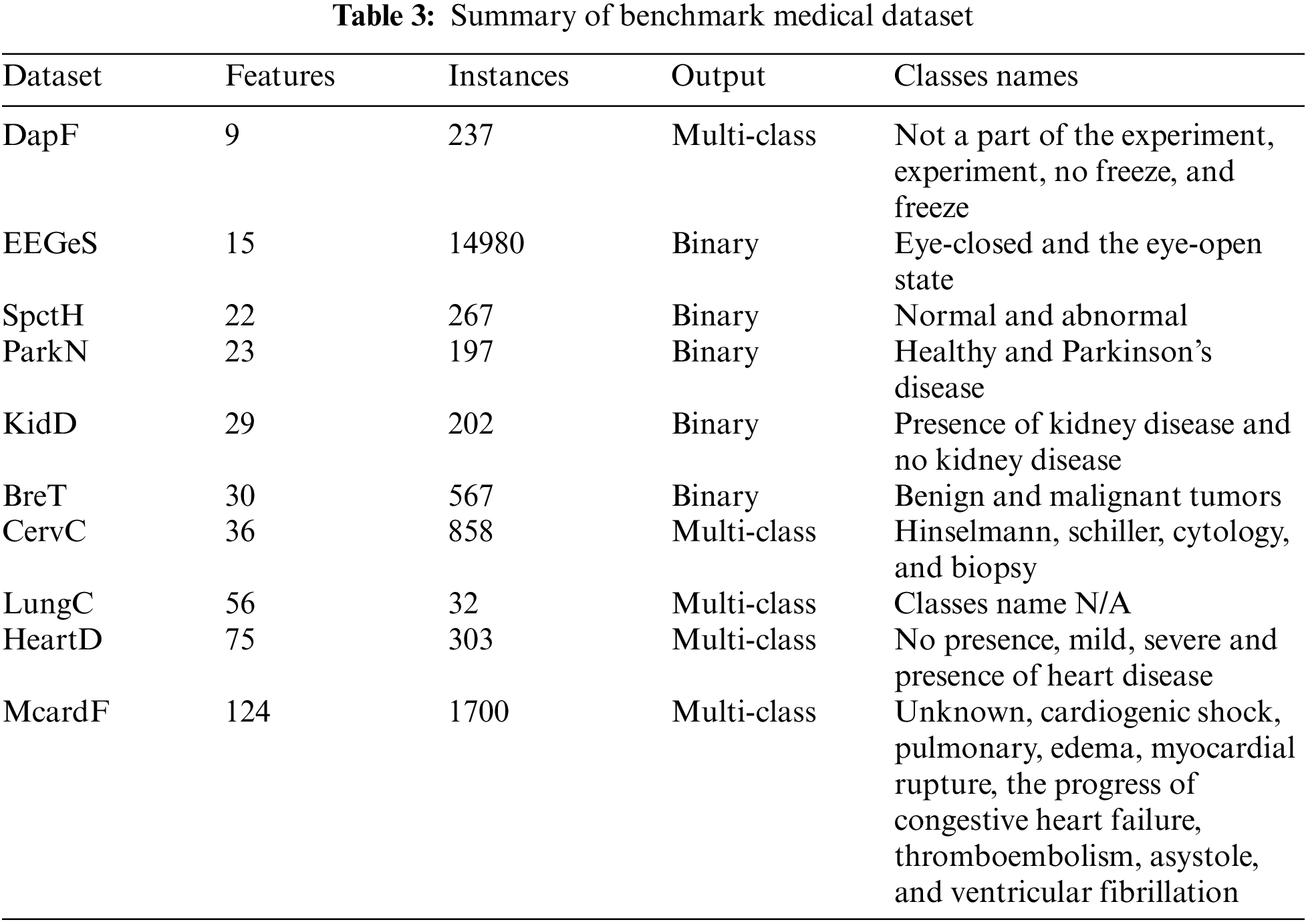
The proposed approach presented in Fig. 1 of FS using SCSO and KNN classifier starts by collecting the ten benchmark medical dataset from the well-known UCI repository of machine learning [74]. The details regarding ten datasets are as; (i) DapF: This dataset was recorded in a laboratory with an emphasis on inducing freeze events by observing daily activities like people fetching coffee and opening doors of different rooms. This dataset includes three acceleration sensor observations from Parkinson’s disease patients who suffer freezing gait problems while engaging in walking activities. The sensors are located at the hip and legs of the patients. (ii) EEGeS: This dataset is comprised of EEG values, each of which represents the eye state determined by a camera during the EEG test. The eye state detected by the camera is manually added to the dataset file after reviewing the 117-s video frames, where values of one and zero denote an open or closed eye, respectively. (iii) SpctH: The dataset provides the diagnosis of cardiac Single Proton Emission Computed Tomography (SPECT) pictures where the patients are divided into two groups normal and abnormal. The dataset contains 267 patient images (SPECT) records in total, and for each patient, 44 discrete feature patterns are generated. Moreover, 22 binary feature patterns were created after the pattern underwent additional processing. (iv) ParkN: This dataset includes several biological voice measures taken from 31 individuals, 23 of whom have Parkinson’s disease. The primary objective of the records is to distinguish between healthy individuals (indicated as 0) and PD patients (indicated as 1). (v) KidD: This dataset relates to a growing medical condition that impairs kidney function by reducing renal capacity production. (vi) BreT: In this dataset, a breast mass digital image of a fine needle aspirate (FNA) is used to compute features that define the properties of the cell nuclei present in the image and classifies between benign or malignant tumors. (vii) CervC: This dataset focuses on predicting cervical cancer using characteristics from past medical records, behaviors, and demographic data. (viii) LungC: No description is available. (ix) HeartD: This dataset reveals whether a patient has cardiac disease using four classes of no presence, mild, severe, or presence of cardiac disease. The names and identification numbers of the patients have been substituted with dummy values to standardize the data. (x) McardF: This dataset solves the important problems of predicting complications of myocardial infarction, phenotyping of disease, dynamic phenotyping, and visualization. There are two types of myocardial infarction: those with or without consequences that do not impact the long-term diagnosis. In addition, 50% of patients in the acute and sub-acute phases experience complications that can exacerbate the condition or possibly result in death. Table 3 summarizes the information regarding features and instances of each dataset.

Before implementing the collected data into the proposed approach, the study has gone through a data preparation stage where the missing values are replaced with mode values. Afterward, 70% of data is used in the training process while the reaming 30% is used to test the performance of the classifier. Next, the data is loaded into the SCSO algorithm to choose the best possible solution/feature from the large collection of features in the medical dataset. Initially, the SCSO algorithm generates a number of random populations as p. The fitness function is used to determine the fitness value of each population. Moreover, the Roulette wheel approach is applied to find the random angle to evaluate the |R|≤1. In the SCSO algorithm, the value of R is used to decide whether the algorithm needs to perform an explorative search or an exploitative search. Once the algorithm meets maximum iteration, the KNN classifier with k = 5 and Euclidean distance is used to determine the effectiveness of the selected feature subset using the following metrics:

The average features size: The proportion of the average size of the features extracted to the entire amount of features is computed after the algorithm runs R times using Eq. (6):

AFS=1R∑r=1RASFAF(6)

In above Eq. (4), AF represents the all features in a medical dataset. The average size of picked features obtained at the r-th run out of a total R runs is presented as ASF.

Average classification accuracy: This score measures how well the classifier selects the most significant features using the following Eq. (7), where BSr refers to the best solution found at the r-th run among the R runs.

ACA=1R∑r=1RBSr(7)

Average computation cost (seconds): Here, when the algorithm runs R times, its computational cost in average is calculated using Eq. (8) where CTr represents the average computational cost spent at r-th run.

ACT=∑r=1RCTr(8)

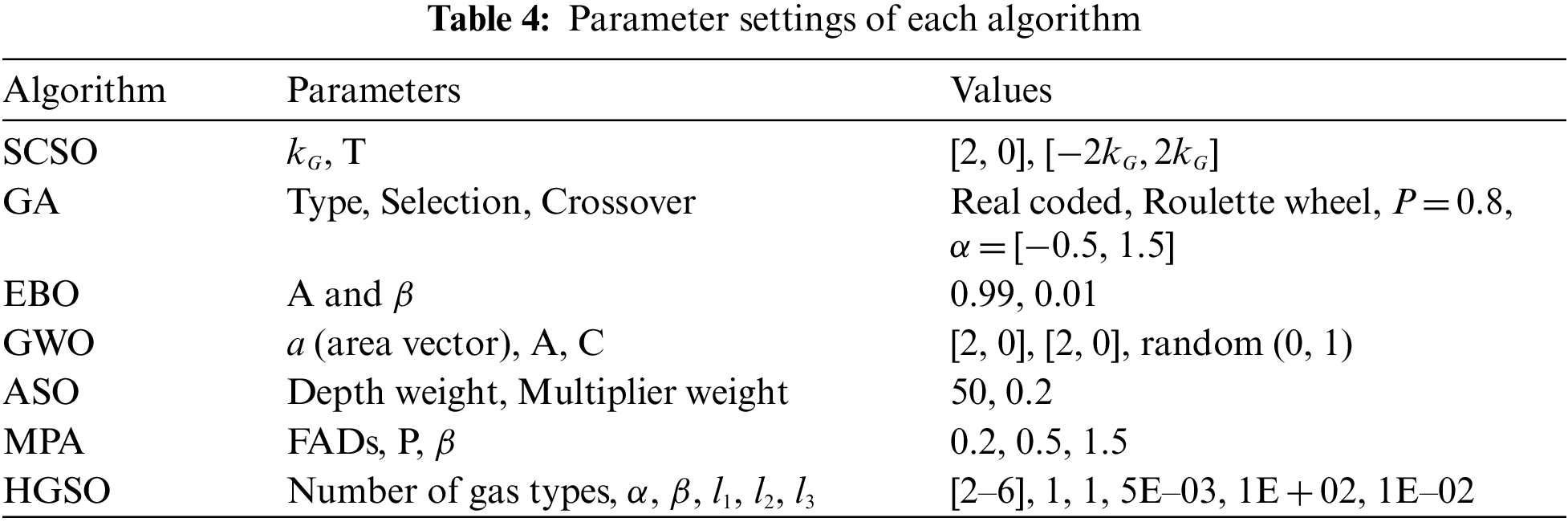
The effectiveness of the SCSO method is compared with GA [75], Equilibrium Optimization (EBO) [76], Grey Wolf Optimization (GWO) [77], Atom Search Optimization (ASO) [43], Marine Predators Algorithm (MPA) [28], and Henry Gas Solubility Optimization (HGSO) [78]. Every algorithm is run 30 times with a total of 200 iterations to calculate the average performance metrics presented in Eqs. (6)–(8). The parameters of each algorithm are summarized in the following Table 4.

Furthermore, the results of statistical analysis have been performed using a Wilcoxon signed-rank test between the proposed SCSO algorithm and comparative algorithms. When the p-value of the test is less than 5.00E-02, it is considered that the results between the proposed and compared algorithms are statistically significant. Otherwise, the results are deliberated insignificant.

5  Results and Discussion

This section has carefully analyzed and discussed the simulation results of the proposed SCSO algorithm and six comparative algorithms of GA, EBO, GWO, ASO, MPA, and HGSO algorithms. From the results presented in Table 5, it is evident that the proposed novel SCSO has successfully selected an overall 14.22 average features on 30 runs for ten medical datasets which are less than all six comparative algorithms. This is due to the SCSO’s effective and balanced explorative and exploitative search mechanism. After SCSO, MPA demonstrated the second-best outcome by selecting the smallest size of features with 18.81 average features on ten medical datasets. The ASO and EBO have selected almost the same size of features as 19.16 and 19.24, hence, becoming the third and fourth best algorithms in this study for selecting less number of features. Whereas, unlike SCSO, ASO, and EBO, HGSO, GA, and GWO have selected more than twenty features with an average feature size of 20.03, 21.17, and 21.83, respectively.

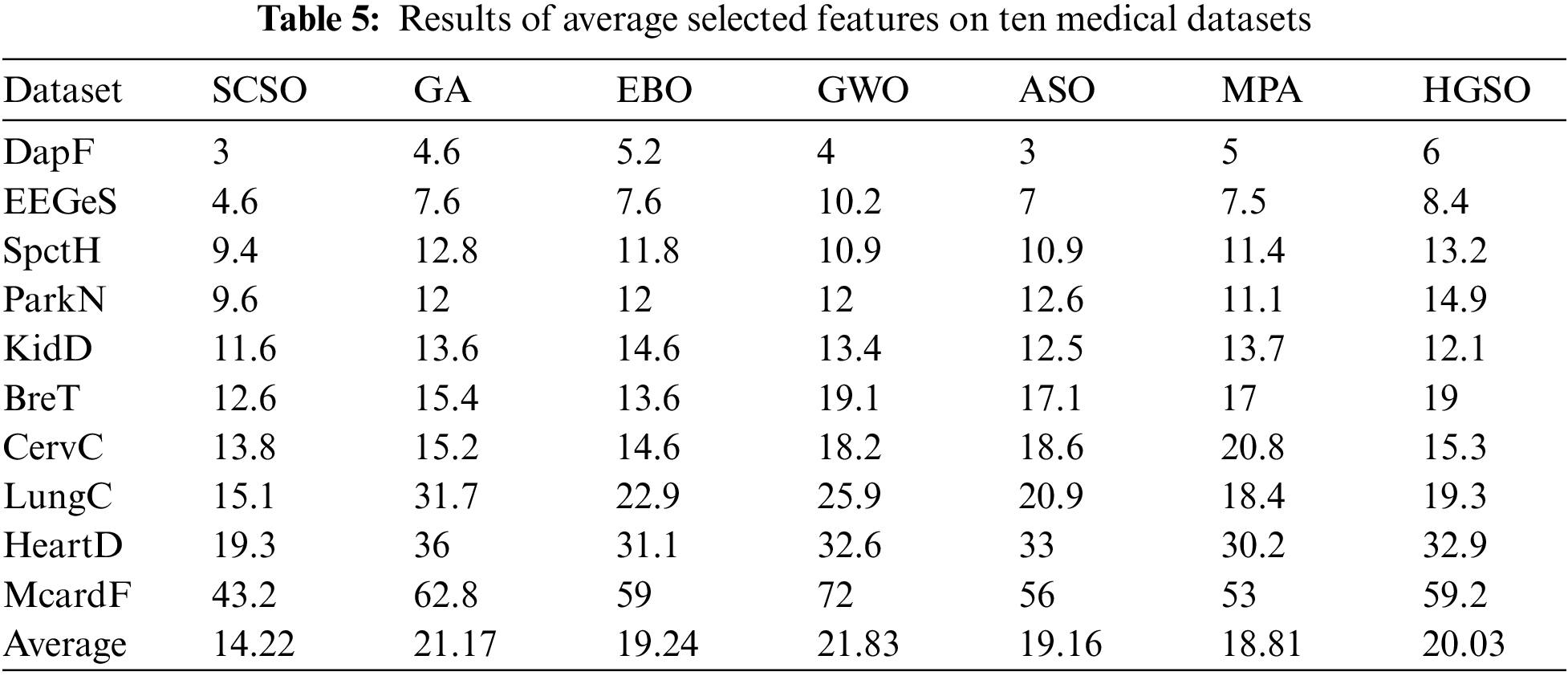
Other than the average selected features, this study has performed a comparative analysis of the proposed SCSO algorithm with GA, EBO, GWO, ASO, MPA, and HGSO algorithms for observing the average classification accuracy obtained by all algorithms. According to the results exhibited in Table 6, we can see that the average classification accuracy produced by the SCSO algorithm outperforms the other methods by securing the first position with the highest classification accuracy of 93.96%. Next, EBO has shown better results following SCSO with 91.79% of classification accuracy. Therefore, EBO appeared to be the second-best algorithm in our study by selecting the least features with best the accuracy. Whereas, GA, GWO, and HGSO have achieved the accuracy of 91.38%, 90.43%, and 89.65%, respectively. Moreover, the MPA and ASO algorithms were successful in getting the least optimum features but the classification accuracy observed by the two algorithms was 89.02% and 88.47% which is very less compared to other algorithms. This finding concludes that the algorithm selecting the least amount of features on the given dataset is not necessarily the best; rather, the potential of an algorithm is defined by the most important factor of classification accuracy on generated feature subset.

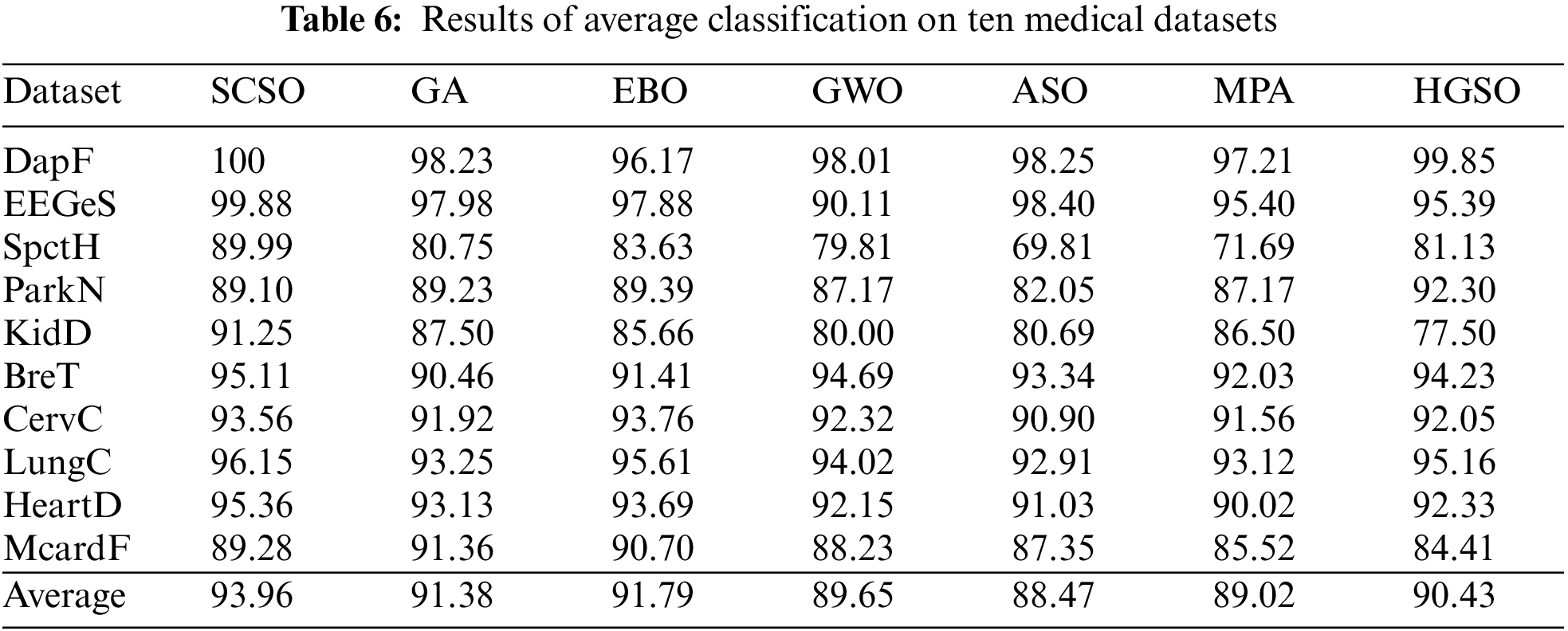
The average computational cost in seconds is the third evaluation metric used in this study to perform the analysis of outcomes generated by each algorithm on ten medical datasets. The following Table 7 provides the obtained results, where surprisingly GWO has outperformed the SCSO algorithm with the least computation cost of 1.15 s on average for all medical datasets. Nevertheless, the proposed SCSO algorithm has shown the highest accuracy with less number of features and the second-best average computational cost of 1.91 s. Just like classification accuracy and selected features, the EBO algorithm remains in the top three algorithms by showing satisfactory accuracy and fewer feature size with a computational cost of 2.24 s. This proves the consistency of the EBO algorithm’s performance on ten medical datasets. Besides, MPA and ASO algorithms showed an average computation cost of 3.56 and 4.02 s. Whereas, HGSO showed satisfactory results in terms of accuracy and selected feature but with the highest computation cost of 12.06 s compared to other algorithms.

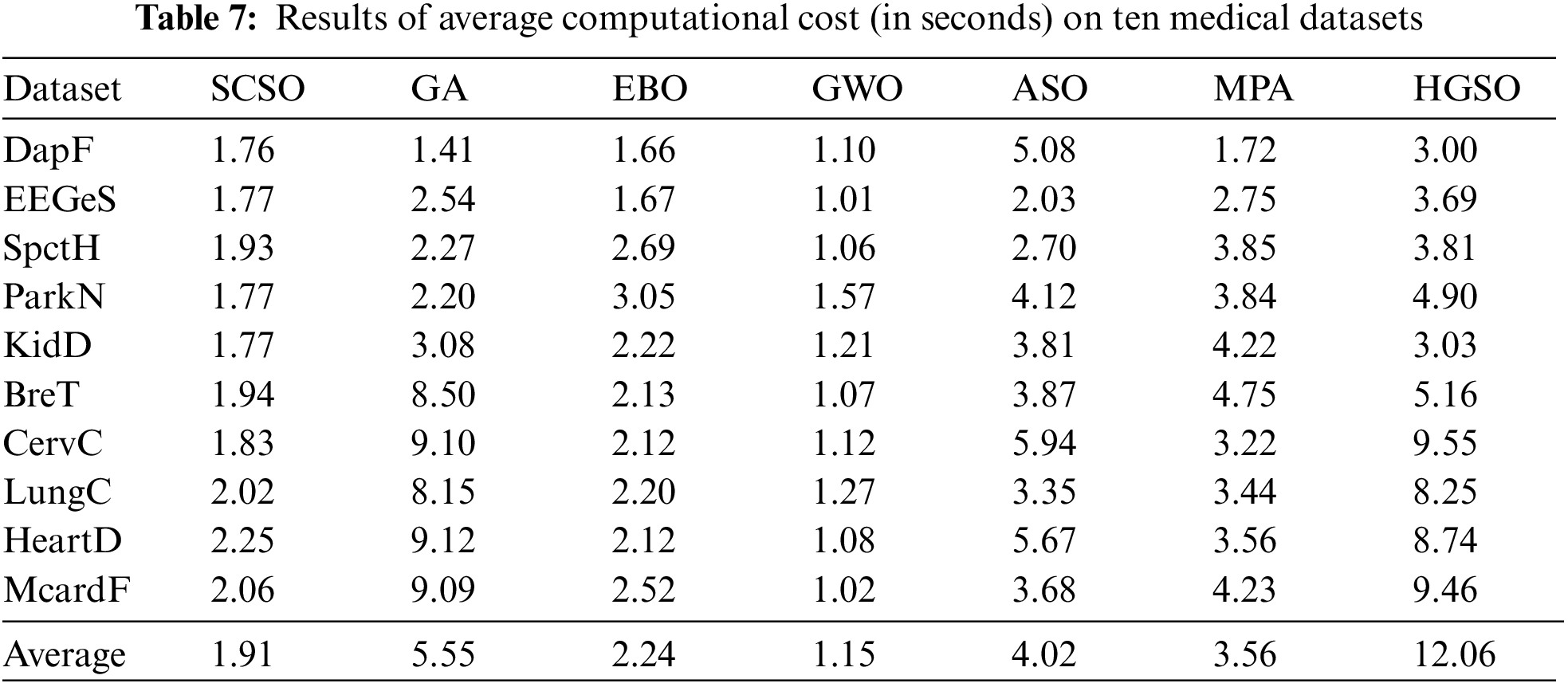
The classification accuracy determines the better performance of the algorithm, however, its effectiveness is highly dependent on convergence. Therefore, in addition to the results in Tables. 5–7, the convergence behavior of the proposed technique and six comparative metaheuristic algorithms for all datasets are presented in Fig. 2. Observing the convergence curves in Fig. 2, it can be seen that the proposed SCSO algorithm provides a fast convergence compared to GA, EBO, GWO, ASO, MPA, and HGSO algorithms for the seven datasets except ParkN, CervC, McardF. This convergence pattern shows that the algorithm’s performance precisely aligns with the optimal accuracy. Thus, it is demonstrated that the SCSO achieves a successful balance between exploration and exploitation search. Moreover, the EBO algorithm has shown better convergence behavior after the SCSO algorithm compared to GA, GWO, ASO, MPA, and HGSO. Besides, Table 8 presents the significance analysis using the Wilcoxon signed-rank test between the proposed approach of SCSO and comparative algorithms using important metrics of classification accuracy.

Figure 2: Convergence curve of the proposed SCSO and comparative algorithms on ten dataset

According to the results in terms of the p-value presented in Table 8, the proposed SCSO algorithm has achieved significant improvement over the GWO, ASO, and MPA algorithms with a p-value of 5.12E-03. Whereas the SCSO algorithm compared to GA and HGSO archived the p-values are 2.85E-02. The comparison between SCSO and EBO showed a p-value of 3.66E-02. All of these values are less than our threshold p-value which is set as 5.00E-02. This highlights the significance of the distinctions between the proposed new SCSO algorithm and comparative algorithms in terms of classification accuracy.

6  Conclusion and Future Works

In this study, a novel metaheuristics method called the Sand Cat Swarm Optimization algorithm was proposed as an FS technique to obtain the best optimum features from ten benchmark medical datasets. Later, the KNN classifier have been used to confirm the efficacy of the selected feature subset. A comparison of results was conducted between the proposed SCSO algorithm and six well-known algorithms of GA, EBO, GWO, ASO, MPA, and HGSO using the evaluation metrics of selected features, classification accuracy, and computational cost on average. The findings indicated that, compared to other algorithms, the novel SCSO has achieved a higher classification accuracy of 93.96% by selecting the fewest features of 14.2 in the least computational time of 14.2 s, respectively. Moreover, the statistical analysis using Wilcoxon signed-rank test for obtained p-value (5.00E-02) using classification accuracy proved that the results achieved by SCSO and comparative algorithms are significantly different.

In the future, the SCSO algorithm can be hybridized with other metaheuristic algorithms to enhance their performance while solving optimization problems. The SCSO algorithm also can be used for effective training and parameter tuning of various machine learning such as neural networks, convolutional neural networks, and hybrid techniques of neuro-fuzzy systems.

Funding Statement: This research was supported by a Researchers Supporting Project Number (RSP2021/309), King Saud University, Riyadh, Saudi Arabia. The authors wish to acknowledge Yayasan Universiti Teknologi Petronas for supporting this work through the research grant (015LC0- 308).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study

References

 1.  A. I. Kadhim, “Survey on supervised machine learning techniques for automatic text classification,” Artificial Intelligence Review, vol. 52, no. 1, pp. 273–292, 2019. [Google Scholar]

 2.  N. Talpur, S. J. Abdulkadir and M. H. Hasan, “A deep learning based neuro-fuzzy approach for solving classification problems,” in 2020 Int. Conf. on Computational Intelligence (ICCI), Bandar Seri Iskandar, Malaysia, pp. 167–172, 2020. [Google Scholar]

 3.  N. Talpur, S. J. Abdulkadir, H. Alhussian, M. H. Hasan, N. Aziz et al., “Deep neuro-fuzzy system application trends, challenges, and future perspectives: A systematic survey,” Artificial Intelligence Review, vol. 55, no. 8, pp. 1–44, 2022. [Google Scholar]

 4.  V. Singh, R. C. Poonia, S. Kumar, P. Dass, P. Agarwal et al., “Prediction of COVID-19 corona virus pandemic based on time series data using support vector machine,” Journal of Discrete Mathematical Sciences and Cryptography, vol. 23, no. 8, pp. 1583–1597, 2020. [Google Scholar]

 5.  H. I. Dino and M. B. Abdulrazzaq, “Facial expression classification based on SVM, KNN and MLP classifiers,” in 2019 Int. Conf. on Advanced Science and Engineering (ICOASE), Zakho-Duhok, Iraq, pp. 70–75, 2019. [Google Scholar]

 6.  Y. Dang, N. Jiang, H. Hu, Z. Ji and W. Zhang, “Image classification based on quantum k-nearest-neighbor algorithm,” Quantum Information Processing, vol. 17, no. 9, pp. 1–18, 2018. [Google Scholar]

 7.  A. P. Gopi, R. N. S. Jyothi, V. L. Narayana and K. S. Sandeep, “Classification of tweets data based on polarity using improved RBF kernel of SVM,” International Journal of Information Technology, vol. 14, no. 6, pp. 1–16, 2020. [Google Scholar]

 8.  P. Agrawal, T. Ganesh, D. Oliva and A. W. Mohamed, “S-shaped and V-shaped gaining-sharing knowledge-based algorithm for feature selection,” Applied Intelligence, vol. 52, no. 1, pp. 81–112, 2022. [Google Scholar]

 9.  F. Saeed, M. Al-Sarem, M. Al-Mohaimeed, A. Emara, W. Boulila et al., “Enhancing Parkinson’s disease prediction using machine learning and feature selection methods,” Computers, Materials & Continua, vol. 71, no. 3, pp. 5639–5658, 2022. [Google Scholar]

10. K. H. Sheikh, S. Ahmed, K. Mukhopadhyay, P. K. Singh, J. H. Yoon et al., “EHHM: Electrical harmony based hybrid meta-heuristic for feature selection,” IEEE Access, vol. 8, pp. 158125–158141, 2020. [Google Scholar]

11. P. Agrawal, T. Ganesh and A. W. Mohamed, “Chaotic gaining sharing knowledge-based optimization algorithm: An improved metaheuristic algorithm for feature selection,” Soft Computing, vol. 25, no. 14, pp. 9505–9528, 2021. [Google Scholar]

12. P. Agrawal, T. Ganesh and A. W. Mohamed, “A novel binary gaining–sharing knowledge-based optimization algorithm for feature selection,” Neural Computing and Applications, vol. 33, no. 11, pp. 5989–6008, 2021. [Google Scholar]

13. R. Al-Wajih, S. J. Abdulkadir, N. Aziz, Q. Al-Tashi and N. Talpur, “Hybrid binary grey wolf with harris hawks optimizer for feature selection,” IEEE Access, vol. 9, pp. 31662–31677, 2021. [Google Scholar]

14. A. W. Mohamed, A. A. Hadi and A. K. Mohamed, “Gaining-sharing knowledge based algorithm for solving optimization problems: A novel nature-inspired algorithm,” International Journal of Machine Learning and Cybernetics, vol. 11, no. 7, pp. 1501–1529, 2020. [Google Scholar]

15. A. Seyyedabbasi and F. Kiani, “Sand cat swarm optimization: A nature-inspired algorithm to solve global optimization problems,” Engineering with Computers, vol. 38, no. 5, pp. 1–25, 2022. [Google Scholar]

16. A. Iraji, J. Karimi, S. Keawsawasvong and M. L. Nehdi, “Minimum safety factor evaluation of slopes using hybrid chaotic sand cat and pattern search approach,” Sustainability, vol. 14, no. 13, pp. 8097, 2022. [Google Scholar]

17. P. Agrawal, H. F. Abutarboush, T. Ganesh and A. W. Mohamed, “Metaheuristic algorithms on feature selection: A survey of one decade of research (2009–2019),” IEEE Access, vol. 9, pp. 26766–26791, 2021. [Google Scholar]

18. K. Hussain, M. N. M. Salleh, S. Cheng and Y. Shi, “Metaheuristic research: A comprehensive survey,” Artificial Intelligence Review, vol. 52, no. 4, pp. 2191–2233, 2019. [Google Scholar]

19. V. K. Prajapati, M. Jain and L. Chouhan, “Tabu search algorithm (TSAA comprehensive survey,” in 2020 3rd Int. Conf. on Emerging Technologies in Computer Engineering: Machine Learning and Internet of Things (ICETCE), Jaipur, India, pp. 1–8, 2020. [Google Scholar]

20. D. Delahaye, S. Chaimatanan and M. Mongeau, “Simulated annealing: From basics to applications,” In: M. Gendreau and J.-Y. Potvin, (Eds.Handbook of Metaheuristics, 3rd ed., vol. 272, pp. 1–35, 2019, Montreal, Canada, Cham: Springer International Publishing. [Google Scholar]

21. A. Rohan, M. Rabah, M. Talha and S. -H. Kim, “Development of intelligent drone battery charging system based on wireless power transmission using hill climbing algorithm,” Applied System Innovation, vol. 1, no. 4, pp. 2–19, 2018. [Google Scholar]

22. S. Hu, Z. Zhang, S. Wang, Y. Kao and T. Ito, “A project scheduling problem with spatial resource constraints and a corresponding guided local search algorithm,” Journal of the Operational Research Society, vol. 70, no. 8, pp. 1349–1361, 2019. [Google Scholar]

23. A. A. Heidari, S. Mirjalili, H. Faris, I. Aljarah, M. Mafarja et al., “Harris hawks optimization: Algorithm and applications,” Future Generation Computer Systems, vol. 97, pp. 849–872, 2019. [Google Scholar]

24. J. M. Abdullah and T. Ahmed, “Fitness dependent optimizer: Inspired by the bee swarming reproductive process,” IEEE Access, vol. 7, pp. 43473–43486, 2019. [Google Scholar]

25. Z. Cui, J. Zhang, Y. Wang, Y. Cao, X. Cai et al., “A pigeon-inspired optimization algorithm for many-objective optimization problems,” Science China Information Sciences, vol. 62, no. 7, pp. 70212, 2019. [Google Scholar]

26. H. Yapici and N. Cetinkaya, “A new meta-heuristic optimizer: Pathfinder algorithm,” Applied Soft Computing, vol. 78, pp. 545–568, 2019. [Google Scholar]

27. J. Xue and B. Shen, “A novel swarm intelligence optimization approach: Sparrow search algorithm,” Systems Science & Control Engineering, vol. 8, no. 1, pp. 22–34, 2020. [Google Scholar]

28. A. Faramarzi, M. Heidarinejad, S. Mirjalili and A. H. Gandomi, “Marine predators algorithm: A nature-inspired metaheuristic,” Expert Systems with Applications, vol. 152, pp. 113377, 2020. [Google Scholar]

29. H. A. Alsattar, A. A. Zaidan and B. B. Zaidan, “Novel meta-heuristic bald eagle search optimisation algorithm,” Artificial Intelligence Review, vol. 53, no. 3, pp. 2237–2264, 2020. [Google Scholar]

30. L. Xie, T. Han, H. Zhou, Z. R. Zhang, B. Han et al., “Tuna swarm optimization: A novel swarm-based metaheuristic algorithm for global optimization,” Computational Intelligence and Neuroscience, vol. 2021, pp. 9210050, 2021. [Google Scholar]

31. L. Abualigah, D. Yousri, M. A. Elaziz, A. A. Ewees, M. A. A. Al-qaness et al., “Aquila optimizer: A novel meta-heuristic optimization algorithm,” Computers & Industrial Engineering, vol. 157, pp. 107250, 2021. [Google Scholar]

32. M. S. Braik, “Chameleon swarm algorithm: A bio-inspired optimizer for solving engineering design problems,” Expert Systems with Applications, vol. 174, pp. 114685, 2021. [Google Scholar]

33. J. S. Chou and D. N. Truong, “A novel metaheuristic optimizer inspired by behavior of jellyfish in ocean,” Applied Mathematics and Computation, vol. 389, pp. 125535, 2021. [Google Scholar]

34. M. Azizi, S. Talatahari and A. H. Gandomi, “Fire hawk optimizer: A novel metaheuristic algorithm,” Artificial Intelligence Review, vol. 55, no. 8, pp. 1–77, 2022. [Google Scholar]

35. P. Trojovský and M. Dehghani, “Pelican optimization algorithm: A novel nature-inspired algorithm for engineering applications,” Sensors, vol. 22, no. 3, pp. 855, 2022. [Google Scholar]

36. A. H. Kashan, R. Tavakkoli-Moghaddam and M. Gen, “Find-fix-finish-exploit-analyze (F3EA) meta-heuristic algorithm: An effective algorithm with new evolutionary operators for global optimization,” Computers & Industrial Engineering, vol. 128, pp. 192–218, 2019. [Google Scholar]

37. M. M. Motevali, A. M. Shanghooshabad, R. Z. Aram and H. Keshavarz, “WHO: A new evolutionary algorithm bio-inspired by wildebeests with a case study on bank customer segmentation,” International Journal of Pattern Recognition and Artificial Intelligence, vol. 33, no. 5, pp. 1959017, 2019. [Google Scholar]

38. M. S. Azqandi, M. Delavar and M. Arjmand, “An enhanced time evolutionary optimization for solving engineering design problems,” Engineering with Computers, vol. 36, no. 2, pp. 763–781, 2020. [Google Scholar]

39. X. Li, Z. Cai, Y. Wang, Y. Todo, J. Cheng et al., “TDSD: A new evolutionary algorithm based on triple distinct search dynamics,” IEEE Access, vol. 8, pp. 76752–76764, 2020. [Google Scholar]

40. X. Xu, Z. Hu, Q. Su, Y. Li and J. Dai, “Multivariable grey prediction evolution algorithm: A new metaheuristic,” Applied Soft Computing, vol. 89, pp. 106086, 2020. [Google Scholar]

41. Z. K. Feng, W. J. Niu and S. Liu, “Cooperation search algorithm: A novel metaheuristic evolutionary intelligence algorithm for numerical optimization and engineering optimization problems,” Applied Soft Computing, vol. 98, pp. 106734, 2021. [Google Scholar]

42. C. M. Rahman and T. A. Rashid, “A new evolutionary algorithm: Learner performance based behavior algorithm,” Egyptian Informatics Journal, vol. 22, no. 2, pp. 213–223, 2021. [Google Scholar]

43. W. Zhao, L. Wang and Z. Zhang, “Atom search optimization and its application to solve a hydrogeologic parameter estimation problem,” Knowledge-Based Systems, vol. 163, pp. 283–304, 2019. [Google Scholar]

44. F. A. Hashim, E. H. Houssein, M. S. Mabrouk, W. Al-Atabany and S. Mirjalili, “Henry gas solubility optimization: A novel physics-based algorithm,” Future Generation Computer Systems, vol. 101, pp. 646–667, 2019. [Google Scholar]

45. A. Kaveh, M. R. Seddighian and E. Ghanadpour, “Black hole mechanics optimization: A novel meta-heuristic algorithm,” Asian Journal of Civil Engineering, vol. 21, no. 7, pp. 1129–1149, 2020. [Google Scholar]

46. S. Talatahari and M. Azizi, “Chaos game optimization: A novel metaheuristic algorithm,” Artificial Intelligence Review, vol. 54, no. 2, pp. 917–1004, 2021. [Google Scholar]

47. F. A. Hashim, K. Hussain, E. H. Houssein, M. S. Mabrouk and W. Al-Atabany, “Archimedes optimization algorithm: A new metaheuristic algorithm for solving optimization problems,” Applied Intelligence, vol. 51, no. 3, pp. 1531–1551, 2021. [Google Scholar]

48. S. Talatahari, M. Azizi and A. H. Gandomi, “Material generation algorithm: A novel metaheuristic algorithm for optimization of engineering problems,” Processes, vol. 9, no. 5, pp. 859, 2021. [Google Scholar]

49. S. Talatahari, M. Azizi, M. Tolouei, B. Talatahari and P. Sareh, “Crystal structure algorithm (CryStAlA metaheuristic optimization method,” IEEE Access, vol. 9, pp. 71244–71261, 2021. [Google Scholar]

50. V. Goodarzimehr, S. Shojaee, S. Hamzehei-Javaran and S. Talatahari, “Special relativity search: A novel metaheuristic method based on special relativity physics,” Knowledge-Based Systems, vol. 254, pp. 109484, 2022. [Google Scholar]

51. S. Balochian and H. Baloochian, “Social mimic optimization algorithm and engineering applications,” Expert Systems with Applications, vol. 134, pp. 178–191, 2019. [Google Scholar]

52. I. Ahmia and M. Aider, “A novel metaheuristic optimization algorithm: The monarchy metaheuristic,” Turkish Journal of Electrical Engineering and Computer Sciences, vol. 27, no. 1, pp. 362–376, 2019. [Google Scholar]

53. H. Ghasemian, F. Ghasemian and H. Vahdat-Nejad, “Human urbanization algorithm: A novel metaheuristic approach,” Mathematics and Computers in Simulation, vol. 178, pp. 1–15, 2020. [Google Scholar]

54. M. Dehghani, M. Mardaneh, O. P. Malik and V. Chahar, “Football game based optimization: An application to solve energy commitment problem,” International Journal of Intelligent Engineering and Systems, vol. 13, no. 5, pp. 514–523, 2020. [Google Scholar]

55. M. F. F. A. Rashid, “Tiki-taka algorithm: A novel metaheuristic inspired by football playing style,” Engineering Computations, vol. 38, no. 1, pp. 313–343, 2021. [Google Scholar]

56. M. A. Al-Betar, Z. A. A. Alyasseri, M. A. Awadallah and I. A. Doush, “Coronavirus herd immunity optimizer (CHIO),” Neural Computing and Applications, vol. 33, no. 10, pp. 5011–5042, 2021. [Google Scholar]

57. T. S. L. V. Ayyarao, N. S. S. Ramakrishna, R. M. Elavarasan, N. Polumahanthi, M. Rambabu et al., “War strategy optimization algorithm: A new effective metaheuristic algorithm for global optimization,” IEEE Access, vol. 10, pp. 25073–25105, 2022. [Google Scholar]

58. M. Braik, M. H. Ryalat and H. Al-Zoubi, “A novel meta-heuristic algorithm for solving numerical optimization problems: Ali baba and the forty thieves,” Neural Computing and Applications, vol. 34, no. 1, pp. 409–455, 2022. [Google Scholar]

59. S. Bashir, I. U. Khattak, A. Khan, F. H. Khan, A. Gani et al., “A novel feature selection method for classification of medical data using filters, wrappers, and embedded approaches,” Complexity, vol. 2022, pp. 8190814, 2022. [Google Scholar]

60. B. Remeseiro and V. Bolon-Canedo, “A review of feature selection methods in medical applications,” Computers in Biology and Medicine, vol. 112, pp. 103375, 2019. [Google Scholar]

61. S. R. S. Chakravarthy and H. Rajaguru, “Lung cancer detection using probabilistic neural network with modified crow-search algorithm,” Asian Pacific Journal of Cancer Prevention, vol. 20, no. 7, pp. 2159–2166, 2019. [Google Scholar]

62. L. Parisi and N. Ravichandran, “Evolutionary feature transformation to improve prognostic prediction of hepatitis,” Knowledge-Based Systems, vol. 200, pp. 106012, 2020. [Google Scholar]

63. A. Abugabah, A. A. AlZubi, M. Al-Maitah and A. Alarifi, “Brain epilepsy seizure detection using bio-inspired krill herd and artificial alga optimized neural network approaches,” Journal of Ambient Intelligence and Humanized Computing, vol. 12, no. 3, pp. 3317–3328, 2021. [Google Scholar]

64. S. R. Kamel and R. Yaghoubzadeh, “Feature selection using grasshopper optimization algorithm in diagnosis of diabetes disease,” Informatics in Medicine Unlocked, vol. 26, pp. 100707, 2021. [Google Scholar]

65. M. A. Elaziz, A. Dahou, N. A. Alsaleh, A. H. Elsheikh, A. I. Saba et al., “Boosting COVID-19 image classification using MobileNetV3 and aquila optimizer algorithm,” Entropy, vol. 23, no. 11, pp. 1383, 2021. [Google Scholar]

66. M. Alweshah, S. Alkhalaileh, M. A. Al-Betar and A. A. Bakar, “Coronavirus herd immunity optimizer with greedy crossover for feature selection in medical diagnosis,” Knowledge-Based Systems, vol. 235, pp. 107629, 2022. [Google Scholar]

67. A. Mabrouk, A. Dahou, M. A. Elaziz, R. P. Díaz Redondo and M. Kayed, “Medical image classification using transfer learning and chaos game optimization on the internet of medical things,” Computational Intelligence and Neuroscience, vol. 2022, pp. 9112634, 2022. [Google Scholar]

68. H. N. AlEisa, E. M. El-kenawy, A. A. Alhussan, M. Saber, A. A. Abdelhamid et al., “Transfer learning for chest x-rays diagnosis using dipper throated algorithm,” Computers, Materials & Continua, vol. 73, no. 2, pp. 2371–2387, 2022. [Google Scholar]

69. X. Han, Q. Xu, L. Yue, Y. Dong, G. Xie et al., “An improved crow search algorithm based on spiral search mechanism for solving numerical and engineering optimization problems,” IEEE Access, vol. 8, pp. 92363–92382, 2020. [Google Scholar]

70. Y. Yan, M. Hongzhong and L. Zhendong, “An improved grasshopper optimization algorithm for global optimization,” Chinese Journal of Electronics, vol. 30, no. 3, pp. 451–459, 2021. [Google Scholar]

71. C. Zhao, Z. Liu, Z. Chen and Y. Ning, “A novel krill herd algorithm with orthogonality and its application to data clustering,” Intelligent Data Analysis, vol. 25, no. 3, pp. 605–626, 2021. [Google Scholar]

72. B. Gao, Y. Shi, F. Xu and X. Xu, “An improved aquila optimizer based on search control factor and mutations,” Processes, vol. 10, no. 8, pp. 1451, 2022. [Google Scholar]

73. N. Talpur, S. J. Abdulkadir, H. Alhussian, N. Aziz and A. Bamhdi, “A comprehensive review of deep neuro-fuzzy system architectures and their optimization methods,” Neural Computing and Applications, vol. 34, pp. 1837–1875, 2022. [Google Scholar]

74. D. Dua and C. Graff, UCI Machine Learning Repository. Irvine, CA, USA: University of California, School of Information and Computer Science, 2019. [Online]. Available http://archive.ics.uci.edu/ml. [Google Scholar]

75. S. Katoch, S. S. Chauhan and V. Kumar, “A review on genetic algorithm: Past, present, and future,” Multimedia Tools and Applications, vol. 80, no. 5, pp. 8091–8126, 2021. [Google Scholar]

76. A. Faramarzi, M. Heidarinejad, B. Stephens and S. Mirjalili, “Equilibrium optimizer: A novel optimization algorithm,” Knowledge-Based Systems, vol. 191, pp. 105190, 2020. [Google Scholar]

77. H. Rezaei, O. Bozorg-Haddad and X. Chu, “Grey wolf optimization (GWO) algorithm,” in Advanced Optimization by Nature-Inspired Algorithms, Singapore: Springer, pp. 81–91, 2018. [Google Scholar]

78. N. Neggaz, E. H. Houssein and K. Hussain, “An efficient henry gas solubility optimization for feature selection,” Expert Systems with Applications, vol. 152, pp. 113364, 2020. [Google Scholar]