New Trends in Fuzzy Modeling Through Numerical Techniques

1  Introduction

The protozoan Entamoeba histolytica causes amoebiasis disease, and it is the second leading cause of protozoan death in the world after malaria [1]. About 50 million people worldwide are infected with this disease, and 0.1 million die yearly [2]. It is a severe public health problem in China and some regions of Latin America, Asia, and Africa. Schaudinn introduced the name Entamoeba histolytica in 1903 for the ability of the parasite to cause tissue lysis [3]. Amoebiasis transfers directly through human-to-human contact or indirectly by eating or drinking food or water contaminated with feces. Its transmission through sexual contact, particularly among homosexual men, may also occur [4,5]. Mature cysts of the Entamoeba histolytica can survive a few weeks in soil, 12 days in a relaxed, moist environment, and 30 days in water for reinfection. They can be kept alive at temperatures below 50°C and above 400°C [6]. The cyst is the infectious, nonmotile form of the parasite that is excised as it progresses through the gastrointestinal tract. Generally, the incubation period is 2 to 4 weeks, but it can last a few months or a few years [7]. Amoebiasis remains a severe health problem in developing countries where health infrastructure and health education are inadequate. Immigration and increased international population movements have had an impact on the occurrence of the disease.

Mathematical modeling has played a vital role in better understanding the behavior of infectious diseases. Chitnis et al. proposed a mathematical model of malaria spread in human and mosquito populations [8]. Niger et al. also studied the malaria model involving three stages of immunity and a backward bifurcation [9]. Many other researchers also studied a malaria model to describe its spread [10–14]. Arif et al. studied a stochastic epidemic model [15]. A stochastic dengue model was checked by Shatanawi et al. [16]. Noor et al. developed a stochastic model to study the Covid 19 dynamics [17]. Yu et al. looked at Covid 19 with a delay factor [18]. Fahmy formulated a boundary element method (BEM) to solve a nonlinear space-time problem of dual-phase-lag fractional bioheat transfer during electromagnetic radiation [19]. Abodayeh et al. studied a vector-borne plant disease model in deterministic and stochastic senses [20].

Most existing mathematical models of disease dynamics are crisp and precise, while many real-world situations are neither crisp nor deterministic. Therefore, these models cannot accurately describe conditions. The idea of the fuzzy set was introduced by Zadeh [21], who assigns each set member a value representing its degree of membership. Considering a fuzzy set representing recovery from infection, we can assign values from 0 to 1. That statement need not be accurate or false when someone says someone is recovering from a disease. The degree to which this recovered person belongs to that population group may be valid. The membership level of 0 indicates low recovery, 0.5 medium recoveries, and one high recovery after infection.

Fuzzy sets and fuzzy logic have been widely used to solve real-world problems in engineering, medicine, economics, and many other fields where human decision-making is critical through evaluation and reasoning [22–26]. Researchers have also used the theory in epidemiology. Barros et al. presented an SI model using fuzzy theory [27]. Torres et al. proposed multiresolution and fuzzy systems to represent cases of dengue and severe dengue, respectively, in Colombia [28]. The obtained results were compared with traditional fuzzy methods. Mondal et al. proposed an SIS model with a treatment control in fuzzy transmission [29]. Li et al. proposed a fuzzy SEIR model and confidence index theory to describe the dynamics of coronavirus disease [30]. Chen et al. proposed a new approach to handle the high-dimensional uncertain SIR model [31]. Abdy et al. presented a SIR model having fuzzy parameters to describe the COVID-19 dynamics [32]. Allehiany et al. studied a fuzzy SIR model by developing Euler, RK-4, and NSFD methods, respectively [33].

Fuzzy reproduction number (FRN) was also studied. The idea of the NSFD scheme was proposed by Mickens [34]. Many researchers have used the theory to solve the system of differential equations [35–38], to mention a few. Dayan et al. constructed an NSFD scheme to solve a SEIQR model describing COVID-19 [39]. Adak et al. studied an SIS model with treatment control using fuzzy numbers [40]. For example, many other researchers also used fuzzy theory to study disease dynamics. Reliable solutions are needed when it comes to issues related to human health. Uncertainties arise due to the variable nature of the parameters used in the mathematical models, as these parameters depend on the virus load of the disease. The virus load is not the same for all individuals in the population for many reasons, such as different age groups, levels of resistance, other habits, customs, etc. Due to these differences, models capable of dealing with these problems are needed. Fuzzy theory is a valuable tool for studying issues that contain uncertainties. With this in mind, the Euler and NSFD schemes for the studied model are developed in a fuzzy way to gain a broader understanding of the disease.

The development, accomplishment, and numerical analysis of the first-order explicit numerical technique with NSFD in a fuzzy environment, especially with fuzzy parameters, is the novelty of the current work. To our knowledge, the model under study has not been analyzed before in NSFD and fuzzy senses in the literature, and this is the first study of this model in this sense.

The remaining paper is designed as we started with a fuzzy SEIR model, and mathematical analysis of the model is presented. The following section contains the formulation of the forward Euler and NSFD mathematical techniques and their simulation results. The final section of the article concludes it.

2  Fuzzy SEIR Model of Amoebiasis Disease

We considered the fuzzy SEIR model describing the dynamics of Amoebiasis disease as follows.

S′=Λ−βIS−μS,(1)

E′=βIS−εE−μE,(2)

I′=εE−(μ+d+γ)I,(3)

R′=γI−μR.(4)

The corresponding fuzzy SEIR model can be written as

S′=Λ−β(ω)IS−μS,(5)

E′=βIS−εE−μE,(6)

I′=εE−(μ+d(ω)+γ(ω))I,(7)

R′=γ(ω)I−μR.(8)

where β(ω), d(ω) and γ(ω) are fuzzy numbers. Firstly, β(ω) can be defined as [41],

β(ω)={0,ω≤ωmin,ω−ωminωM−ωmin,ωmin<ω≤ωM,1,ωM<ω.(9)

The death rate d(ω) is defined as [42],

d(ω)={(1−ξ)−ϵ0ωminω+ϵ0,0≤ω≤ωmin,1−ξ,ωmin<ω.(10)

1−ξ with ξ≥0 is the maximum death.

The recovery rate γ(ω) is given by,

γ(ω)=(γ0−1)ωωM,  0≤ω≤ωM,(11)

where γ0>0 is the lowest rate of recovery.

2.1 Equilibrium Analysis

Case 1: When ω<ωmin, then β(ω)=0, and we get the point E∗(S∗,E∗,I∗,R∗)=(Λμ,0,0,0), where the human population has no Amoebiasis disease, and this is called DFE (Disease Free Equilibrium). From a biological point of view, the Amoebiasis disease is eradicated when the amount of the cyst is lesser than the least required amount in the population for the spread of the disease.

Case 2: When ωmin<ω≤ωM, then β(ω)=ω−ωminωM−ωmin and we obtain E∗∗(S∗∗,E∗∗,I∗∗,R∗∗), where

S∗∗=(μ+ε)(μ+d+γ(ω))εβ(ω),

E∗∗=εβ(ω)Λ−μ(μ+ε)(μ+d+γ(ω))εβ(ω)(μ+ε),

I∗∗=εβ(ω)Λ−μ(μ+ε)(μ+d+γ(ω))β(ω)(μ+ε)(μ+d+γ(ω)),

R∗∗=γ(ω)μ[εβ(ω)Λ−μ(μ+ε)(μ+d+γ(ω))β(ω)(μ+ε)(μ+d+γ(ω))].

Case 3: When ωM<ω<ωmax, then β(ω)=1 and the point E∗∗∗(S∗∗∗,E∗∗∗,I∗∗∗,R∗∗∗) is obtained, where

S∗∗∗=(μ+ε)(μ+d+γ(ω))ε,

E∗∗∗=εΛ−μ(μ+ε)(μ+d+γ(ω))ε(μ+ε),

I∗∗∗=εΛ−μ(μ+ε)(μ+d+γ(ω))(μ+ε)(μ+d+γ(ω)),

R∗∗∗=γ(ω)μ[εΛ−μ(μ+ε)(μ+d+γ(ω))(μ+ε)(μ+d+γ(ω))].

The points E∗∗ and E∗∗∗ are the situations where the Amoebiasis disease virus is higher than the least required amount for Amoebiasis disease spread and the infection persists in the human population.

2.2 The Fuzzy Basic Reproductive Number Raf

The reproductive number Ra is calculated using the next-generation matrix method [41] as

Ra=εβ(ω)Λμ(μ+ε)(μ+d+γ(ω)).(12)

Ra being a function of the Amoebiasis disease can be analyzed for different amounts of the cysts as

Case 1: When ω<ωmin, then β(ω)=0, and we obtain,

Ra=0.(13)

Case 2: When ωmin<ω≤ωM, then β(ω)=ω−ωminωM−ωmin and we obtain,

Ra(ω)=εΛβ(ω)μ(μ+ε)(μ+d+γ(ω)).(14)

Case 3: When ωM<ω<ωmax, then β(ω)=1 and we obtain,

Ra(ω)=εΛμ(μ+ε)(μ+d+γ(ω)).(15)

The basic reproduction number Ra(ω) can be written as a TFN as:

Ra(ω)=(0,εΛβ(ω)μ(μ+ε)(μ+d+γ(ω)),εΛμ(μ+ε)(μ+d+γ(ω))).(16)

The expected value of a TFN A=(a1,a2,a3) is defined as [42]

E[A(ω)]=a1+2a2+a34.(17)

Raf can be estimated as

Raf=E[Ra(ω)].(18)

Now by using Eqs. (17) and (18), we find Raf as follows:

=εΛ(2β(ω)+1)4μ(μ+ε)(μ+d+γ(ω)).(19)

2.3 Sensitivity of Raf

The sensitivity of a variable is defined as [43]

φ(χ)=χRa∂Ra∂χ.

We find sensitivity of the Raf below.

φ(Λ)=ΛRa∂Ra∂Λ=Λεβ(ω)Λμ(μ+ε)(μ+d+γ(ω))∂∂Λεβ(ω)Λμ(μ+ε)(μ+d+γ(ω))=1.

φ(β(ω))=β(ω)Ra∂Ra∂β(ω)=β(ω)εβ(ω)Λμ(μ+ε)(μ+d+γ(ω))∂∂β(ω)εβ(ω)Λμ(μ+ε)(μ+d+γ(ω))=1.

φ(ε)=εRa∂Ra∂ε=εεβ(ω)Λμ(μ+ε)(μ+d+γ(ω))∂∂εεβ(ω)Λμ(μ+ε)(μ+d+γ(ω))=1.

φ(μ)=μRa∂Ra∂μ=μεβ(ω)Λμ(μ+ε)(μ+d+γ(ω))∂∂μεβ(ω)Λμ(μ+ε)(μ+d+γ(ω)),

=−(3μ2+2εμ+2dμ+2μγ(ω)+εd+εγ(ω))(μ+ε)(μ+d+γ(ω)).

φ(d)=dRa∂Ra∂d=dεβ(ω)Λμ(μ+ε)(μ+d+γ(ω))∂∂dεβ(ω)Λμ(μ+ε)(μ+d+γ(ω))=−d(μ+d+γ(ω)).

φ(γ(ω))=γ(ω)Ra∂Ra∂γ(ω)=γ(ω)εβ(ω)Λμ(μ+ε)(μ+d+γ(ω))∂∂γ(ω)εβ(ω)Λμ(μ+ε)(μ+d+γ(ω))=−γ(ω)(μ+d+γ(ω)).

These results show that Λ, β(ω) and ε are the sensitive parameters while the parameters μ, d and γ(ω) are insensitive.

3  Numerical Modeling

3.1 Forward Euler Scheme

Forward Euler scheme for the system (5)–(8) is

Sn+1=Sn+h[Λ−μSn−β(ω)InSn],(20)

En+1=En+h[β(ω)InSn−(μ+ε)En],(21)

In+1=In+h[εEn−(μ+d+γ(ω))In],(22)

Rn+1=Rn+h[γ(ω)In−μRn].(23)

Case 1: When ω<ωmin, then β(ω)=0 and the above scheme becomes

Sn+1=Sn+h(Λ−μSn),(24)

En+1=En−h(μ+ε)En,(25)

In+1=In+h[εEn−(μ+d+γ(ω))In],(26)

Rn+1=Rn+h[γ(ω)In−μRn].(27)

Case 2: When ωmin<ω≤ωM, then β(ω)=ω−ωminωM−ωmin and the above scheme becomes

Sn+1=Sn+h[Λ−μSn−β(ω)InSn],(28)

En+1=En+h[β(ω)InSn−(μ+ε)En],(29)

In+1=In+h[εEn−(μ+d+γ(ω))In],(30)

Rn+1=Rn+h[γ(ω)In−μRn].(31)

Case 3: When ωM<ω<ωmax, then β(ω)=1 and the above scheme becomes

Sn+1=Sn+h[Λ−μSn−InSn],(32)

En+1=En+h[InSn−(μ+ε)En],(33)

In+1=In+h[εEn−(μ+d+γ(ω))In],(34)

Rn+1=Rn+h[γ(ω)In−μRn].(35)

The numerical simulations for the forward Euler’s method are given below for a certain period of time.

The subpopulations for case 1 at DFE are shown in Fig. 1. The results show a convergence at h=0.1, but at the time step value h=10, the forward Euler method produces negative consequences at the start, which is meaningless as any compartment’s negative value is impossible. Fig. 2 presents the subpopulations at the EE for case 2. The method converges for a small matter of h and diverges at h=10. The results of case 3 of the EE are depicted in Fig. 3. Again, the method produces a convergent solution at the start. Still, it diverges and generates nonpositive values for an immense weight of h. From these results, we can conclude that the forward Euler method is unreliable in predicting the Amoebiasis disease dynamics in fuzzy conditions.

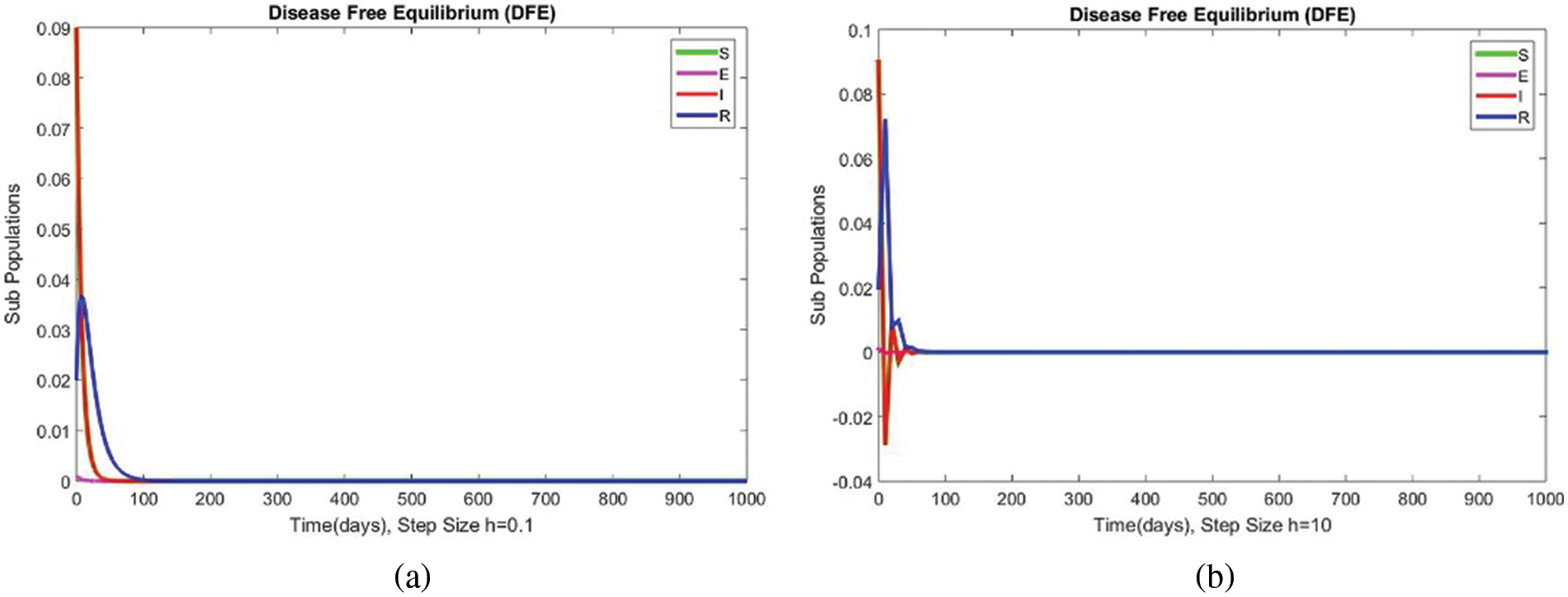
Figure 1: The portion of subpopulations for case 1 at different step sizes

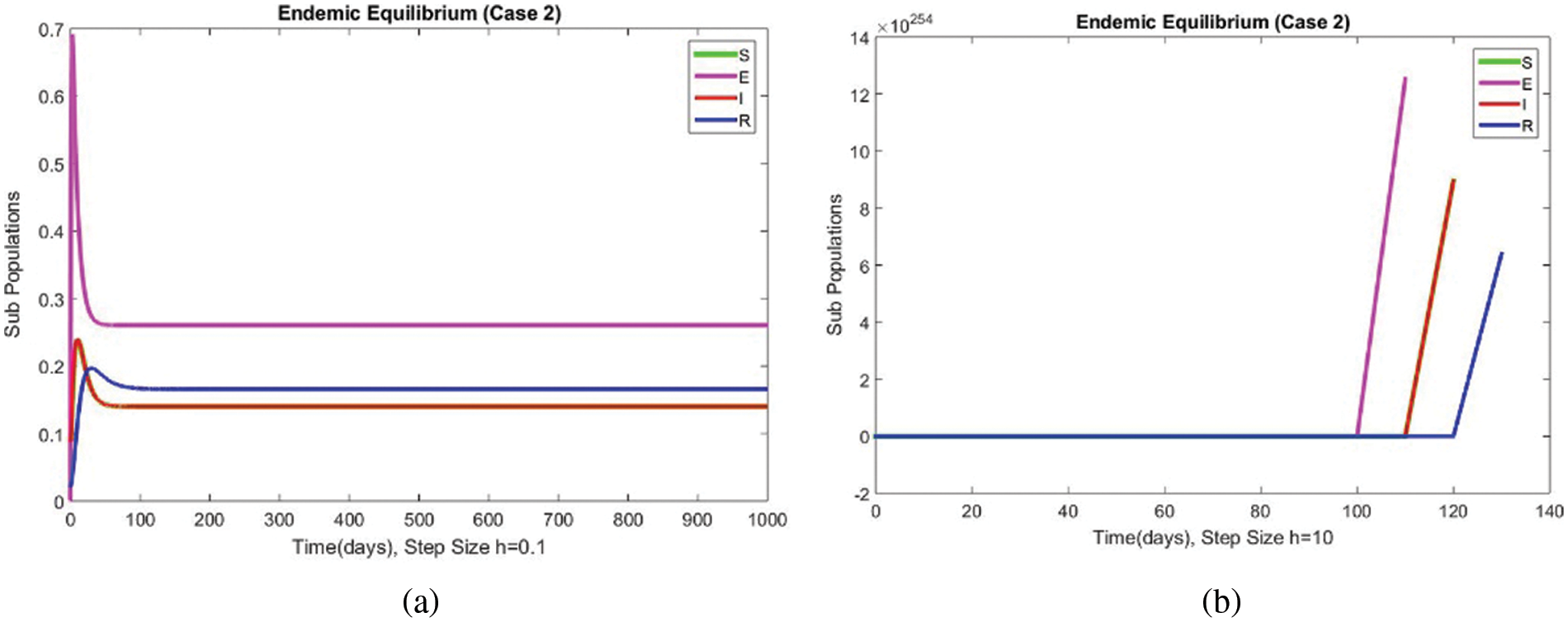
Figure 2: The portion of subpopulations for case 2 at different step sizes

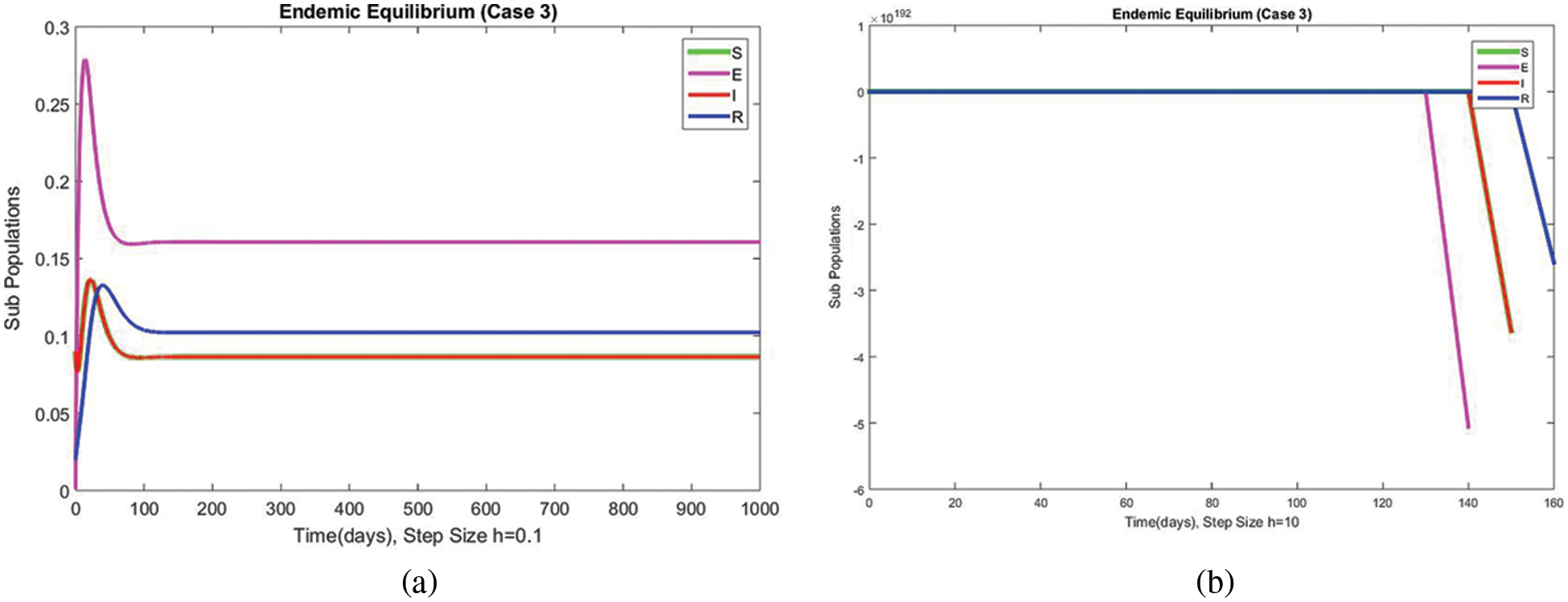
Figure 3: The portion of subpopulations for case 3 at different step sizes

In the following sub-section, we will develop another numerical scheme to overcome these issues and get stable solutions for the studied model.

3.2 Nonstandard Finite Difference (NSFD) Scheme

NSFD scheme for the system (5)–(8) is

Sn+1=Sn+hΛ1+hβ(ω)In+hμ,(36)

En+1=En+hβ(ω)Sn+1In1+h(μ+ε),(37)

In+1=In+hεEn+11+h(μ+d+γ(ω)),(38)

Rn+1=Rn+hγ(ω)In+11+hμ.(39)

Case 1: When ω<ωmin, then β(ω)=0 and the above scheme becomes

Sn+1=Sn+hΛ1+hμ,(40)

En+1=En1+h(μ+ε),(41)

In+1=In+hεEn+11+h(μ+d+γ(ω)),(42)

Rn+1=Rn+hγ(ω)In+11+hμ.(43)

In Fig. 4, the compartment S is shown at minimal and considerable time step values, respectively, at the DFE. In both cases, the results are positive and converge to the same equilibrium points. Convergence and positivity are the core features of the epidemic models, and our proposed method possesses both qualities in this case. Fig. 5 represents the second compartment of the studied model at the DFE. The results are drawn for the time step sizes h=0.1 and h=10, respectively, which converge to the same point. The results of compartments I and R at the DFE are presented in Figs. 6 and 7, respectively. A convergence behavior is reflected in both cases. Fig. 8 illustrates all subpopulations of the model at the DFE. From the above graphs, it can be concluded that the constructed method can be considered a reliable tool for studying the disease of amoebiasis in the human population at DFE.

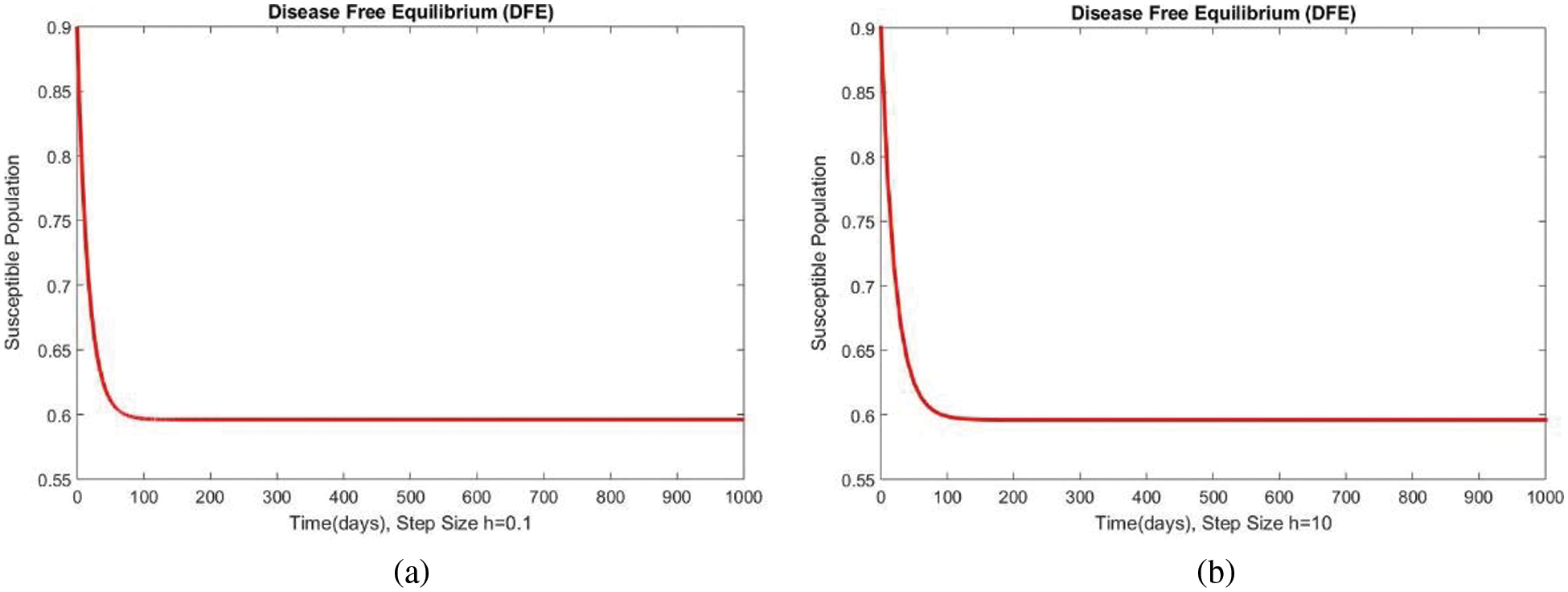
Figure 4: The portion of susceptible populations for case 1 at different step sizes

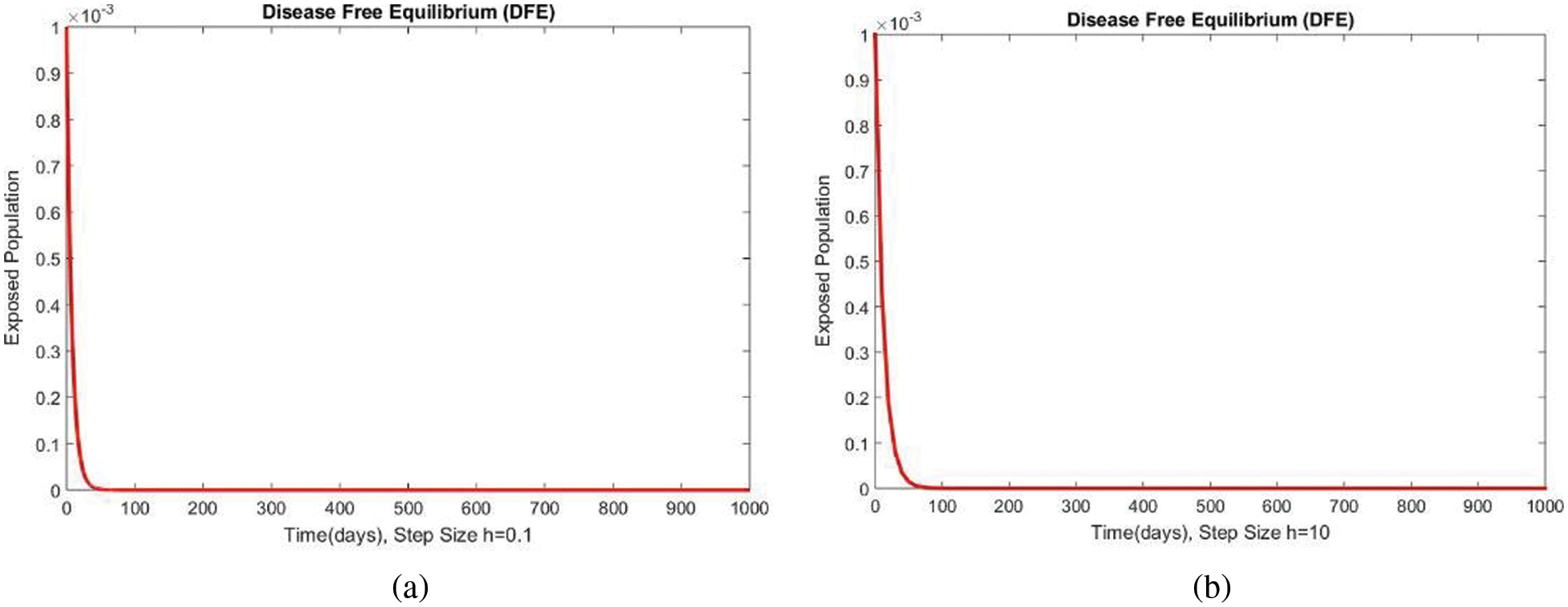
Figure 5: The portion of exposed populations for case 1 at different step sizes

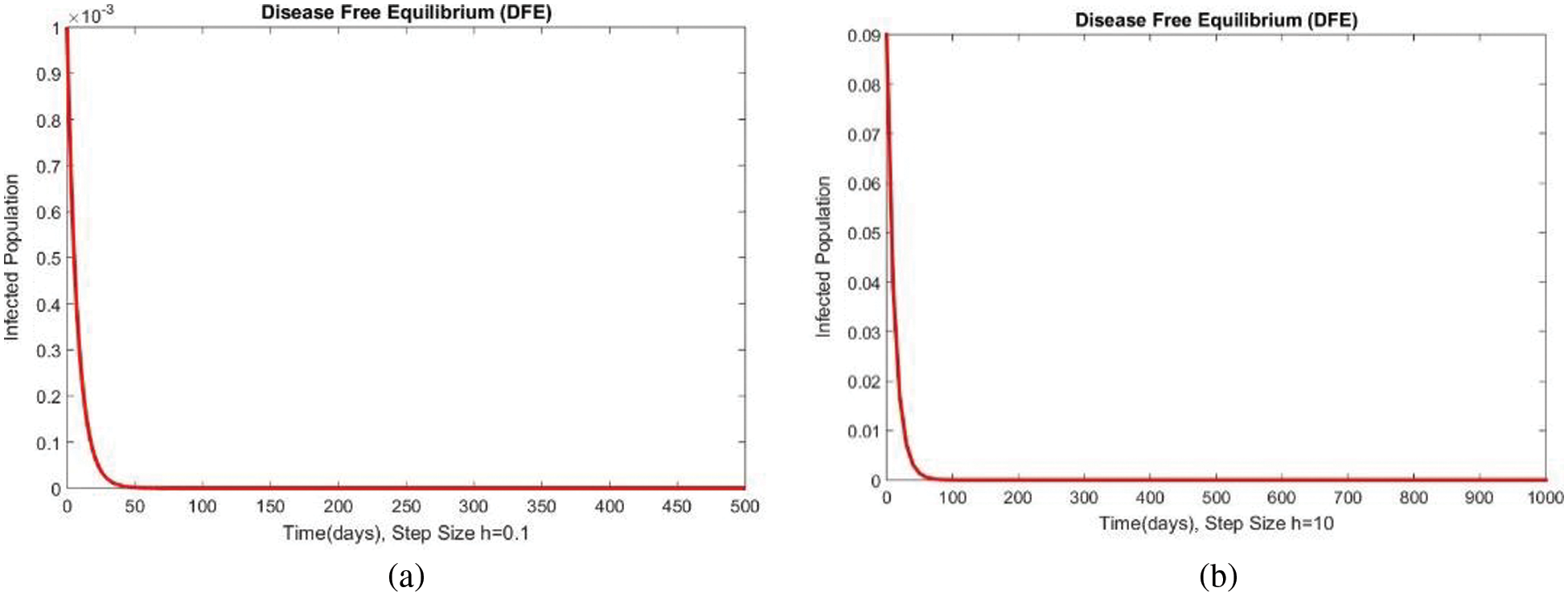
Figure 6: The portion of infected populations for case 1 at different step sizes

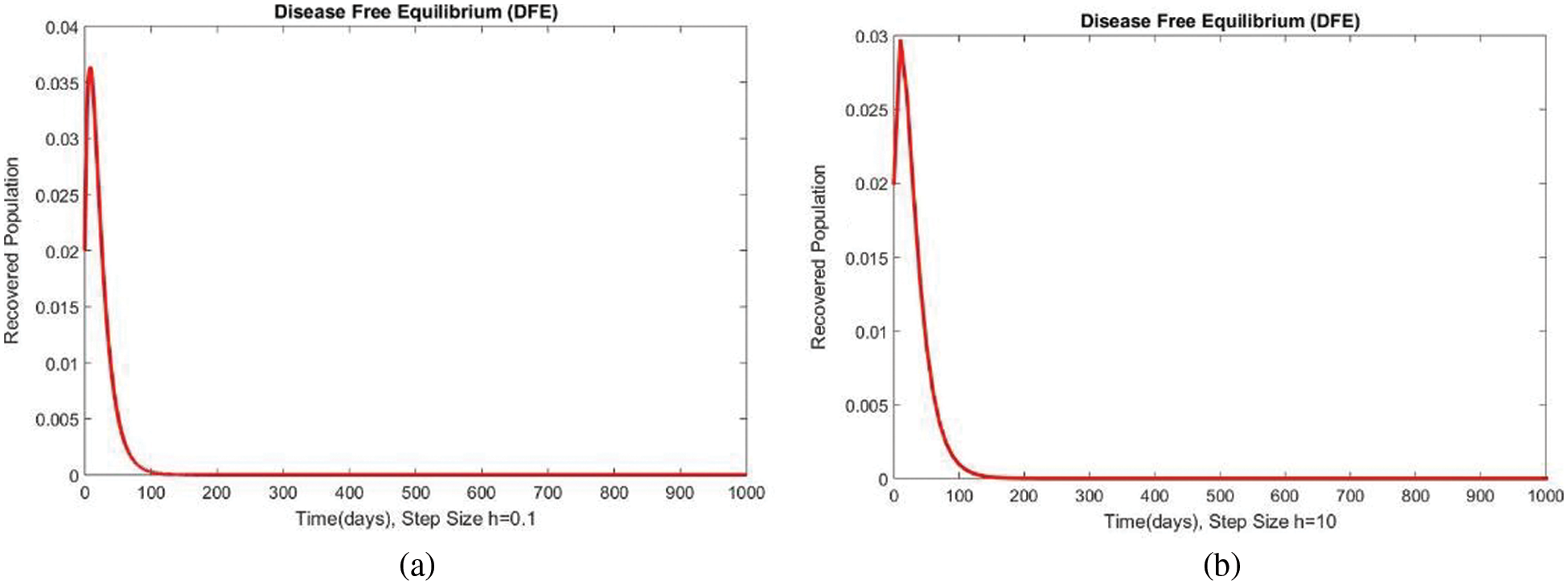
Figure 7: The portion of recovered populations for case 1 at different step sizes

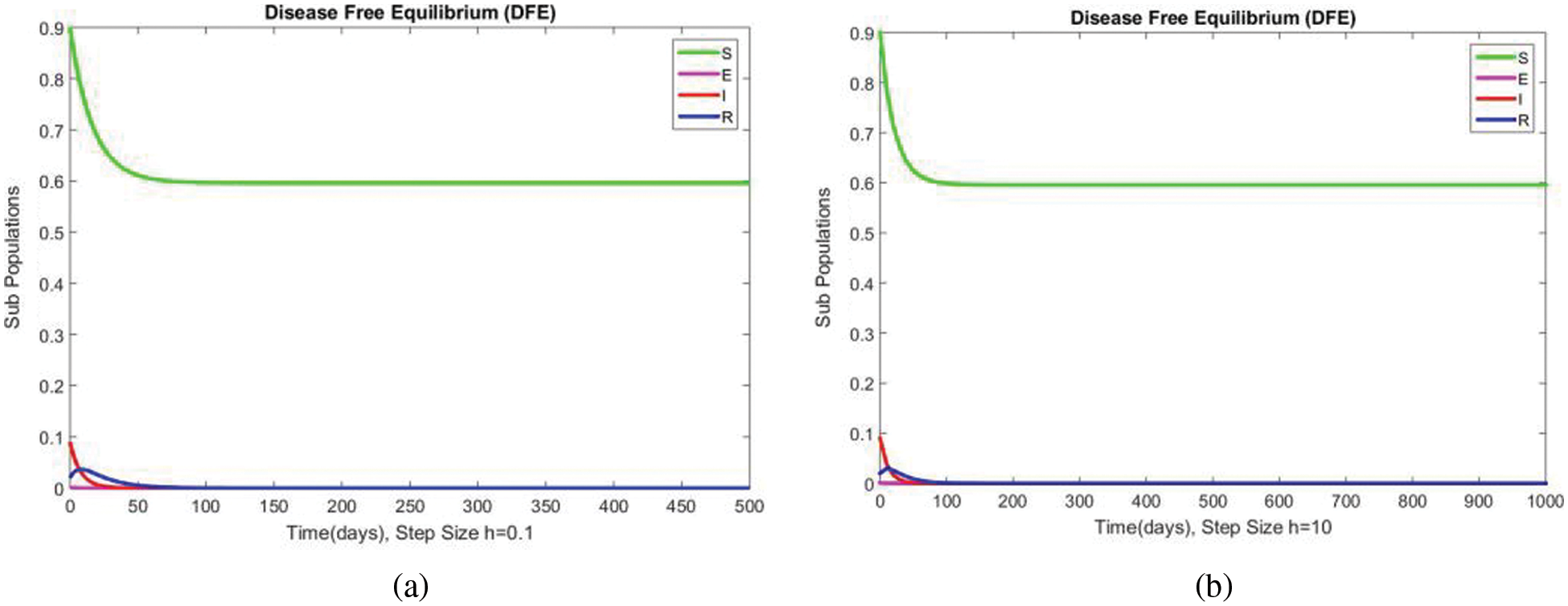
Figure 8: The portion of subpopulations for case 1 at different step sizes

Case 2: When ωmin<ω≤ωM, then β(ω)=ω−ωminωM−ωmin and the above scheme becomes

Sn+1=Sn+hΛ1+hβ(ω)In+hμ,(44)

En+1=En+hβ(ω)Sn+1In1+h(μ+ε),(45)

In+1=In+hεEn+11+h(μ+d+γ(ω)),(46)

Rn+1=Rn+hγ(ω)In+11+hμ.(47)

Figs. 9 and 10 show the results of the exposed and infected compartments, respectively, at the EE for case 2. The graphs reflect a converging behavior at a small and a significant time step size, respectively. The subpopulations at EE for case 2 are shown in Fig. 11. Convergence to the same steady state points is reflected in the above graphs. From this behavior, we conclude that the disease spread procedure at the first EE point, i.e., case 2, can be studied using our proposed method.

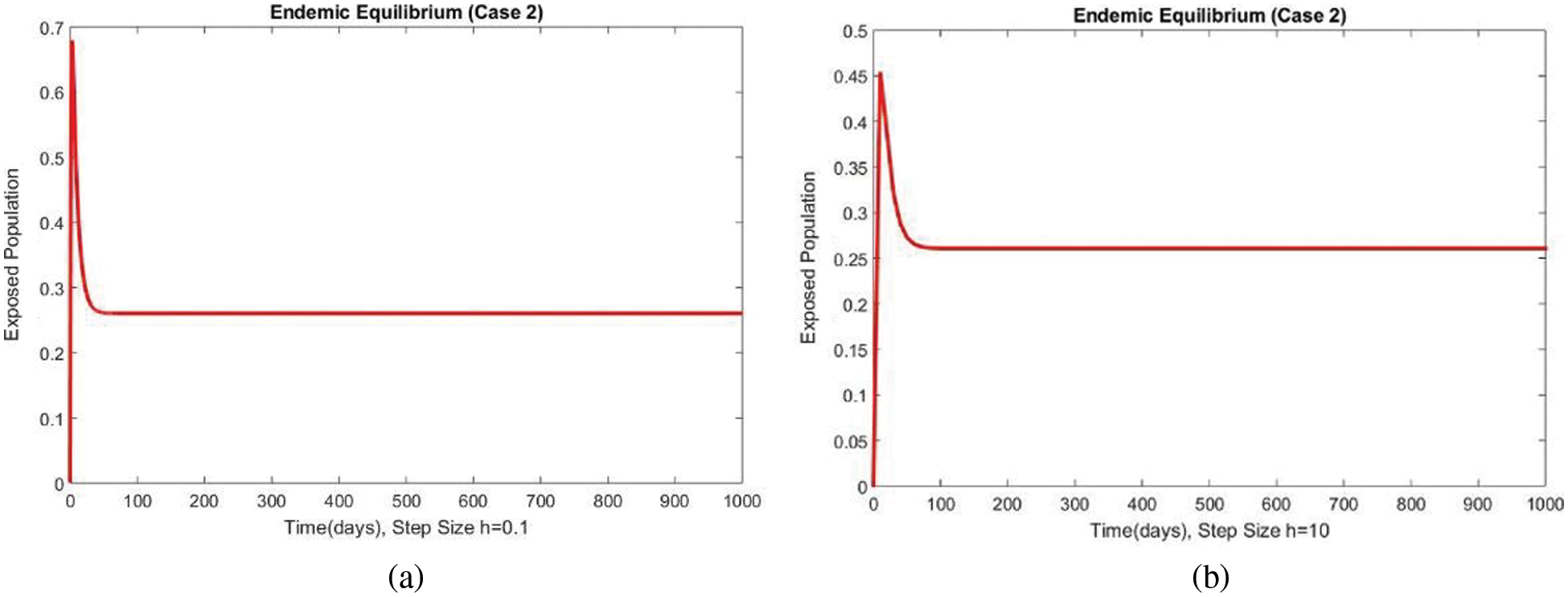
Figure 9: The portion of exposed populations for case 2 at different step sizes

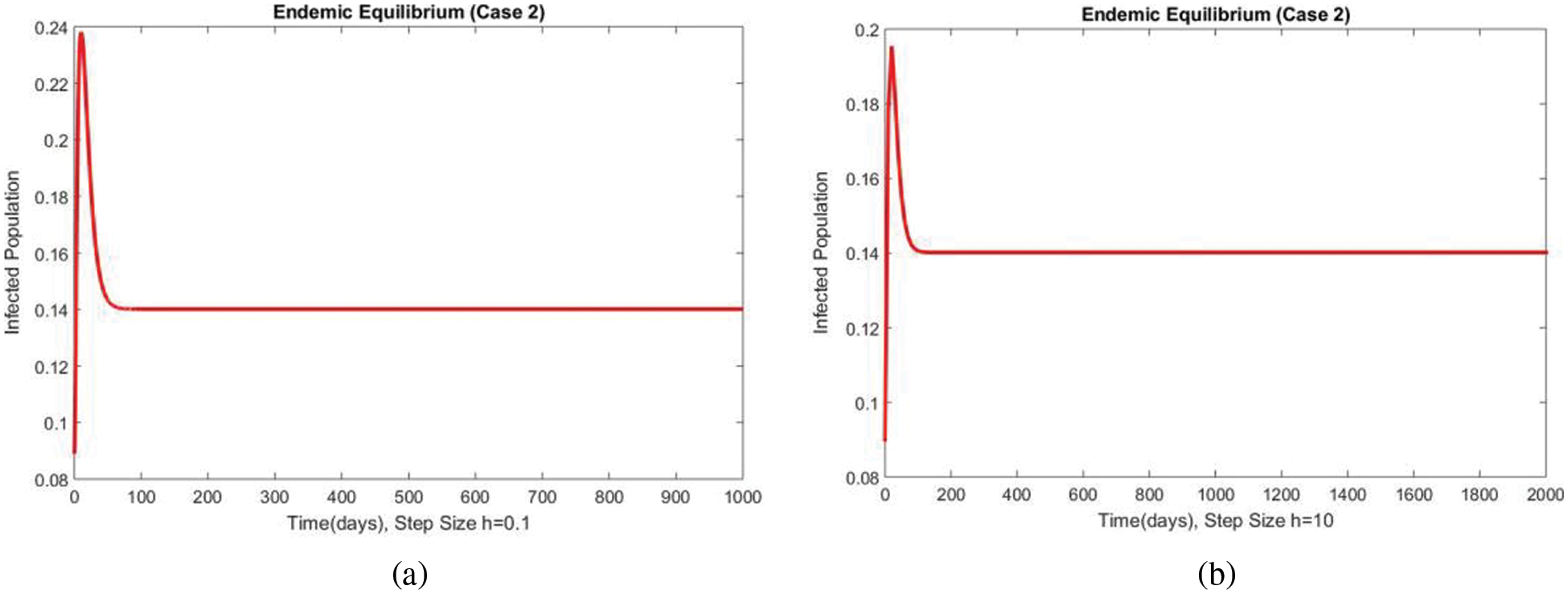
Figure 10: The portion of subpopulations for case 2 at different step sizes

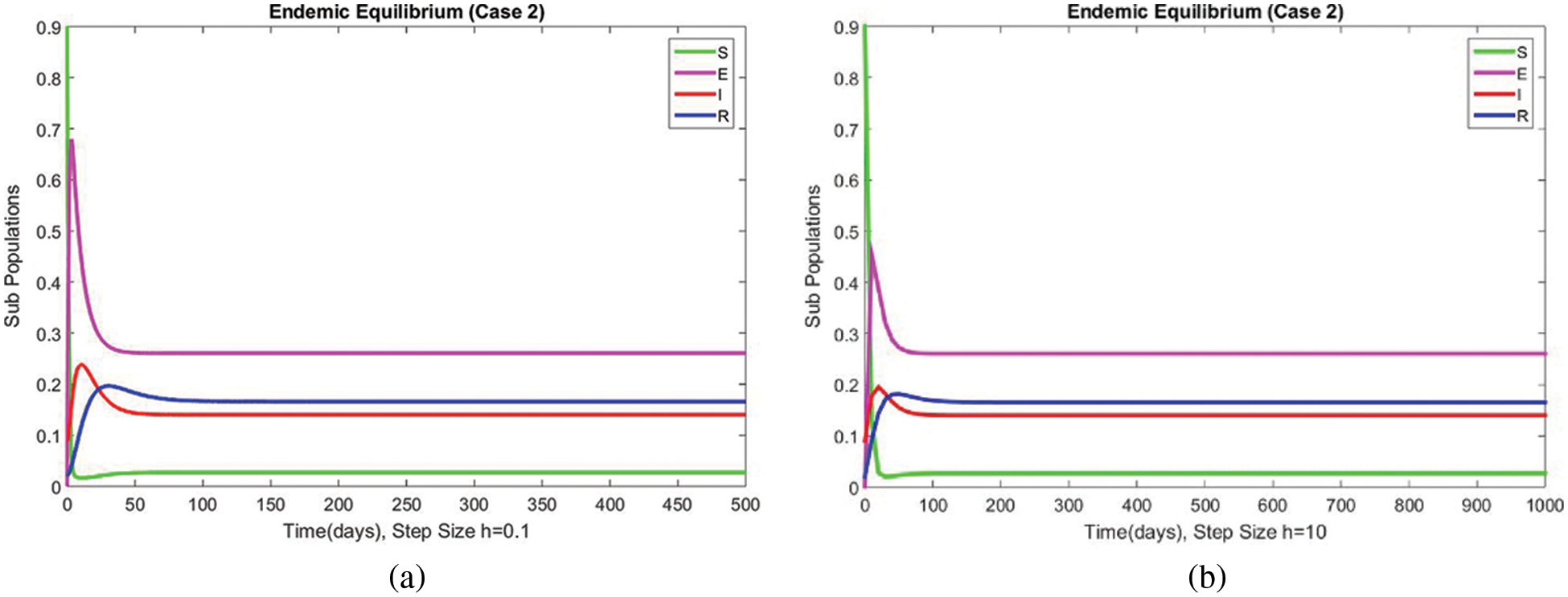
Figure 11: The portion of subpopulations for case 2 at different step sizes

Case 3: When ωM<ω<ωmax, then β(ω)=1 and the above scheme becomes

Sn+1=Sn+hΛ1+hIn+hμ,(48)

En+1=En+hSn+1In1+h(μ+ε),(49)

In+1=In+hεEn+11+h(μ+d+γ(ω)),(50)

Rn+1=Rn+hγ(ω)In+11+hμ.(51)

The graphical behaviors of the exposed and infected compartments are shown in Figs. 12 and 13, respectively, for case 3 at the EE. Convergence to the actual equilibrium points can easily be seen in these graphs. Fig. 14 shows the subpopulations at the EE for case 3. It can be seen that all compartments are converging to the same steady state. From the above numerical experiments, it is easy to conclude that the proposed numerical approach combines unconditionally even for large time step values. Further, it can be supposed that the proposed scheme can be considered a suitable tool to study the spread of amoebiasis in the human population.

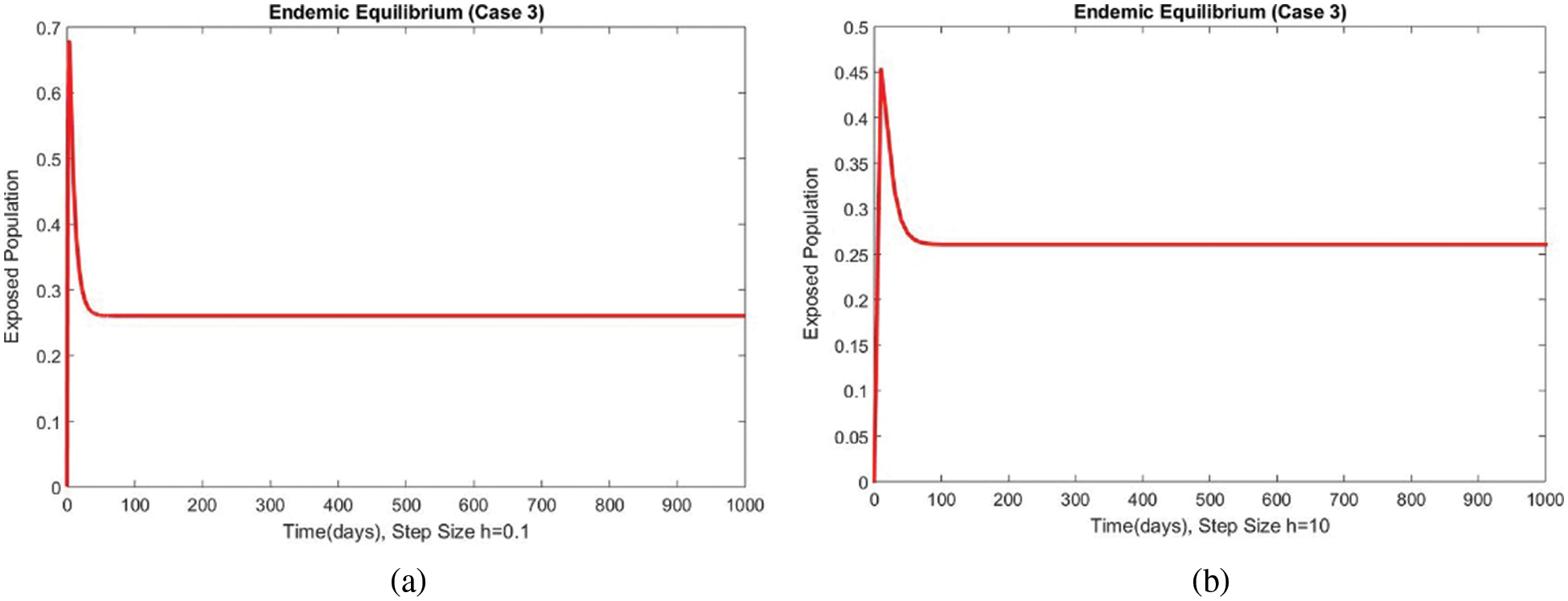
Figure 12: The portion of exposed populations for case 3 at different step sizes

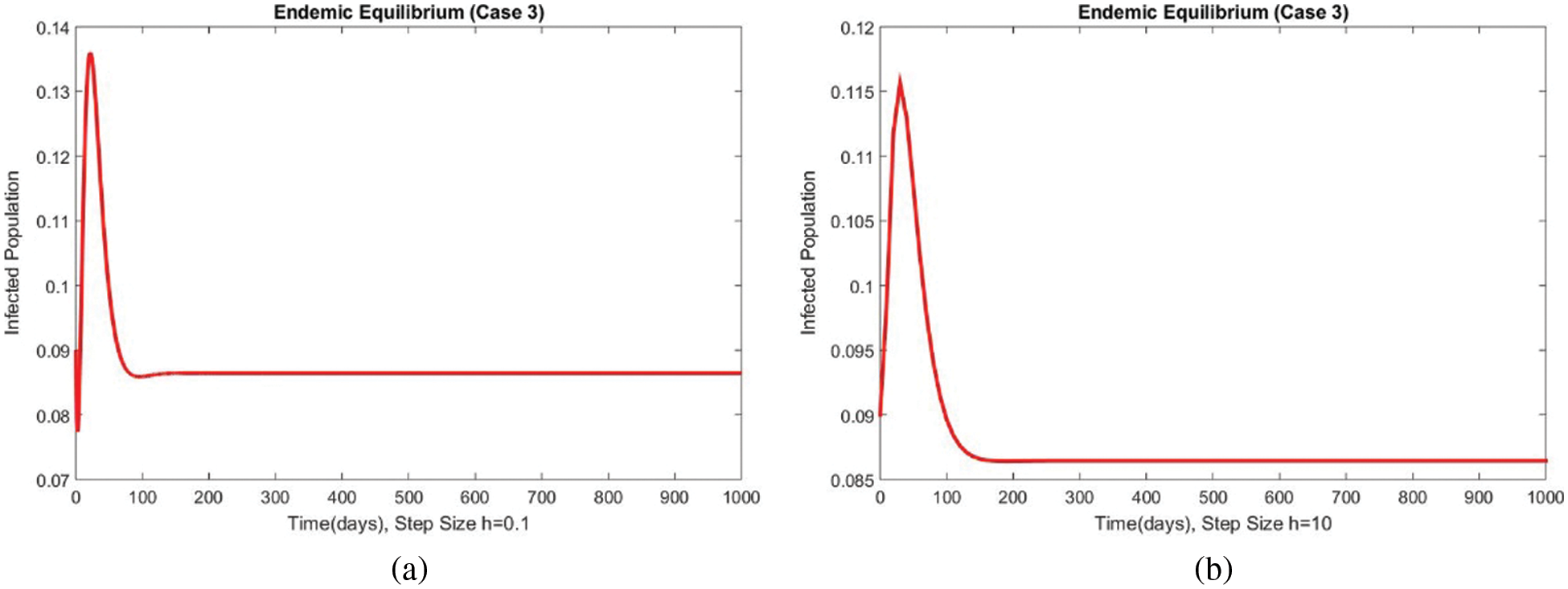
Figure 13: The portion of infected populations for case 3 at different step sizes

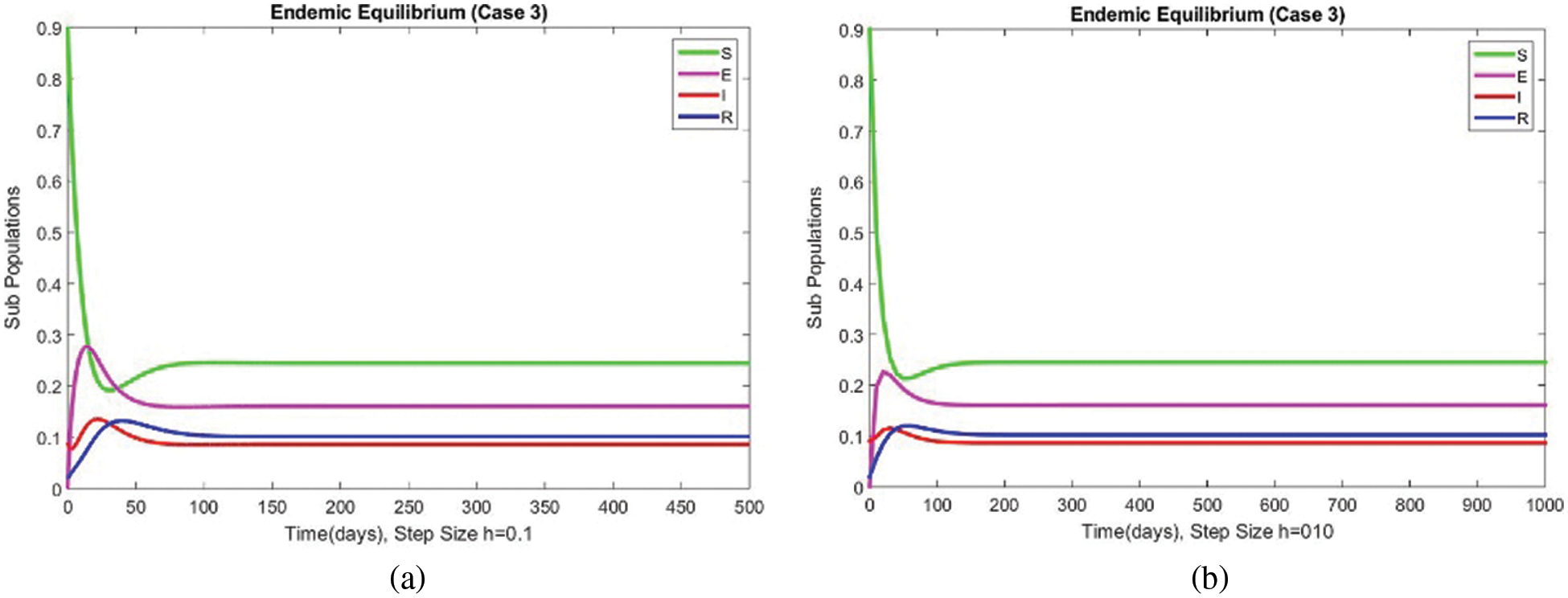
Figure 14: The portion of subpopulations for case 3 at different step sizes

3.3 Convergence of the NSFD Scheme

Let

C1=S+hΛ1+hI+hμ,(52)

C2=E+hSI1+h(μ+ε),(53)

C3=I+hεE1+h(μ+d+γ(ω)),(54)

C4=R+hγ(ω)I1+hμ.(55)

The Jacobian matrix corresponding to the system (52)–(55) is

J=[∂C1∂S∂C1∂I∂C1∂E∂C1∂R∂C2∂S∂C2∂I∂C2∂E∂C2∂R∂C3∂S∂C3∂I∂C3∂E∂C3∂R∂C4∂S∂C4∂I∂C4∂E∂C4∂R]

Jacobian at the DFE is

J=[11+hμ000011+h(μ+ε)000hε1+h(μ+d+γ(ω))11+h(μ+d+γ(ω))000hγ(ω)1+hμ11+hμ]

Eigenvalues of the above jacobian matrix are λ1=11+hμ<1, λ2=11+h(μ+ε)<1, λ3=11+h(μ+d+γ(ω))<1 and λ1=11+hμ. All eigenvalues are less than unity which shows that the system (36)–(39) converges at DFE.

4  Conclusion

This article studies a fuzzy-based model to investigate the dynamics of Amoebiasis infection in humans. The principal objective of this study was to construct and execute a numerical and mathematical model for a better understanding of the dynamics of the disease. We discussed the model’s equilibrium analysis, reproductive number, and sensitivity. For the solution of the studied model, firstly, we developed the forward Euler method and then focused on the formulation of the NSFD scheme. The simulation results reveal that the forward Euler method cannot generate convergent and non-harmful solutions for a considerable value of the time step size.

In contrast, the proposed method produces convergent and positive solutions and is consistent, dynamically, and positively bounded. The exciting feature of the simulation results is the consistency of the graphs’ overall step sizes since many classical methods like Euler, RK-4, Euler’s stochastic, and RK-4 stochastic do not preserve them at large step sizes [44,45]. The fuzzy modeling approach is a reliable and efficient technique to handle the uncertainty in the model. It can be used to study the dynamics of amoebiasis diseases in the human population. The method developed in this work can be extended to delayed, stochastic, and fractional models in fuzzy environments. The idea can also be implemented in machine learning problems [47]. We analyzed the model of the spread of the amoebiasis virus for a general class of parameters taken from the scientific literature in this study. The execution of these findings on real-time data is our future research plan as presented in [47–49].

Acknowledgement: Thanks to our families and colleagues who supported us morally. The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University for funding this work through Large Groups” (Project under Grant Number (RGP.2/116/43)).

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  S. L. Stanley, “Amoebiasis,” The Lancet, vol. 361, no. 9362, pp. 1025–1034, 2003. [Google Scholar]

 2.  G. Choudhuri and M. Rangan, “Amebic infection in humans,” Indian Journal of Gastroenterology, vol. 31, no. 4, pp. 153–162, 2012. [Google Scholar]

 3.  A. E. Pinilla, M. C. Lopez and D. F. Viasus, “Historia del protozoo entamoeba histolytica,” Revista Médica de Chile, vol. 136, no. 1, pp. 118–124, 2008. [Google Scholar]

 4.  D. Stark, S. J. van Hal, G. Matthews, J. Harkness and D. Marriott, “Invasive amebiasis in men who have sex with men, Australia,” Emerging Infectious Diseases, vol. 14, no. 7, pp. 1141–1143, 2008. [Google Scholar]

 5.  I. E. Salit, K. Khairnar, K. Gough and D. R. Pillai, “A possible cluster of sexually transmitted entamoeba histolytica: Genetic analysis of a highly virulent strain,” Clinical Infectious Diseases, vol. 49, no. 3, pp. 346–353, 2009. [Google Scholar]

 6.  A. Samie, A. ElBakri and R. AbuOdeh, “Amoebiasis in the tropics: Epidemiology and pathogenesis,” in Current Topics in Tropical Medicine in Tech, London, UK, chapter 14, pp. 201–226, 2012. [Online]. Available:https://www.intechopen.com/books/825 [Google Scholar]

 7.  C. Xim’enez, P. Mor’an, L. Rojas, A. Valadez and A. G’omez, “Reassessment of the epidemiology of amebiasis: State of the art,” Infection, Genetics and Evolution, vol. 9, no. 6, pp. 1023–1032, 2009. [Google Scholar]

 8.  N. Chitnis, J. M. Cushing and J. M. Hyman, “Bifurcation analysis of a mathematical model for malaria transmission,” SIAM Journal on Applied Mathematics, vol. 67, no. 1, pp. 24–45, 2006. [Google Scholar]

 9.  A. M. Niger and A. B. Gumel, “Mathematical analysis of the role of repeated exposure on malaria transmission dynamics,” Differential Equations and Dynamical Systems, vol. 16, no. 3, pp. 251–287, 2008. [Google Scholar]

10. T. Smith, N. Maire, A. Ross, M. Penny, N. Chitnis et al., “Towards a comprehensive simulation model of malaria epidemiology and control,” Parasitology, vol. 135, no. 13, pp. 1507–1516, 2008. [Google Scholar]

11. A. L. Port, G. Cottrell, C. Dechavanne, V. Briand, A. Bouraima et al., “Prevention of malaria during pregnancy: Assessing the effect of the distribution of IPTp through the national policy in Benin,” American Journal of Tropical Medicine and Hygiene, vol. 84, no. 2, pp. 270–275, 2011. [Google Scholar]

12. F. B. Agusto, N. Marcus and K. O. Okosun, “Application of optimal control to the epidemiology of malaria,” Electronic Journal of Differential Equations, vol. 8, no. 1, pp. 1–22, 2012. [Google Scholar]

13. B. N. Kim, K. Nah, C. Chu, S. U. Ryu, Y. H. Kang et al., “Optimal control strategy of plasmodium vivax malaria transmission in Korea,” Osong Public Health and Research Perspectives, vol. 3, no. 3, pp. 128–136, 2012. [Google Scholar]

14. K. O. Okosun, O. Rachid and N. Marcus, “Optimal control strategies and cost-effectiveness analysis of a malaria model,” Biosystems, vol. 111, no. 2, pp. 83–101, 2013. [Google Scholar]

15. M. S. Arif, A. Raza, K. Abodayeh, M. Rafiq and A. Nazeer, “A numerical efficient technique for the solution of susceptible infected recovered epidemic model,” Computer Modeling in Engineering and Sciences, vol. 124, no. 2, pp. 477–491, 2020. [Google Scholar]

16. W. Shatanawi, A. Raza, M. S. Arif, M. Rafiq, M. Bibi et al., “Essential features preserving dynamics of stochastic dengue model,” Computer Modeling in Engineering and Sciences, vol. 126, no. 1, pp. 201–215, 2021. [Google Scholar]

17. M. A. Noor, A. Raza, M. S. Arif, M. Rafiq, K. S. Nisar et al., “Nonstandard computational analysis of the stochastic COVID-19 pandemic model: An application of computational biology,” Alexandria Engineering Journal, vol. 61, no. 1, pp. 619–630, 2021. [Google Scholar]

18. Z. Yu, R. Arif, M. A. Fahmy and A. Sohail, “Self-organizing maps for the parametric analysis of COVID-19 SEIRS delayed model,” Chaos, Solitons & Fractals, vol. 150, pp. 111202, 2021. [Google Scholar]

19. M. A. Fahmy, “A new boundary element algorithm for a general solution of nonlinear space-time fractional dual-phase-lag bio-heat transfer problems during electromagnetic radiation,” Case Studies in Thermal Engineering, vol. 25, pp. 100918, 2021. [Google Scholar]

20. K. Abodayeh, A. Raza, M. S. Arif, M. Rafiq, M. Bibi et al., “Numerical analysis of stochastic vector-borne plant disease model,” Computers, Materials and Continua, vol. 63, no. 1, pp. 65–83, 2020. [Google Scholar]

21. L. A. Zadeh, “Fuzzy sets,” Information Control, vol. 8, no. 1, pp. 338–353, 1965. [Google Scholar]

22. T. W. Liao, “A fuzzy multicriteria decision-making method for material selection,” Journal of Manufacturing Systems, vol. 15, no. 1, pp. 1–12, 1996. [Google Scholar]

23. J. H. T. Bates and M. P. Young, “Applying fuzzy logic to medical decision making in the intensive care unit,” American Journal of Respiratory and Critical Care Medicine, vol. 167, no. 7, pp. 948–952, 2003. [Google Scholar]

24. N. Fenton and W. Wang, “Risk and confidence analysis for fuzzy multicriteria decision making,” Knowledge-Based Systems, vol. 19, no. 6, pp. 430–437, 2006. [Google Scholar]

25. C. H. Yeh and Y. H. Chang, “Modeling subjective evaluation for fuzzy group multicriteria decision making,” European Journal of Operational Research, vol. 194, no. 2, pp. 464–473, 2009. [Google Scholar]

26. M. Saeed, U. Ali, J. Ali and F. Dayan, “Fuzzy soft relative method and its application in decision making problem,” Proceedings of the Pakistan Academy of Sciences, vol. 57, no. 1, pp. 21–30, 2020. [Google Scholar]

27. L. D. Barros, M. F. Leite and R. C. Bassanezi, “The SI epidemiological models with a fuzzy transmission parameter,” Computers & Mathematics with Applications, vol. 45, no. 10, pp. 1619–1628, 2003. [Google Scholar]

28. C. Torres, S. Barguil, M. Melgarejo and A. Olarte, “Fuzzy model identification of dengue epidemic in Colombia based on multiresolution analysis,” Artificial Intelligence in Medicine, vol. 60, no. 1, pp. 41, 2014. [Google Scholar]

29. P. K. Mondal, S. Jana, P. Haldar and T. K. Kar, “Dynamical behavior of an epidemic model in a fuzzy transmission,” International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, vol. 23, no. 5, pp. 651–665, 2015. [Google Scholar]

30. C. Li, J. Huang, Y. H. Chen and H. Zhao, “A fuzzy susceptible-exposed-infected-recovered model based on the confidence index,” International Journal of Fuzzy Systems, vol. 23, no. 1, pp. 907–917, 2021. [Google Scholar]

31. X. Chen, J. Li, C. Xiao and P. Yang, “Numerical solution and parameter estimation for uncertain SIR model with application to COVID-19,” Fuzzy Optimization and Decision Making, vol. 20, no. 2, pp. 189–208, 2021. [Google Scholar]

32. M. Abdy, S. Side, S. Annas, W. Nur and W. Sanusi, “An SIR epidemic model for COVID-19 spread with fuzzy parameter: The case of Indonesia,” Advances in Difference Equations, vol. 105, no. 2021, pp. 1–17, 2021. [Google Scholar]

33. F. M. Allehiany, F. Dayan, F. F. Al-Harbi, N. Althobaiti, N. Ahmed et al., “Bio-inspired numerical analysis of COVID-19 with fuzzy parameters,” Computers, Materials & Continua, vol. 72, no. 2, pp. 3213–3229, 2022. [Google Scholar]

34. R. E. Mickens, “A fundamental principle for constructing nonstandard finite difference schemes for differential equations,” Journal of Difference Equations and Applications, vol. 11, no. 2, pp. 645–653, 2005. [Google Scholar]

35. J. Cresson and F. Pierret, “Nonstandard finite difference schemes preserving dynamical properties,” Journal of Computational and Applied Mathematics, vol. 303, no. 2, pp. 15–30, 2016. [Google Scholar]

36. M. Naveed, M. Rafiq, A. Raza, N. Ahmed, I. Khan et al., “Mathematical analysis of novel coronavirus (2019-nCov) delay pandemic model,” Computers, Materials & Continua, vol. 64, no. 3, pp. 1401–1414, 2020. [Google Scholar]

37. W. Shatanawi, A. Raza, M. S. Arif, K. Abodayeh, M. Rafiq et al., “An effective numerical method for the solution of a stochastic coronavirus (2019-nCOVID) pandemic model,” Computers, Materials & Continua, vol. 66, no. 2, pp. 1121–1137, 2021. [Google Scholar]

38. N. Shahid, D. Baleanu, N. Ahmed, T. S. Shaikh, A. Raza et al., “Optimality of solution with numerical investigation for coronavirus epidemic model,” Computers, Materials & Continua, vol. 67, no. 2, pp. 1713–1728, 2021. [Google Scholar]

39. F. Dayan, N. Ahmed, M. Rafiq, A. Akgül, A. Raza et al., “Construction and numerical analysis of a fuzzy nonstandard computational method for the solution of an SEIQR model of COVID-19 dynamics,” AIMS Mathematics, vol. 7, no. 5, pp. 8449–8470, 2022. [Google Scholar]

40. S. Adak and S. Jana, “Dynamical behavior of an epidemic model with fuzzy transmission and fuzzy treatment control,” Journal of Applied Mathematics and Computing, vol. 68, no. 3, pp. 1929–1948, 2022. [Google Scholar]

41. L. C. Barros, R. Z. G. Oliveira, M. B. F. Leite and R. C. Bassanezi, “Epidemiological models of directly transmitted diseases: An approach via fuzzy sets theory,” International Journal of Uncertainty, Fuzziness and Knowledge-Based Systems, vol. 22, no. 5, pp. 769–781, 2014. [Google Scholar]

42. R. Verma, S. P. Tiwari and R. K. Upadhyay, “Fuzzy modeling for the spread of influenza virus and its possible control,” Computational Ecology and Software, vol. 8, no. 1, pp. 32–45, 2018. [Google Scholar]

43. P. V. Driessche and J. Watmough, “Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission,” Mathematical Biosciences, vol. 180, no. 1, pp. 29–48, 2002. [Google Scholar]

44. Y. T. Mangongo, J. D. K. Bukweli and J. D. B. Kampempe, “Fuzzy global stability analysis of the dynamics of malaria with fuzzy transmission and recovery rates,” American Journal of Operations Research, vol. 11, no. 6, pp. 257–282, 2021. [Google Scholar]

45. N. Chitnis, J. M. Hyman and M. D. Cushing, “Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model,” Bulletin of Mathematical Biology, vol. 70, no. 5, pp. 1272–1296, 2008. [Google Scholar]

46. M. S. Arif, A. Raza, W. Shatanawi, M. Rafiq and M. Bibi, “A stochastic numerical analysis for computer virus model with vertical transmission over the internet,” Computers, Materials Continua, vol. 61, no. 3, pp. 1025–1043, 2019. [Google Scholar]

47. G. Bhuju, G. R. Phaijoo and D. B. Gurung, “Fuzzy approach analyzing SEIR-SEI dengue dynamics,” BioMed. Research International, vol. 20, no. 1, pp. 1–15, 2020. [Google Scholar]

48. S. C. Mpeshe, “Fuzzy SEIR epidemic model of amoebiasis infection in human,” Advances in Fuzzy Systems, vol. 22, no. 1, pp. 1–14, 2022. [Google Scholar]

49. S. K. Yadav and Y. Akhter, “Statistical modeling for the prediction of infectious disease dissemination with special reference to COVID-19 spread,” Frontiers in Public Health, vol. 680, no. 1, pp. 1–20, 2021. [Google Scholar]