Multimodal Fuzzy Downstream Petroleum Supply Chain: A Novel Pentagonal Fuzzy Optimization

1  Introduction

The manufacturing of products through hand dominated the worldwide economic system as much as in the mid-eighteenth century. However, a good way to meet marketplace needs is to raise manufacturing ranges, which necessitates a transfer from guide labor to steam-powered machines. This marked the beginning of a brand-new generation in global records referred to as the First Industrial Revolution began in England and primarily trusted coal as an essential factor for economic strength and development [1].

Although coal is still widely used in many regions of the world, it is no longer the main energy source because other more powerful sources have been found. Consequently, oil exploration began at the end of the nineteenth century, after the Second Industrial Revolution. Drake drilled the first oil well in Pennsylvania and built refineries that successfully separate kerosene from crude oil for use in lighting and heating. Automobiles were developed in the early 20th century, requiring the extraction of gasoline. This crude oil product was initially an unwanted byproduct [2]. More than 50% of the energy used worldwide is provided by the oil and gas industry. Although alternative energy sources, such as renewables, are becoming more popular [3,4], oil and natural gas are still far from being replaced. Plastics, rubber, solvents, and other petrochemical products have also been produced from crude oil. Oil industry currently supplies most of the world’s energy and there are sufficient proven reserves. The oil industry is constantly in need of the latest technologies for oil exploration, drilling, refining and supply chain.

Oil supply chains are dynamic, complicated, and have significant revenue and expenses. They are divided into three primary areas: upstream, which deals with production and exploration; midstream, which handles refinery processes; and downstream, which considers the supply of oil products [5]. As the upstream sector has been extensively studied, a study of the downstream sector has been conducted [6]. Because this section deals with the distribution of several items, it comprises a variety of services, including storage facilities, wholesale markets, and retail stores that are connected to primary and secondary distribution. The trading consists of multiple transport pathways that may be possibly combinable [7]. As a result, the downstream segment is extremely complex because it deals with the distribution of many products between various storages in the wholesale and retail markets. As a result, the downstream segment is extremely complex because it deals with the distribution of many products between various storages in the wholesale and retail markets, which can be accomplished by a combination of different modes of transportation. Effective management of the oil and gas supply chain requires efficient planning for both oil production and gas production. Well-planned and optimized oil and gas supply chain (OGSC) networks will greatly benefit petroleum producers. Optimizing the oil and gas supply chain is thus seen as a challenging and crucial undertaking by managers, practitioners, and researchers.

2  Literature Review

Diverse origins, such as measurement errors, limited historical and statistical data, imprecise theory, inadequate knowledge expression, or reliance on human judgement, are uncertainties about facts, numbers, and science. Furthermore, in modelling engineering and science challenges, uncertainty theory plays an important role. Recently, significant changes have occurred in this area. Various theories have been developed to measure uncertainity. Zadeh [8] proposed fuzzy set theory in 1965 to address the approximation and generalization of problems. In 1978, Dubois et al. [9] introduced fuzzy numbers to investigate linguistic variables in a fuzzy context; fuzzy numbers were used to develop mathematical models. The decision-making challenge was improved using fuzzy numbers. In addition to triangular and trapezoidal numbers [10,11], pentagonal fuzzy numbers [12] have been introduced.

The modern world would not be able to develop without oil and gas. No country can function smoothly without such resources. Following a recent take of events, the Covid pandemic and decreased manufacturing of petroleum products caused the prices and demand of oil to fall dramatically. This situation makes it difficult to predict the upcoming pricing of oil in the international market. This variability and sinking prices of oil products have pushed international companies in fuel markets to reorganize their corporate structures along with their supply chain networks to manage their expenses and costs. Such restructuring, which makes the business more efficient than before in terms of resources and time, is only effective when it remains an on-going process for improvement [13,14]. The oil and gas industry involves some of the most complicated and technologically advanced supply chain systems in the world. What makes them so complicated is the vertiginous incorporation of tasks spanning from exploring the crude material to then refining it into consumable products and utilizing the logistics to deliver the said product. The process includes manufacturing, shipping, purification, and product placement in the consumer market.

Upstream is an oil supply chain that involves searching for locations that may have hydrocarbons and drilling operations that carry the hydrocarbons to the ground and crude oil transportation. Some authors classify the transportation of crude oil as an upstream activity, whereas others classify it as a midstream activity [15]. Regardless of these differences, the midstream region is concerned with refining operations. The term “downstream” refers to the storage, distribution and marketing of refined products and by refined products we refer to the processed products of oil which are to be stored first at the depots and then afterwards distributed in the retail markets. In the downstream oil supply chain (DOSC), the principal transportation modes include pipelines, railway networks and roads. However, pipelines are the most efficient method to transport oil products, as no weather conditions or any other obstacle can intervene in the. In an existing DOSC, choosing an acceptable pipeline route and construction location is practical and efficient for lowering primary distribution costs and increasing efficiency. This study attempts to develop an optimized design of a prototype for the DOSC considering new pipeline route planning to develop a more efficient DOSC. based on the aforementioned. According to some authors, the petroleum supply chain (PSC) is distributed into two parts: upstream and downstream. Here, the refining operations are downstream activities. Pudasaini [16] focused on the strategic and tactical planning of a DOSC under various sources of uncertainty. Pudasaini developed a stochastic multi-objective MILP in which uncertainty is addressed using fuzzy parameters.

Lima et al. [17] proposed a deterministic MILP model for designing and drafting downstream oil supply chains. The modelling approach determines the distribution plan after defining the strategic network design, while considering multimodal-transportation. Furthermore, by employing the multimodal transportation network equilibrium method proposed in [18], which also considers the capacity restrictions of various modes of travel, the path-overlapping issue in combined modes is resolved. By using public transportation and a combination of modes, the tool provides a framework and tool for developing a traffic management approach. Wang et al. [19] optimized the multimodal problem of the petroleum supply chain with regard to its economy, energy sector, and environmental impacts. A fuzzy min-max goal programming model (FMMGPM) is augmented to analyze the supply chain uncertainty. This study also conducted sensitivity analysis to assess the impact of uncertainty on pipeline design decisions. PSC begins upstream of oil exploration and production. After exploration, oil depots receive crude oil from the tankers . The pipelines then transfer the crude oil to the refineries. Later, refineries and petrochemicals converted crude oil into oil products. Crude oil contains a combination of hydrocarbons that must be fractionated. The products were recovered at different temperatures on a distillation column. Some refineries reprocess the heavy fractions to obtain lighter products, such as liquiefied petroleum gas (LPG), gasoline, and naphtha. Connected refineries can benefit from the complexity of each other. Finally, the downstream segment transports oil products to wholesale distribution centers (DC), and finally to retail stores [20,21]. A variety of optimization techniques can be utilized to deal with uncertainties, including stochastic programming [22], risk management, and robust optimization (see Table 1). If the market possibilities are known, the first two techniques provide viable options. By contrast, fuzzy optimization provides feasible and robust solutions, that is, solutions that can work in various situations [23–25].

According to a literature review, downstream oil and gas supply chain problems contain significant uncertainties. A fuzzy programming strategy has proven highly effective in dealing with a high level of uncertainty in business conditions. This study has the following framework. Section 3 is based on the preliminaries. Section 4 discusses a petroleum supply chain network in a fuzzy environment. The solution methodology used to deal with such a fuzzy environment is discussed in Sections 5 and 6, respectively. To validate this methodology, an illustrative case study is presented in Section 7. Section 8 provides managerial insights and interpretations. Section 9 presents a discussion of the proposed model as well as methodology, and Section 10 presents the conclusions in which the results obtained using the proposed method are presented.

3  Prelimanaries

Here, review some fundamental definitions and results of fuzzy numbers.

3.1 Fuzzy Sets

A fuzzy set A~F in the interval [0, 1] takes its values from its domain or universe of discourse X~ and is defined by

A~F=(x,μ(x),x∈X~).(1)

Here, μ(x) is the grade value of x in the fuzzy set A~F.

3.2 Fuzzy Numbers

A fuzzy number A~F with membership function μA~F is a subset of a real line with property

1.    Membership value of x~ is piecewise continuous in its space

2.    μA~F(xo)=1 for xo∈A~F

3.    μA~F(λx~1+(1−λ)x~2)≥min(λx~1,λx~2) ∀x~1,x~2∈X.

Owing to the various applications of the fuzzy number, two forms of fuzzy numbers, namely, triangular and trapezoidal fuzzy numbers, are introduced in the field of fuzzy algebra.

3.3 Triangular Fuzzy Number

The triangular fuzzy number A~TGF is a number that is represented by the triplet (a~,b~,c~) with a membership function whose mathematical representation is given below:

μTGF(x)={0x≤a~x−a~b~−a~a~≤b~1x=b~c~−xc~−b~b~≤c~0x≥c~(2)

3.4 Trapezoidal Fuzzy Number

The trapezoidal fuzzy number A~TZF is a number defined by the quadruplet (a~,b~,c~,d~) with a membership function, whose mathematical representation is as follows:

μTZF(x)={0x≤a~x−a~b~−a~a~≤b~1b~≤x≤c~c~−xd~−c~c~≤d~0x≥d~(3)

3.5 Pentagonal Fuzzy Number (PFN)

The pentagonal fuzzy number A~PFN is the fuzzy number, which is expressed by (all,al,am,au,auu), where all≤al≤am≤au≤auu with membership have the form

μPFN(x)={(al−all)(x−all)(am−all)(al−all)all≤x≤al1−x−alam−allal≤x≤am1x=am1+x−amam−auuam≤au(all−all)(x−au)(am−auu)(au−auu)au≤auu0x>auu(4)

with graphical representation in Fig. 1.

Figure 1: Pentagonal fuzzy number

3.6 Arithmetic Operations

Some basic arithmetic operations are defined as below:

1)   Addition

Let A1PFN=(a1ll,a1l,a1m,a1u,a1uu) and A2PFN=(a2ll,a2l,a2m,a2u,a2uu) be any two PFN then

A1PFN+A2PFN=(a1ll+a2ll,a1l+a2l,a1m+a2m,a1u+a2u,a1uu+a2uu)(5)

2)   Subtraction

Let A1PFN=(a1ll,a1l,a1m,a1u,a1uu) and A2PFN=(a2ll,a2l,a2m,a2u,a2uu) be two any PFN then

A1PFN−A2PFN=(a1uu−a2uu,a1u−a2u,a1m−a2m,all−a2l,a1ll−a2ll)(6)

3)   Scalar multiplication

Let A1PFN=(a1ll,a1l,a1m,a1u,a1uu) be any PFN and s∈R, then scalar multiplication is defined as:

ifs>0sAPFN=(sall,sal,am,sau,sauu)(7)

ifs<0sAPFN=(sauu,sau,am,sal,sall)(8)

3.7 Defuzzification of Pentagonal Fuzzy Number

Consider the pentagonal fuzzy number A1PFN=(a1ll,a1l,a1m,a1u,a1uu), to obtain the crisp number corresponding to the pentagonal fuzzy number, the accuracy function will be used, which is defined as follows:

Accuracy function =Kf(all+auu)+Km(am)+Kn(al+au).

Here Kf,Km,Kn∈[0,1]with restrictionKm>Kf>Kn.

4  Problem Description

The goal of this section is to construct a single-objective optimization model. To minimize the costs of single-objective, which are primarily transportation-related, it is necessary to consider customer demand, product yield, and storage and transportation capacity constraints.

4.1 Sets

This study addressed an I set of refineries with capacity Si, a set J of depots j, a set K of customer nodes k and an r mode of transportation.

i: refinery i=1,2,3,…,I

j: depots j=1,2,3,…,I

k: customer k=1,2,3,…,K

r: transportation mode r=1,2,3,…,R

p: products p=1,2,3,…,P.

4.2 Parameters

The model includes product p, customer nodes k with annual demand Dp,k for product p and transport modes r that transport p at a cost per unit of p, Ci,j,p,r from i to depots j and transport p at a cost per unit of p, Tp,j,k,r from j to k. Pipelines, rail and trucks are the three modes of shipping addressed in this study. In addition to the fixed cost fj for opening each of the new possible depots, it also has a per-unit capacity cost βn.

D~k,p: Annual demand for product p for end-Users

f~j: Fixed cost of opening depots j

C~i,j,p,r: Cost of transportation per unit of p from i to j using mode r

T~j,k,p,r: Cost of transportation per unit of p from j to k using mode r

S~i: Capacity of i

α~p: Refinery i capacity utilization per p

β~j: Cost per unit capacity at j

M: Large number (109)

4.3 Decision Variables

In the MILP model, binary and continuous decision variables were addressed. A binary variable is an integer with a value of 0 or 1. In this case, Xj is a binary variable with a value of one if depot j is open and zero otherwise. In this case, continuous variables are either positive or real. Therefore, in this model, the real variable is objective variable Z1, which represents the overall cost to be reduced.

Xj: 1 if a depot is opened at j; 0 otherwise

Yi,j,p,r: amount of product p transferred from i to j using mode r

Zj,k,p,r: amount of product p transferred from j to the end users using mode r

Vj: capacity of j.

4.4 Objective Function

The objective function Z1 reduces the overall cost of opening depots and shipping three different products, namely, gasoline, diesel, and jet fuel from the designated refineries to end-users. The first term denotes the fixed cost of locating depots, whereas the second term denotes the capacity cost of the depots that have already been opened. Identify the overall fixed and variable costs of opening depots using the first and second terms. The third term is the cost of moving products from refineries to depots using mode r. Finally, the fourth term includes the cost of moving products from the depots to customer nodes using mode r. In these terms, the coefficients were pentagonal fuzzy numbers.

Z1=min∑j∈J(f~jXj+β~jVj)+∑p∈P∑i∈I∑j∈J∑r∈RC~i,j,p,rYi,j,p,r+∑p∈P∑i∈I∑j∈J∑r∈RT~j,k,p,rZj,k,p,r.(9)

4.5 Constraints

A set of constraints that expresses the problem parameters is presented in the following subsections.

4.5.1 Demand Constraint

∑j∈j∑r∈RZj,k,p,r=D~kp(10)

expression (10) shows that depot receipts meet fuzzy demand of each product.

4.5.2 Big M-Constraint

Vj≤M.Xj(11)

Constraint (11) guarantees that no depot is granted capacity if it will not open and limits the capacity of each depot.

4.5.3 Distribution Capacity Constraint

Each new depot must have a capacity greater than the number of products that pass through it. Adding a factor of 1.10, which multiplies the left-hand side of the equation, ensures that the depot can accommodate an increase in demand of up to 10%.

1.10∗∑p∈P∑k∈K∑r∈RZj,k,p,r≤Vj(12)

4.5.4 Refinery Capacity Constraint

Eq. (13) shows that each product made at refineries equals the amount carried from refineries to depots by taking the fuzzy capacity utilization per product.

∑p∈P∑j∈J∑r∈Rα~pYi,j,p,r≤S~i(13)

4.5.5 Balance Constraint

Balance constraint (14) ensures that all quantities arriving at a refinery’s depot are transferred to each customer node.

∑i∈I∑r∈RYi,j,p,r−∑k∈K∑r∈RZj,k,p,r=0(14)

4.5.6 Non-Negative Constraint

Xj∈{0,1},Yi,j,p≥0,Zj,k,p≥0(15)

5  Proposed Methodology

Consider single-objective optimization problem

Minimize∑j∈Jcj{f(xj)} j=1,2,3,…J(16)

subject to the constraints

gi(x)≤bii=1,2,…,p.(17)

where the decision variables are xj, f(x) represents the objective functions, gi(x) represents the constraints and p represents the number of constraints. Different pentagonal fuzzy models can be constructed by converting crisp linear programming into pentagonal fuzzy linear programming using the concept of pentagonal fuzzy numbers.

1)   Only the cost coefficient is converted into a PFN by taking the remaining parameters and decision variables as crisp values.

2)   Transform the cost coefficient, remaining parameters and decision variables into a pentagonal fuzzy number

3)   Change the cost coefficient and the remaining crisp parameters into a pentagonal fuzzy number.

Here, only one model is discussed: the cost coefficient and the remaining crisp parameters are converted into pentagonal fuzzy numbers to achieve the desired goal. Then, the crisp linear model is converted into pentagonal fuzzy linear programming model using the second model.

Minimize∑j∈Jc~j{f(xj)}j=1,2,3,…J(18)

subject to the constraints

gi(x)≤b~ii=1,2,…,p.(19)

where c~i=(c1,c2,c3,c4,c5) are the pentagonal fuzzy coefficients of the objective function with c3 is the mid-point having membership grades 1 and c2,c4 having membership grades w1,w2 and b~i=(b1,b2,b3,b4,b5) are pentagonal fuzzy parameters, b3 is the mid-point having membership grades 1 and b2,b4 having membership grades w1,w2. The defuzzification of pentagonal fuzzy linear programming was performed using an accuracy function. Equivalent crisp linear programming is solved using any optimization technique to obtain the optimal solution.

6  Solution Methodology

Most decision-making challenges in the real world are ambiguous or uncertain. The use of fuzzy numbers is prevalent in many areas, including fuzzy process modelling and decision making. The management of product supply chains is a critical aspect of today’s dynamic market so that businesses can offer their customers competitive rates. Because of market uncertainty, supply chain management has become more challenging. When dealing with a fuzzy unknown parameter in a supply chain, it seems natural to use a pentagonal fuzzy number instead of a fuzzy number for efficient and improved results. Because the mathematical model effectively addresses uncertainty, the pentagonal fuzzy optimization model can deal with ambiguous data more accurately. A flowchart of thr optimization technique is shown in Fig. 2.

Figure 2: Methodology flowchart

7  Case Study

In this study, the downstream petroleum supply chain according to Pakistan’s region is considered. The under discussed multimode optimization model was further redesigned according to the fuzzy environment. Our natural environment is fuzzy in nature and there are many unpredictable changes that appear on a daily basis in Pakistan due to political, economic or environmental triggers. The fuel prices in Pakistan change abruptly within a month, as shown in Table 2.

As the downstream petroleum supply chain in Pakistan is the main target, the model is formulated accordingly. The main hub for crude oil is Port Qasim Sindh, from which several retailers consume demand through pipelines, ships and roads. Pipelines and ships are cost-effective methods. The Punjab and Khyber Pakhtoon Khawa provinces of Pakistan are not directly connected by any sea port and the cheapest oil transportation mode for these regions is pipeline. The Pak Arab refinery limited (PARCO) transfers crude oil directly from Karachi to Multan’s refinery by an 870 km pipeline, further another 362 km long pipeline transfers that product to nearby Lahore stations. Pakistan’s oil pipeline is based on 16309 km network, 47% of which is shared by different refineries, while 57% is owned by PARCO. For model formulation, the main refineries and oil depots from a specific region were considered to analyze the validity of this study. Two of the six refineries were from Balochistan, Karachi, Multan and Rawalpindi. Petroleum products were further transferred to four distribution centers through different means (see Fig. 3).

Figure 3: Refineries and distribution centers

Based on hypothetical data according to present time this petroleum supply chain network under study is operating six refineries (Cnergyico Pakistan limited (CPL), PARCO, National refiney limited (NRL), ENAR petroleum refining facility (EPRF), Attock refinery limited (ARL) and Pakistan refinery limited (PRL)) four potential depots and further main three customers for each distributor namely as industries, domestic sector and railways. From refinery to distributor and further from distributor to customer dual transportation means are specifically considered as shown in Fig. 4.

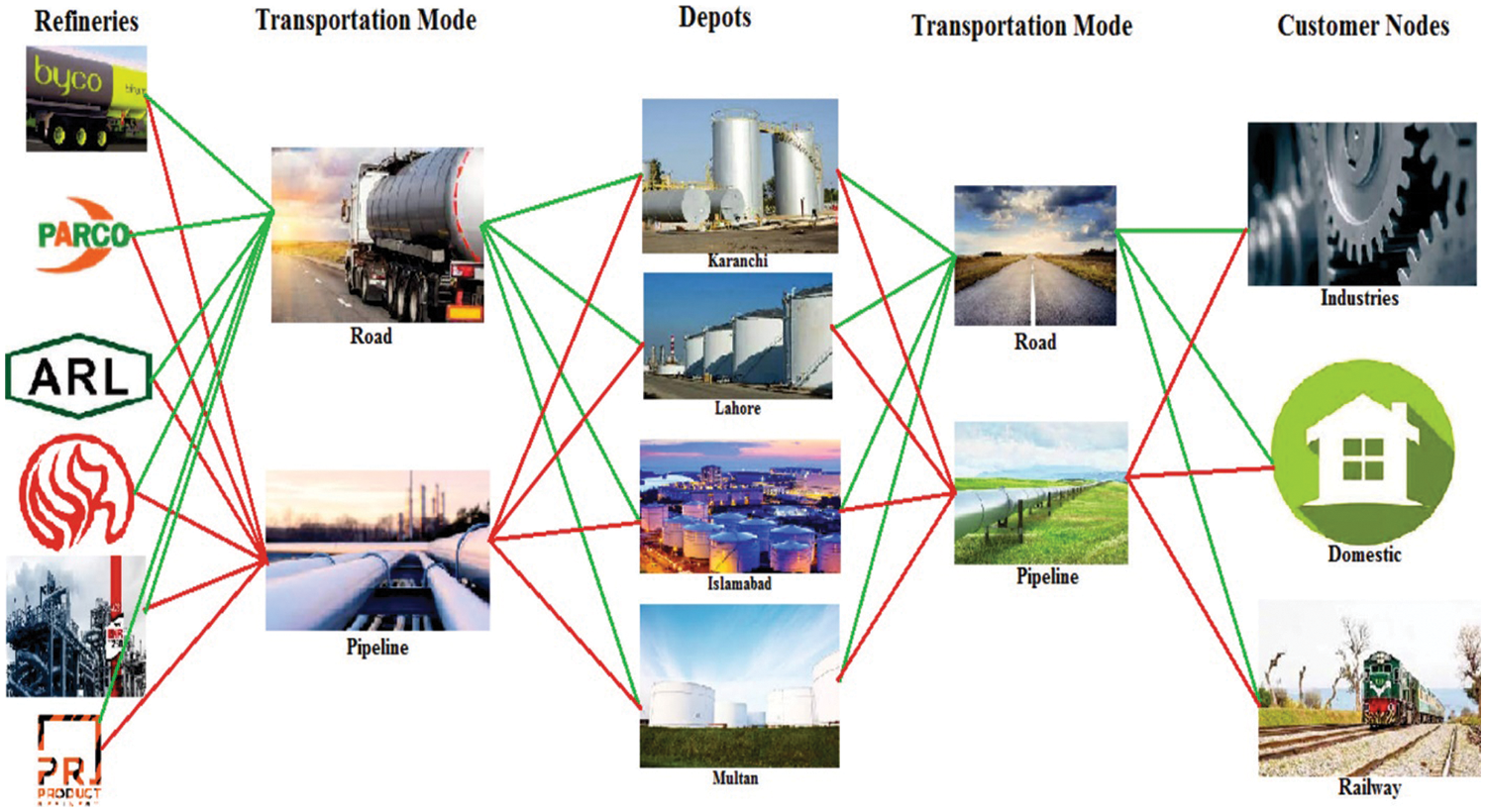
Figure 4: Downstream supply chain network

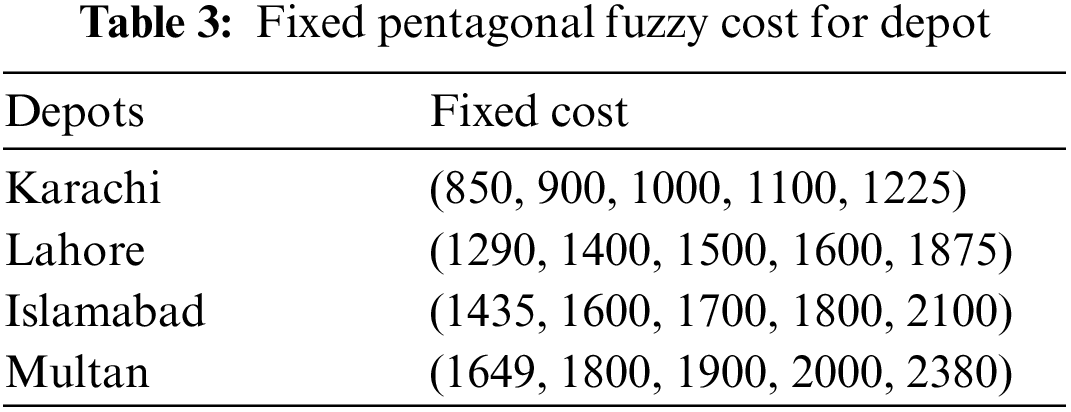
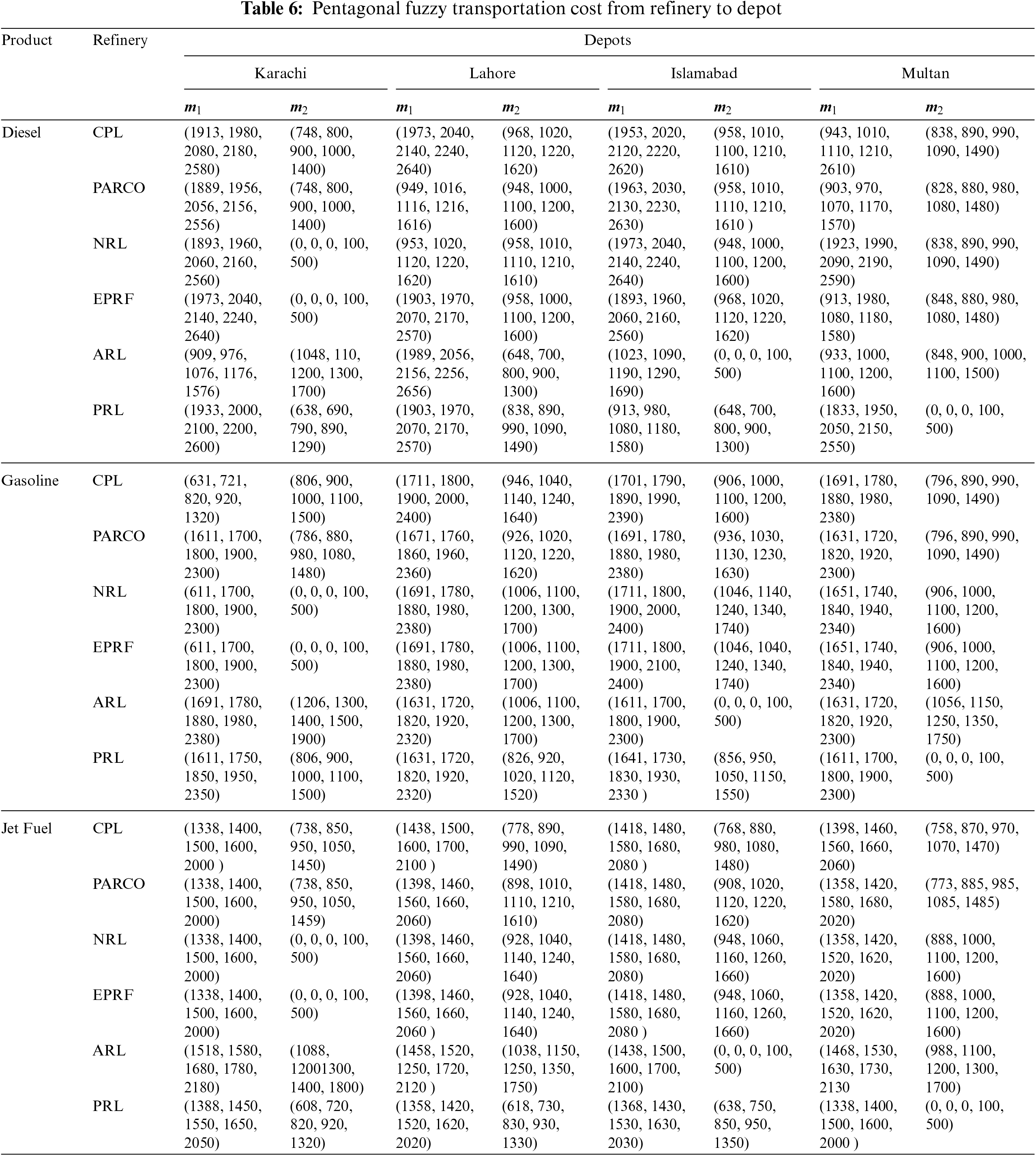
To make the optimization model flexible, it is necessary to consider its fuzzy nature. For this purpose, the considered multi-mode model is further converted into a pentagonal fuzzy multi-mode model by converting the parameters into pentagonal fuzzy numbers (see Tables 3–7).

8  Managerial Insights and Interpretation

The literature examined in this study is categorized as shown in Table 1. Crisp modelling was previously considered to reduce the cost of OGSC. Owing to the uncertainty inherent in real-life applications, it is still unclear how to deal with the fuzzy modelling of downstream supply chains in an uncertain environment. This study used pentagonal fuzzy numbers to examine the fuzzy multimodal oil and gas downstream supply chain (FMOGDSC), while considering uncertainty and imprecision.

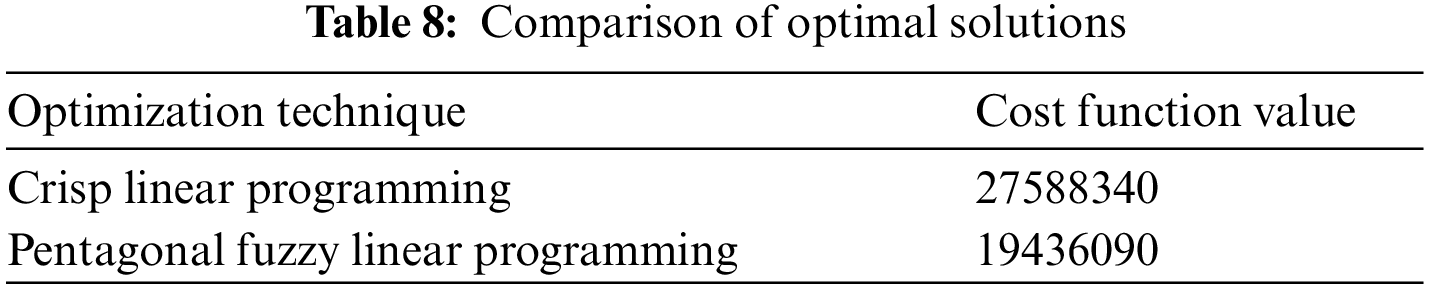
A key conclusion of this study is that pentagonal fuzzy numbers can be used to deal with many uncertain scenarios. Table 8 compares the objective functions of the proposed model with and without uncertainties. In this case, it is shown that adding uncertainty may reduce the cost factor and improve the output.

Pentagonal fuzzy optimization yields the optimum value for each decision variable. As long as the optimization method is effective, the constraints are met while attaining the target. The demand of customer 12910 million tons/year and product supply from the depot to the customer are the same (see Tables 9–11). Consequently, the demand constraint was satisfied.

9  Discussion

Numerical example data were hypothesized because data on oil and gas downstream supply chains (OGDSC) are not accessible. The refineries and distribution centers shown in Fig. 4 were taken into account in this model. Fig. 4 depicts the downstream supply chain network used to create the fuzzy model. In this study, the model was solved using MATLAB software version 2018a on a device with the specification Core (TM) i3-8130U CPU and 4GB RAM. Pentagonal fuzzy optimization was solved in MATLAB using the model (described in the previous section). Furthermore, the inclusion of uncertainty may reduce the cost of our model. However, it is clear that the model includes uncertainties.

10  Conclusion

This study aims to address the gap in the literature review by considering a single objective optimization model for tactical planning decisions of petroleum supply chains products. The model based on the method proposed by Kazemi et al. [26] is intended to minimize costs while decisions are made on opening new depots. Supply chain network uncertainty may be significantly influenced by several factors such as raw material prices, costs and lead times. The key uncertainty factors highlighted in the literature are related to the demand, supply, resource capacity, production costs and transportation costs, which are not considered in the downstream oil and gas supply chain. It seems evident that uncertainty cannot be avoided; therefore, when dealing with a fuzzy unknown parameter in a supply chain, it seems natural to use a pentagonal fuzzy number instead of a fuzzy number for efficient and improved results. When using the novel approach, the optimality gap is also reduced compared with the existing method (see Table 8). Furthermore, the results presented in Table 8 indicates that improvements will be more effective in larger-scale challenges using the novel approach. In addition, the proposed model can be extended by assuming the cost coefficient of the PFN by taking the remaining parameters and decision variables as crisp values and by changing the cost coefficient and the remaining crisp parameters into a pentagonal fuzzy number for the optimal value.

Funding Statement: The authors received no specific funding for this study.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  E. A. Wrigley, “Reconsidering the industrial revolution: England and wales,” The Journal of Interdisciplinary History, vol. 49, no. 1, pp. 9–42, 2018. [Google Scholar]

 2.  D. Yergin, “Oil on the brain: The beginning,” in The Prize: The Epic Quest for Oil, Money & Power, New York, USA: Simon & Schuster, pp. 19–34, 1991. [Google Scholar]

 3.  R. Lofti, N. Mardani and G. W. Weber, “Robust bi-level programming for renewable energy location,” International Journal of Energy Research, vol. 45, no. 5, pp. 7521–7534, 2021. [Google Scholar]

 4.  R. Lofti, B. Kargar, S. H. Hoseini, S. Nazari, S. Safavi et al., “Resilience and sustainable supply chain network design by considering renewable energy,” International Journal of Energy Research, vol. 45, no. 12, pp. 17749–17766, 2021. [Google Scholar]

 5.  C. Lima, S. Relvas and A. Barbosa-Povoa, “Stochastic programming approach for optimal tactical planning of the downstream oil supply chain,” Computers and Chemical Engineering, vol. 108, pp. 314–336, 2018. [Google Scholar]

 6.  L. J. Fermandes, S. Relvas and A. P. Barbosa-Povoa, “Collaborative design and tactical planning of downstream supply chain,” Industrial and Engineering Chemistry Research, vol. 53, no. 44, pp. 17155–17181, 2014. [Google Scholar]

 7.  C. Lima, S. Relvas and A. Barbosa-Povoa, “Downstream oil supply chain management: A critical review and future direction,” Computers and Chemical Engineering, vol. 92, pp. 78–92, 2016. [Google Scholar]

 8.  L. A. Zadeh, “Fuzzy sets,” Information and Control, vol. 8, no. 4, pp. 338–353, 1965. [Google Scholar]

 9.  D. Dubois and H. Prade, “Fuzzy interval analysis,” in Fundamentals of Fuzzy Sets, vol. 7. New York, USA: Springer Science and Business Media, pp. 483–581, 2012. [Google Scholar]

10. D. F. Li, “A ratio ranking method of triangular intuitionistic fuzzy numbers and its application to MADM problem,” Computer and Mathematics with Applications, vol. 60, no. 6, pp. 1557–1570, 2010. [Google Scholar]

11. A. Bansal, “Trapezoidal fuzzy numbers (a, b, c, d); arithmetic behavior,” International Journal of Physical and Mathematical Sciences, vol. 2, no. 1, pp. 39–44, 2011. [Google Scholar]

12. T. Pathinathan and K. Ponnivalavan, “Pentagonal fuzzy numbers,” International Journal of Computing Algorithm, vol. 3, pp. 1003–1005, 2014. [Google Scholar]

13. A. M. Attia, A. M. Ghaithan and S. O. Duffuaa, “A multi-objective optimization model for tactical planning of upstream oil & gas supply chains,” Computers and Chemical Engineering, vol. 128, pp. 216–227, 2019. [Google Scholar]

14. R. B. Amor and A. Ghorbel, “The risk in petroleum supply chain: A review and typology,” International Journal of Scientific and Engineering Research, vol. 9, no. 2, pp. 141–163, 2018. [Google Scholar]

15. A. Leiras, G. Ribas, S. Hamacher and A. Elkamel, “Literature review of oil refineries planning under uncertainty,” International Journal of Oil, Gas and Coal Technology, vol. 4, no. 2, pp. 156–173, 2011. [Google Scholar]

16. P. Pudasaini, “Integrated planning of downstream petroleum supply chain: A multi objective stochastic approach,” Operations Research Perspectives, vol. 8, pp. 100189, 2021. [Google Scholar]

17. C. Lima, S. Relvas and A. Barbosa-Povoa, “A graph modeling framework to design and plan the downstream oil supply chain,” International Transactions in Operational Research, vol. 29, no. 3, pp. 1502–1519, 2021. [Google Scholar]

18. J. -X. Zhu, Q. -Y. Luo, X. -Y. Guan, J. -L. Yang and X. Bing, “A traffic assignment approach for multi-modal transportation networks considering capacity constraints and route correlations,” IEEE Access, vol. 8, pp. 158862–158874, 2020. [Google Scholar]

19. C. N. Wang, N. L. Nhieu, K. P. Tran and Y. H. Wang, “Sustainable integrated fuzzy optimization for multi model petroleum supply chain design with pipeline system: The case study of Vietnam,” Axioms, vol. 11, no. 2, pp. 60, 2022. [Google Scholar]

20. H. Sahebi, S. Nickel and J. Ashaveri, “Strategic and tactical mathematical programming models within the crude oil supply chain context--A review,” Computers and Chemical Engineering, vol. 68, pp. 56–77, 2014. [Google Scholar]

21. S. M. S. Neiro and J. M. Pinto, “A general modeling framework for the operational planning of petroleum supply chains,” Computers and Chemical Engineering, vol. 28, no. 6–7 pp. 871–896, 2004. [Google Scholar]

22. C. Lima, S. Relvas and A. Barbosa-Povoa, “Stochastic programming approach for the optimal tactical planning of the downstream oil supply chain,” Computers and Chemical Engineering, vol. 108, pp. 314–336, 2018. [Google Scholar]

23. Y. Lu, M. Lang, Y. Sun and S. Li, “A fuzzy intercontinental road-rail multimodal routing model with time and train capacity uncertainty and fuzzy programming approaches,” IEEE Access, vol. 8, pp. 27532–27548, 2020. [Google Scholar]

24. Shafiullah, M. Tariq, A. Bari and A. R. Beig, “A new fuzzy multi-objective geometric programming in double sampling in rresence of non-response,” IEEE Access, vol. 8, pp. 45009–45022, 2020. [Google Scholar]

25. M. F. Khan, A. Haq, A. Ahmed and I. Ali, “Multi objective multi product production planning problem using intuitionistic and neutrosophic fuzzy programming,” IEEE Access, vol. 9, pp. 37466–37486, 2021. [Google Scholar]

26. Y. Kazemi and J. Szmerekovsky, “Modeling downstream petroleum supply chain: The importance of multi-mode transportation to strategic planning,” Transportation Research Part E: Logistics and Transportation Review, vol. 83, pp. 111–125, 2015. [Google Scholar]