Securing 3D Point and Mesh Fog Data Using Novel Chaotic Cat Map

1  Introduction

With the expanding prominence of web utilization, 3D point [1] and 3D cross section [2] information portrayals are generally being utilized for the portrayal of articles. Applications like Autodesk123D catch the photo of articles from various points and send them to remote fog-based workers. This information is then recreated to frame 3D models of the articles and are sent to the clients. There are likewise various work area applications for altering the 3D point and cross section fog information. As of late, the Virtual Reality (VR) innovation empowers the clients to encounter the augmented experience 3D climate.

In any case, the principal issue looked by these information is the protection issue since they are put away in the fog. Subsequently, encryption of these information is an indispensable errand. These s3D information are monstrous and multi-dimensional. Likewise, they have a high relationship among the adjoining focuses. Subsequently, conventional encryption calculations like Rivest, Shamir, and Adleman (RSA) [3], Data Encryption Standard (DES) [4], Advanced Encryption Standard (AES) [5] and blowfish [6], Twofish [7], Elliptic Curve Cryptography (ECC) [8], ElGamal encryption [9], Diffie-Hellman key trade [10–14], and so forth, may not be adequate to meet the security issues of 3D information.

The contributions of this paper overall are threefold:

a)   A unique Chaotic Cat map to produce Chaotic Cat sequence for encryption.

b)   A novel two-level encryption framework for the encryption of 3D point fog and 3

c)   D mesh fog data.

d)   Evaluation of the proposed encryption scheme and comparison with the state-of-the-art frameworks.

There are several sections to this essay. Section 2 is devoted to a comprehensive review of prior works in the field of literature. Section 3 explains how the suggested Chaotic Cat map is used to generate Chaotic Cat sequences. Encryption methods are shown in Section 4. Section 5 discusses the conclusion and outcomes. Finally, Section 6 wraps up the research.

2  Literature Survey

An audit of different plans for getting client information in distributed computing dependent on encryption calculations was proposed in [15]. In this exploration, the security issues looked by distributed computing, instruments utilized, the difficulties confronted are investigated exhaustively. Also, different security calculations like RSA, AES, DES and blowfish calculations were executed and examined in this paper. A structure for encoding wellbeing records in distributed computing was proposed in [16]. In this work, a patient-driven plan was proposed in which trait based encryption was performed. This framework accomplished a serious level of safety by using multi-authority encryption. An intermediary based encryption conspire for distributed storage was proposed in [17–22]. In this plan, an intermediary is approved by the sender for information encryption. This scrambled information is transferred to the fog. This structure depends on grid based cryptography. The framework was demonstrated to accomplish protection from the acted up fog workers.

Homomorphic encryption was used in [23] for accomplishing the security of large information put away in the fog. In this work, diverse fog notes were empowered and isolated for performing computational investigation of various pieces of the information. These hubs were made to work autonomously. Subsequently, the presentation of this framework was observed to be superior to the encryption utilizing a solitary distributed computing hub. Encryption plans dependent on bedlam hypothesis are prevalently utilized as of late. Another encryption plot utilizing confusion hypothesis and a solitary round word reference was proposed in [24–28]. In this work, the compressive detecting hypothesis was used to accomplish synchronous pressure and encryption. The estimation lattice utilized for encryption is a turbulent strategic arrangement. Measurement was accomplished utilizing a sigmoid capacity. A solitary round word reference was utilized as a substitute for discrete cosine change (DCT) premise work. Hence, an alternate remarkable word reference was produced for each picture. This assisted with accomplishing great encryption execution.

Encryption utilizing hyperChaotic Cat maps were proposed in [29]. Two kinds of changes were performed. At first, the information was encoded utilizing block changes followed by the bit stages. At long last rearranging was performed at the bit level to upgrade the security. A hash esteem having a length of 256 pieces was utilized for encryption. Another plan for the encryption of 3D point fog information was proposed in [30]. In this work, two sorts of encryptions were proposed, investigated and thought about. The primary plan depended on the age of irregular successions utilizing strategic tumultuous planning. The subsequent plan depended on the projection of the directions of the 3D fog information focuses utilizing a change grid. This network was created utilizing a turn lattice and an interpret vector.

3D fog information encryption utilizing the arrangements produced from the Cat map was proposed in [31]. Here, the succession produced by Cat tumultuous guides was utilized for two kinds of encryptions. The main system depended on arranging the arrangements and rearranging the areas of the 3D information dependent on the arranged successions. In this work, the Haar wavelet change was utilized to implant the cover pictures. The pictures in the spatial space were changed over to the recurrence area. In this space, the information was adjusted utilizing the arbitrary arrangements created by Henon map. This strategy assisted with accomplishing reversible information stowing away with a decent degree of safety.

3  Chaotic Cat Sequence Generation

3.1 Metrics to Validate Chaotic Cat Nature

The two commonly used metrics to validate the Chaotic Cat nature of these maps are approximate entropy and Lyapunov exponent.

3.1.1 Lyapunov Exponent (LE)

A popularly used metric for quantification of the chaos in a Chaotic Cat map is the Lyapunov exponent [32]. It evaluates the average divergence between two trajectories that are obtained with two different initial values that are close to each other. It is mathematically defined as,

LE=limN→∞⁡1N∑n=1N⁡log|dxn+1dxn|(1)

A positive value of Lyapunov exponent indicates that the two trajectories generated by the map will diverge exponentially with respect to time, whereas, a negative value of Lyapunov exponent indicates that the two trajectories will overlap at some point of time. Also, greater the value of LE, the more is the Chaotic Cat nature of the sequence produced by a map.

3.1.2 Approximate Entropy (AE)

Approximate entropy [33] is also used for the quantitative representation of the Chaotic Cat nature of Chaotic Cat maps. Higher values of AE indicate that the complexity of the Chaotic Cat sequence is very high.

3.2 Logistic Map

The logistic map is defined as:

xn+1=μxn(1−xn)(2)

where the control parameter is μ∈[0,4] and the initial condition is x0∈[0,1]. From Fig. 1, from the proposed map we find that the Chaotic Cat in the range μ∈[3.57,4].

Figure 1: Bifurcation of logistic map

To further depict the Chaotic Cat nature of the logistic map, the Lyapunov exponent of the logistic map is shown in Fig. 2. In the Lyapunov exponent graph, the region which is positive refers to the Chaotic Cat region. The logistic map is Chaotic Cat in the region μ∈[3.57,4] is evident from Fig. 2.

Figure 2: Lyapunov exponent of logistic map

3.3 Proposed Chaotic Cat Map

The definition of proposed Chaotic Cat map is given below as:

xn+1=((7000−μ)/7000)∗sin⁡(8πxn)(3)

where x0∈[0,1] is the initial condition and μ∈[0,75] is the control parameter. From Fig. 3, we found that the Chaotic Cat in the range μ∈[0,75] from the proposed map. This range is very much greater than that of the logistic map and logistic sine map. The sequences generated by the suggested map is used for encryption and decryption of the point fog and mesh fog data. In addition, the initial 1000 values generated using a particular key K={x0i,μi} are ignored to avoid the transient effect.

Figure 3: Bifurcation of proposed Chaotic Cat map

Similar to the logistic map and logistic sine maps, the Lyapunov exponent of the proposed map is plotted in Fig. 4. From Fig. 4, we see that the proposed map is completely Chaotic Cat in the region μ∈[0,75]. However, the highest value of LE attained is 1.2881 when μ=75.

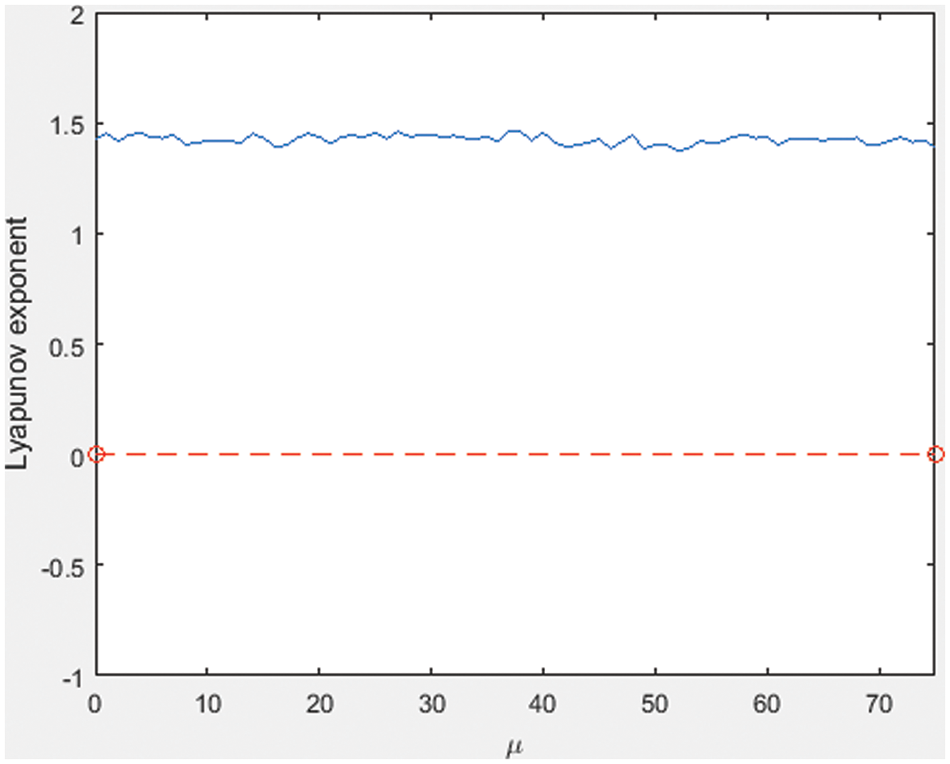
Figure 4: Lyapunov exponent of proposed Chaotic Cat map

Also, to prove the Chaotic Cat properties of the proposed map quantitatively Lyapunov exponent and approximate entropy are evaluated in Tab. 1, which shows the LE and AE values of the proposed map and other existing maps. It can be inferred from the tabulated values that the LE and AE values of the proposed map are high compared to other maps indicating that the proposed map has better Chaotic Cat behavior compared to other existing maps.

4  Proposed Encryption Methodology

This section describes how fog encryption is performed using the sequence generated by the proposed Chaotic Cat map. The keys used for encryption and decryption are securely transmitted between the sender and the receiver. In addition, this technique utilized very few sets of keys hence the problem of data leakage is minimized. The security achieved by the proposed scheme is too high since we have utilized a two-level encryption algorithm. In the first level, the sequences generated by Chaotic Cat maps are sorted in ascending order to shuffle the coordinates of the fog data. In the second level, the sequences generated by Chaotic Cat maps are sorted in descending order to further shuffle the coordinates of the fog data. Thus, double encryption is achieved using ascending sort (AS) and descending sort (DS).

4.1 3D Point Fog Model

The 3D point fog model data comprises a 3-dimensional coordinate system. That is, each point consists of 3 coordinates. Also, the proposed scheme consists of a double encryption methodology. Hence, to encrypt this data, we generate six different random sequences from the proposed Chaotic Cat map. These six sequences are generated using 6 Chaotic Cat keys referred as PK1,PK2,…,PK6 of size 256 bits. Here, each key refers to a pair of key parameters which are the initial value and the control parameter.

4.1.1 Encryption of 3D Point Fog Model

The steps involved in the encryption of the 3D point fog model are shown in Algorithm 1. Initially using the first three keys, three sequences are generated. The sequences are sorted using ascending order. The details of the original and the new locations of the sequences are then stored. Using these stored locations, the locations of the point fog data P1,P2,…,Pn are swapped to obtain intermediate point fog data IP1,IP2,…,IPn. Using the next three Chaotic Cat keys PK4,PK5,PK6, again three new sequences are generated. Using these sequences once again sorting is performed using descending order. The details of the original and new locations are then stored. Now the intermediate point fog data IP1,IP2,…,IPn is again swapped based on this location information to obtain encrypted point fog data EP1,EP2,…,EPn. The entire process is depicted in Fig. 5.

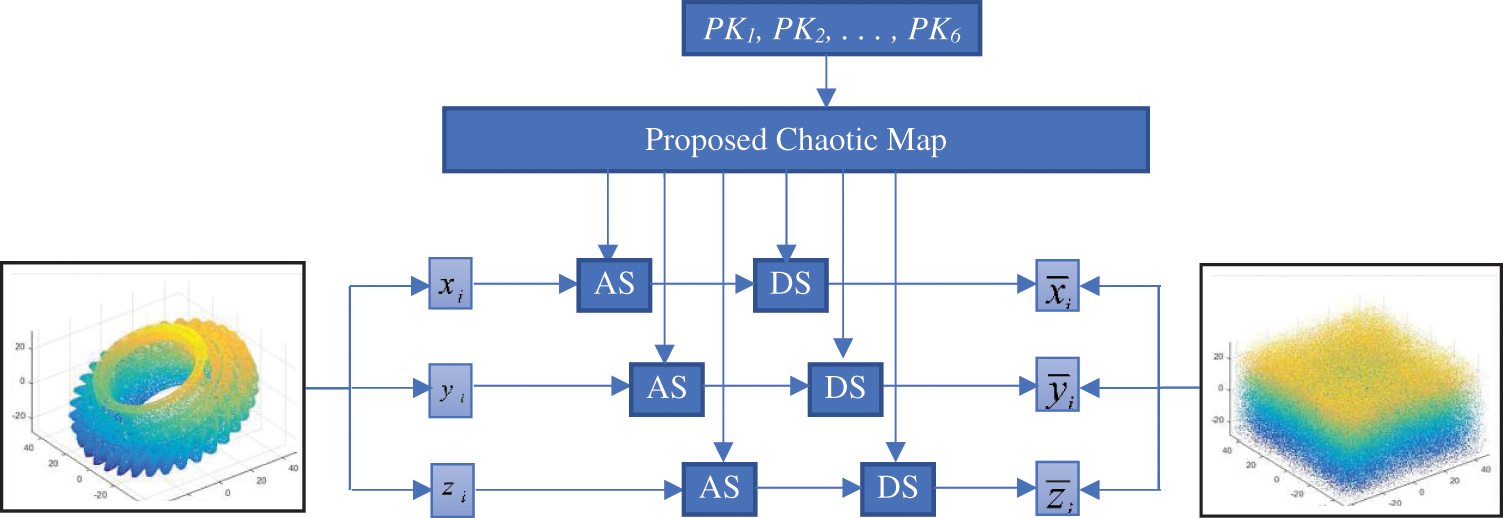
Figure 5: Proposed two-level encryption scheme for point fog data

4.1.2 Decryption of 3D Point Fog Model

The decryption of 3D point fog is done to reverse the effect of encryption and to get back the original data P1,P2,…,Pn from the encrypted data EP1,EP2,…,EPn. This is given in Algorithm 2. Here, using the Chaotic Cat keys PK4,PK5,PK6, three sequences namely S4,S5,S6 are generated. Then, these sequences are sorted in descending order and their location details are stored. Based on this information, the encrypted data is swapped to obtain the intermediate point fog data IP1,IP2,…,IPn. Now, using the Chaotic Cat keys PK1,PK2,PK3 three new Chaotic Cat sequences S1,S2,S3 are once again generated. The new Chaotic Cat sequences are again sorted in ascending order and the new location of each value is then stored. Using this information, the intermediate point fog data IP1,IP2,…,IPn is swapped to get the original data P1,P2,…,Pn. This process is illustrated in Fig. 6.

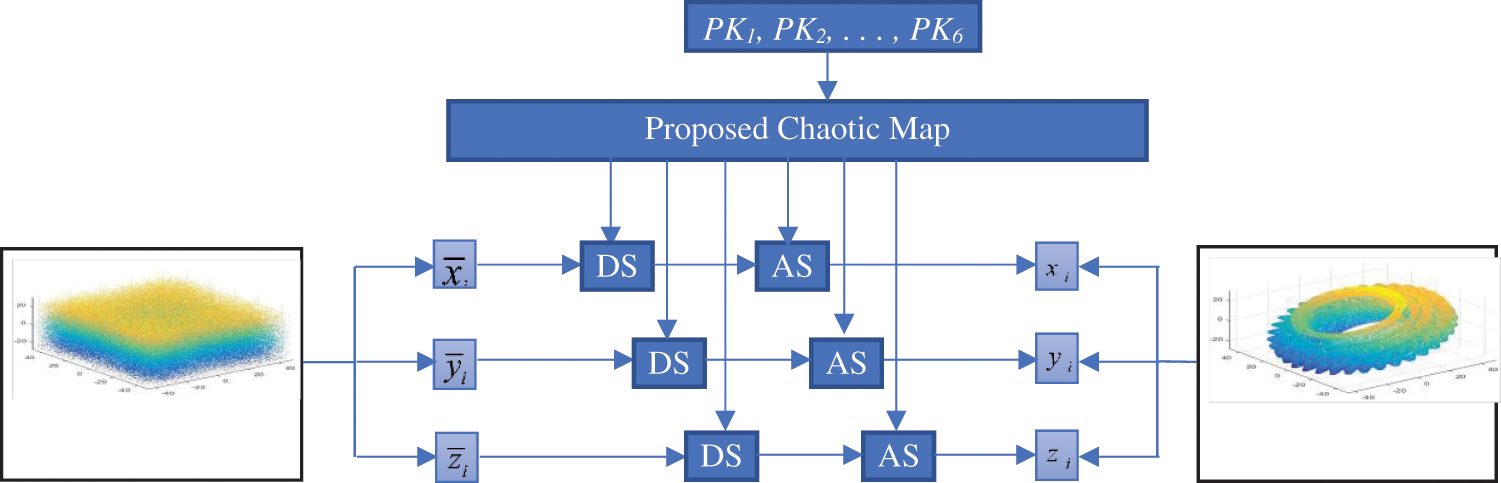
Figure 6: Proposed two-level decryption scheme for point fog data

4.1.3 Encryption of 3D Mesh Fog Model

The steps involved in the encryption of 3D mesh fog model are shown in Algorithm 3. Initially using the nine Chaotic Cat keys MK1,MK2,…,MK9, nine sequences are generated. The sequences are sorted using ascending order. The details of the original and the new locations of the sequences are then stored. Using these stored locations, the locations of the mesh fog data M1,M2,…,Mn are swapped to obtain intermediate point fog data IM1,IM2,…,IMn. Using the next nine Chaotic Cat keys MK10,MK2,…,MK18, again nine new sequences are generated. Using these sequences once again sorting is performed using descending order. The details of the original and new locations are then stored. Now the intermediate point fog data IM1,IM2,…,IMn is again swapped based on this location information to obtain the encrypted mesh fog data EM1,EM2,…,EMn. The entire process is depicted in Fig. 7.

Figure 7: Proposed two-level encryption scheme for mesh fog data

4.1.4 Decryption of 3D Mesh Fog Model

The decryption of 3D mesh fog is done to reverse the effect of encryption and to get back the original data M1,M2,…,Mn from the encrypted data EM1,EM2,…,EMn. This is given in Algorithm 4. Here, using the Chaotic Cat keys MK10,MK11,…,MK18, nine sequences namely S10,S11,…,S18 are generated. Then, these sequences are sorted in descending order and their location details are stored. Based on this information, the encrypted data is swapped to obtain the intermediate mesh fog data IM1,IM2,…,IMn. Now, using the Chaotic Cat keys MK1,MK2,…,MK9 nine new Chaotic Cat sequences S1,S2,…,S9 are once again generated. The new Chaotic Cat sequences are again sorted in ascending order and the new location of each value is then stored. Using this information, the intermediate mesh fog data IM1,IM2,…,IMn is swapped to get the original data M1,M2,…,Mn. This process is illustrated in Fig. 8.

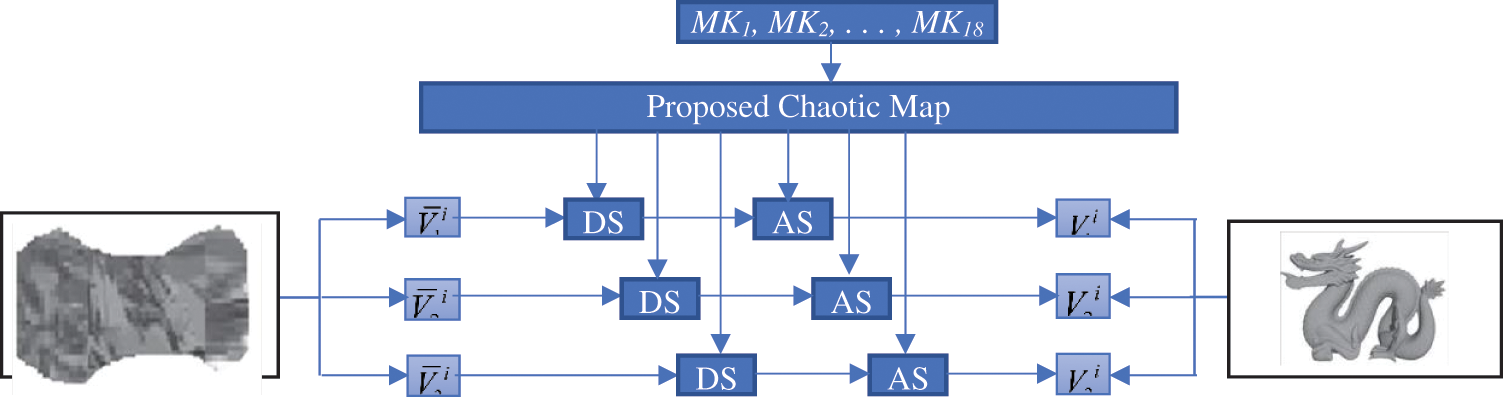
Figure 8: Proposed two-level decryption scheme for mesh fog data

5  Results and Discussion

The analysis of 3D point fog and 3D mesh fog data was performed using data in the Artec 3D [34] and Stanford 3D scanning repository [35] datasets respectively.

5.1 Security Analysis of 3D Point fog

The security analysis of 3D point fog data is performed using secret key space analysis, secret key sensitivity analysis and speed of encryption analysis.

5.1.1 Secret Key Sensitivity Analysis

Since the proposed encryption scheme is based on chaos theory, it is highly sensitive to key parameters which are the initial condition and the control parameter. Thus, to test the secret key sensitivity we change the secret keys by a very small Δ = 10−15 value. The decryption is then performed using new set of keys where PKi={x0i+Δ,μi+Δ} and i=1,2,…,6. Fig. 9 shows the original data, encrypted data and the result obtained after decryption using the new set of keys. From the Fig. 9, it is evident that the data cannot be retrieved back even if there is a small change in the key parameter values. Thus, our proposed framework possesses very high secret key sensitivity. The sensitivity level is in the order of 10−15 which a is very low value.

Figure 9: Results obtained using secret key sensitivity analysis of point fog data

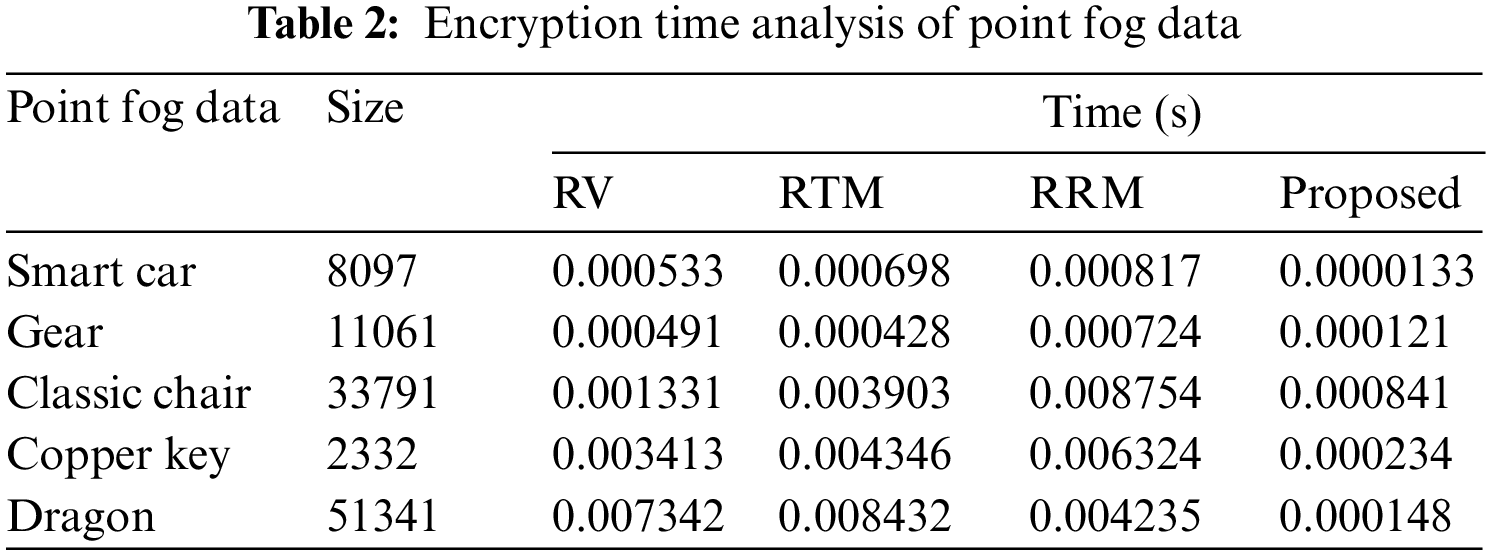
5.1.2 Speed of Encryption Analysis

The suggested system was simulated using MATLAB R2016b on a Windows PC with an Intel i3 core processor and 6GB of RAM. The proposed system has a temporal complexity of O (6 N). It is shown in Tab. 2 that the suggested framework for encryption consumes less time than previously proposed techniques. From Tab. 2, we can deduce that the proposed system takes a lot less time than the most recent state-of-the-art works. It was compared with previously proposed techniques like random variable (RV) [36], random transformation matrix (RTM) [37–39] and random reversible matrix (RRM) [40–43].

5.2 Security Analysis of 3D Mesh fog

The security analysis of 3D mesh fog data is performed using secret key space analysis, secret key sensitivity analysis and entropy analysis.

5.2.1 Secret Key Sensitivity Analysis

Since the proposed encryption scheme is based on chaos theory, it is highly sensitive to key parameters which are the initial condition and the control parameter. Thus, to test the secret key sensitivity for mesh data we change the secret keys again by a very small Δ = 10−15 value. The decryption is then performed using new set of keys where PKi={x0i+Δ,μi+Δ} and i=1,2,…,18. Fig. 10 shows the original data, encrypted data and the result obtained after decryption using the new set of keys.

Figure 10: Results obtained using secret key sensitivity analysis of mesh fog data

5.2.2 Entropy Analysis

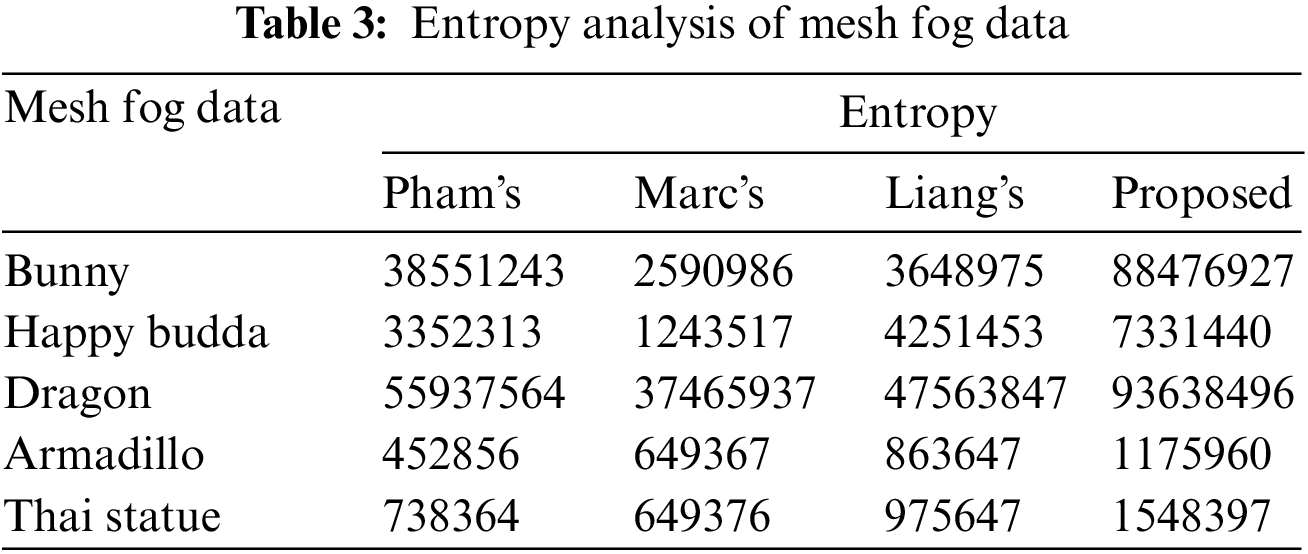
The best way to quantize the security of mesh encryption is by means of entropy analysis is given in Tab. 3. This is because entropy gives the uncertainty of an information source. It can be also defined as a measure of confusion. Thus, the amount of difficulty to retrieve the original mesh data without the use of the secret key is given by entropy. We compare the proposed scheme with state-of-the-art works like Pham’s [44], Marc’s [45], Liang’s [46].

6  Conclusion

In this examination, we have introduced an original plan for encryption of point and lattice fog information. The proposed plot uses the successions produced by a clever tumultuous guide for encryption. The tumultuous properties of the proposed turbulent guide were demonstrated utilizing bifurcation investigation, Lyapunov type and surmised entropy. Through quantitative examination, it was shown that the arbitrariness of the proposed map was more noteworthy than that delivered by regularly utilized calculated and sine strategic guides. Also, the proposed twofold encryption plot delivered amazing outcomes as far as security examination. For continuous execution, the fundamental angle is encryption time. The proposed point fog encryption plot used least encryption time contrasted with best in class works in the writing. Further, the entropy of the scrambled lattice information was additionally processed and contrasted and that accomplished by cutting edge works. It was seen that our framework creates the best outcomes. To limit the issue of information spillage there should be less keys. Since our structure depends on tumultuous guides, not very many keys were used and along these lines information spillage issue was additionally destroyed.

Acknowledgement: Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R151), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Funding Statement: This work was supprted by Princess Nourah bint Abdulrahman University Researchers Supporting Project number (PNURSP2022R151), Princess Nourah bint Abdulrahman University, Riyadh, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  K. Guo, D. Zou and X. Chen, “3D mesh labeling via deep convolutional neural networks,” ACM Transactions on Graphics, vol. 35, no. 1, pp. 215–227, 2015. [Google Scholar]

 2.  A. Quadir, “Efficient algorithm for CSP selection based on three-level architecture,” in Artificial Intelligence and Technologies, Springer, Chennai, India, vol. 23, no. 2, pp. 515–531, 2022. [Google Scholar]

 3.  Y. Li, H. Yu, B. Song and J. Chen, “Image encryption based on a single-round dictionary and chaotic cat sequences in fog computing,” Concurrency and Computation, vol. 5182, no. 21, pp. 1–15, 2019. [Google Scholar]

 4.  C. P. Schnorr and M. Jakobsson, “Security of signed ElGamal encryption,” Lecture Notes in Computer Science, vol. 1976, no. 12, pp. 73–89, 2000. [Google Scholar]

 5.  J. Solomon and I. V. Be, “A study of two fish algorithm,” International Journal of Engineering Research and Development, vol. 4, no. 2, pp. 2321–9939, 2016. [Google Scholar]

 6.  R. Dhanalakshmi, J. Anand, A. K. Sivaraman and S. Rani, “IoT-based water quality monitoring system using cloud for agriculture use,” in Cloud and Fog Computing Platforms for Internet of Things, CRC Press, United Kingdom, vol. 28, no. 3, pp. 1–14, 2022. [Google Scholar]

 7.  R. Gayathri, R. Vincent, M. Rajesh, A. K. Sivaraman and A. Muralidhar, “Web-acl based dos mitigation solution for cloud,” Advances in Mathematics: Scientific Journal, vol. 9, no. 7, pp. 5105–5113, 2020. [Google Scholar]

 8.  R. Rajakumaran, S. Gayathri, N. Venkataraman and A. Quadir, “Early detection of LDOS attack using SNMP MIBs,” in ITM Web of Conf., EDP Sciences, Chennai, India, vol. 37, no. 3, pp. 213–221, 2021. [Google Scholar]

 9.  M. Steiner, G. Tsudik and M. Waidner, “Diffie-hellman key distribution extended to group communication,” in Proc. of the ACM Conf. on Computer and Communications Security, Malaysia, vol. 102, no. 12, pp. 31–37, 1996. [Google Scholar]

10. A. Shashank, R. Vincent, A. K. Sivaraman, A. Balasundaram, M. Rajesh et al., “Power analysis of household appliances using IoT,” in Int. Conf. on System, Computation, Automation and Networking (ICSCAN), IEEE Xplore, Puducherry, India, pp. 1–5, 2021. [Google Scholar]

11. D. L. Turcotte, “Logistic map,” Fractals and Chaos in Geology and Geophysics, vol. 23, no. 7, pp. 231–244, 2012. [Google Scholar]

12. A. Quadir, V. Varadarajan and K. Mandal, “Correction to: Efficient algorithm for identification and cache based discovery of cloud services,” Mobile Networks and Applications, vol. 24, no. 4, pp. 1198–1198, 2019. [Google Scholar]

13. M. Ganga, N. Janakiraman, A. K. Sivaraman, A. Balasundaram, R. Vincent et al., “Survey of texture based image processing and analysis with differential fractional calculus methods,” in Int. Conf. on System, Computation, Automation and Networking (ICSCAN), IEEE Xplore, Puducherry, India, pp. 1–6, 2021. [Google Scholar]

14. C. K. Huang and H. H. Nien, “Multi chaotic cat systems based pixel shuffle for image encryption,” Optics Communications, vol. 282, no. 11, pp. 2123–2127, 2009. [Google Scholar]

15. S. Lian, J. Sun and Z. Wang, “A block cipher based on a suitable use of the chaotic cat standard map,” Chaos, Solitons and Fractals, vol. 26, no. 1, pp. 117–129, 2005. [Google Scholar]

16. D. Kothandaraman, A. Balasundaram, R. Dhanalakshmi, A. K. Sivaraman, S. Ashokkumar et al., “Energy and bandwidth based link stability routing algorithm for IoT,” Computers, Materials & Continua, vol. 70, no. 2, pp. 3875–3890, 2021. [Google Scholar]

17. J. Prassanna and A. Quadir, “Secrecy protector: A novel data analytics based credit score management system,” International Journal of Scientific & Technology Research, vol. 9, no. 3, pp. 29–38, 2020. [Google Scholar]

18. A. M. D. Rey, “A method to encrypt 3D solid objects based on three-dimensional cellular automata,” Lecture Notes in Artificial Intelligence, vol. 9121, no. 21, pp. 427–438, 2015. [Google Scholar]

19. R. Sornalatha, N. Janakiraman, K. Balamurugan, A. K. Sivaraman, R. Vincent et al., “FPGA implementation of protected compact AES s-box using CQCG for embedded applications,” Advances in Parallel Computing (Smart Intelligent Computing and Communication Technology) & IOS Press, vol. 38, no. 3, pp. 396–401, 2021. [Google Scholar]

20. R. Arora and A. Parashar, “Secure user data in fog computing using encryption algorithms,” International Journal of Engineering Research and Applications, vol. 3, no. 4, pp. 1922–1926, 2013. [Google Scholar]

21. A. Quadir and V. Vijayakumar, “Combined preference ranking algorithm for comparing and initial ranking of cloud services,” Recent Advances in Electrical & Electronic Engineering (Formerly Recent Patents on Electrical & Electronic Engineering), vol. 13, no. 2, pp. 260–275, 2020. [Google Scholar]

22. M. Li, S. Yu, Y. Zheng, K. Ren and W. Lou, “Scalable and secure sharing of personal health records in fog computing using attribute-based encryption,” IEEE Transactions on Parallel and Distributed Systems, vol. 24, no. 1, pp. 131–143, 2013. [Google Scholar]

23. M. Ganga, N. Janakiraman, A. K. Sivaraman, R. Vincent, A. Muralidhar et al., “An effective denoising and enhancement strategy for medical image using Rl-gl-caputo method,” Advances in Parallel Computing (Smart Intelligent Computing and Communication Technology) & IOS Press, vol. 38, no. 3, pp. 402–408, 2021. [Google Scholar]

24. X. Zhang, Y. Tang, H. Wang, C. Xu, Y. Miao et al., “Lattice-based proxy-oriented identity-based encryption with keyword search for fog storage,” Information Sciences, vol. 494, no. 10, pp. 193–207, 2019. [Google Scholar]

25. A. Quadir, “An efficient algorithm to detect DDOS amplification attacks,” Journal of Intelligent & Fuzzy Systems, vol. 39, no. 6, pp. 8565–8572, 2020. [Google Scholar]

26. Y. Zhang, C. Xu, J. Ni, H. Li and X. S. Shen, “Blockchain-assisted public-key encryption with keyword search against keyword guessing attacks for fog storage,” IEEE Transaction in Fog Computing, vol. 16, no. 5, pp. 1–12, 2019. [Google Scholar]

27. A. Balasundaram, G. Dilip, M. Manickam, A. K. Sivaraman, K. Gurunathan et al., “Abnormality identification in video surveillance system using DCT,” Intelligent Automation & Soft Computing, vol. 32, no. 2, pp. 693–704, 2021. [Google Scholar]

28. V. Kakkad, M. Patel and M. Shah, “Biometric authentication and image encryption for image security in fog framework,” Multiscale and Multidisciplinary Modeling, Experiments and Design, vol. 2, no. 4, pp. 233–248, 2019. [Google Scholar]

29. J. Li, “An efficient attribute-based encryption scheme with policy update and file update in fog computing,” IEEE Transactions on Industrial Informatics, vol. 15, no. 12, pp. 6500–6509, 2019. [Google Scholar]

30. H. Sabireen and V. Neelanarayanan, “A review on fog computing: Architecture, fog with IoT, algorithms and research challenges,” ICT Express, vol. 7, no. 2, pp. 162–176, 2021. [Google Scholar]

31. T. Wang, Y. Mei, W. Jia, X. Zheng, G. Wang et al., “Edge-based differential privacy computing for sensor–fog systems,” Journal of Parallel and Distributed Computing, vol. 136, no. 9, pp. 75–85, 2020. [Google Scholar]

32. A. Quadir, D. Agrawal, M. Mehta, A. K. Sivaraman and K. F. Tee, “Time optimization of unmanned aerial vehicles using an augmented path,” Future Internet, MDPI, vol. 13, no. 12, pp. 1–13, 2021. [Google Scholar]

33. A. Alabdulatif, I. Khalil and X. Yi, “Towards secure big data analytic for fog-enabled applications with fully homomorphic encryption,” Journal of Parallel and Distributed Computing, vol. 137, no. 9, pp. 192–204, 2020. [Google Scholar]

34. T. Xiang, J. Hu and J. Sun, “Outsourcing chaotic cat selective image encryption to the fog with steganography,” Digital Signal Processing, vol. 43, no. 12, pp. 28–37, 2015. [Google Scholar]

35. S. Karthik, R. S. Bhadoria, J. G. Lee, A. K. Sivaraman, S. Samanta et al., “Prognostic kalman filter based Bayesian learning model for data accuracy prediction,” Computers, Materials & Continua, vol. 72, no. 1, pp. 243–259, 2022. [Google Scholar]

36. M. Mishra, P. Singh and C. Garg, “A new algorithm of encryption and decryption of images,” International Journal of Computational Science and Engineering, vol. 4, no. 7, pp. 741–746, 2014. [Google Scholar]

37. N. K. Pareek, V. Patidar and K. K. Sud, “Image encryption using chaotic cat logistic map,” Image and Vision Computing, vol. 24, no. 9, pp. 926–934, 2006. [Google Scholar]

38. S. Rani, A. Kataria, M. Chauhan, P. Rattan, R. Kumar et al., “Security and privacy challenges in the deployment of cyber-physical systems in smart city applications: State-of-art work,” in Int. Conf. on Innovative Technology for Sustainable Development (ICITSDMaterials Today: Proc., Elsevier, Chennai, India, pp. 103–112, 2022. [Google Scholar]

39. S. Som, A. Mitra, S. Palit and B. B. Chaudhuri, “A selective bitplane image encryption scheme using chaotic Cat maps,” Multimedia Tools and Applications, vol. 78, no. 8, pp. 10373–10400, 2019. [Google Scholar]

40. S. A. Rajesh, A. K. Sivaraman and M. Lakshmi, “A routing optimization algorithm via fuzzy logic towards security in wireless ad-hoc networks,” in Int. Conf. on Circuits, Power & Computing Technologies, ICCPCT & IEEE Xplore, Kumaracoil, India, pp. 1321–1323, 2014. [Google Scholar]

41. P. Panja, A. Abilash, J. Christy and A. Quadir, “An approach to skin cancer detection using keras and tensorflow,” Journal of Physics: Conference Series, IOP Publishing, vol. 1911, no. 1, pp. 23–29, 2021. [Google Scholar]

42. K. A. K. Patro, B. Acharya and V. Nath, “Secure multilevel permutation-diffusion based image encryption using chaotic Cat and hyper-chaotic Cat maps,” Microsystem Technologies, vol. 25, no. 12, pp. 4593–4607, 2019. [Google Scholar]

43. R. Gayathri, A. Magesh, A. Karmel, R. Vincent and A. K. Sivaraman, “Low cost automatic irrigation system with intelligent performance tracking,” Journal of Green Engineering, vol. 10, no. 12, pp. 13224–13233, 2020. [Google Scholar]

44. X. Jin, Z. Wu, C. Song, C. Zhang and X. Li, “3D point fog encryption through chaotic cat mapping,” In Lecture Notes in Computer Science, vol. 9916, no. 23, pp. 119–129, 2016. [Google Scholar]

45. C. Jia, T. Yang, C. Wang, B. Fan and F. He, “Encryption of 3D point fog using chaotic cat cat mapping,” 3D Research, vol. 10, no. 1, pp. 342–357, 2019. [Google Scholar]

46. X. Wang, M. Xu and Y. Li, “Fast encryption scheme for 3D models based on chaos system,” Multimedia Tools and Applications, vol. 78, no. 23, pp. 33865–33884, 2019. [Google Scholar]