Partially Deep-Learning Encryption Technique

1  Introduction

In the past decades, for enhancing the transmission and security of electronic data, it is essential to continue the development of digital network communications technology. During transmission of data over open communication networks, it was a prerequisite to protect and keep the secrecy of data. Especially, over the doubtful network. One of the solutions is cryptography which hides secret data from all but authorized persons [1,2]. The cryptography categories are asymmetric key cryptography, hash functions, and symmetric key cryptography [3]. The shared key is used to encrypt or decrypt data in symmetric key encryption [1]. The public key for encryption and the private key for decryption are used in the asymmetric key cryptography class. An example of this class is ECC (Elliptic-curve cryptography) [4] and RSA algorithm (Rivest-Shamir-Adleman) [5]. No key is used but the hash value is used in the third class that is named hash functions [6].

The researchers to solve the problem of digital data security proposed many cryptographic systems. In the past forty years, numerous robust and effective encryption systems are proposed based on the above-mentioned cryptography categories. As is known, encryption is the process of changing clear data into an incomprehensible form and is used to provide data authentication and confidentiality.

A well-built encryption technology should have high statistical advantages and fulfill the requirements of confusion and diffusion [7]. During encryption, confusion is incomprehension and canceling the relationship between the secret data and the key. But diffusion rearranges and moves bits from one location to another to make the encrypted data appear randomly [8]. Some encryption techniques achieve good diffusion and confusion for encrypting data, but these techniques do not apply to all digital data [9,10]. Cryptography systems based on different categories are widely used for transmitting information/data over secure/insecure communication. For achieving enough protection, the authors’ implementation of cryptosystems depends on the transposing of the byte and changing its value in clear data [11–13]. In [14], the authors proposed a hybrid technique to protect handwritten signatures using the RSA algorithm to encrypt them and randomly embed them over the carrier image. There are researchers proposed encryption systems using 1-D and high-dimensional chaotic maps [15–17]. Some authors consider using a combination of DNA and chaotic maps in cryptosystems to realize authentication and confidentiality for digital data [18–20]. Many researchers proposed cryptosystems to enhance the quality of the encrypted data using evolutionary computation, metaheuristic algorithms, and fuzzy logic systems [21–23]. Another cryptographic property is the elliptic curve that uses to encrypt image applications [24,25]. A hybrid Gaussian backward and forward interpolation formula and RSA is proposed to increase the integration of RSA [26]. The authors present the framework to authenticate the image based-on double random phase encoding and watermarking combined with a Walsh Hadamard transform for encrypting the image scheme in [27].

In recent years and shortly, the risks and threats of breaching security systems will increase and the probability of revealing secret data will increase significantly as a result of increasing computing power and new technologies. The main contributions to this paper are 1) the PD-LET encryption technique, which is hard to break and resists new generation attacks; 2) designing a multi-tier encryption technique that significantly improved the quality of encrypted data based on multiple rounds of the block cipher; 3) using a convolutional layer (CL) that comprises a group of filters (or kernels) with variable sizes and values at every round in the proposed encryption technique; and 4) PD-LET merges substitution, transposition and key expansion based on CLs and its other stages, which creates a large amount of diffusion and confusion. To achieve a reliable security system, symmetric cryptography and iterative process technique have been proposed. The proposed technique is built on some standard deep learning algorithm processes, zigzag transformation, image partitioning, and keys. In this section, the basic definition and some properties of previous encryption techniques are briefly summarized and discussed.

The rest of this manuscript is organized as follows. Section 2 is devoted to the construction of the proposed technique. Section 3 depicts the results of the proposed encryption and its comparison with the existing results. The last section concludes the discussion.

2  The Proposed Technique

In general, all people try to protect their sensitive information and data. Especially, if it is private data or top secret. The most important parameters that make security algorithms robust and unbreakable are computational and time complexity. As a result of increasing computing power, the threats and risks of breaching security systems will increase and the likelihood of unauthorized disclosure of secret data will increase. To achieve a reliable security system, symmetric cryptography and iterative process technique are proposed. The Partially Deep-Learning Encryption Technique (PD-LET) is built on some standard deep learning algorithm processes, zigzag transformation, image partitioning, and keys.

This technique encrypts any digital data type. The main steps of the proposed technique are preprocessing, image partitioning, part interchanging, adding value, convolution stage, zigzag transformation, and symmetric key encryption as shown in Fig. 1. They are explained as follows.

Figure 1: Proposed technique stages

Algorithm 1 represents the encoding processes of PD-LET to encrypt secret data. Algorithm 2 represents the decoding processes to reconstruct the original data from an encrypted image.

2.1 Preprocessing Stage

The main objective of this stage is to convert the secret data into a two-dimensional (2D) array of bytes. Padding is used by completing the data with zeros so that the dimension of the array is divisible by an integer in preparation for dividing the data into several equal parts as shown in Figs. 2a and 2b. For example, if secret data is a grayscale/color image, it is ready because it is a 2D array. The secret data is reshaped to an appropriate array dependent on its size if it is not in the form of a 2D array.

Figure 2: Pre-processing stage

The secret square-shaped data is divided into several equal parts as shown in Fig. 2c. Each part is placed in a cluster based on its data content and then rotated or flipped its data as predefined or using a chaotic function for each class. After that, these parts are swapped diagonally, horizontally, or vertically as predetermined or using a chaotic function.

2.2 Addition/XOR Value Key

At this stage, the predefined value is added or/and XOR to each byte of the secret data, then the data is normalized to be represented from the range of image scale values represented between 0 and 255.

2.3 Convolution Layer

A convolutional layer (CL) is an important layer of a CNN (Convolutional Neural Network) architecture. This layer comprises a group of filters (or kernels), these kernels convolve with the data and extract features of input data. The filter’s size is generally smaller than the input data. The objective of this stage is to replace and change the position and value of data.

The dimension of the filter may be from 2 × 2 up to the half size of the part (secret square-shaped data). The kernel size is used to scramble the input data by swapping them diagonally, horizontally, or vertically. The values of kernel weights alter the output of the convolutional layer.

A linear process is used to encrypt the data. A kernel is a small set of numbers that is applied across the input data. Every output byte of each CL is the result of the sum of the product of each element of the kernel and its corresponding input data using zero padding to retain dimensions.

The stride of the kernel is one. After the kernel completes scanning the entire data, the normalized process converts the convoluted output to the range 0 and 255. Fig. 3 shows an example of input data, 2 × 2 kernel weights values, and normalized output values in the range between 0 and 255 for three consecutive convolution layers. Fig. 4 shows an example of input data, 3 × 3 kernel weights values, and normalized output values in the range. Fig. 5 shows an example of an inverse process for three consecutive convolution layers of the input data (mentioned in Fig. 3), 2 × 2 kernel weights values, and normalized output values in the range between 0 and 255.

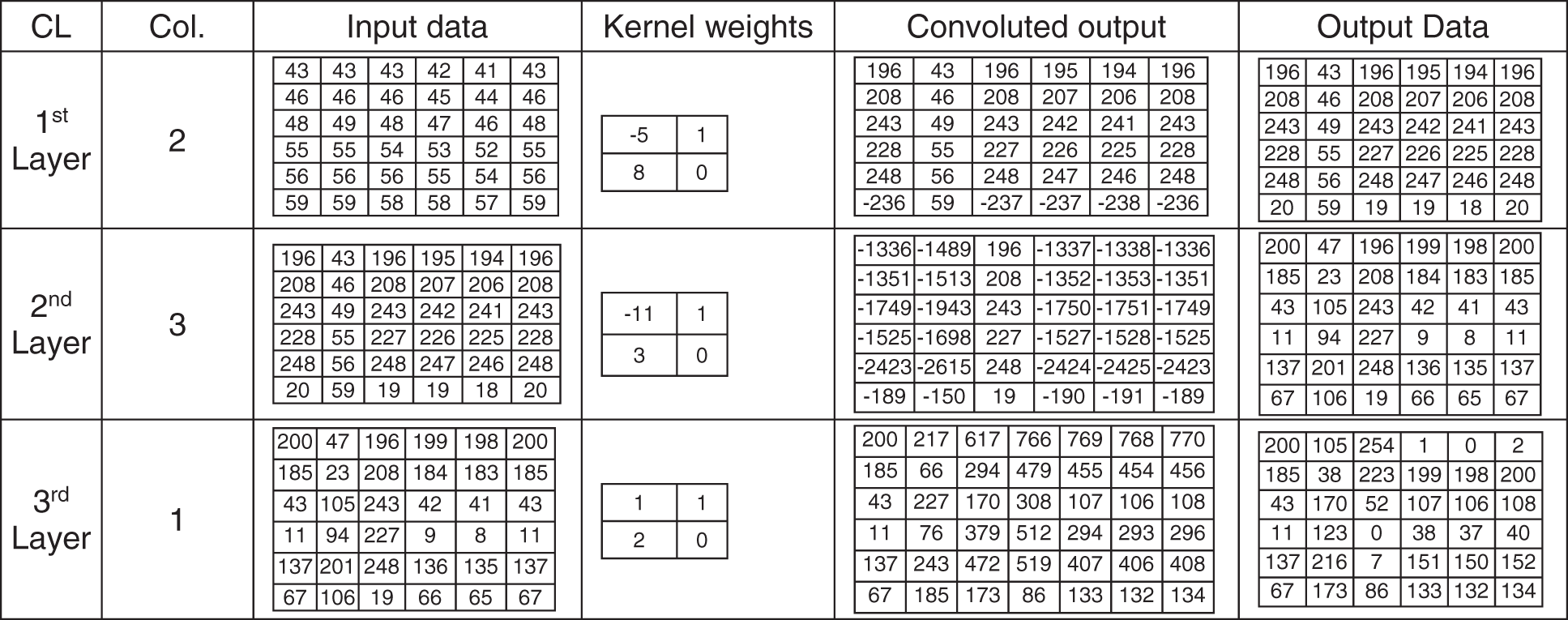
Figure 3: Convolutional layer example (input data, 2 × 2 kernel weights values and output values)

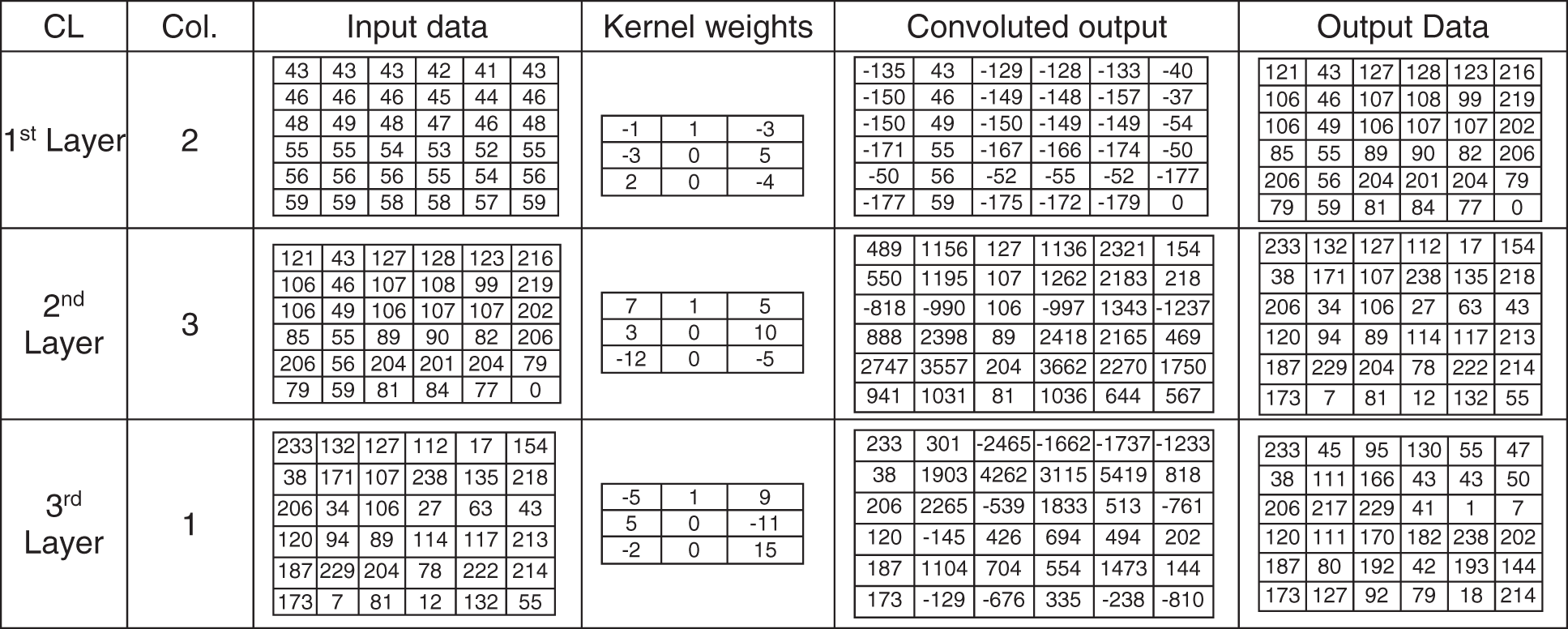
Figure 4: Convolutional layer example (input data, 3 × 3 kernel weights values and output values)

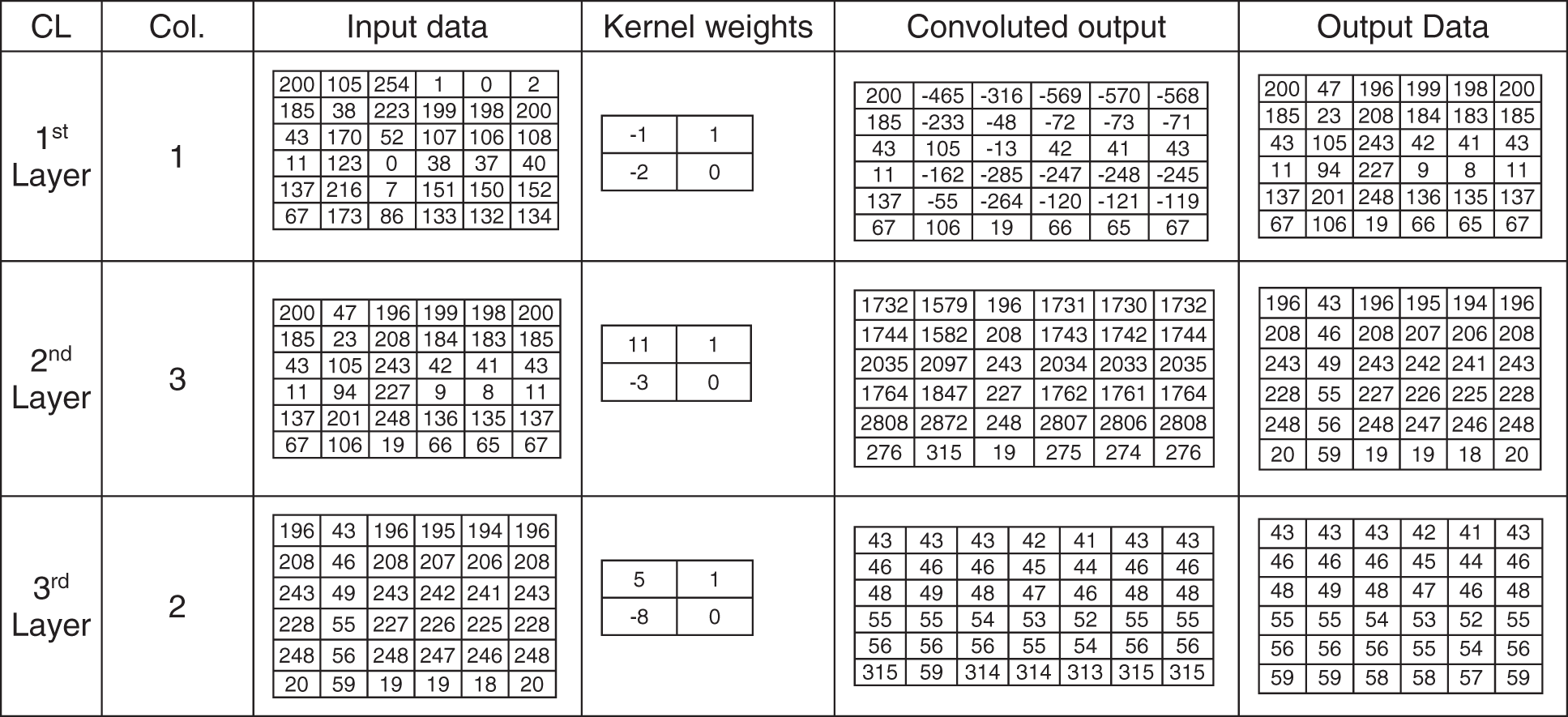
Figure 5: Deconvolutional layer example (input data, 2 × 2 kernel weights and output values)

2.4 Zigzag Transformation

2D zigzag scanning is important in many applications such as the graphic compression algorithm and medical imaging. 2D zigzag scrambles the data by changing their locations. There are several types of zigzag scanning depending on the starting point and direction [28]. The zigzag transformation is applied to the whole data as one unit or each part separately. Fig. 6 shows a sample of 2D zigzag inputs and outputs.

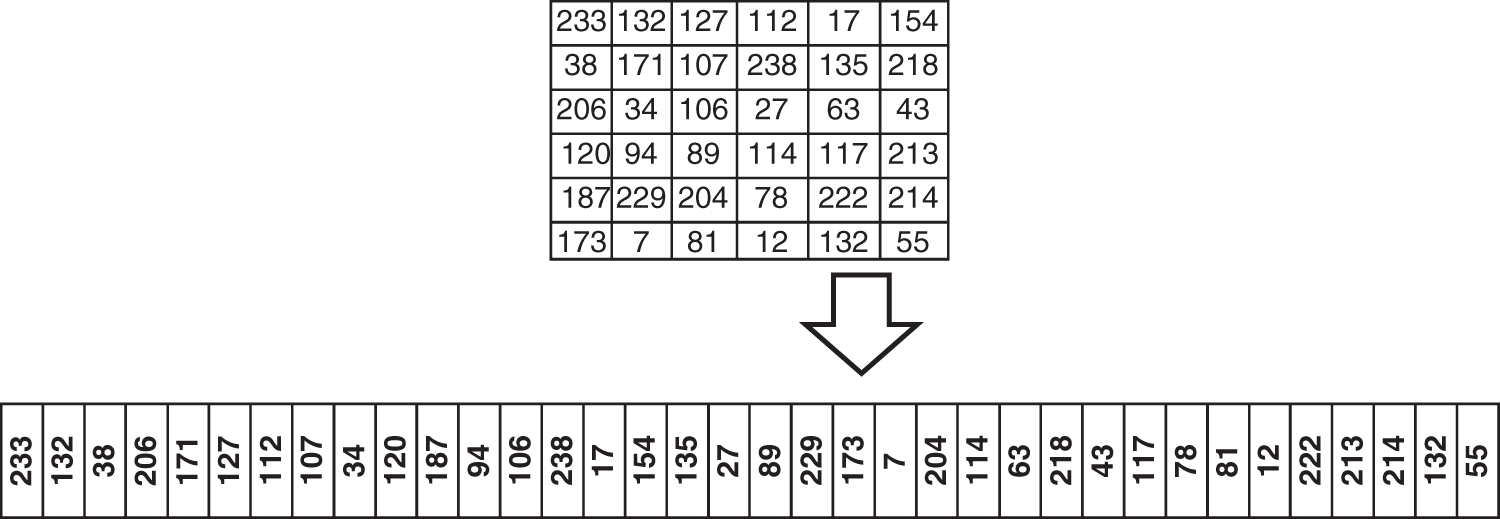
Figure 6: Two-dimensional zigzag input and output

3  Implementation and Evaluation Results

For implementation purposes, the proposed is designed and developed to protect data in a 2D format using MATLAB 2020A. The proposed system is executed on Windows 10, a 64-bit Operating system in Intel Pentium G2020 Dual-core (2 Core) 2.90 GHz Processor and 8 GB RAM. For testing the efficiency of the proposed technique, several experiments are made using different image types and sizes. To illustrate the effects of CL round and kernel weights in encrypted output, Fig. 7 shows the encrypted output of a CL Layer, two consecutive CLs, three consecutive CLs, and the change of kernel weights.

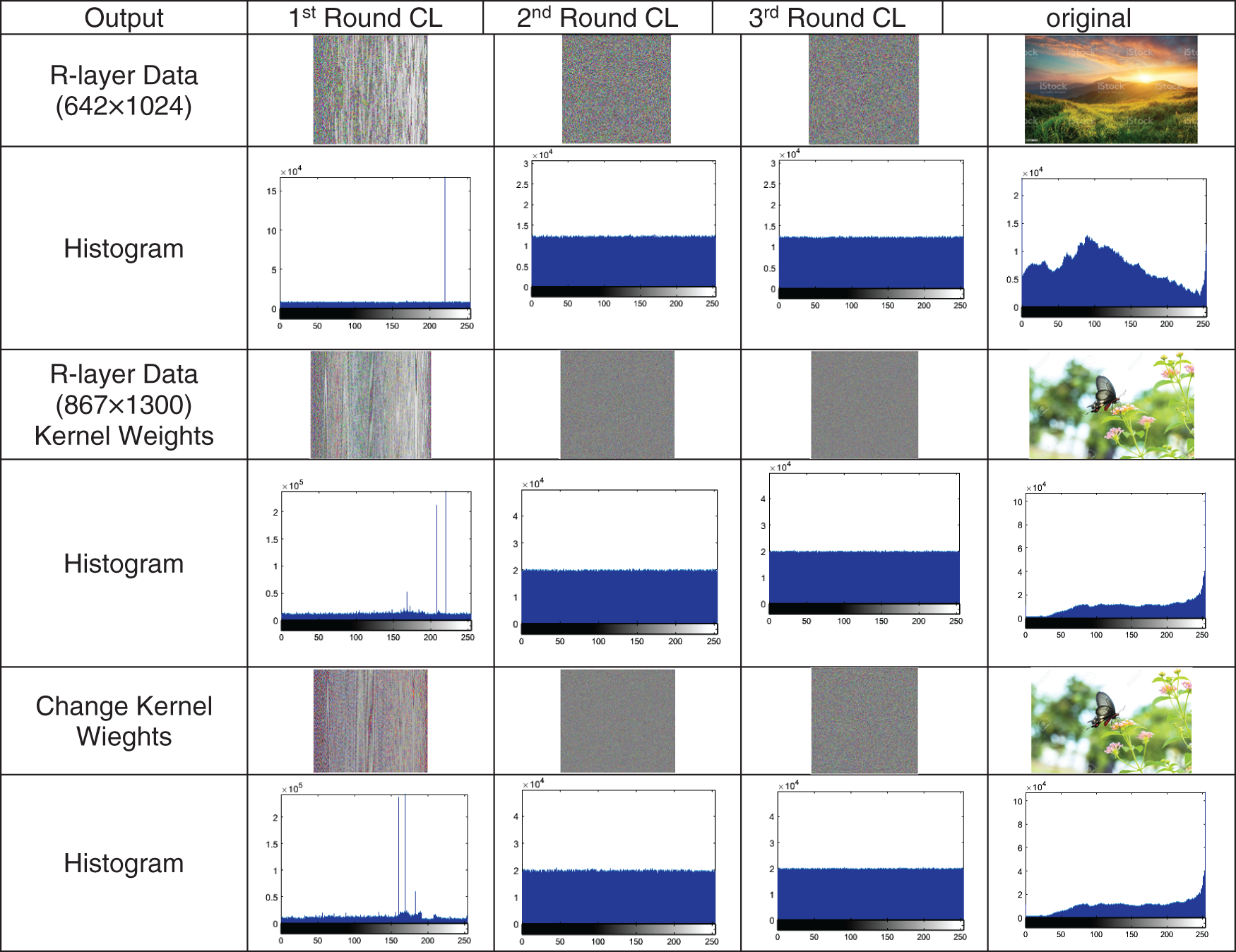
Figure 7: The effects of convolutional layer round and change kernel weights in the encrypted output

3.1 Security Analysis

Security analysis is important to judge the quality of a cryptosystem as it is determined if a cryptosystem is strong enough to resist any type of attack. The quality and strength of the proposed technique are verified based on key space, visual testing, histogram analysis, differential analysis, information entropy, and correlation coefficient analysis. The restored data is a copy of the original one.

3.2 Key Space Analysis

A key space is defined as the number of attempts an attacker must make to read confidential data. The rule says: “the larger the key space, the fewer the chances of a brute attack”. In the proposed technique, the weight values of kernel filters in convolution layers and added values combine the key space of the proposed technique and it is also the initial parameters of chaotic function and keys. A small change in these values will affect the output. A brute force attack is almost impossible and impractical due to the large key size. All other parameters of the proposed technique increase key space size. The sequence of the phased implementation of the proposed technique and its repetition are good resistance to brute force attacks. Any slight change in the value of the secret key makes a complete difference in the encryption and decryption output. Fig. 8 shows the test of the key that displays encrypted images of Barbara using the user key with a 1-bit difference. The mean absolute error between encrypted images equals 85.3508.

Figure 8: Original and encrypted images with a slight key difference

3.3 Visual Testing

The efficiency of the encryption system is excellent if only an authorized person can read the secret data. Fig. 9 shows the original image and its corresponding image. By examining the two images with the naked eye, there is no relationship between them, and no attacker can extract any information that helps in reading the hidden data.

Figure 9: Original images and their encrypted

3.4 Histogram Analysis

Using histogram (intensity function) that represents the distribution of pixel intensity values in graphic form, to test the effectiveness of the encryption technique. Fig. 10 shows the secret image, their corresponding hidden data image, and their histograms. There is no relationship between the obtained histogram of the secret image and its hidden data. The histogram of the hidden data is almost pure randomness. It is indicated that the proposed technique is truly effective.

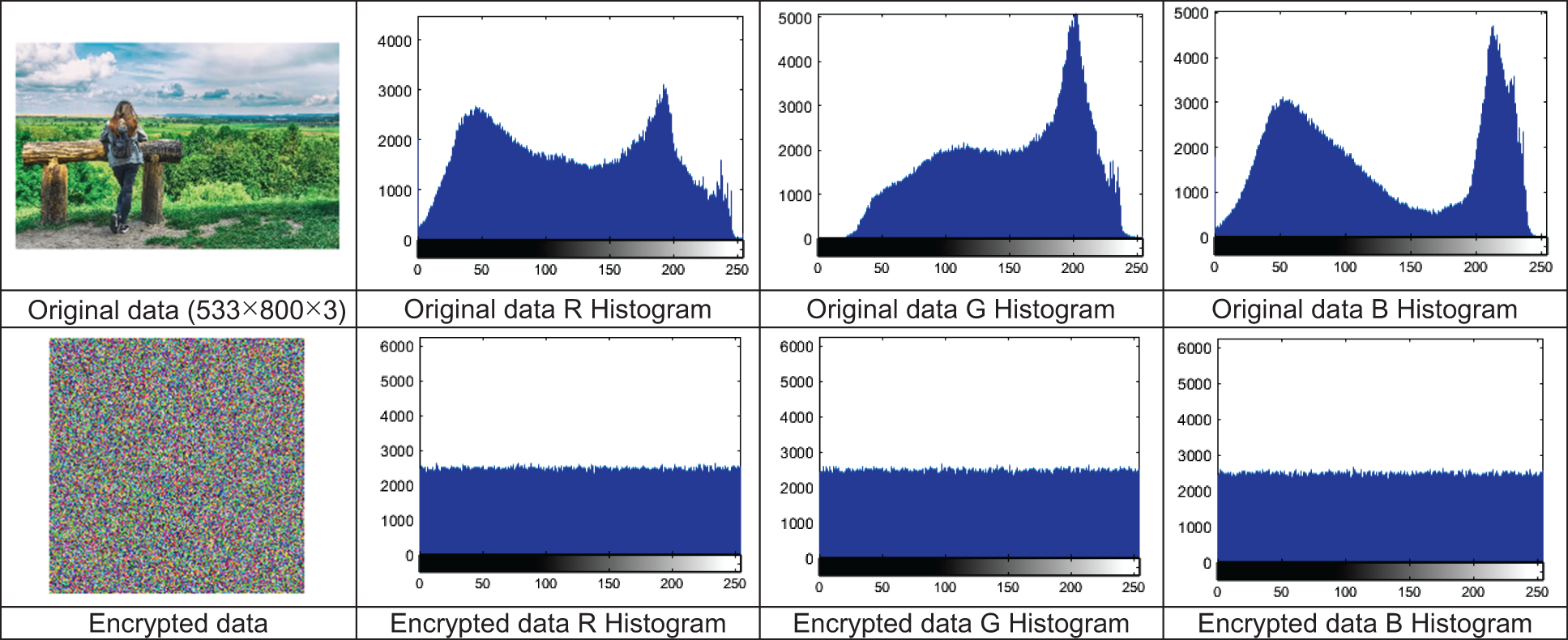
Figure 10: Original image, encrypted image and their corresponding histograms

3.5 Correlation Coefficient Analysis

There is a mutual relationship between any two contiguous pixels in an unvarying image. Scatter plots in Fig. 11 appears the horizontal, vertical, and diagonal correlation of two neighboring bytes in the cameraman image distributions. Scatter plots in Fig. 11 appear the horizontal, and diagonal correlation of two neighboring bytes in the cipher data distributions of the cameraman image.

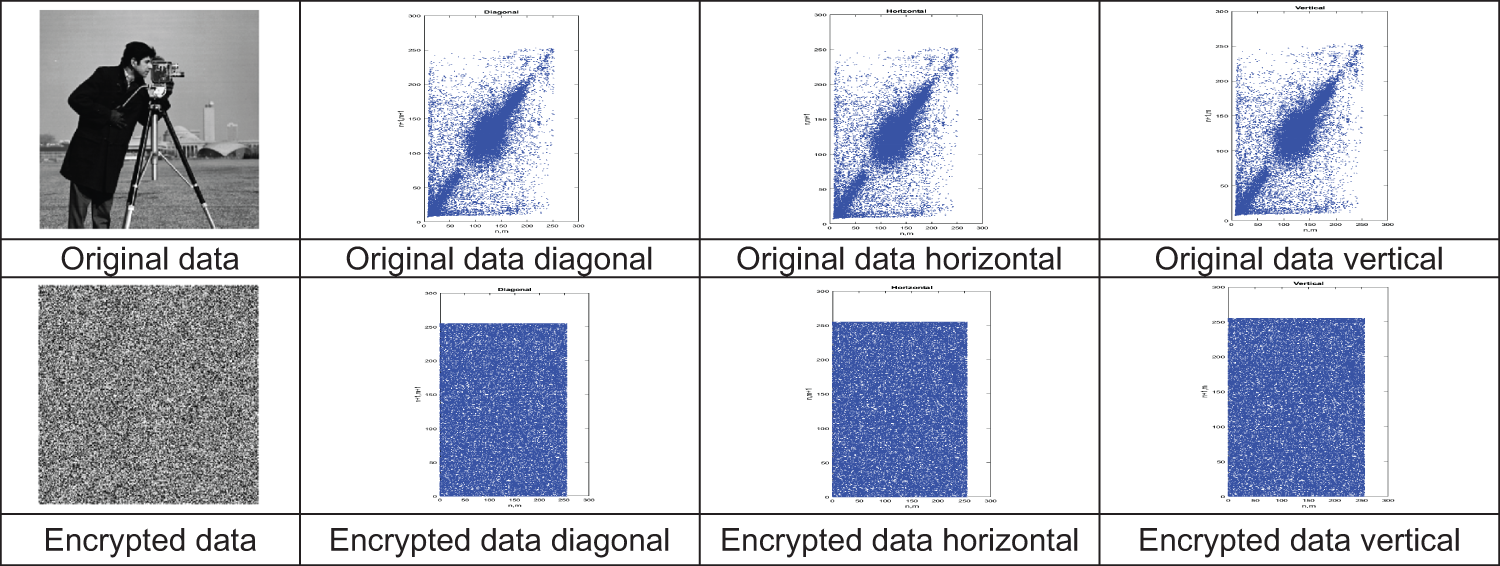
Figure 11: Scatter plots of the original image and encrypted image

The correlation coefficient (CorrCoff) is one of the most widely used statistical measures to determine the relationship between two variables. The range of the correlation coefficient is −1.0 to 1.0. If the absolute value of the correlation coefficient is one, there is a strong relationship between the two variables. If the correlation coefficient is almost zero, then there is no relationship between the two variables. The following formula defines the common correlation coefficient:

CorrCoeff=∑m∑n(Omn−O¯¯)(Emn−E¯¯)∑m∑n(Omn−O¯¯)2(Emn−E¯¯)2(1)

where O and E are original data and encrypted data. O¯¯ and E¯¯ are Average of O and E elements respectively. For a well-hidden technique, it must be that the correlation coefficient is a little between neighboring bytes in the encrypted data [29].

As a result of the obtained correlation coefficient value in the range of −0.0034 to 0.0026, the attacker cannot extract any information about the original data from the encrypted data, and the relationship of the original data with the encrypted data is almost negligible.

3.6 Information Entropy Analysis

Entropy is defined as a degree of the randomness of data. The following equation defines Information entropy (Entropy):

Entropy=−∑i=0255Hilog2(Hi)(2)

where Hi is the count of the values (that equals i). A sample of the original data, its corresponding encrypted data, and calculated entropy values for them is displayed in Fig. 12. The encrypted data is considered random data due to the entropy value for encrypted data being very close to eight [30]. So, the proposed technique can withstand entropy attacks, and the possibility of occurrence of this type of attack is negligible.

Figure 12: Sample of the original data, its corresponding encrypted and its entropy

3.7 Chi-Square Analysis

The chi-square value shows the distribution of encrypted data values that is estimated using the following equation:

chi−square=∑i=0255(Oi−Ei)2Ei(3)

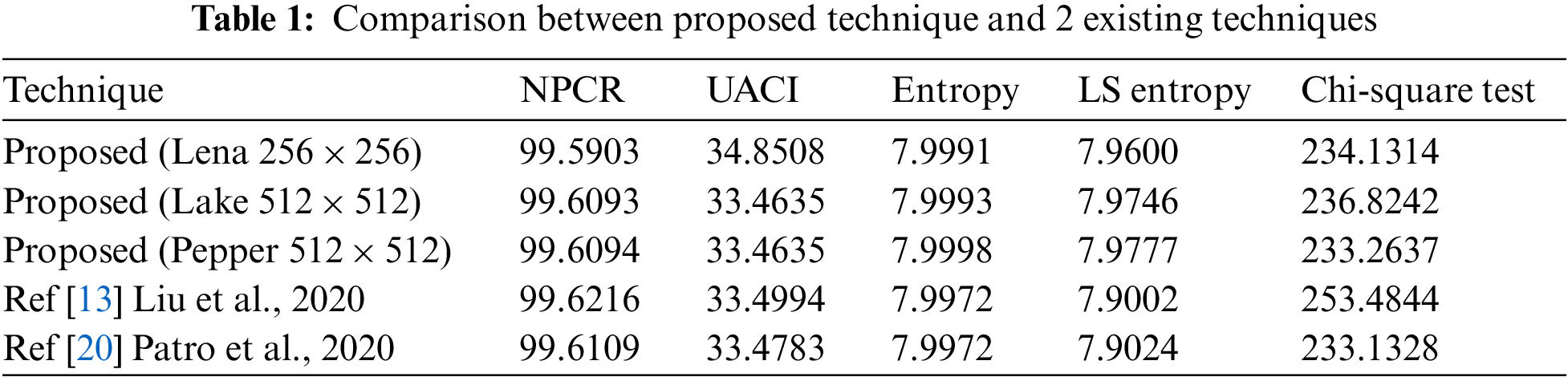
where Oi and Ei represent the observed and expected values respectively. The significance of the results in Table 1 is that the encrypted data has a uniform distribution and the proposed technique successes the chi-square test because all values of the chi-square test of the encrypted data are lower than the theoretical value (293) [31].

3.8 Differential Attack

The rule of the encryption schema states: Minor modifications in the regular data should make a big difference to the encryption technique outcome. To break the encryption scheme, The attacker slightly modifies the plain data and checks the encrypted data. There are two formulas for tracking the alternation level NPCR (rate of pixel change) and UACI (uniform average change intensity) [32]. It is known that: a high NPCR/UACI score is usually interpreted as high resistance to differential attacks.

In general, an encryption technique is good if its output is completely different when making slight modifications to the input (secret data). The ability to resist differential attacks is confirmed by NPCR/UACI tests [33,34]. The higher the NPCR/UACI score, the higher resistance against differential attacks. NPCR measures the rate of the pixel change in the encrypted data due to varying only one-pixel value of the original data and determines that:

NPCR(A,B)=1m×n(∑i,jsim(i,j))×100%(4)

where A and B are two corresponding secret and encrypted data to the same secret data, m and n are dimensions of A and B, and the following equation defines sim:

sim(i,j)={1ifA(i,j)−B(i,j)≠00ifA(i,j)−B(i,j)=0(5)

UACI is estimated as the percentage of a difference value between the encrypted data and the secret data divided by the maximum value into the secret data (max_value) as the following equation:

UACI(A,B)=1m×n{∑i.j|A(i,j)−B(i,j)max_value|}×100%(6)

Using these two scores to study the output of the proposed technique when changing a single byte in secret data and to verify the resistance of the proposed technique to differential attacks [35].

We randomly change only one value in secret data that is called ‘‘I1’’ and the result data after changing is called ‘‘I2’’. After that, these two data (I1 and I2) are encrypted, and the outputs of the proposed technique are encrypted data (A and B) respectively. Fig. 13 shows a sample of the input and encrypted output of the proposed technique. The average of NPCR and UACI are 99.6033 and 33.4120 respectively.

Figure 13: Sample of input and encrypted output with only one-pixel change

3.9 Local Shannon Entropy

Infrequently the encrypted data contains some blocks with very low entropy information values [36]. In this case, the effectiveness of the encryption technique is in doubt. As a precaution to eliminate this doubt, Shannon’s local entropy is the answer to confirm its efficacy. Shannon’s local entropy calculates the randomness of some blocks extracted from the encrypted data. The local Shannon entropy (LS) of the encrypted data block is defined as [37].

LSEntropy=∑i=1KH(Bi)K(7)

where Bi is non-overlapping blocks of cipher image and H(Bi) is the entropy information of block (Bi). For the test, we select K non-overlapping blocks with suitable sizes.

Table 1 represents the information of local Shannon entropy which shows that the results of cipher images possess high randomness. From Table 1, the values of NPCR, UACI, Entropy, and LS Entropy for the proposed method are higher than 99, 34, 7.99, and 7.99, respectively which are almost equal to or higher than the previous techniques’ values. The higher the NPCR/UACI score, the higher resistance against differential attacks. In general, the values of NPCR and UACI of the proposed technique are sufficient to resist differential attacks. The homogeneity of a random variable is measured by entropy. If the entropy value for encrypted data is very close to eight, the encrypted data is considered random data. The proposed technique can withstand entropy attacks because the achieved entropy is almost eight. The proposed technique succeeds the chi-square test because all values of the chi-square test of the encrypted data are lower than the theoretical value (293) so, the encrypted data has a uniform distribution. From these results, the proposed technique achieved the best value of all above mention metrics and the gotten output is random data.

3.10 Structural Similarity Index Analysis

SSI (Structural Similarity Index) measures the different degrees of an image’s texture after processing. The SSI value is usually in the range of 0 to 1. If two images match, the SSI value is one. The smaller the value, the greater the difference between them [38].

Using the MATLAB (SSIM) function to calculate SSI. The SSI value between the original and the encrypted image is on average 0.049. As a result of the small value of SSI, there is no correlation between them.

3.11 Plain-Text Attack Analysis

The proposed technique is tested with a full-black and full-white data image to verify its suitability and ability to resist the plain-text attack. Fig. 14 shows the results of full-black and full-white data image, and their encrypted data with their corresponding entropy values. The entropy values of encrypted data are close to 8 indicating the proposed technique is appropriate to protect from plain-text attacks.

Figure 14: Full-black, full-white data image, and their encrypted data

3.12 Comparison and Discussion with Other Encryption Techniques

The results of the proposed technique are compared with previous encryption systems based on statistical score metrics. From the results presented in Table 1, the comparison between the proposed encryption and some previous encryption systems is demonstrated that the superiority of the proposed technique due to its achieving a) good NPCR, UACI, and chi-square results, b) high local Shannon entropy and high entropy information c) close to zero correlation coefficient. d) uniform histogram. This shows that the proposed technique has robustness against statistical attack, high resistance against cryptanalysis, and without loss of information.

4  Conclusions

This paper proposes a strong multi-stage cryptographic system. The proposed technique is called Partially Deep-Learning Encryption Technique (PD-LET). The first stage is preprocessing which scrambles data by reshaping and transposing the secret data. Deep learning and zigzag transformation processes are responsible for increasing encryption efficiency. It also included random image partitioning and encryption keys for encryption quality. The results show the resistance of the PD-LET technique against different attacks based on its operations sequence. There is no indication of the original data in the encrypted data so the cryptanalysis possibilities of attacks are negligible. Furthermore, the size of encrypted data is frequently different from the original which gives additional security, and protects against discovery and revealing. Performance is evaluated by estimating entropy, plain-text attack analysis, structural similarity index, Local Shannon Entropy, Chi-Square test, Histogram, NPCR, and UACI values. There is a 100% match between the original and reconstructed data. In future work, we will be trying to decrease the encryption data size and computation cost. Data encryption systems based on full deep learning algorithms will be proposed because quantum computers can crack most encryption algorithms in the future.

Acknowledgement: The author expresses his appreciation to God almighty and to those who carry the torches of knowledge to light the way of mankind.

Funding Statement: The author received no specific funding for this study.

Conflicts of Interest: The author declares that he has no conflicts of interest to report regarding the present study.

References

 1.  W. Stallings, Cryptography and Network Security: Principles and Practice, 7th ed., Essex, England: Pearson Education, pp. 19–91, 2017. [Google Scholar]

 2.  C. Paar and J. Pelzl, Understanding Cryptography, Heidelberg, Berlin, Germany: Springer-Verlag, pp. 1–23, 2010. [Google Scholar]

 3.  J. Daemen and V. Rijmen, The Design of Rijndael: The Advanced Encryption Standard (AES), 2nd ed., Heidelberg, Berlin, Germany: Springer-Verlag, pp. 1–8, 2020. [Google Scholar]

 4.  Z. K. Obaidand and N. F. Al Saffar, “Image encryption based on elliptic curve cryptosystem,” International Journal of Electrical and Computer Engineering, vol. 11, no. 2, pp. 1293–1302, 2021. [Google Scholar]

 5.  J. S. Kraft and L. C. Washington, An Introduction to Number Theory With Cryptography, 2nd ed., New York, USA: CRC Press, pp. 209–219, 2018. [Google Scholar]

 6.  J. Katz and Y. Lindell, Introduction to Modern Cryptography, 3rd ed., New York, USA: CRC Press, pp. 167–202, 2021. [Google Scholar]

 7.  A. Qayyum, J. Ahmad, W. Boulila, S. Rubaiee, A. Arshad et al., “Chaos-based confusion and diffusion of image pixels using dynamic substitution,” IEEE Access, vol. 8, pp. 140876–140895, 2020. [Google Scholar]

 8.  A. J. Menezes, P. C. V. Oorschot and S. A. Vanstone, Handbook of Applied Cryptography, New York, USA: CRC Press, pp. 1–48, 1997. [Google Scholar]

 9.  B. Schneier, Applied Cryptography: Protocols, Algorithms and Source Code in C, New York, USA: John Wiley & Sons Inc., pp. 189–232, 1996. [Google Scholar]

10. D. R. Stinson and M. B. Paterson, Cryptography: Theory and Practice, 4th ed., New York, USA: CRC Press, pp. 415–488, 2019. [Google Scholar]

11. J. Fridrich, “Symmetric ciphers based on two-dimensional chaotic maps,” International Journal of Bifurcation and Chaos, vol. 8, no. 6, pp. 1259–1284, 1998. [Google Scholar]

12. H. Liu, Z. Zhu, H. Jiang and B. Wang, “A novel image encryption algorithm based on improved 3D chaotic cat map,” in Proc. 9th IEEE Int. Conf. for Young Computer Scientists, Hunan, China, pp. 3016–3021, 2008. [Google Scholar]

13. L. Liu, Y. Lei and D. Wang, “A fast chaotic image encryption scheme with simultaneous permutation-diffusion operation,” IEEE Access, vol. 8, pp. 27361–27374, 2020. [Google Scholar]

14. Y. M. Wazery, S. G. Haridy and A. A. Ali, “A hybrid technique based on RSA and data hiding for securing handwritten signature,” International Journal of Advanced Computer Science and Applications, vol. 12, no. 4, pp. 726–735, 2021. [Google Scholar]

15. S. Fu-Yan, L. Shu-Tang and L. Zong-Wang, “Image encryption using high-dimension chaotic system,” Chin. Phys, vol. 16, no. 12, pp. 3616–3623, 2007. [Google Scholar]

16. B. Norouzi, S. Mirzakuchaki, S. M. Seyedzadeh and M. R. Mosavi, “A simple, sensitive and secure image encryption algorithm based on hyper-chaotic system with only one round diffusion process,” Multimedia Tools Appl., vol. 71, no. 3, pp. 1469–1497, Aug. 2014. [Google Scholar]

17. H. M. Mousa, “Chaotic genetic-fuzzy encryption technique,” International Journal of Computer Network and Information Security, vol. 10, no. 4, pp. 10–19, 2018. [Google Scholar]

18. H. M. Mousa, “DNA-genetic encryption technique,” I. J. Computer Network and Information Security, vol. 8, no. 7, pp. 1–9, 2016. [Google Scholar]

19. Q. Zhang, L. Guo and X. Wei, “Image encryption using DNA addition combining with chaotic maps,” Mathematical and Computer Modelling, vol. 52, pp. 2028–2035, 2010. [Google Scholar]

20. K. A. K. Patro, B. Acharya and V. Nath, “Secure, lossless, and noise resistive image encryption using chaos, hyper-chaos, and DNA sequence operation,” IETE Technical Review, vol. 37, no. 3, pp. 223–245, May 2020. [Google Scholar]

21. N. A. Azam, “A novel fuzzy encryption technique based on multiple right translated AES gray s-boxes and phase embedding,” Security and Communication Networks, vol. 2017, pp. 1–9, 2017. [Google Scholar]

22. K. GaneshKumar and D. Arivazhagan, “New cryptography algorithm with fuzzy logic for effective data communication,” Indian Journal of Science and Technology, vol. 9, no. 48, pp. 1–6, December 2016. [Google Scholar]

23. H. M. Mousa, “Bat-genetic encryption technique,” International Journal of Intelligent Systems and Applications, vol. 11, no. 11, pp. 1–15, 2019. [Google Scholar]

24. S. Behnia, A. Akhavan, A. Akhshani and A. Samsudin, “Image encryption based on the Jacobian elliptic maps,” Journal of Systems and Software, vol. 86, no. 9, pp. 2429–2438, Sep. 2013. [Google Scholar]

25. F. Amounas and E. H. El Kinani, “Fast mapping method based on matrix approach for elliptic curve cryptography,” International Journal of Information and Network Security, vol. 1, no. 2, pp. 54–59, Jun. 2012. [Google Scholar]

26. J. K. Dawson, F. Twum, J. B. Acquah and B. K. Ayawli, An Enhanced RSA Algorithm for Data Security Using Gaussian Interpolation Formula, Durham, NC, USA: Research Square, 2022. [Online]. Available: https://www.researchsquare.com/article/rs-1326669/v1. [Google Scholar]

27. W. El-Shafai, H. A. Abd El-Hameed, A. A. M. Khalaf, N. F. Soliman, A. A. Alhussan et al., “A hybrid security framework for medical image communication,” Computers, Materials & Continua, vol. 73, no. 2, pp. 2713–2730, 2022. [Google Scholar]

28. C. Pu, “Image scrambling algorithm based on image block and zigzag transformation,” Computer Modelling & New Technologies, vol. 18, no. 12, pp. 489–493, 2014. [Google Scholar]

29. A. Ikram, M. Abdul Jalil, A. Bin Ngah, N. Iqbal, N. Kama et al., “Encryption algorithm for securing non-disclosure agreements in outsourcing offshore software maintenance,” Computers, Materials & Continua, vol. 73, no. 2, pp. 3827–3845, 2022. [Google Scholar]

30. X. Meng, J. Li, X. Di, Y. Sheng and D. Jiang, “An encryption algorithm for region of interest in medical DICOM based on one-dimensional eλ-cos-cot map,” Entropy, vol. 24, no. 7, 901, pp. 1–28, 2022. [Google Scholar]

31. S. Ma, Y. Zhang, Z. Yang, J. Hu and X. Lei, “A new plaintext-related image encryption scheme based on chaotic sequence,” IEEE Access, vol. 7, pp. 30344–30360, 2019. [Google Scholar]

32. W. Zhang, Z. Zhu and H. Yu, “A symmetric image encryption algorithm based on a coupled logistic-Bernoulli map and cellular automata diffusion strategy,” Entropy, vol. 21, no. 5, 504, pp. 1–23, 2019. [Google Scholar]

33. H. Khanzadi, M. Eshghi and S. E. Borujeni, “Image encryption using random bit sequence based on chaotic maps,” Arabian Journal for Science and Engineering, vol. 39, no. 2, pp. 1039–1047, Feb. 2014. [Google Scholar]

34. S. Somaraj and M. A. Hussain, “Performance and security analysis for image encryption using key image,” Indian Journal of Science and Technology, vol. 8, no. 35, pp. 1–4. Dec. 2015. [Google Scholar]

35. G. Hu and B. Li, “Coupling chaotic system based on unit transform and its applications in image encryption,” Signal Processing, vol. 178, pp. 1–17, 2021. [Google Scholar]

36. R. E. Boriga, A. C. Dăscălescu and A. V. Diaconu, “A new fast image encryption scheme based on 2D chaotic maps,” International Journal of Computer Science, vol. 41, no. 4, pp. 249–258, 2014. [Google Scholar]

37. Y. Wu, Y. Zhou, G. Saveriades, S. Agaian, J. P. Noonan et al., “Local shannon entropy measure with statistical tests for image randomness,” Information Sciences, vol. 222, pp. 323–342, 2013. [Google Scholar]

38. Z. Wang, A. C. Bovik, H. R. Sheikh and E. P. Simoncelli, “Image quality assessment: From error visibility to structural similarity,” IEEE Transactions on Image Processing, vol. 13, no. 4, pp. 600–612, 2004. [Google Scholar]