Intelligent Systems and Photovoltaic Cells Empowered Topologically by Sudoku Networks

1  Introduction

Sudoku, initially named number place, is a famous game that can be found in many mobile applications, magazines and newspapers. Analysts have been particularly enthused about seeing the number of conceivable sudoku puzzles, which ended up being around 6.671 × 1021 by Felgenhauer and Jarvis by composing a PC program [1]. The field of graph theory is completely developing and expecting an excellent part in the subject of cheminformatics which is the blend of chemistry, mathematics, and information technology that concentrates on the assorted substance arrangement and their physicochemical properties. Specifically, Graph theory is utilized in a part of numerical chemistry which is known as compound graph theory [2]. Settling the sudoku puzzle should be visible as a case of an organized result forecast issue, where the riddle task is the classifier input and the riddle arrangement is addressed by the result marks to be anticipated [3]. Sudoku network is used in many fields like interconnection networks of intelligent systems, PV cells, puzzle games, multiprocessors and chemical structures, etc.

Solar energy is the most well-known and generally utilized environmentally friendly power asset because of its overflow and availability consistently. Solar energy is likewise a spotless type of energy and requires negligible upkeep contrasted with other energy assets. Despite the benefits, numerous challenges limit the successful utilization of solar energy. For instance, the generally low effectiveness of solar PV expands the expense of PV power age per kW, and the PV power age altogether depends on temperature and illumination. Managing the inbuilt obstruction of a PV module is a difficult task. This will become mind-boggling when the PV exhibit gets various degrees of light. Unique levels of illumination happen in light of mists development, shadows of trees and structures, dust particles, also, droppings. The event of non-uniform illumination is known as halfway overshadowing. During the concealing circumstances, the concealed PV cells create less current. Since a PV module is made by several series cells in association, consequently, the concealed PV cells are constrained to convey the same current as different cells can produce a high current. During this condition, the concealed cells act as a heap and empty power out of the non-concealed cells. These outcomes in an expansion in temperature inside the cells and cause problem areas, which obliteration the PV modules.

The issues of problem areas can be overwhelmed by utilizing sidestep diodes. Nonetheless, these detour diodes produce various tops over a P-V bend, in this manner diminishes the power age. Consequently, the variables introduced previously make a hole between the introduced energy limit and the real energy age. To overcome the impacts of halfway shade and to upgrade how much power age, scientists have zeroed in on creating the greatest power extraction strategies [4]. So, the present study finds the gap in terms of enhancing the topology of PV cells for reducing the power losses and high conversion of solar energy into usable power energy [5]. Fig. 1 shows the sudoku network with 2 × 2 vertices used in different games, intelligent systems, photovoltaic cells and chemical structures, etc. Fig. 2 shows the sudoku network with 3 × 3 vertices used in different games, intelligent systems, photovoltaic cells and chemical structures, etc.

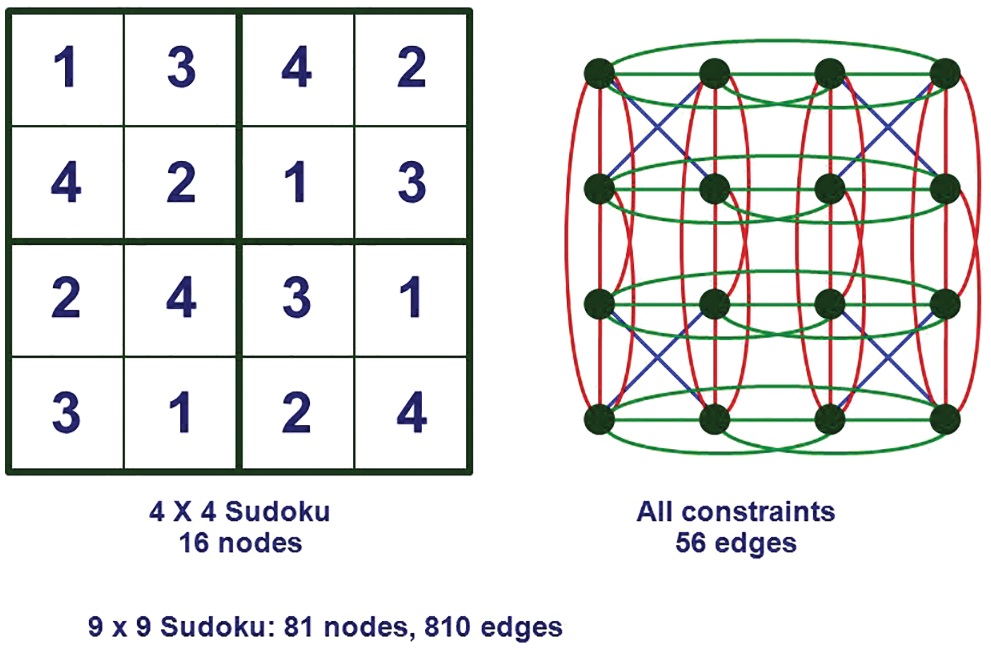
Figure 1: Puzzle game where r is 2 × 2

Figure 2: Puzzle game where r is 3 × 3

In 2021, Gutman define the chance of sombor indices. Another vertex degree-based invariant graph named sombor index is used to get the sharp lower and upper constraints of the related network and the properties of the network showing up at the cutoff points. There are two varieties of KBSO indices, the first is the KBSO index and the second is its reduced variation [6]. A KBSO Index is a topological index that is a number related to a network graph that gets the equilibrium of the network structure and gives a consistent language to predict the characteristics of the network [7]. In 2021, V. R Kulli introduced some topological degree-based indices following Gutman’s sombor indices. These indices are called dharwad indices. It has several unique structures like lessened dharwad, diminished dharwad astounding, and δ-dharwad index which are used to handle the geography of sweet-smelling compounds [8].

In 2022 V. R Kulli introduced new topological invariants called CQIs which have two forms. Chemical Graph Theory is a part of mathematical chemistry that critically affects the improvement of the chemical sciences. The review presents the CQI of a sub-atomic graph. This paper chooses the CQI of a few standard classes of graphs. The study additionally registers the CQI of certain significant nanostar dendrimers [9]. In 2021 V. R Kulli introduced the ISO index. In Chemical Graph Theory, a few degree-based topological indices were presented and examined [10].

As another arising science is made with the help of computer science, mathematics, and chemistry called cheminformatics, whose basic segments solidify Quantitative structure-development relationship (QSAR) and Quantitative structure-property associations (QSPR) and the sections can add to the appraisal of the physicochemical characteristics of fabricated mixes. QSAR is a showing gadget used to handle the geography of networks or structure of blends and to show the user and best performer networks or structures. QSPR is similarly a showing gadget that relates the properties of network structures with the help of mathematical circumstances or verbalizations. It similarly gives the quantitative association between the properties of networks or compound structures. Marks of geography as numeric characteristics can be portrayed with the help of a graph because of invariance. It is done because of the automorphism property of the graph. In the fields of computer science and chemistry, there are a lot of usages of graph theory [11,12].

A topological index is planned by transforming a network structure into a number. Originally, the aim was to introduce new computer architectures and networks that profit by both efficiencies and advance with the assistance of topological indices in context with puzzle games and chemical structures like silicon and iodine compounds. In this load of cases, this study can compute boundaries called Topological invariants (TIs) that mathematically depicted the connectedness designs (structure) between the hubs or entertainers in a network. So this study can construct a brain shocking network of general sets of laws partner laws (hubs) that direct typical organic subjects for instance. QSAR and QSPR are providing the foundation for these models. A final remark is that the utilization of the measurement in the network plane facilitates a quantitative evaluation of various geography safeguarding mapping algorithms [13,14].

This paper first introduces the problem statement with sudoku networks, KBSO indices, CQIs, ISOs and dharwad indices, secondly reviews the literature, thirdly discusses objectives, significance, research gap, and method in the research methodology section, the fourth section analyzes data, and the last section write results and conclude the research. The study has implications in the fields of computer science, physics, electronics, chemistry, mathematics, and bioinformatics for modeling purposes of networks of the PV system, intelligent systems, puzzle games and chemical compounds [15]. KBSO, CQIs, ISOs and dharwad invariants with their reduced forms allow us to accumulate information about algebraic structures and mathematically predict hidden properties of various structures such as Sudoku networks [16–18].

2  Literature Review

The study addresses the issue of learning a visual of the sudoku solver from models. We consider the solver to be an occasion of Markov Network (MN) based organized yield classifier. As of late proposed expansion of the Maximum Margin Markov Network (M3N) algorithm can become familiar with the direct MN classifier with an inconsistent area structure utilizing commented on and to some extent clarified preparing models. In this postulation, the study proposes to coordinate the MN classifier with neural networks. We tell the best way to utilize the M3N algorithm to get familiar with the boundaries of the MN classifier at the same time with a neural network to remove the highlights of the classifier. We show tentatively that the visual Sudoku solver advanced by the proposed technique beats all baselines, accomplishing a test exactness of 97% [19].

This paper investigates how to change the pursuit-based thinking process utilized by such specialists to create all the more effectively human-logical arrangements, utilizing the space of Sudoku puzzles as our proving ground. The study models the apparent human mental exertion of utilizing different recognizable Sudoku addressing methods. In light of that, we tell the best way to find a clarification reasonable to human players of changing master levels and assess the calculation exactly on many riddles of various trouble [20].

The field of graph theory is completely developing and expecting a remarkable part in the subject of cheminformatics which is the mix of chemistry, mathematics, and information technology that studies the different synthetic arrangement and their physicochemical properties. In specific, Graph theory is utilized in a part of numerical chemistry which is known as synthetic graph theory. Compound graph theory gives a phase to focus on the physicochemical properties of the sub-atomic graph with the help of topological indices (TIs). TIs are the mathematical numbers that are related to different synthetic designs of sub-atomic graphs and expect the structural, toxicological, biological, and physicochemical properties of the synthetic mixtures existing in the sub-atomic graphs [21].

Probabilistic graphical models (PGMs) are devices for settling complex probabilistic connections. Notwithstanding, less-than-ideal PGM structures are utilized practically speaking. This paper presents three commitments to PGM writing. The first is a correlation between factor graphs and cluster graphs on graph shading issues like sudokus - demonstrating a critical benefit for leaning toward cluster graphs. The second is the use of cluster graphs for a functional issue in cartography: land cover characterization supporting. The third is a PGMs plan for limitation fulfillment issues and a calculation called cleanse and converge to tackle such issues excessively complex for customary PGMs [22].

Another AdDoKu strategy for PV module course of action for absolute cross-tied (TCT) interconnection design has been presented in this paper. This game plan is pointed toward limiting the PV exhibit (PVA) misfortunes brought about by incomplete concealing circumstances and, subsequently, building the influence yield. Simulations are completed on a broad scale to approve the improvement in execution when contrasted with the TCT association. Examinations are likewise made between the recently proposed AdDoKu design and the sudoku arrangement. The information acquired during this correlation place the proposed conspire at standard with the sudoku design regarding functional qualities. The actual area of modules is modified without modifying any electrical associations. The information acquired from the simulation tests shows that the AdDoKu course of action design decreases the number of nearby tops in the P-V qualities and, subsequently, makes the worldwide most extreme power point (GMPP) following algorithm a lot less complex and more exact [23].

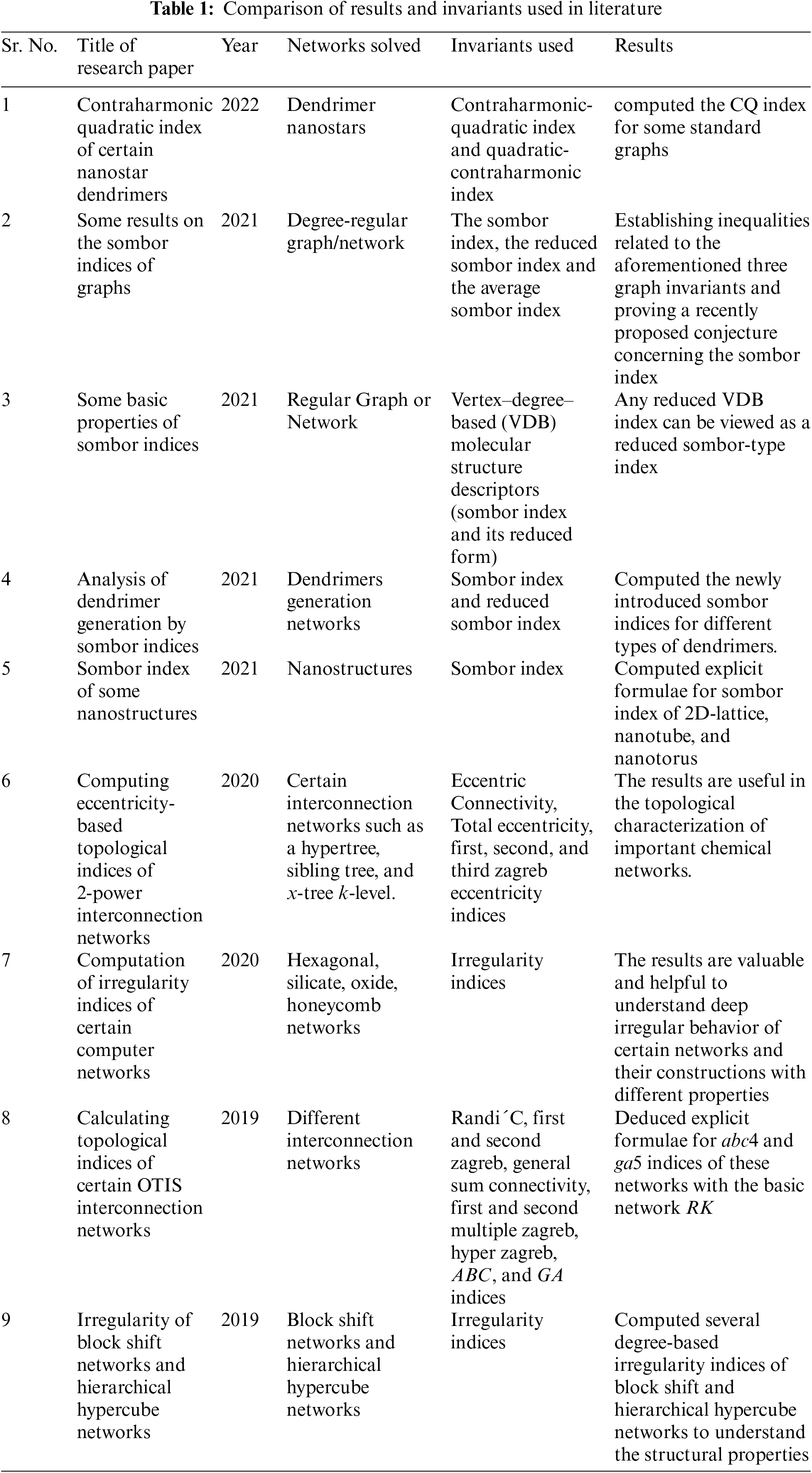
This article centers on the reworking of the design of the photovoltaic (PV) cluster under various concealing circumstances. It means breaking down the jumble power misfortunes (MPLs) because of unpredictable brightening over PV exhibit (PVA). The effect of halfway irradiance influences the electrical power as well as the goals of different tops in the P-V and I-V bends. The definition of the best PVA design (PVAC) to accomplish the greatest result considerably under incomplete concealing circumstances is the game-changer for the geographies considered. To help the greatest power extraction, another Sudoku PVAC is planned like hyper Sudoku (HS). This new construction is contrasted and the all-around existing PVACs, for example, span connect, honeycomb, series-equal, complete cross-tied, and Sudoku in the impact of impressive instances of shadowing. MatLab/Simulink is utilized for the planning, and PC-based modeling of every one of these PVACs is viewed in this review [24]. The paper proposed a warm and numerical model which can be utilized for deciding the PV board temperature. The paper presents an examination between traditional designs and the Sudoku strategy. The fact that the sudoku topology performs better makes it shown for different layouts [25]. We have shown a comparison of results and invariants in Tab. 1.

From the above literature, it is noticed that the sudoku networks are used in PV cells, intelligent systems, memory interconnection networks, processor interconnection networks, power generation interconnection networks, integrated circuits and some chemical compounds also. There is also a need for improvements in all these systems. This study solved the topology of sudoku networks used in these systems and try to find lower bounds, upper bounds and irregularities in the networks.

3  Research Methodology

The methodology is based on quantitative inquiry, detailed as follows.

3.1 Objectives

The main objective of this study is to investigate the topological invariants of the sudoku networks. The study explains the KBSO indices, dharwad indices their reduced forms, and ISOs. The work deduced some results which are used in the modeling, and scalability of the sudoku networks used in interconnection networks, power interconnection networks, PV cells, puzzle games, and chemical structures [26].

3.2 Significance

It is also discovering new and significant solutions or formulas for modeling the sudoku networks because no adequate solution has been found till now due to its incremental and fast nature. It constructs new network architectures with different properties by using deduced results. The applications of these produced results are in the fields of computer networks, interconnection networks of processors, power interconnection networks, chemical structures, PV cells, puzzle games, artificial intelligence-based systems, parallel computing, biological structures, etc. [27].

3.3 Hypothesis

The analysis provides the strength to develop error-free, failure-free, and best-performer computer networks, interconnection networks of processors, power interconnection networks, PV cells, and intelligent systems, etc.

3.4 Method

This systematic study will take an existing sudoku network, associate it with a graph, perform mapping over it and solve the topology of the graph with the help of KBSO indices, dharwad indices, CQIs, their reduced forms and ISO indices. The concerning results in the form of formulas will compare with existing results. These deduced results will apply to many other networks in the fields of computer networks, processor interconnection networks, power interconnection networks, parallel computing, PV cells, intelligent systems and puzzle games afterward [28]. The methodology diagram also shows the step-by-step flow of the study.

Fig. 3 represents the road map for the precedence of the study for mapping, linking, solving, comparing and modeling the sudoku network by deduced results.

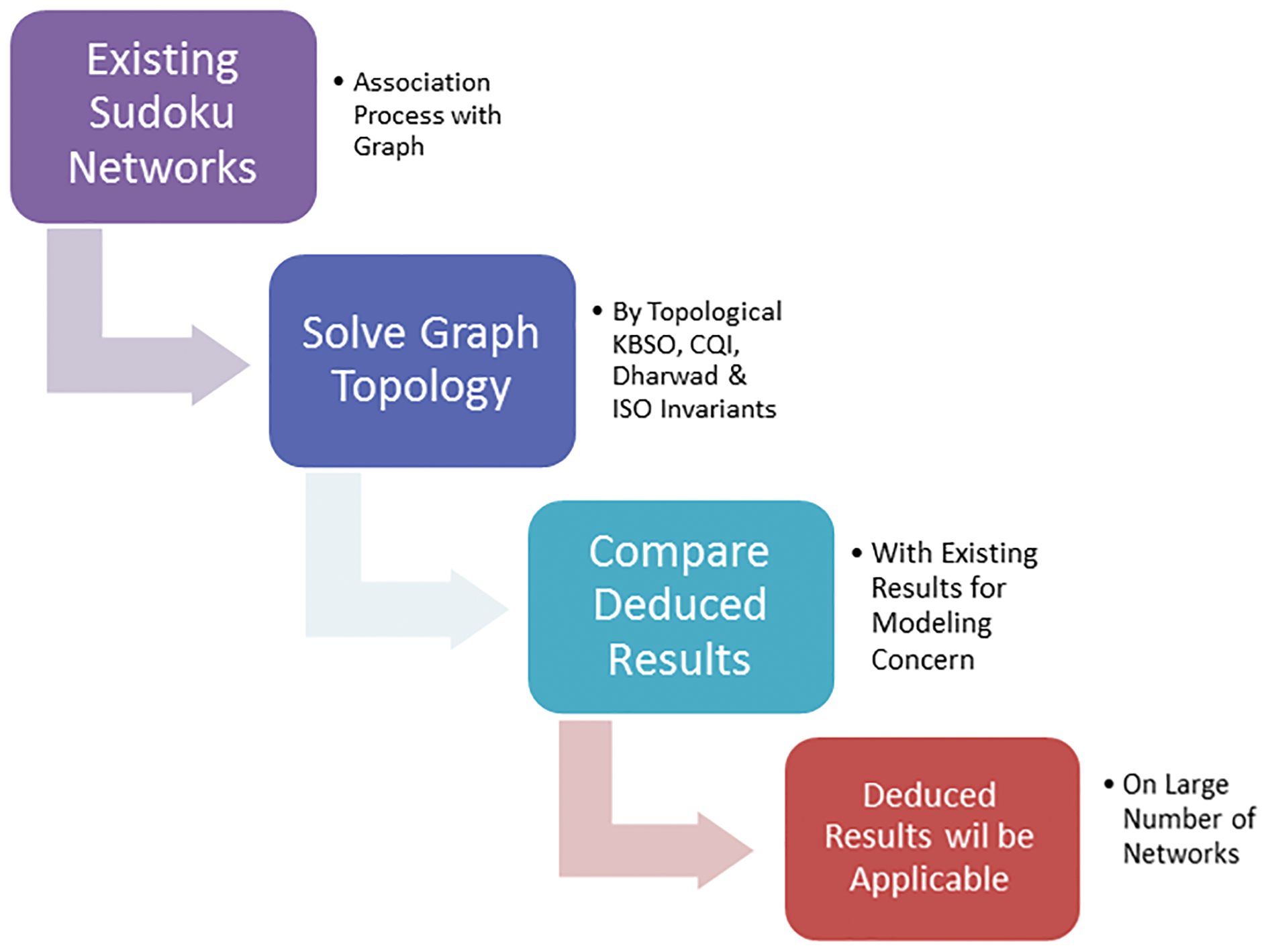
Figure 3: Methodology flow diagram

4  Experimental Results

Sudoku graphs Srxr are the graphs of the bipartite graphs. Sudoku is the graphs typically portrayed by the set number of repetitions of fully connected graphs. The number of edges of the sudoku graph is r(34r−6) and the edge segment relies upon the level of end vertices of edges. Edges are divided by something similar and various levels of vertices hold edges. KBSO indices have two variants, the KBSO index and its reduced version.

KBSO(G)=∑uedu2+dϱ2(1)

Eq. (1) shows the KBSO index which will be used for the solution of the sudoku computer network mentioned in Fig. 4. KBSO is a vertex-degree-based index used to find the upper and lower bounds at boundaries for solving the network.

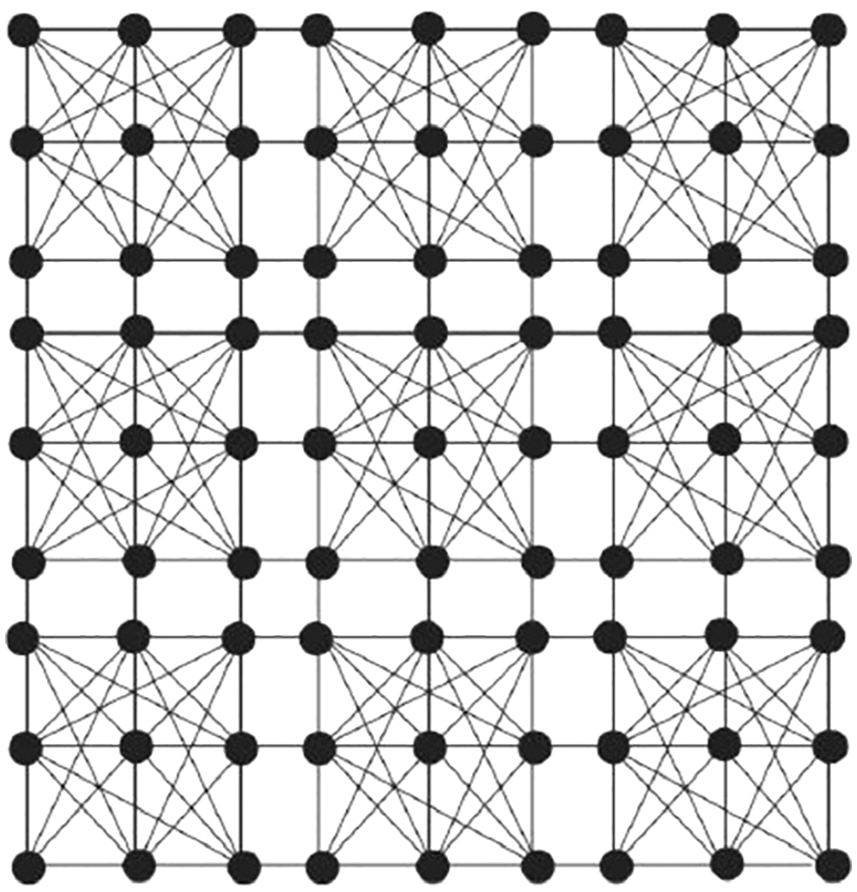
Figure 4: Sudoku network (Srxr)

KBSOrϱd_(G)=∑ue(du−1)2+(dϱ−1)2(2)

Eq. (2) shows the KBSO reduced index which will be used for the solution of the sudoku computer network mentioned in Fig. 4.

CQI(G)=∑uv∈E(G)2(dG(u)2+dG(v)2)dG(u)+dG(v)(3)

QCI(G)=∑uv∈E(G)(dG(u)+dG(v))2(dG(u)2+dG(v)2)(4)

Eqs. (3) and (4) show the CQI and QCI which will be used for the solution of the sudoku computer network mentioned in Fig. 4.

D(G)=∑uedu3+dv3(5)

RD(G)=∑ue(du−1)3+(dv−1)3(6)

These Eqs. (5) and (6) represent new vertex-degree based invariants called dharwad index and its reduced form. It is used for the solution of the sudoku network for the sake of improvements in existing networks and the development of new architectures.

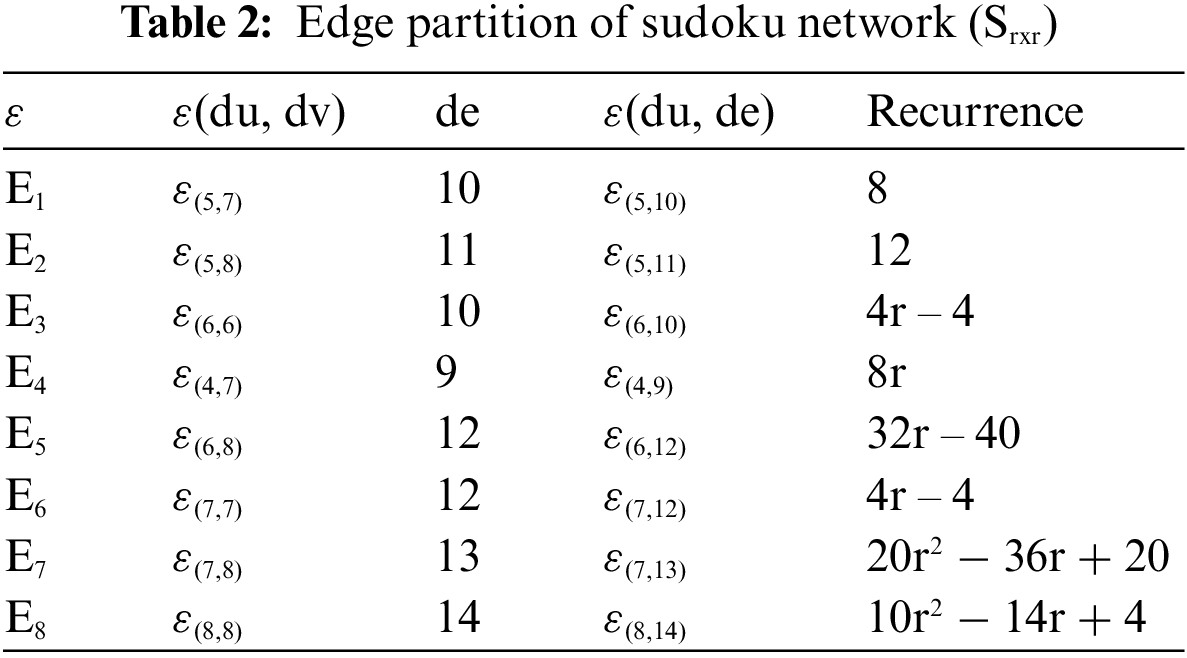
Table 2 describes the edge partitions of graph Srxr of the sudoku network graph given in Fig. 4 with frequencies.

4.1 Main Results of Modern Topological Invariants

Fig. 4 shows the sudoku network (Srxr) with distinct edges generalizing the network or graph.

4.1.1 Sudoku Network (Srxr)

If E (Srxr) represents the edge set. Fig. 4 shows that there are distinct kinds of edges present in the graph of (Srxr). Table 2, explains in detail the edges partition.

4.1.2 Theorem 1

Let Srxr be a graph of the sudoku network used in PV cells, intelligent systems, sudoku puzzle games and different chemical structures also, then, KBSO and KBSOred indices are

KBSO(Srxr)=405+12146+234(4r−4)+897r+65(32r−40)+193(4r−4)+218(20r2−36r+20)+265(10r2−14r+4)(7)

KBSOred(Srxr)=897+2429+106(4r−4)+873r+146(32r−40)+157(4r−4)+65(20r2−36r+20)+218(10r2−14r+4)(8)

Eqs. (7) and (8) represent the proven results of the graph of the sudoku network used in intelligent systems, PV cells, the sudoku puzzle games, and different electronic and chemical structures also mentioned in Fig. 4.

4.1.3 Investigation of Sudoku Graph by KBSO Indices

Proof:

KBSO(G)=∑uedu2+dϱ2

KBSO(Srxr)=52+102(8)+52+112(12)+62+102(4r−4)−42+92(8r)+62+122(32r−40)+72+122(4r−4)+72+132(20r2−36r+20)−82+142(10r2−14r+4)

KBSO(Srxr)=405+12146+234(4r−4)+897r+65(32r−40)+193(4r−4)+218(20r2−36r+20)+265(10r2−14r+4)

KBSOrϱd_(G)=∑ue(du−1)2+(dϱ−1)2

KBSOred(Srxr)=(5−1)2+(10−1)2(8)+(5−1)2+(11−1)2(12)+(6−1)2+(10−1)2(4r−4)+(4−1)2+(9−1)2(8r)+(6−1)2+(12−1)2(32r−40)+(7−1)2+(12−1)2(4r−4)+4(7−1)2+(13−1)2(20r2−36r+20)+(8−1)2+(14−1)2(10r2−14r+4)

KBSOred(Srxr)=897+2429+106(4r−4)+873r+146(32r−40)+157(4r−4)+65(20r2−36r+20)+218(10r2−14r+4)

Fig. 5 shows the results of KBSO and its reduced form in green and blue respectively. The above figure represents the sharp upper and lower bounds of the solved Srxr network.

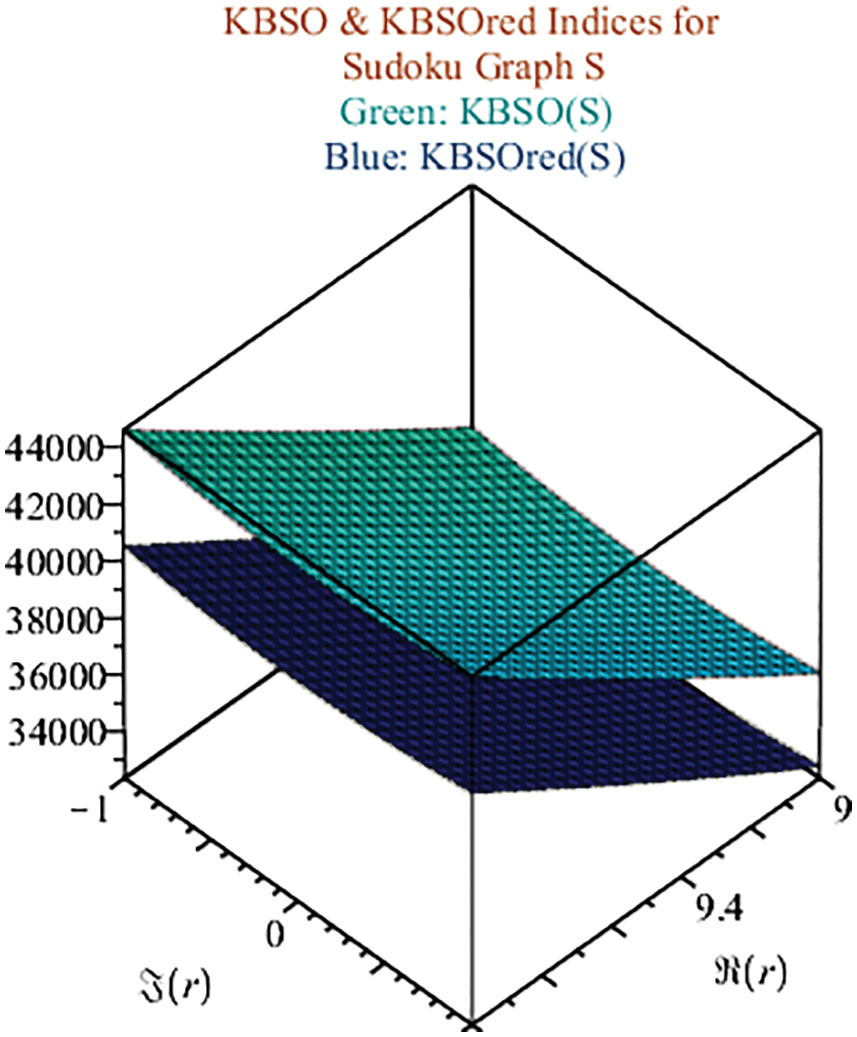
Figure 5: Results for KBSO and KBSOred

4.1.4 Theorem 2

Let G be a graph of the sudoku network, then, CQI and QCI indices are

CQI(Srxr)=4337+1213178−6r−4+811130r−572(32r−4)+115226(20r2−36r+20)+10r2(9)

QCI(Srxr)=483737+7889178−6r−4+4465130r+7102(32r−4)+15226226(20r2−36r+20)+10r2(10)

Eqs. (9) and (10) represent the proven results of the graph of the sudoku structure mentioned in Fig. 4.

4.1.5 Investigation of Sudoku Graph by CQI Indices

CQI(G)=∑uv∈E(G)2(dG(u)2+dG(v)2)dG(u)+dG(v)

CQI(Srxr)=2((5)2+(7)2)5+7(8)+2((5)2+(8)2)5+8(12)+2((6)2+(6)2)6+6(4r−4)+2((4)2+(7)2)4+7(8r)+2((6)2+(8)2)6+8(32r−40)+2((7)2+(7)2)7+7(4r−4)+2((7)2+(8)2)7+8(20r2−36r+20)+2((8)2+(8)2)8+8(10r2−14r+4)

CQI(Srxr)=4337+1213178−6r−4+811130r−572(32r−4)+115226(20r2−36r+20)+10r2

QCI(G)=∑uv∈E(G)(dG(u)+dG(v))2(dG(u)2+dG(v)2)

QCI(Srxr)=5+72((5)2+(7)2)(8)+5+82((5)2+(8)2)(12)+6+62((6)2+(6)2)(4r−4)+4+72((4)2+(7)2)(8r)+6+82((6)2+(8)2)(32r−40)+7+72((7)2+(7)2)(4r−4)+7+82((7)2+(8)2)(20r2−36r+20)+8+82((8)2+(8)2)(10r2−14r+4)

QCI(Srxr)=483737+7889178−6r−4+4465130r+7102(32r−4)+15226226(20r2−36r+20)+10r2.

Fig. 6 shows the results of CQI and QCI in green and blue respectively. The above figure represents the sharp upper and lower bounds of the solved Srxr network.

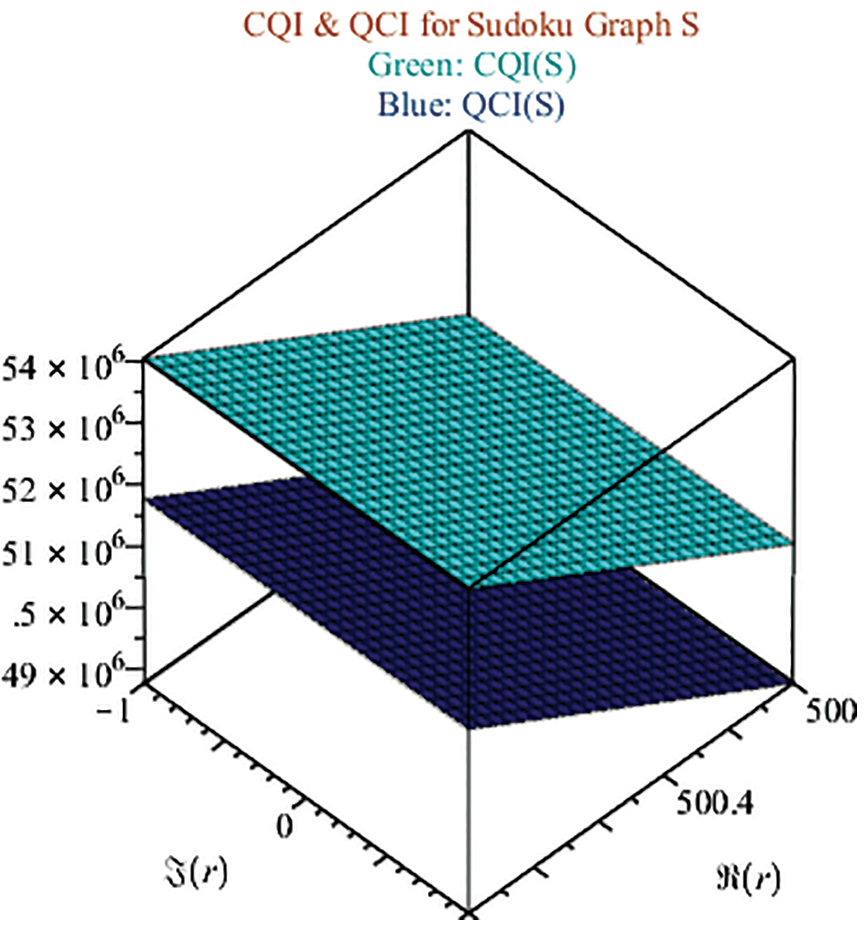
Figure 6: Results for CQI and QCI

4.1.6 Theorem 3

Let Srxr be a graph of the Sudoku network used in PV cells, intelligent systems, sudoku puzzle games and different chemical structures also, then, dharwad and dharwadred indices are

D(Srxr)=13213+123(4r−4)+8407r−2182(32r−40)+714(4r−4)+395(20r2−36r+20)+320r2−448r+128(11)

RD(Srxr)=1670+12407+510(4r−4)+723r+613(32r−40)+1213(4r−4)+559(20r2−36r+20)+714(10r2−14r+4)(12)

Eqs. (11) and (12) represent the proven results of the graph of the sudoku network used in intelligent systems, PV cells, sudoku puzzle games, and different electronic and chemical structures also mentioned in Fig. 4.

4.1.7 Investigation of Sudoku Graph by Dharwad Indices

Proof:

D(G)=∑uedu3+dv3

D(Srxr)=53+73(8)+53+83(12)+63+63(4r−4)−43+73(8r)+63+83(32r−40)+73+73(4r−4)+73+83(20r2−36r+20)−83+83(10r2−14r+4)

D(Srxr)=13213+123(4r−4)+8407r−2182(32r−40)+714(4r−4)+395(20r2−36r+20)+320r2−448r+128

RD(G)=∑ue(du−1)3+(dv−1)3

RD(Srxr)=(5−1)3+(7−1)3(8)+(5−1)3+(8−1)3(12)+(6−1)3+(6−1)3(4r−4)+(4−1)3+(7−1)3(8r)+(6−1)3+(8−1)3(32r−40)+(7−1)3+(7−1)3(4r−4)+(7−1)3+(8−1)3(20r2−36r+20)+(8−1)3+(8−1)3(10r2−14r+4)

RD(Srxr)1670+12407+510(4r−4)+723r+613(32r−40)+1213(4r−4)+559(20r2−36r+20)+714(10r2−14r+4)

Fig. 7 shows the results of dharwad and dharwadrxr in green and blue respectively. The above figure represents the sharp upper and lower bounds of the solved Srxr network.

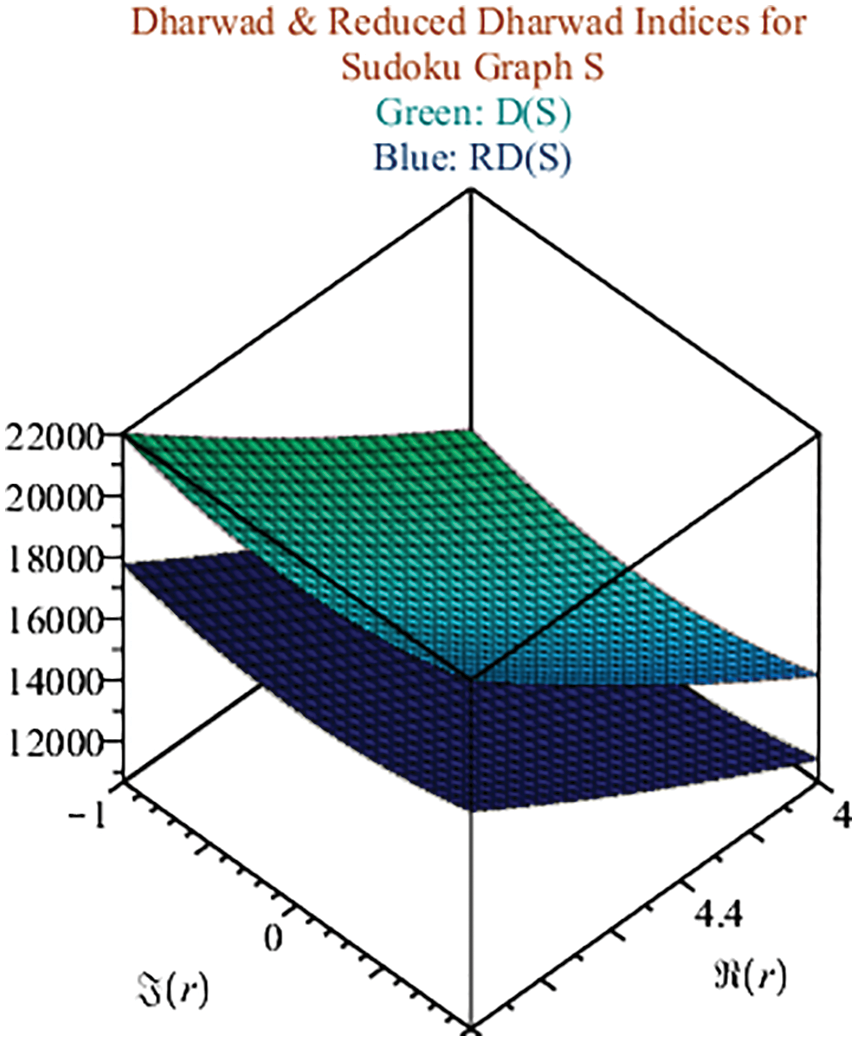
Figure 7: Results for dharwad and dharwadred indices

4.2 Main Results for Irregularity Index

4.2.1 Theorem 4

Let Srxr be a graph of the sudoku network used in intelligent systems, PV cells, sudoku puzzle games and different chemical structures also, then, the ISO index is

ISO(Srxr)=405+486+32r−32+865r+63(32r−40)+95(4r−4)+230(20r2−36r+20)+233(10r2−14r+4)(13)

Eq. (13) represents the proven result of the graph of the sudoku network used in sudoku puzzle games and different chemical structures also mentioned in Fig. 4.

4.2.2 Investigation of Sudoku Graph by Irregularity Sombor Index

Proof

ISO(G)=∑ue|du2−dv2|

ISO(Srxr)=|52−102|(8)+|52−112|(12)+|62−102|(4r−4)+|42−92|(8r)+|62−122|(32r−40)+|72−122|(4r−4)+|72−132|(20r2−36r+20)+|82−142|(10r2−14r+4)

ISO(Srxr)=405+486+32r−32+865r+63(32r−40)+95(4r−4)+230(20r2−36r+20)+233(10r2−14r+4)

Fig. 8 shows the result of the ISO index and represents the sharp upper and lower bounds of the solved Srxr network.

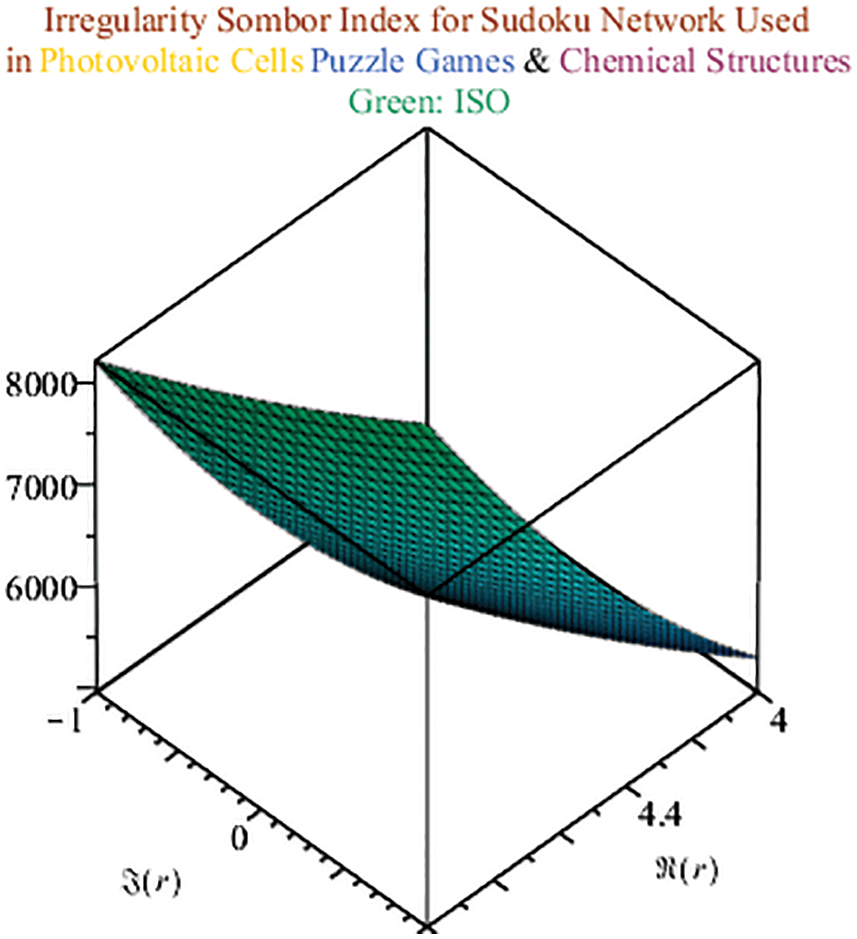
Figure 8: ISO index for Sudoku network

Table 3 describes the comparison of topological invariants for the Sudoku graph for investigation of different properties of the Sudoku network like sharp lower bound, sharp upper bound, performance efficiency, effectiveness, scalability, boiling, melting points, chemical reactivity and connectivity, etc.

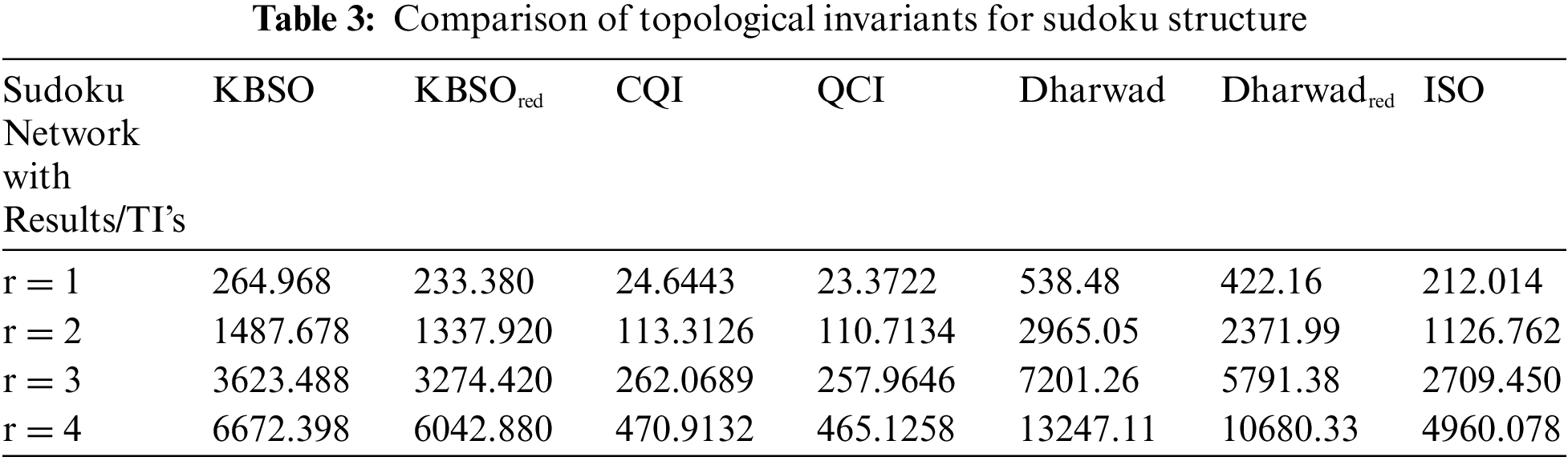
Fig. 9 shows the comparison of different topological invariants KBSO in red, KBSOred in navy blue, CQI in leaf green, QCI in cyan, Dharwad in purple and dharwadred in blue colors. The above figure represents the sharp upper and lower bounds of the solved Srxr network with different invariants.

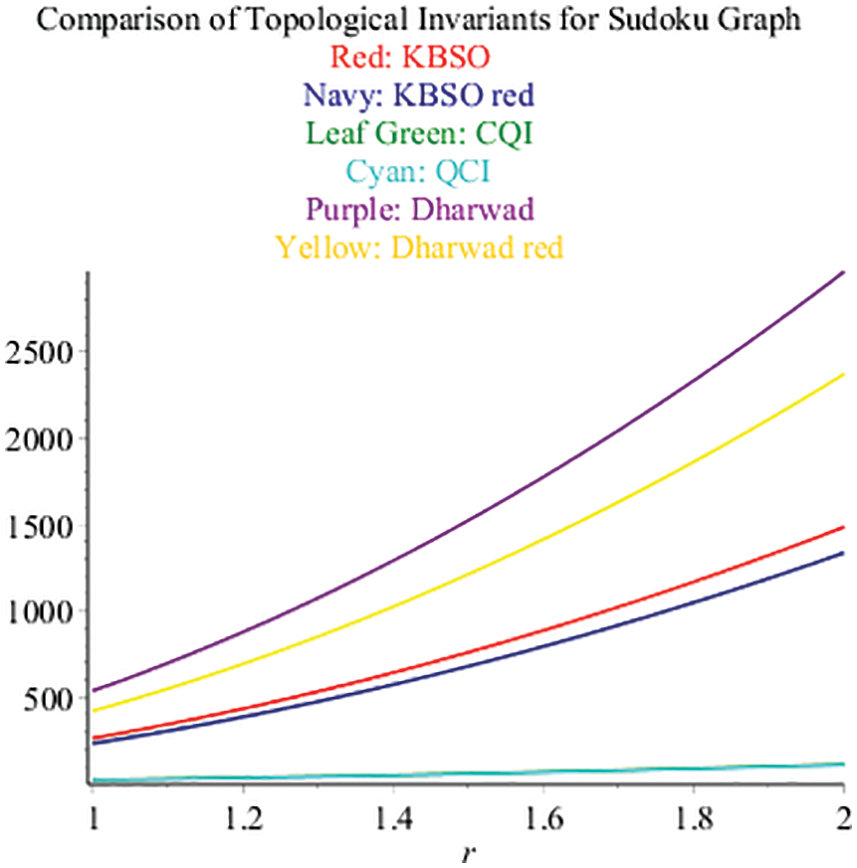
Figure 9: Comparison of topological invariants for sudoku network

5  Conclusions

Topological indices have lots of purposes and executions in many fields of computer science, electronics, chemistry, informatics, math, and some more. The best conceivable degree of enormous application is in the non-accurate QSPR and QSAR. TIs are connected with the plan of networks, parallel processors interconnections, intelligent systems, PV cell arrangements and synthesis of chemical compounds. The present article looks at the KBSO invariants, CQIs, ISO and dharwad invariants which are recently presented and have excellent prediction characteristics for different varieties of sudoku graphs or networks. The graphical results of KBSO indices for referenced sudoku graphs of the network are with exact parameters values for finding lower and upper bounds. In parallel dharwad indices and CQIs are also newly presented having the quality of prediction for different physical properties of the sudoku network under discussion. The graphical results of dharwad indices and CQIs for the Sudoku network are also with exact parametric values for modeling purpose. The study also presented graphical result of ISO invariant which is used to find irregularities from the sudoku network. These solved results will be used for the demonstration and modeling of the sudoku network used in intelligent systems, PV cells and puzzle games, for their scalability, make them more intelligent, minimizing power losses, maximizing energy conversion into usable power in the field of computer science, physics, electronics, chemistry, and so forth. In the end, the study compared different topological invariants for upper and lower bounds and irregularities of the sudoku network.

Acknowledgement: The authors extend their appreciation to King Saud University for funding this work through Researchers Supporting Project number (RSP2022R426), King Saud University, Riyadh, Saudi Arabia.

Funding Statement: This work was supported by King Saud University through Researchers Supporting Project number (RSP2022R426), King Saud University, Riyadh, Saudi Arabia.

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  M. Hashmi, A. Virk, A. J. M. Khalaf and M. Farahani, “Computing irregularity measures for sudoku graph,” Journal of Discrete Mathematical Sciences & Cryptography, vol. 24, no. 1, pp. 487–498, 2021. [Google Scholar]

 2.  B. Tosuni, “Graph theory in computer science—An overview,” International Journal of Academic Research & Reflection, vol. 3, no. 4, pp. 55–62, 2015. [Google Scholar]

 3.  M. B. Ali, E. Bonyah and M. Javaid, “Computing connection-based topological indices of sudoku graphs,” Journal of Mathematics, vol. 2022, no. 1, pp. e4279702, 2022. [Google Scholar]

 4.  A. Ajmal, S. B. Thanikanti, V. Ramachandaramurthy, D. Yousri and J. Ekanayake, “Static and dynamic reconfiguration approaches for mitigation of partial shading influence in photovoltaic arrays,” Sustainable Energy Technologies & Assessments, vol. 40, no. 1, pp. 100738, 2020. [Google Scholar]

 5.  M. Prabhu, “Sudoku reconfiguration technique to enhance the maximum power under partial shading conditions in PV arrays,” International Journal of Scientific Development & Research, vol. 5, no. 12, pp. 275, 2020. [Google Scholar]

 6.  I. Gutman, “Some basic properties of Sombor indices,” Open Journal of Discrete & Applied Mathematics, vol. 4, no. 1, pp. 1–3, 2021. [Google Scholar]

 7.  H. Khalid, M. W. Iqbal, A. U. R. Virk, M. U. Ashraf, A. M. Alghamdi et al., “K-Banhatti sombor invariants of certain computer networks,” Computers, Materials & Continua, vol. 73, no. 1, pp. 15–31, 2022. [Google Scholar]

 8.  V. R. Kulli, “Dharwad index,” International Journal of Engineering Sciences & Research Technology, vol. 10, no. 4, pp. 17–21, 2021. [Google Scholar]

 9.  V. Kulli, “Contraharmonic quadratic index of certain nanostar dendrimers,” International Journal of Mathematical Trends & Technology, vol. 13, no. 1, pp. 1–7, 2022. [Google Scholar]

10. V. Kulli, “New irregularity sombor indices and new adriatic (a, b)-KA indices of certain chemical drugs,” International Journal of Mathematics Trends & Technology, vol. 67, no. 1, pp. 105–113, 2021. [Google Scholar]

11. M. W. Sarwar, A. Riaz, S. M. R. Dilshad, A. Al-Qahtani, M. S. N. U. Rehman et al., “Structure activity relationship (SAR) and quantitative structure activity relationship (QSAR) studies showed plant flavonoids as potential inhibitors of dengue NS2B-NS3 protease,” BMC Structural Biology, vol. 18, no. 1, pp. 6–16, 2018. [Google Scholar]

12. J. F. Zhong, A. Rauf, M. Naeem, J. Rahman and A. Aslam, “Quantitative structure-property relationships (QSPR) of valency based topological indices with COVID-19 drugs and application,” Arabian Journal of Chemistry, vol. 14, no. 7, pp. 103240, 2021. [Google Scholar]

13. K. S. Hirpara and U. D. Patel, “Quantitative structure-activity relationship (QSAR) models for color and COD removal for some dyes subjected to electrochemical oxidation,” Environmental Technology, vol. 2022, pp. 1–12, 2022. [Google Scholar]

14. K. G. Mirajkar, A. V. Deshpande and H. H. Budihal, “QSPR analysis of KCD coindices for some chemical compounds,” in AIP Conf. Proc. in Int. Conf. on Advances in Materials, Computing and Communication Technologies, Kanyakumari, KM, India, pp. 130037, 2022. [Google Scholar]

15. Z. Hussain, M. Munir, S. Rafique and S. Min Kang, “Topological characterizations and index-analysis of new degree-based descriptors of honeycomb networks,” Symmetry, vol. 10, no. 10, pp. 478, 2018. [Google Scholar]

16. M. K. Siddiqui, M. Naeem, N. A. Rahman and M. Imran, “Computing topological indices of certain networks,” Journal of Optoelectronics & Advanced Materials, vol. 18, no. 2016, pp. 884–892, 2016. [Google Scholar]

17. J. Liu, L. Cai, A. R. Virk, W. Akhtar, S. A. Maitla et al., “Computation of irregularity indices of certain computer networks,” Mathematical Problems in Engineering, vol. 2020, no. 1, pp. e2797286, 2020. [Google Scholar]

18. I. Ahmad, M. A. Chaudhry, M. Hussain and T. Mahmood, “Topological descriptors on some families of graphs,” Journal of Chemistry, vol. 2021, no. 1, pp. e6018893, 2021. [Google Scholar]

19. Y. Bai, D. Chen and C. P. Gomes, “CLR-DRNets: Curriculum learning with restarts to solve visual combinatorial games,” in Proc. Int. Conf. on Principles & Practice of Constraint Programming, Dagstuhl, DT, Germany, pp. 1–17, 2021. [Google Scholar]

20. A. M. Lynch, “A human centered approach to logic puzzles,” in Proc. Annual Symp. on Computer-Human Interaction in Play, New York, NY, USA, pp. 397–398, 2021. [Google Scholar]

21. P. Kaur, P. Nand, S. Naseer, A. A. Gardezi, F. Alassery et al., “Ontology-based semantic search framework for disparate datasets,” Intelligent Automation & Soft Computing, vol. 32, no. 1, pp. 1717–1728, 2022. [Google Scholar]

22. S. Streicher, “Incremental inference on higher-order probabilistic graphical models applied to constraint satisfaction problems,” arXiv, vol. 1, no. 1, pp. 1296, 2022. [Google Scholar]

23. S. Anjum, V. Mukherjee and G. Mehta, “Modelling and simulation of AdDoKu based reconfiguration technique to harvest maximum power from photovoltaic array under partial shading conditions,” Simulation Modelling Practice & Theory, vol. 115, no. 1, pp. 102447, 2022. [Google Scholar]

24. S. Anjum, V. Mukherjee and G. Mehta, “Hyper sudoku-based solar photovoltaic array reconfiguration for maximum power enhancement under partial shading conditions,” Journal of Energy Resources Technology, vol. 144, no. 3, pp. 4051427, 2021. [Google Scholar]

25. A. M. Ajmal, V. K. Ramachandaramurthy, A. Naderipour and J. B. Ekanayake, “Comparative analysis of two-step GA-based PV array reconfiguration technique and other reconfiguration techniques,” Energy Conversion & Management, vol. 230, no. 1, pp. 113806, 2021. [Google Scholar]

26. K. Hamid, M. W. Iqbal, H. A. B. Muhammad, Z. Fuzail, Z. T. Ghafoor et al., “Usability evaluation of mobile banking applications in digital business as emerging economy,” International Journal of Computer Science & Network Security, vol. 22, no. 1, pp. 250–260, 2022. [Google Scholar]

27. K. Hamid, M. W. Iqbal, H. A. B. Muhammad, Z. Fuzail, Z. T. Ghafoor et al., “Detection of brain tumor from brain MRI images with the help of machine learning and deep learning,” International Journal of Computer Science & Network Security, vol. 22, no. 5, pp. 709–721, 2022. [Google Scholar]

28. K. Hamid, M. W. Iqbal, E. Arif, Y. Mahmood, A. S. Khan et al., “K-Banhatti invariants empowered topological investigation of bridge networks,” Computers, Materials & Continua, vol. 73, no. 3, pp. 5423–5440, 2022. [Google Scholar]