Topological Evaluation of Certain Computer Networks by Contraharmonic-Quadratic Indices

1  Introduction

A network of single topology performed well in the field of computer science and others like chemistry, bioinformatics and physics [1]. But in the case of a merger of two or more networks in the form of a bridge network the efficiency and effectiveness is being compromised [2]. The purpose of this study is to evaluate the topology of bridge networks before developing and using them in any field [3]. Bridge graphs [4] are introduced by Mansour et al. [5] which is a mix of networks bridged together in a single network. These are also called certain computer networks. A bridge graph is a graph acquired from the number of graphs G1, G2, G3, …, Gm by partner the vertices vi and vi + 1 by an edge∀, I = 1, 2, …, m−1 [2]. Then again, V.R. Kulli in 2022, define another vertex degree-based invariant graph named QCIs are utilized to catch the sharp lower and upper bounds of the associated networks and the attributes of the network arriving at the boundaries. There are two variations of QCIs, the first one is QCI and the second one is CQI [6]. A QCI is a Topological invariant (TI) which is a number associated with a network graph [7] that catches the symmetry of the network structure and gives a logical language to anticipating the attributes of the network.

For the most part networks of various geographies are performed well and productive independently yet the blend of at least two effectiveness split the difference. For the proper explanation, the study talks about and settles the topology of bridge networks with the assistance of the graph hypothesis mathematically.

As one more emerging science is created with the assistance of computer science, math and chemistry called Cheminformatics, whose huge fragments consolidate Quantitative structure-activity relationship (QSAR) and Quantitative structure-property relationships (QSPR) and the portions can include the assessment of physicochemical qualities of engineered blends [8]. QSAR is a modeling device used to tackle the topology of networks or structure of compounds and demonstrated the effective and best entertainer networks or structures. QSPR is likewise a modeling apparatus that corresponds to the properties of a network structure with the assistance of numerical conditions or articulation. It likewise gives the quantitative relationship between properties of networks or chemical structures. Points of topology as the numeric worth can be depicted with the assistance of a graph due to invariance. It is done because of the automorphism property of the graph. In the fields of computer sciences, chemistry, mathematics and robotics there is a ton of utilizations of the graph hypothesis [4].

Its first eminent application in chemistry was the examination of paraffin edges bubbling over by wiener. Different topological indices were introduced following this assessment that explained physicochemical properties. The progress of enormous scope incorporated circuit advancement has engaged the improvement of complex interconnected networks. Graph theory gives a vital mechanical assembly to planning and assessing such networks. Interconnected networks and graph theory gives a point-by-point perception of these associated networks. Electric power interconnections prerequisite to unendingly screening the state of their structures under the voltage size at loads and the machine stage point at generators. In the electric power system, a vertex tends to be an electric center and an edge tends to be a transmission line joining two electrical focuses. Chemical graph theory is a piece of mathematical science where in it applies gadgets of graph theory to show the chemical marvel mathematically. In the design of a network interconnection point tends to be the processor and an edge tends to be a network way through which transmission is finished. In a network, the vertex addresses the network center point like Personal (PC), switch, another contraption and an edge tends to a network way through which transmission finished. This theory contributes an observable work in the fields of chemical sciences [5].

A chemical graph is a fundamental finite graph in which vertices show the atoms or molecules and edges connote the chemical bondings in the essential chemical development. The topological indices are a numeric sum related to the chemical constitution demonstrating the association of the chemical structure development with various properties of physiochemical nature, the reactivity of chemicals and natural activities. These topological indices or invariants are additionally numeric quantities related to computer networks, their interconnections and their properties and so forth this assessment gives a premise to understand the significant topologies of some significant bridge networks and how these networks can be created based on the best topological properties. This highlight likewise gives possible help to researchers to consider network qualities better. Additionally, assuming that the connected networks are supplanted by various networks, this study can likewise compute and get the contrasting equations [3].

A topological index is arranged by changing a network structure into a number. Initially, our point is to present new computer structures and networks that benefit both productivities and advance with the help of topological indices. An interconnection network's structure can be numerically exhibited by a graph. The geography of a graph concludes with the way where vertices are associated by edges. From the geography of a network, certain properties can without much of a stretch be settled. The most extreme distance is settled between any two center points in the network. The degree of the center point is distinguished by the number of associations connected with it. Computer networks from intranet to overall networks, electric power interconnection, social networks, robotics interconnected networks, and the sexual ailment of networks of transmission and genome networks are comparable with graph theory with the assistance of complex network analysis apparatus. These multitudes of networks are at the top level of their utilization and differentiated. In this heap of cases, this study can figure boundaries called Topological invariants (TIs) that numerically portrayed the connectedness plans (structure) between the centers or performers in a network. So this study can build a mind-stunning network of general arrangements of regulations accomplice regulations (centers) that direct ordinary natural subjects for example. QSAR and QSPR are giving the establishment to these models. The last comment is that the use of the estimation in the network plane works with a quantitative assessment of different geography shielding planning calculations [4].

To expand the viability of noticing and preservation attempts, it is of key significance to encourage sound quantitative strategies that can show which key regions and landscape parts play a recognizable and basic job in the working of an area mosaics. In this article, a new arising study will figure out different indices of bridge networks. The outcomes will assume a crucial part in deciding the properties of these networks and their uses in the computer industry, robotics, chemistry and drug industry and so forth. It will likewise perform index analysis on certain networks which might be gainful for people groups who are working in the field of computer science, mathematics, robotics and the chemical industry too. In the end, form a numerical expression to build a computer network or processor designing or chemical compound, really take a look at the properties of bothered previously and likewise check the attainability of anyone which talks about prior [9].

This paper at first presents the issue declaration with bridge graph and QCIs, likewise reviews the concerning writing, thirdly discuss targets, significance, research hole and procedure in research approach region, in the fourth portion analyze data and in the last fragment create results and wrap up the assessment with the end. The survey has ideas in the fields of the computer industry, electronics, chemical industry, math, robotics and bioinformatics for modeling purposes behind networks, network interconnections, power age interconnection networks and chemical mixtures. QCIs grant us to accumulate information about arithmetical designs and mathematically anticipate hidden away properties of various designs, for instance, bridge networks.

2  Literature Review

TIs are widely utilized for laying out the connection between the nanostructure and their physical-substance properties. The development of new nanostructures gives a feature to industry, gadgets, drugs, clinical medicines, correspondence, data and food science, etc. In this paper, the Sombor index is tried with physiochemical properties of octane isomers like entropy, acentric component, enthalpy of vaporization (HVAP) and standard enthalpy of vaporization (DHVAP) utilizing the straight models. The Sombor index shows a brilliant relationship with these compound properties. Extraordinarily high relationship with DHVAP. Further, we get the Sombor index of the 2D-cross section, nanotube and nanotorus of TUC4C8 [p; q] and region diagram of 2D-grid, nanotube and nanotorus of TUC4C8 [p; q] [10].

Chemical Graph Theory is a part of Mathematical Chemistry that importantly affects the development of the Chemical Sciences. We present the CQI of a molecular graph. In this paper, we determine the CQI of some standard classes of graphs. the study likewise computes the CQI of certain important nanostar dendrimers. The analysis presents the adjusted first and second K-Banhatti Indices of a graph. Likewise, the study presents the symphonious Sombor indices of a graph. The study of newly prepared invariants is started. The study figure out the adjusted first and second Banhatti Sombor indices and symphonious Banhatti Sombor index of a few standard graphs, TUC4C8[p, q] nanotubes and TUC4[p, q] nanotubes [11,12].

The review is characterized and determined various types of indices in setting with topology like degree based, distance based and counting related topological indices and so forth. The molecular structures of cross sections are hexagonal; honeycomb structures network structures and framework structures networks. The Atom-bond connectivity (ABC) and Geometric number juggling (GA) correspond to different physical and chemical properties of chemicals having the above structures, similar to robustness and strain energy and the edge of boiling over and so forth Bunch theory and development of graphs can utilize the Cayley graphs (CG) of gatherings for deciding properties. In this review, they register conditions of the general randi’ c index for different potential gains of α, first zagreb index, ABC index, GA index, the fourth ABC index (ABC4 ), fifth GA index (GA5) for certain gatherings of graphs [13]. These graphs give the premise for ascertaining numerous different groups of graphs for chemical compounds and computer networks [14].

From the perspective of study, the progress of enormous scope integrated circuit advancement has to understand the improvement of complex interconnected networks. Graph theory gives a critical contraption to planning and assessing such networks. Interconnected networks and graph theory give an itemized cognizance of these associated networks. Chemical graph theory is a piece of mathematical science wherein they apply gadgets of graph theory to exhibit the chemical miracle mathematically. In network vertex addresses the network center like PC, switch, switch another contraption and an edge tends to a network way through which transmission finished. These topological indices or invariants are additionally numeric qualities related to computer networks, their interconnections and their properties and so forth. It computes the different topological indices of unpredictability based on the paired tree up to the k-level. The concluded results of a paper can be utilized for computer networks and chemical networks in topological portrayal [15].

The estimation of the irregularity indices of honeycomb networks, hexagonal networks, oxide networks and silicate networks is finished. The outcomes are extremely useful in understanding the conduct of various computer networks and chemical networks. After understanding these expressions various scientists can develop their own best networks in the chemical and computer industries likewise [16]. Further, the study explains that graph theory is a field through which they compute topological indices for tracking down the properties of various chemicals and networks without playing out any sorts of investigations on them. It very well might be understanding just numerical expressions or conditions which are reasoned for them. It likewise works out topological indices for m-polynomial square shift networks which is a piece of various chemical compounds with the assistance of division of edge [17].

The research topic elaborates that topological indices can be designed by changing over a chemical structure into a mathematical means. These topological indices accomplice certain physiochemical properties like cutoff, security and strain energy and so on of synthetic mixes. Graph theory has found an amazing use around here of investigation. The properties of the topology of explicit networks are concentrated lately. In this paper, they loosen up this assessment to interconnection networks and decide logical shut delayed consequences of General randi c’ index R (G) for different potential gains of “α” for octagonal network, toroidal polyhex and summarized precious crystal. Interconnection networks of multiprocessor are routinely expected to communicate a large number of homogeneously imitated processor-memory consolidates, all of which is known as handling center [18].

Readings of the work show how a high thickness of catalytic destinations got together with specific spatial bearings of those sites can cause a supra molecular catalytic machine that works intentionally to work with the improvement of relevant advancement states and, in this manner, redesign reaction rates. The enduring assortment of MOF topologies recommends that these porous frameworks will turn out to be useful network structures for a rich variety of multisite-catalyzed compound reactions [19].

As per the exploration of this paper, physicochemical properties and topological indices are talked about and thoroughly analyzed in the QSAR/QSPR, for instance, randić, zagreb and ABC indices are used to predict the bioactivity of the manufactured blends. Graph theory has found huge use in computer science and chemistry, particularly in exhibiting substance structures. Topological indices are arranged in a general sense by changing a molecular graph into a number. In this paper, they register the randić, zagreb and ABC index of silicate, honeycomb and hexagonal networks. Gathered recursively using the hexagon enrichment, honeycomb networks are extensively used in PC outlines, telephone base stations, image processing and in the chemical industry as the depiction of benzenoid hydrocarbons [20]. This similarly gives conceivable help to analysts to consider better attributes of networks [21].

Another review conveyed that since computers as devices utilized on the planet for the wellspring of data, they expanding in numbers variously. So much, today, it is difficult to find any space, intelligent or other, which isn't subject to their application. To be sure, even broad arrangements of regulations have been impacted by original handling and information systems. An impressive part of these QSAR strategies relies upon the usage of topological boundaries, which are numerical courses of action that order to accommodate primary information and sympathy relationships among structure and regular properties [22].

In all of these cases, they can register boundaries considered TIs that numerically portrayed the connectedness plans between the hubs or performers in a network. Accordingly, TIs are useful as commitments for QSPR models at every underlying level. Without a doubt, even broad arrangements of regulations may be advanced toward using figuring and information systems like networks. So they can foster a flighty network of generally speaking arrangements of regulations partner regulations (hubs) that oversee fundamental natural focuses for instance. On the other hand, a precise legal structure is relied upon to provide legitimate and relevant guidance to addressing different enlisting methodologies as applied to coherent examination [23].

The examination concentrate on told that graphs are considered a fabulous modeling device that can be used to show and explain assorted kind of relations between genuine issues. A lot of issues and issues can be researched comprehensively with the help of graph theory. In this paper, researchers focused on different kinds of issues related to graph theory and their executions and ideas in the field of programming to show the ampleness of graph theory. These applications are familiar particularly with loosening up graph theory and showing its goal and importance in network designing. This paper is wanted to help the under examinations of programming to get important information on graph theory and its importance with various subjects like working systems, networks, data sets, software engineering and so on this paper zeroed in on the different employments of colossal graph theory that have congruity to the field of computer programming and applications [24].

The speculative contemplations of the graph are particularly used by computer programming applications. Particularly in research spaces of programming such as data mining, picture division, gathering, picture getting, networking and so forth For instance, a data configuration can be sorted out as a tree which thus used vertices and edges. Moreover, modeling of network geographies should be possible by utilizing graph considerations. Additionally, central considered graph covering is used in resource dispersion and booking. Besides, ways, strolls and circuits in graph theory are utilized in huge applications say adaptable arrangements issues, database course of action contemplations and asset networking. This prompts the progress of new assessments and new speculations that can be utilized in enormous applications. It has been allocated to two locales. The first locale gives a certain foundation of graph theory and a few uses in the booking. The second area underlines how graph theory is used in different computer applications [25].

Consequently, these fields have braced the improvement of different new outline speculative considerations and prompted many testing graph theory issues. They can expect that the continued trade between graph theory and different spaces of utilization will incite basic new turns of events. The basic control of graph theory in PC applications is the improvement of graph assessments [26].

TIs engage us to assemble data about logarithmic structures and give us a numerical strategy to figure out the secret properties of various structures [27]. Various strategies are available in history to check the nature of a topological index. CQI and other versions had a good potential for prediction in the field of computer science, mathematics, chemistry, pharmacy, bio-informatics and parallel computing in context with properties of structures and networks.

3  Research Methodology

The reason for this study is to investigate and foster understanding with regards to basic and critical worries like blunder-free, faultless, best execution and having advanced abilities in computer networks, interconnection networks of processors, chemical structures, robotics interconnections and power interconnection networks.

3.1 Objectives

The principal objective of this study is to research the TIs of bridge computer networks. The review figures out the force of reality of topological indices in bridge networks like workstation networks, interconnection network of processors, power interconnection networks and chemical structures and so forth In this paper study clarifies the QCIs, and their different structures and their advantages. This article clarifies and mindful ongoing utilization of QCIs. Its great goal is to foster formulas, so it can check the topology, and execution of bridge networks without doing/performing tests and likewise before assembling them. The work derived a few outcomes which are utilized in the modeling of bridge networks utilized in terminal networks, interconnection networks, power interconnection networks, chemical structures and robotics interconnection networks.

3.2 Significance

The study is exceptionally critical these days since it makes mindfulness about TIs of bridge networks like terminal networks, interconnection networks of processors, power interconnection networks, chemical structures and mechanical technology interconnection networks and so forth It additionally finds new and critical arrangements or equations for modeling bridge networks because no any satisfactory arrangement has been found till now because of steady and quick nature.

3.3 Hypothesis

The reading considers the accompanying hypothesis for the advancement of bridge networks utilized in computer networks, interconnection networks of processors, power interconnection networks, chemical structures and mechanical technology interconnection networks since merchants and makers need to understand the complexity and force of execution and disappointment-free items. The analysis gives solidarity to create mistake-free, disappointing free and best entertainer workstation networks, interconnection networks of processors, power interconnection networks and mechanical technology interconnection networks.

3.4 Method

This deliberate study, it will take a current bridge network, partner it with a graph and address the topology of the graph with the assistance of QCIs and their other forms. The concluded results about the type of numeric expression will contrast with existing outcomes. These concluded outcomes will be pertinent to numerous different networks in the fields of computer networks, processor interconnection networks, memory interconnection networks, power interconnection networks and picture handling subsequently. This model is especially unsettling as it tackled the topology of a bridge network in numeric and graphical structure and gives exact outcomes. After analysis, a recreation apparatus maple is utilized for the confirmation and approval of results [28].

The flow of systematic study involves the steps in which take existing bridge networks associate it with graph theory, solve the topology of the graph by QCIs and compare the results and deduced results will be used for modeling of bridge networks utilized in certain networks.

4  Experimental Results

A bridge graph is a graph obtained from the number of graphs G1, G2, G3, …, Gm by associating the vertices vi and vi + 1 by an edge∀, i = 1, 2,…, m−1. QCIs have two main forms CQI and QCI Indices [29].

CQI(G)=∑uv∈E(G)2(dG(u)2+dG(v)2)dG(u)+dG(v)(1)

QCI(G)=∑uv∈E(G)(dG(u)+dG(v))2(dG(u)2+dG(v)2)(2)

Eqs. (1) and (2) show the CQI and QCI which will be used for the solution of bridge networks mentioned in Figs. 1, 3 and 5.

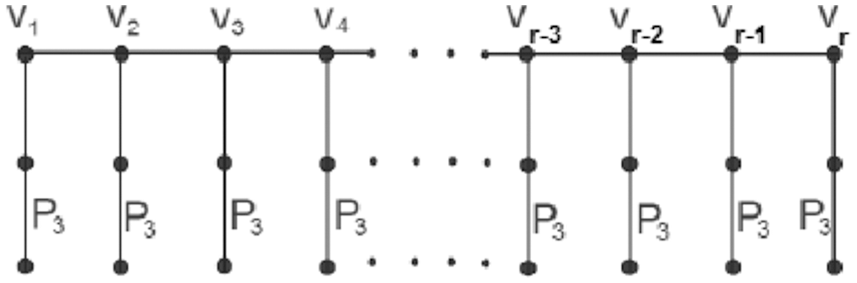
Figure 1: Gr (Ps, v) over Ps for the bridge network

Tab. 1 describes the edge partitions of graph Gr (Ps, v) over Ps of the bridge graph.

4.1 Main Results

Fig. 1 shows bridge networks in which bus networks and star networks bridge in a tree-like structure.

4.1.1 Bridge Graph Gr (Ps, v) Over Path

If the vertex set is V then by the observation of Fig. 2, it can order this vertex set into four subsets V1, V2, V3 and V4, Such that V = V1 + V2 + V3 + V4. If E represents the edge set. Fig. 2 shows that there are four distinct kinds of edges present in the graph bridge graph Gr (Ps, v) over the path of hybrid networks. Tab. 1, explains in detail the edges partition.

Figure 2: CQI and QCI for Gr (Ps, v) over Ps

4.1.2 Theorem 1

Let G be a graph of Gr (Ps, v) over Ps, then, CQI and QCI indices are

CQI(G)=1310r+4r−1+1526r(3)

QCI(G)=31010r+4r−1+52626r(4)

Eqs. (3) and (4) represent the proven results of the graph of Gr (Ps, v) over Ps mentioned in Fig. 2.

4.1.3 Investigation of Bridge Graphs by CQI and QCI

Proof

CQI(G)=∑uv∈E(G)2(dG(u)2+dG(v)2)dG(u)+dG(v)

CQI(G)=2((1)2+(2)2)1+2 r+2((2)2+(2)2)2+2(3 r+2)+2((2)2+(3)2)2+3 r+2((3)2+(3)2)3+3(r−3)

CQI(G)=1310r+4r−1+1526r

QCI(G)=∑uv∈E(G)(dG(u)+dG(v))2(dG(u)2+dG(v)2)

QCI(G)=1+22((1)2+(2)2)r+2+22((2)2+(2)2)(3 r+2)+2+32((2)2+(3)2) r+3+32((3)2+(3)2)(r−3)

QCI(G)=31010r+4r−1+52626r

Fig. 2 shows the optimized results (Eqs. (1) & (2)) of the CQI and QCI in red and blue lines respectively.

Tab. 2 describes the edge partitions of graph Gr (Ks, v) Over Ks of the bridge graph given in Fig. 5 with frequencies.

4.2 Main Results

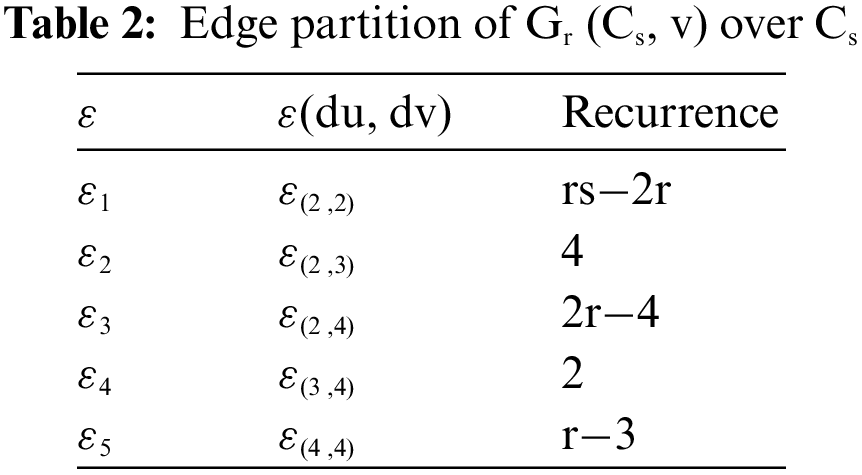
Fig. 3 shows the bridge networks in which bus networks and ring networks bridge together.

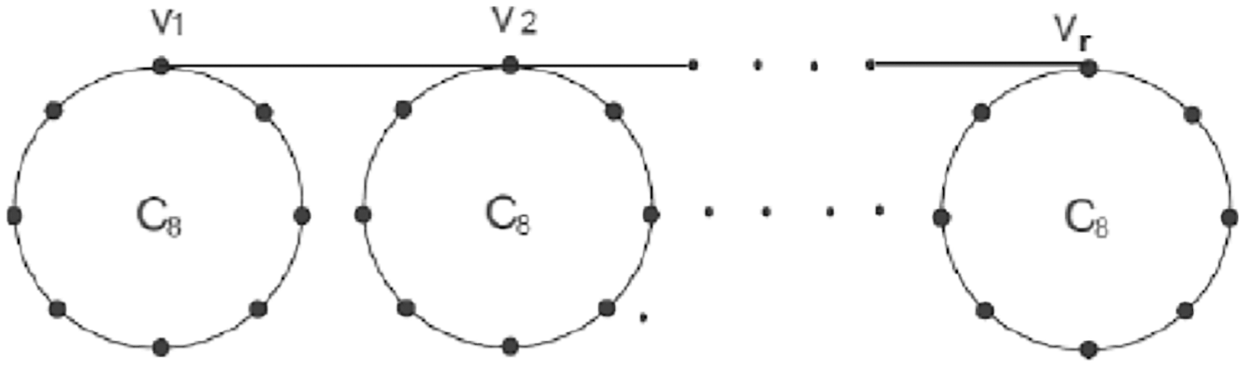
Figure 3: Gr (Cs, v) over Cs for the bridge network

4.2.1 Bridge Graph Gr (Cs, v) Over Cycle

Assuming V is the arrangement of vertices seen in Fig. 4, this arrangement of vertices can be parted into four subsets V1, V2, V3 and V4 to V = V1 + V2 + V3 + V4. When ε(D2 (m)) addresses an edge set. Fig. 4 shows a half-and-half network cycle with five distinct kinds of edges in the network graph of the bridge graph Gr (Cs, v). Tab. 2 provides a detailed description of the edge set.

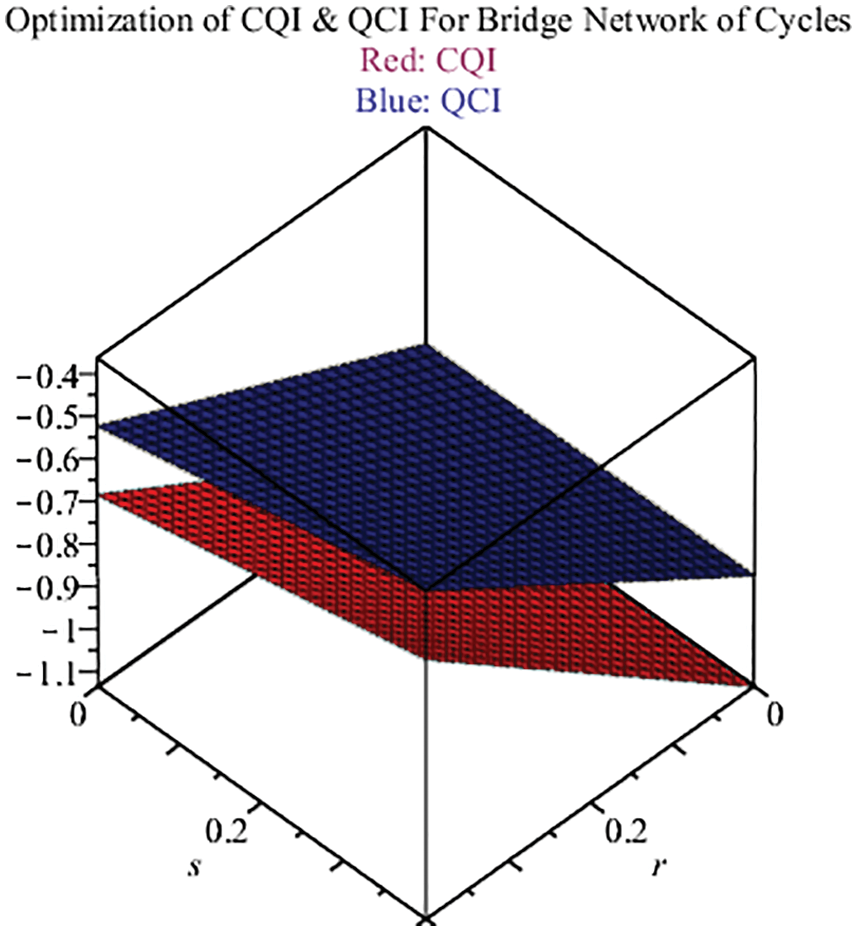
Figure 4: CQI and QCI for Gr (Cs, v) over cycle

4.2.2 Theorem 2

Let G be a graph of Gr (Cs, v) over Cs Then CQI and QCI indices are

CQI(G)=rs−r+4526+1310(2 r−4)+1072−3(5)

QCI(G)=rs−r+101326+31010(2 r−4)+752−3(6)

Eqs. (5) and (6) represent the proven results of the graph of Gr (Cs, v) over Cs for Bridge Network mentioned in Fig. 3.

4.2.3 Investigation of Bridge Graphs by CQI and QCI

Proof

CQI(G)=∑uv∈E(G)2(dG(u)2+dG(v)2)dG(u)+dG(v)

CQI(G)=2((2)2+(2)2)2+2(rs−2r)+2((2)2+(3)2)2+3(4)+2((2)2+(4)2)2+4(2r−4)+2((3)2+(4)2)3+4(2)+2((4)2+(4)2)4+4(r−3)

CQI(G)=rs−r+4526+1310(2 r−4)+1072−3

QCI(G)=∑uv∈E(G)(dG(u)+dG(v))2(dG(u)2+dG(v)2)

QCI(G)=2+22((2)2+(2)2)(rs−2r)+2+32((2)2+(3)2)(4)+2+42((2)2+(4)2)(2r−4)+3+42((3)2+(4)2)(2)+4+42((4)2+(4)2)(r−3)

QCI(G)=rs−r+101326+31010(2 r−4)+752−3

Fig. 4 shows the optimized results (Eqs. (1) & (2)) of the CQI and QCI in red and blue colors respectively in the 3D version.

Tab. 3 describes the edge partitions of graph Gr (Ks, v) Over Ks of the bridge graph given in Fig. 5 with the number of occurrences.

Figure 5: Gr (Ks, v) over Ks

4.3 Main Results

Fig. 5 shows the bridge networks in which bus networks and fully connected networks are bridged together.

4.3.1 Bridge Graph Gr (Ks, v) Over Complete Graph

Assuming that the vertices set are V, understanding Fig. 5 allows us to sort this set of vertices into three subsets V1, V2 and V3 so that V = V1 + V2 + V3. If E shows the edge set, Fig. 5 shows the bridge graph Gr (Ks, v) of the complete graph of the hybrid network. The bridge graph of the network graph has five different edges. Tab. 3 provides a detailed description of the edge set.

4.3.2 Theorem 3

Let G be a graph of Gr (Ks, v) over Ks. Then CQI and QCI indices are

CQI(G)=2982+232+2(s−1)23+s+(r−2)+50+2(s−1)24+s(r−2)+2(s−1)2+12rs(r−1)−r−12s−2(7)

QCI(G)=94182+2(3+s)32+2(s−1)2+(r−2)+(4+s)50+2(s−1)2(r−2)+12(2s−2)((12rs(r−1)−r−1)(s−1)2(8)

Eqs. (7) and (8) represent the proven results of the graph of Gr (Ks, v) over the complete graph mentioned in Fig. 5.

4.3.3 Investigation of Bridge Graphs by CQI and QCI

Proof

CQI(G)=∑uv∈E(G)2(dG(u)2+dG(v)2)dG(u)+dG(v)

CQI(G)=2((4)2+(5)2)4+5(2)+2((4)2+(s−1)2)4+(s−1)(2)+2((5)2+(5)2)5+5(r−2)+2((5)2+(s−1)2)5+(s−1)(r−2)+2((s−1)2+(s−1)2)(s−1)+(s−1)(rs(r−1)−2(r+1))/2

CQI(G)=2982+232+2(s−1)23+s+(r−2)+50+2(s−1)24+s(r−2)+2(s−1)2+12rs(r−1)−r−12s−2

QCI(G)=∑uv∈E(G)(dG(u)+dG(v))2(dG(u)2+dG(v)2)

QCI(G)=4+52((4)2+(5)2)(2)+4+(s−1)2((4)2+(s−1)2)(2)+5+52((5)2+(5)2)(r−2)+5+(s−1)2((5)2+(s−1)2)(r−2)+(s−1)+(s−1)2((s−1)2+(s−1)2)(rs(r−1)−2(r+1))/2

QCI(G)=94182+2(3+s)32+2(s−1)2+(r−2)+(4+s)50+2(s−1)2(r−2)+12(2s−2)((12rs(r−1)−r−1)(s−1)2

Fig. 6 shows the optimized results (Eqs. (1)) & (2)) of the CQI and QCI in red and blue colors respectively in the 3D version.

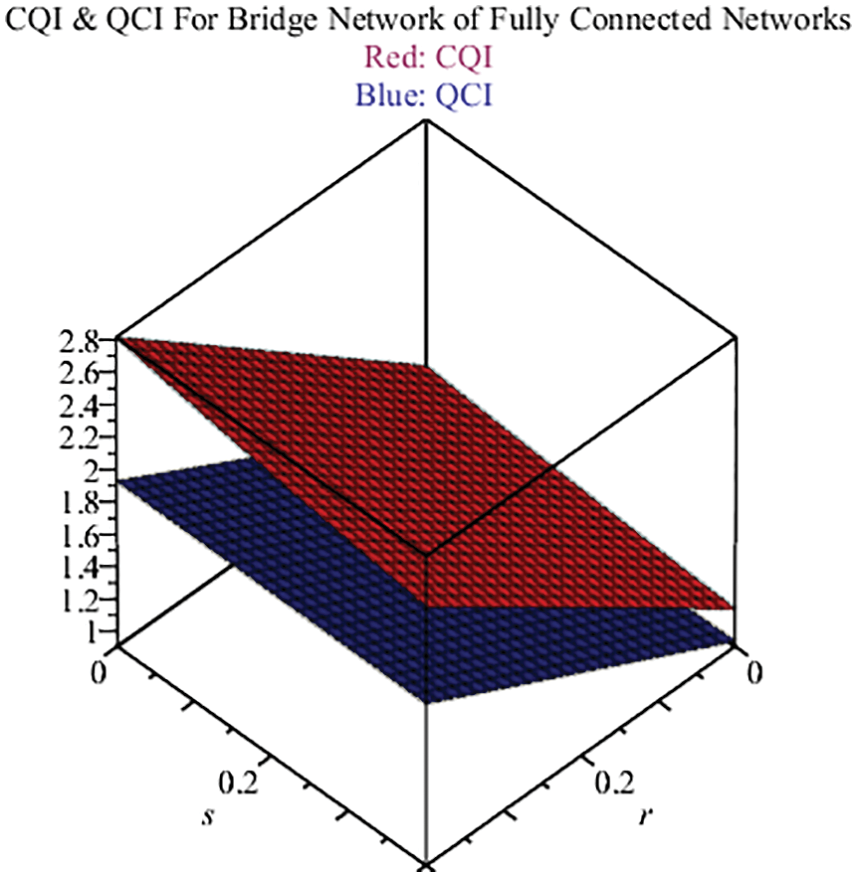
Figure 6: CQI and QCI for Gr (Ks, v) over Ks

5  Conclusion

Bridge networks are tremendously utilized in various fields of computer science like parallel computing, processor interconnection, memory interconnection and the internet too. Then again TIs have bunches of purposes and executions in many fields of computer science, Biology, chemistry, informatics, arithmetic, material sciences and mechanical technology and so on, in any case, the greatest possible level of huge application is in the non-exact QSPR and QSAR. TIs are related to the design of networks, the spine of the internet, processor interconnection, memory interconnection and synthesis of chemical structures. The present article examines the CQI with QCI which is newly introduced. These have various forecast qualities for various variations of bridge graphs or networks, for example, Gr (Ps, v), Gr (Cs, v) and Gr (Ks, v). Figs. 2, 4 and 6 give the graphical portrayal of CQI and QCI for the above-mentioned bridge networks. These concluded outcomes will be helpful for the modeling of computer networks, the spine of the internet, massively large processors, power generation networks, synthetic constructions, picture handling, bio-informatics, memory interconnection networks and agricultural water management system and so on. These generated results provide the guidelines for the development of new architectures and networks with the best possible characteristics.

Acknowledgement: The authors acknowledge with thank the University of Jeddah technical and financial support.

Funding Statement: This work was funded by the University of Jeddah, Jeddah, Saudi Arabia, under Grant No. (UJ-22-DR-14).

Conflicts of Interest: The authors declare that they have no conflicts of interest to report regarding the present study.

References

 1.  C. Gao, L. Zhong, X. Li, Z. Zhang and N. Shi, “Combination methods for identifying influential nodes in networks,” International Journal of Modern Physics C, vol. 26, no. 6, pp. 1550067, 2015. [Google Scholar]

 2.  L. Huang, J. Wang and M. Cheng, “Coded caching for combination networks with multiaccess,” ArXiv:2108.09612 [cs, math], vol. 1, no. 1, pp. 1–14, 2021. [Google Scholar]

 3.  S. J. Webb, T. Hanser, B. Howlin, P. Krause and J. D. Vessey, “Feature combination networks for the interpretation of statistical machine learning models: Application to Ames mutagenicity,” Journal of Cheminformatics, vol. 6, no. 1, pp. 8, 2014. [Google Scholar]

 4.  X. Bei, S. Chen, J. Guan, Y. Qiao and X. Sun, “From independent sets and vertex colorings to isotropic spaces and isotropic decompositions: Another bridge between graphs and alternating matrix spaces,” SIAM Journal of Computing, vol. 50, no. 3, pp. 924–971, 2021. [Google Scholar]

 5.  T. Mansour and M. Schork, “The vertex PI index and szeged index of bridge graphs,” Discrete Applied Mathematics, vol. 157, no. 7, pp. 1600–1606, 2009. [Google Scholar]

 6.  V. Kulli, “Contraharmonic quadratic index of certain nanostar dendrimers,” International Journal of Mathematical Trends & Technology, vol. 13, no. 1, pp. 1–7, 2022. [Google Scholar]

 7.  A. F. Bouarab, J. P. Harvey and C. Robelin, “Viscosity models for ionic liquids and their mixtures,” Physical Chemistry Chemical Physics, vol. 23, no. 2, pp. 733–752, 2021. [Google Scholar]

 8.  J. F. Zhong, A. Rauf, M. Naeem, J. Rahman and A. Aslam, “Quantitative structure-property relationships (QSPR) of valency based topological indices with COVID-19 drugs and application,” Arabian Journal of Chemistry, vol. 14, no. 7, pp. 103240, 2021. [Google Scholar]

 9.  S. Hayat and M. Imran, “Computation of topological indices of certain networks,” Applied Mathematics and Computation, vol. 240, pp. 213–228, 2014. [Google Scholar]

10. A. Alsinai, B. Basavangoud, M. Sayyed and M. Farahani, “Sombor index of some nanostructures,” Journal of Prime Research in Mathematics, vol. 17, no. 1, pp. 123–133, 2021. [Google Scholar]

11. V. Kulli, “New k-banhatti topological indices,” International Journal of Fuzzy Mathematical Archive, vol. 12, no. 1, pp. 29–37, 2017. [Google Scholar]

12. V. Kulli, “On k banhatti indices of graphs,” Journal of Computer and Mathematical Sciences, vol. 7, no. 1, pp. 213–218, 2016. [Google Scholar]

13. S. Sultan, W. Gharibi and A. Ahmad, “Computing the topological indices for certain families of graphs,” Science International, vol. 27, no. 6, pp. 1–10, 2015. [Google Scholar]

14. K. C. Das, F. M. Bhatti, G. Lee and I. Gutman, “Spectral properties of the He matrix of hexagonal systems,” MATCHCommunications in Mathematical and in Computer Chemistry, vol. 65, no. 2011, pp. 753–774, 2011. [Google Scholar]

15. M. Imran, M. A. Iqbal, Y. Liu, A. Q. Baig, W. Khalid et al., “Computing eccentricity-based topological indices of 2-power interconnection networks,” Journal of Chemistry, vol. 2020, no. 1, pp. 1–10, 2020. [Google Scholar]

16. J. Liu, L. Cai, A. R. Virk, W. Akhtar, S. A. Maitla et al., “Computation of irregularity indices of certain computer networks,” Mathematical Problems in Engineering, vol. 2020, no. 1, pp. e2797286, 2020. [Google Scholar]

17. M. Cancan, I. Ahmad and S. Ahmad, “Study of topology of block shift networks via topological indices,” Proyecciones (Antofagasta), vol. 39, no. 4, pp. 887–902, 2020. [Google Scholar]

18. M. K. Siddiqui, M. Naeem, N. A. Rahman and M. Imran, “Computing topological indices of certain networks,” Journal of Optoelectronics and Advanced Materials, vol. 18, no. 2016, pp. 884–892, 2016. [Google Scholar]

19. P. Deria, D. A. G. Gualdrón, I. Hod, R. Q. Snurr, J. T. Hupp et al., “Framework-topology-dependent catalytic activity of zirconium-based (porphinato) zinc (II) MOFs,” Journal of the American Chemical Society, vol. 138, no. 43, pp. 14449–14457, 2016. [Google Scholar]

20. A. W. Bharati Rajan, C. Grigorious and S. Stephen, “On certain topological indices of silicate, honeycomb and hexagonal networks,” Journal of Computer and Mathematical Sciences, vol. 3, no. 5, pp. 498–556, 2012. [Google Scholar]

21. A. Hussain, M. Numan, N. Naz, S. I. Butt, A. Aslam et al., “On topological indices for new classes of benes network,” Journal of Mathematics, vol. 2021, no. 1, pp. e6690053, 2021. [Google Scholar]

22. M. Šestak, M. Heričko, T. W. Družovec and M. Turkanović, “Applying k-vertex cardinality constraints on a Neo4j graph database,” Future Generation Computer Systems, vol. 115, no. 1, pp. 459–474, 2021. [Google Scholar]

23. A. H. Göller, L. Kuhnke, A. T. Laak, K. Meier and A. Hillisch, “Machine learning applied to the modeling of pharmacological and admetabsorption, distribution, metabolism, excretion and toxicity (ADMET) endpoints,” in Artificial Intelligence in Drug Design, vol. 1, Humana, New York, NY, USA: Springer, pp. 61–101, 2022. [Google Scholar]

24. V. V. Mitic, G. Lazovic, B. Randjelovic, V. Paunovic, I. Radovc et al., “Graph theory applied to microelectronics intergranular relations,” Ferroelectrics, vol. 570, no. 1, pp. 145–152, 2021. [Google Scholar]

25. J. Nazir, M. W. Iqbal, T. Alyas, D. Hamid, S. Malik et al., “Load balancing framework for cross-region tasks in cloud computing,” Computer, Materials and Continua, vol. 70, no. 1, pp. 1479–1490, 2021. [Google Scholar]

26. B. Huang, L. Ge, G. Chen, M. Redenkovic, X. Wang et al., “Nonlocal graph theory based transductive learning for hyperspectral image classification,” Pattern Recognition, vol. 116, no. 1, pp. 107967, 2021. [Google Scholar]

27. Y. H. He, “Machine-learning mathematical structures,” International Journal of Data Science in the Mathematical Sciences, vol. 2022, pp. 1–10, 2022. [Google Scholar]

28. K. Hamid, M. W. Iqbal, A. U. R. Virk, M. U. Ashraf, A. M. Alghamdi et al., “K-Banhatti sombor invariants of certain computer networks,” Computer, Materials and Continua, vol. 73, no. 1, pp. 15–31, 2022. [Google Scholar]

29. S. Khlood, K. Alsubhi, A. Alzahrani and M. U. Ashraf, “Machine learning-based botnet detection in software-defined network: A systematic review,” Symmetry, vol. 13, no. 5, pp. 866–902, 2021. [Google Scholar]